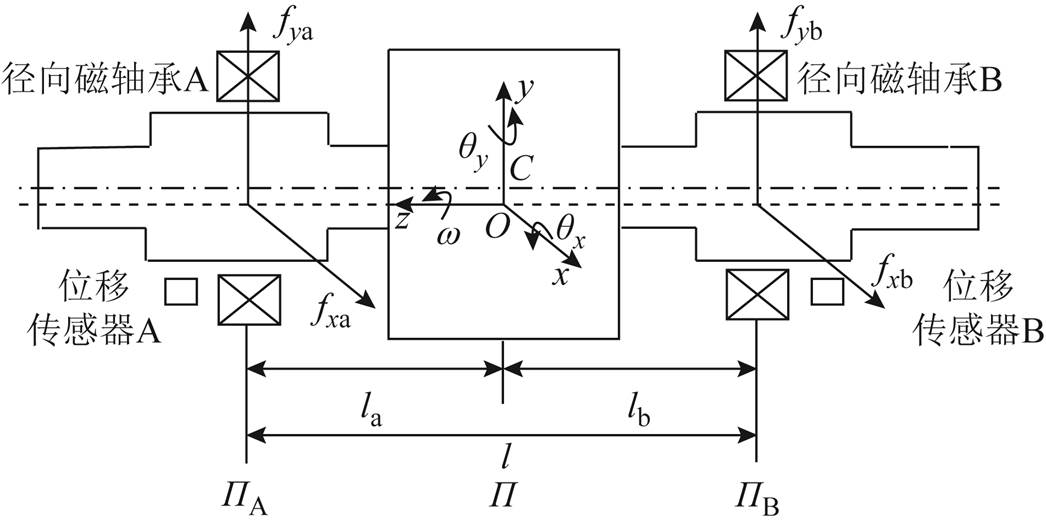
图1 磁悬浮高速电机刚性转子结构
Fig.1 Structure of magnetically levitated high-speed motor rigid rotor
摘要 针对磁悬浮高速电机刚性转子的不平衡振动,提出一种基于极性切换自适应陷波器的自动平衡方法。首先结合磁悬浮高速电机刚性转子系统径向动力学模型,分析自适应陷波器的原理和自动平衡策略;其次根据磁悬浮高速电机刚性转子径向振动系统的广义根轨迹得到极性切换规律,构造陷波器的反馈控制和前馈控制,实现转子系统在整个转速范围内稳定运行和自动平衡;最后,在搭建的仿真和实验平台上验证了不同工况下基于极性切换自适应陷波器的自动平衡控制策略能够有效地抑制转子系统的不平衡同步振动及对基础的传递力。
关键词:磁悬浮高速电机 刚性转子 自动平衡 陷波器 根轨迹
主动电磁轴承(Active Magnetic Bearing, AMB)具有无摩擦、适合高速运行以及使用寿命长等优点[1-3]。采用主动电磁轴承的高速电机具有体积小、功率密度高等优点,额定转速可达每分钟几万甚至十几万转,因此AMB广泛应用于涡轮分子泵、压缩机、飞轮储能等高速旋转机械领域。
在旋转机械中,转子不平衡产生的离心力将引起转子的不平衡振动,转速越高,不平衡激励力就越大,引起转子的振动就越剧烈。因此有必要采取主动控制策略对转子的不平衡振动进行抑制。不平衡补偿和自动平衡是AMB刚性转子系统不平衡振动主动控制的两种有效方法。
不平衡补偿是通过对位移进行补偿,实现位移最小控制,能够提高转子的转动精度。不平衡补偿既可以直接对转子的不平衡力进行补偿,也可以对转子的不平衡位移进行补偿,前者与转子的转速相关,而后者与转子的转速无关。毛川等提出了一种基于实时变步长的转子等效不平衡力系数的多边形迭代寻优算法,使AMB产生一个与等效不平衡力大小相同、相位相反的补偿力,以有效地减少转子的振动[4]。蒋科坚等根据转子不平衡质量的实时位置,进而产生控制信号,对不平衡质量位置进行补偿,从而克服了控制器连续频繁计算,实现了转子不平衡的补偿[5]。N. Taiki等研究了AMB刚性转子系统不平衡振动的补偿器峰值增益控制和相变控制方法,并证明了峰值增益控制可以有效抑制不平衡振动[6-7]。Fang Jiancheng等基于带通滤波器提出了一种不平衡补偿控制策略,使转子绕其几何轴旋转[8]。孙玉坤等针对传统磁悬浮开关磁阻电机存在的多变量非线性强耦合问题,提出一种混合双定子磁悬浮开关磁阻电机[9]。蓝益鹏等采用混合灵敏度H∞控制策略设计了鲁棒控制器[10],孙鲲鹏等[11]和孙玉坤等[12]分别基于无速度传感器控制和滑模控制算法设计了鲁棒控制器,均可实现高速电机的稳定运行。宋腾等研究了基于最小位移的AMB转子变极性最小均方(Least Mean Square, LMS)反馈不平衡补偿方法来抑制转子不平衡振动[13]。这些研究结果均表明,不平衡补偿虽然提高了转子旋转的精度,但高速时易造成功放饱和,甚至导致系统失稳。另外,引入的不平衡补偿器也增加了控制系统的复杂性和设计难度。
自动平衡是通过对电流或者电磁力进行补偿,实现电流或者电磁力的最小控制。宋立伟等分析了力耦合特性对混合式磁轴承的影响[14]。D. Saito等将传统转子系统径向不平衡振动控制的增益峰值控制、自动平衡控制和相位变量控制等方法用于轴向振动的控制[15]。S. L. Chen等采用侵入流不变型原理研究了三磁极结构AMB转子系统的自适应不平衡力补偿,但分析过程十分复杂[16]。S. K. Mohamed等将不平衡力看作是导致转子在旋转过程中的周期性谐波扰动,用二阶滑模控制器来实现AMB转子系统在宽速度范围内的稳定运行,但滑模面的高频切换容易引起高频振荡,引入高频噪声且不易消除[17]。Zheng Shiqiang等研究了基于同步旋转框架变换的AMB转子自动平衡新方法,通过优化电磁力以抑制不平衡力[18-19]。N. Amin等研究了一种多输入多输出AMB转子系统的辨识与鲁棒控制,既考虑了转子静止时的恒定扰动,又考虑了旋转时离心力和质量不平衡引起的正弦扰动,但该模型过于依赖系统的建模[20]。Lin Chao等提出了一种基于自定心控制等效电磁力的刚性转子在线动平衡方法,有效地消除了转子不平衡对系统稳定性和运动精度的影响[21]。Gao Hui等将LMS算法与不平衡前馈补偿相结合,并引入H∞控制,实现自动平衡[22]。Zheng Shiqiang等提出一种基于坐标变换的陷波器结合前馈补偿的方法,但适用于转速变化不大的情况[23]。Chen Qi等将自适应陷波器和自适应频率估计器用于自动平衡,但需调整两个参数,而且仅在恒定转速下进行了验证[24]。
针对以上研究中存在的问题,本文将极性切换自适应陷波器应用于磁悬浮高速电机刚性转子系统的自动平衡控制。其创新点体现在两个方面:第一,为实时有效地消除由不平衡力产生的与转速同频的径向振动分量,设计了自适应陷波器,以实现最小电流或电磁力控制,提高转子在高速区悬浮的稳定性;第二,针对磁悬浮刚性转子在径向刚体临界转速附近运行时系统闭环稳定性条件不同的问题,提出了基于极性切换的自动平衡控制,并结合自适应陷波器实现AMB高速电机刚性转子系统在包含刚体临界的全转速范围内的稳定运行。
文中首先通过陷波器反馈控制和前馈控制,实现电磁力最小控制。然后,利用广义根轨迹法分析加入了基于自适应陷波器的自动平衡控制后,转子系统径向的稳定性,通过极性切换,实现转子系统在包含刚体临界的全转速范围内的稳定运行。最后,在磁悬浮高速电机刚性转子系统试验平台上对该方法的有效性进行了验证。
本文研究的磁悬浮高速电机刚性转子的结构如图1所示。轴对称刚性转子的轴向由一对永磁轴承支承,径向由两个AMB支承。由于转子的工作转速远低于转子的一阶弯曲临界转速,所以转子可以简化为一个四自由度的刚性转子系统。

图1 磁悬浮高速电机刚性转子结构
Fig.1 Structure of magnetically levitated high-speed motor rigid rotor
为了便于描述磁悬浮高速电机刚性转子的运动状态,在图1中定义了相关平面及坐标系。假设两端AMB-A和-B的中心平面分别为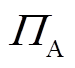 和
和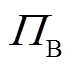 。平衡转子的质心为C,由于对称性,质心C必将位于转子几何中心线上,过
。平衡转子的质心为C,由于对称性,质心C必将位于转子几何中心线上,过 点作平行于两端AMB中心平面
点作平行于两端AMB中心平面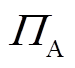 和
和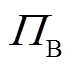 的平面
的平面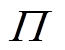 ,
,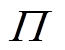 平面与定子几何中心线交于
平面与定子几何中心线交于 点。C点到两端AMB中心平面
点。C点到两端AMB中心平面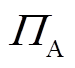 和
和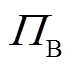 的距离分别为la和lb,平面
的距离分别为la和lb,平面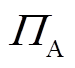 和
和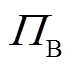 之间的距离为
之间的距离为 。磁悬浮高速电机转子的质量为m;
。磁悬浮高速电机转子的质量为m;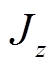 及J分别为转子绕
及J分别为转子绕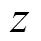 轴及绕
轴及绕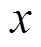 轴(
轴(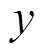 轴)的转动惯量;fxa、fya、fxb、fyb分别为AMB-A和AMB-B在
轴)的转动惯量;fxa、fya、fxb、fyb分别为AMB-A和AMB-B在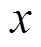 及
及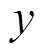 方向上的电磁力,也等于AMB传递到基础上的传递力;
方向上的电磁力,也等于AMB传递到基础上的传递力; 为电机的旋转角速度。
为电机的旋转角速度。
建立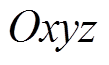 固定坐标系,其中
固定坐标系,其中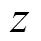 轴为旋转轴,
轴为旋转轴,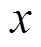 、
、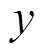 和
和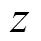 之间形成右手系。转子的运动状态可以用转子质心在
之间形成右手系。转子的运动状态可以用转子质心在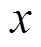 和
和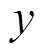 方向的平动位移(x,y)和转子绕
方向的平动位移(x,y)和转子绕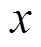 及
及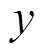 轴的角位移(
轴的角位移( ,
,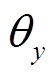 )来描述。
)来描述。
当两端AMB处转子离开平衡位置的位移分别为(xa, ya)和(xb, yb)时,质心C的位移为
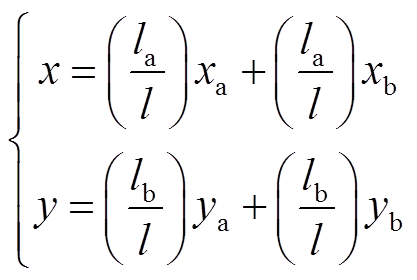 (1)
(1)转子绕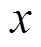 轴和
轴和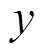 轴逆时针转动的角度为
轴逆时针转动的角度为
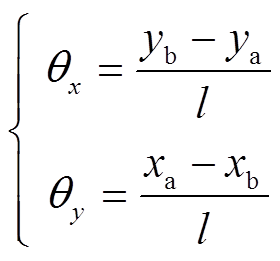 (2)
(2)
为了建立径向四自由度磁悬浮高速电机刚性转子系统的动力学方程,假设:①转子附加不平衡质量与转子的质量相比很小,不足以影响转子质心位置的偏移,不平衡转子的运动状态仍然用平衡转子质心C点的广义坐标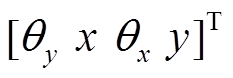 来描述;②转子为轴对称刚性转子,转子绕x轴和绕y轴的转动惯量相同;③两端的AMB-A和AMB-B与位移传感器A和B不在同一个平面上;④径向四个自由度的AMB结构和参数均相同;⑤忽略轴向轴承对转子径向运动的影响。
来描述;②转子为轴对称刚性转子,转子绕x轴和绕y轴的转动惯量相同;③两端的AMB-A和AMB-B与位移传感器A和B不在同一个平面上;④径向四个自由度的AMB结构和参数均相同;⑤忽略轴向轴承对转子径向运动的影响。
基于上面的假设,容易得到四自由度平衡刚性转子系统在稳态运动过程中的径向运动方程为
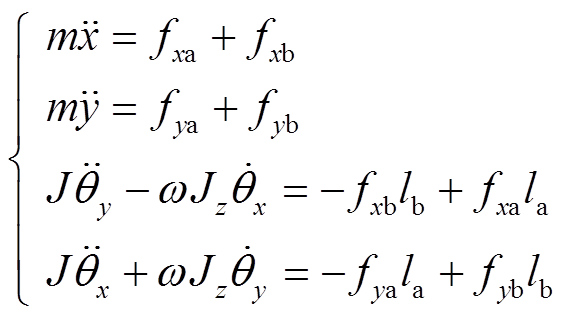 (3)
(3)四自由度平衡刚性转子系统径向传递函数框图如图2所示。由图2可见:①在转子的四个径向运动中,转子在x、y轴方向上的力可同时影响转子在x、y轴方向的平移与其绕y、x轴的旋转,通常把这种在同一坐标平面内的力耦合称之为结构耦合;②转子在x、y轴方向上的力在导致其绕y、x轴旋转的同时,通过耦合项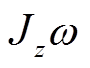 影响转子绕x、y轴的旋转,这种交叉耦合称为陀螺(耦合)效应。
影响转子绕x、y轴的旋转,这种交叉耦合称为陀螺(耦合)效应。

图2 四自由度刚性转子系统径向传递函数框图
Fig.2 Radial transfer function diagram of AMB rigid rotor system with four radial degrees of freedom
对于不平衡的转子,转子的不平衡可等效为由一个不在平衡转子系统质心C处的附加不平衡质量产生。转子不平衡示意图如图3所示。假设该附加转子不平衡质量在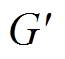 点位置,
点位置,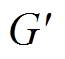 在平衡转子几何中心平面
在平衡转子几何中心平面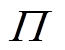 内的投影为
内的投影为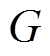 ,在
,在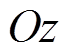 轴上的投影长度为
轴上的投影长度为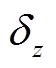 ,
,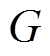 点到
点到 点的偏心距为
点的偏心距为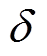 , r为C点到O点的距离。
, r为C点到O点的距离。
为便于描述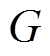 点在转子几何中心平面
点在转子几何中心平面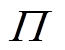 内的运动,以
内的运动,以 为原点,建立
为原点,建立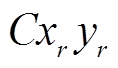 旋转坐标系,当
旋转坐标系,当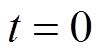 时,旋转坐标系
时,旋转坐标系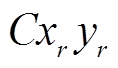 的
的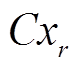 轴与
轴与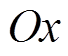 轴平行;当
轴平行;当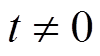 时,
时,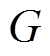 的瞬态旋转角度为
的瞬态旋转角度为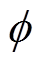 。当转子稳定运行时,
。当转子稳定运行时,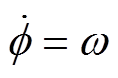 ,
,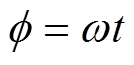 。
。
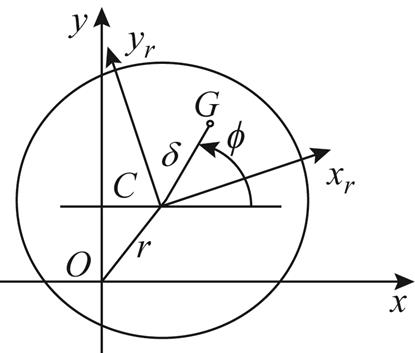
图3 转子不平衡示意图
Fig.3 Schematic diagram of rotor imbalance
同理可以得到四自由度不平衡刚性转子系统在非稳态运动过程中的径向运动方程为
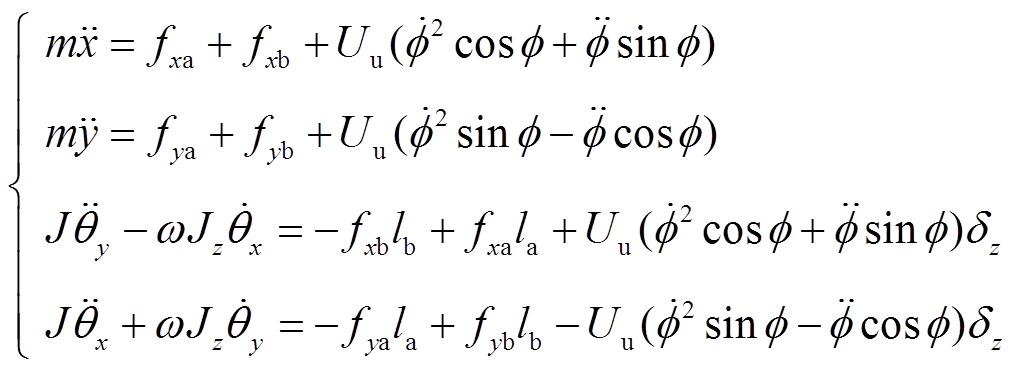 (4)
(4)式中,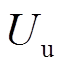 为不平衡量,
为不平衡量,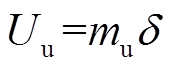 ,
,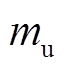 及
及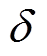 分别为不平衡质量及偏心距。
分别为不平衡质量及偏心距。
传统自适应陷波器用于磁悬浮高速电机转子系统中时,在径向刚体临界转速附近存在稳定性问题。如果采用传统自适应陷波器来消除转子系统中不平衡量引起的同频干扰,只能去除AMB中电流刚度力中的同频成分,而无法去除AMB中位移刚度力中的同频成分,因此无法最大限度地抑制不平衡振动。本文在传统自适应陷波器的基础上提出了变极性不平衡振动控制方式,即在传统陷波器反馈控制基础上增加前馈控制,同时对电流刚度和位移刚度进行补偿,实现对转子的振动及传递力的最小控制。
自适应陷波滤波器的结构如图4所示。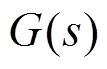 为AMB转子系统的传递函数,Gc(s)、GP(s)及GS(s)分别为PID控制器、功率放大器及位移传感器的传递函数。Nf(s)是陷波器的反馈环节,
为AMB转子系统的传递函数,Gc(s)、GP(s)及GS(s)分别为PID控制器、功率放大器及位移传感器的传递函数。Nf(s)是陷波器的反馈环节,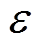 是陷波器的可调参数,
是陷波器的可调参数, 为角频率。
为角频率。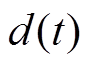 是反馈环节Nf(s)的输入,
是反馈环节Nf(s)的输入,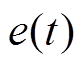 是反馈环节Nf(s)的输出,则有
是反馈环节Nf(s)的输出,则有
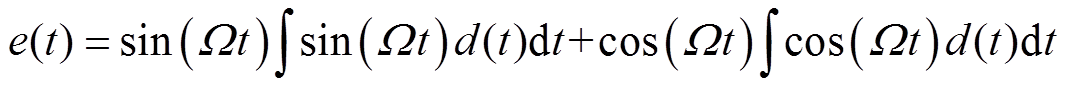 (5)
(5)对式(5)两边同时求导可得

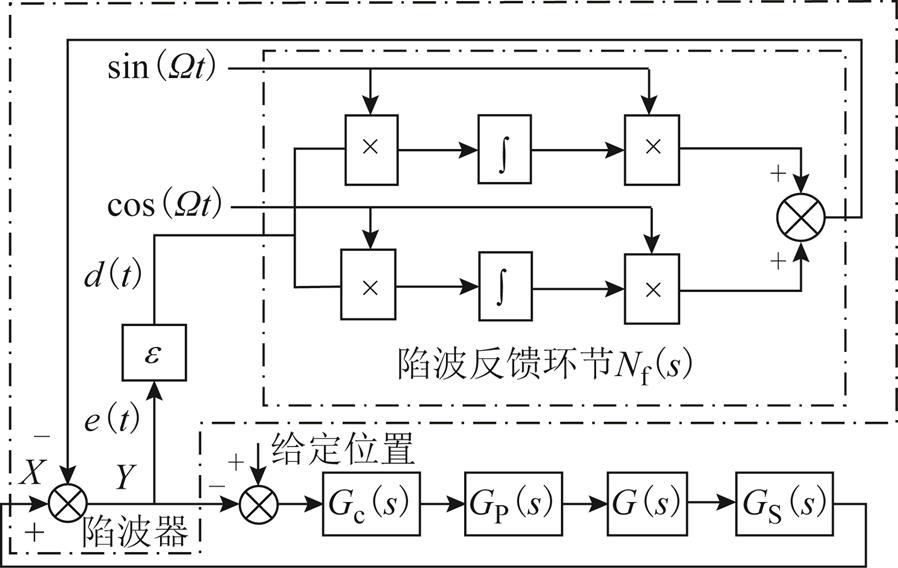
图4 自适应陷波滤波器的结构
Fig.4 Structure of adaptive notch filter
再对式(6)两边同时求导并化简可得
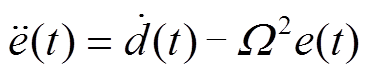 (7)
(7)则可以得到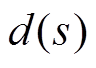 与
与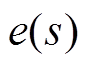 之间的关系为
之间的关系为
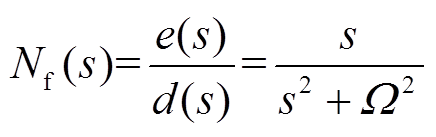 (8)
(8)
由图4和式(8)可知,陷波器输入和输出之间满足
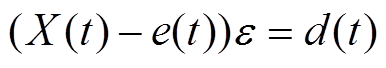 (9)
(9)给式(9)两边同时除以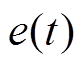 并结合式(8)可得
并结合式(8)可得
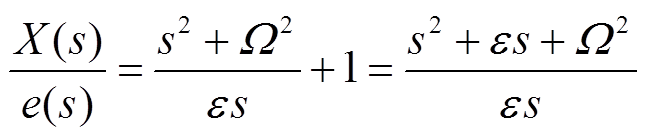 (10)
(10)
不同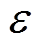 值对陷波器性能的影响如图5所示。可见,随着
值对陷波器性能的影响如图5所示。可见,随着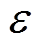 变大,阻带宽度变大,甚至引起失稳。因此,实际应用中,在确保算法能够稳定跟踪振动信号的情况下,应选取较小的
变大,阻带宽度变大,甚至引起失稳。因此,实际应用中,在确保算法能够稳定跟踪振动信号的情况下,应选取较小的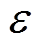 值。
值。

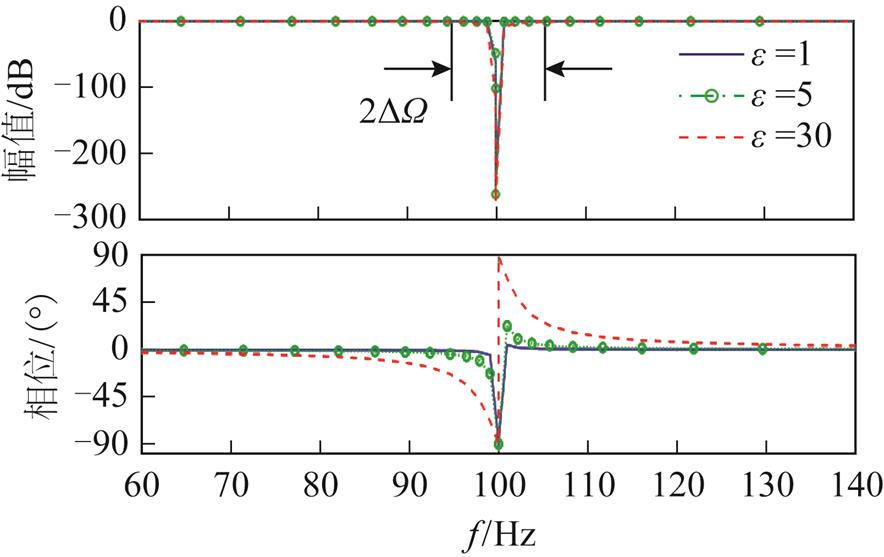
图5 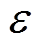 对自适应陷波器性能的影响
对自适应陷波器性能的影响
Fig.5 Influence of 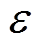 on adaptive notch filter
on adaptive notch filter
令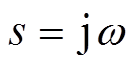 (
(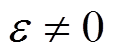 时),由图5可得
时),由图5可得
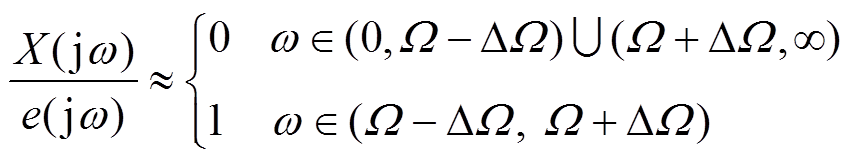 (11)
(11)式中,DW为陷波器阻带宽度的一半,其值远小于W。由式(11)可知,陷波器经过若干拍之后,输入 中与转速同频的分量可被完全消除,实现同频振动分量的抑制。
中与转速同频的分量可被完全消除,实现同频振动分量的抑制。
为了验证自适应陷波器的跟踪能力和滤波性能,分别在恒定频率和频率以恒定速率变化条件下进行仿真分析。图6为恒定频率120Hz时和频率0~240Hz变化时自适应陷波器的仿真结果。可见,无论是在恒定频率还是频率变化的条件下,自适应陷波器均表现出了良好的信号跟踪能力和滤波性能。
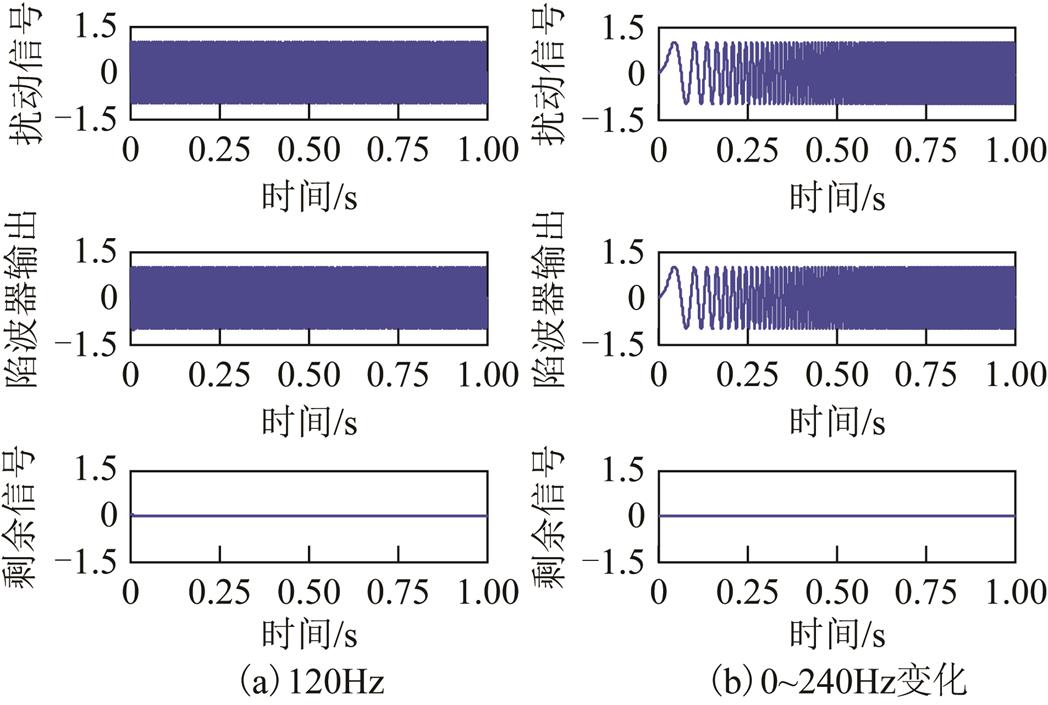
图6 频率为120Hz和在0~240Hz变化时自适应陷波器仿真结果
Fig.6 Simulation results of adaptive notch filter with constant frequency of 120Hz and frequencies of 0~240Hz
图7为基于自适应陷波器的AMB高速电机刚性转子系统自动平衡控制的框图。图中,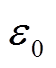 为极性切换开关。通过陷波器反馈控制以及前馈控制,实现电磁力最小控制。
为极性切换开关。通过陷波器反馈控制以及前馈控制,实现电磁力最小控制。
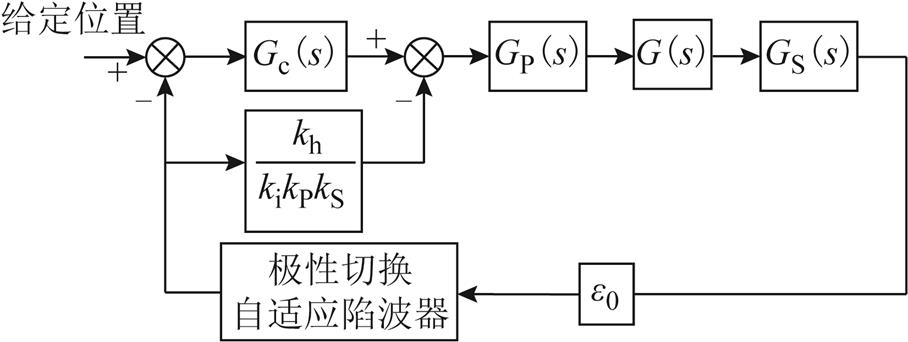
图7 基于自适应陷波器反馈及前馈控制的自动平衡
Fig.7 Automatic balancing based on feedback and feedforward control of adaptive notch filter
AMB刚性转子系统可看作是一个二阶系统,其传递函数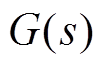 为
为
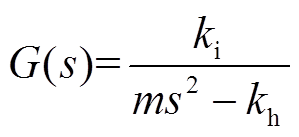 (12)
(12)式中,ki为电流刚度系数;kh为位移刚度系数。
PID控制器的传递函数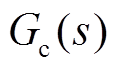 为
为
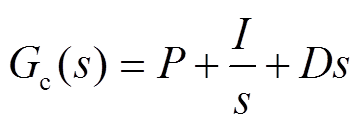 (13)
(13)式中,P为比例增益系数;I为积分增益系数;D为微分增益系数。
如果不考虑功放及传感器的动态特性,它们均可视为一阶线性系统,其传递函数分别为
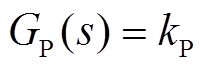 (14)
(14)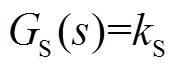 (15)
(15)
式中,kP及kS分别为功率放大器及传感器的放大系数。
当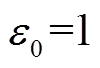 时,基于自适应陷波器自动平衡控制的等效框图如图8所示。
时,基于自适应陷波器自动平衡控制的等效框图如图8所示。
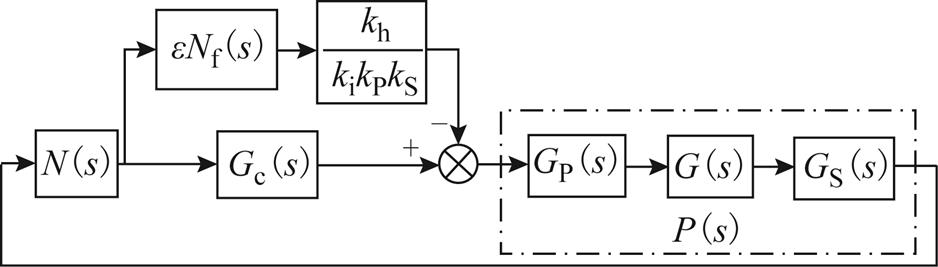
图8 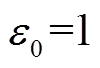 时基于自适应陷波器自动平衡的等效框图
时基于自适应陷波器自动平衡的等效框图
Fig.8 Equivalent block diagram of automatic balancing based on adaptive notch filter when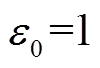
陷波器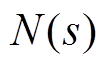 的传递函数为
的传递函数为
 (16)
(16)转子系统的传递函数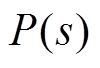 为
为
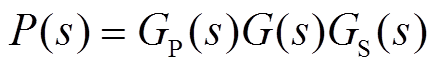 (17)
(17)
转子系统的闭环特征方程为
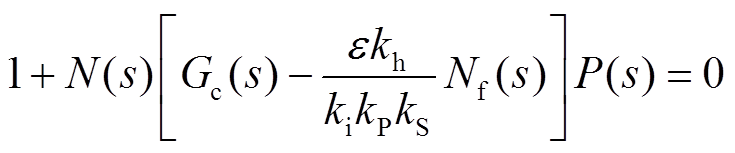 (18)
(18) 当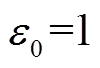 时,以
时,以 为变量,绘制转子系统的广义根轨迹,如图9a所示。可见,转子系统根轨迹有两条分支位于虚轴附近,其余分支均位于s左半平面且离虚轴较远。因此,离虚轴较近的两条分支为主导根轨迹。随着
为变量,绘制转子系统的广义根轨迹,如图9a所示。可见,转子系统根轨迹有两条分支位于虚轴附近,其余分支均位于s左半平面且离虚轴较远。因此,离虚轴较近的两条分支为主导根轨迹。随着 变大,两条主导根轨迹分支从s右半平面越过虚轴进入s左半平面。低于转子系统的刚体临界转速时,闭环系统发散。
变大,两条主导根轨迹分支从s右半平面越过虚轴进入s左半平面。低于转子系统的刚体临界转速时,闭环系统发散。
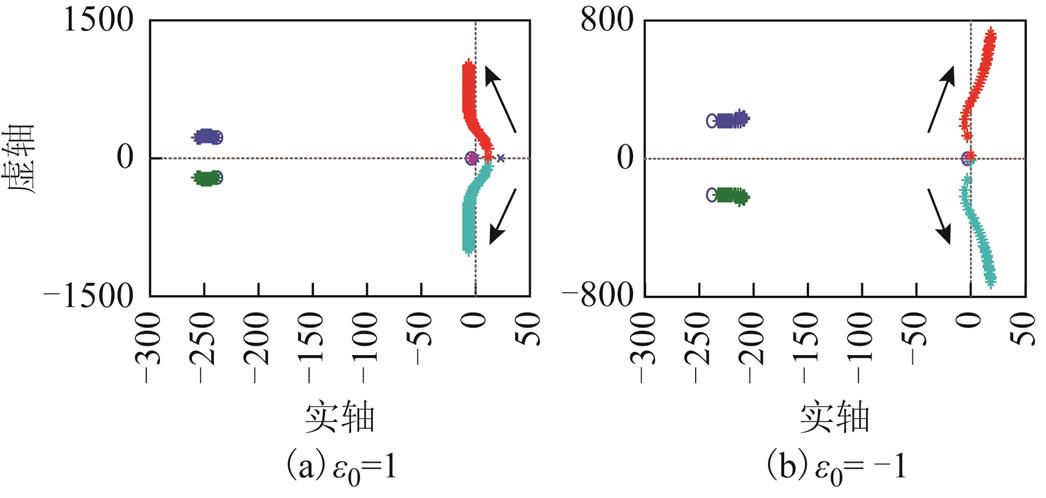
图9 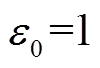 和
和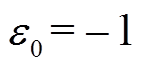 时闭环系统的根轨迹
时闭环系统的根轨迹
Fig.9 Root loci of closed loop system when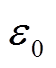 =1, -1
=1, -1
当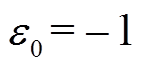 时,基于自适应陷波器的自动平衡控制等效框图类似于图8,只是传递函数
时,基于自适应陷波器的自动平衡控制等效框图类似于图8,只是传递函数 替换了
替换了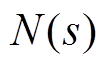 。其中,
。其中, 表示为
表示为
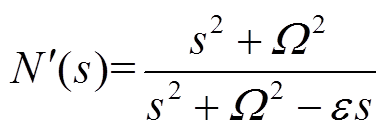 (19)
(19)则转子系统的闭环特征方程为
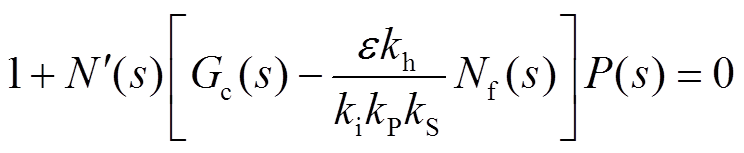 (20)
(20)
类似地,当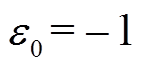 时,转子系统的广义根轨迹如图9b所示。不同于
时,转子系统的广义根轨迹如图9b所示。不同于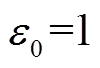 的是,当转子速度高于转子系统的刚体临界转速时,闭环系统发散。
的是,当转子速度高于转子系统的刚体临界转速时,闭环系统发散。
从以上分析可知,当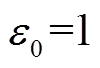 ,低于转子系统的刚体临界转速时,闭环系统发散,高于刚体临界转速时,闭环系统稳定;当
,低于转子系统的刚体临界转速时,闭环系统发散,高于刚体临界转速时,闭环系统稳定;当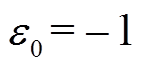 ,低于刚体临界转速时,闭环系统稳定,高于刚体临界转速时,闭环系统发散。为此,本文提出通过极性切换策略来实现转子系统在包含刚体临界的全转速范围内的自动平衡控制。
,低于刚体临界转速时,闭环系统稳定,高于刚体临界转速时,闭环系统发散。为此,本文提出通过极性切换策略来实现转子系统在包含刚体临界的全转速范围内的自动平衡控制。
采用陷波器反馈结构极性切换的AMB高速电机刚性转子闭环系统的虚轴附近的根轨迹分支如图10所示。具体切换策略为:当转子转速低于其刚性临界转速时,取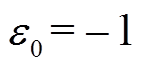 ;当转子转速高于其刚性临界转速时,取
;当转子转速高于其刚性临界转速时,取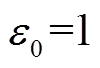 。当转子转速位于临界稳定附近以及等于临界转速时,取
。当转子转速位于临界稳定附近以及等于临界转速时,取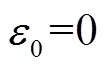 ,此时由于凹陷反馈环节Nf(s)中积分器的作用,对AMB高速电机刚性转子闭环系统进行开环补偿。
,此时由于凹陷反馈环节Nf(s)中积分器的作用,对AMB高速电机刚性转子闭环系统进行开环补偿。
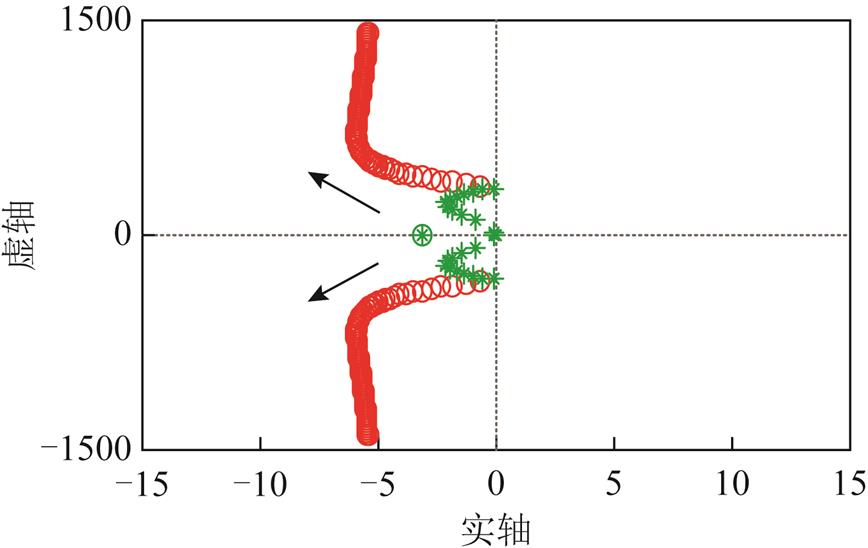
图10 采用极性切换后的主导根轨迹分支
Fig.10 Major root locus after switching polarity
为方便说明,以采用负极性陷波器反馈结构为例,讨论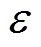 取值对AMB高速转子闭环系统的影响。
取值对AMB高速转子闭环系统的影响。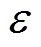 对AMB高速电机刚性转子闭环系统虚轴附近的根轨迹的影响如图11所示。
对AMB高速电机刚性转子闭环系统虚轴附近的根轨迹的影响如图11所示。
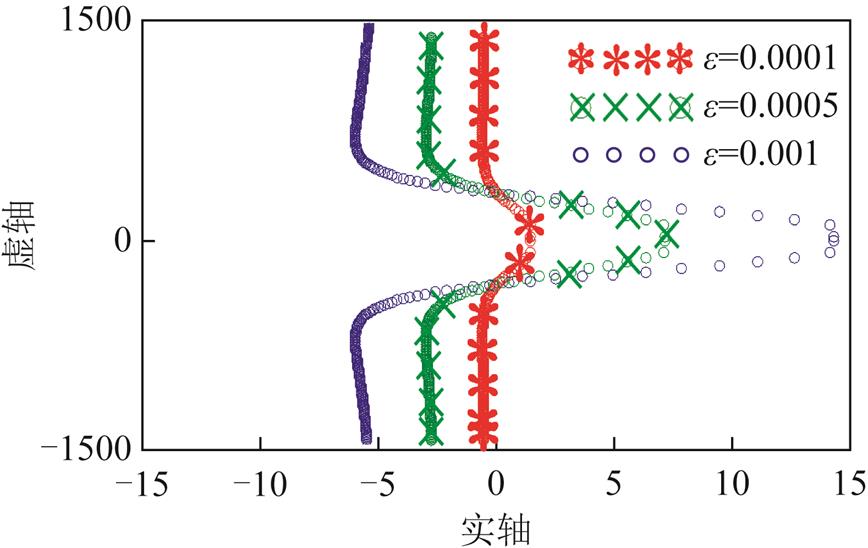
图11 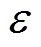 对闭环系统虚轴附近的根轨迹影响
对闭环系统虚轴附近的根轨迹影响
Fig.11 Influence on the root locus near the imaginary axis of the closed-loop system with different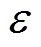
随着 增加,不同
增加,不同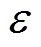 时的闭环系统虚轴附近的根轨迹分支变化趋势相同,并从同一点越过虚轴进入s左半平面,且临界稳定转速相同。可得,在
时的闭环系统虚轴附近的根轨迹分支变化趋势相同,并从同一点越过虚轴进入s左半平面,且临界稳定转速相同。可得,在 相同的条件下
相同的条件下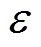 取值越大,根轨迹实部离虚轴越远,算法收敛速度越快,响应时间越短。但由图6可知,
取值越大,根轨迹实部离虚轴越远,算法收敛速度越快,响应时间越短。但由图6可知,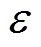 也决定了陷波器的带宽,较大的
也决定了陷波器的带宽,较大的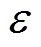 使陷波效果变差,影响了算法对不平衡量的辨识效果。因此,实际中应选取较小的
使陷波效果变差,影响了算法对不平衡量的辨识效果。因此,实际中应选取较小的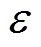 值。
值。
通过AMB高速电机刚性转子系统闭环根轨迹的分析,可知转子系统的刚体临界转速对应的频率在85Hz附近。因此,分别在亚刚体临界和超刚体临界区进行仿真分析。仿真中转子系统的各项参数见表1。
表1 磁悬浮高速电机转子系统的参数
Tab.1 Parameters of magnetically levitated high-speed motor rotor system

参数数值 转子质量m/kg18.09 转子绕x和y轴的转动惯量J/(kg×m2)0.2 转子绕z轴的转动惯量Jz/(kg×m2)0.02 A端到中心平面距离la/m0.13 B端到中心平面距离lb/m0.13 单边理想气隙c0/mm0.35 电磁轴承电流刚度系数ki/(N/A)577.96 电磁轴承位移刚度系数kh/(N/m)2.75×106 电机功率PN/kW75 电机轴向长度l/mm420 电机径向半径r/mm120 额定电压UN/V380 额定电流IN/A167 额定转速nN/(r/min)24 000 额定转矩TL/(N×m)30
为了验证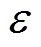 取值对磁悬浮高速电机刚性转子不平衡振动控制的影响,
取值对磁悬浮高速电机刚性转子不平衡振动控制的影响,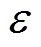 值分别为0.000 05,0.000 1,0.000 15 和0.000 2,在恒定频率120Hz下进行仿真,在0.2s 时开启不平衡振动控制,AMB-A处电磁力(即传递力)的变化如图12所示。可知,
值分别为0.000 05,0.000 1,0.000 15 和0.000 2,在恒定频率120Hz下进行仿真,在0.2s 时开启不平衡振动控制,AMB-A处电磁力(即传递力)的变化如图12所示。可知,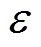 取值越大,电磁力收敛越快。
取值越大,电磁力收敛越快。
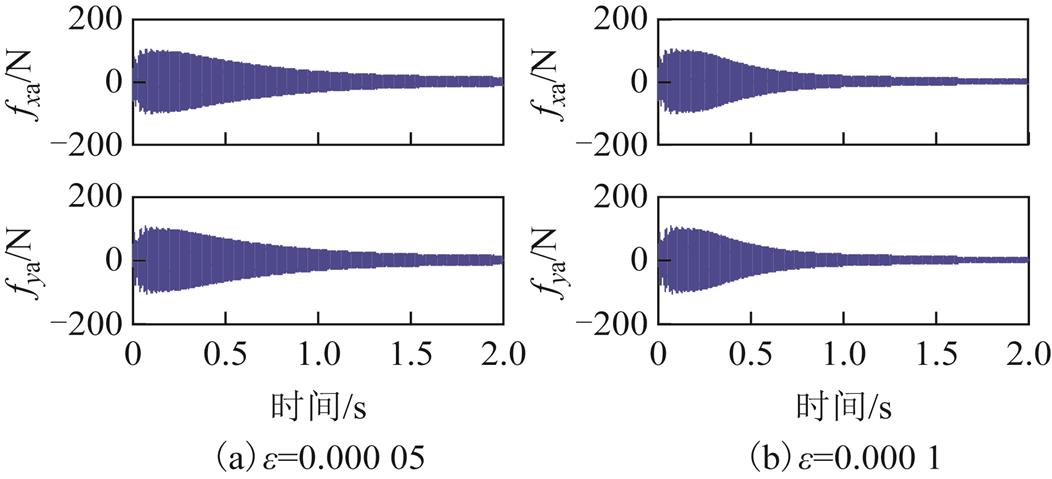
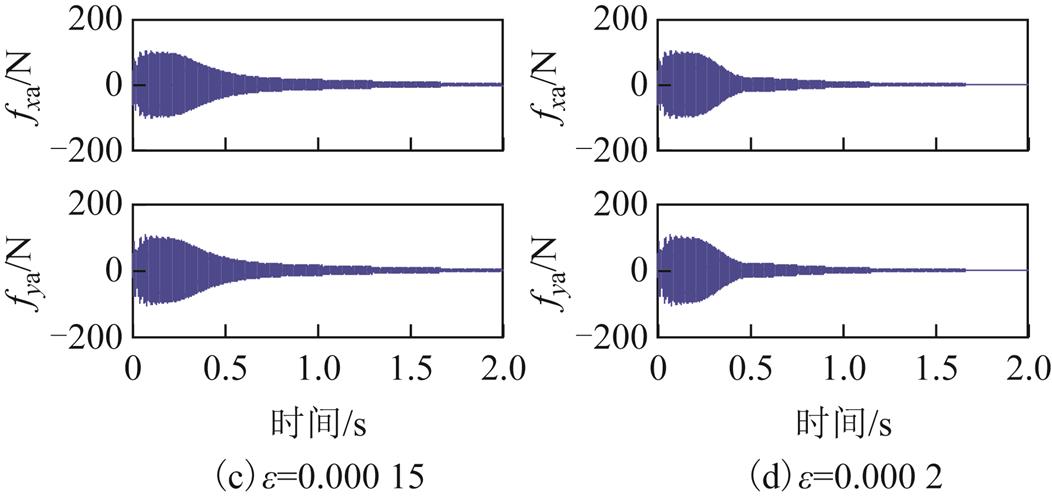
图12 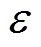 取不同值时AMB-A处的电磁力
取不同值时AMB-A处的电磁力
Fig. 12 Electromagnetic force at AMB-A side with different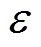
当低于刚体临界频率85Hz时,AMB高速电机刚性转子系统采取正极性陷波器反馈补偿方式;当转子转速高于刚体临界稳定转速时,采取负极性自适应陷波器反馈补偿方式。当转子的旋转频率分别为60Hz、70Hz、120Hz及150Hz时,在转子水平和垂直方向加入正弦干扰,该干扰分别加在执行器的输出电磁力F=[fxA fxB fyA fyB]上,四自由度AMB高速电机刚性转子系统的不平衡分量引起的干扰由式(4)可知,同频干扰信号幅值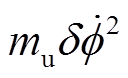 =
= (
(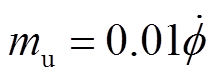 ,
,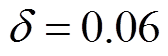 ,
,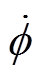 为转子旋转频率),水平和垂直方向的正弦干扰相位相差90°。在0.2s时分别开启
为转子旋转频率),水平和垂直方向的正弦干扰相位相差90°。在0.2s时分别开启 及
及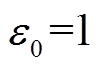 的基于自适应陷波器的自动平衡控制,AMB-A处电磁力和转子位移如图13所示。其中,e=0.000 2。
的基于自适应陷波器的自动平衡控制,AMB-A处电磁力和转子位移如图13所示。其中,e=0.000 2。
由于转子为轴对称刚性转子,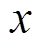 及
及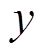 方向的电磁力和转子位移响应几乎一致,因此选取
方向的电磁力和转子位移响应几乎一致,因此选取 方向为例进行仿真。结果表明,开启自动平衡控制后,AMB-A处的电磁力和转子位移均能很快收敛。
方向为例进行仿真。结果表明,开启自动平衡控制后,AMB-A处的电磁力和转子位移均能很快收敛。
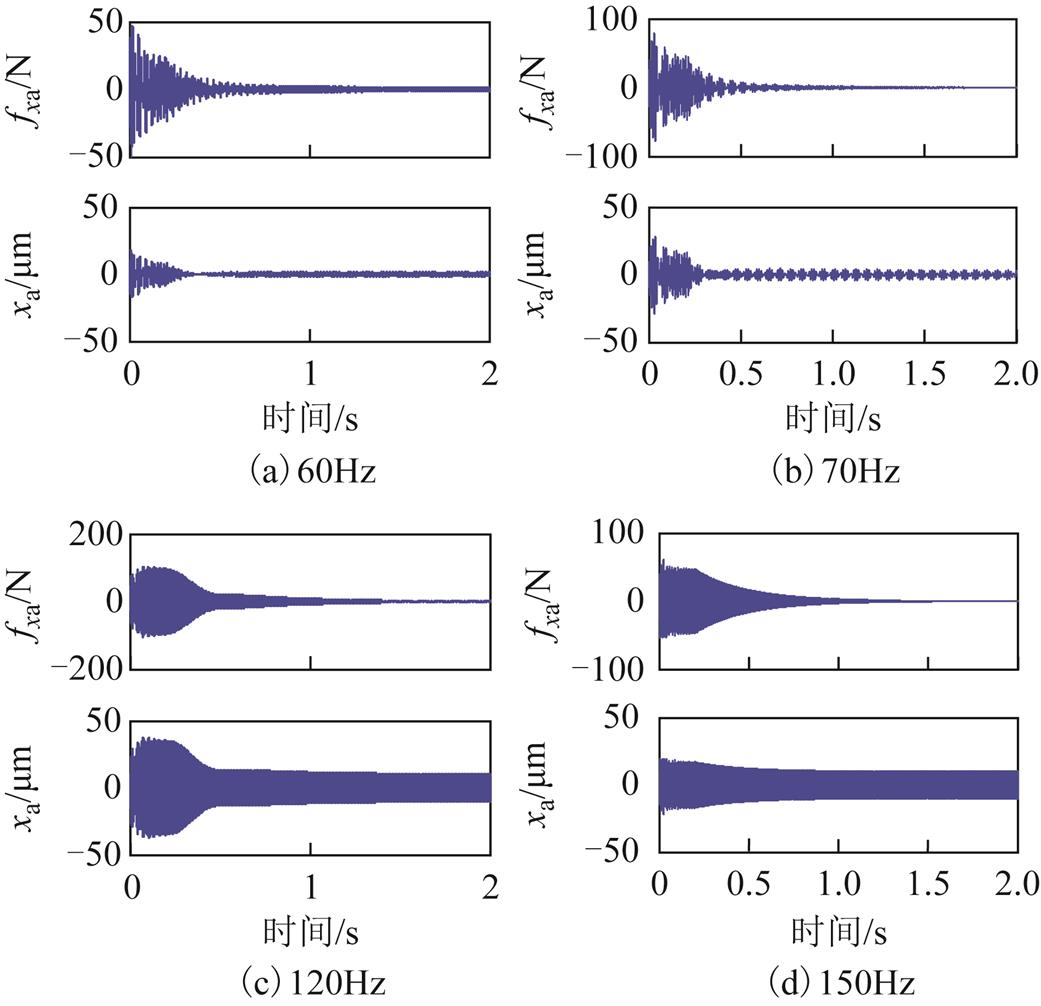
图13 AMB-A处的电磁力和转子位移
Fig.13 Electromagnetic force and rotor displacement at AMB-A side
在磁悬浮高速电机刚性转子系统实验平台实际调试过程中,由于硬件设备等多方面因素影响可能存在频率失配,因此有必要针对这种情况进行仿真研究。取转子旋转频率为120Hz,进行频率失配性能仿真,失配误差频率分别为118Hz、118.5Hz、119Hz、121Hz、121.5Hz及122Hz。在0.2s时开启基于自适应陷波器的自动平衡控制,AMB-A处电磁力和转子位移分别如图14~图16所示。其中,e=0.000 2。
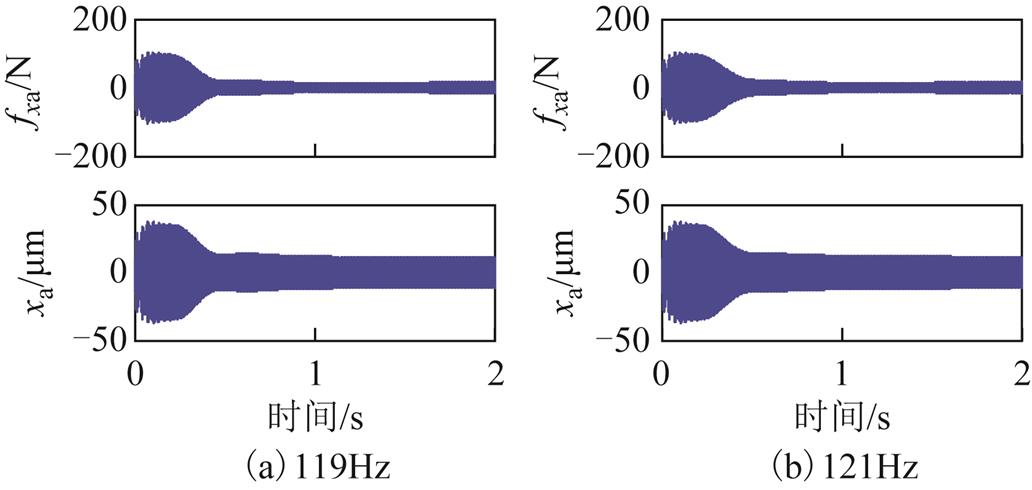
图14 频率误差为1Hz时AMB-A处电磁力和转子位移
Fig.14 Electromagnetic force and rotor displacement at AMB-A side with a frequency error of 1Hz

图15 频率误差为1.5Hz时AMB-A处电磁力和转子振动位移
Fig.15 Electromagnetic force and rotor displacement at AMB-A side with a frequency error of 1.5Hz

图16 频率误差为2Hz时转子A端电磁力和转子位移
Fig.16 Electromagnetic force and rotor displacementt AMB-A side with a frequency error of 2Hz
结果表明,采用基于自适应陷波器的自动平衡控制,当失配频率误差为1Hz时,转子的电磁力和位移分别减小了约85%及80%;当失配频率误差为1.5Hz时,转子的电磁力和位移均减小了约60%;当失配频率误差为2Hz时,转子的电磁力和位移均减小了约50%。因此,在一定频率误差范围内,采用自适应陷波器的自动平衡控制,依然能够起到较好的控制效果。
在磁悬浮高速电机刚性转子实验平台实际调试过程中,由于功率放大器噪声、传感器噪声等硬件设备噪声的存在,会对实验结果产生影响,因此有必要针对这种情况进行仿真研究。信号的信噪比用振动信号与噪声的比值SNR表示。在120Hz的恒定转速下,分别加入SNR为2、4、10、20的白噪声干扰。采用基于自适应陷波器的自动平衡控制前后,非驱动端AMB-A处电磁力和转子位移如图17所示。
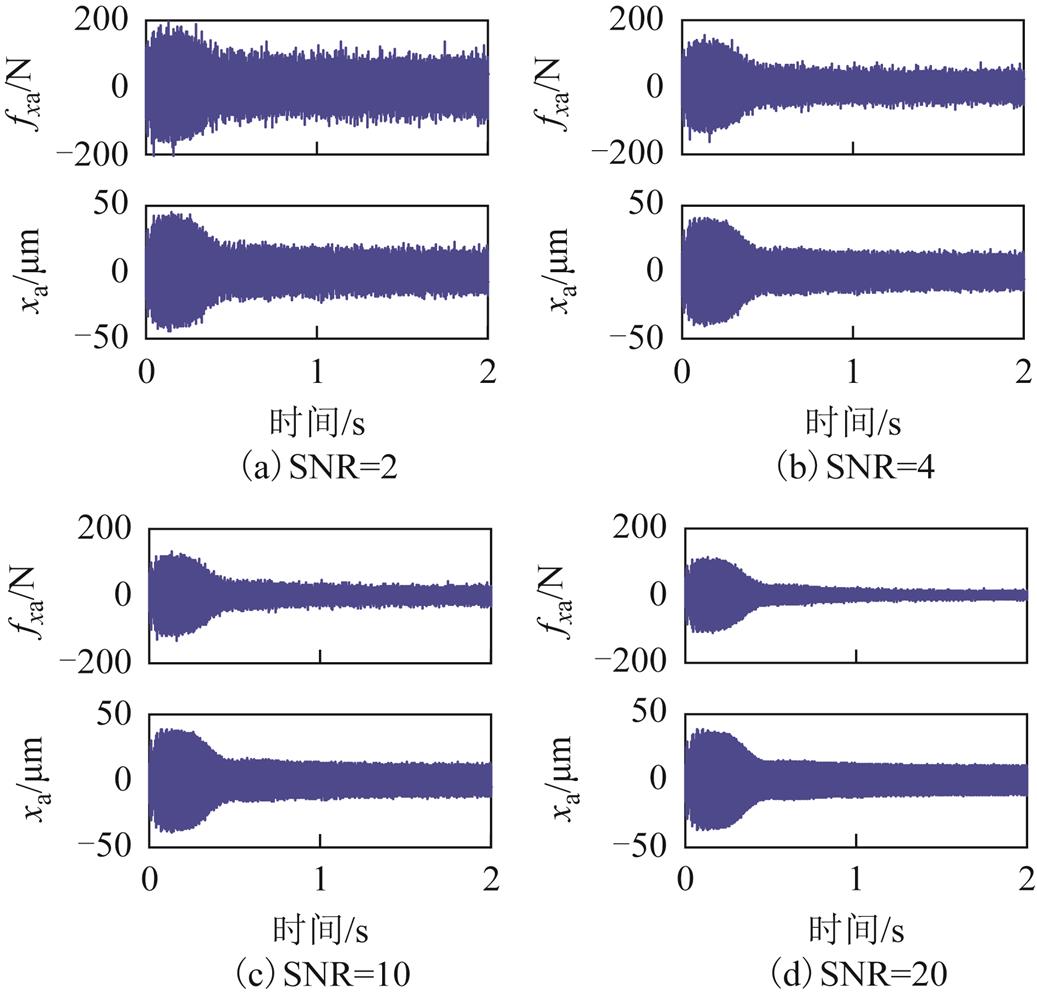
图17 不同噪声水平下AMB-A处电磁力和转子位移
Fig.17 Electromagnetic force and rotor displacement at AMB-A side with different SNRs
结果表明,采用基于自适应陷波器的自动平衡控制时,加入一定量的噪声后,并没有影响算法的收敛性,依然能够起到较好的控制效果。
为了研究基于自适应陷波器变极性不平衡振动控制的性能,分别在不同恒加速度的情况下进行了仿真。图18~图21分别给出了加速度为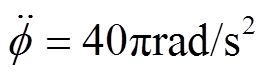 和
和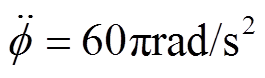 条件下,采用基于自适应陷波器的自动平衡控制前后,AMB-A端的电磁力、转子位移及控制电流的仿真结果。
条件下,采用基于自适应陷波器的自动平衡控制前后,AMB-A端的电磁力、转子位移及控制电流的仿真结果。
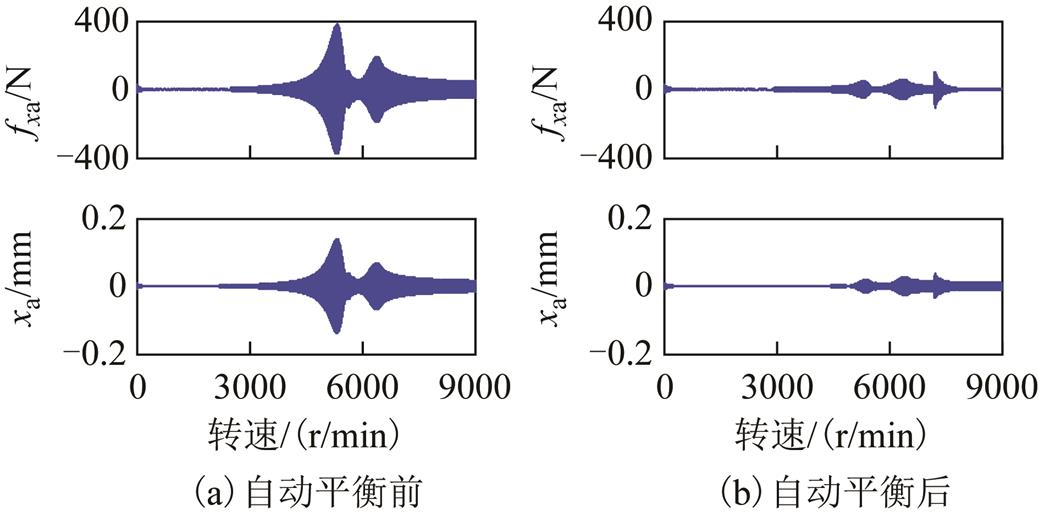
图18 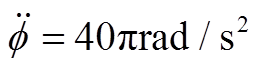 时自动平衡前后AMB-A端的电磁力和转子位移
时自动平衡前后AMB-A端的电磁力和转子位移
Fig. 18 Electromagnetic force and rotor displacement under constant acceleration 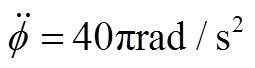 at AMB-A side before and after automatic balancing
at AMB-A side before and after automatic balancing
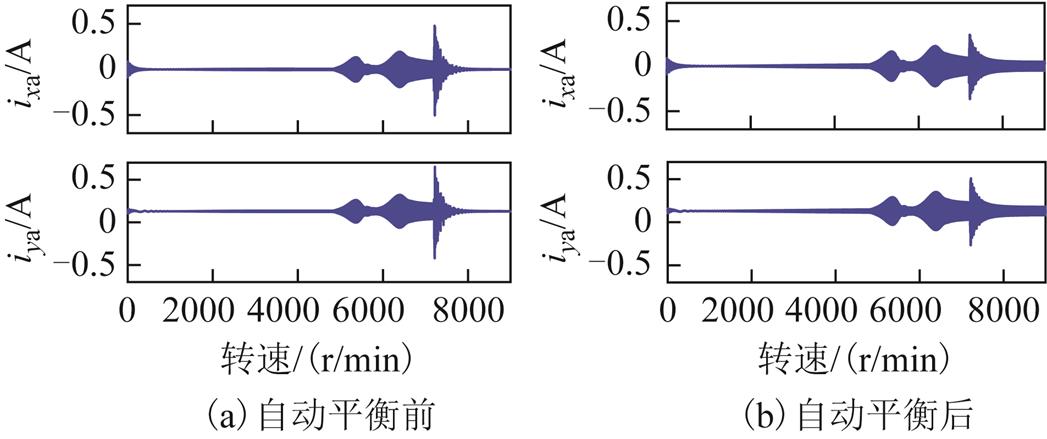
图19 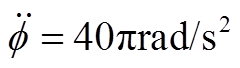 时自动平衡前后AMB-A端的控制电流
时自动平衡前后AMB-A端的控制电流
Fig.19 Control current under constant acceleration 
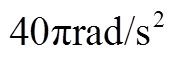 at AMB-A side before and after automatic balancing
at AMB-A side before and after automatic balancing
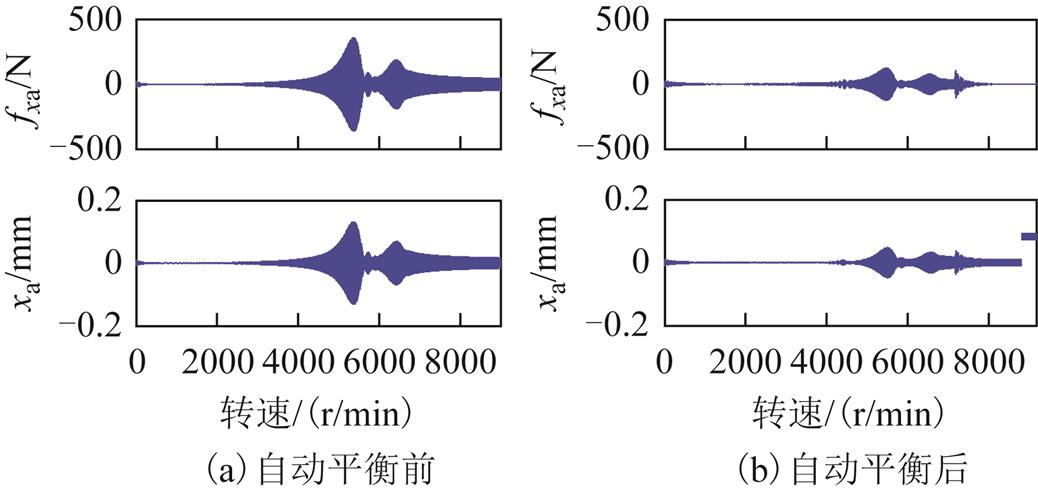
图20 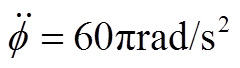 时自动平衡前后AMB-A端的电磁力和转子位移
时自动平衡前后AMB-A端的电磁力和转子位移
Fig.20 Electromagnetic force and rotor displacement under constant acceleration 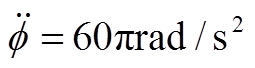 at AMB-A side before and after automatic balancing
at AMB-A side before and after automatic balancing
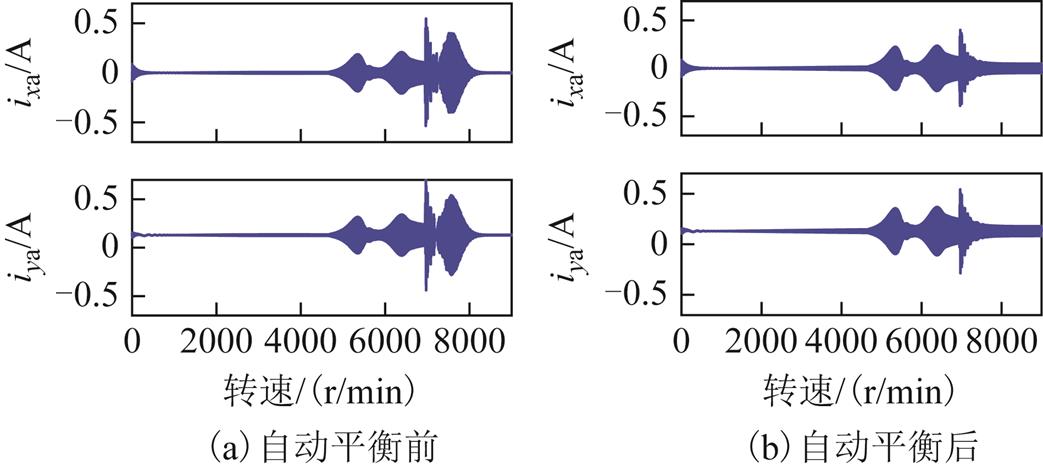
图21 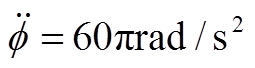 时自动平衡前后AMB-A端的控制电流
时自动平衡前后AMB-A端的控制电流
Fig. 21 Control current under constant acceleration 
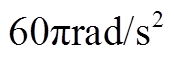 at AMB-A side before and after automatic balancing
at AMB-A side before and after automatic balancing
可见,在采用基于自适应陷波器的自动平衡控制前,转子在两个刚体临界转速区出现了明显的共振峰;在采用基于自适应陷波器的自动平衡控制后,转子在两个刚体临界转速区的共振峰明显减小。加入基于自适应陷波器的变极性自动平衡控制后,磁悬浮高速电机刚性转子的不平衡响应得到了明显的抑制,电磁力和控制电流的幅值也都得到了削减。
由于重力的影响,y垂直方向上的控制电流相比于x水平方向的控制电流,其波形被抬高了。这是因为为克服重力,垂直方向上端磁极中的控制电流需大于下端磁极中的控制电流,即上端磁极电磁力大于下端磁极电磁力,最终使转子悬浮所致。
相关实验是在图22所示额定功率为75 kW的磁悬浮高速电机试验平台上进行的。磁悬浮转子系统主要由dSPACE控制平台、上位机、功率放大器、测速模块及电涡流位移传感器等组成。其中,位置传感器实物图及其安装位置如图22右上角所示。电涡流位移传感器的具体参数为:线性范围为0.27~1.27mm;线性中点为0.77mm;标准灵敏度为10.00V/mm;非线性为0.3%;中点输出值为4.962V;灵敏度偏差为-0.1%。由于转子在0~10 000 r/min转速范围内振动比较明显,所以这里主要给出这个转速区的实验结果。图23为实验平台控制系统的示意图,其中,DS1006 PPC为dSPACE的标准内核控制板,DS2103和DS2002分别为dSPACE提供的多通道D-A和A-D采集板。

图22 磁悬浮高速电机转子系统实验平台
Fig.22 Magnetically levitated high-speed motors rotor system test platform
在进行旋转实验之前,一般先进行在线模拟调试,以验证控制算法的合理性和有效性。
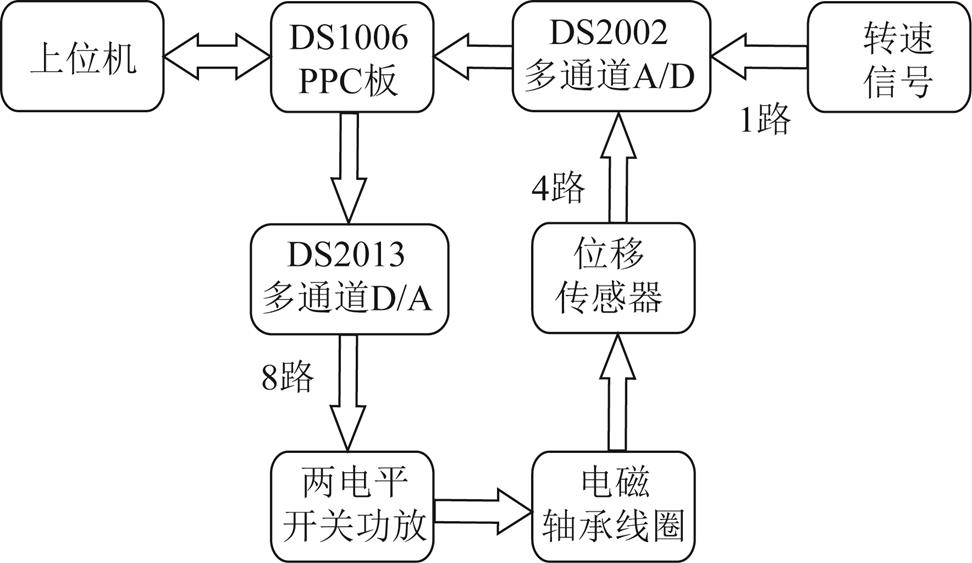
图23 系统试验平台原理示意图
Fig. 23 Schematic diagram of system test platform
转子不平衡力的影响通过采用外加激励的方式来模拟,也就是通过控制器在转子水平及垂直方向加入一个与转速同频的正弦及余弦激励信号,模拟转子在旋转时产生的同频不平衡力。四自由度磁悬浮高速电机刚性转子系统实验平台是轴对称的,AMB-A处和AMB-B处转子径向的振动信号几乎一致,这里用AMB-A处的振动信号来说明自适应陷波器自动平衡控制的有效性。电机模拟转速分别为3 600 r/min及9 000r/min时,采用自适应陷波器自动平衡控制前后,AMB-A处转子的径向位移及运动轨迹分别如图24和图25所示。
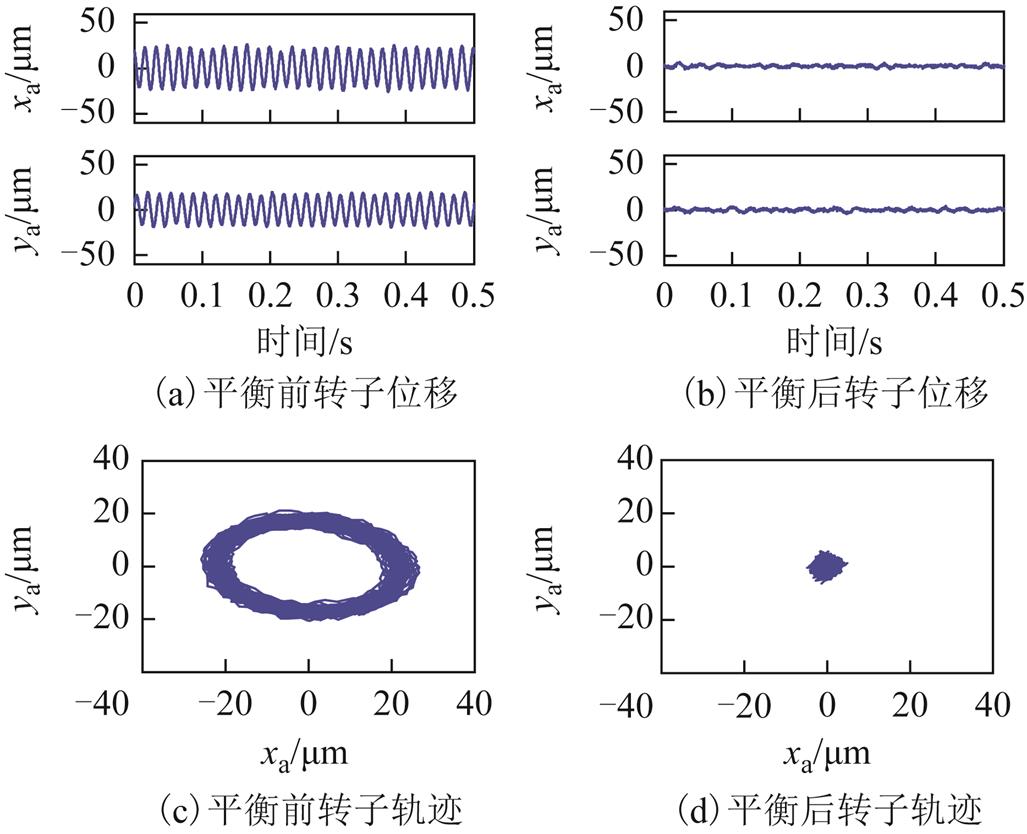
图24 转速3 600 r/min时自动平衡前后在线模拟调试结果
Fig.24 Online simulation results under 3 600 r/min before and after automatic balancing
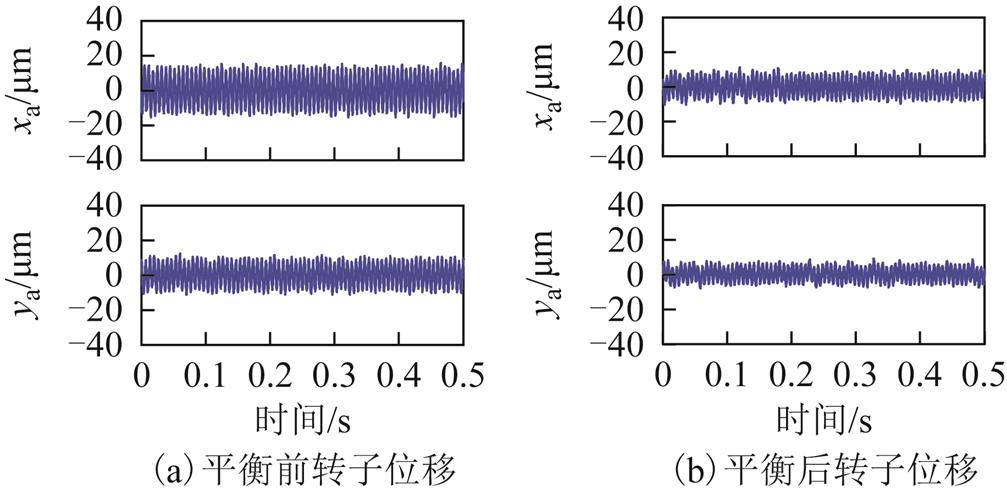
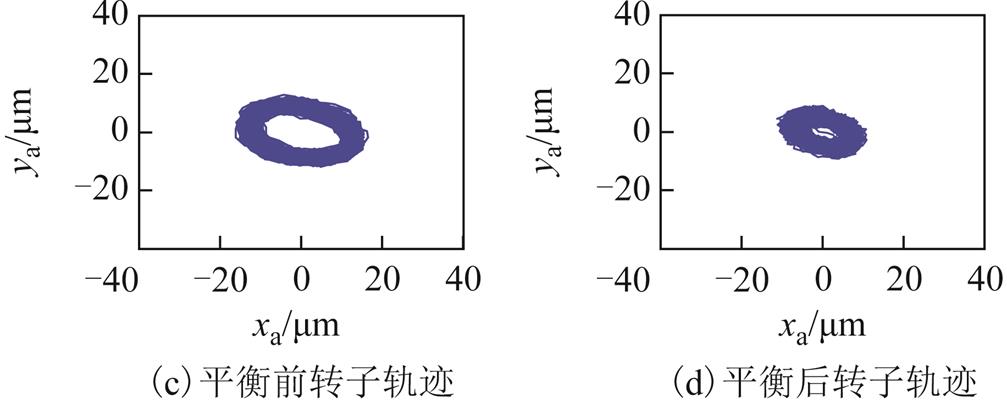
图25 转速9 000 r/min时自动平衡前后在线模拟调试结果
Fig.25 Online simulation results under 9 000 r/min before and after automatic balancing
由图24和图25可知,加入采用基于自适应陷波器自动平衡控制后,转子振动被明显地抑制。恒加速运行条件下,采用基于自适应陷波器自动平衡控制前后,转子振动信号瀑布图如图26所示。

图26 自动平衡前后在线模拟调试AMB-A处振动信号瀑布图
Fig.26 Vibration signal waterfall of online simulation at AMB-A side before and after automatic balancing
由图26可知,在恒加速条件下,采用基于自适应陷波器自动平衡控制后,同频振动得到了有效的抑制,特别是在刚体转子的刚体临界转速附近。
根据在线模拟调试结果,再进行磁悬浮高速电机刚性转子系统的旋转实验。
采用基于自适应陷波器自动平衡控制前后,AMB-A处转子径向振动信号的瀑布图如图27所示。采用自动平衡控制前,转子转速为5 200r/min时,AMB-A处转子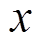 方向上的振幅已经达到了90μm,y方向振幅已经达到了80μm。当转速稍有增加时,转子会因振动过大而失稳,难以通过转子系统的刚体临界转速。采用自动平衡控制后,转子能够以较小的振动顺利穿越刚体临界转速。在整个转速范围内,
方向上的振幅已经达到了90μm,y方向振幅已经达到了80μm。当转速稍有增加时,转子会因振动过大而失稳,难以通过转子系统的刚体临界转速。采用自动平衡控制后,转子能够以较小的振动顺利穿越刚体临界转速。在整个转速范围内,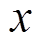 方向上转子的最大振幅不超过36μm,振动幅值减小约60%。
方向上转子的最大振幅不超过36μm,振动幅值减小约60%。
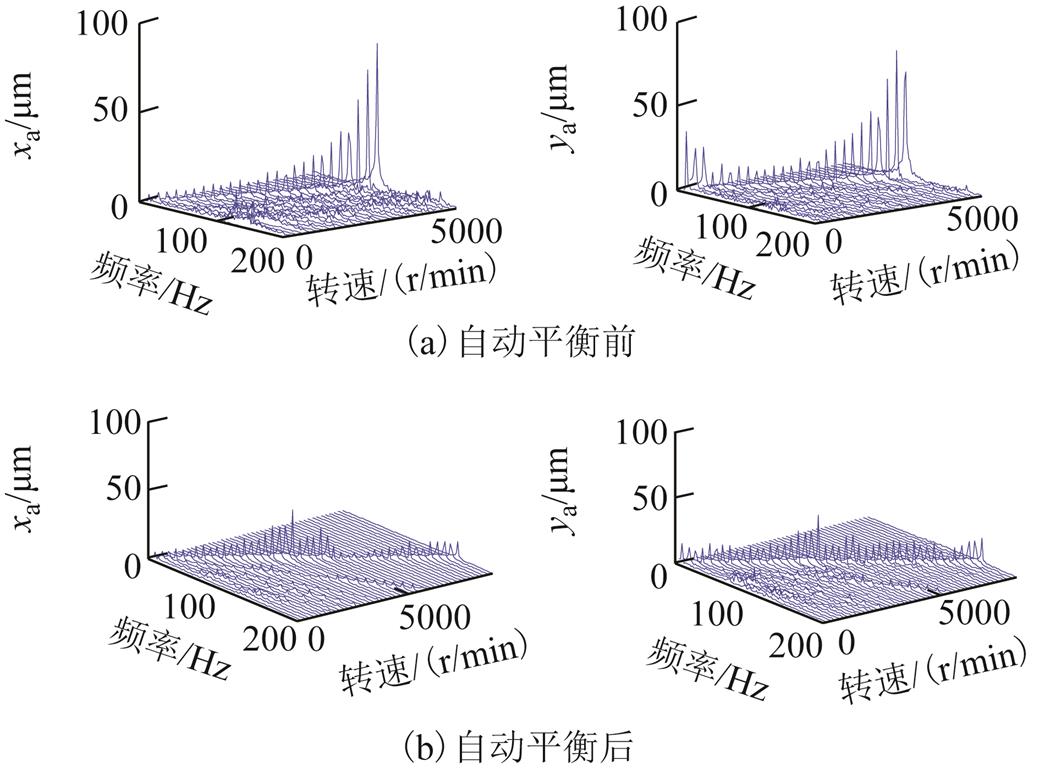
图27 加入自动平衡前后实验时AMB-A处转子振动信号瀑布图
Fig.27 Vibration signal waterfall of experiment at AMB-A side before an d after automatic balancing
针对磁悬浮高速电机刚性转子系统的不平衡振动,建立了磁悬浮高速电机刚性转子系统的径向动力学模型,通过分析自适应陷波器的原理提出了基于极性切换自适应陷波器的自动平衡策略,利用闭环系统的根轨迹得到了极性切换规律,进而构造陷波器反馈控制和前馈控制,实现磁悬浮高速电机刚性转子系统径向电磁力最小控制和在包含刚体临界的全转速范围内稳定运行。仿真和实验均验证了多种工况下基于自适应陷波器自动平衡控制策略能够有效地抑制磁悬浮高速电机刚性转子系统不平衡同步振动及传递力。
参考文献
[1] 张涛, 刘欣凤, 莫丽红, 等. 磁悬浮高速电机系统建模与控制[J]. 电机与控制学报, 2018, 22(4): 98-104. Zhang Tao, Liu Xinfeng, Mo Lihong, et al. Modeling and control of magnetic suspension high-speed motor[J]. Electric Machines and Control, 2018, 22(4): 98-104.
[2] 秦伟, 范瑜, 徐洪泽, 等. 高温超导运动磁场电磁Halbach初级结构直线感应磁悬浮电机[J]. 电工技术学报, 2018, 33(23): 5427-5434. Qin Wei, Fan Yu, Xu Hongze, et al. A linear induction maglev motor with HTS traveling magnetic electromagnetic Halbach array[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5427-5434.
[3] 吴磊涛, 王东, 苏振中, 等. 异极式永磁偏置径向磁轴承的建模与实验[J]. 电工技术学报, 2018, 33(5): 1051-1057. Wu Leitao, Wang Dong, Su Zhenzhong, et al. Modeling and experiment of permanent magnetic biased radial heter-polar magnetic bearing[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1051-1057.
[4] Mao Chuan, Zhu Changshen. Unbalance compensation for active magnetic bearing rotor system using a variable step size real-time iterative seeking algorithm[J]. IEEE Transactions on Industrial Electronics, 2018, 65(5): 4177-4186.
[5] Jiang Kejian, Zhu Changshen, Chen Liangliang. Unbalance compensation by recursive seeking unbalance mass position in active magnetic bearing-rotor system[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5655-5664.
[6] Taiki N, Shinji W, Yukinori N. An interpretation of unbalance vibration compensator for five-axes active magnetic bearing systems based on internal model principle[C]//Proceedings of the 2015 International Conference on Advanced Mechatronic Systems, Beijing, China, 2015: 137-142.
[7] Taiki N, Shinji W, Yukinori N. A phase stabilization method for unbalance vibration control of five-axes active magnetic bearing systems[C]//Proceedings of the 2014 International Conference on Advanced Mechatronic Systems, Besacon, France, 2014: 150- 155.
[8] Fang Jiancheng, Wang Yingguang, Han Bangcheng, et al. Field balancing of magnetically levitated rotors without trial weights[J]. Sensors, 2013, 13(12): 16000-16022.
[9] 孙玉坤, 于丰源, 袁野, 等. 一种混合双定子磁悬浮开关磁阻电机[J]. 电工技术学报, 2019, 34(1): 1-10. Sun Yukun, Yu Fengyuan, Yuan Ye, et al. A hybrid double stator bearingless switched reluctance motor[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 1-10.
[10] 蓝益鹏, 陈其林, 胡学成, 等. 磁悬浮永磁直线电动机控制系统非脆弱鲁棒控制的研究[J]. 电工技术学报, 2016, 31(7): 26-32. Lan Yipeng, Chen Qilin, Hu Xuecheng, et al. Research on non-fragile robust control for magnetic levitation permanent magnet linear motor control system[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 26-32.
[11] 孙鲲鹏, 葛琼璇, 王晓新, 等. 磁悬浮列车在双端供电模式下的无速度传感器控制[J]. 电工技术学报, 2018, 33(18): 4249-4258. Sun Kunpeng, Ge Qiongxuan, Wang Xiaoxin, et al. Speed sensorless control of maglev train with double-end power supply[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4249-4258.
[12] 孙玉坤, 林文威, 袁野, 等. 磁悬浮开关磁阻电机二阶滑模直接转矩控制[J]. 电机与控制学报, 2018, 22(10): 76-86. Sun Yukun, Lin Wenwei, Yuan Ye, et al. Direct torque control based on second order sliding mode for bearingless switched reluctance motor[J]. Electric Machines and Control, 2018, 22(10): 76-86.
[13] 宋腾, 韩邦成, 郑世强, 等. 基于最小位移的磁悬浮转子变极性LMS反馈不平衡补偿[J]. 振动与冲击, 2015, 34(7): 24-32. Song Teng, Han Bangcheng, Zheng Shiqiang, et al. Variable polarity LMS feedback based on displacement nulling to compensate unbalance of magnetic bearing[J]. Journal of Vibration and Shock, 2015, 34(7): 24-32.
[14] 宋立伟, 李书培. 力耦合特性对混合式磁轴承的影响[J]. 电工技术学报, 2017, 32(1): 190-196. Song Liwei, Li Shupei. Coupling mechanical characteristics and its effect on hybrid magnetic bearings[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 190-196.
[15] Saito D, Wakui S. Trial of applying the unbalance vibration compensator to axial position of the rotor with AMB [C] //Proceedings of the 2017 International Conference on Advanced Mechatronic Systems, Xiamen, China, 2017: 249-254.
[16] Chen S L, Lin S Y. Adaptive imbalance compensation for a three-pole AMB system[C] //Proceedings of 12th IEEE International Conference on Control and Automation, Kathmandu, Nepal, 2016: 962-965.
[17] Mohamed S K, Maxime R D, Loicq S B, et al. Application of second-order sliding-mode concepts to active magnetic bearings[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 855-864.
[18] Zheng Shiqiang, Han Bangcheng, Feng Rui, et al. Vibration suppression control for AMB-supported motor driveline system using synchronous rotating frame transformation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5700-5708.
[19] Zheng Shiqiang, Li Haitao, Cong Peng, et al. Experimental investigations of resonance vibration control for noncollocated AMB flexible rotor systems [J]. IEEE Transactions on Industrial Electronics, 2017, 64(3): 2226-2235.
[20] Amin N, Juan S, Wee S L, et al. System identification and robust control of multi-input multi-output active magnetic bearing systems[J]. IEEE Transactions on Control Systems Technology, 2016, 24(4): 1227-1239.
[21] Liu Chao, Liu Gang. Field dynamic balancing for rigid rotor-AMB system in a magnetically suspended flywheel[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(2): 1140-1150.
[22] Gao Hui, Xu Longya. Real-time feed-forward force compensation for active magnetic bearings system based on H∞ controller[J]. Chinese Journal of Mechanical Engineering, 2011, 24(1): 58-66.
[23] Zheng Shiqiang, Feng Rui. Feedforward compensation control of rotor imbalance for high-speed magnetically suspended centrifugal compressors using a novel adaptive notch filter[J]. Journal of Sound and Vibration, 2016, 366: 1-14.
[24] Chen Qi, Liu Gang, Han Bangcheng. Suppression of imbalance vibration in AMB-rotor systems using adaptive frequency estimator[J]. IEEE Transactions on Industrial Electronics, 2015, 62(12): 7696-7705.
Automatic Balancing for Rigid Rotor of Magnetically Levitated High-Speed Motors Based on Adaptive Notch Filter with Polarity Switching
Abstract For unbalance vibration of rigid rotor system on magnetically levitated high-speed motors,an algorithm based on adaptive notch filter with polarity switching is proposed to achieve automatic balancing. Firstly, according to radial dynamic model of a rigid rotor system with a magnetically levitated high-speed motor, the principle of adaptive notch filter and the strategy of automatic balancing are analyzed. Then a polarity switching strategy is proposed by using of generalized root locus based the magnetically levitated high-speed rigid rotor system, stable operation and automatic balancing in the whole rotational speed range are achieved by adopting adaptive notch filter feedback control and feedforward control. Finally, simulation and experiment results show that the proposed method could suppress the synchronous imbalance vibration and transmitter force to the base effectively in case of different operation conditions.
keywords:Magnetically levitated high-speed motors, rigid rotor, automatic unbalancing, notch filter, root locus
DOI:10.19595/j.cnki.1000-6753.tces.190228
中图分类号:TM351
巩 磊 男,1993年生,博士研究生,研究方向为高速转子系统振动主动控制。E-mail:gong_lei@zju.edu.cn
祝长生 男,1963年生,教授,博士生导师,研究方向为转子系统动力学、高速电机及飞轮储能等。E-mail:zhu_zhang@zju.edu.cn(通信作者)
国家自然科学基金(11632015)和国家重点研发计划(2018YFB0905500)资助项目。
收稿日期2019-03-08
改稿日期2019-05-20
(编辑 郭丽军)