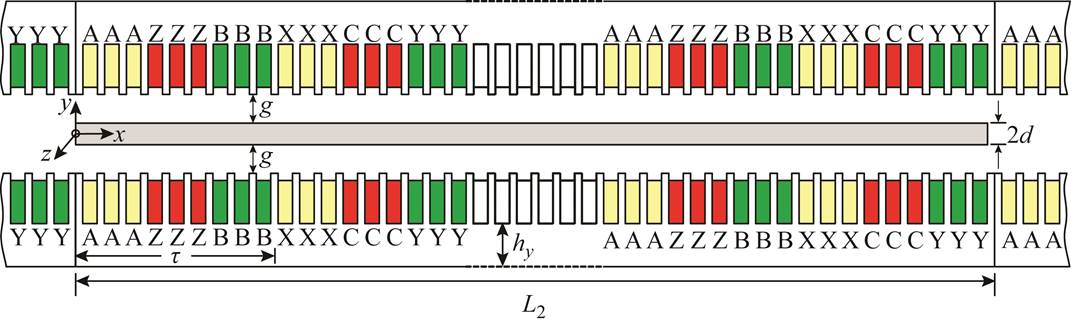
图1 长初级双边直线感应电机横截面示意图
Fig.1 Cross section of long primary DLIM
摘要 根据一维电磁场理论建立以次级板为运动参考坐标系的长初级双边直线感应电机(DLIM)解析模型。首先推导气隙磁通密度在实数域的表达式,分析端部效应引起的前进和后退行波磁场的时空分布特点及其对基波气隙磁场的影响;然后推导考虑前进和后退行波磁场的电机推力密度和稳态推力表达式,分析推力密度在次级板纵向的分布特点、各电磁推力分量随速度的分布特征以及端部效应对总电磁推力的影响;最后建立电机的有限元模型,对电机的气隙磁场分布和不同频率下推力特性进行计算,并与解析计算的结果对比,证实解析计算方法的准确性,为长初级DLIM的初始设计和后续优化提供理论依据和方法。
关键词:双边直线感应电机 后退行波 解析法 电磁性能 端部效应
直线感应电机在中低速的城市轨道交通车辆牵引系统、低速磁悬浮以及线性伺服系统有着广泛的应用[1-3]。双边直线感应电机(Double Sided Linear Induction Machine, DLIM)根据初级长短分为短初级双边直线感应电机(Short Primary DLIM)和长初级双边直线感应电机(Long Primary DLIM)。短初级双边直线感应电机成本较低、供电简单、效率较高,适合应用在需要长时间、远距离运行的场合,如轨道交通的牵引系统[4]。长初级双边直线感应电机次级为一块轻质量金属铝板或者铜板,便于加速和制动,适合应用在较短时间和短距离内将负荷加速到预定速度的场合,比如汽车碰撞实验平台、无人机弹射、航母舰载机电磁弹射系统等[5-6],由于长初级DLIM由多段定子组成,为了节约电能,通常都采用分段供电[7-8]。
对直线感应电机性能的求解计算及优化,主要采用有限元和理论解析计算两种方法[9-10]。用于电磁弹射的长初级双边直线感应电机,驱动电流通常达到数千安培甚至上万安培,电机不可避免地出现饱和状态。铁心饱和对电机性能的影响主要体现在励磁电感和定子漏感参数,通过对磁化曲线分段拟合、实验测试以及有限元计算等方法均能有效地考虑电机的饱和特性[11-13]。对直线电机参数和性能的计算除了通过等效电路[12,14-15],还能通过等效磁路的方法来计算[16]。为了获得大推力,文献[11,15]中电机采用多定子结构,分析了双定子之间的耦合作用;为提升电机的功率密度,文献[16]提出一种无槽结构的直线感应电机;为了解决电力电子器件容量和系统冗余问题,文献[18]提出了十二相长定子直线感应电机,建立了仿真模型并分析了电机性能,分析表明多相电机比多定子电机提升了效率,降低了损耗。
长初级DLIM的气隙磁场分布受次级两端开断导致的端部效应影响,其磁场方程在纵向边界条件上与短初级DLIM有所不同,从而导致其气隙磁场的分布以及性能的差异。对长初级DLIM性能的分析计算,通常都是以初级作为运动参考坐标系建立其矢量磁位方程[17-21],并建立考虑端部效应的等效电路并分析其性能。文献[22]在分析推力波动的基础上,基于磁动势理论推导了动子和定子的不对称阻抗矩阵,提出了利用推力数据计算动子不对称电感的方法。文献[19-20]证明了在转差率极小时可以忽略气隙磁场表达式中的后退行波分量,但没有考虑次级运动导致边界条件的变化,得到的推力波动频率与实际不相符[23]。文献[23-24]建立了以次级为运动参考坐标系的长初级DLIM解析计算模型,但对电机的性能计算忽略了后退行波磁场的影响,仅推导了气隙磁场在复数域内的表达式,磁场的后退分量在整个调速范围内对气隙磁场以及电机性能的影响均被忽略。
为了全面考虑纵向端部效应的影响,基于文献[23-24]的分析方法,建立以次级板为运动参考坐标系的长初级DLIM的解析计算模型,推导了长初级DLIM在恒流源驱动时气隙磁场在实数域内的解析表达式,并分析了端部效应引起的前进和后退行波磁场的时空分布特点,以及各磁场分量对合成气隙磁场的影响。通过理论分析推导了考虑气隙磁场纵向端部效应前进和后退行波磁场之后的电磁推力密度和电磁推力在实数域内的表达式,以及推力密度在次级纵向上的分布特点;根据推力性质和来源将推力表达式分解成与基波推力相关的推力分量;计算了各电磁推力分量随速度变化的情况,定量分析了端部效应,特别是后退气隙磁场分量对电磁推力的影响。最后,建立电机的有限元模型,对电机的气隙磁场分布和不同频率下推力特性进行计算和分析,并验证了解析方法求解的气隙磁场和电磁推力表达式的准确性。
当长初级直线感应电机采用双层叠绕组时,其每段初级的两端均存在半填充槽。次级运动时,随着次级与初级相对位置的不断变化,将引起气隙磁场的脉振,导致气隙磁场畸变,影响推力的平稳性。为消除每段初级端部半填充槽对气隙磁场的影响,长初级DLIM宜采用单层全填充绕组以改善气隙磁场分布,提升电机的推力密度,次级板的长度通常设计为整数倍极距,以降低电机的推力脉动。当电机气隙与极距的比值小于0.25时,采用一维场分析,计算结果在精度上完全可以满足工程需求[25]。采用单层同心式绕组的长初级双边直线感应电机横截面示意图如图1所示。为了简化一维场的分析计算,作如下基本假设[24]:①初级铁心的磁导率无穷大 (μ=∞),电导率σ1为0;②各场量是时间的正弦函数;③气隙磁场只有y方向分量;④初级、次级电流均为z方向;⑤忽略铁心饱和、磁滞损耗、次级导体板的趋肤效应;⑥齿槽对气隙磁通密度分布不均匀的影响通过气隙系数表示。

图1 长初级双边直线感应电机横截面示意图
Fig.1 Cross section of long primary DLIM
根据行波磁动势完全相同的原则,用初级电流层密度代替初级绕组电流[24],并建立以次级板为运动参考坐标系的长初极DLIM的数学模型,如图2所示,模型分为初级与次级耦合区域Ⅰ,无次级非耦合区域Ⅱ和Ⅲ。
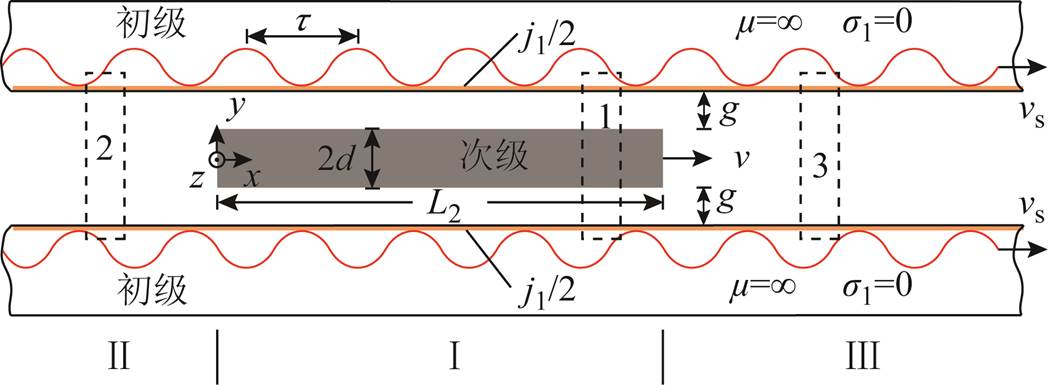
图2 长初级双边直线感应电机数学模型
Fig.2 Mathematical model of long primary DLIM
初级双边合成的电流层密度为
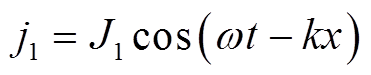 (1)
(1)为方便计算,将式(1)写成复指数形式为
 (2)
(2)
其中

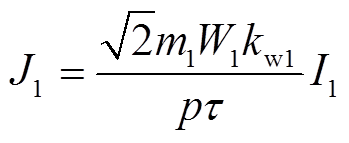
式中,s为转差率;ω为电源角频率;τ为极距;m1为相数;W1为每相串联匝数;kw1为绕组基波因数;I1为初级绕组相电流有效值;p为极对数。
为简化表达,在后续推导中均略去取实部符号Re。将运动参考坐标固定在次级,可得初级电流层密度为
 (3)
(3)根据Maxwell基本方程组,对图2中区域Ⅰ、Ⅱ、Ⅲ内的矩形1、2、3分别应用安培环路定理,可得
 (4)
(4)
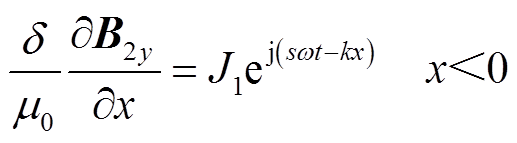 (5)
(5)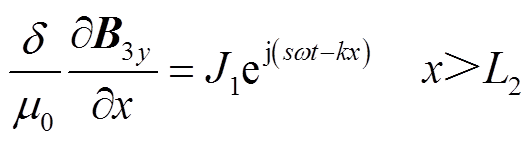 (6)
(6)
式中,B1y、B2y、B3y分别为区域Ⅰ、Ⅱ、Ⅲ中气隙磁通密度y方向分量;j1、j2分别为区域Ⅰ中初级和次级线电流密度瞬时值;δ为等效电磁气隙长度;μ0为真空磁导率。
在耦合区域Ⅰ中,引入矢量磁位A,将其z方向分量记为A1z,且 ,有
,有
 (7)
(7)式中,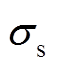 为次级导体面电导率。
为次级导体面电导率。
将式(7)代入式(4),可得气隙磁场方程为
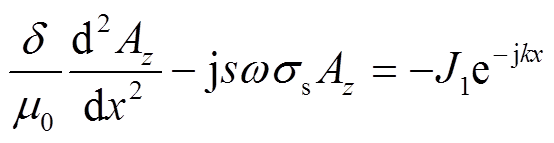 (8)
(8)式(8)为二阶常系数非齐次微分方程,其通解为
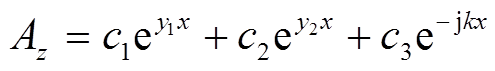 (9)
(9)
从而得到区域Ⅰ的气隙磁场表达式
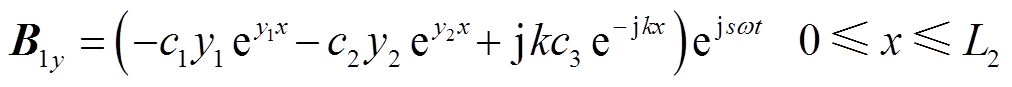 (10)
(10)其中
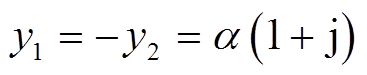
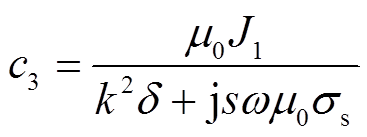
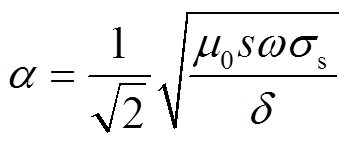
式中,c1、c2。
根据磁通密度的连续性,在x=0、x=L2处的边界条件分别为
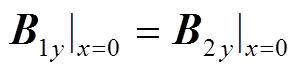 (11)
(11)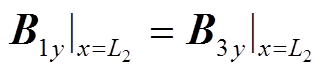 (12)
(12)
利用边界条件式(11)、式(12)可求得式(9)中待定系数C1和C2的表达式,进而得到初、次级耦合区域Ⅰ内的气隙磁场表达式为

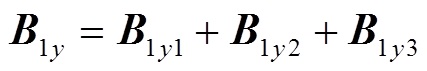 (13)
(13)式中
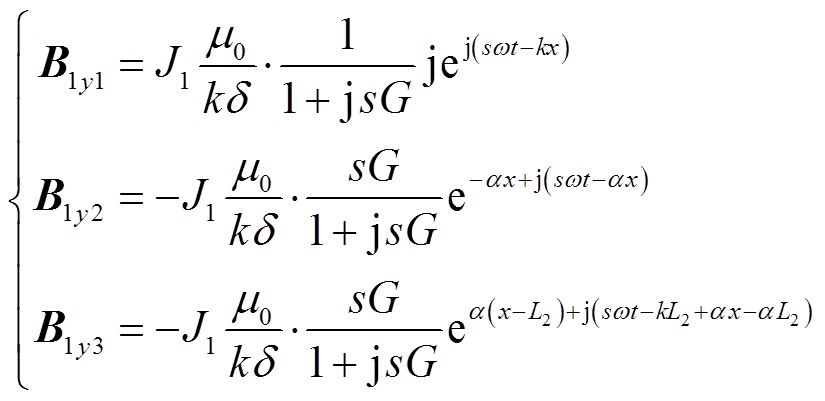 (14)
(14)
式中,G为电机的品质因数,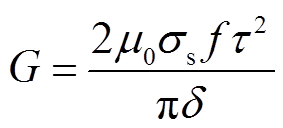 ;f为初级绕组电流频率。
;f为初级绕组电流频率。
非耦合区域Ⅱ、Ⅲ中气隙磁场表达式分别为
 (15)
(15)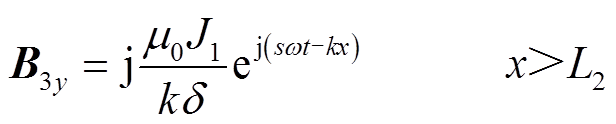 (16)
(16)
将耦合区域气隙磁场表达式(14)变换到实数域,可得
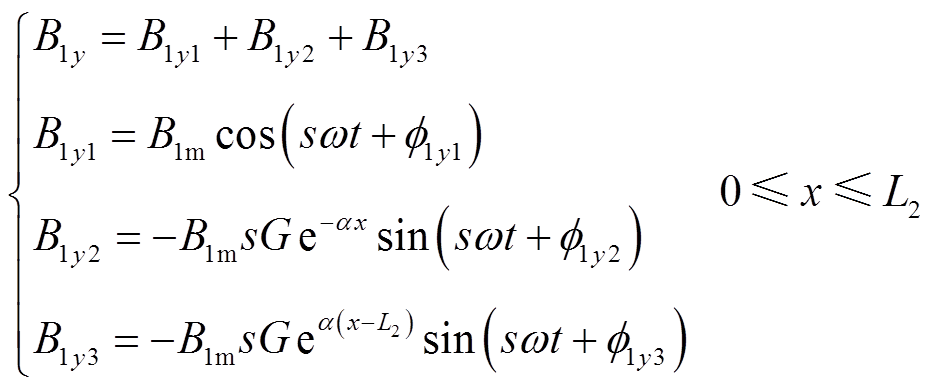 (17)
(17)式中

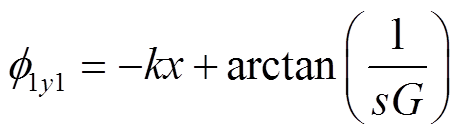
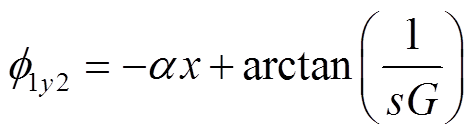
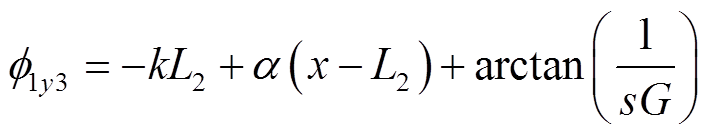
非耦合区域Ⅱ、Ⅲ中气隙磁场在实数域表达式为
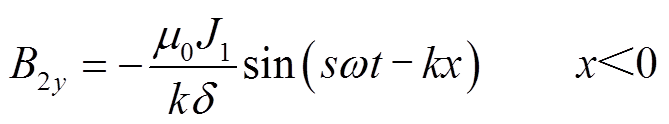 (18)
(18)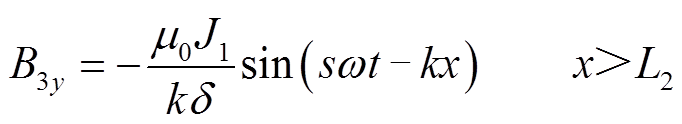 (19)
(19)
令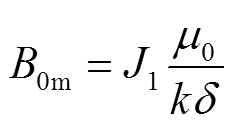 ,则式(18)、式(19)变为B2y= -B0msin(sωt-kx);B3y=-B0msin(sωt-kx)。
,则式(18)、式(19)变为B2y= -B0msin(sωt-kx);B3y=-B0msin(sωt-kx)。
可见,耦合区域Ⅰ中的气隙磁场由三部分组成:等幅值的正常行波磁场(基波磁场)B1y1、幅值正向衰减的前进行波磁场B1y2和幅值反向衰减的后退行波磁场B1y3。耦合区域气隙磁场的前进分量是由入口端部效应引起的,以时间常数1/α沿x轴正方向以指数规律衰减;后退分量是由出口端部效应引起的,以时间常数1/α沿x轴负方向以指数规律衰减,该时间常数由电机的品质因数以及转差率决定。电机空载运行时,气隙磁通密度的前进和后退分量为0,即空载时无纵向端部效应,气隙磁通密度幅值为B0m,此时B1y与j1在相位上正交。电机负载运行时,s>0,气隙磁通密度基波分量幅值B1m<B0m。
非耦合区域Ⅱ、Ⅲ中气隙磁场幅值和相位相同,为等幅的正弦行波磁场,幅值为B0m,与空载气隙磁通密度幅值相等。与文献[20]相比,以次级为运动参考坐标求解的气隙磁通密度表达式更简洁。
采用恒流驱动的以次级为运动参考坐标系的长初级双边直线感应电机,其平均电磁推力Fem可通过对初级电流层密度j1的共轭与耦合区域气隙磁通密度B1y乘积的积分得到
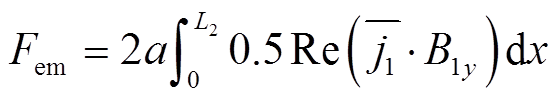 (20)
(20)式中,2a为初级铁心宽度;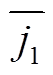 为j1的共轭复数。
为j1的共轭复数。
根据式(17)可知,耦合区域气隙磁通密度由三部分组成,因此,其电磁推力也由三部分组成,分别为正常行波磁场、前进行波磁场、后退行波磁场产生的电磁推力,将式(3)和式(17)代入式(20)可得
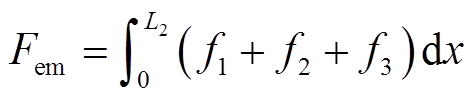 (21)
(21)式中
 (22)
(22)
式中,f1、f2、f3分别为B1y1产生的基波推力密度、B1y2产生的前进行波推力密度和B1y3产生的后退行波推力密度。式(22)反映了推力密度在次级板纵向的分布特点:基波推力密度为常数,与电机参数以及转差率有关,沿次级板纵向均匀分布;前进和后退行波推力密度分别是沿x轴正方向和负方向衰减的正弦函数,主要分布在次级板入口端和出口端。前进和后退行波推力密度均可用基波推力密度表示,式(21)推力表达式可写成
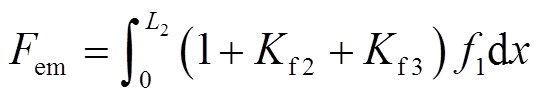 (23)
(23)式中,(1+Kf2+Kf3)f1为总的推力密度,Kf2f1和Kf3f1分别为用基波推力密度表示的前进和后退行波推力密度。因此,纵向端部效应产生的推力密度可用系数Kf2和Kf3修正基波推力密度得到。
在基本行波磁场基础上考虑纵向端部效应前进行波磁场和后退行波磁场所产生的总电磁推力为
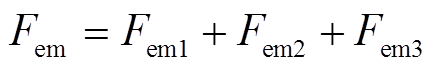 (24)
(24)由式(17)、式(20)可得,基本行波磁场产生的电磁推力Fem1为
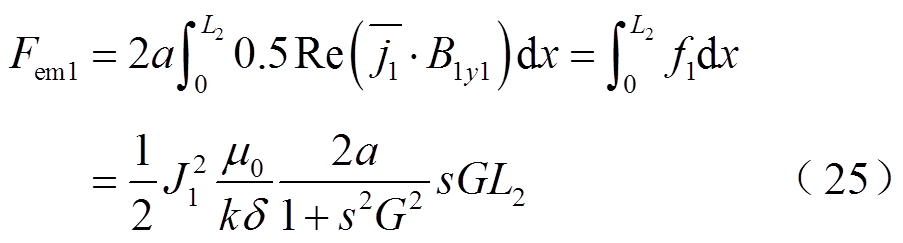
前进行波磁场产生电磁推力Fem2为

后退行波磁场产生的电磁推力Fem3为
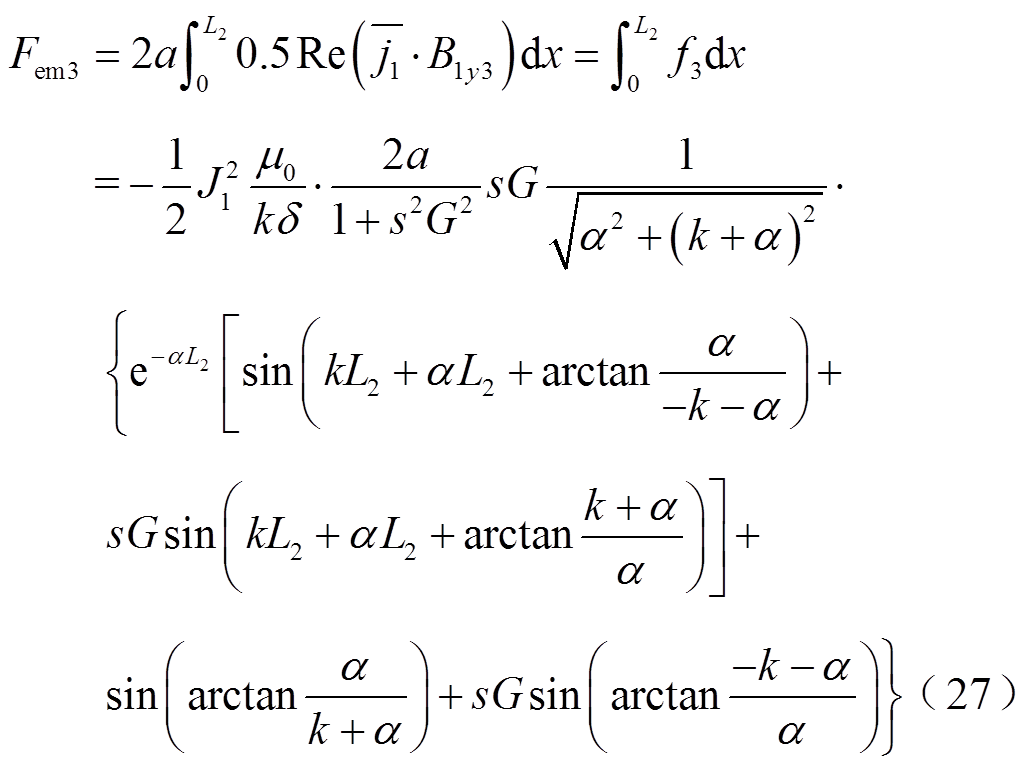
基波推力Fem1为常量,与次级板的长度成正比,通过对Fem1求导,可得基波推力最大时转差率为s=1/G。转差率s≠0时,前进行波平均推力Fem2和后退行波平均推力Fem3值不为0,表明纵向端部效应产生一定的电磁推力增加或减小了基波推力。
前进行波平均推力Fem2和后退行波平均推力Fem3均由两部分组成:一部分为不包含衰减系数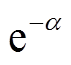 的稳态分量Fem21、Fem31;另一部分为包含气隙磁场衰减系数
的稳态分量Fem21、Fem31;另一部分为包含气隙磁场衰减系数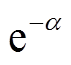 的衰减分量Fem22、Fem32,在DLIM中该项数值通常较小,可以忽略。由式(26)、式(27)可知,上述推力分量表达式均包含两项,因此,由前进行波和后退行波产生的平均电磁推力可以写成
的衰减分量Fem22、Fem32,在DLIM中该项数值通常较小,可以忽略。由式(26)、式(27)可知,上述推力分量表达式均包含两项,因此,由前进行波和后退行波产生的平均电磁推力可以写成
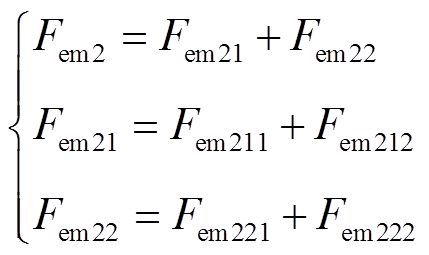 (28)
(28)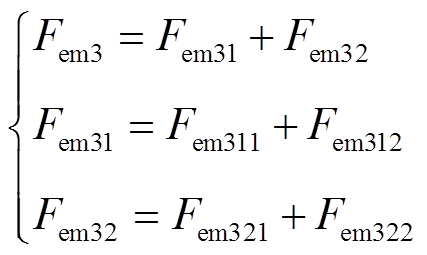 (29)
(29)
端部效应产生的不包含衰减系数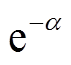 的推力稳态分量Fem211、Fem212、Fem311和 Fem312用基波推力Fem1表示为
的推力稳态分量Fem211、Fem212、Fem311和 Fem312用基波推力Fem1表示为
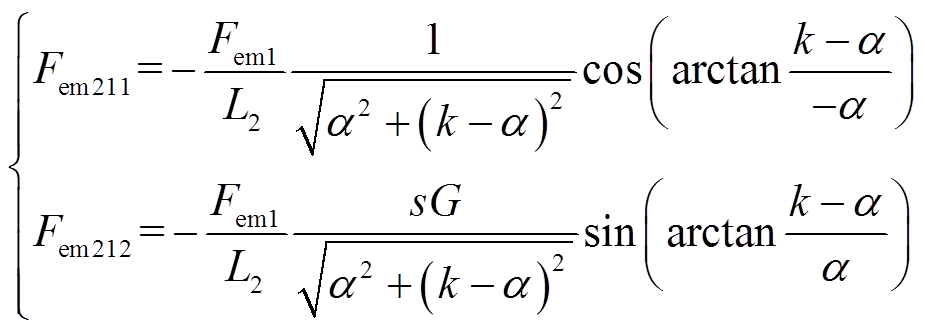 (30)
(30)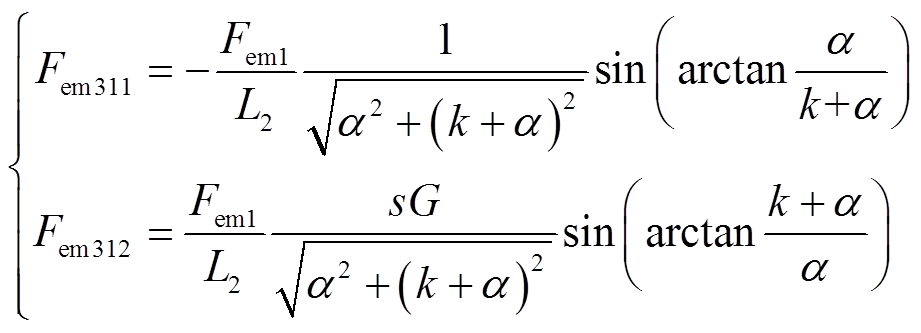 (31)
(31)
由式(30)和式(31)可知,Fem211、Fem311恒为负值,与基波推力方向相反。为减弱基波推力的制动力,Fem212数值与k-α有关,当α<k时,Fe212为与基波推力方向相反的制动力,可减小基波推力;而Fem312恒大于0,增强了基波推力。与文献[21]相比,本文的推力表达式得到简化。
本文以一台长初级双边直线感应电机为例分析计算其电磁性能,电机参数见表1。定子采用单层同心式绕组,端部无半填充槽,避免了采用双层叠绕组出现端部半填充槽引起的气隙磁场脉振,降低了电机的推力波动。此外,单层同心式绕组便于将每对极做成一个模块,也便于安装和故障时替换,且同一槽内导线为同一相,避免了槽内相间击穿。
表1 长初级双边直线感应电机参数
Tab.1 The parameters of long primary DLIM

参数数值 单段初级长度L1/m1.704 极对数p4 每极每相槽数q13 初级宽度2a/mm230 极距τ/m0.213 槽宽bs/mm12 齿距t1/mm23.67 定子槽数Q72 绕组节距y19 并联支路数a12 每相串联线圈匝数N136 次级板长L2/m1.704 次级板厚2d/mm8 次级板宽2c/mm500 次级电导率σ2/(S/m)38×106 机械气隙g/mm10
根据式(17)可得,转差率s为0.02,电源频率f为47.66Hz时,耦合区域Ⅰ气隙磁通密度基波分量B1y1随时间和空间的分布如图3所示。气隙磁通密度的基波分量是位置和时间的正弦函数,其在空间、时间上均按正弦规律分布,其幅值为B1m。
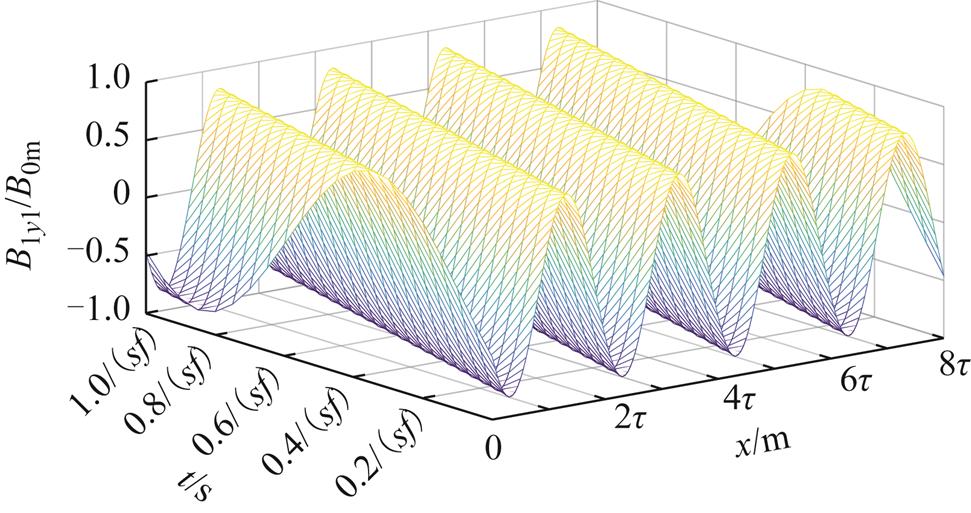
图3 气隙磁通密度基波分量
Fig.3 Fundamental component of air-gap flux density
当电机的参数和电流确定后,基波气隙磁通密度幅值大小仅与电机的转差率s(速度v)有关,负载气隙磁通密度幅值B1m小于空载气隙磁通密度幅值B0m,且随着转差率s增大,气隙磁通密度基波分量幅值呈现衰减趋势;其相位与转差率s及位置x等有关。
转差率s=0.02时,耦合区域Ⅰ气隙磁通密度前进分量和后退分量随时间和空间的分布如图4和图5所示,二者关于次级板纵向(x轴方向)中心对称分布。耦合区域内气隙磁通密度的前进分量是时间的正弦函数、幅值是位置的正向衰减函数;后退分量是时间的正弦函数、幅值是位置的反向衰减函数;气隙磁通密度前进分量在x=0处、后退分量在x=L2处有相同的最大幅值,在电机参数和电流层密度确定后,两处的幅值大小仅与转差率相关。
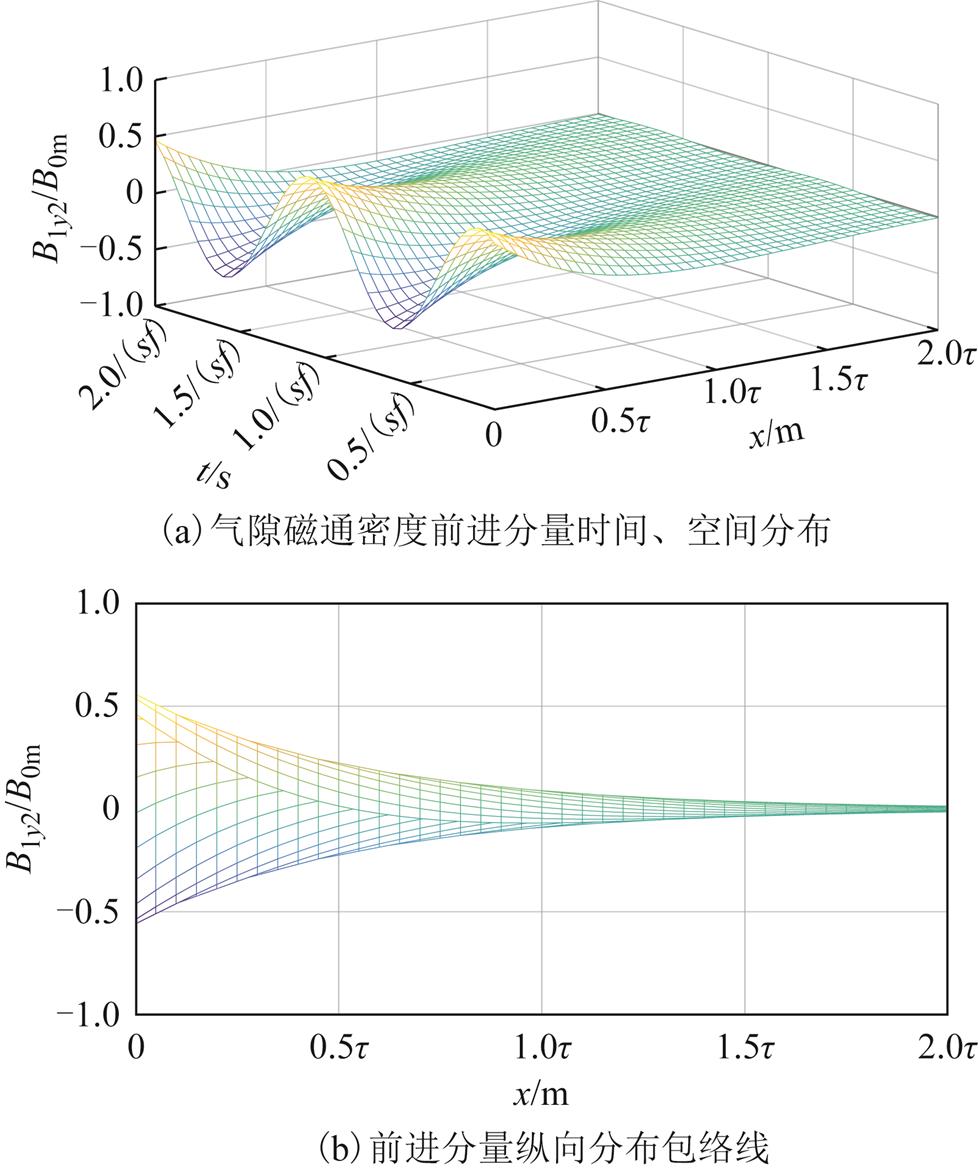
图4 气隙磁通密度前进分量(s=0.02)
Fig.4 Forward component of air-gap flux density
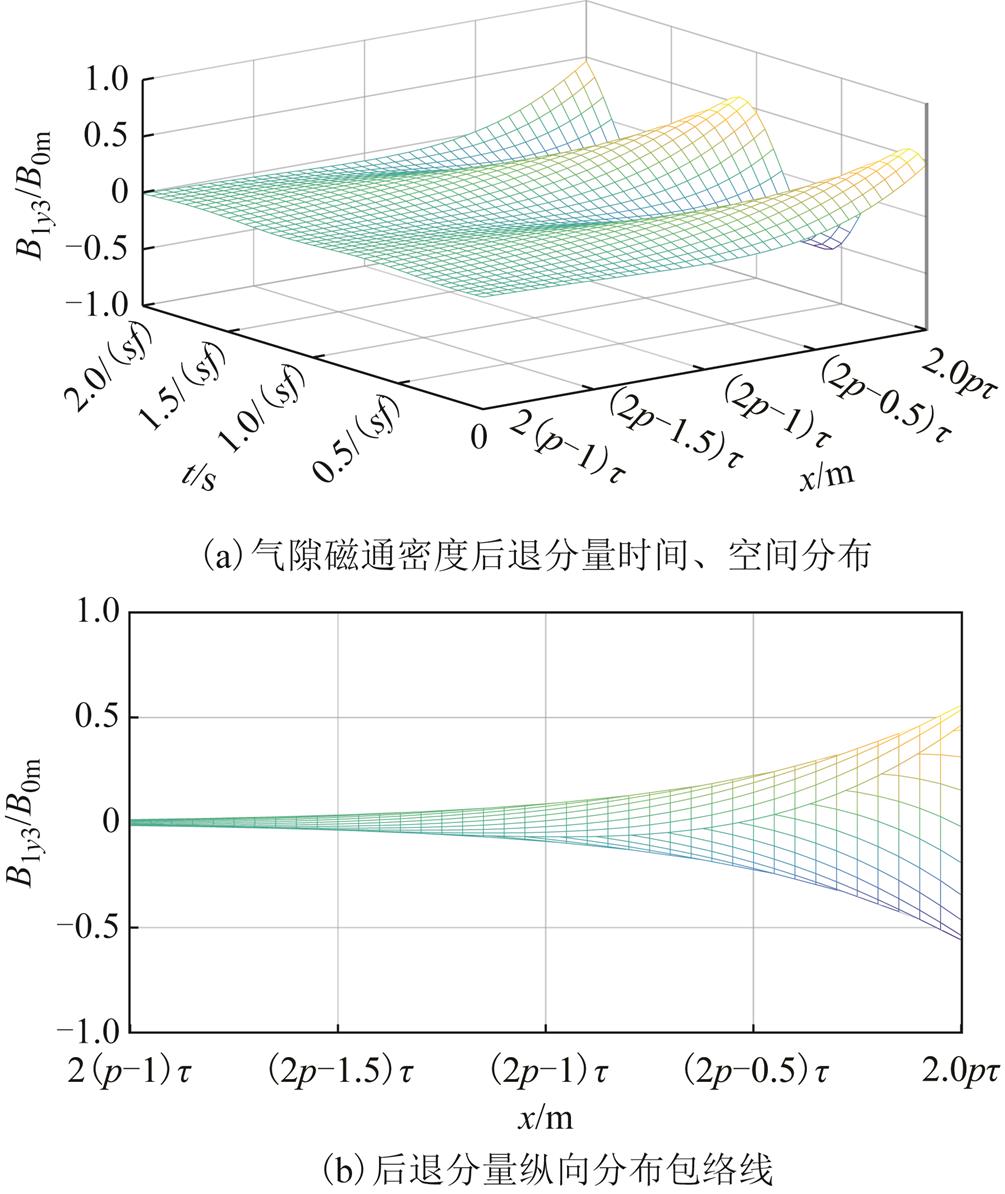
图5 气隙磁通密度后退分量(s=0.02)
Fig.5 Backward component of air-gap flux density
s=0.02时,气隙磁通密度前进分量和后退分量幅值在次级入端和出端一对极距内衰减至较小值。气隙磁场的前进、后退分量幅值随转差增大而增大,在耦合区域内衰减越快,在s较大(s>0.1)时二者幅值明显高于基波磁场幅值,对次级的出端、入端一对极影响显著,对中间极影响可以忽略,如图6所示,因此在次级长度不变情况下增加极对数能削弱纵向端部效应。
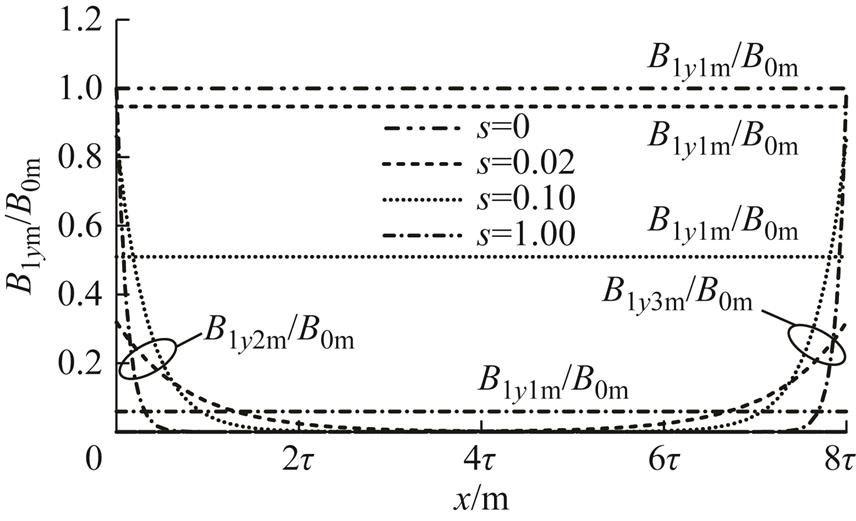
图6 气隙磁通密度各分量幅值
Fig.6 The amplitude of each component of air-gap flux density
与短初级DLIM不同的是,长初级DLIM靠近耦合区域两端的非耦合区域存在激励。s=0.02时,耦合区域Ⅰ考虑气隙磁场前进分量和后退分量的合成气隙磁通密度,以及非耦合区域Ⅱ、Ⅲ的气隙磁通密度分布如图7a和图7b所示。图中0~8τ为次级板与初级耦合区域,该区域内合成气隙磁通密度为时间的正弦函数,空间上由于端部效应的存在,其纵向分布存在畸变,具体表现为耦合区域出端磁场增强、入端磁场减弱,端部效应的影响在出端和入端一对极距范围较为显著。
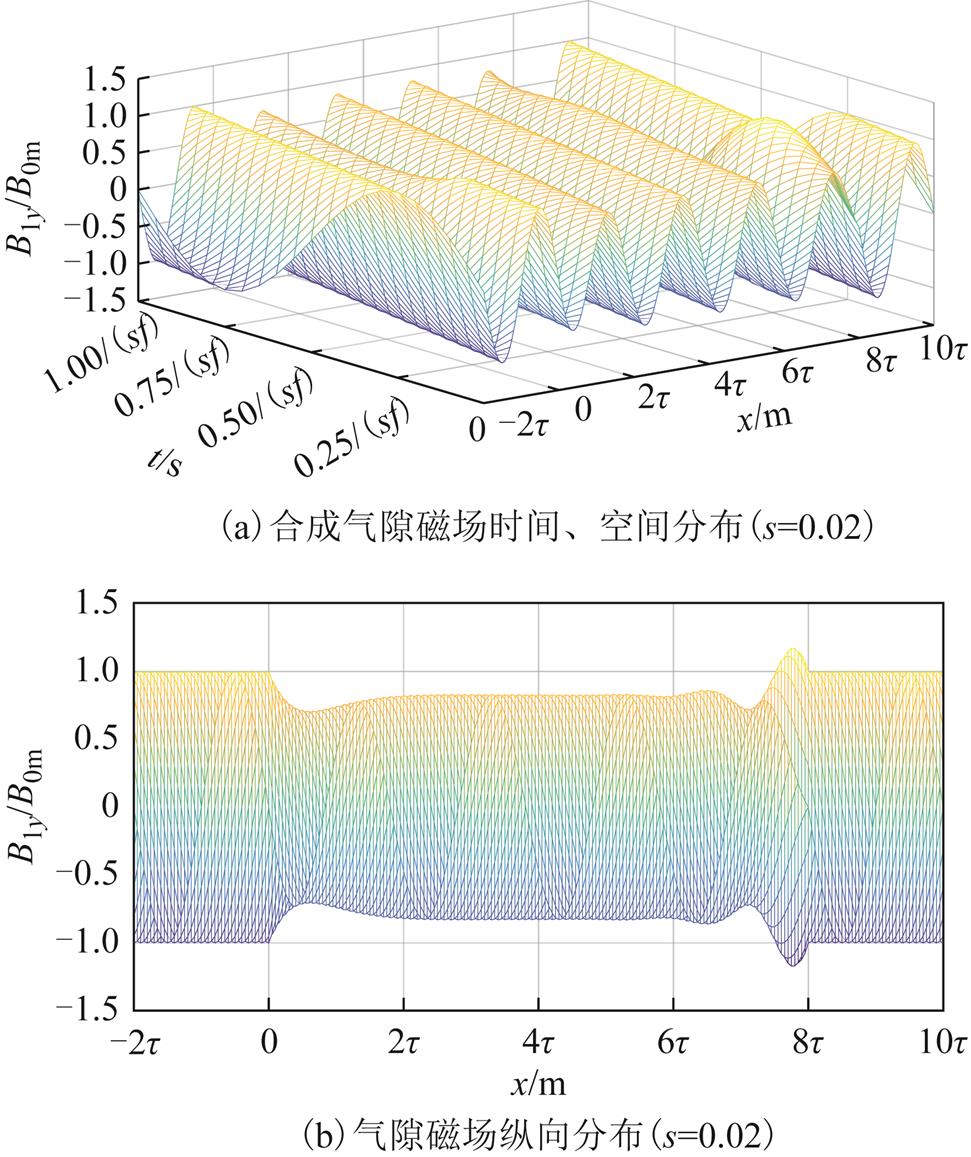
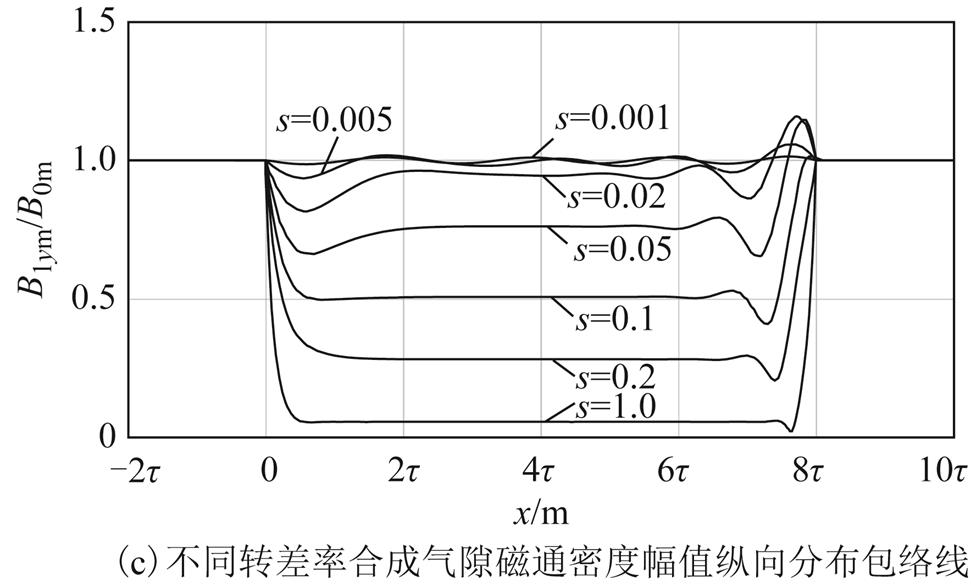
图7 合成气隙磁通密度分布
Fig.7 Air-gap flux density distribution
不同转差率时,合成气隙磁通密度幅值纵向分布如图7c所示。转差率极小时(s<0.05),由于气隙磁场的前进、后退分量衰减时间常数1/α较大,二者在耦合区域内均存在且衰减缓慢,但幅值较小,因而合成气隙磁场幅值波形畸变并不严重。电机速度越高,合成气隙磁通密度幅值越接近空载磁通密度幅值,畸变越小。电机以较小转差率运行时,端部效应使耦合区域的入端磁通密度幅值增大、出端磁通密度幅值减小;转差较大时(s>0.1),端部效应增强了耦合区域入端和出端气隙磁场磁通密度。
非耦合区域(x<-2τ,x>8τ)气隙磁通密度在空间和时间上均是正弦分布,幅值仅与电机参数有关,与转差率s无关。
通过分析可以看出,恒流驱动长初级DLIM气隙磁通密度的分布规律明显与短初级DLIM[26]不同。
推力密度反映了推力在次级板上的分布规律,根据式(22)和式(23)可得考虑气隙磁场前进和后退分量后,频率为47.66Hz,不同转差率,以基波推力密度f1为基准、采用系数表示的推力密度沿次级板前进方向的分布如图8所示。前进和后退行波推力密度分别沿x轴正向和反向正弦衰减,转差率极小(s=0.001)时,由于衰减时间常数较大,衰减较慢,二者分布在整个次级板范围内;随着转差率增大,时间常数减小,二者主要分布在入端和出端一对极距范围内,次级中间位置的推力密度主要由基波推力密度决定。与气隙磁场分布不同,前进与后退行波推力密度纵向分布不再关于次级板x轴方向中心对称分布,转差率较低时(s<0.1),推力密度最大值分布在次级出端。在电机参数确定情况下,前进与后退行波推力密度对基波推力密度增强还是减弱取决于转差率的大小。
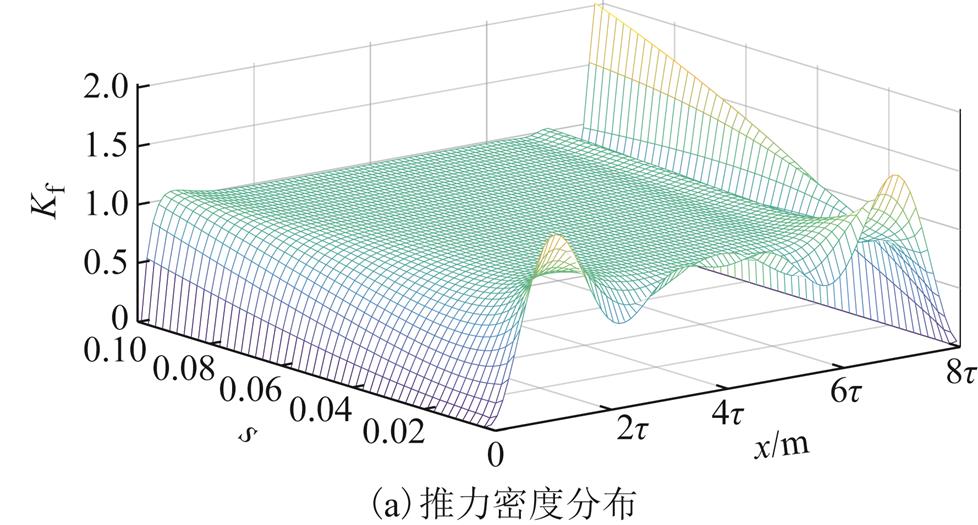
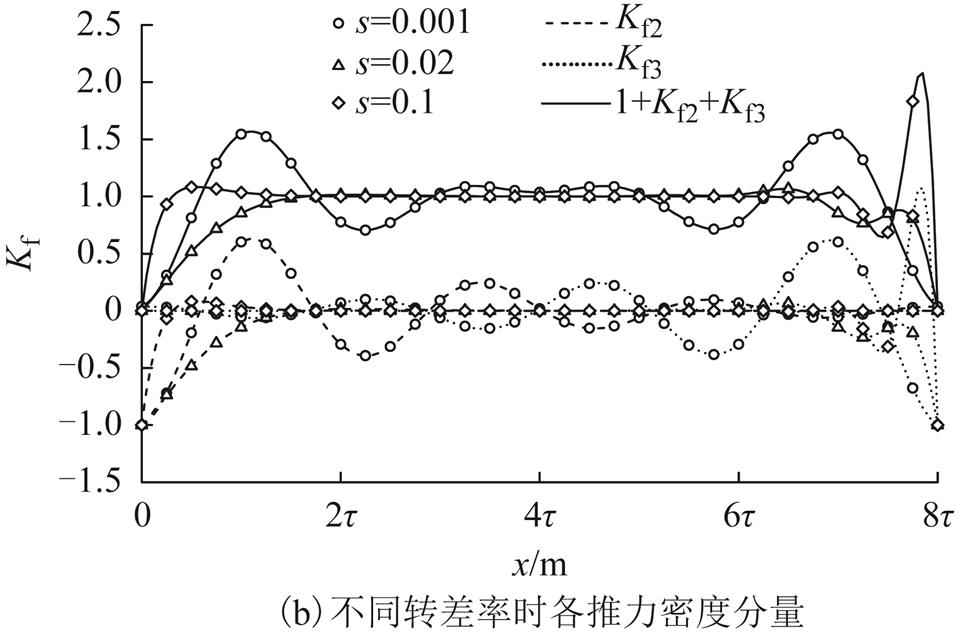
图8 推力密度纵向分布
Fig.8 Longitudinal distribution of thrust density
与推力密度相对应,电机的电磁推力主要包含三部分,分别与气隙磁通密度三个分量相对应。由式(25)可得不考虑端部效应的基波电磁推力在不同频率时随速度变化的曲线,如图9所示。电机以恒流驱动时,长初级DLIM的推力特性与旋转感应电机转矩特性类似,不同电源频率,最大电磁推力相等,均为6.4kN。
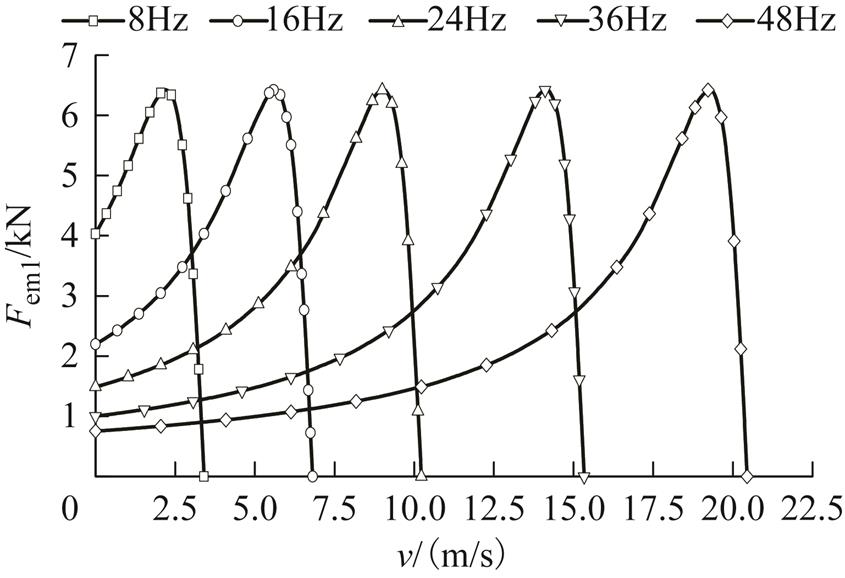
图9 基波电磁推力
Fig.9 Electromagneticthrust with end effects neglected
由式(26)~式(31)得,不同频率下端部效应产生的各电磁推力分量随速度变化波形如图10所示。气隙磁场前进分量产生的电磁推力中不包含衰减系数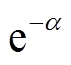 的稳态分量Fem21及其组成Fem211、Fem212,如图10a所示。Fem211数值恒为负值,表现为阻碍次级运动的制动力,Fem211随着次级速度增加先不断减小后不断增加,在低速时Fem211数值较小,在速度较高时随速度增加Fem211数值基本线性减小,阻碍次级运动的制动力逐渐减弱;Fem212在转差率s>2/G时为正值,对基波电磁推力起增强作用,转差率s<2/G时,该部分推力数值为负值,其数值比Fem211小;Fem21在
的稳态分量Fem21及其组成Fem211、Fem212,如图10a所示。Fem211数值恒为负值,表现为阻碍次级运动的制动力,Fem211随着次级速度增加先不断减小后不断增加,在低速时Fem211数值较小,在速度较高时随速度增加Fem211数值基本线性减小,阻碍次级运动的制动力逐渐减弱;Fem212在转差率s>2/G时为正值,对基波电磁推力起增强作用,转差率s<2/G时,该部分推力数值为负值,其数值比Fem211小;Fem21在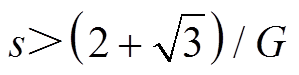 时为正值,增强基波电磁推力,在
时为正值,增强基波电磁推力,在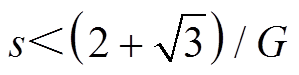 时,该部分推力减弱基波电磁推力。
时,该部分推力减弱基波电磁推力。
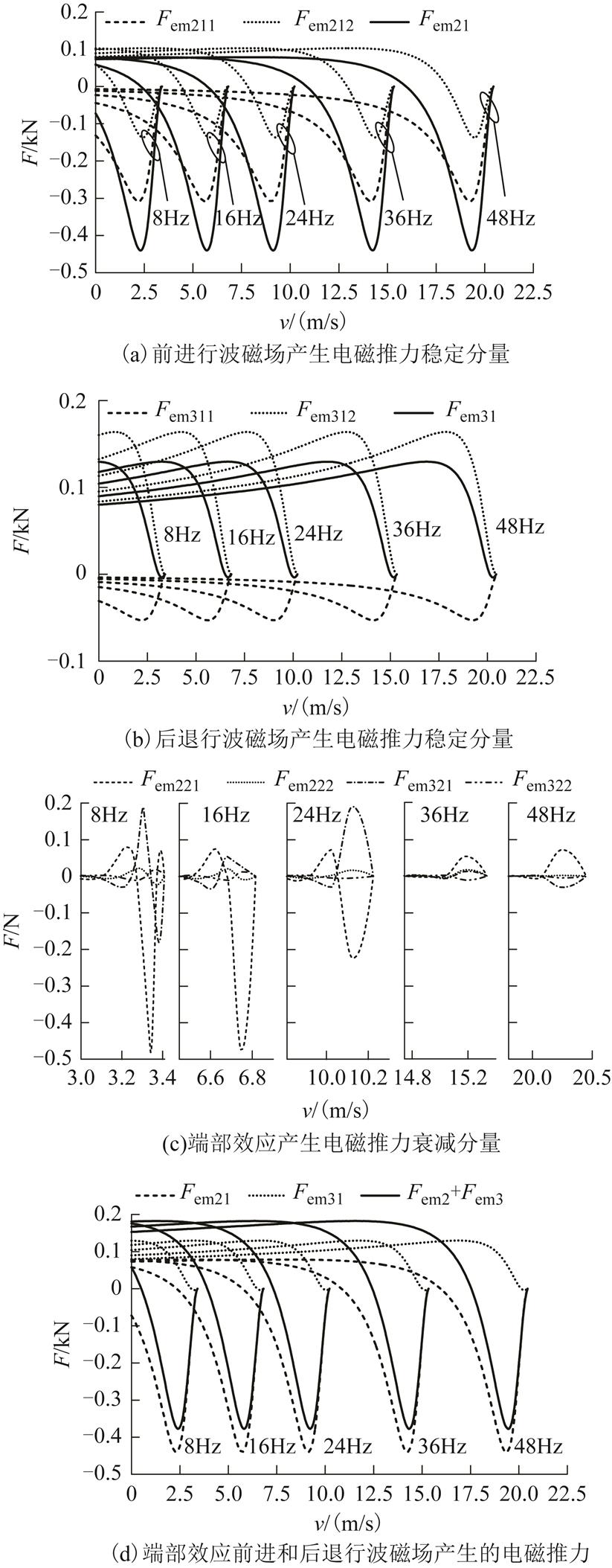
图10 端部效应前进和后退行波磁场产生的电磁推力
Fig.10 Electromagnetic thrust produced by forward and backward traveling waves of end effects
与Fem21类似,气隙磁场后退分量产生的电磁推力中不包含衰减系数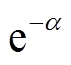 的稳态分量Fem31及其组成Fem311、Fem312,如图10b所示。Fem311数值恒为负值,其数值相对较小,为阻碍次级运动的制动力;Fem312数值恒为正值,其数值随速度先增大后减小,对基波电磁推力起增强作用;Fem31在较宽的速度范围内增强基波电磁推力,仅在接近同步时为负值,数值极小,对总的电磁推力贡献较小。
的稳态分量Fem31及其组成Fem311、Fem312,如图10b所示。Fem311数值恒为负值,其数值相对较小,为阻碍次级运动的制动力;Fem312数值恒为正值,其数值随速度先增大后减小,对基波电磁推力起增强作用;Fem31在较宽的速度范围内增强基波电磁推力,仅在接近同步时为负值,数值极小,对总的电磁推力贡献较小。
气隙磁场前进、后退分量产生的电磁推力中包含衰减系数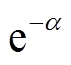 的衰减分量Fem22(包含Fem221和Fem222)、Fem32(包含Fem321和Fem322)在不同频率下随速度变化曲线如图10c所示,这四个分量随转差率s增加迅速衰减,其数值小于1N,在计算电磁推力时可以将其忽略不计。
的衰减分量Fem22(包含Fem221和Fem222)、Fem32(包含Fem321和Fem322)在不同频率下随速度变化曲线如图10c所示,这四个分量随转差率s增加迅速衰减,其数值小于1N,在计算电磁推力时可以将其忽略不计。
气隙磁场前进、后退分量产生的电磁推力Fem2、Fem3以及二者的合力,即纵向端部效应产生的推力如图10d所示。电机以较低频率(8Hz)起动时,Fem21主要是阻碍次级运动的制动力,Fem31主要增加基波电磁推力。由于Fem31的数值比Fem21小,总的端部效应产生的电磁推力在低频时表现为减小基波电磁推力的制动力。频率较高时,低速工况下,Fem21和Fem31共同作用增加电磁推力,高速工况下,Fem31抵消了Fem21部分制动力,端部效应产生电磁推力总体仍为阻碍次级运动的制动力。电机运行在同步速时,端部效应产生推力的大小为0。
对于以极小转差率运行的长初级DLIM,后退分量产生的电磁推力Fem3相对前进行波推力Fem2值小,采用数值计算额定推力时可以忽略。若计算电机在整个速度范围内的推力特性,或者电机额定转差率较大时,此项不应忽略。
考虑端部效应之后长初级DLIM总的电磁推力Fem特性如图11所示。端部效应减弱了基本行波推力的最大值;在电机的稳定工作区,端部效应减弱了基波推力Fem1,随着速度增加,端部效应减弱,对基波推力Fem1影响减弱,推力波动也将降低。电机以较高频率起动时,端部效应的存在增大了电机起动推力。
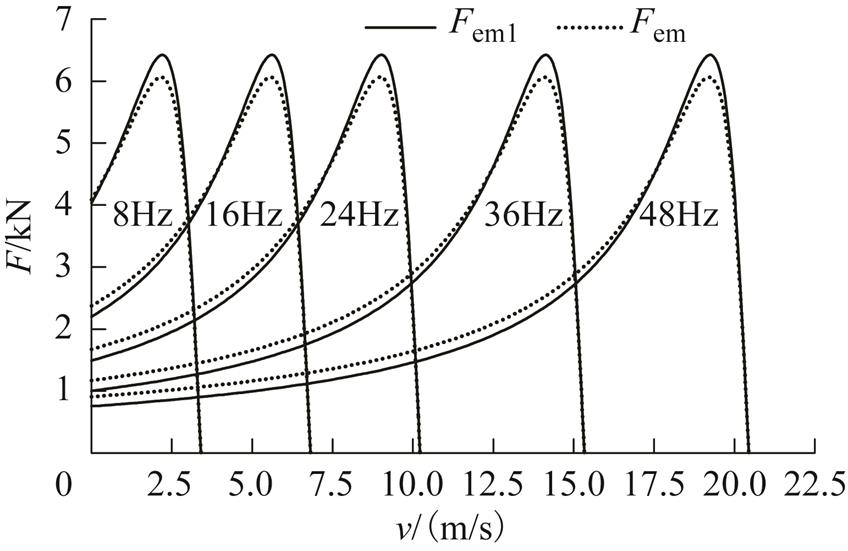
图11 总电磁推力
Fig.11 Resultant electromagnetic thrust
采用有限元(Finite Element Mothod, FEM)仿真软件Ansys建立了设计电机的二维瞬态场模型,计算了电机气隙磁场分布以及电磁推力特性曲线。电机的有限元模型如图12所示,对电机的两端施加主从边界,仿真模型中参数与表1相同。

图12 长初级双边直线电机有限元模型
Fig.12 FEM model of long primary DLIM
采用有限元(FEM)计算了以47.66Hz、900A恒流驱动的电机在不同转差率时的气隙磁场分布,并与解析表达式(17)~式(19)计算的结果进行了比较,计算结果如图13所示。有限元和解析方法计算的气隙磁通密度在纵向上分布一致,由于有限元计算考虑了电机定子齿槽效应,其气隙磁通密度分布包含了齿谐波分量;解析计算采用气隙系数考虑齿槽对磁通密度分布的影响,因此无齿谐波分量。随着转差率增大,初级、次级耦合区域(0≤x≤8τ)磁通密度幅值逐渐减小,非耦合区域(x<0,x>8τ)磁通密度幅值与转差率无关。
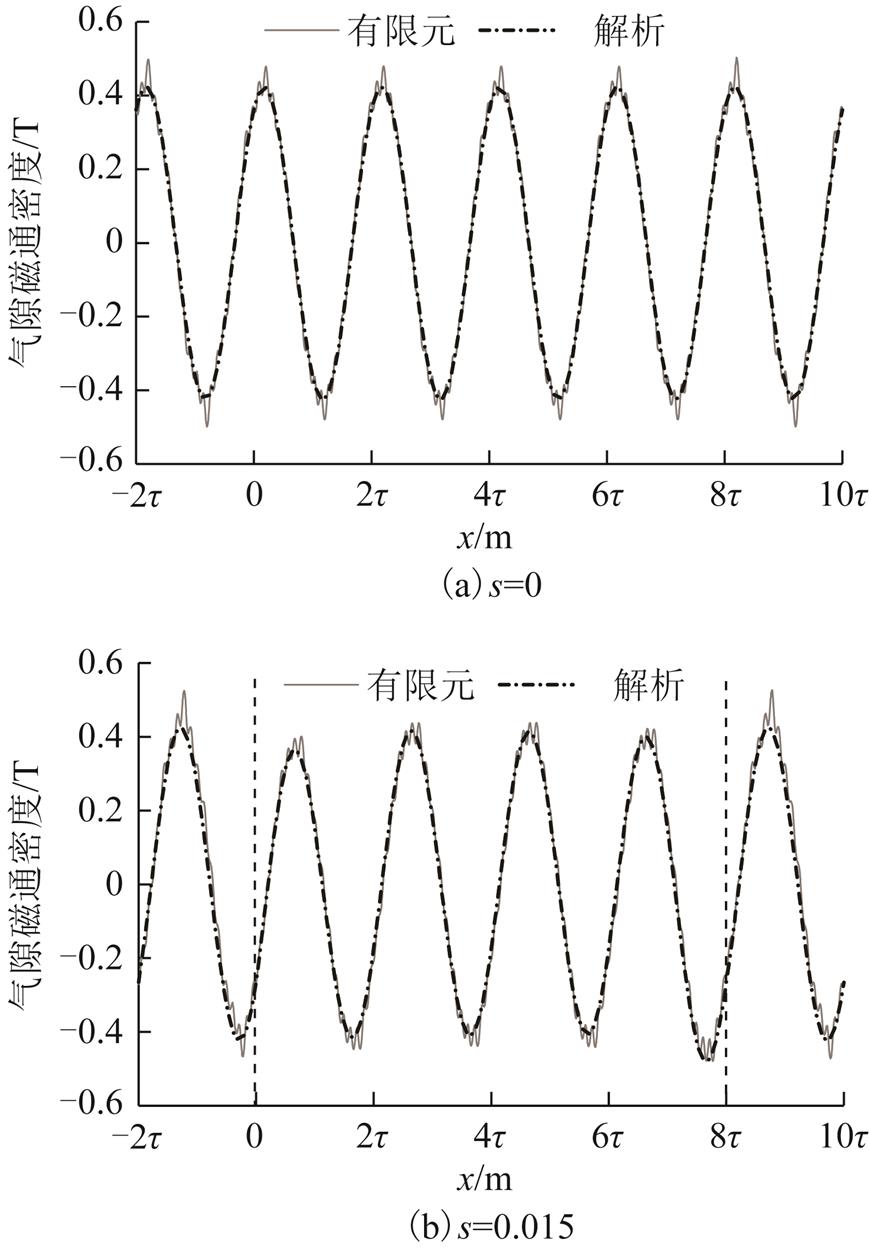
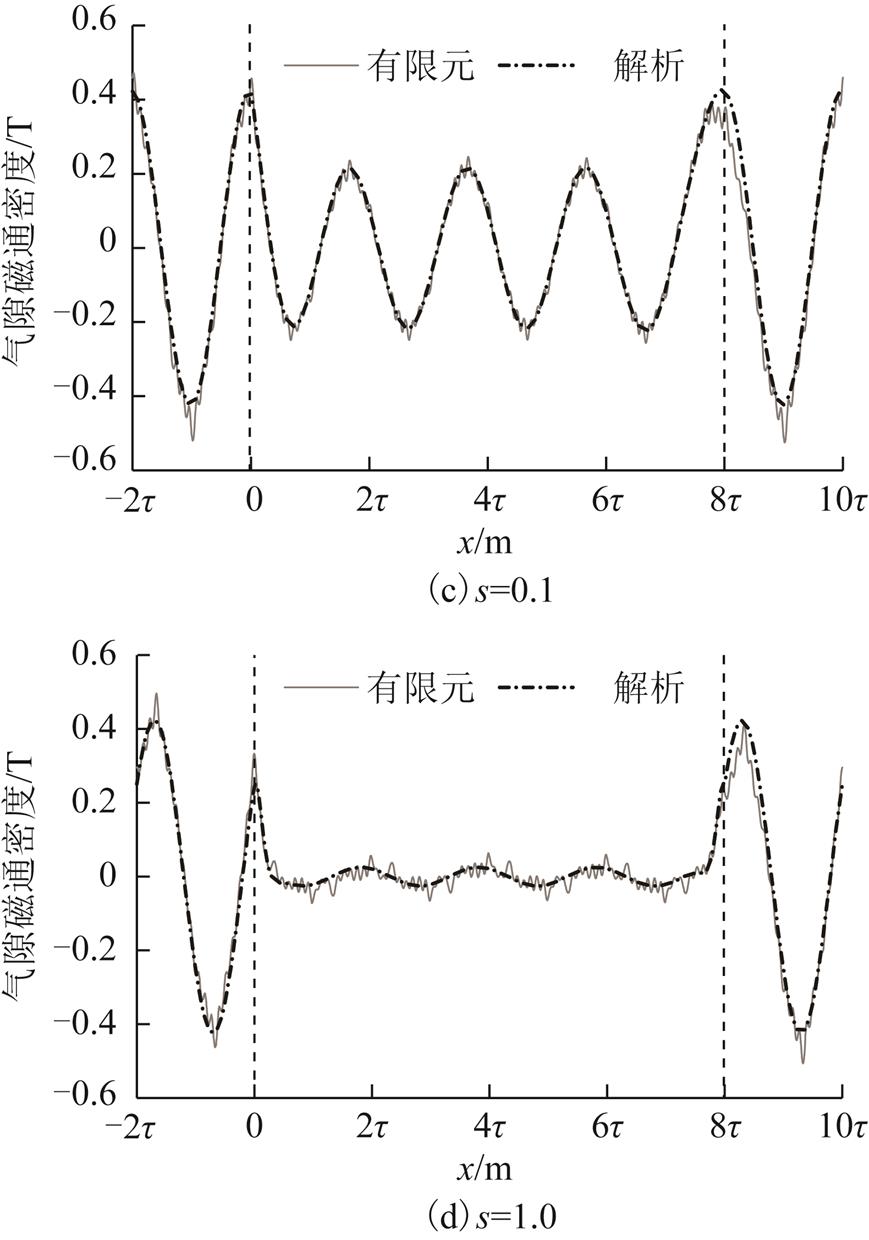
图13 有限元和解析计算不同转差率时的气隙磁密分布
Fig.13 Air-gap flux density distribution at different slip calculated by FEM and analytical
对有限元计算的空载气隙磁通密度进行傅里叶分解,结果如图14所示。气隙磁场的主要高次谐波(17次)为一阶齿谐波,有限元计算的基波分量为0.4346T,解析计算的空载气隙磁通密度幅值为0.4232T,解析计算与有限元计算结果能较好地吻合。
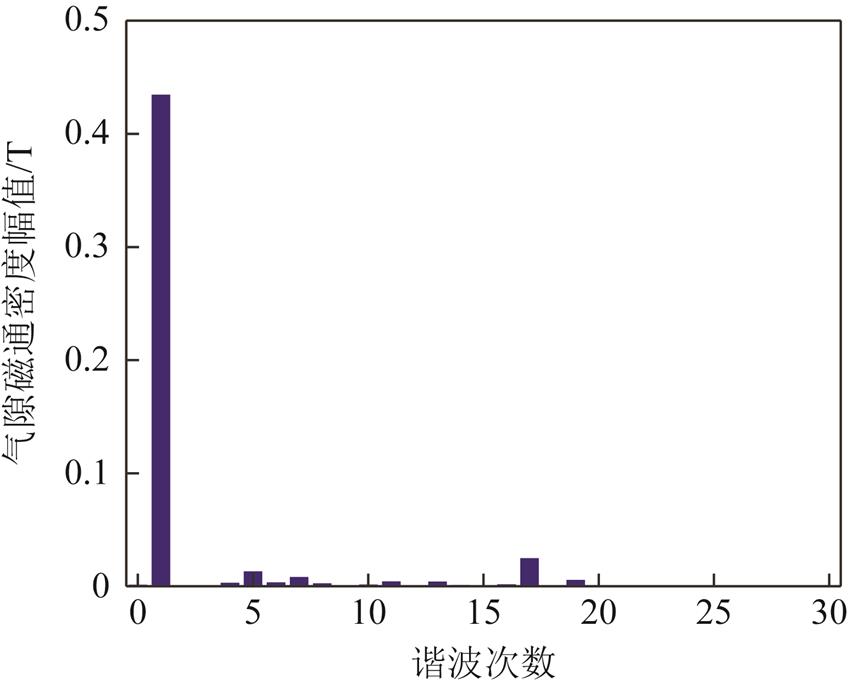
图14 空载气隙磁通密度谐波含量
Fig.14 Harmonics of air-gap flux density
不同电源频率、电流为900A时,采用解析计算不考虑端部效应和考虑端部效应,包括气隙磁场前进、后退分量之后的电磁推力与有限元计算的结果如图15所示,由图15可知,解析法与有限元法计算结果吻合。由于忽略了磁动势的高次谐波对推力的影响,以及采用等效气隙系数来考虑齿槽效应,因此解析计算的推力值与有限元仿真计算结果存在一定的误差。
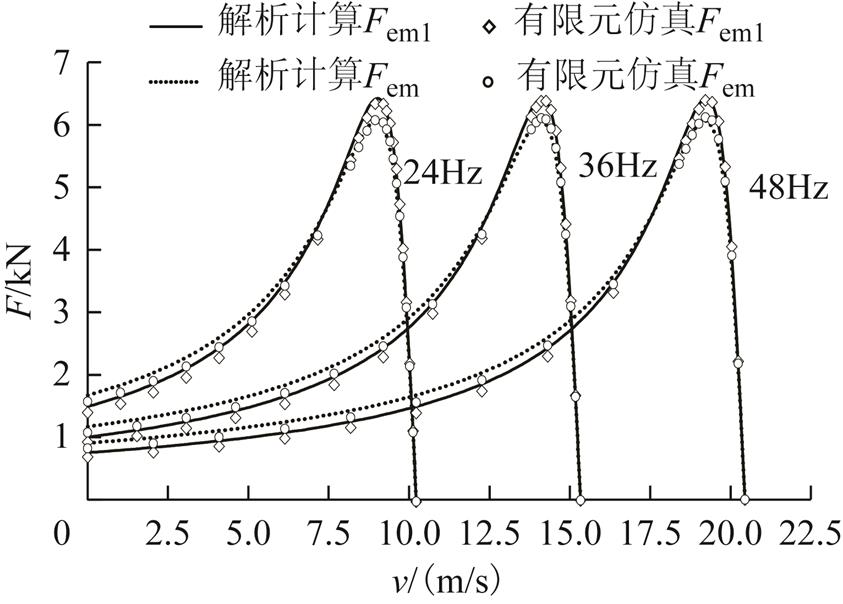
图15 解析计算电磁推力有限元验证
Fig.15 Verification of analytical Electromagnetic thrust by FEM
采用解析法和有限元法计算的不同频率时由气隙磁场前进分量和后退分量产生的电磁力-速度曲线如图16所示。两种方法计算的端部效应产生的推力随速度变化趋势一致,均体现出纵向端部效应在电机起动时增加了起动推力,电机稳定运行时表现为阻碍次级运动的制动力。有限元计算结果证实了解析法求解的电磁推力表达式的准确性。
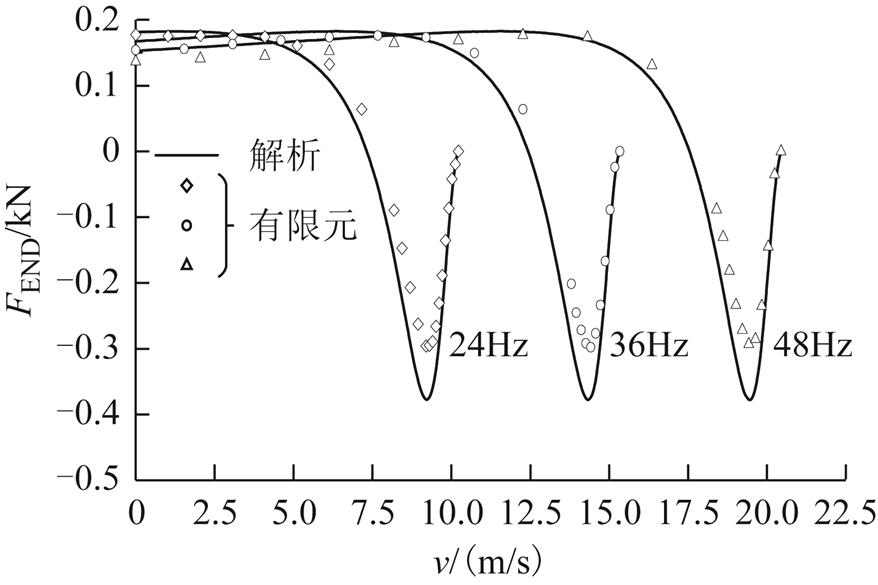
图16 端部效应产生的电磁推力验证
Fig.16 Verification of electromagnetic force by end effects
本文根据一维电磁场理论建立了以次级板为运动参考坐标系的长初级DLIM解析模型,推导了气隙磁通密度在实数域的解析表达式,以及考虑端部效应前进和后退行波磁场的推力密度和推力的解析表达式。并利用有限元计算的气隙磁场分布和电磁推力,验证了解析计算方法所求解的气隙磁场以及电磁推力表达式的准确性,得出如下结论:
1)考虑后退行波磁场所求解的气隙磁场分布、推力特性与实际更吻合。后退和前进行波磁场在空间上关于次级板运动方向中心对称分布,对次级入端和出端一对极距范围内磁场分布影响最显著,是时间的正弦函数;二者幅值以相同的时间常数按照相反的方向衰减,衰减时间常数与电机参数和转差率有关;合成气隙磁场分布由电机品质因数和转差率决定,在低转差率时,耦合区域合成气隙磁场表现为出端增强、入端减弱。
2)前进和后退行波磁场使推力密度最大值分布在次级的两端,低转差率时主要分布在次级的出端。
3)前进行波磁场产生的电磁推力低速时增加基波电磁推力,在接近同步速时为阻碍次级加速的制动力;后退行波磁场产生电磁推力总体表现为增加基波电磁推力,在接近同步速时为较小负值。
4)端部效应前进和后退行波磁场产生的电磁力,在接近同步速时为减小基本电磁推力的制动力,在起动时增加起动推力。
参考文献
[1] 秦伟, 范瑜, 徐洪泽, 等. 高温超导运动磁场电磁Halbach初级结构直线感应磁悬浮电机[J]. 电工技术学报, 2018, 33(23): 5427-5433. Qin Wei, Fan Yu, Xu Hongze, et al. A linear induction maglev motor with HTS traveling magnetic electromagnetic Halbach array[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5427-5433.
[2] Boldea I. Linear electric machine, drives, and MAGLEVs handbook[M]. London, UK: CRC Press, 2013.
[3] Zou Janqiao, Xu Wei, Yu Xinghuo, et al. Multistep model predictive control with current and voltage constraints for linear induction machine based urban transportation[J]. IEEE Transactions on Vehicular Technology, 2017, 66(12): 10817-10829.
[4] Abdollahi S E, Mirzayee M, Mirsalim M. Design and analysis of a double-sided linear induction motor for transportation[J]. IEEE Transactions on Magnetics, 2015, 51(7): 1-7.
[5] Meeker D C, Newman M J. Indirect vector control of a redundant linear induction motor for aircraft launch[J]. Proceedings of the IEEE, 2009, 97(11): 1768-1776.
[6] Xu Jin, Yang Xidang, Ma Weiming, et al. Nonlinear calculation methods of long primary double-sided linear induction motor[C]//IEEE International Conference on Electrical Machines & Systems, Hangzhou, 2014: 1774-1778.
[7] 徐兴华, 马伟明, 崔小鹏, 等. 分段供电直线电机切换开关的关断故障在线诊断方法[J]. 电机与控制学报, 2018, 22(12): 1-10. Xu Xinghua, Ma Weiming, Cui Xiaopeng, et al. Online diagnosis method of turnoff faults in the switch of sectionalized power-supply linear induction motor[J]. Electric Machines & Control, 2018, 22(12): 1-10.
[8] 腾腾, 赵治华, 马伟明. 基于数据驱动的分段供电直线电机故障诊断研究[J]. 电机与控制学报, 2019, 23(1): 1-8. Teng Teng, Zhao Zhihua, Ma Weiming. Data driven fault diagnosis for segment-powered linear induction motor[J]. Electric Machines & Control, 2019, 23(1): 1-8.
[9] 宫金林, 王秀和. 基于多目标有效全局优化算法的直线感应电动机优化设计[J]. 电工技术学报, 2015, 30(24): 32-37. Gong Jinlin, Wang Xiuhe. Optimal design of a linear induction motor using multi-objective efficient global optimization[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 32-37.
[10] 邸珺, 范瑜, 刘亚静. 基于等效次级的直线感应电机的电磁分析与参数辨识[J]. 电工技术学报, 2017, 32(11): 145-154. Di Jun, Fan Yu, Liu Yajing. Electromagnetic analysis and parameter estimation for the linear induction motor based on equivalent secondary[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 145-154.
[11] 张育兴, 马名中, 马伟明, 等. 双定子直线感应电机饱和特性分析[J]. 中国电机工程学报, 2012, 32(36): 102-108. Zhang Yuxing, Ma Mingzhong, Ma Weiming, et al. Analysis of saturation characteristics of double-stator linear induction motors[J]. Proceedings of the CSEE, 2012, 32(36): 102-108.
[12] 孙兆龙, 刘德志, 马伟明, 等. 计及铁心饱和直线感应电动机模型及参数研究[J]. 中国电机工程学报, 2011, 31(33): 144-150. Sun Zhaolong, Liu Dezhi, Ma Weiming, et al. Modeling and parameters of linear induction motors with iron saturation[J]. Proceedings of the CSEE, 2011, 31(33): 144-150.
[13] 许金, 马伟明, 鲁军勇, 等. 长定子直线感应电机饱和特性和非线性计算[J]. 电工技术学报, 2012, 27(9): 183-190. Xu Jin, Ma Weiming, Lu Junyong, et al. Saturation characteristics analysis and nonlinear calculation methods of long-stator linear induction motors[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 183-190.
[14] 饶金, 刘德志, 许金, 等. 长初级短次级十二相直线感应电动机数学模型分析[J]. 海军工程大学学报, 2014, 26(2): 10-14. Rao Jin, Liu Dezhi, Xu Jin, et al. Analysis of mathematical model for long-primary short- secondary twelve-phase linear induction motor[J]. Journal of Naval University of Engineering, 2014, 26(2): 10-14.
[15] 许金, 马伟明, 鲁军勇, 等. 一种四定子双边直线感应电动机数学模型和工作特性[J]. 电工技术学报, 2011, 26(9): 5-12. Xu Jin, Ma Weiming, Lu Junyong. Mathematical Model and performance analysis of a four-stator double-sided linear induction motor[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 5-12.
[16] 许金, 聂世雄, 马伟明, 等. 无槽双边长定子直线感应电动机磁路计算方法[J]. 中国电机工程学报, 2016, 36(10): 2793-2799. Xu Jin, Nie Shixiong, Ma Weiming, et al. Magnetic circuit calculation of slot-less double-sided long primary linear induction motor[J]. Proceedings of the CSEE, 2016, 36(10): 2793-2799.
[17] Yang Tong, Zhou Libing, Li Langru. Influence of design parameters on end effect in long primary double-sided linear induction motor[J]. IEEE Transactions on Plasma Science, 2011, 39(1): 192-197.
[18] Yang Tong, Zhou Libin, Li Langru. Performance calculation for double-sided linear induction motor with short secondary[C]//IEEE International Conference on Electrical Machines & Systems, Wuhan, 2008: 3478-3483.
[19] Lu Junyong, Ma Weiming. Research on end effect of linear induction machine for high-speed industrial transportation[J]. IEEE Transactions on Plasma Science, 2011, 39(1): 116-120.
[20] 杨通, 周理兵. 长初级双边直线感应电机纵向动态端部效应第一部分: 气隙磁场[J]. 电机与控制学报, 2014, 18(4): 52-59. Yang Tong, Zhou Libing. Longitudinal dynamic end effect in long primary double-sided linear induction motor part 1: air gap magnetic field[J]. Electric Machines & Control, 2014, 18(4): 52-59.
[21] 杨通, 周理兵. 长初级双边直线感应电机纵向动态端部效应第二部分: 性能计算[J]. 电机与控制学报, 2014, 18(8): 67-74. Yang Tong, Zhou Libing. Longitudinal dynamic end effect in long primary double-sided linear induction motor part 2: performance calculation [J]. Electric Machines & Control, 2014, 18(8): 67-74.
[22] 聂世雄, 付立军, 许金, 等. 分段供电直线感应电机动子不对称模型及参数计算[J]. 电机与控制学报, 2017, 21(2): 10-17. Nie Shixiong, Fu Lijun, Xu Jin, et al. Asymmetrical model and parameter calculation of segment-powered linear inductive motor mover[J]. Electric Machines & Control, 2017, 21(2): 10-17.
[23] 聂世雄, 马伟明, 李卫超, 等. 对称电流激励长初级直线感应电机推力波动研究[J]. 中国电机工程学报, 2015, 35(21): 5585-5591. Nie Shixiong, Ma Weiming, Li Weichao, et al. Research on thrust ripple of long primary linear induction motors with symmetrical current excited[J]. Proceedings of the CSEE, 2015, 35(21): 5585-5591.
[24] 龙遐令. 直线感应电机的理论和电磁设计方法[M]. 北京: 科学出版社, 2006.
[25] 上海工业大学, 上海电机厂. 直线异步电动机[M]. 北京: 机械工业出版社, 1979.
[26] Gieras J F. Linear induction drives[M]. Oxford, UK: Clarendon Press, 1994.
Calculation of Electromagnetic Performance for Long Primary Double Sided Linear Induction Motors Considering Backward Traveling Wave
Abstract One dimensional electromagnetic theory is applied to establish the analytical model of long primary double sided linear induction machine (DLIM) with secondary as moving reference frame. Firstly, the expression of the air-gap flux density in the real domain is derived by numerical method. The temporal-spatial distribution characteristics of the forward and backward traveling waves caused by the end effect and the influence of these two traveling waves on the normal component of the air-gap flux density are analyzed. And then the expressions of thrust force density and thrust which considering the forward and backward traveling waves are deduced, and the longitudinal distribution characteristics of thrust density on the secondary are investigated. The characteristics of each thrust component with velocity and the effect of end effect on the fundamental thrust are studied. Finally, the air-gap magnetic field distribution and thrust characteristics of the DLIM at different frequencies are calculated based on the FEM model, and the results are compared with those of the analytical method. The accuracy of the analytical method is verified, which contributes to the initial design and subsequent optimization of long primary DLIMs.
keywords:Double sided linear induction machine(DLIM), backward traveling wave, analytic method, electromagnetic performance, end effect
DOI:10.19595/j.cnki.1000-6753.tces.190215
中图分类号:TM359.4; TM153
张 千 男,1986年生,博士研究生,工程师,研究方向为电机及其控制。E-mail:qianzh@bjtu.edu.cn(通信作者)
刘慧娟 女,1967年生,教授,博士生导师,研究方向为新型电机的运行理论及控制。E-mail:hjliu@bjtu.edu.cn
中央高校基本科研业务费专项资金(2018YJS161)和北京交通大学科研项目(E18L00100)资助。
收稿日期2019-03-05
改稿日期 2019-06-06
(编辑 郭丽军)