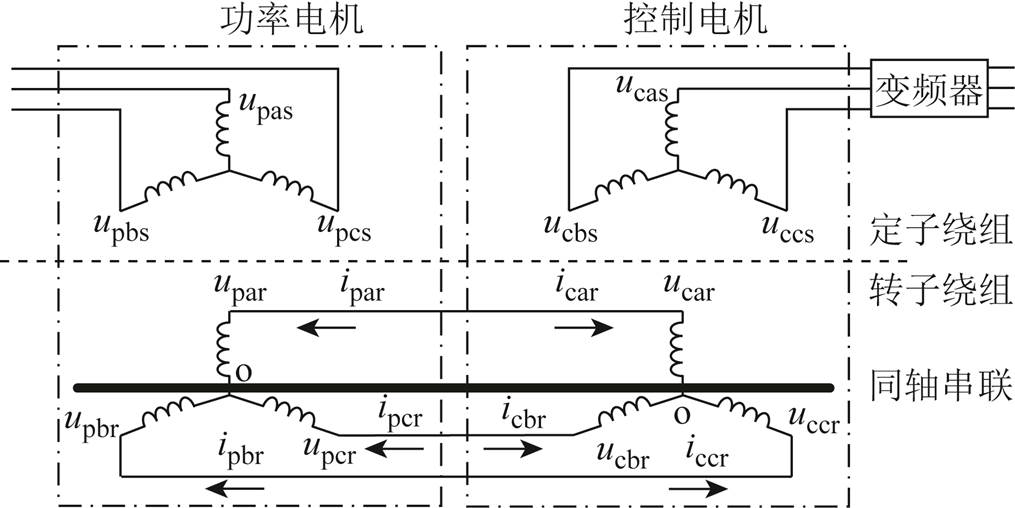
图1 级联绕线转子无刷双馈电机结构
Fig.1 The structure of cascade wound-rotor BDFM
摘要 该文首先给出控制电机电流源供电时无刷双馈电机在转子坐标系下的状态空间模型，经旋转坐标变换得到控制电机同步坐标系下的仿射非线性状态空间模型，分析其静态直流特性。以此为基础应用反馈线性化方法解决无刷双馈电机的解耦控制问题，得到控制电机同步坐标系下的解耦控制方法及其实现的必要条件，给出相关参数的折算方法和测试方法。仿真结果证明该文给出的控制方案的有效性和鲁棒性。
关键词：无刷双馈电机 反馈线性化 解耦控制 同步坐标系 鲁棒性
无刷双馈电机（Brushless Doubly Fed Machine, BDFM）因为取消了双馈电机的集电环和电刷，维护成本大幅度降低，而且可靠性高，可以使用较小容量的逆变器控制较大功率的电机，在水力发电和风力发电、车载和船载轴带发电、新能源汽车动力耦合装置等领域有广阔的应用前景[1-3]。然而无刷双馈电机的非线性、交叉强耦合问题突出且参数多，其控制问题至今尚未得到很好地解决。随着对无刷双馈电机研究的深入，国内外学者提出的控制策略有标量控制、直接转矩控制和矢量控制等。其中，标量控制[4-5]即变频控制，虽然实现简单，但控制效果差，应用场合受到很大限制。直接转矩控制[6-9]则沿用异步电机直接转矩控制的方法，将转矩和磁链的观测值与给定值经滞环比较选择电压矢量进行控制。由于无刷双馈电机本身的特点，并非像异步电机通过控制定子磁场相对于转子的旋转速度就可以控制电机转矩，而是通过控制功率电机定子磁场和控制电机定子磁场间的角度差来控制电机转矩。由于异步转矩和同步转矩间的相互影响，直接转矩控制方法只适用于大容量电机，其转子感抗远大于转子阻抗，转子损耗小至可以忽略的情况下才能得到好的控制效果，其并不适合于中小容量电机[8-9]。无刷双馈电机的矢量控制策略主要有两种：一种是采用所谓双同步坐标模型，即把无刷双馈电机分为功率电机和控制电机两个子系统，采用功率电机定子磁场对功率子系统定向，采用控制电机转子磁场对控制子系统定向[10-13]，从相关研究论文给出的几种设计方案看，主要问题是根据转矩和磁链给定计算控制电机电流给定的过程太复杂，需要在线求解非线性方程，对电机参数的依赖性强，且未能实现转矩和磁链控制的解耦；另一种矢量控制则是基于所谓统一坐标系模型[14]，即将控制电机或功率电机之一的相关变量通过取共轭变换，使两电机各相关变量相对于转子同方向旋转，再旋转到同步坐标系。统一坐标系模型将功率电机转子磁链和控制电机转子磁链的矢量和作为混合转子磁链，这使得它并不适用于转子磁场定向及控制策略，而是更适合于定子磁场定向及控制策略，例如在风力发电系统中实现对有功功率和无功功率的控制等[15-16]，同时也只对大容量电机，转差频率较大、转子感抗远大于阻抗、混合转子磁链幅值和异步转矩较小的情况，才可能有好的控制效果。
对于共用磁路的无刷双馈电机来说，功率电机和控制电机的极对数不同，两电机定子、转子绕组只交链各自的磁场。极对数不同、相对转子旋转方向相反的两电机磁场，在电机内部并不形成真正意义上矢量和，而是沿气隙分布的逐点叠加，这将导致共用磁路的设计加倍。而对于杯型转子的无刷双控电机来说，两电机的磁场分别通过杯型转子的内侧和外侧，不共用磁路。另外，由异步电机矢量控制可知，只有按转子磁场定向才可以得到电机磁场和转矩严格意义上的去耦控制。因此，研究无刷双馈电机转子磁场定向控制策略和实现方案有着重要的理论和实际意义。
对于可以进行机理建模的多变量非线性系统，输入输出反馈线性化是一种标准化的设计方法，文献[17]提出了混合励磁同步电机的反馈线性化设计方法，文献[18]提出了一种不引入零动态的异步电机反馈线性化设计方法。本文结果说明只依靠磁场定向无法解决无刷双馈电机的解耦控制问题，反馈线性化是实现无刷双馈电机高性能解耦控制的有效方法。另外，从本文所得结果可以看出，异步电机转子磁场定向控制和转差型矢量控制的实现方案，正是本文所提方法中当功率电机定转子互感等于零时的特例。
无刷双馈电机按转子结构分为绕线转子式、笼型和磁阻式，本文仅以绕线转子无刷双馈电机为例进行说明。绕线转子无刷双馈电机的数学模型可以根据级联无刷双馈电机得到，级联绕线转子BDFM结构如图1所示。它由两台转子绕组反相序联结的绕线转子异步电机同轴串联而成，其中一台电机定子接定频定压电源，一般不对其进行控制，称为功率电机；另一台电机定子接变频器，称为控制电机，通过调节控制电机定子电压的大小和频率来控制整个电机的转速、转矩。
图1 级联绕线转子无刷双馈电机结构
Fig.1 The structure of cascade wound-rotor BDFM
应该指出，由于绕线转子和笼型无刷双馈电机的数学模型类似[10]（除由于转子绕组联结方式不同引起的控制电机的电压方程中有两项符号不同外，并无其他不同），本文给出的设计方法同时适用于这两种无刷双馈电机的控制问题，对本文给出的结果稍加改动便可用于实现笼型无刷双馈电机的解耦控制。
本文中，r为绕组电阻，l为绕组电感，wr为电机转子的机械角速度，nr为电机转速，J为电机的转动惯量，Te为电机的电磁转矩。下标p、c分别表示功率电机和控制电机，下标d、q表示转子坐标系的直轴和交轴，下标m、t表示任意旋转坐标系或同步坐标系的直轴和交轴，下标s、r表示电机的定子、转子，绕组电感的下标m表示互感。i、u、y为向量形式的电流、电压和磁链，i、u、y为它们在两相坐标上的投影。pp和fp为功率电机的极对数和供电频率，pc和fc为控制电机的极对数和供电频率。上标“·”表示对时间求导。
无刷双馈电机稳定运行的条件是两个电机转子中的电流频率相同，即功率电机和控制电机的转差频率相等，由此得到稳态时无刷双馈电机的转速与两电机定子绕组供电频率的关系为
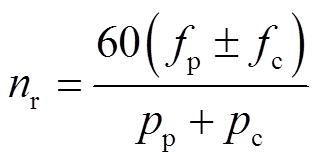（1）式中，当控制电机供电相序与功率电机供电相序相同时取“+”，此时电机运行于超同步状态；当控制电机供电相序与功率电机供电相序相反时取“-”，此时电机运行于欠同步状态。fc=0时的转速为无刷双馈电机的同步转速，即
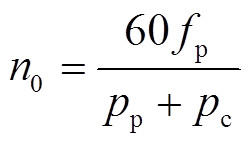（2）
容易看出，无刷双馈电机与同步电机具有类似的工作特性，即电机的稳态转速仅由功率电机和控制电机的供电频率确定。
功率电机和控制电机在转子dq坐标系下的电压电流模型分别为
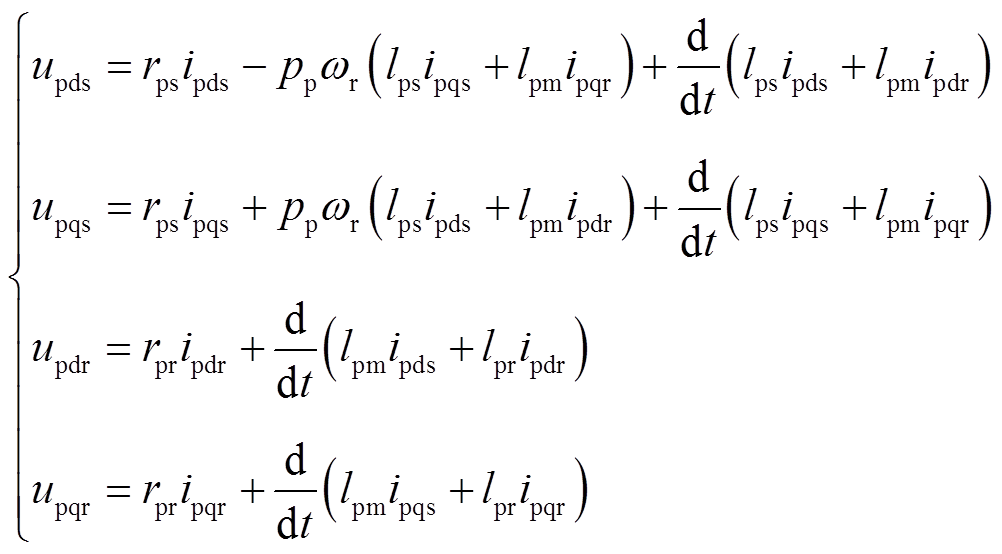（3）
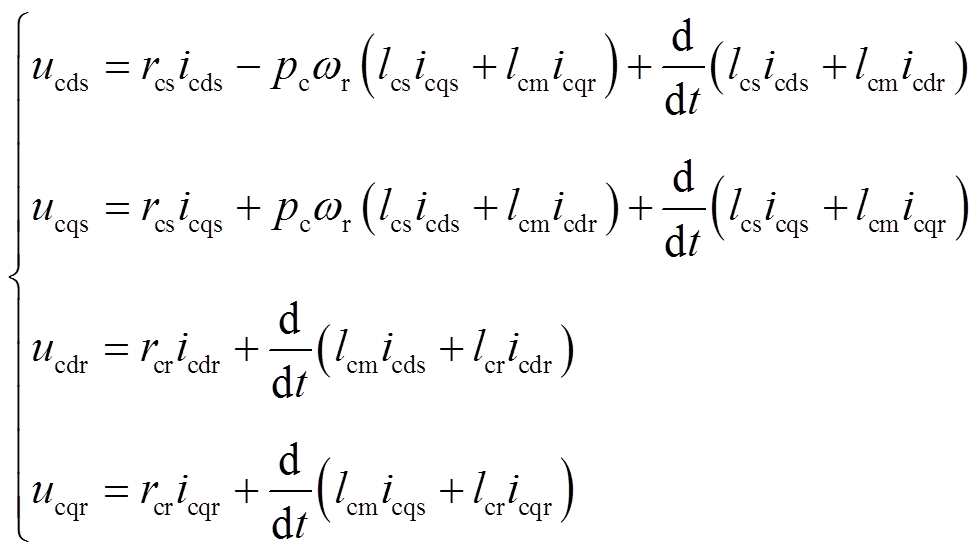（4）
电机输出转矩是功率电机和控制电机电磁转矩的和，即有
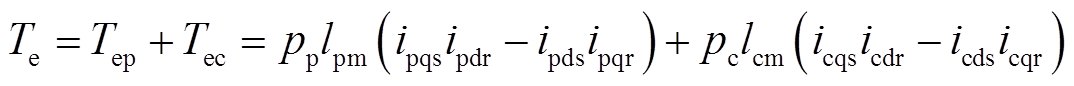（5）如图1所示，两个电机的转子绕组反相序相连，两电机转子相电压和线电流之间有如下关系
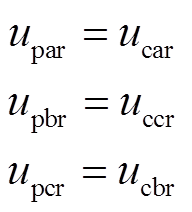
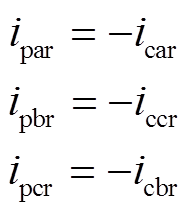
转子两相dq坐标系与转子三相abc坐标系间的关系如图2所示，其中d轴与a轴重合，于是两电机转子相电压和线电流有如下关系
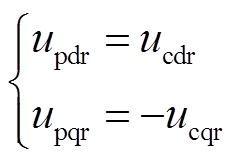
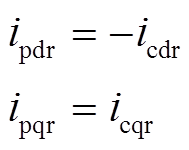（6）
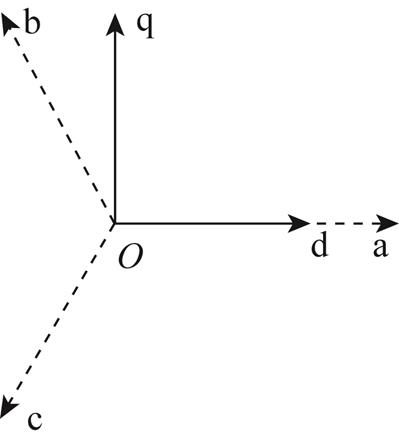
图2 转子dq坐标系与转子abc坐标系间关系
Fig.2 Relationship between rotor dq reference frame and rotor abc reference frame
将式（6）代入式（3）和式（4），得到电机在转子dq坐标下的电压电流模型为
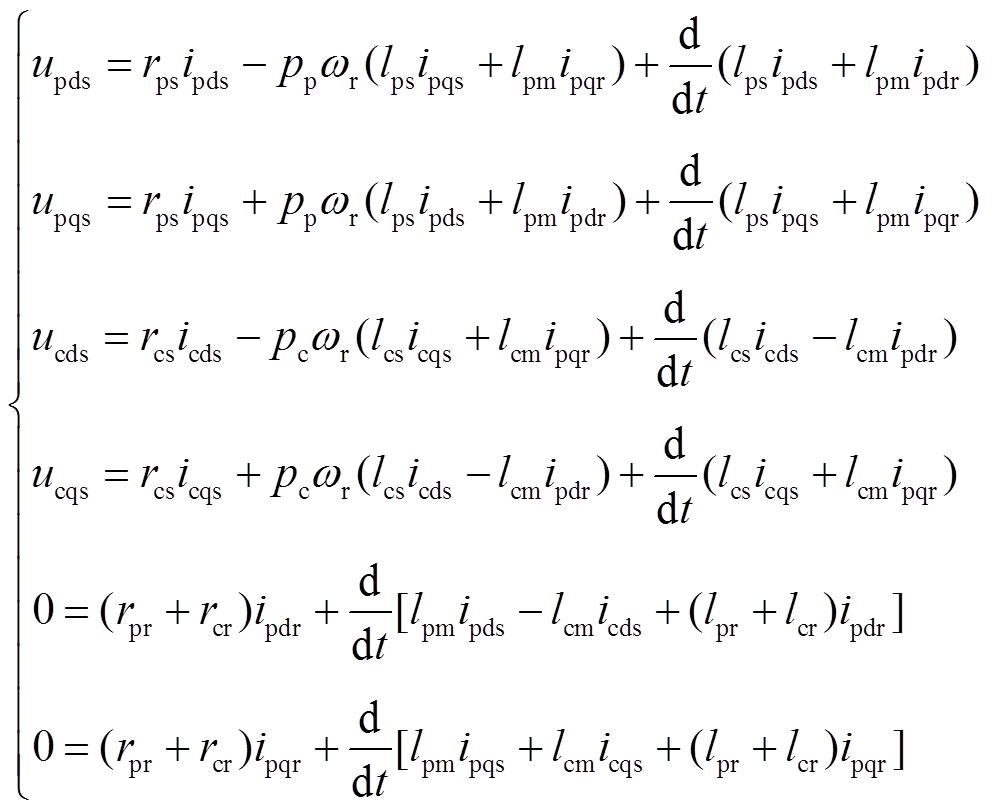（7）实际中，从快速性和安全性考虑控制电机一般都设计有电流环，将控制电机快速响应的电流环等效为电流源供电，为得到以控制电机定子电流和功率电机定子电压作为输入的状态方程描述，需要寻找合适的状态变量，使当输入发生有界阶跃变化时，状态变量是连续变化的。由于定子、转子互感的存在，控制电机定子电流发生阶跃变化时，转子电流和功率电机定子电流也会发生阶跃变化，故不能选为状态变量。本文选取功率电机的定子磁链为
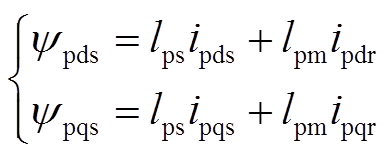（8）
新定义的控制电机转子磁链为
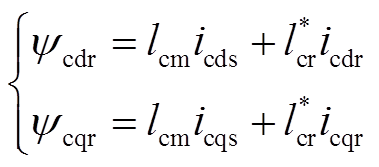（9）式中，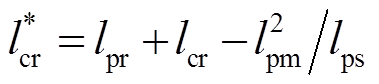
，转子磁链这样定义是为了在所得状态方程描述中，转子磁链方程与控制电机定子电压无关。以式（8）、式（9）中定子磁链和转子磁链作为状态变量，经状态变量变换得到BDFM在转子dq坐标系下以功率电机定子电压和控制电机定子电流为输入的4阶状态方程为
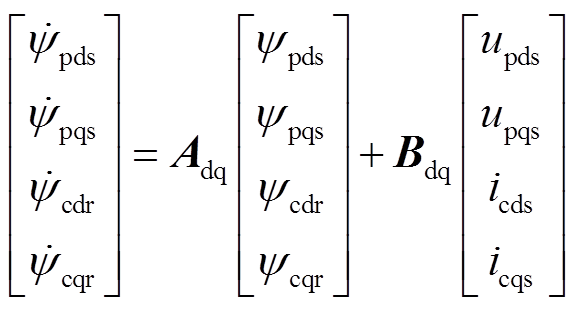（10）
其中
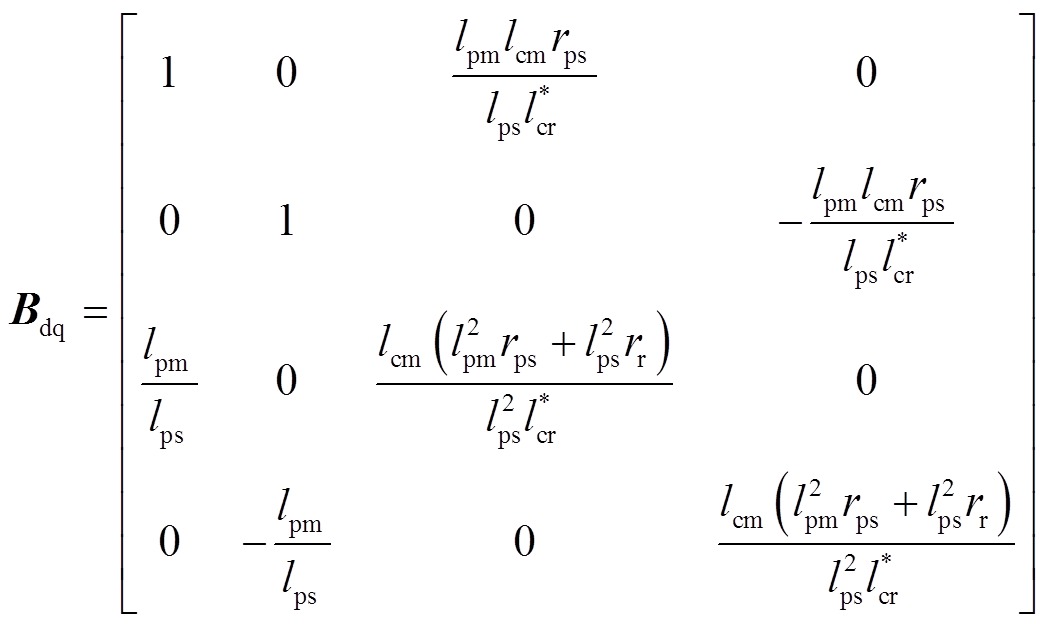
式中，rr为转子电阻，rr=rpr+rcr。用新的状态变量则电机的转矩方程变为
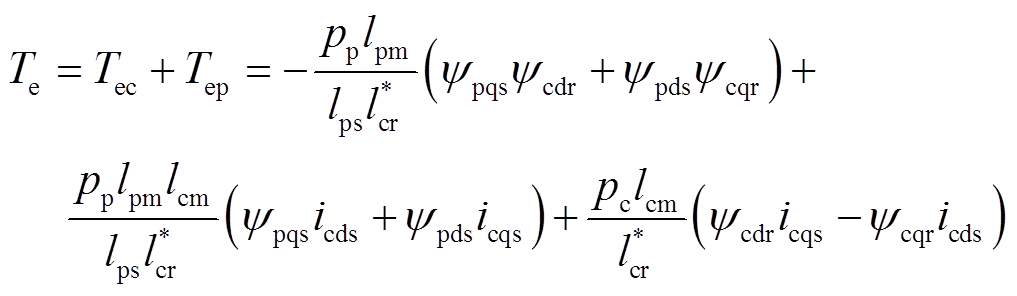（11）为了便于测量电机参数，进一步将功率电机的定子漏感全部折算到转子侧（具体方法见附录），折算后除功率电机定子电阻rps、电感lps、电流ips、磁链yps和控制电机的定子电流ics不变外，转子侧参数和相关变量都用折算值，并用上标“′”表示。注意到折算后有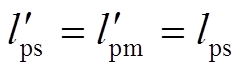
，得到折算后系统的定子磁链满足
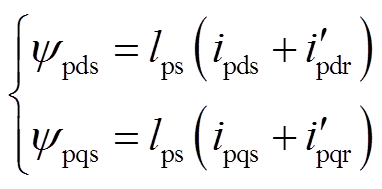（12）
控制电机的转子磁链为
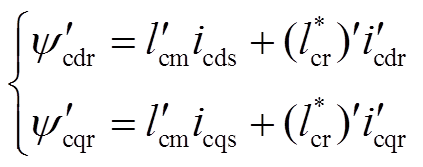（13）状态方程描述为
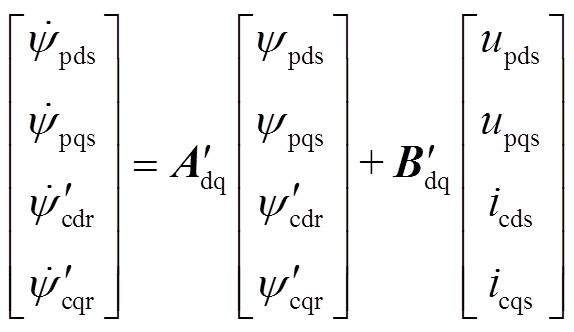（14）
其中
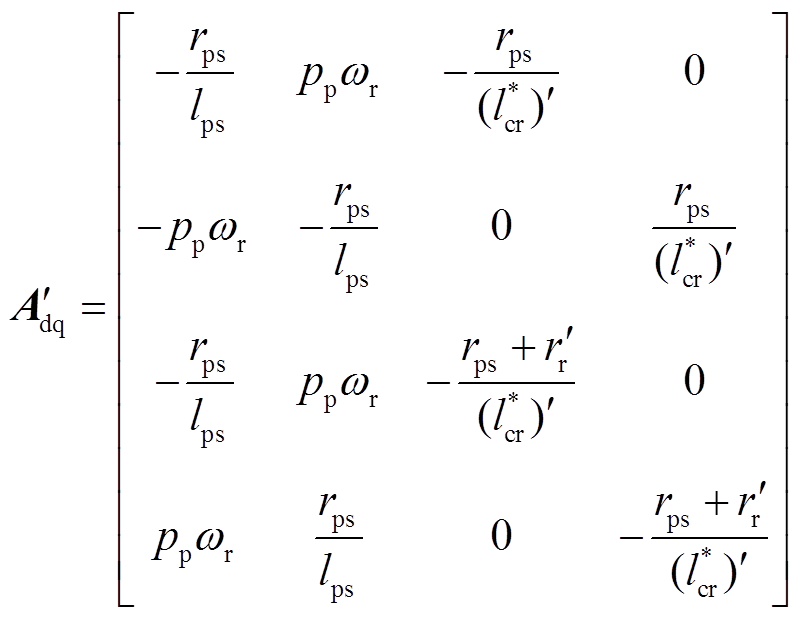
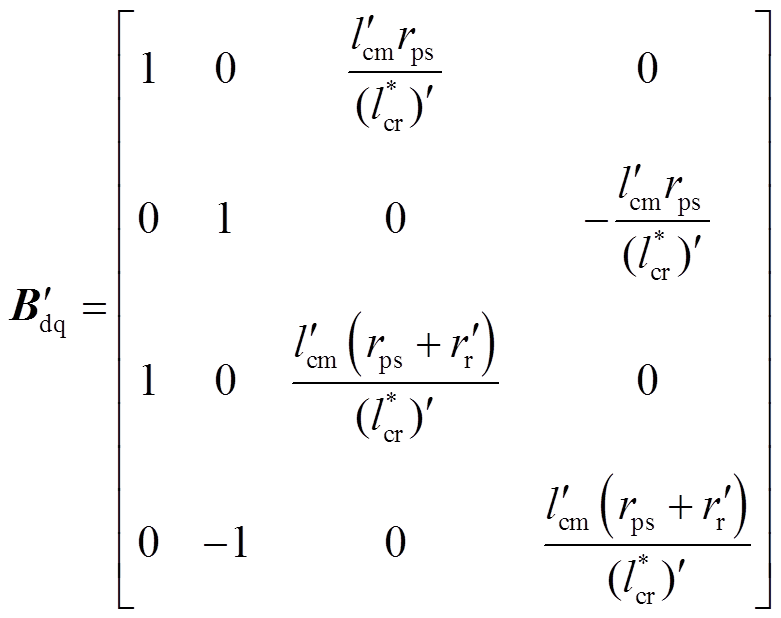
式中，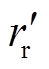
为折算后的转子电阻，
；
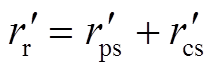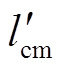为折算后控制电机的转子互感，因为有
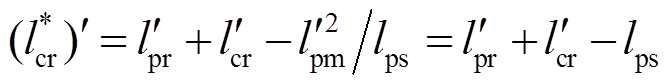，故按式（13）的定义，
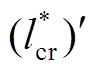为折算后与转子互感和全部转子漏感交链的磁链，故将
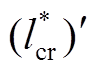称为转子电感。根据附录的内容可知，折算前后时间常数
、
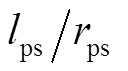维持不变。
用折算后参数和状态变量表示电机的转矩为
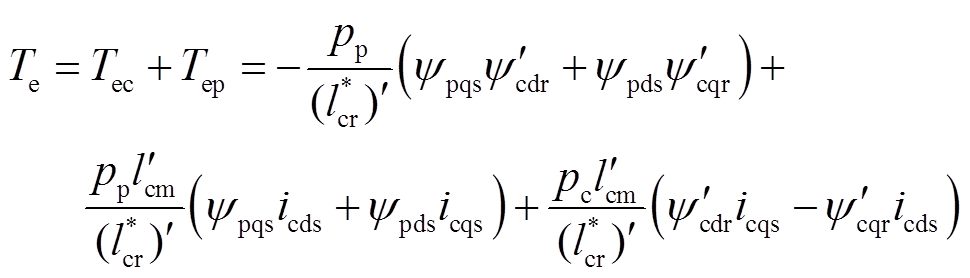（15）显然，在转子dq坐标系中，状态方程式（14）中的变量都是交流量，为了便于控制，需要将状态空间方程变换到控制电机同步坐标系中以得到直流控制量。静止αβ、转子dq和任意mt坐标系的关系如图3所示，由图3可知，任意两相旋转mt坐标系m轴与转子坐标系d轴间的夹角为lc。对式（14）的状态变量、输入变量做旋转变换，得到
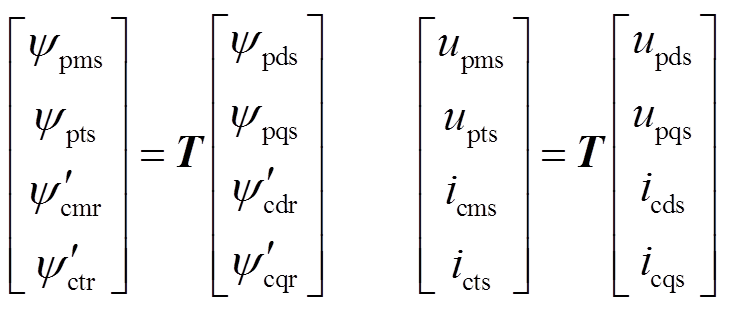
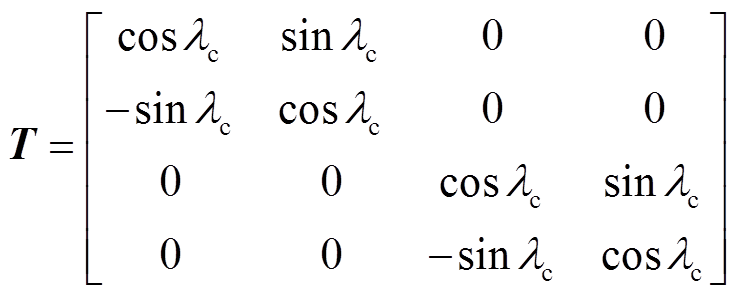
进而得到任意两相旋转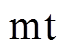
坐标系下BDFM的状态方程为
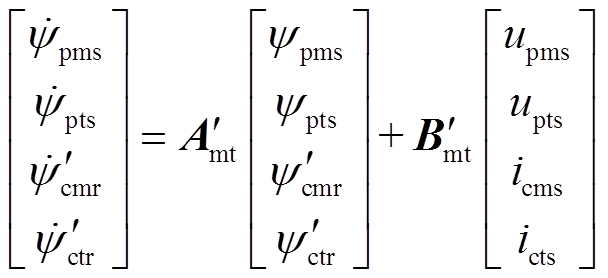（16）其中
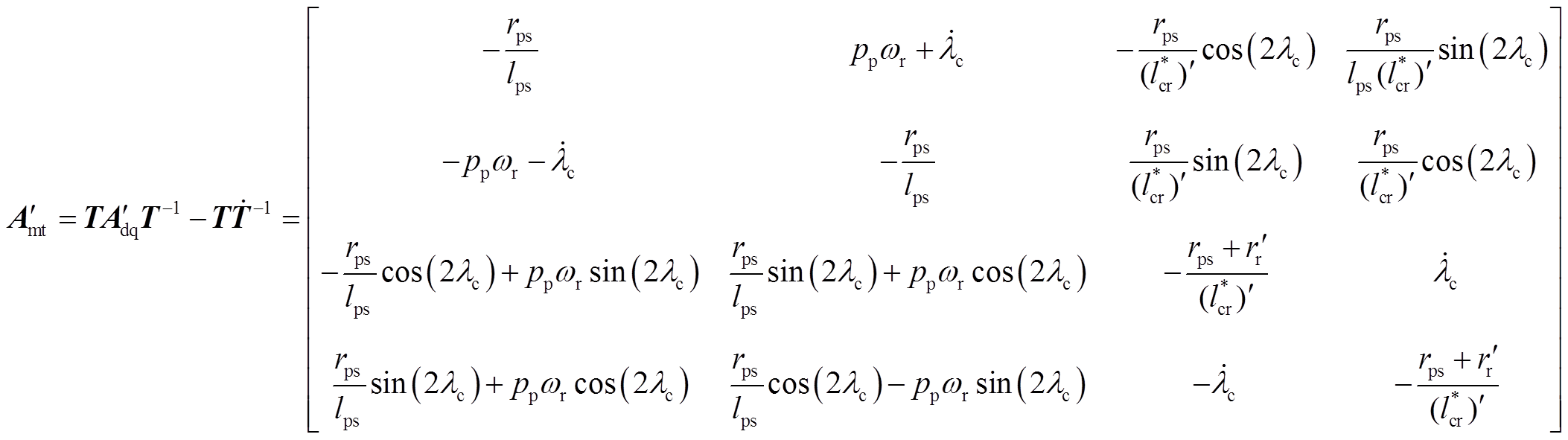
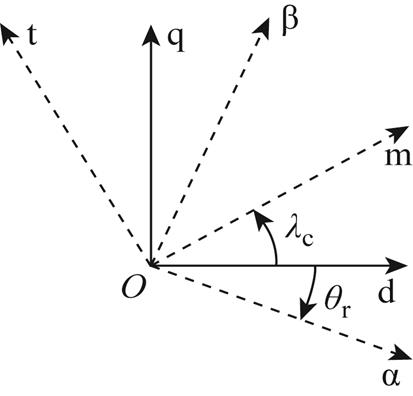
图3 静止ab、转子dq和任意旋转mt坐标系的关系
Fig.3 Relationships among static reference frame, rotor reference frame and arbitrary rotating reference frame
两相旋转mt坐标系下电机转矩表示为
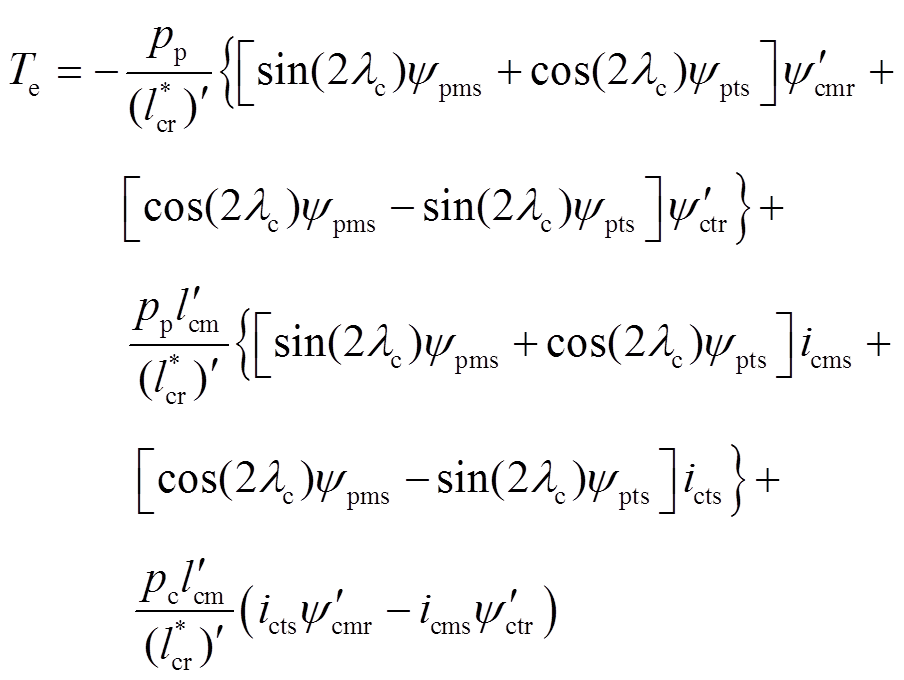
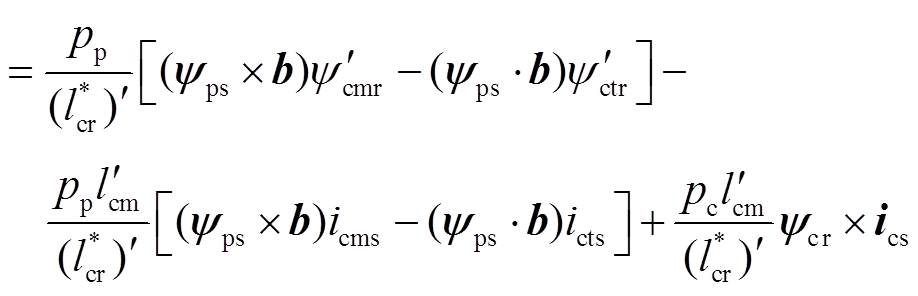（17）
其中
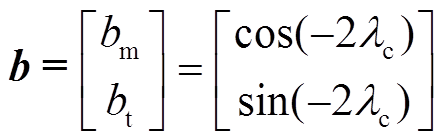
式中，b为单位矢量；“·”和“×”分别表示两向量的点积和叉积。由第1节给出的无刷双馈电机的工作原理可知，电机稳速运行时控制电机磁场和功率电机磁场相对于转子的旋转角速度分别为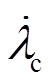
和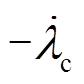
，大小相等方向相反。由此可知，功率电机各变量相对于控制电机各变量以角速度
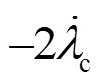旋转，这表明静态下yps与b之间的夹角及ups与b之间的夹角均为常数值，因此静态下yps×b、yps´b、ups×b也都为常数值（对式（16）也可以做类似的分析）。在式（17）中，除去上述三项外，其他变量都是控制电机侧的变量，它们在控制电机同步坐标系下均为直流量，这说明在控制电机同步坐标系下可以得到直流控制量，应用简单的PI调节器可以实现无差调节，所谓双同步坐标系[10]的处理方法并非必要。
当采用控制电机转子磁场定向时，有
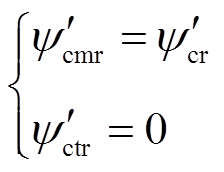（18）式中，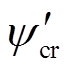
为控制电机转子磁链的幅值。将式（18）代入式（16），由式（16）的第3行和转矩表达式（17），可将控制电机转子磁链和电机转矩输出表示为
（19）
其中
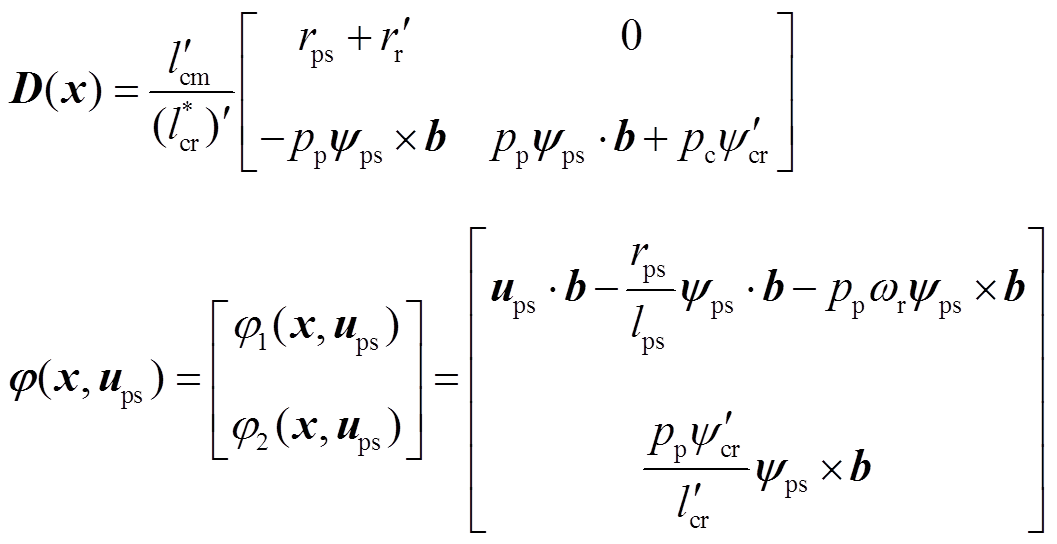
根据反馈线性化理论，输出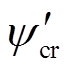的相对阶为1，Te的相对阶为0。
定义一个新的控制输入为
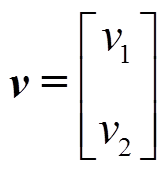
当D(x)非奇异时，系统可以进行输入输出反馈线性化控制，令
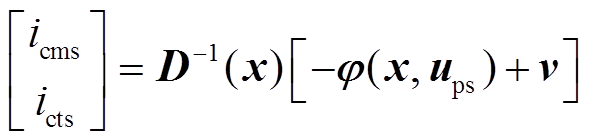（20）
其中
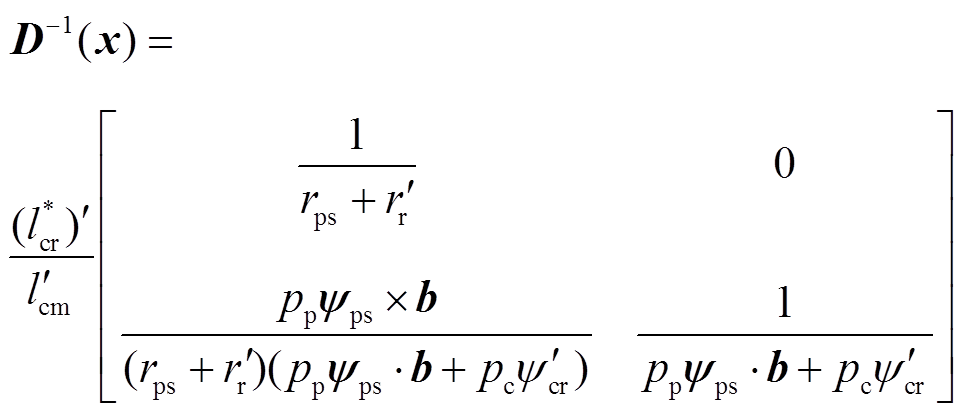
则有
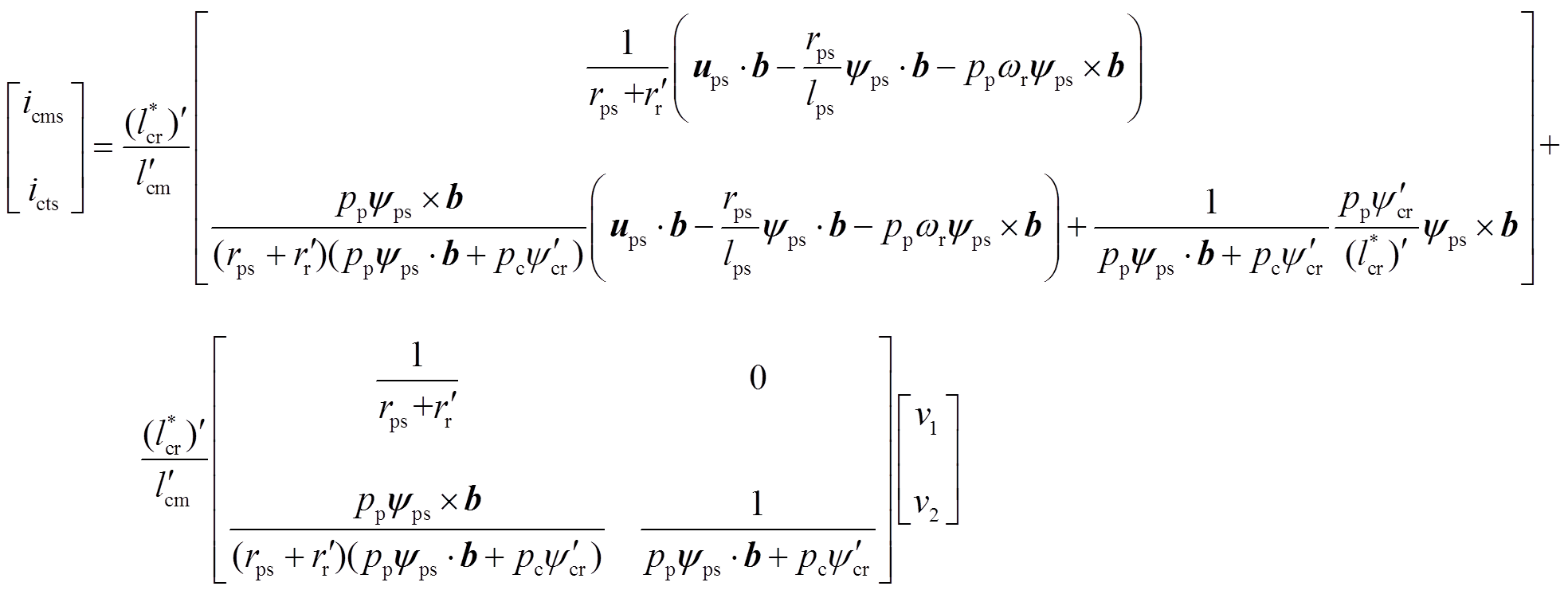
得到反馈线性化后系统的描述为
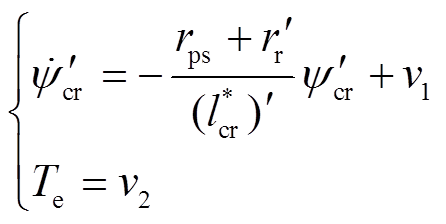（21）在反馈线性化控制律式（20）中，ups和wr通过测量获得，yps、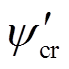
和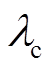
通过观测器得到。
可以看出，由于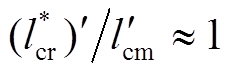
，在反馈线性化控制律式（20）中，除与功率电机定子磁场、控制电机转子磁场相关各量外，只用到了功率电机定子回路时间常数以及功率电机定子电阻与转子电阻的和。
另外，在上述得到的结果中令功率电机定子电感lps=0，则可得到异步电机转子磁场定向控制策略。与异步电机的情况类似，根据转子磁场定向后式（16）的第4行，还可以得到无刷双馈电机的转差型矢量控制策略[19]。最后，着重指出，在转子坐标系下将功率电机相关变量取负共轭或共轭变换改变其旋转方向，得到同步坐标系下的直流控制量[8-9]，取或不取上述变换，只是导致公式表示和处理方法的不同，并不影响其实质性内容。
根据式（19）中的第1式，磁链幅值指令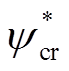
为常值，即有
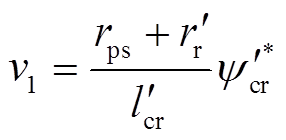
得到无刷双馈电机反馈线性化解耦控制框图如图4所示。
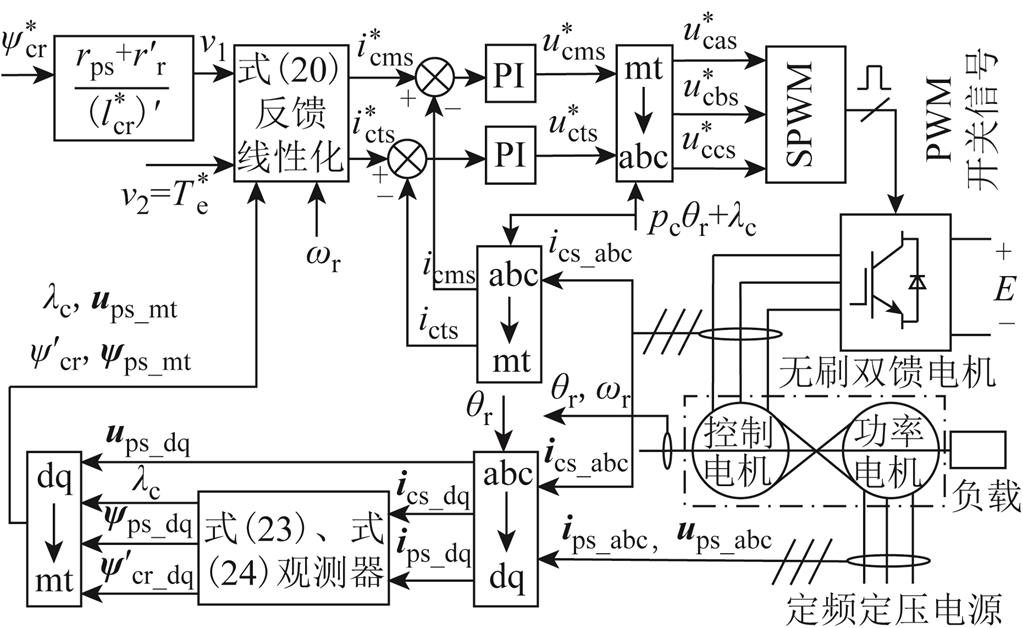
图4 BDFM输入输出反馈线性化解耦控制原理
Fig.4 Input-output feedback linearization decoupling control schematic of BDFM
系统实现反馈线性化的前提条件是矩阵D(x)非奇异，即要求
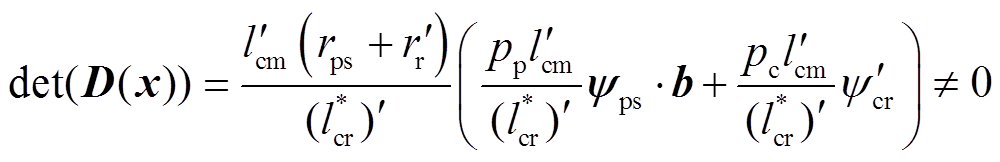
并且，根据电磁转矩表达式（17）可以看出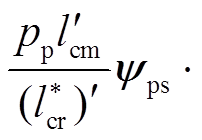
b+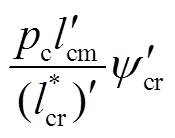
是控制电机转矩电流icts到转矩Te的增益，在控制过程中希望它一直为正。因此，D(x)非奇异的条件从本质上揭示了无刷双馈电机输出稳定转矩的必要条件，即在控制过程中，从icts到Te的增益不能过零，否则将引起转矩振荡，造成转矩失控。显然，当控制电机转子磁链幅值满足式（22）时，上述要求可以得到满足
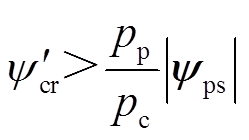（22）
在本文的仿真中，无刷双馈电机由Matlab Simulink中的两台异步电机级联而成，如图5所示，两台电机的转子绕组反相序相连，控制电机的转子角速度作为功率电机的机械输入，功率电机的电磁转矩作为控制电机的机械输入，以上设置保证了仿真中的BDFM与实际中的无刷双馈电机一致。功率电机由220V/50Hz的定频定压电源供电，控制电机通过逆变器供电，逆变器的调制频率为10kHz，逆变器放大倍数为300，逆变器直流电压为300V。仿真在变量测量中加入了测量滤波环节，考虑了电压(1ms)、电流(0.1ms)和转速(1ms)的测量延时。
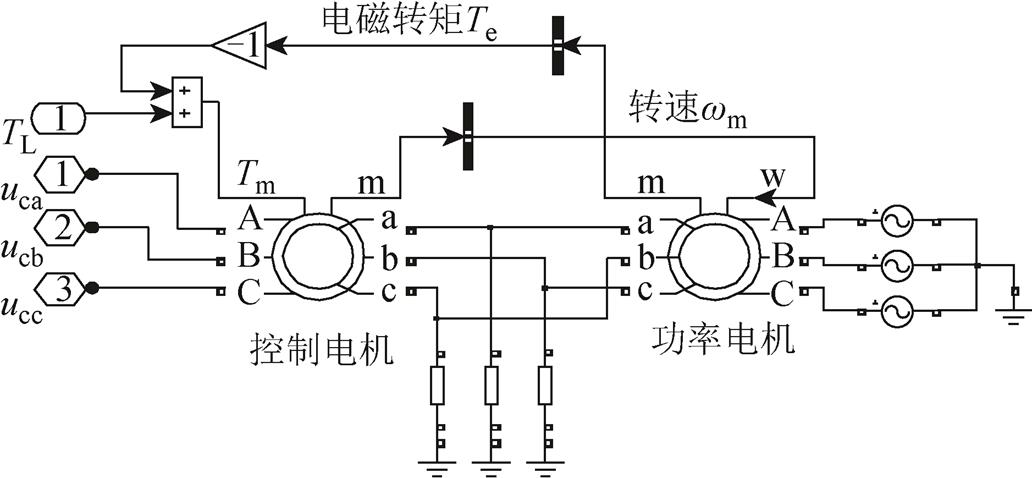
图5 仿真中级联无刷双馈电机示意图
Fig.5 Cascaded BDFM in the simulation system
仿真中采用的无刷双馈电机参数如下：rps=1.71W, rcs=1.71W, rpr=1.49W, rcr=1.49W, lps=0.13H, lcs=0.13H, lpr=0.13H, lcr=0.13H, lpm=0.125H, lcm= 0.125H, pp=1, pc=3, J=0.1kg×m2, 额定功率为3.7kW、额定电压为380V，额定电流为9.2A、额定转速为908r/min。
由式（20）可知，控制过程中需要观测电机磁链，将磁链表达式（8）、式（9）代入系统方程式（7），消去转子电流，得到转子dq坐标系下的磁链观测模型，并用折算后的值替换后，有
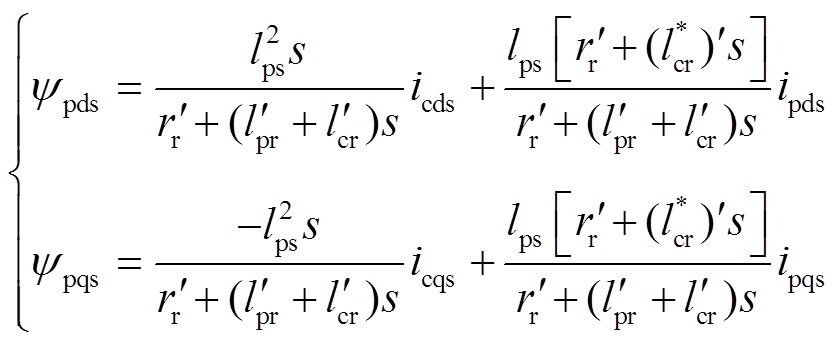（23）
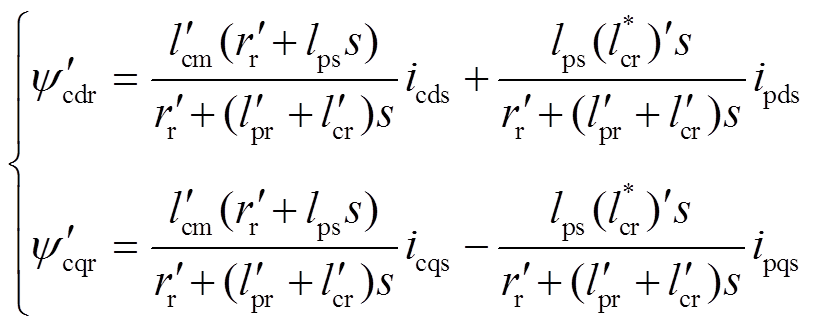（24）
当然，功率电机的定子磁链也可以使用静止坐标系下的电压电流模型，通过大惯性环节进行近似积分得到。
根据图4搭建反馈线性化控制系统模型进行仿真，仿真结果如图6所示，其中磁链给定为在0.7~ 0.5Wb之间变化的阶跃信号，转矩给定值在8.5N×m、0 N×m和-8.5 N×m三个值之间切换，电机空载起动。图6所示依次为控制电机转子磁链、电机电磁转矩、电机转速和控制电机定子电流的波形，实线为给定信号曲线，虚线为跟踪曲线。
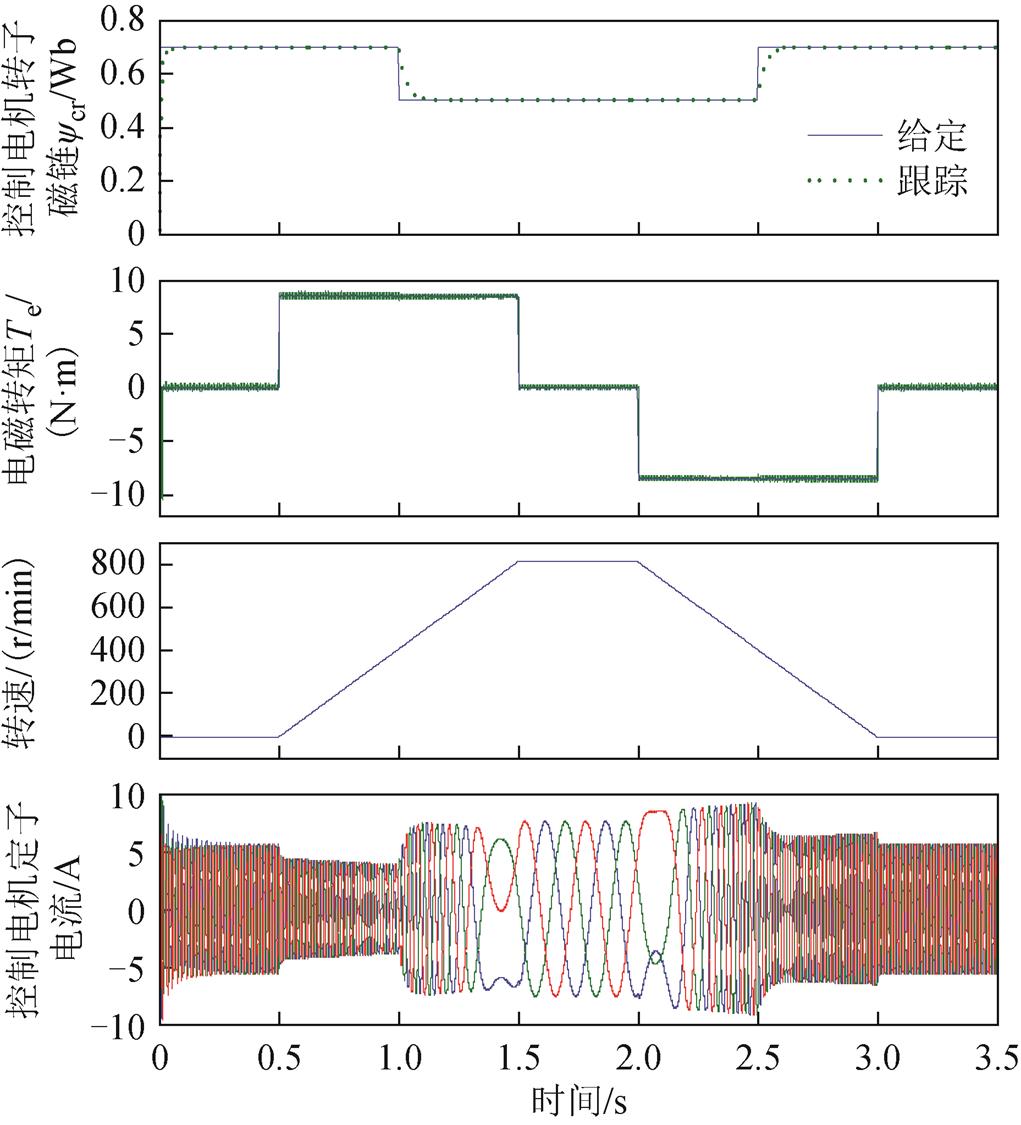
图6 BDFM磁链幅值和电机转速输入输出反馈线性化控制效果图
Fig.6 The input-output feedback linearization control effect diagram of BDFM Flux amplitude and speed
从图6可以看出，控制电机转子磁链幅值ycr和电机电磁转矩Te能够快速准确地跟踪给定信号，并且当磁链和转矩发生变化时对彼此不产生影响。以上结果说明本文给出的解耦控制方法从根本上消除了磁链和转矩之间的耦合影响，实现了系统的高性能解耦控制。
由控制电机定子电流波形可以看出，在1.4s时电机转速上升，超过同步速750 r/min，控制电机由负相序供电变为正相序供电，电机运行在超同步状态；在2.1s，转速下降，低于750 r/min时，控制电机由正相序供电变为负相序供电，此时电机运行在欠同步状态。
根据3.1节磁链和转矩开环的控制效果，可以设计闭环控制系统，如图7所示。这是以反馈线性化解耦控制为内环，磁链和转速为外环的BDFM控制系统，对其进行仿真研究，以检验系统的抗扰能力和鲁棒性能。
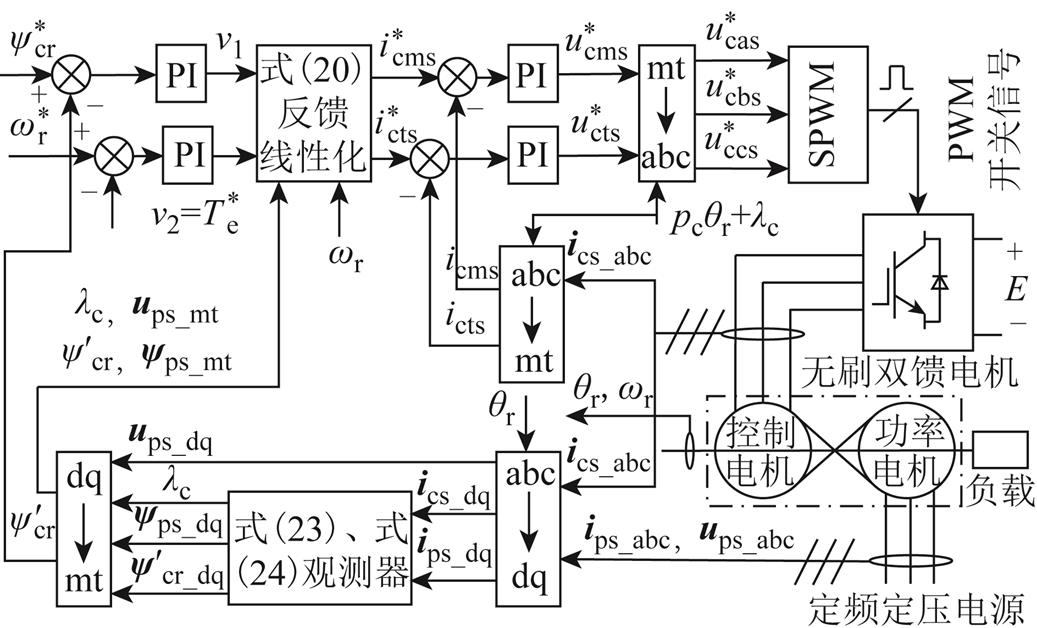
图7 BDFM反馈线性化闭环控制系统框图
Fig.7 The closed-loop control schematic of BDFM based on input-output feedback linearization
仿真条件设置为：磁链给定值为0.7 Wb，转速给定值在1s时由0 r/min阶跃至400 r/min，功率电机初始由220V(50Hz)的电源供电，在2.5s时电源幅值升至250V，电机空载起动，在3s时加3N×m负载。磁链和转速PI调节器的输出限幅值分别为±40和±6。
为了证明该策略对参数偏差的鲁棒性，仿真中将BDFM的转子电阻rr提高20%，将电机电感lps、lcs、lr、lpm和lcm等参数提高10%，而反馈线性化环节和观测器中的参数不做改变。图8所示波形从上至下依次为控制电机转子磁链、电机电磁转矩、电机转速和电机转速在电源与负载变化时的调节效果细节。
从图8可以看出，存在参数偏差时，转速仍然可以准确地跟踪给定值；而对于电机磁链来说，电感参数变化会引起磁链的观测偏差，实际磁链与给定值有一定的误差，比给定值大5.4%左右。当1s和1.7s转矩发生变化时，磁链也产生波动，波动幅值最大达到了稳态值的3.1%，但磁链能够快速地回到稳态值。根据以上结果可以看出，参数偏差影响了反馈线性化部分的解耦性能，但不影响系统的稳定性，这证明了本文提出的控制策略对参数偏差具有鲁棒性。
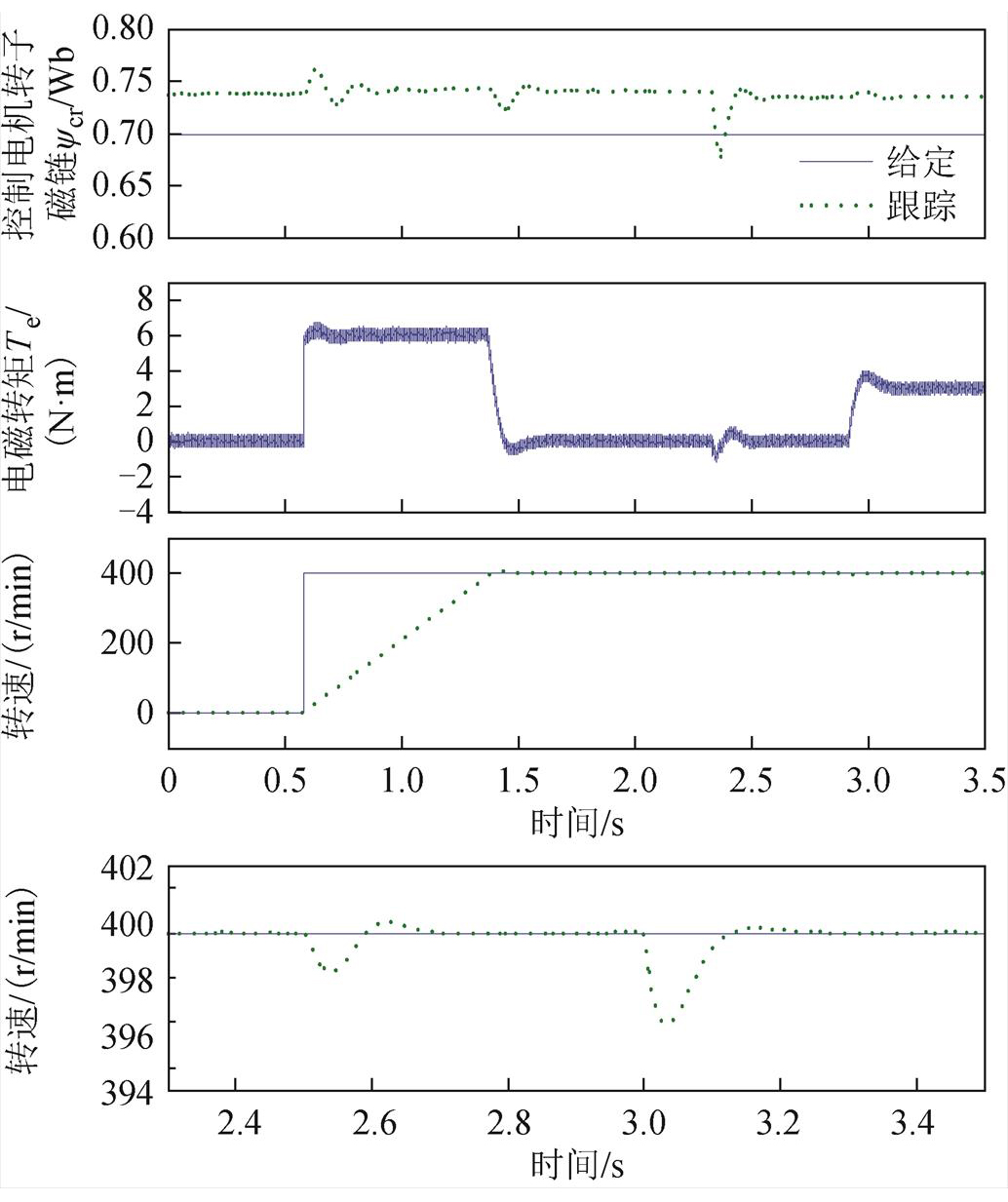
图8 电机电阻提高20%，电感提高10%时的控制效果
Fig.8 System responses when resistance increased by 20%, inductance and mutual inductance increased by 10%
另外，在2.5s时供电电压升高，磁链和转速都发生了波动，磁链波动值达到了稳态值的9.3%，转速波动值达到了给定值的0.5%，但是很快都回到了稳态值；在3s时，电机突然加载3N×m，磁链和转速再次产生波动，同样能够快速回到稳态值，此时电机转矩也快速升至3N×m。
本文给出了控制电机同步坐标系下BDFM的仿射非线性状态空间模型，基于该模型应用输入输出反馈线性化方法实现了BDFM磁链和转矩的解耦控制，给出了控制算法和系统设计方案，以及相关参数的折算方法和测试方法。本文给出的控制方法和系统设计方案适用于各种容量等级的无刷双馈电机，仿真结果证明了该控制方法的有效性和鲁棒性。
附 录
电机参数测试等效电路如附图1所示，控制电机由电流源供电，功率电机由电压源供电，电机保持静止，用加固定方向脉振电流和电压激励的方法得到电机参数。因为dq轴施加的激励成固定比例，可省掉dq下标。
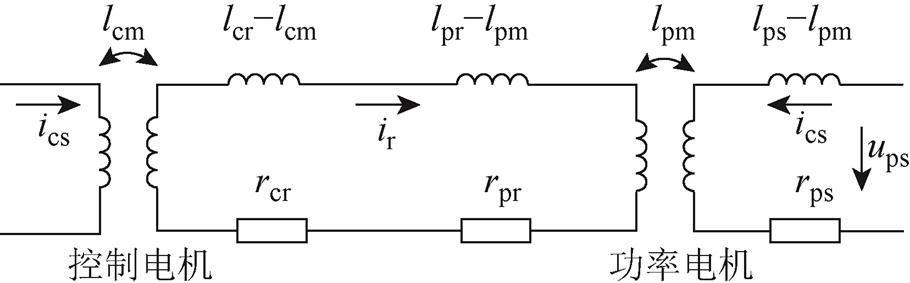
附图1 电机参数测试等效电路
App.Fig.1 The equivalent circuit diagram for motor parameter test
根据附图1有
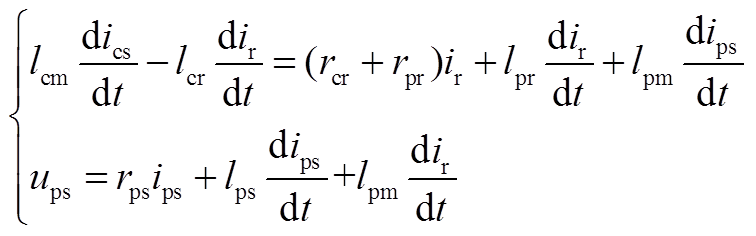（A1）拉氏变换得到
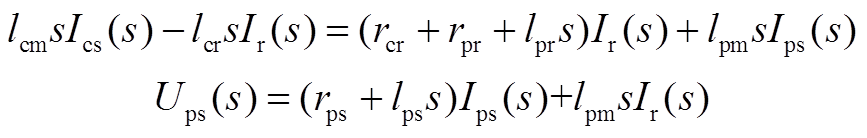
从式（A1）的第1式解出Ir(s)为
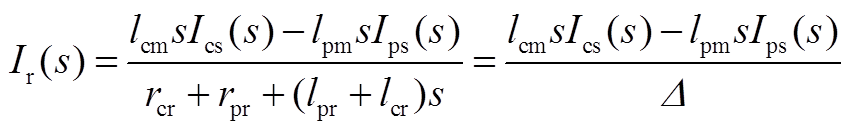（A2）式中，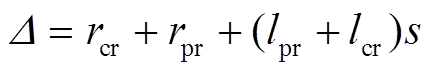
。代入式（A1）的第2式得到
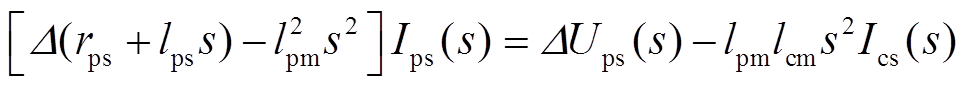
这是一个两阶系统，共有5个独立的系数。而在附图1等效电路中，将控制电机转子漏感和功率电机转子漏感加在一起，控制电机转子电阻和功率电机转子电阻加在一起，共有6个独立参数。因此，在参数测量时必须做一个假设。本文将功率电机定子漏感全部折算到转子侧，令折算后的电机参数rps和lps不变，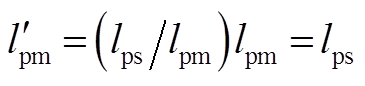
，功率电机的定子漏感等于零，
，
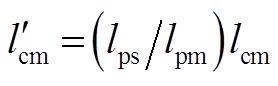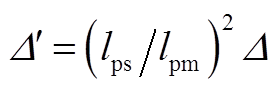，即
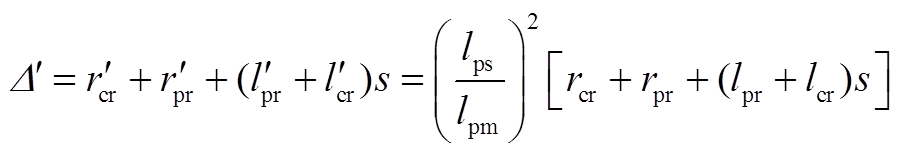
由此得到
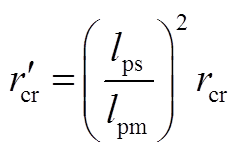
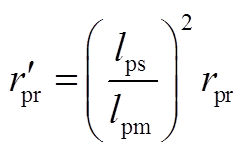
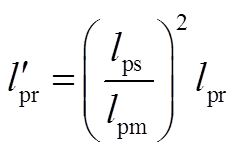
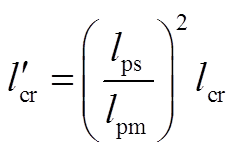
从式（26）容易看出，折算后的转子电流减小了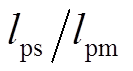
倍，即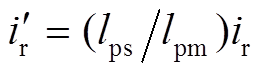
，因此有式（8）的定子磁链不变，即
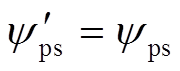，式（9）的控制电机转子磁链增加了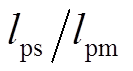倍。根据式（11），用折算后参数和转子电流计算电机的转矩为
参考文献
[1] 欧先朋, 韩力, 韩雪峰, 等. 两种不同笼型转子结构无刷双馈电机的稳态运行性能对比[J]. 电工技术学报, 2017, 32(23): 61-71. Ou Xianpeng, Han Li, Han Xuefeng, et al. Comparison of Steady state operating performances on brushless doubly-fed machine with two different cage rotors[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 61-71.
[2] Cheng Ming, Luo Rensong, Wei Xinchi. Design and analysis of current control methods for brushless doubly fed induction machines[J]. IEEE Transactions on Industrial Electronics, 2019, 66(1): 717-727.
[3] 阚超豪, 赵威, 储成龙, 等. 基于变极绕组的无刷双馈电机起动特性研究[J]. 电工技术学报, 2019, 34(7): 1392-1403. Kan Chaohao, Zhao Wei, Chu Chenglong, et al. Research on starting characteristics of brushless doubly-fed machines based on pole changing winding[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1392-1403.
[4] Sarasola I, Poza J, Oyarbide E, et al. Stability analysis of a brushless doubly-fed machine under closed loop scalar current control[C]//IEEE 32nd Annual Conference on Industrial Electronics, Paris, France, 2006: 1527-1532.
[5] Gao Xinmai, Wang Xuefan, Ou Lezhi, et al. Instability analysis and mitigation of oscillation in wound rotor brushless doubly-fed machine[C]//2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, South Korea, 2018: 1486-1491.
[6] 张爱玲, 许永顺, 王昕. 直接转矩控制的无刷双馈感应电机的异步启动[J]. 电机与控制学报, 2012, 16(6): 69-74. Zhang Ailing, Xu Yongshun, Wang Xin. Asynchronous starting for BDFIM based on direct torque control strategy[J]. Electric Machines and Control, 2012, 16(6): 69-74.
[7] 夏超英, 霍克强, 侯晓鑫. 无刷双馈电机直接转矩控制失控分析[J]. 太阳能学报, 2017, 38(7): 1838-1846. Xia Chaoying, Huo Keqiang, Hou Xiaoxin. DTC out of control analysis and improved for brushless doubly-fed machine[J]. Acta Energies Solaris Sinica, 2017, 38(7): 1838-1846.
[8] Xia Chaoying, Hou Xiaoxin. Study on the static load capacity and synthetic vector direct torque control of brushless doubly fed machines[J]. Energies, 2016, 9(11): 966.
[9] Xia Chaoying, Hou Xiaoxin, Chen Feng. Flux-angle-difference feedback control for the brushless doubly fed machine[J]. Energies, 2017, 10(7): 1840.
[10] Zhou D, Spee R. Synchronous frame model and decoupled control development for doubly-fed machines[C]//IEEE Power Electronics Specialists Conference(PESC), Taipei, 1994: 1229-1236.
[11] Zhou D, Spee R, Alexander G C, et al. A simplified method for dynamic control of brushless double-fed machines[C]//Proceedings of the 1996 22nd International Conference on Industrial Electronics, Control, and Instrumentation, Taipei, 1996: 946-951.
[12] Zhou D, Spee R, Alexander G C, et al. Experimental evaluation of a rotor flux oriented control algorithm for brushless doubly-fed machines[J]. IEEE Transaction on Power Electronics, 1997, 12(1): 72-78.
[13] Zhou D, Spee R. Field oriented control development for brushless doubly-fed machines[C]//IEEE Industry Applications 31th IAS Annual Meeting, California, America, 1996: 304-310.
[14] Zhang Guanguan, Yang Jian, Sun Yao, et al. A robust control scheme based on ISMC for the brushless doubly fed induction machine[J]. IEEE Transactions on Power Electronics, 2018, 33(4): 3129-3140.
[15] 张迪, 魏艳君, 杨宗丰, 等. 不平衡电网电压下基于滑模变结构控制的双馈风电系统转子侧变流器控制策略[J]. 电工技术学报, 2016, 31(17): 121-131. Zhang Di, Wei Yanjun, Yang Zongfeng, et al. Sliding-mode control for rotor-side converters of DFIG-based wind-power generation system under unbalanced grid voltage conditions[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 121-131.
[16] 赵荣理, 张爱玲, 田慕琴, 等. 笼型转子无刷双馈发电机的间接功率控制[J]. 电机与控制学报, 2019, 23(9): 1-8.Zhao Rongli, Zhang Ailing, Tian Muqin, et al. Indirect power control strategy for brushless doubly-fed induction generator[J]. Electric Machines and Control, 2019, 23(9): 1-8.
[17] 李生民, 张泽灵, 郭思语, 等. 混合励磁同步电机反馈线性化控制[J]. 电工技术学报, 2019, 34(增刊1): 39-51. Li Shengmin, Zhang Zeling, Guo Siyu, et al. Feedback linearization control of hybrid excitation synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 39-51.
[18] 李洁,孔维超,钟彦儒.一种不引入零动态的异步电机反馈线性化控制[J]. 电工技术学报, 2014, 29(1): 110-115. Li Jie, Kong Weichao, Zhong Yanru. Feedback linearization control of induction machines without introducing zero dynamics[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 110-115.
[19] 夏超英, 于佳丽, 田聪颖, 等. 无刷双馈电机的转差型矢量控制[J]. 控制与决策, 2019, 34(3): 649-654. Xia Chaoying, Yu Jiali, Tian Congying, et al. Slip frequency type vector control for brushless doubly-fed machine[J]. Control and Design, 2019, 34(3): 649-654.
Feedback Linearization Control Approach of Brushless Doubly Fed Machine
Abstract Based on the description of brushless doubly fed machine state space model in the rotor reference frame, the brushless doubly fed machine (BDFM) affine nonlinear state space model in arbitrary rotating reference frame is derived by rotating coordinate transformation, and its static DC characteristic is analyzed. On the basis, The decoupling control method of BDFM in the control motor synchronous reference frame is obtained by means of input-output feedback linearization. The necessary condition of the implementation of the presented control strategy is demonstrated. The conversion method and identification method of parameters are also given. Simulation results confirm the effectiveness and the robustness of the proposed strategy.
keywords：Brushless doubly fed machine, feedback linearization, decoupled control, synchronous reference frame, robustness
DOI: 10.19595/j.cnki.1000-6753.tces.190517
中图分类号：TM301.2
夏超英 男，1958年生，教授，博士生导师，研究方向为控制理论、电力电子与电力传动和新能源汽车等。E-mail：xiachaoying@126.com（通信作者）
张耀华 男，1994年生，硕士，研究方向为电力电子与电力传动。E-mail：17302259960@163.com
收稿日期2019-04-30
改稿日期 2019-07-25
（编辑 郭丽军）