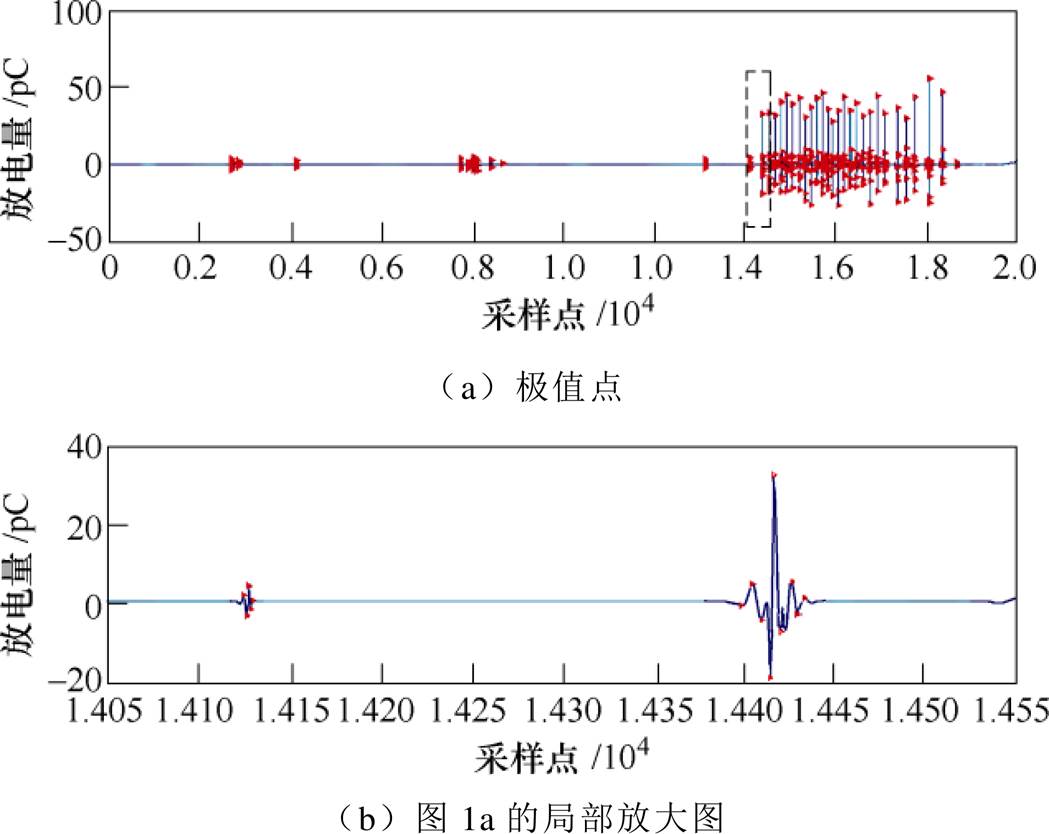
图1 电晕放电去噪后的放电波形极值点分布
Fig.1 Corona discharge after denoising and its extremum points
摘要 局部放电（PD）信号处理是电力设备绝缘状态评估的基础，而特征量提取又是信号处理的关键环节。特征量提取包括局部放电脉冲分割和放电特征量提取两个步骤。放电脉冲分割提取是后续PD信号特征提取及故障分类的前提。为尽可能保留放电信息，同时减少人工干涉，该文提出了一种基于聚类算法的PD脉冲分割提取方法。该方法采用小波分解算法进行滤波处理，使用噪声抑制比（NRR）表征滤波效果；以所有局部放电信号半波脉冲为对象，计算各半波脉冲的能量（即信号瞬时值平方对时间的积分），从而使该方法能更准确地描述局部放电过程。应用Otsu算法自适应计算能量阈值并结合密度峰值聚类算法（DPC）实现PD脉冲的自动分割。在实验室建立了三种不同类型局部放电模型，采集得到10组电晕放电、11组悬浮放电和30组锥板放电数据，以对该文方法进行验证。结果都取得了80%以上的识别率，比同类算法更高或相当，表明了该文方法的优越性。
关键词：局部放电 最大类间方差法 自适应能量阈值 脉冲分割 密度峰值聚类
局部放电（Partial Discharge, PD）是导致电气设备绝缘故障的主要原因，科技工作者研发了多种PD在线监测或带电检测手段，主要包括电测量法、超声波[1-2]、特高频[3]、光测量法[4]，还有气谱法[5]及其他非电测量方法[6-7]。不同的采集量可以构造不同的局部放电模式[8]。目前应用最广泛的是基于电测法的构造模式[9-11]方法，而电测法主要有常规脉冲电流法[2]和宽频带脉冲电流法[12]。对PD信号的去噪和模式分析（放电类型判定）一直是电力设备绝缘状态监测和评估研究的重点[13]。
对于PD模式分析而言，PD信号中脉冲部分是至关重要的，而其他部分没有多少价值。如果采样频率足够高，非脉冲部分会产生大量冗余数据，对存储及计算都会带来挑战。解决办法是对测得的某个较长时间段内的局放信号进行脉冲提取，亦可称脉冲分割，它是指在PD信号中去掉非放电信号段，并记录各个放电信号段的起止时间和脉冲信号最大值的发生时刻。
局部放电的模式识别包括模式构造、特征量提取及模式分类器设计三种方式，几种主要PD放电模式构造[14]有时间分布模式[15]（Time Resolved Partial Discharge, TRPD）、相位分布模式（Phase Resolved Partial Discharge, PRPD）、脉冲序列相位分布模式[16]（Phase Resolved Pulse Sequence, PRPS）、Du及Du/Df 模式和混沌模式[17]。上述这些模式构造方法都依赖于对放电脉冲的分割。
PD信号脉冲分割技术大体上分为两类[18]：①去噪加脉冲检测；②特征提取加脉冲识别。信噪比较大的情况下一般采用第①类方法，即先采用各种去噪手段，然后通过检测波峰实现脉冲识别，这类方法需要确定最小的放电时间间隔，该间隔随着脉冲时间长度的变化而变化，该间隔确定不合理时会造成同一次放电的多个波峰可能被识别为多次放电。信噪比较小的情况下一般采用第②类方法，在此情况下即使去噪也难以识别信号中的放电脉冲，需要从信号中提取特征来进行脉冲识别，提取的特征包括小波能量分布特征[19]、纹理特征[20]等，这类方法存在的困难在于特征的选择及特征维的减少。
目前存在的脉冲分割方法主要有：①基于形态学的方法。文献[18]采用多尺度形态学技术得到PD信号的包络曲线，通过包络曲线的极值点与瞬时相位的关系来判断脉冲起止点，取得了较好的脉冲分割效果。②基于时域能量的方法。文献[21]通过把幅值阈值设置为噪声平均值的5倍来判断放电起点，并通过计算平均能量及近似曲率来判断放电终点；文献[22-23]采用滑动时窗法采集单次脉冲；文献[24]利用背景与脉冲能量的差异来确定脉冲边沿；文献[25]利用时窗能量法结合峭度计算来判断PD信号的发生并确定脉冲边沿。③基于数理统计方法。文献[26]通过计算各点发生PD信号脉冲的概率来判定脉冲起点；文献[27]提出了一种逻辑判断法，以第一个过阈值点的半波零点为脉冲起点，最后一个过阈值点的半波零点为脉冲终点。④基于图像分割的方法。文献[28]基于Otsu算法自适应地得到幅值阈值和时间间隔阈值，通过双阈值判断脉冲发生点，该方法能够较好地识别出放电相位。
上述大多数方法都仅根据放电信号峰值抓取放电脉冲，会把冲击干扰错误地统计为放电脉冲。为了在脉冲分割过程中尽可能保留原有的放电信息并减少人工干预，本文提出一种基于聚类算法的PD脉冲分割方法。该算法首先将PD信号由过零点分成许多半波，计算各半波的能量，建立能量集；然后采用Otsu算法对能量集进行一次分割，分割过程中会把能量小的元素滤除，便可去掉干扰脉冲，得到放电集；最后以放电集为待聚类对象，采用DPC聚类算法，把属于同一次放电的半波聚为一类，记一次放电。对分割得到的所有放电脉冲分别取头尾过零点，即可得到脉冲起点和终点。本文利用在实验室采集到的各类型PD数据，验证了所提方法的正确性。
PRPD模式的三个基本参数为放电次数n、视在放电量q及放电相位j。其中，视在放电量q一般都是用PD采集过程中的放电幅值来表征。鉴于每个放电脉冲都存在升降过程，而能量是信号瞬时值的平方对时间的积分，故可用放电能量来刻画局部放电。由于波形分割的目的是将所有放电脉冲分离开，脉冲的边界显然是过零点，这些过零点将PD脉冲序列划分为许多的半波。将所有半波作为放电信号脉冲分割的基本对象，计算出各半波的能量，根据该能量大小进行分割。这样，能量小的冲击干扰采样点就可以被滤掉。图1为电晕放电信号去噪后的波形，图中标示出了所有极值点分布。
图1 电晕放电去噪后的放电波形极值点分布
Fig.1 Corona discharge after denoising and its extremum points
从每个极值点分别向前、向后寻找并记录最近的过零点，得到所有半波。计算每个半波的能量并归一化处理，最后得到原始PD脉冲半波能量集。对图1所示共2×104个采样点的局部放电信号，计算其中的半波能量，得到图2所示半波序列能量 分布。
设原始PD脉冲半波能量集为{Ei}，i表示半波序号，Ei表示第i个半波的能量。从图2中可以看出，样本中含有大量能量值很小的元素，它们不是放电半波，一般为干扰，需要先排除掉。应用一次分割算法，得到分割阈值Th，将能量集{Ei}分为放电集{Ei1}和非放电集{Ei2}。对图2所示的半波序列能量集处理后，可得去除小能量半波后的放电集{Ei1}，其元素在图3a中标记出来。
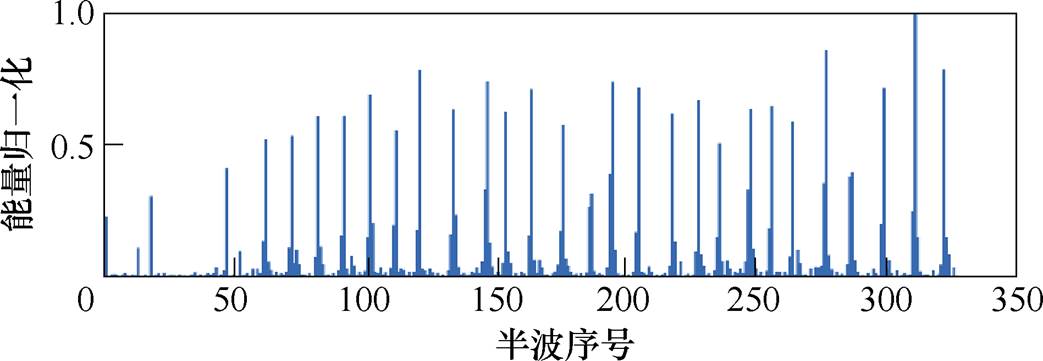
图2 原始PD脉冲半波序列及其能量分布
Fig.2 Original PD pulse half-wave sequence and its energy distribution
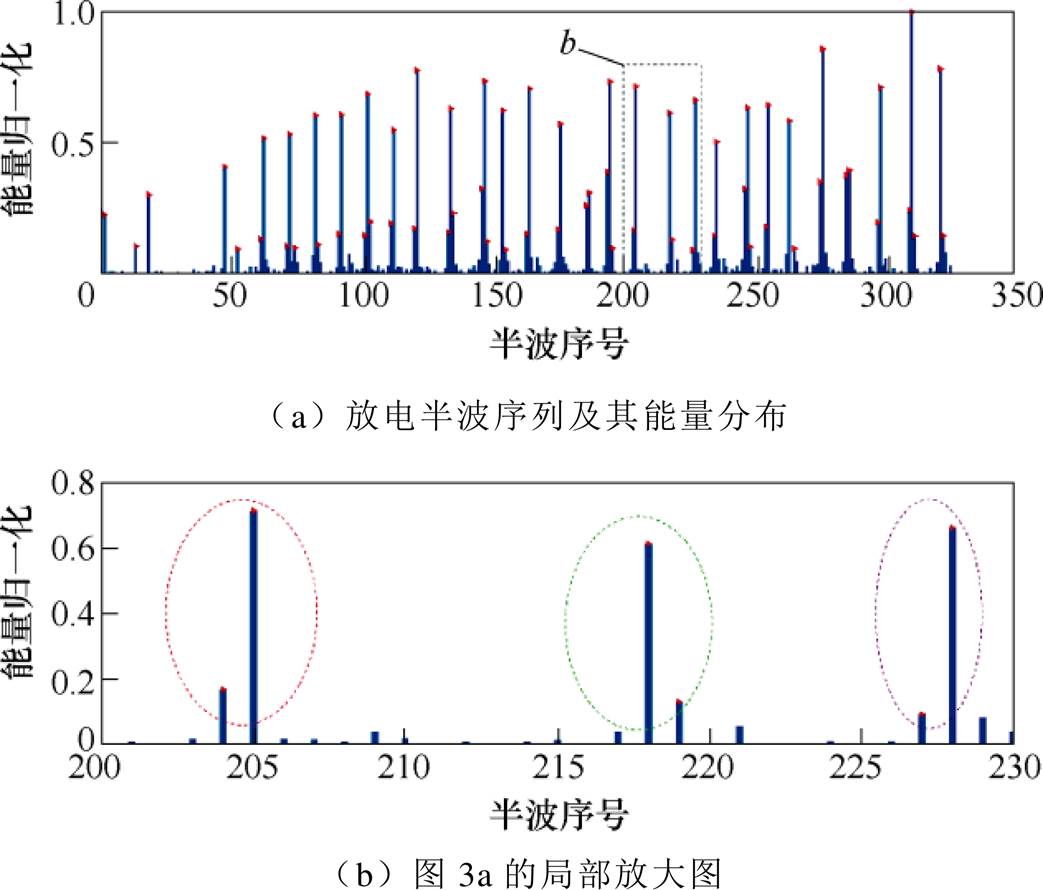
图3 放电半波序列及其能量分布
Fig.3 Discharge half-wave sequence and its energy distribution
记局部放电信号中一次放电脉冲为Pi，则有Pi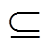
{Ei1}，且Pi中的元素序号是相连的。本文脉冲分割的准则：①若多个半波元素在放电集中的序号很近，且放电时刻距离很近，则这些半波被视为一个放电脉冲，并以该次放电的最大值点为放电位置；②若多个半波元素在放电集中的序号较远，放电时刻距离也较远，则被划分为不同的放电脉冲。图3b中，处于同一个椭圆中的半波可认为属于同一次局部放电，而不同椭圆代表不同次的放电。注意，当放电频率高，相邻两次放电的间隔小于局部放电仪的放电检测时间分辨率时，相邻两次甚至多次放电将被视为一次放电，这会影响放电次数的统计，但不影响各种类型放电脉冲的相位分布规律。
根据以上分析，本文使用聚类算法将属于同一次放电的半波聚为一类，从而实现脉冲分割。在本文模型下，唯一的变量是半波之间的采样点时间距离，是一维聚类问题。
1.2.1 Otsu分割算法
Otsu算法[29]由日本学者Otsu于1979年提出，它基于最大类间方差原则，能够根据背景类和目标类的灰度直方图自适应地计算出合适的分割阈值，一直是自适应分割问题的最佳算法。本文采用Otsu算法计算能量分割阈值。
样本集被阈值k分为背景类CB与目标类CO两类，各自均值分别为
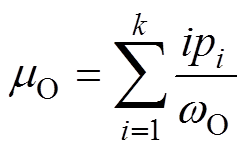（1）
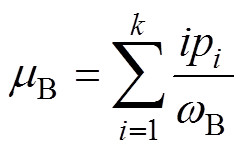（2）
式中，w0和wB分别为目标类和背景类的概率；pi为灰度级i出现的概率，i∈[0, 255]取整。
令
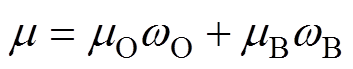（3）从而得到类间方差为
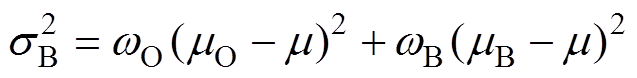（4）
Otsu算法求取分割阈值的公式为
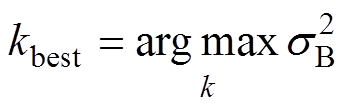（5）文献[30]证明，Otsu算法在处理类间方差相差较大的情况时得到的最佳阈值会偏向方差较大的一类。因此，本文根据文献[28]，采用二次Otsu算法计算所得最佳阈值如图4所示。
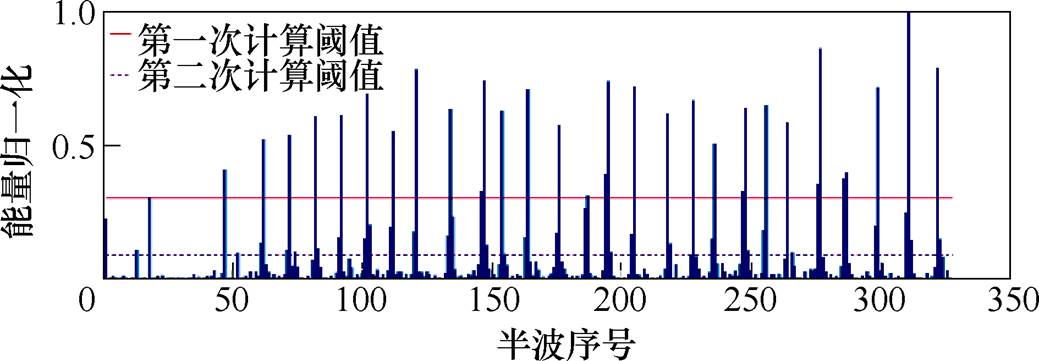
图4 Otsu算法计算阈值
Fig.4 calculates threshold through Otsu algorithm
从图4中可以得到结论，当第一次计算阈值偏大时，会漏掉一些小的放电半波，而在第二次计算过后，基本上能够提取到大部分属于放电脉冲的半波，同时滤除干扰半波。这些半波构成了放电集{Ei1}。
1.2.2 DPC聚类算法
在进行半波聚类时，只需考虑到各半波间的间隔。该间隔关系着放电半波的分布密度，因此脉冲分割适合使用基于密度分布[31]的聚类算法。
DPC算法[32]，即密度峰值聚类法，由Rodriguez和Laio等于2014年首次提出，能自动确定出任意形状样本集的聚类中心，因其计算快速及原理简单受到重视。算法基于两个对簇类中心的基本假设：
（1）簇类中心的局部密度大于其邻居点。
（2）不同簇类中心的距离较远。
局部密度ri的计算公式为
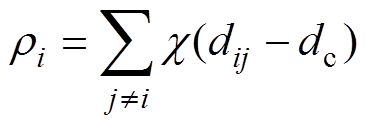（6）式中，dij为i、j两样本点的距离；dc为选定截断距离，而函数χ的定义为
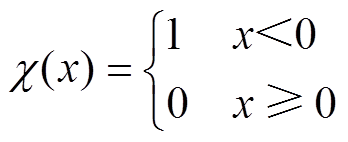（7）
设I={i}为样本序号集，则有样本i的距离参数δi的计算公式为
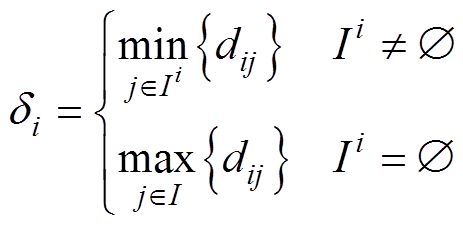（8）式中，对每个样本i，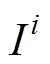
是I的子集，其由满足式（9）的点序号组成。
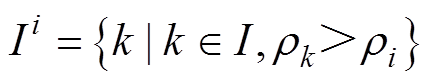（9）
DPC算法需要调节的参数只有一个，即截断距离dc。
计算局部密度时，除选择如式（7）所示的Cut-off Kernel外，亦可选择其他Kernel函数，关于局部密度和截断距离的详细论述参见文献[32]。
对放电集{Ei1}中的每个元素分别计算ρ和δ及gi=ridi，作出决策图来决定簇类中心，如图5所示。图5a为r-d 图，圈中数值为放电集{Ei1}中元素的编号，每一个数字编号代表一次放电脉冲。对于同时具有较大的r （密度）和d（距离）的点，会从其他点中“突出”，如68号和34号点。有些放电脉冲会远离其他放电脉冲，其d 很大但r 很小，在图中表现为离群点，如1号和74号点，以这两类点作为候选聚类中心。但是用肉眼观察r-d 图以寻找聚类中心时主观性较强，有时候无法确定准确的聚类中心，如图5a所示。为进行定量判断，本文对{gi}降序排列，其结果如图5b所示，从其局部放大图中可以看出，g 的取值存在一个明显的跳跃，于是此次聚类算法以g =200为界，选择若干g 值大于200的点作为各簇的聚类中心。
确定完中心点后，进一步利用边界区域对每个簇计算平均局部密度上界raver，判断所有非中心点归属。大于该密度上界的点属于当前簇，否则属于其他簇（边界区域由这样的点构成：属于该簇，但是与其他簇样本的距离小于截断距离dc）。
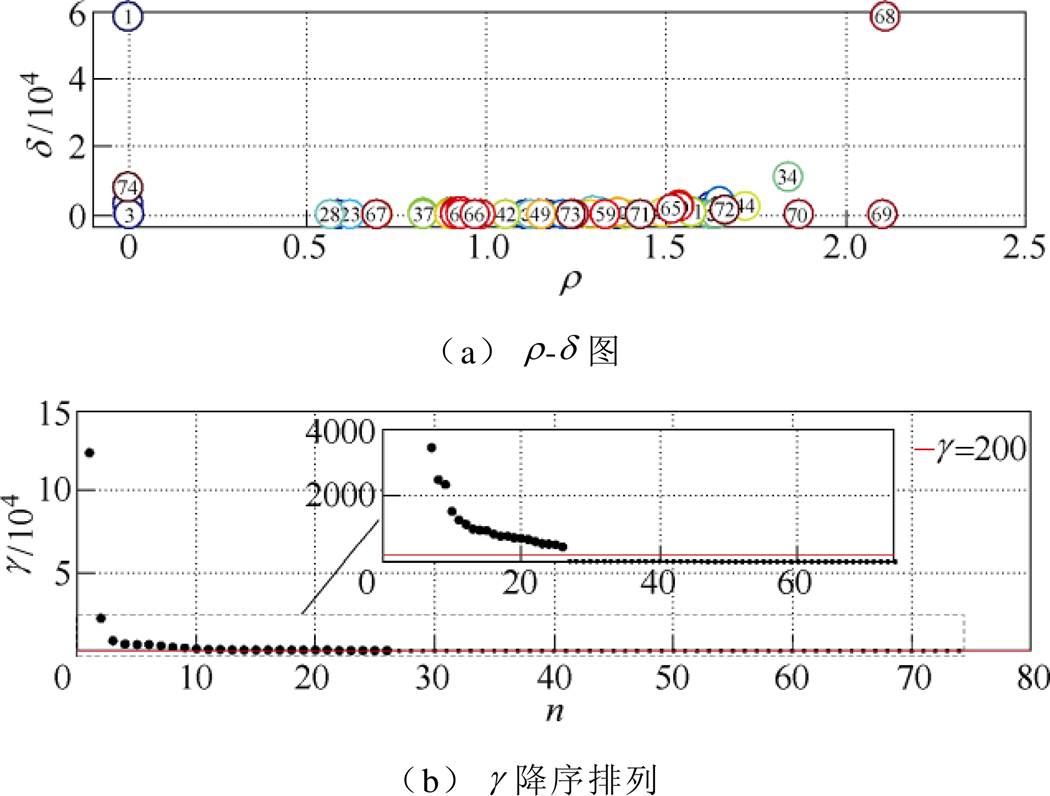
图5 聚类中心决策图
Fig.5 Clustering center decision graph
本文提出的脉冲分割算法主要有三部分：数据处理与原始PD脉冲半波能量集的建立、自适应阈值计算和聚类计算。自适应PD脉冲分割流程如图6所示。
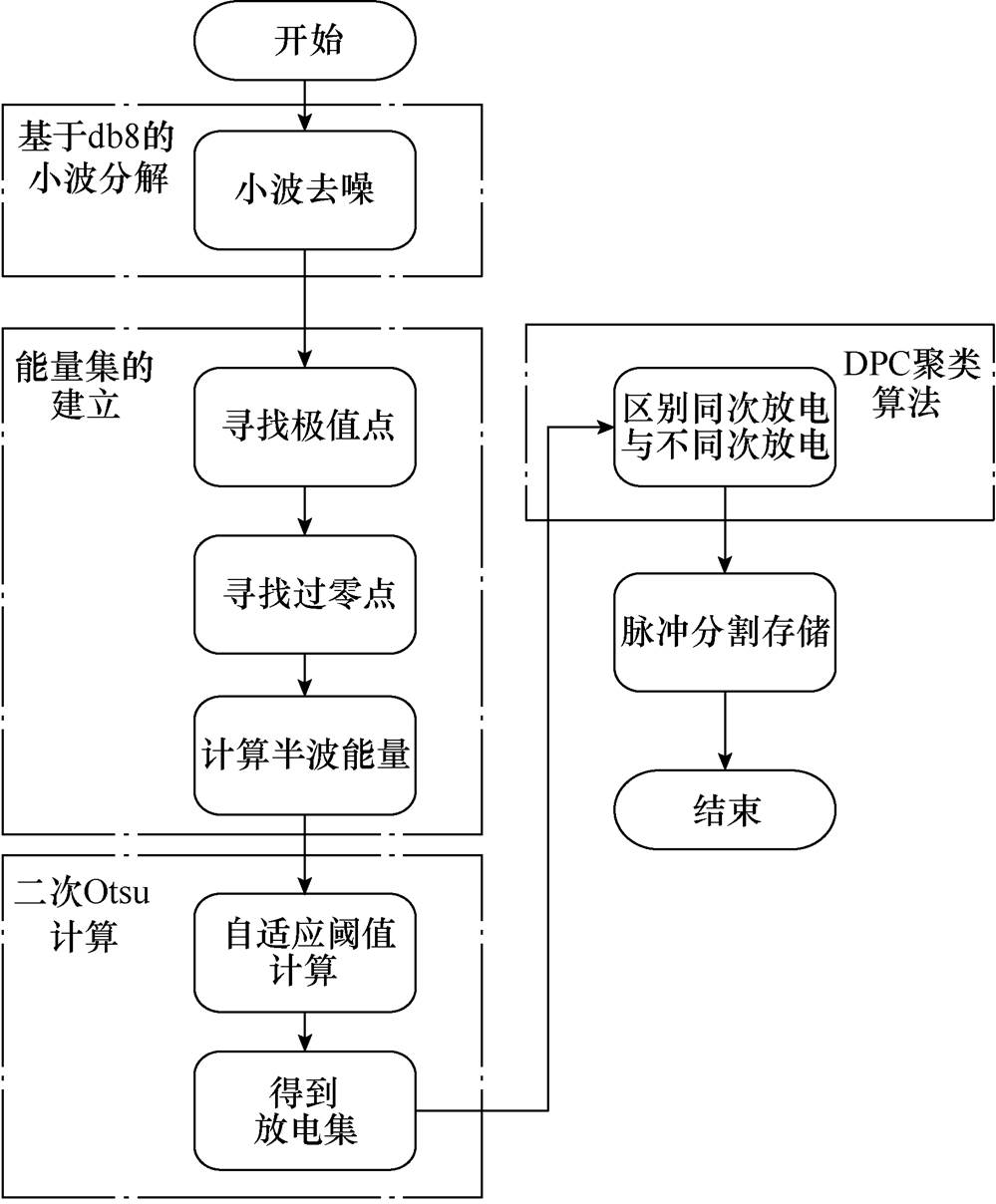
图6 自适应PD脉冲分割流程
Fig.6 Flow chart of adaptive PD pulse segmentation
为验证本文提出的PD脉冲分割算法准确性，在实验环境下设计了不同PD放电模型进行放电实验，信号采集系统原理接线图如图7所示。使用的PD分析仪为TWPD-2F局部放电综合分析仪，一组PD数据采集时间为1个工频周期，即20ms，采样频率是1MHz。
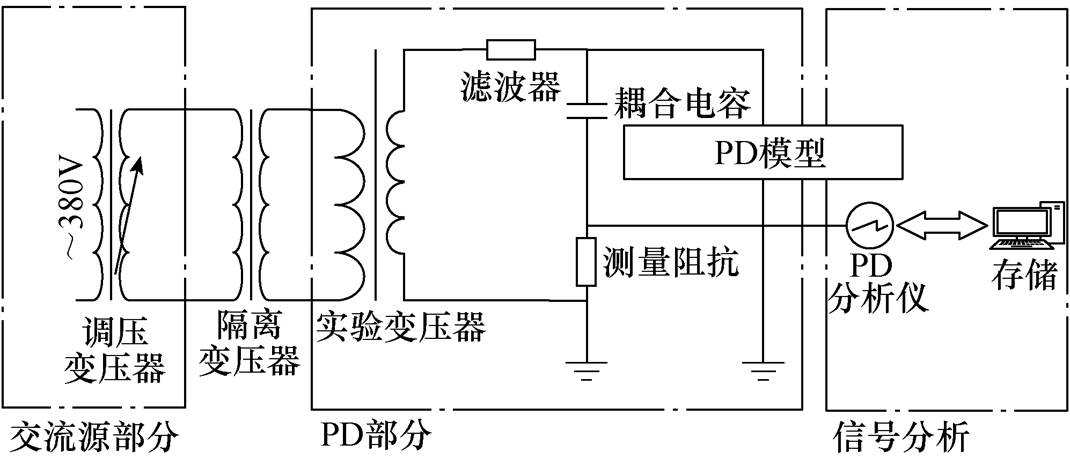
图7 实验室高压PD信号采集系统原理接线图
Fig.7 Principle wiring diagram of high voltage PD signal acquisition system in laboratory
选择三种典型的PD类型，其脉冲分布各有特点：电晕放电量相对较大，而且比较密集；悬浮放电则放电量相对较小，且比较分散；锥板放电的脉冲分布最分散。
图8为实验室中采用的三种放电模型，其中电晕放电是外部放电，是对空气放电；悬浮放电与锥板放电都是在油中的放电。电晕放电实验采用铜线，悬浮放电采用螺母作悬浮颗粒，锥板放电采用绝缘纸分开两侧的锥和板电极。
图8 电晕放电模型、悬浮放电模型和锥板放电模型
Fig.8 Corona discharge model、suspended discharge model and cone-plate discharge model
PD信号容易受到干扰，采集或实验现场环境又非常复杂，如图9所示，是三种受到明显噪声影响的PD采集信号。
从图9可知原始PD信号中噪声较多，需要对其进行必要的滤波处理。小波变换非常适合处理非平稳信号[33]，在时频域都有良好的表现。在众多小波基函数中，Daubechies小波基是一种应用广泛的正交小波基，与PD信号之间具有极高的相似度，特别是db4和db8小波基[34]，本文选择db8小波基进行小波变换。
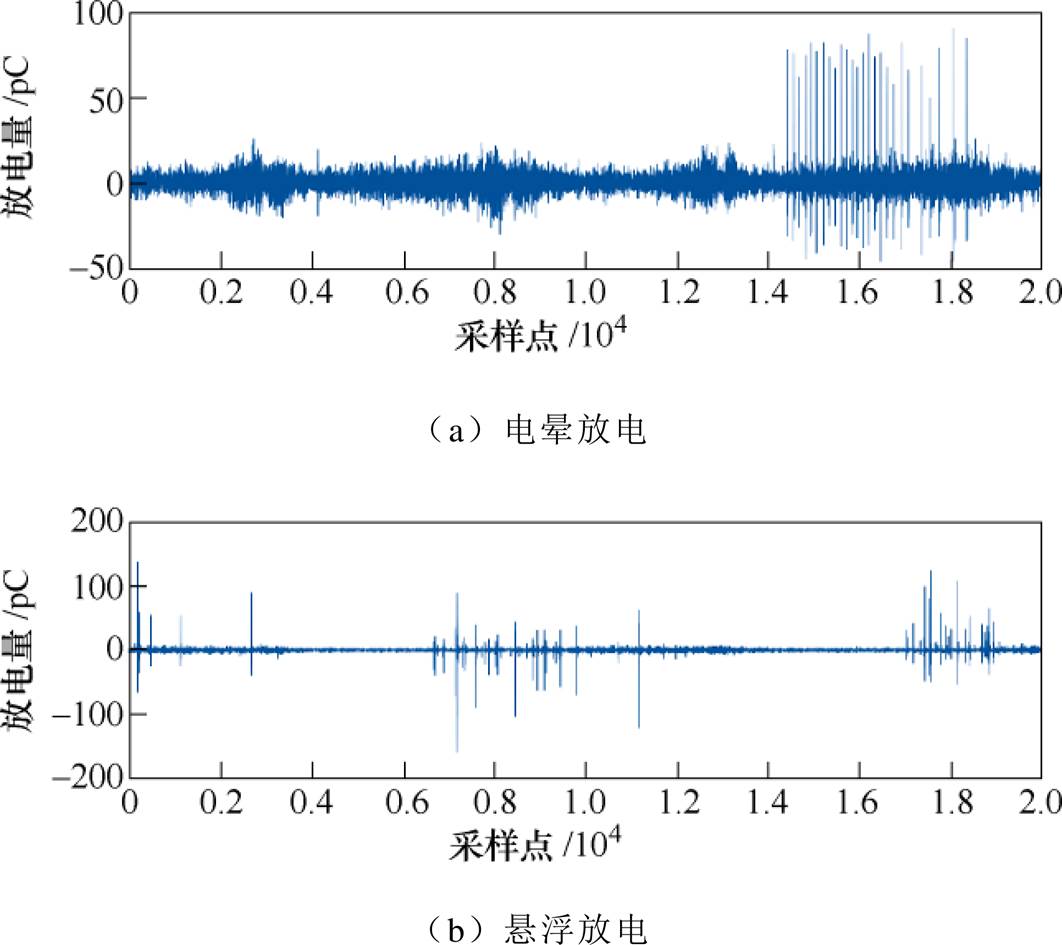
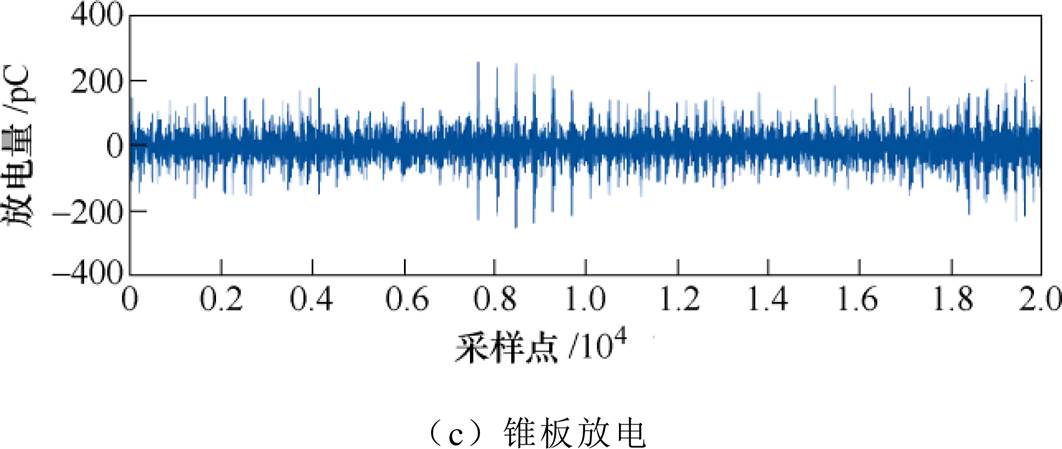
图9 典型放电模型的放电波形
Fig.9 Discharge waveforms of typical discharge models
由于无法得到原始无噪信号，故不能得到信噪比（Signal to Noise Ratio, SNR）、波形相似度（Normalized Correlation Coefficient, NCC）等参数。鉴于此，本文采用噪声抑制比（Noise Rejection Ratio, NRR）[35]来描述滤波效果，NRR计算公式为
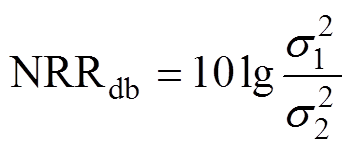（10）式中，s1和s2分别表示滤波前后的信号方差；NRR越大表示滤波效果越好。
对染噪信号进行基于db8小波基的分解，得到不同分解层级下滤波后的NRR，如图10所示。
综合考虑后，选择小波分解层级为9，用x代表原局放信号，根据固定值原则计算的小波去噪阈值为
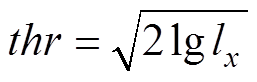（11）
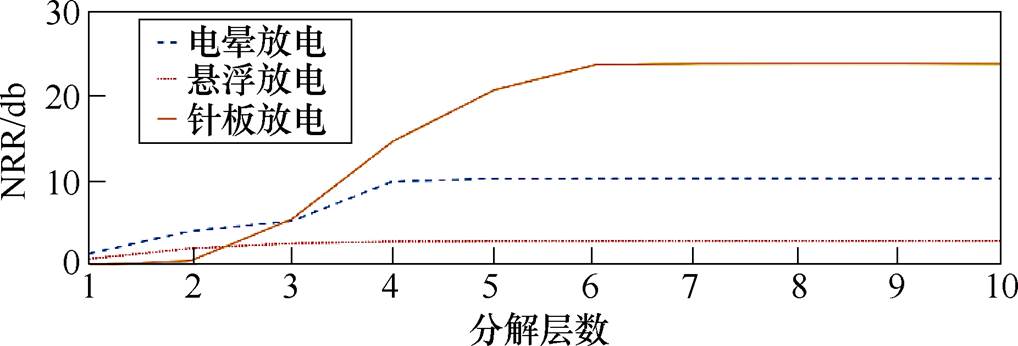
图10 不同小波分解层级下的NRR
Fig.10 NRRs at different wavelet decomposition levels
式中，lx表示原信号的长度。将该阈值与各尺度下的噪声方差相乘得到修正后的阈值，然后利用软阈值函数过滤含噪的小波系数，滤波后的结果如图11所示。
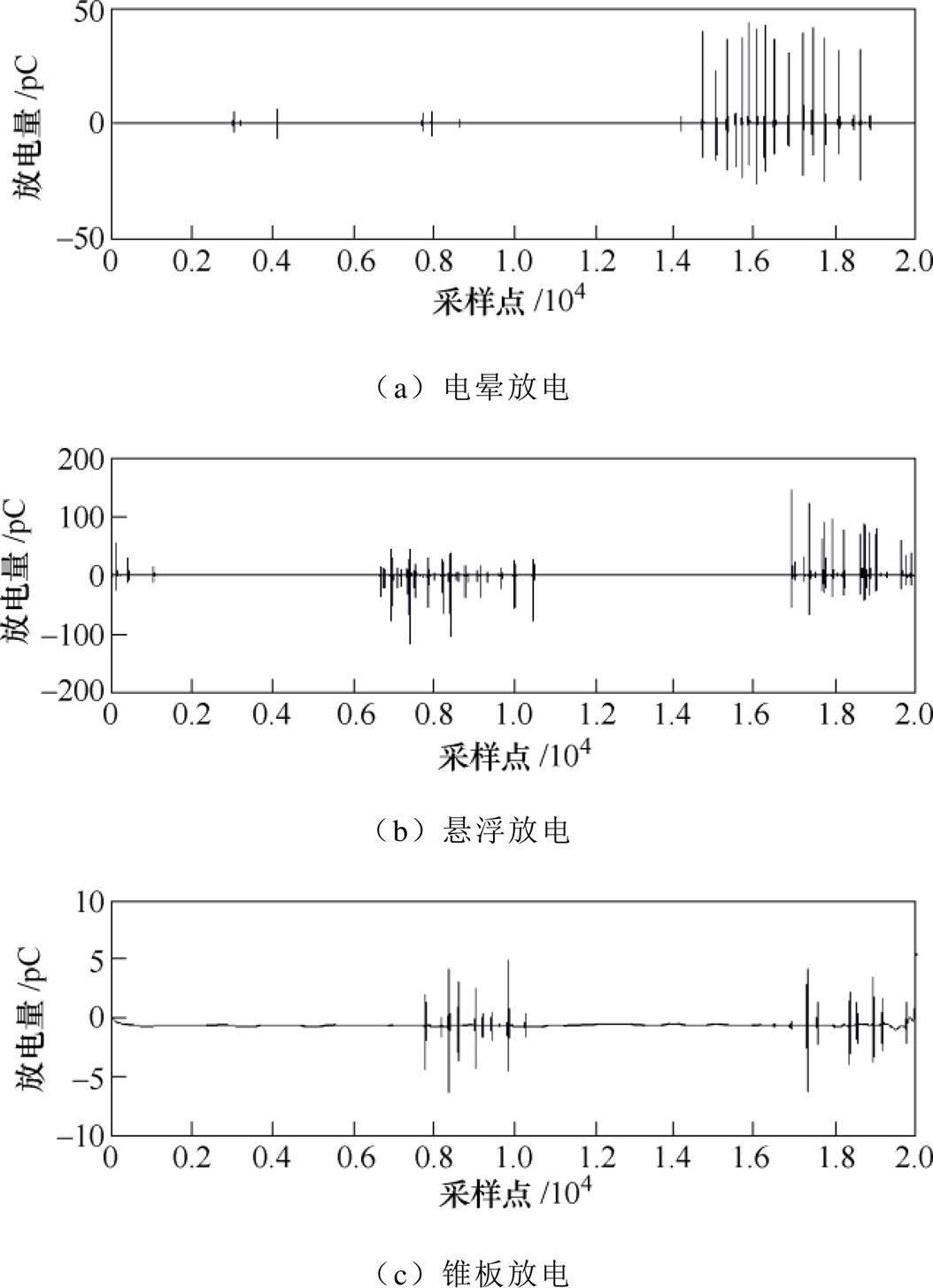
图11 小波去噪后的PD波形
Fig.11 PD waveforms after wavelet denoising
由图11可以看出，小波去噪基本能去除噪声干扰，同时很好地保留一些放电细节。
对去噪后的PD信号应用二次Otsu算法进行自适应能量阈值计算，根据本文提出的PD信号脉冲分割原理可获得放电脉冲如图12所示，图中标识出的放电半波序列是根据第二次Otsu计算的阈值进行分割得来（图12各图左侧为能量分布图及两次Otsu计算所得的阈值，较大的为第一次，右侧为放电半波序列）。
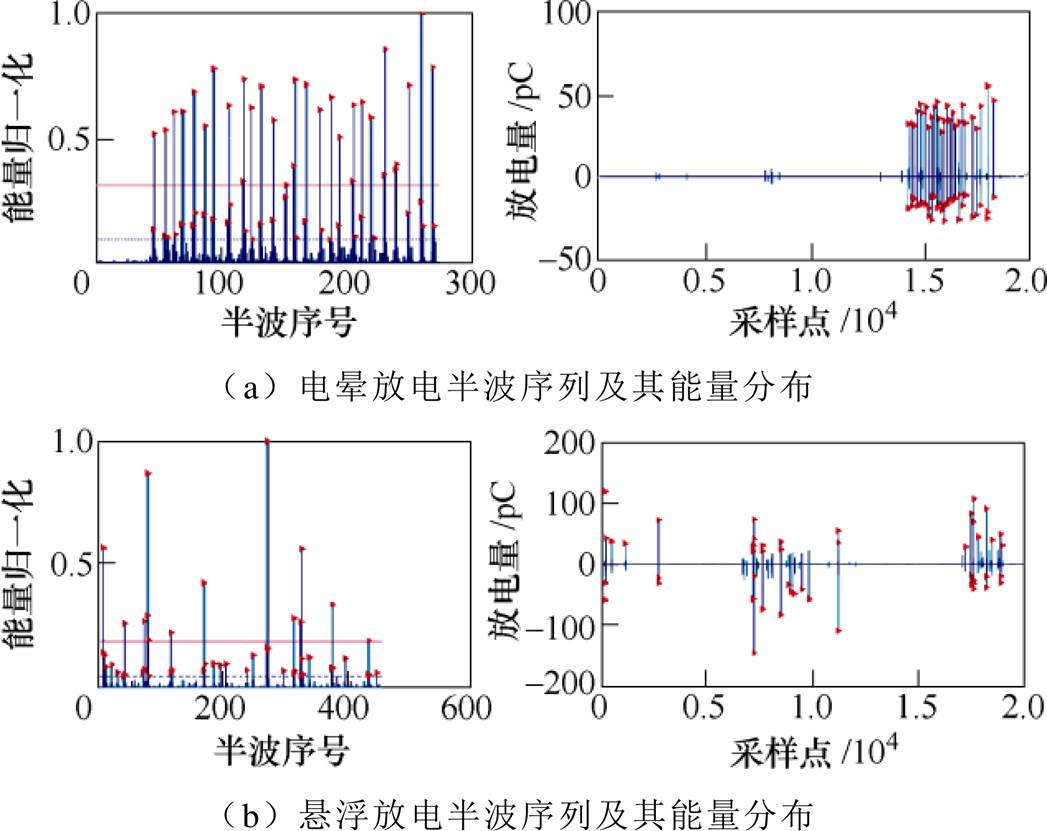
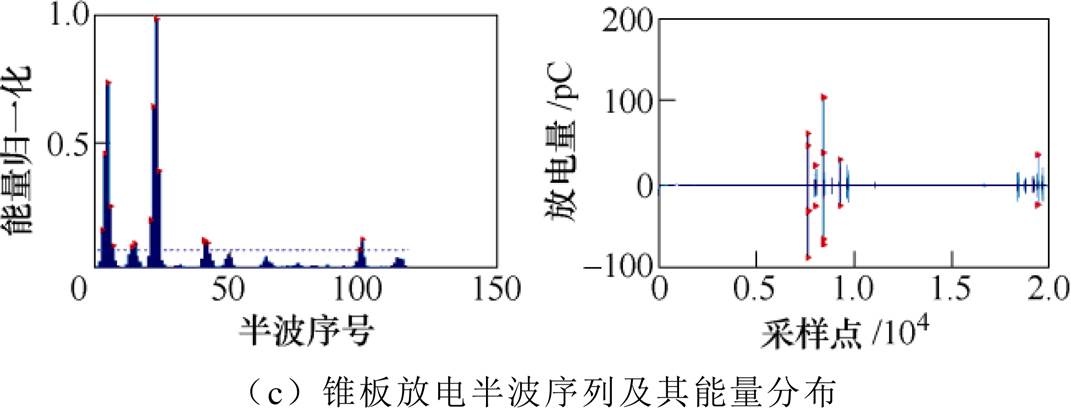
图12 PD信号放电半波序列及其能量分布
Fig.12 PD pulse and its energy distribution and adaptive threshold
对放电集应用DPC聚类算法聚类，结果如图13所示。
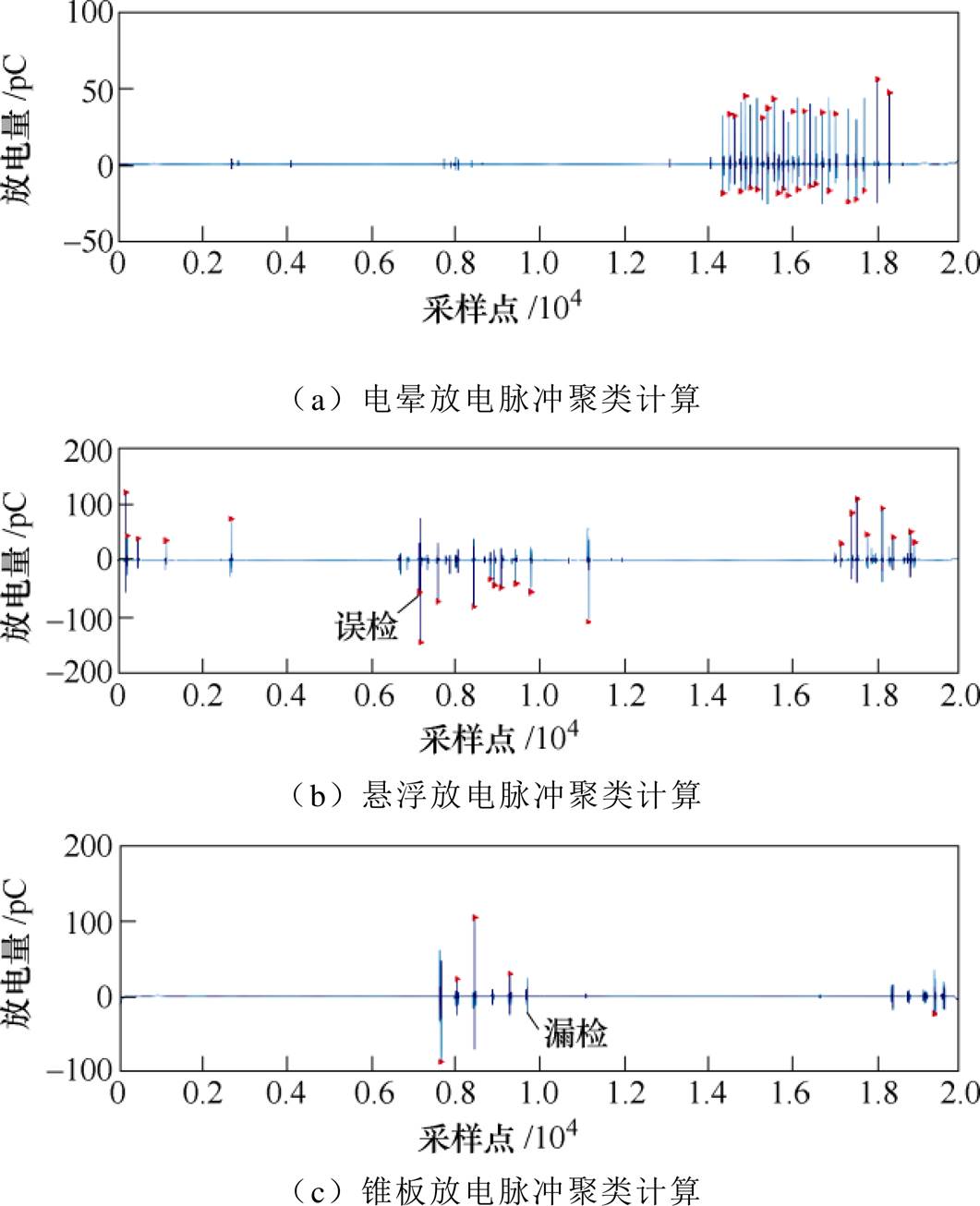
图13 聚类计算及PD脉冲识别
Fig.13 Cluster computing and PD pulse recognition
对原始PD放电信号进行脉冲分割之后，需要存储识别出的各个放电脉冲的编号、峰值、起始和终止时刻，以便进行进一步的放电模式识别。表1为某一PD信号经本文脉冲分割方法分割后所得结果的脉冲存储格式。
表1 脉冲存储格式
Tab.1 Pulse storage format
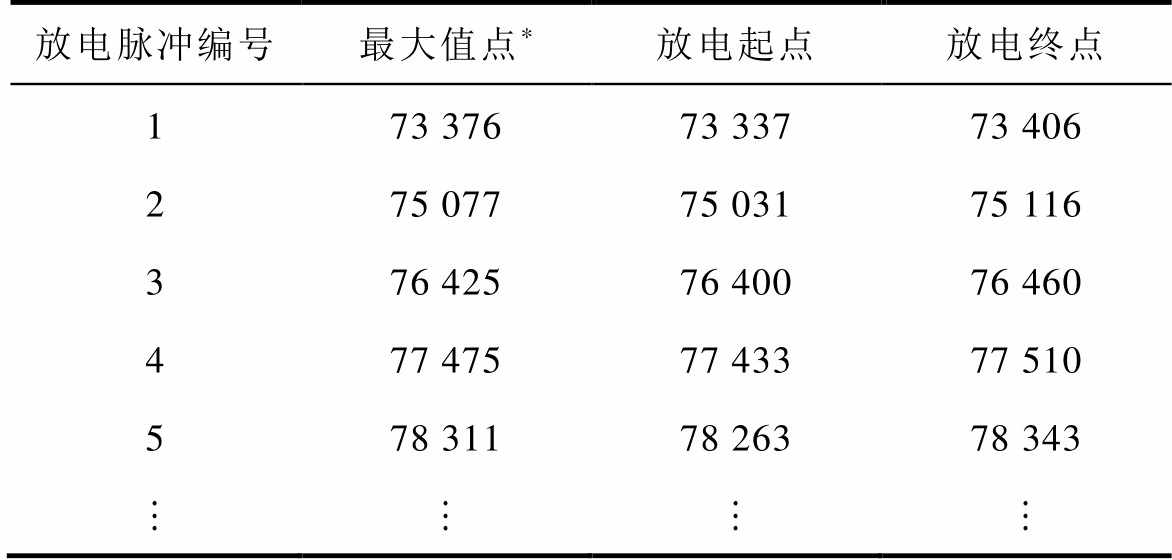
放电脉冲编号最大值点*放电起点放电终点 173 37673 33773 406 275 07775 03175 116 376 42576 40076 460 477 47577 43377 510 578 31178 26378 343
注：*为以最大值点表示该次放电的位置。
从表1可以看到，每个脉冲储存长度在50～100个点，在采样率1M/s下相当于每个放电脉冲在几十ms左右（图7中的测量阻抗会把实际几十ns[13]的放电电流脉宽拉长到ms级）。
为了验证本文所提方案的准确性，选择逻辑判断法[27]和双阈值法[28]做对比实验，各算法的参数设置可在相应文献中查到，文献中未明确指出的按照经验值设置。分别取电晕放电信号10组，悬浮放电信号11组，锥板放电信号30组，统计放电次数，结果见表2。
表2 放电次数统计
Tab.2 Statistics of discharge number
放电类型识别方法 聚类分割法双阈值法逻辑法 电晕放电次数752714691 误检19(2.582%)3(0.408%)0 漏检1(0.136%)25(3.40%)45(6.11%) 悬浮放电次数169165209 误检8(4.47%)11(6.15%)30(16.8%) 漏检18(10.1%)25(14.0%)0 锥板放电次数208158144 误检48(19.6%)30(17.8%)5(3.07%) 漏检3(1.84%)35(19.0%)24(14.7%)
由于本文采用的局放数据是无标签数据，因此在统计表2中的放电次数及误检和漏检时，采用的是人工法。误检是指将本不是放电的脉冲误计为放电脉冲，漏检是指将本为放电的脉冲漏统计。表2的结果说明本文方法能够较好地分割各放电脉冲。双阈值法和逻辑判断法算法的脉冲分割识别结果如图14所示。
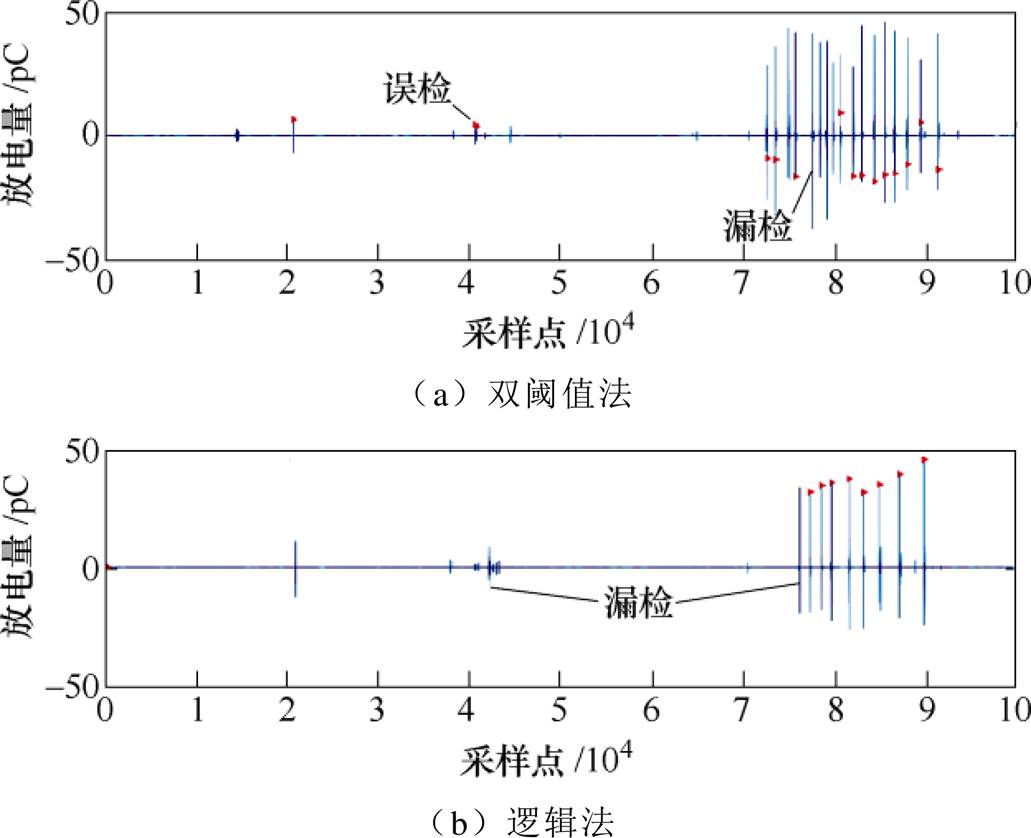
图14 双阈值法和逻辑判断法算法的PD脉冲识别结果
Fig.14 PD pulse recognition results of each methods
从上面的实验结果可以看出，各算法对电晕放电都能取得不错的识别率，而对悬浮放电和锥板放电的识别率逐步下降。原因在于电晕放电一般能量较大，且放电位置相对集中，有利于对放电点的判断及对放电位置的确定，故提高了算法的识别率。悬浮放电能量次之，锥板放电能量最小，且放电分布最分散。对锥板放电来说，在其放电过程中一个放电脉冲后往往紧接着一个距离很近的能量较小的放电脉冲，而且放电位置分布不具有规律性，表现出更强的随机性，导致各算法识别率下降。但总体上看，本文所提的算法识别率更高或与同类算法相当，证实了基于密度峰值聚类算法的脉冲识别方法的优越性。
本文从数据处理和模式构造两方面论证了局部放电脉冲分割的必要性，进而提出一种脉冲分割算法，能够在减少人工干预的情况下，尽量保留多的局部放电信息。考虑到采集的PD信号一般都存在噪声干扰，需要进行滤波。db小波基非常适合于处理非平稳信号，因此本文采用db8小波基对PD放电进行滤波处理，得到了相对理想的PD信号。由于通过放电幅值来识别放电脉冲并不充分（不能识别放电时间很短但幅值大的脉冲干扰），故本文提出了使用放电能量来刻画放电过程，只有放电能量超过指定阈值的脉冲被识别为放电脉冲。使用Otsu算法能自适应地得到脉冲分割能量阈值，利用该阈值可将能量集分为放电集与非放电集。考虑到同一次PD的放电脉冲分布集中，而不同次PD的放电脉冲距离较远，可用密度来描述各放电脉冲的分布。于是使用基于密度峰值的聚类算法，对放电集脉冲进行聚类计算，将属于同一次PD的放电脉冲分为一类，不同次PD的放电脉冲分属为不同类，从而实现了放电脉冲的自适应分割。实验证明了本文所提方法是一种有效的脉冲分割手段。
参考文献
[1] 齐伟强, 李俭, 陈柏超, 等. 基于COMSOL的变压器中超声波传播特性[J]. 电工技术学报, 2015, 30(增刊2): 195-200.
Qi Weiqiang, Li Jian, Chen Baichao, et al. Ultrasonic wave propagation characteristics of the transformer based on COMSOL[J]. Transactions of China Electrotechnical Society, 2015, 30(S2): 195-200.
[2] 周加斌, 陈玉峰, 井雨刚, 等. 特高压变压器磁屏蔽接地线断裂引起局部放电异常的检测与分析[J]. 电力系统保护与控制, 2018, 46(3): 110-115.
Zhou Jiabin, Chen Yufeng, Jing Yugang, et al. Detection and analysis of abnormal partial discharge caused by the fracture of magnetic shielding ground line in UHV transformer[J]. Power System Protection and Control, 2018, 46(3): 110-115.
[3] 李臻, 罗林根, 盛戈皞, 等. 基于压缩感知的特高频局部放电定位法[J]. 电工技术学报, 2018, 33(1): 202-208.
Li Zhen, Luo Lingen, Sheng Gehao, et al. Ultrahigh frequency partial discharge localization methodology based on compressed sensing[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 202- 208.
[4] 司文荣, 李军浩, 袁鹏, 等. 局部放电光测法的研究现状与发展[J]. 高压电器, 2008, 44(3): 261-264.
Si Wenrong, Li Junhao, Yuan Peng, et al. Current situation and development of optical detection for partial discharge[J]. High Voltage Apparatus, 2008, 44(3): 261-264.
[5] 张晓星, 董星辰, 陈秦川. 锐钛矿型(101)晶面吸附SF6局部放电分解组分的气敏机理分析[J]. 电工技术学报, 2017, 32(3): 200-209.
Zhang Xiaoxing, Dong Xingchen, Chen Qinchuan. Gas sensing mechanism analysis of SF6 decomposed gases adsorption on anatase (101) surface under partial discharge[J]. Transactions of China Electro- technical Society, 2017, 32(3): 200-209.
[6] 郭俊, 吴广宁, 张血琴, 等. 局部放电检测技术的现状和发展[J]. 电工技术学报, 2005, 20(2): 29-35.
Guo Jun, Wu Guangning, Zhang Xueqin, et al. The actuality and perspective of partial discharge detection techniques[J]. Transactions of China Elec- trotechnical Society, 2005, 20(2): 29-35.
[7] 程养春. 发电机定子绝缘局部放电非接触式在线监测方法的研究[D]. 北京: 华北电力大学, 2005.
[8] Krivda A. Automated recognition of partial dis- charges[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1995, 2(5): 796-821.
[9] 贾亚飞, 朱永利, 王刘旺, 等. 基于VMD和多尺度熵的变压器内绝缘局部放电信号特征提取及分类[J]. 电工技术学报, 2016, 31(19): 208-217.
Jia Yafei, Zhu Yongli, Wang Liuwang, et al. Feature extraction and classification on partial discharge signals of power transformers based on VMD and multiscale entropy[J]. Transactions of China Electro- technical Society, 2016, 31(19): 208-217.
[10] 王刘旺, 朱永利, 贾亚飞, 等. 局部放电大数据的并行PRPD分析与模式识别[J]. 中国电机工程学报, 2016, 36(5): 1236-1244.
Wang Liuwang, Zhu Yongli, Jia Yafei, et al. Parallel phase resolved partial discharge analysis for pattern recognition on massive PD data[J]. Proceedings of the CSEE, 2016, 36(5): 1236-1244.
[11] Wei Gang, Tang Ju, Zhang Xiaoxing, et al. Gray intensity image feature extraction of partial discharge in high-voltage cross-linked polyethylene power cable joint[J]. International Transactions on Elec- trical Energy Systems, 2014, 24(2): 215-226.
[12] 沈煜, 阮羚, 谢齐家, 等. 采用甚宽带脉冲电流法的变压器局部放电检测技术现场应用[J]. 高电压技术, 2011, 37(4): 937-943.
Shen Yu, Ruan Ling, Xie Qijia, et al. On-site application of partial discharge detection of trans- former using very wide bandwidth pulse current method[J]. High Voltage Engineering, 2011, 37(4): 937-943.
[13] 邱昌容, 王乃庆. 电工设备局部放电及其测试技术[M]. 北京: 机械工业出版社, 1994.
[14] 唐志国, 唐铭泽, 李金忠, 等. 电气设备局部放电模式识别研究综述[J]. 高电压技术, 2017, 43(7): 2263-2277.
Tang Zhiguo, Tang Mingze, Li Jinzhong, et al. Review on partial discharge pattern recognition of electrical equipment[J]. High Voltage Engineering, 2017, 43(7): 2263-2277.
[15] 李剑. 局部放电灰度图象识别特征提取与分形压缩方法的研究[D]. 重庆: 重庆大学, 2001.
[16] Lapp A, Kranz H G. The use of the CIGRE data format for PD diagnosis applications[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2000, 7(1): 102-112.
[17] Lim Yun-Seog, Kim Sung-Hong, Ko Jae-Ho, et al. Identification of chaotic characteristics in partial discharge[C]//Dielectric Liquids, Proceedings of the IEEE 13th International Conference on Dielectric Liquids, Nara, Japan, 1999: 556-559.
[18] Long Jiachuan, Wang Xianpei, Tian Meng, et al. A novel automatic pulse segmentation approach and its application in PD-induced electromagnetic wave detection[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(1): 304-315.
[19] Bajwa Abdullah Akram, Habib Salman, Kamran Muhammad. An investigation into partial discharge pulse extraction methods[J]. International Journal of Electrical Power & Energy Systems, 2015, 73: 964-982.
[20] Darabad V P, Vakilian M, Blackburn T R, et al. An efficient PD data mining method for power transformer defect models using SOM technique[J]. International Journal of Electrical Power & Energy Systems, 2015, 71: 373-382.
[21] Nagesh V, Gururaj B I. Automatic detection and elimination of periodic pulse shaped interferences in partial discharge measurements[J]. IEE Proceedings- Science, Measurement and Technology, 1994, 141(5): 335-342.
[22] 刘明军. 变压器局放超高频监测与基于知识的分析方法研究[D]. 武汉: 华中科技大学, 2011.
[23] 王鹏, 吴广宁, 罗杨, 等. 连续高压脉冲方波下局部放电测试系统设计[J]. 高电压技术, 2012, 38(3): 587-593.
Wang Peng, Wu Guangning, Luo Yang, et al. Design of partial discharge testing system under continuous square pulse voltage[J]. High Voltage Engineering, 2012, 38(3): 587-593.
[24] 万元, 李朝晖, 薛松, 等. 水轮发电机局部放电在线监测中的脉冲识别方法[J]. 高电压技术, 2009, 35(9): 2169-2175.
Wang Yuan, Li Chaohui, Xue Song, et al. Pulses recognition method in partial discharge online monitoring of hydro-generators[J]. High Voltage Engineering, 2009, 35(9): 2169-2175.
[25] 张安安, 何聪, 孙茂一, 等. 基于峭度和时域能量的局放脉冲提取算法[J]. 电子科技大学学报, 2017, 46(4): 559-564.
Zhang Anan, He Cong, Sun Maoyi, et al. Partial discharge pulse extraction algorithm based on kurtosis and time domain energy[J]. Journal of University of Electronic Science and Technology of China, 2017, 46(4): 559-564.
[26] 贾嵘, 赵佳佳, 武桦, 等. 相关概率小波变换在局部放电检测中的应用[J]. 高电压技术, 2017, 43(9): 2896-2902.
Jia Rong, Zhao Jiajia, Wu Hua, et al. Application of correlated probabilistic wavelet transform in partial discharge detection[J]. High Voltage Engineering, 2017, 43(9): 2896-2902.
[27] 张士宝, 董旭柱, 林渡, 等. 局部放电监测中现场干扰的分析与抑制[J]. 清华大学学报: 自然科学版, 1997, 37(8): 109-112.
Zhang Shibao, Dong Xuzhu, Lin Du, et al. Analysis and suppression of field disturbance in partial discharge monitoring[J]. Journal of Tsinghua University: Sci & Tech, 1997, 37(8): 109-112.
[28] 王刘旺, 朱永利, 李莉, 等. 基于自适应双阈值的局部放电基本参数提取[J]. 高电压技术, 2016, 42(4): 1268-1274.
Wang Liuwang, Zhu Yongli, Li Li, et al. Extraction of fundamental parameters in partial discharge based on adaptive dual threshold[J]. High Voltage Engin- eering, 2016, 42(4): 1268-1274.
[29] Otsu Nobuyuki. A threshold selection method from gray-level histograms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1): 62-66.
[30] 许向阳, 宋恩民, 金良海. Otsu准则的阈值性质分析[J]. 电子学报, 2009, 37(12): 2716-2719.
Xu Xiangyang, Song Enming, Jin Lianghai. Charac- teristic analysis of threshold based on Otsu criterion[J]. Acta Electronica Sinica, 2009, 37(12): 2716-2719.
[31] 高诗莹, 周晓锋, 李帅. 基于密度比例的密度峰值聚类算法[J]. 计算机工程与应用, 2017, 53(16): 10-17.
Gao Shiying, Zhou Xiaofeng, Li Shuai. Clustering by fast search and find of density peaks based on density-raito[J]. Computer Engineering and Appli- cations, 2017, 53(16): 10-17.
[32] Rodriguez Alex, Laio Alessandro. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496.
[33] Glowacz Adam. DC motor fault analysis with the use of acoustic signals, coiflet wavelet transform, and K-nearest neighbor classifier[J]. Archives of Acoustics, 2015, 40(3): 321-327.
[34] 肖俊安. 基于稀疏分解算法的局部放电信号干扰抑制技术的学习与思考[D]. 武汉: 华中科技大学, 2016.
[35] Chang Dah-Chung, Chu Feitao. Feedforward active noise control with a new variable tap-length and step-size filtered-x LMS algorithm[J]. IEEE/ACM transactions on audio, speech, and language processing, 2014, 22(2): 542-555.
Partial Discharge Pulse Segmentation Based on Clustering by Fast Search and Find of Density Peaks
Abstract Partial discharge (PD) signal processing is the basis of insulation state evaluation of electric power equipment, and feature extraction is the key link of signal processing. The feature extraction includes two steps: partial discharge pulse segmentation and discharge feature extraction. Pulse segmentation extraction is the premise of subsequent feature extraction and fault classification of PD signals. In order to preserve discharge information as much as possible and reduce manual interference, a PD pulse segmentation method based on clustering algorithm is proposed in this paper. The wavelet decomposition algorithm is used for filtering, and the noise rejection ratio (NRR) is used to characterize the filtering effect. The method takes all the partial discharge half-wave pulses into consideration to calculate the energy of each half-wave which is the integral of squared instant value of the PD signal over time. Therefore, it can describe the process of partial discharge more accurately. The Otsu algorithm is used to calculate the energy threshold adaptively, and one density peak clustering algorithm, called as clustering by fast search and find of density peaks (DPC), is used to achieve automatic segmentation of PD pulses. Three types of partial discharge models are established in the laboratory. Data from 10 sets of corona discharge, 11 sets of suspension discharge and 30 sets of cone-plate discharge are collected to verify the method. The results have achieved a recognition rate of more than 80%, which is higher or equivalent to the existing similar algorithms, demonstrating the superiority of this method.
keywords：Partial discharge, Otsu adaptive energy threshold, adaptive energy threshold, pulse segment, clustering by fast search and find of density peaks (DPC)
中图分类号：TM85
DOI: 10.19595/j.cnki.1000-6753.tces. 190020
国家自然科学基金重点项目（51677072）和中央高校基本科研业务费专项资金项目（2018QN078）资助。
收稿日期 2019-01-03
改稿日期 2019-04-09
朱永利 男，1963年生，教授，博士生导师，研究方向为网络化监控与智能信息处理、电力设备监测大数据处理。E-mail: yonglipw@163.com（通信作者）
蒋 伟 男，1991年生，博士研究生，研究方向为输变电设备故障诊断。E-mail: paul_j@foxmail.com
（编辑 赵 鹏）