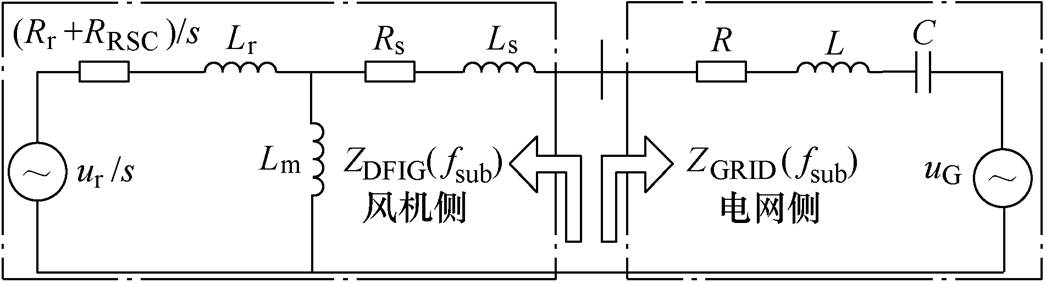
图1 DFIG接入串补系统在次同步频率下的等效电路
Fig.1 Equivalent circuit of DFIG integrated to a series-compensated system in sub-synchronous frequency
摘要 针对双馈风电场经串补系统外送功率时存在次同步控制相互作用（SSCI）问题，该文提出一种应用静止同步串联补偿器（SSSC）抑制SSCI的等效正电阻控制方法。该方法采用网侧线路中的电流作为输入信号，通过SSSC附加有源电阻控制（SARC）策略生成与线路中次同步电流同相位的次同步电压信号。SSSC实时跟踪该次同步电流信号，使其在次同步频率下等效为一正电阻。通过在网侧串接SSSC使网侧电阻增大，从而系统等值电阻被抬升至正值区域，进而达到抑制SSCI的效果。此外，详细介绍了SARC的结构及参数设计方法。最后，在PSCAD/EMTDC上搭建了华北某实际风电场时域仿真模型。仿真结果表明：多种运行工况下，SSSC可等效成正电阻使系统等值电阻处在正值区域，从而避免了系统发生SSCI。该方法具有参数整定简便、便于实现等优点。
关键词：双馈风电场 串补系统 次同步控制相互作用 SSSC 附加有源电阻控制
新能源技术的快速发展推动我国风电装机容量不断攀升。大型风电基地经固定串补外送电能时存在次同步振荡（Sub-Synchronous Oscillation, SSO）的风险[1-2]。其中，主流双馈风电机组（Doubly-Fed Induction Generator, DFIG）的稳定性问题尤为突出且备受关注[3-4]。2009年美国Texas某双馈风电场发生由固定串补引起的次同步振荡事故，造成大量风电机组脱网及撬棒电路损毁[5]；加拿大Buffalo Ridge地区及我国华北地区双馈风电场也相继出现此类事件[6-7]。
研究表明，该问题主要由DFIG换流器控制与线路串补之间的相互耦合引发，无机组轴系扭振参与，故称其为次同步控制相互作用（Sub-Synchronous Control Interaction, SSCI）[8]。不同于传统火电机组的次同步振荡问题，SSCI的振荡频率取决于换流器控制与输电系统的网架结构，同时与风电场出力情况密切相关[9]。由于风电机组出力存在波动性及随机性，致使其振荡频率具有显著时变的新特点[10]。2012年华北地区某双馈风电场出现6～8Hz的SSCI事件，其振荡频率随着风速和并网风机台数的增大而增大[7, 10]。因此，研究多运行工况下的SSCI抑制方法对提升风电场并网稳定运行具有显著的工程意义。
目前，针对抑制DFIG-串补系统的SSCI问题已提出诸多解决方案。由于DFIG换流器控制对SSCI起关键作用，因此提出在DFIG换流器中附加控制策略达到抑制SSCI的效果[8, 11]。其中代表性的附加控制策略包括在转子侧换流器内环控制或网侧换流器功率外环控制中引入抑制信号，从而达到在风机侧抑制SSCI的目的。另一方面，部分文献在风电场或电网侧接入含附加抑制策略的灵活交流输电系统（Flexible AC Transmission System, FACTS）装置，通过提升振荡频率下的系统阻尼达到抑制SSCI的效果[12-14]。其中代表性的含附加抑制策略的FACTS装置包括线路中并接的静止同步补偿器（Static Synchronous Compensator, STATCOM）和静止无功补偿器（Static Var Compensator, SVC）。虽然上述抑制措施具有一定效果，但基于附加控制策略的抑制方法，其参数整定对运行工况的适用性较差，并且对已投运的风电机组进行改造工程量较大；并联型FACTS装置注入电流存在分流稀释效应导致抑制效果有限，制约着其在工程中应用。
静止同步串联补偿器（Static Synchronous Series Compensator, SSSC）作为串联型FACTS家族的一员，通过向系统注入一个与线路电流几乎正交的电压，可实现对线路潮流的迅速调整[15]。因SSSC良好的控制灵活性，应用SSSC抑制火电机组次同步振荡问题的理论研究成果较多[15-18, 27]，但尚未有文献提出应用SSSC抑制风电次同步振荡问题。目前，世界上首套单独SSSC装置已在天津石各庄变电站成功投运，其功能仅用于潮流控制。在此背景下，研究利用SSSC附加控制策略抑制风电次同步振荡问题具有实际工程意义。
本文基于DFIG-串补系统SSCI的发生机理，提出一种增大系统在次同步振荡频率下电阻的SSSC附加控制策略，该策略可避免并联型FACTS装置注入电流的分流稀释效应。首先，阐述了SSSC等效正电阻抑制SSCI的原理；其次，介绍了SSSC的附加有源电阻控制（Supplementary Active Resistance Control, SARC）策略及SARC参数设计方法；最后，通过搭建华北某实际风电场PSCAD/ EMTDC仿真模型，验证SSSC附加控制策略在多种工况下对SSCI的良好抑制效果；SARC参数表现出较优的鲁棒性。
DFIG经固定串补并网时，在次同步频率fsub下的等效电路如图1所示[7,19-23]。
图1中DFIG经固定串补并网系统可分为风机侧和电网侧两部分，相关变量的说明如下。
图1 DFIG接入串补系统在次同步频率下的等效电路
Fig.1 Equivalent circuit of DFIG integrated to a series-compensated system in sub-synchronous frequency
风机侧：Ls、Lm、Lr分别为定子漏感、励磁电感及转子漏感。Rs为定子电阻；转子等值电阻包含两部分：一部分为转子电阻Rr/s；另一部分为转子侧换流器（Rotor Side Converter, RSC）控制器对次同步振荡影响的等效电阻RRSC/s[20]；s为转子转差率，且s=( fsub-fr)/fsub，fr为转子频率。通常情况下，fsub＜fr，所以s＜0[19]。ur/s为fsub下的RSC输出电压，即转子电压。
电网侧：R、L、C分别为等值电阻、等值电感及线路串补电容；uG为fsub下的系统电压。
由图1等效电路可知，风机侧和电网侧在fsub下的等值阻抗分别为ZDFIG( fsub)=RDFIG+jXDFIG( fsub)和ZGRID( fsub)=R+j(wsubL-1/wsubC)。其中
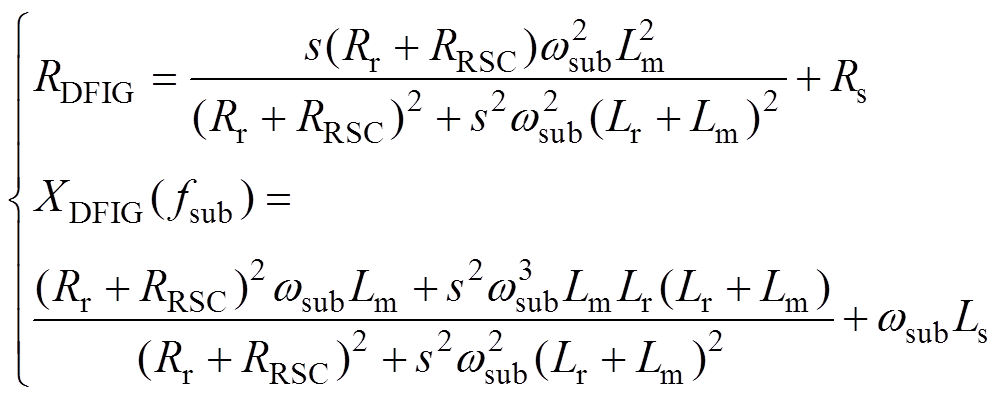（1）式中，wsub为次同步角频率，wsub=2pfsub。
由文献[22]可知，一般励磁电感Lm很大且Lm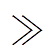
Rr+RRSC，对式（1）化简后，可得到fsub下的系统等值阻抗Zeq( fsub)=ZDFIG( fsub)+ZGRID( fsub)=Req+jXeq( fsub)。其中，系统等值电阻Req及等值电抗Xeq( fsub)为
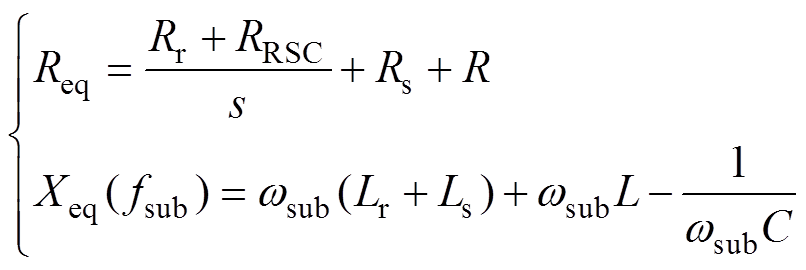（2）根据文献[19-20]的分析，转子绕组中的扰动电流Di会引起RSC输出扰动电压Du，且Du=-KRSCDi，KRSC为比例系数。把RSC对次同步振荡的影响等效成转子负电阻RRSC/s，且RRSC/s的大小主要由电流内环比例增益主导[20, 23]。由于RSC响应速度及跟踪精度的较高要求，一般内环比例增益不会设置太小，从而增加了式（2）中Req＜0的风险。
当系统受到扰动时，若系统满足式（3），则会发生持续发散的电气振荡。
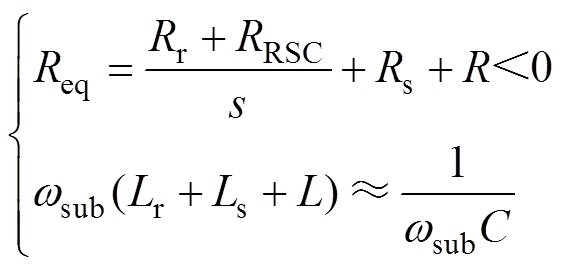（3）当Req＜0，即系统阻尼为负时，系统受到扰动后缺乏正阻尼而失稳振荡。其中，由于RSC的正反馈环助增了转子绕组中的次同步电流，使换流器与线路串补电容相互耦合作用不断加强[24]，进而RSC等效成较大负电阻而导致Req变为负值。
由第1节分析可知，系统因Req＜0而缺乏抑制SSCI的正阻尼，使得系统发散振荡。而风机侧的负电阻是使Req处在负值区域的主要原因。文献[19, 25-26]提出通过RSC附加控制策略使RSC等效成正电阻，进而减小风机侧负电阻，使Req重回正值区域；系统因具有正阻尼而避免发生SSCI。然而，实际风电场并网风电机组数目众多且型号参数各异，对其升级改造面临诸多困难。为解决该问题，通过在电网侧串接一个振荡频率下的正电阻，同样可保证Req＞0。
SSSC是以电压源换流器（Voltage Source Converter, VSC）为核心部件的电力电子装置，其控制较灵活。将SSSC装置接入风电外送汇集线路中，当系统发生SSCI时，利用SSSC输出与线路中次同步电流相位一致、幅值可控的次同步电压，此时SSSC等效为振荡频率下的正电阻，从而把Req抬升至正值区域。值得指出，工频下SSSC表现为开路，不影响系统工频运行状态。
图2所示为SSSC抑制SSCI的原理，ZDFIG( fsub)为所有风电机组及变压器T的串并联阻抗；ZGRID( fsub)包含串补线路阻抗ZCL及系统阻抗Zsys。接入SSSC后，线路电流i经滤波环节提取到次同步电流isub；isub再经增益K及限幅后，即可得到抑制SSCI的电压参考指令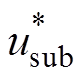
；该指令输入至SSSC使其输出次同步电压usub。从而SSSC等效为串入系统中的电阻Rseries，此时Req如式（4）所示。为有效抑制SSCI，Rseries的大小应保证Req＞0。K增加可使Rseries增大，系统稳定性增强。
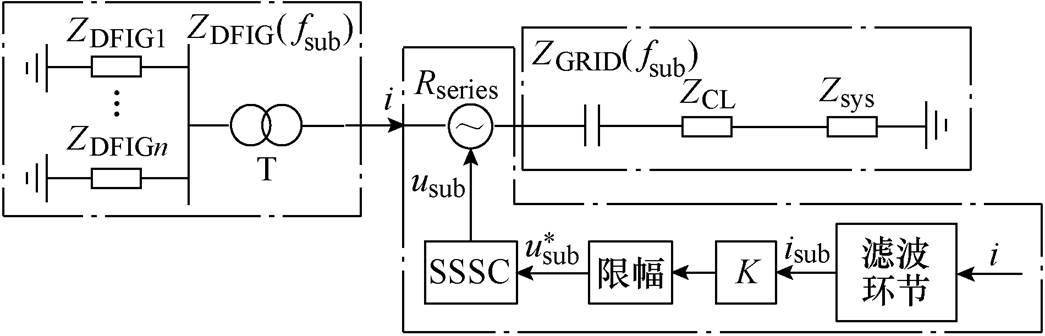
图2 SSSC抑制SSCI的原理
Fig.2 Principle of SSSC mitigating SSCI
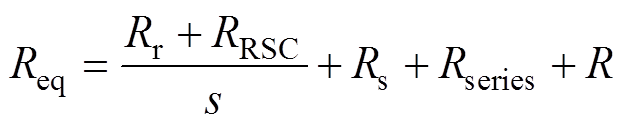（4）SSSC通过耦合变压器串联接入线路中，拓扑结构采用星形联结H桥结构，其整体控制策略包含基本控制策略和附加有源电阻控制（Supplementary Active Resistance Control, SARC）策略，如图3所示。图中，基本控制策略包括dq解耦双环控制[27]和三级均压控制。其中，相间及单元均压均采用基于叠加有功电压矢量控制的原理[28]，故图3中仅给出相间均压控制框图。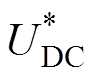
为H桥单元模块直流电容电压参考值，UDC为三相总平均直流电容电压测量值，Ua_ave为A相总平均直流电容电压测量值。qi为通过锁相环得到的线路电流的相位；外环电压参考值
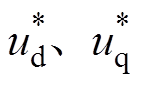分别由全局均压和定电压控制给定；ud、uq分别为SSSC输出电压中dq轴分量测量值。交叉反馈解耦项w0C与w0L用于实现SSSC输出电压中dq轴分量之间的解耦控制。
SARC策略的输入信号为线路电流，输出信号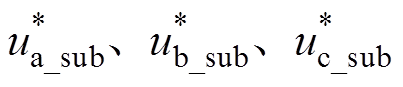
为抑制SSCI的次同步电压指令值；
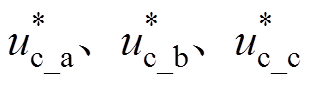为叠加抑制SSCI指令值和相间均压指令值的调制指令，该指令经载波相移正弦脉宽调制环节后，产生PWM信号并输入至SSSC级联H桥单元模块。
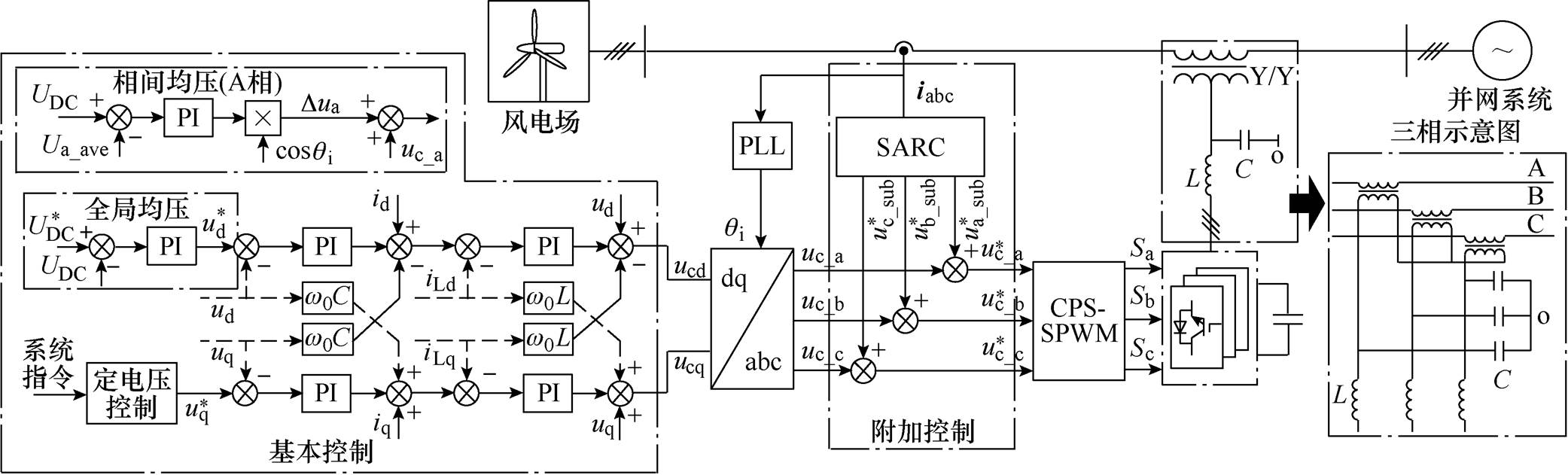
图3 SSSC抑制SSCI的整体控制策略
Fig.3 Overall control strategy of SSSC mitigating SSCI
SARC基于线路电流反馈信号中的次同步电流分量生成同相位的次同步电压参考信号，其构成工作原理框图如图4所示，包括宽频带滤波器、相位校正环节及比例限幅3部分。宽频带滤波器包括低通滤波器（LP filter）和带阻滤波器（BS filter）；相位校正环节对宽频带滤波器滤出的次同步电流信号进行相位补偿，fsub0为折中补偿频率；次同步电流信号iabc_sub经增益Ku及限幅环节后，得到SSSC抑制SSCI的参考指令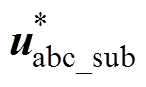
。该指令叠加至SSSC主调制波后，其可输出与iabc_sub相位一致的uabc_sub，此时SSSC等效为次同步振荡频率下的正电阻，使Req抬升至正值区域，达到抑制SSCI的目的。
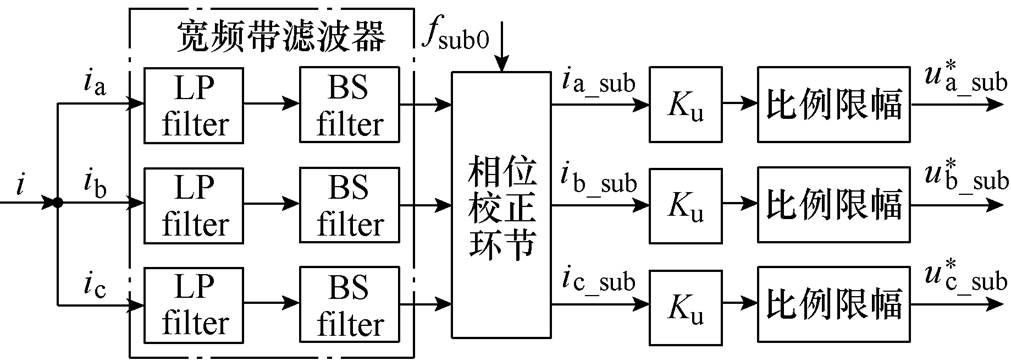
图4 SARC的构成原理框图
Fig.4 Configuration and principle of SARC
3.3.1 宽频带滤波器
风电SSCI频率具有显著的时变特性，滤波器的动态响应性能直接影响到对线路中次同步电流的提取精度。为精确获得线路中的次同步电流分量，本文采用LP filter+BS filter的信号提取方法。首先，采用二阶巴特沃斯LP filter GLP(s)滤除掉高次谐波；其次，利用四阶巴特沃斯BS filter GBS(s)将工频量滤除；二者传递函数为
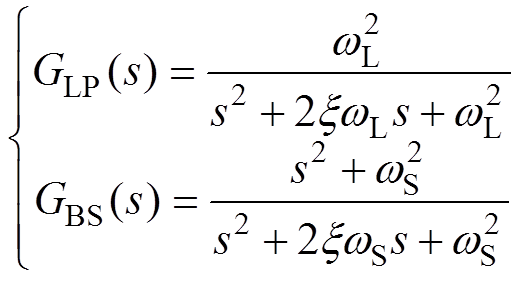（5）式中，wL为LP filter截止角频率，根据实际风电系统发生SSCI的频率范围，其取值应不影响滤波器在次同步频率范围内的幅频及相频特性；wS为BS filter中心角频率，考虑兼顾滤波器的滤波性能与动态特性，然后根据实际指标要求选取合适的带宽；x 为阻尼系数，本文取x ＝0.7。
3.3.2 相位校正环节
因宽频带滤波器的参数选取兼顾多种因素，导致次同步电流信号经过滤波器后产生相位偏移。为保证SSSC在次同步频率下可近似等效成纯电阻，需加相位校正环节进行相位补偿。相位校正环节GC(s)为
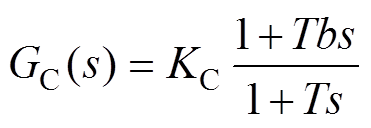（6）式中，KC为补偿增益，其保证补偿频率下宽频带滤波器的幅频特性不会发生改变；T为时间常数；b为构造参数。各参数取值为
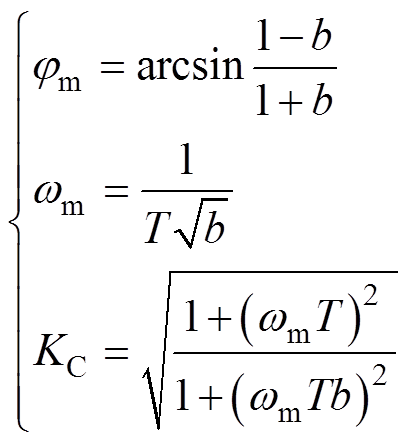（7）
式中，wm为折中补偿角频率，wm=2pfm。根据实际风电系统发生SSCI的主要频率范围，选取折中频率fm进行相位校正；jm为折中频率fm下宽频带滤波器的相频特性偏移角度。
3.3.3 增益Ku
SARC中的增益Ku直接决定SSSC可等效成正电阻的大小，增益Ku越大，式（4）中Req则越大，SSCI的抑制效果越好。但Ku过大，抑制初始时刻SSSC与系统交换的瞬时有功功率会很大，这将造成H桥直流电容电压波动剧烈；继而容易造成稳压控制环节达到限幅设定值。
实际系统运行工况多变，不同运行工况下由不同原因引起的SSCI振荡幅值差异较大。在相位校正环节确定之后，通过整定Ku的大小保证Req＞0，进而达到抑制SSCI的目的。
为了避免抑制初始时刻直流电容电压波动较大并同时有效抑制SSCI，本文通过大量的数字仿真，选取系统在最恶劣的运行工况下，能够抑制SSCI的最小增益Ku作为设定值。
以华北某风电场的实际参数与系统结构建立如图5所示的等效系统模型[21]：160台额定电压0.69kV、容量1.5MW的DFIG经箱变及线路变压器升压，并入40%串补度的500kV输电线路进行远距离输送。图5中，XT1、XT2、XT3为升压变压器电抗；XL1、XL2为线路电抗；RL1、RL2为线路电阻；XC为串联容抗；CDC为直流电容；DFIG及系统等效参数见 表1。级联H桥型SSSC装置串联接入220kV输电线路中，其装置参数见表2。
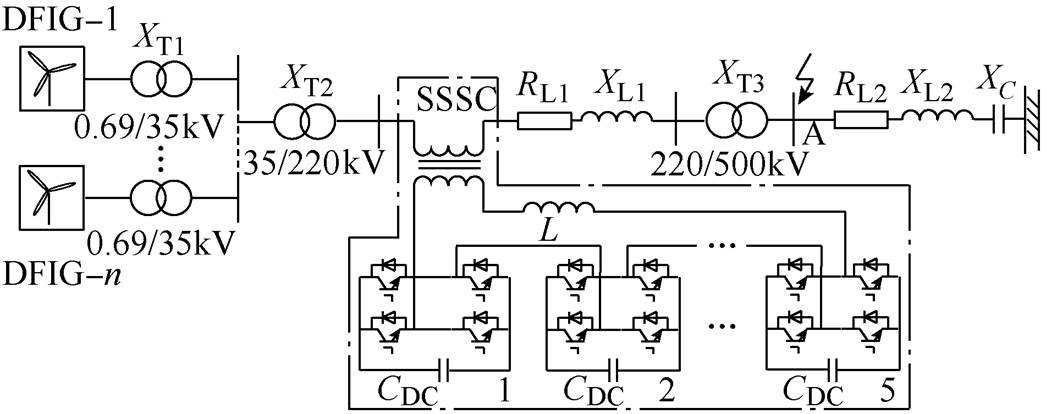
图5 DFIG风电场接入串补系统等效模型
Fig.5 Equivalent model of DFIG-based wind farms integrated to a series-compensated system
表1 DFIG及系统等效参数
Tab.1 Equivalent parameters of DFIG and system
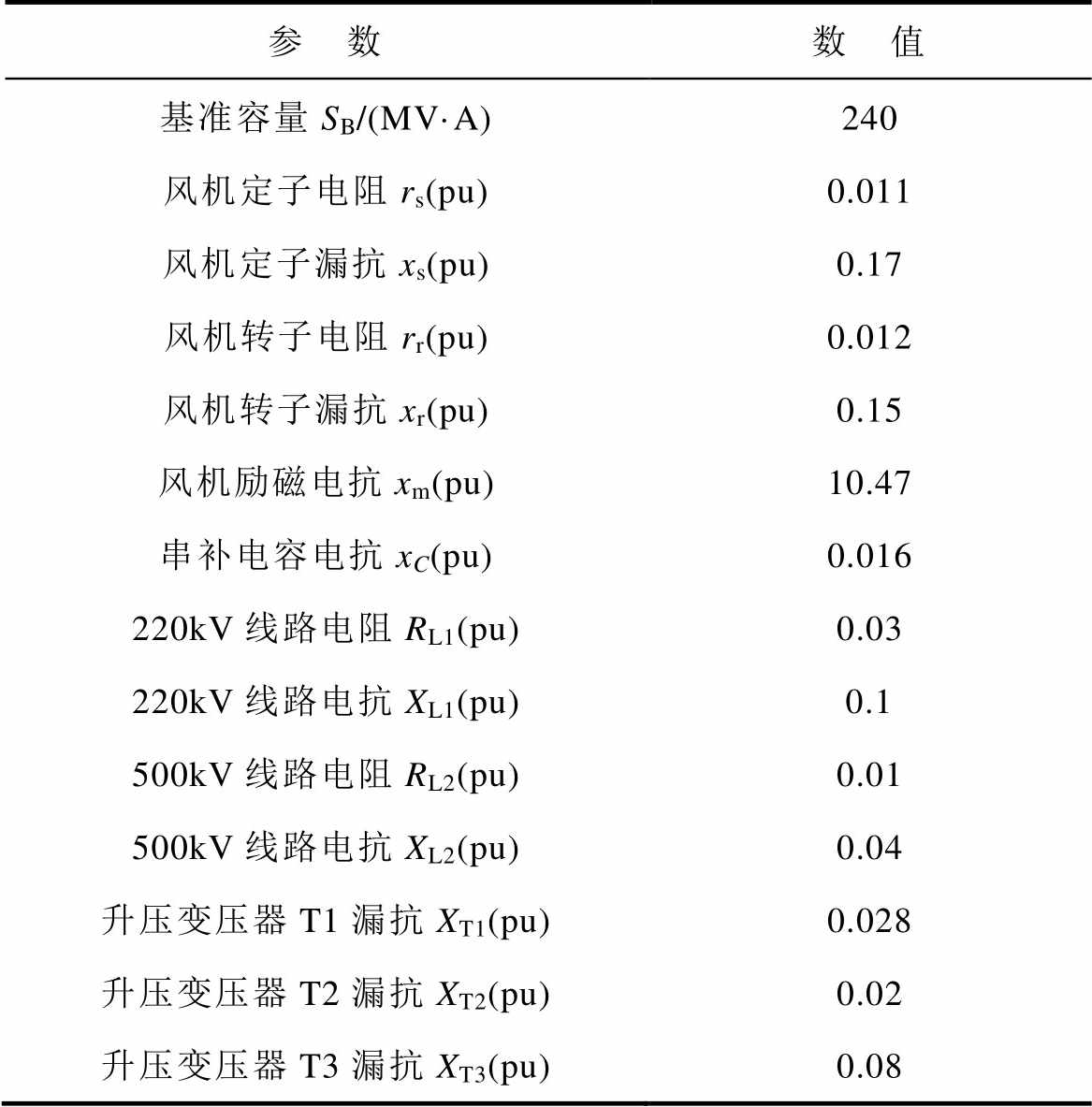
参 数数 值 基准容量SB/(MV·A)240 风机定子电阻rs(pu)0.011 风机定子漏抗xs(pu)0.17 风机转子电阻rr(pu)0.012 风机转子漏抗xr(pu)0.15 风机励磁电抗xm(pu)10.47 串补电容电抗xC(pu)0.016 220kV线路电阻RL1(pu)0.03 220kV线路电抗XL1(pu)0.1 500kV线路电阻RL2(pu)0.01 500kV线路电抗XL2(pu)0.04 升压变压器T1漏抗XT1(pu)0.028 升压变压器T2漏抗XT2(pu)0.02 升压变压器T3漏抗XT3(pu)0.08
表2 级联H桥SSSC拓扑结构参数
Tab.2 Topological parameters of cascaded H bridge SSSC
参 数数 值 耦合变压器电压比k1 滤波电感/mH0.01 滤波电容/mF14 直流电容/mF6 000 直流电容电压/kV1.5 开关频率/Hz500 级联模块数5
根据该风电场发生SSCI的频率范围（4～10Hz），并兼顾宽频带滤波器的性能指标，设计二阶巴特沃斯LP filter的截止频率为100Hz，四阶巴特沃斯BS filter的中心频率为50Hz，带宽范围为[49, 51]Hz。基于Matlab计算得到数字滤波器的传递函数参数值，见表3。基于滤波器传递函数得到宽频带滤波器伯德图，如图6所示。
表3 宽频带滤波器参数
Tab.3 The parameters of broadband filter
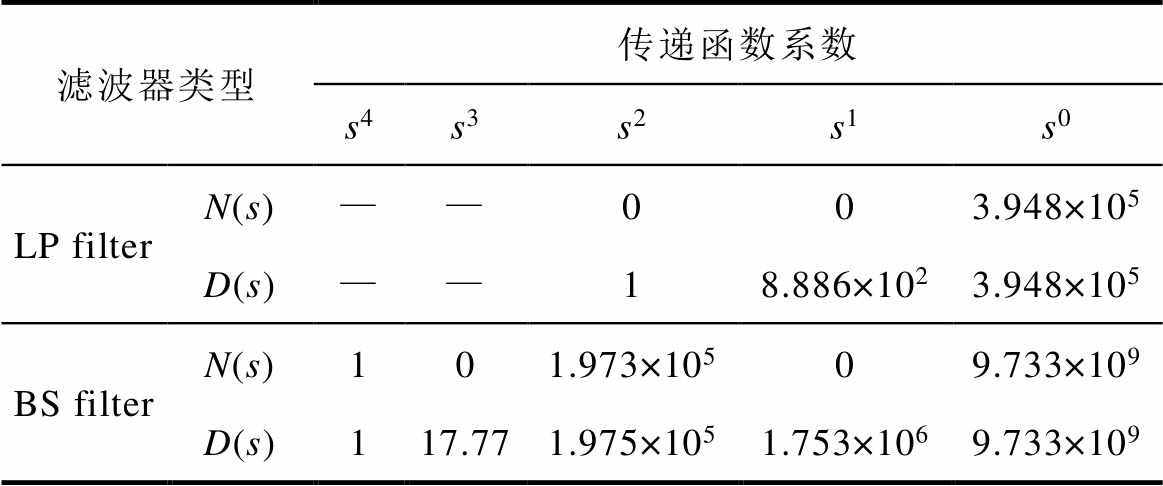
滤波器类型传递函数系数 s4s3s2s1s0 LP filterN(s)——003.948×105 D(s)——18.886×1023.948×105 BS filterN(s)101.973×10509.733×109 D(s)117.771.975×1051.753×1069.733×109
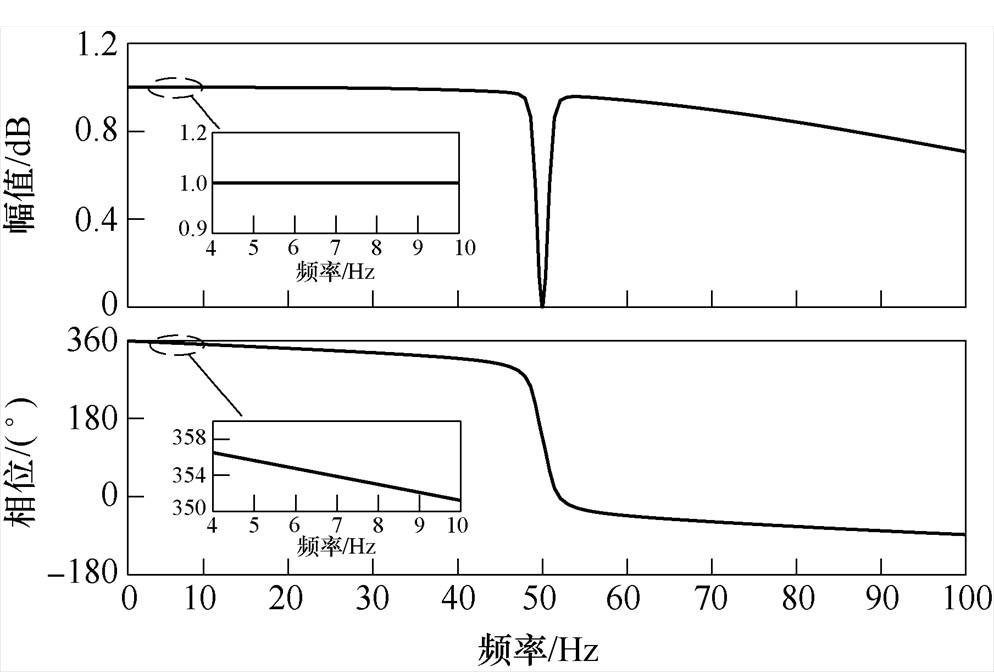
图6 宽频带滤波器伯德图
Fig.6 The Bode diagram of broadband filter
由图6可知，4～10Hz频率范围内滤波器幅频特性的增益为1，表明可以较好地滤出次同步电流信号；50Hz对应的增益为0，滤波器可以较好地滤除工频量。此外，滤波器对相应的超同步频率范围分量具有一定的衰减作用。然而，相频特性在该频率范围内出现4°～9°不等的相位滞后。
为保证SSSC在该频率范围内近似等效成纯电阻，考虑到该系统发生SSCI的频率范围主要集中在6～8Hz，故选取折中频率fm=7Hz进行相位校正。由图6得到fm=7Hz对应的补偿角度jm=-6.2°，并结合式（7）求得KC=0.900 4，T=0.020 5s，b=1.233 5。
经相位校正环节后的宽频带滤波器相频特性如图7所示。图中，7Hz对应的相位偏移为0°，且6～8Hz频率范围内的相位偏移不足±1°，该频率范围内可认为SSSC等效电阻为1(pu)。相比于未经相位校正环节的相频特性，4～10Hz频率范围内的相位偏移已经很小。系统振荡频率不在6～8Hz范围内时，如10Hz对应的相位偏移为-3°，SSSC在该频率下的等效电阻为0.998 6(pu)；4Hz对应的相位偏移为+2°，SSSC在该频率下的等效电阻为0.999 4(pu)。所以，SSSC在整个系统振荡频率范围内近似等效成纯电阻。
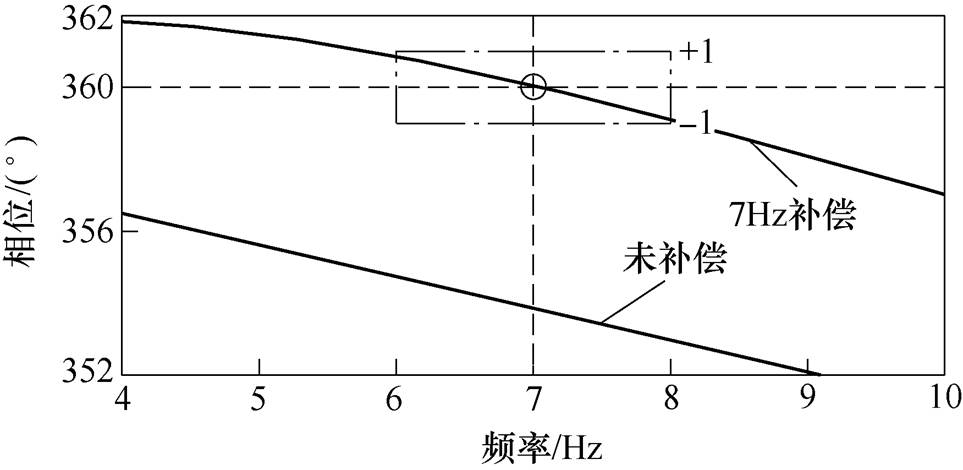
图7 相位校正后伯德图
Fig.7 The Bode diagram after phase correction
为验证SSSC抑制SSCI的有效性，在PSCAD/ EMTDC仿真软件中搭建如图5所示的华北某实际DFIG风电场经串补系统送出的时域仿真模型。利用频率扫描分析法，分别研究在典型风速变化、串补度变化工况下，对有无投入SSSC的图5系统等值阻抗特性进行分析；并结合时域仿真分析法进行验证。
4.3.1 风速变化
在线路串补度为40%时，分别选取风速9m/s、7m/s、5m/s三种工况。仿真开始之前串补电容设为投入状态，待系统稳定运行后，在风电场并网点向系统依次注入1～20Hz幅值很小的谐波电流。从而扫描出风机侧及网侧在4～10Hz范围的阻抗，通过叠加原理获得Req及Xeq。图8为三种风速工况下有无投入SSSC的系统频率扫描分析结果。
由图8可知，随着风速的降低，未投SSSC时，Xeq=0W 对应频率下的Req由正变负，表明系统发生SSCI的风险增加。而投入SSSC时，三种风速工况下Req均为正值，表明SSSC等效为正电阻增大了Req，使系统免于发生SSCI的风险。
图8 不同风速下有无SSSC时的Req/Xeq
Fig.8 Req/Xeq with or without SSSC under different wind speeds
频率扫描分析方法为一种近似线性化方法，为验证频率扫描分析结果，可进行时域仿真验证。工况条件不变，仿真开始之前，串补电容被旁路，其在仿真时刻t =5s时被投入。图9为三种风速工况下有无投入SSSC的线路有功功率P响应特性，其振荡频率与系统振荡频率互补[29]。
由图9可知，风速为9m/s时，串补电容投入后，有无投入SSSC，系统均收敛，但投入SSSC时的收敛速度比未投SSSC时要快。风速为7m/s且未投SSSC时，投入串补电容后，功率振荡的幅值不断增大，最终系统失稳；FFT分析结果表明，其振荡频率为44Hz。投入SSSC时，功率振荡得到抑制，系统由发散转为收敛。风速为5m/s且未投SSSC时，串补电容被投入后，功率振荡发散导致系统失稳，其振荡频率为44Hz；投入SSSC时，系统快速收敛趋于稳定。
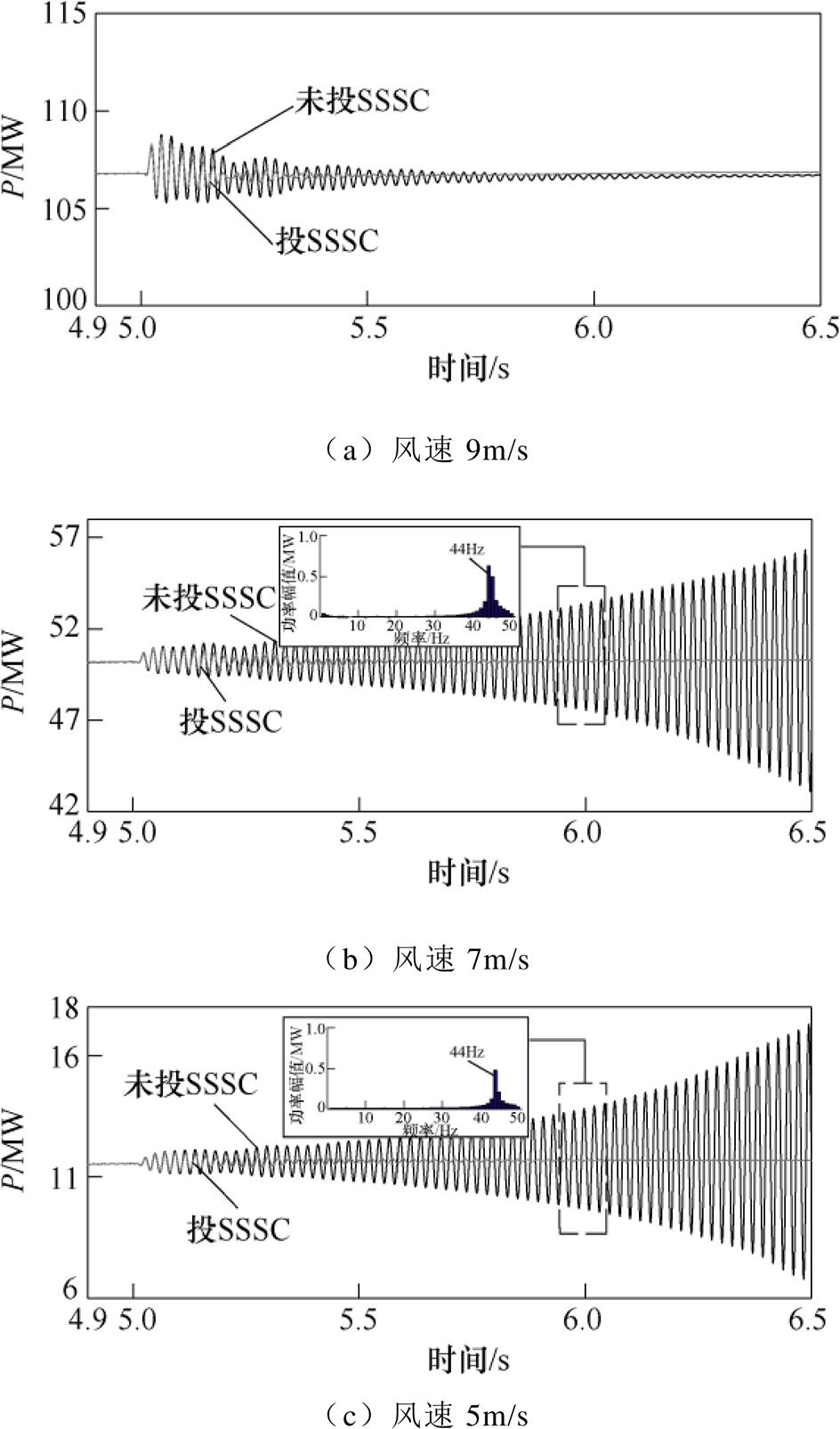
图9 不同风速下有无SSSC时的线路有功功率
Fig.9 The active power with or without SSSC under different wind speeds
上述仿真结果表明，在低风速工况下发生SSCI时，SSSC等效为正电阻抬升Req至正值区域，使系统不具备失稳的条件。
4.3.2 串补度变化
在风速为9m/s时，分别选取线路串补度60%、80%两种工况，系统频率扫描分析过程同4.3.1节。图10为两种串补度工况下有无投入SSSC的系统频率扫描分析结果。
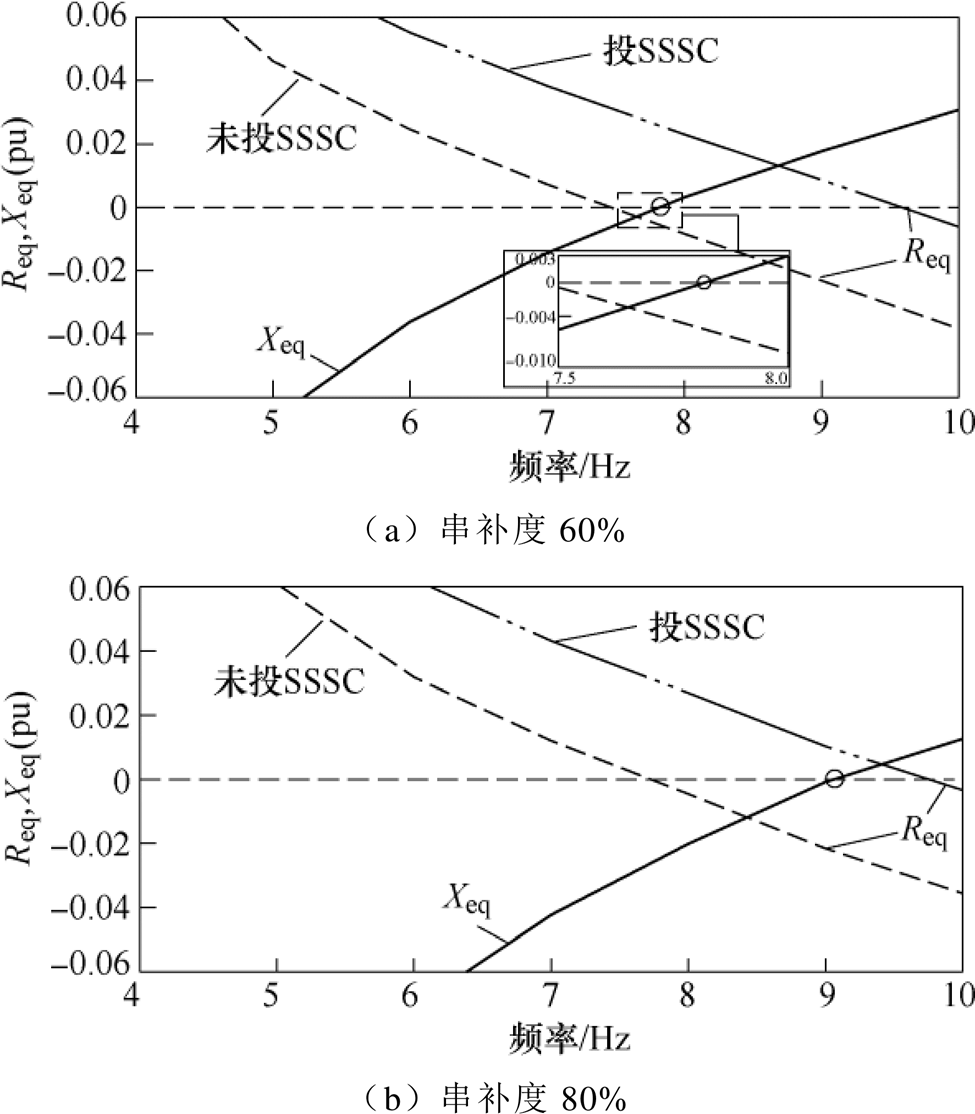
图10 不同串补度下有无SSSC时的Req和Xeq
Fig.10 Req and Xeq with or without SSSC under different compensated levels
由图10可知，未投入SSSC时，两种工况下Xeq=0W 对应频率下的Req均为负值，表明系统存在发生SSCI的风险。投入SSSC时，两种工况下Req均为正值，系统无发生SSCI的风险。此外，系统振荡频率因串补度改变而发生偏移，但SSSC仍可有效提供正电阻，表明SARC具有较好的输入输出特性。
除工况条件不同，时域仿真设置同4.3.1节。图11为两种串补度工况下有无投入SSSC的线路有功功率P响应特性。
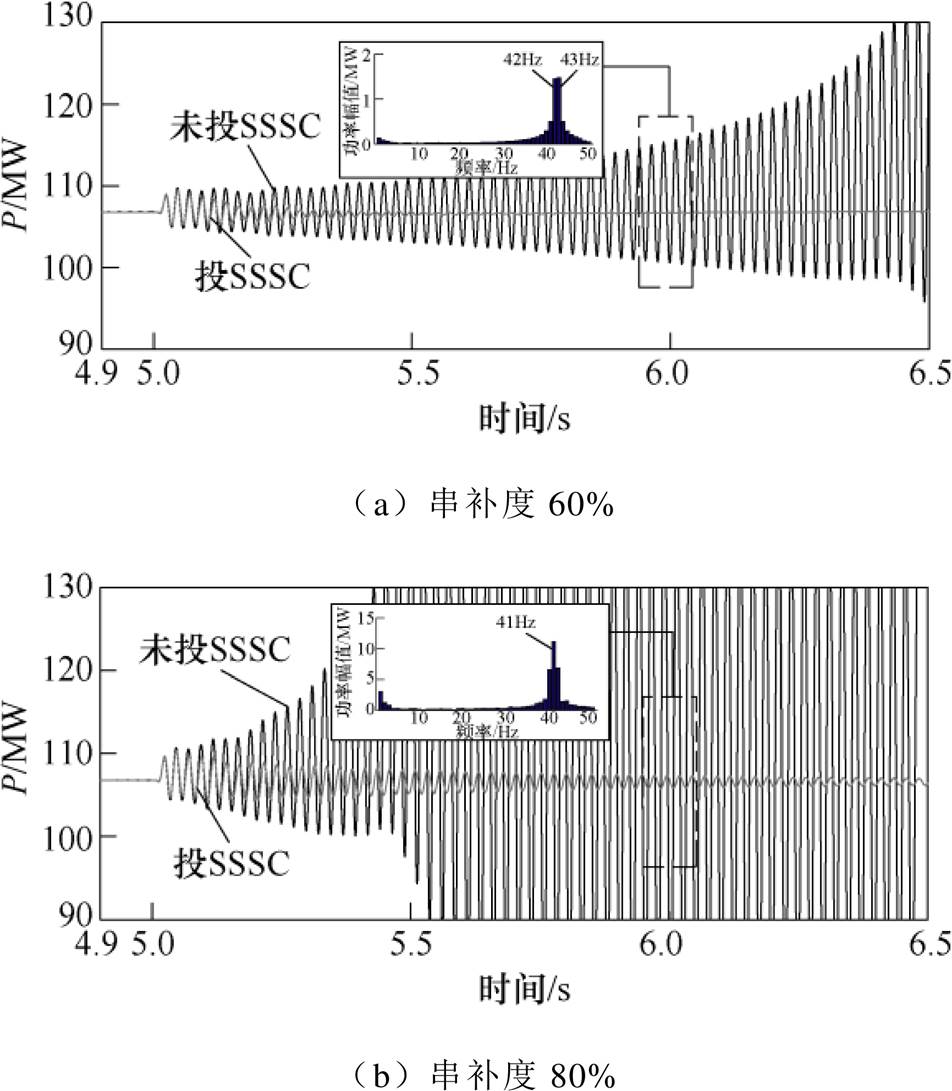
图11 不同串补度下有无SSSC时的线路有功功率
Fig.11 The active power with or without SSSC under different compensated levels
由图11可知，串补度60%且未投SSSC时，投入串补电容后，功率振荡的幅值缓慢增加，直至系统发散，失去稳定；投入SSSC时，功率振荡得到抑制，系统由发散转为收敛。当串补度增加至80%时，未投SSSC时，串补电容被投入后，系统快速发散失稳；而投入SSSC时，系统能够快速收敛。
上述仿真结果表明，较高串补度运行工况下，SSSC仍可有效抑制SSCI。SSSC的抑制效果受系统运行工况的影响较小，显著增强了系统的稳定性。
4.3.3 三相接地故障
为验证SSSC在故障情况下抑制SSCI的有效性，在仿真开始之前，串补电容设为投入状态。风电场风速设置为7m/s，线路串补度设置为60%。系统进入稳态后，t =5s时在220/500kV升压变高压侧设置三相接地短路故障（见图5中A点），故障持续时间100ms。设置SSSC在5.5s投入，线路有功功率P及SSSC A相输出电压如图12和图13所示。
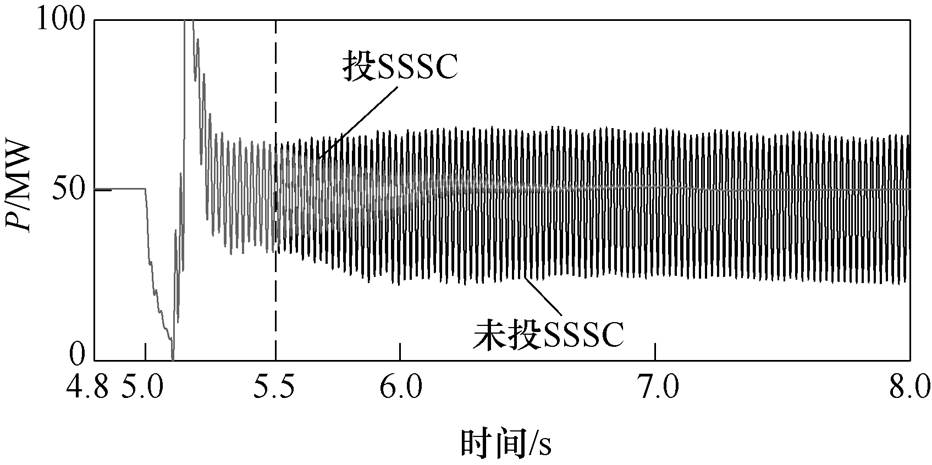
图12 三相故障下有无SSSC时的线路有功功率
Fig.12 The active power with or without SSSC under three-phase fault
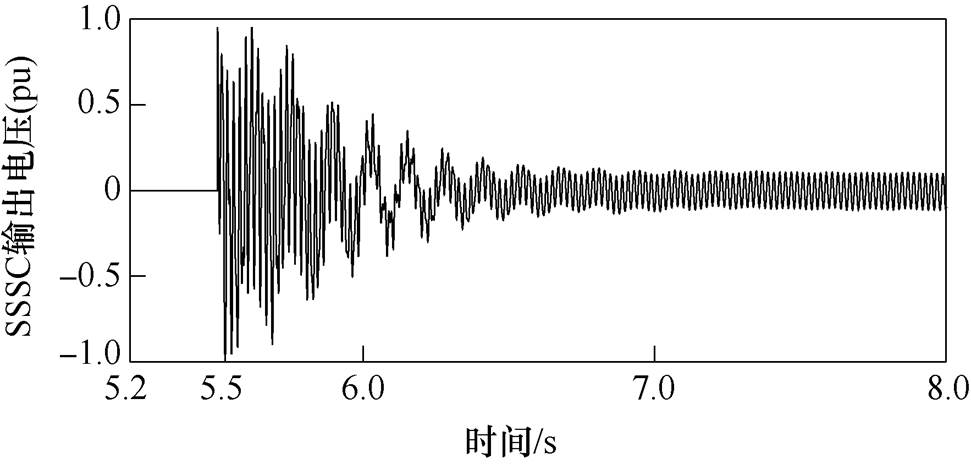
图13 SSSC A相输出电压
Fig.13 A phase output voltage of SSSC
由图12可知，故障后系统发生严重的SSCI，未投入SSSC时，线路有功功率出现等幅振荡，系统失稳；而5.5s时投入SSSC，功率振荡缓慢收敛，7s后系统趋于稳定。
由图13可知，SSSC刚投入时，由于系统中次同步电流分量较大，导致SSSC输出电压实际值接近装置额定值。大约1.5s后振荡被平抑，系统趋于稳定，SSSC输出电压中只含工频分量。在系统中含有较大的次同步电流分量情况下，SSSC的投入有效抑制了SSCI，由此验证SSSC在故障情况下可发挥良好的抑制效果。
1）基于双馈风电场与串补系统发生SSCI的机理，提出利用SSSC产生正电阻的附加有源电阻控制（SARC）策略。通过在网侧增加次同步振荡频率下的电阻，确保系统具有正电阻而不具备发生SSCI的条件。结合实际工程模型，频域及时域仿真结果验证了该策略的可行性及有效性。
2）与现有的附加控制策略参数对系统动态运行工况适用性较差相比，SARC参数整定简便，并且在多种运行工况下均具有较好的适用性，因而工程应用性较强。
参考文献
[1] 肖湘宁, 罗超, 廖坤玉. 新能源电力系统次同步振荡问题研究综述[J]. 电工技术学报, 2017, 32(6): 85-97.
Xiao Xiangning, Luo Chao, Liao Kunyu. Review of the research on sub-synchronous oscillation issues in electric power system with renewable energy sources[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 85-97.
[2] 高本锋, 刘晋, 李忍, 等. 风电机组的次同步控制相互作用研究综述[J]. 电工技术学报, 2015, 30(16): 154-161.
Gao Benfeng, Liu Jin, Li Ren, et al. Studies of sub-synchronous control interaction in wind turbine generators[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 154-161.
[3] 边晓燕, 施磊, 宗秀红, 等. 多运行方式下风电机组变频器参与次同步相互作用的分析与抑制[J]. 电工技术学报, 2017, 32(11): 38-47.
Bian Xiaoyan, Shi Lei, Zong Xiuhong, et al. Analysis and mitigation of wind turbine converters in sub-synchronous interaction under multi-operating conditions[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 38-47.
[4] 姚骏, 曾欣, 李嘉伟. 并网双馈感应风电系统轴系振荡特性[J]. 电工技术学报, 2017, 32(6): 123-135.
Yao Jun, Zeng Xin, Li Jiawei. Shaft oscillation characteristics of grid-connected doubly-fed induction generator-based wind power generation system[J]. Transactions of China Electrotechnical Society 2017, 32(6): 123-135.
[5] Adams J, Carter C, Huang S H. ERCOT experience with sub-synchronous control interaction and pro- posed remediation[C]//IEEE Transmission and Distri- bution Conference and Exposition (T&D), PES Orlando, FL, USA, 2012: 1-5.
[6] Narendra K, Fedirchuk D, Midence R, et al. New microprocessor based relay to monitor and protect power systems against sub-harmonics[C]//IEEE Elec- trical Power and Energy Conference, Winnipeg, MB, 2011: 438-443.
[7] Xie Xiaorong, Zhang Xa, Liu Huakun, et al. Charac- teristic analysis of sub-synchronous resonance in practical wind farms connected to series-compensated transmissions[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1117-1126.
[8] 王玉芝, 王亮, 姜齐荣. 基于STATCOM的风电场SSCI附加阻尼抑制策略[J]. 电力系统自动化, 2019, 43(15): 49-59.
Wang Yuzhi, Wang Liang, Jiang Qirong. STATCOM based supplementary damping mitigation strategy for subsynchronous control interaction in wind farms[J]. Automation of Electric Power Systems, 2019, 43(15): 49-59.
[9] 董晓亮, 谢小荣, 杨煜, 等. 双馈风机串补输电系统次同步谐振影响因素及稳定区域分析[J]. 电网技术, 2015, 39(1): 189-193.
Dong Xiaoliang, Xie Xiaorong, Yang Yu, et al. Impacting factors and stable area analysis of sub- synchronous resonance in DFIG based wind farms connected to series-compensated power system[J]. Power System Technology, 2015, 39(1): 189-193.
[10] 廖坤玉, 陶顺, 姚黎婷, 等. 考虑励磁的DFIG静止坐标系输入阻抗的频域建模与时变特性研究[J]. 中国电机工程学报, 2018, 38(16): 4886-4897.
Liao Kunyu, Tao Shun, Yao Liting, et al. Study on frequency-domain modeling and time-varying characteri- stics of DFIG input impedance with excitation under static reference frame[J]. Proceedings of the CSEE, 2018, 38(16): 4886-4897.
[11] Fan Lingling, Miao Zhixin. Mitigating SSR using DFIG-based wind generation[J]. IEEE Transactions on Sustainable Energy, 2012, 3(3): 349-358.
[12] 曹建春, 项祖涛, 燕翚, 等. 抑制双馈风电场次同步谐振的STATCOM研究[J]. 电网技术, 2019, 43(3): 902-909.
Cao Jianchun, Xiang Zutao, Yan Hui, et al. Research on mitigating DFIG wind farm SSR with STATCOM[J]. Power System Technology, 2019, 43(3): 902-909.
[13] 张旭, 谢小荣, 刘辉, 等. 网侧次同步阻尼控制器的设计及其RTDS测试[J]. 中国电机工程学报, 2018, 38(22): 6503-6511.
Zhang Xu, Xie Xiaorong, Liu Hui, et al. Design and RTDS test of the grid-side sub-synchronous damping controller[J]. Proceedings of the CSEE, 2018, 38(22): 6503-6511.
[14] 边晓燕, 施磊, 周歧斌, 等. 基于概率法的并网双馈风电场次同步相互作用及其抑制措施[J].高电压技术, 2016, 42(9): 2740-2747.
Bian Xiaoyan, Shi Lei, Zhou Qibin, et al. Sub- synchronous interaction and its suppression measurement caused by grid-integration of DFIG-based wind farms using probabilistic method[J]. High Voltage Engin- eering, 2016, 42(9): 2740-2747.
[15] 肖湘宁, 郭春林, 高本锋, 等. 电力系统次同步振荡及其抑制方法[M]. 北京: 机械工业出版社, 2014.
[16] 郑翔, 徐政, 屠卿瑞, 等. 静止同步串联补偿器次同步谐振多模式阻尼控制器设计[J]. 高电压技术, 2011, 37(9): 2321-2327.
Zheng Xiang, Xu Zheng, Tu Qingrui, et al. Static synchronous series compensator multimode damping controller design for sub-synchronous resonance suppression[J]. High Voltage Engineering, 2011, 37(9): 2321-2327.
[17] 高本锋, 肖湘宁, 赵成勇, 等. 混合串联补偿装置抑制次同步谐振的研究[J]. 电工技术学报, 2010, 25(11): 142-147.
Gao Benfeng, Xiao Xiangning, Zhao Chengyong, et al. Study of hybrid series compensator on sub- synchronous resonance damping[J]. Transactions of China Electrotechnical Society, 2010, 25(11): 142- 147.
[18] 鹿建成, 李啸骢, 黄维, 等. 基于SSSC和励磁协调抑制次同步振荡的线性最优控制器设计[J]. 电力系统保护与控制, 2015, 43(1): 21-27.
Lu Jiancheng, Li Xiaocong, Huang Wei, et al. Linear optimal controller of static series synchronous compensator and excitation to suppress sub- synchronous oscillation[J]. Power System Protection and Control, 2015, 43(1): 21-27.
[19] 吴熙, 关雅静, 宁威, 等. 双馈风机转子侧变换器参数对次同步振荡的交互影响机理及其应用研究[J]. 电网技术, 2018, 42(8): 2536-2544.
Wu Xi, Guan Yajing, Ning Wei, et al. Mechanism of interactive effect of RSC parameters in DFIG on SSO and its application[J]. Power System Technology, 2018, 42(8): 2536-2544.
[20] 王亮, 谢小荣, 姜齐荣, 等. 大规模双馈风电场次同步谐振的分析与抑制[J]. 电力系统自动化, 2014, 38(22): 26-31.
Wang Liang, Xie Xiaorong, Jiang Qirong, et al. Analysis and mitigation of SSR problems in large- scale wind farms with doubly-fed wind turbines[J]. Automation of Electric Power Systems, 2014, 38(22): 26-31.
[21] 董晓亮, 田旭, 张勇, 等. 沽源风电场串补输电系统次同步谐振典型事件及影响因素分析[J]. 高电压技术, 2017, 43(1): 321-328.
Dong Xiaoliang, Tian Xu, Zhang Yong, et al. Practical SSR incidence and influencing factor analysis of DFIG-based series-compensated transmission system in Guyuan farms[J]. High Voltage Engineering, 2017, 43(1): 321-328.
[22] 张学广, 邱望明, 方冉, 等. 双馈风电机组静止坐标系下阻抗建模及次同步谐振抑制策略[J]. 电力系统自动化, 2019, 43(6): 41-48, 106.
Zhang Xueguang, Qiu Wangming, Fang Ran, et al. Impedance modeling and sub-synchronous resonance mitigation strategy of DFIG based wind turbine in static reference frame[J]. Automation of Electric Power Systems, 2019, 43(6): 41-48, 106.
[23] 陈斐泓, 杨健维, 廖凯, 等. 基于频率扫描的双馈风电机组次同步控制相互作用分析[J]. 电力系统保护与控制, 2017, 45(24): 84-91.
Chen Feihong, Yang Jianwei, Liao Kai, et al. Sub- synchronous control interaction analysis in doubly- fed induction generator based on frequency scanning[J]. Power System Protection and Control, 2017, 45(24): 84-91.
[24] 张剑, 肖湘宁, 高本锋, 等. 双馈风力发电机的次同步控制相互作用机理与特性研究[J]. 电工技术学报, 2013, 28(12): 142-149.
Zhang Jian, Xiao Xiangning, Gao Benfeng, et al. Mechanism and characteristic study on sub- synchronous control interaction of a DFIG-based wind-power generator[J]. Transactions of China Electrotechnical Society, 2013, 28(12): 142-149.
[25] 胡应宏, 邓春, 谢小荣, 等. 双馈风机-串补输电系统次同步谐振的附加阻尼控制[J]. 电网技术, 2016, 40(4): 1169-1173.
Hu Yinghong, Deng Chun, Xie Xiaorong, et al. Additional damping control of DFIG series compensated transmission system[J]. Power System Technology, 2016, 40(4): 1169-1173.
[26] 朱玲, 许翔, 侯玉强, 等. 基于宽频带转子附加阻尼的双馈型风机次同步振荡抑制策略[J]. 电力系统保护与控制, 2018, 46(2): 37-42.
Zhu Ling, Xu Xiang, Hou Yuqiang, et al. A supper- ssion strategy for DFIG sub-synchronous oscillation based on broadband rotor additional damping[J]. Power System Protection and Control, 2018, 46(2): 37-42.
[27] 张帆, 徐政. 静止同步串联补偿器控制方式及特性研究[J]. 中国电机工程学报, 2008, 28(19): 75-80.
Zhang Fan, Xu Zheng. Study on control and characte- ristics of static synchronous series compensator[J]. Proceedings of the CSEE, 2008, 28(19): 75-80.
[28] 刘钊, 刘邦银, 段善旭, 等. 链式静止同步补偿器的直流电容电压平衡控制[J]. 中国电机工程学报, 2009, 29(30): 7-12.
Liu Zhao, Liu Bangyin, Duan Shanxu, et al. DC capacitor voltage balancing control for cascade multilevel STATCOM[J]. Proceedings of the CSEE, 2009, 29(30): 7-12.
[29] 栗然, 卢云, 刘会兰, 等. 双馈风电场经串补并网引起次同步振荡机理分析[J]. 电网技术, 2013, 37(11): 3073-3079.
Li Ran, Lu Yun, Liu Huilan, et al. Mechanism analysis on sub-synchronous oscillation caused by grid-integration of doubly fed wind power generation system via series compensation[J]. Power System Technology, 2013, 37(11): 3073-3079.
The Suppression Method of Wind Power Sub-Synchronous Oscillation Using Static Synchronous Series Compensator
Abstract In view of the problem of sub-synchronous control interaction (SSCI) when the doubly-fed wind farms transmit power through the series-compensated system, this paper proposes an equivalent positive resistance control method based on SSSC to suppress SSCI. The method uses the current in the grid side as an input signal and produces sub-synchronous voltage reference signal corresponding to sub-synchronous current in the line through the SSSC supplementary active resistance control (SARC) strategy. The SSSC traces sub-synchronous current to make it equivalent to a positive resistance at the sub-synchronous frequency. The grid side resistance is increased by connecting the SSSC in the line, and the system equivalent resistance is increased to a positive value region, thereby mitigating SSCI. In addition, the structure and parameter design method of SARC are introduced in detail. Finally, based on an actual wind farm structure in North China, the simulation model was built in PSCAD/EMTDC. The results show that the system equivalent resistance is in the positive region because SSSC is equivalent to a positive resistance under various operating conditions, thereby avoiding SSCI in the system. The method has advantages of simple parameters setting and easy realization.
keywords：Doubly-fed wind farms, series-compensated system, sub-synchronous control inter- action, static synchronous series compensator, supplementary active resistance control
中图分类号：TM712
DOI: 10.19595/j.cnki.1000-6753.tces.190033
国家电网公司科技项目“串联型次同步振荡抑制器关键技术研究”（GEIRI-DL-71-18-005）和教育部中央高校基本科研业务费专项基金（2018MS087）资助项目。
收稿日期 2019-01-16
改稿日期 2019-06-11
高本锋 男，1981年生，博士，副教授，研究方向为高压直流输电和电力系统次同步振荡。E-mail: gaobenfeng@126.com（通信作者）
王飞跃 男，1993年生，硕士研究生，研究方向为电力系统次同步振荡。E-mail: Feiyue_W@163.com
（编辑 赵 鹏）