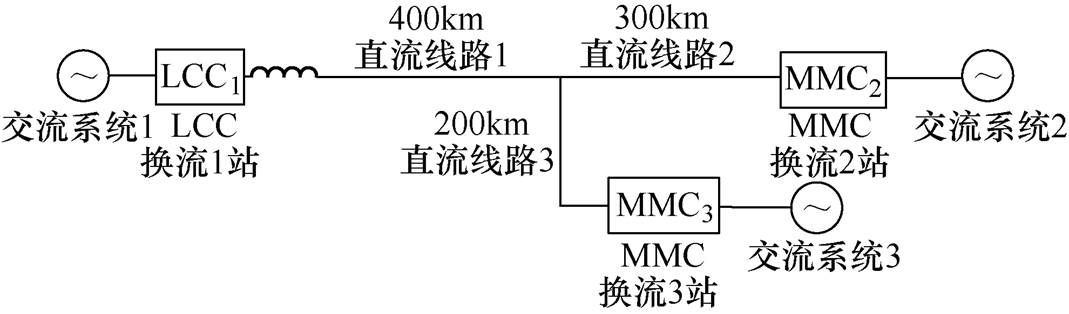
图1 混合三端直流输电系统结构
Fig.1 Configuration of hybrid three-terminal HVDC system
摘要 整流站采用电网换相型换流器（LCC）、逆变站采用模块化多电平换流器（MMC）的混合多端直流输电系统（H-MTDC）连接弱交流系统时，若控制参数设置不合理，系统可能出现小干扰失稳现象，限制了混合多端直流输电系统在弱交流场合下的应用。该文提出一种提高弱交流系统下混合多端直流输电系统小干扰稳定性的控制参数优化调节方法。首先，基于混合多端直流输电系统的小干扰模型，采用特征根分析法研究不同换流站所联接的交流系统强度对混合多端直流输电系统小干扰稳定性的影响，结果表明不合理的控制参数会降低系统的稳定裕度，继而诱发小干扰失稳问题。然后以混合三端直流输电系统为例，给出一种基于灵敏度分析的控制参数优化调节方法，优化了混合三端直流输电系统的控制参数。PSCAD/EMTDC的详细电磁暂态仿真结果表明，采用优化后的控制系统参数提高了连接弱交流系统时混合三端直流输电系统的小干扰稳定性。
关键词：混合多端直流输电系统 弱交流系统 控制参数优化 灵敏度分析
整流站采用电网换相型换流器（Line Com- mutated Converter, LCC）、逆变站采用模块化多电平换流器（Modular Multilevel Converter, MMC）的混合多端直流输电系统（Hybrid Multi-Terminal HVDC, H-MTDC）结合了LCC和MMC各自的优势[1-5]，因其不存在换相失败问题，可以向弱交流系统供电且降低了成本及系统损耗，引起了广泛关注[6-9]。2018年5月，乌东德混合三端直流输电系统在我国南方电网开始建设[10]，乌东德项目的建成在提高受端电网的电压稳定性，改善已有常规直流运行环境等方面都具有很大的意义。混合多端直流输电系统在未来也将具有较为广阔的工程应用前景。
目前，已有学者针对整流侧为LCC、逆变侧为MMC的混合多端直流输电系统开展了相关的研究，主要集中在运行特性和控制策略方面。文献[11]提出了受端多端的混合直流系统输送风电的控制策略。文献[12]分析对比了不同控制策略下混合多端直流输电的交流故障响应。文献[13]提出特高压混合多端直流输电系统各站的控制模式及系统的启停方案。文献[14-15]研究了混合多端直流输电系统的故障特性与相应的控制保护策略。上述文献研究了混合多端直流输电系统的暂稳态特性，然而并未涉及混合多端直流输电系统小干扰稳定性。
已有研究表明，含有LCC与电压源型换流器（Voltage Source Converter, VSC）的交直流混联系统的小干扰稳定性随交流系统强度减小而降低[16]。文献[17]分析了混合两端直流输电系统的小干扰稳定性，研究结果表明控制器参数对混合两端直流输电系统特别是对于弱交流电网条件下系统的小干扰稳定裕度影响较大。文献[18-19]建立了整流侧为LCC、逆变侧为VSC的混合多端直流输电系统的小信号模型，并分析了其小干扰稳定性，但是建模时没有考虑MMC换流站的内部谐波，无法基于该模型研究与MMC内部谐波相关的混合多端系统小干扰稳定性问题。因此，连接弱交流系统时混合多端直流输电系统的小干扰稳定裕度还有待深入研究。
本文提出一种提高弱交流系统下混合多端直流输电系统小干扰稳定性的控制参数优化调节方法。首先，基于混合多端直流输电系统的小干扰模型，采用特征根分析法研究了交流系统强度对混合多端直流输电系统小干扰稳定性的影响，并获得了可能引起系统失稳的主导模态。根据主导模态的特征并基于控制参数的灵敏度分析方法，给出一种控制参数的优化调节方法，结果表明，该方法可以提高连接弱交流系统时混合多端直流输电系统的小干扰稳定裕度。
混合三端直流输电系统的结构如图1所示，该系统送端为一个LCC换流站，受端为两个MMC换流站。系统的等效电路如图2所示，LCC站的交流滤波器和无功补偿装置参照CIGRE标准测试模型[20]。图2中，交流系统由等值电压源us_x（x =1, 2, 3，分别代表3个换流站）和戴维南阻抗Rs_x、感抗Ls_x表示，换流变压器由Lt_x、Rt_x表示。直流线路采用T型等效，Loh_x、Roh_x与Ccdc_x分别为三站直流侧T型线路的等值电感、等值电阻与等值电容，Udc_N为三站直流侧连接点的电压，Ldc_1为LCC1站出口的平波电抗器。
图1 混合三端直流输电系统结构
Fig.1 Configuration of hybrid three-terminal HVDC system
混合三端直流输电系统的控制系统如图3所示。LCC1站的控制系统包含锁相环（Phase-Lock Loop, PLL）以及定直流电流控制，MMC2站、MMC3站的控制系统包含锁相环电流矢量控制（Vector Current Control, VCC）以及环流抑制控制（Circulating Current Suppression Control, CCSC），MMC2站采用定直流电压控制与定无功功率控制，MMC3站采用定有功功率控制与定无功功率控制。
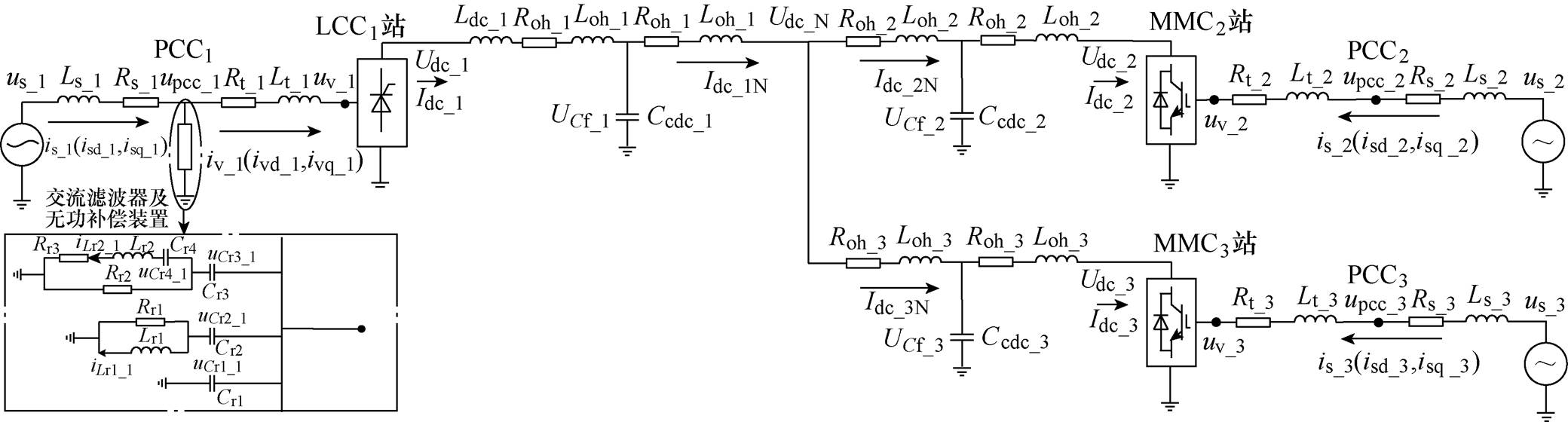
图2 混合三端直流输电系统等效电路
Fig.2 Equivalent circuit diagram of hybrid three-terminal HVDC system
图3 混合三端直流输电系统的控制系统
Fig.3 Control system of hybrid three-terminal HVDC system
混合三端直流输电系统小干扰模型包括LCC子系统、MMC子系统以及直流线路。LCC子系统包含三部分：交流系统、LCC换流站以及控制系统，MMC子系统也包含交流系统、MMC换流站以及控制系统。本文基于文献[21]建立了LCC子系统1的状态空间模型，基于文献[22]建立了MMC子系统2、3的状态空间方程，不再详述，LCC子系统1状态变量及其物理意义见表1，MMC子系统2、3状态变量及其物理意义见表2。
表1 LCC子系统1状态变量及其物理意义
Tab.1 State variables and physical meanings of LCC subsystem 1
结构物理意义状态变量 LCC侧交流系统交流母线电压upccd_1, upccq_1 交流滤波器uCr2d_1, uCr2q_1, uCr3d_1, uCr3q_1, uCr4d_1, uCr4q_1, iLr1d_1, iLr1q_1, iLr2d_1, iLr2q_1 交流系统电流isd_1, isq_1 LCC1站控制系统直流电流控制器及测量环节x1_1,Idcm_1, Idc_1 PLL1x2_1, xpll_1
直流线路起到联接LCC子系统与MMC子系统的作用，状态变量及其物理意义见表3。
根据图2列写LCC子系统1侧直流线路上的电感电流Idc_1N和电容电压UCf_1的状态方程，有
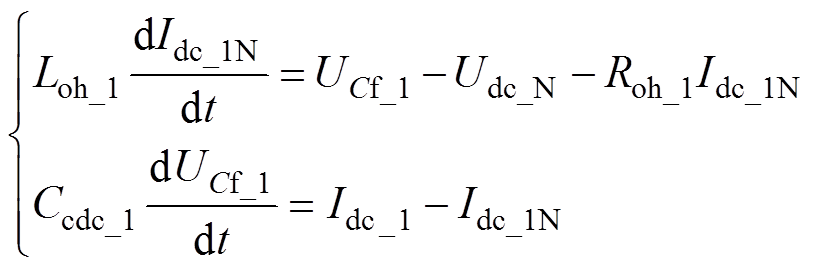（1）式中，Idc_1为LCC子系统1直流侧出口电流；Loh_1、Roh_1、Ccdc_1分别为LCC子系统1直流侧T型线路的等值电感、等值电阻与等值电容；Udc_N为三站直流侧连接点的电压。
MMC子系统3侧直流线路的电感电流Idc_3N和电容电压UCf_3的状态方程为
表2 MMC子系统2、3状态变量及其物理意义
Tab.2 State variables and physical meanings of MMC subsystem2 and 3
结构物理意义状态变量 MMC2、MMC3侧交流系统交流母线电压upccd_2, upccq_2, upccd_3, upccq_3 交流系统电流isd_2, isq_2, isd_3, isq_3 MMC2、MMC3换流站子模块直流电压分量ucdc_2, ucdc_3 子模块基频电压分量uc1d_2, uc1q_2, uc1d_3, uc1q_3 子模块二倍频电压分量uc2d_2, uc2q_2, uc2d_3, uc2q_3 子模块三倍频电压分量u3x_2, u3y_2, u3x_3, u3y_3 桥臂基频电流isd_2, isq_2, isd_3, isq_3 桥臂二倍频环流icird_2, icirq_2, icird_3, icirq_3 换流站出口直流电流Idc_2, Idc_3 MMC2、MMC3站控制系统交流母线电压测量值upccdm_2, upccqm_2, upccdm_3, upccqm_3 交流系统电流测量值isdm_2, isqm_2, isdm_3, isqm_3 内环d轴控制x1_2, x1_3 内环q轴控制x2_2, x2_3 VSC外环定有功类控制x3_2, x3_3 VSC外环定无功类控制x4_2, x4_3 CCSC的d轴控制f1_2, f1_3 CCSC的q轴控制f2_2, f2_3 PLL2x5_2, xpll_2, x5_3, xpll_3
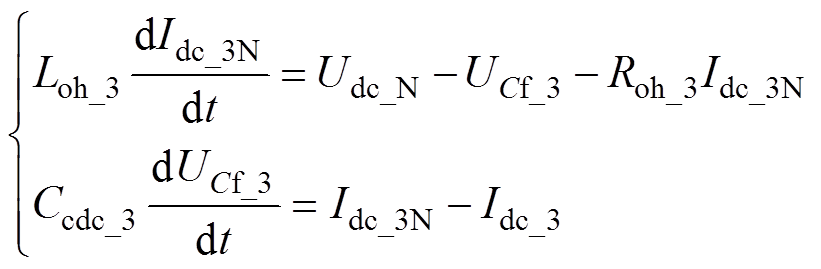（2）表3 直流线路状态变量及其物理意义
Tab.3 State variables and physical meanings of DC system
物理意义状态变量 电容电压UCf_1, UCf_2, UCf_3 电感电流Idc_1N, Idc_3N
式中，Idc_3为MMC子系统3直流侧出口电流；Loh_3、Roh_3与Ccdc_3分别为MMC子系统3直流侧T型线路的等值电感、等值电阻与等值电容。
根据基尔霍夫电流定律，MMC子系统2侧直流线路的电感电流Idc_2N为LCC子系统1侧直流线路的电感电流与MMC子系统3侧电流之差（Idc_2N= Idc_1N-Idc_3N），因此MMC子系统2侧直流线路的电容电压UCf_2的状态方程为
（3）式中，Idc_2为MMC子系统2直流侧出口电流；Ccdc_2为MMC子系统2直流侧T型线路的等值电容。
式（1）、式（2）中的线路公共连接处电压Udc_N用状态变量表示为
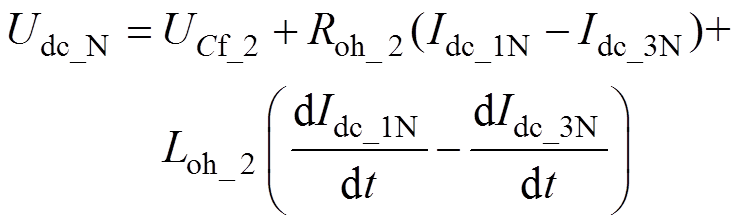（4）将式（1）、式（2）代入式（4），整理后得到Udc_N最终的表达式为
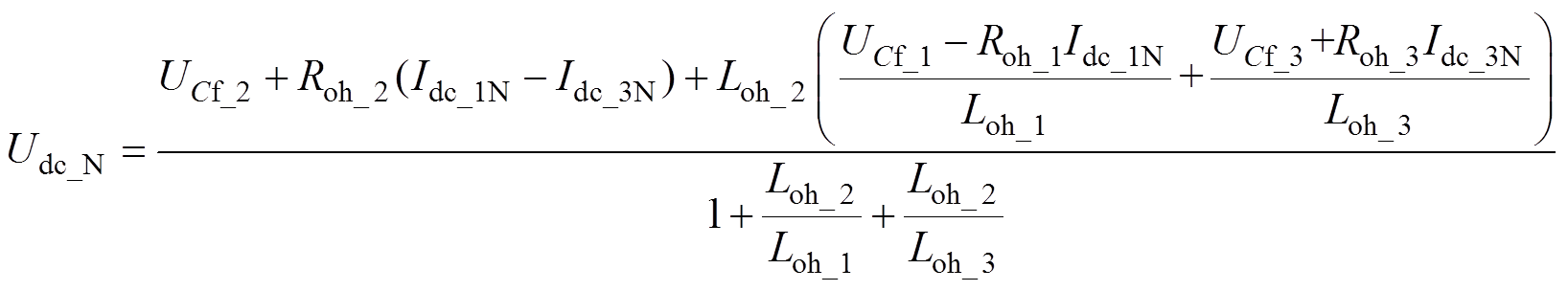（5）
将式（5）代入式（1）、式（2），结合式（3）即可得到直流线路的最终状态空间模型。
对LCC子系统、MMC子系统以及直流线路的状态空间方程进行线性化，即可得到74阶的混合三端直流输电系统的小干扰动态模型为
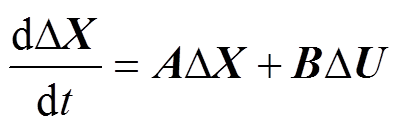（6）式中，X为状态变量；U为输入变量。状态变量X见表1～表3，输入变量为LCC子系统定电流指令值及MMC子系统电流矢量控制指令值，即U= [Idcref_1 Udcref_2 Pref_3 Qref_2 Qref_3]T；A为状态矩阵，B为输入矩阵，A阵为74阶方阵，B阵为74×5阶矩阵。由于论文篇幅有限，矩阵A、B的表达式由74阶状态空间模型线性化可容易得到，此处不再给出矩阵表达式。
为了验证所建立的混合三端直流输电系统小干扰模型的准确性，本节详细对比了Matlab中的系统小干扰模型与PSCAD中的详细电磁模型的动态响应，系统参数见表4。
混合三端直流输电系统初始以额定参数运行，5.0s时MMC3换流站的定有功功率参考值Pref_3从-1.00(pu)阶跃上升5%到-0.95(pu)，5.5s时恢复至-1.00(pu)。在Matlab建立的小干扰模型和在PSCAD中搭建的详细电磁暂态模型的仿真结果对比如图4所示。
表4 混合三端直流输电系统参数
Tab.4 Parameters of hybrid three-terminal HVDC system
参 数数 值 LCC子系统1额定功率P1/MW1 500 交流系统短路比SCR13∠85° 交流系统电压us_1(pu)1.0 换流变漏抗Lt_1(pu)0.18 额定交流母线电压upcc_1(pu)1.0 MMC 子系统2、子系统3额定功率P2, P3/MW750 交流系统短路比SCR2、SCR32.5∠85° 交流系统电压us_2, us_3(pu)1.0 换流变漏抗Lt_2, Lt_3(pu)0.15 子模块数N2, N3200 桥臂电感Larm_2, Larm_3/mH70 桥臂电阻Rarm_2, Rarm_3/W1 子模块电容CSM_2, CSM_3/mF10 000 直流线路平波电抗器Ldc_1/H0.29 线路长度l1N, lN2, lN3/km400, 300, 200 电阻R0/(W/km)0.0127 电感L0/(mH/km)0.88 电容C0/(mF/km)0.013
图4a～图4d分别表示LCC1站直流电流Idc_1、MMC2站直流电压Udc_2、MMC3站有功功率Pm_3以及子模块电容电压uC_3的动态响应波形，图4d中点画线框内波形为MMC3站子模块电容电压uC_3在5s左右波形的放大图，其中实线波形为PSCAD中的详细电磁暂态模型仿真结果，虚线波形为Matlab中的小干扰模型仿真结果。由图4可看出，各物理量的电磁暂态模型仿真结果与小干扰模型仿真结果基本一致，有效地验证了混合三端直流输电系统小干扰模型的正确性。
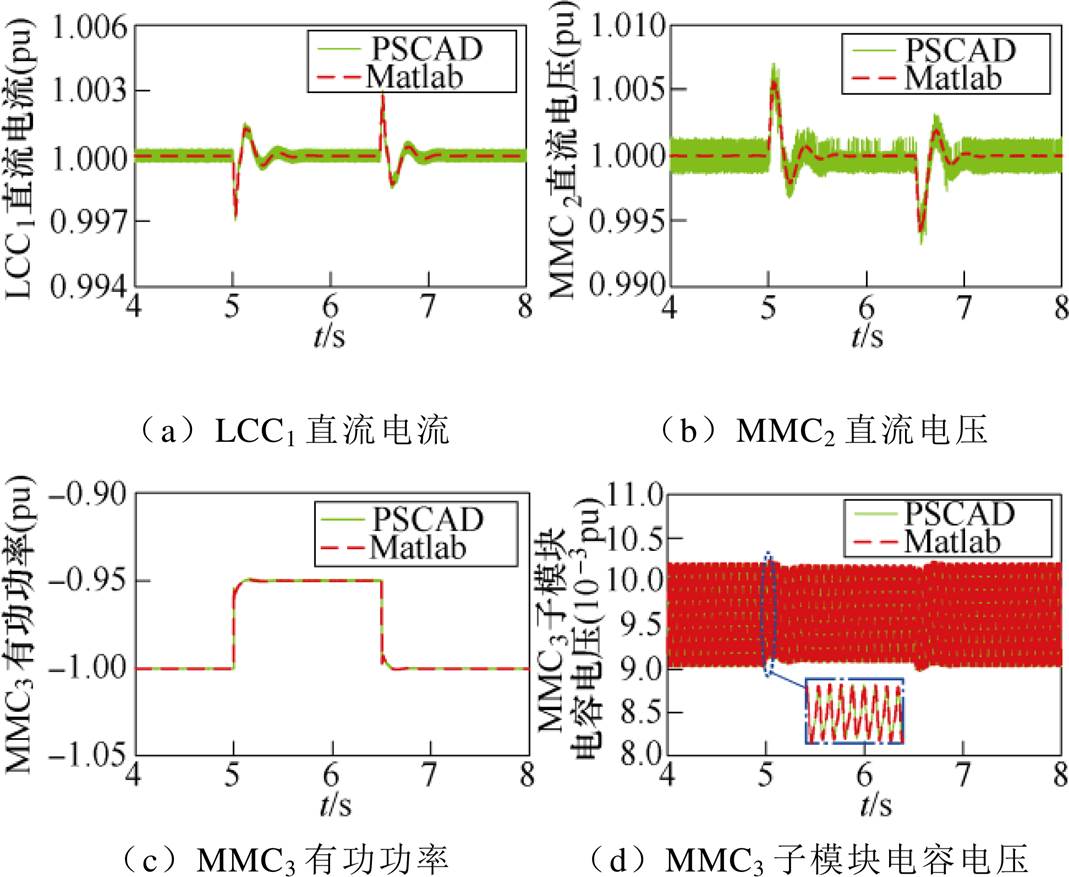
图4 Pref_3阶跃时系统的动态特性
Fig.4 System dynamic characteristics when Pref_3 step-change
为研究弱交流系统下混合三端直流输电系统的小干扰稳定裕度，基于第2节建立的混合三端直流输电系统小干扰模型研究三站交流系统的强度对混合三端直流输电系统小干扰稳定性的影响。
保持逆变侧联接MMC的两个交流系统的短路比（SCR2=2.5、SCR3=2.5）以及系统其他参数不变，令LCC侧交流系统的短路比SCR1从3减小至2，混合三端直流输电系统的根轨迹如图5所示。
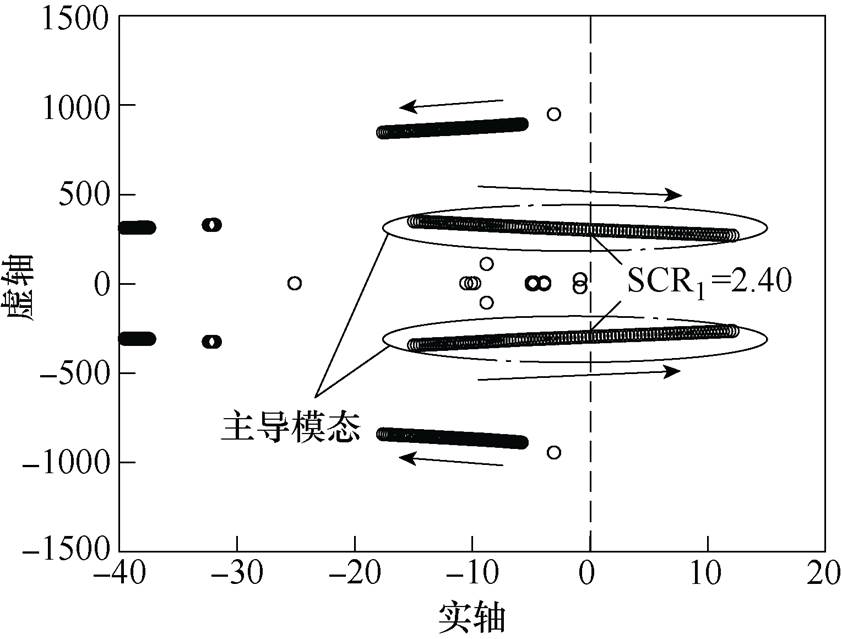
图5 SCR1减小时的根轨迹
Fig.5 Eigenvalue locus when SCR1 changes
由图5可知，LCC侧交流系统短路比下降到2.40时，主导模态穿越虚轴进入右半平面，混合三端直流系统面临小干扰失稳，此时引起系统失稳的主导模态的振荡频率f =47.60Hz。
同理，保持LCC1侧交流系统、MMC3侧交流系统短路比（SCR1=3、SCR3=2.5）以及系统其他参数不变，令MMC2侧交流系统的短路比从2.5减小至1.5，混合三端直流输电系统的根轨迹如图6所示。
由图6可知，MMC2侧交流系统短路比下降至2.12时，主导模态与虚轴相交，系统处于临界稳定状态，当短路比小于2.12时，系统将出现小干扰失稳现象，其主导模态的振荡频率f =3.15Hz。
保持LCC1侧交流系统、MMC2侧交流系统短路比（SCR1=3、SCR2=2.5）以及系统其他参数不变，令MMC3侧交流系统的短路比从2.5减小至1.5时，混合三端直流输电系统的根轨迹如图7所示。
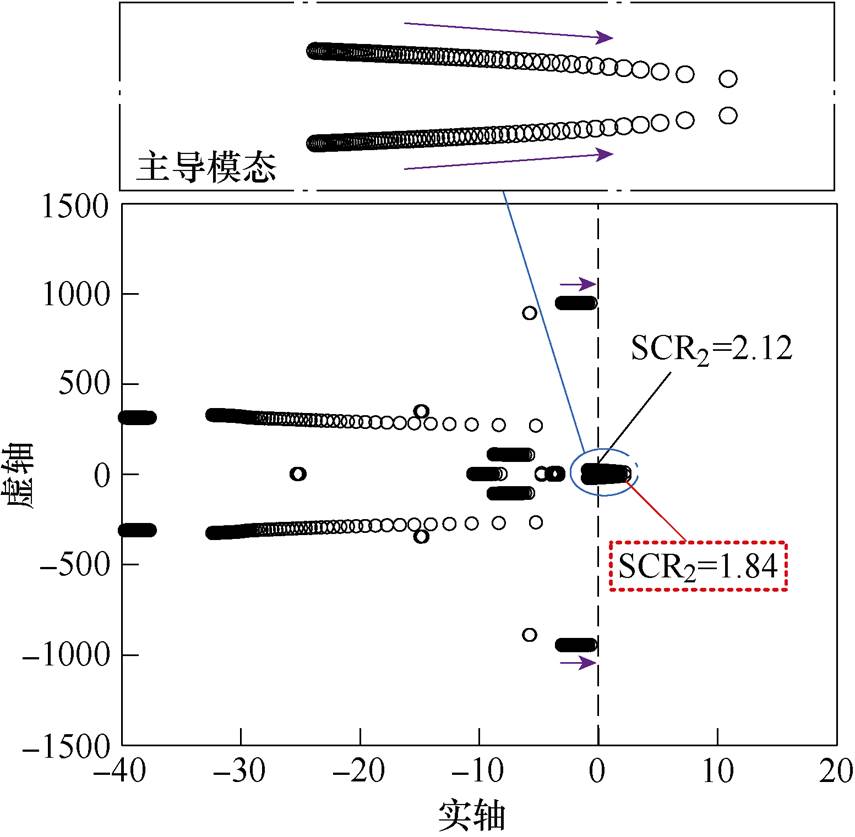
图6SCR2变化时的根轨迹
Fig.6 Eigenvalue locus when SCR2 changes
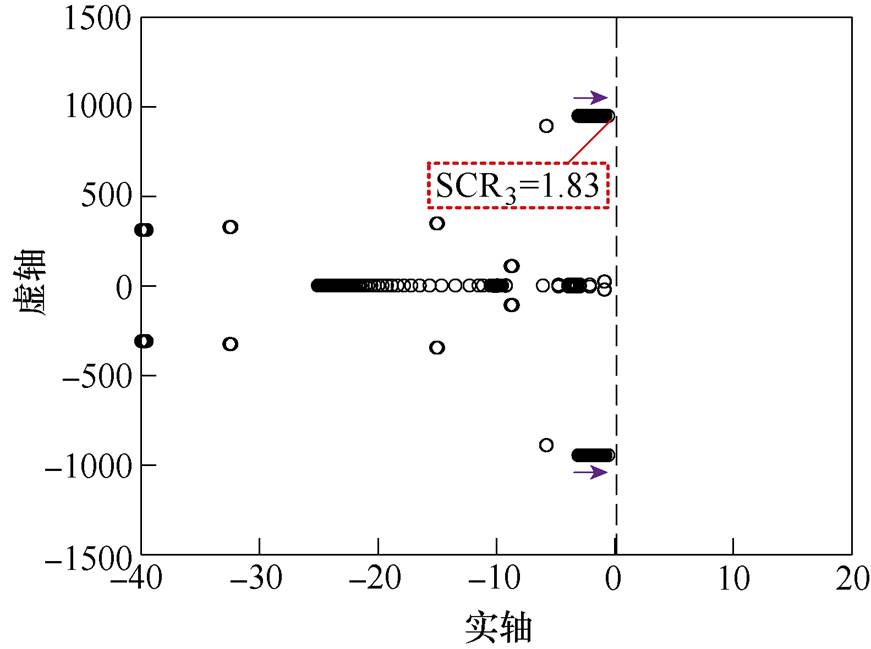
图7 SCR3变化时的根轨迹
Fig.7 Eigenvalue locus when SCR3 changes
由图7可知，随着MMC3侧交流系统的短路比下降，其主导模态向虚轴移动但始终保持在左半平面，表明系统可以维持小干扰稳定性。需要强调的是，图6、图7方框中所示的SCR2=1.84或SCR3= 1.83为不考虑控制系统参数影响时由混合三端直流输电系统潮流方程约束条件得到的系统静态稳定极限，因此SCR2＜1.84以及SCR3＜1.83时系统特征根变化趋势没有在图6和图7中表示出来。由此可见，随着MMC3侧交流系统短路比下降，系统到达静态稳定极限，即MMC3侧交流系统的短路比降低不会引起由于控制参数设置不合理造成的系统小干扰失稳；而对于MMC2侧交流系统短路比降低的情况，混合三端直流输电系统在未达到其静态稳定限值（SCR2=1.84）时，系统在SCR2＜2.12时将出现小干扰失稳现象，也就是说在本文研究的算例中，当MMC2站连接弱交流系统时，控制系统参数影响了整个混合三端直流输电系统的稳定性。考虑到MMC2换流站采用的是定直流电压控制，其具有与交流系统中平衡节点类似的平衡系统整体功率的功能，因此其在弱交流系统下的稳定裕度直接影响整个混合三端系统的稳定运行。因此，非常有必要研究如何通过控制参数的合理调节来提高整个混合三端直流输电系统的小干扰稳定性。
对于采用定直流电压控制的MMC2换流站，其控制系统包括PLL、VCC控制以及CCSC控制，该换流站同时也可能由于换流站间的耦合作用受到其他换流站控制系统的影响。而对于本文研究的混合三端直流输电系统，包含的控制参数很多，且各个控制参数的调节规律（增大或减小）不清楚，需要定位可提高稳定性的灵敏性控制参数及确定其调节方向，这就给提高定直流电压换流站连接弱交流系统时混合三端输电系统的小干扰稳定性带来了很大困难。本节基于该难点，给出一种可以提高连接弱交流系统时混合多端直流输电系统小干扰稳定裕度的控制参数优化调节方法，并针对定直流电压换流站连接弱交流系统时混合三端直流输电系统存在由控制系统引起的小干扰失稳现象，通过对控制系统参数的合理调节提高整个系统的小干扰稳定性。
参数优化调节方法的思路是每次参数调节时（即每次迭代）都需要基于参数的灵敏度分析方法获得对主导模态最灵敏的控制参数，并根据控制参数变化（增大或减小）时主导模态移动的特征，来调节控制参数。下面先简要介绍灵敏度分析的原理，再基于灵敏度分析给出参数优化调节的具体步骤。
特征值ln对控制参数am的灵敏度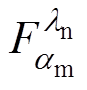
可由状态矩阵A的右特征向量和左特征向量计算得到[23-24]。参数灵敏度实部的正负表示随着控制参数的增大，模态沿实轴移动的方向（向实轴正半轴移动或向实轴负半轴移动），灵敏度实部若为正数表示参数的减小会使对应的模态向左半平面移动，该模态的阻尼比增强，即系统的稳定性提高；灵敏度实部的大小表示模态沿实轴移动的速度，灵敏度实部的绝对值越大，表示模态对该参数越敏感，随着控制参数的变化，模态沿实轴移动越快。本节将灵敏度的实部作为控制参数优化调节的基础，给出了一种基于灵敏度分析的控制参数优化调节方法。
基于灵敏度分析的控制参数优化调节方法的特点是，在每一次迭代过程中以提高混合三端直流输电系统的最小阻尼比为目的调整灵敏性控制参数。首先对采用初始控制参数得到的状态矩阵A进行特征值分析，确定阻尼比最小的模态为临界模态lc。然后计算临界模态对所有控制参数的灵敏度，选择灵敏度绝对值最大的控制参数ac，并通过每次迭代中的比例系数Da对控制参数ac进行优化，优化方 程为
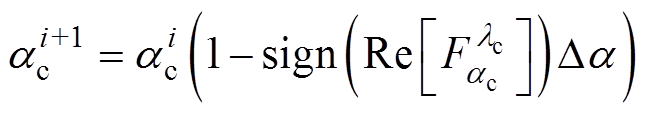（7）式中，i为迭代次数。控制参数灵敏度的实部符号决定了控制参数是减小还是增大才能使临界模态向左半平面移动，从而提高系统的稳定性。每次迭代时都要重新识别阻尼最小的临界模态，并重新计算对临界模态最敏感的控制参数。由于本文中参数优化的目的是提高整个系统的最小阻尼比，所以对临界模态阻尼比的要求可以设置为结束条件，有
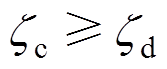（8）
式中，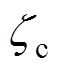
为临界模态的阻尼比；
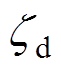为所需的临界模态阻尼比。一旦满足结束条件则优化过程结束，另外，为了防止由于所需的临界阻尼比设置不合适导致迭代无法跳出，设置了最大迭代次数，当达到最大迭代次数（本文中设置为500），参数优化迭代 终止。
令SCR1=2.5、SCR2=2、SCR3=2为初始运行状态，此时混合三端直流输电系统与弱交流系统联接，由于MMC2换流站所联接的交流系统的短路比低于其小干扰稳定临界值（如图6所示，SCR2=2.12），整个系统将出现小干扰失稳现象。以第一次迭代为例，对参数优化调节方法进行说明。首先，基于运行参数确定临界模态，计算此时临界模态对于控制系统各参数的灵敏度，其结果如图8所示。
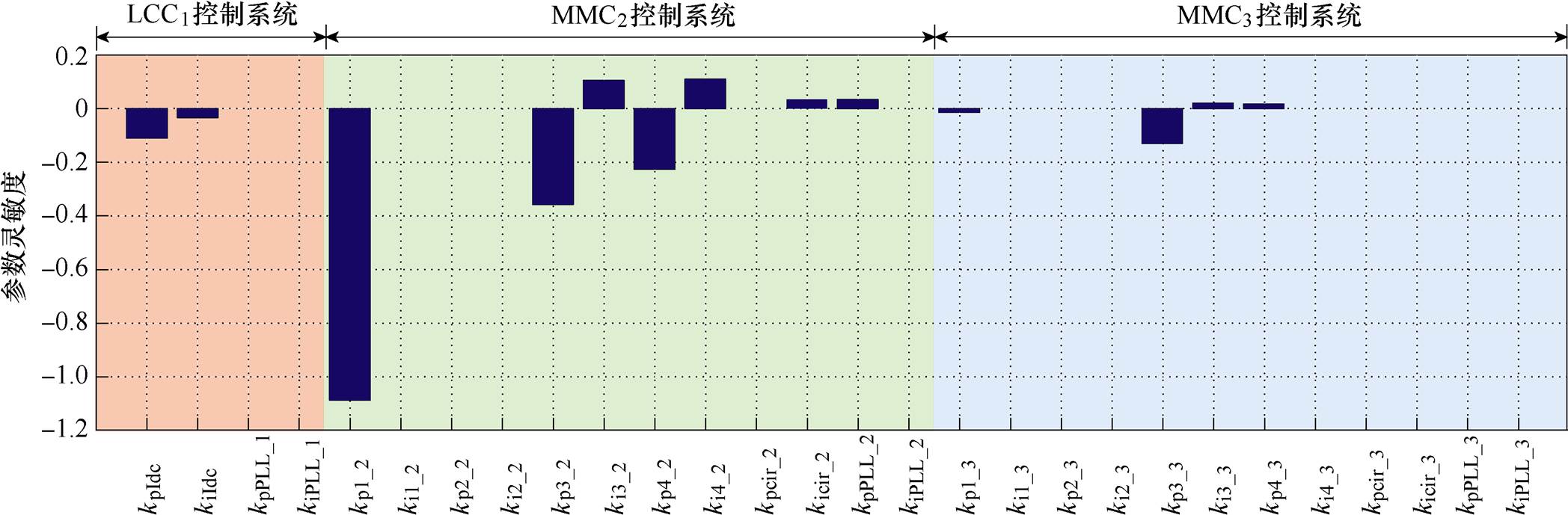
图8 临界模态对于控制系统参数变化的灵敏度
Fig.8 Parametric sensitivity of critical mode to different control parameter
由图8可知，此时灵敏度绝对值最高的控制参数为MMC2站定直流电压控制器的外环比例增益kp1_2，表明此时临界模态主要受MMC2站定直流电压控制器的外环比例增益的影响，则在本次迭代中优化的参数为定直流电压控制器的外环比例增益。临界模态对定直流电压控制器的外环比例增益灵敏度为负值，表明增大kp1_2将使临界模态向左半平面移动，将MMC2站定直流电压控制器的外环比例增益kp1_2的数值乘以1+Da 后，检查此时系统是否符合迭代结束条件，即系统最小阻尼比满足要求或者达到了最大迭代次数，如果不满足迭代结束条件，进入下一次迭代。如此往复迭代，直至满足优化终止条件。
采用基于灵敏度分析的控制参数优化调节方法对混合三端直流输电系统控制参数进行优化，控制系统参数优化前后见表5。
由表5结果可知，为了有效抑制连接弱交流系统时混合三端直流输电系统存在由控制系统引起的小干扰失稳现象，调节的主要控制参数不仅有MMC2站的定直流电压控制外环参数，还有MMC2站的内环d轴和q轴控制参数及CCSC控制参数；同时还调节了MMC3站的定有功功率控制外环，内环d轴和q轴控制参数及CCSC控制参数。
为了验证上述参数优化调节方法的有效性，在PSCAD中基于详细电磁暂态仿真进行了验证。混合三端直流输电系统初始以额定功率稳定运行（SCR1= 2.5、SCR2=2.5、SCR3=2），t =0.5s时MMC2侧交流系统短路比SCR2由2.5降低至2（由图6可知，此时短路比小于2.12，系统将出现小干扰失稳现象）；t =1.5s时，系统控制参数由表5的初始值调整为优化后的值，整个过程的仿真结果如图9所示。
表5 混合三端系统的控制系统参数
Tab.5 Parameters of control system of the overall system
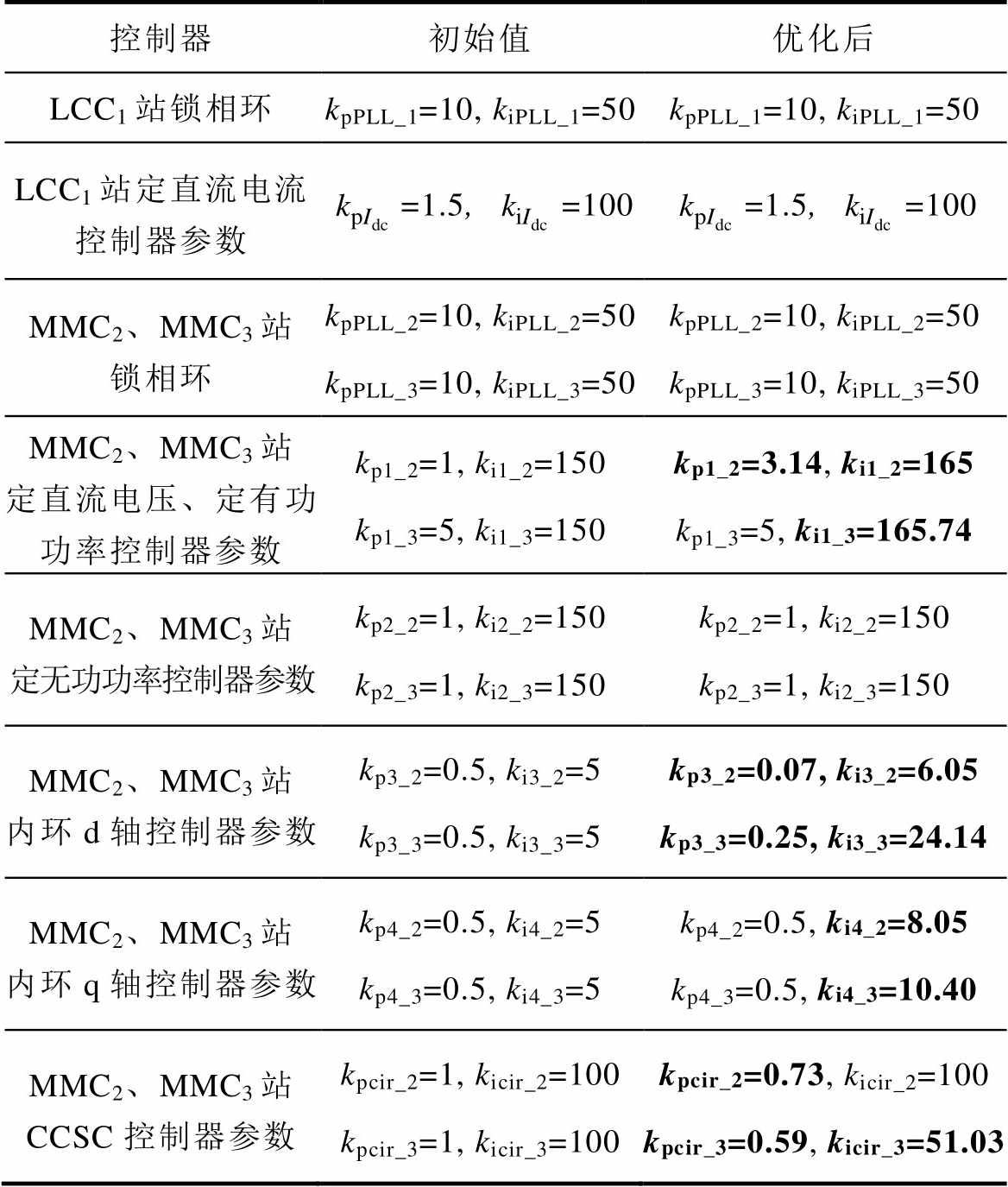
控制器初始值优化后 LCC1站锁相环kpPLL_1=10, kiPLL_1=50kpPLL_1=10, kiPLL_1=50 LCC1站定直流电流控制器参数=1.5, =100=1.5,=100 MMC2、MMC3站锁相环kpPLL_2=10, kiPLL_2=50kpPLL_3=10, kiPLL_3=50kpPLL_2=10, kiPLL_2=50kpPLL_3=10, kiPLL_3=50 MMC2、MMC3站定直流电压、定有功功率控制器参数kp1_2=1, ki1_2=150kp1_3=5, ki1_3=150kp1_2=3.14, ki1_2=165kp1_3=5, ki1_3=165.74 MMC2、MMC3站定无功功率控制器参数kp2_2=1, ki2_2=150kp2_3=1, ki2_3=150kp2_2=1, ki2_2=150kp2_3=1, ki2_3=150 MMC2、MMC3站内环d轴控制器参数kp3_2=0.5, ki3_2=5kp3_3=0.5, ki3_3=5kp3_2=0.07, ki3_2=6.05kp3_3=0.25, ki3_3=24.14 MMC2、MMC3站内环q轴控制器参数kp4_2=0.5, ki4_2=5kp4_3=0.5, ki4_3=5kp4_2=0.5, ki4_2=8.05kp4_3=0.5, ki4_3=10.40 MMC2、MMC3站CCSC控制器参数kpcir_2=1, kicir_2=100kpcir_3=1, kicir_3=100kpcir_2=0.73, kicir_2=100kpcir_3=0.59,kicir_3=51.03
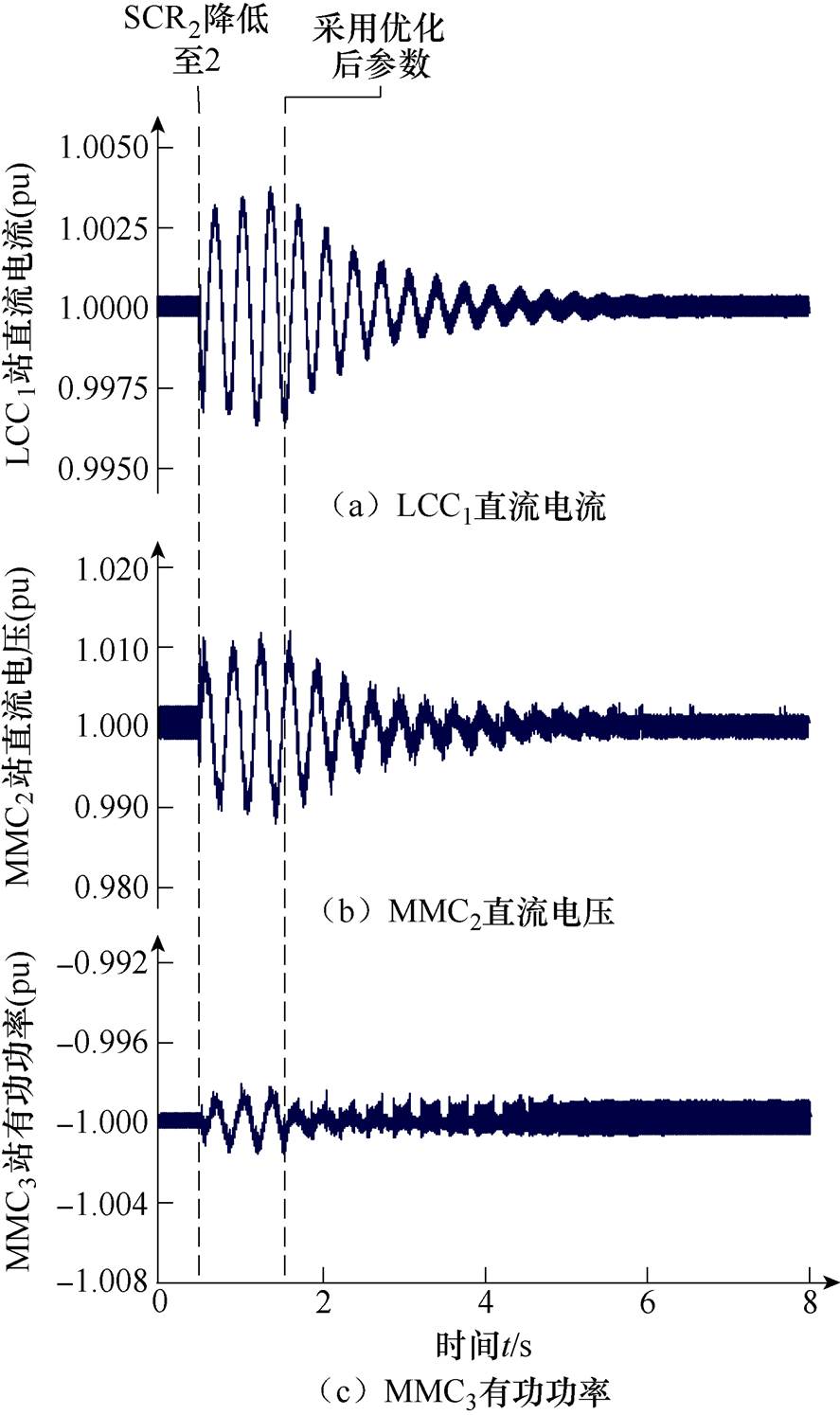
图9 SCR2=2时采用优化后参数的系统动态响应
Fig.9 Dynamic response of the system with optimized parameters whenSCR2=2
由图9可知，t =0.5s时，当混合三端直流输电系统中MMC2侧交流系统短路比SCR2降低到2后，LCC1站直流电流、MMC2站直流电压以及MMC3站有功功率逐渐发散，表明此时系统出现了振荡失稳现象，该结果也进一步验证了图6特征根分析结果的正确性。在t =1.5s时将控制系统参数调整为优化的参数后系统逐渐恢复稳定。因此，该结果进一步验证了所建立小干扰模型的正确性与所给出的参数优化调节方法的有效性，即通过所给出方法对控制参数进行合理调节后，可以有效抑制连接弱交流系统时混合三端直流输电系统存在由控制系统引起的小干扰失稳现象。
本文针对混合三端直流输电系统控制参数设置不合理导致其连接弱交流系统时出现的小干扰稳定性问题，提出了一种控制参数优化调节方法。首先基于混合三端直流输电系统的小干扰模型采用特征根分析方法，探究了交流系统强度对整个系统小干扰稳定性的影响。结果表明，在弱交流系统场景下，当控制参数设置不合理时，将使系统的小干扰稳定裕度小于其静态稳定裕度，可能出现由控制系统引起的小干扰失稳现象。为了提高混合三端直流输电系统连接弱交流系统时的小干扰稳定裕度，本文给出了一种基于灵敏度分析的控制参数优化调节方法。PSCAD/EMTDC的详细电磁暂态仿真结果表明，采用优化后控制参数的系统在连接弱交流系统时小干扰稳定性得到提升，有效地验证了参数优化调节方法的有效性。
参考文献
[1] 赵畹君. 高压直流输电工程技术[M]. 2版. 北京: 中国电力出版社, 2011.
[2] 肖湘宁, 李伟, 罗超, 等. 特高压直流孤岛运行特性与稳定控制研究综述[J]. 电工技术学报, 2017, 32(10): 1-11.
Xiao Xiangning, Li Wei, Luo Chao, et al. Survey on operational characteristics and stability control of ultra-HVDC transmission system in islanded mode[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 1-11.
[3] 吴杰, 王志新. 多端柔性直流输电系统的改进下垂控制策略[J]. 电工技术学报, 2017, 32(20): 241-250.
Wu Jie, Wang Zhixin. Improved droop control strategy for multi-terminal voltage source converter-HVDC[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 241-250.
[4] 姚骏, 谭义, 裴金鑫, 等. 模块化多电平变流器高压直流输电系统直流故障改进控制策略[J]. 电工技术学报, 2018, 33(14): 3306-3318.
Yao Jun, Tan Yi, Pei Jinxin, et al. Improved control strategy for DC fault in modular multi-level converter HVDC system[J]. Transactions of China Electro- technical Society, 2018, 33(14): 3306-3318.
[5] 王增平, 刘席洋, 李林泽, 等. 多馈入直流输电系统换相失败边界条件[J]. 电工技术学报, 2017, 32(10): 12-19.
Wang Zengping, Liu Xiyang, Li Linze, et al. Boundary conditions of commutation failure in multi-infeed HVDC systems[J]. Transactions of China Electro- technical Society, 2017, 32(10): 12-19.
[6] 唐庚, 徐政, 薛英林. LCC-MMC混合高压直流输电系统[J]. 电工技术学报, 2013, 28(10): 301-310.
Tang Geng, Xu Zheng, Xue Yinglin. A LCC-MMC hybrid HVDC transmission system[J]. Transactions ofChina Electrotechnical Society, 2013, 28(10): 301-310.
[7] Zhao Zhenyu, Iravani M R. Application of GTO voltage source inverter in a hybrid HVDC link[J]. IEEE Transactions on Power Delivery, 1994, 9(1): 369-377.
[8] Li Chenghao, Zhan Peng, Wen Jinyu, et al. Offshore wind farms integration and frequency support control utilizing hybrid multi-terminal HVDC transmission[J]. IEEE Transactions on Industry Applications, 2014, 50(4): 2788-2797.
[9] 李建国, 刘文华, 王久和, 等. 基于LCC和双钳位MMC混联高压直流输电的实验[J]. 电工技术学报, 2018, 33(16): 3677-3685.
Li Jianguo, Liu Wenhua, Wang Jiuhe, et al. Experi- ment of hybrid high voltage direct current trans- mission based on LCC and clamp double sub module MMC[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3677-3685.
[10] 杨燕, 林勇, 徐蔚, 等. 乌东德多端直流输电对广东电网安全稳定的影响[J]. 广东电力, 2017, 30(11): 44-50.
Yang Yan, Lin Yong, Xu Wei, et al. Influence of Wudongde multi-terminal HVDC on security and stability of Guangdong power grid[J]. Guangdong Electric Power, 2017, 30(11): 44-50.
[11] 葛廷利, 宁博扬, 陈金辉. 受端多端的混合直流系统输送风电的控制策略研究[J]. 电力系统保护与控制, 2016, 44(24): 191-195.
Ge Tingli, Ning Boyang, Chen Jinhui. Research on control strategy of received multiterminal DC system transporting mixed by the wind[J]. Power System Protection and Control, 2016, 44(24): 191-195.
[12] 杨健, 洪潮, 张野, 等. 不同控制策略下混合多端直流输电的交流故障响应对比[J]. 南方电网技术, 2017, 11(7): 39-44, 50.
Yang Jian, Hong Chao, Zhang Ye, et al. Comparison on AC fault response of hybrid multi-terminal HVDC with differnet control strategies[J]. Southern Power System Technology, 2017, 11(7): 39-44, 50.
[13] 李婧靓, 黄伟煌, 刘涛, 等. 特高压多端混合直流输电系统的控制策略研究[J]. 南方电网技术, 2018, 12(2): 47-55.
Li Jingjing, Huang Weihuang, Liu Tao, et al. Research on control strategy of multi-terminal hybrid UHVDC transmission system[J]. Southern Power System Technology, 2018, 12(2): 47-55.
[14] 时伯年, 洪潮, 张野, 等. LCC-MMC三端混合直流输电系统整流站交流故障穿越协调控制策略[J]. 南方电网技术, 2017, 11(7): 11-18.
Shi Bonian, Hong Chao, Zhang Ye, et al. Rectifier side AC fault ride-through coordination control strategy for three-terminal LCC-MMC hybrid HVDC system[J]. Southern Power System Technology, 2017, 11(7): 11-18.
[15] 洪潮, 时伯年, 孙刚, 等. 基于LCC-MMC的三端混合直流输电系统故障特性与控制保护策略[J]. 电力建设, 2017, 38(8): 73-79.
Hong Chao, Shi Bonian, Sun Gang, et al. Fault characteristics and control & protection strategy of three-terminal LCC-MMC hybrid HVDC transmission system[J]. Electric Power Construction, 2017, 38(8): 73-79.
[16] Bidadfar A, Nee H P, Zhang Lidong, et al. Power system stability analysis using feedback control system modeling including HVDC transmission links[J]. IEEE Transactioins on Power Systems, 2016, 31(1): 116-124
[17] Guo Chunyi, Yin Zihan, Zhao Chengyong, et al. Small-signal dynamics of hybrid LCC-VSC HVDC systems[J]. International Journal of Electrical Power and Energy Systems, 2018, 98: 362-372
[18] Kotba O, Ghandharia M, Erikssonb R, et al. On small signal stability of an AC/DC power system with a hybrid MTDC network[J]. Electric Power Systems Research, 2016, 136: 79-88.
[19] Zhang Hailin, Yao Shujun, Zhao Peng. Research on small-signal stability of hybrid multi-terminal HVDC system and control system parameter design[J]. The Journal of Engineering, 2017, 13: 2401-2406.
[20] Szechtman M, Wess T, Thio C V. A benchmark model for HVDC system studies[C]//International Conference on AC and DC Power Transmission, London, 1991: 374-378.
[21] Guo Chunyi, Zhao Chengyong, Iravani R, et al. Impact of phase-locked loop on small-signal dynamics of the line commutated converter-based high-voltage direct-current station[J]. IET Generation Trans- mission & Distribution, 2017, 11(5): 1311-1318.
[22] 李探, Aniruddha M Gole, 赵成勇. 考虑内部动态特性的模块化多电平换流器小信号模型[J]. 中国电机工程学报, 2016, 36(11): 2890-2899.
Li Tan, Aniruddha M Gole, Zhao Chengyong. Small- signal model of the modular multilevel converter considering the internal dynamics[J]. Proceedings of the CSEE, 2016, 36(11): 2890-2899.
[23] Kundur P. Power system stability and control[M]. New York: McGrawHill, 1994.
[24] D'Arco S, Suul J A, Fosso O B. Automatic tuning of cascaded controllers for power converters using eigenvalue parametric sensitivities[J]. IEEE Transa- ctions on Industry Applications, 2015, 51(2): 1743- 1753.
Optimal Adjustment Method of Control Parameters for Improving Small-Signal Stability of Hybrid Multi-Terminal HVDC System under Weak AC Condition
Abstract The hybrid multi-terminal high voltage direct current (H-MTDC) system uses the Line Commutated Converter (LCC) for rectifiers and the Modular Multilevel Converter (MMC) for inverters. When the H-MTDC system is connected to a weak AC system, if the control parameters are set unreasonably, small-signal instability may occur in the system, which limits the application of the H-MTDC system under weak AC condition. In this paper, a control parameter optimization method was proposed to improve the small-signal stability of H-MTDC system under weak AC condition. First, based on the small-signal model of H-MTDC system, the eigenvalue analysis method was used to study the impact of the strength of AC grid connected at different converter stations on the small-signal stability of H-MTDC. The results show that unreasonable selection of control parameters will reduce the stability margin of the system, and then induce the corresponding small-signal instability. Taking the hybrid three-terminal high voltage direct current (HVDC) system as an example, this paper presented a control parameter optimization method based on sensitivity analysis, and optimized the control parameters of the hybrid three-terminal HVDC system. The detailed electromagnetic transient simulation results in PSCAD/EMTDC show that the small-signal stability of hybrid three-terminal HVDC system under weak AC grid condition can be improved by the optimized control system parameters.
keywords：Hybrid multi-terminal high voltage direct current system, weak AC condition, control parameters optimization, sensitivity analysis
中图分类号：TM721.1
DOI: 10.19595/j.cnki.1000-6753.tces.190160
国家自然科学基金面上资助项目（51877077）。
收稿日期2019-02-15
改稿日期 2019-05-20
郑安然 女，1995年生，硕士研究生，研究方向为直流输电等。E-mail: zhenganran1995@126.com
郭春义 男，1984年生，博士，副教授，研究方向为直流输电、FACTS等。E-mail: chunyiguo@outlook.com（通信作者）
（编辑 崔文静）