弱电网下具有定稳定裕度的并网逆变器阻抗重塑分析与设计
涂春鸣1 高家元1 赵晋斌2 张云飞2 郭 祺1
(1. 国家电能变换与控制工程技术研究中心(湖南大学) 长沙 410082 2. 上海电力大学电气工程学院 上海 200090)
摘要 针对弱电网下并网逆变器的稳定性控制问题进行了研究。该文以重塑的基于阻抗的稳定性判据为理论基础,以电流双闭环控制三相LCL型并网逆变器为模型,建立并网系统的诺顿等效串、并联阻抗数学模型;通过分析等效输出阻抗的特点,选择对逆变器的并联等效输出阻抗进行重塑;该阻抗重塑控制技术包含电网阻抗检测、相位裕度补偿和幅值矫正三个单元,重塑后的等效阻抗模型在电网阻抗宽范围变化时始终能够保持逆变器并网系统具有恒定的稳定裕度,与此同时在考虑电网阻抗存在检测误差的情况下,依旧能够保证系统具有良好的稳态和动态性能。最后,通过仿真和实验验证了文中理论分析的正确性以及所提阻抗重塑控制技术的有效性。
关键词:弱电网 LCL 并网逆变器 阻抗判据 阻抗重塑 稳定裕度
0 引言
随着煤、石油以及天然气等不可再生能源的日益枯竭,环境问题日益严重,利用可再生能源发电的分布式发电技术得到快速发展,故其在电网中所占的容量也在不断增加[1]。由于分布式发电系统呈散落分布状,需要大量变压器及较长的输电线路接入大电网,造成电网存在不可忽略的电网阻抗,这种电网通常称为弱电网[2]。同时,电网运行方式的变化也导致了电网阻抗呈宽范围变化的特点[3]。而并网逆变器作为可再生能源发电与电网的接口,电网阻抗的存在会严重影响逆变器并网系统的控制性能甚至导致系统不稳定[4-6]。
目前针对弱电网下并网逆变器的稳定性控制问题,许多学者采用不同的分析方法给出了多种解决方案。文献[7]通过时域分析方法,分别研究了比例积分(PI)控制器、比例谐振(PR)控制器及滞环控制器在弱电网下的动态性能变化以及系统稳定性问题。文献[8]对应用有源阻尼控制、谐波振荡控制、重复控制及电网电压前馈控制四种控制方法的并网逆变器在弱电网下工作的稳定性问题分别进行了评估。文献[9-11]主要关注逆变器系统中滤波器谐振和电流环设计,通常使用虚拟阻抗法来提高系统稳定性。文献[12]表明弱电网下数字控制延时会影响有源阻尼的效果,进而影响系统对电网阻抗的鲁棒性,为削弱数字控制延时的不利影响,提出一种相位超前补偿方法来提高系统对电网阻抗的鲁棒性。文献[13-14]提出逆变器的自适应控制策略,通过实时检测电网阻抗值,根据控制算法关系来实时动态调整相应控制环参数,实现逆变器并网系统的稳定、优化运行。以上的这些研究多关注于逆变器控制器本体的稳定性,系统稳定性分析过程较为复杂[15]。为此,专家们提出基于阻抗的稳定性分析方法[16],该方法把逆变器和电网视为两个单独的子系统,以阻抗的形式来表示其外特性,并采用基于阻抗的稳定性判据来分析二者之间的交互稳定性[17]。文献[4,18-19]通过定义阻抗控制环节直接作用于并网逆变器的等效输出阻抗实现阻抗控制。文献[20]介绍了目前虚拟阻抗的不同实施方式,对基于虚拟阻抗控制的电流源和电压源型变换器进行了系统的总结。文献[21]指出传统的基于阻抗的稳定性判据在用阻抗比表征系统的稳定性裕度过程中存在表征误差,同时在弱电网下并网逆变器自适应控制过程中有可能因等效电流源不稳定而变得不再适用。为此该文对阻抗判据进行了重塑,重塑后的阻抗判据不仅能够利用阻抗比准确表征系统真实的相位裕度,而且适用于弱电网下并网逆变器的自适应控制。
通过上述分析,本文在重塑基于阻抗的稳定性判据理论基础上[21],采用数学方法推导并建立了电流双闭环控制LCL型并网逆变器的诺顿等效串、并联阻抗模型。通过对阻抗模型的阻抗特性进行分析,提出一种保持等效电流源串联输出阻抗不变,优化并联输出阻抗特性的阻抗重塑控制技术。该阻抗重塑技术包含三部分:电网阻抗检测单元、相位裕度定点补偿单元和幅值矫正单元。其中电网阻抗检测单元实现电网阻抗的实时在线检测,并将其检测信息送入到相位裕度定点补偿单元;相位裕度定点补偿单元首先根据送入的电网阻抗信息利用重塑的基于阻抗的稳定性判据计算得到交截频率与对应的相位裕度,然后根据获取的交截频率与相位裕度确定补偿环节参数,实现相位裕度的精确补偿;同时为了实现定点补偿需要幅值矫正单元进行幅值修正。本文所提阻抗重塑控制技术不仅能够在电网阻抗宽范围变化过程中保持逆变器并网系统具有恒定的稳定裕度,而且在考虑电网阻抗存在检测误差的情况下,依旧能够保证系统具有良好的稳态和动态性能。最后,通过仿真和实验验证了本文理论分析的正确性以及所提控制策略的有效性。
1 LCL型并网系统阻抗模型建立
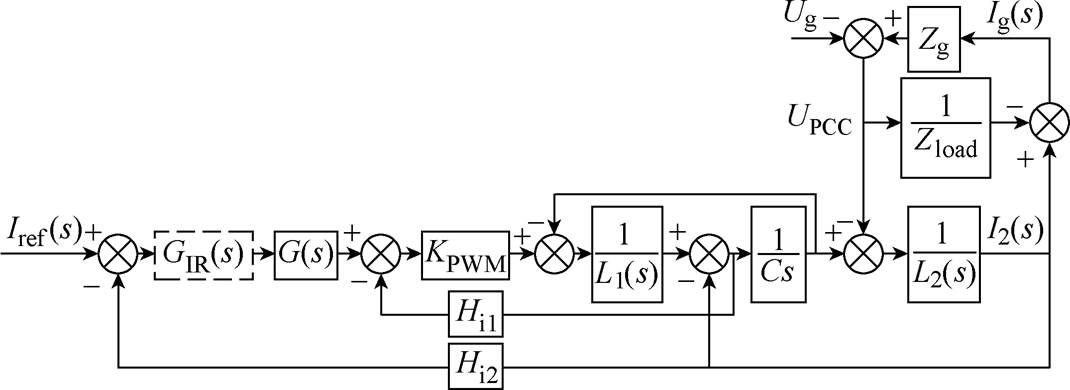
为了分析弱电网下本文所提阻抗重塑控制技术的可行性,在文献[4]逆变器控制结构的基础上加入阻抗重塑单元。该系统的总体控制结构如图1所示,其控制系统数学框图模型如图2所示。
在图1和图2中,L1、C和L2构成LCL滤波器;Zload为负载等效阻抗,Zg为电网阻抗;i1为逆变桥侧电感电流,iC为滤波电容电流,i2为逆变器输出电流,ig为并网电流,iCa、iCb 分别为电容电流在ab 坐标系下的分量,i2a、i2b 分别为逆变器输出电流在ab 坐标系下的分量,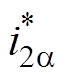 、
、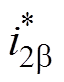 分别为逆变器输出电流在ab 坐标系下的给定值;UPCC为公共耦合点(Point of Common Coupling, PCC)的电压,Ug为电网电压,Udc为直流母线电压。wt为锁相环(Phase Locked Loop, PLL)输出相位,G(s)为外环控制器,Hi1为电容电流比例反馈系数,Hi2为并网电流采样系数,KPWM为脉宽调制增益,Zo1(s)、Zo2(s)分别为逆变器等效输出并联、串联阻抗,k1、k2为相位裕度补偿系数,k3为幅值矫正系数;fcross为阻抗判据交截频率,PM为闭环系统相位裕度,GIR(s)为阻抗重塑单元等效传递函数。由于负载具有不确定性且不是本文研究重点,因此取一个特殊情况研究,即负载阻抗为无穷大。
分别为逆变器输出电流在ab 坐标系下的给定值;UPCC为公共耦合点(Point of Common Coupling, PCC)的电压,Ug为电网电压,Udc为直流母线电压。wt为锁相环(Phase Locked Loop, PLL)输出相位,G(s)为外环控制器,Hi1为电容电流比例反馈系数,Hi2为并网电流采样系数,KPWM为脉宽调制增益,Zo1(s)、Zo2(s)分别为逆变器等效输出并联、串联阻抗,k1、k2为相位裕度补偿系数,k3为幅值矫正系数;fcross为阻抗判据交截频率,PM为闭环系统相位裕度,GIR(s)为阻抗重塑单元等效传递函数。由于负载具有不确定性且不是本文研究重点,因此取一个特殊情况研究,即负载阻抗为无穷大。
在对逆变器并网系统进行阻抗重塑之前,根据控制框图等效变换可得等效框图,如图3所示。
图3中,G1(s)、G2(s)以及系统环路增益TA(s)的表达式分别为
为了简化,令A(s)=L1Cs2+Hi1KPWMCs+1,则有
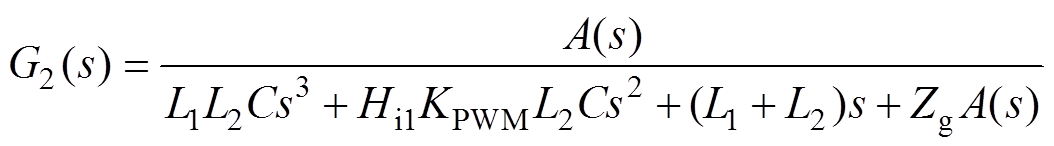 (2)
(2)
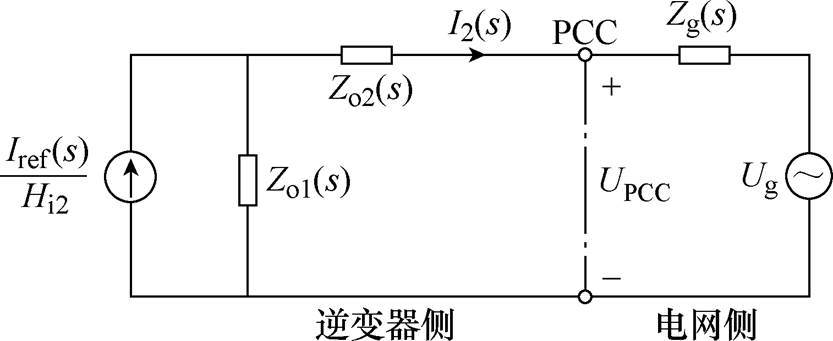
图4中,Zo1(s)、Zo2(s)的表达式分别为
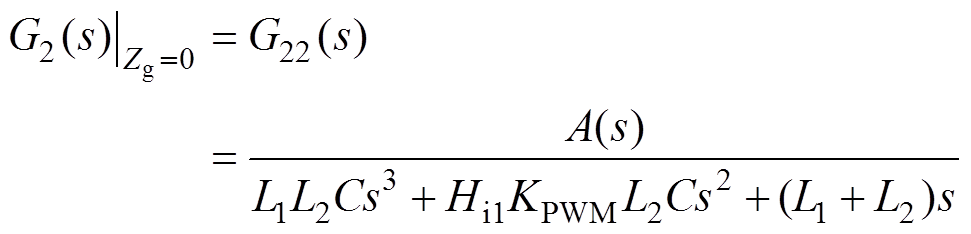 (5)
(5)
根据图4的诺顿等效阻抗模型可以求得并网电流I2(s)的表达式为
根据文献[21]的相关结论可知:逆变器的稳定性可以用(Zo2(s)+Zg(s))/Zo1(s)所表征的单位前向通道增益负反馈控制系统来进行判定,同时原系统真实的相位裕度PM可以计算为
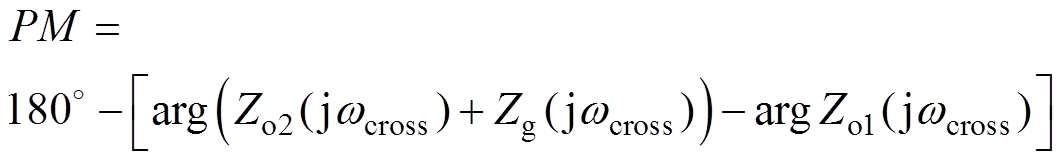 (7)
(7)
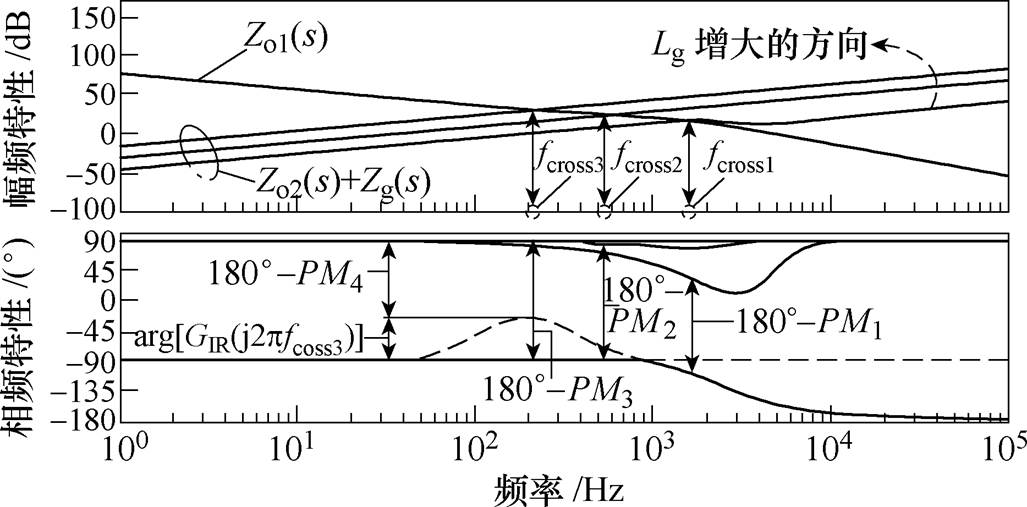
式中,wcross为Zo2(s)+Zg(s)与Zo1(s)的交截角频率,wcross=2pfcross。图5给出了该阻抗判据随电网阻抗变化的Bode图。
从图5的分析结果可以看出:当电网阻抗不断增加时,Zo2(s)+Zg(s)与Zo1(s)的交截频率在不断减小,这就意味着系统的响应速度变慢、动态性能变差;同时系统的相位裕度PM也随着电网阻抗的增加而不断减小(PM3<PM2<PM1),过小的PM会恶化系统的稳态和动态性能,甚至有可能导致系统振荡以及不稳定。通过观察阻抗判据可以看出:Zo2(s)+Zg(s)的频率特性会随着电网阻抗的变化而实时动态调整,具有不确定性,但是Zo1(s)的频率特性在逆变器并网系统参数确定后具有唯一不变性,易于重塑。基于上述阻抗特点,本文选择对并联输出阻抗Zo1(s)的阻抗特性进行重塑。如果重塑后的Zo1(s)始终能够保证在与Zo2(s)+Zg(s)的交截频率处具有满意的相位裕度,则就能够保证弱电网下并网逆变器系统的安全稳定运行。具体的阻抗重塑控制技术的分析与设计将会在下一节中详细讨论。
2 阻抗重塑控制技术的分析与设计
为了提高逆变器并网系统对弱电网的适应性,本文基于系统的阻抗模型提出一种阻抗重塑控制技术,该技术旨在保证逆变器并网系统具有理想的相位裕度,进而保障系统的安全稳定运行。
2.1 电网阻抗检测算法设计
在利用重塑的基于阻抗的稳定性判据判定系统的稳定性以及求取系统真实相位裕度的过程中需要实时获取电网阻抗信息,因此电网阻抗的实时在线检测就显得至关重要。本文充分考虑阻抗重塑控制技术优化逆变器并网电流的工作特性,结合并网电流的总谐波畸变率(Total Harmonic Distortion, THD),提出一种选择性注入非特征谐波的电网阻抗检测方法,尽量减少注入谐波对逆变器输出电能质量的影响。
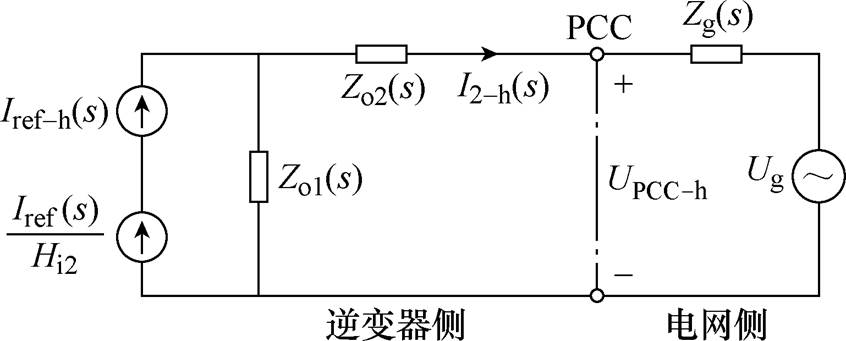
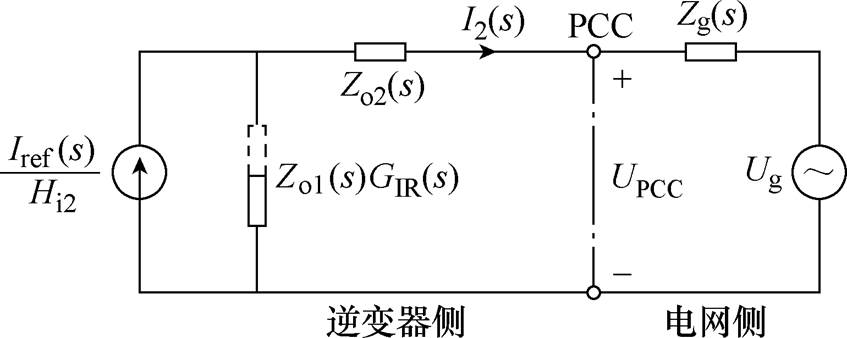
非特征谐波注入逆变器的小信号等效电路如图6所示。
在并网电流参考值上叠加一定幅值的非特征检测谐波,对PCC电压和并网电流进行快速傅里叶变换(Fast Fourier Transform, FFT),分别得到它们在非特征谐波频率fh处的幅值和相位信息,则可以计算得到电网阻抗Lg的数值为
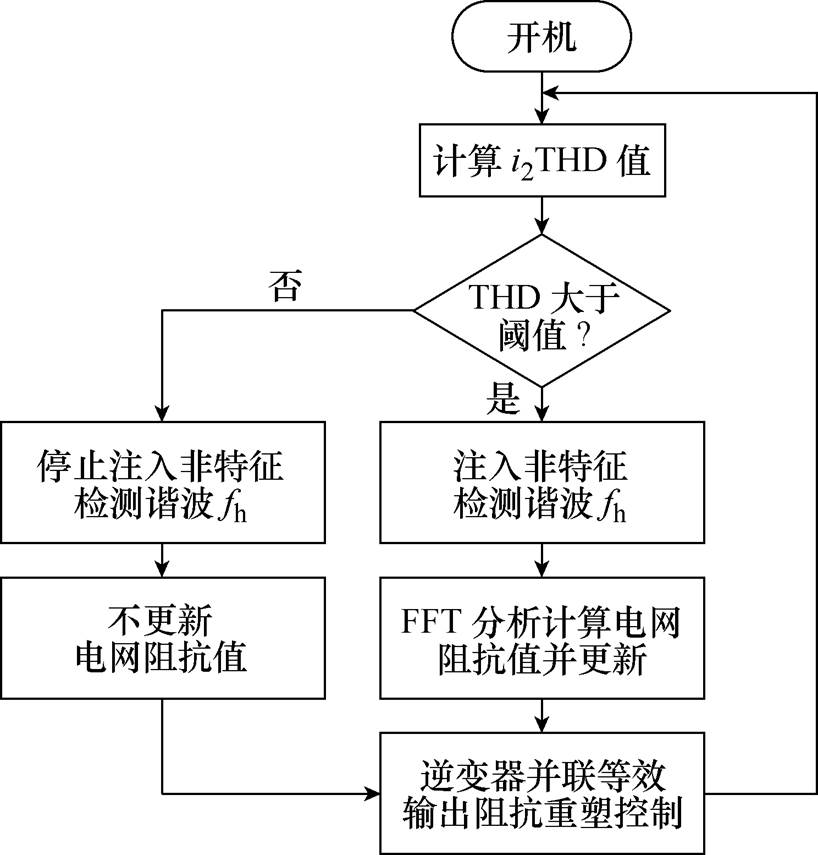
与本文所提阻抗重塑控制技术相结合的电网阻抗检测算法流程如图7所示。在投入电网阻抗检测算法时,首先计算得到并网电流的THD值,并与事先设定的阈值进行比较,如果超出阈值,则注入非特征谐波并采样PCC电压与并网电流,通过FFT分析计算得到电网阻抗值,实现对逆变器并联等效输出阻抗的重塑,优化并网电流质量;如果并网电流的THD值没有超出阈值,满足要求,则停止注入非特征检测谐波,并保留上一次计算得到的电网阻抗值,来对逆变器并联等效输出阻抗进行重塑。本文选取注入的非特征检测谐波的频率fh=500Hz,电流幅值为3A[22],THD阈值设置为3%。
2.2 阻抗重塑控制技术设计
为了保证逆变器并网系统在电网阻抗宽范围变化时依旧具有良好的稳定裕度,本文在电网阻抗检测的基础上选择对逆变器的并联等效输出阻抗Zo1(s)进行阻抗重塑,重塑后的诺顿等效阻抗模型如图8所示。
根据重塑的基于阻抗的稳定性判据可知,原逆变器并网系统的稳定性以及系统的真实相位裕度可以由式(9)的等效负反馈控制系统来判定。
为了实现对(Zo2(s)+Zg(s))/Zo1(s)的定点相位裕度补偿,要求GIR(s)不仅具有相位补偿单元还要具有幅值矫正单元,于是可构造GIR(s)的结构为
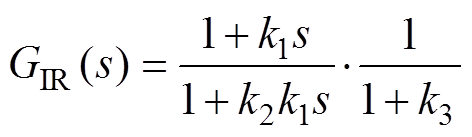 (10)
(10)
根据式(10)可以求得GIR(s)的补偿相位j (w)的表达式为
补偿函数j (w)的最大补偿相位的角频率选在(Zo2(s)+Zg(s))/Zo1(s)的交截频率处,由此可得
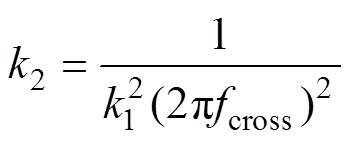 (12)
(12)
假设补偿后原系统的相位裕度为PMideal,则GIR(s)的补偿相位jideal的数值大小为
式中,PMreal为补偿前系统的相位裕度。结合式(11)~式(13)可以求得k1的表达式为
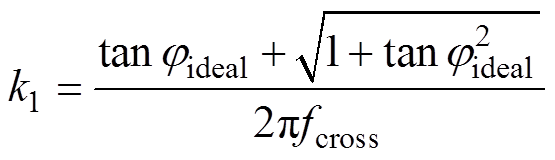 (14)
(14)
同时为了实现GIR(s)的定点相位裕度补偿,需要对其幅值进行矫正,即要保证|GIR(j2pfcross)|=1成立,由此可求得幅值矫正系数k3的数值为
从上述理论分析可以得出如下结论:当阻抗重塑单元GIR(s)按照上述设计要求选取参数时,逆变器并网系统在电网阻抗实时变化时始终能够保持预先设计的理想相位裕度PMideal,保证系统在弱电网下具有良好的稳态和动态性能。如图5中阻抗重塑后系统的相位裕度示意图PM4所示,相较于重塑之前的相位裕度PM3,系统的相位裕度得到了显著的提升。
3 仿真与实验验证
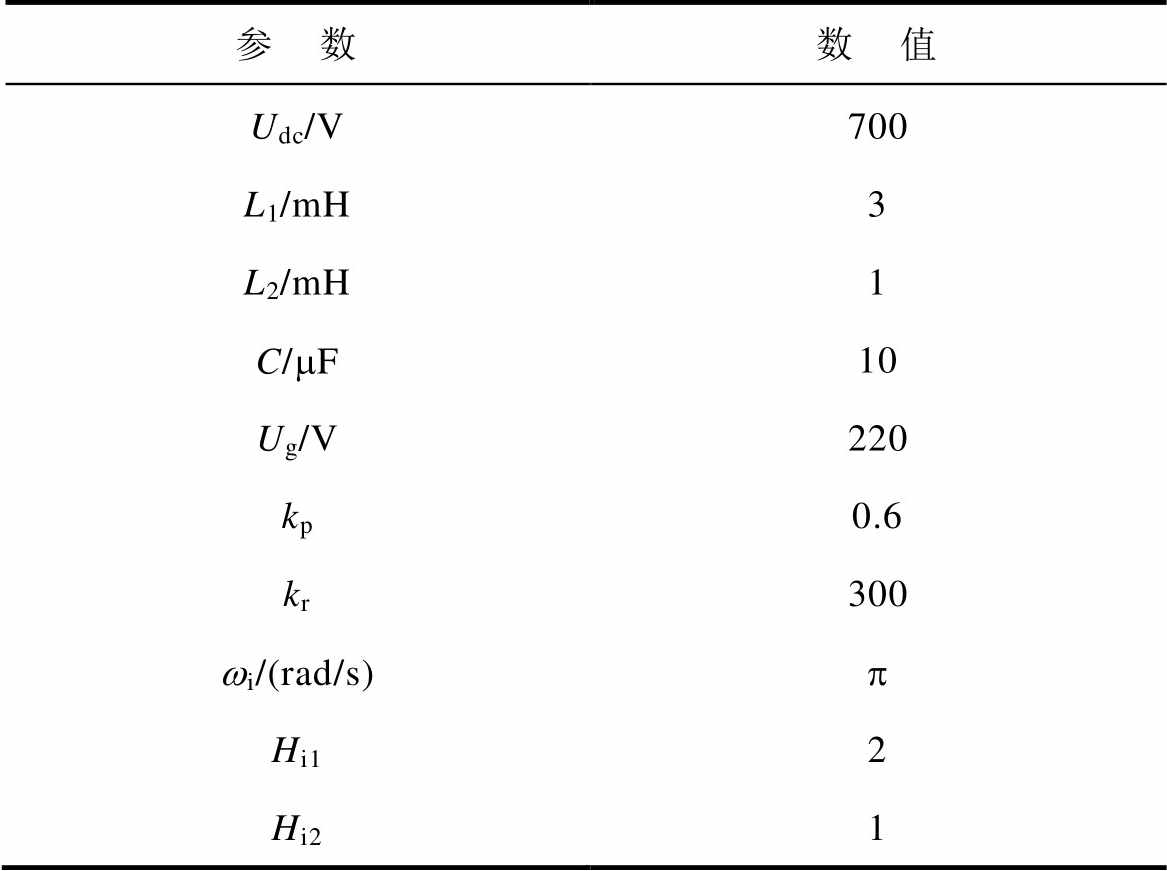
为了验证本文理论分析的正确性与所提控制策略的合理性,利用Matlab/Simulink软件搭建了一套电压220V、频率50Hz、额定功率14kW的LCL型并网逆变器模型并进行了仿真验证。主要仿真参数见表1。
表1 主要仿真参数
Tab.1 Main simulation parameters
参 数数 值 Udc/V700 L1/mH3 L2/mH1 C/mF10 Ug/V220 kp0.6 kr300 wi/(rad/s)p Hi12 Hi21
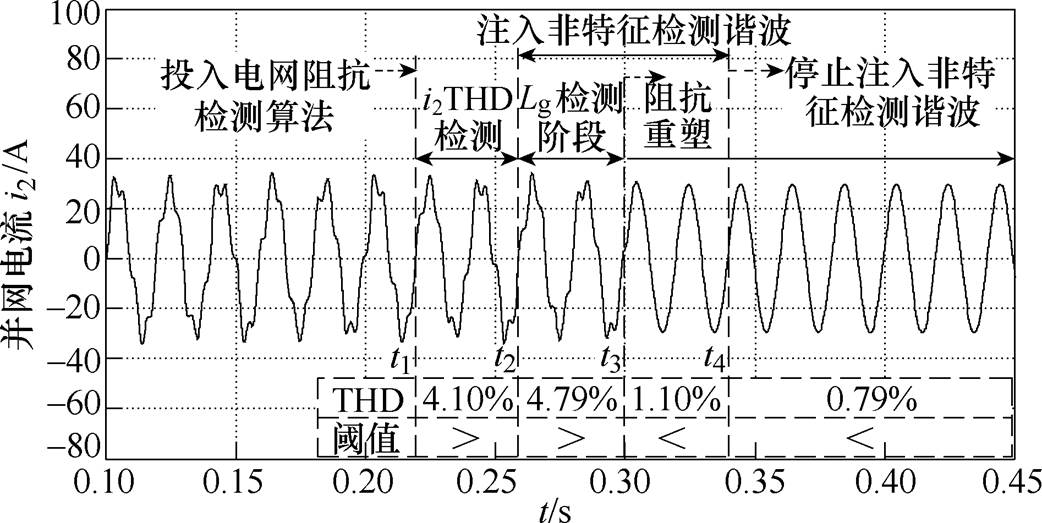
为了验证本文所提阻抗重塑控制技术中电网阻抗检测算法的有效性,图9给出了在Lg=4.8mH时电网阻抗检测算法的检测过程。
根据图9电网阻抗检测过程的t2~t3时段可以测得此时UPCC-h=19.42∠-71.8°V、I2-h=1.31∠198°A。根据式(8)可以求得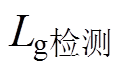 =4.721mH,与实际值基本相符。表2给出了不同电网阻抗值的检测结果。
=4.721mH,与实际值基本相符。表2给出了不同电网阻抗值的检测结果。
表2 电网阻抗检测结果
Tab.2 The results of Lg detection

Lg实际值/mHUPCC-h/VI2-h/ALg检测值/mH 318.18∠-58.4°1.93∠211.6°2.999 4.819.42∠-71.8°1.31∠198°4.721 5.1427.66∠-30.7°1.72∠239.2°5.121
为了验证本文所提阻抗重塑控制技术的有效性,搭建了RT-LAB硬件在环实验平台,实验参数与仿真参数一致,控制器采用TI公司的TMS320F2812。结合不同电网阻抗值对逆变器并网系统阻抗重塑前后的输出波形进行了一系列对比实验验证。
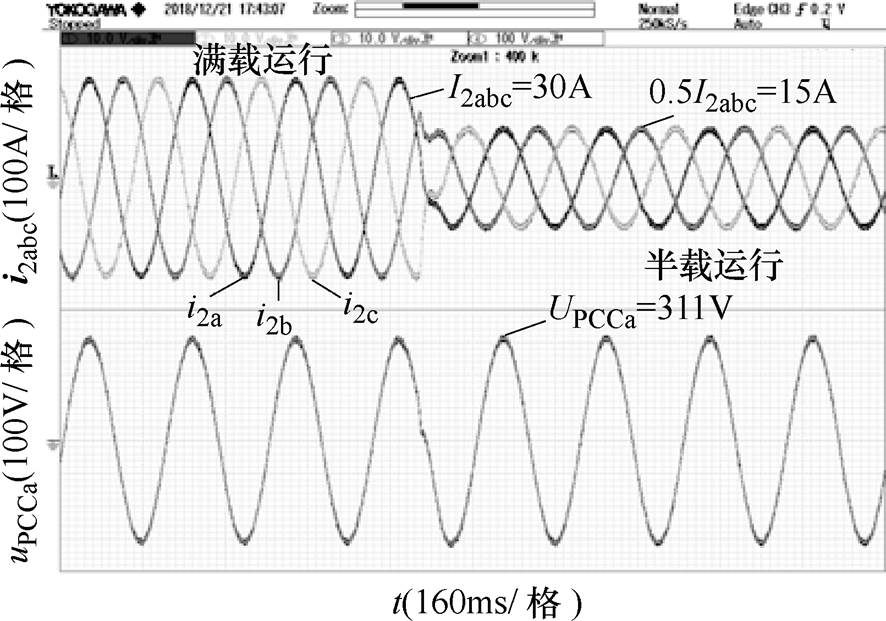
图10给出了逆变器并网系统在Lg=0mH时三相电流实验波形,可以看出,在不考虑电网阻抗条件下,原系统控制性能良好,满载时并网电流i2的THD= 1.05%,半载时THD=1.84%。
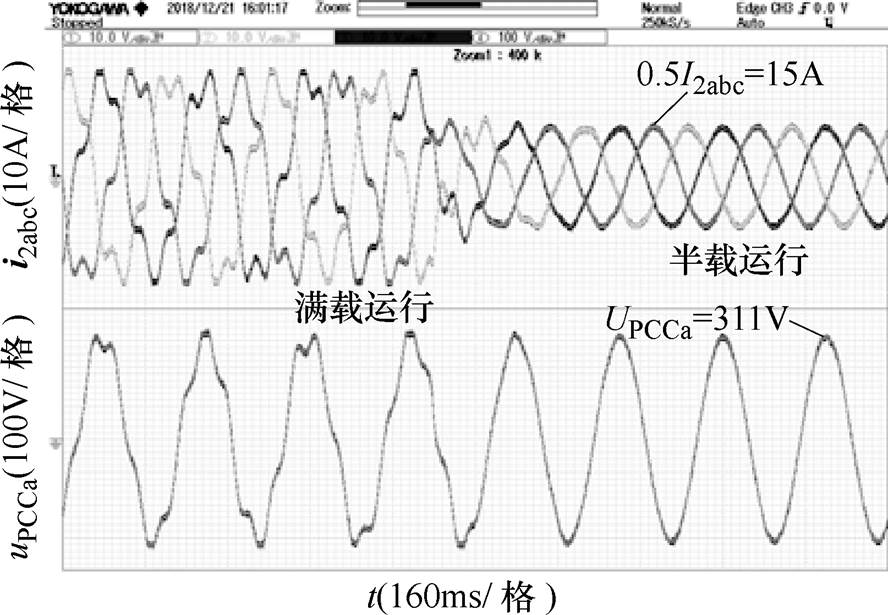
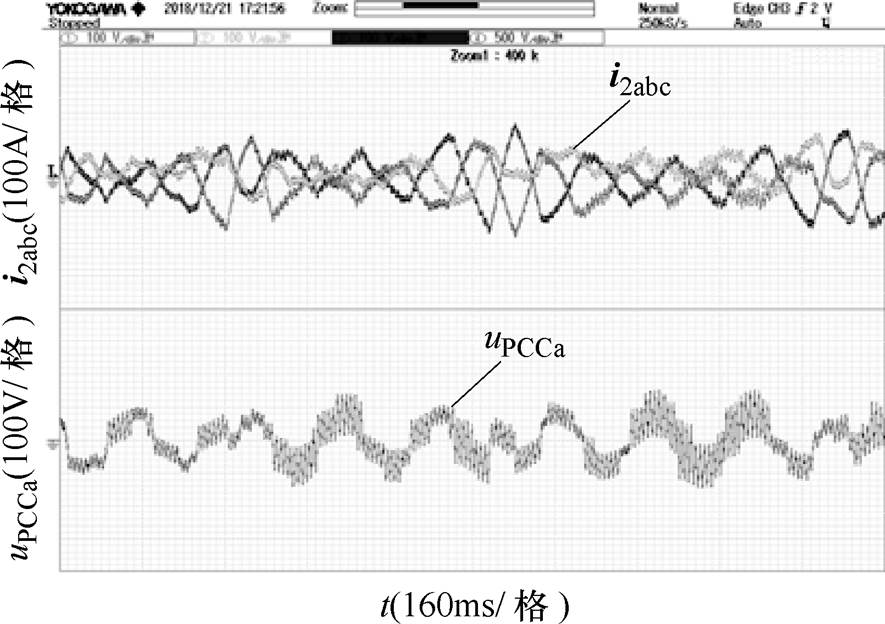
随着电网阻抗增加,系统的相位裕度逐渐减小,稳态和动态性能变差,图11给出了Lg=4.8mH时阻抗重塑之前的并网电流波形。
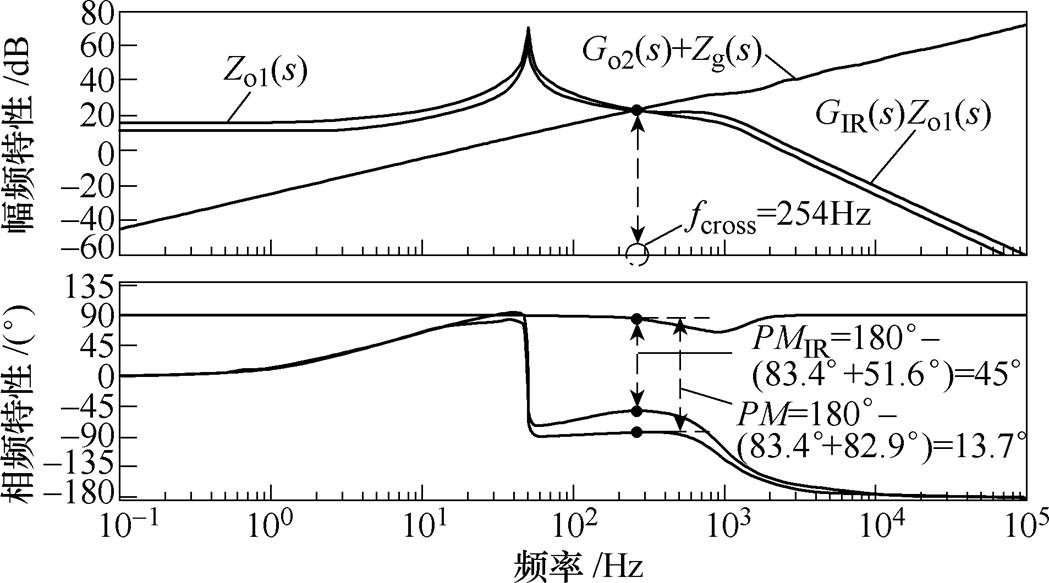
此时并网电流i2满载时的THD=4.59%,半载时THD=2.66%,并网电流质量明显变差,不利于系统的安全稳定运行。对逆变器并联等效输出阻抗进行GIR(s)阻抗重塑,本文设计PMideal=45°,按照2.2小节参数设计要求,可以求得k1=0.001 1,k2= 0.316 2,k3=0.778 3。此时系统阻抗判据的Bode图如图12所示。
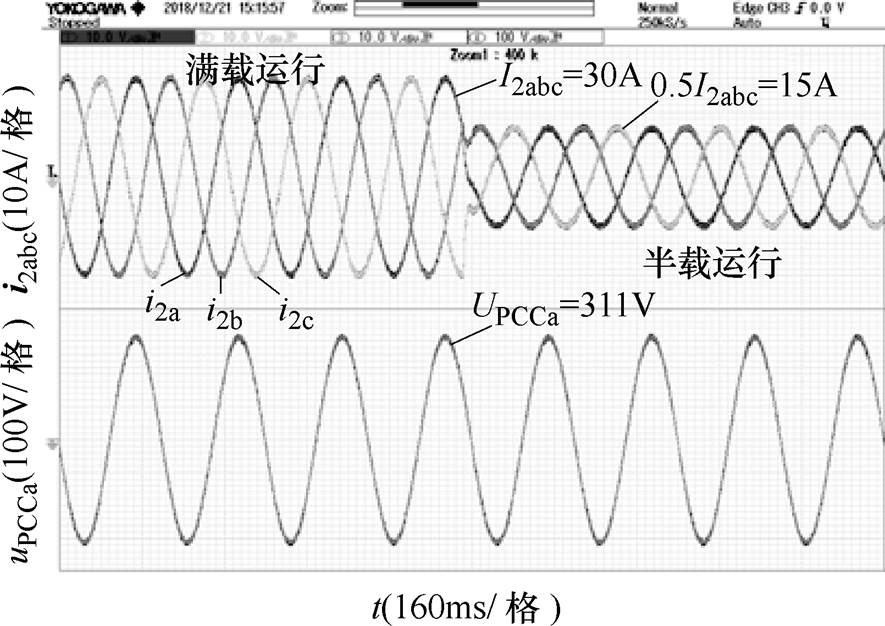
从图12的仿真结果可以看出,在Lg=4.8mH时,阻抗重塑之前系统的相位裕度只有13.7°,系统的稳态和动态性能都将恶化;阻抗重塑之后,系统的相位裕度按照预先设定值达到PMIR=45°。实验结果如图13所示,此时并网电流i2满载时的THD= 0.95%,半载时THD=0.99%,可见阻抗重塑之后系统性能得到了明显改善。
电网的强弱一般通过短路比SCR(short-circuit ratio)来度量[5],当SCR<10时认为电网处于弱电网状态。本文选取SCR=6.5,根据短路比的定义,可以求得此时电网阻抗的最大值为5.14mH。
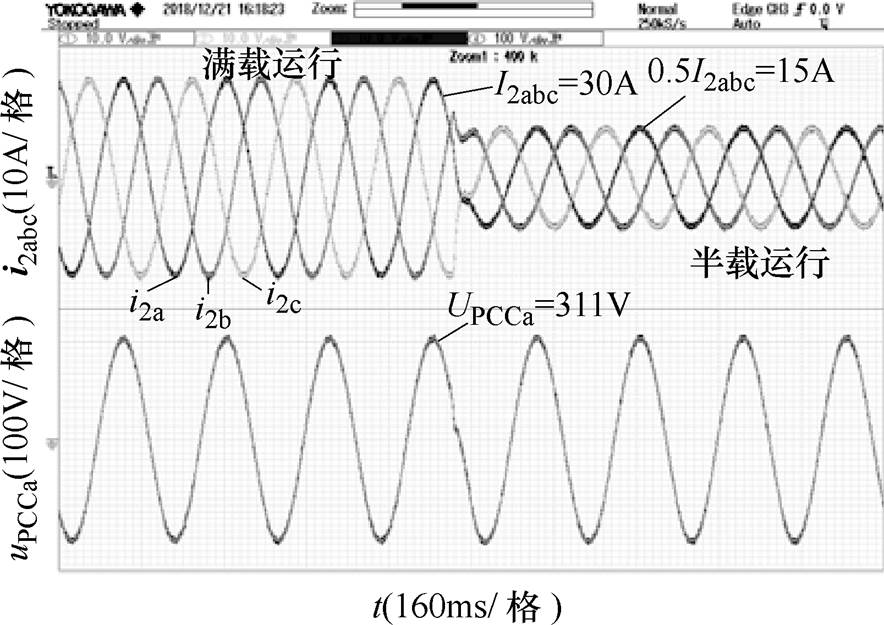
当电网阻抗Lg=5.14mH时,系统阻抗重塑前的并网电流波形如图14所示,此时系统的相位裕度仅为13.3°,相位裕度过小,造成并网电流发生明显振荡,甚至是不稳定。按照PMideal=45°的阻抗重塑要求,根据2.2节理论公式可以求得k1=0.001 1,k2= 0.311 1,k3=0.793,阻抗重塑之后的并网电流波形如图15所示,此时并网电流i2满载时的THD= 1.03%,半载时THD=1.06%。
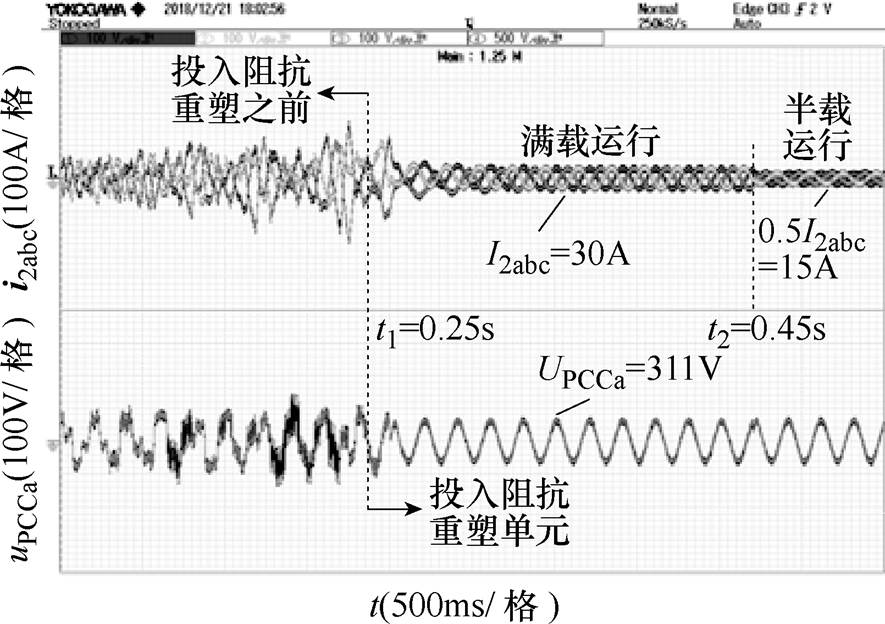
为了验证本文提出的阻抗重塑控制技术具有切换平滑,响应速度快的优点,图16给出了逆变器并网系统在Lg=5.14mH下的动态实验结果。其中在t1= 0.25s之前未投入阻抗重塑单元,在t1=0.25s时投入阻抗重塑单元,且在t2=0.45s时并网电流从满载运行跳变到半载运行。
从图16的实验结果可以看出,在投入算法之前,并网电流与PCC电压严重畸变,在t1时刻投入阻抗重塑单元后,并网电流大约经过两个工频周期的动态调节,便可以趋于稳定,系统具有良好的动态响应性能;同时系统在投入阻抗重塑单元之后,并网电流由满载跳变到半载的动态过程中具有响应速度快、动态性能好的优点。
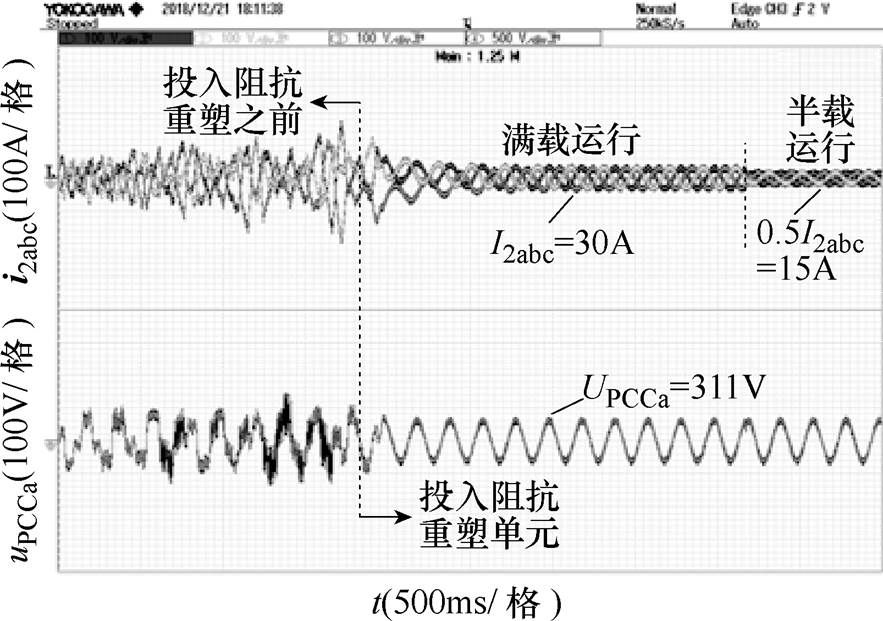
考虑电网阻抗存在±20%的检测误差,由于电网阻抗越大越不利于逆变器并网系统的安全稳定运行,因此本文只考虑+20%的检测误差情况。在Lg= 5.14mH时考虑+20%的检测误差,此时送入阻抗重塑单元的电网阻抗信息为Lg=6.2mH,根据阻抗重塑要求可以求得:k1=0.001 2,k2=0.294 8,k3=0.841 8,由这些参数构成的阻抗重塑单元对逆变器并联等效输出阻抗Zo1(s)进行阻抗重塑之后,系统的相位裕度为46.4°,此时并网电流实验波形如图17所示,满载时THD=0.99%,半载时THD=1.04%。
从图17的实验结果可以看出,在电网阻抗存在检测误差的情况下,本文提出的阻抗重塑控制技术依旧能够保证系统具有良好的稳定裕度,使系统具有优良的稳态和动态性能。上述实验结果进一步证明本文所提阻抗重塑控制技术的合理性与有效性。
4 结论
本文针对弱电网下并网逆变器的稳定性控制问题进行了研究,提出一种阻抗重塑控制技术。该控制技术依托于重塑的基于阻抗的稳定性判据,在对该判据的串、并联阻抗特性进行分析后,做出重塑并联阻抗的选择。该阻抗重塑控制技术包含电网阻抗检测单元、相位裕度补偿单元以及幅值矫正单元,能够在阻抗判据交截频率处实现定点定裕度相位补偿,并且在电网阻抗存在检测误差的情况下依旧能够很好地改善系统的阻抗特性,使逆变器并网系统在电网阻抗宽范围变化下始终能够保持优良的稳态和动态性能;而且本文所提阻抗重塑控制技术在投入系统后具有响应速度快、动态性能好的优点。最后,通过仿真和实验验证了本文理论分析的正确性以及所提控制策略的有效性。
参考文献
[1] 杨树德, 同向前, 尹军, 等. 增强并网逆变器对电网阻抗鲁棒稳定性的改进前馈控制方法[J]. 电工技术学报, 2017, 32(10): 222-231.
Yang Shude, Tong Xiangqian, Yin Jun, et al. An improved grid voltage feedforward strategy for grid- connected inverter to achieve high robust stability against grid-impedance variation[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 222- 231.
[2] Kothari D P, Singal K C, Ranjan R. Renewable energy sources andemerging technologies[M]. 2nd ed. New Delhi: PHI Learning Private Limited, 2012: 196-197.
[3] Etxegarai A, Eguia P, Torres E, et al. Impact of wind power in isolated power systems[C]//IEEE Mediter- ranean Electrotechnical Conference, Yasmine Hammamet, Tunisia, 2012: 63-66.
[4] 杨东升, 阮新波, 吴恒. 提高LCL型并网逆变器对弱电网适应能力的虚拟阻抗方法[J]. 中国电机工程学报, 2014, 34(15): 2327-2335.
Yang Dongsheng, Ruan Xinbo, Wu Heng. A virtual impedance methodto improve the performance of LCL-type grid-connected inverters under weak grid conditions[J]. Proceedings of the CSEE, 2014, 34(15): 2327-2335.
[5] 中国电力科学研究院. Q/GDW 480-2010 分布式电源接入电网技术规定[S]. 北京: 国家电网公司, 2010.
[6] 张旸, 陈新, 王昀, 等. 弱电网下并网逆变器的阻抗相角动态控制方法[J]. 电工技术学报, 2017, 32(1): 97-106.
Zhang Yang, Chen Xin, Wang Yun, et al. Impedance- phased dynamic control method of grid-connected inverters under weak grid condition[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 97- 106.
[7] Midtsund T, Suul J A, Undeland T. Evaluation of current controller performance and stability for voltage source converters connected to a weak grid[J]. IEEE International Symposium on Power Electronics for Distributed Generation Systems, 2010, 24(1): 382-388.
[8] Xu Jinming, Xie Shaojun, Tang Ting. Evaluations of current control in weak grid case for grid-connected LCL-filtered inverter[J]. IET Power Electronics, 2013, 6(2): 227-234.
[9] 殷进军, 刘邦银, 段善旭. LCL滤波并网逆变器双环控制参数设计与优化[J]. 电力系统自动化, 2013, 37(9): 123-128.
Yin Jinjun, Liu Bangyin, Duan Shanxu. Parameters design and optimization of dual-loop controller for grid-connected inverters with LCL filters[J]. Auto- mation of Electric Power Systems, 2013, 37(9): 123-128.
[10] Tang Yi, POH C L, Wang Peng, et al. Exploring inherent damping characteristic of LCL-filters for there-phase grid-connected voltage source inver- ters[J]. IEEE Transactions on Power Electronics, 2012, 27(3): 1433-1443.
[11] 陈燕东, 王伊, 周乐明, 等. 弱电网下LCL逆变器阻尼谐振抑制与功率快速调节方法[J]. 电工技术学报, 2018, 33(11): 2565-2575.
Chen Yandong, Wang Yi, Zhou Yueming, et al. Damping resonance suppression and fast power regulation method for LCL-type inverter under weak grid[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2565-2575.
[12] 方天治, 黄淳, 陈乃铭, 等. 一种提高弱电网下LCL型并网逆变器鲁棒性的相位超前补偿策略[J].电工技术学报, 2018, 33(20): 4813-4822.
Fang Tianzhi, Huang Chun, Chen Naiming, et al. A phase-lead compensation strategy on enhancing robustness of LCL-type grid-tied inverters under weak grid conditions[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4813-4822.
[13] 何超杰, 赵晋斌, 杨旭红, 等. 弱电网下基于系统敏感度的逆变器自适应控制[J]. 电网技术, 2016, 40(1): 238-244.
He Chaojie, Zhao Jinbin, Yang Xuhong, et al. Adaptive controlstrategy for grid-tied inverter based on system sensitivity in weak grid[J]. Power System Technology, 2016, 40(1): 238-244.
[14] 许津铭, 谢少军, 唐婷. 弱电网下LCL滤波并网逆变器自适应电流控制[J]. 中国电机工程学报, 2014, 34(24): 4031-4039.
Xu Jinming, Xie Shaojun, Tang Ting. An adaptive current control for grid-connected LCL-filtered inverters in weak grid case[J]. Proceedings of the CSEE, 2014, 34(24): 4031-4039.
[15] Wang Yanbo, Wang Xiongfei, Blaabjerg F, et al. Harmonic instability assessment using state-space modeling and participation analysis in inverter-fed power systems[J]. IEEE Transactions on Industrial Electronics, 2017, 64(1): 806-816.
[16] Sun Jian. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.
[17] Chen Xin, Sun Jian. Characterization of inverter-grid interactions using a hardware-in-the-loop system test-bed[C]//Proceedings of IEEE 8th International Conference on Power Electronics and ECCE Asia, Jeju, Korea, 2011: 2180-2187.
[18] 张庆海, 罗安, 陈燕东, 等. 并联逆变器输出阻抗分析及电压控制策略[J]. 电工技术学报, 2014, 29(6): 98-105.
Zhang Qinghai, Luo An, Chen Yandong, et al. Analysis of output impedance for parallel inverters and voltage control strategy[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 98-105.
[19] 杨立滨, 张海宁, 李春来, 等. 基于虚拟导纳的大型光伏电站谐波抑制策略研究[J]. 电力系统保护与控制, 2016, 44(18): 120-126.
Yang Libin, Zhang Haining, Li Chunlai, et al. Harmonic suppression strategy of large-scale photo- voltaic plants based on virtual admittance[J]. Power System Protection and Control, 2016, 44(18): 120-126.
[20] Wang Xiongfei, Li Yunwei, Frede B, et al. Virtual- impedance-based control for voltage-source con- verters[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 7019-7037.
[21] 高家元, 赵晋斌, 陈晓博, 等. 弱电网条件下基于阻抗的稳定性判据重塑[J]. 电网技术, 2017, 41(9): 2762-2768.
Gao Jiayuan, Zhao Jinbin, Chen Xiaobo, et al. Reconstruction of impedance-based stability criteria in weak grid[J]. Power System Technology, 2017, 41(9): 2762-2768.
[22] 汤婷婷, 张兴, 谢东. 基于高频注入阻抗检测的孤岛检测研究[J]. 电力电子技术, 2013, 47(3): 70-72.
Tang Tingting, Zhang Xing, Xie Dong. Islanding detection method based on impedance detection using high frequency signal injection[J]. Power Electronics, 2013, 47(3): 70-72.
Analysis and Design of Grid-Connected Inverter Impedance Remodeling with Fixed Stability Margin in Weak Grid
Tu Chunming1 Gao Jiayuan1 Zhao Jinbin2 Zhang Yunfei2 Guo Qi1
(1. National Electric Power Conversion and Control Engineering Technology Research Center Hunan University Changsha 410082 China 2. School of Electrical Engineering Shanghai University of Electric Power Shanghai 200090 China)
Abstract The stability control of grid-connected inverter in weak grid is studied. Based on the reconstructed impedance-based stability criterion, the current double closed-loop control of three-phase LCL grid-connected inverter is used as a model to establish a Norton equivalent series and parallel impedance mathematical model for the inverter grid-connected system. By analyzing the characteristics of inverter equivalent output impedance, the parallel equivalent output impedance of inverter is selected to be reconstructed. The impedance reconstruction control technology includes three units: grid impedance detection, phase margin compensation and amplitude correction. The reconstructed equivalent impedance model can always maintain a constant stability margin for the inverter grid-connected system when the grid impedance varies widely, meanwhile, considering the detection error of the grid impedance, the system can still maintain good steady-state and dynamic performance. Simulation and experimental measurements verify the analysis.
keywords:Weak grid, LCL, grid-connected inverter, impedance criterion, impedance remodeling, stability margin
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.190027
国家自然科学基金资助项目(51577055)。
收稿日期 2019-01-08
改稿日期 2019-04-24
作者简介
涂春鸣 男,1976年生,教授,博士生导师,研究方向为电力电子技术及其在电力系统中的应用。E-mail: chunming_tu@263.net
高家元 男,1991年生,博士研究生,研究方向为电力电子技术、分布式发电和逆变器控制技术。E-mail: Jiayuan_gao@163.com(通信作者)
(编辑 崔文静)
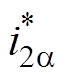 、
、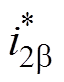 分别为逆变器输出电流在ab 坐标系下的给定值;UPCC为公共耦合点(Point of Common Coupling, PCC)的电压,Ug为电网电压,Udc为直流母线电压。wt为锁相环(Phase Locked Loop, PLL)输出相位,G(s)为外环控制器,Hi1为电容电流比例反馈系数,Hi2为并网电流采样系数,KPWM为脉宽调制增益,Zo1(s)、Zo2(s)分别为逆变器等效输出并联、串联阻抗,k1、k2为相位裕度补偿系数,k3为幅值矫正系数;fcross为阻抗判据交截频率,PM为闭环系统相位裕度,GIR(s)为阻抗重塑单元等效传递函数。由于负载具有不确定性且不是本文研究重点,因此取一个特殊情况研究,即负载阻抗为无穷大。
分别为逆变器输出电流在ab 坐标系下的给定值;UPCC为公共耦合点(Point of Common Coupling, PCC)的电压,Ug为电网电压,Udc为直流母线电压。wt为锁相环(Phase Locked Loop, PLL)输出相位,G(s)为外环控制器,Hi1为电容电流比例反馈系数,Hi2为并网电流采样系数,KPWM为脉宽调制增益,Zo1(s)、Zo2(s)分别为逆变器等效输出并联、串联阻抗,k1、k2为相位裕度补偿系数,k3为幅值矫正系数;fcross为阻抗判据交截频率,PM为闭环系统相位裕度,GIR(s)为阻抗重塑单元等效传递函数。由于负载具有不确定性且不是本文研究重点,因此取一个特殊情况研究,即负载阻抗为无穷大。

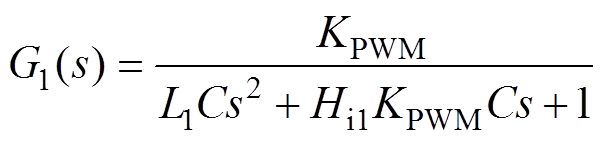 (1)
(1)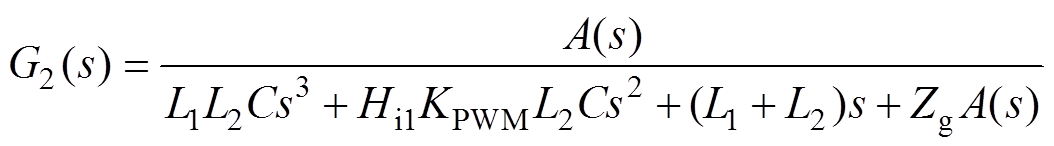 (2)
(2)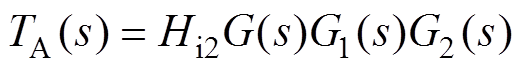 (3)
(3)
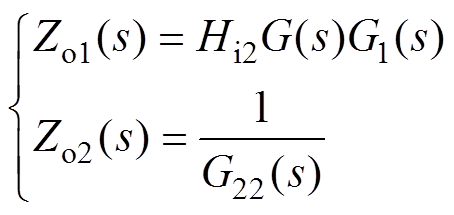 (4)
(4)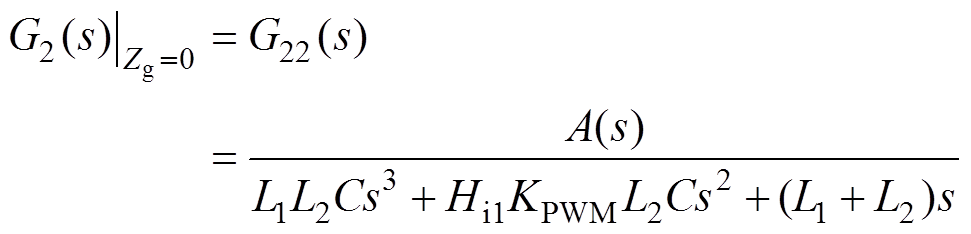 (5)
(5)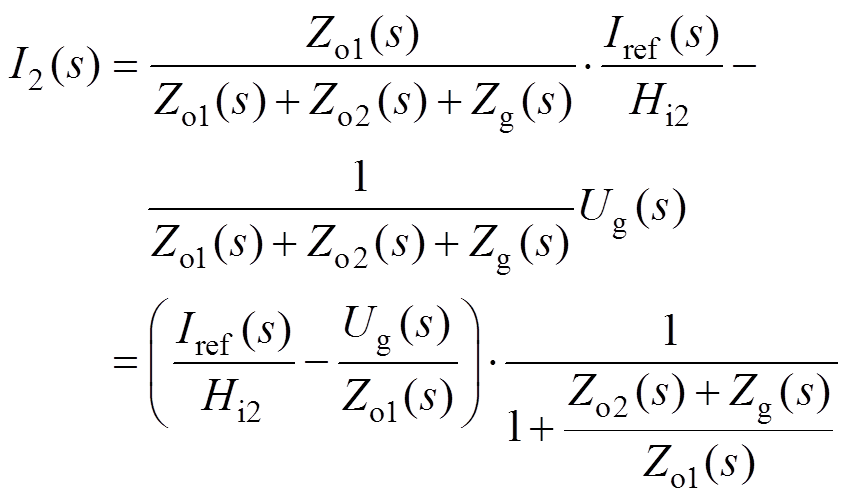 (6)
(6)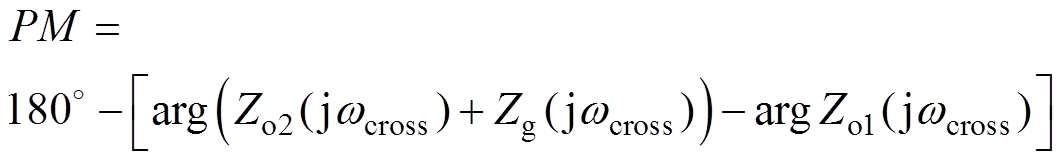 (7)
(7)
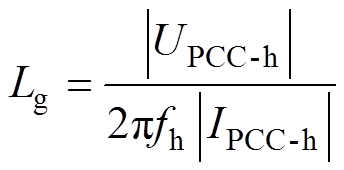 (8)
(8)
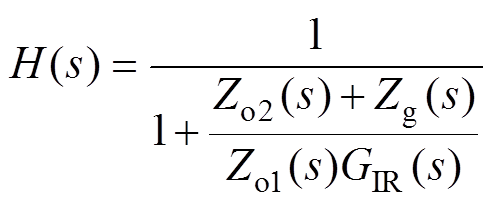 (9)
(9)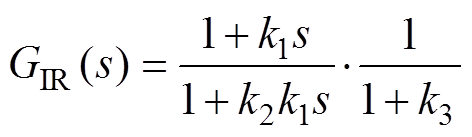 (10)
(10)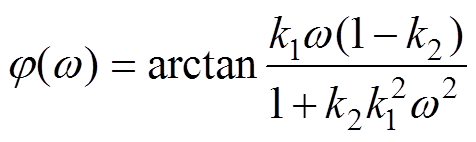 (11)
(11)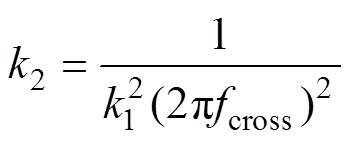 (12)
(12)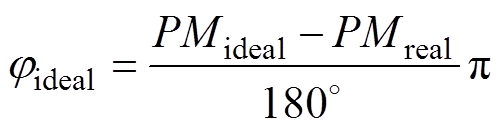 (13)
(13)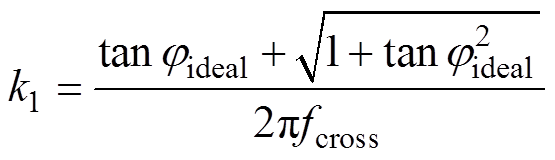 (14)
(14)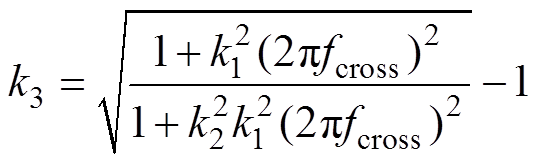 (15)
(15)
 =4.721mH,与实际值基本相符。表2给出了不同电网阻抗值的检测结果。
=4.721mH,与实际值基本相符。表2给出了不同电网阻抗值的检测结果。