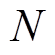 和
和 。为解决低频电容电压波动问题,网侧MMC需要为机侧MMC提供一个宽范围可调的直流电压[12-13]。半桥子模块没有负电平输出能力,无法实现输出直流电压宽范围可调,因此,网侧MMC需要采用全桥子模块。机侧MMC无需负电平输出,采用半桥子模块。
。为解决低频电容电压波动问题,网侧MMC需要为机侧MMC提供一个宽范围可调的直流电压[12-13]。半桥子模块没有负电平输出能力,无法实现输出直流电压宽范围可调,因此,网侧MMC需要采用全桥子模块。机侧MMC无需负电平输出,采用半桥子模块。摘要 最近电平逼近调制(NLM)是模块化多电平变换器(MMC)中最常用的调制方式。电平数较少时,NLM的输出电压电流谐波严重畸变,使其无法用于电平数较少的变频调速场合。该文通过详细分析NLM下无差拍电流控制的开关过程,指出NLM调制下MMC无差拍电流控制具有滞环特性。定量分析了NLM下MMC无差拍电流控制的滞环环宽,得到了滞环环宽和输出电流波动范围的表达式。同时,设计了MMC背靠背变频调速系统的综合控制方案。与传统方案相比,所提方案具有控制结构简单、开关频率低、环流抑制容易实现和动态特性好等优点。在Matlab/Simulink中搭建了十一电平背靠背MMC中高压变频调速模型,验证了所提控制方案的正确性和有效性。
关键词:模块化多电平变换器 中高压变频调速 最近电平逼近调制 无差拍控制 滞环特性
近年来,模块化多电平变换器(Modular Multilevel Converter, MMC)在大功率应用场合中受到了广泛关注。该变换器最初是针对高压直流输电系统提出的[1],但因其具有高度模块化的直接级联结构、可背靠背四象限运行和无需体积庞大的隔离变压器等优点,在中高压变频领域也颇具应用前景[2-5]。
在MMC变频调速中,随着频率的降低,电容电压波动逐渐增大。在频率接近0时,电压波动理论上可达到无穷大,电机无法正常运行[6]。近年来,为解决这一问题,研究人员提出了若干方法。文献[5]将这些方法总结归纳为三类:高频注入法[7-9]、功率通道法[10]和变运行模式法[11-13]。随着对上述方法的不断研究和改进,MMC低频电容波动的问题已逐渐得到解决,相信未来会推出应用于机车牵引、轧钢机等高性能大转矩传动场合的工程产品[5]。
现阶段变频调速用MMC的研究主要集中在低频电容电压波动问题的解决上,缺乏与此相关的优化控制策略的研究。现有控制方案结构多采用电容电压分层控制和移载波调制相结合的方案[7-13],同时辅以相应的环流抑制环节。这样的设计方案存在如下缺点:①移相载波调制需要对每个子模块加入闭环电压控制,需对每个子模块配以单独的比例-积分(PI)调节器,增加了数字处理器的负担。同时,要求各子模块都采用频率相同、相位不同的载波,载波生成复杂;②将负载控制环、稳压控制环和环流控制环三环解耦独立控制,分别设计相应的控制器,控制结构复杂。每个控制环节都要用到一组或多组PI调节器,多组PI参数需协调配合工作,参数整定十分困难;③复杂的控制结构设计,和大量PI控制器的使用,降低了整个变频调速系统的动态性能。
与移相载波调制相比,最近电平逼近调制(Nearest Level Modulation, NLM)实现简单,没有复杂的载波生成过程。但最近电平调制属于阶梯波调制,当电平数较少时,输出电压电流谐波畸变率大[14],限制了其在电平数少的场合的应用。为解决该问题,不同的改进方案相继被提出[15-19]。文献[15]在排序算法上做了改进,使得原本只能输出N+1个电平的NLM可以输出2N+1个电平。这样的做法简单有效,但优化效果有限。电平数很低时,其输出电流谐波依旧很大,系统无法正常工作。文献[16-18]对NLM和PWM的混合调制策略进行了研究。这样的设计没能完全取消载波生成环节,同时当PWM载波频率较低时,输出电流波形质量和环流抑制效果不理想。文献[19-20]提出了一种基于电流滞环原理的NLM调制策略,具有一定的输出电流谐波优化能力,但其滞环环节输出值的设置存在局限性。
为解决上述问题,本文提出一种基于最近电平逼近调制的MMC中高压变频调速系统运行控制方案。在文献[21]的基础上,结合桥臂电流误差控制原理,详细分析了无差拍电流控制的开关过程,指出NLM调制下MMC无差拍电流控制具有滞环特性。定量分析了NLM下MMC无差拍电流控制的滞环环宽,得到了滞环环宽和输出电流波动范围的表达式,为变频调速综合控制方案的设计提供了理论基础。同时,设计了MMC背靠背变频调速系统的综合控制方案。与传统方法相比,本文所提方法具有控制结构简单、环流抑制实现简单、开关频率更小和动态特性好等优点。最后,在Matlab/Simulink中搭建了十一电平背靠背MMC中高压变频调速模型,验证了所提控制方案的正确性和有效性。
背靠背MMC电机驱动拓扑结构如图1所示,网侧MMC作为整流器与电网相连,始终运行在工频50Hz。机侧MMC作为逆变器与电机相连用于驱动电机,运行频率在0~50Hz之间变化。网侧和机侧MMC的子模块数目和子模块电容电压额定值均相同,分别为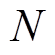 和
和 。为解决低频电容电压波动问题,网侧MMC需要为机侧MMC提供一个宽范围可调的直流电压[12-13]。半桥子模块没有负电平输出能力,无法实现输出直流电压宽范围可调,因此,网侧MMC需要采用全桥子模块。机侧MMC无需负电平输出,采用半桥子模块。
。为解决低频电容电压波动问题,网侧MMC需要为机侧MMC提供一个宽范围可调的直流电压[12-13]。半桥子模块没有负电平输出能力,无法实现输出直流电压宽范围可调,因此,网侧MMC需要采用全桥子模块。机侧MMC无需负电平输出,采用半桥子模块。
图1中,“g”和“m”分别用来描述网侧MMC和机侧MMC的电气量。直流电压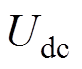 将不再定义为一个定值量,而是一个随电机转速或频率变化的量。
将不再定义为一个定值量,而是一个随电机转速或频率变化的量。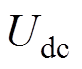 可以表示为
可以表示为
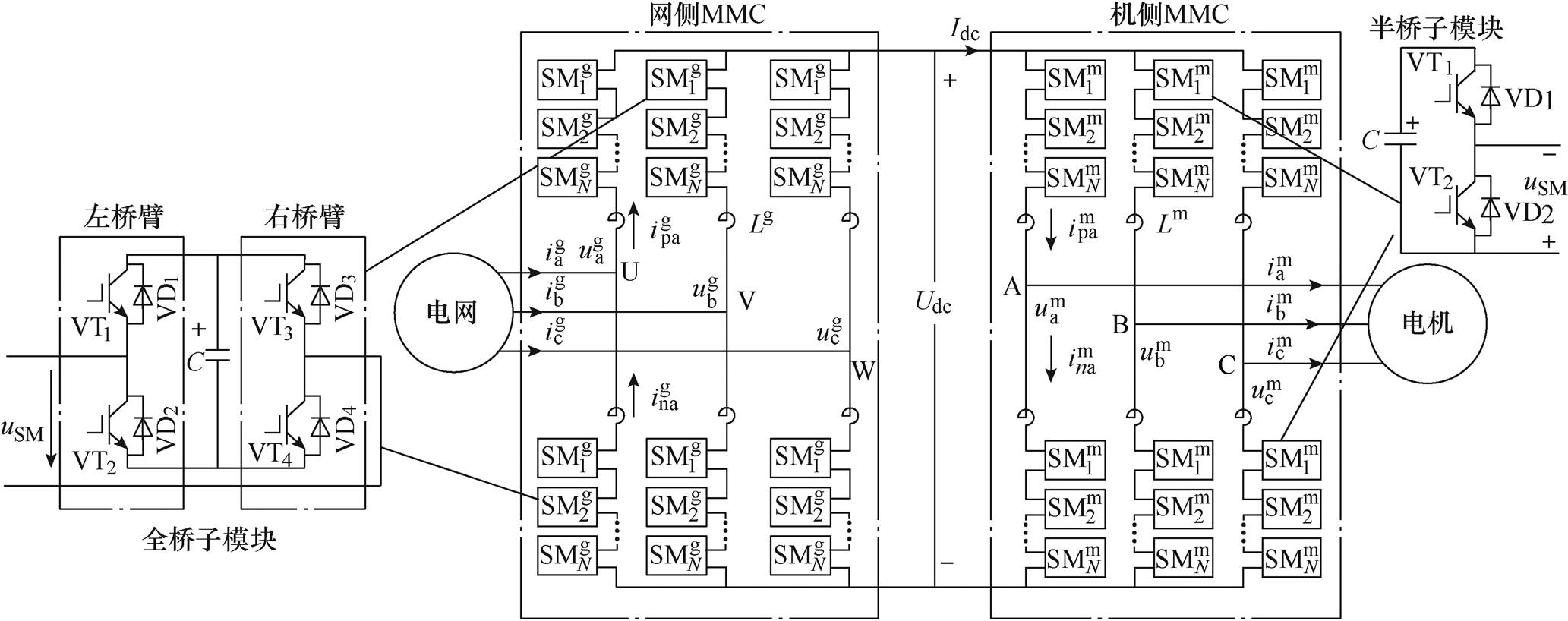
图1 背靠背MMC电机驱动拓扑结构
Fig.1 Topology of back-to-back MMC for motor drive
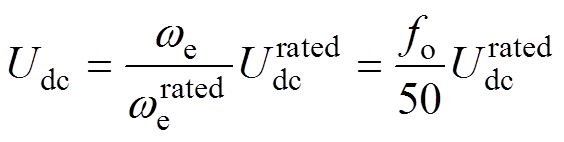 (1)
(1)式中,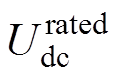 为直流母线电压额定值;
为直流母线电压额定值;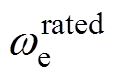 和
和 分别为电机额定转速和实际转速;
分别为电机额定转速和实际转速;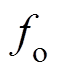 为机侧MMC输出频率,也就是电机运行频率。
为机侧MMC输出频率,也就是电机运行频率。
以机侧MMC为例,图2a为机侧MMC单相等效电路a。设j相上桥臂电流为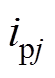 ,下桥臂电流为
,下桥臂电流为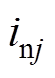 ,上桥臂所有导通的子模块电压之和为
,上桥臂所有导通的子模块电压之和为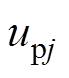 ,下桥臂所有导通的子模块电压之和为
,下桥臂所有导通的子模块电压之和为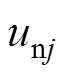 ,输出电流为
,输出电流为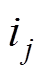 ,直流侧与桥臂之间的环流为
,直流侧与桥臂之间的环流为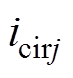 ,电机电动势为
,电机电动势为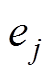 ,桥臂电感值为
,桥臂电感值为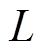 ,下标
,下标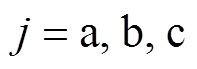 。
。
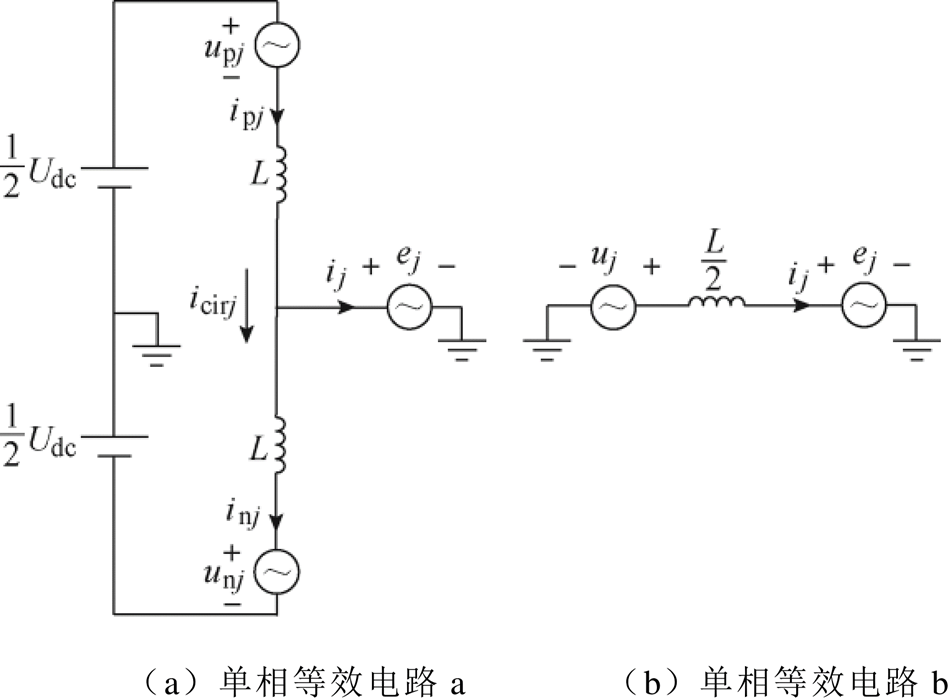
图2 MMC单相等效电路
Fig.2 Single-phase equivalent circuit of MMC
根据基尔霍夫电压定律可得
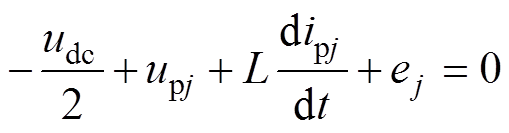 (2)
(2)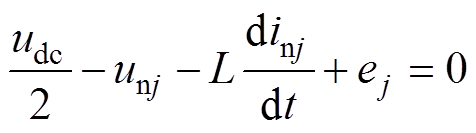 (3)
(3)
将式(2)和式(3)相加后除以2,可得
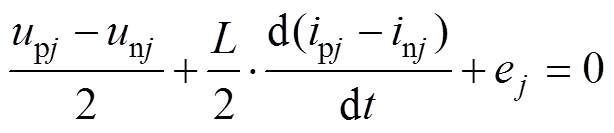 (4)
(4)根据文献[14],MMC输出电流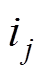 和输出电压
和输出电压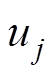 分别为
分别为
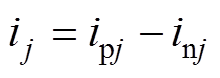 (5)
(5)
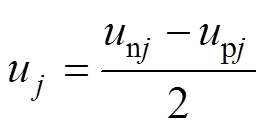 (6)
(6)根据基尔霍夫电流定律和上、下桥臂严格对称性,可得
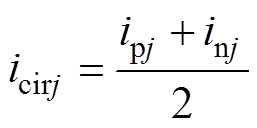 (7)
(7)
结合式(5)和式(7),桥臂电流可表示为
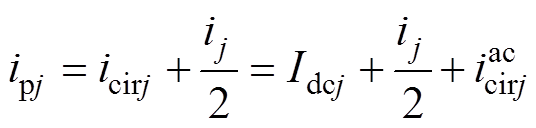 (8)
(8)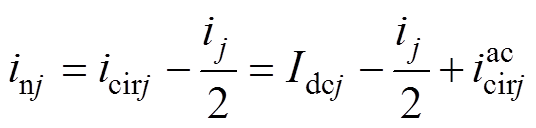 (9)
(9)
式中,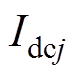 为
为 相环流的直流分量,即
相环流的直流分量,即 相流过的直流电流;
相流过的直流电流;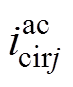 为
为 相环流的交流分量。
相环流的交流分量。
将式(5)和式(6)代入式(4),可得图2b所示等效电路,即
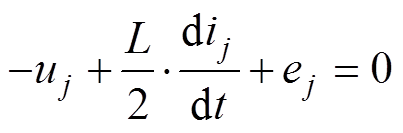 (10)
(10)结合式(4)与式(10)分析得出,通过调制上、下桥臂所有导通子模块电压之和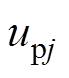 和
和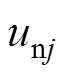 ,可以控制MMC输出相电压,从而实现对MMC工作状态的灵活控制。上、下桥臂电压的参考值分别表示为
,可以控制MMC输出相电压,从而实现对MMC工作状态的灵活控制。上、下桥臂电压的参考值分别表示为
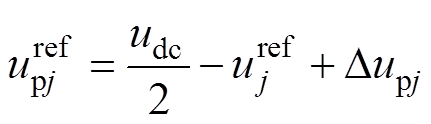 (11)
(11)
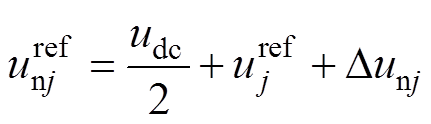 (12)
(12)式中,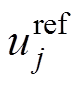 为相电压调制值;
为相电压调制值;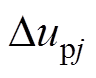 和
和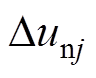 分别为由稳压、环流等附加控制器得到电压调整项。
分别为由稳压、环流等附加控制器得到电压调整项。
无差拍控制的基本思想是:根据系统的状态方程和输出反馈信号以及所要求的下一时刻参考输出量计算出下一个开关周期的控制量,如图3所示。MMC无差拍电流控制的控制结构分为环流控制、无差拍电流跟踪控制和调制策略三部分[20]。
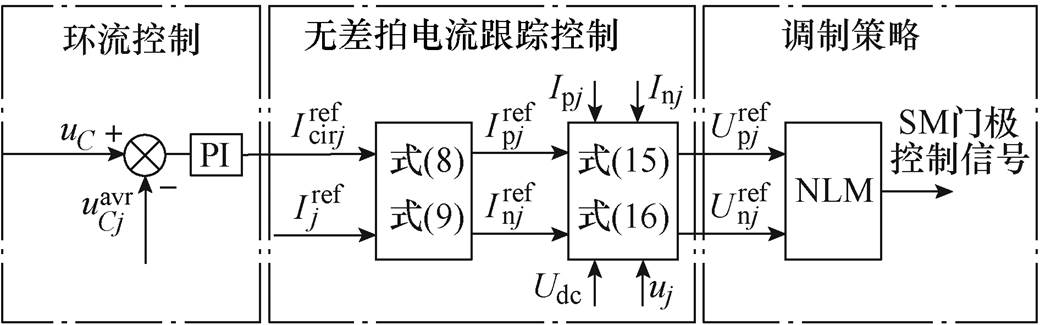
图3 无差拍电流控制
Fig.3 The deadbeat control block
图3中, 为子模块电容电压参考值,
为子模块电容电压参考值,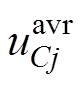 为j相所有子模块电容电压的平均值。子模块电容电压平均值可以表示为
为j相所有子模块电容电压的平均值。子模块电容电压平均值可以表示为
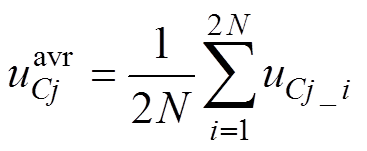 (13)
(13)将 与
与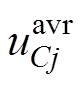 作差后,通过一个PI调节器,可以获得j相环流参考值
作差后,通过一个PI调节器,可以获得j相环流参考值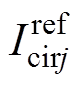 为
为
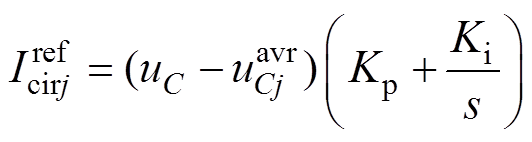 (14)
(14)
该环流的作用是对SM的电容进行充放电,以维持整体电压稳定。环流参考值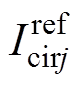 与输出电流参考值
与输出电流参考值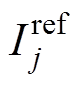 分别经过式(8)和式(9)计算得到上、下桥臂参考电流
分别经过式(8)和式(9)计算得到上、下桥臂参考电流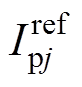 和
和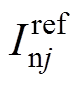 。再经过式(15)和式(16)计算得到上、下桥臂的参考电压
。再经过式(15)和式(16)计算得到上、下桥臂的参考电压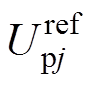 和
和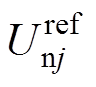 [20]分别为
[20]分别为
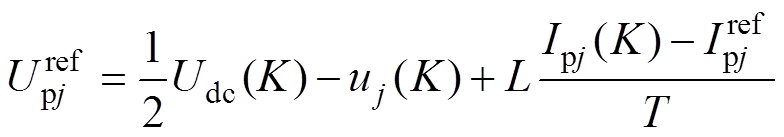 (15)
(15)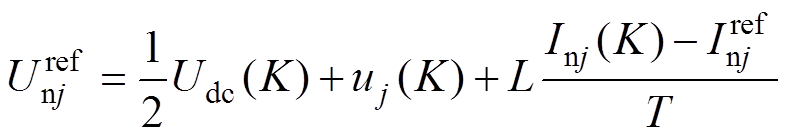 (16)
(16)
式中,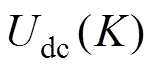 为第
为第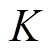 个控制周期的直流侧电压;
个控制周期的直流侧电压;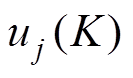 为j相第
为j相第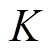 个控制周期的负载电压;
个控制周期的负载电压;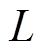 为桥臂电感值;
为桥臂电感值;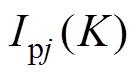 为j相第
为j相第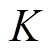 个控制周期上桥臂电流;
个控制周期上桥臂电流;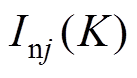 为j相第
为j相第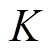 个控制周期下桥臂电流。
个控制周期下桥臂电流。
得到上、下桥臂电压的参考值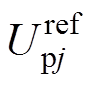 和
和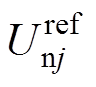 后,经过最近电平逼近调制策略便可得到开关控制信号。
后,经过最近电平逼近调制策略便可得到开关控制信号。
文献[21]在提出MMC无差拍电流控制后,分析了电感参数的偏移对系统稳定性的影响,并对该控制策略进行了仿真和实验验证。仿真和实验结果均表明,相比于传统控制方法,MMC无差拍电流控制的输出电流谐波明显减小。但文献[21]并没有对此做出解释,论文建模和理论分析中也均未提及,未能阐明所设计控制策略的本质规律。因此有必要对NLM下MMC无差拍电流控制的开关过程进行详细分析,从而揭示其工作机理,解释其输出电流谐波畸变率(Total Harmonic Distortion, THD)显著减小的原因。
将式(2)进行变形,有
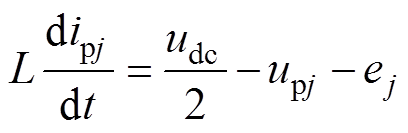 (17)
(17)对式(17)进行积分,有
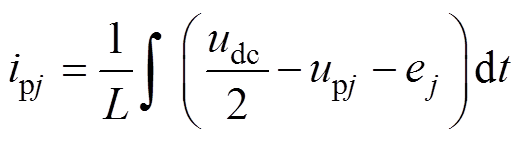 (18)
(18)
若在理想情况下,MMC上桥臂输出其电压调制值,则j相上桥臂电流为参考值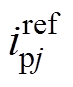 ,则有
,则有
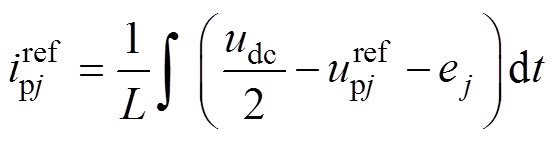 (19)
(19)将MMC上桥臂电流的实际值和参考值之差定义为上桥臂电流误差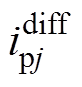 。由式(18)减去式(19),有
。由式(18)减去式(19),有
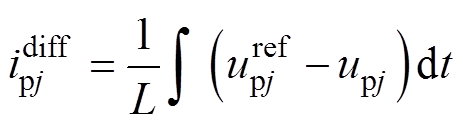 (20)
(20)
式(20)表明,通过控制MMC的上、下桥臂所有导通子模块的电压和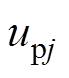 和
和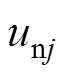 ,可以将上桥臂电流误差
,可以将上桥臂电流误差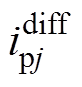 限制在一定范围之内。
限制在一定范围之内。
图4为桥臂电流误差控制原理。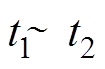 时刻,上桥臂导通子模块数为y。此时,
时刻,上桥臂导通子模块数为y。此时,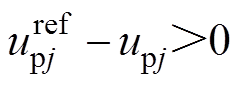 ,由式(20)可知,
,由式(20)可知,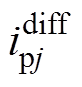 的值将增大。到
的值将增大。到 时刻,若上桥臂电平数不改变(仍保持为y),
时刻,若上桥臂电平数不改变(仍保持为y),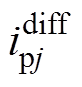 将继续增大。若
将继续增大。若 时刻,上桥臂导通子模块数升高至y+1,
时刻,上桥臂导通子模块数升高至y+1,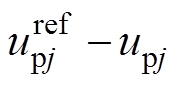 的值将由大于0转变为小于0。根据式(20),
的值将由大于0转变为小于0。根据式(20),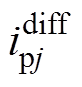 将开始减小,直至
将开始减小,直至 时刻上桥臂导通子模块数重新回落至y,
时刻上桥臂导通子模块数重新回落至y,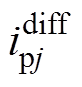 重新开始增大。
重新开始增大。
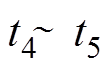 时刻,上桥臂导通子模块数为y+1。此时,
时刻,上桥臂导通子模块数为y+1。此时,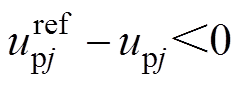 ,由式(20)可知,
,由式(20)可知,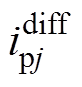 的值将减小。到
的值将减小。到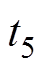 时刻,若上桥臂电平数不改变(仍保持为y+1),
时刻,若上桥臂电平数不改变(仍保持为y+1),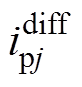 将继续减小。若
将继续减小。若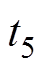 时刻,上桥臂导通子模块数降低至y,
时刻,上桥臂导通子模块数降低至y,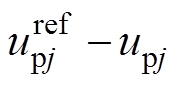 的值将由小于0转变为大于0。根据式(20),
的值将由小于0转变为大于0。根据式(20), 将开始增大,直至
将开始增大,直至 时刻上桥臂导通子模块数重新上升至y+1,
时刻上桥臂导通子模块数重新上升至y+1, 重新开始减小。
重新开始减小。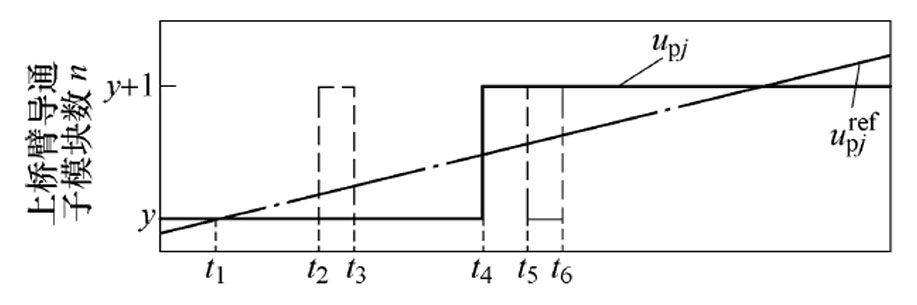
图4 桥臂电流误差控制原理
Fig.4 Arm current error control principle
由上面分析可以看出,通过微调上桥臂导通子模块数,可以调节上桥臂误差电流的变化趋势。若要将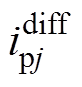 控制在区间
控制在区间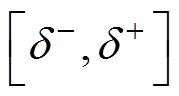 之内,其控制规则需按如下要求执行:
之内,其控制规则需按如下要求执行:
(1)当上桥臂电流误差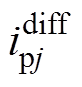 高于
高于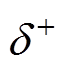 时,使上桥臂导通子模块数增加1,
时,使上桥臂导通子模块数增加1,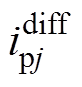 将开始减小。
将开始减小。
(2)当上桥臂电流误差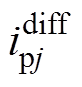 低于
低于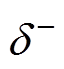 时,使上桥臂导通子模块数减小1,
时,使上桥臂导通子模块数减小1,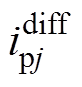 将开始增大。
将开始增大。
同理,对于下桥臂电流,可以得到完全一致的结论。
在式(11)中若不考虑电压调整项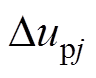 ,控制中参考电压
,控制中参考电压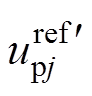 可表示为
可表示为
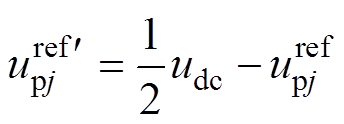 (21)
(21)考虑电压调整项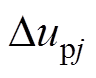 的参考电压为
的参考电压为
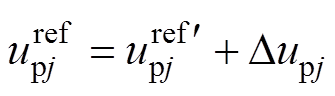 (22)
(22)
最近电平逼近调制下,不考虑电压调整项时,上桥臂导通子模块数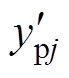 可表示为
可表示为
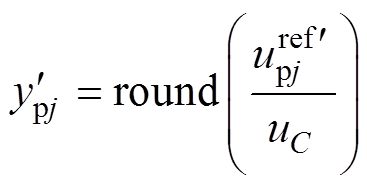 (23)
(23)考虑电压调整项时,上桥臂导通子模块数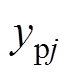 可表示为
可表示为
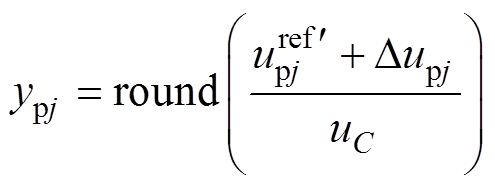 (24)
(24)
由式(24)可以看出,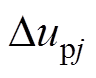 的存在将对
的存在将对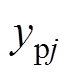 产生影响。为分析
产生影响。为分析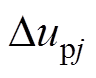 对
对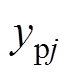 的影响,根据最近电平逼近的基本原理,可得电压调整项与桥臂导通子模块数关系如图5所示。
的影响,根据最近电平逼近的基本原理,可得电压调整项与桥臂导通子模块数关系如图5所示。
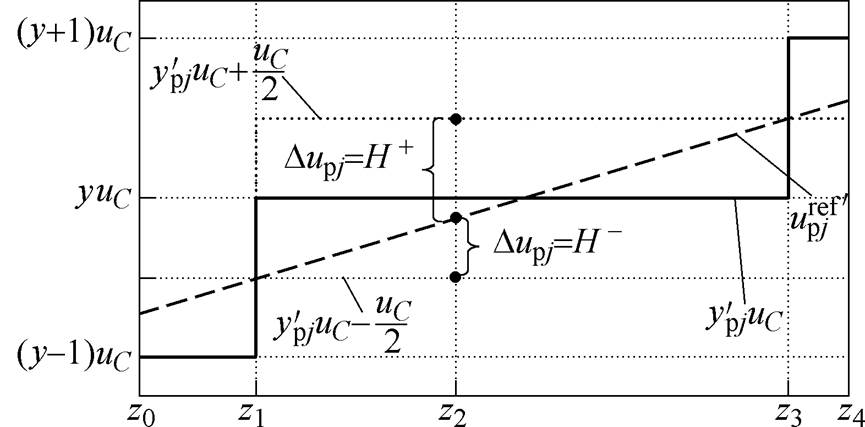
图5 电压调整项与桥臂导通子模块数关系
Fig.5 Analysis of the relationship between the voltage adjustment term and the arm conduction sub-module
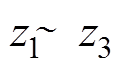 时间区间,
时间区间,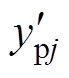 的值将保持不变,其值为y;
的值将保持不变,其值为y;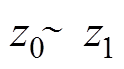 时间区间,
时间区间,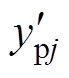 的值为
的值为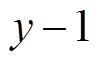 ;
;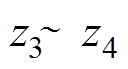 时间区间,
时间区间,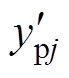 的值为
的值为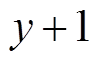 。
。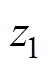 、
、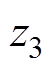 时刻为
时刻为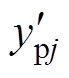 变化的临界点,
变化的临界点,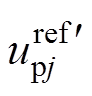 的值可分别表示为
的值可分别表示为
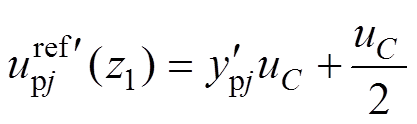 (25)
(25)
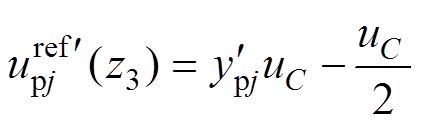 (26)
(26)
定义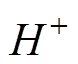 、
、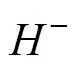 分别为
分别为
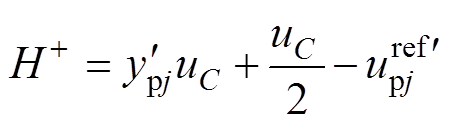 (27)
(27)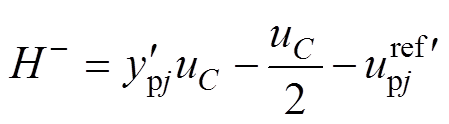 (28)
(28)
对于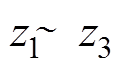 时间区间的任意时刻
时间区间的任意时刻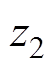 ,有
,有
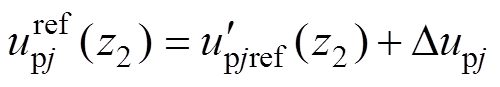 (29)
(29)当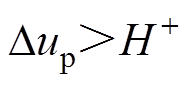 时
时
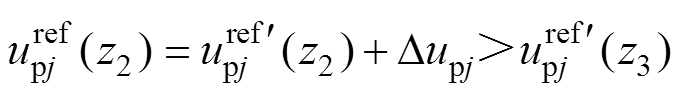 (30)
(30)
则有
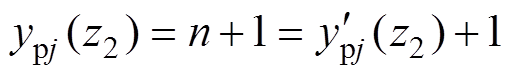 (31)
(31)同理,当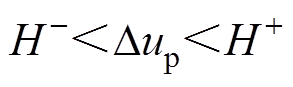 时,
时,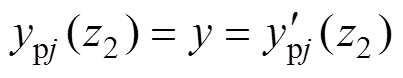 ;而当
;而当 时,有
时,有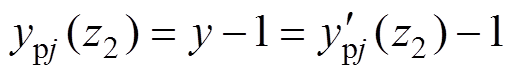 。
。
至此,可以得到如下结论:电压调整项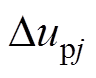 具有调整上桥臂电压导通子模块数的能力,使得
具有调整上桥臂电压导通子模块数的能力,使得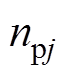 可在
可在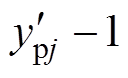 、
、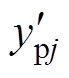 和
和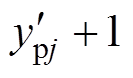 之间变化。
之间变化。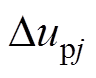 以
以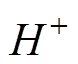 为上边界,一旦
为上边界,一旦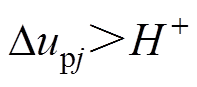 ,上桥臂电压导通子模块数增加1。
,上桥臂电压导通子模块数增加1。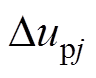 以
以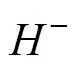 为下边界,一旦
为下边界,一旦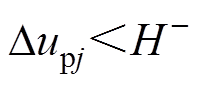 ,上桥臂电压导通子模块数减小1。当
,上桥臂电压导通子模块数减小1。当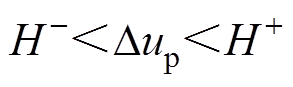 时,上桥臂电压导通子模块数维持原有值不变。对于下桥臂的情形,通过类似地推导,可以得到同样的结论。
时,上桥臂电压导通子模块数维持原有值不变。对于下桥臂的情形,通过类似地推导,可以得到同样的结论。
对比式(10)和式(15),可以发现,无差拍电流控制中,电压修正项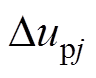 为
为
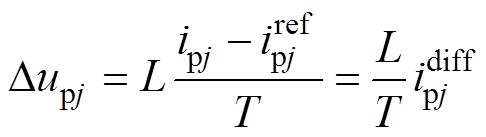 (32)
(32)在式(32)中,桥臂电感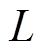 和控制周期
和控制周期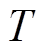 一旦选定后就不再变化,决定电压修正项
一旦选定后就不再变化,决定电压修正项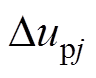 大小的是上桥臂电流误差
大小的是上桥臂电流误差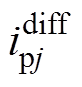 ,
,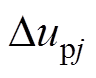 与
与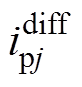 呈正比关系。令
呈正比关系。令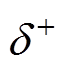 、
、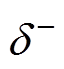 分别为
分别为
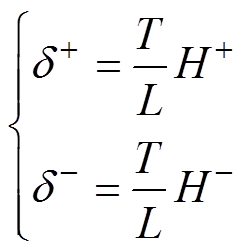 (33)
(33)
结合2.2节和2.3节的分析,可得到如下结论:
(1)当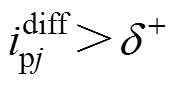 ,即
,即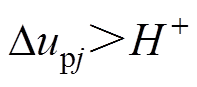 时,上桥臂导通子模块数将增加1,
时,上桥臂导通子模块数将增加1,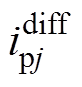 开始减小。
开始减小。
(2)当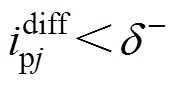 ,即
,即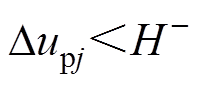 时,上桥臂导通子模块数将减小1,
时,上桥臂导通子模块数将减小1,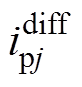 开始增大。
开始增大。
综合上面的分析可知,NLM下MMC无差拍电流控制具有滞环特性。其滞环环宽上限为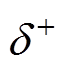 ,下限为
,下限为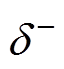 。
。
根据round函数的性质和式(27),有
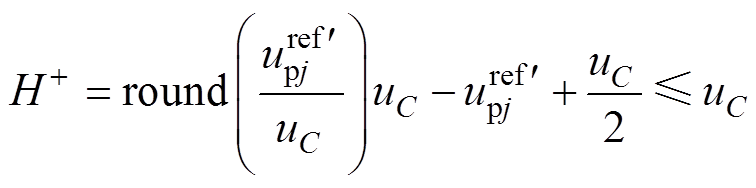 (34)
(34)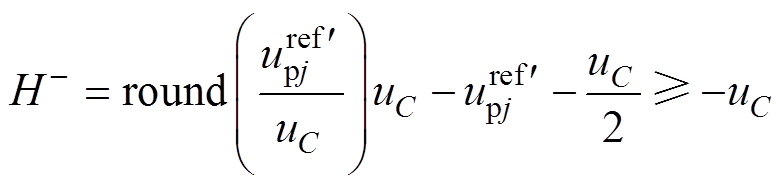 (35)
(35)
则有
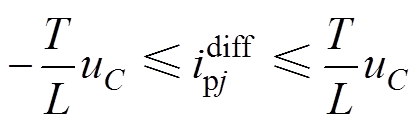 (36)
(36)可以看出,上桥臂电流误差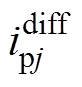 的波动范围为
的波动范围为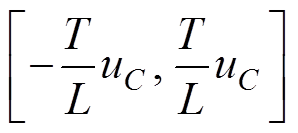 。上桥臂电流误差波动范围与控制周期和电容电压参考值呈正比,与桥臂电感值呈反比。
。上桥臂电流误差波动范围与控制周期和电容电压参考值呈正比,与桥臂电感值呈反比。
根据式(20),取调制比为0.9,当MMC桥臂子模块数为4时,传统NLM下的上桥臂电流误差如图6所示。由于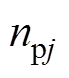 在一个电平区间始终为定值,当
在一个电平区间始终为定值,当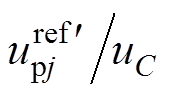 <
<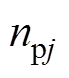 时,桥臂电流误差将一直保持减小的趋势。
时,桥臂电流误差将一直保持减小的趋势。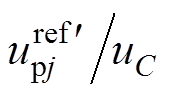 >
>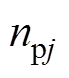 时,桥臂电流误差始终保持增加的趋势。当
时,桥臂电流误差始终保持增加的趋势。当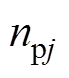 由0变为1的瞬间,即波谷所在电平区间结束时,桥臂实际电流最大程度正偏离其参考值。当
由0变为1的瞬间,即波谷所在电平区间结束时,桥臂实际电流最大程度正偏离其参考值。当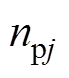 由4变为3的瞬间,即波峰所在电平区间结束时,桥臂实际电流最大程度负偏离其参考值。随着电平数的减少,每个电平区间的保持时间延长,将导致误差电流绝对值持续增大,尤其是在波峰和波谷所在电平区间,造成很大的跟踪误差。
由4变为3的瞬间,即波峰所在电平区间结束时,桥臂实际电流最大程度负偏离其参考值。随着电平数的减少,每个电平区间的保持时间延长,将导致误差电流绝对值持续增大,尤其是在波峰和波谷所在电平区间,造成很大的跟踪误差。
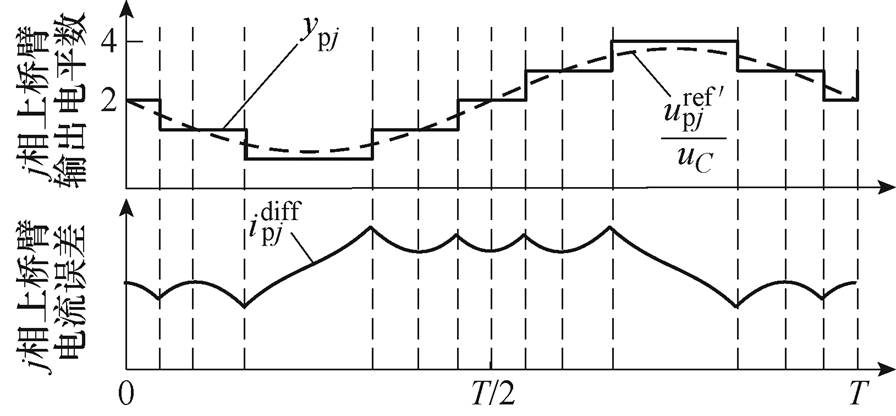
图6 传统NLM调制方法与上桥臂电流误差
Fig.6 Traditional NLM module method and differential current of upper-arm
实际上,在传统NLM控制下,稳压或者环流控制环节也会生成一个对应于式(11)的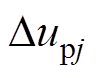 。但对应稳压控制的电压调整量通常很小,不足以使
。但对应稳压控制的电压调整量通常很小,不足以使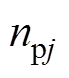 发生变化。而对应环流控制的电压调整量即便能使
发生变化。而对应环流控制的电压调整量即便能使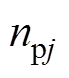 发生变化,也只能起到抑制环流的作用,无法降低桥臂电流误差。
发生变化,也只能起到抑制环流的作用,无法降低桥臂电流误差。
图7给出了NLM下无差拍电流控制与上桥臂电流误差。在MMC实际应用中,其控制周期通常在几十到几百微秒,即T的值通常很小。式(32)中,T作为分母,在电流误差较大时无差拍控制产生的电压调整相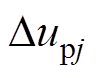 足以接近或超过子模块额定电压值,以此改变
足以接近或超过子模块额定电压值,以此改变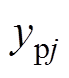 的值。一旦桥臂电流误差正偏离值超过式(33)中的
的值。一旦桥臂电流误差正偏离值超过式(33)中的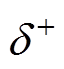 ,或者负偏离值超过
,或者负偏离值超过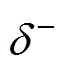 时,桥臂输出电平调整机制便起动,使得
时,桥臂输出电平调整机制便起动,使得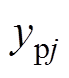 在一个电平区间不断变化,以此将桥臂电流误差控制在滞环环宽范围之内。
在一个电平区间不断变化,以此将桥臂电流误差控制在滞环环宽范围之内。

图7 NLM下无差拍电流控制与上桥臂电流误差波形
Fig.7 Deadbeat current control based NLM module method and differential current of upper-arm
由误差电流的定义有
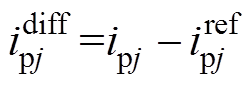 (37)
(37)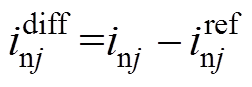 (38)
(38)
根据式(5)、式(37)和式(38),有
 (39)
(39)由2.4节结论可知
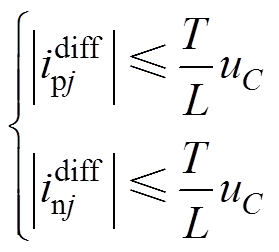 (40)
(40)
由式(39)结合不等式的性质,有
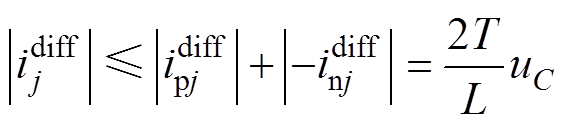 (41)
(41)式(41)表明,输出电流误差的波动范围为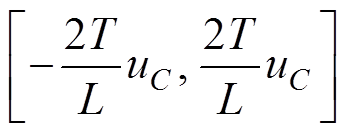 。输出电流误差波动范围只受控制周期、电容电压参考值和桥臂电感值的影响,与电平数无关。因此,NLM下MMC无差拍电流控制的输出电流质量不受电平数影响。即便在电平数很低的情况下,也能保证良好的输出电流波形质量。
。输出电流误差波动范围只受控制周期、电容电压参考值和桥臂电感值的影响,与电平数无关。因此,NLM下MMC无差拍电流控制的输出电流质量不受电平数影响。即便在电平数很低的情况下,也能保证良好的输出电流波形质量。
由式(8)和式(9)可知,桥臂电流由环流直流分量、交流侧电流和环流交流分量三部分组成。直流分量用于MMC与直流侧的功率交换,交流侧电流用于电网或电机与MMC的功率交换,而环流交流分量是有害分量,需要加以抑制。
实际运行中,MMC的子模块电压的波动随调制反映在直流母线电压与输出电压上,导致桥臂电流中存在偶次谐波环流,其中高次谐波环流相比于二倍频环流很小,可以忽略。NLM下MMC无差拍电流控制中,上、下桥臂电流各自独立以滞环的形式跟踪其电流参考值。利用该特点,只需在桥臂电流参考值中滤除环流二倍频分量,就可以达到抑制桥臂电流中二倍频环流的目的。
在滤除2次谐波时,可采用低通滤波器,也可采用陷波器[22]。陷波器传递函数为
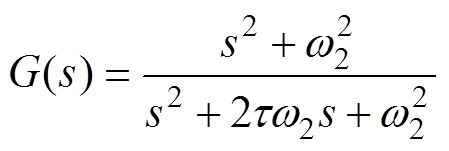 (42)
(42)式中,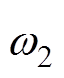 为陷波器的二倍频角频率;
为陷波器的二倍频角频率;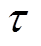 为与陷波器品质因数有关的参数。
为与陷波器品质因数有关的参数。
因此只需将图3控制框图中的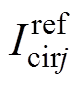 经过低通滤波器或陷波器后再送入式(8)和式(9),就可达到环流抑制的目的。
经过低通滤波器或陷波器后再送入式(8)和式(9),就可达到环流抑制的目的。
系统运行过程中,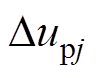 根据电流误差不停地改变上、下桥臂开通子模块数,这将导致子模块开关频率增加。由于电流误差与控制周期呈正比,为获得更好滞环跟踪效果,需要使用更小的控制周期(阀控周期)。这也将导致开关频率增大,因此均压环节需采用开关频率优化的均压策略,以降低子模块开关频率。
根据电流误差不停地改变上、下桥臂开通子模块数,这将导致子模块开关频率增加。由于电流误差与控制周期呈正比,为获得更好滞环跟踪效果,需要使用更小的控制周期(阀控周期)。这也将导致开关频率增大,因此均压环节需采用开关频率优化的均压策略,以降低子模块开关频率。
NLM的均压优化方法主要分为两类:第一类为基于子模块间最大电压偏差量的优化均压策略;第二类为基于子模块虚拟电容电压的优化均压策略。文献[23]详细分析了这两类均压策略的优化机理,并指出这两类均压算法都可以明显降低子模块开关频率;同时指出,在最大电压偏差和虚拟电容电压偏移量一致的情况下,基于最大电压偏差的优化均压算法的开关频率比基于虚拟电容电压的均压算法高。因此,本文采用基于子模块虚拟电容电压的优化均压策略[23-24]。
文献[5]通过分析MMC变换器的功率脉动和周期能量变化,给出MMC电容电压波动系数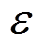 的表达式为
的表达式为
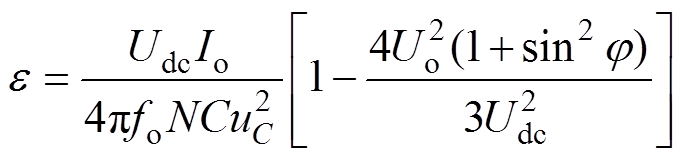 (43)
(43)式中,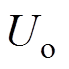 和
和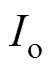 分别为机侧MMC输出电压和电流的幅值;
分别为机侧MMC输出电压和电流的幅值;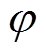 为功率因数角。
为功率因数角。
由式(43)可知,若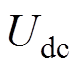 可以随电机频率(转速)成比例变化,表达式
可以随电机频率(转速)成比例变化,表达式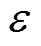 的值将保持不变。此时,表达式
的值将保持不变。此时,表达式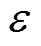 的左边第一项中
的左边第一项中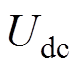 和
和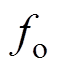 分别作为分子和分母成比例变化。最右侧项中,
分别作为分子和分母成比例变化。最右侧项中,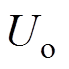 和
和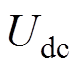 也分别作为分子和分母成比例变化。其余项均为定量,因此表达式
也分别作为分子和分母成比例变化。其余项均为定量,因此表达式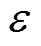 的值也为定值,即电容电压波动范围恒定,不再受频率变化的影响。
的值也为定值,即电容电压波动范围恒定,不再受频率变化的影响。
因此,为保证机侧MMC低频运行时的电容电压波动不增大,网侧MMC需为机侧MMC提供一个随频率变化的直流电压。MMC整流器常作为一个升压拓扑,文献[25]指出全桥子模块MMC整流器具有降压运行能力,并对此做出了详细分析和实验验证,此处不再重复分析。
根据NLM下无差拍电流控制的滞环特性,MMC整流器部分只需按经典的电压源整流器的滞环控制方案[26]进行设计即可。其控制框图如图8所示。其中,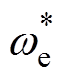 为转速参考值,通过式(1)得到直流母线电压参考值
为转速参考值,通过式(1)得到直流母线电压参考值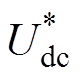 。直流母线电压参考值
。直流母线电压参考值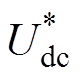 与实测值
与实测值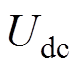 相减经过PI调节器乘以单位化的网侧三相相电压交流信号(锁相)得到三相交流电流的正弦指令信号
相减经过PI调节器乘以单位化的网侧三相相电压交流信号(锁相)得到三相交流电流的正弦指令信号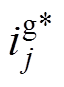 。
。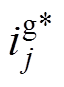 、
、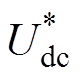 和三相电流反馈信号
和三相电流反馈信号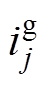 再经过无差拍电流控制即可得到开关脉冲信号。
再经过无差拍电流控制即可得到开关脉冲信号。
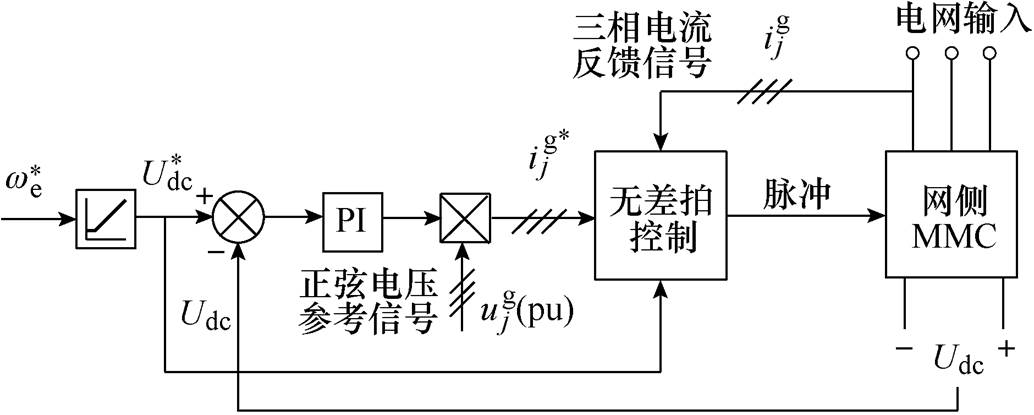
图8 网侧MMC控制框图
Fig.8 Control block diagrams for grid side MMC
本文所用电机为永磁同步电机,电机控制部分采用SPWM矢量控制[27],电流控制部分参照经典滞环控制进行设计。电机控制框图如图9所示,转速参考值 与实测值
与实测值 相减经过PI调节器得到q轴电流参考值
相减经过PI调节器得到q轴电流参考值 。d轴电流参考值
。d轴电流参考值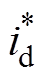 设置为0,与q轴电流参考值
设置为0,与q轴电流参考值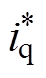 和转子位置角
和转子位置角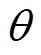 经过坐标变换得到机侧MMC输出电流参考值
经过坐标变换得到机侧MMC输出电流参考值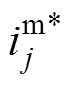 ,再经过机侧MMC无差拍电流控制便可得到开关控制信号驱动电机。
,再经过机侧MMC无差拍电流控制便可得到开关控制信号驱动电机。
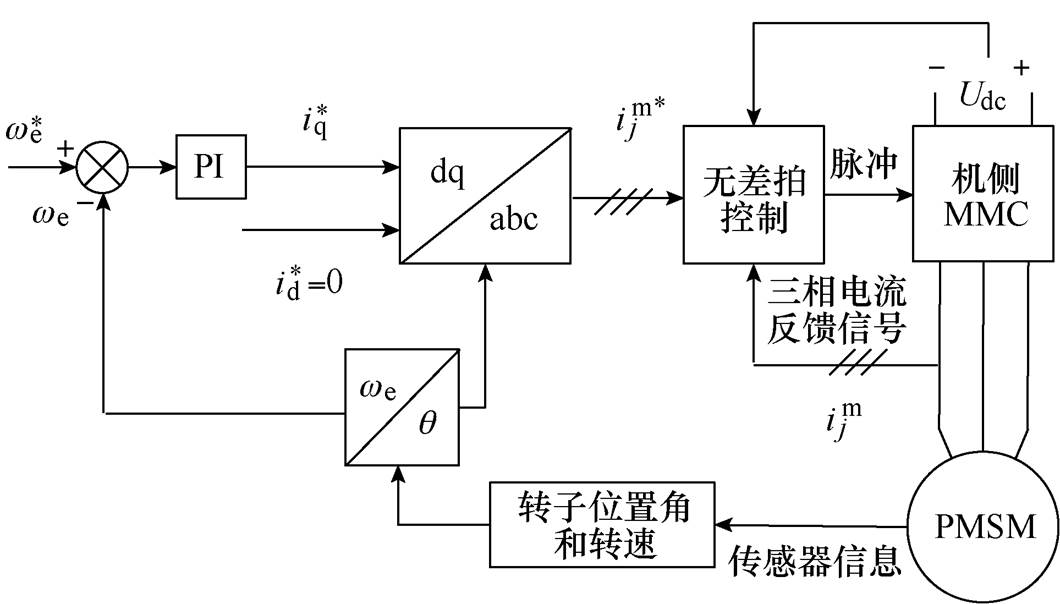
图9 电机控制框图
Fig.9 Control block diagrams for motor drive
为了验证本文所提出控制策略的正确性和有效性,利用Matlab软件搭建仿真模型,仿真参数见表1。
表1 MMC仿真参数
Tab.1 Simulation parameters of the MMC
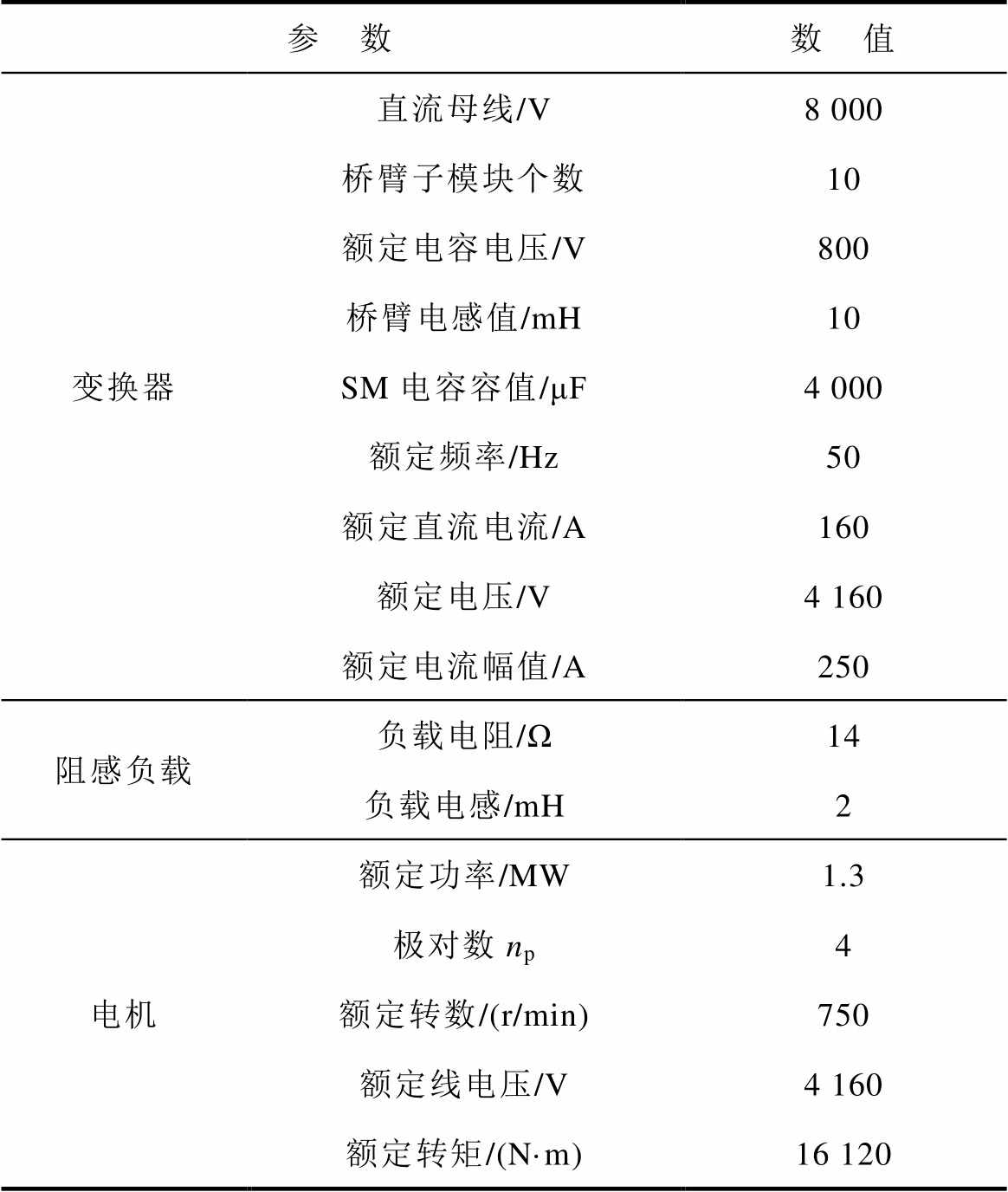
参 数数 值 变换器直流母线/V8 000 桥臂子模块个数10 额定电容电压/V800 桥臂电感值/mH10 SM电容容值/μF4 000 额定频率/Hz50 额定直流电流/A160 额定电压/V4 160 额定电流幅值/A250 阻感负载负载电阻/Ω14 负载电感/mH2 电机额定功率/MW1.3 极对数np4 额定转数/(r/min)750 额定线电压/V4 160 额定转矩/(N·m)16 120
网侧和机侧MMC的桥臂子模块数、桥臂电感值、电容容值和交流电流额定值均保持一致,此处不再分别列出。
图10给出了滞环特性仿真,此部分仿真中桥臂子模块数为10。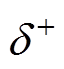 和
和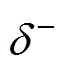 由式(27)、式(28)和式(33)得到。从图10中可以看出,
由式(27)、式(28)和式(33)得到。从图10中可以看出,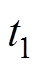 时刻,
时刻,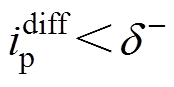 ,上桥臂子模块导通数由9降为8,上桥臂误差电流
,上桥臂子模块导通数由9降为8,上桥臂误差电流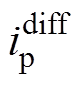 开始增大。
开始增大。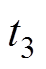 时刻,
时刻,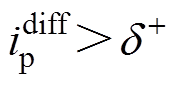 ,上桥臂子模块导通数由9升为10,上桥臂误差电流
,上桥臂子模块导通数由9升为10,上桥臂误差电流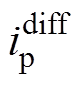 开始减小。这与本文2.2节的推导和2.4节的分析相一致。
开始减小。这与本文2.2节的推导和2.4节的分析相一致。

图10 滞环特性仿真
Fig.10 Hysteresis characteristic simulation diagram
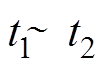 时刻,
时刻,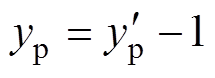 ;
;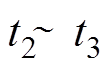 时刻,
时刻,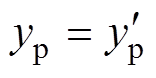 ;
;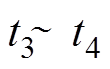 时刻,
时刻,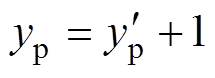 。不同于传统最近电平逼近调制的
。不同于传统最近电平逼近调制的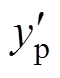 在一个电平区间始终为定值,NLM下的无差拍电流控制开通子模块数
在一个电平区间始终为定值,NLM下的无差拍电流控制开通子模块数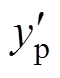 在不停地微调。这样的微调将桥臂误差电流控制在一定的区间。
在不停地微调。这样的微调将桥臂误差电流控制在一定的区间。
电流误差仿真如图11所示,0.2s投入式(32)的电压调整项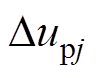 。0~0.2s为传统最近电平调制,0.2~0.4s即为无差拍电流控制。可以看出,较之于传统最近电平调制,无差拍电流控制的桥臂电流误差和输出电流误差明显减小。此处,
。0~0.2s为传统最近电平调制,0.2~0.4s即为无差拍电流控制。可以看出,较之于传统最近电平调制,无差拍电流控制的桥臂电流误差和输出电流误差明显减小。此处,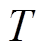 为50ms,将本文的仿真参数代入式(36)和式(41),可得到桥臂电流误差的波动范围为[-4, 4]A,输出电流误差的波动范围为[-8, 8]A。图11中桥臂电流误差和输出电流误差的范围,与2.4节和3.1节的理论计算值一致。
为50ms,将本文的仿真参数代入式(36)和式(41),可得到桥臂电流误差的波动范围为[-4, 4]A,输出电流误差的波动范围为[-8, 8]A。图11中桥臂电流误差和输出电流误差的范围,与2.4节和3.1节的理论计算值一致。
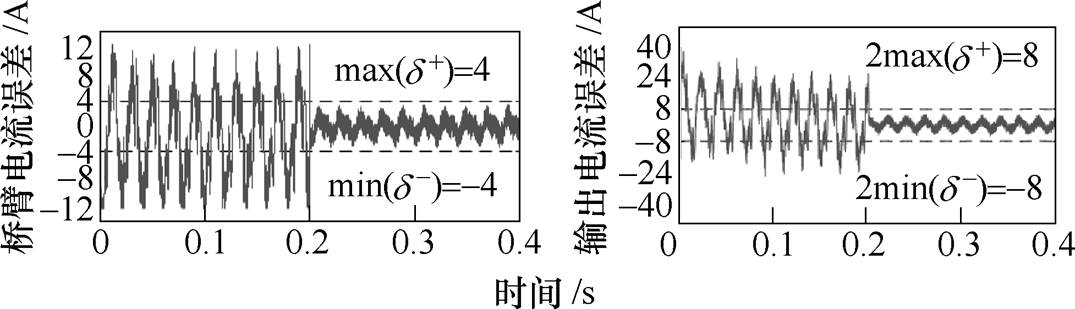
图11 电流误差仿真
Fig.11 The simulation diagram current error
保持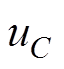 和
和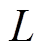 的值不变,在桥臂子模块数为10、8、6、4和2的情况下,分别选取
的值不变,在桥臂子模块数为10、8、6、4和2的情况下,分别选取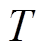 为100ms、50ms和20ms,测得无差拍电流控制下输出电流THD的值。从表2中可以看出,即便在电平数很低的情况下,无差拍电流控制都可以保证输出电流良好的谐波特性。
为100ms、50ms和20ms,测得无差拍电流控制下输出电流THD的值。从表2中可以看出,即便在电平数很低的情况下,无差拍电流控制都可以保证输出电流良好的谐波特性。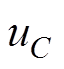 、
、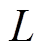 和
和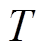 值相同时,不同子模块数情况下的输出电流THD相近,说明NLM下无差拍电流控制的输出电流THD不受电平数的影响。
值相同时,不同子模块数情况下的输出电流THD相近,说明NLM下无差拍电流控制的输出电流THD不受电平数的影响。
表2 不同桥臂子模块数下输出电流THD
Tab.2 The THD values of output current under different bridge arm sub-modules
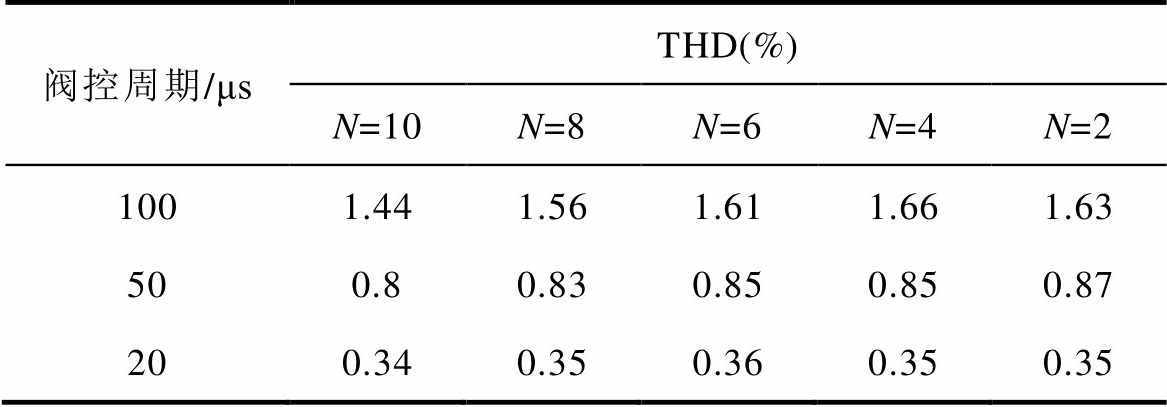
阀控周期/μsTHD(%) N=10N=8N=6N=4N=2 1001.441.561.611.661.63 500.80.830.850.850.87 200.340.350.360.350.35
由图10可以看出,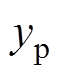 较之于
较之于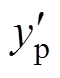 改变更为频繁,对应的子模块开关频率越大。为此,需对本文方法的输出电流谐波优化效果和子模块开关频率与其他控制策略进行比较。对比控制策略中,对比方法一为电容电压分层控制下的移相载波调制策略[12-13];对比方法二为参考文献[19-20]中的基于滞环原理的输出电流谐波优化算法,该方法也是通过实时调整上、下子模块开通数目,达到优化输出电流的目的;对比方法三为参考文献[14]中的结合电容电压排序的移相载波调制策略。
改变更为频繁,对应的子模块开关频率越大。为此,需对本文方法的输出电流谐波优化效果和子模块开关频率与其他控制策略进行比较。对比控制策略中,对比方法一为电容电压分层控制下的移相载波调制策略[12-13];对比方法二为参考文献[19-20]中的基于滞环原理的输出电流谐波优化算法,该方法也是通过实时调整上、下子模块开通数目,达到优化输出电流的目的;对比方法三为参考文献[14]中的结合电容电压排序的移相载波调制策略。
将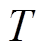 分别选取为500ms、100ms、50ms、20ms和10ms,采用本文方法得到各自对应的子模块平均开关频率。将得到的开关频率值作为对比方法一和对比方法三的载波频率,得到这两种方法不同载波频率下的输出电流THD。将输出电流滞环环宽分别设为16、4、2、1和0.5,得到对比方法二的子模块平均开关频率和输出电流THD。
分别选取为500ms、100ms、50ms、20ms和10ms,采用本文方法得到各自对应的子模块平均开关频率。将得到的开关频率值作为对比方法一和对比方法三的载波频率,得到这两种方法不同载波频率下的输出电流THD。将输出电流滞环环宽分别设为16、4、2、1和0.5,得到对比方法二的子模块平均开关频率和输出电流THD。
四种方法的数据汇总得到开关频率与输出电流THD的关系如图12(部分数据在表3中给出)所示。从图12中可以看出,相同的子模块平均开关频率下本文方法的输出电流THD最小。对比方法一作为目前电平数较少场合应用最广泛的调制方法,只需选取合适的载波频率,就能获得很好的输出电流谐波特性。平均开关频率大于700Hz时,其输出电流谐波THD已经小于1%。子模块平均开关频率大于700Hz时,对比方法三可以获得十分接近对比方法一的调制效果。对比方法二同样可以获得较好的输出电流谐波特性,其输出电流优化效果与滞环环宽成反比。滞环环宽越小,优化效果越好,但同时开关频率越大。只需保证足够的开关频率,对比的三种方法都可以获得很好的输出电流谐波特性,但本文方法在开关频率上占优。
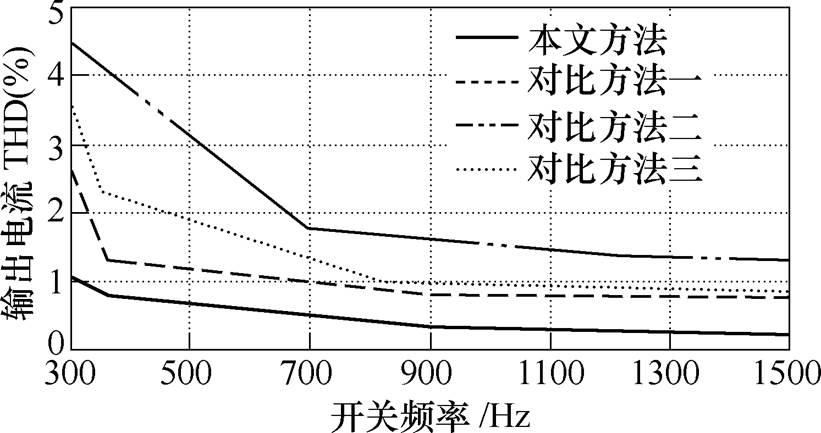
图12 开关频率与输出电流THD关系
Fig.12 The relationship diagram between switching frequency and THD value of output current
表3 不同方法下开关频率与输出电流THD
Tab.3 Switching frequency and THD value of output current under different methods
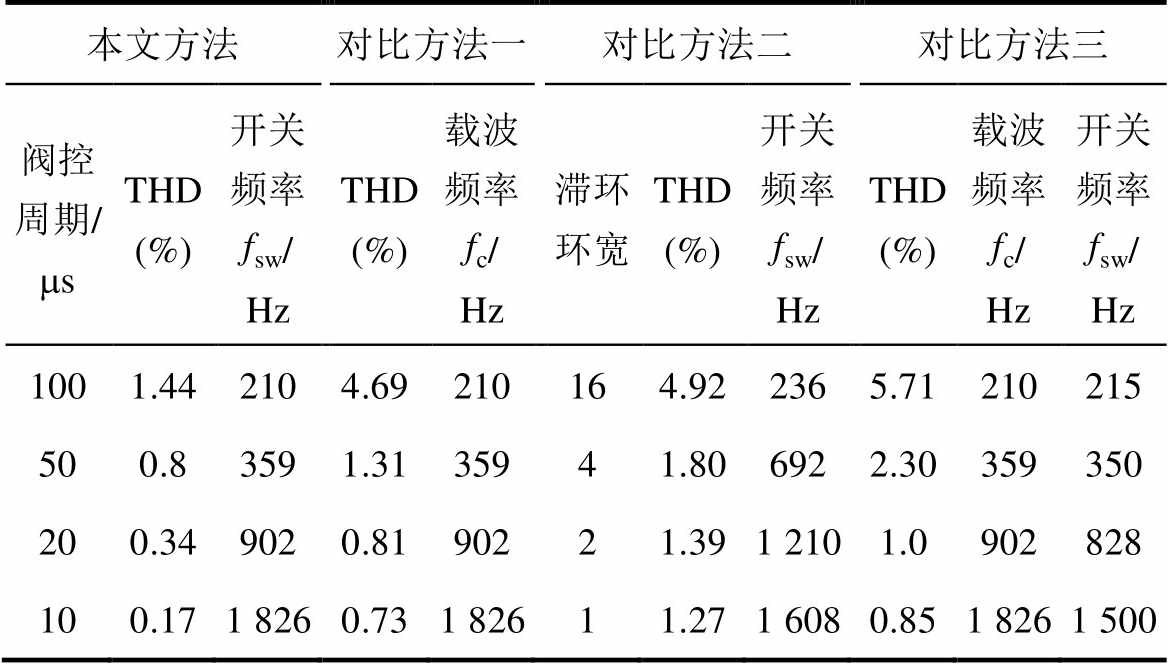
本文方法对比方法一对比方法二对比方法三 阀控周期/msTHD (%)开关频率fsw/ HzTHD (%)载波频率fc/ Hz滞环环宽THD (%)开关频率fsw/ HzTHD (%)载波频率fc/ Hz开关频率fsw/ Hz 1001.442104.69210164.922365.71210215 500.83591.3135941.806922.30359350 200.349020.8190221.391 2101.0902828 100.171 8260.731 82611.271 6080.851 8261 500
图13给出了无差拍电流控制下环流抑制的仿真。0.2s后,在图3控制框图的PI调节器后加入低通滤波器或陷波器。仿真结果显示,通过在环流参考值中滤除环流二倍频分量,环流交流分量均得到有效抑制。无差拍电流控制下,环流抑制实现简单,与陷波器相结合的环流抑制方案动态性能和环流抑制效果都要更好。

图13 环流抑制仿真
Fig.13 Circulating current suppressing simulation diagram
图14给出了电机起动过程的仿真波形。从图中可以看出,两种方法的电容电压波动都在合理范围之内(小于10%)。转矩经过0.2s由零值增至额定转矩(16 120N·m),转速经过2s由零值增至额定转速(750r/min)。两种控制方法的转矩和转速都均匀平滑上升,进入稳态后,转矩和转速的波动范围一致。与传统方法相比,本文方法的直流母线电压更加平滑。文献[9]指出PWM引入了开关波纹,在电机定子绕组上表现为共模电压,该共模电压约为子模块电容电压的一半。本文方法的共模电压控制在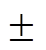 600V之内,而移相载波方法的共模电压最大值超过1 000V,有效避免了由PWM额外带来的共模电压。
600V之内,而移相载波方法的共模电压最大值超过1 000V,有效避免了由PWM额外带来的共模电压。
图15分别给出了两种频率下,本文方法和传统方法在转矩突变的情况下的仿真波形。50Hz时,稳定转速为750r/min,2.5s时转矩由16 120N·m阶跃变为8 000N·m。5Hz时,稳定转速为75r/min,0.52s时转矩由16 120N·m阶跃变为8 000N·m。从图15 可以看出,两种不同频率下,本文方法经过0.05s后,转速恢复稳定。而传统方法,50Hz时经过0.11s后转速恢复稳定,5Hz时经过0.16s后转速恢复稳定。本文方法的动态性能优于传统方法。
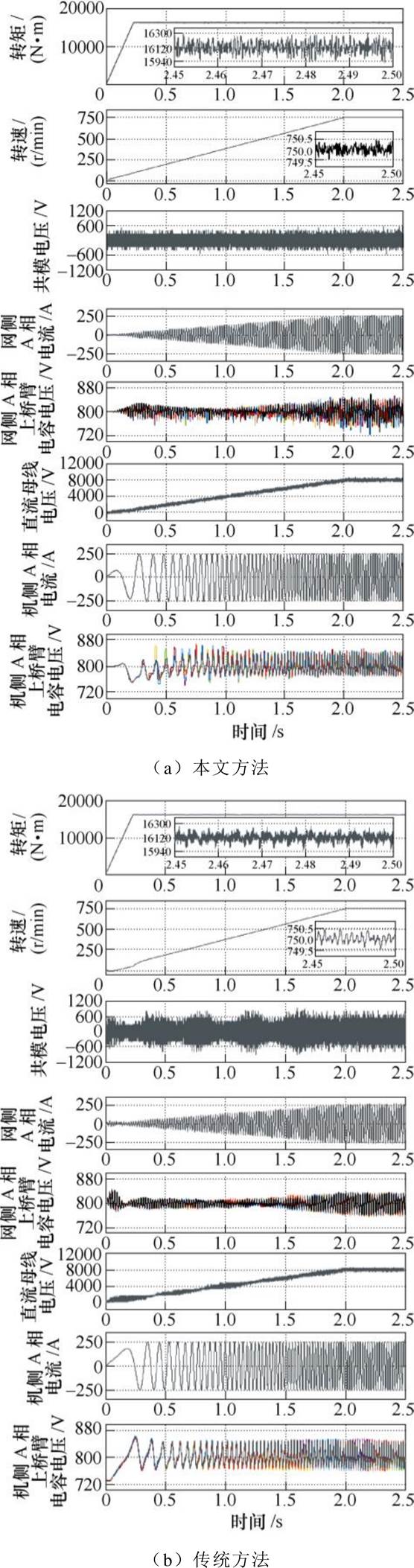
图14 永磁同步电机起动仿真波形
Fig.14 Simulation waveforms of a PMSM driven
电机起动过程和负载突变过程中,本文方法的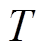 值均为50ms,对比方法的载波频率为902Hz。图15中给出了子模块平均开关频率。50Hz时,本文方法和对比方法的平均开关频率分别为394Hz和978Hz。5Hz时,本文方法和对比方法的平均开关频率分别为374Hz和918Hz。可以看出,本文方法在开关频率上有明显的优势。
值均为50ms,对比方法的载波频率为902Hz。图15中给出了子模块平均开关频率。50Hz时,本文方法和对比方法的平均开关频率分别为394Hz和978Hz。5Hz时,本文方法和对比方法的平均开关频率分别为374Hz和918Hz。可以看出,本文方法在开关频率上有明显的优势。
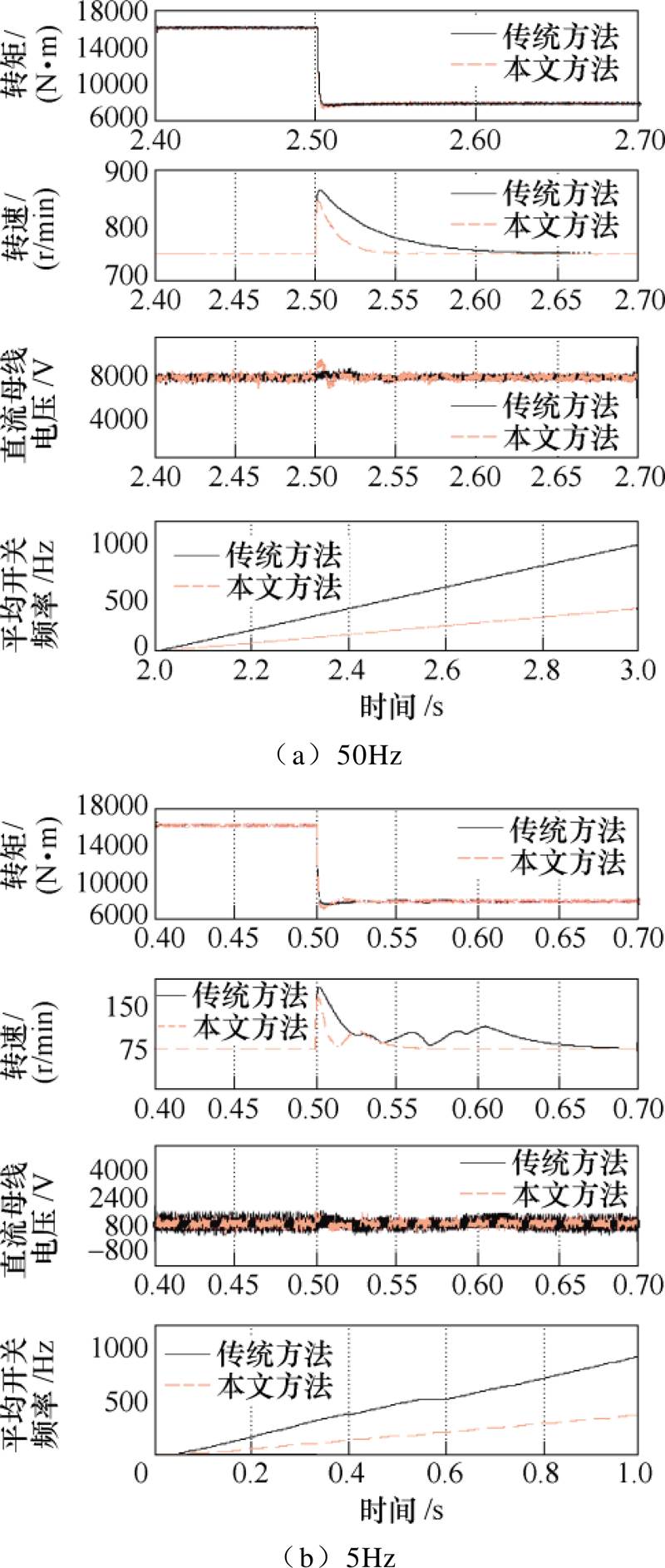
图15 负载突变仿真波形
Fig.15 The simulation waveforms under sudden load change
本文设计了一种基于最近电平逼近调制的背靠背MMC中高压变频调速系统控制策略。可得如下结论:
1)NLM下MMC无差拍电流控制具有滞环特性,桥臂电流误差波动范围与控制周期和电容电压参考值呈正比,与桥臂电感值呈反比。
2)NLM下无差拍电流控制的滞环特性,使其具有输出电流谐波优化能力。相同的开关频率下,本文所提方法的输出电流THD小于移相载波控制。
3)无差拍电流控制中上、下桥臂独立控制,互不影响。只需在参考电流中滤除环流二倍频分量,便可实现对环流二倍频分量的抑制。
4)将无差拍电流控制用于背靠背MMC变频调速系统,可大大简化控制系统的结构。相比于传统方案,本文所设计方案具有共模电压更小、动态性能更好和开关频率更低等优点。
参考文献
[1] Marquardt R, Lesnicar A, Hildinger J. Modulares stro-mrichterkonzept für netzkupplungsanwen- dungen bei hohen spannungen[C]//ETG-Fachtagung, Bad Nauheim, Germany: Fachtagung des VDE, 2002: 1-7.
[2] Hagiwara M, Nishimura K, Akagi H. A medium- voltage motor drive with a modular multilevel PWM inverter[J]. IEEE Transactions on Power Electronics, 2010, 25(7): 1786-1799.
[3] Li He, Potty K, Ke Ziwei, et al. Hardware design of a 1.7kV SiC MOSFET based MMC for medium voltage motor drives[C]//2018 IEEE Applied Power Elec- tronics Conference and Exposition (APEC), San Antonio, TX, 2018: 1649-1655.
[4] 徐殿国, 李彬彬, 周少泽. 模块化多电平高压变频技术研究综述[J]. 电工技术学报, 2017, 32(20): 104-116.
Xu Dianguo, Li Binbin, Zhou Shaoze. Overview of the modular multilevel converter based high voltage motor drive[J]. Transactions of China Electro- technical Society, 2017, 32(20): 104-116.
[5] 王奎, 郑泽东, 李永东. 新型模块化多电平变换器电容电压波动规律及抑制方法[J]. 电工技术学报, 2011, 26(5): 8-14.
Wang Kui, Zheng Zedong, Li Yongdong. Voltage ripple principle and restrain method of floating capacitors in a new modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 8-14.
[6] 王泽, 张凯, 陈济民, 等. 应用于模块化多电平变频器的电容电压脉动抑制技术综述[J]. 电工技术学报, 2018, 33(16): 3756-3771.
Wang Ze, Zhang Kai, Chen Jimin, et al. A summary of capacitor voltage ripple suppression techniques applied to modular multilevel converters for AC motor drives[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3756-3771.
[7] 殷实, 谭国俊, 方磊, 等. 模块化多电平变流器调速系统变频控制[J]. 电工技术学报, 2016, 31(20): 139-150.
Yin Shi, Tan Guojun, Fang Lei, et al. Variable- frequency control strategy of modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 139-150.
[8] Li Binbin, Zhou Shaoze, Xu Dianguo, et al. An improved circulating current injection method for modular multilevel converters in variable-speed drives[J]. IEEE Transactions on Industrial Electronics, 2016, 66(11): 7215-7225.
[9] Du Sixing, Wu Bin, Zargari N. Common-mode voltage elimination for variable-speed motor drive based on flying-capacitor modular multilevel con- verter[J]. IEEE Transactions on Power Electronics, 2017, 33(7): 5621-5628.
[10] Diab M S, Massoud A M, Ahmed S, et al. A dual modular multilevel converter with high-frequency magnetic links between submodules for MV open-end stator winding machine drives[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5142-5159.
[11] Kumar S, Poddar G. Control of medium-voltage AC motor drive for wide speed range using modular multilevel converter[J]. IEEE Transactions on Industrial Electronics, 2017, 64(4): 2742-2749.
[12] 周少泽, 李彬彬, 王景坤, 等. 改进型模块化多电平高压变频器及其控制方法[J]. 电工技术学报, 2018, 33(16): 3772-3781 .
Zhou Shaoze, Li Binbin, Wang Jingkun, et al. A hybrid modular multilevel high-voltage converter and its control method[J]. Transactions of China Electro- technical Society, 2018, 33(16): 3772-3781.
[13] Guan Mingxu, Li Binbin, Zhou Shaoze, et al. Back- to-back hybrid modular multilevel converters for AC motor drive[C]//IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, 2017: 1822-1827.
[14] 屠卿瑞. 模块化多电平换流器型直流输电若干问题研究[D]. 杭州: 浙江大学, 2013.
[15] Hu Pengfei, Jiang Daozhuo. A level-increased nearest level modulation method for modular multilevel converters[J]. IEEE Transactions on Power Electro- nics, 2014, 30(4): 1836-1842.
[16] Long Yunbo, Xiao Xiangning, Xu Yonghai, et al. A hybrid modulation method for improved modular multilevel converter applied for power quality compensation in medium voltage[C]//Future Energy Electronics Conference, Tainan, 2013: 789-793.
[17] Fan Shengfang, Zhang Kai, Xiong Jian, et al. An improved control system for modular multilevel converters with new modulation strategy and voltage balancing control[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 358-371.
[18] Wang Yi, Hu Can, Ding Ruoyu, et al. A nearest level PWM method for the MMC in DC distribution grids[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9209-9218.
[19] Hassanpoor A, Angquist L, Norrga S, et al. Tolerance band modulation methods for modular multilevel converters[J]. IEEE Transactions on Power Elec- tronics, 2015, 30(1): 311-326.
[20] 彭也伦, 黄守道, 张文娟, 等. 一种基于电流滞环控制的模块化多电平变流器调制策略[J]. 电工技术学报, 2016, 31(17): 94-101.
Peng Yelun, Huang Shoudao, Zhang Wenjuan, et al. A modulation strategy based on current hysteresis control for modular multilevel converter[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(17): 94-101.
[21] 荣飞, 龚喜长, 黄守道, 等. 模块化多电平换流器的无差拍控制策略[J]. 中国电机工程学报, 2017, 37(6): 1753-1763.
Rong Fei, Gong Xichang, Huang Shoudao, et al. Deadbeat control strategy of modular multilevel converter[J]. Proceedings of the CSEE, 2017, 37(6): 1753-1763.
[22] 徐千鸣, 罗安, 马伏军, 等. 考虑低频振荡的MMC有源阻尼环流抑制方法[J]. 电工技术学报, 2015, 30(24): 118-126.
Xu Qianming, Luo An, Ma Fujun, et al. Circulating current suppressing method based on active damping control of MMC considering low-frequency oscil- lation[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 118-126.
[23] 廖武. 模块化多电平变换器(MMC)运行与控制若干关键技术研究[D]. 长沙: 湖南大学, 2016.
[24] Lee H J, Jung J J, Sul S K. A switching frequency reduction and a mitigation of voltage fluctuation of modular multilevel converter for HVDC[C]//IEEE Energy Conversion Congress & Exposition, Pittsburgh, PA, USA, 2014, DOI: 10.1109/ECCE.2014.6953433.
[25] Lin Weixin, Jovcic D, Nguefeu S, et al. Full-bridge MMC converter optimal design to HVDC operational requirements[J]. IEEE Transactions on Power Deli- very, 2016, 31(3): 1342-1350.
[26] 张崇巍, 张兴. PWM整流器及其控制[M] . 北京: 机械工业出版社, 2003.
[27] 黄守道, 邓建国, 罗德荣. 电机瞬态过程分析的Matlab建模与仿真[M]. 北京: 电子工业出版社, 2013.
A Medium-Voltage Motor Drive with Modular Multilevel Converter Based on Nearest Level Modulation
Abstract Nearest level modulation (NLM) is the most commonly used modulation method for modular multilevel converter (MMC). When the number of levels is small, the output voltage and current harmonics of the NLM are severely distorted, and it cannot be used in MMC based medium-voltage motor drive system. In this paper, the switching process of the deadbeat current control under NLM is analyzed in detail, and it is pointed out that the MMC deadbeat current control under NLM modulation has hysteresis characteristics. The hysteresis loop width of MMC deadbeat current control under NLM is quantitatively analyzed, and the expression of hysteresis loop width and output current fluctuation range is obtained. At the same time, the integrated control scheme of MMC based motor drive system is designed. Compared with the traditional scheme, the proposed scheme has the advantages of simple control structure, low switching frequency, easy realization of circulating current suppression and good dynamic characteristics. The 11-level back-to-back MMC motor drive model was built in Matlab/Simulink to verify the correctness and effectiveness of the proposed control scheme.
keywords:Modular multilevel converter, medium-voltage motor drive, nearest level modulation, deadbeat current control, hysteresis characteristics
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.190103
国家自然科学基金项目(61572417)和国家自然科学基金重点项目(51737004)资助。
收稿日期 2019-01-24
改稿日期 2019-04-21
易灵芝 女,1966年生,博士,教授,主要研究方向为交流调速与电力电子装置、新能源发电与直流微网。E-mail: ylzwyh@sohu.com
黄晓辉 男,1992年生,硕士研究生,主要研究方向为多电平变换器及其控制技术。E-mail: 751011718@qq.com(通信作者)
(编辑 崔文静)