图1 多相整流永磁同步发电机相间短路示意图
Fig.1 Schematic diagram of phase-to-phase short-circuit of multi-phase PMSG with rectifier load system
摘要 该文将多回路法与有限元法相结合,建立了多相整流永磁同步发电机系统绕组内部相间短路的通用数学模型,可计算永磁电机正常及绕组内部故障工况的电气量分布,不仅适用于每相单分支的多相电机,还适用于每相多分支的情况。在一台特制的六相双分支永磁同步发电机样机上进行了故障实验,实验结果和仿真结果相吻合,验证了数学模型的正确性。在准确计算绕组电流的基础上,进一步计算了故障前后样机内部的温度场分布,结果表明故障导致样机内部温度不再均匀分布。根据仿真和实验结果,分析了该样机相间短路的故障特点,并说明了短路点附近明显升温对永磁电机的严重影响以及不同组三相绕组间相间短路引起整流桥中某些二极管过电流的潜在危害。该文研究为多相永磁同步发电机内部相间短路故障检测提供了依据。
关键词:多相永磁同步发电机 多分支 整流系统 相间短路 多回路-有限元数学模型
多相整流发电机提供的直流电源,具有直流脉动小、电磁干扰小、可靠性高和效率高等优点[1],已广泛应用于航空航天、船舶推进等移动平台[2]。作为各种移动体(如飞机、舰船)电源的核心部分,多相发电机带整流系统的安全运行至关重要。由于常用于移动体中,发电机运行的工况和外界环境都比较复杂,在这些复杂条件的作用下,系统更容易出现故障,不仅可能损坏电机,甚至可能直接威胁乘客或工作人员的安全,造成严重事故[3]。
目前对多相同步发电机整流系统的故障研究主要集中在电励磁电机[4-11]。对于永磁同步发电机,虽然转子上没有绕组,结构比电励磁电机简单,但各种材料、形状和安装位置的永磁体产生的磁场却比电励磁电机复杂,而且绕组内部短路故障还会使磁场发生畸变[12],进一步增大了计算分析的难度。此外,一旦检测到短路故障,电励磁电机在停机操作中可采取灭磁措施,以减小停机过程中对电机的损害;而永磁电机由于无法直接调节永磁体产生的磁场,只能逐渐降低转速直至故障电机停机。在停机过程中绕组内部一直存在较大的短路电流,可能烧毁电机,所以对短路故障检测的快速性要求更高。因此,对永磁发电机定子内部短路故障的研究更有必要。
发电机定子内部短路故障包括匝间短路故障和相间短路故障。目前对三相永磁电机匝间短路故障的研究已经比较深入,例如,文献[13-14]在abc坐标系下建立了三相永磁电机匝间短路故障的数学模型;文献[15]和文献[16]分别利用故障引起的3次谐波电流和高频谐波注入法,研究了永磁电机匝间短路的故障检测方法;文献[17]基于PNN神经网络建立了永磁电机匝间短路故障的诊断模型等。但以上研究仅针对传统三相永磁电机的定子绕组匝间短路故障,缺乏对内部相间短路故障的研究,并且基本不涉及整流负载。而相间短路故障比匝间短路故障的破坏性更强[13],所以本文将主要针对多相整流永磁同步发电机系统定子内部相间短路故障进行深入研究,为及时发现并排除故障提供依据。
现有文献中对多相永磁同步发电机整流系统及其故障的研究还不够全面,建立的数学模型仅限于某种特定的多相电机。例如,文献[18]只研究了发电机转子失磁故障,建立的永磁发电机整流系统数学模型没有涉及定子绕组内部故障;文献[19]对永磁发电机进行了定子内部故障的仿真研究,但是缺乏实验验证,而且其数学模型只适用于每相单分支的发电机。实际上在一些需要大功率输出的场合(如等离子高压脉冲实验等),每相绕组通常采用多分支并联的结构。文献[20]就研究过一台每相8个并联分支的六相脉冲电励磁发电机,类似地,多相永磁整流同步发电机也存在每相多分支的情况。
为了具有更广泛的适用性,本文将多回路分析法与有限元法相结合,建立了多相多分支永磁同步发电机带整流负载系统定子绕组内部相间短路故障的通用数学模型,不仅适用于每相单分支的十二相等多相电机,还适用于每相多分支的情况(比如六相双分支电机)。本文在一台六相双分支永磁同步发电机样机上进行了实验,验证了该数学模型的正确性。在此基础上,还分析了实验样机故障前后的温度场分布。最后结合仿真和实验,分析了样机定子绕组相间短路的故障特点及危害,可为故障的及时检测提供依据。
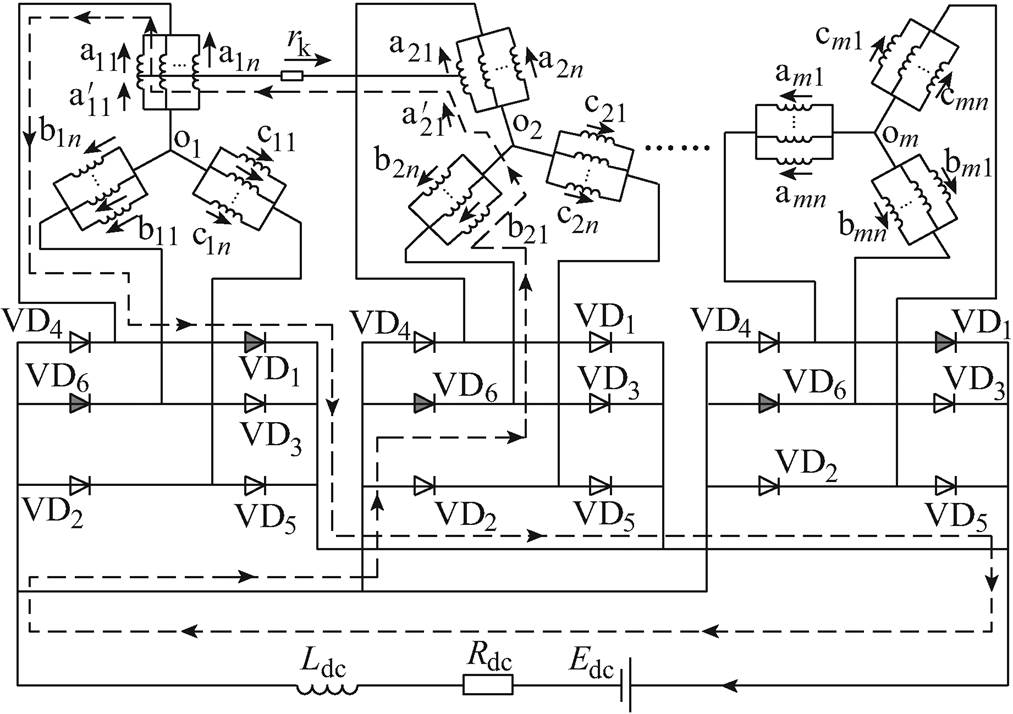
图1是3m相整流永磁同步发电机的绕组及整流桥连接示意图(m为自然数)。3m相定子绕组,由m个星形联结的三相绕组(A1B1C1~AmBmCm)组成,每组在空间上互差180°/(3m)(电角度),每组中性点相互独立;每相绕组由n个分支并联(如A1相的n个分支a11~a1n);每组三相绕组连接一个三相整流桥(其中开关管可以是二极管也可以是晶闸管,本文采用二极管,VD1~VD6为二极管编号),m个三相整流桥在直流侧并联,共同为负载供电。图1中,Rdc、Ldc和Edc分别为直流侧负载电阻、电感和反电动势。

图1 多相整流永磁同步发电机相间短路示意图
Fig.1 Schematic diagram of phase-to-phase short-circuit of multi-phase PMSG with rectifier load system
不同于传统的三相电机,这种多相电机的内部相间短路故障有两种情况:同桥相间短路(比如a11与b11短路)和异桥相间短路(比如a11与a21短路)。考虑到多相电机异桥相间短路与以往研究过的三相电机内部相间短路有明显区别,本文将以异桥相间短路为例,建立多相永磁同步发电机整流系统绕组内部相间短路故障的数学模型。
以图1中所示A1相第1分支a11与A2相第1分支a21之间的内部短路故障为例,列写定子绕组电压方程。图中正常分支可看作一个绕组元件(如a12、a22等),而故障分支从短路点被分为两个绕组元件(如故障绕组a11和故障附加绕组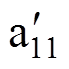 ),另外故障发生后还增加了一条短接线元件k。按照图中的参考方向,列写各绕组元件的电压方程,即
),另外故障发生后还增加了一条短接线元件k。按照图中的参考方向,列写各绕组元件的电压方程,即
 (1)
(1)式中,p =d/dt为微分算子;Us、ys和Is为定子绕组所有元件的电压向量、磁链向量和电流向量,都是3mn+3行的列向量,即
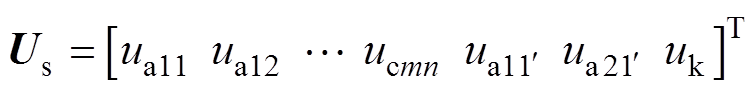

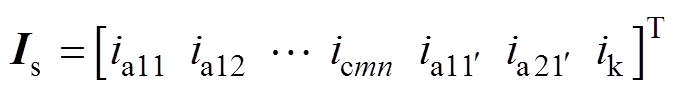
定子绕组电阻矩阵为
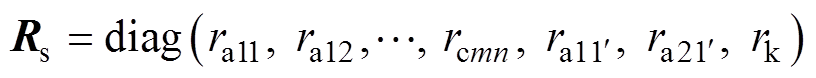
式中,ua11~ucmn、ya11~ycmn、ia11~icmn、ra11~rcmn为绕组元件a11~cmn(包括正常绕组元件和故障绕组元件)的电压、磁链、电流和电阻;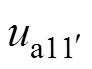 和
和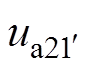 、
、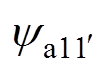 和
和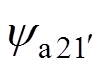 、
、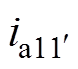 和
和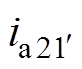 、
、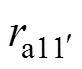 和
和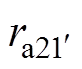 为故障附加绕组元件
为故障附加绕组元件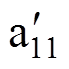 和
和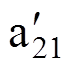 的电压、磁链、电流和电阻;uk和ik、rk为故障短接线元件k的电压、电流和电阻。
的电压、磁链、电流和电阻;uk和ik、rk为故障短接线元件k的电压、电流和电阻。
对正常绕组(没有内部短路故障的情况),Us、ys和Is只有前3mn行,Rs只有前3mn行和3mn列。
永磁电机中,绕组磁链由两部分组成,分别由定子电流和永磁体产生。定子绕组所有元件的磁链向量可表示为
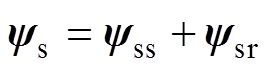 (2)
(2)式中,yss为定子电流产生的磁场匝链定子各绕组元件的磁链向量,在多回路数学模型中可计算得到
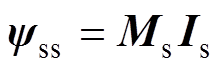 (3)
(3)
式中,Ms为正常绕组、故障绕组和故障附加绕组的自感以及互感构成的电感矩阵。计算绕组电感系数有多种方法,如文献[21]提到的气隙磁导分析法。考虑到永磁体形状及安装位置多种多样,尤其是内嵌式永磁电机的等效气隙不均匀,等效磁导的计算比较复杂,因此本文采用二维有限元法计算定子绕组电感系数。这种方法能计及气隙磁场与槽漏磁场的共同作用,但无法考虑端部漏磁场引起的电感系数。本文根据文献[21]的方法另外计算了定子端部漏电感。受本文篇幅所限,将另外撰文阐述永磁电机中定子电感系数的具体计算过程。
式(2)中ysr为永磁体产生的磁场匝链定子各绕组元件的磁链向量,本文采用有限元法进行计算,可考虑磁极形状、齿槽效应及永磁体工作点等因素。通过有限元计算,可得到永磁体产生的气隙磁通密度空间函数为
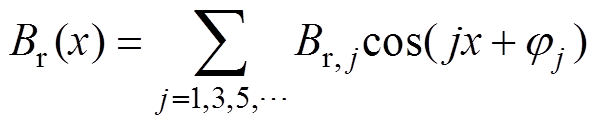 (4)
(4)式中,x为建立在转子坐标系中的空间位置角(电角度),x =0处为磁极中心线;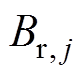 和
和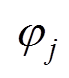 为永磁体产生气隙磁通密度的空间j次谐波的幅值和相位。结构正常的永磁体(不考虑失磁故障)产生气隙磁密的空间周期为1对极,气隙磁通密度只包含基波和3、5等奇数次谐波,即j =1, 3, 5,…。
为永磁体产生气隙磁通密度的空间j次谐波的幅值和相位。结构正常的永磁体(不考虑失磁故障)产生气隙磁密的空间周期为1对极,气隙磁通密度只包含基波和3、5等奇数次谐波,即j =1, 3, 5,…。
对式(4)在定子中单个线圈横截面进行积分,得到永磁体磁场在该线圈中匝链的磁链为
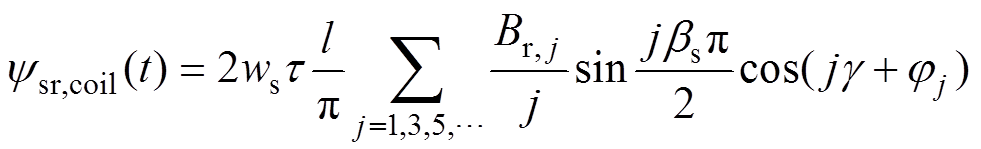 (5)
(5)式中,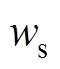 和
和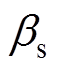 为定子单个线圈的匝数和短距比;
为定子单个线圈的匝数和短距比;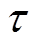 为极距;l为定子轴向长度;
为极距;l为定子轴向长度;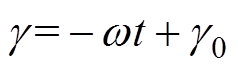 (其中
(其中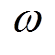 为电角速度,t为时间,
为电角速度,t为时间, 为t =0时线圈中心线落后转子d轴的电角度)。
为t =0时线圈中心线落后转子d轴的电角度)。
由式(5)可得永磁体在该线圈中产生的电动 势为
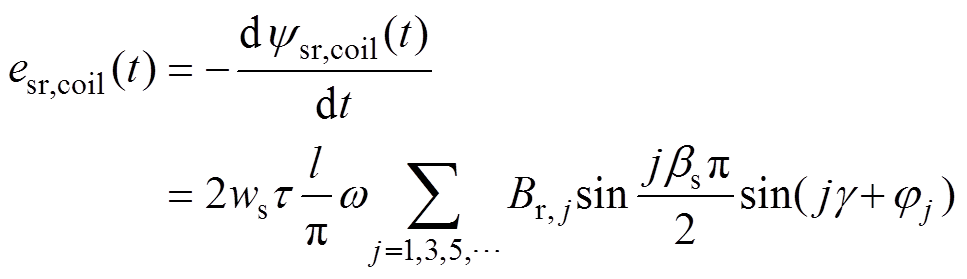 (6)
(6)类似地,可以得到定子所有线圈的电动势,然后根据电机正常或者故障时,定子绕组的实际连接情况,将绕组元件中所有线圈的电动势叠加,得到永磁体在定子绕组元件中产生的电动势esr[18-19]。其向量形式为
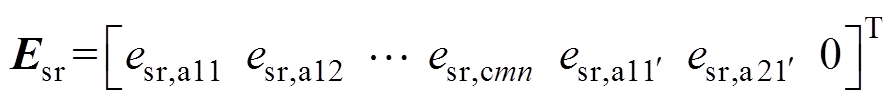
式中,Esr是3mn+3行的列向量,当电机绕组正常时,Esr只有前3mn行;esr,a11~esr,cmn为永磁体在绕组元件a11~cmn(包括正常绕组元件和故障绕组元件)中产生的电动势; 和
和 为永磁体在故障附加绕组元件
为永磁体在故障附加绕组元件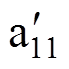 和
和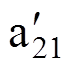 中产生的电动势。
中产生的电动势。
综合式(1)~式(3)和式(6)得发电机绕组所有元件的电压方程为
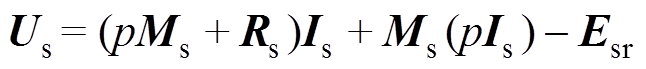 (7)
(7)如图1所示,根据电压与电流的关系[4, 10]可得
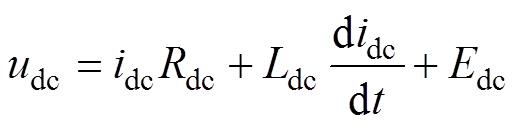 (8)
(8)式中,udc和idc分别为直流侧电压、电流。
将式(7)和式(8)联立,得到
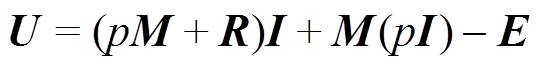 (9)
(9)式中,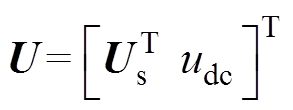 ;
;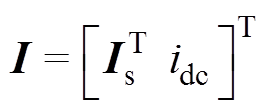 ;
;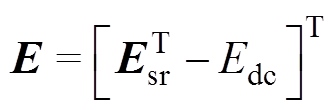 ;
;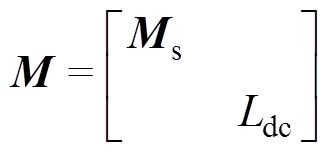 ;
;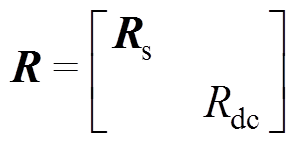 。
。
式(9)实际上是系统中各元件的电压方程,并没有考虑发电机定子绕组元件和整流桥直流侧负载元件之间通过整流桥形成的实际导通回路[22]。本文采用关联矩阵T [21]来描述导通回路与发电机绕组和直流侧负载的拓扑关系。以图1中所示相间短路故障为例形成关联矩阵。根据图中二极管的导通情况(图中实心二极管为导通状态,空心二极管为关断状态),关联矩阵如下
 (10)
(10)在图1所示状态下,关联矩阵T为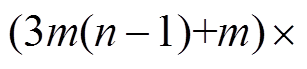
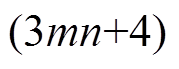 矩阵。列代表绕组元件,包括定子各相绕组各分支元件(a11~cmn)、两个故障附加分支元件(
矩阵。列代表绕组元件,包括定子各相绕组各分支元件(a11~cmn)、两个故障附加分支元件(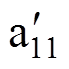 和
和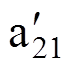 )、短接线元件k和直流负载元件dc,列数是固定不变的;行代表实际导通回路。矩阵T1~Tm分别表示1~m组三相绕组元件与导通回路的关系。矩阵Tm+1表示故障附加分支元件、短接线元件和直流侧负载元件与导通回路的关系。
)、短接线元件k和直流负载元件dc,列数是固定不变的;行代表实际导通回路。矩阵T1~Tm分别表示1~m组三相绕组元件与导通回路的关系。矩阵Tm+1表示故障附加分支元件、短接线元件和直流侧负载元件与导通回路的关系。
对于每相多分支的整流发电机,系统运行时导通回路可分为两类:①同相各分支元件形成的固有回路;②发电机定子绕组与直流侧负载形成的回路。前者与整流桥的导通模式无关,比如当电机空载且无故障运行时,关联矩阵T(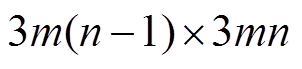 矩阵)为
矩阵)为
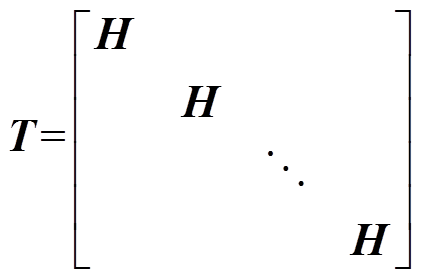 (11)
(11)式中, ,
, 为
为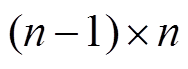 矩阵,矩阵h中每一行代表同相绕组内部相邻分支所形成的固有回路。
矩阵,矩阵h中每一行代表同相绕组内部相邻分支所形成的固有回路。
发电机负载运行时,关联矩阵T前3m(n-1)行如式(11)所述;此外,每组三相绕组之间还会通过导通二极管形成经过负载的回路,对应关联矩阵T中3m(n-1)行之后。由于本文研究的短路故障发生在第1组与第2组三相绕组之间,所以关联矩阵T中对应这两组三相绕组导通回路的行为
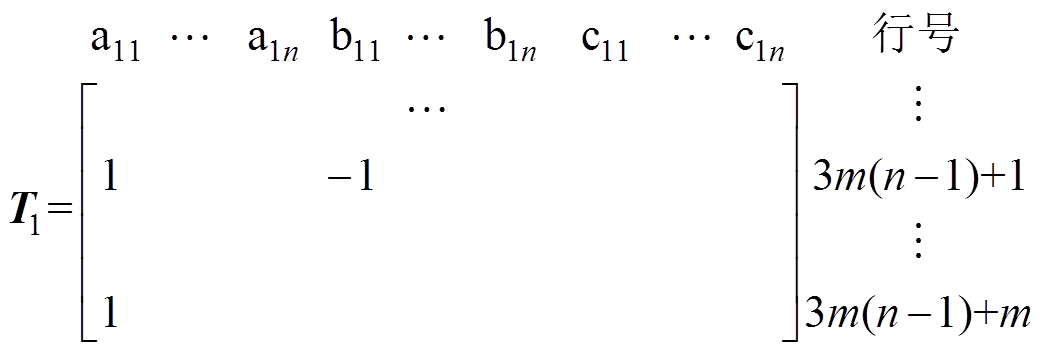 (12)
(12)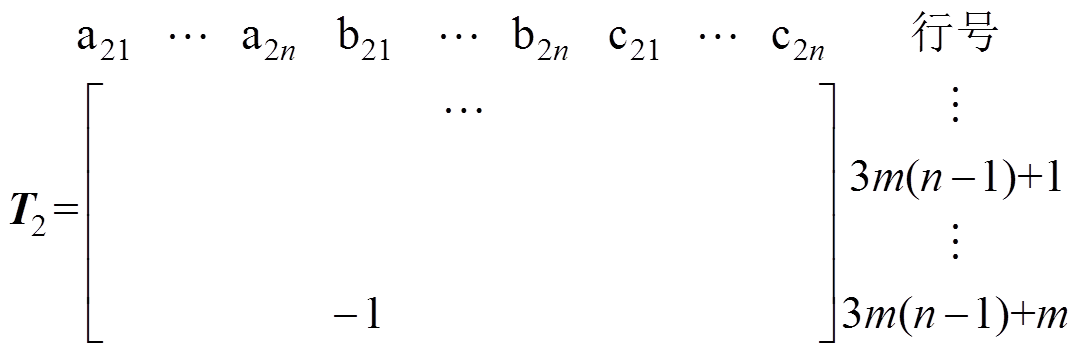 (13)
(13)
 (14)
(14)
而没有发生短路的三相绕组的导通回路对应行( )为
)为
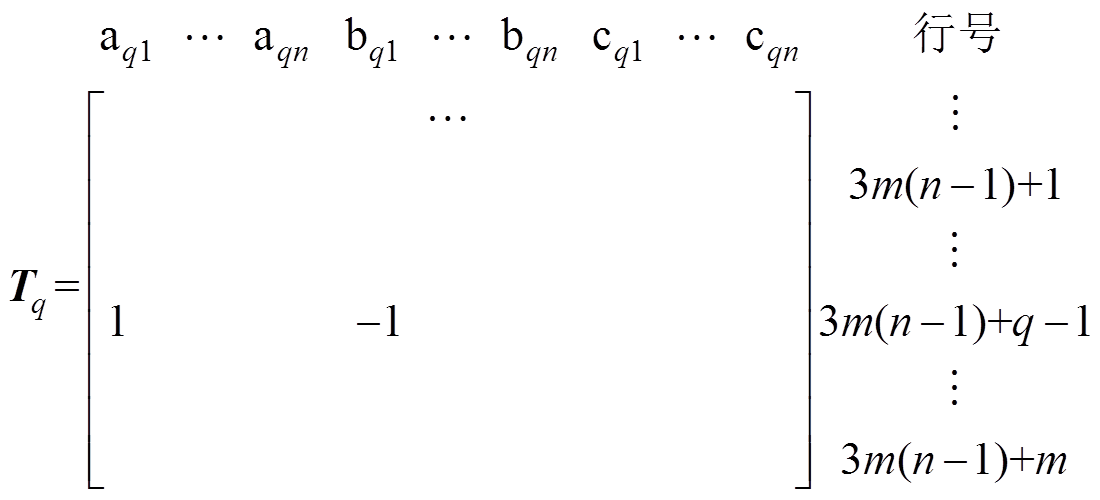 (15)
(15)关联矩阵T的最后一行表示发生相间短路后形成的故障附加回路。其中元素的符号按照实际导通回路与各绕组规定的参考方向是否一致来确定,除了标记出的数值,其他元素的值都为0。
得到关联矩阵T后,由系统绕组电压、电流与系统回路电压、电流的关系可得
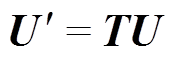 (16)
(16)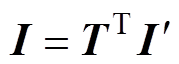 (17)
(17)
式中,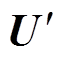 为系统回路电压向量;
为系统回路电压向量;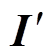 为系统回路电流向量。
为系统回路电流向量。
将式(16)、式(17)代入式(9)中,得到系统的状态方程为
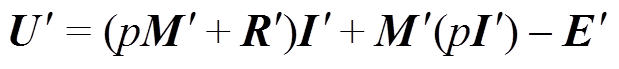 (18)
(18)式中, ;
;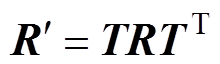 ;
;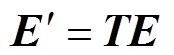 。式(18)为微分方程组,在系统运行时,由于
。式(18)为微分方程组,在系统运行时,由于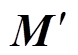 是时变的,所以只能通过数值积分的方法(如四阶龙格库塔法)求解[23]。
是时变的,所以只能通过数值积分的方法(如四阶龙格库塔法)求解[23]。
事实上,系统状态方程的形式是随整流桥导通模式变化不断变化的。因此,经过求解以后,需要根据所求电气量来判断整流桥的工作状态是否发生变化。若发生变化,则修改关联矩阵T;若没有发生变化,则关联矩阵T保持不变。以此实现多相整流永磁同步发电机系统的数字仿真。
考虑到永磁体产生磁场的大小受到电机运行工况的影响,本文将多回路计算程序与有限元计算程序相互迭代计算永磁整流发电机的绕组电流、电压等电气量,不仅能够考虑整流桥开关管导通模式变化对系统状态方程的影响,还能够考虑电机电枢电流变化对永磁体工作点的影响。基于多回路-有限元数学模型的迭代仿真流程如图2所示。
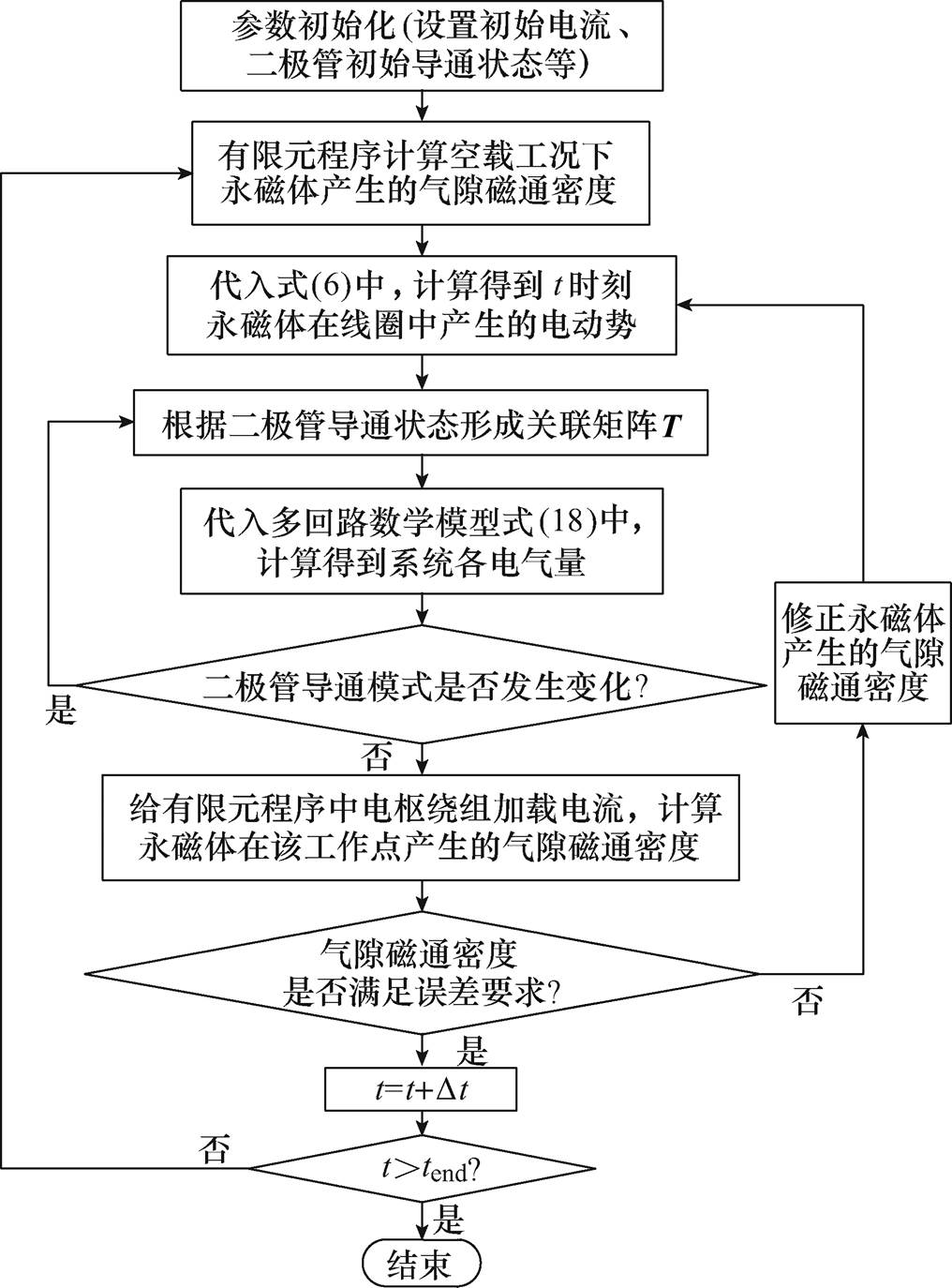
图2 基于多回路-有限元数学模型的迭代仿真流程
Fig.2 Iterative simulation flow chart based on multi-loop and FEM mathematical model
本文在一台特制的六相双分支永磁同步发电机样机上进行了带整流负载的实验,样机主要参数见表1。为实现定子内部短路故障实验,在实验样机定子绕组中设置了抽头,引出抽头方案如图3所示。由图3可以看出,每个分支由4个线圈串联组成,所以抽头从分支的25%、50%和75%处引出。
下面以A1相a11分支(相对中性点)25%对A2相a21分支25%的定子内部相间短路故障为例(即图3中u11抽头与x11抽头发生短路),进行实验和相应的仿真计算。实验中发电机转速保持额定同步速1 500r/min,负载为阻性负载Rdc=1.14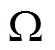 。本文进行了金属性短路实验,考虑到线路电阻以及短路开关的接触电阻,仿真计算时短接线元件的电阻设置为rk=0.04
。本文进行了金属性短路实验,考虑到线路电阻以及短路开关的接触电阻,仿真计算时短接线元件的电阻设置为rk=0.04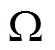 。故障前后整个过渡过程中各电气量的实验波形和对应工况下仿真波形如图4所示。
。故障前后整个过渡过程中各电气量的实验波形和对应工况下仿真波形如图4所示。
表1 六相实验样机主要参数
Tab.1 Main parameters of the model machine

参 数数 值 直流输出额定功率/kW4 直流输出额定电压/V40 直流输出额定电流/A100 额定转速/(r/min)1 500 额定频率/Hz50 极对数2 相数6 每相分支数2
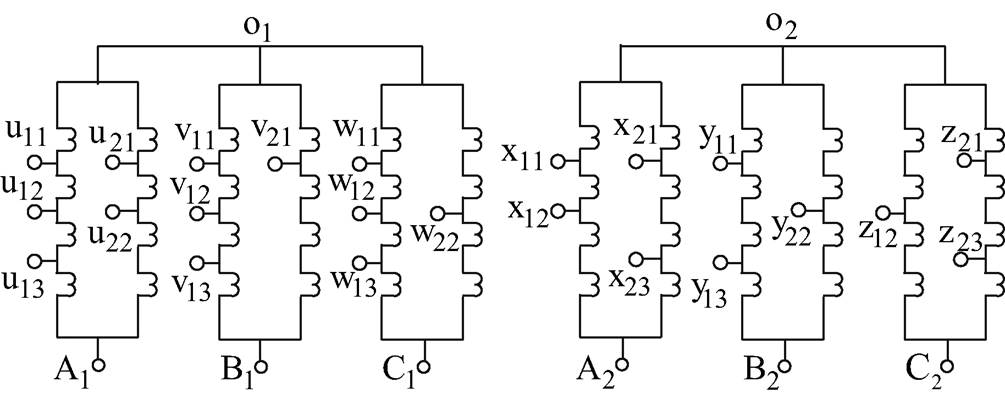
图3 定子绕组内部抽头引出方案示意图
Fig.3 Diagram of the internal taps of the stator windings
六相整流永磁同步发电机系统正常运行时,虽然整流桥开关管的通断状态变化会导致各相电流呈非正弦波形,但理论上其波形完全相同,每组三相(如A1相、B1相和C1相)电流互差120°电角度,两组三相对应相电流(如A1和A2相)互差30°电角度[11],从图4g~图4j中正常运行部分(即t<1.156s)可以看出这一特点。


图4 定子绕组A1相a11分支对A2相a21分支金属性相间短路的过渡过程
Fig.4 Transient waveforms of the metallic short-circuit of a11 branch of A1 phase to a21 branch of A2 phase in the stator windings
从图4中实验波形和仿真波形可以看出,发生相间短路故障后(即t>1.156s),各相(分支)电流发生了明显畸变,各相电流对应二极管的导通时间发生变化,如A1相和B1相导通时间明显增加,C1相导通时间明显减小;短路附加回路中出现了频率为50Hz的故障电流ik,波形呈非正弦状。
通过对比可以看出,各电流、电压实验与仿真波形基本一致。为进一步分析说明,本文对各电流和电压进行谐波分解,限于篇幅,仅给出部分结果,见表2。
表2 定子绕组A1相a11分支对A2相a21分支金属性相间短路故障前后的稳态电压、电流谐波分析
Tab.2 Harmonic analysis of steady-state voltages and currents of model machine before and after the metallic short circuit of a11 branch of A1 phase to a21 branch of A2 phase in the stator winding

各电气量稳态分量有效值故障前(正常负载稳态)故障稳态 计算值实验值误差(%)计算值实验值误差(%) a11分支电流各次谐波/A基波7.787.592.619.479.380.98 3次00.09—4.524.490.71 5次5.345.41-1.292.612.542.65 7次3.743.79-1.263.193.025.77 a12分支电流各次谐波/A基波7.397.43-0.569.569.81-2.59 3次00.08—1.651.69-2.24 5次5.495.450.763.013.14-4.18 7次3.753.75-0.092.862.6010.16 a21分支电流各次谐波/A基波7.017.08-0.934.584.345.44 3次00.07—4.244.42-4.14 5次5.215.32-2.092.932.5315.84 7次3.723.92-5.293.143.072.31 a22分支电流各次谐波/A基波7.757.84-1.166.536.58-0.65 3次00.09—0.750.84-11.55 5次5.435.70-4.714.254.38-3.13 7次3.803.86-1.583.032.991.22 A1相电流各次谐波/A基波15.1814.991.2218.9119.05-0.76 3次00.01—6.076.050.33 5次10.8310.84-0.155.505.441.12 7次7.487.53-0.676.055.598.15 A2相电流各次谐波/A基波14.7614.92-1.0710.9910.821.63 3次00.02—4.855.2-6.72 5次10.6411.02-3.477.166.913.58 7次7.517.78-3.446.156.012.28 短路回路电流各次谐波/A基波00—12.1711.892.33 3次00—15.8515.621.48 5次00—5.595.96-6.19 7次00—2.022.56-20.91 直流输出电压各种交、直流分量/V直流分量43.1244.04-2.0943.8844.88-2.22 2次00.05—0.900.890.50 4次00.02—0.740.689.15 6次00.20—0.790.6817.04 12次1.091.22-10.461.131.26-9.69
(续)

各电气量稳态分量有效值故障前(正常负载稳态)故障稳态 计算值实验值误差(%)计算值实验值误差(%) 直流输出电流各种交、直流分量/A直流分量37.1737.87-1.8637.8338.52-1.78 2次00.06—0.770.6519.25 4次00.03—0.640.4637.54 6次00.36—0.680.81-16.03 12次0.940.931.060.980.970.88
从表2中可以看出,稳态分量的计算误差绝大多数都在15%以内,验证了数学模型的正确性和仿真计算的准确性。其中,故障引起的某些谐波分量、尤其是高次谐波分量,比如故障后直流输出电流的2次和4次谐波分量、短路回路电流的7次谐波等,虽然计算结果的相对误差超过15%,但考虑到这些谐波分量本身比较小或者在相应电气量中所占比例较小,计算结果的绝对误差比较小,总体上不会影响计算结果的准确性。另外可以发现,发生相间短路故障后,相电流和分支电流中出现了正常时没有的3次谐波分量。至于正常工况实验中相电流和分支电流中出现的少量3次谐波,主要由电机制造误差等因素引起,是仿真计算无法考虑的。
从表2中还可以看出,直流输出电压及电流出现了正常时没有的2次等偶数次谐波,这是由于故障后,各相电流不再对称,不像正常运行时直流侧输出12脉波,但是每相电流本身呈现奇对称,所以通过整流以后,将会在直流输出电压及电流中出现2次等偶数次谐波[10]。
在第2节已经验证了本文建立的多回路-有限元数学模型的正确性,用该模型还可以计算得到故障前后电机内部磁场分布如图5所示。从图中可以看出,故障前后电机内部磁场分布变化不大。虽然故障后交流侧电流发生畸变,但是各分支中故障电流的幅值与故障前相当,电枢反应对永磁体产生的影响差别不大。这种发生在连接到不同整流桥的相绕组之间的内部短路故障,由于短路回路经过直流侧负载,负载电阻对短路电流起到了限制作用,使得短路回路电流的幅值不会太大,短路电流对电机内部磁场影响较小,所以故障前后电机内部磁场分布变化不明显。
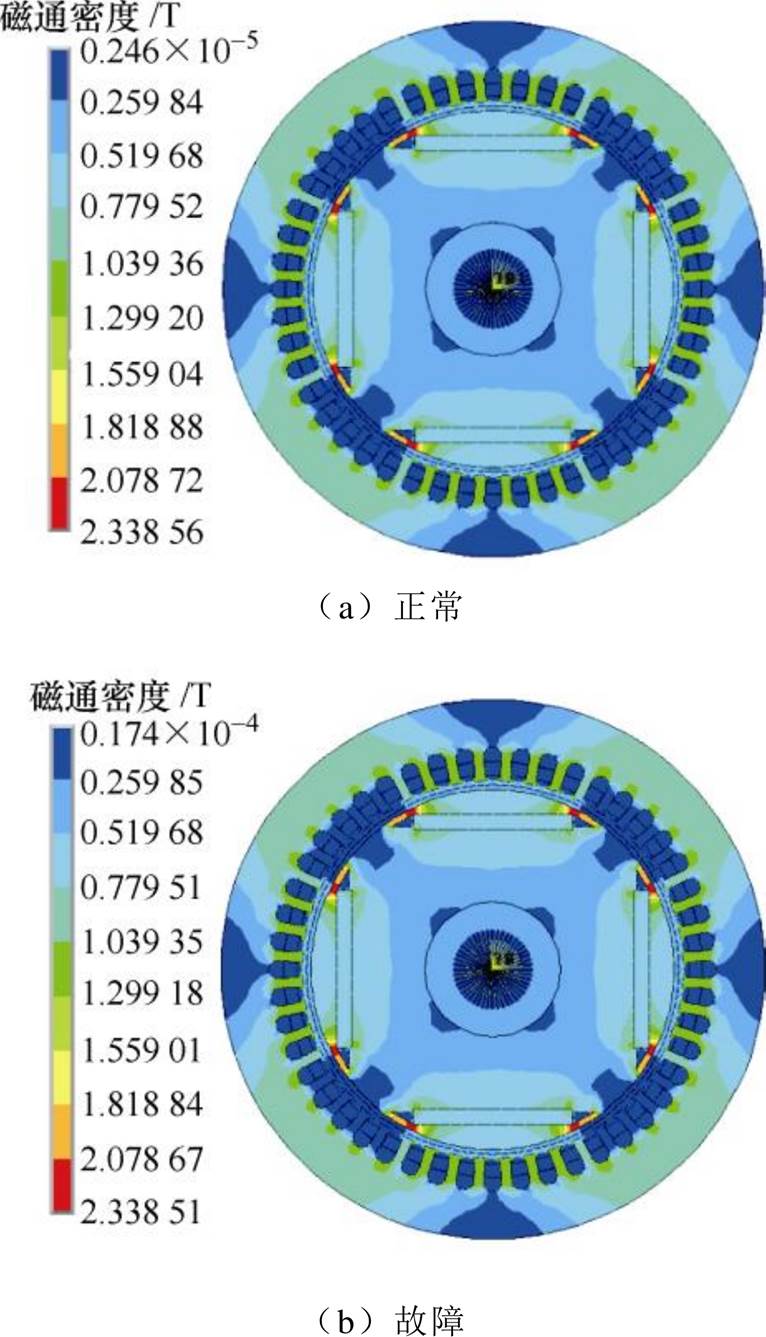
图5 故障前后电机内部磁场分布
Fig.5 Distribution diagram of internal magnetic field of model machine before and after the fault
虽然故障后对电机内部磁场分布影响不大,但由于短路电流经过了整流桥,改变了整流桥的工作模式。如图6a和图6b所示,分别为第1桥6号二极管(即B1相的共阳极管)和第2桥3号二极管(即B2相的共阴极管)电流仿真波形。从图中可以看出,二极管的导通时间都发生了变化。第1桥6号二极管的导通占空比由0.24增加到0.28,电流的有效值由14.36A增加到18.65A;而第2桥3号二极管的导通占空比则由0.24降低到0.14,电流的有效值由14.32A下降到10.83A。可以看出,故障后整流桥的工作方式将会发生很大变化。各二极管流过电流的有效值不同,二极管不同程度发热,将会导致整流桥温度分布不均,局部可能出现过热,从而影响二极管的使用寿命,增加了整流桥发生故障的概率。

图6 故障前后二极管电流的仿真波形
Fig.6 Simulation waveforms of diode current before and after the fault
从图4a看到,这种相间短路故障引起了较大的短路回路电流,并影响到各绕组电流,尤其是故障附加绕组的电流会出现明显畸变,从而使发电机中损耗与温度分布发生变化。为了更直观地显示故障对电机温度场的影响,本文在23℃的初始温度下,通过仿真计算,得到电机分别在正常和相间短路故障情况下,运行相同时间后电机的温度分布如图7所示。从图7中可以看出,电机正常运行时,温度分布均匀,绕组最高温度为55.47℃,电机健康良好运行;而内部相间短路故障发生后,电机温度分布不再均匀,特别是短路回路所在位置的温度升高明显,最高达到72.46℃。同时,其他部分的温度也发生了一定的变化,比如故障附加绕组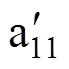 和
和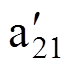 附近(见图7b中左上部分)的定子铁心温度有所上升,而正常绕组b21和b22附近(见图7b中右边和右下部分区域)的绕组和定子铁心温度则有所下降。故障点附近的明显升温,会导致邻近绕组的绝缘进一步恶化,可能造成故障不断扩大,甚至可能导致永磁体失磁或烧毁电机的严重后果,必须尽快停机切除故障。
附近(见图7b中左上部分)的定子铁心温度有所上升,而正常绕组b21和b22附近(见图7b中右边和右下部分区域)的绕组和定子铁心温度则有所下降。故障点附近的明显升温,会导致邻近绕组的绝缘进一步恶化,可能造成故障不断扩大,甚至可能导致永磁体失磁或烧毁电机的严重后果,必须尽快停机切除故障。
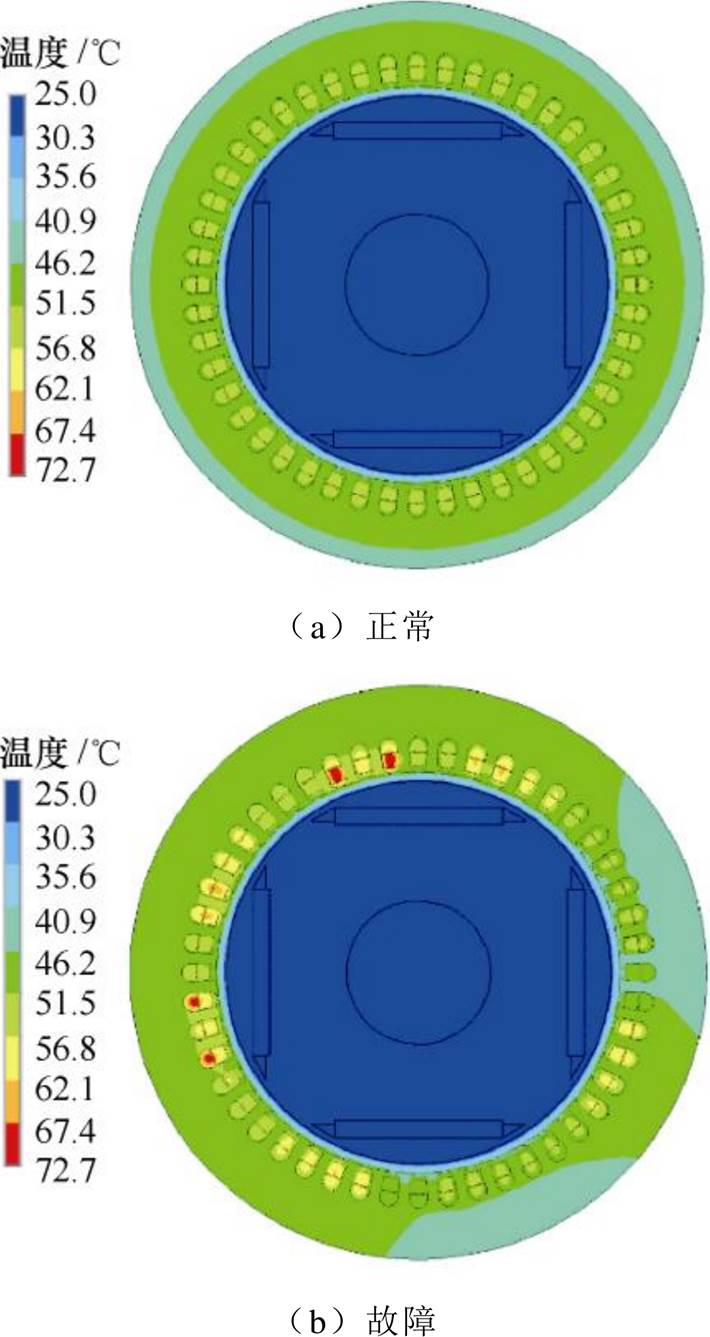
图7 故障前后电机内部温度场分布
Fig.7 Distribution diagram of internal temperature field of model machine before and after the fault
本文将多回路分析法和有限元法相结合,建立了多相整流永磁同步发电机系统相间短路故障的通用数学模型,实现了故障前后交流侧和直流侧各电压、电流的数字仿真。样机实验得到各电气量的实验波形和仿真波形基本一致,验证了数字模型的正确性和仿真计算的准确性。
实验和仿真结果表明,发生相间短路故障后,六相整流永磁同步发电机的相电流和分支电流中会出现正常时没有的3次等谐波分量;短路回路中会出现较大的短路电流,主要包含基波、3次等奇数次谐波;直流侧电压、电流中除正常时存在的12次谐波外,还出现了2次等偶数次谐波,严重影响了供电品质。发生在不同桥间的内部相间短路,会在整流元件中产生过电流,将影响整流桥的使用寿命。同时,故障后电机整体温度会上升且不再均匀分布,特别是短路回路所在绕组,温度明显升高,可能使相间短路故障进一步恶化。所以有必要及时采取监测或保护等措施,保障系统安全、稳定运行。
参考文献
[1] 马伟明. 电力集成技术[J]. 电工技术学报, 2005, 20(1): 16-20.
Ma Weiming. Power system integration technique[J]. Transactions of China Electrotechnical Society, 2005, 20(1): 16-20.
[2] 郑晓钦, 王东. 十五相感应电机对称缺相运行时的定子漏抗计算[J]. 电工技术学报, 2016, 31(15): 26-31.
Zheng Xiaoqin, Wang Dong. Calculation of stator reactance of fifteen-phase induction motor under symmetrical fault condition[J] Transactions of China Electrotechnical Society, 2016, 31(15): 26-31.
[3] 辛鹏, 戈宝军, 陶大军, 等. 多极隐极发电机励磁绕组匝间短路时的定子分支环流谐波特性[J]. 电工技术学报, 2017, 32(7): 67-76.
Xin Peng, Ge Baojun, Tao Dajun, et al. Stator branch circulating current harmonic characteristics of multi- pole non-salient-pole generator with field winding inter-turn short circuits[J] Transactions of China Electrotechnical Society, 2017, 32(7): 67-76.
[4] 孙宇光, 黄子果, 魏锟, 等. 十二相整流同步发电机系统异桥相间短路的故障分析[J]. 中国电机工程学报, 2017, 37(3): 889-897.
Sun Yuguang, Huang Ziguo, Wei Kun, et al. Analysis of stator internal phase-to-phase short circuit between different bridge-rectifiers in the 12-phase synchronous generator with rectifier-load system[J]. Proceedings of the CSEE, 2017, 37(3): 889-897.
[5] 马伟明, 胡安, 王令蓉. 基于电压波形分析的十二相整流装置故障诊断[J]. 电工技术学报, 1997, 12(6): 49-54.
Ma Weiming, Hu An, Wang Lingrong. 12-phase rectifier fault diagnosis based on voltage waveform analysis[J]. Transactions of China Electrotechnical Society, 1997, 12(6): 49-54.
[6] 马伟明, 胡安, 袁立军. 十二相同步发电机整流系统直流侧突然短路的研究[J]. 中国电机工程学报, 1999, 19(3): 31-36.
Ma Weiming, Hu An, Yuan Lijun. Sudden DC-side short circuit of a 12-phase synchronous generator- rectifier system[J]. Proceedings of the CSEE, 1999, 19(3): 31-36.
[7] 马伟明, 郑逢时. 十二相同步发电机突然不对称短路的分析[J]. 清华大学学报: 自然科学版, 1996, 36(9): 42-50.
Ma Weiming, Zheng Fengshi. Transients of sudden unbalance short-circuited fault between different Y-winding[J]. Journal of Tsinghua University: Science & Technology, 1996, 36(9): 42-50.
[8] 吴新振, 张伟玲, 董海涛, 等. 十二相整流发电机二极管开路的故障运行分析[J]. 电工技术学报, 2017, 32(3): 157-163.
Wu Xinzhen, Zhang Weiling, Dong Haitao, et al. Analysis of diode-open fault operation for 12-phase rectifier generators[J]. Transactions of China Electro- technical Society, 2017, 32(3): 157-163.
[9] 张伟玲, 吴新振, 魏锟, 等. 十二相整流发电机缺桥故障运行分析[J]. 中国电机工程学报, 2016, 36(6): 1724-1730.
Zhang Weiling, Wu Xinzhen, Wei Kun, et al. Analysis of bridge-loss fault operation of 12-phase generators with rectifier-load[J]. Proceedings of the CSEE, 2016, 36(6): 1724-1730.
[10] 孙宇光, 黄子果, 陈丽, 等. 十二相整流同步发电机定子匝间短路故障计算[J]. 电工技术学报, 2014, 29(3): 57-64.
Sun Yuguang, Huang Ziguo, Chen Li, et al. Calcu- lation of stator winding inter-turn short circuit in 12-phase synchronous generators with rectifier load system[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 57-64.
[11] 孙宇光, 黄子果, 王善铭, 等. 十二相整流同步发电机同组星形连接绕组的相间短路故障[J]. 电力系统自动化, 2017, 41(8): 153-158.
Sun Yuguang, Huang Ziguo, Wang Shanming, et al. Phase-to-phase short circuit fault between same group of star-connected phase winding in 12-phase synchronous generator with rectifier load system[J]. Automation of Electric Power System, 2017, 41(8): 153-158.
[12] 赵洪森, 戈宝军, 陶大军, 等. 大型核电汽轮发电机定子内部短路故障时局部电磁力分布研究[J]. 电工技术学报, 2018, 33(7): 1497-1507.
Zhao Hongsen, Ge Baojun, Tao Dajun, et al. Local electromagnetic force distribution study on giant nuclear turbo-generators with stator short-circuit fault[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 1497-1507.
[13] 苏晓丹, 纪志成. PMSM定子匝间短路故障建模与仿真研究[C]//中国控制与决策年会, 无锡, 中国, 2007: 615-618.
[14] Vaseghi B, Nahid-Mobarekeh B, Takorabet N, et al. Experimentally validated dynamic fault model for PMSM with stator winding inter-turn fault[C]// Proceedings of IEEE Industry Applications Con- ference, Edmonton, AB, Canada, 2008: 1-5.
[15] Refaat S S, Abu-Rub H, Saad M S, et al. Discri- mination of stator winding turn fault and unbalanced supply voltage in permanent magnet synchronous motor using ANN[C]//Power Engineering, Energy and Electrical Drives (POWERENG), Istanbul, Turkey, 2013: 858-863.
[16] Arellano-Padilla J, Summer M, Gerada C. Winding condition monitoring scheme for a permanent magnet machine using high-frequency injection[J]. Electric Power Applications, 2011, 5(1): 89-99.
[17] 付朝阳, 刘景林, 张晓旭. 双余度永磁无刷直流电机匝间短路故障诊断[J]. 电工技术学报, 2014, 29(1): 104-109.
Fu Zhaoyang, Liu Jinglin, Zhang Xiaoxu. Research on inter-turn short circuit fault diagnosis of dual redundancy permanent magnet brushless DC motor[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 104-109.
[18] 王炳辉. 多相整流永磁同步发电机转子失磁故障的分析与检测[M]. 北京: 清华大学, 2016.
[19] 陈丽. 十二相可控整流永磁同步发电机定子内部短路故障研究[M]. 北京: 清华大学, 2014.
[20] 栾庆伟, 杨怀海, 潘波. 六相脉冲发电机稳态负序能力分析[J]. 防爆电机, 2017, 52(2): 19-22.
Luan Qingwei, Yang Huaihai, Pan Bo. Analysis on steady-state negative-sequence ability of six-phase pulse generator[J]. Explosion-Proof Electric Machine, 2017, 52(2): 19-22.
[21] 高景德, 王祥珩, 李发海. 交流电机及其系统分析 [M]. 2版. 北京: 清华大学出版社, 2005.
[22] 陈丽, 孙宇光, 黄子果, 等. 六相永磁同步发电机整流系统的数学模型[J]. 微特电机, 2015, 43(6): 37-40.
Chen Li, Sun Yuguang, Huang Ziguo, et al. Mathe- matical model of 6-phase high-speed permanent- magnet synchronous generator with controlled rectifier system[J]. Small & Special Electrical Machines, 2015, 43(6): 37-40.
[23] 关治, 陆金普. 数值分析基础[M]. 2版. 北京: 高等教育出版社, 2010.
Analysis of Stator Internal Phase-to-Phase Short-Circuit in the Multiphase Permanent Magnet Synchronous Generator with Rectifier Load System
Abstract Combining the multi-loop method with the finite element method (FEM), this paper established a general mathematical model for the internal phase-to-phase short-circuit in the multiphase permanent magnet synchronous generator (PMSG) with rectifier load system. With this mathematical model, all the voltages and currents of stator windings are calculated under normal operation and internal short-circuit fault conditions. In addition, the model is applicable to both single-branch and multi-branch generators. The fault experiment was carried on a customized 6-phase dual-branch PMSG. The experimental results are consistent with the simulation results, which verifies the correctness of the mathematical model. Based on the accurate calculation of the winding current, the temperature field of the model machine before and after the fault was also calculated. The results show that the fault changes the distribution of the internal temperature field of the model machine. According to the simulation and experimental results, the characteristics of the phase-to-phase short-circuit fault were analyzed. Furthermore, the severe influence of the obvious temperature rise near the short-circuit position on the model machine was analyzed, and the potential hazard of over-current in some rectifier bridges caused by phase-to-phase short-circuit between different groups of three-windings was illustrated. This paper provides the basis for the detection of phase-to-phase short-circuit faults in multiphase PMSG.
keywords:Multiphase permanent magnet synchronous generator, multi-branch, rectifier load system, phase-to-phase short-circuit, multi-loop and finite element method mathematic model
中图分类号:TM341
DOI: 10.19595/j.cnki.1000-6753.tces.181920
国家自然科学基金资助项目(51277103)。
收稿日期2018-12-18
改稿日期 2019-04-08
田代宗 男,1990年生,硕士研究生,研究方向为多相永磁电机系统内部故障分析。E-mail: 1067237823@qq.com
王善铭 男,1972年生,教授,研究方向为特殊电机设计分析、发电机内部故障分析和电机电磁场分析。E-mail: wangsm96@mails.tsinghua.edu.cn(通信作者)
(编辑 赵 鹏)