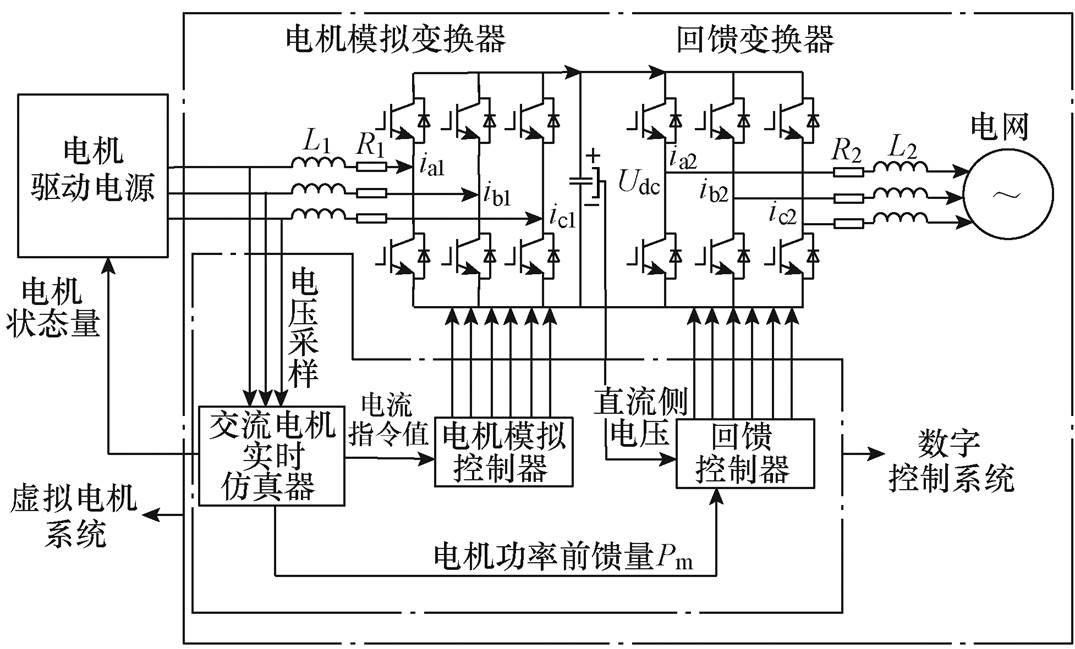
图1 基于虚拟电机的电机系统测试平台示意图
Fig.1 Schematic diagram of motor system test platform based on virtual motor
摘要 因交流传动在现代工业中应用广泛,针对电机驱动电源的性能测试备受重视。基于此,该文提出一种利用背靠背变换器代替交流电机及其机械负载的虚拟电机系统设计方案。针对交流电机运行工况复杂,需考虑暂态过程和故障状态,数学建模和端口特性实时模拟存在困难等实际问题,该文建立考虑定子绕组故障的异步电机模型,通过方案对比选取了四阶龙格库塔数值求解法。电机电流跟踪控制则选用准比例谐振控制器,在考虑数字控制延时的前提下,以提高控制器带宽和动态响应能力为目标完成控制参数优化设计。仿真和实验表明,该虚拟电机系统可以准确模拟异步电机在正常状态以及定子绕组匝间故障状态下的端口特性,即可作为交流电子负载用于电机驱动电源的开发与测试。
关键词:虚拟电机 异步电机 匝间短路 准比例谐振控制器
交流电机作为一种常见的电力传动设备,在工业生产、国防科技以及航空航天等领域[1]中应用广泛。其中异步电机由于拥有结构简单可靠、制造维护方便和工作性能良好等优势一直受到研究者的亲睐,同时电机本体以及电机驱动电源的开发一直是学界和工业界非常关注的学科领域[2]。
在开发电机驱动电源时需要对其进行大量测试,传统的测试平台是利用电动机和同轴发电机形成的对拖平台。在实际工程应用中,部分特殊类型电机本体设计开发周期长,严重影响了电机驱动电源的测试开发进度。同时,传统测试平台成本高、电能浪费严重、电机参数无法灵活调节[3]。在开发电机容错算法或者设计电机故障保护措施时,还需要对电机进行破坏性试验,操作不便。
由于对电机驱动电源的开发和测试主要关注的是电机端口电压电流特性,如果可以使用交流电子负载模拟电机端口特性,将会为电机驱动电源的研发和测试带来便利。
利用交流电子负载代替实际电机的“虚拟电机”技术一直受到研究者的重视。文献[4-5]最早提出了“虚拟电机”的概念,并介绍了基本框架结构以及实现“虚拟电机”的基本思路。文献[6]采用了基于遗传算法的PID控制器提高电流控制的精度,但是对电机模型的数值计算问题未详细讨论。文献[7]采用滞环电流控制策略对整流器进行控制,逆变器则使用幅相控制,并利用Matlab/Simulink对异步电动机及其负载特性模拟进行仿真分析,但未进行实验验证。文献[3, 8-9]讨论了异步电机数学模型的数值计算方法,使用比例积分控制器、比例谐振控制器以及无差拍控制器对电机模拟变换器进行控制,并进行仿真和实验验证,但未考虑到端口电压变化和电机故障等复杂工况。文献[10]使用了双星斩波单元变换器搭建虚拟电机系统,提高了虚拟电机模拟电机端口特性的能力,但依然未考虑电机故障状态。文献[11]内容涉及到了电机故障状态,但是模型比较复杂,且未详细讨论具体的数值求解方法。
基于现有研究成果,本文首先介绍了“虚拟电机”系统的基本原理,然后在对异步电机进行数学建模时,考虑到定子绕组匝间短路故障这一复杂工况,讨论了数学模型在常用数字信号处理器(Digital Singnal Processor, DSP)中的实时数值计算问题。电机模拟变换器选择了基于内模原理的准比例谐振控制器(Quasi Proportional Resonant, QPR)控制策略[12],并且在考虑数字控制延时的前提下,以提高控制器带宽和动态响应能力为目标进行参数优化设计,从而实现对不平衡以及动态电流指令的快速跟踪。
对于电机驱动电源而言,如果三相交流电子负载可以准确模拟电机端口电压电流特性,则可以称之为虚拟电机系统[3]。
基于虚拟电机的电机系统测试平台示意图如图1所示,虚拟电机系统由功率电路和数字控制系统组成。功率电路包括电机模拟变换器和回馈变换器。电机模拟变换器实时模拟电机端口特性,回馈变换器将电能快速高效地回馈至电网,同时维持直流侧电压的稳定。

图1 基于虚拟电机的电机系统测试平台示意图
Fig.1 Schematic diagram of motor system test platform based on virtual motor
数字控制系统包括交流电机实时仿真器、电机模拟控制器和回馈控制器。交流电机实时仿真器采集电机驱动电源输出侧的电压值,并计算出电流指令。电机模拟控制器对电机模拟变换器进行实时控制,使得电机模拟变换器输入侧电流ia1、ib1、ic1快速且准确地跟踪电流指令;回馈控制器则需控制回馈变换器,实现能量回馈,ia2、ib2、ic2为馈网电流。
电机状态量(电机转速、电磁转矩)可以由交流电机实时仿真器计算得出。
实现“虚拟电机”的前提是实时获取实际异步电机的端口电压电流特性。异步电机故障种类繁多,主要包括定子故障、转子故障、气隙偏心故障和轴承故障,其中定子故障最为常见[13],故本节在对异步电机进行数学建模时将定子绕组匝间短路故障纳入考虑范畴。
在对考虑定子故障的异步电机进行数学建模时,应兼顾准确性和简易性。异步电机在abc静止坐标系下的数学模型变量之间耦合严重,旋转坐标系下的数学模型[14]则需要考虑转子位置角的计算。因此在ab 轴坐标系下对电机进行数学建模较为恰当。
考虑定子绕组故障的异步电机示意图如图2所示。图2中,异步电机定子侧A相绕组发生匝间短路故障,相绕组的总匝数为Ns,匝间短路的故障程度为m,即有mNs匝绕组发生短路故障,当m =0时,该异步电机未发生故障,借此可将故障模型和无故障模型做统一化处理。
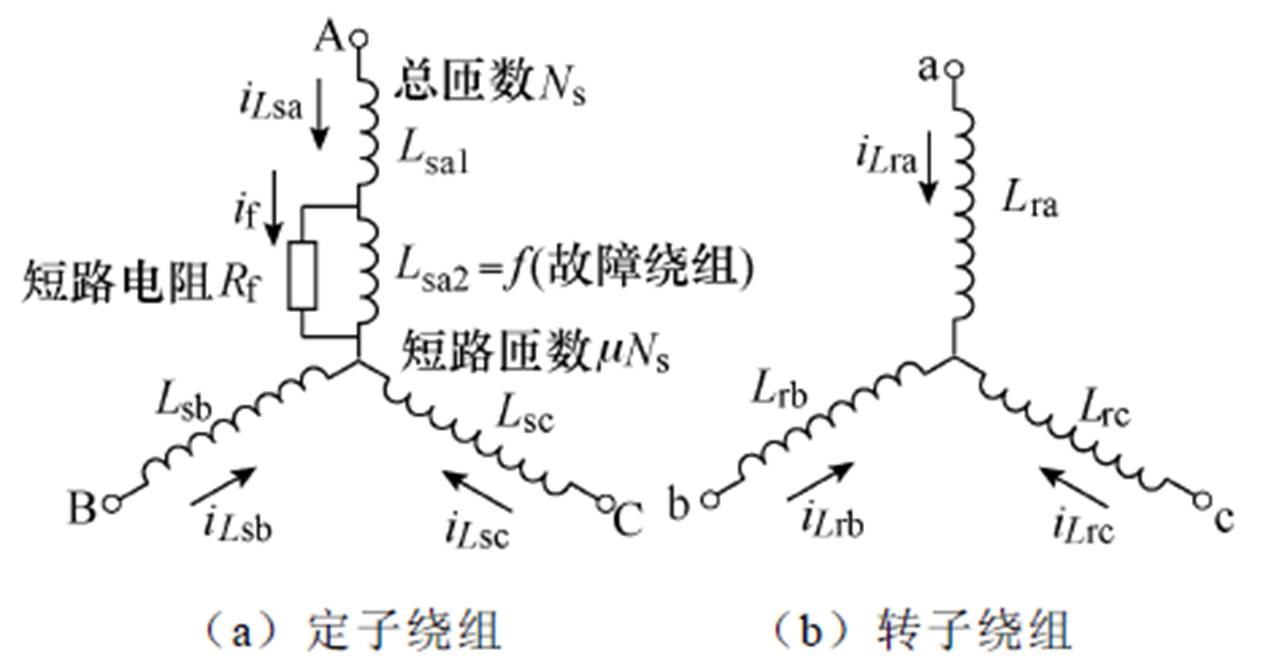
图2 考虑定子绕组故障的异步电机示意图
Fig.2 Schematic diagram of asynchronous motor considering stator winding failure
在ab 轴坐标系下建立考虑定子故障的异步电机数学模型[15]为
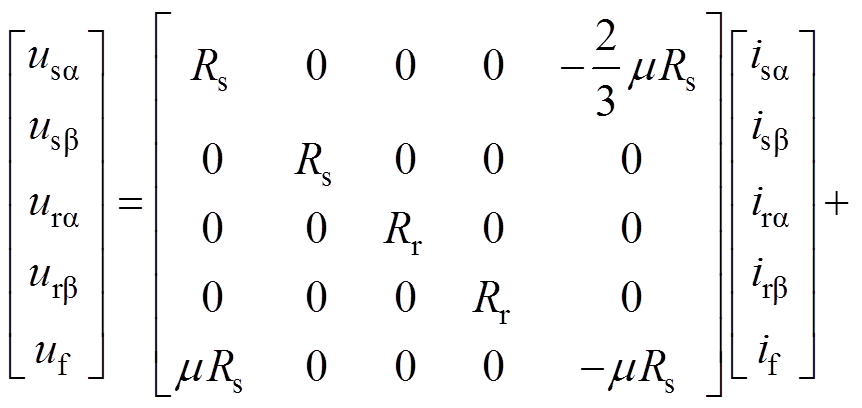
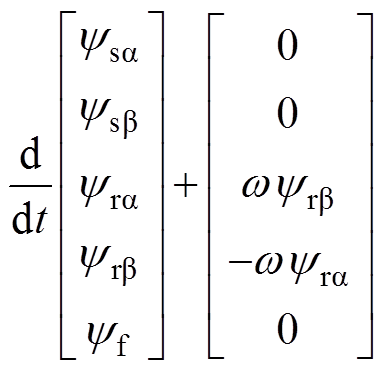 (1)
(1)
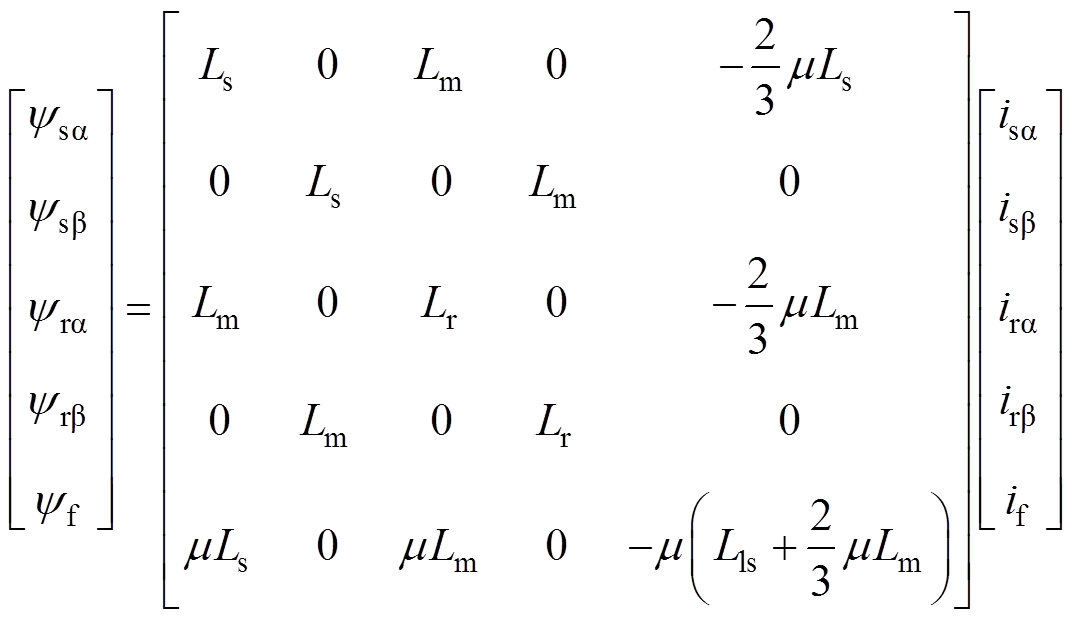 (2)
(2)
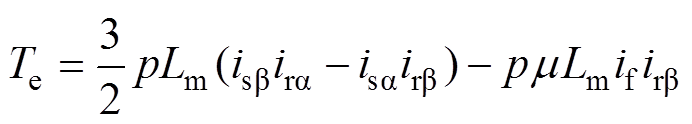 (3)
(3)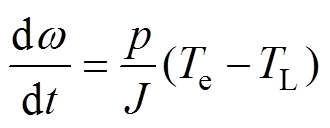 (4)
(4)
式中,usa、usb,isa、isb和ysa、ysb 为异步电机定子侧在ab 轴下的电压、电流和磁链;ura、urb,ira、irb和yra、yrb 为异步电机转子侧在ab 轴下的电压、电流和磁链;Rs为定子电阻;Rr为转子电阻;w 为电机的电角速度;Ls为定子绕组自感;Lm为定转子绕组互感;Lls为定子漏电感;Lr为转子绕组自感;yf和if为故障绕组的磁链以及短路电流;Te为电磁转矩;TL为负载转矩;p为极对数;J为转动惯量。
为方便实时数值计算,选择ysa、ysb、yra、yrb、yf和w 为状态变量,求取状态方程。
当m =0时,求得无故障异步电机的5阶动态数学模型为
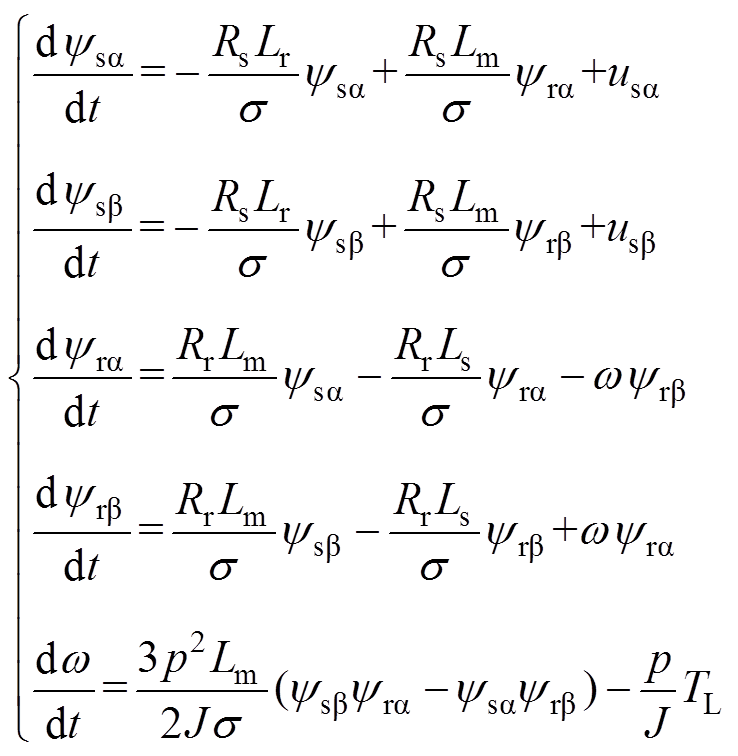 (5)
(5)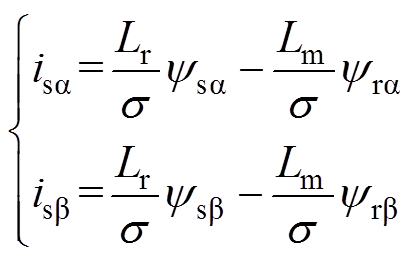 (6)
(6)
当m ¹0时,求得发生定子故障的异步电机6阶数学模型为
 (7)
(7)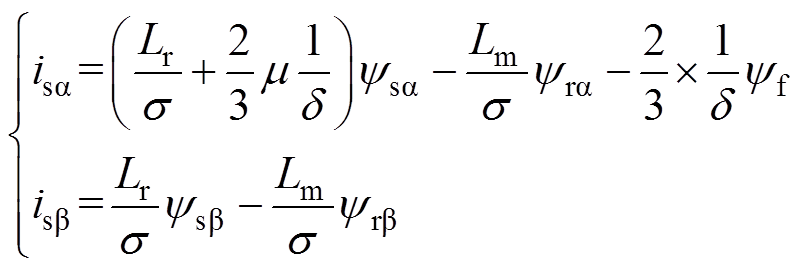 (8)
(8)
其中
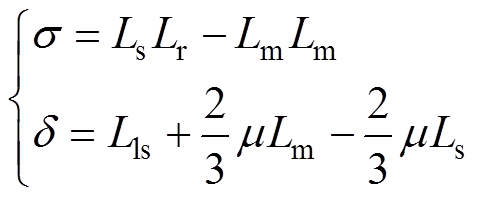 (9)
(9)根据式(5)~式(9)可以实现对考虑定子故障的异步电机数学模型的求解。
数值计算方法是交流电机仿真的关键技术之一。速度、精度、稳定性、能否自起动以及是否选择定步长是数值计算方法选取的基本准则[16]。
虚拟电机数字控制系统的核心是一块TMS320F28335芯片,用以实现交流电机实时仿真和相关控制算法。考虑到计算资源的限制以及变步长算法实现的难 度[17],选择定步长算法。
数值计算稳定性与该计算方法的收敛域有关,可以利用状态方程的特征根进行分析[8]。
由于显式欧拉法计算精度偏低,两步阿达姆斯法和四阶龙格库塔法成为交流电机实时数值计算的备选方案,这两种算法都可以自起动。
2.2.1 两步阿达姆斯法求解电机数学模型
两步阿达姆斯法的基本计算公式[16]为
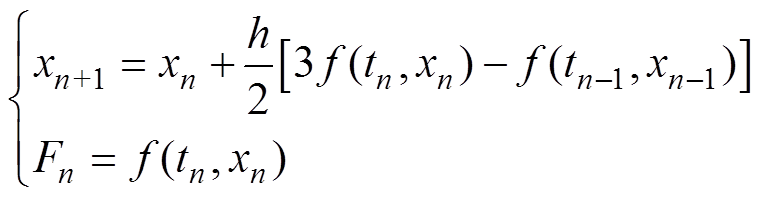 (10)
(10)多步法的优势在于可以利用已经求解出的函数值来计算新的函数值,提高数值计算的精度和数据的利用率。
2.2.2 四阶龙格库塔法求解电机数学模型
龙格库塔法是一种高精度的单步法,基本实现思路是在区间[x(n), x(n+1)]内多取几个点,将它们的斜率进行加权平均,作为导数的近似。算法[16]为
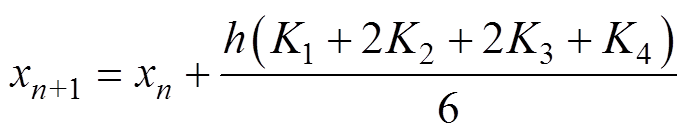 (11)
(11)其中
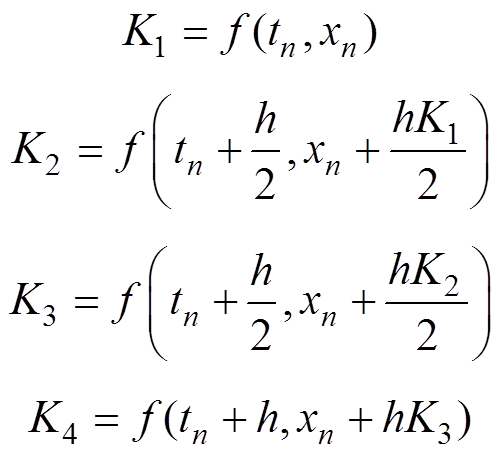
2.2.3 两种数值计算方法对比分析
选择一台220V/50Hz异步电机作为研究对象,电机参数见表1。
表1 电机参数
Tab.1 Motor parameters
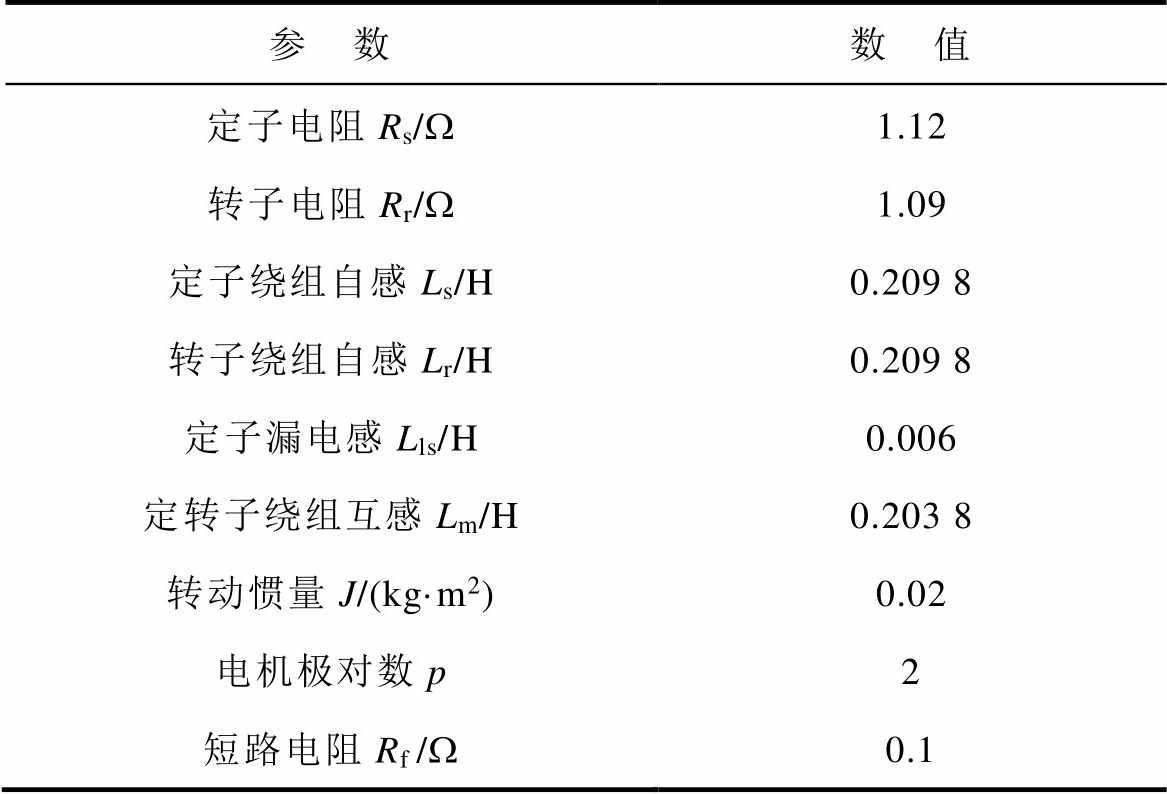
参 数数 值 定子电阻Rs/W1.12 转子电阻Rr/W1.09 定子绕组自感Ls/H0.209 8 转子绕组自感Lr/H0.209 8 定子漏电感Lls/H0.006 定转子绕组互感Lm/H0.203 8 转动惯量J/(kg·m2)0.02 电机极对数p2 短路电阻Rf/W0.1
分别利用式(10)、式(11)对式(5)~式(8)中的电机状态方程进行离散化处理。选择50Hz正弦电压为电机驱动电源,为了与硬件实验条件吻合,仿真计算时,端口电压有效值在1s内由0V调压至110V后稳定不变,虚拟电机驱动电压波形如图3所示。
利用Matlab/Simulink软件的s-function函数对电机模型进行离散域数值计算,并同连续模型进行对比。异步电机首先在无故障状态下空载调压起动,1.1s时刻负载转矩增加至12N·m,1.25s时刻,电机A相绕组发生故障程度为4%的匝间短路故障。仿真结果如图4所示。当交流电机实时仿真器计算步长为100ms时,四阶龙格库塔法和二阶阿达姆斯法对电机电流的仿真结果都十分接近连续模型的仿真结果,二者差异不明显。但是四阶龙格库塔对电机转速的仿真结果更接近连续模型,因此优先考虑四阶龙格库塔法。
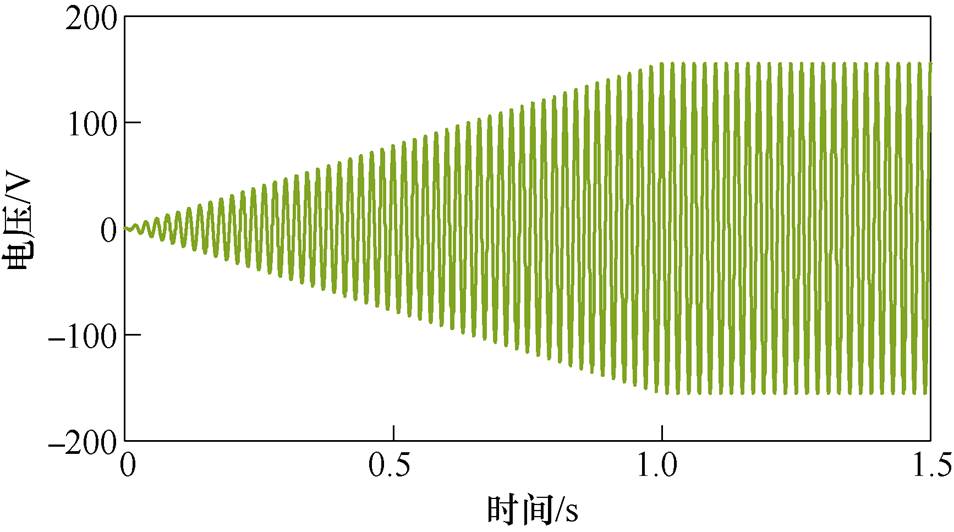
图3 虚拟电机驱动电压波形
Fig.3 Driving voltage waveform of virtual motor
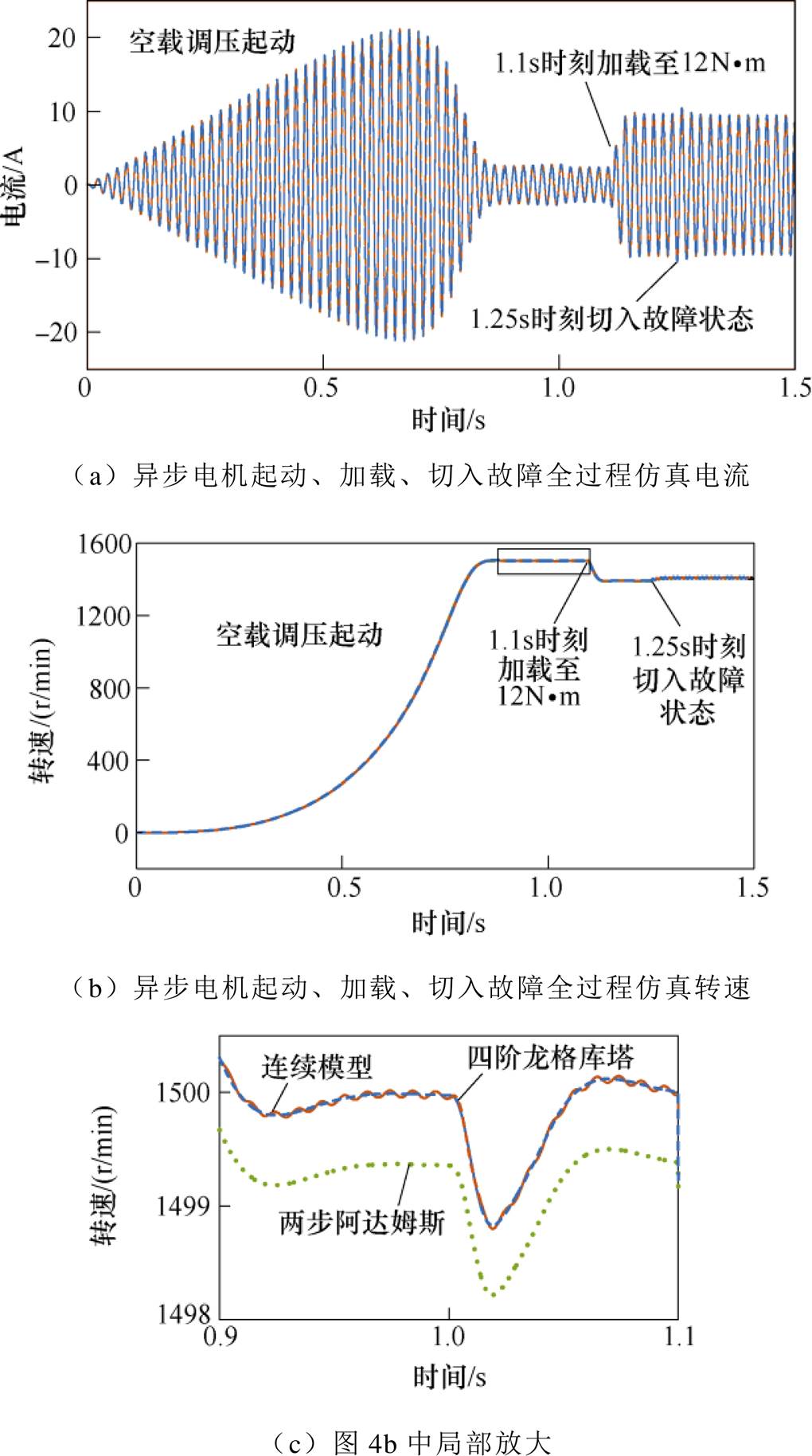
图4 步长为100ms时实时仿真器仿真结果
Fig.4 Real-time simulator calculation results with a step size of 100ms
评估数字芯片TMS320F28335对电机模型的实时计算能力时,利用CCS上位机软件的断点功能测试代码的运行时钟数即可获取代码运行时间。虚拟电机系统各功能模块运行时间见表2。
表2 虚拟电机系统各功能模块运行时间
Tab.2 Running time of virtual motor system function module
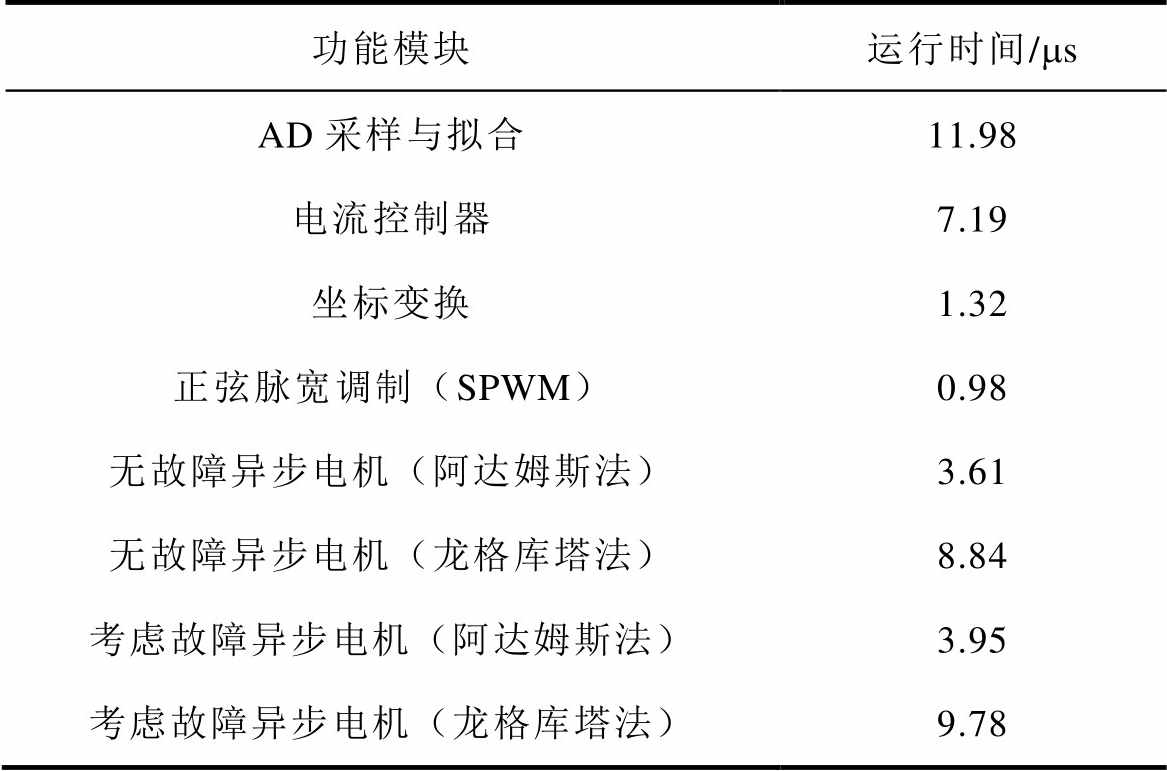
功能模块运行时间/ms AD采样与拟合11.98 电流控制器7.19 坐标变换1.32 正弦脉宽调制(SPWM)0.98 无故障异步电机(阿达姆斯法)3.61 无故障异步电机(龙格库塔法)8.84 考虑故障异步电机(阿达姆斯法)3.95 考虑故障异步电机(龙格库塔法)9.78
四阶龙格库塔法代码的运行时间略长于两步阿达姆斯法,但仍可在10ms内计算完毕,所以当计算步长选择为100ms时,TMS320F28335可以满足实时仿真的需要。
综合以上分析,选择四阶龙格库塔法代替传统的两步阿达姆斯法作为交流电机的数值计算方法。
电机模拟变换器工作性能的优劣主要取决于直流侧的稳压性能以及电机模拟控制器的电流跟踪能力。变换器参数见表3。
表3 变换器参数
Tab.3 Parameters of PWM converter

参 数数 值 变换器交流侧滤波电感L1, L2/mH2.5 变换器交流侧寄生电阻R1, R2/W0.1 直流母线电容C/mF2 200 PWM开关频率/kHz10 交流侧电压有效值/V110 直流侧电压/V400
电机起动和负载切换过程中,电流信号的幅值和频率处于快速变化中,谐波含量丰富。电机出现定子绕组匝间短路故障时,三相电流不对称。dq旋转坐标系下电流指令含2次谐波分量,比例积分控制器难以实现无差跟踪。故三相可独立控制的QPR成为电机模拟控制器首选。
电机模拟变换器控制系统结构如图5所示。图5中,Gc(s)为QPR,Kpwm为变换器等效增益,GL(s)为进线电感的数学模型。电机驱动电源的频率往往是不确定的,所以需要利用锁相环(Phase Locked Loop, PLL)获取电源频率,供控制器参数设计所用。
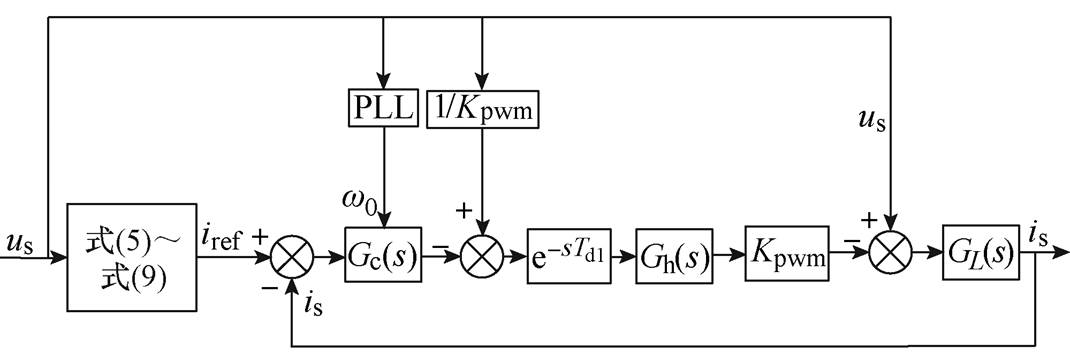
图5 电机模拟变换器控制系统结构
Fig.5 Structure diagram of motor simulation converter control system
为了更接近实际数字控制的运行状态,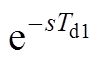 将用来表征AD采样、交流电机实时仿真器和电流控制算法的计算延时[18],Gh(s)为PWM的零阶保持延时[19],此处将其表示为
将用来表征AD采样、交流电机实时仿真器和电流控制算法的计算延时[18],Gh(s)为PWM的零阶保持延时[19],此处将其表示为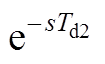 ,具体数学模型为
,具体数学模型为
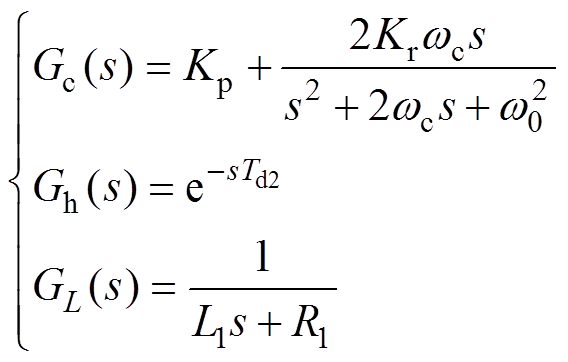 (12)
(12)式中,Kp为比例系数;wc为截止频率;w0为谐振频率;Kr为谐振系数[20]。
数字控制系统的延时说明如图6所示,Ts为PWM波的开关周期,DSP的ePWM模块使用增减计数模式,在计数寄存器的值为0时(即A点)触发ADC中断,Td1为采样计算延迟时间,当Td1>Ts时,控制系统不稳定。DSP工作在影子装载模式时,新求出的占空比不会立刻写入比较寄存器中,而是等待特定的装载条件。当装载条件为计数寄存器等于0(即C点)时,占空比实现更新,如图6a所示,此时零阶保持延时为Td2,数字控制系统的总延时Td=Td1+Td2=Ts。若装载条件为计数寄存器的值最大,那么当Td1<0.5Ts时,总延时Td=0.5Ts,如图6b所示;当0.5Ts<Td1<Ts时,总延时Td=1.5Ts,如图6c所示。为考虑最恶劣工况,本文将基于最长延时1.5Ts进行分析。
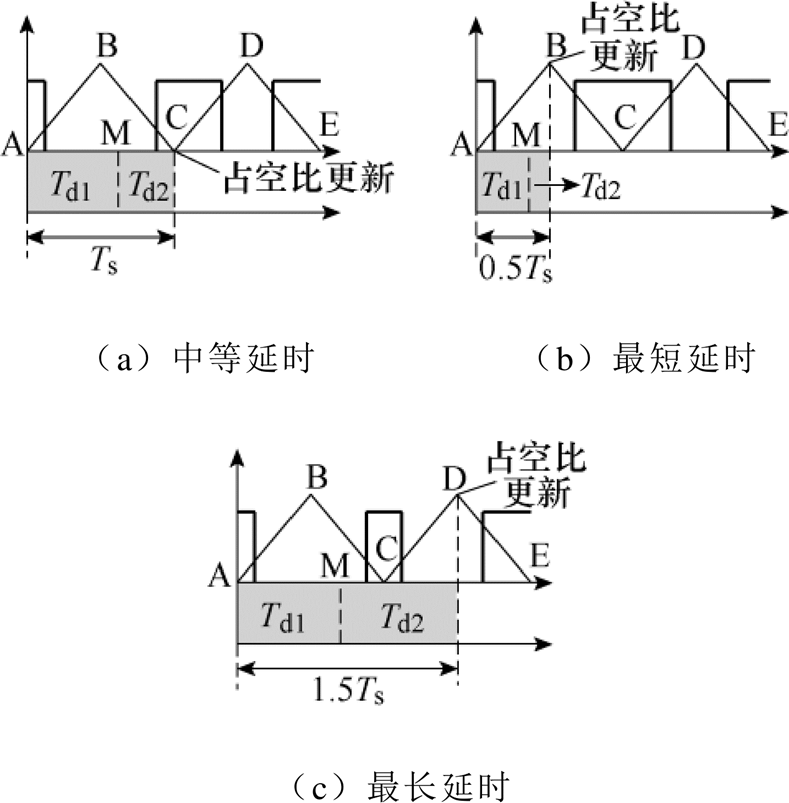
图6 数字控制系统的延时说明
Fig.6 Delay description of digital control system
实验中电机驱动电源频率为50Hz,w0=100p。首先对异步电机调压起动以及负载切换过程中的电机端口电流进行频谱分析。
异步电机起动以及负载切换电流频谱如图7所示。起动电流频谱集中在30~70Hz之间,其他频率段谐波电流幅值已下降至0.02A以下;负载切换时,从直流分量到150Hz段的电流频谱分量都不容忽视。所以电机实时模拟要求电流控制器能够提供足够的带宽以及尽可能高的动态响应能力。
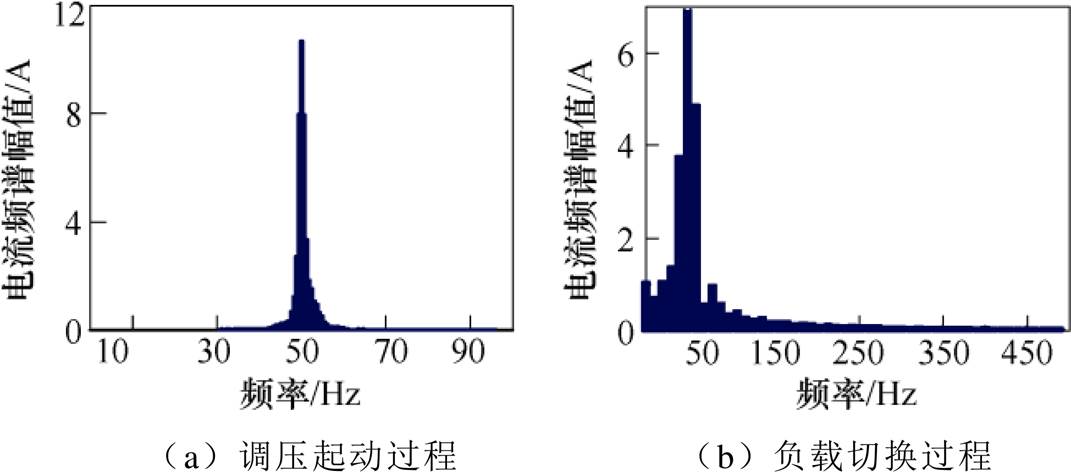
图7 异步电机起动以及负载切换电流频谱
Fig.7 Asynchronous motor start-up and load mutation current spectrum
QPR的谐振项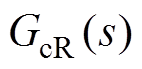 在谐振频率处有一个比较大的增益,Kr需保证系统在该频率处的开环增益在50~60dB之间,即
在谐振频率处有一个比较大的增益,Kr需保证系统在该频率处的开环增益在50~60dB之间,即
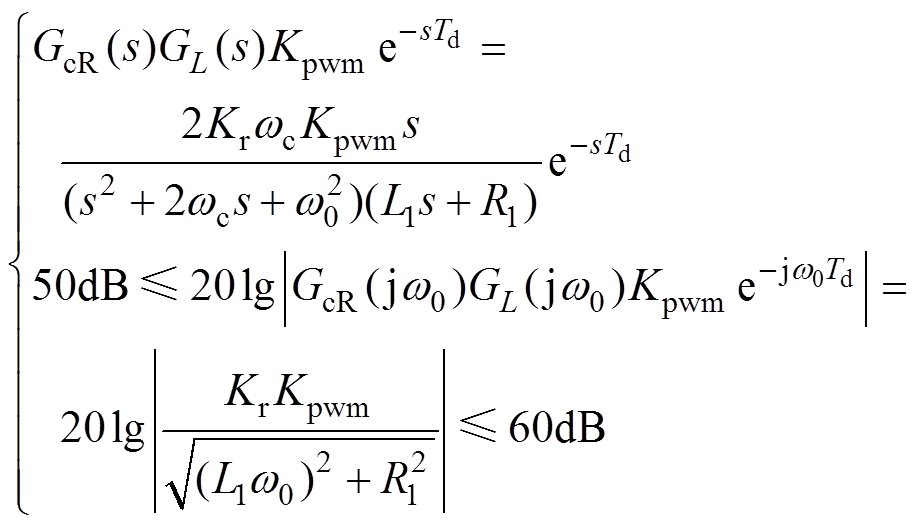 (13)
(13)根据式(13)计算得到Kr的取值范围为
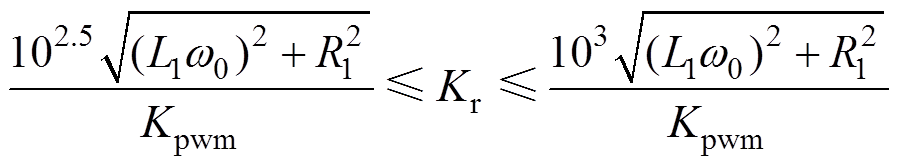 (14)
(14)
谐振项提供的带宽Dw =2wc,而wc的取值范围一般是p~10,因此谐振项难以提供足够的带宽。
比例系数Kp可以提高系统动态响应能力[21],扩展系统带宽。因此设计目标为在保障系统稳定的前提下尽可能增大Kp值。电流环开环传递函数为
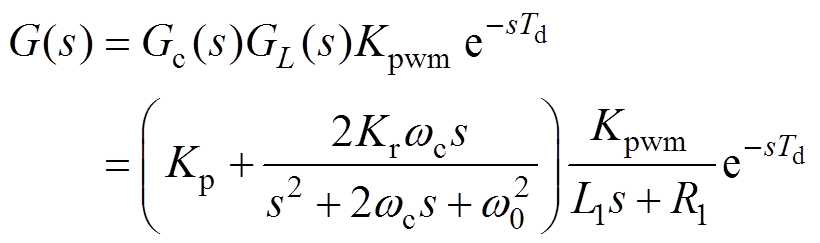 (15)
(15)wc取8,谐振系数Kr可以由式(14)获取。为了得到Kp的取值范围,将式(15)做进一步处理为
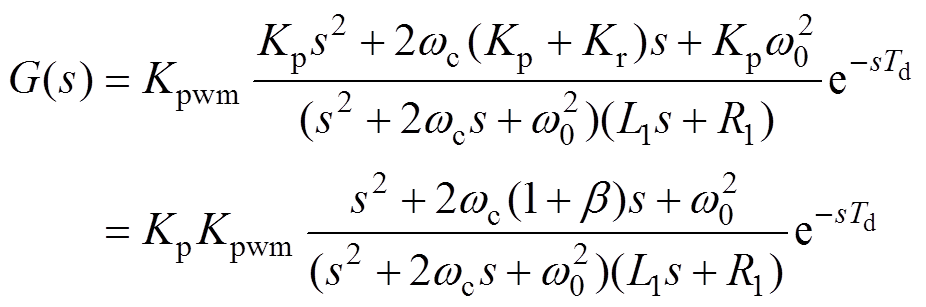 (16)
(16)
其中
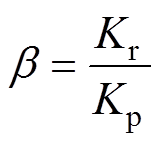
结合表3中的参数,Kpwm=200。当b 取不同的值时,求得当Kp变化时,整个闭环控制系统的根轨迹簇如图8所示。
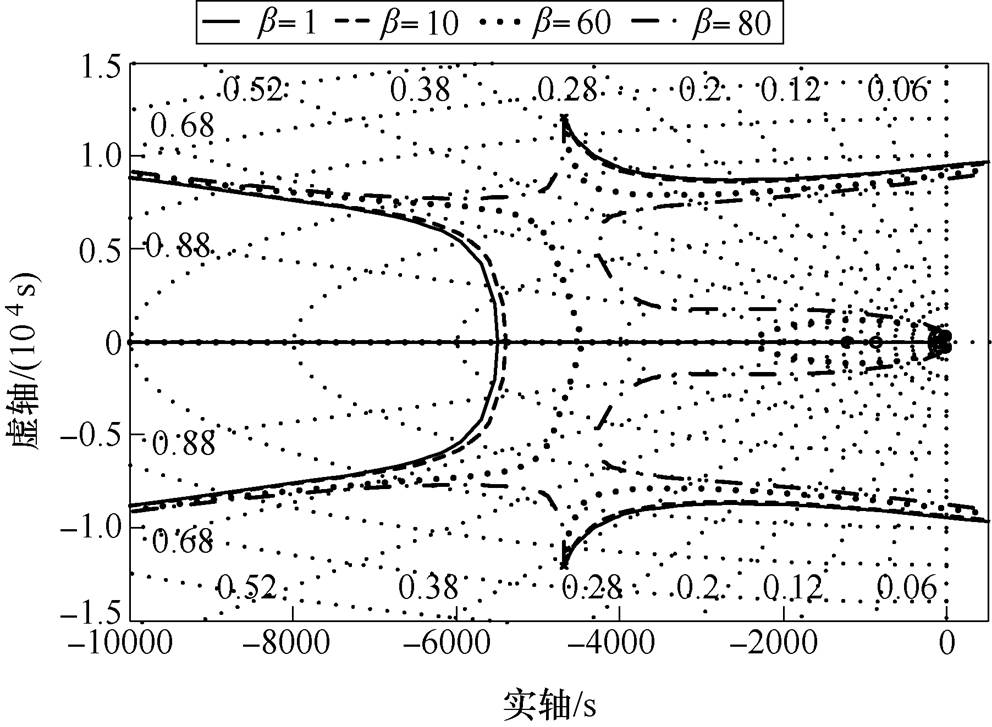
图8 闭环控制系统的根轨迹簇
Fig.8 Root track cluster of closed-loop control system
为了满足带宽要求,带宽初步设计目标在1 000Hz左右,参数设计应当在实轴数值-6 000左右进行;当b <10时,根轨迹基本不变,而且b 取得过小时,可能因为Kp过大导致系统失稳;当 b >60时,根轨迹与负实轴无绝对值较大的交点,参数设计范围不够,且b 取得过大时,可能因为Kp过小导致系统带宽不足。综合上述分析,b 的初步取值范围是[10, 60]。
为了在最大化Kp的同时保证系统有足够的相位裕度,对式(15)进一步处理可以得到
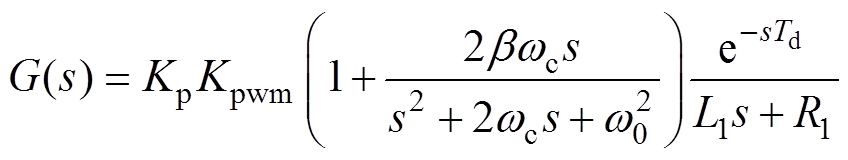 (17)
(17)开环系统的剪切频率wx与闭环系统的带宽具有同向性,wx越大,闭环系统带宽越高。且wx远大于wc和w0,将其代入式(17),可以推导出
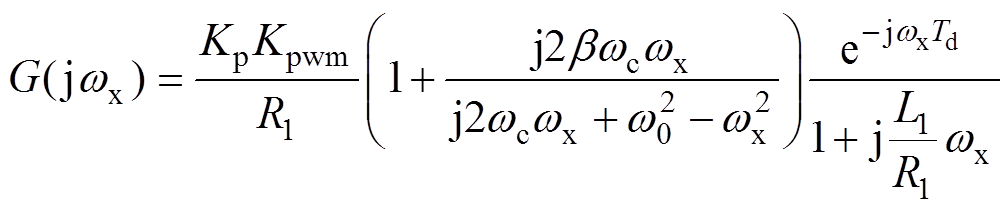
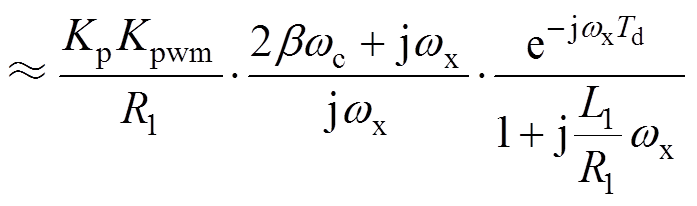 (18)
(18)考虑到进线电感上的电阻可以忽略,根据式(18)求得开环传递函数的幅频表达式为
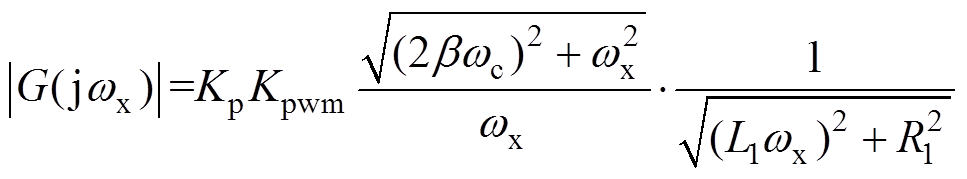
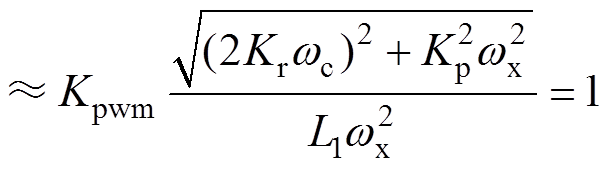 (19)
(19)根据式(19)可以得到剪切频率wx的表达式为
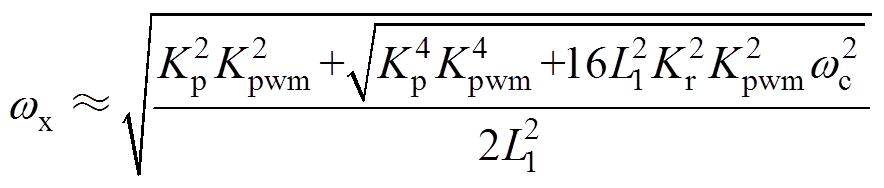 (20)
(20)
式(20)表明wx与Kp呈正相关。
同样根据式(18)求得开环传递函数的相频表达式为
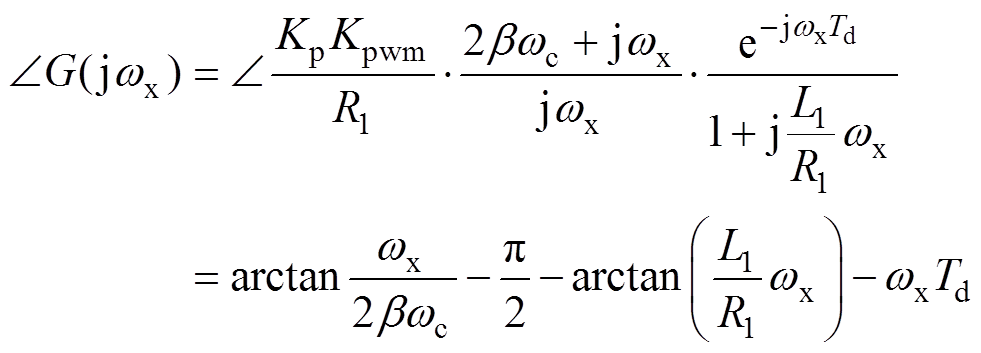
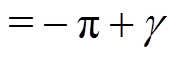 (21)
(21)
由于R1数值较小,所以系统的相位裕度g 为
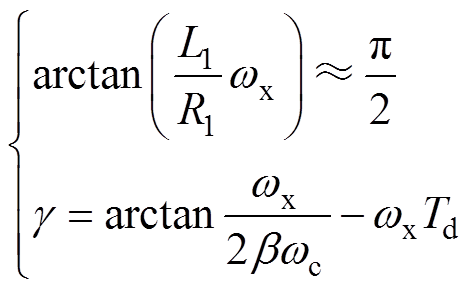 (22)
(22)为了维持系统稳定,一般将相位裕度设计在 30°~60°之间。设计目标为开环剪切频率最大,对式(22)进一步处理[21]得到
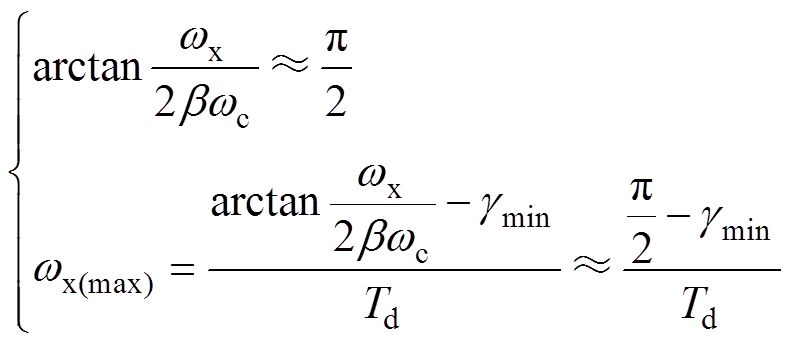 (23)
(23)
将式(23)代入式(19)可以求得Kp的理论优化值为
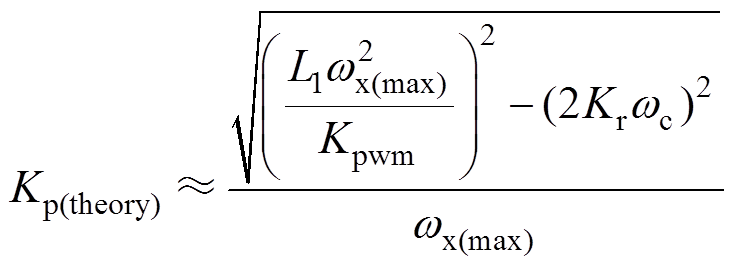 (24)
(24)由于上述推导过程中做了大量近似和简化,式(24)中的Kp的理论优化值还需要结合伯德图做进一步调整。
结合式(14),求得谐振系数Kr的取值范围是[1.25, 3.96],取Kr=3。根据根轨迹的分析结果,Kp的初步取值范围是[0.05, 0.3]。根据式(24),最小相位裕度gmin取30°,Kp的理论优化值为0.087,在上述取值范围之内。
图9为改变比例系数Kp时,电流环开环传递函数的伯德图,Kp的改变对谐振频率处增益影响不明显,证明了该点增益由Kr决定。当Kp=0.3时,剪切频率高达3.82kHz,但是相位裕度为负,系统不稳定。当Kp取理论优化值0.087时,相位裕度为 25.8°,还需要进行调整。当Kp减小至0.078时,剪切频率达到998Hz,相位裕度为30.8°,略大于30°,为最佳设计状态。若继续减小Kp,系统可以保持稳定,但是剪切频率明显降低。式(24)中的比例系数理论优化值虽然不是最佳,但是仍然能够为参数设计提供有力依据。
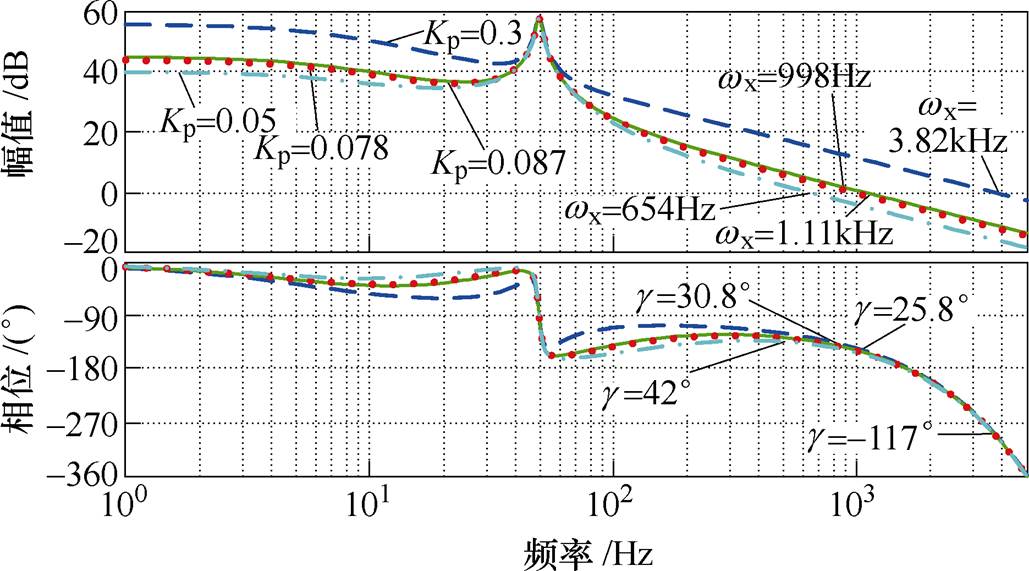
图9 比例系数对带宽和稳定性的影响
Fig.9 The effect of Kp on bandwidth and stability
综上所述,比例系数Kp将选定为0.078。由于本系统中闭环带宽高于开环剪切频率,该闭环系统为电流指令跟踪提供的带宽将高于998Hz,系统动态响应快,满足电机模拟需求。
上述分析是基于数字控制系统延时Td=1.5Ts的,但是Td的取值并不是固定的,接下来将分析延迟时间对系统性能的影响。改变延迟时间,延迟时间对稳定性的影响如图10所示。
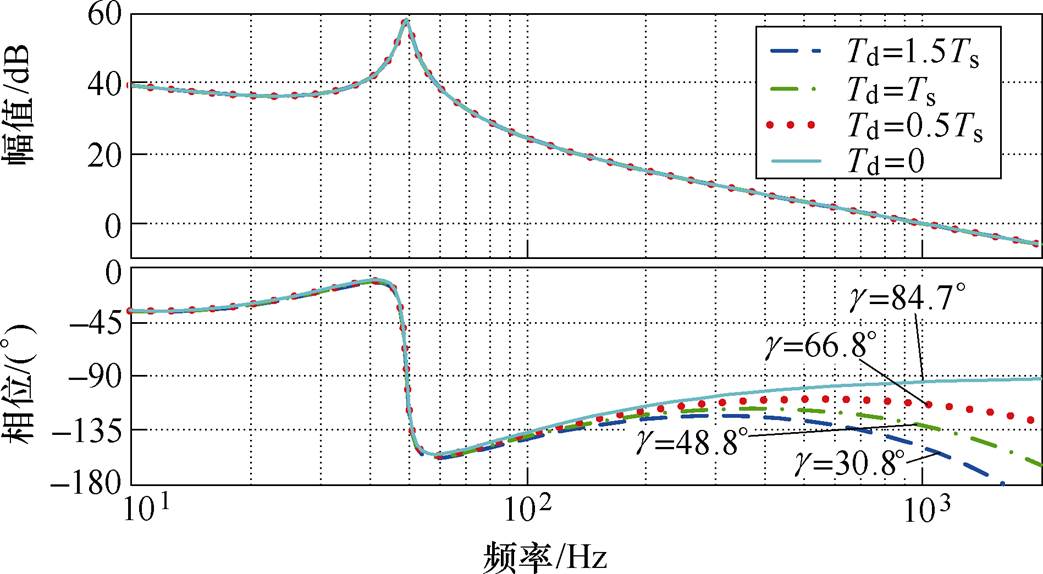
图10 延迟时间对稳定性的影响
Fig.10 The effect of Td on stability
数字控制延时的大小虽然对开环系统的幅频特性没有影响,但是对相频特性作用明显。Td越大,系统相位裕度越小,系统稳定性越差,所以减少数字控制的延时时间将有利于系统稳定性的提高,同时也为扩展控制器带宽提供更大裕度。
电机模拟变换器控制系统框图如图11所示。
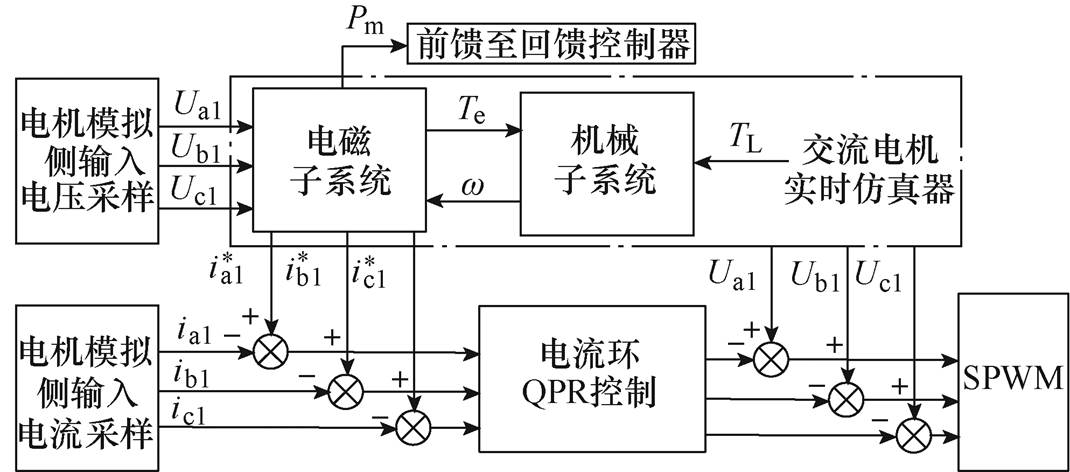
图11 电机模拟变换器控制系统框图
Fig.11 Block diagram of motor simulation converter control system
回馈变换器将采用电压电流双闭环[22]控制系统,并利用电机功率前馈的策略抑制虚拟电机暂态过程对直流侧电压的扰动[23],最终得到如图12所示的回馈变换器控制系统框图。
基于上述原理分析,搭建5kV·A的实验样机进行原理验证,异步电机参数见表1,样机参数见表3。
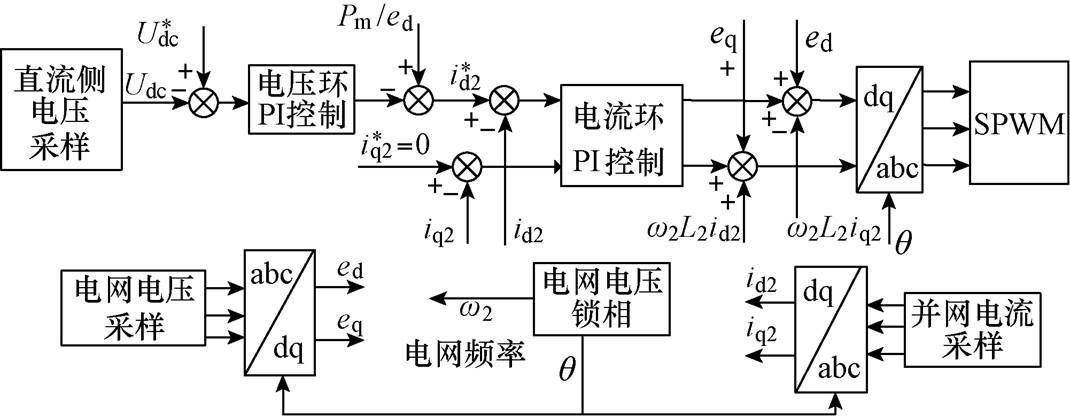
图12 回馈变换器控制系统框图
Fig.12 Block diagram of the feedback converter control system
利用三相对称正弦电压作为虚拟电机的驱动电源,虚拟电机实验平台如图13所示。

图13 虚拟电机实验平台
Fig.13 Virtual motor experiment platform
利用电网模拟器将电机模拟变换器输入侧相电压在1s时间内由0V调压至110V,随后维持不变,观测虚拟电机端口特性,此时异步电机未发生故障,虚拟电机调压起动过程波形如图14所示。
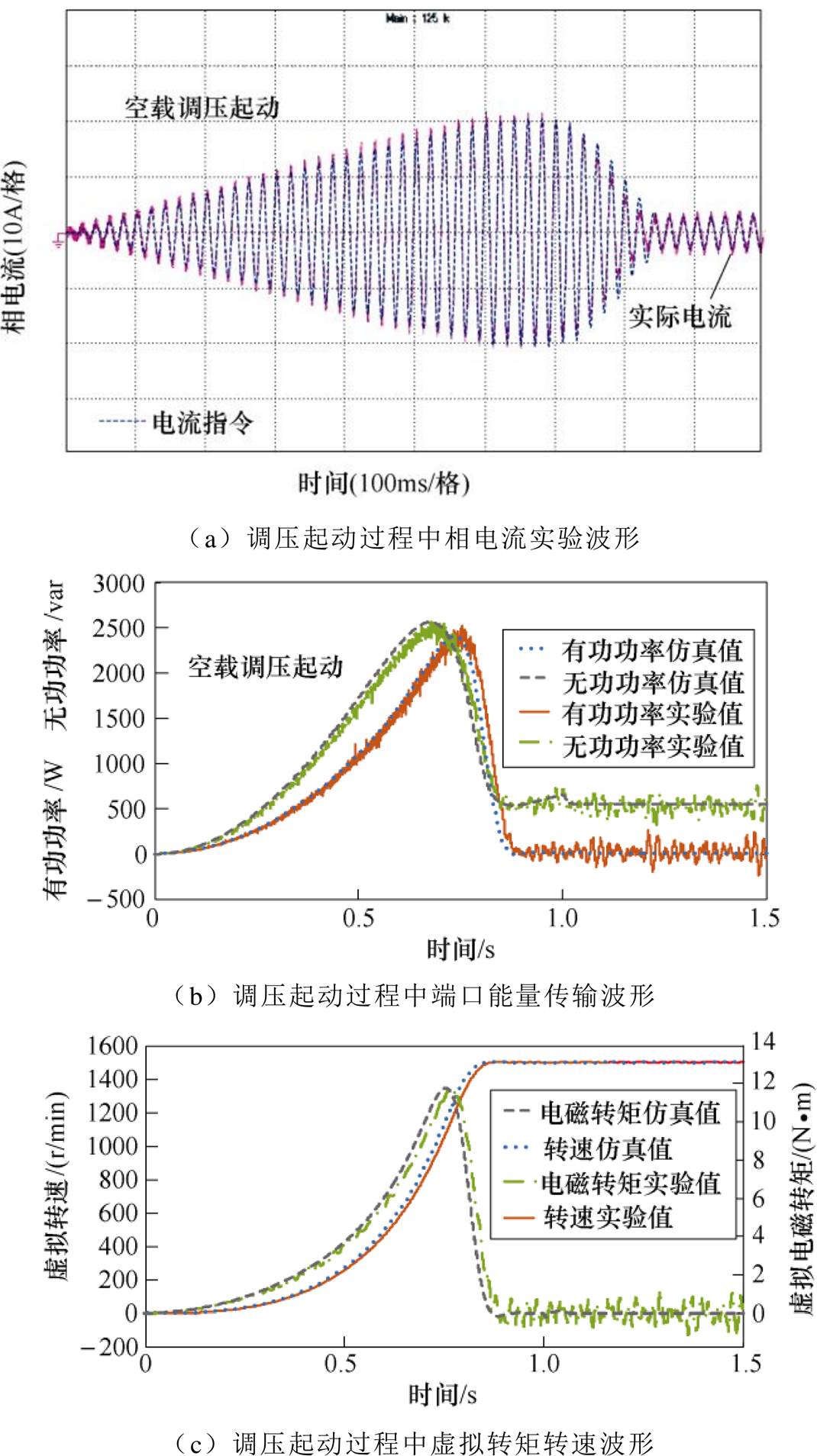
图14 虚拟电机调压起动过程波形
Fig.14 Waveforms diagram of virtual motor voltage regulation starting process
空载调压起动过程中,虚拟电机端口电流先逐渐上升,最大电流接近20A,随后在电机稳定运行时,电流下降至3A左右,图14a表明电机模拟变换器对电机实时仿真器中的电流指令跟踪良好。电机加速需要足够的有功以及无功功率支撑,如图14b所示,仿真结果与实验结果变化趋势基本相同。
虚拟电机端口虽不能直接呈现出电机转速与电磁转矩等信息,但是根据交流电机实时仿真器中的计算结果,虚拟电机起动过程开始后,虚拟电机转速上升,最后稳定在1 500r/min左右,供加速所用的电磁转矩先逐渐上升至12N·m,待异步电机以恒定转速稳定运行时,电磁转矩降至0N·m附近。根据上述分析,虚拟电机在调压起动过程中呈现出异步电机的端口特性。
虚拟电机在恒定正弦电压下空载稳定运行,于0.2s时刻将电机实时仿真器中的负载转矩从0N·m增加至12N·m。虚拟电机负载切换过程波形如图15所示。
0~0.2s内,异步电机处于空载稳态运行状态,相电流幅值在3A左右,转速约为1 500r/min,有功功率接近0W,无功功率接近550var,电磁转矩在0N·m附近波动;在0.2s时刻,负载转矩由0N·m切换至12N·m,相电流幅值增大至9A左右,由图15b可知,实际电流对指令电流跟踪性能良好,注入电机模拟变换器的功率增大至2 000W与900var左右,异步电机转速降至为1 390r/min左右,虚拟电磁转矩在12N·m左右波动,实验结果和仿真结果也比较贴合。综合上述分析,虚拟电机在负载切换过程中呈现出异步电机的端口特性。
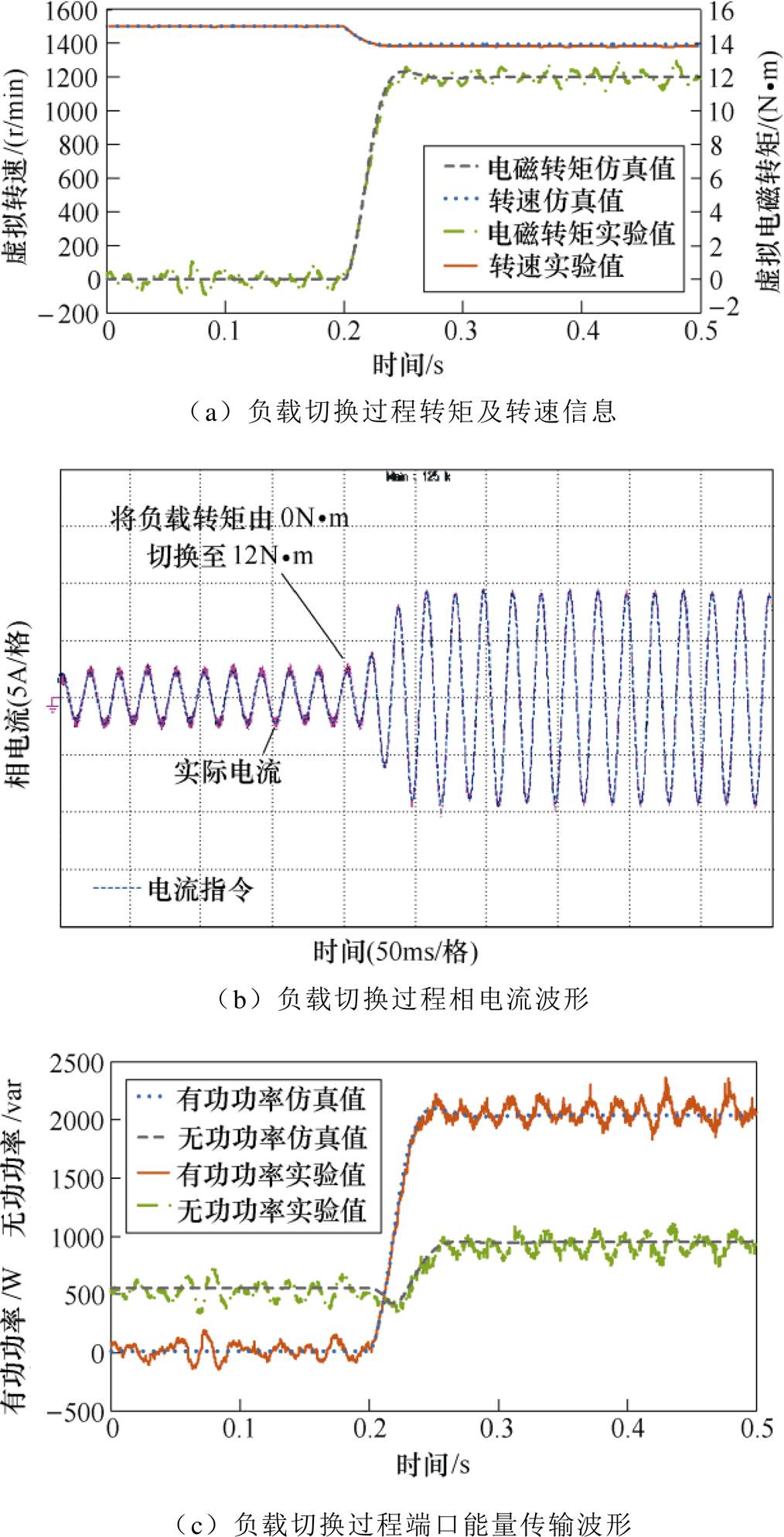
图15 虚拟电机负载切换过程波形
Fig.15 Waveforms diagram of virtual motor load mutation process
当虚拟电机模拟故障程度为0.04的异步电机端口特性时,虚拟电机相电流如图16所示。
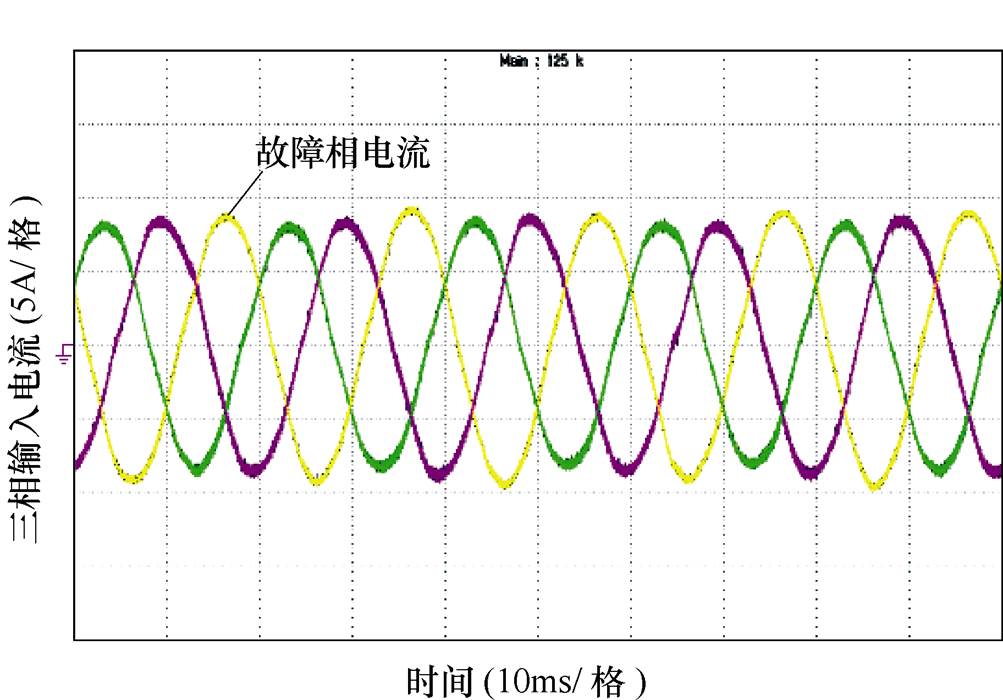
图16 故障程度为0.04时虚拟电机相电流
Fig.16 Virtual motor phase current when the fault level is 0.04
当异步电机未发生故障时,三相电流基本平衡;当某一相绕组发生定子匝间短路故障时,如图16所示,故障相电流明显增大,三相电流出现不平衡现象,实验结果与相关理论[15]保持一致。
负序电流是判断异步电机定子绕组匝间短路故障是否发生以及估计故障严重程度的重要指标,该特征量可以衡量三相电流的不平衡度。利用Hilbert变换可以提取电机模拟变换器侧负序电流分量[15]。虚拟电机负序电流如图17所示。
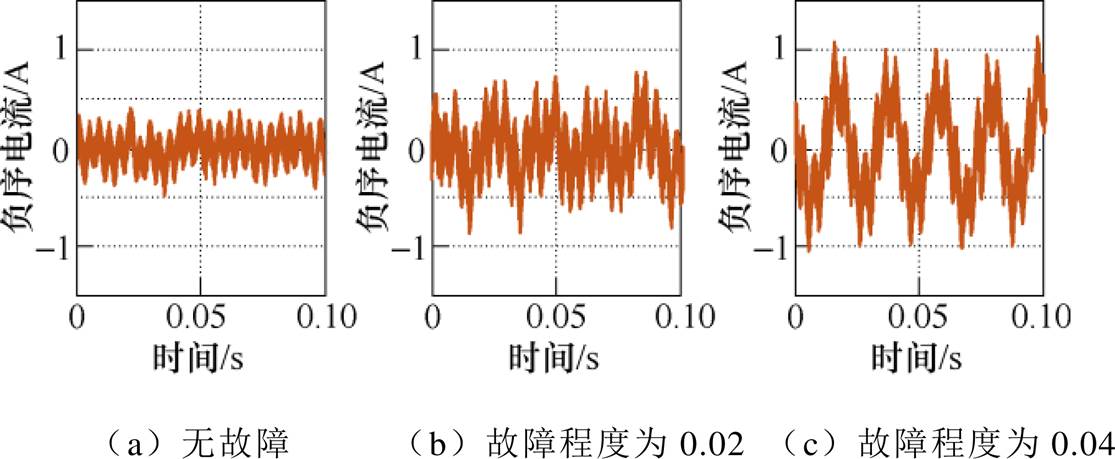
图17 虚拟电机负序电流
Fig.17 Negative sequence current of virtual motor
当故障由无到有,程度由浅及深,虚拟电机模拟变换器侧的负序电流幅值依次增加,表明虚拟电机系统呈现出异步电机发生定子绕组匝间短路故障时的端口电流特性。
1)在ab 轴下建立的考虑定子匝间短路故障的异步电机数学模型可以通过故障系数对正常模型和故障模型做统一化处理,以绕组磁链作为状态变量后求得的状态方程可以为实时数值计算带来便利。
2)四阶龙格库塔法可以在相同的计算步长下达到更高精度,相较于传统两步阿达姆斯法更适合应用于交流电机实时仿真器。
3)对于电机模拟控制器,QPR优势明显,数字控制延时会降低系统稳定性,针对性的参数优化设计方法可以有效提高系统动态响应能力并且提供足够的带宽。
仿真和实验表明,本文设计的交流电子负载系统可以对异步电机起动、负载切换过程以及发生定子匝间短路故障时的端口特性进行模拟,可以用于电机驱动电源的开发测试。
参考文献
[1] 宋向金, 王卓, 胡静涛, 等. Hilbert解调制方法诊断异步电机轴承故障[J]. 电工技术学报, 2018, 33(21): 45-52.
Song Xiangjin, Wang Zhuo, Hu Jingtao, et al. Hilbert's demodulation method for diagnosis of asynchronous motor bearing faults[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 45-52.
[2] Zhang Qian, Liu Huijuan, Zhang Zhenyang, et al. A cast copper rotor induction motor for small commercial EV traction: electromagnetic design, analysis, and experimental tests[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(4): 417-424.
[3] 宋鹏先, 李耀华, 王平, 等. 交流电机端口特性的数字化实现方法[J]. 电工技术学报, 2015, 30(14): 184-192.
Song Pengxian, Li Yaohua, Wang Ping, et al. Digital implementation of AC motor port characteristics[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 184-192.
[4] Jack A G, Atkinson D J, Slater H J. Real-time emulation for power equipment development. Part 1: real-time simulation[J]. IEE Proceedings-Electric Power Applications, 1998, 145(2): 92-97.
[5] Slater H J, Atkinson D J, Jack A G. Real-time emulation for power equipment development II. the virtual machine[J]. IEE Proceedings-Electric Power Applications, 1998, 145(3): 153.
[6] 姚剑锋. 基于PWM技术的电动机模拟器[D]. 天津:天津大学, 2006.
[7] 陈志博. 基于PWM换流器的异步电动机及其负载特性数字模拟[D]. 武汉: 华中科技大学, 2007.
[8] 黄清军, 孙牧村, 邹旭东, 等. 模拟电机端口特性的电力电子负载系统设计[J]. 电力系统自动化, 2014, 38(3): 71-77.
Huang Qingjun, Sun Mucun, Zou Xudong, et al. Design of power electronic load system for simulating motor port characteristics[J]. Automation of Electric Power Systems, 2014, 38(3): 71-77.
[9] 宋鹏先, 张郁颀, 李耀华, 等. 基于无差拍控制的交流电机端口特性模拟[J]. 电工电能新技术, 2016, 35(6): 24-28.
Song Pengxian, Zhang Yuxin, Li Yaohua, et al. Simulation of port characteristics of AC motor based on deadbeat control[J]. Advanced Technology of Electrical Engineering and Energy, 2016, 35(6): 24-28.
[10] Kenichiro Saito, Hirofumi Akagi. A power hardware- in-the-loop (P-HIL) test bench using two modular multilevel DSCC converters for a synchronous motor drive[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 4563-4573.
[11] Rao S, Chandorkar. Electrical load emulator for unbalanced loads and with power regeneration[C]// 21st IEEE International Symposium on Industrial Electronics, Hangzhou, 2012: 320-327.
[12] 麦志勤, 肖飞, 刘计龙, 等. 基于准比例谐振级联PI的双三相永磁同步电机谐波电流抑制策略[J]. 电工技术学报, 2018, 33(24): 117-125.
Mai Zhiqin, Xiao Fei, Liu Jilong, et al. Harmonic current suppression strategy for two-phase three- phase permanent magnet synchronous motor based on quasi-proportional resonant cascade PI[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(24): 117-125.
[13] 刘赫. 基于逆变器谐波的交流电机定子匝间短路故障诊断研究[D]. 杭州: 浙江大学, 2017.
[14] Tallam R M. Transient model for induction machines with stator winding turn faults[J]. IEEE Transactions on Industry Applications, 2000, 38(3): 632-637.
[15] 刘卉圻. 异步电机定子绕组匝间短路故障建模与检测方法研究[D]. 成都: 西南交通大学, 2014.
[16] 钱积新, 王慧, 邵之江. 控制系统的数字仿真及计算机辅助设计[M]. 杭州: 浙江大学出版社, 2004.
[17] 王洁聪, 刘崇茹, 徐东旭, 等. 基于RTDS的模块化多电平换流器闭锁状态仿真建模方法[J]. 电工技术学报, 2018, 33(16): 3686-3696.
Wang Jiecong, Liu Chongru, Xu Dongxu, et al. Modeling method for latching state of modular multilevel converter based on RTDS[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3686-3696.
[18] 方天治, 黄淳, 陈乃铭, 等. 一种提高弱电网下LCL型并网逆变器鲁棒性的相位超前补偿策略[J]. 电工技术学报, 2018, 33(20): 171-180.
Fang Tianzhi, Huang Chun, Chen Naiming, et al. A phase advance compensation strategy for improving the robustness of LCL grid-connected inverters in weak grids[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 171-180.
[19] Zhang X, Spencer J W, Guerrero J M. Small-signal modeling of digitally controlled grid-connected inverters with LCL filters[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3752-3765.
[20] 宋卫章, 余丰, 戴智豪, 等. 带负载电流前馈的VIENNA整流器PR控制[J]. 电机与控制学报, 2019, 23(5): 76-83.
Song Weizhang, Yu Feng, Dai Zhihao, et al. PR control of VIENNA rectifier with load current feedforward [J]. Electric Machines and Control, 2019, 23(5): 76-83.
[21] Holmes D G, Lipo T A, Mcgrath B P, et al. Optimized design of stationary frame three phase AC current regulators[J]. IEEE Transactions on Power Electronics, 2009, 24(11): 2417-2426.
[22] 刘博, 贲洪奇, 白银龙. 一种抑制PWM整流器起动冲击电流的缓给定方法[J]. 电工技术学报, 2018, 33(12): 2758-2766.
Liu Bo, Ben Hongqi, Bai Yinlong. A slow method for suppressing the starting current of PWM rectifier[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2758-2766.
[23] 姚骏, 廖勇, 庄凯. 永磁直驱风电机组的双PWM变换器协调控制策略[J]. 电力系统自动化, 2008, 32(20): 88-92.
Yao Jun, Liao Yong, Zhuang Kai. Coordinated control strategy for dual PWM converters of permanent magnet direct drive wind turbines[J]. Automation of Electric Power Systems, 2008, 32(20): 88-92.
Virtual Motor System Considering Fault Characteristic Simulation and Its Control Strategy
Abstract AC motors are widely used in modern industry, and performance tests for motor drivers have received much attention. This paper presents a design scheme of a virtual motor system that uses a back-to-back converter instead of actual motor and its load. Since the operating conditions of AC motors are complicate, it is necessary to consider the transient processes and fault conditions. Therefore, the mathematical modeling and real-time simulation are difficult. This paper presented an asynchronous motor model considering stator winding fault, and selected quasi proportional resonant (QPR) controller for dynamic current tracking by the comparison of numerical calculation methods. Under the premise of digital control delay estimation, parameter optimization design was achieved with the goal of improving bandwidth and dynamic response capability. Simulation and experiments show that the virtual motor system can simulate port characteristics of asynchronous motor under normal conditions and the condition of stator winding turn-to-turn short-circuit fault. It can be used as an AC electronic load for the development and testing of motor drivers.
keywords:Virtual motor, asynchronous motor, turn-to-turn short-circuit fault, quasi proportional resonant controller
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.190135
国家自然科学基金资助项目(51677167,51690182)。
收稿日期 2019-01-30
改稿日期 2019-07-26
杨庆文 男,1994年生,硕士研究生,研究方向为高效能电机系统,交流电子负载。E-mail: yangqingwen@zju.edu.cn
杨 欢 男,1981年生,教授,博士生导师,研究方向为分布式发电与微电网、智能配用电、高效能电机系统等。E-mail: yanghuan@zju.edu.cn(通信作者)
(编辑 陈 诚)