 (1)
(1)摘要 针对永磁直线同步电动机(PMLSM)伺服系统易受参数变化、外部扰动等不确定性因素影响,该文提出了一种将时滞控制(TDC)与自适应控制(AC)相结合的自适应时滞控制(ATDC)方案。首先,建立了含有不确定性因素的PMLSM伺服系统动态模型;然后,利用TDC估计系统不确定性因素的值,使系统的动态模型更精确,进而得出时滞控制率;但是,由于TDC过程中增益固定,存在较大的时滞估计误差,因此,采用AC在线调整控制增益来补偿时滞估计误差;最后,通过系统实验验证了所提出的控制方案是有效可行的,与TDC相比,基于ATDC的伺服系统具有更好的跟踪性能和鲁棒性能,明显减小了跟踪误差。
关键词:永磁直线同步电动机 自适应时滞控制 时滞估计误差 鲁棒性
目前,随着工业快速发展,永磁直线同步电动机(Permanent Magnet Linear Synchronous Motor, PMLSM)因其精度高、响应速度快、机械结构简单以及高效等优点,被广泛应用于精密加工、装配检验、工业机器人等行业[1-3]。但是,PMLSM省去了电机与负载中间的传动环节,由于这种固有的机械结构,PMLSM的性能容易受到参数变化、外部负载扰动、非线性摩擦力等不确定因素的影响,增加了伺服控制的难度[4]。为了满足伺服控制的需求,国内外专家提出了多种控制方案,如神经网络控制[5]、模糊控制[6]、滑模控制(Sliding Mode Control, SMC)[7]、自适应控制(Adaptive Control, AC)[8]以及模型预测控制[9]等。虽然智能控制有很强的自学习功能,能用来解决系统的非线性以及不确定性等问题,但是神经网络权值和模糊规则训练太复杂。SMC具有强鲁棒性、收敛速度快和设计简单等优点,但是,SMC无法预先获得不确定性因素的边界,并且存在抖振现象,影响PMLSM在一些高精度场合的应 用[10]。AC虽然可以通过在线调节控制增益,改善系统的跟踪性能,但是不确定性因素对系统的影响依然存在,而且存在收敛速度不够快的缺点。时滞控制(Time Delay Control, TDC)作为非线性控制,利用时滞信号来解决系统存在的不确定性问题,但是时滞信号引起的时滞估计误差会引起较大的跟踪误差,从而降低系统的性能[11]。
为了补偿时滞估计误差,很多方法被提出。文献[12]采用模糊SMC补偿时滞估计误差,并且使用模糊规则来减少抖振。文献[13]采用监督切换控制来补偿时滞估计误差。上述控制方法,虽然在一定程度上补偿了时滞估计误差,提高了系统的跟踪性能,取得较好的控制效果,但是,由于采用固定增益控制,仍然存在较大的时滞估计误差。如果采用自适应增益控制将会获得更好的控制效果[14]。
为了克服TDC固定增益控制的缺陷,本文提出一种自适应时滞控制(Adaptive Time Delay Control, ATDC)方案。首先,通过TDC估计系统不确定性因素的值。将不确定因素的估计值与建立的含有不确定性因素的PMLSM伺服系统动态方程相结合得出时滞控制率。采用AC与SMC相结合在线调整控制增益,以补偿时滞估计误差。ATDC中控制增益在滑模面附近一个任意小的领域内适当调整。当系统的状态轨迹偏离滑模面时,控制增益增大,以实现良好的瞬态响应。当系统的状态轨迹靠近滑模面附近时,控制增益减小,避免由于过高的控制增益和噪声影响导致瞬态响应变差。通过调整控制增益,避免了SMC过高的切换增益,有效抑制了抖振。此外,通过AC和SMC相结合,AC直接反映滑模变量,从而系统的收敛速度更快。因此,通过调整控制增益获得较好的控制效果。最后,通过实验验证了所提出的控制方案能有效地提高系统跟踪性能,实现高精密伺服控制。
采用基于磁场定向的矢量控制方法,在电流内环d轴电流分量id=0的条件下,PMLSM的电磁推力方程和机械运动方程分别为
 (1)
(1)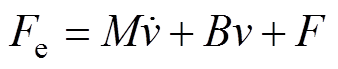 (2)
(2)
式中,Fe为电磁推力;pn为极对数;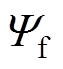 为基波磁链;
为基波磁链; 为极距;iq为q轴电流;Kf为电磁推力常数;M为动子质量;
为极距;iq为q轴电流;Kf为电磁推力常数;M为动子质量;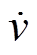 为动子加速度;B为黏滞摩擦因数;v为动子速度;F为扰动,包括参数变化、外部扰动以及非线性摩擦力等。
为动子加速度;B为黏滞摩擦因数;v为动子速度;F为扰动,包括参数变化、外部扰动以及非线性摩擦力等。
考虑F的影响,根据式(1)和式(2)可得PMLSM的动态方程为
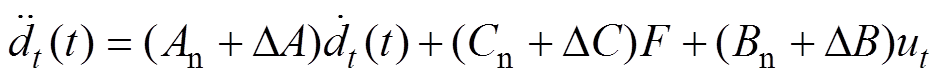 (3)
(3)式中,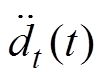 为动子加速度;
为动子加速度; 为动子的速度;
为动子的速度;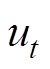 为控制器的输出,
为控制器的输出,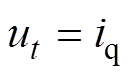 ;
;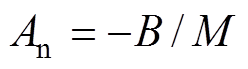 ;
;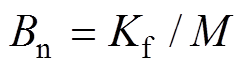 ;
;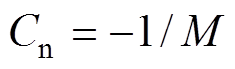 。
。
为了简化PMLSM的动态方程,式(3)可重写为
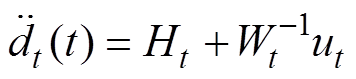 (4)
(4)式中,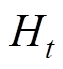 为系统的总不确定因素,表示为
为系统的总不确定因素,表示为
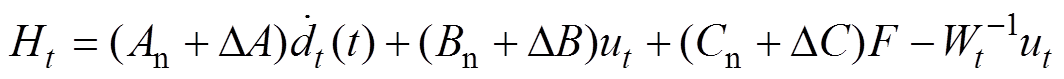 (5)
(5)
式中,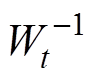 为控制增益。此处,假设
为控制增益。此处,假设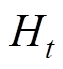 有界,
有界, ,其中,
,其中,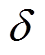 为给定的正常数。
为给定的正常数。
在传统的伺服控制系统中,由于无法建立准确的系统数学模型,而且对于系统的不确定因素难以测量,为了在最大程度上减少建模不准确和不确定因素等对系统的影响,保证伺服控制精度,提出多种鲁棒控制、补偿方法、人工智能算法等。为获得较好的控制效果,控制算法和控制结构均变得复杂。
TDC作为一种众所周知的非线性控制方法,首先,由于不需要事先获得系统不确定性因素的边界,而是通过延时一个采样周期来估计系统不确定性因素的值。因此,在算法上比智能算法等控制方案简单。其次,对系统不确定性因素的估计值可以使系统的动态方程变得更精确。于是,在控制过程中,可以省去对系统不确定量的补偿环节。因此,在控制结构上也比较简单。
PMLSM时滞控制系统框图如图1所示。为使PMLSM精确地跟踪参考轨迹,通过延时一个采样周期来获得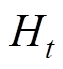 的估计值
的估计值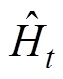 。当延时时间L充分小的时候,
。当延时时间L充分小的时候,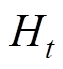 可以看作一个连续函数。近似满足
可以看作一个连续函数。近似满足
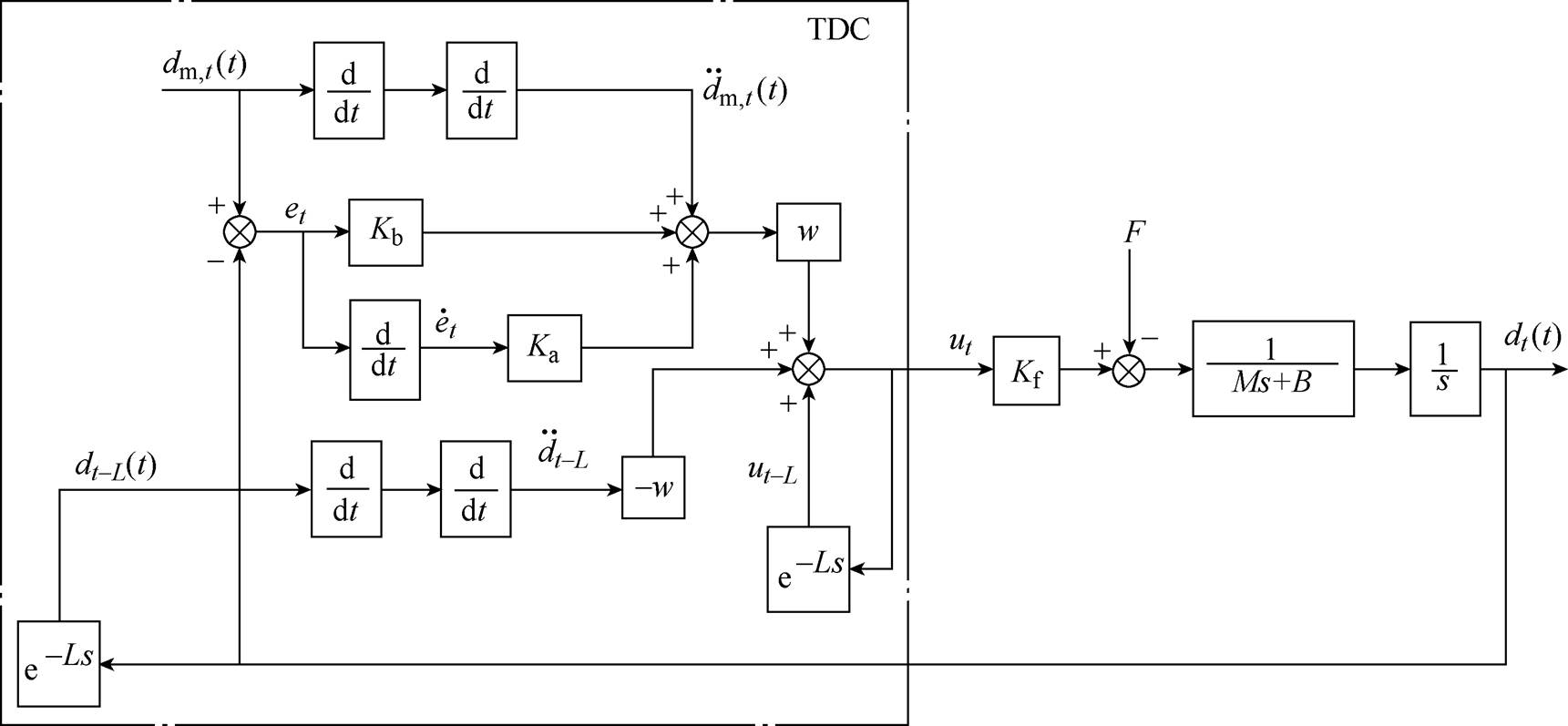
图1 PMLSM时滞控制系统框图
Fig.1 Block diagram of time delay control system for PMLSM
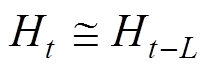 (6)
(6)根据式(6),对不确定量的估计可表示为
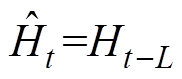 (7)
(7)
由式(4)可得
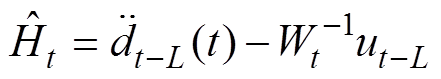 (8)
(8)式中,L为一个采样周期。
由式(5)可看出,电机参数主要包含在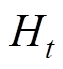 中。通过延时一个采样周期的方式,采用TDC对
中。通过延时一个采样周期的方式,采用TDC对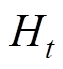 直接估计得到式(8),通过简单的表达式来表示复杂的电机参数以及系统中的不确定量,摆脱了控制系统对系统动态方程的依赖,从而摆脱了传统伺服控制中电机主要参数对控制率设计的限制,降低了控制率设计的难度。
直接估计得到式(8),通过简单的表达式来表示复杂的电机参数以及系统中的不确定量,摆脱了控制系统对系统动态方程的依赖,从而摆脱了传统伺服控制中电机主要参数对控制率设计的限制,降低了控制率设计的难度。
定义系统的跟踪误差为
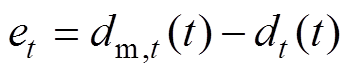 (9)
(9)式中, 、
、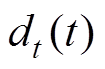 分别为动子的给定位置和实际位置。
分别为动子的给定位置和实际位置。
根据式(4)、式(8)和式(9)得出TDC的控制律为
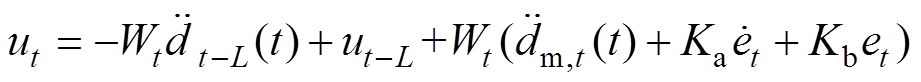 (10)
(10)式中,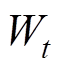 、
、 和
和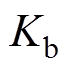 均为正常数。为了避免与2.2节提出的ATDC的控制律中的参数混淆,把式(10)中的
均为正常数。为了避免与2.2节提出的ATDC的控制律中的参数混淆,把式(10)中的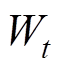 改写为w。式(10)重写为
改写为w。式(10)重写为
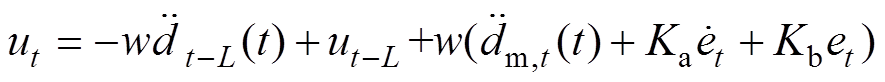 (11)
(11)
PMLSM自适应时滞控制系统框图如图2所示。在TDC的基础上结合SMC和AC,设计了自适应时滞控制器。定义滑模面为
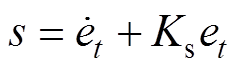 (12)
(12)式中,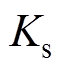 为正常数。
为正常数。
根据式(10)和式(12),得出ATDC的控制律为
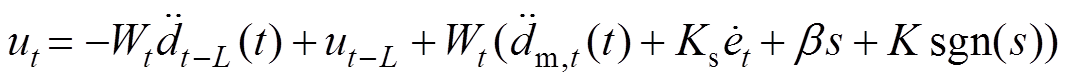 (13)
(13)式中,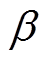 、K为正常数,K代表切换增益;
、K为正常数,K代表切换增益;![]() 为符号函数,即
为符号函数,即
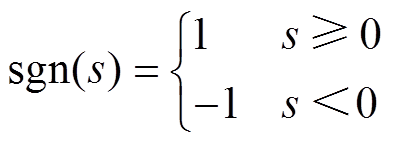 (14)
(14)
根据自适应法在线调整的控制增益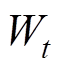 为
为
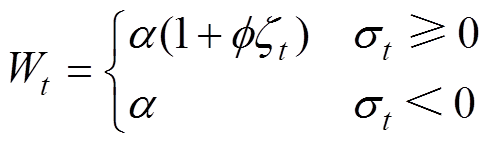 (15)
(15)式中,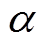 、
、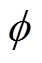 为正常数。
为正常数。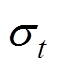 表示为
表示为
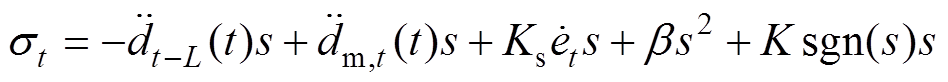 (16)
(16)
通过自适应法的更新参数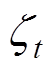 的不断变化,
的不断变化,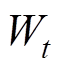 自动调整控制增益的大小。
自动调整控制增益的大小。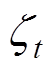 为
为
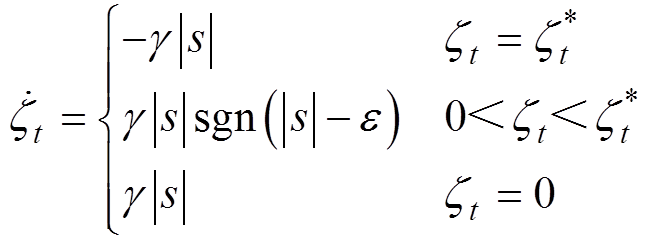 (17)
(17)式中,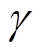 、
、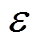 都是正常数。可以明显地看出,自适应法直接反映了滑模变量,因此系统的收敛速度更快。由式(17)可知,
都是正常数。可以明显地看出,自适应法直接反映了滑模变量,因此系统的收敛速度更快。由式(17)可知,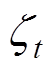 的上边界为
的上边界为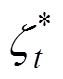 ,当
,当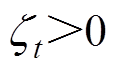 时,根据符号函数的输出,自适应法有
时,根据符号函数的输出,自适应法有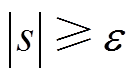 和
和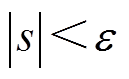 两种情况,当
两种情况,当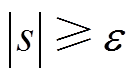 时,
时,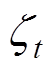 的值一直增大,直到
的值一直增大,直到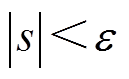 为止。从而
为止。从而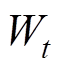 随着
随着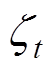 增大而增大,因此系统获得较快的收敛速度。当
增大而增大,因此系统获得较快的收敛速度。当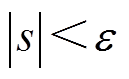 时,
时,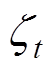 的值一直减小,
的值一直减小,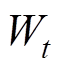 会随着
会随着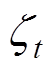 的减小而减小,因此改善了系统的瞬态响应,避免了增益过高。当
的减小而减小,因此改善了系统的瞬态响应,避免了增益过高。当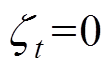 时,
时,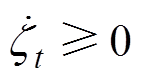 ,
,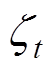 的值一直增大,又回到
的值一直增大,又回到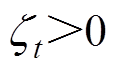 的状况下。可以看出,通过AC与SMC相结合来调整控制增益,不仅减小了时滞估计误差,还提高了系统的跟踪性能,同时也减小了SMC的切换增益,从而减小抖振的影响,保证了ATDC系统的稳定性。综上所述,可以通过适当调整控制增益来改善系统的跟踪能力。
的状况下。可以看出,通过AC与SMC相结合来调整控制增益,不仅减小了时滞估计误差,还提高了系统的跟踪性能,同时也减小了SMC的切换增益,从而减小抖振的影响,保证了ATDC系统的稳定性。综上所述,可以通过适当调整控制增益来改善系统的跟踪能力。
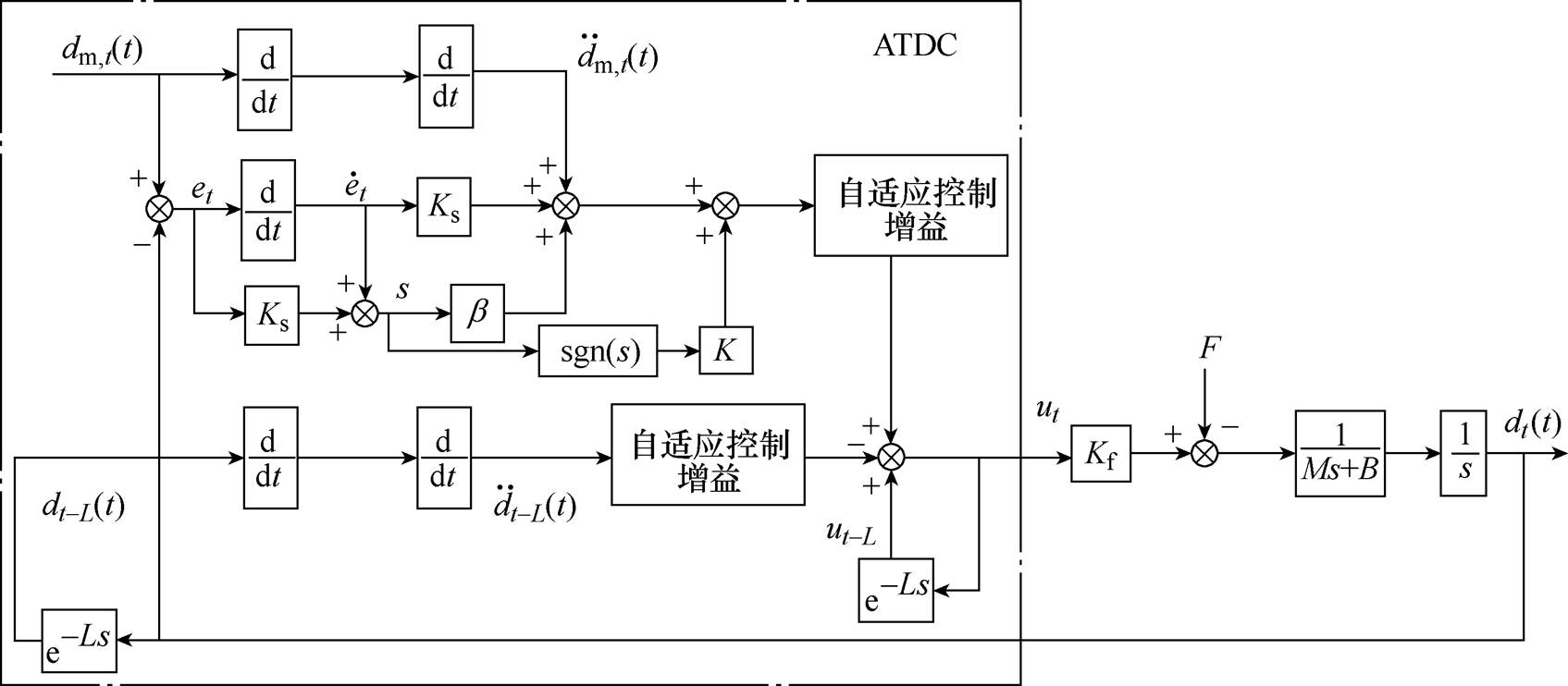
图2 PMLSM自适应时滞控制系统框图
Fig.2 Block diagram of adaptive time delay control system for PMLSM
对ATDC采用的李雅普诺夫函数为
对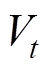 求导得
求导得
![]() (19)
(19)
将式(4)代入式(19)得
将式(13)代入式(20)得
![]() (21)
(21)
式中,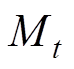 为时滞估计误差,
为时滞估计误差,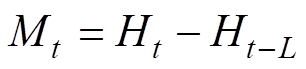 。假设
。假设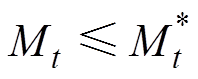 ,可以得出
,可以得出
如果切换增益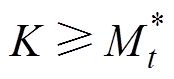 ,那么可以得到
,那么可以得到
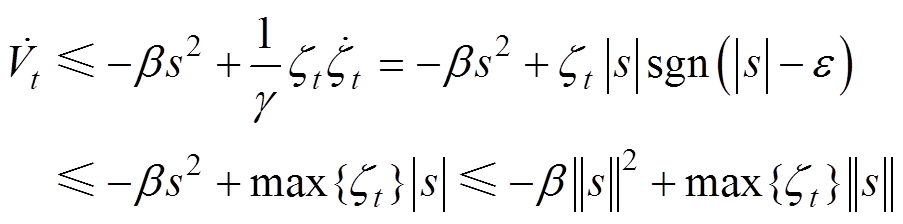 (23)
(23)
如果![]() ,那么对于任意给定的正常数
,那么对于任意给定的正常数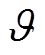 ,
,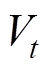 都会以非零的速度减小。在有限的时间内,滑模变量s会进入
都会以非零的速度减小。在有限的时间内,滑模变量s会进入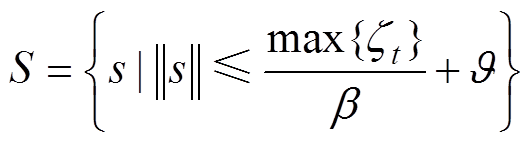 集合。如果s一直在集合的范围内,
集合。如果s一直在集合的范围内,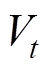 将有一个上边界
将有一个上边界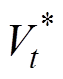 ,表示为
,表示为
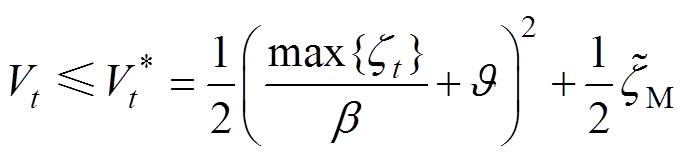 (24)
(24)式中,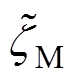 为式(18)中
为式(18)中![]() 的上边界值。即使
的上边界值。即使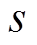 不在集合的范围内,由于当
不在集合的范围内,由于当![]() 时,
时,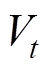 也会减少,所以不等式仍然成立。
也会减少,所以不等式仍然成立。
由式(24)得,式(18)中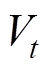 的范围为
的范围为
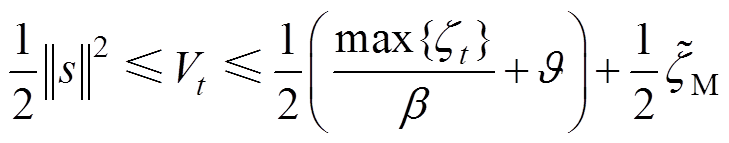 (25)
(25)最后,可以得出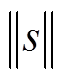 是有界的,表示为
是有界的,表示为
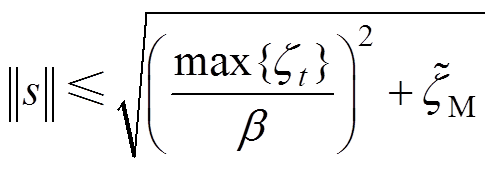 (26)
(26)
由于s有界,因此,跟踪误差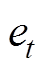 有界,于是更新参数
有界,于是更新参数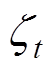 和控制增益
和控制增益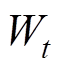 也有界。
也有界。
采用TMS320F2812A的DSP作为控制算法核心,为了消除输入信号中的高频信号对系统的干扰,在控制程序中设计了FIR低通滤波程序,采样频率为1kHz,截止频率为300Hz。实验中利用TDC和ATDC两种控制方法进行对比分析,验证所得控制方案的有效性。基于DSP的PMLSM控制系统结构如图3所示,实验装置采用PMLSM、PC+DSP、IPM、动子电流检测模块和直线光栅尺位置检测模块等。
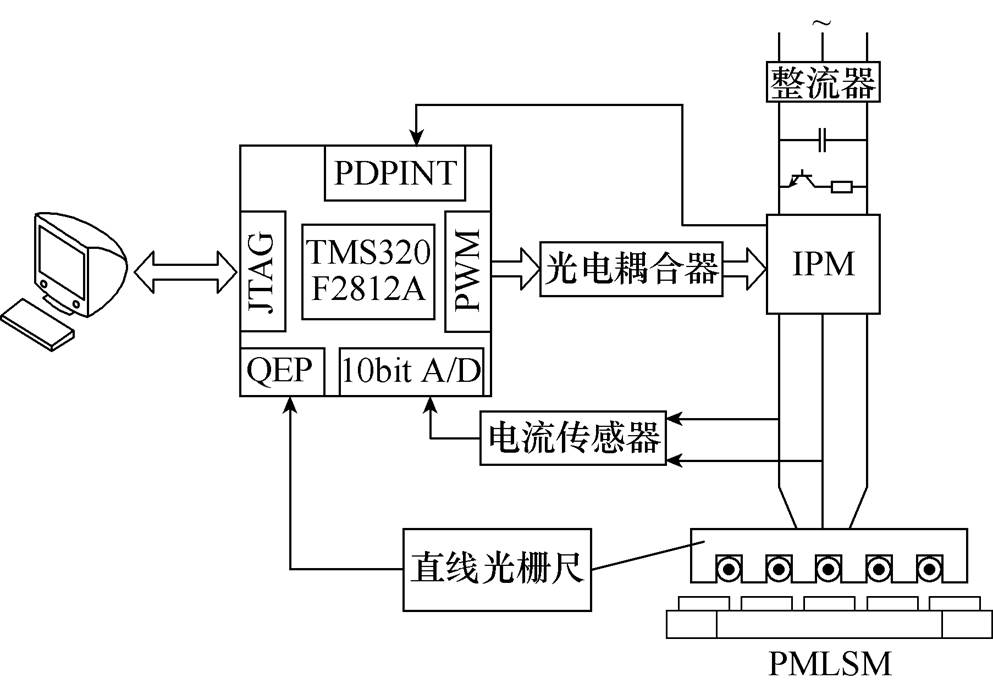
图3 PMLSM控制系统结构
Fig.3 Structure diagram of PMLSM control system
PMLSM参数为Kf=50.7N/A,Ld=Lq=26.7mH,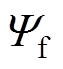 =0.24Wb,
=0.24Wb,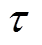 =18mm,B=0.2N·s/m,M=6.6kg,pn=2。对PMLSM输入的信号分别为:①阶跃信号,其幅值大小为1mm,并且在0.5s时刻突加50N的负载扰动;②阶跃信号,其幅值大小为1mm,并且在0.5s时刻突加变负载扰动;③正弦信号,其幅值为1mm,频率为1rad/s;④正弦信号,其幅值为1mm,频率为1rad/s,并加入周期性扰动信号。根据输入的信号,对ATDC和TDC均延时一个采样周期L=1ms。通过使用控制变量法,反复调节ATDC和TDC中的参数,经过多次实验最终选定最优参数。TDC中的参数:w=0.1,
=18mm,B=0.2N·s/m,M=6.6kg,pn=2。对PMLSM输入的信号分别为:①阶跃信号,其幅值大小为1mm,并且在0.5s时刻突加50N的负载扰动;②阶跃信号,其幅值大小为1mm,并且在0.5s时刻突加变负载扰动;③正弦信号,其幅值为1mm,频率为1rad/s;④正弦信号,其幅值为1mm,频率为1rad/s,并加入周期性扰动信号。根据输入的信号,对ATDC和TDC均延时一个采样周期L=1ms。通过使用控制变量法,反复调节ATDC和TDC中的参数,经过多次实验最终选定最优参数。TDC中的参数:w=0.1, =15,
=15,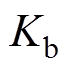 =55。ATDC中的参数:
=55。ATDC中的参数: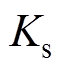 =164,
=164,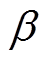 =7.38,自适应控制率中的增益越大,系统的收敛速度越快,但同时会降低系统的稳定性,因此在满足跟踪误差以及收敛速度要求的前提下选取参数为
=7.38,自适应控制率中的增益越大,系统的收敛速度越快,但同时会降低系统的稳定性,因此在满足跟踪误差以及收敛速度要求的前提下选取参数为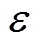 =0.014 4,
=0.014 4,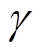 =12.246,K=54.35,
=12.246,K=54.35, =1.03,
=1.03,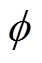 =1.01,
=1.01,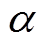 =0.1。
=0.1。
在信号①情况下,分别采用TDC和ATDC的系统进行位置跟踪。位置跟踪曲线图如4a所示,位置误差曲线如图4b所示。通过TDC和ATDC的系统跟踪曲线对比,明显可以看出,在给定信号后,ATDC的系统迅速响应,在0.18s开始收敛,相比之下TDC的系统响应速度较慢,在0.2s才开始收敛,因此ATDC的系统具有更好的瞬态响应能力。在0.5s对系统突加扰动的情况下,ATDC的系统位置误差并没有较大的变化,位置误差始终维持在-1~0.6mm之间,而TDC的系统位置误差由0.5mm迅速增大到5mm,并且在此后伴随有小幅度振荡,在0.95s附近位置误差达到最大约为7.7mm,接着在1s处位置误差开始逐步减少,慢慢地收敛到2mm左右,恢复到稳定状态。很明显,ATDC的抗扰性更强,系统能更快地回到稳定状态,具有更快的瞬态响应。
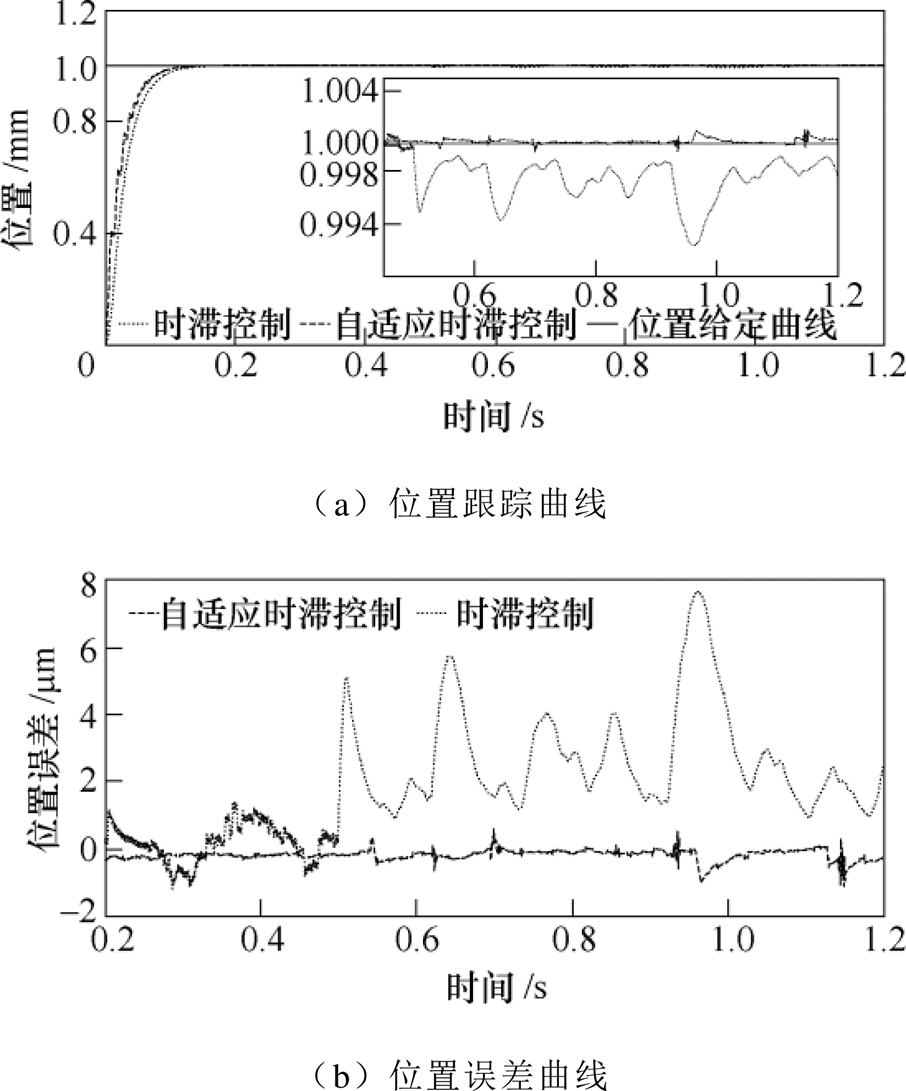
图4 阶跃信号下突加负载扰动的位置曲线
Fig.4 Position curves of sudden load disturbance under step signal
在信号②情况下,分别采用TDC和ATDC的系统进行位置跟踪。位置跟踪曲线图如5a所示,位置误差曲线如图5b所示。由图5a明显可以看出,在给定信号后,ATDC的系统迅速响应,在0.18s开始收敛,而TDC的系统响应速度较慢,在0.2s才开始收敛,因此ATDC系统具有更好的瞬态响应能力。在0.5s对系统突加变负载扰动如图5c所示,在0.5~1.0s由图5b可以看出,ATDC的系统位置误差由0.2mm增大到2.5mm,并且系统在0.64s恢复到稳定状态,TDC系统位置误差由0.5mm迅速增大到8.6mm,并且此后伴随有小幅度振荡,在0.75s附近位置误差开始逐步减少,恢复到稳定状态。在1.0~2.0s,ATDC的系统位置误差快速增大到5.5mm,并经过0.2s恢复到稳定状态。很明显,TDC的位置误差远大于ATDC的位置误差,约为11.3mm。而且收敛的时间也较长,经过0.3s才收敛。在2.0~2.5s,ATDC的系统位置误差由0.1mm快速增大为-2mm,然后在2.13s恢复到稳态。而TDC的系统位置误差由0.4mm快速增大到-5mm,然后缓慢收敛,在2.3s恢复到稳态。很明显ATDC的系统抗扰性更强,瞬态响应更快。
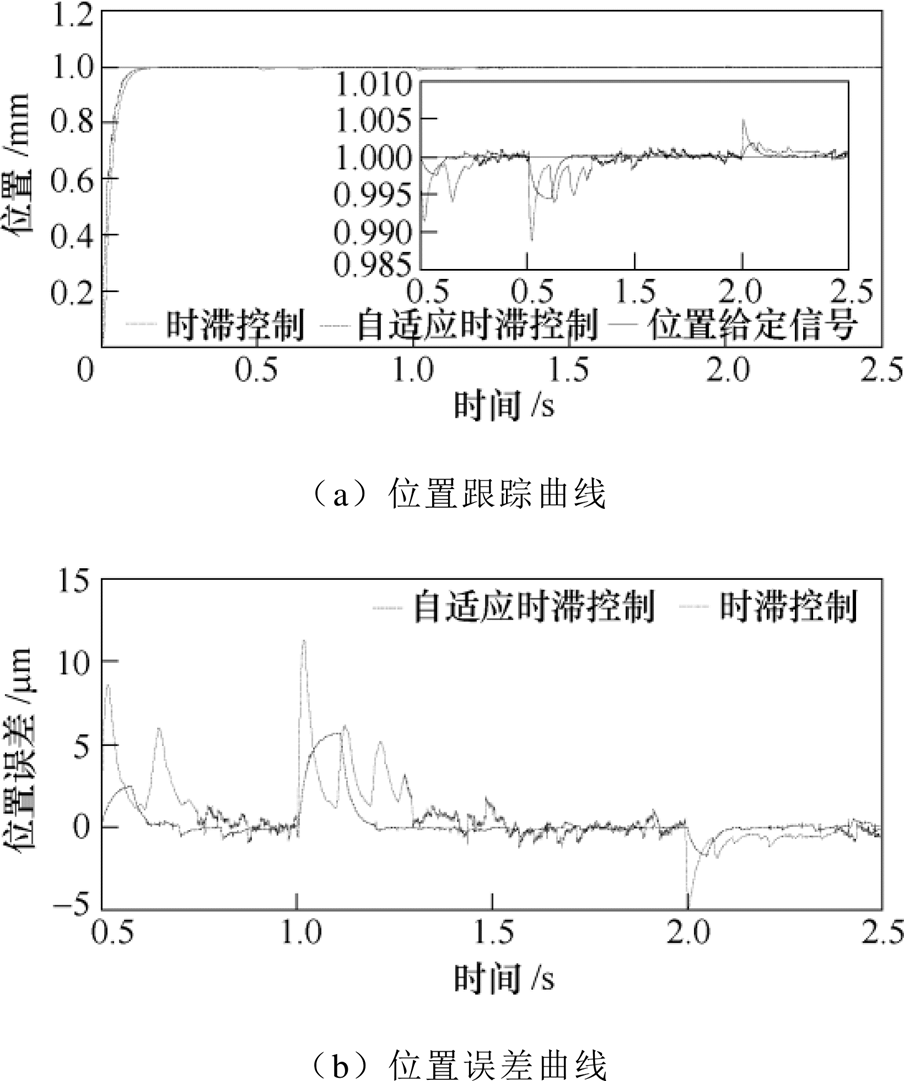
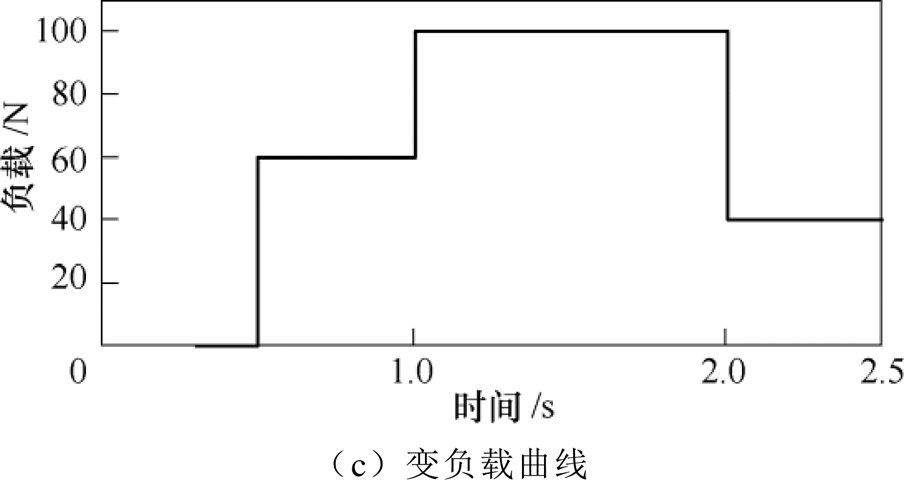
图5 阶跃信号下突加变负载扰动的位置曲线
Fig.5 Position curves of sudden variable load disturbance under step signal
在信号③情况下,分别采用TDC和ATDC的系统跟踪正弦信号的位置跟踪曲线如图6a所示,基于TDC的系统位置误差曲线如图6b所示,基于ATDC的系统位置误差曲线如图6c所示。通过对比TDC和ATDC的系统跟踪曲线,明显可以看出,给定参考正弦信号后,TDC的系统和ATDC的系统迅速跟踪给定位置曲线,在跟踪的过程中,TDC的系统位置误差变化幅度较大,误差变化范围为-15~13mm,最大位置误差为-15mm。而ATDC的系统位置误差变化幅度较小,位置误差变化范围为-1.25~1.27mm,最大误差为1.27mm。ATDC的最大位置误差约为TDC最大位置误差的10%。通过比较系统的位置误差可以得ATDC的系统位置误差更小,控制精度更高。
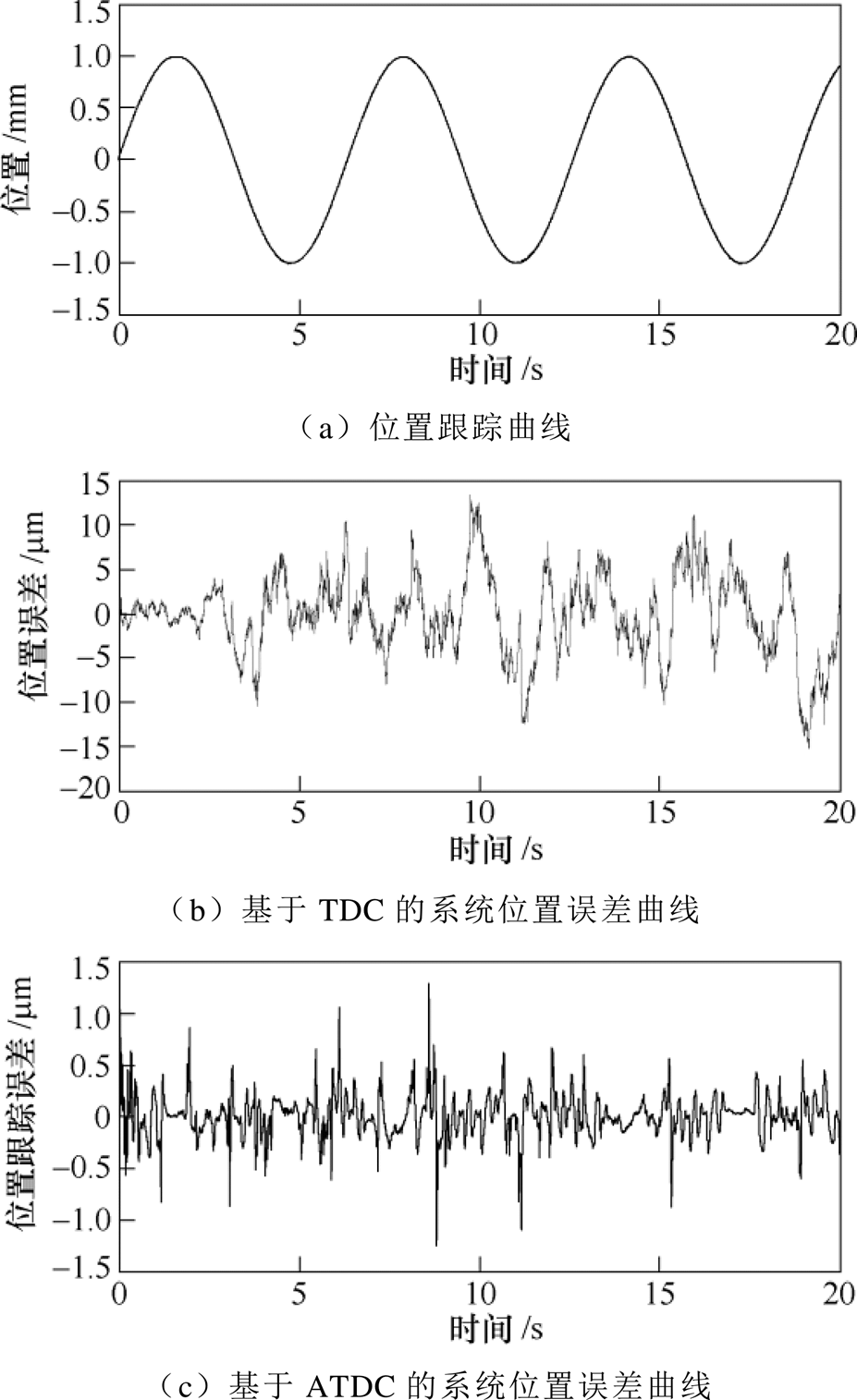
图6 正弦信号下的位置曲线
Fig.6 System position curves under sinusoidal signal
在信号④情况下进行仿真实验,给定位置信号如图7a所示,加入周期性的扰动信号如图7b所示。采用TDC和ATDC的系统跟踪正弦信号的位置误差曲线分别如图7c、图7d所示。在输入位置信号时,两个系统开始跟踪位置信号,由图7c可以看出,TDC的位置误差变化幅度较大,误差变化范围为-20~18mm,最大误差为-20mm。由图7d得,ATDC的位置误差明显小于TDC的位置误差,而且误差变化幅度较小,误差的变化范围为-1.4~1.6mm。其最大位置误差为1.6mm。由此可见,在加入周期性负载扰动的情况下,ATDC的系统依然能够保持强鲁棒性,具有较高的控制精度。
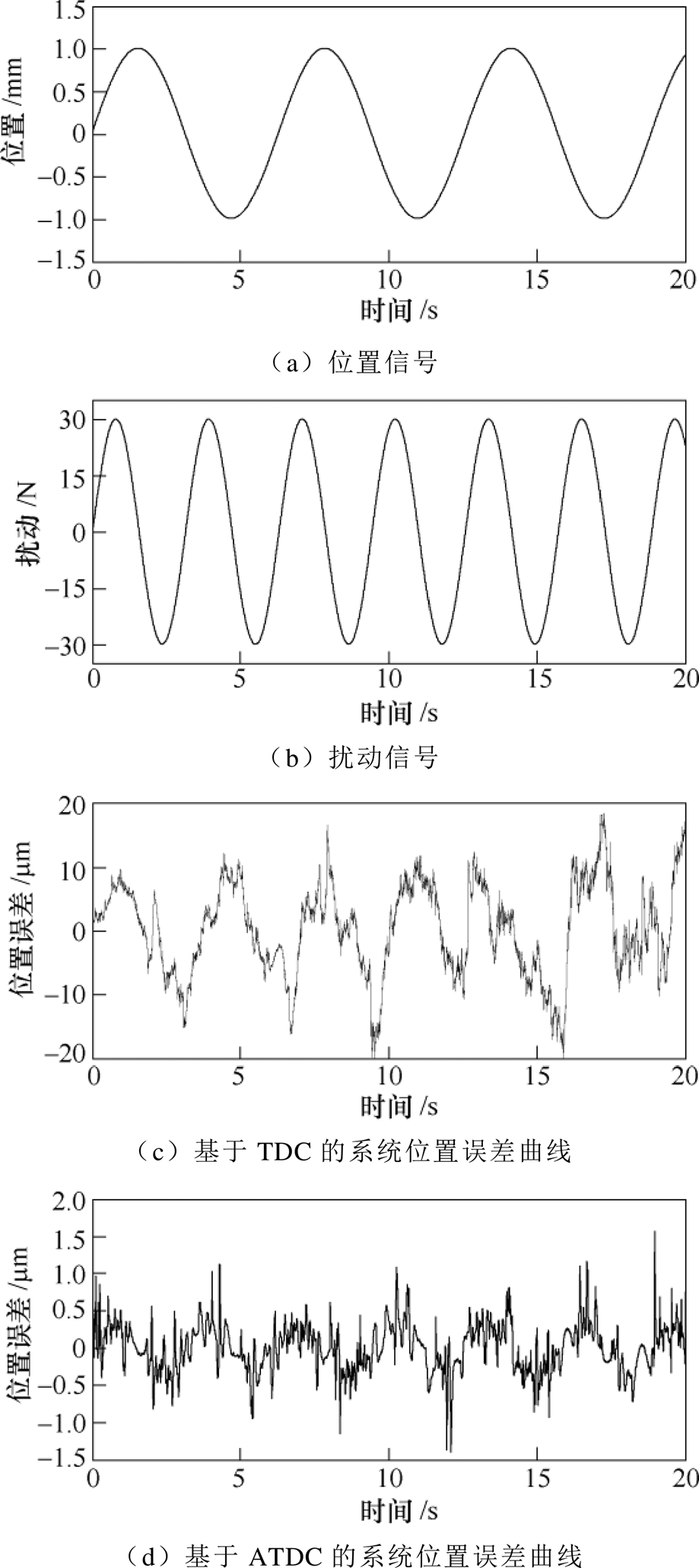
图7 正弦信号下加周期性扰动的位置曲线
Fig.7 Position curves adding periodic disturbance under sinusoidal signal
针对PMLSM伺服系统易受不确定性因素等影响,考虑到TDC由于采用固定增益控制,而产生较大的时滞估计误差,降低系统的跟踪性能,提出了一种ATDC方案。通过TDC实现了对系统不确定性因素的估计,使系统的动态方程更加精确;采用AC和SMC相结合对控制增益进行适当地调整,使时滞估计误差减小,系统的控制性能更优。最后,实验结果表明,ATDC的系统与TDC的系统相比,跟踪误差明显减小,收敛速度更快。
参考文献
[1] 朱国昕, 雷鸣凯, 赵希梅. 永磁同步电机伺服系统自适应迭代学习控制[J]. 沈阳工业大学学报, 2018, 40(1): 6-11.
Zhu Guoxin, Lei Mingkai, Zhao Ximei. Adaptive iterative learning control of permanent magnet synchronous motor servo system[J]. Journal of Shenyang University of Technology, 2018, 40(1): 6-11.
[2] 孙兴法, 聂子玲, 朱俊杰, 等. 基于低阶串行双扩展卡尔曼滤波的永磁直线同步电机无速度传感器控制策略[J]. 电工技术学报, 2018, 33(12): 2685- 2694.
Sun Xingfa, Nie Ziling, Zhu Junjie, et al. A speed sensorless control strategy for a permanent magnet linear synchronous motor based on low-order serial dual extended Kalman filters[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2685- 2694.
[3] 夏加宽, 毕亮, 李瑞泽, 等. 车用永磁同步电机MT坐标系下DTC控制[J]. 沈阳工业大学学报, 2018, 40(3): 241-247.
Xia Jiakuan, Bi Liang, Li Ruize, et al. DTC in MT coordinate system for permanent magnet synchronous motor used in electric vehicle[J]. Journal of Shenyang University of Technology, 2018, 40(3): 241-247.
[4] Cheng Shengting, Lieu J F, Liu Chunshan, et al. An adaptive FNN control design of PMLSM in stationary reference frame[J]. Journal of Control, Automation and Electrical Systems, 2016, 27(4): 391-405.
[5] He Wei, David A O, Zhao Yin, et al. Neural network control of a robotic manipulator with input deadzone and output constraint[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2016, 46(6): 759-770.
[6] Sun Fuchun, Pan Yongping, Cheng Badong, et al. Disturbance observer based composite learning fuzzy control of nonlinear systems with unknown dead zone[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 47(8): 1854-1862.
[7] 王要强, 冯玉涛, 秦明, 等. 表贴式永磁同步电机全阶滑模观测与控制策略[J]. 电工技术学报, 2018, 33(24): 5688-5699.
Wang Yaoqiang, Feng Yutao, Qin Ming, et al. Full- order sliding mode observation and control strategy for surface permanent magnet synchronous motor[J], Transactions of China Electrotechnical Society, 2018, 33(24): 5688-5699.
[8] Jung J W, Leu V Q, Do T D, et al. Adaptive PID speed control design for permanent magnet syn- chronous motor drives[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 900-908.
[9] Hu Yuansheng, Hu Cungang, Zhang Pingjia, et al. A novel hybrid seven-level converter for permanent magnet synchronous motor driving system based on model predictive control[J] CES Transactions on Electrical Machines and Systems, 2019, 3(4): 389- 396.
[10] 赵希梅, 吴勇慷. 基于多阶段速度规划的PMLSM自适应反推滑模控制[J]. 电工技术学报, 2018, 33(3): 662-669.
Zhao Ximei, Wu Yongkang. Adaptive backstepping sliding mode control for PMLSM based on multi- segment velocity planning[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 662-669.
[11] Jin Maolin, Jin Yi, Chang P H, et al. High-accuracy trajectory tracking of industrial robot manipulators using time delay estimation and terminal sliding mode[C]//Conference of the IEEE Industrial Electro- nics Society, Porto, Portugal, 2009: 65-78.
[12] Bae H J, Jin Maolin, Suh J, et al. Control of robot manipulators using time-delay estimation and fuzzy logic systems[J]. Journal of Electrical Engineering & Technology, 2017, 12(3): 1271-1279.
[13] Cho S J, Jin Maolin, Kuc T Y, et al. Control and synchronization of chaos systems using time-delay estimation and supervising switching control[J]. Nonlinear Dynamics, 2014, 75(3): 549-560.
[14] Cho S J, Jin Maolin, Kuc T Y, et al. Stability guaranteed auto-tuning algorithm of a time-delay controller using a modified nussbaum function[J]. International Journal of Control, 2014, 87(9): 1926- 1935.
Adaptive Time Delay Control of Permanent Magnet Linear Synchronous Motor
Abstract The permanent magnet linear synchronous motor (PMLSM) servo system is sensitive to the uncertainties, such as parameter variations, external disturbance and so on. This paper proposed an adaptive time delay control (ATDC) scheme by combining the time delay control (TDC) and the adaptive control (AC). Firstly, the dynamic model of the PMLSM servo system with uncertainties was established. Then, the values of the uncertainties of the system were estimated by the TDC to make the dynamic model of the system more accurate, and then the TDC rate was obtained. However, because the control gain was fixed during the process of TDC, there is a large time delay estimation error. Therefore, the AC online adjustment control gain was used to compensate the error. Finally, the experimental results show that the proposed control scheme is effective and feasible. Compared with TDC, the servo system based on ATDC has better tracking performance and robustness, and significantly reduces tracking errors.
keywords:Permanent magnet linear synchronous motor, adaptive time-delay control, time-delay estimation error, robustness
中图分类号:TP351
DOI: 10.19595/j.cnki.1000-6753.tces.181837
辽宁省自然科学基金计划重点项目(20170540677)和辽宁省教育厅科学技术研究项目(LQGD2017025)资助。
收稿日期2018-11-26
改稿日期 2019-06-18
姬相超 男,1995年生,硕士研究生,研究方向为电机控制。E-mail: jxc2532847877@163.com
赵希梅 女,1979年生,教授,博士生导师,研究方向为电机控制、机器人控制和智能控制等。E-mail: zhaoxm_sut@163.com(通信作者)
(编辑 赵 鹏)