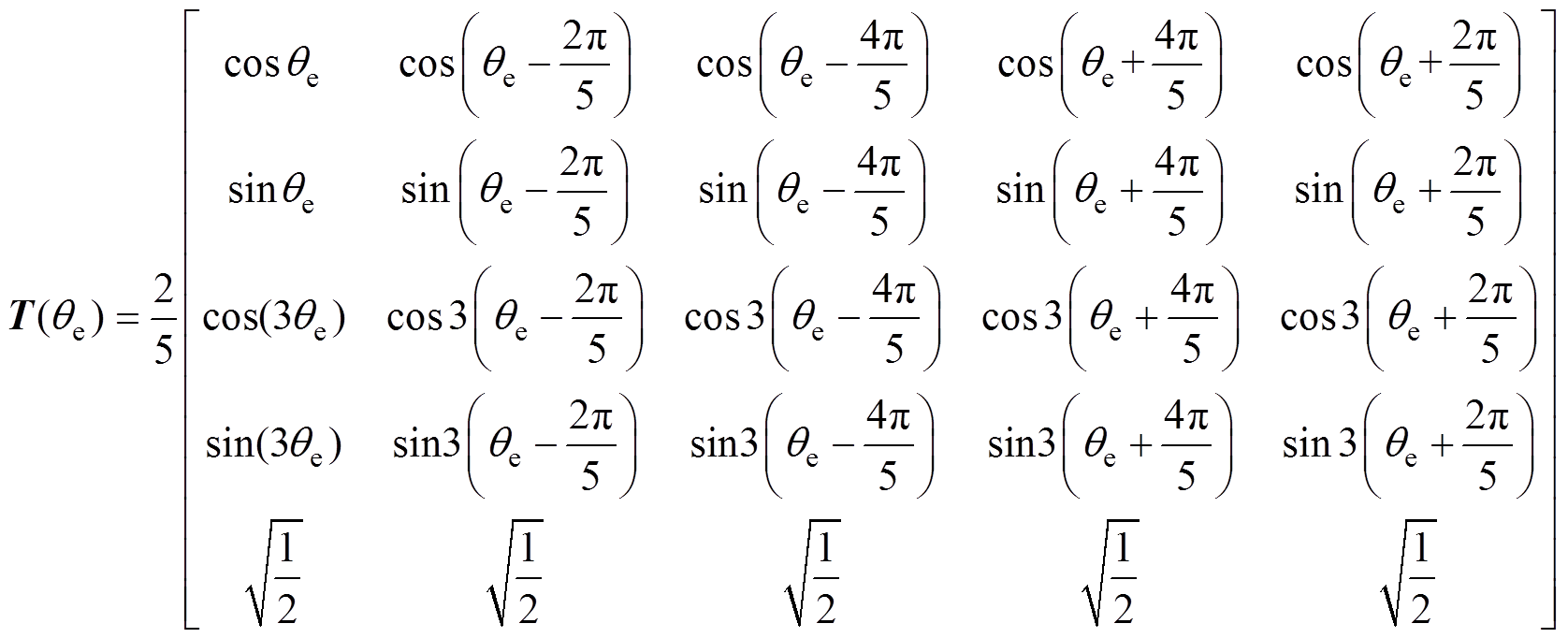 (1)
(1)摘要 同步坐标系下比例积分(PI)控制性能易受参数摄动、转子永磁体谐波磁链以及逆变器死区效应等扰动的影响,限制了其在高性能驱动系统中的应用。为此,该文首先对五相永磁同步电机驱动系统中的扰动进行了特征分析和建模。分析表明,电机驱动性能主要受到系统中的低频和周期扰动影响。其次,设计一个增强型扰动观测器,同时对系统内的低频和周期扰动进行估计,并通过内部反馈通道对扰动进行补偿。再次,对扰动观测器参数的设计进行理论分析并给出参数设计方法。最后,实验结果表明,该文所提方法提高了PI控制器对参数摄动的鲁棒性,并有效抑制了由周期扰动引起的低次谐波电流。
关键词:五相永磁同步电机 周期扰动 增强型扰动观测器 比例积分控制 鲁棒性
永磁同步电机(Permanent Magnet Synchronous Machine, PMSM)具有高功率密度、高效率等优点,在工业界、学术界引起了广泛关注和研究。多相PMSM同时兼具PMSM的优点和多相电机的优点:①每相输出功率低,降低了对开关器件的要求,十分适合低压大功率传动的场合[1-2];②可通过优化转子磁场,提高电机的输出转矩[3-5];③输出转矩脉动频率增加,幅值减小;④可实现容错运行,十分适合电动汽车、航空航天、船舶等对可靠性有严格要求的场合[6];⑤具有多个控制自由度,为高性能控制算法提供更多的可能性[7]。
由于多相PMSM具有以上突出的优点,国内外学者对其进行了大量研究,包括多相PMSM建模[8],多相PWM算法研究[9],多相模型预测控制[10],容错控制技术研究[7]等。现阶段常用的五相PMSM电流控制策略是双同步旋转坐标系下的比例积分(Proportional-Integral, PI)控制器[11]。但是,PI控制性能的抗扰动性能差。学者通过采用鲁棒控制[12],自适应控制[13-14]或者滑模控制[15]来提高系统对参数摄动的鲁棒性,但它们都无法有效地抑制由周期扰动引起的谐波电流。并且鲁棒控制是基于最坏条件设计,需牺牲一部分参考信号跟踪性能,滑模控制容易引起系统抖振。
为了减小由死区效应引起的谐波电流,文献[16-17]提出了一种死区时间补偿方法,但是该方法需要电流极性检测。文献[18-19]采用谐振控制器有效地抑制了谐波电流,但是谐振控制器的引入会降低系统控制器的稳定裕度。文献[20]采用重复控制策略对谐波电流进行抑制,但它增加了系统所需的存储量,且动态性能较差。文献[21-22]分别将模糊控制和线性神经网络应用于抑制定子电流中的谐波电流,但是它们计算复杂,不易于在微控制器中实现。以上方法都是基于反馈的控制系统,它们只具有单个自由度,所以一般需牺牲一部分参考信号跟踪性能用于抑制扰动[23]。
基于扰动观测器的控制器(Disturbance Observer Based Controller, DOBC)具有两个控制自由度,可以在不牺牲参考信号跟踪性能的前提下有效补偿系统中的扰动[23-24],并且扰动观测器可以将被控对象标称化,简化了控制器参数的设计过程[25-27]。文献[28-29]采用扰动观测器,提高了系统对参数摄动的鲁棒性。文献[30]采用二阶滑模扰动观测器有效地减小了模型预测控制中由参数变化引起的稳态跟踪误差。文献[31]采用一个Luenberger状态观测器估计和补偿周期转矩扰动,有效抑制了转矩脉动。目前,大多数DOBC都是针对单一扰动的系统,但实际电机驱动系统受到的扰动一般都是多源的,即同时存在由参数变化引起的低频扰动和由死区时间以及永磁体谐波磁链引起的周期扰动。文献[32]将扰动观测器与重复控制相结合用于抑制多源扰动,但重复控制需增加计算量和存储量,且动态性能较差。
针对五相PMSM驱动系统存在的低频和周期扰动,本文提出了一种增强型扰动观测器(Enhanced Disturbance Observer, EDO),可同时对这两类扰动进行估计。通过将扰动估计值反馈到被控对象的输入端,对系统内的扰动进行补偿,并对基于增强型扰动观测器的比例积分(Enhanced Disturbance Observer Based Proportional Integral, EDOB-PI)控制器的参数设计进行理论分析,给出控制参数设计原则。同时,为了便于观测器的数字实现,给出了其等效实现方法。最后,实验结果验证了文中所提方法的正确性和有效性。
为实现五相永磁同步电机的解耦控制,采用推广派克变换矩阵为
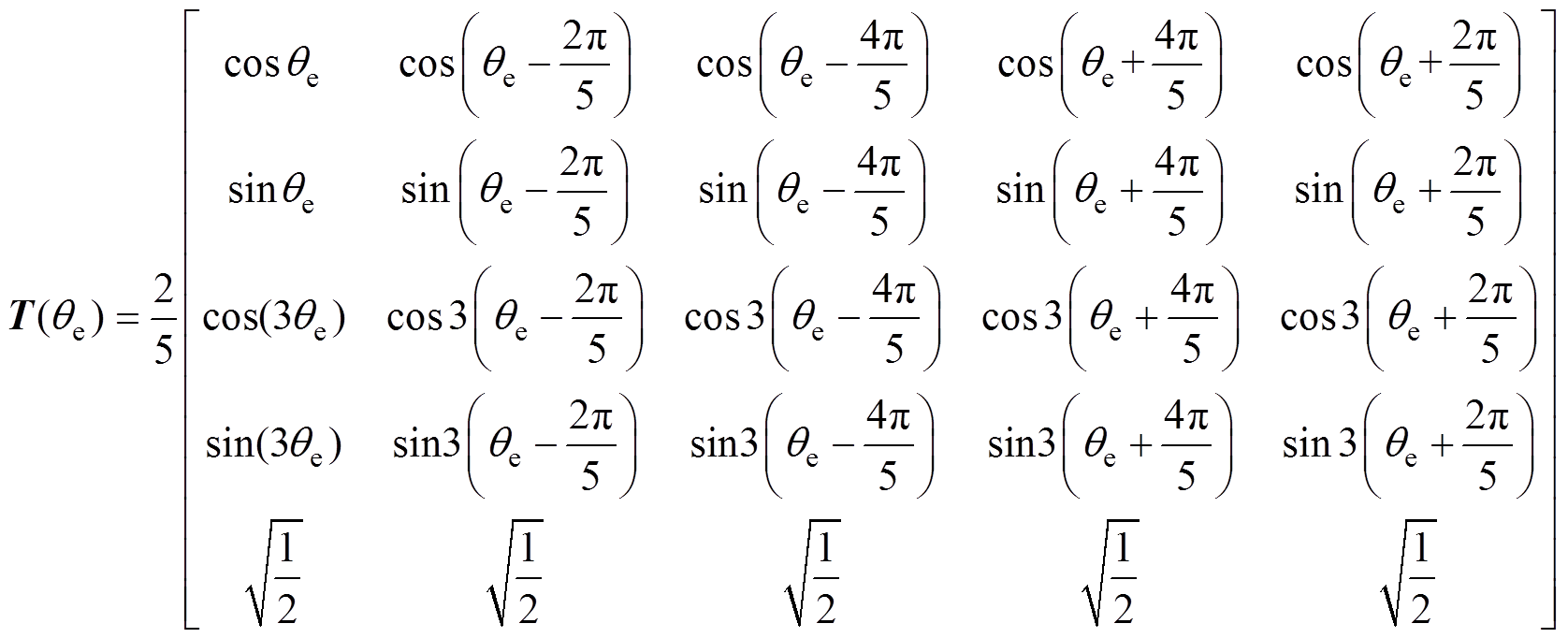 (1)
(1)式中,qe为转子电角度,建立其在同步坐标系下的数学模型。
通过坐标变换矩阵式(1),可将电机变量中基波和10k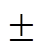 1(k=1, 3, 5, …)次谐波映射到d1-q1平面,也称基波平面,3次谐波和10k
1(k=1, 3, 5, …)次谐波映射到d1-q1平面,也称基波平面,3次谐波和10k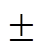 3(k=1, 3, 5, …)次磁链映射到d3-q3平面,也称3次谐波平面。那么,五相表贴式永磁同步电机在同步坐标系下的电压方程为
3(k=1, 3, 5, …)次磁链映射到d3-q3平面,也称3次谐波平面。那么,五相表贴式永磁同步电机在同步坐标系下的电压方程为
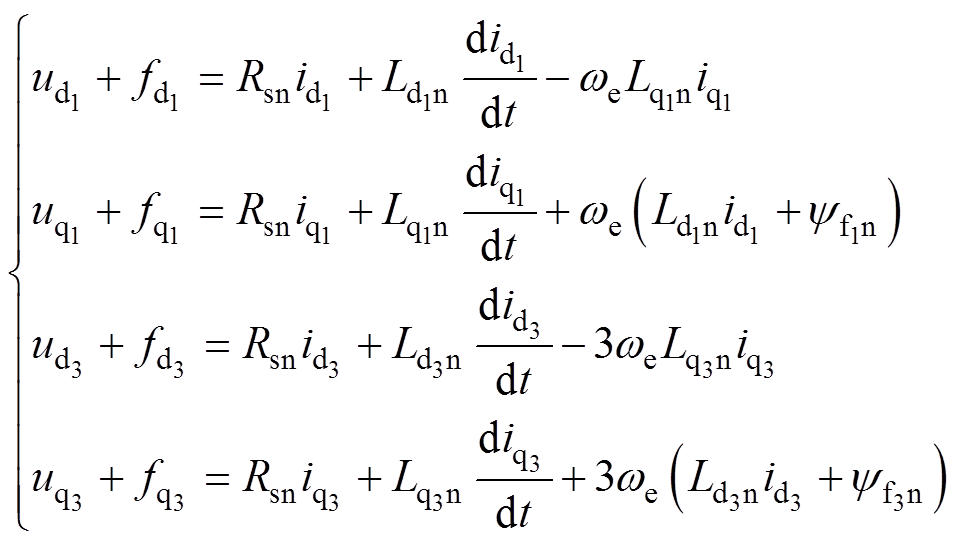 (2)
(2)式中,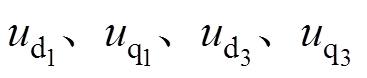 分别为
分别为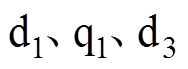 和
和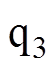 轴电压;
轴电压;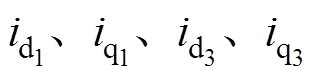 为分别为
为分别为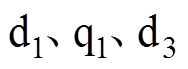 和
和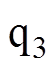 轴电流;
轴电流;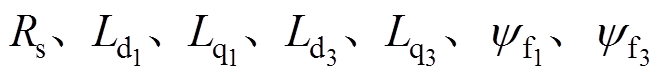 分别为定子电阻、
分别为定子电阻、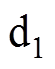 轴直轴电感、
轴直轴电感、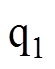 轴交轴电感、
轴交轴电感、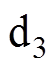 轴直轴电感、
轴直轴电感、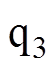 轴交轴电感、永磁体基波和3次谐波磁链的实际值;带有下标“n”的符号为其对应参数的标称值;we为电角速度;
轴交轴电感、永磁体基波和3次谐波磁链的实际值;带有下标“n”的符号为其对应参数的标称值;we为电角速度;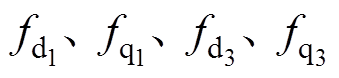 分别表示
分别表示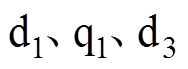 和
和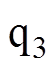 轴的集中扰动。
轴的集中扰动。
由参数变化及不确定性引起的扰动分量为
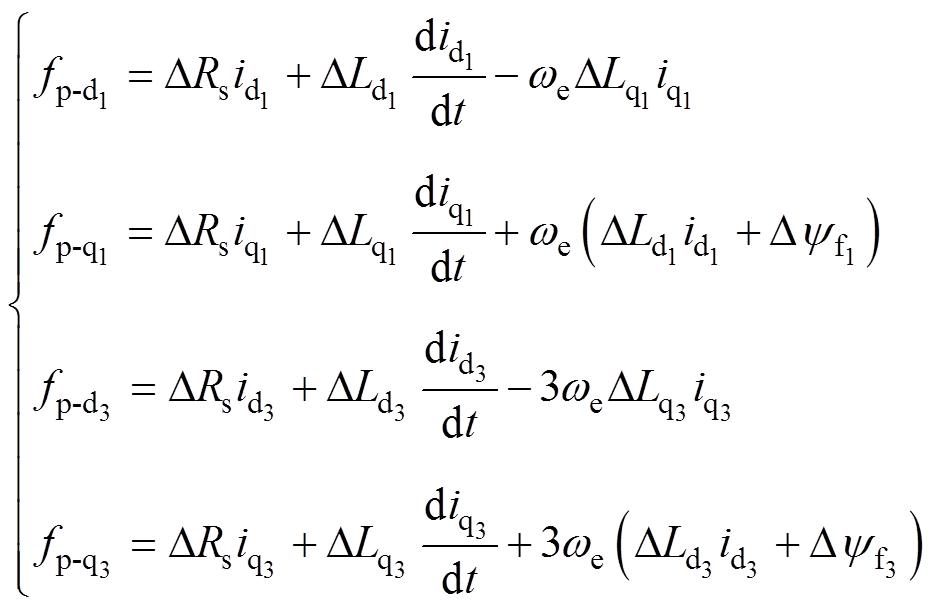 (3)
(3)式中,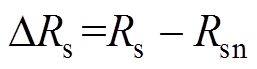 ,
, 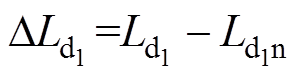 ,
, 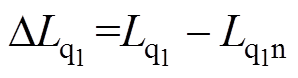 ,
, 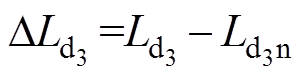 ,
, 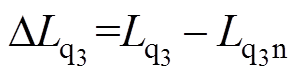 ,
, 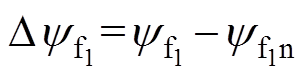 ,
, 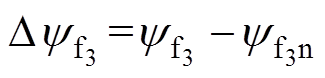 ;
;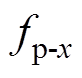 表示由参数变化引起的扰动分量,x
表示由参数变化引起的扰动分量,x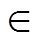 {d1, q1, d3, q3}。考虑到电机参数变化缓慢,在电机稳态时,
{d1, q1, d3, q3}。考虑到电机参数变化缓慢,在电机稳态时,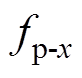 可近似为一个常值分量,在电机动态时,其是一个非周期连续变化的量。
可近似为一个常值分量,在电机动态时,其是一个非周期连续变化的量。
自然坐标系下的奇次谐波反电动势通过坐标变换式(1)映射为同步坐标系下的10次以及10的倍数次谐波反电动势。与三相系统类似[18, 22],死区效应同样会在五相系统中引起基波及奇次谐波的相电压误差,其可通过式(1)映射为同步坐标系下的常值、10次以及10的倍数次电压误差。例如,自然坐标系下的7次和13次信号,通过坐标变换式(1)映射为d3-q3平面的10次信号,而自然坐标系下的9次和11次信号映射为d1-q1平面的10次信号。那么,由转子永磁体谐波分量和死区效应引起的扰动之和可表示为
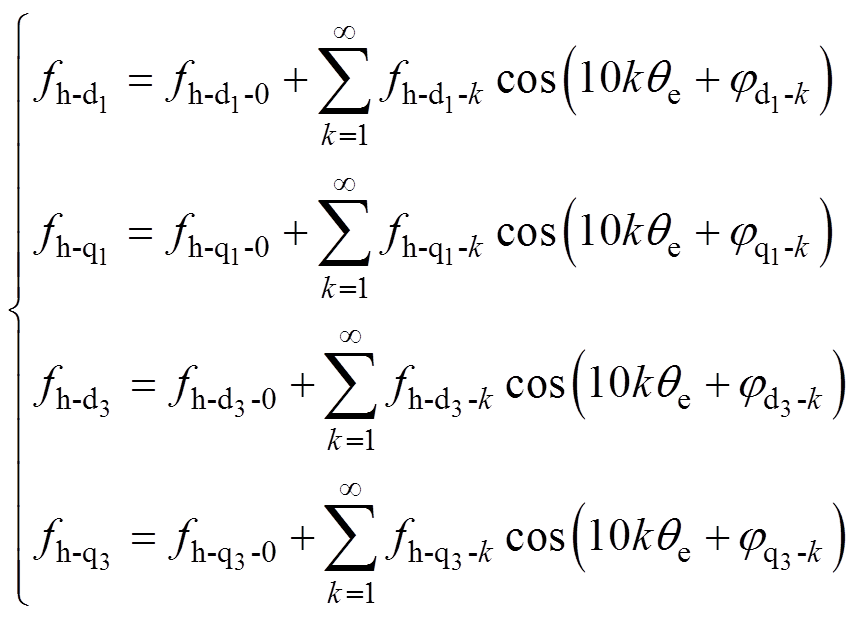 (4)
(4)式中,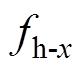 表示由转子永磁体谐波和死区效应引起的扰动分量,x
表示由转子永磁体谐波和死区效应引起的扰动分量,x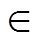 {d1, q1, d3, q3};
{d1, q1, d3, q3};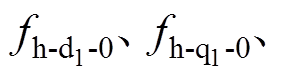
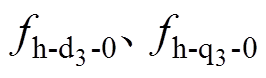 为
为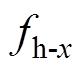 的常值分量;
的常值分量;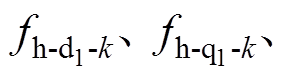
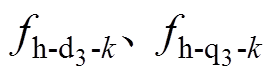 为
为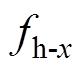 的10k次周期分量的幅值;
的10k次周期分量的幅值;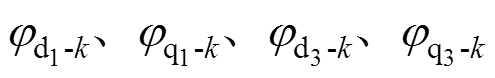 为初始相位。
为初始相位。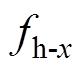 的幅值和相位与电机运行的工况、电机温度以及逆变器非线性有关,无法通过建模精确得到,但其频率是10次及10的倍数次基波频率,可通过测量电机转速获取,后文可知周期扰动的观测只需获取扰动的频率信息。由式(3)和式(4)可知,电流环集中扰动中包含常值分量、非周期连续变化分量以及周期连续变化分量三类分量。其可表示为
的幅值和相位与电机运行的工况、电机温度以及逆变器非线性有关,无法通过建模精确得到,但其频率是10次及10的倍数次基波频率,可通过测量电机转速获取,后文可知周期扰动的观测只需获取扰动的频率信息。由式(3)和式(4)可知,电流环集中扰动中包含常值分量、非周期连续变化分量以及周期连续变化分量三类分量。其可表示为
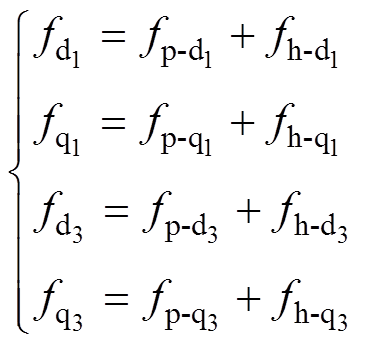 (5)
(5)
图1给出了扰动观测器的结构。频率在滤波器Q通带范围内的集中扰动f,即使在被控对象标称模型与实际模型不匹配时,依然可以被完全抑制[23-26]。
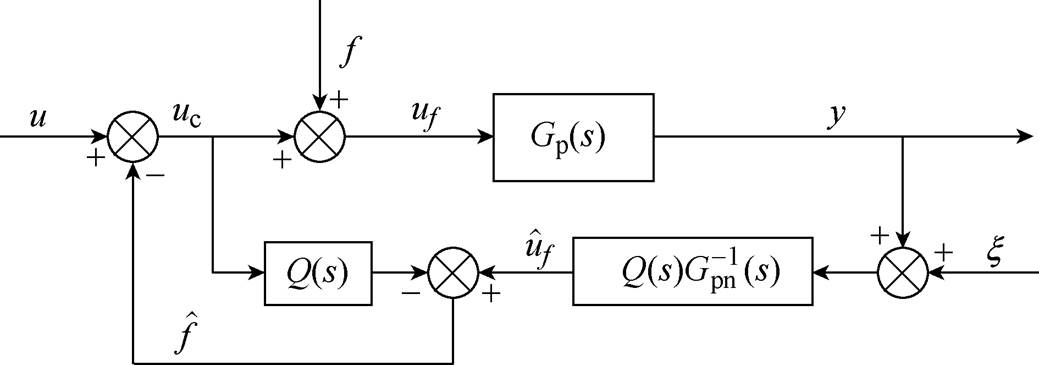
图1 扰动观测器的估计与补偿示意图
Fig.1 The block diagram of the disturbance observer
图2给出了基于扰动观测器的比例积分控制(DOB-PI)的结构框图,r表示参考信号,Gc为控制器,x 为测量噪声。本文采用PI控制器,即
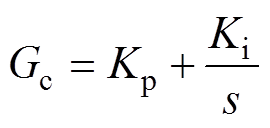 (6)
(6)式中,Kp为比例增益系数;Ki为积分增益系数。
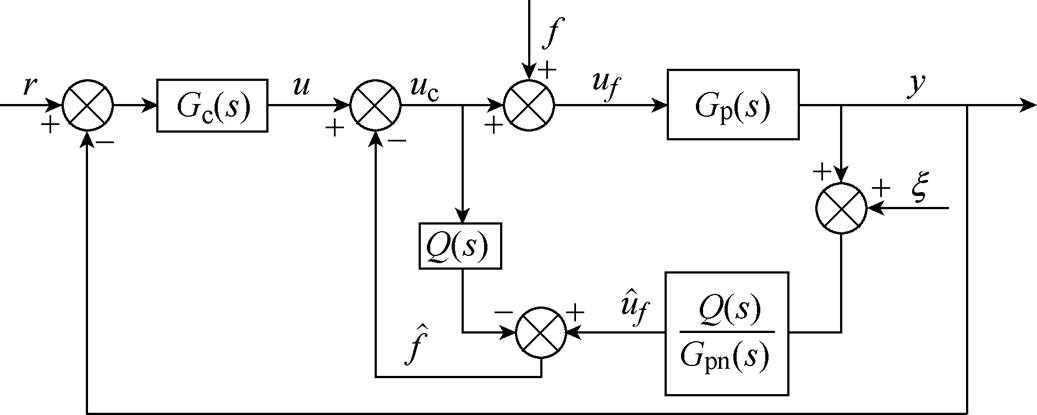
图2 基于扰动观测器的比例积分控制的结构框图
Fig.2 The block diagram of the DOB-PI
由图2可得以下闭环传递函数
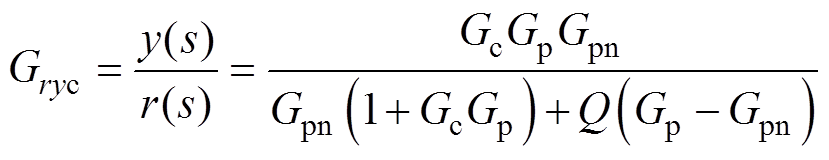 (7)
(7)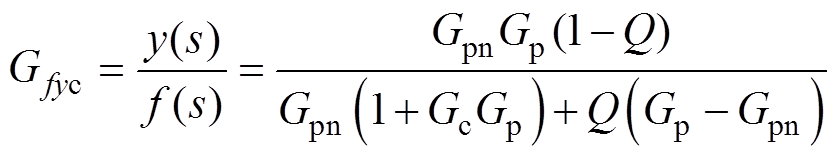 (8)
(8)
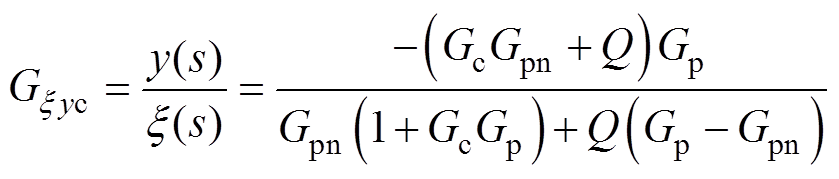 (9)
(9)
由式(7)可知,在滤波器Q的通带范围内,即Q的幅值为1,受到外界干扰的不确定参数的系统Gp对参考输入信号的响应性能/跟踪性能与标称参数系统Gpn对参考输入信号的跟踪性能基本一致。由式(8)可知,在滤波器Q的通带范围内,外界和内部的扰动对系统基本无影响。可以得出结论,基于扰动观测器的控制器不仅不会影响系统的跟踪性能,而且能够完全消除频率在滤波器Q带宽内的扰动对系统输出的影响;在滤波器的阻带,系统在该频带内的响应与传统PI控制器作用于系统时一致。电流环的参考值一般为直流量,并且扰动的频率特性一般表现为低频或者10倍基波频带,所以在滤波器阻带内的响应特性对系统控制性能影响不大。
在传统扰动观测器的设计过程中,一般只考虑常值或者低频扰动,所以滤波器Q一般选择低通滤波器。但由第1节可知,电流环中的扰动不仅包含常值和低频扰动,还包含周期扰动。考虑到10的倍数次周期扰动含量较少,对系统性能的影响较小,因此,本文只考虑同步坐标系下的10次周期扰动。下文将以q1轴电流环控制器为例设计基于增强型扰动观测器的比例积分(EDOB-PI)控制,其他轴电流环的设计过程类似,被控对象标称模型为
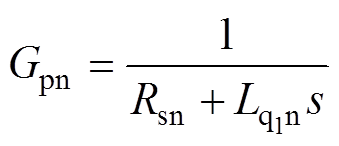 (10)
(10)分别采用低通滤波器GLP和带通滤波器GBP对低频扰动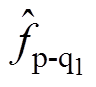 和周期扰动
和周期扰动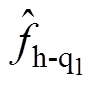 进行观测,EDOB-PI控制器的结构框图如图3所示,构成增强型扰动观测器。图3中,
进行观测,EDOB-PI控制器的结构框图如图3所示,构成增强型扰动观测器。图3中,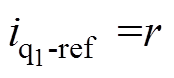 为电流环参考值,
为电流环参考值,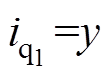 为电流环输出信号。
为电流环输出信号。
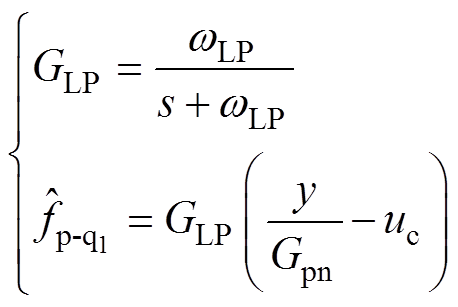 (11)
(11)
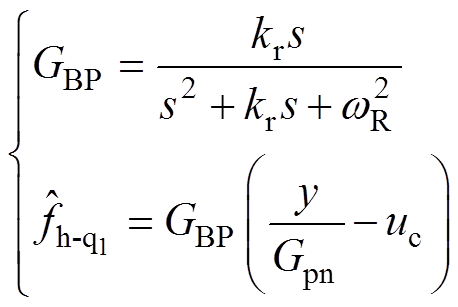 (12)
(12)式中,wLP为低通滤波器截止频率;wR为带通滤波器的中心频率;kr为带通滤波器质量因子。本文为了抑制10次周期扰动,令wR=10we。
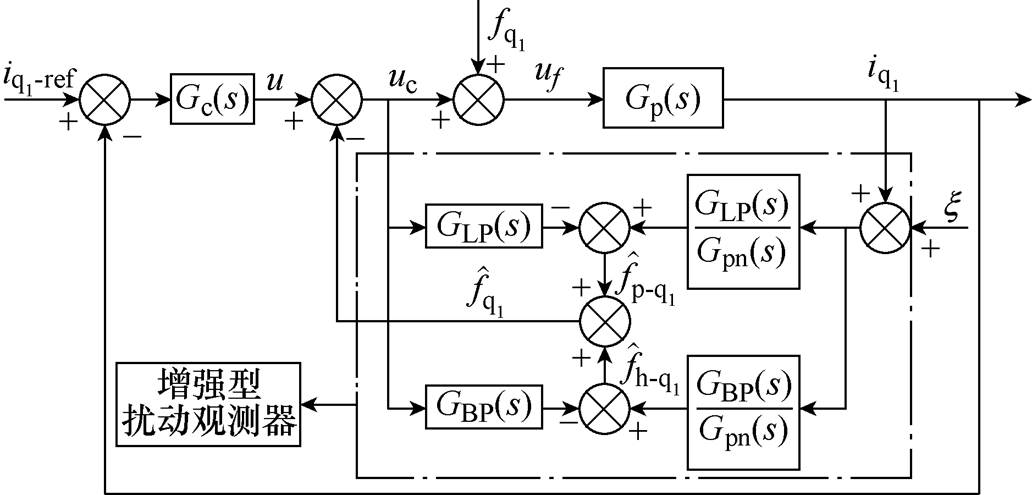
图3 EDOB-PI控制器的结构框图
Fig.3 Block diagram of the EDOB-PI controller
图4给出了低通滤波器和带通滤波器的伯德图。当转速较低时,周期扰动会被低通滤波器和带通滤波器重复观测。本文为了实现扰动观测的解耦,采用解耦低通滤波器GLPC代替低通滤波器GLP。
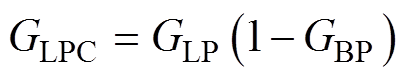 (13)
(13)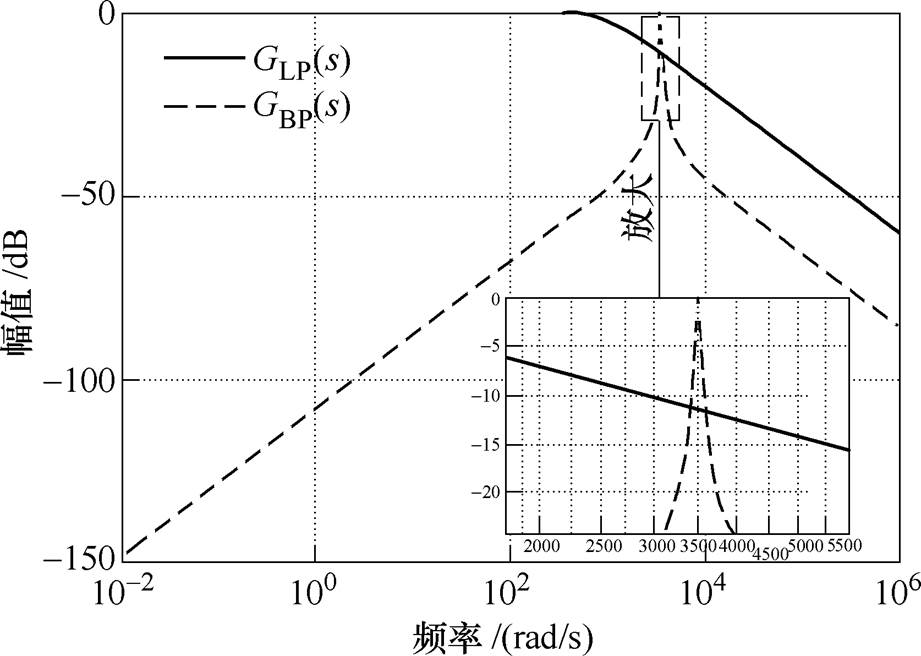
图4 低通滤波器GLP和带通滤波器GBP的幅频特性
Fig.4 Bode plot of the filter GLP and GBP
本文采用的五相永磁同步电机的参数见表1。为了便于控制器参数的设计,下文中的论述将结合表1中的参数。由于被控对象可以被扰动观测器标称化[25],PI调节器的比例增益系数与积分增益系数可通过零极点对消法来设计[28]。那么式(6)中的参数Kp和Ki的设计值分别如式(14)和式(15)所示。在Q =1时,电流环的闭环传递函数如式(16)所示,电流环的闭环响应呈无超调的一阶惯性响应。
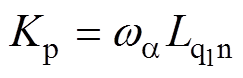 (14)
(14)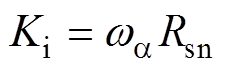 (15)
(15)
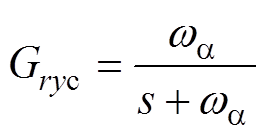 (16)
(16)
式中,wa为根据电流参考值跟踪性能需求选取的电流环带宽,本文选定wa=1 500rad/s。
表1 五相PMSM参数
Tab.1 Parameters of five-phase PMSM
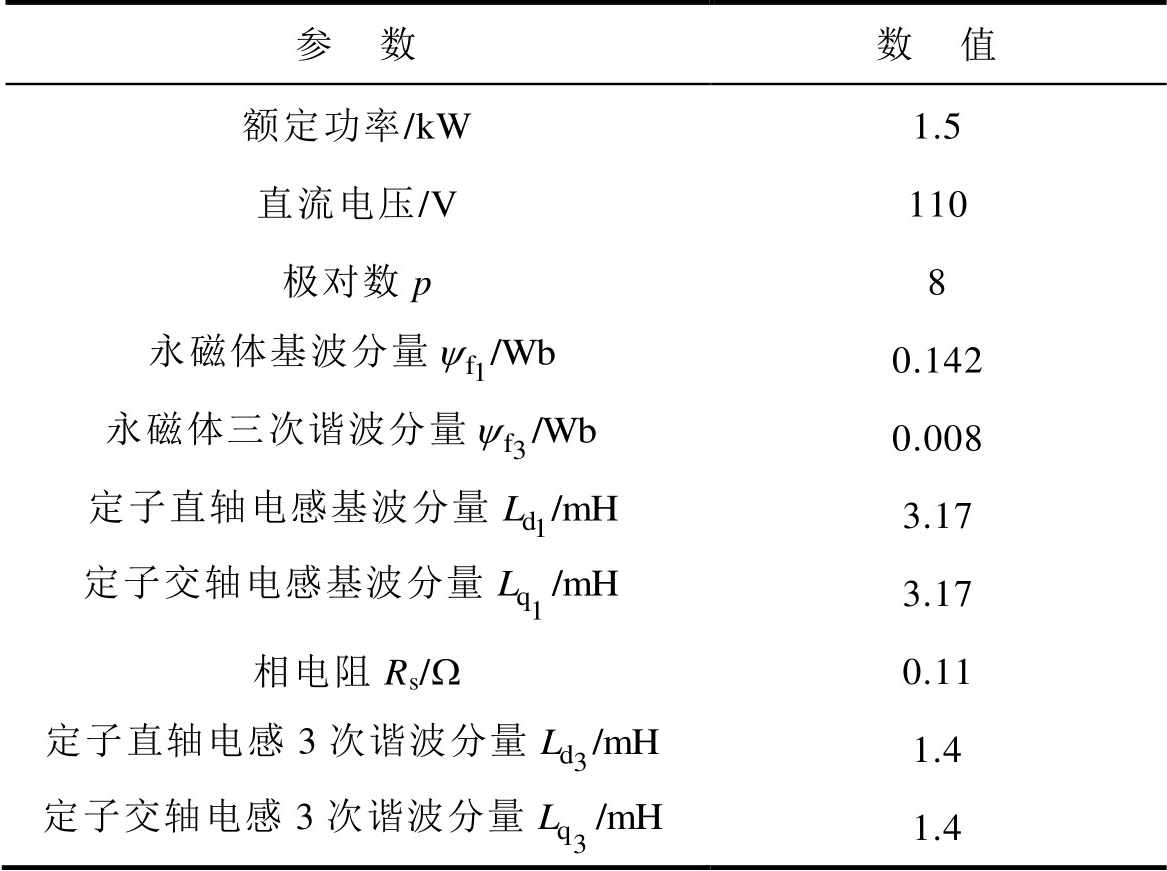
参 数数 值 额定功率/kW1.5 直流电压/V110 极对数p8 永磁体基波分量0.142 永磁体三次谐波分量0.008 定子直轴电感基波分量3.17 定子交轴电感基波分量3.17 相电阻Rs/W0.11 定子直轴电感3次谐波分量1.4 定子交轴电感3次谐波分量1.4
本文设计的增强型扰动观测器中包含参数wLP和kr,其中wLP决定了低频扰动抑制能力,kr决定了周期扰动的抑制能力。为了使得被控对象在其闭环带宽内被标称化,那么低通滤波器的带宽wLP需大于或等于闭环带宽wa。图5和图6分别给出了wLP取不同值时的传递函数Gfyc和Gz yc的伯德图。图5中,wLP=0时表示不加扰动观测器时的PI调节器情况,可以看出扰动观测的引入,显著增强了系统的低频扰动抑制能力,且wLP越大,扰动抑制能力越强,但是对测量噪声的抑制能力越弱,如图6所示。所以,wLP的选取需在低频扰动抑制能力和测量噪声抑制能力之间折中选择。本文根据实测情况,选定wLP=3wa。
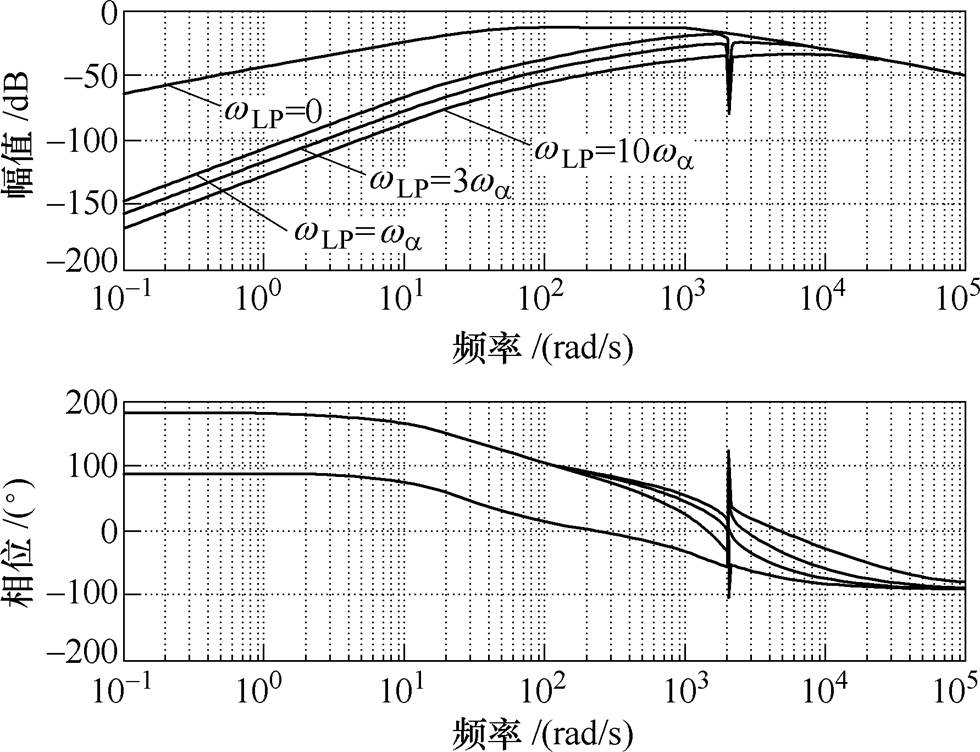
图5 扰动到输出闭环传递函数Gfyc的伯德图
Fig.5 Bode plot of the transfer function Gfyc
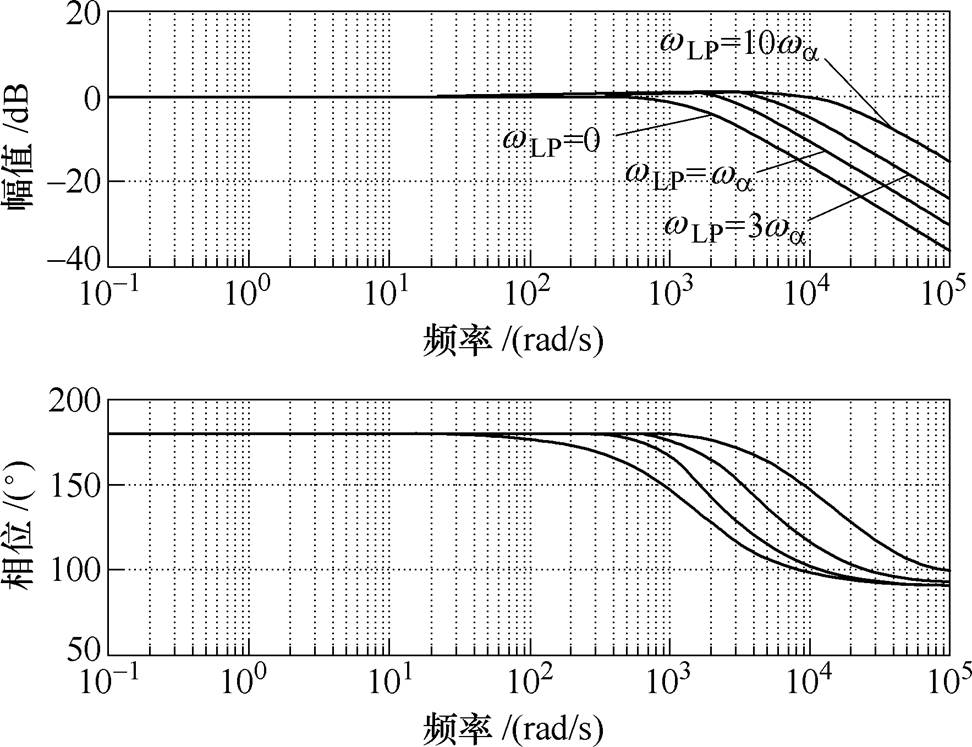
图6 测量噪声到输出闭环传递函数Gz yc的伯德图
Fig.6 Bode plot of the transfer function Gzyc
图7和图8分别给出了kr取不同值时的带通滤波器GBP和扰动到输出闭环传递函数Gfyc的伯德图。由图7中可见,kr越大,带通滤波器的带宽越大,观测器对电机转速波动的敏感性越低。由图8可见,kr=0,Gfyc增益很大,表示传统PI调节器对周期扰动的抑制能力有限。而采用扰动观测器后,Gfyc增益在中心频率附近的增益明显小于-60dB,可近似为无穷小,表明周期扰动得到了有效抑制,且kr越大,Gfyc在中心频率附近的增益越小,对周期扰动的抑制能力越强。同样,kr的选取也需在扰动抑制能力和测量噪声抑制能力之间折中选择。本文根据实测情况,选择kr=50。
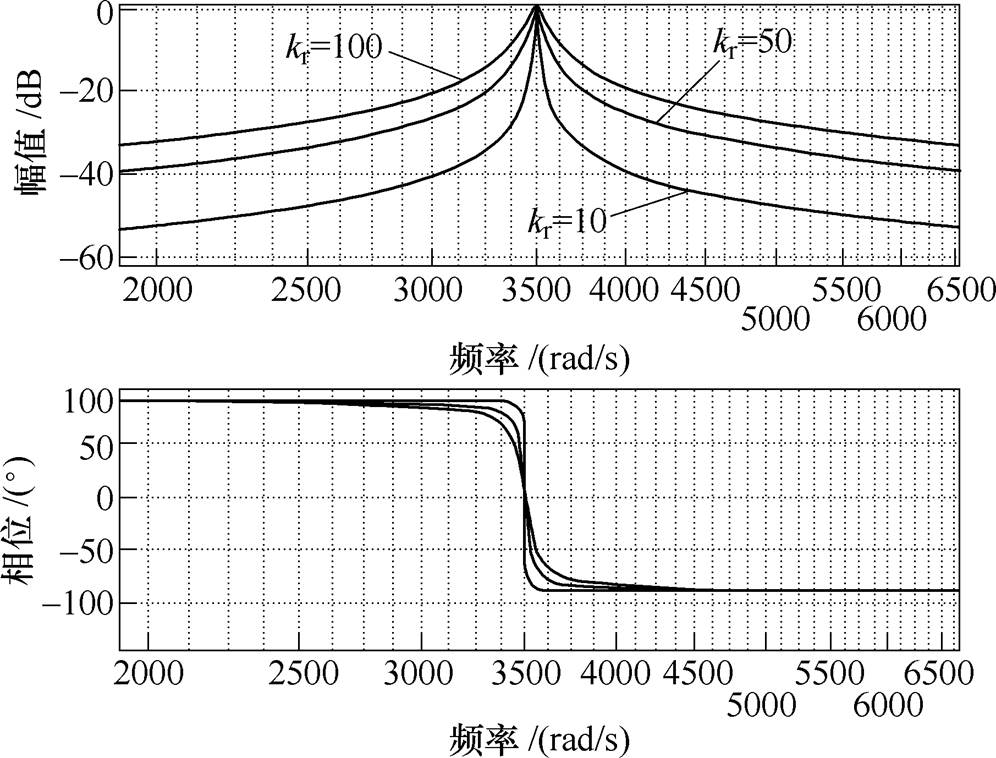
图7 kr取不同值时的带通滤波器GBP的伯德图
Fig.7 Bode plot of the band pass filter GBP with different kr
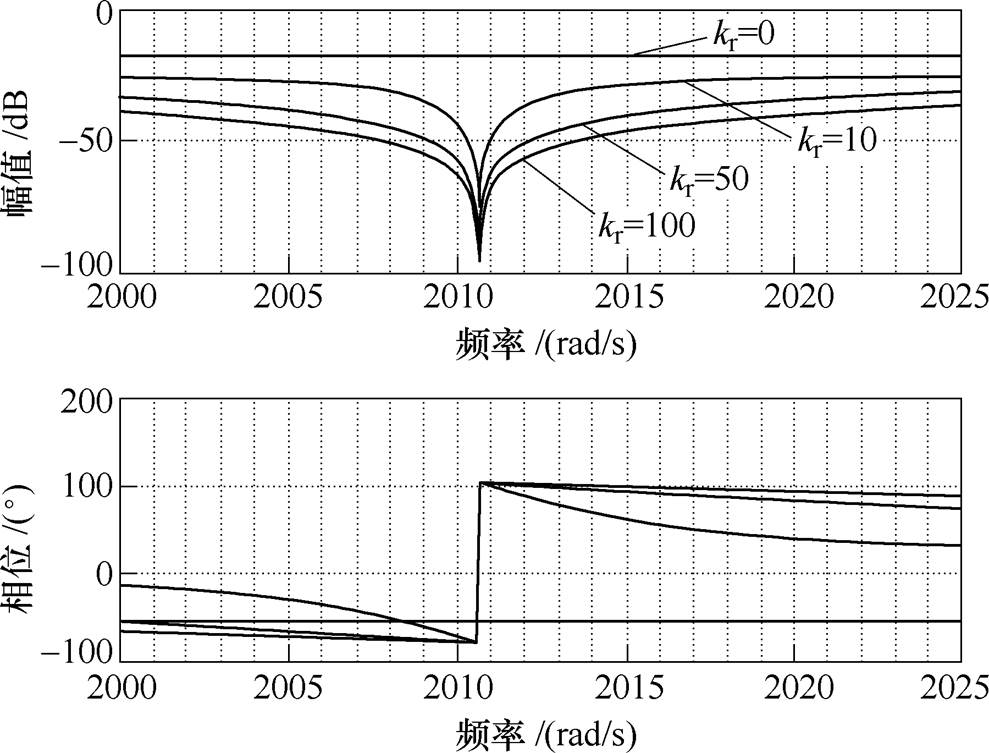
图8 kr取不同值时扰动到输出传递函数Gfyc的伯德图
Fig.8 Bode plot of transfer function Gfyc with different kr
为验证基于EDOB-PI控制系统对参数变化的鲁棒性,图9给出了控制器采用三种不同模型参数(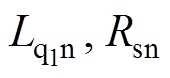 )时的电流环闭环传递函数的伯德图。可以看出,图中三条幅频增益曲线基本重合,系统带宽(-3dB处)为1 500rad/s,与设定值一致,三条曲线只在高频段有所区别,但高频段的增益很小,对系统性能基本无影响。可得出结论,即使控制器采用的标称参数与被控对象实际参数不一致时,系统响应都表现为标称模型响应,表明EDOB-PI控制具有较强的对参数变化的鲁棒性。由图9可见,扰动观测器的引入对PI控制器的电流参考跟踪性能没有影响,间接表明EDOB-PI控制器是一个两自由度控制器。
)时的电流环闭环传递函数的伯德图。可以看出,图中三条幅频增益曲线基本重合,系统带宽(-3dB处)为1 500rad/s,与设定值一致,三条曲线只在高频段有所区别,但高频段的增益很小,对系统性能基本无影响。可得出结论,即使控制器采用的标称参数与被控对象实际参数不一致时,系统响应都表现为标称模型响应,表明EDOB-PI控制具有较强的对参数变化的鲁棒性。由图9可见,扰动观测器的引入对PI控制器的电流参考跟踪性能没有影响,间接表明EDOB-PI控制器是一个两自由度控制器。
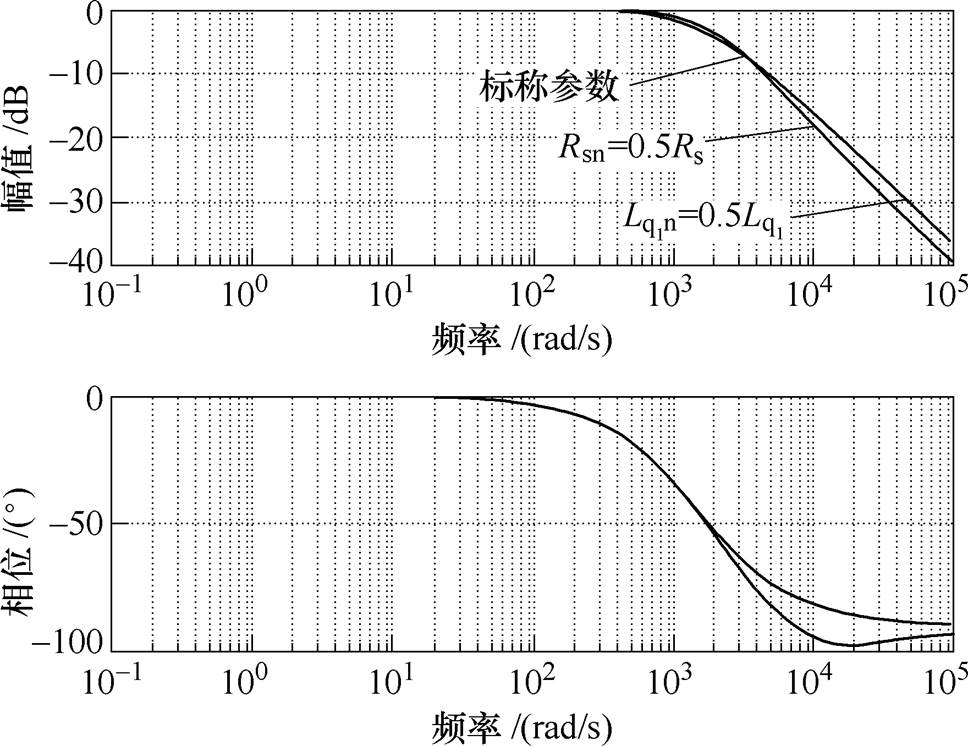
图9 不同参数设置时闭环传递函数Gryc的伯德图
Fig.9 Bode plot of Gryc with different parameter settings
为分析EDOB-PI控制器的闭环稳定性,图10给出了电流环的开环Nyquist曲线,由于电流环的开环传递不存在正实部极点,且w 从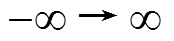 变化时,增补完整的开环频率特性极坐标图不包含点(-1, j0)。由Nyquist稳定判据可知,在PI控制的基础上加入增强型扰动观测器后,闭环系统仍然稳定的,且系统的稳定裕度几乎不受电机参数变化的影响,验证了EDOB-PI控制对参数变化的鲁棒性。由式(8)可知,在闭环系统稳定的前提下,本文所提的EDOB-PI控制器能够有效地抑制频率在滤波器Q带宽内的扰动对系统输出的影响。
变化时,增补完整的开环频率特性极坐标图不包含点(-1, j0)。由Nyquist稳定判据可知,在PI控制的基础上加入增强型扰动观测器后,闭环系统仍然稳定的,且系统的稳定裕度几乎不受电机参数变化的影响,验证了EDOB-PI控制对参数变化的鲁棒性。由式(8)可知,在闭环系统稳定的前提下,本文所提的EDOB-PI控制器能够有效地抑制频率在滤波器Q带宽内的扰动对系统输出的影响。
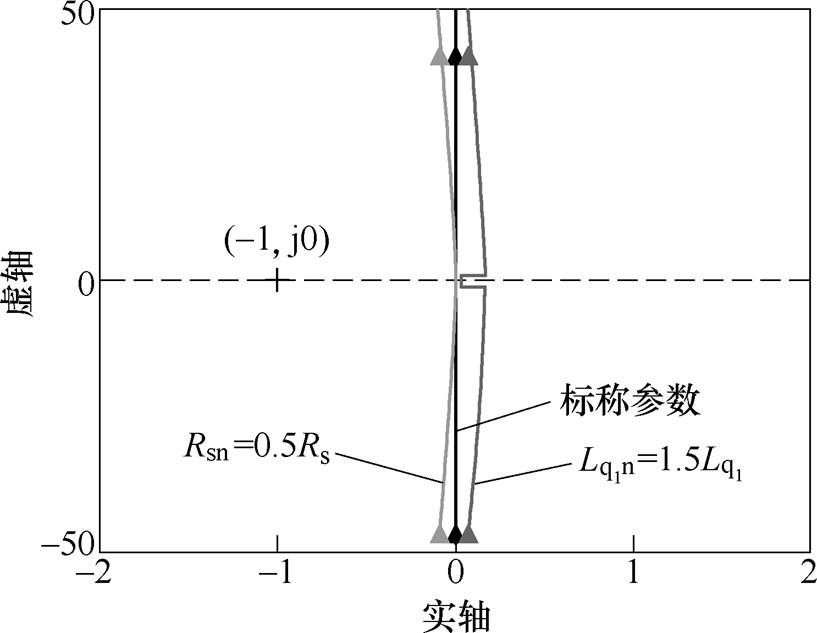
图10 采用EDOB-PI控制的电流环的Nyquist曲线
Fig.10 Nyquist curves of current loop with EDOB-PI
式(13)实现了扰动观测的解耦,但其增加了扰动观测器实现的难度,为此,本节提出了一种等效解耦方法。由式(13)得
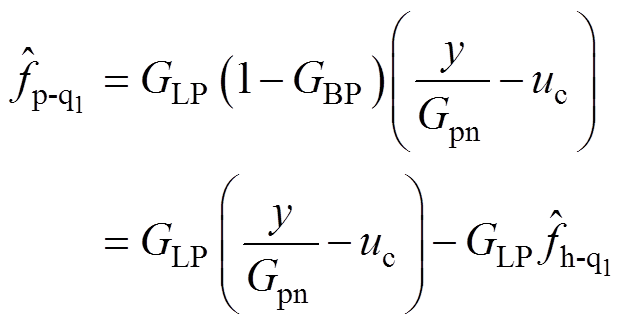 (17)
(17)由式(17)可得等效扰动观测解耦方法的控制框图如图11所示,即将周期扰动的估计值反馈到低频扰动观测器的输入端uc,用于补偿低通滤波器GLP观测得到的周期扰动,从而实现解耦。图中只用到了GLP和GBP,而未使用GLPC,简化了实现过程。
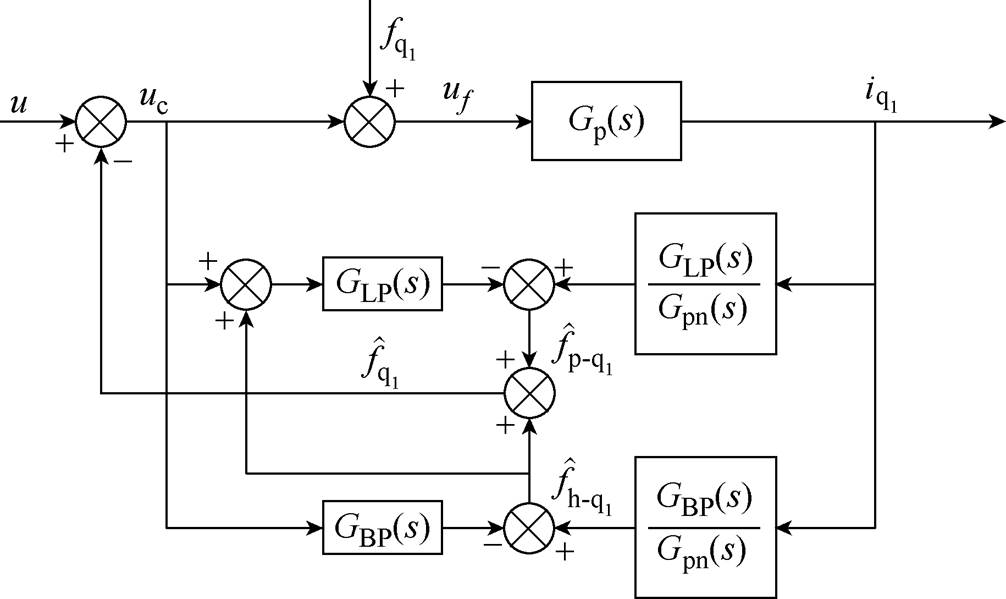
图11 增强型扰动观测器的等效控制框图
Fig.11 Equivalent control block diagram of EDO
本文采用低通滤波器对低频扰动进行观测,低通滤波器的数字实现过程较为容易,这里不作介绍。周期扰动的观测过程采用了带通滤波器,带通滤波器的中心频率与电机转速呈正比。直接对带通滤波器传递函数进行离散化,需要计算三角函数,所以实现过程较为复杂[33]。本文将带通滤波器传递函数GBP分解为两个积分器,那么周期扰动观测环节的等效控制框图如图12所示。两个积分器结构的等效带通滤波器简化了离散化过程,便于在微控制器中进行数字实现。

图12 周期扰动观测环节的等效控制框图
Fig.12 Equivalent control block diagram of periodic disturbance observation
基于扰动观测器的比例积分控制在以TI公司DSP芯片TMS320F28335为核心控制器的五相永磁同步电机驱动平台上进行验证。五相PMSM驱动实验平台如图13所示,实验平台所用的电机参数见 表1。五相PMSM驱动的控制框图如图14所示。整个闭环系统由转速环和电流环构成,转速环采用比例积分控制器,转速环的输出为q1轴电流的参考值。基波和3次谐波电流都采用EDOB-PI控制器。基波平面d1轴和3次谐波平面的电流参考值都设置为零。文献[28]提出了基于扰动观测器的PI控制器(DOB- PI),提高了系统对参数变化的鲁棒性,但该方法未考虑系统中存在的周期扰动。本节对比分析了PI、DOB-PI和EDOB-PI的抗扰动性能。

图13 五相PMSM驱动实验平台
Fig.13 Experimental platform of five phase PMSM drives
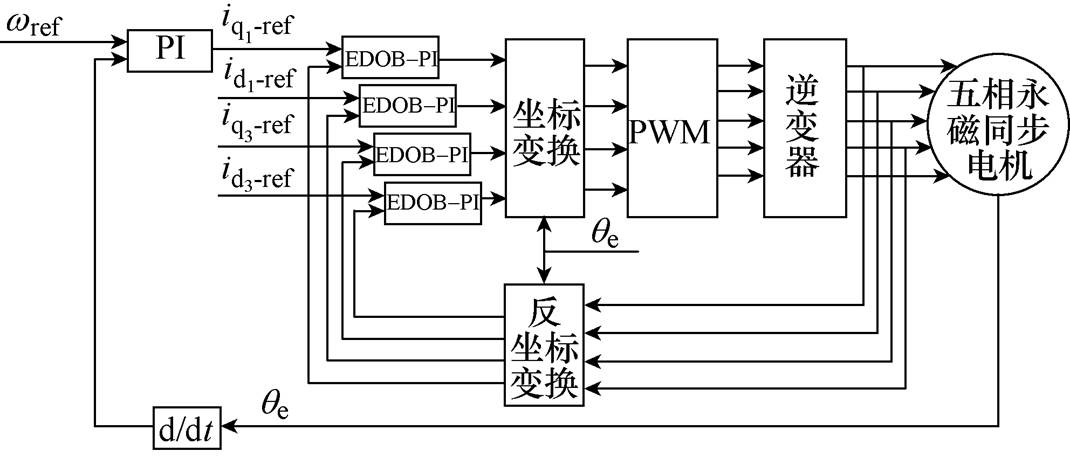
图14 五相PMSM驱动系统控制框图
Fig.14 Block diagram of five phase PMSM drives
4.2.1 稳态下周期扰动抑制性能验证
图15和图16分别给出了负载转矩为9N·m,转速为240r/min时EDO的观测结果和采用PI、DOB-PI和EDOB-PI控制方法时定子相电流稳态波形及频谱。由图15可见,电流环中的扰动同时包含常值分量和周期分量。由图16可见,受逆变器死区效应的影响,采用PI和DOB-PI控制器的电机相电流中包含较大的低次谐波,存在零电流钳位现象,而采用EDOB-PI控制器可以观测并补偿死区效应引起的周期扰动,从而有效地抑制了电流中的7次和9次谐波,减小了电流的总谐波畸变率(Total Harmonics Distortion, THD)值,三种方法稳态性能比较见表2,与DOB-PI控制器相比,EDOB-PI控制器可以降低电流THD值47.5%,降低7次谐波电流83.2%,且降低9次谐波电流44.8%。
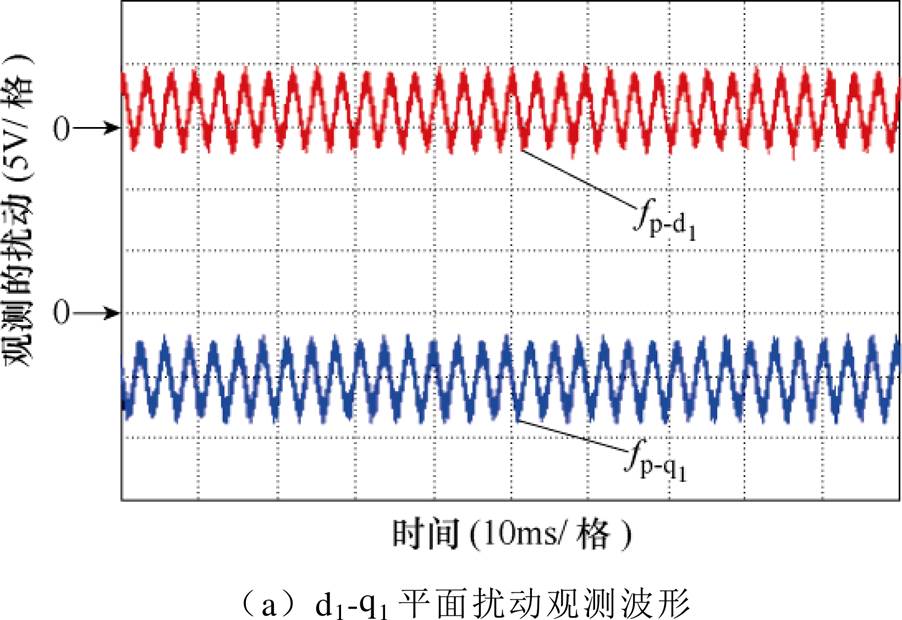
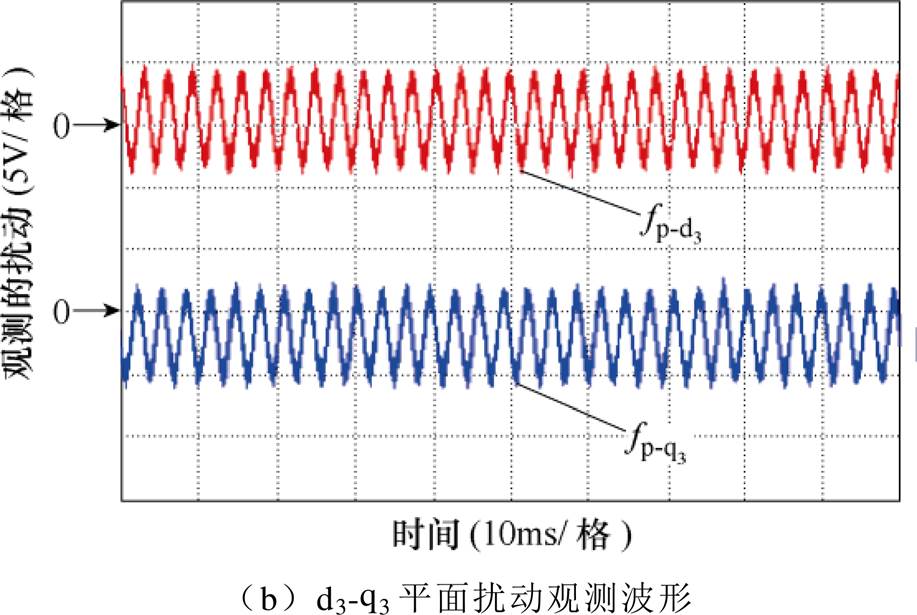
图15 增强型扰动观测器(EDO)的估计结果
Fig.15 Estimation results of EDO
4.2.2 动态情况下周期扰动抑制性能验证
图17给出了电机转速从100r/min加速到360r/min的过程中,采用EDOB-PI控制器的定子电流波形。可以看出,在转速变化过程中,EDOB-PI控制也能很好地抑制周期扰动引起的谐波电流,改善由死区效应引起的零电流钳位现象。
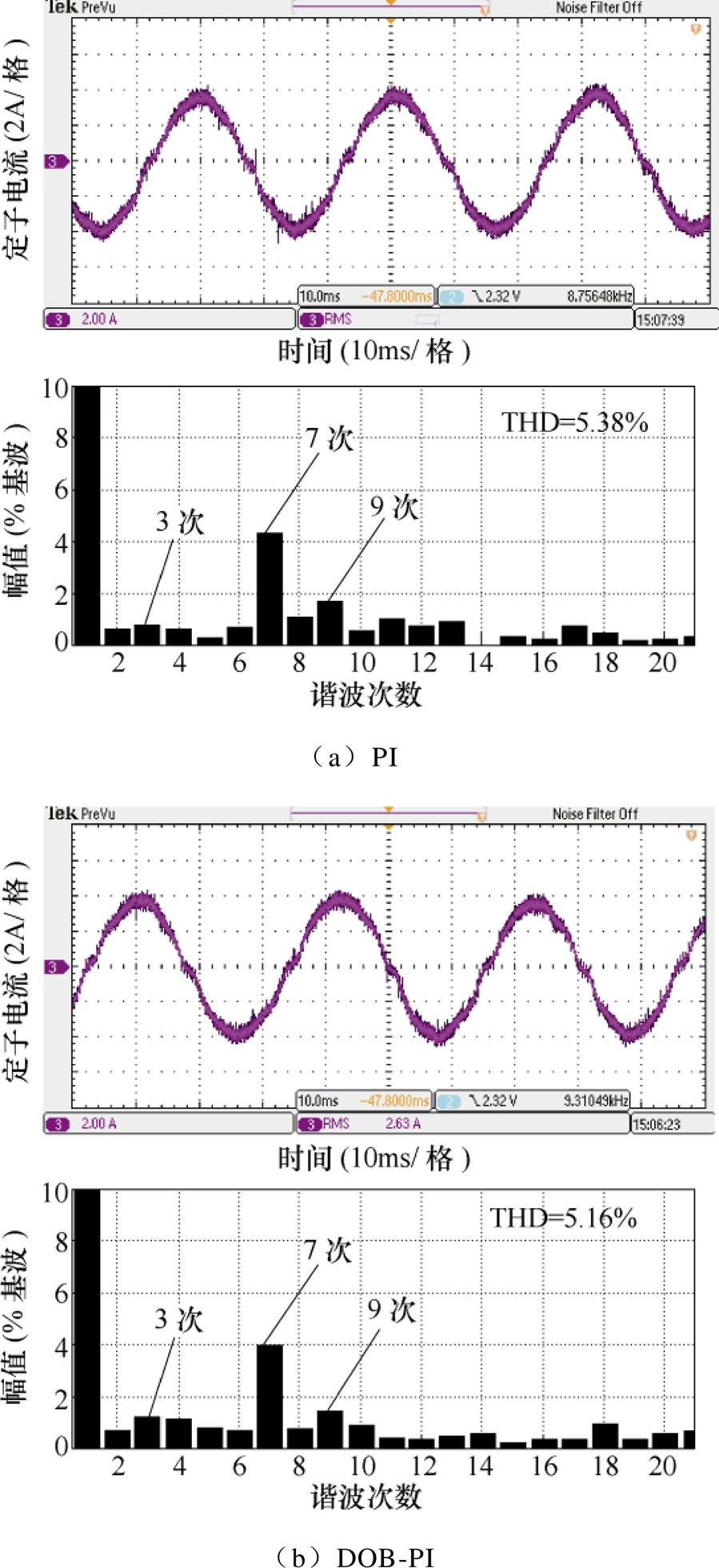
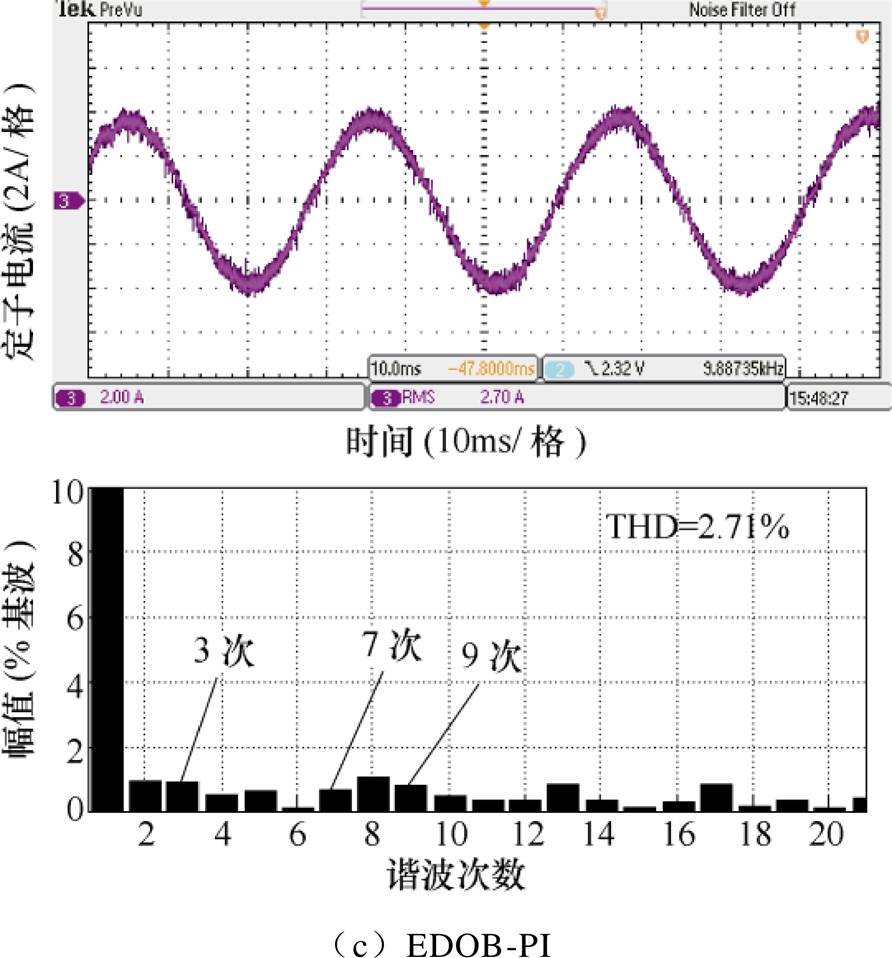
图16 三种控制方法的相电流波形及频谱
Fig.16 Steady state stator-current waveforms and its spectrum
表2 三种方法稳态性能比较
Tab.2 Performance comparison for three methods
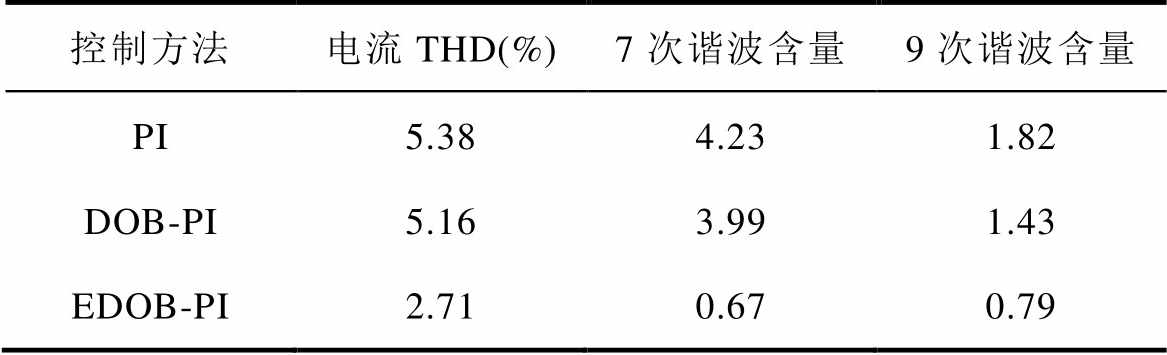
控制方法电流THD(%)7次谐波含量9次谐波含量 PI5.384.231.82 DOB-PI5.163.991.43 EDOB-PI2.710.670.79
图18和图19分别给出了EDOB-PI控制器取定子电阻阻值为标称值的1/2时和取定子电感感值为标称值的1.5倍时的定子电流波形及其频谱。将图18和图19的电流波形及频谱与图16c进行对比,可以看出,当电机参数发生变化时,采用EDOB-PI控制器依然能有效地抑制周期扰动引起的谐波电流,验证了EDOB-PI控制器在稳态时对参数变化的鲁棒性。
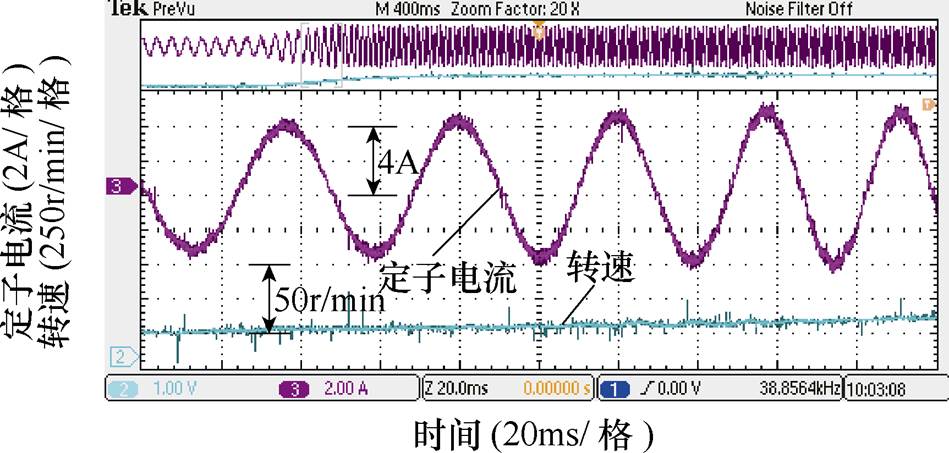
图17 电机转速变化过程中定子相电流输出波形
Fig.17 Stator current and speed waveforms when speed is increased from 100r/min to 360r/min.
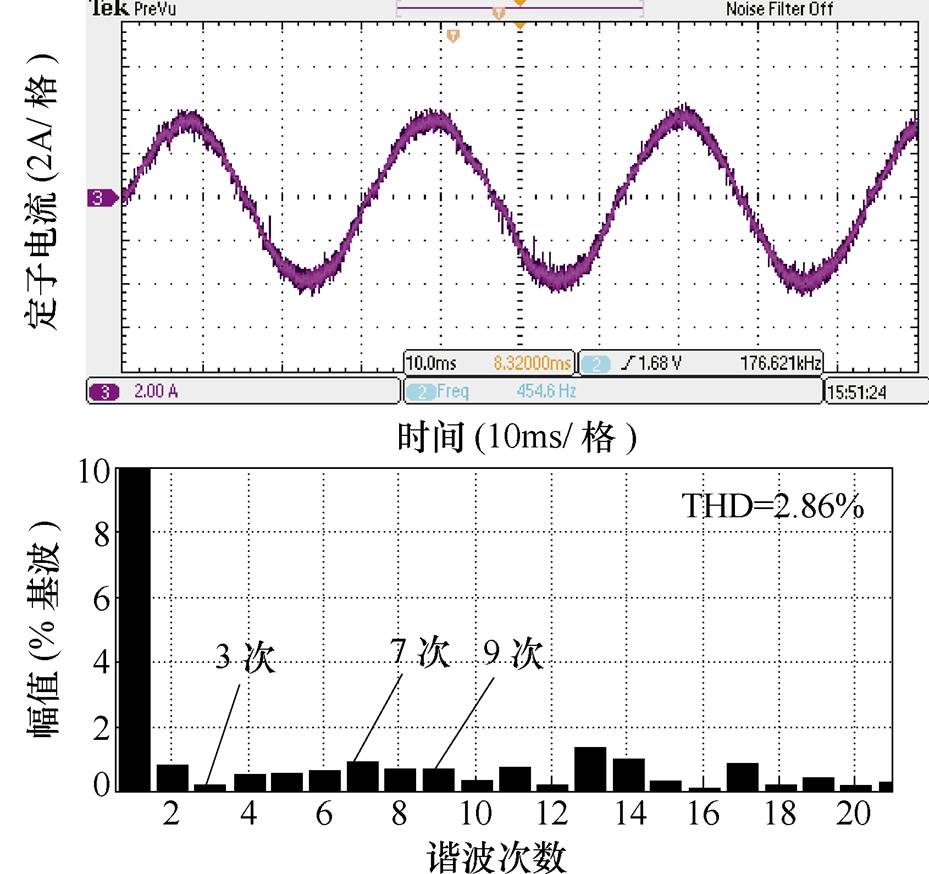
图18 定子电流波形及其频谱(Rsn=0.5Rs)
Fig.18 Stator current waveform and its spectrum with Rsn=0.5Rs
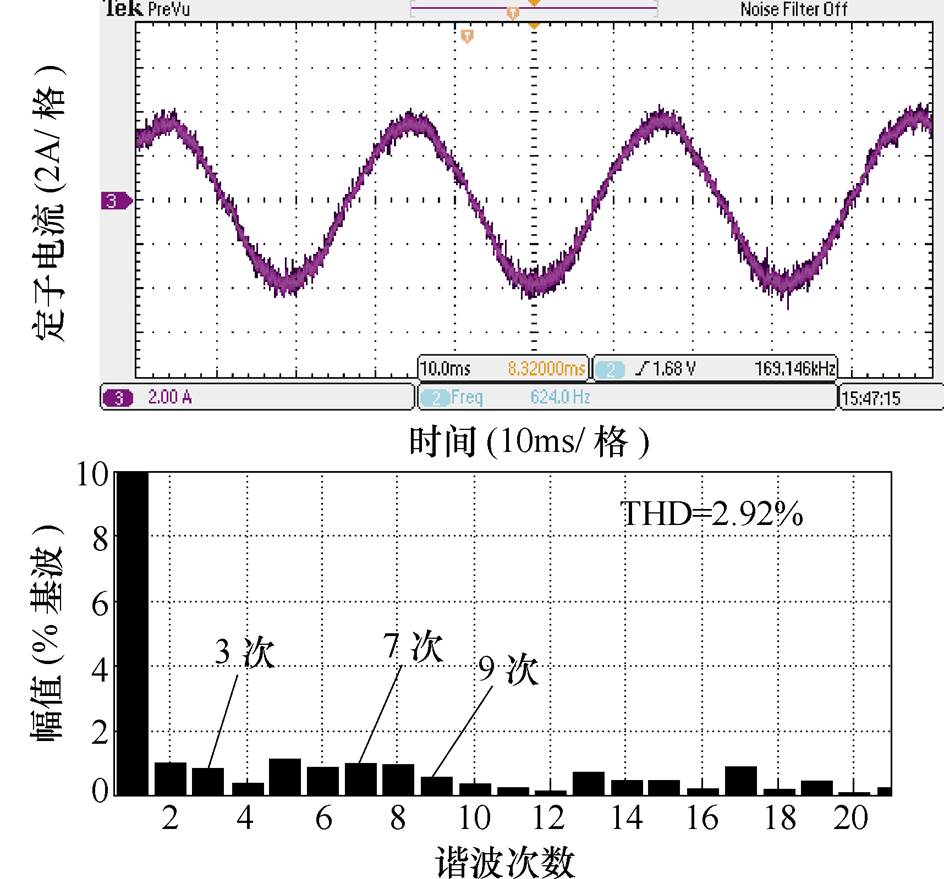
图19 定子电流波形及其频谱(Lsn=1.5Ls)
Fig.19 Stator current waveform and its spectrum with Lsn=1.5Ls
图20给出了采用PI、DOB-PI和EDOB-PI控制器时取电机参数等于标称值、取定子电阻阻值为标称值的1/2以及取电感值为标称值的1.5倍情况下的q1轴电流动态波形。q1轴电流参考值在6ms时由1A突变为3A。从图20中电流响应曲线可以看出,DOB-PI和EDOB-PI控制器在参数不匹配时依然具有很好的电流跟踪性能,表明DOB-PI和EDOB-PI控制器可以有效地观测并补偿参数变化引起的扰动,验证了DOB-PI和EDOB-PI控制在动态过程中对参数变化的鲁棒性。而PI的控制性能容易受到电感参数不匹配的影响,输出响应存在15.3%的超调量,且调节时间比参数匹配时增加47.4%。
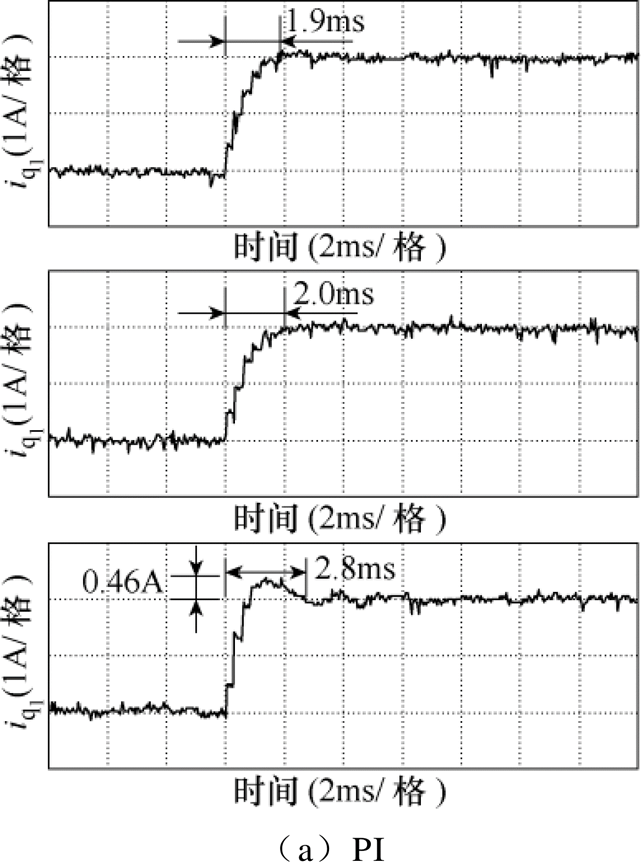

图20 三种控制器的q1轴电流动态响应(从上到下依次为取电机参数为标称值、取定子电阻阻值为标称值的1/2和取定子基波电感感值为标称值的1.5倍)
Fig.20 Step reference response of q1-axis current for three different strategies (from the top row to the bottom row: with nominal parameters, with Rsn=0.5Rs, and with 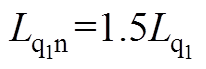 )
)
针对采用同步坐标系下的比例积分控制器的五相永磁同步电机驱动系统容易受到转子永磁体磁链、逆变器死区效应以及参摄摄动的影响,难以达到高性能控制的要求,本文设计了基于扰增强型扰动观测器的比例积分控制器。基于扰动模型,设计了一种增强型扰动观测器,可同时对系统内的低频和周期扰动进行观测,并给出了PI控制器和扰动观测器参数的设计原则。最后,实验结果表明,基于增强型扰动观测器的比例积分控制可以有效地抑制由周期扰动引起的低次谐波电流,并且提高了控制系统对参数变化的鲁棒性,改善了系统的稳态和动态性能。
参考文献
[1] Levi E. Multiphase electric machines for variable- speed applications[J]. IEEE Transactions on Indu- strial Electronics, 2008, 55(5): 1893-1909.
[2] 刘自程, 李永东, 郑泽东. 多相电机控制驱动技术研究研究综述[J]. 电工技术学报, 2017, 32(24): 17-29.
Liu Zicheng, Li Yongdong, Zheng Zedong. Control and drive techniques for multiphase machines: a review[J]. Transactions of China Electrotechnical Society, 2017, 32(24): 17-29.
[3] Gu Z Y, Wang K, Zhu Z Q, et al. Torque improvement in five-phase unequal tooth SPM machine by injecting third harmonic current[J]. IEEE Transactions on Vehicular Technology, 2018, 67(1): 206-215.
[4] 赵品志, 杨贵杰, 李勇. 三次谐波注入式五相永磁同步电机转矩密度优化[J]. 中国电机工程学报, 2010, 30(33): 71-77.
Zhao Pinzhi, Yang Guijie, Li Yong. Torque density optimization for five-phase PMSM with third harmonic injection[J]. Proceedings of the CSEE, 2010, 30(33): 71-77.
[5] 王东, 马伟明, 郭云, 等. 基于非正弦供电方式的多相感应电动机建模[J]. 电工技术学报, 2010, 25(2): 6-14.
Wang Dong, Ma Weiming, Guo Yun, et al. Modelling of multiphase induction motor with non-sinusoidal supply[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 102-110.
[6] 周长攀, 杨贵杰, 苏健勇, 等. 基于正常解耦变换的双三相永磁同步电机缺相容错控制策略[J]. 电工技术学报, 2017, 32(3): 86-96.
Zhou Changpan, Yang Guijie, Su Jianyong, et al. The control strategy for dual three-phase PMSM based on normal decoupling transformation under fault con- dition due to open phases[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 86-96.
[7] Levi E. Advances in converter control and innovative exploitation of additional degrees of freedom for multiphase machines[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1): 433-448.
[8] Barrero F, Duran M J. Recent advances in the design, modeling, and control of multiphase machines—part I[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1): 449-458.
[9] Ryu Hyung Min, Kim Jang Hwan, Sul S K. Analysis of multiphase space vector pulse-width modulation based on multiple d-q spaces concept[J]. IEEE Transactions on Power Electronics, 2005, 20(6): 1364-1371.
[10] 张杰, 柴建云, 孙旭东, 等. 双三相异步电机电流预测控制算法[J]. 电工技术学报, 2015, 30(9): 12-21.
Zhang Jie, Chai Jianyun, Sun Xudong, et al. Predictive current control methods for dual three phase induction machine[J]. Transactions of China Electrotechnical Society, 2015, 30(9): 12-21.
[11] Parsa L, Toliyat H A. Five-phase permanent-magnet motor drives[J]. IEEE Transactions on Industry Applications, 2005, 41(1): 30-37.
[12] Errouissi R, Ouhrouche M, Chen W H, et al. Robust nonlinear predictive controller for permanent-magnet synchronous motors with an optimized cost fun- ction[J]. IEEE Transactions on Industrial Electronics, 2012, 59(7): 2849-2858.
[13] Mohamed Y A-R I, El-Saadany E F. An improved deadbeat current control scheme with a novel adaptive self-tuning load model for a three-phase PWM voltage-source inverter[J]. IEEE Transactions on Industrial Electronics, 2007, 54(2): 747-759.
[14] Kung Y S, Tsai M H. FPGA-based speed control IC for PMSM drive with adaptive fuzzy control[J]. IEEE Transactions on Power Electronics, 2007, 22(6): 2476-2486.
[15] Chang S H, Chen P Y, TingY H, et al. Robust current control-based sliding mode control with simple uncer- tainties estimation in permanent magnet synchronous motor drive systems[J]. IET Electric Power Appli- cations, 2010, 4(6): 441-450.
[16] 王高林, 于泳, 杨荣峰, 等. 感应电机空间矢量PWM控制逆变器死区效应补偿[J]. 中国电机工程学报, 2008, 28(25): 79-83.
Wang Gaolin, Yu Yong, Yang Rongfeng, et al. Dead-time compensation of space vector PWM inverter for induction motor[J]. Proceedings of the CSEE, 2008, 28(25): 79-83.
[17] Lee D H, Ahn J W. A simple and direct dead-time effect compensation scheme in PWM-VSI[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3017-3025.
[18] 张海洋, 许海平, 方程, 等. 基于比例积分-准谐振控制器的直驱式永磁同步电机转矩脉动抑制方法[J]. 电工技术学报, 2017, 32(19): 41-51.
Zhang Haiyang, Xu Haiping, Fang Cheng, et al. Torque ripple suppression method of direct-drive permanent magnet synchronous motor based on proportional-integral and quasi resonant controller[J]. Transactions of China Electrotechnical Society, 2017, 32(19): 41-51.
[19] Zhou Zhanqing, Xia Changliang, Yan Yan, et al. Disturbances attenuation of permanent magnet synchronous motor drives using cascaded predictive- integral-resonant controllers[J]. IEEE Transactions on Power Electronics. 2018, 33(2): 1514-1527.
[20] Tang Zhuangyao, Akin B. Suppression of dead-time distortion through revised repetitive controller in PMSM drives[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 918-930.
[21] 刘栋良, 武瑞斌, 张遥, 等. 基于模糊控制零电流钳位逆变器死区补偿[J]. 电工技术学报, 2011, 26(8): 119-124.
Liu Dongliang, Wu Ruibing, Zhang Yao, et al. Inverter dead time compensation of zero current clamping based on fuzzy control[J]. Transactions of China Electrotechnical Society, 2011, 26(8): 119-124.
[22] Qiu Tengfei, Wen Xuhui, Zhao Feng. Adaptive-linear- neuron-based dead-time effects compensation scheme for PMSM drives[J]. IEEE Transactions on Power Electronics, 2016, 31(3): 2530-2538.
[23] Chen Wenhua, Yang Jun, Guo Lei, et al. Disturbance observer based control and related methods-an overview[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(2): 1083-1095.
[24] Yang Jun, Chen Wenhua, Li Shihua. Disturbance/ uncertainty estimation and attenuation techniques in PMSM drives-a survey[J]. IEEE Transactions on Industrial Electronics, 2017, 64(4): 3273-3285.
[25] Sariyildiz E, Ohnishi K. A guide to design distur- bance observer based motion control systems[C]// International Power Electronics Conference, Hiro- shima, Japan, 2014: 2483-2488.
[26] Sariyildiz E, Ohnishi K. Stability and robustness of disturbance-observer-based motion control systems[J]. IEEE Transactions on Industrial Electronics, 2015, 62(1): 414-422.
[27] 易伯瑜, 康龙云, 冯自成, 等. 基于扰动观测器的永磁同步电机预测电流控制[J]. 电工技术学报, 2016, 31(18): 37-45.
Yi Boyu, Kang Longyun, Feng Zicheng, et al. Predictive current control for permanent magnet synchronous motor based on disturbance observer[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 37-45.
[28] Ren Jianjun, Ye Yongqiang, Xu Guofeng, et al. Uncertainty and disturbance estimator based current control scheme for PMSM drives with a simple parameter tuning algorithm[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5712-5722.
[29] Yang Haitao, Zhang Yongchang, Liang Jiejunyi, et al. Robust deadbeat predictive power control with a discrete-time disturbance observer for PWM rectifiers under unbalanced grid conditions[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(1): 287-300.
[30] Wang Bo, Dong Zhen, Yu Yong, et al. Static-errorless deadbeat predictive current control using second- order sliding-mode disturbance observer for induction machine drives[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2395-2403.
[31] Ruderman M, Ruderman A, Bertram T. Observer- based compensation of additive periodic torque disturbances in permanent magnet motors[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 1130-1138.
[32] 赵希梅, 郭庆鼎. 基于扰动观测器和重复控制器的永磁直线同步电动机鲁棒控制[J]. 中国电机工程学报, 2010, 30(15): 64-69.
Zhao Ximei, Guo Qingding. Robust control based on the disturbance observer and repetitive controller for permanent magnet linear synchronous motor[J]. Proceedings of the CSEE, 2010, 30(15): 64-69.
[33] Yepes A G, Freijedo F D, Doval Gandoy J, et al. Effects of discretization methods on the performance of resonant controllers[J]. IEEE Transactions on Power Electronics, 2010, 25(7): 1692-1712.
A Robust Current Control Scheme for Five-Phase Permanent Magnet Synchronous Motor Based on Enhanced Disturbance Observer
Abstract The dual synchronous rotating frame proportional integral (PI) control is most frequently employed in five-phase permanent magnet synchronous motor drives. However, its control performance is easily affected by disturbances such as parameter perturbation and inverter nonlinearity. Due to the limited bandwidth of the PI controller, there is usually a low-order harmonic current caused by the dead time of the inverter in the stator current. Therefore, this paper proposes a proportional integral control method based on the enhanced disturbance observer (EDOB-PI). The disturbances existing in the five-phase permanent magnet synchronous motor are classified and modeled. Then a disturbance observer is designed to observe the disturbance. Finally, the disturbance is compensated by the feed-forward channel. This method can improve parameter perturbation robustness and suppress low-order harmonic current caused by dead time and harmonic rotor permanent magnet flux. The experimental results have verified the proposed method.
keywords:Five-phase permanent magnet synchronous motor, harmonic disturbance, enhanced disturbance observer, proportional-integral (PI) control, robustness
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.181814
熊 聪 男,1991年生,博士研究生,研究方向为多相永磁同步电机驱动控制。E-mail: xiongcong@mail.iee.ac.cn
许海平 男,1973年生,研究员,博士生导师,研究方向为电力电子技术、交流电机与变频调速、电动汽车。E-mail: hpxu@mail.iee.ac.cn(通信作者)
(编辑 赵 鹏)