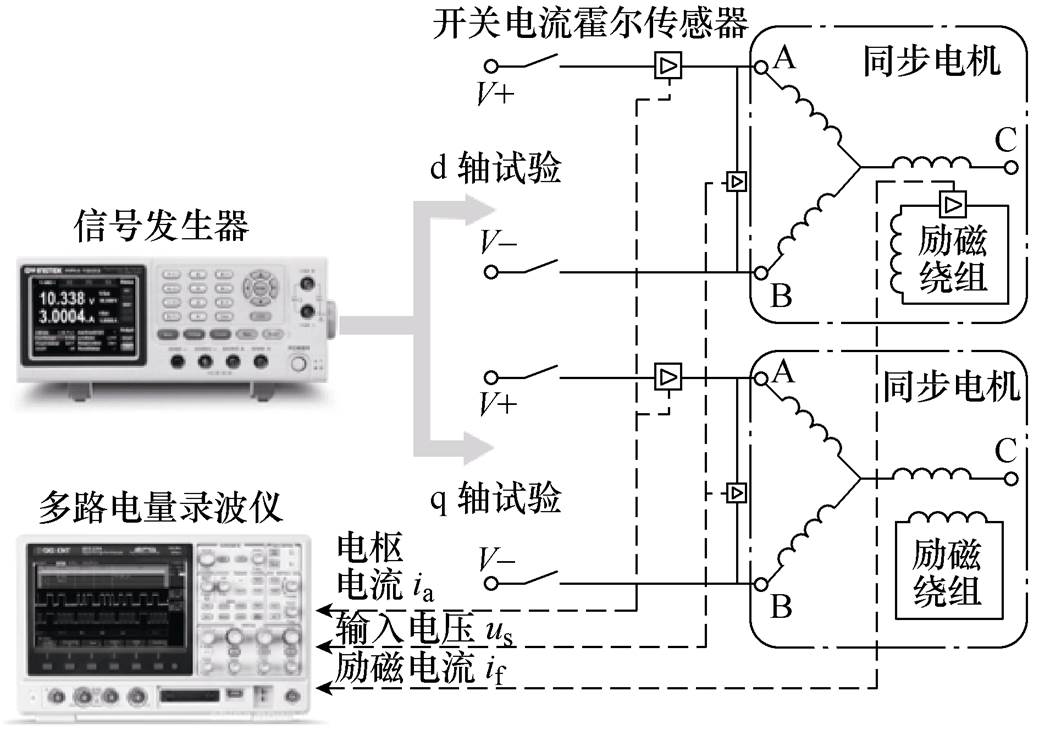
图1 信号输入实验接线示意图
Fig.1 Schematic of signal input experiment
摘要 大型同步电机瞬态参数的测量一般通过三相突然短路实验进行,实验过程复杂且存在一定的危险性。以静止频率响应实验、信号输入实验等为代表的静止实验方法可在一定程度上解决安全性问题,但此类方法必须进行转子预定位,对于大型同步电机实施难度较大,且定位误差也会影响测量的准确性。针对上述问题,该文基于信号输入实验原理,提出了一种任意转子位置下的同步电机全参数辨识实验方法,其中包括一种扩展至频域的Dalton-Cameron变换方法,以此为基础提出任意转子位置下的实验方案并加以应用分析,实现了dq轴参数的同时辨识。第三代非支配排序进化算法(NSGA3)被用于时域拟合过程以获取所需电枢电流响应信号的表达式。最后,通过对一台动态模拟实验样机进行实验,验证了所提出的参数辨识方法的有效性和准确性。该文提出的实验方案及参数辨识方法不仅适用于采用其他形式信号的信号输入实验,同样可为其他类别的静止实验方法提供参考。
关键词:同步电机 参数辨识 任意转子位置 静止实验方法
同步电机的参数,特别是以各阶瞬变电抗与瞬态时间常数为主的动态参数,是电机运行特性的决定性因素,同样也是对电机进行考核评估、运行控制及保护整定的基础。
实验测量是获取电机参数的重要途径之一,目前应用最广的同步电机动态参数的实验测试方法仍是GB/T 1029—2005推荐的三相突然短路法与电压恢复法等[1]。三相突然短路法是在电机以额定转速旋转于一定的空载电压下,利用开关在机端进行三相突然对称短路,根据短路电流提取出电机的动态参数的方法[2-3]。然而,当在大型同步电机上开展三相突然短路实验时,机端产生过大的瞬态电流引起的安全性问题不可忽视。电压恢复实验虽然能一定程度上解决三相突然短路实验的安全隐患,但仍无法解决这两类实验仅能用于获取d轴参数的弊端。
为增加实验的安全性,同时实现对q轴参数的准确测量,静止频率响应实验被IEEE标准所推荐[4]。但是,此类方法对设备要求较高且数据处理过程复杂[5-6],难以推广运用。近年来,基于信号输入的同步电机参数辨识方法由于具有安全性高、实验过程简单和设备要求低等优点而被国内外一些学者所推崇[7-11]。这类实验的特征是:在特定的转子位置下,通过在机端输入某种形式的电压信号以在机端产生瞬态电流响应。在现有的文献中,包括直流阶跃信号[7]、脉冲信号[8]、Chirp信号[9]、sinc信号[10]在内的多种信号已见应用。在获得电流响应后,需要对电流响应进行时域拟合来分别辨识出同步电机的d轴与q轴参数[7]。一系列人工智能的寻优方法被用于这一过程,包括单目标的遗传算法[11]、粒子群算法[12-13]、多目标的应用第二代非支配排序进化算法(Nondominated Sorting Genetic Algorithms II, NSGA2)[14]等。人工智能算法的应用能够有效地减轻传统算法对初值的依赖,降低拟合难度。同时,考虑到实验时输入电压信号较小,瞬态电流响应中会含有大量的噪声,在拟合前通常需要对电流响应进行去噪,以提升曲线拟合的精度,如可以采用结构简单、易于拓展的小波阈值去噪算法[15-16]。
目前,在进行包括静止频率响应实验、信号输入实验、直流衰减实验等同步电机静止参数测量实验时,最不可或缺的一个步骤是转子的预定位,即必须要在实验之前将电机转子轴线置于进行d轴与q轴参数实验所需的特定位置下,这也意味着电机d轴与q轴的参数必须分别进行实验与辨识。具体的定位方法在IEEE标准与相关文献中进行了详细介绍[4-6],定位时电机需要以稳定的低转速进行旋转,通过判断励磁绕组感应电压大小来确定转子位置。这一过程对于小容量电机是容易进行的,但是在大型同步电机上操作起来极为困难,特别是对于不具有原动机的大型同步电机,转子的预定位需要额外配备一台原动机或其他盘车设备方可进行。同时,由于定位过程中不可避免地产生误差,对于具有多极对数的电机,定位时较小的机械角度误差就会引起较大的电角度误差,进而大大降低参数辨识的准确度[17]。为使静止实验方法在大型同步电机上应用的可操作性更强,有必要提出无需转子预定位操作的实验方法。
针对任意转子位置下的静止参数测量实验,Dalton与Cameron早先提出了一种变换方法用于测试任意转子位置下的dq轴负序电抗与超瞬变电抗[18]。2004年,Edson等基于Dalton-Cameron变换(以下简称D-C变换)提出了一种任意转子位置下的静止频率响应实验方法[19]。Simond等在2006年提出一种利用传递函数的零点与极点进行任意转子位置参数辨识的直流衰减实验方法[20],类似的方法在文献[21]也有提及。然而,目前国内外尚未有文献针对信号输入实验提出相应的任意转子位置参数辨识实验方法。
本文工作的主要内容包括:首先,介绍信号输入实验及其参数辨识的基本原理;然后,针对任意转子位置下的信号输入实验,建立输入的电压信号与产生的电流响应信号的传递函数并以此传递函数为基础,提出并证明一种扩展至频域的D-C变换方法,进而给出在任意转子位置下进行实验的方法,并针对扩展D-C变换式的适用性进行讨论。接着,介绍实验数据处理方法,包括对实测电流响应的小波阈值去噪[15]与应用第三代非支配排序进化算法(Nondominated Sorting Genetic Algorithms III, NSGA3)[22]的电流响应时域拟合方法。最后,通过对一台同步电机的动模实验样机进行实验,验证了该实验方法及其参数辨识方法的有效性与准确性。文中使用的变量及其定义汇总见附表1。
与静止频率响应实验类似,信号输入实验需要在电机处于静止状态时进行。实验接线示意图如图1所示。实验时,首先需要将转子轴线分别置于进行dq轴实验的特定位置,并将励磁绕组短路。然后,在电枢绕组两相之间施加一定形式的电压信号,并对施加信号后的电枢回路与励磁回路瞬态电流响应数据进行录波。

图1 信号输入实验接线示意图
Fig.1 Schematic of signal input experiment
基于同步电机的运算电感表达式与dq轴电压平衡方程,可以建立电流响应与电机具体参数之间的解析关系[7],其中,励磁电流响应用于确定两轴的电枢反应电感。根据具体的电机模型与输入电压信号形式即可确定电枢与励磁电流响应的时域通解形式。考虑电机d轴与q轴均具有N条等效阻尼回路,dq轴的运算电感Ld(s)与Lq(s)可分别表示为
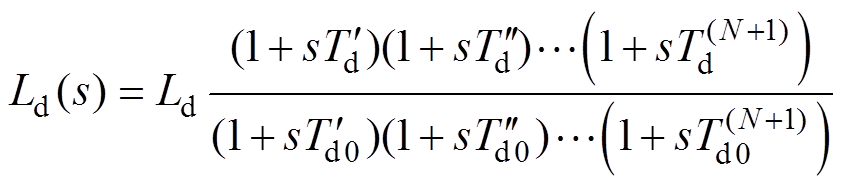 (1)
(1) (2)
(2)
式中,带有下标0的参数表示电枢回路开路时的时间常数。最后,根据电流响应的时域通解形式对实测响应进行时域拟合,最终计算得到同步电机的d轴与q轴参数。具体的参数计算过程可以参考文 献[7]。
在上述信号输入实验过程中,转子的预定位操作是必不可少的。假设电压信号施加于定子绕组的A相与B相之间,则进行d轴参数测量实验时,转子轴线必须与C相绕组轴线垂直;而进行q轴参数测量实验时,转子轴线必须与C相绕组轴线平行,即dq轴参数必须分两次进行实验。
为研究任意转子位置下输入电压信号与输出电流信号之间的关系,需首先建立两者之间的传递函数。下面以转子处于任意位置,励磁绕组短路,电机dq轴分别具有一个阻尼绕组,输入电压信号施加于定子A相与B相为例进行说明。在上述条件下,定子端电压、电流满足如下关系
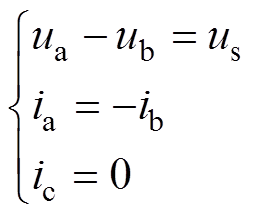 (3)
(3)根据式(3)以及dq轴各绕组的电压平衡方程,频域中A相电流响应与输入电压信号有如下传递函数(具体的推导过程见附录)
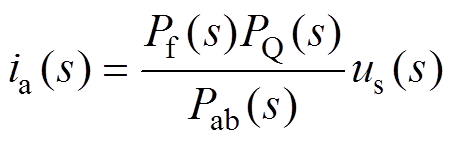 (4)
(4)
其中
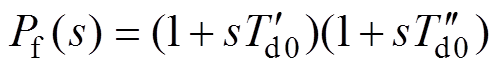 (5)
(5)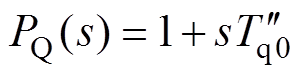 (6)
(6)
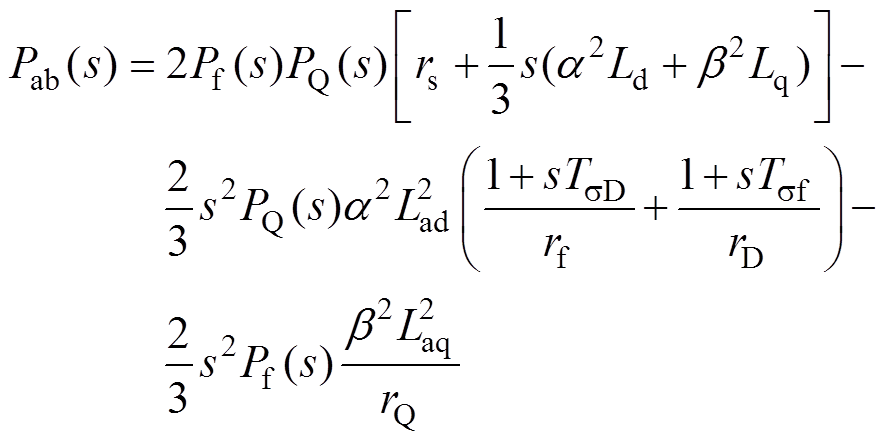 (7)
(7)
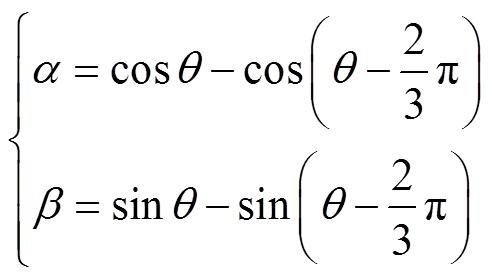 (8)
(8)由式(4)可知,电流响应及输入电压之间的传递函数与电机dq轴参数及转子位置角q 相关。文献[20]中提到可以利用此传递函数的零点与极点对两轴参数进行辨识,然而此方法依赖于不同转子位置角下的多套实验数据以寻找出不同的零点与极点,在此过程中仍需要旋转电机转子,对大型同步电机来说可操作性低,且大大增加了所需的实验次数。因此,有必要提出更为简便且容易实施的实验方案及参数辨识方法。
针对dq轴超瞬变电抗的静测法实验[1],Dalton与Cameron给出一种任意转子位置下的实验与参数计算方法。在文献[18]中给出的实验方法为:将一个单相额定频率的电压信号依次施加于电枢两相绕组之间,共进行3次静测法实验。在d轴超瞬变电抗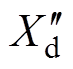 大于q轴超瞬变电抗
大于q轴超瞬变电抗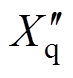 且两轴完全解耦的前提下,该文献基于在一对极的转角范围内超瞬变电抗的变化规律满足正弦周期函数形式的假设,给出了以下的变换式求解超瞬变电抗,即
且两轴完全解耦的前提下,该文献基于在一对极的转角范围内超瞬变电抗的变化规律满足正弦周期函数形式的假设,给出了以下的变换式求解超瞬变电抗,即
 (9)
(9)其中
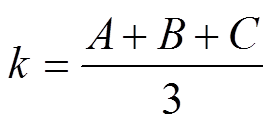 (10)
(10)
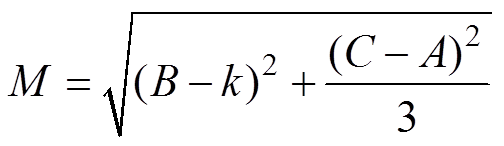 (11)
(11)式中,A、B、C分别表示在电枢A-B相、B-C相、C-A相施压时测得的电抗值。分析其引入的辅助运算量k与M可知,k表示超瞬变电抗变化式的偏置量,M表示超瞬变电抗变化式中余弦函数部分的幅值。传统的D-C变换仅针对超瞬变电抗进行求解,基于以上分析及2.1节中建立的传递函数,接下来提出一种扩展至频域的D-C变换以实现dq轴的全部动态参数的辨识。
首先,根据式(4)可知,在A-B相施加信号时,对应的频域阻抗应满足
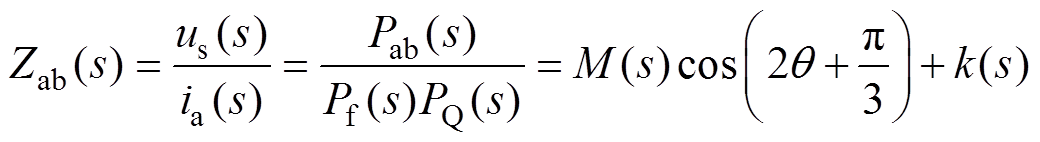 (12)
(12)其中
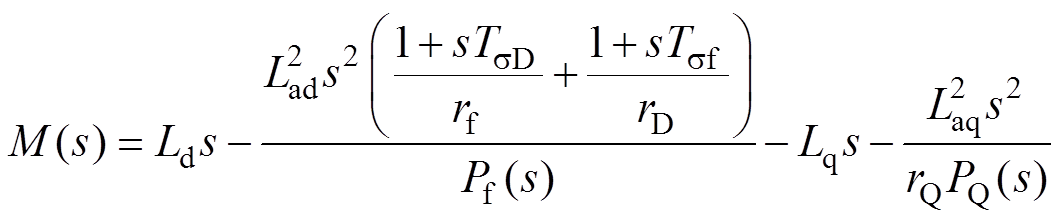 (13)
(13)
 (14)
(14)若输入电压信号施加于B-C相与C-A相,对应的阻抗表达式应为
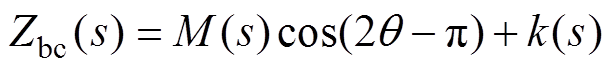 (15)
(15)
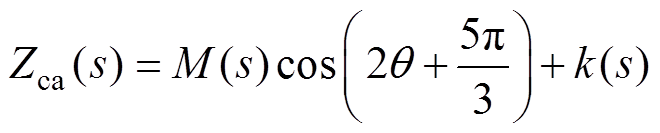 (16)
(16)以上过程得到的式(12)、式(15)、式(16)与图2相对应,频域阻抗变换曲线如图2所示。
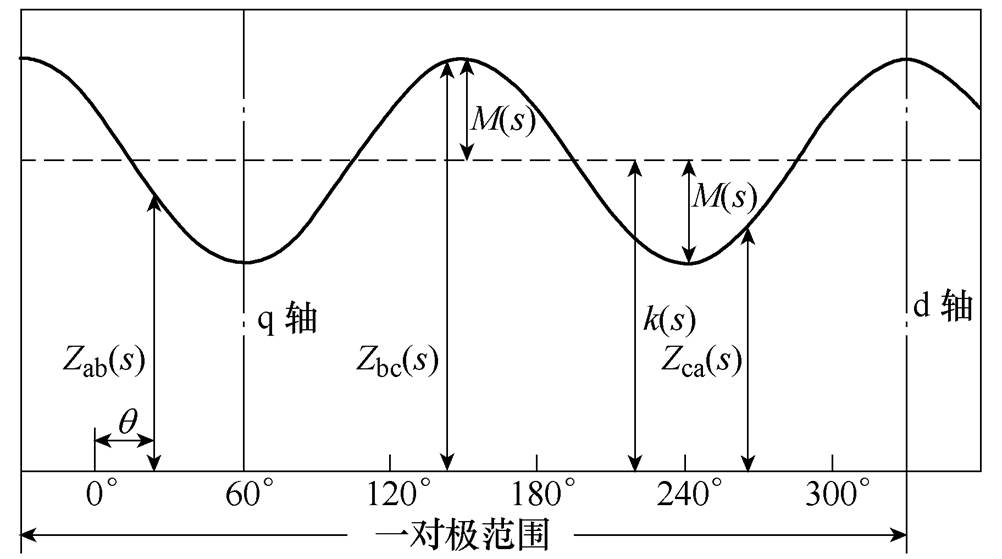
图2 频域阻抗变换曲线
Fig.2 Curve of frequency domain impedance
由图2可知,M(s)等效于余弦函数部分的幅值,而k(s)等效于此变换曲线的偏置值。因此,M(s)与k(s)可以分别表示为
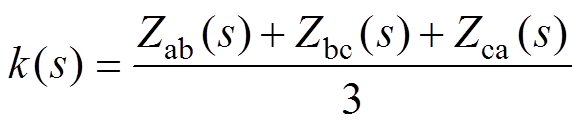 (17)
(17)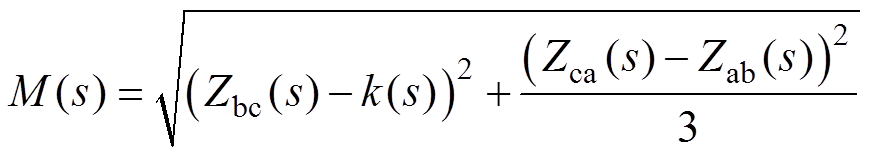 (18)
(18)
一般情况下,电励磁同步电机均满足d轴阻抗大于q轴阻抗,所以频域阻抗在d轴位置取得最大值,q轴位置取得最小值。这可由励磁绕组感应电流进行判断,越靠近d轴,励磁绕组的感应电流越大。当在不同绕组组合下施加信号产生的励磁感应电流大小与计算出的频域阻抗大小相同时,Zd(s)>Zq(s)[18],满足
 (19)
(19)采用转子定位的方法进行d轴实验时,q =-30°,将此值代入式(12)计算,同样可以证明式(19)的正确性。
进一步地,可以求得dq轴运算电感分别为
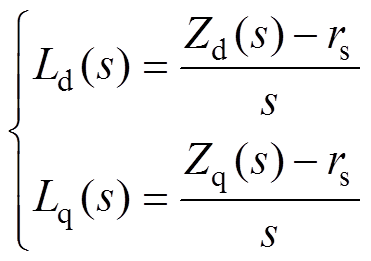 (20)
(20)根据电机的具体建模方式与由式(20)获得的运算电感表达式,即可对比式(1)与式(2)获取dq轴各时间常数与同步电感,进而可以计算得到其他阶次的瞬变电感。以d轴仅具有一个阻尼绕组为例[7],即
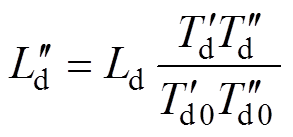 (21)
(21)
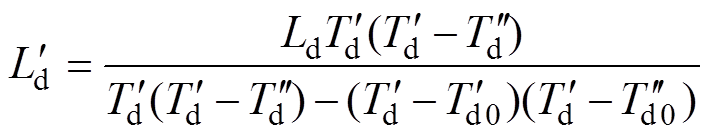 (22)
(22)根据2.2节建立的扩展D-C变换,可以形成如下的实验方案以求取任意转子位置下的dq轴等效电路参数:
(1)电机处于静止状态,将励磁绕组短路。
(2)在不同的两相定子绕组组合下,由定子绕组端口施加某种形式的电压信号。
(3)对定子绕组瞬态电流进行录波。
(4)由三次实验的电流响应波形计算dq轴参数。
三种不同的两相定子绕组组合见表1。
表1 不同定子绕组组合
Tab.1 Different couplings of stator winding
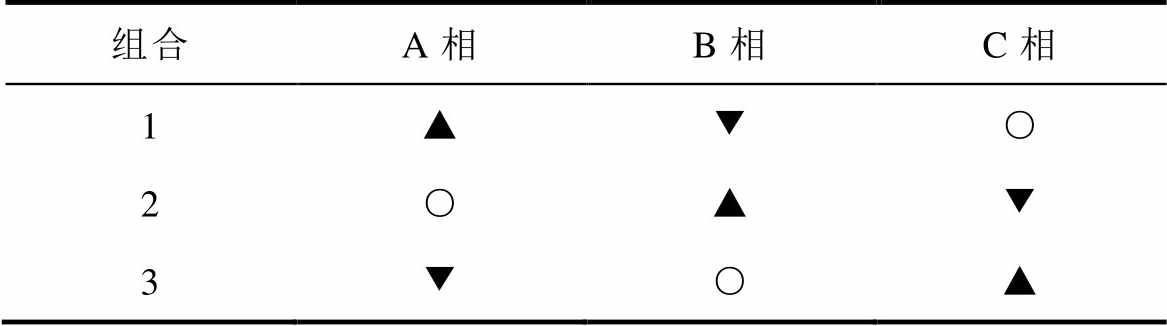
组合A相B相C相 1▲▼○ 2○▲▼ 3▼○▲
注:▲接于信号发生器正端;▼接于信号发生器负端;○悬空。
2.4.1 定子电阻rs的影响
在2.2节对扩展D-C变换的解析证明过程中,为了与原始的D-C变换式对应,k(s)与M(s)分别由式(17)与式(18)进行了定义。这两个公式成立的前提在于在不同定子端口输入电压信号时,定子电阻rs均相同。以输入信号为直流阶跃电压为例,各次实验rs不变等效于各次实验的电流稳态值相等。事实上,rs中还包括了外接实验设备引入的电阻以及接触电阻,特别是接触电阻,难以保证每次实验均是不变的。由于定子绕组电阻本身很小,外部电阻的变化会对电枢电流瞬态过程产生较大的影响,各次实验时电阻的不平衡也可能会在参数辨识过程中引入误差。
现对2.2节中的变换式进行改进,由式(14)可知,与rs有关的项是独立存在的。因此,为排除定子电阻不平衡对参数辨识结果的影响,可在计算各次实验对应的频域阻抗时,首先减去2rs,即
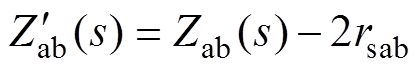 (23)
(23)式中,rsab为A-B相施压时对应的定子相电阻。同理,可获得在其他端口施压时的 与
与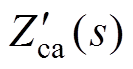 ,并将其代入式(17)与式(18)重新计算获得
,并将其代入式(17)与式(18)重新计算获得 与
与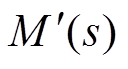 。则最终获得的运算电感表达式为
。则最终获得的运算电感表达式为
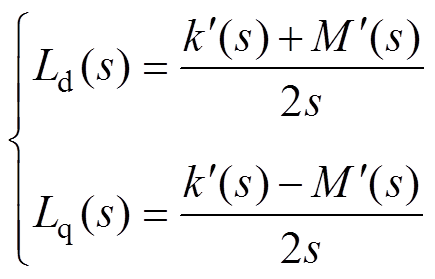 (24)
(24)
2.4.2 转子位置角q 的计算
通过此实验,不仅dq轴参数可以被同时辨识出来,还可以进一步对转子位置角q 进行计算。根据式(12)、式(15)与式(16),由三角函数的和差化积公式可得
 (25)
(25)运用上述扩展D-C变换进行参数辨识的前提在于能够准确获取在不同端口施加电压信号后产生的电枢电流响应信号的时域表达式,即Iab(s)、Ibc(s)与Ica(s)。因此,对电流响应实测数据的时域拟合是参数辨识过程中至关重要的问题。为减小曲线拟合的误差,在拟合前,有必要对电流响应进行去噪预处理。
基于SURE阈值选择方法的梯度迭代优化小波阈值去噪方法能够针对较为平稳的信号取得良好的去噪效果[23]。本文在文献[23]的算法基础上加入模拟退火算子,形成了结合模拟退火粒子群(Simulated Annealing Particle Swarm Optimization, SAPSO)算法的自适应阈值小波去噪算法对电流波形进行去噪,选择的阈值函数为
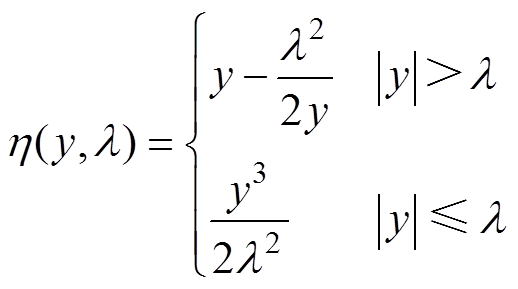 (26)
(26)式中,h(y, l)为阈值函数;l 为阈值。
去噪完成后,需要对电流响应曲线进行时域拟合。根据2.3节提出的实验方案,实验后共获得三条电流响应曲线。在此,采用NSGA3对三条电流响应的时域表达式进行同时寻优求解。NSGA3在2014年由学者K. Deb等提出[22],该算法采用基于参考点的选择机制获得子代染色体,有效地避免了处理高维多变量问题时仍采用基于拥挤距离的子代选择方式时容易造成局部最优的问题。
下面以输入信号为直流阶跃电压形式为例说明优化目标函数的构造方法。
首先,对传递函数式(4)的分母Pab(s)进行整理,Pab(s)可以写为如下的多项式形式(具体的系数表达式见式(A11)~式(A15))。
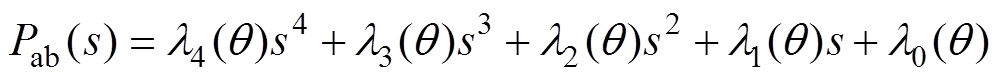 (27)
(27)由式(27)可知,Pab(s)最高幂次为4,即对应有四个非零解。再考虑输入为直流阶跃电压信号,uab(s)=uab/s,则电枢电流中应包含4个衰减分量和一个稳态分量,进而产生时域通解形式为
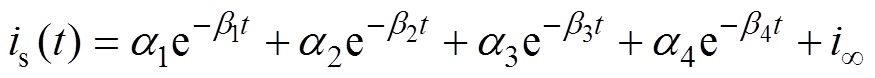 (28)
(28)
式中,a1~a4表示衰减分量的幅值系数;b1~b4表示衰减分量的衰减系数;is(t)表示电枢电流;i¥表示电流的稳态值。根据电机瞬态分析理论[24-25],易知4个衰减分量分别对应于定子绕组、励磁绕组、d轴阻尼绕组与q轴阻尼绕组的衰减过程。
基于电枢电流响应的时域通解形式和电流响应实测值,可以构造三个优化目标函数,其中电流稳态值由波形直接进行判断,以A-B相施加信号为例,有
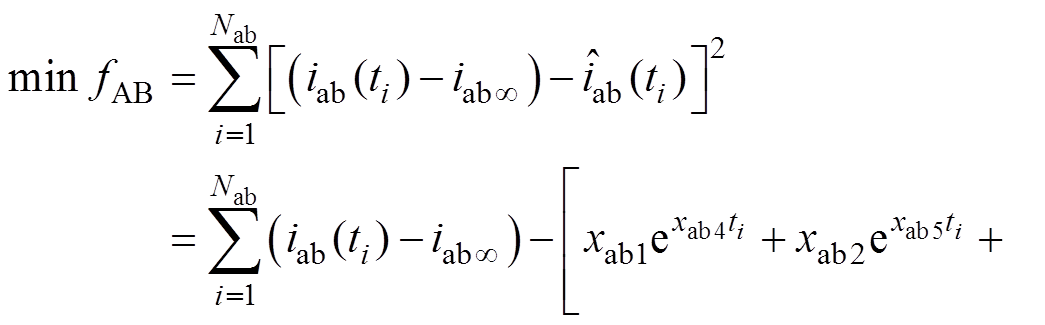
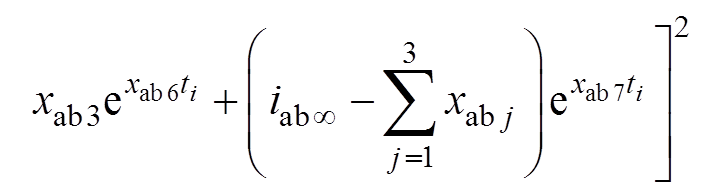 (29)
(29)
式中,xab1, xab2, …, xab7为优化目标量;iab(t)为A-B相施压的电流响应实测值;iab¥为电流稳态值;下标i表示第i个测量点;Nab为测量点的个数。类似地,可以构造对应于另外两个电流响应的优化函数。
根据三个表达式构造目标函数,利用NSGA3得到Pareto最优解集。以X方向为min fAB,Y方向为min fBC,Z方向为min fCA绘制得到Pareto前沿面,优化结果的优劣通过Pareto误差曲线进行表征。获取Pareto前沿面上切平面与原点距离最近的点,读取对应的染色体信息,得到各优化目标量的值。
由各优化目标量的值,获得3次实验的电流响应时域解,并将其变换至频域。然后,可以根据第2节中提出的扩展D-C变换对dq轴运算电感进行求解,其中定子电阻rs可根据电流稳态值进行计算,进而可以同时求得dq轴各阶瞬变电感与各瞬态时间常数。参数辨识过程的流程如图3所示。

图3 参数辨识流程
Fig.3 Flowchart of parameters identification
为验证提出的任意转子位置信号输入类实验的实验方案及其参数辨识方法,选择输入信号为直流阶跃电压形式,对一台376MV·A同步电机的15kW动态模拟实验样机进行了此实验。动模样机的额定线电压为UN=230V,额定线电流为IN=37.65A,实验时设定直流电源的输出电压为1V。实验设备如图4所示。

图4 实验设备
Fig.4 Equipmental of the proposed test
实验分别在两个不同的任意转子位置下进行,以其中一个任意转子位置为例,根据2.3节的实验方案,3次实验实测的电枢电流响应波形及其去噪结果如图5所示,将电流瞬态过程开始时刻作为时间零点以方便比较与数据处理。
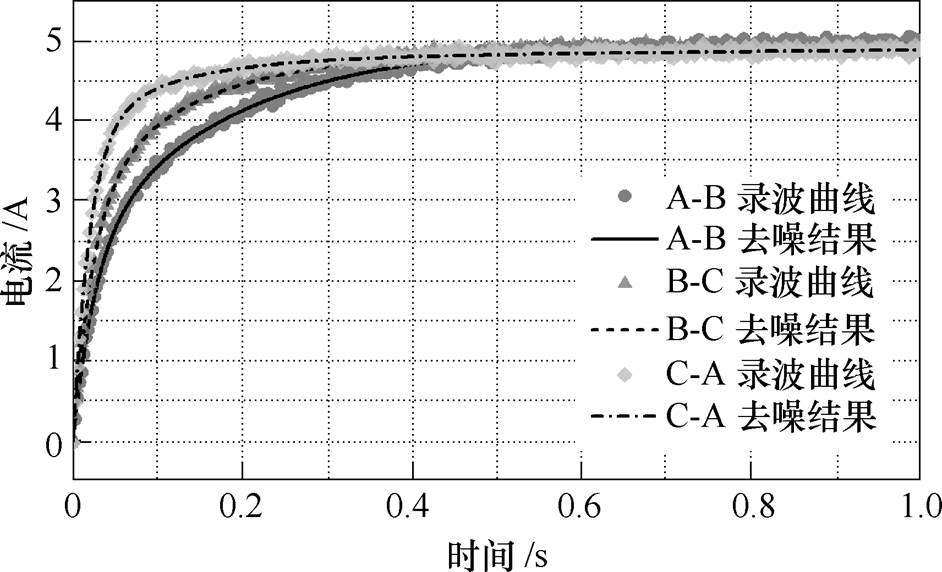
图5 电流响应去噪结果
Fig.5 Denoising result of current responses
基于第3节建立的电枢电流响应时域通解式(28),使用NSGA3对所构造的目标函数进行优化拟合,拟合数据见表2,算法生成的Pareto面如图6所示,电流响应拟合曲线如图7所示。
表2 电流响应的时域拟合数据
Tab.2 Current response curve fitting data
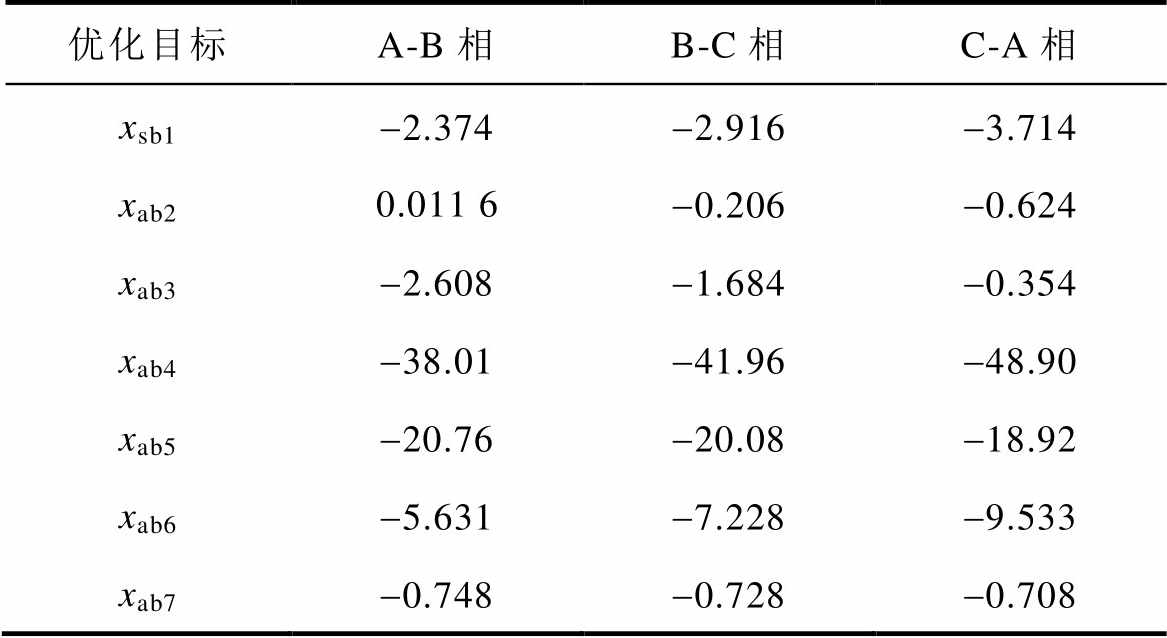
优化目标A-B相B-C相C-A相 xsb1-2.374-2.916-3.714 xab20.011 6-0.206-0.624 xab3-2.608-1.684-0.354 xab4-38.01-41.96-48.90 xab5-20.76-20.08-18.92 xab6-5.631-7.228-9.533 xab7-0.748-0.728-0.708
注:三相电阻平衡,i¥≈4.98A;xab1~xab7对应于式(29)中的优化目标量。

图6 NSGA3 Pareto面
Fig.6 Pareto surface of NSGA3 algorithm
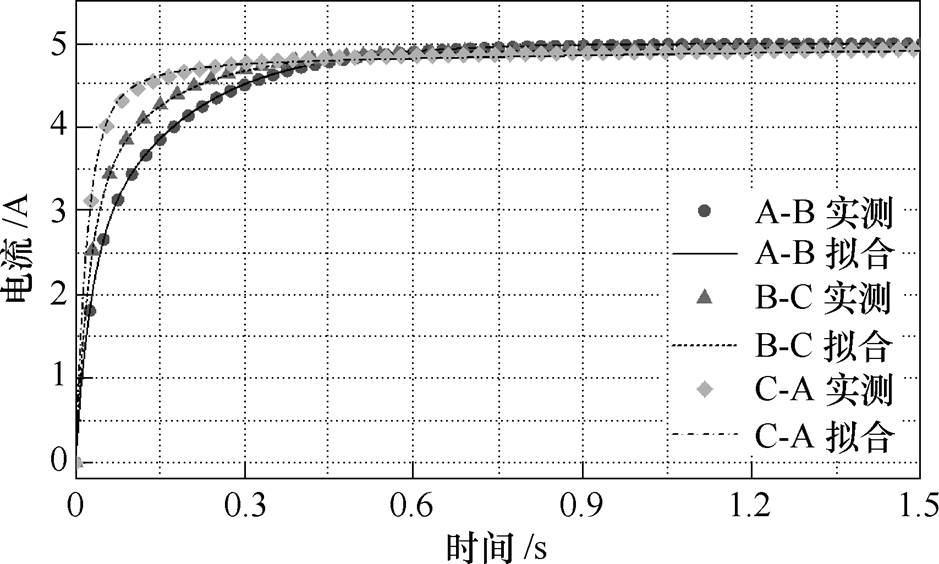
图7 电流响应拟合曲线
Fig.7 Current response fitting curves
由图7可见,拟合出的电流响应曲线能够与实测曲线良好匹配,进而可以由扩展D-C变换对其dq轴等效电路的参数进行求取。
表3与表4分别给出了不同转子位置下d轴与q轴参数的辨识结果,根据式(25)计算得到的转子位置角同样在表3、表4中给出。为方便比较,电感参数折算为额定频率50Hz下的电抗标幺值,定子侧阻抗基值ZB=6.2W。转子位置3与4下的参数辨识结果是通过传统直流阶跃电压实验方法获得[8],与文中提出的新实验方法的辨识结果进行对比。表3与表4中的误差项分别表示转子位置1、2下的参数辨识结果相对于转子位置3与转子位置4下的结果的相对误差的较大值。
表3 d轴参数辨识结果
Tab.3 Identification results of d-axis parameters
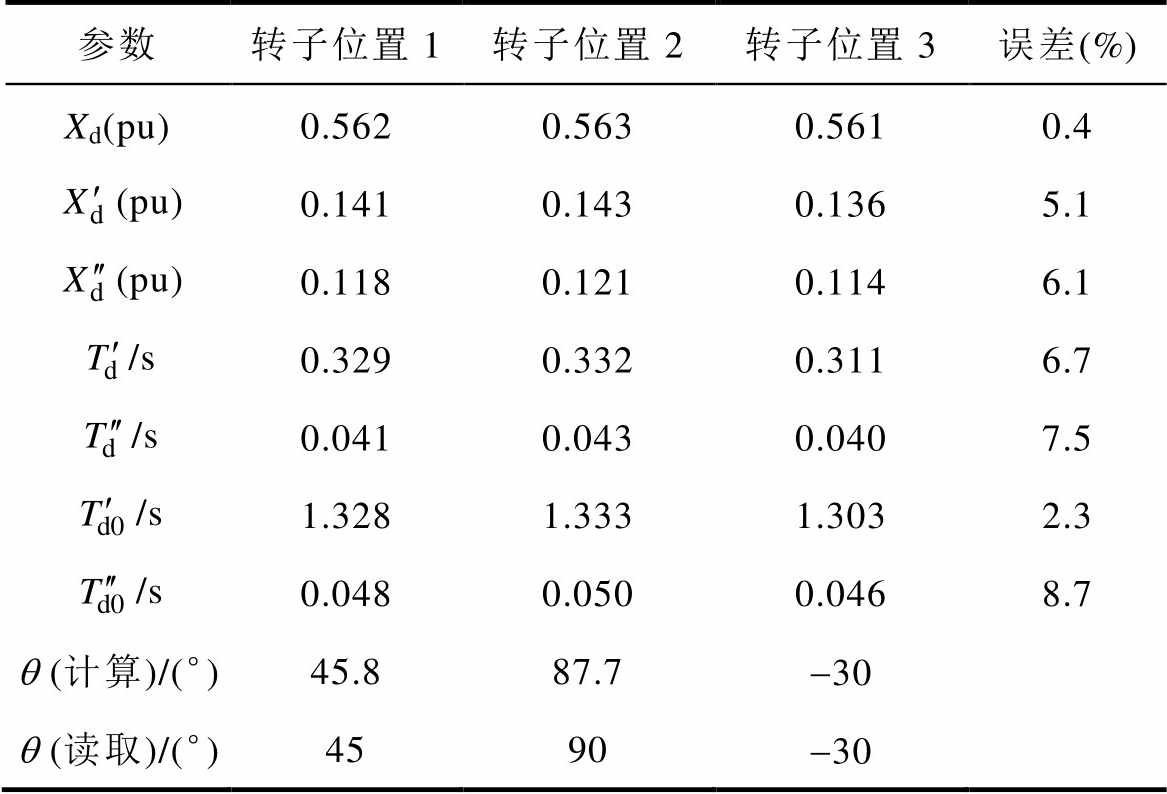
参数转子位置1转子位置2转子位置3误差(%) Xd(pu)0.5620.5630.5610.4 (pu)0.1410.1430.1365.1 (pu)0.1180.1210.1146.1 /s0.3290.3320.3116.7 /s0.0410.0430.0407.5 /s1.3281.3331.3032.3 /s0.0480.0500.0468.7 q (计算)/(°)45.887.7-30 q (读取)/(°)4590-30
表4 q轴参数辨识结果
Tab.4 Identification results of q-axis parameters

参数转子位置1转子位置2转子位置4误差(%) Xq(pu)0.3200.3190.3210.6 (pu)0.1430.1450.1403.6 /s0.0440.0470.0439.3 /s0.0990.1030.0967.3 q/(°)45.887.7-120
由表3与表4可以看出,在不同的转子位置下,运用第2节提出的实验方法与变换方法均能得到与传统直流阶跃电压实验相近的结果,各参数的最大误差在10%以内,证明了所提出的方法的有效性。
为探究定子电阻不平衡对辨识结果的影响,在B-C相加压实验时,串入0.1W 的电阻;在C-A相加压实验时,串入0.2W 的电阻。在转子位置1处进行以上实验,定子电阻不平衡情况下得到电流响应拟合结果如图8所示,其辨识结果见表5。
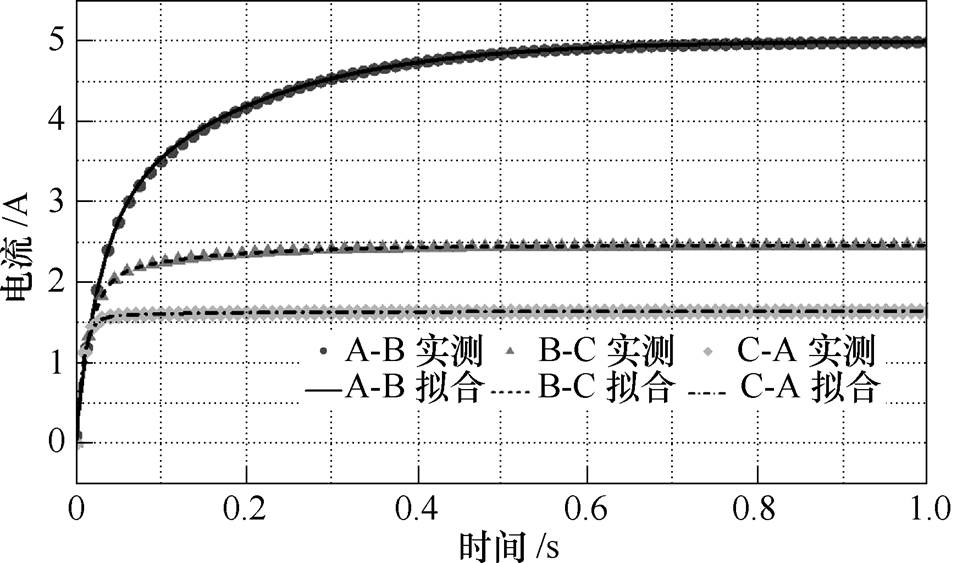
图8 电阻不平衡时的电流响应拟合曲线
Fig.8 Current fitting curves of unbalance resistance
由表5可知,在3次实验定子电阻不平衡的情况下,通过计算端口等效阻抗Zab(s)、Zbc(s)与Zca(s)时先将与rs有关的项减去再进行变换,同样可以获得准确的参数辨识结果,由此可以排除由设备电阻与接触电阻引起的辨识误差。
相比于传统的信号输入实验方法,本文提出的任意转子位置下的实验方案在继承了原方法的安全性好、设备简单等优点的基础上,具有更强的适用性,无需转子定位的特点使得其对设备要求更低,总体所需的实验次数更少,且能够同时进行dq轴动态参数的辨识。
表5 电阻不平衡时的辨识结果
Tab.5 Identification results of unbalance resistance
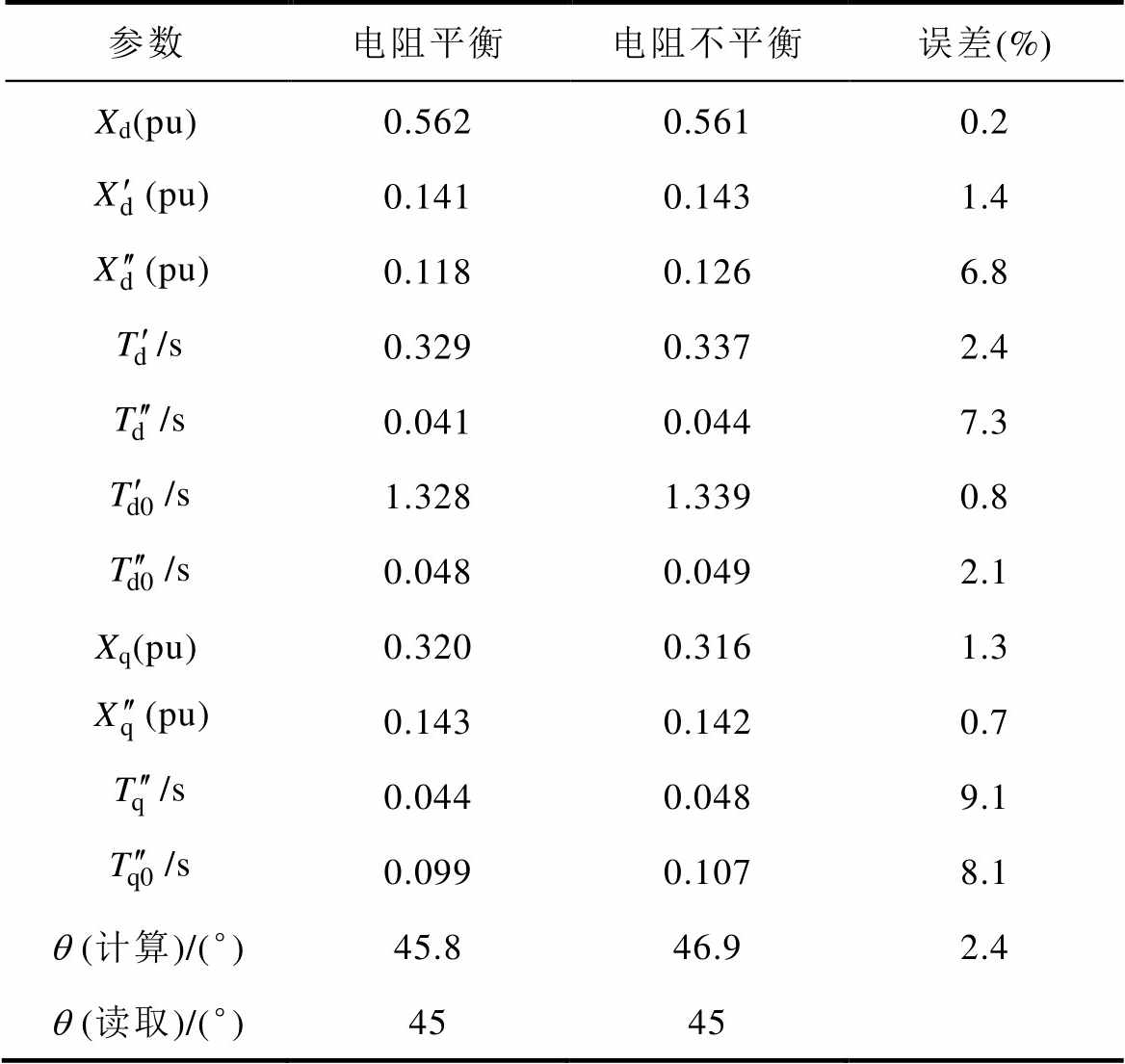
参数电阻平衡电阻不平衡误差(%) Xd(pu)0.5620.5610.2 (pu)0.1410.1431.4 (pu)0.1180.1266.8 /s0.3290.3372.4 /s0.0410.0447.3 /s1.3281.3390.8 /s0.0480.0492.1 Xq(pu)0.3200.3161.3 (pu)0.1430.1420.7 /s0.0440.0489.1 /s0.0990.1078.1 q (计算)/(°)45.846.92.4 q (读取)/(°)4545
本文基于信号输入实验提出了一种任意转子位置下的同步电机全参数辨识实验方法。通过建立输入电压信号与电流响应信号的传递函数,提出并证明了一种扩展至频域的Dalton-Cameron变换方法,实现了任意转子位置下的参数辨识;利用小波阈值去噪算法和NSGA3,由实测电流波形数据获得了电流响应信号的精确时域表达式;最后通过动模样机实验验证了所提出方法的有效性和准确性。
该方法的优势在于实验前无需进行转子预定位操作,在继承了传统的信号输入实验方法安全性好、设备简单等优点的基础上,具有更强的适用性,不仅能够大大简化实验过程及设备要求,降低总体所需的实验次数,还能够实现dq轴全部动态参数的一次性辨识。
由于静止参数测量实验的理论基础均是对dq轴运算电感的求解,因此,本文的实验方法及变换思想不仅适用于采用其他形式信号的信号输入类实验,同样能被用于进行其他类型的静止参数测量实验,如静止频率响应实验、直流衰减实验等。
给出2.1节传递函数的详细推导过程,推导中dq轴仅考虑一条等效阻尼回路,阻尼绕组数量更多时可以进行类推。假设在A-B相施加电压信号,电压电流关系满足正文的式(2),基于Xad基值系统进行推导。首先,由定子电流的Park方程,d轴的励磁绕组D与阻尼绕组f满足以下的电压平衡方程为
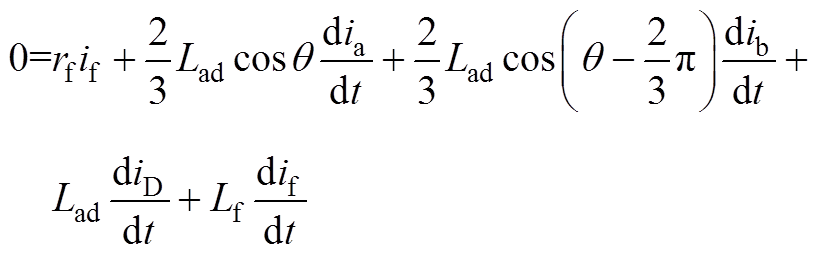 (A1)
(A1)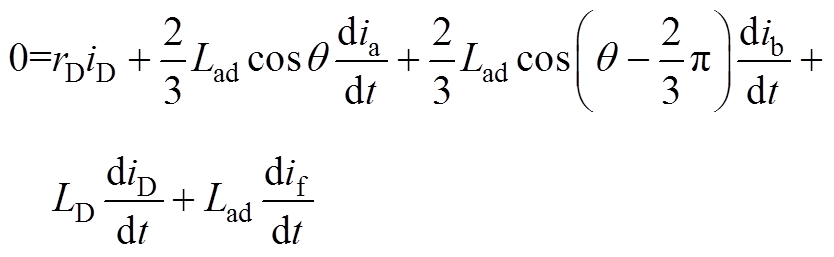 (A2)
(A2)
考虑ia=-ib,将式(A1)、式(A2)进行拉氏变换至频域,同时求解形成的频域表达式,频域中的励磁绕组电流if(s)与阻尼绕组电流iD(s)用A相电流ia(s)来表示为
 (A3)
(A3)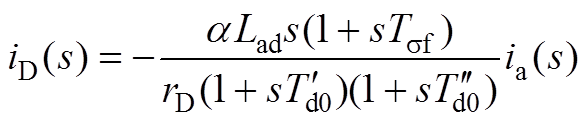 (A4)
(A4)
同理,对q轴阻尼绕组Q有电压平衡方程为
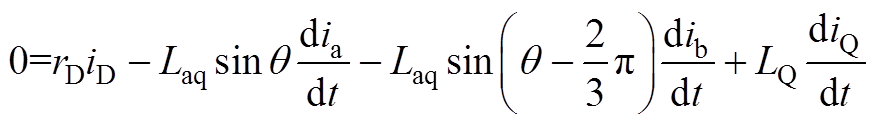 (A5)
(A5)将式(A5)整理至频域,得
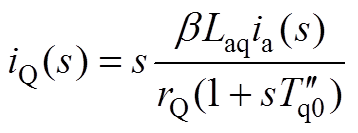 (A6)
(A6)
进一步地,定子相电压可由各绕组的电流与各电感进行表示。对于A相电压
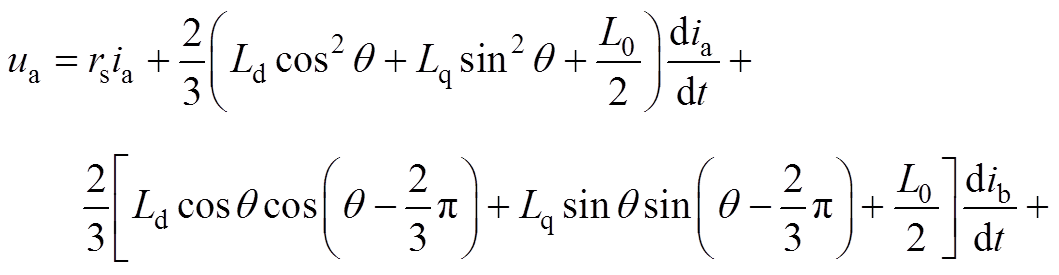
 (A7)
(A7)
对于B相电压
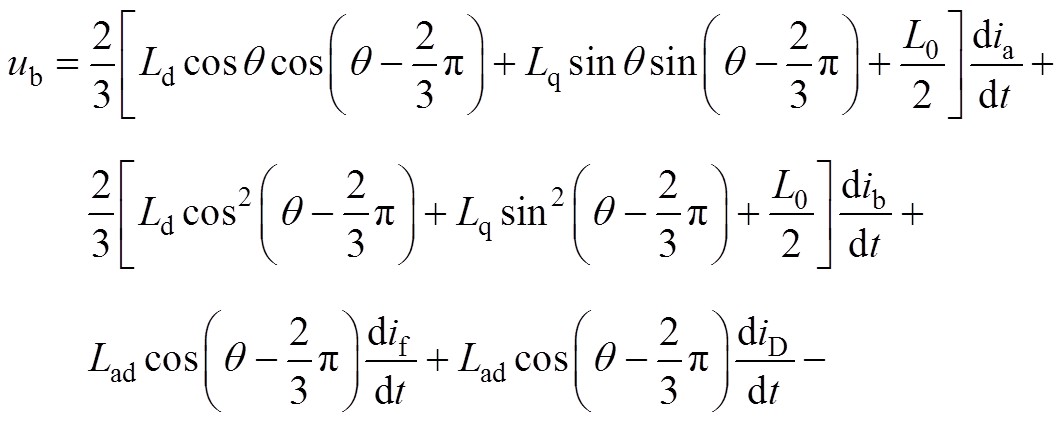
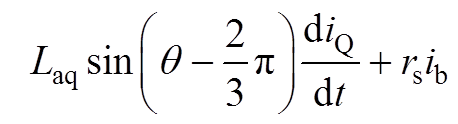 (A8)
(A8)
根据接线方式,输入电压us=ua-ub,因此uab可以表示为
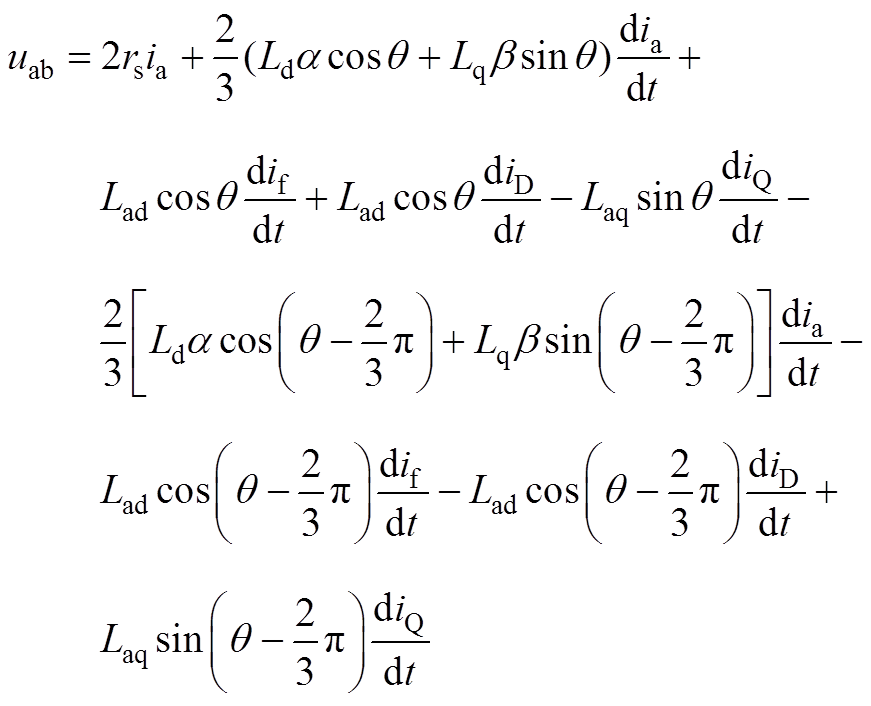 (A9)
(A9)将式(A9)变换至频域得
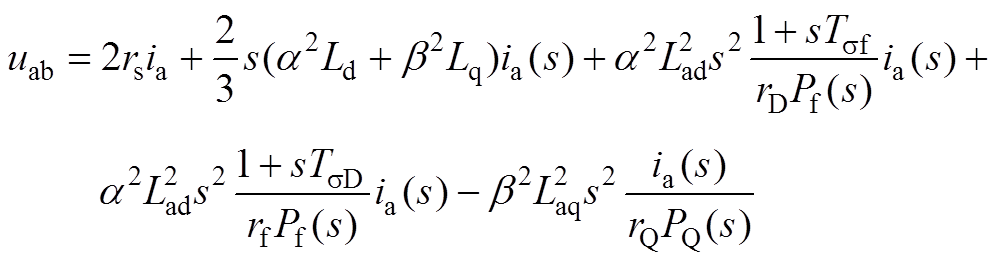
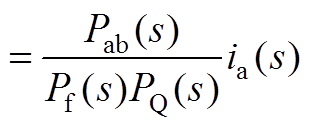 (A10)
(A10)Pab(s)可以整理为一个最高幂次为4的多项式见式(27)。式中,各系数为
 (A11)
(A11)

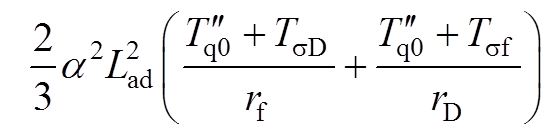 (A12)
(A12)
 (A13)
(A13)
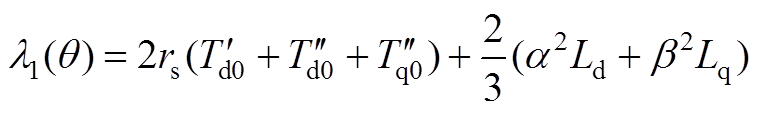 (A14)
(A14)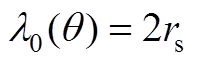 (A15)
(A15)
附表1 变量
App.Tab.1 Variables

变 量定 义 uabc定子三相电压 us定子输入电压 iabc定子三相电流 rs定子电阻 Ldd轴同步电感 Lqq轴同步电感 Ladd轴电枢反应电感 Laqq轴电枢反应电感 d轴瞬态电感 d轴超瞬态电感 q轴超瞬态电感 d轴瞬态时间常数 d轴超瞬态时间常数 q轴超瞬态时间常数 d轴阻尼回路N时间常数 q轴阻尼回路N时间常数 Tsf绕组f漏磁时间常数 TsD绕组D漏磁时间常数 rf励磁绕组电阻 rD阻尼绕组D电阻 rQ阻尼绕组Q电阻 s拉普拉斯算子
参考文献
[1] GB/T 1029—2005 三相同步电机实验方法[S]. 2005.
[2] 王亮, 王公宝, 马伟明, 等. 基于小波变换和神经网络的同步电机参数辨识新方法[J]. 电力系统自动化, 2007, 27(3): 1-6.
Wang Liang, Wang Gongbao, Ma Weiming, et al. A new method for parameters identification of synchronous electric machine based on wavelet transform and neural network[J]. Proceedings of the CSEE, 2007, 27(3): 1-6.
[3] 张宇辉, 陈峰, 李慧敏, 等. 基于小波变换和矩阵束算法的同步电机参数辨识[J]. 电力系统保护与控制, 2012, 40(9): 87-92.
Zhang Yuhui, Chen Feng, Li Huimin, et al. Parameter identification of synchronous machine based on wavelet transform and matrix pencil algorithm[J]. Power System Protection and Control, 2012, 40(9): 87-92.
[4] IEEE Std 115-1995 IEEE guide: test procedures for synchronous machines[S]. 1995.
[5] Saunders R M. Standstill frequency-response methods and salient-pole synchronous machines[J]. IEEE Transactions on Energy Conversion, 1999, 14(4): 1033-1037.
[6] Radjeai H, Barakat A, Tnani S, et al. Identification of synchronous machine by standstill frequency response (SSFR) method-influence of the stator resistance[C]//IEEE International Conference on Electrical Machines, Rome, 2010: 1-5.
[7] Sellschopp F S, Arjona M A. Semi-analytical method for determining d-axis synchronous generator parameters using the DC step voltage test[J]. IET Electric Power Applications, 2007, 1(3): 348-354.
[8] Makela O, Repo A K, Arkkio A. Numerical(pu)lse test for synchronous machines[J]. Compel Inter- national Journal for Computation & Mathematics in Electrical & Electronic Engineering, 2013, 29(5): 1151-1158.
[9] Cisneros-Gonzalez M, Hernandez C, Morales-Caporal R, et al. Parameter estimation of a synchronous- generator two-axis model based on the standstill chirp test[J]. IEEE Transactions on Energy Conversion, 2013, 28(1): 44-51.
[10] Arjona M A, Cisneros-Gonzalez M, Hernandez C. Parameter estimation of a synchronous generator using a sine cardinal perturbation and mixed stochastic-deterministic algorithms[J]. IEEE Transa- ctions on Industrial Electronics, 2011, 58(2): 486- 493.
[11] Gao Jian, Dai Litao, Zhang Wenjuan. Improved genetic optimization algorithm with subdomain model for multi-objective optimal design of SPMSM[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(1): 160-165.
[12] Ma Yiming, Ling Zaixun, Cai Wanli, et al. A novel coast-down no-load characteristic test and curve conversion method for large-scale synchronous condenser[J]. Electric Power Systems Research, 2019, 172: 77-85.
[13] 孙曙光, 于晗, 杜太行, 等. 基于多特征融合与改进QPSO-RVM的万能式断路器故障振声诊断方法[J]. 电工技术学报, 2017, 32(19): 107-117.
Sun Shuguang, Yu Han, Du Taihang, et al. Vibration and acoustic joint fault diagnosis of conventional circuit breaker based on multi-feature fusion and improved QPSO-RVM[J]. Transactions of China Electrotechnical Society, 2017, 32(19): 107-117.
[14] 刘东奇, 王耀南, 袁小芳. 电动汽车充放电与风力/火力发电系统的协同优化运行[J]. 电工技术学报, 2017, 32(3): 18-26.
Liu Dongqi, Wang Yaonan, Yuan Xiaofang. Co- operative dispatch of large-scale electric vehicles with wind-thermal power generating system[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 18-26.
[15] 邢家维, 金能, 林湘宁, 等. 基于小波包变换的电流互感器饱和识别及有效数据运用策略研究[J]. 电工技术学报, 2018, 33(6): 1170-1179.
Xing Jiawei, Jin Neng, Lin Xiangning, et al. A novel strategy of current transformer saturation identi- fication and valid data application based on wavelet packet[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1170-1179.
[16] 周凯, 黄永禄, 谢敏, 等. 短时奇异值分解用于局放信号混合噪声抑制[J]. 电工技术学报, 2018, 33(11): 2435-2443.
Zhou Kai, Huang Yonglu, Xie Min, et al. Mixed noises suppression of partial discharge signal employing short-time singular value decom- position[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2435-2443.
[17] Dandeno P L, Karmaker H C, Azuaje C, et al. Experience with standstill frequency response (SSFR) testing and analysis of salient pole synchronous machines[J]. IEEE Transactions on Energy Con- version, 2002, 14(4): 1209-1217.
[18] Dalton F K, Cameron A W W. Simplified measurement of subtransient and negative sequence reactances in salient-pole synchronous machines[J]. Transactions of the American Institute of Electrical Engineers Part III Power Apparatus & Systems, 2008, 71(1): 752-757.
[19] Bortoni E C, José Antônio Jardini. A standstill frequency response method for large salient pole synchronous machines[J]. IEEE Transactions on Energy Conversion, 2005, 19(4): 687-691.
[20] Vicol L, Xuan M T, Wetter R, et al. On the identification of the synchronous machine parameters using standstill DC decay test[C]//IEEE International Conference on Electrical Machines, Chania, Greece, 2006: 229-233.
[21] Sellschopp F S, Arjona M A. DC decay test for estimating d-axis synchronous machine parameters: a two-transfer-function approach[J]. IEE Proceedings of Electric Power Applications, 2006, 153(1): 123- 128.
[22] Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577-601.
[23] 江天炎, 李剑, 杜林, 等. 粒子群优化小波自适应阈值法用于局部放电去噪[J]. 电工技术学报, 2012, 27(5): 77-83.
Jiang Tianyan, Li Jian, Du Lin, et al. De-noising for partial discharge signals using PSO adaptive wavelet threshold estimation[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 77-83.
[24] 汤蕴璆, 王成元. 交流电机动态分析[M]. 北京: 机械工业出版社, 2015.
[25] 赵洪森, 戈宝军, 陶大军, 等. 核电汽轮发电机定子内部短路故障对转子涡流损耗影响[J]. 电机与控制学报, 2018, 22(8): 17-25.
Zhao Hongsen, Ge Baojun, Tao Dajun, et al. Influence of stator internal short-circuit fault on rotor eddy current losses in nuclear power turbo- generator[J]. Electric Machines and Control, 2018, 22(8): 17-25.
A Novel Full Parameters Identification Method for Synchronous Machine Based on an Expanded Dalton-Cameron Transformation in Arbitrary Rotor Position
Abstract The measurement of transient parameters of large synchronous machines is generally carried out by a three-phase sudden short-circuit test, which is complicated and has certain dangers. Standstill test methods, such as static frequency response tests and signal input tests, can solve the above problem to some extent. However, such kind of tests must align the rotor with specific positions, which is difficult to implement for SMs of high capacity, and the positioning error also affects the accuracy. Aiming at the above problems, this paper proposed a novel full parameter test method based on signal input test for arbitrary rotor positions. A novel expanded Dalton-Cameron transformation was proposed and the corresponding test scheme was also given and analyzed, so that d and q axes parameters could be identified synchronously. NSGA3 algorithm was used for the curve fitting part. The test scheme and parameter identification method were verified by the test result of a dynamic simulation test prototype. The transformation and test method proposed in this paper are not only applicable to the tests using other forms of signals, but also provide reference for other standstill tests.
keywords:Synchronous machine, parameters identification, arbitrary rotor position, standstill experiment
中图分类号:TM341
DOI: 10.19595/j.cnki.1000-6753.tces.190134
国家重点研发计划资助项目(2018YFB0606000)。
收稿日期 2019-01-30
改稿日期 219-05-17
马一鸣 男,1995年生,硕士研究生,研究方向为大型电机特殊试验及参数辨识。E-mail: hust_maym@hust.edu.cn
王 晋 男,1979年生,副教授,硕士生导师,研究方向为大型与特种电机设计及其控制。E-mail: jinwang@hust.edu.cn(通信作者)
(编辑 陈 诚)