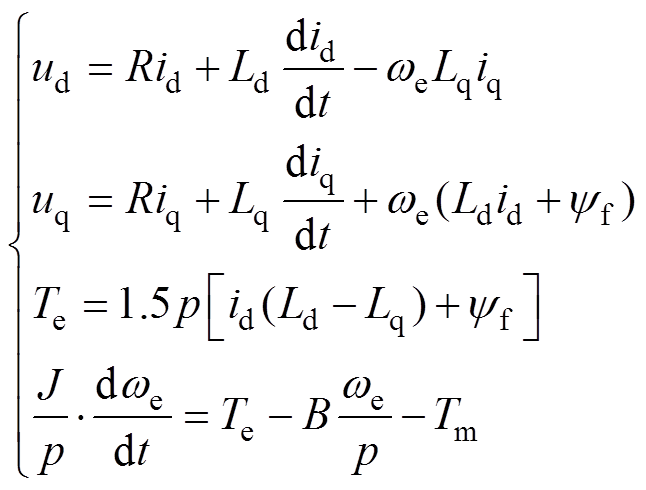（1）摘要 针对永磁同步电机（PMSM）多参数辨识困难的问题，该文提出一种初始参数优化的混沌变异小生镜粒子群优化（NCOPSO）算法，并设计一个含有5个待辨识参数（定子绕组电阻，定子绕组交、直轴电感，永磁体磁链，转动惯量）的满秩数学方程组。该算法首先使用粒子群算法优化基本粒子群算法3个初始参数（惯性系数w，学习因子c1、c2）。再对优化后的粒子群使用小生镜策略，以连续多次迭代适应值变化小的粒子为中心构造一个小生镜群体。最后使用混沌变异策略，在每次迭代过程中，以每个小生镜群体最优粒子为基础迭代生成一个混沌序列，将序列中最优粒子随机替换当前小生镜群体某一粒子，同时对小生镜群体最差粒子进行初始化。经电机仿真与实验验证了该算法的可行性与准确性。
关键词：永磁同步电机 参数辨识 粒子群优化 优化初始参数 小生镜 混沌变异
今年来，永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）以结构简单、重量轻、体积小、损耗小和功率密度高等诸多优点而被广泛用于民用、工业和军事等领域[1-2]。电机控制系统的设计需要精确获取定子绕组电阻，定子绕组交、直轴电感，永磁体磁链等关键参数[3-4]。例如，电机转矩控制需要获取磁链参数[5]，电流环控制器需要获取电阻和电感参数[6]，另外转动惯量对于速度控制器动态性能的设计也相当重要[7]。因此，获取准确的电机参数有助于提高整个PMSM驱动系统的控制性能。由于PMSM驱动系统是一个非线性时变系统，在实际运行中，电阻、电感和磁链参数受温度、磁饱和、负载扰动的影响而发生改变[8]，转动惯量随机械载荷的变化而变化，这些参数的任何变化都会引起系统运行状态的变化，因此对这些参数进行精确辨识很有必要。
为此国内外诸多学者提出了不同的参数辨识方法，有最小二乘法[9]、扩展卡尔曼算法[10]、模型参考自适应方法[11-12]、神经网络[13-14]、遗传算法[15-16]和粒子群算法[17-18]等。最小二乘法具有收敛速度快的优点，但在非稳态条件下，该算法的计算量大、跟踪能力差。文献[9]在三种准稳态条件下采集数据构成满秩方程组来辨识3个参数，但采集三种准稳态数据较困难，且辨识参数较少。文献[10]提出一种估计PMSM转子转速和位置的扩展卡尔曼算法，但由于该算法一阶线性化精度低，在系统非线性较强时，滤波效果不佳[19]。文献[11]使用模型自适应方法分步辨识参数，先辨识电感，再辨识电阻和磁链，但电阻和磁链的精度受电感的影响。文献[12]通过设定其他参数为标称值来估计一些参数，然而，当PMSM参数非线性变化时，标称值和实际值存在偏差，其估计值可能存在偏差。文献[13]用神经网络结合最小方均权值收敛算法，精度较高、收敛较快，但是辨识系统的稳定性和速度取决于收敛因子选取是否合适，且神经网络函数逼近对训练数据非常敏 感[20]。文献[15]使用遗传算法帕德逼近并离散化数学模型，先辨识出离散化方程系数再求待辨识参数，步骤较复杂，且遗传算法具有搜索精度不高、易陷入局部最优等缺点[21]。文献[16]使用量子遗传算法，该算法采用多状态基因量子比特编码方式和通用量子旋转门操作，引入动态调整旋转角机制和量子交叉，比遗传算法更具有通用性，且效率更高，但算法每次迭代都需要进行量子旋转门操作，数据处理量大、运行时间较长。文献[17]使用柯西变异的粒子群算法，但与文献[15]相似，在数学模型方程欠秩条件下辨识多个参数缺乏理论依据。文献[18]将待辨识参数初始值与电机设计值设置得较近，然而实际工况为一台未知参数的电机，很难估计其参数值相对大小。
本文在PMSM定子d轴注入负序弱磁电流，与矢量控制id=0两种状态下采集相同数量数据，使得PMSM机电数学方程满秩。运用初始参数优化的混沌变异小生镜粒子群优化（Niche based on Chaotic mutation with initial parameter Optimization Particle Swarm Optimization, NCOPSO）算法可同时精确辨识定子绕组电阻，定子绕组交、直轴电感，永磁体磁链和转动惯量5个参数。
PMSM可分为电气系统和机械系统两个子系统，其在同步旋转dq坐标系下的机电方程通常表示为
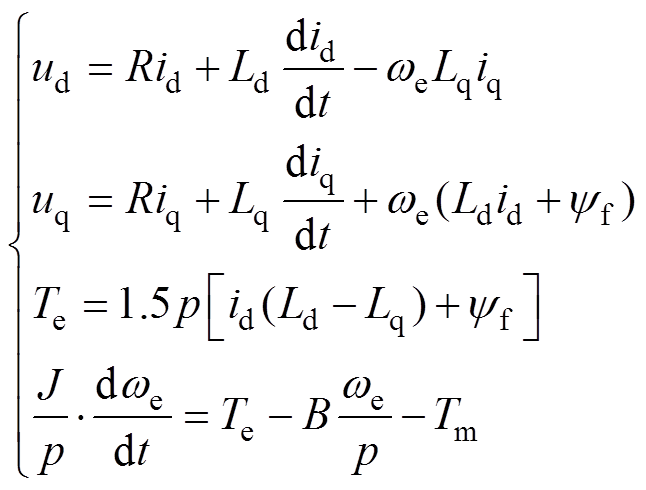（1）式中，ud、uq为定子直轴、交轴电压；R为定子电阻；id、iq为定子直轴、交轴电流；Ld、Lq为定子直轴、交轴电感；we为电角速度；yf为永磁体磁链；p为极对数；Te为电磁转矩；Tm为负载转矩；B为转动惯量；J为阻尼系数。
当电机处于稳态运行时，定子交、直轴电流，转速变化很小，近似认为
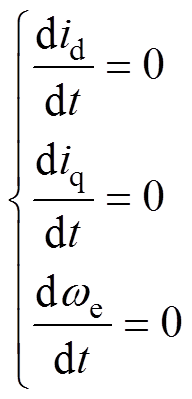
其稳态运行时的数学模型为
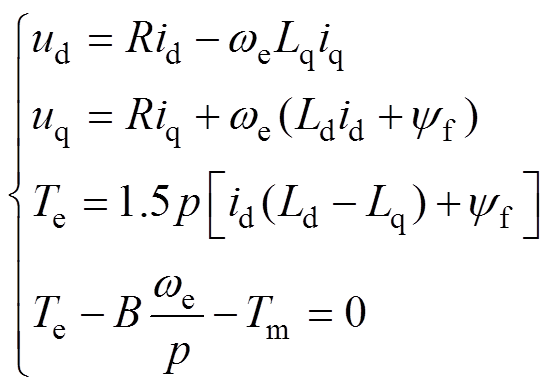（2）
将式（2）中Te消去得
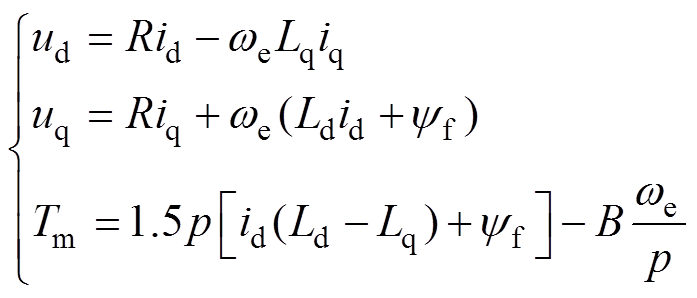（3）一般矢量控制设为id=0，用来解耦磁通和转矩控制。上述方程为含有5个未知数（R、Ld、Lq、yf、B），秩为3的方程组，方程组有无数组解，目前多数学者采用在d轴注入id≠0的负序弱磁电流策略，数据采样如图1所示。
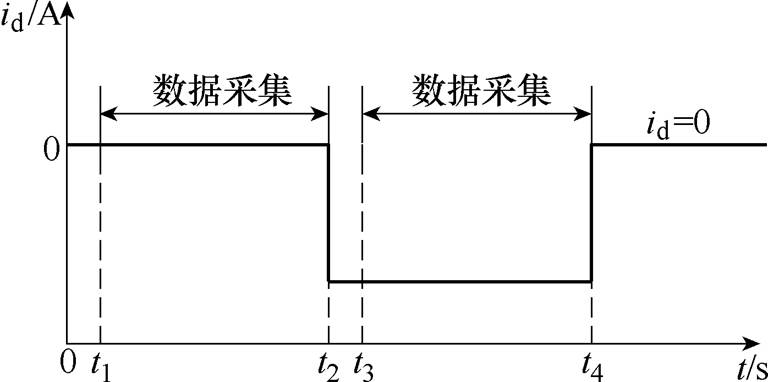
图1 数据采样
Fig.1 Data sampling diagram
在两种控制策略下采集相同数量的数据构成满秩方程组，即
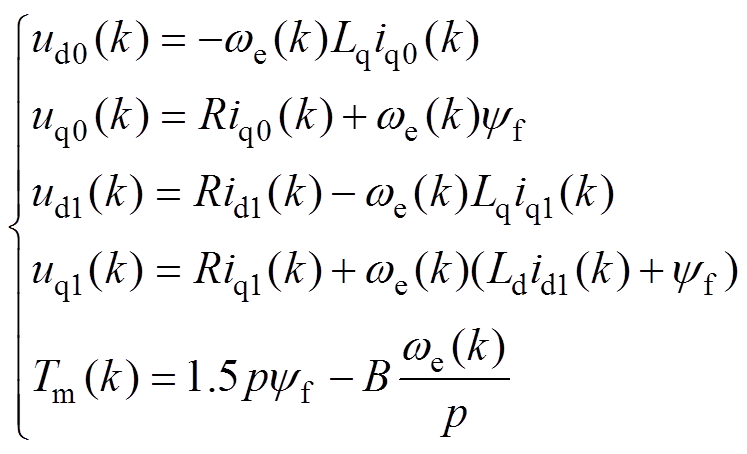（4）式中，ud0(k)、iq0(k)、uq0(k)、we(k)、Tm(k)分别为图1中t1～t2时间段第k次的采样数据；ud1(k)、iq1(k)、uq1(k)、id1(k)分别为图1中t3～t4时间段第k次的采样数据。方程组式（4）满秩，解唯一。
基本粒子群优化（Particle Swarm Optimization, PSO）算法，起源于对鸟群捕食行为的研究。在每次迭代中，更新粒子位置和速度为
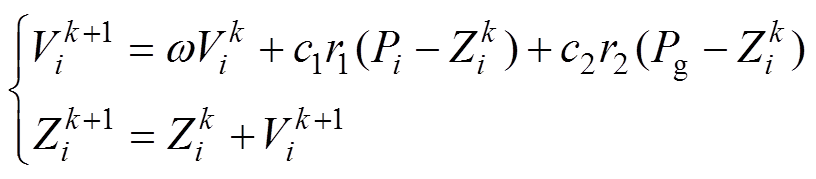（5）式中，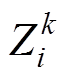
、
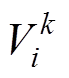分别为粒子i在第k代的位置与速度；Pi为粒子i所经历的最优位置；Pg为整个粒子群经历的最优位置；c1、c2为学习因子；r1、r2为[0, 1]之间的随机数；w 为惯性权重系数。PSO具有较强的小数据寻优能力，能解决较复杂的优化问题，但随着迭代次数的增加，易陷入局部最优[22]。
Shi和Eberhart通过大量实验，研究了w 对算法优化性能的影响，发现较大的w 有利于算法跳出局部最优解，能提高全局搜索能力，而较小的w 能提高算法的局部搜索能力，c1表示对粒子历史位置的认识和肯定，鼓励粒子飞向自身发现的最佳位置；c2为社会部分，表示粒子对群体社会位置的学习，引导粒子飞向群体所经历的最好位置，三者对算法性能好坏有着本质的影响[23]。因此，选择合适的初始参数w、c1、c2能较好地提高算法的收敛速度和搜索精度。
当三个初始参数设为m1、m2、m3时，粒子群算法对目标函数f多次寻优后平均适应度值为a，改变三个初始参数，设为n1、n2、n3，对应平均适应度值为b，当b＞a时（目标函数越复杂，数据量越大时，差距越明显），可以认定后者好于前者。不同的初始参数对应的平均适应度值不同，为了找到能使平均适应度值最小的3个初始参数，可以使用粒子群优化算法来对这3个初始参数寻优。设需要初始参数寻优的基本粒子群算法为粒子群1，粒子解是3个初始参数的为粒子群2。粒子群2的作用为将不同的初始参数都传递给粒子群1，并获取每组初始参数对应的粒子群1的适应度值，将其作为此粒子的适应度值。粒子群2迭代结束后输出的即为能使粒子群1适应度值最小的初始参数。粒子群优化初始参数流程如图2所示。
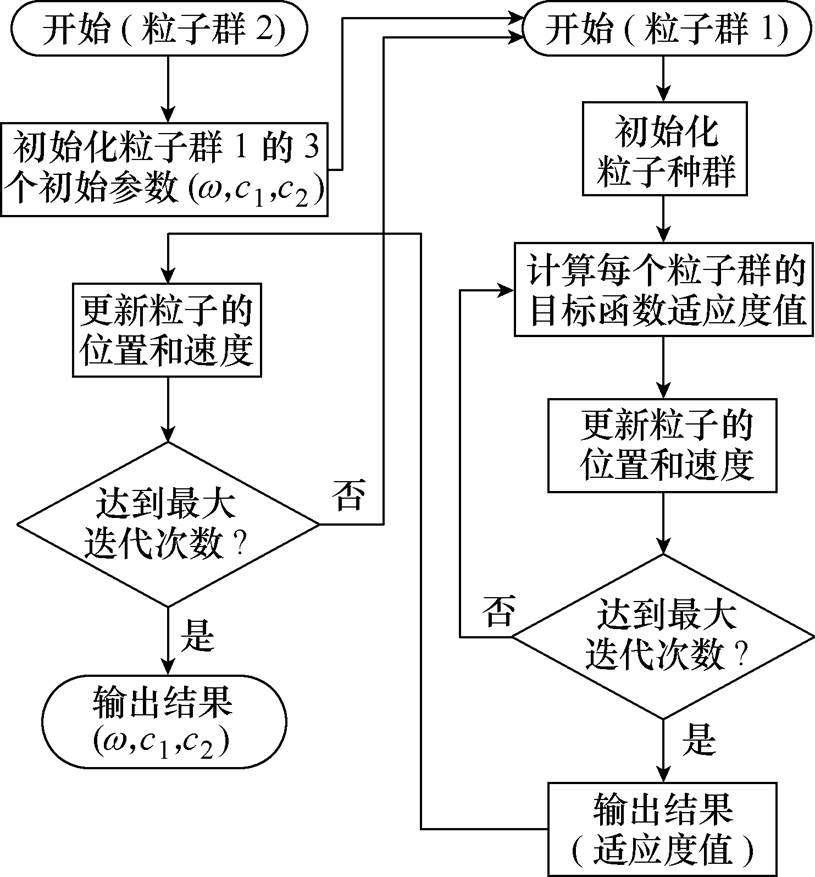
图2 粒子群优化初始参数流程
Fig.2 Flow chart of initial parameters for particle swarm optimization
经多次粒子群算法优化不同目标函数实验发现，对目标函数f寻求的最优初始参数w、c1、c2，对其他目标函数同样具有较好的收敛速度和搜索 精度。
自然界中的小生镜是指在特定条件下的生存策略。在进化过程中，生物通常与自己的物种生活在一起，并共同繁殖后代。2002年Brits、Engelbrchta等将小生镜策略引入基本粒子群优化算法中，提出小生镜粒子群算法（Niche PSO, NPSO）[24]。
在NPSO中，当一个粒子多次迭代适应度值变化幅度很小时，以此粒子为半径，构造一个圆形小生镜群体，半径的大小为与其最近粒子的距离。多次迭代后小生镜群体半径公式为
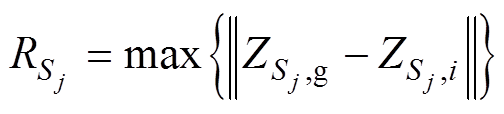（6）式中，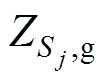
、
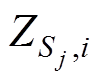分别为小生镜群体Sj中的最优粒子和除最优粒子以外的粒子。
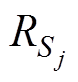算法有两个重要步骤：
1）若粒子Zi进入小生镜群体Sj区域内，即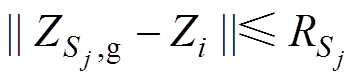
，则此粒子将被Sj接受。
2）若两个小生镜群体Sj、Sk区域相交，即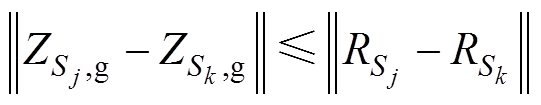
，两个小生镜群体合并。
NPSO具体步骤如下：
（1）设置算法参数并初始化主粒子群。
（2）计算主粒子群各粒子的适应度值，根据基本粒子群的位置和速度式（5）产生子粒子群，并计算子粒子群的适应度值。
（3）通过如下方式更新小生镜群体：
①使用一般收敛粒子群算法更新子粒子群，即
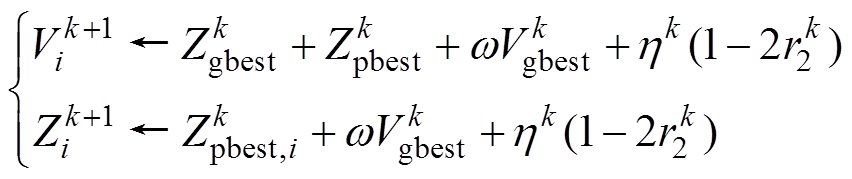（7）式中，k为更新次数；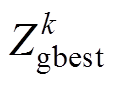
、
分别为第k次更新时种群全局最优位置和粒子i历史最优位置；h 为搜索范围的最大值；r2为[0, 1]之间的随机数。
②计算每个子粒子的适应度值。
③对未形成小生镜群体的子粒子，计算其主粒子，更新前的子粒子，子粒子三者间适应度变化量，若变化量很小，以此子粒子为中心生成小生镜群体，对已在小生镜群体中的子粒子，则更新其所在小生镜群体的半径。
④如果其他粒子满足步骤1），则被此小生镜群体接受。
⑤如果两个小生镜群体满足步骤2），则两个小生镜群体合并。
⑥返回步骤（2）直到达到最大迭代次数。
混沌是自然界广泛存在的一种非线性现象，具有随机性、遍历性等特点，已被广泛运用于随机优化[25]。混沌Logistice方程[26]为
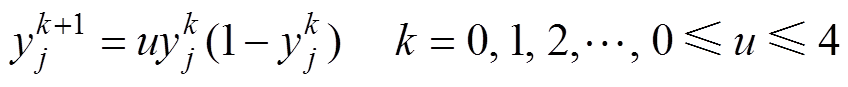（8）式中，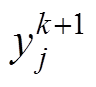
为混沌变量；u为控制参数；k为迭代次数，实验证明，当3.57≤u≤4时，方程值的变化非常大，进而每次迭代的解都是随机的，此时，Logistice方程成为混沌系统[27]。
基于混沌变异的小生镜粒子群（Niche based on Chaotic mutation PSO, NCPSO）算法具体步骤如下：
（1）设置算法参数并初始化主粒子群。
（2）生成小生镜群体，记录小生镜中最优粒子和最差粒子。
（3）对每个小生镜最优粒子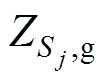进行混沌优化：
①将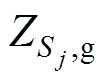映射到Logistice方程的定义域[0, 1]上，即
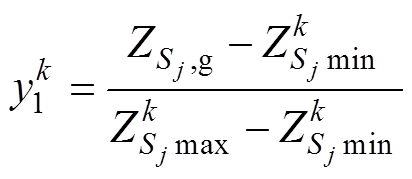（9）式中，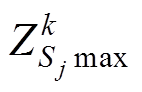
、
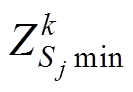分别为小生镜群体Sj第k次迭代后最大和最小值。
②对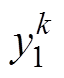
通过式（8）进行N次迭代，得到混沌序列
。
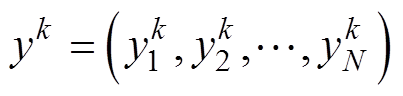③将混沌序列逆映射到原解空间，即
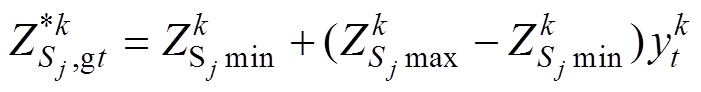
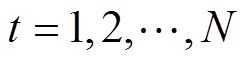（10）从而产生一个混沌变量可行解列为
④计算可行解序列中每个粒子的适应值，并保留最优粒子，记为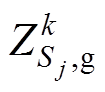
。
（4）从当前小生镜群体中随机选择一个粒子，并用最优粒子替换选出的粒子。
（5）初始化小生镜群体最差粒子。
（6）返回步骤（2）直到算法达到最大迭代次数。
NCPSO算法具有小生镜策略的全局优化能力和混沌变异策略精细化搜索各自的优点，因此比NPSO有更快的寻优能力和更高的搜索精度。
永磁同步电机参数辨识可转化为系统优化问题。ud、uq、Tm被作为PMSM辨识模型和测量信号的输入，NCOPSO选取待PMSM辨识参数的合适值，使得辨识模型与测量信号之间的误差二次方和目标函数适应度值达到最小值，适应度值越小，其辨识模型输入与测量模型输入越接近，待辨识参数和真实值也越近。目标函数如下
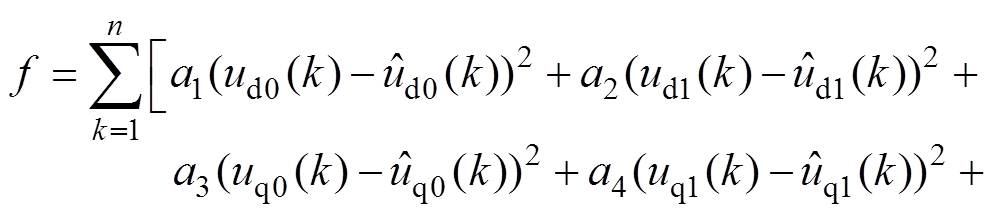
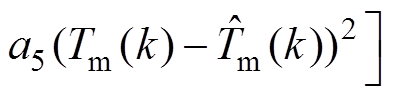（11）
式中，a1、a2、a3、a4、a5为权重系数；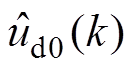
、
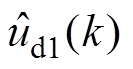为辨识模型定子d轴输出电压值；
、
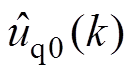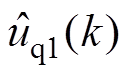为辨识模型定子q轴输出电压值；
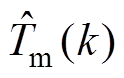为辨识模型输出电压、转矩值。在相同的适应度值条件下，不同的权重系数可以改变各个待辨识参数的精度。图3为NCOPSO算法辨识原理。
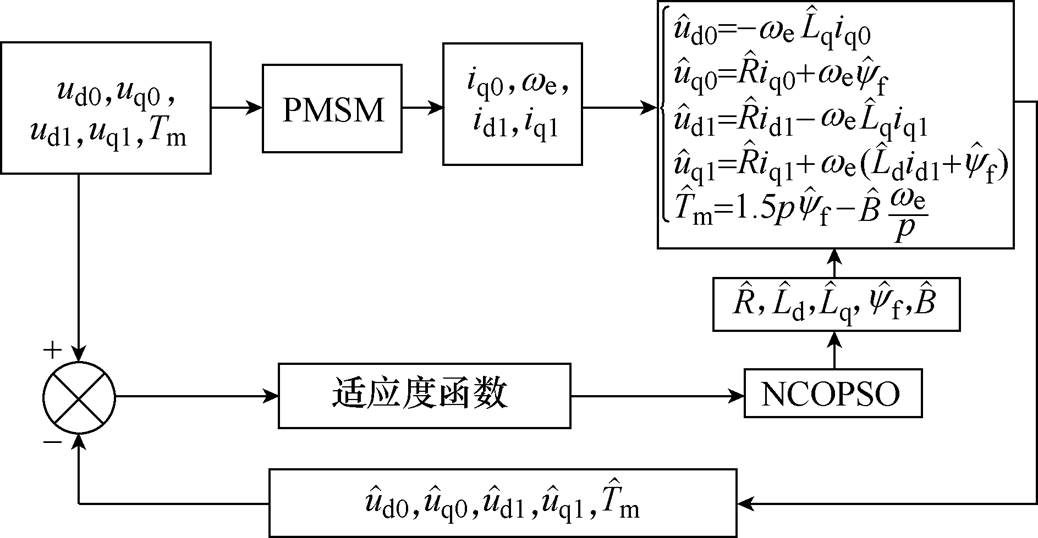
图3 NCOPSO算法辨识原理
Fig.3 Identification schematic diagram of NCOPSO algorithm
与实验相比，仿真不受不同工况条件下的扰动和采样精度的影响，能很好地检验算法的辨识性能。
为验证NCOPSO较PSO、NPSO、NCPSO在PMSM多参数辨识中的优越性，基于Matlab2016b/ Simulink8.8环境下搭建如图4所示的粒子群算法在线辨识模型。模型的上半部分采集除待辨识参数以外的所有数据；模型的下半部分为算法辨识模块。
实验中的电机参数采用仿真电机参数设计值，仿真模型参数值见表1，仿真中电机负载转矩设为5N·m，转速设为2 500r/min。
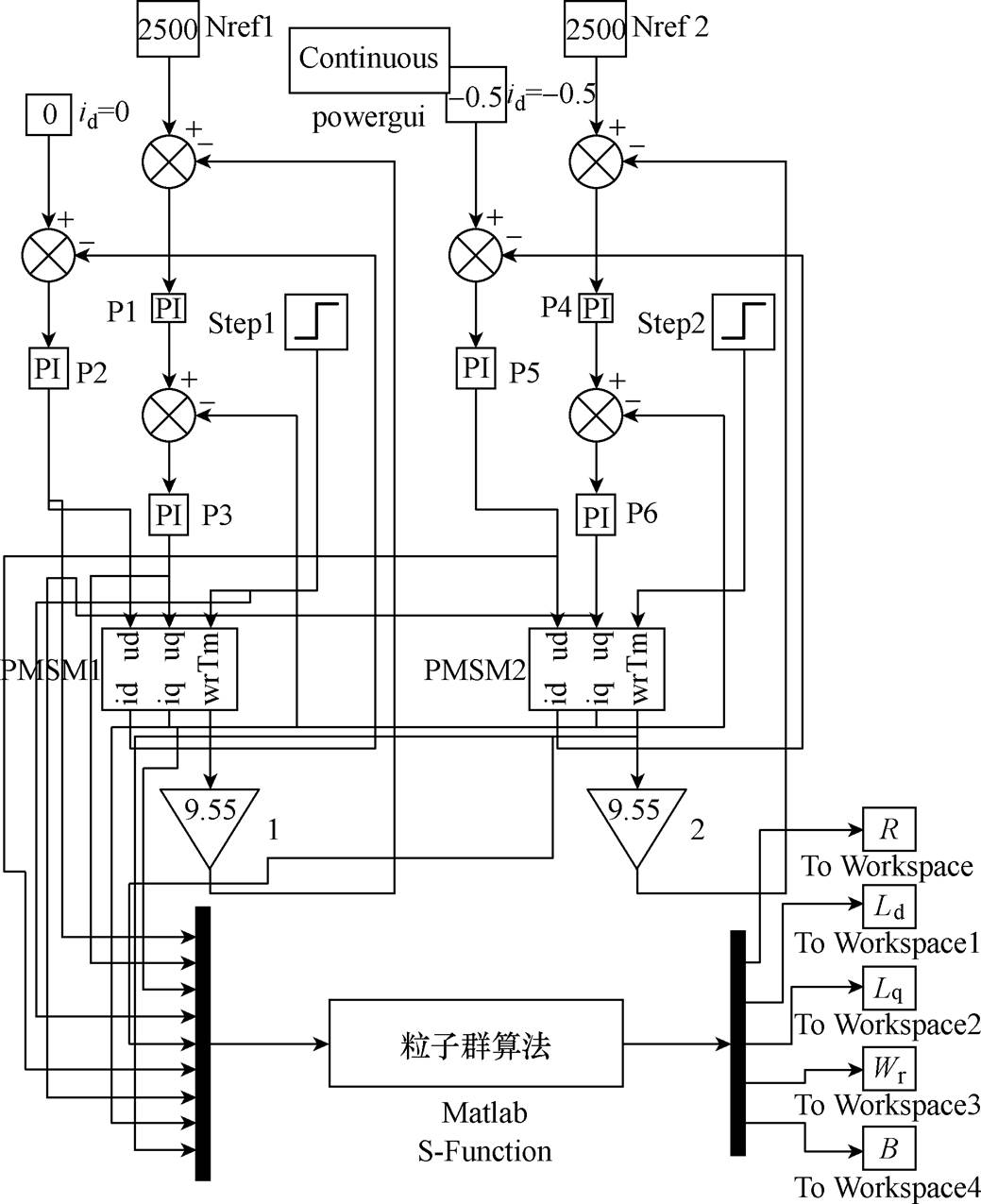
图4 粒子群算法在线辨识模型
Fig.4 On-line identification model of particle swarm optimization
表1 仿真模型参数值
Tab.1 Parameters of simulation model
参 数数 值 额定功率/kW1.0 额定转速/(r/min)2 500 额定转矩/(N·m)4 峰值转矩/(N·m)12 额定线电流/A4.0 额定线电压/V220 定子电阻R/W2.76 d轴电感Ld/mH6.42 q轴电感Lq/mH6.42 磁链yf/Wb0.204 转动惯量B/(104kg·m2)8.5 极对数4
为了确保仿真分析的合理性，PSO、NPSO、NCPSO的3个初始参数均设为w =0.4，c1=c2=2；NCOPSO使用优化的初始参数，所有算法的最大迭代次数相同，为150次，种群规模相同为100。仿真实验数据采集时长为0.5s，共10 000组数据，五个待辨识参数的初始域为[0, 5]，远离仿真电机设计值。为了减少单次算法的随机性带来的测试误差，所有仿真实验独立运行30次，取其平均值作为最终输出值。四种算法迭代满150次各参数的波形曲线如图5所示，仿真结果见表2。
图5 PMSM仿真参数辨识曲线
Fig.5 Parameter identification curves of PMSM
表2 仿真结果
Tab.2 Simulation result
参 数数 值 PSONPSONCPSONCOSPO R/W3.4443.6042.6542.767 Ld/mH36.364.486.176.422 Lq/mH16.426.066.796.419 yf/Wb0.3040.256 40.229 40.204 1 B/(104kg·m2)30.5742.628.948.46 平均适应值350 917.510 611.619.50.7
从图5的平均适应度值可以看出，四种算法平均在15代左右就进入了局部精细化搜索，不同的是随后PSO陷入局部最优，这主要是因为仿真采集数据较多，目标函数为多模态问题存在局值，而改进的NPSO、NCPSO、NCOPSO效果明显好于PSO，其中NCOPSO效果最好，其适应度值非常小，准确地辨识出5个参数。NCOPSO在寻优过程中，当最优粒子适应度值变化很小时，混沌变异策略能使其跳出局部最优，以致粒子的各个解向量都朝着设计值快速收敛。NCOPSO的电感、磁链的辨识值非常接近设计值，说明在式（4）中，三者的波动对适应度函数影响较大，而对电阻、转动惯量的影响较低。
为了在动态工况条件下验证算法的辨识性能，搭建如图6所示的实验平台。
图6 实验平台
Fig.6 Experimental platform
永磁同步电机参数见表1。动态转矩传感器采集动态转矩、转速和功率等信号，并传输给动态转矩测控仪显示。动态转矩传感器与动态转矩测控仪构成高精度、智能型的动态转矩测控系统。磁粉制动器是自动控制元件，模拟负载使用，磁粉控制器控制模拟负载大小。DSP控制板采集传感器信号、控制电机和显示电机状态等信息。计算机用于实现辨识功能。
文献[28]指出在定子d轴注入电流分量，可能导致永磁体不可逆退磁，然而在动态工况条件下辨识参数需要较长时间的d轴注入电流，为减少因注入电流而导致的永磁体退磁，注入电流不易过大，本文注入的直轴电流为-0.5A。通过改变电机转速和负载大小来模拟在动态工况条件下电机的运行状态，将电机处于2 000r/min，负载6N·m稳定运行时开始计时，采集数据总时长为8s。在第1s时开始匀速提高转速直到2 500r/min，在第4s时开始将扭矩匀速提高直到10N·m，将采样数据发送到上位机后，再传递给基于VC++6.0的NCOPSO程序，便可实现在线辨识[20]。在动态工况条件下PMSM各实验参数辨识曲线如图7所示。
从图7可以看出，当电机运行状态发生变化时，NCOPSO各参数的辨识值和真实值很接近，其辨识效果相比PSO、NPSO、NCPSO较好，且对于变化的电机参数可以准确跟踪，鲁棒性强，具有较好的实用性。在动态工况条件下，电机参数会发生一定的偏移，电阻随着时间有着轻微的上升趋势、磁链有下降的趋势，原因为电机在运行时产生热量，导致电机本体温度上升，温度上升又导致磁通密度下降。升温使得电阻增大，磁通密度下降使得磁链减小。当电机转速匀速提高时，负载转矩方程是动态的，电角速度微分项产生较大干扰，使得转动惯量和磁链辨识值与真实值发生较大偏移。当负载转矩匀速提高时，电机机电数学模型不是稳态方程式（4），而是动态方程式（1），但负载转矩均匀提高导致的定子交轴电流微分项产生的干扰较小，使得辨识值偏移较小。
图7 动况条件下PMSM实验参数辨识曲线
Fig.7 Parameter identification curve of PMSM experiment under dynamic condition
本文在矢量控制基础上，通过注入id≠0的弱磁负序电流使电机机电数学模型达到满秩，运用基于初始参数优化的混沌变异小生镜粒子群算法能同时精确辨识定子绕组电阻，定子绕组交、直轴电感，永磁体磁链，转动惯量5个参数，该算法在基本粒子群算法基础上运用优化初始参数、小生镜、混沌变异三种策略，在全局搜索性能、收敛速度、搜索精度取得了较好的效果。仿真验证了NCOPSO算法较PSO、NPSO、NCPSO算法在永磁同步电机参数辨识的优越性，实验验证了在动态工况条件下的辨识性能。另外，该算法具有适用广、鲁棒性强等优点，能广泛运用于寻求最优化的工程中。
参考文献
[1] Masahiro Aoyama, Deng Jianing. Visualization and quantitative evaluation of eddy current loss in bar-wound type permanent magnet synchronous motor for mild-hybrid vehicles[J].CES Transactions on Electrical Machines and Systems, 2019, 3(3): 269-278.
[2] 李键, 牛峰, 黄晓艳, 等. 永磁同步电机有限控集模型预测电流控制预测误差分析[J]. 电机与控制学报, 2019, 23(4): 2-7.
Li Jian, Niu Feng, Huang Xiaoyan, et al. Prediction error analysis of finite-controlset model predictive current control for PMSMs[J]. Electric Machines and Control, 2019, 23(4): 2-7.
[3] Underwood S J, Husain I. Online parameter estimation and adaptive control of permanent-magnet synchronous machines[J]. IEEE Transactions on Industrial-Electronics, 2010, 57(7): 2435-2443.
[4] Babel A S, Cintron-Rivera J G, Foster S N, et al. Evaluation of a parameter identification method for permanent magnet AC machines through parametric sensitivity analysis[J]. IEEE Transactions on Energy Conversion, 2014, 29(1): 240-249.
[5] Huang Wenqing, Zhang Yontong, Zhang Xingchun, et al. Accurate torque control of interior permanent magnet synchronous machine[J]. IEEE Transactions on Energy Conversion, 2014, 29(1): 29-37.
[6] Underwood S J, Husain I. Online parameter estimation and adaptive control of permanent-magnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2435-2443.
[7] Zhang Xiaoguang, Li Zhengxi. Sliding mode observer-based mechanical parameter estimation for permanentmagnet synchronous motor[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5732-5745.
[8] Liu Kan, Zhu Z Q, Stone D A. Parameter estimation for condition monitoring of PMSM stator winding and rotor permanent magnets[J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5902-5913.
[9] 刘金海, 陈为. 表贴式永磁同步电机准稳态多参数在线辨识[J]. 电工技术学报, 2016, 31(17): 155-160.
Liu Jinghai, Chen Wei. Online multi-parameter identification for surface-mounted permanent magnet synchronous motors under quasi-steady-state[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 155-160.
[10] Shi Yuchao. Online identification of permanent magnet flux based on extended Kalman filter for IPMSM drive with position sensorless control[J]. IEEE Transactions on Industrial Electronics, 2012, 59(11): 4169-4178.
[11] 杨宗军, 王莉娜. 表贴式永磁同步电机的多参数在线辨识[J]. 电工技术学报, 2014, 29(3): 112-118.
Yang Zongjun, Wang Lina. Online multi-parameter identification for surface-mountrd permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 112-118.
[12] Zhang Yanqing, Yin Zhonggang, Sun Xiangdong, et al. On-line identification- methods of parameters for permanent magnet synchronous motors based on cascade MRAS[C]//9th International Conference on Power Electronics and E-CCE Asia, 2015: 345-353.
[13] 谷鑫, 胡升, 史婷娜, 等. 基于神经网络的永磁同步电机多参数解耦在线辨识[J]. 电工技术学报, 2015, 30(6): 115-121.
Gu Xin, Hu Sheng, Shi Tingna, et al. Muti-parameter decoupling online identification of permanent magnet synchronous motor based on neural network[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 115-121.
[14] 张立伟，张鹏，刘曰峰, 等. 基于变步长Adaline神经网络的永磁同步电机参数辨识[J]. 电工技术学报, 2018, 33(2): 378-384.
Zhang Liwei, Zhang Peng, Liu Yuefeng, et al. Parameter identification of permanent magnet synchronous motor based on variable step-size adaline neural network[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 378-384.
[15] 肖曦, 许青松, 王雅婷, 等. 基于遗传算法的内埋式永磁同步电机参数辨识方法[J]. 电工技术学报, 2014, 29(3): 22-26.
Xiao Xi, Xu Qingsong, Wang Yating, et al. Parameter identification of interior permanent magnet synchronous motors based on genetic algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 22-26.
[16] Liu Kan, Zhu Z Q. Quantum genetic algorithm-based parameter estimation of PMSM under variable speed control accounting for system identifiability and VSI nonlinearity[J]. IEEE Transactions on Industrial- Electronics, 2015, 62(4): 2363-2371.
[17] 傅小利, 顾红兵, 陈国呈, 等. 基于柯西变异粒子群算法的永磁同步电机参数辨识[J]. 电工技术学报, 2014, 29(5): 127-131.
Fu Xiaoli, Gu Hongbing, Chen Guocheng, et al. Permanent magnet synchronous motors parameters identification based on cauchy mutation particle swarm optimization[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 127-131.
[18] 刘朝华, 李小花, 周少武, 等. 面向永磁同步电机参数辨识的免疫完全学习型粒子群算法[J]. 电工技术学报, 2014, 29(5): 119-126.
Liu Chaohua, Li Xiaohua, Zhou Shaowu, et al. Comprehensive learning particle swarm optimization algorithm based on immune mechanism for permanent magnet synchronous motor parameter identification[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 119-126.
[19] 谷苗, 夏超英, 田聪颖. 基于综合型卡尔曼滤波的锂电池荷点状态估算[J]. 电工技术学报, 2019, 34(2): 420-426.
Gu Miao, Xia Chaoying, Tian Congying, Li-ion battery state of charge estimation based on comprehensive Kalman filter[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 420- 426.
[20] 赵希梅, 吴勇慷. 基于自适应修正拉盖尔递归神经网络的永磁直线同步电机反推控制[J]. 电工技术学报, 2018, 33(10): 2393-2399.
Zhao Ximei, Wu Yongkang. Backstepping control based on adaptive modified laguerre ecurrent neural network for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(10): 2393-2399.
[21] 杜林, 杨峰, 蔚超, 等. 基于频域介电谱的油纸绝缘宽频等效模型参数辨识研究[J]. 电工技术学报, 2018, 33(5): 1159-1166.
Du Lin, Yang Feng, Wei Chao, et al. Parameter identification of the wide-band model of oil- impregnated paper insulation using frequency[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1159-1166.
[22] 彭道刚, 陈跃伟, 钱玉良, 等. 基于粒子群优化-支持向量回归的变压器绕组温度软测量模型[J]. 电工技术学报, 2018, 33(8): 1743-1749.
Peng Daogang, Chen Yuewei, Qian Yuliang, et al. Transformer winding temperature soft measurement model based on particle swarm optimization suport vector regression[J]. Transactions of China Elec- trotechnical Society, 2018, 33(8): 1743-1749.
[23] 介婧, 徐新黎. 智能粒子群优化计算控制方法、协同策略及优化应用[M]. 北京: 科学出版社, 2016.
[24] Brits R, Engelbrecht A P, Bergh F V D. A niching particle swarm optimizer[C]//Conference on Simulated Evolution & Learning, South Africa, 2002: 1037- 1040.
[25] 贾东立, 张家树, 张超. 基于混沌遗传算法的基元提取[J]. 西南交通大学学报, 2005, 40(4): 496-500.
Jia Dongli, Zhang Jiashu, Zhang Chao. Geomet ricpri-mitive extraction using chaos genetic algo- rithm[J]. Journal of Southwest Jiaotong University, 2005, 40(4): 496-500.
[26] 施特凡格雷席克. 混沌与其秩序[M]. 上海: 百家出版社, 2001.
[27] 纪震, 廖惠连, 吴青华. 粒子群算法与应用[M]. 北京: 科学出版社, 2009.
[28] 李立毅, 于吉坤, 曹继伟, 等. 新型定子结构永磁同步电机弱磁调速性能分析[J]. 电工技术学报, 2015, 30(14): 87-93.
Li Liyi, Yu Jikun, Cao Jiwei, et al. Analysis of permanent magnet synchronous motor with new stator- design for adjustable-speed by flux weakening[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 87-93.
Research on Multi-Parameter Identification Method of Permanent Magnet Synchronous Motor
Abstract Aiming at the difficulty of multi-parameter identification of permanent magnet synchronous motor (PMSM), this paper proposed a chaotic mutation niche particle swarm optimization algorithm with initial parameter optimization (NCOPSO), and designed a full-rank mathematical system with five parameters (stator winding resistance, stator cross-axis and direct-axis inductance, permanent magnet flux, moment of inertia) to be identified. Firstly, the particle swarm optimization was used to optimize the three initial parameters (inertia coefficient w, learning factor c1, c2) of the basic particle swarm optimization algorithm. Then the niche strategy was applied to the optimized particle swarm: a niche population centering on the particles with small adaptive value changes in successive iterations was constructed. Finally, the chaotic mutation strategy is used: in each iteration process, a chaotic sequence was generated based on the optimal particles of each niche group. The optimal particles in the sequence were randomly replaced by a certain particle of the current niche population, and the worst particle of the niche mirror population was initialized at the same time. The feasibility and accuracy of the algorithm were verified by motor simulation and experiment.
keywords：Permanent magnet synchronous motor, parameter identification, particle swarm optimization, initial paramter optimization, niche, chaotic mutation
中图分类号：TM315
DOI: 10.19595/j.cnki.1000-6753.tces.190122
国家自然科学基金项目（51767009），江西省科技项目（20153BCB23012，20151BBE50109，GJJ160598，20181BAB206035）和江西理工大学清江青年英才计划资助。
收稿日期2019-01-28
改稿日期 2019-05-06
刘细平 男，1976年生，博士，教授，硕士生导师，研究方向为稀土永磁电机设计、风力发电及其相关控制、电力电子技术。E-mail: liuxp211@163.com（通信作者）
胡卫平 男，1991年生，硕士研究生，研究方向为智能优化算法、电机与控制。E-mail: 2061139702@qq.com
（编辑 陈 诚）