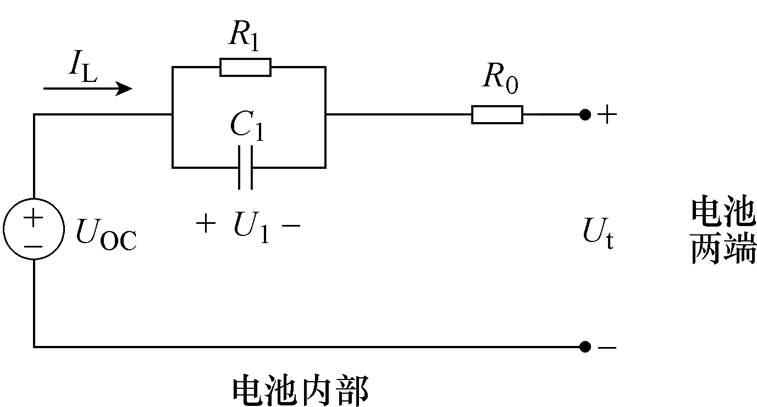
图1 锂离子电池一阶RC模型
Fig.1 First order RC model for lithium-ion battery
摘要 电池剩余寿命(RUL)预测是电池管理系统的核心技术之一。为了以较少的数据量准确地在线预测电池RUL,提出新陈代谢灰色粒子滤波(MGM-PF)算法。首先利用一阶RC模型在线估算电池容量;然后基于估算的容量数据,利用新陈代谢灰色模型动态更新的灰色发展系数作为模型参数,构建表征电池容量退化的动态状态空间模型;并融合粒子滤波跟踪电池容量退化,实现电池RUL预测并给出预测结果的不确定性表达。实验结果表明,所提出的基于在线容量估算的MGM-PF算法能准确预测电池RUL。
关键词:新陈代谢灰色模型 粒子滤波 电池剩余寿命 在线容量估算
随着能源危机和温室气体排放问题日益凸显,节能低碳的电动汽车已成为汽车工业的重点发展方向。锂离子电池因能量密度大、循环寿命长和自放电率低等优点成为电动汽车动力电池的首选,但其寿命衰减带来的性能下降会影响到整车性能与行车安全[1-4]。因此,电池剩余寿命(Remaining Useful Life, RUL)预测是动力电池管理的重点和难点之一。准确预测电池RUL能够为系统维护和电池更换提供参考,降低维护成本并减少致命故障发生概率。
近年来,RUL预测方法发展迅速,其中基于电池退化模型的RUL预测方法发展已经较为成熟[5]。粒子滤波(Particle Filter, PF)因具有处理非线性、非高斯且能提供不确定性表达等优点[6],被广泛应用于电池RUL预测;苗强等构建容量退化双指数模型,利用已知容量数据更新初始化退化模型,最后引入标准粒子滤波算法实现电池RUL预测,但电池容量数据无法直接在线测量,且粒子滤波算法需要大量的样本数据量才能很好地近似系统后验概率密度[7]。随着机器学习方法的研究深入,支持向量机、相关向量机以及神经网络等机器学习类方法逐渐广泛运用于电池RUL预测[8]。如Liu等利用相关向量机实现电池RUL预测,但进行RUL预测前需要先对模型进行训练,因此对数据量要求较高[9]。Wei等为准确描述电池老化过程容量退化特性,利用支持向量机建立容量退化模型,然后以粒子滤波更新退化模型参数,最终实现电池RUL预测[10]。虽然关于RUL预测方法的研究众多,但现阶段大部分研究都利用电池容量或者内阻作为电池退化表征量,而这些参数并不容易在线获取[11-12]。
由于不同于传统退化模型过于依赖模型精度,又优于数据驱动类算法所需数据量大,灰色系统理论逐渐被应用于电池健康管理方向[13]。Chen等利用多种灰色模型进行电池容量预测,经验证,新陈代谢灰色模型(Metabolic Grey Model, MGM)在不同充放电倍率和温度下均能实现电池容量准确预测[14]。潘海鸿等基于灰色预测模型所需数据量少、预测精度高的优点,利用带滑窗的GM(1, 1),即MGM替代传统扩展卡尔曼滤波(Extended Kalman Filte, EKF)中的Jacobian矩阵,实现电池荷电状态(State of Charge, SOC)估算[4]。以上文献表明,MGM在电池健康管理上的研究已取得一定成果,但还有待进一步挖掘。
基于上述研究基础,首先利用一阶RC模型和带遗忘因子的递推最小二乘算法(Recursive Least Squares method with Forgetting Factor, FFRLS)在线估算出电池容量;然后以估算的容量数据为基础,引入MGM动态更新电池容量退化趋势,获取表征容量退化的灰色发展系数;然后将灰色发展系数作为电池老化模型参数,建立PF动态状态空间模型;最后通过新陈代谢灰色粒子滤波(Metabolic Grey Model Particle Filter, MGM- PF)算法对电池容量进行跟踪迭代直至失效阈值,实现电池RUL预测。
传统电池容量测试为:在一定温度(通常为25℃)下,以一定倍率(一般设为0.2C)将满充电池放电至截止电压所放出电量。但在实际应用中电池通常不会完全充放电,因此传统电池容量测试方法并不适用。为此提出构建简单电池模型并辨识出模型参数间接求出电池容量的方法。
1.1.1 电池模型
由于一阶RC模型在满足模型精度的同时,计算较为简单,因此采用一阶RC[15]模型作为锂离子电池模型,如图1所示。

图1 锂离子电池一阶RC模型
Fig.1 First order RC model for lithium-ion battery
图1中,锂离子电池一阶RC模型表达式如下
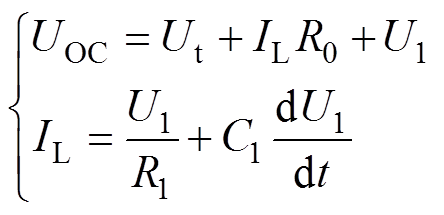 (1)
(1)式中,IL为电池负载电流;UOC为锂离子电池开路电压,UOC=f (SOC);Ut为电池端电压;U1为RC网络结的极化电压;R0为锂离子电池欧姆内阻;R1和C1分别为极化内阻和极化电容。
1.1.2 电池模型参数辨识
电池参数会随工作环境的改变而发生变化,而固定参数的模型精度必然会随电池老化而逐渐降低,无法满足电池状态准确估算要求。因此根据电池系统状态变化快、参数变化缓慢的特点,需要降低历史数据对参数估算的影响权重,同时增大新信息对系统参数辨识影响程度,且数据越新权重越大。为此,采用带遗忘因子的递推最小二乘算法[16-18]在线辨识锂离子电池模型参数R0、R1、C1及UOC。
1.1.3 电池容量在线估算
电池容量在线估算流程如图2所示,首先以辨识出的电池开路电压UOC为基础,然后通过OCV- SOC关系得出电池SOC;最后基于电池SOC和电流积分值估算出电池容量为
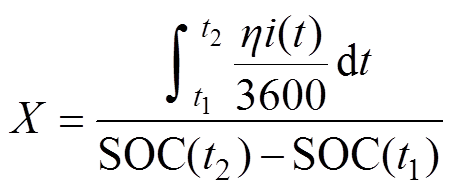 (2)
(2)式中,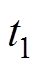 为放电起始时间;
为放电起始时间;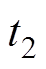 为放电终止时间;
为放电终止时间;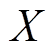 为电池容量;
为电池容量;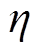 为库伦效率系数,相比铅酸电池和镍氢电池等,锂离子电池内部副反应程度较低,可近似认为
为库伦效率系数,相比铅酸电池和镍氢电池等,锂离子电池内部副反应程度较低,可近似认为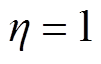 [19]。
[19]。
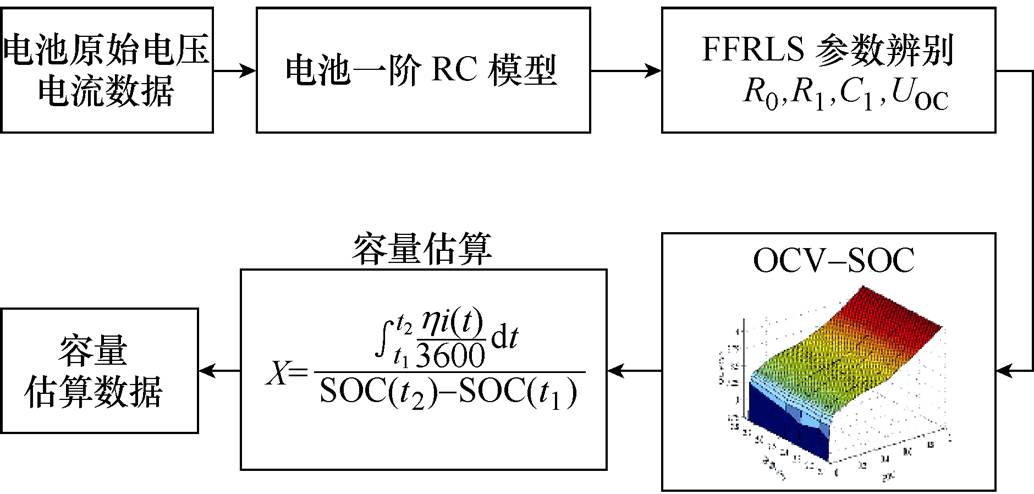
图2 基于RC模型和FFRLS算法的容量估算
Fig.2 Capacity estimation based on RC model andFFRLS algorithm
新陈代谢灰色模型[14]由于建模所需数据量少,因此适用于电池早期预测历史数据量少的情况;并可根据电池老化状态的变化更新模型参数,提高预测精度,因此选用MGM作为电池容量退化模型。而粒子滤波算法具有可处理非线性、非高斯问题且对状态变量没有过多约束的优点。因此针对电池RUL预测已知历史数据量少、退化过程为非线性非高斯、退化过程复杂的特点,提出以1.1节在线估算出的容量数据为已知历史数据,在PF框架基础上融入MGM,构建MGM-PF算法来实现电池RUL预测。MGM-PF算法的步骤如下。
1)构建MGM获取灰色发展系数a。
MGM即在灰色模型(Grey Model, GM)的基础上采取滑窗机制,假定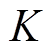 时刻窗口内有
时刻窗口内有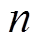 个历史数据,进行GM建模后预测出一个新数据,然后滑窗向前移动代谢早期历史数据加入预测新数据。随着预测进行,滑动窗口内数据量保持不变,但窗口不断向前滑动,代谢早期历史数据带入最新预测数据以减小历史数据对系统的影响。新陈代谢灰色原理如图3所示,算法如下。
个历史数据,进行GM建模后预测出一个新数据,然后滑窗向前移动代谢早期历史数据加入预测新数据。随着预测进行,滑动窗口内数据量保持不变,但窗口不断向前滑动,代谢早期历史数据带入最新预测数据以减小历史数据对系统的影响。新陈代谢灰色原理如图3所示,算法如下。
假定在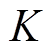 时刻窗口内有
时刻窗口内有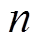 个容量历史数据,构成时间序列
个容量历史数据,构成时间序列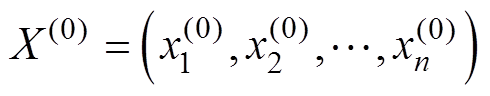 。为挖掘序列
。为挖掘序列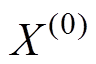 变化趋势,对该序列进行一次累加变换得到
变化趋势,对该序列进行一次累加变换得到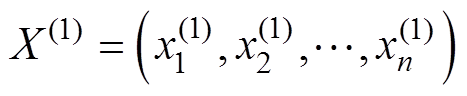 ,其中
,其中
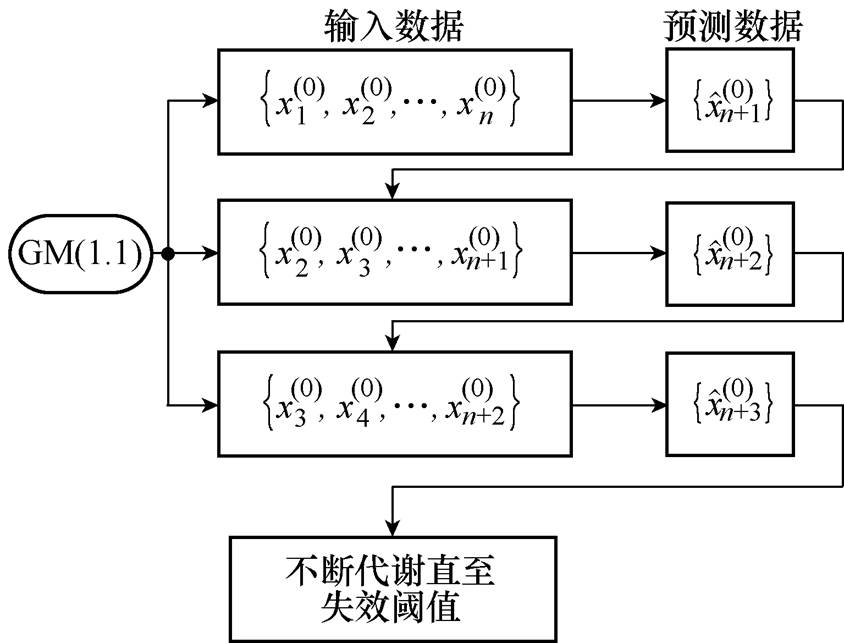
图3 新陈代谢灰色原理
Fig.3 Schematic diagram of metabolic grey
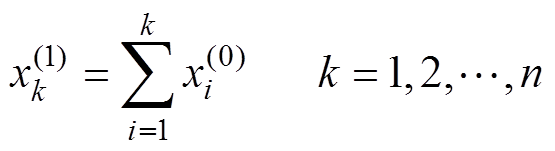 (3)
(3)则MGM的一阶方程表达式为
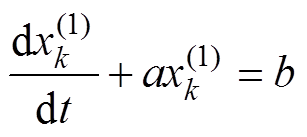 (4)
(4)
式中,a为灰色发展系数,代表时间序列发展态势;b为灰色作用量,反映外部因素作用大小。
由最小二乘算法求解式(4)中灰色发展系数和灰色作用量的最优解分别为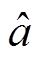 和
和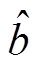 。
。
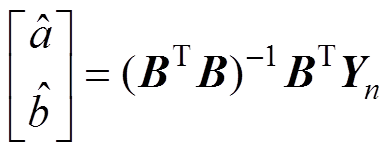 (5)
(5)其中
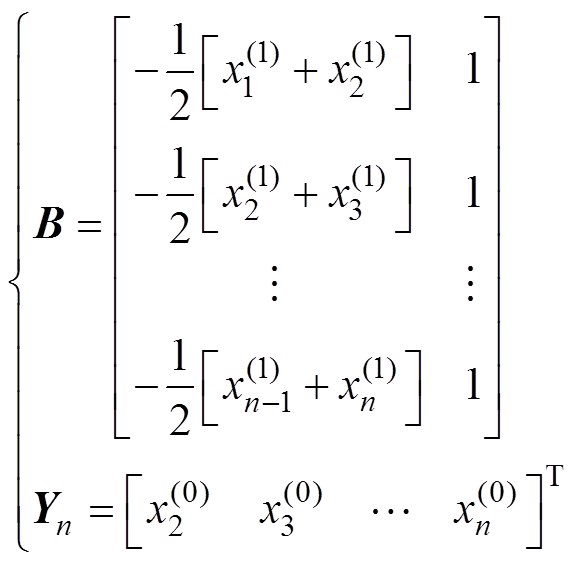 (6)
(6)
将计算出的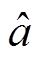 、
、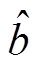 代入式(4),并还原可得
代入式(4),并还原可得
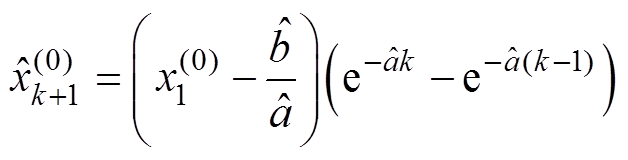 (7)
(7)2)利用灰色发展系数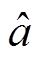 构建PF算法[20-21]的动态状态空间模型。
构建PF算法[20-21]的动态状态空间模型。
根据第一步结果可得递推表达式为
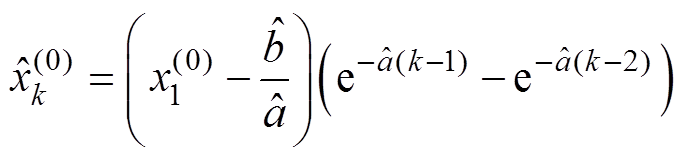 (8)
(8)将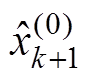 与
与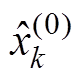 相除得MGM递推关系式为
相除得MGM递推关系式为
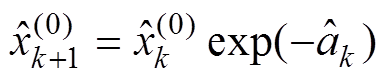 (9)
(9)
由式(9)构建PF算法的动态状态空间模型,有
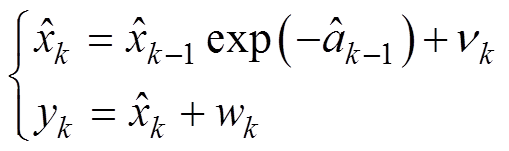 (10)
(10)式中,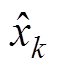 为K时刻电池容量估计值;
为K时刻电池容量估计值;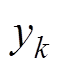 为K时刻电池容量实测值;
为K时刻电池容量实测值;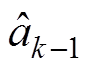 为窗口在K-1时刻灰色发展系数;
为窗口在K-1时刻灰色发展系数;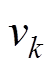 、
、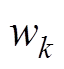 分别为系统噪声与观测噪声,均利用随机函数生成。
分别为系统噪声与观测噪声,均利用随机函数生成。
3)基于动态状态空间模型的RUL预测。
(1)初始化PF。设置相关参数:采样粒子数N、有效粒子数阈值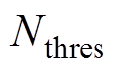 、电池容量失效阈值
、电池容量失效阈值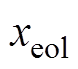 。
。
(2)以动态状态空间模型预测电池容量。根据建议分布函数随机采样N个粒子,有
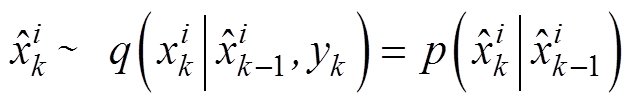
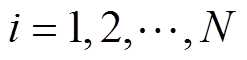 (11)
(11)式中,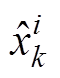 为第k时刻的第i个粒子;
为第k时刻的第i个粒子;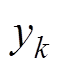 为观测值;
为观测值;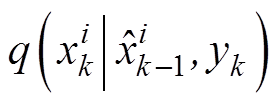 为建议分布密度;
为建议分布密度;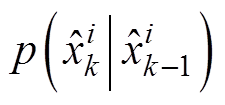 为先验分布密度。
为先验分布密度。
(3)计算各粒子权重,有
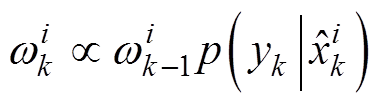 (12)
(12)式中,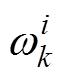 为第k时刻第i个粒子权重。
为第k时刻第i个粒子权重。
(4)设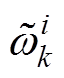 为归一化后粒子权重,则归一化的权重为
为归一化后粒子权重,则归一化的权重为
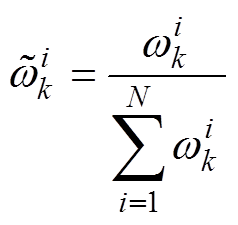 (13)
(13)(5)计算粒子退化指标为
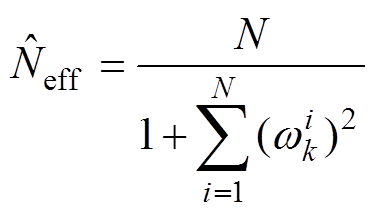 (14)
(14)
判断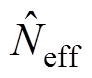 是否小于设定的阈值
是否小于设定的阈值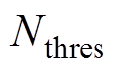 ,若
,若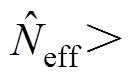
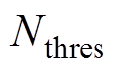 ,则进行状态估算,即容量更新;否则进行重采样,重新设置粒子权重
,则进行状态估算,即容量更新;否则进行重采样,重新设置粒子权重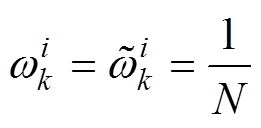 ,得到新的粒子集合
,得到新的粒子集合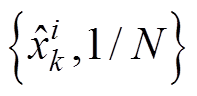 。
。
(6)状态估算,有
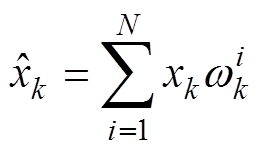 (15)
(15)4)判断是否达到电池容量失效阈值。
若达到电池容量失效阈值,算法结束;否则,将电池容量预测值引入到第一步的容量历史数据序列中,同时剔除最老的容量数据,构建新的容量历史数据序列,重复执行算法。
实验平台由三星锂离子电池、充放电系统、恒温箱三部分组成。充放电系统由直流电源、电子负载仪、内阻测试仪和中央控制电脑组成,用于电池充电和模拟动态工况放电。恒温箱用于控制电池工作环境温度。从同类型相同批次的三星锂离子电池ICR18650-26F中随机挑选两颗电池进行老化实验,编号分别为S29和S30,其详细参数见表1。
表1 电池参数
Tab.1 Battery parameters

额定容量/(A·h)额定电压/V充电截止电压/V放电截止电压/V 2.603.704.202.75
依据电池使用手册,设计了锂离子电池老化实验,包括电池容量测试、动态工况测试和电池老化测试三部分,具体实验步骤如下。
(1)容量测试
为获取最大可用真实容量,先将电池以标准CC-CV(constant-current and constant-voltage)充电后静置1h,以小倍率恒流放电至截止电压,并记录最大可用容量。
(2)动态工况测试
先将电池以标准CC-CV充电法满充后静置1h,将电池统一以NEDC(new european driving cycle)(见图4a)动态工况放电至截止电压。
(3)电池老化测试
规范一:为加速锂离子电池老化速率,将S29号电池老化测试实验温度提高到45℃。加速老化工况由UDDS(urban dynamometer driving schedule)工况、2.6A恒流放电30s和5.2A恒流放电120s组成(见图4b)。
规范二:S30号电池老化测试实验温度设定为35℃,其老化工况为脉冲放电工况,由1.95A恒流放电60s和5.2A恒流放电15s组成,静置15s后重复放电(见图4c)。
重复上述步骤直至两颗电池容量都衰退至初始容量的80%,即2.08A·h。
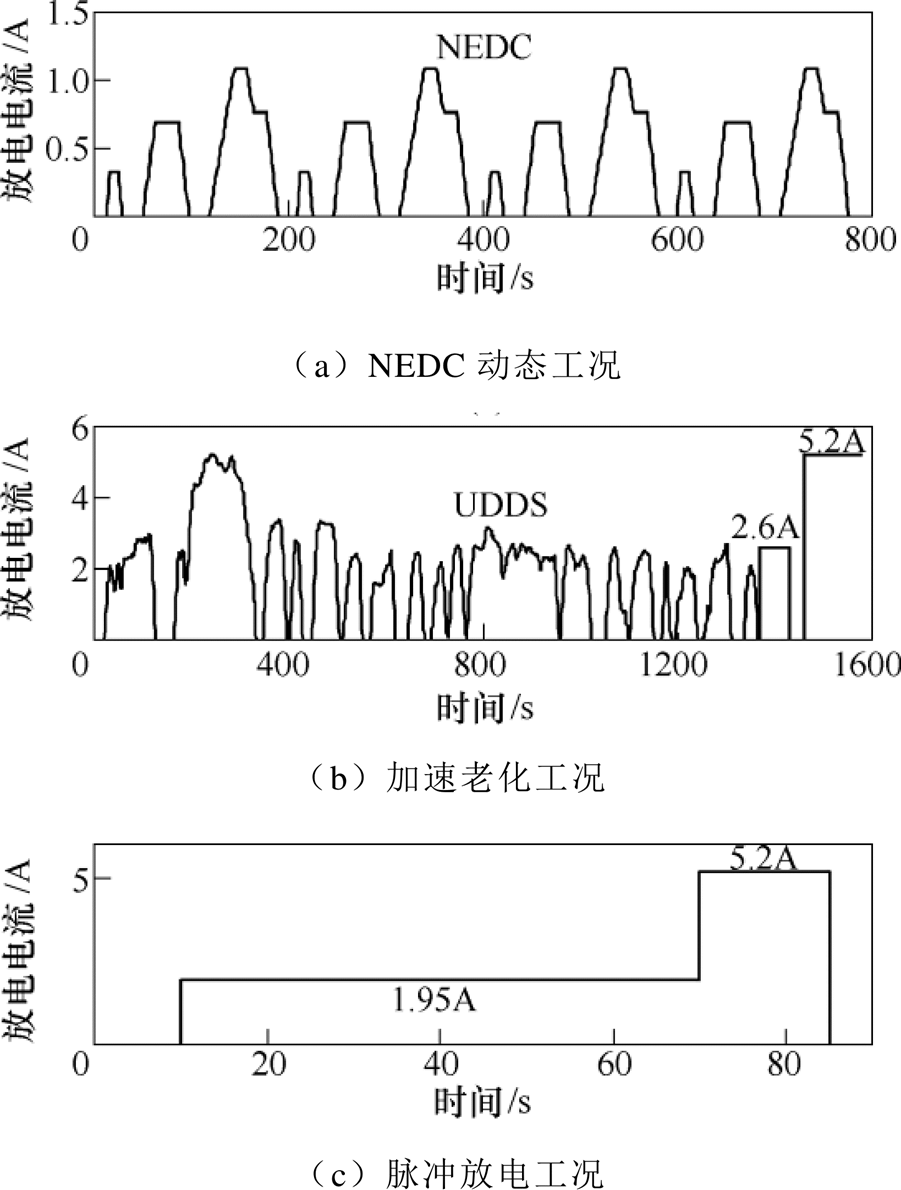
图4 不同工况下老化测试放电电流
Fig.4 Aging test discharge current under different working conditions
根据容量估算流程,首先建立电池一阶RC模型,再采用FFRLS辨识模型参数。即当实时采集到电压电流值时,对电池特性实验中的动态工况测试数据进行电池模型参数辨识,当辨识算法充分收敛后,模型估算端电压与实测端电压误差不超过电池放电截止电压的1%,则认为电池模型精度合理[2]。且在放电过程中进行多次容量估算,最后取容量估算均值。根据不同老化阶段的实验数据,分别选取S29号电池前450个循环和S30号电池前500个循环下容量估算值,容量测试参考值以及容量预测误差如图5所示,并计算误差,见表2。
图5中,S29和S30号电池估算容量基本与参考容量保持一致,由表2可知,各老化阶段下电池容量的估算都很准确。S29和S30号电池容量的估算平均误差分别为0.034 9A·h、0.039 0A·h,考虑到电池额定容量为2.6A·h,则稳定后容量估算平均相对误差小于2%。最大误差也仅分别为0.098 3A·h和0.135 9A·h,最大相对误差小于5%,达到精度要求。
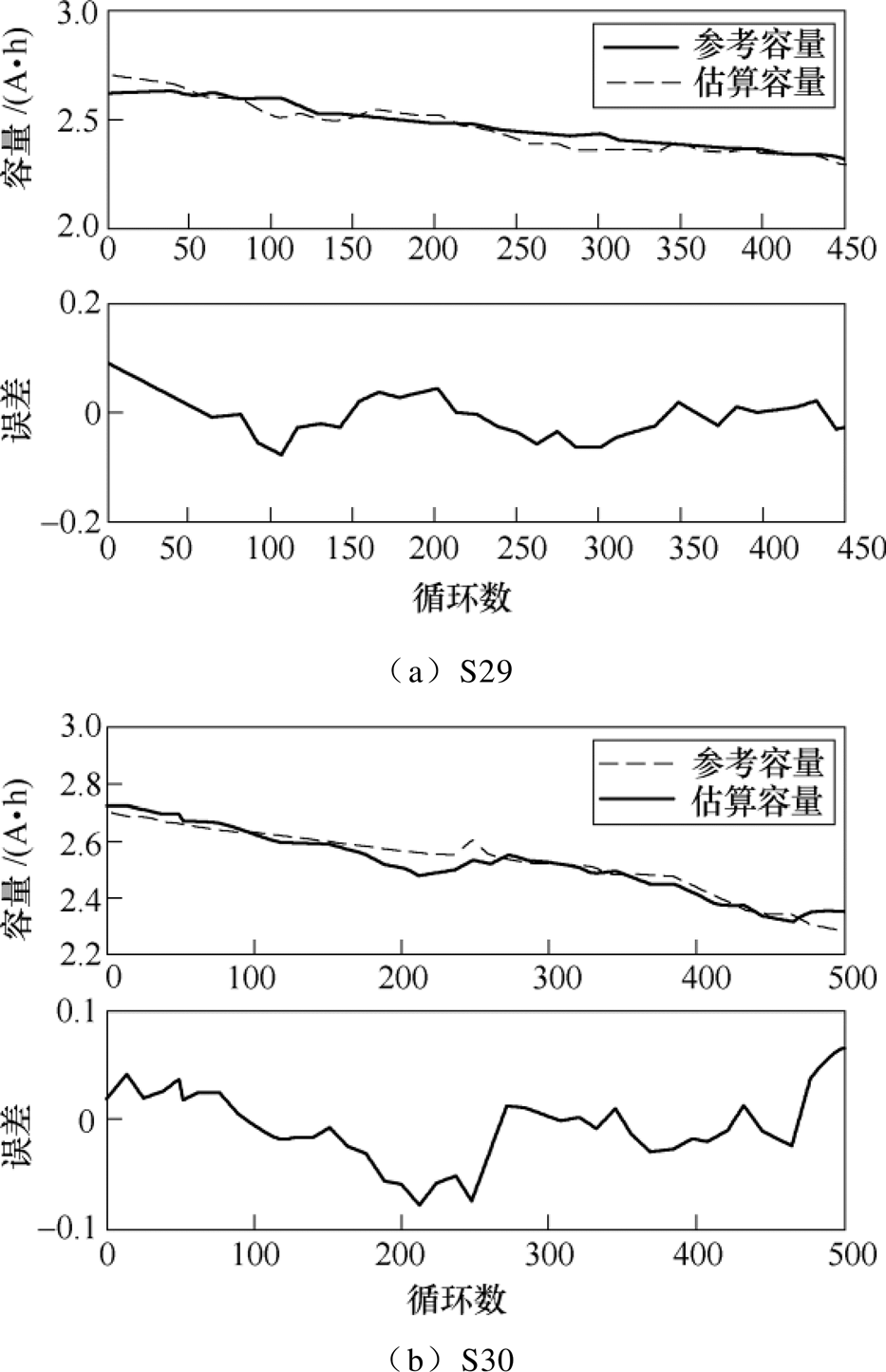
图5 容量估算结果
Fig.5 Capacity estimation results
表2 容量估算误差
Tab.2 Capacity estimation error

电池号误差最大值/ (A·h)误差最小值/ (A·h)平均误差/ (A·h)方均根误差 S290.098 30.001 80.034 90.027 3 S300.135 90.030 00.039 00.036 5
综上所述,所提出电池容量在线估算方法能准确估算出电池容量,满足实际应用中精度需求。
根据1.2节算法,灰色发展系数a的变化能动态反映容量退化趋势。为验证算法有效性,绘制两者的变化轨迹如图6所示,图中灰色发展系数的动态变化与电池容量退化呈现出一定的相关性。当电池容量退化趋势较为平稳时,灰色发展系数波动较小;如S30号电池100~200循环时,容量退化趋势平稳,而灰色发展系数波动也较小;而当容量发生回升时,灰色发展系数也波动较大,例如S29号电池100~200循环容量发生回升现象,灰色发展系数也产生较大变化,即两者存在明显相关性。为定量评估灰色发展系数a和电池容量退化的关系,采用灰色关联分析方法,计算S29和S30号电池灰色发展系数a和电池容量退化的关联度,见表3。

图6 灰色发展系数与电池容量退化关系
Fig.6 Relationship between grey development coefficient and battery capacity degradation
表3 灰色发展系数与电池容量退化的灰色关联度
Tab.3 Grey correlation degree between the grey development coefficient and battery capacity degradation

电池号灰色关联度 S290.881 S300.884
灰色关联分析是根据因素之间发展趋势的相似或相异程度,衡量因素之间关联程度的一种方法,灰色关联度越接近于1,则说明两组数据之间近似关系越明显。由表3可知,S29和S30号电池的灰色发展系数a与电池容量退化的灰色关联度都大于0.88,接近1,表明电池灰色发展系数a与电池容量之间有较高关联度,即灰色发展系数a的动态特性能有效反映了电池容量退化趋势,说明所提出的采用灰色发展系数a建立电池状态空间模型具有可行性。
设置新陈代谢灰色理论中滑动窗口内已知容量数据量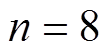 ;采样粒子数N=200,有效粒子数阈值
;采样粒子数N=200,有效粒子数阈值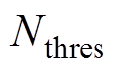 =133,电池容量失效阈值
=133,电池容量失效阈值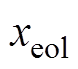 =2.08A·h;为反映在不同老化阶段基于容量估算RUL预测性能,分别选取不同起始预测点,本次实验中S29和S30号电池分别选取第150、250、350、450循环作为算法预测起始点。循环误差计算以预测循环数目减去寿命截止循环数。限于篇幅原因,给出基于容量估算S30号电池在各个不同老化阶段RUL预测结果,如图7所示。
=2.08A·h;为反映在不同老化阶段基于容量估算RUL预测性能,分别选取不同起始预测点,本次实验中S29和S30号电池分别选取第150、250、350、450循环作为算法预测起始点。循环误差计算以预测循环数目减去寿命截止循环数。限于篇幅原因,给出基于容量估算S30号电池在各个不同老化阶段RUL预测结果,如图7所示。
从图7可以看出,随着预测起始点推后,使用数据增多,S30号电池的RUL预测值越来越接近真实RUL。然而S30号电池在起始预测循环为250时,RUL预测误差比150循环处稍微偏大。分析实验记录后发现,由于锂离子电池在老化至250循环时,实验中一段较长时间静置,出现电池容量再生现象,容量突然上升导致容量估算出现偏差。但整体来看,RUL误差呈逐步减小趋势。
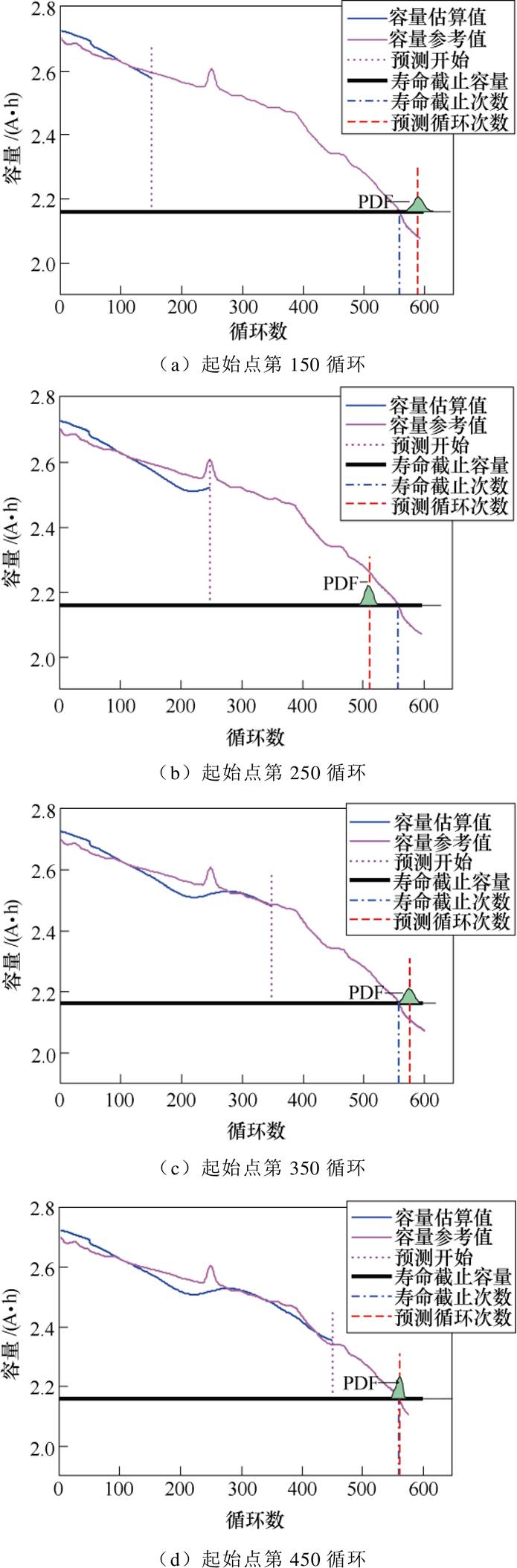
图7 S30号电池RUL预测结果
Fig.7 S30 battery RUL prediction results
表4分别给出以MGM-PF和PF进行RUL预测的结果对比,可知MGM-PF算法比PF算法对RUL预测的误差更小,表明MGM-PF算法能够准确预测电池RUL。且针对MGM-PF算法,S29号电池虽然在电池老化前期预测时误差较大,但随着使用数据增多,RUL误差逐步减小,老化后期RUL预测误差仅为2.58%。而S30号电池在电池老化的前期,预测起始点为150循环时,RUL预测误差为31个循环,预测寿命截止循环误差为5.55%;当预测起点为250循环时,预测误差为8.23%,预测误差呈现上升趋势,是因为实验中一段较长时间静置,出现电池容量再生现象;在电池老化后期,起始预测点为350循环时,RUL误差进一步减小,为17循环,预测的寿命截止循环误差为2.8%;在预测起始为450循环时,预测误差仅为1个循环,接近真实寿命截止循环次数。两颗电池预测结果均说明,随着预测使用数据的增加,建立的灰色预测模型能够更好地反映出电池老化速率,同时PF算法能更准确跟踪电池容量退化状态,使得粒子分布更为趋近真实值。因此所提出的算法能准确估算电池容量和跟踪电池老化状态,实现了电池RUL预测。
表4 基于不同算法电池RUL预测误差
Tab.4 Battery RUL prediction error based on different algorithms (单位: 次)

电池号预测起始点RUL实际值预测方法RUL预测值RUL预测误差95%置信区间 S29150393MGM-PF324-69[295, 353] PF46471[434, 494] 250293MGM-PF235-58[208, 262] PF36067[324, 396] 350193MGM-PF169-24[145, 193] PF25461[234, 274] 45093MGM-PF10714[94, 120] PF13845[122, 154] S30150409MGM-PF44031[420, 460] PF273-136[256, 290] 250309MGM-PF263-46[246, 280] PF243-66[225, 261] 350209MGM-PF192-17[177, 207] PF161-48[145, 177] 450109MGM-PF1081[99, 117] PF14637[136, 156]
1)利用一阶RC模型辨识出的模型参数为基础在线估算电池容量数据,得到的容量数据与容量测试参考值保持一致,最大误差仅为0.135 9A·h。
2)利用MGM在仅使用8个历史容量数据的情况下建立容量退化模型,动态跟踪容量退化过程,提高电池老化建模的动态特性。分析灰色发展系数与电池容量灰色关联度,表明灰色发展系数的动态特性能有效表征电池容量退化,证明所构建容量退化模型的有效性。
3)融合MGM和PF构建MGM-PF算法,通过PF算法对电池容量跟踪迭代,动态调整PF算法状态空间模型中的灰色发展系数,实现准确RUL预测。
参考文献
[1] Lu Langguang, Han Xuebing, Li Jianqiu, et al. A review on the key issues for lithium-ion battery management in electric vehicles[J]. Journal of Power Sources, 2013, 226: 272-288.
[2] Waag W, Fleischer C, Sauer D U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles[J]. Journal of Power Sources, 2014, 258: 321-339.
[3] 焦东升, 王海云, 朱洁, 等. 基于离散Fréchet距离的电动汽车电池健康状态诊断方法[J]. 电力系统保护与控制, 2016, 44(12): 68-74.
Jiao Dongsheng, Wang Haiyun, Zhu Jie, et al. EV battery SOH diagnosis method based on discrete Fréchet distance[J]. Power System Protection and Control, 2016, 44(12): 68-74.
[4] 潘海鸿, 吕治强, 李君子, 等. 基于灰色扩展卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报, 2017, 32(21): 1-8.
Pan Haihong, Lü Zhiqiang, Li Junzi, et al. Estimation of lithium-ion battery state of charge based on grey prediction model-extended Kalman filter[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(21): 1-8.
[5] 刘大同, 周建宝, 郭力萌, 等. 锂离子电池健康评估和寿命预测综述[J]. 仪器仪表学报, 2015, 36(1): 1-16.
Liu Datong, Zhou Jianbao, Guo Limeng, et al. Survey on lithium-ion battery health assessment and cycle life estimation[J]. Journal of Scientific Instrument, 2015, 36(1): 1-16.
[6] Jouin M, Gouriveau R, Hissel D, et al. Particle filter-based prognostics: review, discussion and perspectives[J]. Mechanical Systems and Signal Processing, 2016, 72-73: 2-31.
[7] 苗强, 崔恒娟, 谢磊, 等. 粒子滤波在锂离子电池剩余寿命预测中的应用[J]. 重庆大学学报, 2013, 36(8): 47-52, 60.
Miao Qiang, Cui Hengjuan, Xie Lei, et al. Remaining useful life prediction of the lithium-ion battery using particle filtering[J]. Journal of Chongqing University, 2013, 36(8): 47-52, 60.
[8] Zhou Yapeng, Huang Miaohua, Chen Yupu, et al. A novel health indicator for on-line lithium-ion batteries remaining useful life prediction[J]. Journal of Power Sources, 2016, 321: 1-10.
[9] Liu Datong, Zhou Jianbao, Liao Haitao, et al. A health indicator extraction and optimization frame- work for lithium-ion battery degradation modeling and prognostics[J]. IEEE Transactions on Systems Man Cybernetics-Systems, 2015, 45(6): 915-928.
[10] Wei Jingwen, Dong Guangzhong, Chen Zonghai. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5634-5643.
[11] Wang Dong, Miao Qiang, Pecht M. Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model[J]. Journal of Power Sources, 2013, 239: 253-264.
[12] Walker E, Rayman S, White R E. Comparison of a particle filter and other state estimation methods for prognostics of lithium-ion batteries[J]. Journal of Power Sources, 2015, 287: 1-12.
[13] 熊瑞. 基于数据模型融合的电动车辆动力电池组状态估计研究[D]. 北京: 北京理工大学, 2014.
[14] Chen Lin, Lin Weilong, Li Junzi, et al. Prediction of lithium-ion battery capacity with metabolic grey model[J]. Energy, 2016, 106: 662-672.
[15] 陈息坤, 孙冬, 陈小虎. 锂离子电池建模及其荷电状态鲁棒估计[J]. 电工技术学报, 2015, 30(15): 141-147.
Chen Xikun, Sun Dong, Chen Xiaohu. Modeling and state of charge robust estimation for lithium-ion batteries[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 141-147.
[16] 杨帆, 代锋, 姚德贵, 等. 基于最小二乘QR分解算法的接地网磁场重构方法及应用[J]. 电工技术学报, 2016, 31(5): 184-191.
Yang Fan, Dai Feng, Yao Degui, et al. Least square QR factorization arithmetic based magnetic field reconstruction for grounding grid and its appli- cation[J]. Transactions of China Electrotechnical Society, 2016, 31(5): 184-191.
[17] 谷苗, 夏超英, 田聪颖. 基于综合型卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报, 2019, 34(2): 419-426.
Gu Miao, Xia Chaoying, Tian Congying. Li-ion battery state of charge estimation based on com- prehensive Kalman filter[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 419-426.
[18] 刘伟龙, 王丽芳, 廖承林, 等. 充电模态下电动汽车动力电池模型辨识[J]. 电工技术学报, 2017, 32(11): 198-207.
Liu Weilong, Wang Lifang, Liao Chenglin, et al. Parameters identification method of battery model for electric vehicles under the charging mode[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 198-207.
[19] Farmann A, Waag W, Marongiu A, et al. Critical review of on-board capacity estimation techniques for lithium-ion batteries in electric and hybrid electric vehicles[J]. Journal of Power Sources, 2015, 281: 114-130.
[20] Zhang Lijun, Mu Zhongqiang, Sun Changyan. Remaining useful life prediction for lithium-ion batteries based on exponential model and particle filter[J]. IEEE Access, 2018, 6: 17729-17740.
[21] 谢长君, 费亚龙, 曾春年, 等. 基于无迹粒子滤波的车载锂离子电池状态估计[J]. 电工技术学报, 2018, 33(17): 3958-3964.
Xie Changjun, Fei Yalong, Zeng Chunnian, et al. State estimation of on-board lithium-ion battery based on unscented particle filter[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 3958-3964.
Remaining Useful Life Prediction of Battery Using Metabolic Grey Particle Filter
Abstract Remaining useful life (RUL) prediction is one of the core technologies of battery management systems. In order to accurately predict the battery RUL with less data volume, a metabolic grey model particle filter (MGM-PF) algorithm is proposed. Firstly, the first-order RC model is used to estimate the battery capacity online. Then, based on the obtained capacity data, the grey development coefficient is dynamically updated by the metabolic grey model, and the coefficient is used as the model parameter to construct a dynamic state space model that characterizes the battery capacity degradation. Finally, the particle filter is used to track the battery capacity degradation to realize the battery RUL prediction and derive the uncertainty expression of the prediction results. The experimental results show that the proposed MGM-PF algorithm based on online capacity estimation can accurately predict the battery RUL.
keywords:Metabolic grey model, particle filter, remaining useful life of battery, online capacity estimation
中图分类号:TM911
DOI: 10.19595/j.cnki.1000-6753.tces.190082
国家自然科学基金(51667006)和广西自然科学基金(2015GXNSFAA139287)资助项目。
收稿日期2019-01-18
改稿日期 2019-06-28
韦海燕 女 1963年生,副教授,硕士生导师,研究方向为内燃机节能与排放控制,电动汽车。E-mail: gxwhytu@163.com
陈 琳 女,1973年生,教授,博士生导师,研究方向为信号检测与处理和电池管理。E-mail: gxdxcl@163.com(通信作者)
(编辑 崔文静)