0 引言
随着现代工业的发展，在电动汽车、船舶推进、轨道牵引和风力发电等领域，低速大转矩直驱电机以其简化的传动链和改善的系统效率，受到了越来越多的青睐[1-3]。早期的低速传动系统一般是高速电机加减速箱的驱动结构，减速箱的使用不但会增加系统的体积和质量，降低传动效率，而且会产生振动和噪声。相比而言，低速直驱电机不需要配备减速装置便可实现转矩的低速传动，从而简化传动链结构并提升了系统效率[4]。然而，传统的直驱永磁同步电机，通常采用增加电机极对数的方式来实现低速运行，极对数的增加往往会导致电机本体体积增大、制造成本高、运输和安装困难等问题[5]。近年来，一类基于“磁齿轮原理”的场调制永磁电机受到了国内外电机领域学者的广泛关注。该类电机的工作原理是利用调磁极实现对低速磁场和高速磁场的双向调制，进而通过谐波磁场耦合作用实现机电能量转换[6-9]。例如：转子采用较多的永磁体极对数，低速旋转直接驱动负载；定子电枢绕组则按气隙中磁场调制产生的极对数较少的高速谐波磁场极对数进行绕制，从而能够减少定子槽数，简化绕组设计[10]。最新研究表明，该类场调制永磁电机具有功率密度高、结构紧凑、控制灵活等优点，在电气牵引、航空航天、风力发电等低速直驱领域具有潜在的应用前景[11-13]。
为了进一步提高该类电机的转矩密度等驱动性能，同时考虑诸如电气牵引等应用场合的宽调速范围需求，本文将“双定子电机”结构和电励磁方式融入场调制电机，提出一种电励磁双定子场调制（Electric-Excitation Double-Stator Filed-Modulated, EEDSFM）电机。该电机设计成内外双定子、中间调磁极转子的“三明治”式结构，电枢绕组置于外定子，励磁绕组置于内定子，充分利用电机的内部空间，且通过控制励磁电流可方便地调节磁场，从而满足电机的宽调速性能要求。但与传统单定子场调制电机相比，该电机结构略显复杂，这对电机的高效优化设计方法提出了新的挑战。如何在保证高转矩密度的同时，尽可能地抑制转矩纹波、降低转矩脉动也是该电机优化设计是否成功的关键[14-15]。
近年来，有学者提出诸如基于单参扫描法、响应面法、遗传算法和模拟退火算法等多种电机优化分析方法[16]，但是所针对的优化目标往往比较单一，而且上述某一方法的单独使用均存在一定的局限性[17]。例如，文献[18]针对磁通切换永磁电机，以高转矩密度作为单一优化目标，根据经验选取一系列极弧系数或永磁体充磁厚度等参数，利用有限元分析基于单参扫描法反复调整结构参数进行电机优化设计，该方法的多参数交叉、多目标优化以及全局寻优能力较差。文献[19]则基于响应面法对双凸极永磁型双定子电机进行了优化设计分析，通过对结构参数的分组较好地处理了参数间交叉影响的问题，但是每次只能同时分析优化两个相关的结构参数，当需要优化的关键尺寸参数较多时，很难同时考虑所有参数之间的相互影响。文献[20]中，将遗传算法和模拟退火算法理论相结合，重点优化分析了双定子永磁电机的永磁磁链，虽然能够较准确地得到最优结构尺寸，但是其优化过程缓慢、耗时长且效率低。
本文所提出的EEDSFM 电机具有双定子和两层气隙的特殊结构，这使得优化分析过程中需要考虑的结构参数众多，其对优化目标的交叉影响进一步增加了电机优化设计的难度。另一方面，该电机的设计分析是一个复杂的多维统筹优化过程，涉及电磁转矩、定位力矩、转矩纹波等多个优化目标。传统的电机优化设计方法要么优化目标单一，要么过度依赖经验值，要么全局寻优能力差，要么过程繁琐效率低[21-22]。因此，本文将以高转矩密度和低转矩纹波为优化设计目标，基于敏感性分析对关键尺寸参数进行敏感度分层，在此基础上根据参数敏感度层次将基于遗传算法的多目标优化分析以及响应面法和单参扫描法等多种优化方法相结合，充分发挥不同优化方法的优势，最终确定所提电机的最优结构尺寸参数。在电机电磁性能分析的基础上，制作原理样机，搭建实验平台，并进行实验测试。理论分析和实验结果均表明，基于参数敏感度分层的多手段优化设计方法，能满足该类电励磁双定子场调制电机的高效优化设计需求。
1 电机结构与工作原理
1.1 拓扑结构
EEDSFM 电机结构如图1 所示，两层气隙将电机隔成三部分：内定子、调磁极转子、外定子，三者相互之间存在磁耦合。其中，内定子作为励磁的主体，仅放置励磁绕组，内定子的存在能够充分利用电机的内部空间，从而为该类电机转矩密度的提高创造了条件。调磁极转子的磁场调制作用能够使气隙获得旋转谐波磁场，取消了传统电励磁同步电机所必需的集电环和电刷，从而提高了电机运行的可靠性。外定子作为功率转换的载体，采用三相集中式电枢绕组，可以减小绕线端部长度，从而有利于降低铜耗，改善电机效率。基于磁场调制原理，本文中所提到的电励磁双定子场调制电机，外定子设置为42 槽/28 极电枢绕组，内定子放置4 对极励磁绕组，调磁极转子间隔设置18 个导磁极，满足调磁极转子导磁极个数等于电枢绕组极对数和励磁绕组极对数之和的关系，能够保证电机正常工作，从而获得低速大转矩的输出特性。
图1 EEDSFM 电机结构
Fig.1 Structure of EEDSFM machine
1.2 工作原理及尺寸方程
本文提到的电励磁双定子场调制电机借助旋转的调磁极转子的磁场调制作用，实现静止的励磁磁场和旋转的电枢磁场之间的磁耦合作用，从而实现机电能量转换。具体而言，在忽略铁心饱和及漏磁影响的情况下，内定子励磁绕组产生静止磁动势，由于调磁极转子中导磁极和非导磁极交替排列导致圆周磁阻分布不均匀，从而使外气隙中产生一系列旋转的谐波磁场。当外定子电枢绕组绕制的极对数与气隙中某一谐波磁场极对数一致时，该谐波磁场匝链电枢绕组，能够感应出有效电动势，电机则可稳定运行。
有限元分析表明，本文所提到的电励磁双定子场调制电机能够产生正弦感应电动势。为简化分析，当其作发电运行时，假设施加三相对称纯电阻负载，此时电机的电磁功率Pe 可以表示为
式中，m 为相数；E0m 为相空载感应电动势幅值；Iam为相电流幅值；cosφ 为内功率因数。
根据电励磁双定子场调制电机的工作原理和设计理论，E0m 和Iam 可分别表示为
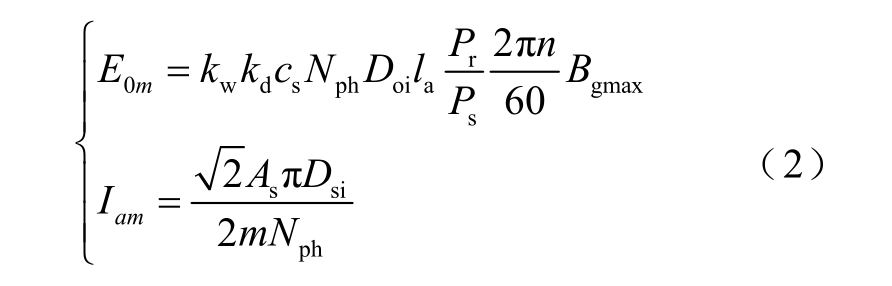
式中，Pr 为调磁极转子导磁极个数；Ps 为外定子电枢绕组极对数；Doi 为外定子内径；la 为电机铁心轴向长度；Nph 为电枢绕组每相匝数；n 为转子转速；kw 为相绕组系数；kd 为漏磁系数；cs 为外定子齿极弧系数；Bgmax 为外气隙中14 对极磁场磁通密度幅值；As 为线负荷。将式（2）代入式（1），可得电磁功率Pe 表达式为
若忽略铜耗，上述电磁功率即为EEDSFM 电机发电运行时的输出电功率。此时，电磁转矩Te 可表示为
式中，Vg=πlaDsi2/4 表示外气隙所包围的体积。所以该电机的转矩密度ξT 可定义为
此外，转矩纹波Tri 可根据定义表示为
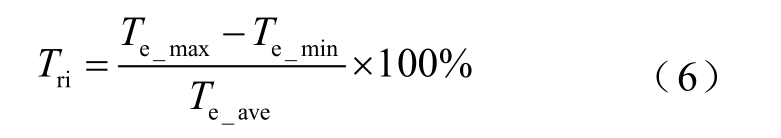
基于上述尺寸方程，根据应用场合选择电机的功率、电磁负荷、额定转速后，就可以确定电机的主要结构尺寸。在此基础上，利用二维有限元分析软件JMAG，对EEDSFM 电机进行参数化建模，从而为后期结构参数的优化设计提供条件。
2 电机的优化设计
2.1 优化设计思路
EEDSFM 电机所具有的双层气隙、双定子特殊结构，导致其优化设计过程中需要考虑的结构参数众多。而且，为满足电机的高性能要求，优化目标也由单目标上升为多目标。因此，综合考虑优化时效和优化精度的需求，需要根据不同结构参数对多个优化目标的影响程度，分别采取有针对性的优化设计分析方法。图2 所示为构建的EEDSFM 电机优化设计流程。
图2 EEDSFM 电机优化设计流程
Fig.2 Flow chart of EEDSFM machine design
本文在充分考虑EEDSFM 电机低速大转矩特性的基础上，合理确定优化目标、选取合适的待优化结构参数，并依据场调制电机的设计经验及理论推导得到的电机尺寸方程，确定电机主要尺寸参数的设计初值及合理变化范围。然后建立EEDSFM 电机的参数化模型，对电机的电磁性能进行初步评估。考虑到待优化的结构参数众多，有些结构参数对优化目标存在交叉影响，而有些结构参数则较为独立，若对不同的结构参数均采用单一相同的优化方法，则会降低电机优化的时效并导致很难寻得最优结构尺寸。因此，本文首先利用有限元分析结果，合理评价优化目标对不同结构参数的敏感度，从而将待优化的结构参数分为强敏感性（Ⅰ型）和弱敏感性（Ⅱ型）两大类。针对强敏感性的结构参数（称为Ⅰ型参数），采用基于遗传算法的优化方法对多维参数同时进行寻优分析；针对弱敏感性的结构参数，则继续进行分层处理，对于在局部结构上具有关联性的弱敏感性结构参数（称为Ⅱ-1 型参数）进行分组，采用基于响应面法的优化方法进行二维参数的优化分析，而对于在局部结构上相对孤立的弱敏感性结构参数（称为Ⅱ-2 型参数），则采用单参数扫描的方法进行单参数的优化设计分析。最后，通过有限元计算判断是否达到优化目标，在反复优化调整后，最终确定电机的最优结构尺寸。
2.2 优化设计目标
EEDSFM 电机基于磁场调制原理，能够实现低速大转矩的输出特性，适用于低速直驱应用场合，因此，该电机低速运行时的电磁转矩Te 是需要重点考虑的性能指标。此外，由于定位力矩能够影响电机空载运行时的振动和噪声，它的大小和电机空载磁场分布相联系。而转矩纹波则是电机负载运行时的转矩波动，虽然定位力矩大小会对转矩纹波产生一定影响，但是转矩纹波同时还受电动势波形、控制方式、电枢磁场引起的气隙磁场畸变等因素影响。可见，转矩纹波和定位力矩之间存在差别，其受影响的因素不尽相同，所反映的电机性能指标也不相同，二者不能相互替代，有必要在电机设计中同时考虑。综合分析，针对EEDSFM 电机的优化设计，可以将电磁转矩Te、定位力矩Tcog、转矩纹波Tri 作为优化目标。此时，EEDSFM 电机设计的多目标优化函数f(xi)可以定义为
式中， eT′、 cogT′ 、 riT′为优化前电机电磁转矩、定位力矩、转矩纹波的大小；
为结构尺寸参数xi 的函数，分别表示xi 取某定值时电机电磁转矩、定位力矩、转矩纹波的大小。优化目标要求是尽可能地增大电磁转矩，减小定位力矩和转矩纹波。纵观多目标优化函数f(xi)，电磁转矩的优化初值 eT′放在分子上，而定位力矩和转矩纹波的优化初值 cogT′ 、 riT′则放在分母上。此时，当优化后所得电磁转矩fTe(xi)越大时，
则越小，同时，当优化后所得定位力矩fTcog(xi)和转矩纹波fTri(xi)越小时，
也会越小。因此，根据电机设计要求，需要寻求多目标优化函数f(xi)的最小值 f(xi)min。需要注意的是，本文所提到的EEDSFM 电机适用于低速大转矩应用场合，对电机高转矩密度要求更高，因此多目标优化函数f(xi)中的权重系数λ1 取为0.5，而λ2、λ3 则分别取为0.25，满足λ1+λ2+λ3=1 的关系。
2.3 结构参数敏感性分析
借鉴传统场调制电机的设计经验并充分考虑EEDSFM 电机双气隙、双定子结构的特殊性，本文选取12 个关键结构尺寸参数进行EEDSFM 电机的多目标优化设计分析。图3 所示为EEDSFM 电机的结构参数示意图。表1 为给定的待优化结构尺寸参数设计初值及其合理变化范围。
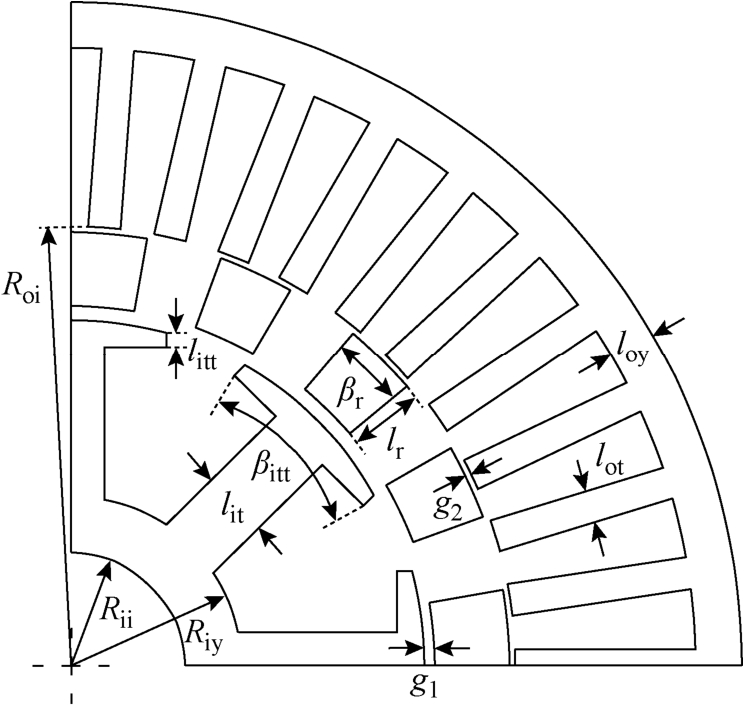
图3 EEDSFM 电机结构参数
Fig.3 Structural parameters of EEDSFM machine
表1 EEDSFM 电机待优化结构参数初值及变化范围
Tab.1 Initial value and variation range of structural parameters of EEDSFM machine
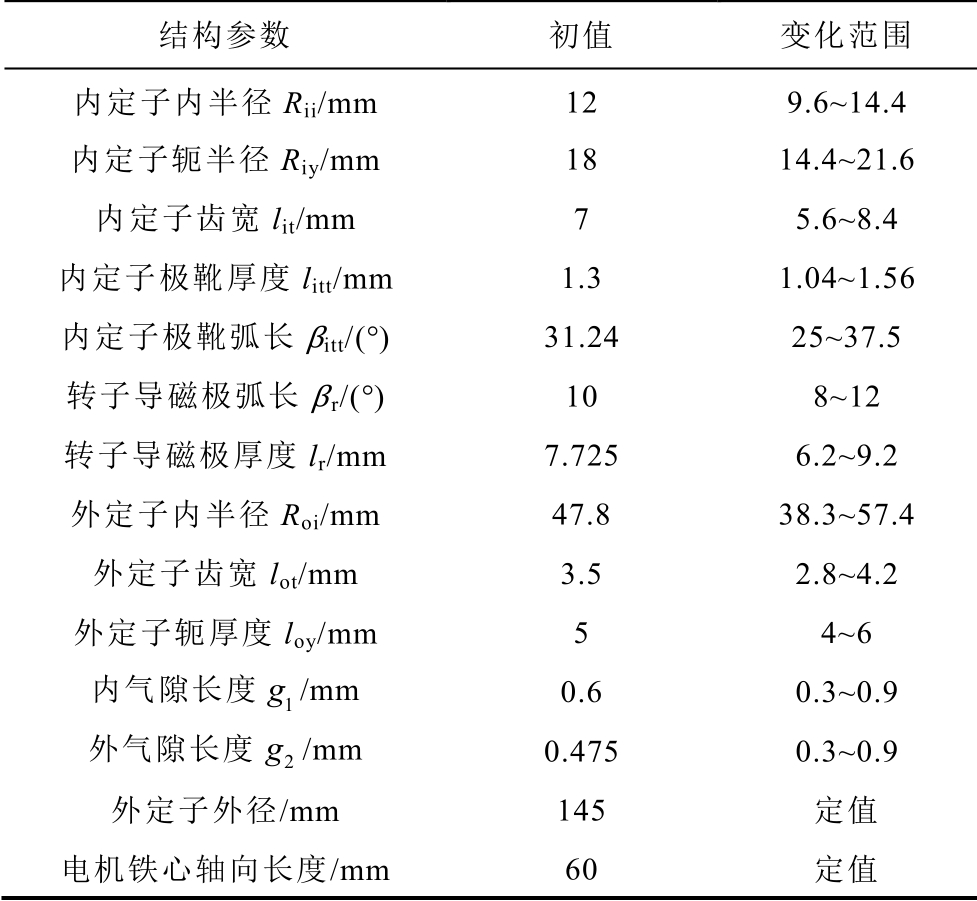
结构参数 初值 变化范围 内定子内半径Rii/mm 12 9.6～14.4 内定子轭半径Riy/mm 18 14.4～21.6 内定子齿宽lit/mm 7 5.6～8.4 内定子极靴厚度litt/mm 1.3 1.04～1.56 内定子极靴弧长βitt/(°) 31.24 25～37.5 转子导磁极弧长β r/(°) 10 8～12 转子导磁极厚度lr/mm 7.725 6.2～9.2 外定子内半径Roi/mm 47.8 38.3～57.4 外定子齿宽lot/mm 3.5 2.8～4.2 外定子轭厚度loy/mm 5 4～6 内气隙长度 1g /mm 0.6 0.3～0.9 外气隙长度 2g /mm 0.475 0.3～0.9 外定子外径/mm 145 定值 电机铁心轴向长度/mm 60 定值
在EEDSFM 电机中，需要设计的结构参数众多，而且不同结构参数对优化目标的影响程度并不相同，若对各个参数均基于单参扫描法逐一进行分析设计，则无法顾及参数间相互影响的问题，难以寻得最优结构尺寸；若基于遗传算法同时对所有结构参数进行优化分析，则容易导致优化过程耗时长、效率低。因此，本文首先利用有限元对电机性能进行初步分析，并据此对各个结构参数xi 进行敏感性评估，得到结构参数xi 针对某一优化目标的敏感因子G(xi)，再综合分析三个优化目标，得到各个结构参数xi 对于多目标的敏感度S(xi)。敏感因子G(xi)和敏感度S(xi)定义为
式中，V(y/xi)为结构参数xi 取某定值时，优化目标y的方差； y¯ 为结构参数xi 取不同数值时，优化目标y的平均值；Ge(xi)、Gcog(xi)、Gri(xi)分别为结构参数xi针对电磁转矩、定位力矩、转矩纹波等不同优化目标的敏感因子。表2 给出了各个结构参数的敏感性分析结果，对应的柱状图如图4 所示。根据表2 和图4 可以看出不同结构参数对电磁转矩、定位力矩和转矩纹波的影响是有差异的。例如，外定子齿宽lot 和内气隙长度 1g 对电磁转矩的影响较为明显；外定子齿宽lot 和外气隙长度 2g 对定位力矩的影响较大；内气隙长度 1g 和外气隙长度 2g 是影响转矩纹波的最主要因素。
表2 结构参数的敏感性分析结果
Tab.2 Sensitivity of the structural parameters
结构参数xi Ge(xi) Gcog(xi) Gri(xi) S(xi) 敏感度分层 Rii 0.070 2 -0.092 2 -0.033 9 0.066 0 Ⅱ-1 型Riy 0.057 2 0.041 5 0.060 7 0.054 2 Ⅱ-1 型lit 0.284 8 0.355 0 0.113 0 0.259 4 Ⅰ型 litt 0.056 3 0.133 4 -0.084 0 0.082 5 Ⅱ-1 型βitt 0.123 7 -0.160 3 -0.080 5 0.122 1 Ⅱ-1 型β r -0.125 1 0.269 4 0.131 6 0.162 8 Ⅱ-2 型lr 0.256 8 -0.102 4 -0.106 9 0.180 7 Ⅱ-1 型Roi 0.256 8 -0.102 4 -0.106 9 0.180 7 Ⅱ-1 型lot 0.545 6 0.883 4 0.291 3 0.566 5 Ⅰ型 loy -0.115 6 -0.043 3 -0.019 2 0.073 4 Ⅱ-2 型g1 -0.550 4 -0.179 7 -0.379 4 0.415 0 Ⅰ型 g2 -0.143 4 -0.773 4 -0.495 8 0.389 0 Ⅰ型
图4 结构参数的敏感性分析结果
Fig.4 Sensitivity of the structural parameters
2.4 结构参数优化调整
在上述参数敏感性分析的基础上，将敏感度S(xi)＞0.2 的4 个结构参数lit、lot、 1g 、 2g 划归为强敏感性参数（Ⅰ型参数），该类Ⅰ型参数对优化目标存在交叉影响，相互之间作用性强，因此采用基于遗传算法的优化方法同时进行优化分析。而将敏感度小于0.2 的剩余8 个结构参数：Rii、Riy、litt、βitt、lr、Roi、βr、loy 则归为弱敏感性参数（Ⅱ型参数）。对于该类Ⅱ型参数，考虑到局部结构和磁路的关联性，可以进一步将其划分为关联性较强的Ⅱ-1 型参数Rii、Riy、litt、βitt、lr、Roi 和相对独立的Ⅱ-2 型参数βr、loy。针对Ⅱ-1 型参数，分别将Rii 和Riy、βitt和litt、lr 和Roi 分为一组，采用基于响应面法的优化方法对其进行二维参数的优化分析；针对Ⅱ-2 型参数，由于参数敏感度较低且与其他结构参数关联性低，则采用单参扫描法单独进行优化分析。此外，电机优化设计过程中，考虑到实际运行情况，还需要设置一些约束条件，例如，线电流密度J≈5A/mm2；当结构参数改变导致槽面积发生变化时，通过计算得到相应的绕组匝数，需保证槽满率kfill≈0.65 基本不变。
在采用基于遗传算法的优化方法对上述Ⅰ型参数进行设计分析时，其总体目标函数F(x)通过多元非线性回归模型确定，表达式为
首先通过变量变换，将每个Ⅰ型参数所对应的多目标优化函数f(xi)转换为线性回归模型，用线性回归方法确定每个Ⅰ型参数xi 与F(x)的关系，按最小二乘法原理确定每个Ⅰ型参数xi 所对应的多目标优化函数f(xi)在遗传算法总体目标函数F(x)中的系数值αi，寻优目标则是求F(x)的最小值。遗传算法的种群大小设置为100，采用二进制编码方式，设置交叉概率为0.6，变异概率为0.01，适应度函数为1/F(x)。考虑到传统遗传算法存在着收敛速度慢、寻优效率低的不足，为减少遗传代数、提高寻优时效，设置初始种群随机分布在0.8xi～1.2xi，并设置结构参数的阈值也为0.8xi～1.2xi。在迭代过程中，经过交叉、变异操作，不断更新种群染色体的基因，根据适应度函数筛选出适应度高的个体，保留优秀的基因并淘汰适应度低的个体。图 5 所示为目标函数F(x)的迭代收敛情况，经过变量的全局寻优，迭代次数仅为70 次时，总体目标函数F(x)则可稳定到最小值，约为0.26。
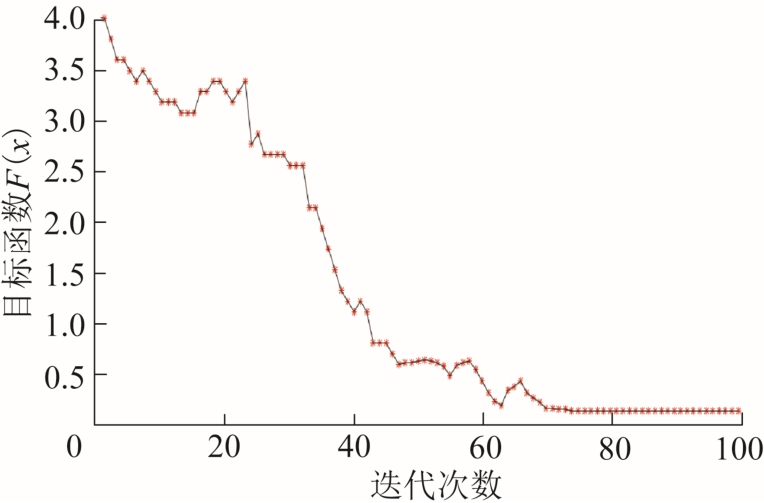
图5 基于遗传算法的目标函数收敛情况
Fig.5 Objective function value change based on the genetic algorithm
图6 三个优化目标在结构参数Rii 和Riy 下的响应
Fig.6 Response of three optimization objectives to the structural parameters Rii and Riy
针对三组Ⅱ-1 型参数，采用响应面法进行优化设计分析，结果如图6、图7 和图8 所示。从图6a和图6c 可以看出，随着Riy 的增大，电磁转矩和定位力矩都逐渐增大，综合图6b 所示转矩纹波的变化情况，并结合多目标优化函数分析，最终选取Rii=12.3mm、Riy=17.6mm。由图7 可知，当βitt 增大时，电磁转矩先增大后减小，而定位力矩和转矩纹 波则先减小后增大；对于参数litt，电磁转矩随其增加也是先增大后减小，而定位力矩和转矩纹波几乎不随其发生变化，再结合多目标优化函数进行分析，最终确定βitt=30°、litt=1.1mm。同理，基于图8 所示的结构参数 lr 和 Roi 的响应面分析结果，当选取lr=7.4mm、Roi=46.7mm 时，既能保证电机具有较低的定位力矩和转矩纹波，又能获得较高的电磁转矩。
图7 三个优化目标在结构参数βitt 和litt 下的响应
Fig.7 Response of three optimization objectives to the structural parameters βitt and litt
图8 三个优化目标在结构参数lr 和Roi 下的响应
Fig.8 Response of three optimization objectives to the structural parameters lr and Roi
对于Ⅱ-2 型参数loy 和βr，采用单参扫描法进行优化分析，二者的设计初值分别选为5mm 和10o，变化范围分别为4～6mm、8o～12o。选取合适的参数值变化步长，借助有限元分析，并结合式（7），得到的多目标优化函数f(xi)随loy、βr 的变化情况分别如图9a 和图9b 所示。由图9 可以看出，当loy=5.3mm、βr=10.5o 时，对应的f(xi)分别可以取得最小值。
图9 单参扫描法优化结构参数loy 和βr
Fig.9 Optimization of structural parameters loy and βr by using single parameter scanning method
表3 结构参数和优化目标的优化前后结果对比
Tab.3 Comparison of results before and after optimization
参 数 数 值 优化前 优化后 g1/mm 0.6 0.55 g2/mm 0.475 0.5 lot/mm 3.5 2.9 lit/mm 7 6.2 litt/mm 1.3 1.1 loy/mm 5 5.3 lr/mm 7.725 7.4 Roi/mm 47.8 46.7 βr/(°) 10 10.5 Riy/mm 18 17.6 Rii/mm 12 12.3 βitt/(°) 31.24 30 Te/(N·m) 4.22 4.74 Tcog/(N·m) 0.28 0.23 Tri(%) 22.04 16.84
基于以上对Ⅰ型、Ⅱ-1 型和Ⅱ-2 型参数的优化设计和有限元分析，可以对比得到结构参数和优化目标在电机优化前后的变化情况见表3。可以看到， 经过结构参数的优化设计后，电机的电磁转矩提高约 12.3%，而定位力矩和转矩纹波则分别降低约17.9%和23.6%。
3 电磁性能分析
为了验证优化效果，利用二维有限元分析方法，对比研究了优化前后电机的电磁性能，主要包括定位力矩、电磁转矩和相空载感应电动势。由于EEDSFM 电机具有双层气隙，因此其转子定位力矩为内外气隙齿槽转矩的叠加，图10a 给出了优化前和优化后电机转子定位力矩的有限元分析对比曲线。可以明显看出，通过对关键结构参数（主要是外定子齿宽lot，转子导磁极弧长βr、内定子极靴弧长βitt）进行优化设计后，周期变化的定位力矩峰值有明显 减小。电机定位力矩峰值由优化前的最大值0.28N·m 降低到优化后的最大值0.23N·m，减小了约17.9%，这将有利于降低电机运行时的转矩脉动、振动和噪声水平。
图10 优化前后电机的电磁性能对比
Fig.10 Comparison of electromagnetic performances before and after optimization
此外，对 EEDSFM 电机施加额定励磁电流（If=5A）和额定电枢电流（Ia=5A），并采用无刷交流控制方案中的id=0 控制方法，可以得到电机加载时的电磁转矩。图10b 对比给出了优化前后电机的电磁转矩有限元计算结果。分析表明，优化设计后EEDSFM 电机一个电周期内的电磁转矩平均值提高了约12.3%，即由优化前的4.22N·m 提高到优化后的4.74N·m。此外，优化前电机的电磁转矩最大值为4.53N·m，最小值为3.8N·m，根据式（6）计算得到的转矩纹波约为17.3%；而优化后电机的电磁转矩最大值为4.99N·m，最小值为4.45N·m，计算得到的转矩纹波约为11.4%。因此，经过优化设计，所提EEDSFM 电机的转矩纹波下降约6%。仿真分析结果验证了结构参数优化设计的有效性，即：提高转矩密度的同时降低了转矩纹波。
有限元分析中，设置转子运行在额定转速167r/min，可以得到EEDSFM 电机的三相空载感应电动势波形如图10c 所示。由图可见，优化前后的三相空载感应电动势波形均对称分布，且相感应电动势幅值由优化前的6.96V 增加到优化后的8.07V，提高了约15.9%。此外，通过傅里叶分解进行谐波分析表明，优化前电机的相空载电动势波形总谐波畸变率（Total Harmonic Distortion, THD）约为5.94%，而优化后电机的相空载电动势波形THD 仅为1.46%。综合上述分析，EEDSFM 电机转矩纹波的降低一方面得益于优化后定位力矩的减小，另一方面则得益于相感应电动势波形正弦度的提高。
4 原理样机实验测试
为验证所提优化设计方法的有效性和有限元分析的正确性，制造了一台原理样机，并搭建了实验测试平台，如图11 所示。
图11 EEDSFM 原理样机及实验测试平台
Fig.11 Prototype and experimental testing platform
样机在施加额定励磁电流 If=5A、额定转速n=167r/min 运行时，实测空载感应电动势波形如图12 所示。由图可得实测相空载感应电动势幅值接近7.4V，比有限元计算值下降约8.3%，经傅里叶分析可得实测相空载感应电动势波形THD 约为7.35%。对比分析图10c 和图12 可见，实测相空载感应电动势波形及幅值与有限元计算结果略有差别，这主要是由于有限元计算忽略端部漏磁效应及样机加工工艺误差（主要考虑气隙不均匀）等因素造成的。
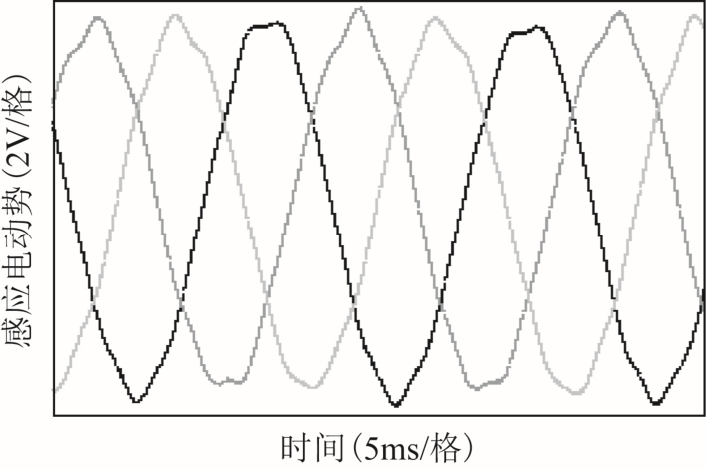
图12 实测空载感应电势波形( I f=5A, n N=167r/min)
Fig.12 Measured no-load EMF waveforms at I f=5A, n N=167r/min
图13 所示为在施加额定励磁电流If =5A 时，样机定位力矩实测波形，其峰值为0.39N·m，比有限元计算值略大0.16N·m，这主要是由于样机加工装配精度和测量误差引起的。此外，对比分析图10a和图13 可见，定位力矩实测波形的周期性并不明显，这主要是由于力矩测试仪器的采样频率过低所致。在额定励磁情况下，采用 di =0 控制方法，施加额定电枢电流Iaq=5A 时，实验测得样机输出转矩波形如图14 所示。分析实验数据可得，样机输出转矩平均值约为4.33N·m，比有限元计算值小0.41N·m，而实测转矩纹波则为29.7%，过大的转矩纹波及实测转矩结果与有限元计算值之间的差异，主要由样机加工工艺误差导致的空载感应电动势波形和幅值均未达到理论预期所引起。总体而言，样机实验测试结果虽然与有限元分析结果略有偏差，但能够在一定程度上验证设计方法的有效性。
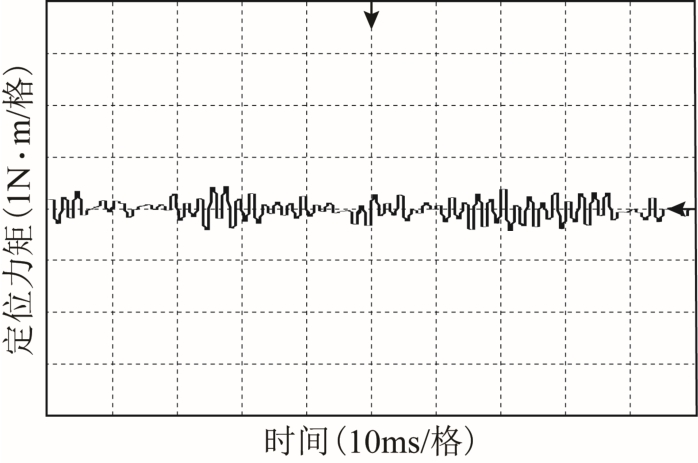
图13 定位力矩实测波形( fI =5A)
Fig.13 Measured cogging torque at fI =5A
图14 输出转矩实验波形( fI =5A, aqI =5A)
Fig.14 Measured output torque at fI =5A, aqI =5A
5 结论
本文针对EEDSFM 电机双层气隙、双定子的复杂结构，提出了一种基于参数敏感度分层的多种优化手段相结合的多目标优化分析方法。在建立多目标优化函数的基础上，根据敏感度将结构参数进行分类，并针对性地采用遗传算法、响应面法和单参扫描法对不同敏感度的结构参数进行多目标优化设计分析，从而快速有效地确定了电机的最优结构尺寸参数。本文提出的遗传优化算法所具有的优势及进行多目标优化设计后对电机性能的改善可以总结如下：
1）相较于JMAG 软件自带的遗传算法，本文提出的遗传算法通过编程能够方便地实现多维优化目标的自由组合及权重的灵活设定，并可合理地控制待设计参数的阈值范围、交叉概率及变异概率，从而保证其在寻优时效和精度方面更具优势。
2）经过多目标优化分析设计，EEDSFM 电机的转矩提高了约12.3%，转矩纹波下降约6%，同时，相感应电动势幅值提高了约15.9%。
3）经过优化分析设计，所提EEDSFM 电机的相感应电动势波形的正弦度进一步提高，其波形总谐波畸变率由优化前的 5.94%改善为优化后的1.46%，这将利于抑制无功损耗，提高效率。
最终，本文结合样机实验分析，进一步验证了所提优化设计方法的有效性和有限元分析的正确性。
[1] Hua Wei, Zhang Hengliang, Cheng Ming, et al. An outer-rotor flux-switching permanent-magnet-machine with wedge-shaped magnets for in-wheel light traction[J]. IEEE Transactions on Industrial Electronics, 2017, 64(1): 69-80.
[2] Li Xianglin, Chau K T, Cheng Ming. Analysis, design and experimental verification of a field-modulated permanent-magnet machine for direct-drive wind turbines[J]. IET Electric Power Applications, 2015, 9(2): 150-159.
[3] 鲍晓华, 刘佶炜, 孙跃, 等. 低速大转矩永磁直驱电机研究综述与展望[J]. 电工技术学报, 2019, 34(6): 1148-1160.
Bao Xiaohua, Liu Jiwei, Sun Yue, et al. Review and prospect of low-speed high-torque permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1148-1160.
[4] Cheng Ming, Zhu Ying. The state of the art of wind energy conversion systems and technologies: a review[J]. Energy Conversion and Management, 2014, 88: 332-347.
[5] Gao Yuting, Qu Ronghai, Li Dawei, et al. Design of a dual-stator LTS vernier machine for direct-drive wind power generation[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 5204505.
[6] Du Yi, Xiao Feng, Hua Wei, et al. Comparison of fluxswitching PM motors with different winding configurations using magnetic gearing principle[J]. IEEE Transactions on Magnetics, 2016, 52(5): 8201908.
[7] Cheng Ming, Han Peng, Hua Wei. General airgap field modulation theory for electrical machines[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6063-6074.
[8] Cheng Ming, Wen Honghui, Han Peng, et al. Analysis of airgap field modulation principle of simple salient poles[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 2628-2638.
[9] Du Yi, Zhang Chao, Zhu Xiaoyong, et al. Principle and analysis of doubly salient PM motor with πshaped stator iron core segments[J]. IEEE Transactions on Industrial Electronics, 2019, 66(3): 1962-1972.
[10] 李祥林, 程明, 邹国棠, 等. 聚磁式场调制永磁风力发电机工作原理与静态特性[J]. 电工技术学报, 2014, 29(11): 1-9.
Li Xianglin, Cheng Ming, Chau K T, et al. Principle and analysis of a new flux-concentrating fieldmodulated permanent-magnet wind power generator[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 1-9.
[11] Zhao Wenxiang, Wang Shiyuan, Ji Jinghua, et al. A new mover separated linear magnetic-field modulated motor for long stroke applications[J]. IEEE Transactions on Magnetics, 2017, 53(11): 4002205.
[12] Bai Jingang, Zheng Ping, Cheng Luming, et al. A new magnetic-field-modulated brushless double-rotor machine[J]. IEEE Transactions on Magnetics, 2015, 51(11): 8112104.
[13] Li Xianglin, Chau K T, Cheng Ming, et al. Performance analysis of a flux-concentrating fieldmodulated permanent-magnet machine for directdrive applications[J]. IEEE Transactions on Magnetics, 2015, 51(5): 8104911.
[14] Lei Gang, Liu Chengcheng, Zhu Jianguo, et al. Techniques for multilevel design optimization of permanent magnet motors[J]. IEEE Transactions on Energy Conversion, 2015, 30(4): 1574-1584.
[15] Xu Liang, Zhao Wenxiang, Liu Guohai, et al. Design optimization of a spoke-type permanent-magnet vernier machine for torque density and power factor improvement[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3446-3456. [
16] 鲍晓华, 吴长江, 胡云鹏, 等. 一种优化表插式永磁电机性能的方法[J]. 电工技术学报, 2018, 33(2): 238-244.
Bao Xiaohua, Wu Changjiang, Hu Yunpeng, et al. A method for optimizing performance of inset permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 238-244.
[17] 莫丽红, 全力, 朱孝勇, 等. 定子永磁式双转子电机设计与实验研究[J]. 电工技术学报, 2014, 29(9): 74-82.
Mo Lihong, Quan Li, Zhu Xiaoyong, et al. Optimal design and experiment of a novel double-rotor machine with PMs in stator[J]. Transactions of China Electrotechnical Society, 2014, 29(9): 74-82.
[18] Li Feng, Hua Wei, Tong Minghao, et al. Nine-phase flux-switching permanent magnet brushless machine for low-speed and high-torque applications[J]. IEEE Transactions on Magnetics, 2015, 51(3): 8700204.
[19] 陈云云, 朱孝勇, 全力, 等. 基于参数敏感度的双凸极永磁型双定子电机的优化设计和性能分析[J]. 电工技术学报, 2017, 32(8): 160-168.
Chen Yunyun, Zhu Xiaoyong, Quan Li, et al. Parameter sensitivity optimization design and performance analysis of double-salient permanentmagnet double-stator machine[J]. Transactions of China Electrotechnical Society, 2017, 32(8): 160-168.
[20] Gao Jian, Dai Litao, Zhang Wenjuan. Improved genetic optimization algorithm with subdomain model for multi-objective optimal design of SPMSM[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(1): 160-165.
[21] 陈云云, 全力, 朱孝勇, 等. 双凸极永磁双转子电机优化设计与电磁特性分析[J]. 中国电机工程学报, 2014, 34(12): 1912-1921.
Chen Yunyun, Quan Li, Zhu Xiaoyong, et al. Optimal design and electromagnetic performance analysis of double-salient permanent-magnet double-rotor motors[J]. Proceedings of the CSEE, 2014, 34(12): 1912-1921.
[22] Zhu Xiaoyong, Xiang Zixuan, Quan Li, et al. Multimode optimization design methodology for a flux-controllable stator permanent magnet memory motor considering driving cycles[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5353-5366.