0 引言
基于磁齿轮原理的场调制型永磁游标电机具有低速大转矩、高功率密度的特点，在风力发电等领域具有广阔的应用前景[1-4]。与此同时，场调制效应导致永磁体内磁通密度变化明显，这会在永磁体内感应出较大的涡流损耗[5]。此外，为实时控制电机的转矩与转速，这些永磁电机通常都是和电压源型逆变器（Voltage Source Inverter, VSI）配合使用[6]。它会在永磁体内感应出额外的脉宽调制（Pulse Width Modulation，PWM）谐波损耗。这些损耗不仅降低了电机系统效率，还会引起永磁体温度升高[7]，增加永磁体不可逆退磁的风险[8]。
快速、准确地计算逆变器供电下永磁体涡流损耗是确保电机安全运行、进行电机系统优化设计的前提。基于PWM 电压源为输入的三维时步有限元分析（Time-Stepping Finite Element Analysis, TSFEA）可以准确计算永磁体涡流损耗[9]。然而三维模型和一个电周期内数千步的时步有限元计算使得这种方法非常耗时，无法应用于优化设计阶段。此外，永磁游标电机的定转子的对称性不同，使得分析这种电机的有限元模型也比一般永磁同步电机复杂，进一步增加了计算时间。
文献[10]中采用二维TSFEA 和永磁体涡流损耗解析模型相结合的方法计算了一种聚磁式场调制型（ Flux-Concentrating Field-Modulated Permanent Magnet, FCFMPM）游标电机逆变器供电下的永磁涡流损耗。这种方法虽然省去了三维TSFEA，但需要的数千步二维TSFEA 仍非常耗时。本文继续以该电机为例， 提出一种结合高效有限元分析（Computationally Efficient Finite Element Analysis, CE-FEA）[11]和频域小信号分析[12]快速计算逆变器供电下游标电机中PM 涡流损耗的方法。针对基波电流和齿槽效应引起的低频涡流损耗，采用CE-FEA结合永磁体涡流损耗模型计算；而永磁体中PWM谐波损耗则采用频域小信号分析结合解析损耗模型得到。该方法相较于传统三维TSFEA 的方法，相对误差小于4%，而且计算速度则提高了数百倍。
1 基于CE-FEA 计算低频涡流损耗
1.1 FCFMPM 模型参数
图1 中给出了分析该18 槽/8 极FCFMPM 电机所需的最小有限元模型[3-5,10,13]，该模型为整个电机截面的1/2。而普通的8 极分布绕组永磁同步电机仅需采用1/8 截面的有限元模型即可计算。因此，在剖分精度相同的情况下，用于分析FCFMPM 电机的有限元模型网格数更多。表1 给出了本文计算中使用的FCFMPM 电机参数，该样机的详细参数在文献[3-5]中已经给出。
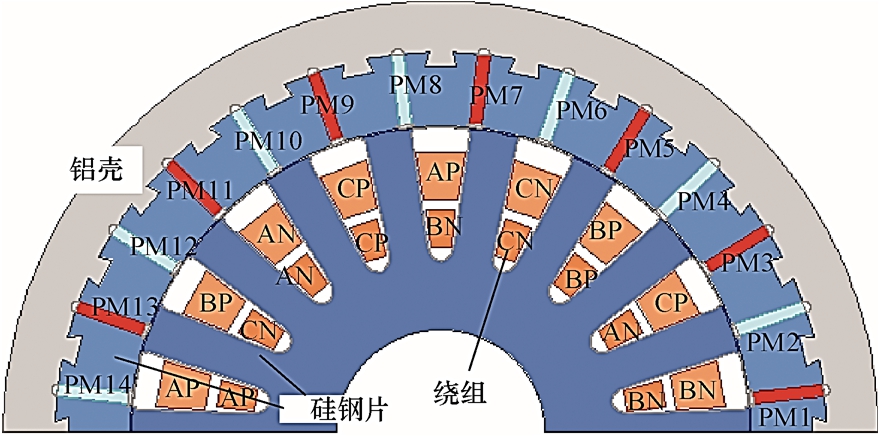
图1 18 槽/8 极FCFMPM 电机最小有限元模型
Fig.1 The minimum finite element model for the 18-slot/ 8-pole FCFMPM machine
表1 FCFMPM 电机模型参数
Tab.1 Parameters of the FCFPM machine
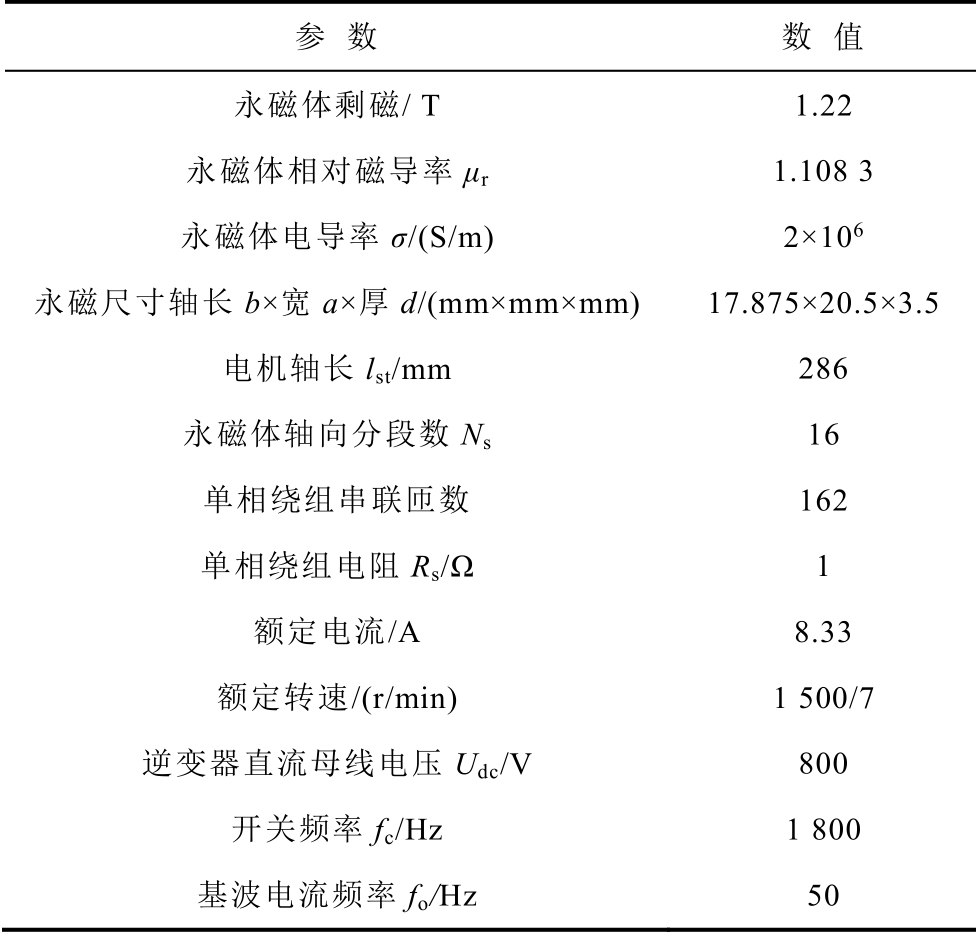
参 数 数 值 永磁体剩磁/ T 1.22 永磁体相对磁导率μr 1.108 3 永磁体电导率σ/(S/m) 2×106 永磁尺寸轴长b×宽a×厚d/(mm×mm×mm) 17.875×20.5×3.5 电机轴长lst/mm 286 永磁体轴向分段数Ns 16 单相绕组串联匝数 162 单相绕组电阻Rs/Ω 1 额定电流/A 8.33 额定转速/(r/min) 1 500/7 逆变器直流母线电压Udc/V 800 开关频率fc/Hz 1 800 基波电流频率fo/Hz 50
1.2 采用CE-FEA 计算永磁体中磁通密度变化
计算样机在额定工况下永磁体中的涡流损耗通常采用正弦基波电流激励下的TSFEA。由于定子有18 个槽，齿槽交替所引起的永磁体中磁密变化的周期为20°的机械角度，当转子以额定转速运行时，对应的周期为140/9ms。而基波电流的变化周期为20ms，考虑到三相电流的对称性，其在永磁体中引起磁通密度变化的周期为20/3ms。两个磁通密度变化周期的最小公倍数为永磁体中磁通密度交变周期，即140/3ms，其对应转子旋转的机械角度为60°[13]。
假设在一个电周期20ms 中进行30 步TSFEA，则获取一个周期的永磁体中的磁通密度变化需要进行70 步的TSFEA。而采用文献[11]中的CE-FEA 法，只需要进行5 步TSFEA 即可构造出永磁体中一个周期的磁密变化波形。CE-FEA 的具体原理是利用14 块永磁体中磁密变化波形的相位差规律，只需将5 步TSFEA 计算得到的每块永磁体中的磁密变化波形依照相位差规律移相，即可得到一块永磁体一个周期的磁密变化波形。
在进行有限元计算时，应尽量控制每块永磁体剖分情况相同，穿过永磁体的平均磁密计算式为
式中，A1、A2、A3 和A4 分别为图2 中节点1、2、3、4 的磁矢位。
图2 一块永磁的网格
Fig.2 Mesh of one PM
图3 中给出了利用CE-FEA 的原理，根据5 步TSFEA 的计算结果构造出一个周期内PM1 中Bav 变化波形的方法。其中，定义转子电角度为
式中，θi 为转子机械角度； PMp 为永磁体极对数14。
根据图3 所示，穿过与PM1 极性相同的永磁体的平均磁密，按照图中的规律依次超前120°电角度。而与PM1 极性相反的永磁体上的平均磁密需要先取相反数，再按照图中规律移相即可构建出一个周期内穿过PM1 的平均磁密波形。构建的磁密波形与采用70 步TSFEA 计算得到的波形完全一致。
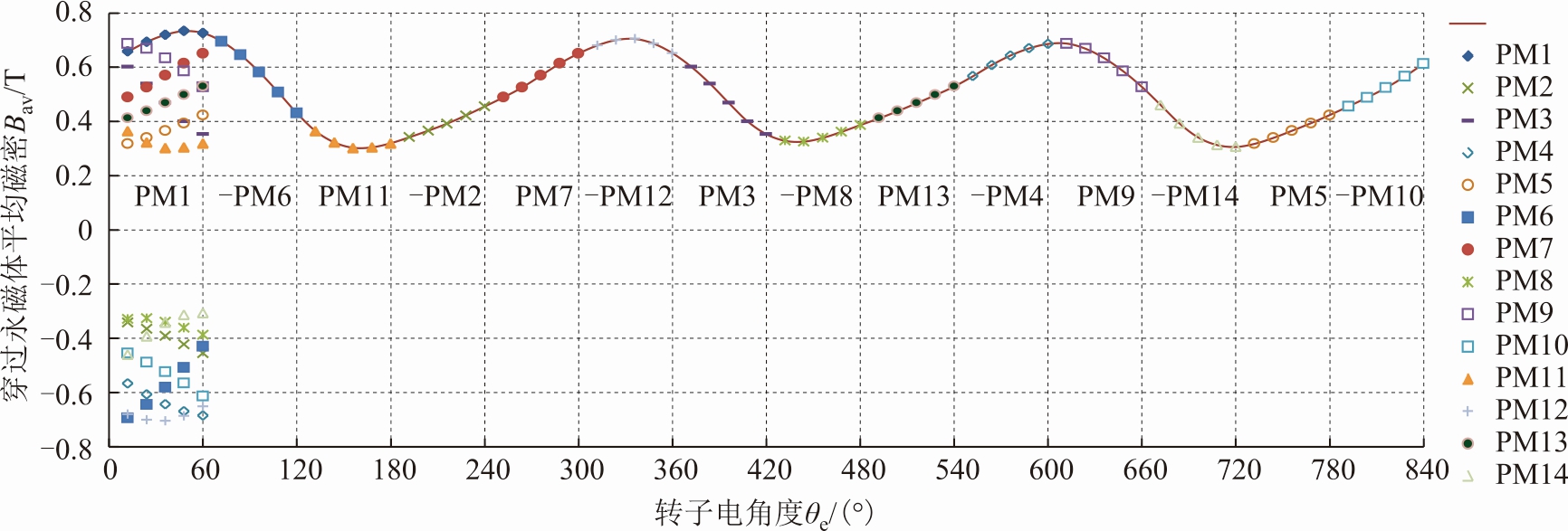
图3 通过5 步TSFEA 的计算结果构造穿过PM1 一个周期的平均磁密变化波形
Fig.3 Construction of the average flux density passing through PM1 according to the 5-step TSFEA results
CE-FEA 有效地减少了计算电机性能所需的TSFEA 的步数[11]。另外需要指出，这里采用每60°电角度进行5 步TSFEA 只是一个示例，事实上，所需进行的TSFEA 的步数还可能更少，这取决于所要分析的谐波的最高频率。图4 中对比了分别通过5步和1 步TSFEA 构造的磁密变化波形。
图4 通过不同步数TSFEA 构造的Bav 波形对比
Fig. 4 Waveforms of Bav constructed from the TSFEAs with different number of steps
图5 通过不同步数TSFEA 构造的Bav 频谱对比
Fig. 5 Frequency spectra of Bav constructed from the TSFEAs with different number of steps
图5 给出了通过不同步数TSFEA 构造的Bav 频谱对比。由于一个周期磁密波形对应的时间为140/3ms，因此频谱中的基波频率为150/7Hz。尽管从图4 来看，通过1 步TSFEA 构造的磁密波形较为粗糙，但从图5 频谱对比中可以看出通过1 步TSFEA计算出的频谱的最高频次为6，这已经包含了交变 磁密的主要分量。
1.3 永磁体涡流损耗解析计算模型
根据交变磁密的频谱，即可使用文献[10,12]中的解析模型计算各次交变磁密产生的涡流损耗，进而叠加得到总的涡流损耗。不考虑轴向分段影响的涡流损耗二维解析模型为
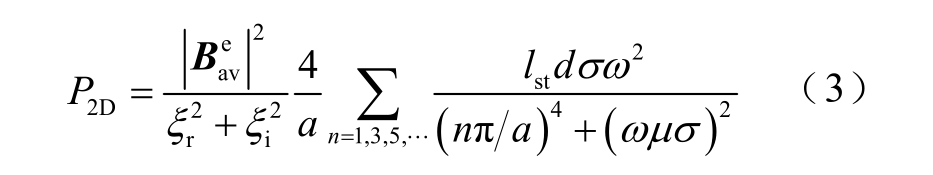
式中，ω 为某次谐波的角频率；
为存在涡流反应时，该频率分量的交变磁密幅值，在计算低频涡流损耗时可以认为其等于图5 中不考虑涡流反应时得到的值；μ 为永磁体的磁导率；ξ 为定量反应涡流反应强弱的参数，ξr 和ξi 分别为其实部和虚部，在二维模型中的表达式为
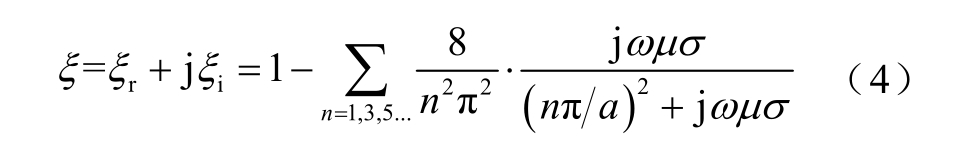
考虑轴向分段影响的三维涡流损耗计算模型为
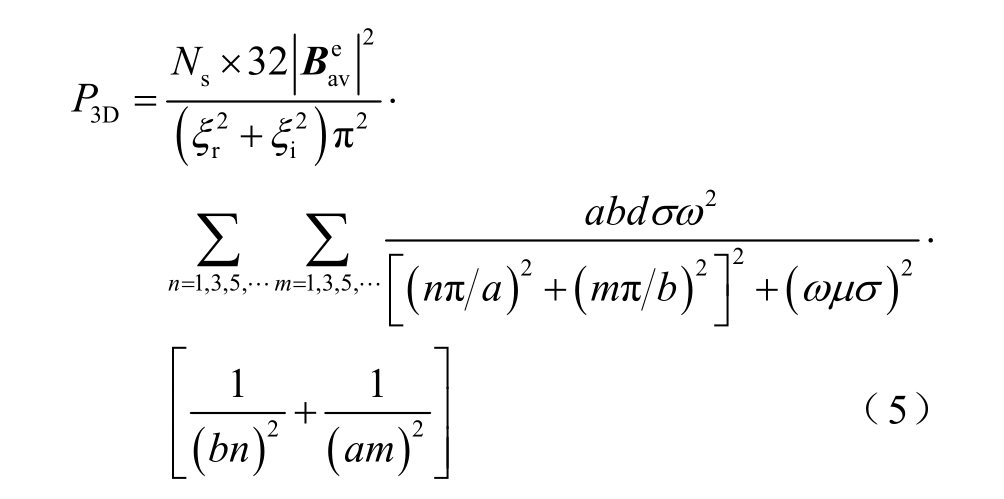
其中ξ 在三维模型中表达式为
1.4 计算结果对比
传统计算永磁体涡流损耗的方法是基于TSFEA 计算永磁体内部涡流密度，进而得到损耗密度，并在永磁体区域进行积分得到总的涡流损耗[5]。这种方法的计算精度会受计算时间步长的影响，如图6 所示，每60°电角度仅进行1 步TSFEA 时，计算的涡流损耗会明显小于进行5 步TSFEA 的结果。而当每60°电角度进行的TSFEA 步数增加至20 时，增加已不再明显，说明此时已达到真实值。此外，采用传统TSFEA 计算永磁体涡流损耗时，还需要经历计算值从0 增加到稳定值的一个瞬态过程。选取采用TSFEA_20 计算结果在θe 位于60°～120°的20个点的平均值作为参考，与本文所提的计算方法进行对比。采用传统TSFEA 计算永磁体涡流损耗所需要的时间被认为是进行40 步TSFEA 所需的时间。详细的对比情况见表2。
图6 传统TSFEA 计算的永磁体涡流损耗
Fig. 6 PM eddy current loss calculated with the traditional TSFEA
表2 不同方法计算永磁体低频涡流损耗对比
Tab.2 Comparison of the low-frequency PM eddy current losses obtained with different methods
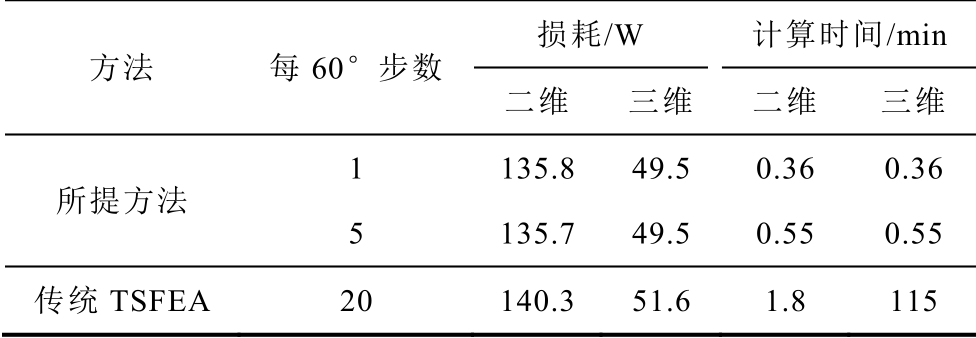
方法 每60°步数损耗/W 计算时间/min二维 三维 二维 三维所提方法 1 135.8 49.5 0.36 0.36 5 135.7 49.5 0.55 0.55传统TSFEA 20 140.3 51.6 1.8 115
从表2 中明显可以看出，所提方法在低频涡流损耗计算方法的速度具有明显优势，尤其是在三维情况下，可将计算速度提升300 倍，而计算相对误差小于4%。所提方法最少只需要进行1 步二维有限元计算。而且可以看出采用传统二维的方法会显著高估永磁涡流损耗，必须采用三维的方法才能准确计算。
2 基于小信号分析计算PWM 谐波损耗
基于PWM 谐波电压在永磁电机中引入的高频谐波电流幅值很小、不足以影响硅钢片饱和状态的假设，文献[14]中提出采用冻结增量磁导率法（Frozen Differential Permeability Method，FDPM）和以电压源为输入的时谐有限元分析（Time-Harmonic Finite Element Analysis，THFEA）研究PWM 电压中的高频分量与永磁体中高频交变磁密，进而快速计算永磁体中的PWM 谐波损耗。文献[12]进一步发展了该方法，指出采用冻结增量张量磁阻率法（ Frozen Differential Tensor Reluctivity Method, FDTRM）进行局部线性化更加合理。此外还指出，采用转子坐标系下的PWM 电压频谱计算永磁体内部涡流损耗更加合理，而不是采用线电压频谱。这种方法的实现思想类似于对晶体管交流放大特性进行小信号分析，故将这种分析方法称为永磁电机频域小信号分析，简称小信号分析。将由FDPM 或FDTRM 实现的局部线性化模型称为永磁电机小信号模型[15]。本节将采用这种分析方法计算FCFMPM电机中的PWM 谐波损耗。
2.1 转子坐标系的PWM 电压频谱
本文参照文献[9]的方法生成PWM 电压波形，进而通过快速傅里叶变换（Fast Fourier Transformation, FFT）计算其频谱，所选用的调制策略是自然采样的空间脉宽矢量调制。图7 中给出了d、q 轴的PWM电压分量udh 和uqh 的幅值。udh 和uqh 的相位差没有明显分布规律，在此不再给出[12]。一个电周期采样点数为2 016，频谱中最高频率为50.35kHz。过高频率的谐波电压幅值已不再显著，故未在图7 中给出。
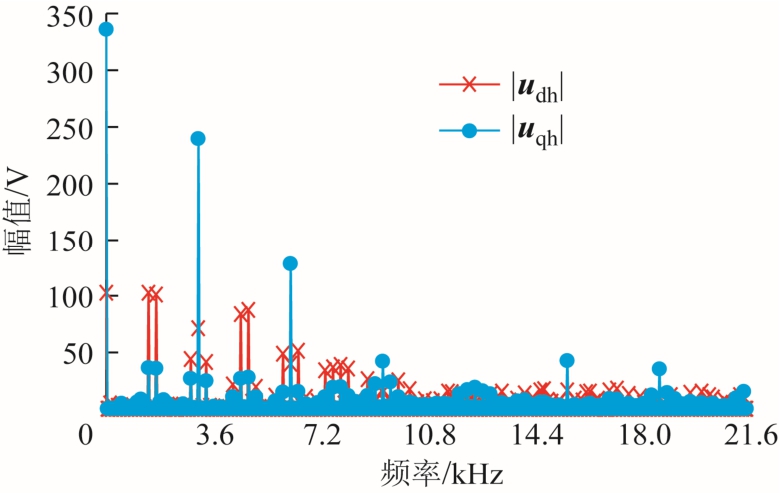
图7 转子坐标系下PWM 电压频谱
Fig. 7 Frequency spectra of PWM voltage in rotor reference frame
2.2 谐波电压与谐波损耗关系
2.2.1 转子位置与相位差影响
基于FDPM 和二维THFEA 可计算不同转子位置下，谐波电压在永磁体中产生的交变磁密和损耗，详细步骤见文献[12]。对于转子饱和程度较低的FCFMPM 电机，FDPM 和FDTRM 差别不大，在此直接使用FDPM。图8 给出了2kHz 的不同谐波电压组合在所有永磁体中产生的涡流总损耗。可以看出，与文献[12]中的内埋式永磁电机不同，转子位置对谐波电压与损耗之间的关系影响不大。此外，udh 和 uqh 之间的相位差也不会明显影响总损耗，且udh 和uqh 组合产生的永磁体涡流损耗可分别由udh 和uqh 单独产生的损耗叠加得到。FCFMPM电机的这两个特性有助于简化文献[12]中的计算流程。
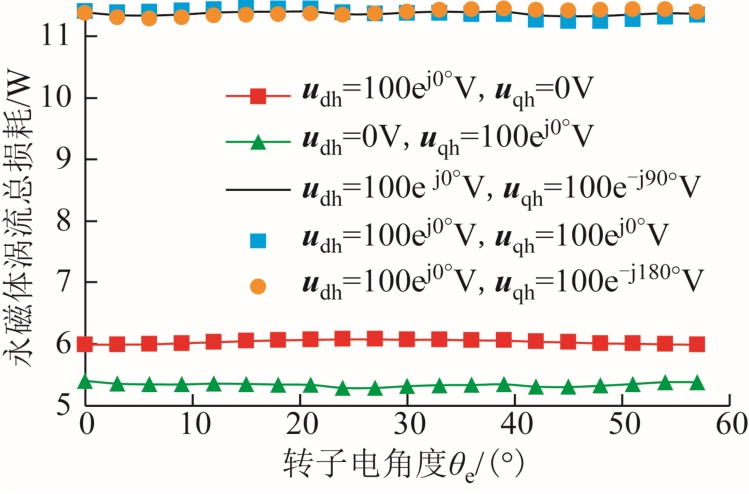
图8 2kHz 不同谐波电压组合产生的永磁涡流总损耗
Fig.8 Total PM eddy current loss generated by different combinations of harmonic voltages at 2kHz
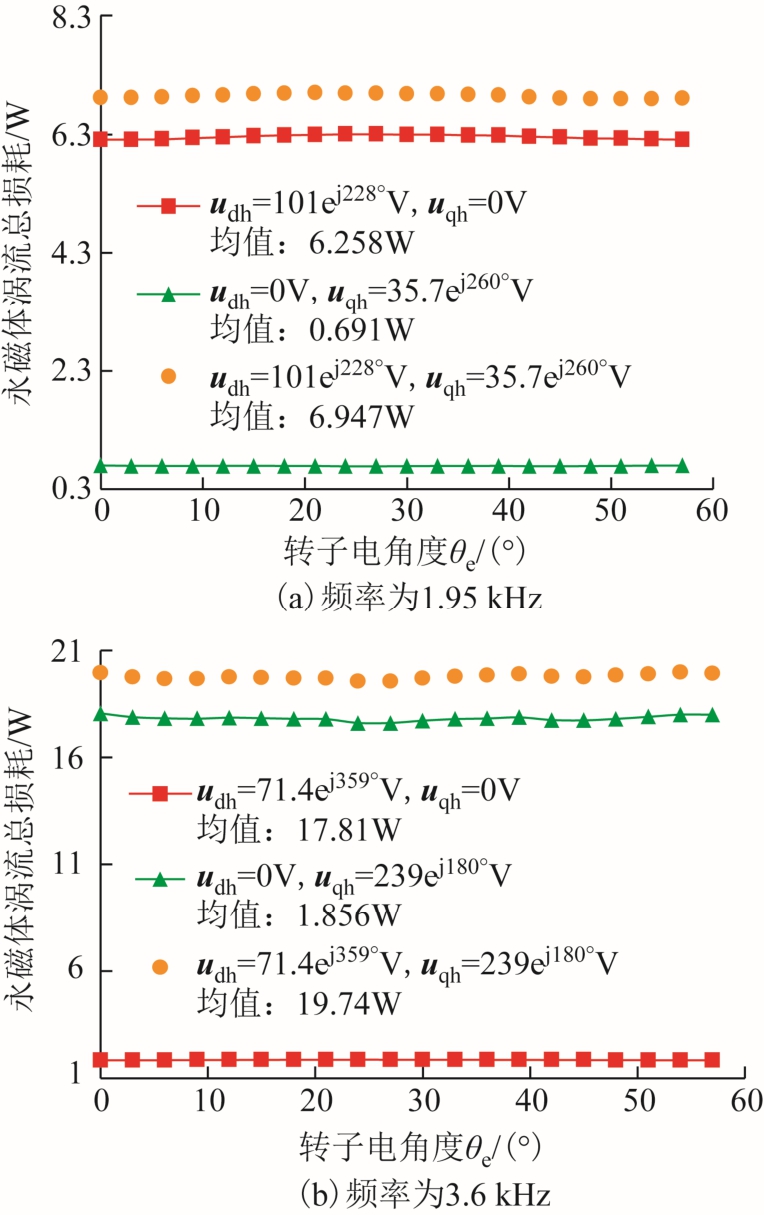
图9 不同频率的谐波电压激励下损耗随转子位置关系
Fig.9 Total PM eddy current losses generated by different harmonic voltages at different frequencies
对于该FCFMPM 电机，udh 与uqh 间的相位差及转子位置对永磁体涡流总损耗的影响可以忽略的结论适用于任意频率的电压谐波。为进一步验证这一点，选取图7 中实际存在的两组谐波电压进行计算。第一组的频率为1.95kHz、udh 为101ej228°V、uqh 为 35.7ej260°V；第二组频率为 3.6kHz、udh 为71.4ej359°V、uqh 为239ej180°V。图9 中给出了这两组谐波电压激励下损耗随转子位置的变化关系，同时给出了udh 或uqh 单独激励下的损耗。可以看出转子位置对永磁体中总损耗的影响可以忽略，而且无论udh 与uqh 之间相位差如何，udh 和uqh 共同激励下 的永磁体总损耗可近似认为等于udh和uqh 单独激励下的损耗和。
另外，根据THFEA 计算的结果，可对式（3）中解析模型的计算结果进行验证。在采用式（3）模型计算永磁体涡流损耗时，直接用θe 为0°处，udh或uqh 单独激励下考虑涡流反应时，穿过每块永磁体的平均磁密代入计算，进而得到所有永磁体中总损耗。而udh 和uqh 共同激励时的解析损耗，直接用两者单独激励时计算的损耗之和计算。表3 中对比了不同情况下的计算结果，可以看出解析模型计算结果与THFEA 得到的结果非常接近。而且，任意udh 和uqh 组合激励下的损耗可通过两者分别激励下的损耗进行叠加计算得到，进一步证明了本小节的结论。
表3 解析法与THFEA 计算永磁涡流损耗对比
Tab.3 Comparison of PM eddy current losses obtained from the analytical method and THFEA
udh/V uqh/V 频率/ kHz THFEA /W 式（3）模型计算值/W θe=0° 平均值 100ej0° 0 2 5.983 6.028 5.833 0 100ej0° 5.399 5.335 5.250 100ej0° 100e-j90° 11.38 11.36 11.08 100ej0° 100ej0° 11.40 11.36 11.08 100ej0° 100ej180° 11.36 11.37 11.08 100ej0° 0 7.2 1.581 1.592 1.501 0 100ej0° 1.340 1.321 1.261 100ej0° 100e-j90° 2.921 2.913 2.762 100ej0° 100ej0° 2.901 2.879 2.762 100ej0° 100ej180° 2.941 2.947 2.762 101ej228° 0 1.95 6.211 6.258 6.056 0 35.7ej260° 0.699 0.691 0.680 101ej228° 35.7ej260° 6.916 6.947 6.736 71.4ej359° 0 3.6 1.842 1.856 1.780 0 239ej180° 18.05 17.81 17.36 71.4ej359° 239ej180° 19.92 19.74 19.14
2.2.2 谐波电压与穿过永磁体平均磁密的关系
既然转子位置对谐波电压与涡流损耗关系的影响可以忽略，则只需分析一个转子位置的情况，本文选取θe=0°的位置进行分析。图10 中对比了在3.6kHz、100V 的
或
单独激励下，穿过每块永磁体的平均磁密幅值。其中，
表示忽略永磁体涡流反应时计算结果，
表示考虑涡流反应时的计算结果。可以看出每块永磁体中的磁密分布区别明显，且 
的幅值明显小于 
不同编号永磁体的位置参见图1。
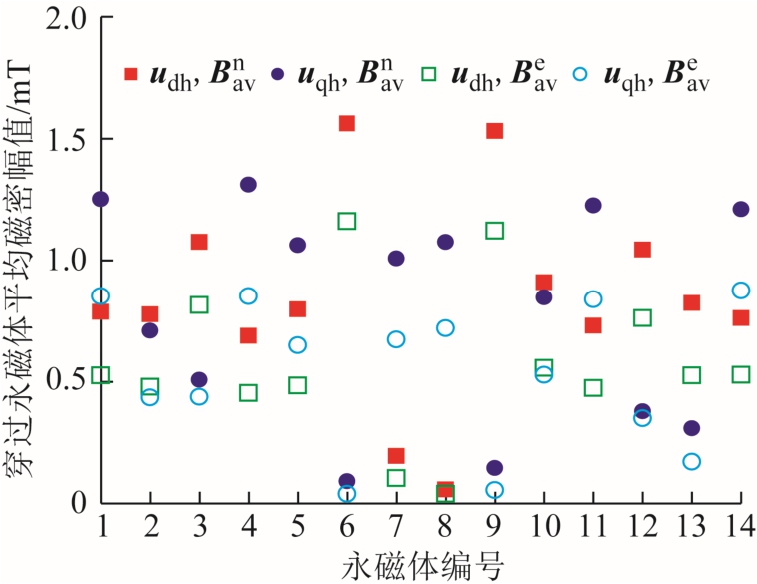
图10 在3.6kHz 分别忽略与考虑涡流反应时磁密对比
Fig. 10 Comparison of flux densities obtained when neglecting and considering eddy reaction effect at 3.6kHz
根据文献[10,12]中的结论，在高频情况下忽略电阻影响，
与谐波电压幅值U 及频率f 的关系为
式中，U 可以是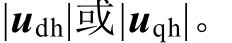
根据这个关系即可通过一组频率和电压下的THFEA 计算值推算任意频率和电压下的
但式（3）和式（5）中需要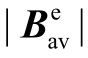
计算损耗，而根据文献[10]中假设的模型，两者之间关系为
式中，p 为漏磁系数，它由二维THFEA 的计算结果拟合得到。分别计算在考虑与不考虑涡流反应时，100V 的udh 或uqh 在fc/2、fc、2fc、4fc 和10fc时穿过每块永磁体的平均磁密。然后计算不同频率时的
和二维情况下的ξ。用式（8）拟合每块永磁体在udh 或uqh 激励下的p 值，拟合效果如图11 所示。图11a 中给出了在3.6kHz、100V 的udh 激励下，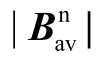
＞0.5mT 的永磁体的情况。如图10所示，除了7 和8 号永磁体之外，所有的永磁体都满足这个条件。在这些永磁体中，式（8）非常好地拟合了
与
但是在图11b 中所示的磁密较小的情况，模型拟合效果较差，但由于磁密较小，在这两块永磁体中产生的损耗也较小，这种拟合误差不会对计算总损耗产生明显影响。如图11c和图11d 所示，在uqh 激励情下的情况类似，在此不再赘述。
图11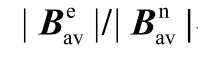 
与
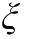关系拟合
Fig. 11 Fitting the relationship between 
2.3 逆变器供电下永磁体涡流损耗计算流程
根据2.2 节内容可以计算出任意udh 或uqh 激励下的
然后即可代入式（3）或式（5）中计算永磁体涡流损耗。在三维情况下，需将式（6）计算出的ξ 代入计算。图12 中总结了计算逆变器供电下永磁体涡流总损耗的流程。由1.2 节的分析可知，只需要进行1 步TSFEA，即可准确计算出低频涡流损耗，根据图8 可知只需要研究一个转子位置下的谐波电压-损耗关系即可。当然这个结论只对本文中的FCFMPM 适用，对于其他类型的电机可能要研究若干个转子位置的情况再取均值。
图12 计算逆变器供电下永磁体涡流总损耗流程
Fig.12 Flow chart for calculating the total PM eddy current loss
另外，2.2.2 节通过5 个频率点下的THFEA 结果去拟合p。由于该模型对交变磁密显著的永磁体拟合效果非常好，说明这个模型准确地反映涡流反应对磁密变化影响的物理规律，因此可以只在2fc 这一个频率下进行二维THFEA，且只用这一个点的计算结果去拟合p 即可。这样可以进一步将所需的THFEA 步数由20 步减少到4 步，具体影响将在下节进行对比分析。
2.4 计算结果对比
图13 中给出了以电压源为输入的传统TSFEA法计算的涡流损耗波形。和1.4 节一样，取θe 位于60°～120°范围内涡流损耗平均值作为参考值。计算时间为从0°计算至120°所需时间，共需进行672 步TSFEA。
图13 PWM 电压供电下传统TSFEA 计算损耗
Fig.13 Losses calculated with the traditional TSFEA using PWM voltage as input
表4 逆变器供电下不同方法计算永磁体涡流损耗对比
Tab.4 Comparison of the PM eddy current losses obtained with different methods under PWM VSI supply
方法 THFEA步数 PWM 谐波损耗/W 总损耗/W 计算时间/min二维 三维 二维 三维 二维 三维传统 — 42.3 27.3 182.6 78.9 42.5 1220本文所提20 43.9 29.5 179.7 79 3.52 4.07 4 44.4 29.6 180.2 79.1 2.51 3.06
表 4 给出了所提方法计算的逆变器供电下损耗与传统方法的对比。其中，由于传统PWM 电压源供电下的TSFEA 只能计算出总的永磁体涡流损耗，无法分离其中的高频和低频分量，所以认为传统TSFEA 计算的PWM 谐波损耗等于PWM 谐波电压供电下计算的永磁损耗减去表 2 中正弦电流供电下TSFEA 得到的结果。从表4 中可以看出，所提方法计算的PWM 谐波损耗比传统方法计算的值略大，最大相对误差低于8.4%。而从表2 中可以看出，所提方法计算的低频谐波损耗略低于传统TSFEA 的计算值。综合起来使得逆变器供电下总损 耗的相对误差仅有2%。而且，仅采用2fc 时的4 步THFEA 计算就可以准确地拟合出p，进而准确计算PWM 谐波损耗。在三维情况下，将PWM 谐波损耗的计算时间降低至约为传统方法的1/400，其中的计算时间已经包含了低频损耗的计算、网格剖分和解析计算时间。
3 结论
基于CE-FEA 和永磁体涡流损耗解析模型相结合可以快速计算FCFMPM 电机内部的低频涡流损耗；而基于小信号分析与解析损耗模型相结合可以快速计算永磁体中的PWM 谐波损耗。最少仅需要1 步二维TSFEA 和4 步二维THFEA 即可快速计算逆变器供电下的永磁体涡流损耗。与传统TSFEA 相比，所提方法低频谐波损耗计算相对计算误差小于4%，PWM 谐波损耗计算相对误差小于8.4%，计算时间缩短了数百倍以上。本文证明了基于频域小信号分析快速计算永磁电机的PWM 谐波损耗的方法同样适用于场调制型永磁电机。
[1] 鲍晓华, 刘佶炜, 孙跃, 等. 低速大转矩永磁直驱电机研究综述与展望[J]. 电工技术学报, 2019, 34(6): 1148-1160.
Bao Xiaohua, Liu Jiwei, Sun Yue, et al. Review and prospect of low-speed high-torque permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1148-1160.
[2] 李岱岩, 白保东, 杨晨, 等. 基于调磁块阵列的永磁游标电机研究[J]. 电工技术学报, 2018, 33(增刊2): 359-366.
Li Daiyan, Bai Baodong, Yang Chen, et al. Study of permanent magnet vernier machine by using magnetic tuning block array[J]. Transactions of China Electrotechnical Society, 2018, 33 (S2): 359-366.
[3] 李祥林, 程明, 邹国棠, 等. 聚磁式场调制永磁风 力发电机工作原理与静态特性分析[J]. 电工技术学报, 2014, 29(11): 1-9.
Li Xianglin, Cheng Ming, Chau K T, et al. Principle and analysis of a new flux-concentrating field modulated permanent-magnet wind power generator[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 1-9.
[4] 李祥林, 程明, 邹国棠. 聚磁式场调制永磁风力发电机输出特性改善的研究[J]. 中国电机工程学报, 2015, 35(16): 4198-4206.
Li Xianglin, Cheng Ming, Chau K T. Research on improvement of output characteristics of the flux concentrating field-modulated permanent-magnet wind power generator[J]. Proceedings of the CSEE, 2015, 35(16): 4198-4206.
[5] 朱洒, 程明, 李祥林, 等. 新型外转子低速直驱永磁游标电机的损耗[J]. 电工技术学报, 2015, 30(2): 14-20.
Zhu Sa, Cheng Ming, Li Xianglin, et al. Loss analysis of a new low-speed direct-drive permanent-magnet vernier machine[J]. Transactions of China Electrotechnical Society, 2015, 30(2): 14-20.
[6] 陈晓, 赵文祥, 吉敬华, 等. 考虑边端效应的双边直线永磁游标电机模型预测电流控制[J]. 电工技术学报, 2019, 34(1): 49-57.
Chen Xiao, Zhao Wenxiang, Ji Jinghua, et al. Model predictive current control of double-side linear vernier permanent magnet machines considering end effect[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 49-57.
[7] Tong Wenming, Wang Yunxue, Sun Ruolan, et al. Simulation and experimental study on no-load loss distributions of an IPM motor under the conditions of both sinusoidal supply and converter supply[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-6.
[8] Zhu Sa, Cheng Ming, Hua Wei, et al. Finite element analysis of flux-switching PM machine considering oversaturation and irreversible demagnetization[J]. IEEE Transactions on Magnetics, 2015, 51(11): 1-4.
[9] Yamazaki K, Abe A. Loss investigation of interior permanent-magnet motors considering carrier harmonics and magnet eddy currents[J]. IEEE Transactions on Industry Applications, 2009, 45(2): 659-665.
[10] Cheng Ming, Zhu Sa. Calculation of PM eddy current loss in IPM machine under PWM VSI supply with combined 2-D FE and analytical method[J]. IEEE Transactions on Magnetics, 2017, 53(1): 1-12.
[11] Zhang Peng, Sizov G Y, He Jiangbiao, et al. Calculation of magnet losses in concentrated-winding permanent-magnet synchronous machines using a computationally efficient finite-element method[J]. IEEE Transactions on Industry Applications, 2013, 49(6): 2524-2532.
[12] Zhu Sa, Wang Hao, Zhang Jingwei, et al. Fast calculation of carrier harmonic loss in permanent magnet of IPMSM under PWM VSI supply over entire working range[J]. IEEE Transactions on Energy Conversion, 2019, 34(3): 1581-1592.
[13] 朱洒. 新型永磁电机损耗计算与多物理场分析[D]. 南京：东南大学, 2017.
[14] Zhu Sa, Cheng Ming, Zhu Ying. Fast calculation of PM eddy current loss in IPMSM under PWM VSI supply based on the spectra of line-line voltage[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.
[15] Alberti L, Bianchi N, Morandin M, et al. Finiteelement analysis of electrical machines for sensorless drives with high-frequency signal injection[J]. IEEE Transactions on Industry Applications, 2014, 50(3): 1871-1879.