0 引言
永磁电机在质量和体积上均较小，结构相对比较简单，具有高效率、低损耗等明显优势，已应用于现代科技生产和社会生产生活的相关领域[1-3]。要实现直驱式永磁电机低速大转矩传递，需增加永磁体极对数，增大电机体积，电机转矩虽有所增加，但电机转矩密度显著降低。磁力齿轮与永磁电机配合构成复合电机具有较高的转矩密度[4-6]，在低速高转矩如电动汽车[7]、风力涡轮机场合[8]，这种复合电机将发挥它的巨大优势。
影响电机性能和设计的关键因素之一是如何获取准确的气隙磁场。针对气隙磁场的求解，目前主要有数值法[9-11]、半解析法[12-13]、解析法[14-18]。虽然数值法具有较高的计算精度，但时间上花费较长，气隙网格在转子旋转过程中易发生畸变，难以保证网格的剖分质量；尤其是对于具有多个气隙的复合电机，两个转子的旋转速度和方向是不同的，并且任一侧的相对运动将不可避免地影响另一侧，转子的旋转对网格的影响更加严重。如果气隙层不存在网格剖分，可以使转子灵活旋转，问题自然得以解决。永磁电机磁钢采用Halbach 阵列，其气隙磁场比常规永磁电机气隙磁场正弦度更好，磁通密度幅值的增大和谐波含量的减小都有利于增加输出转矩；弱磁侧具有自屏蔽特性，可大大降低电机体积，提升转矩密度[19-20]。
针对磁力变速永磁无刷复合电机结构特点，L. Jian 和K. Chau 采用有限元法开展了较为丰富的研究[21-22]。而本文是基于文献[23-25]，将永磁无刷电机（Permanent Magnet Brushbess Machine, PMBM）嵌入磁力齿轮（Magnetic Geared, MG）中形成复合电机，高速内转子永磁体均为 Halbach 阵列，低速外转子永磁体为径向充磁，建立永磁体充磁解析模型；应用解析法对复合电机气隙磁场进行计算，可以有效地解决数值法计算复合电机模型时在气隙网格剖分和转动位置上的缺陷，从而实现转子的自由旋转。以一台内电机转子永磁体极对数为10、磁力齿轮传动比为26/3 的Halbach 阵列磁力变速永磁无刷电机为例，计算分析了复合电机内层气隙磁场、反电动势和电磁转矩，并对比数值法计算结果。计算了该复合电机的效率和功率因数，并与试验样机测试值进行对比，验证了所提方法的合理性和有效性。
1 电机结构及参数
图1 是Halbach 阵列磁力变速永磁无刷复合电机结构模型。该复合电机由两大部件构成：内部是一个带外转子的永磁无刷电机（PMBM）；外部是一个磁力齿轮（MG）。复合电机的高速内转子由PMBM 转子和MG 高速转子通过一个不锈钢圈连接组成；复合电机低速外转子是MG 的低速转子。复合电机低速和高速转子磁体分别采用径向充磁和Halbach 阵列结构，利用Halbach 阵列的磁场自屏蔽效应，使电机与磁力齿轮主磁通相互解耦。由于采用Halbach 阵列，转子铁心轭部的磁场相对很弱，可适当减小轭部厚度，不但节省硅钢片材料，还可缩小复合电机总体积。试验样机的结构参数见表1。
图1 Halbach 阵列磁力变速永磁无刷复合电机模型
Fig.1 Structure of MG-PMBM with Halbach arrays
表1 样机参数
Tab.1 Parameters of prototype
参 数 数 值 电机永磁体极数2p 20 MG 高速转子极对数 3 MG 低速转子极对数 26 MG 调磁铁块数 29 电机永磁体每极块数 3 MG 高速转子每极块数 8 永磁体剩磁/T 1.1 定子槽数Q 18 定子外径/mm 77.1 电机永磁体内径/mm 77.9 电机转子铁心内径/mm 81.4 电机转子铁心外径/mm 84.4 MG 高速转子铁心内径/mm 87.4 MG 高速转子铁心外径/mm 94.2 MG 高速转子永磁体外径/mm 102.2 调磁环内径/mm 103 调磁环外径/mm 117.5 低速转子永磁体内径/mm 118.3 低速转子铁心内径/mm 123.7 低速转子铁心外径/mm 135.5 电机轴向长度/mm 60
2 磁场解析计算
2.1 Halbach 阵列解析模型
Halbach 阵列具有聚磁效应，但需要有正确的磁化角度来获得正弦分布磁场。图2 是内电机高速转子一对永磁体磁化平面图，其中永磁体每一极均分三小块，每隔60°依次充磁，箭头代表的是每小块磁体磁化方向。
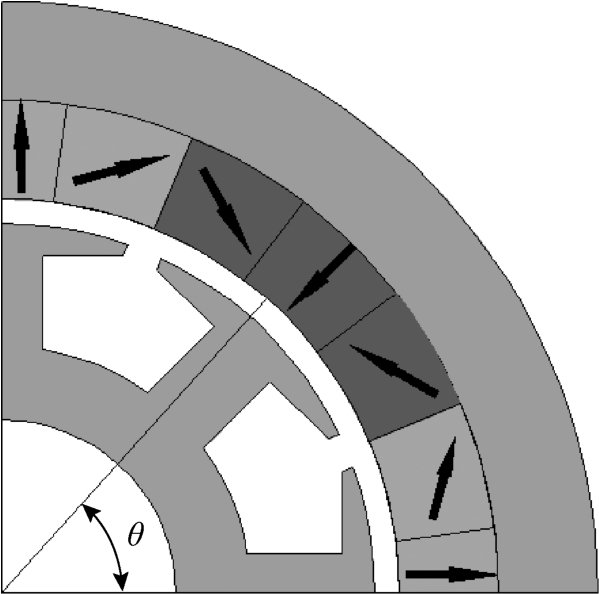
图2 永磁体磁化平面示意图
Fig. 2 Arrangements of PM segments
永磁体磁化强度M 表达式为
其中
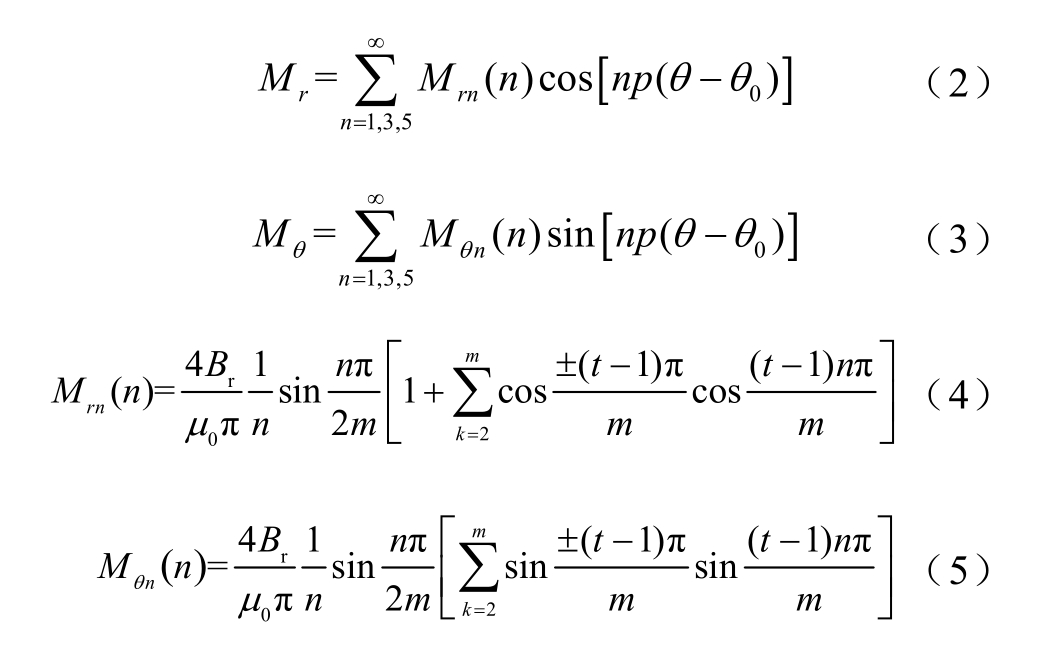
式中，“+”代表外转子；“-”代表内转子；p 为内电机转子极对数；m 为每一极下永磁体分块数； t 为m 块中的第t 块； 0θ 为设定的初始角；Br 为永磁体剩磁；μ0 为真空磁导率。
2.2 空载气隙磁场解析模型
为了分析方便，作如下假设：①在r-θ坐标下进行2D 计算，无端部效应；②永磁体相对磁导率μr=1；③定子、转子铁心磁导率无穷大；④定子槽型是半闭口扇形，槽中没有电流。
根据以上假设，矢量磁位在2D 极坐标下只有z轴有分量，所以内层气隙区域矢量磁位A1 在极坐标下的拉普拉斯方程为
同理，槽域i 矢量磁位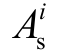
的拉普拉斯方程可表示为
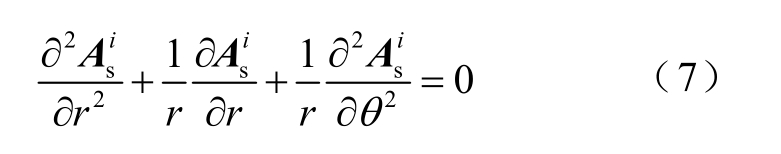
而内外转子永磁体矢量磁位A2 在2D 极坐标下泊松方程可表示为
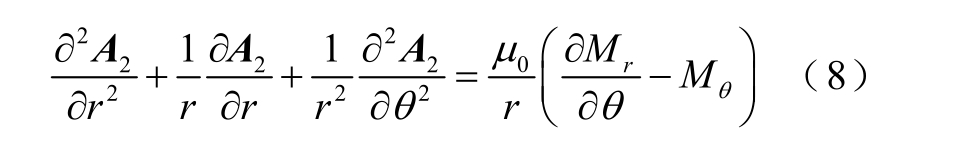
运用分离变量法，可以得到各矢量磁位表达式为
式中，系数 
是常数；β 为槽口角度； iθ 为第i 槽的初始角度； k 为第i 槽区域傅里叶展开次数；h 为2p 和Q 的最大公约数；Rs 为定子外半径；Rs1 为区域Si 和区域Sj 交界处半径。
由麦克斯韦应力张量法可知，在空载状态下，该电磁转矩即齿槽定位转矩，表达式为
式中，Lef 为电机轴向长度。从式（12）可以看出，齿槽转矩大小只与内层气隙矢量磁位A1(r,θ )表达式系数有关。
通过对槽域矢量磁位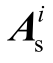 
的面积分可以得到磁链的表达式，由于本文绕组为双层绕组，则槽内某一相绕组磁链可表示为
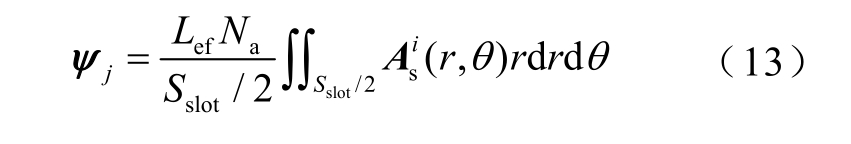
式中，Na 为绕组导体数；Sslot 为定子槽面积。
感应电动势可以通过对磁链进行微分，其表达式为
式中，ω 为转子机械角速度。
2.3 电枢反应磁场解析模型
同样，作如下假设：①不考虑饱和与涡流；②永磁体不充磁；③铁磁导率无穷大；④定子槽为半闭口扇形，电流均匀分布在槽内。
极坐标系下，j 槽内矢量磁位
满足泊松方程
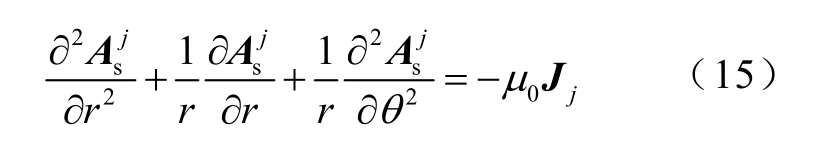
式中，Jj 为第j 槽内的电流密度。
若j 槽中上层绕组区域Sj1 和下层绕组区域Sj2内电流密度分别为
根据边界连续条件，相应区域内矢量磁位可表示为
其中
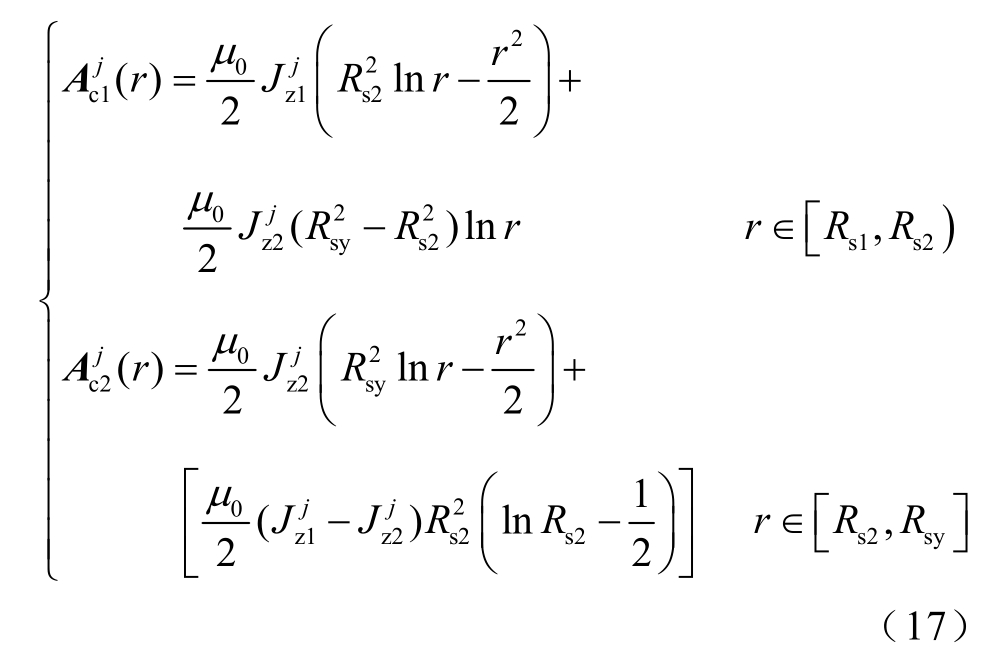
式中，Rs2 为区域Sj1 和区域Sj2 交界处半径；Rsy 为定子槽轭部半径；δ 为槽身张开角度；第j 槽初始角度为θi+(β－δ)/2；m 为区域Sj 内傅里叶展开次数；
为待定系数。
3 计算结果与验证分析
根据图1 及样机结构参数可知，Halbach 阵列磁力变速永磁无刷复合电机采用传动比为-8.67:1，电机采用10 对极18 槽配合，其有限元分析场量如图3 所示。图4a 和图4b 分别为两种不同充磁方式复合电机的磁力线分布图。
图3 MG-PMBM 有限元场量图
Fig.3 FE analysis field measurement of MG-PMBM
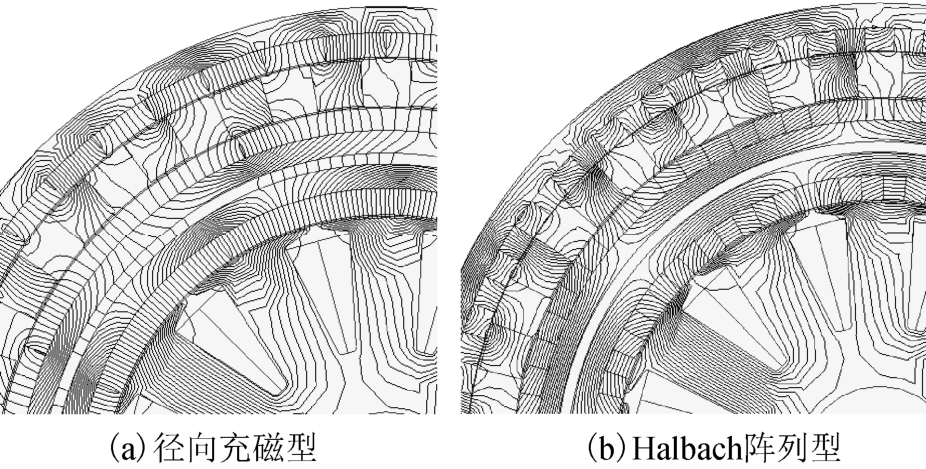
图4 复合电机磁力线图
Fig.4 Magnetic flux distributions of MG-PMBM
图4 a 所示为转子永磁体径向充磁型复合电机， 磁力线在磁力齿轮与电机之间形成闭合回路，说明主磁通耦合程度较高，各层气隙谐波分量较大。图4b 为Halbach 阵列型复合电机，内电机与磁力齿轮磁力线彼此隔离，说明电机与磁力齿轮的主磁通相互解耦，气隙谐波分量小。
图5 给出了内层气隙中间部位r=77.5mm 处磁通密度分布曲线。
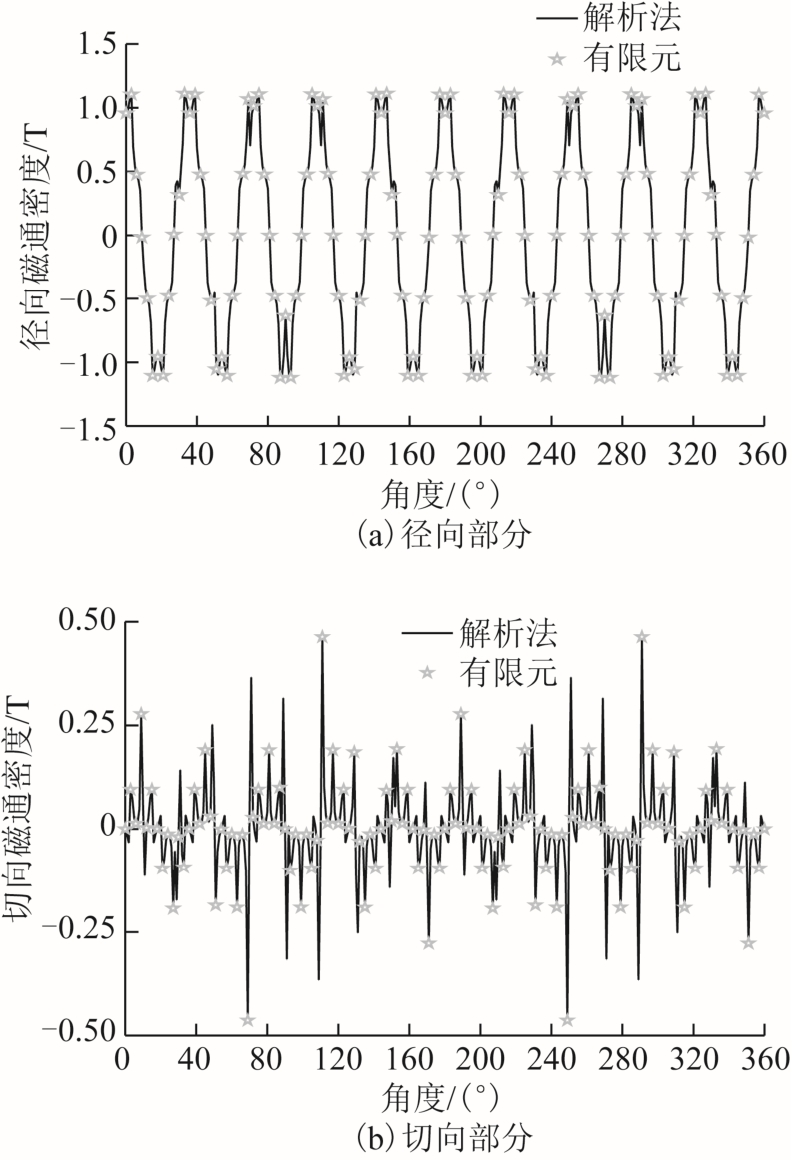
图5 内气隙磁通密度
Fig. 5 Flux density distribution at r=77.5mm
从图5 可以看出，磁通密度解析计算值与有限元计算结果在波形上基本一致，这也证实了本方法是正确有效的。
图6a 和图6b 分别表示该复合电机齿槽转矩计算结果和傅里叶分解结果。由图6 可知，齿槽转矩周期是20°电角度，幅值约为117.3mN·m。齿槽转矩两种计算值波形吻合良好。
图7 为电枢反应磁场气隙磁通密度的径向分量 和切向分量。解析结果与有限元分析结果相符，电枢反应磁场描述准确。同样证实了本方法是正确有效的。
图8a～图8e 所示为Halbach 阵列磁力变速永磁无刷电机样机部分实物图和试验平台。图8d 所示为Halbach 阵列磁力变速永磁无刷复合电机高速转子内电机侧10 对极Halbach 阵列磁钢，经磁粉显影试纸可以观察到，其磁场分布呈现较好的正弦性，磁极非常明显。
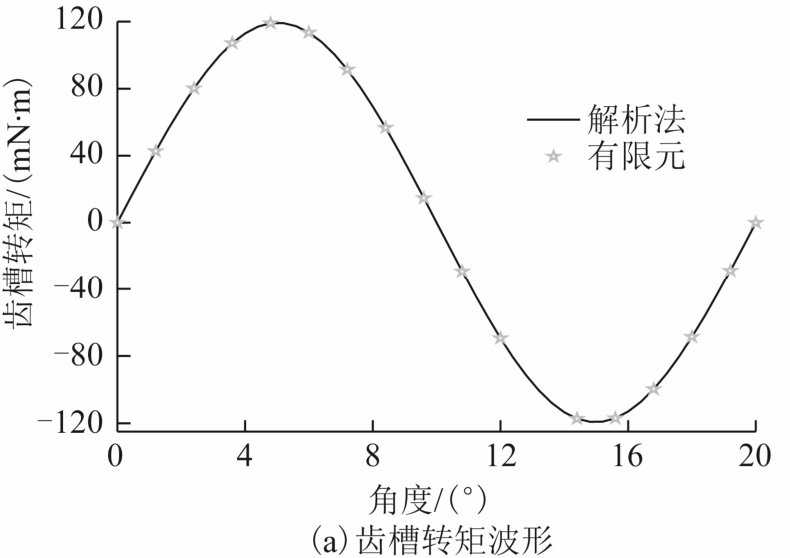
图6 齿槽转矩
Fig. 6 Cogging torque
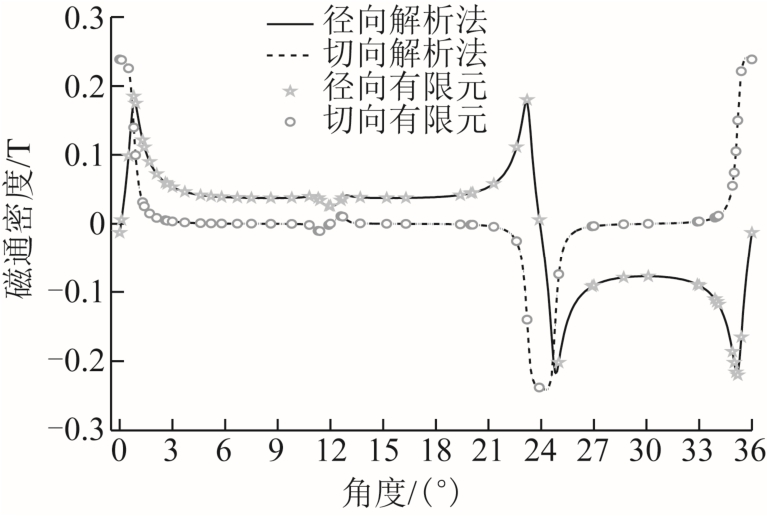
图7 电枢反应磁通密度
Fig.7 Flux density of armature reaction field
图8 样机及试验平台
Fig.8 Prototype and test platform
当Halbach 阵列磁力变速永磁无刷复合电机高速内转子转速为120r/min，即频率为20.07Hz 时，空载感应电动势的解析计算波形与试验测试波形如图9 所示，二者波形基本一致。
图9 感应电动势
Fig.9 Back-EMF
从图9a 可知，解析法计算感应电动势最大值为31V；而图9b 中，样机测试的感应电动势幅值为28.8V。两者之所以有偏差，可能是以下两方面原因：①贴装永磁体时，每块之间都有气隙，留有余量，而在解析计算中没有考虑；②充磁角度存在误差，和有限元模型存在一定的差异，可能造成样机整个磁场性能的变化。不过，两数值之间的偏差仍在合理区间之内，证实了解析计算的正确性与合理性。
样机传递效率曲线如图10 所示。从图中可知，在转速为15r/min，输出转矩为40N·m、80N·m 和120N·m 时，传递效率均低于90%。这是因为空载损耗占相对较大比值，复合电机在低速、轻载运行时，传递效率相对较低，而随着输入功率的增大，空载损耗所占的比例逐渐下降，效率逐步提高，基本都在91%以上。
图10 传递效率
Fig.10 Transmission efficiency
图11 为不同负载下，复合电机功率因数的变化曲线。由图11 可以看出，功率因数曲线随着转速的升高整体呈现下降的趋势。与传递效率相似，负载较轻时，功率因数较小；大负载运行时，功率因数较高。样机运行最大功率因数可以达到0.905。
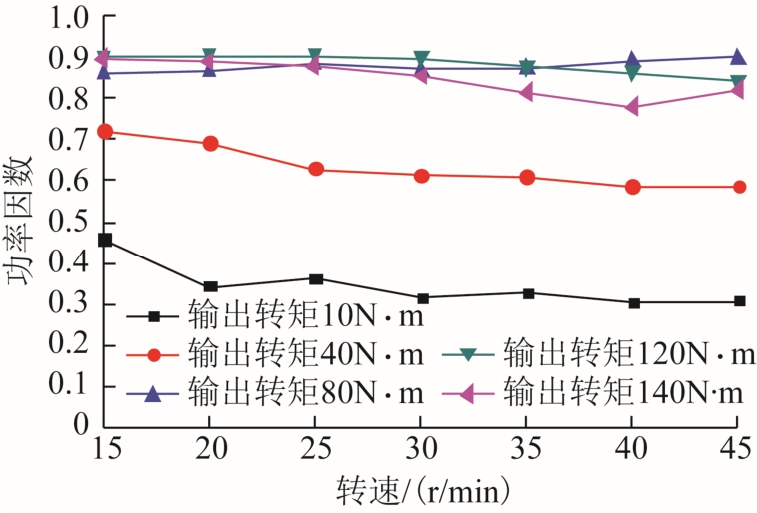
图11 功率因数
Fig.11 Power factor
图12 为A 相绕组在不同负载下的电流波形。从图12 可知，Halbach 阵列磁力变速永磁无刷复合 电机电流的频率基本维持在28Hz 左右，波形有较高的正弦度，而且幅值随着负载增大而增大。
图13 是Halbach 阵列磁力变速永磁无刷复合电机转矩响应曲线。该曲线可以在上位机软件中直接读取。在t =0.5s 时，给磁粉制动器加压，从0V 突然上升到1.3V，电机输出转矩在t =1.25s 左右跟随到负载转矩108N·m；在t =3.0s 时，磁粉制动器的电压突然降到0V，电机输出转矩在t =3.25s 左右回到0 N·m。
由图13 可以看到，Halbach 阵列磁力变速永磁无刷复合电机的输出转矩动态响应性能良好，跟随速度快，转矩稳定且脉动较小。
图12 负载电流
Fig.12 Load currents
图13 负载响应
Fig. 13 Load response
4 结论
本文采用解析法计算了Halbach 阵列磁力变速永磁无刷复合电机磁场，建立了Halbach 阵列充磁解析模型、各子区域矢量表达式。计算了复合电机内层气隙磁通密度和电机齿槽转矩，解析计算波形与有限元法计算波形结果一致，较有限元法计算时间短，证明了解析法的有效性和正确性；同时能快速改变复合电机的主要电磁参数尺寸，达到优化预设计的目的。从试验结果知，样机效率可以达到90%以上，且比较稳定；负载运行的最大功率因数可达0.905，随着转速的升高，功率因数整体呈下降的趋势。而且，采用Halbach 阵列结构，可以节约成本，有效减小电机体积，提高电机转矩密度。本研究方法可以为磁力齿轮复合电机设计提供一种有力的工具。
[1] Gao Yuting, Qu Ronghai, Li Jian, et al. Design of three-phase flux reversal machines with fractional-slot windings[J]. IEEE Transactions on Industry Applications, 2016, 52(4):2856-2864.
[2] 王天煜, 温福强,张凤阁, 等. 兆瓦级高速永磁电机转子多场耦合强度分析[J]. 电工技术学报, 2018, 33(19): 4508-4516.
Wang Tianyu, Wen Fuqiang, Zhang Fengge, et al. Analysis of multi-field coupling strength for MW high-speed permanent magnet machine[J]. Transactions of China Electrotechnical Society, 2018, 33(19):4508-4516.
[3] 李伟, 程明, 朱洒. 磁通切换永磁电机固有轴电压分析[J]. 电工技术学报, 2017, 32(15):1-9.
Li Wei, Cheng Ming, Zhu Sa. Analysis of inherent shaft voltage in flux-switching permanent magnet machine[J]. Transactions of China Electrotechnical Society, 2017, 32(15):1-9.
[4] 井立兵,高起兴,王冲,等.双转子混合励磁电机优化设计和特性分析[J]. 电机与控制学报, 2019, 23(9): 43-50.
Jing Libing, Gao Qixing, Wang Chong, et al. Optimization design and characteristic analysis of dual-rotor hybrid excitation motor[J]. Electric Machines and Control, 2019, 23(9): 43-50.
[5] 沈建新, 王利利. 磁场调制型永磁电机的设计与实验[J]. 电工技术学报, 2013, 28(11): 28-34.
Shen Jianxin, Wang Lili. Design and experimental study of permanent magnet machines with magnetic field modulation[J]. Transactions of China Electrotechnical Society, 2013, 28(11): 28-34.
[6] 谢颖, 黑亮声, 华邦杰, 等. 新型永磁游标电机的设计与研究[J]. 电机与控制学报, 2019, 23(2): 68-74.
Xie Ying, Hei Liangsheng, Hua Bangjie, et al. Design and analysis of a new vernier permanent magnet motor[J]. Electric Machines and Control, 2019, 23(2): 68-74.
[7] Zhao Xing, Niu Shuangxia. Design and optimization of a new magnetic-geared pole-changing hybrid excitation machine[J]. IEEE Transactions on Industrial Electronics, 2017, 64 (12) :9943-9952.
[8] Lee H T, Chau K T, Liu C H, et al. Design and analysis of a magnetless flux-switching DC-excited machine for wind power generation[J]. Journal of International Council on Electrical Engineering, 2014, 4(1):80-87.
[9] Jing Libing, Luo Zhenghao, Qu Ronghai, et al. Investigation of a surface PM machine with segmented eccentric magnet poles[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(3): 5204305.
[10] Shi Chaojie, Qu Ronghai, Li Dawei, et al. A novel linear permanent magnet vernier machine with consequent-pole permanent magnets and Halbach permanent magnet arrays[J]. IEEE Transactions on Magnetics, 2017, 53(11): 2501404.
[11] Jing L B, Liu Lin, Qu R H, et al. A novel method of reducing the cogging torque in SPM machine with segmented stator[J]. Journal of Electrical Engineering & Technology, 2017, 12(2): 718-725.
[12] 林楠, 王东, 魏锟, 等. 新型混合励磁同步电机的数学模型与等效分析[J].电工技术学报, 2017, 32(3): 149-156.
Lin Nan, Wang Dong, Wei Kun, et al. Mathematical model and equivalent analysis of a novel hybrid excitation synchronous machine[J]. Transactions of China Electrotechnical Society, 2017, 32 (3) :149-156.
[13] 章跃进, 江建中, 崔巍. 数值解析结合法提高电机磁场后处理计算精度[J]. 中国电机工程学报, 2007, 27(3):68-72.
Zhang Yuejin, Jiang Jianzhong, Cui Wei. Accuracy enhancement of post process of magnetic field computation for rotational electric machines by numerical-analytical method[J]. Proceedings of the CSEE, 2007, 27(3): 68-72.
[14] Zhu Z Q, Howe D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors, Part II: armature-reaction field[J]. IEEE Transactions on Magnetics, 1993, 29(1): 136-142.
[15] Jing L B, Luo Z H, Liu Lin, et al. Optimization design of magnetic gear based on genetic algorithm toolbox of Matlab[J]. Journal of Electrical Engineering & Technology, 2016, 11(5): 1202-1209.
[16] Qiu Z J, Dai J, Yang J. Research on rotor eccentricity compensation control for bearingless surface mounted permanent magnet motors based on an exact analytical method[J]. IEEE Transactions on Magnetics, 2015, 51(11): ID: 8114004.
[17] 寇宝泉, 曹海川, 李伟力, 等. 新型双层Halbach 永磁阵列的解析分析[J]. 电工技术学报, 2015, 30 (10): 68-76.
Kou Baoquan, Cao Haichuan, Li Weili, et al. Analytical analysis of a novel double layer Halbach permanent magnet array[J]. Transactions of China Electrotechnical Society, 2015, 30 (10): 68-76.
[18] Ojaghi M, Sabouri M, Faiz J, et al. Analytic model for induction motors under localized bearing faults[J]. IEEE Transactions on Energy Conversion, 2018, 33(2): 617-626.
[19] Jing Libing, Huang Zhangxian, Chen Junlin et al. An asymmetric pole coaxial magnetic gear with unequal Halbach arrays and spoke structure[J]. IEEE Transactions on Applied Superconductivity, 2020, 30(4): 1-4.
[20] 秦伟, 范瑜, 徐洪泽, 等. 高温超导运动磁场电磁Halbach 初级结构直线感应磁悬浮电机[J]. 电工技术学报, 2018, 33(23): 5427-5434.
Qin Wei, Fan Yu, Xu Hongze, et al. A linear induction maglev motor with HTS traveling magnetic electromagnetic Halbach array[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5427-5434.
[21] Jian Linni, Chau K T, Jiang J Z. A magnetic-geared outer-rotor permanent-magnet brushless machine for wind power generation[J]. IEEE Transactions on Industry Applications, 2009, 45(3): 954-962.
[22] Jian Linni, Shi Yujun, Liu Cheng, et al. A novel dual permanent magnet excited machine for low speed large torque applications[J]. IEEE Transactions on Magnetics, 2013, 49(5): 2381-2384.
[23] 井立兵, 章跃进. Halbach 阵列同心式磁力齿轮磁场全局解析法分析[J].电机与控制学报, 2014, 18(10): 50-54, 67. Jing Libing, Zhang Yuejin. Exact analytical method for magnetic field computation in concentric magnetic gear with Halbach permanent magnet arrays[J]. Electric Machines and Control, 2014, 18(10): 50-54, 67.
[24] Lubin T, Mezani S, Rezzoug A. 2-D exact analytical model for surface-mounted permanent-magnet motors with semi-closed slots[J].IEEE Transactions on Magnetics, 2011, 47(2): 479-492.
[25] 井立兵, 柳霖, 章跃进, 等. Halbach 阵列同心式磁力齿轮参数分析与优化设计[J]. 电机与控制学报, 2016, 20(3): 6-12.
Jing Libing, Liu Lin, Zhang Yuejin, et al. Parameters analysis and optimization design for concentric magnetic gear with Halbach permanent magnet arrays[J]. Electric Machines and Control, 2016, 20(3): 6-12.