0 引言
电机是第一次工业革命的产物,诞生于1830 年代,至今已有180 余年的历史。随着电气化和自动化技术的普及,电机的应用场合已经从常规工业驱动,全面拓展至航空航天、交通运输、数控设备、机器人等高科技领域,应用地点也从地面立体化延伸拓展到深空、深海、深地。与此同时,不同应用领域对电机的性能要求不断细化,传统的有刷直流电机、感应电机和同步电机已无法满足新领域、新应用的苛刻要求。因此,各种不同结构特点、不同工作原理、不同性能优势的新型电机大量涌现,如无刷双馈感应电机(Brushless Doubly-Fed Induction Machine, BDFIM)[1-2]、开关磁阻电机(Switched Reluctance Machine, SRM)[3-4]、定子永磁电机(Stator Permanent Magnet Machine, SPMM)[5-6]、永磁游标电机(Permanent Magnet Vernier Machine, PVM)[7-8]、磁齿轮复合电机(Magnetically-Geared Machine, MGM)[9]等。然而,面对上述新型/特种电机时,经典电机学理论不再完全适用,或者说,经典电机学理论已难以适用于这些新型电机的工作原理解释和性能参数分析。举例来说,根据经典电机学理论与机电能量转换原理[10-11],电机能够实现机电能量转换的前提之一是定子绕组极对数必须等于转子磁场极对数。而对于如图1 所示的永磁电机[7],其电枢绕组通电后形成1 对极的电枢磁场,但其转子却有17 对永磁磁极,直观地看,其定子、转子极对数明显不等,电机无法运行,即使考虑绕组磁动势谐波,17 次谐波磁动势幅值很小,与转子磁场作用产生的转矩基本可以忽略,该类电机似乎没有实用价值。但仿真计算和实验结果表明,该类电机不仅能实现机电能量转换,而且其转矩密度等性能还要优于常规永磁电机。
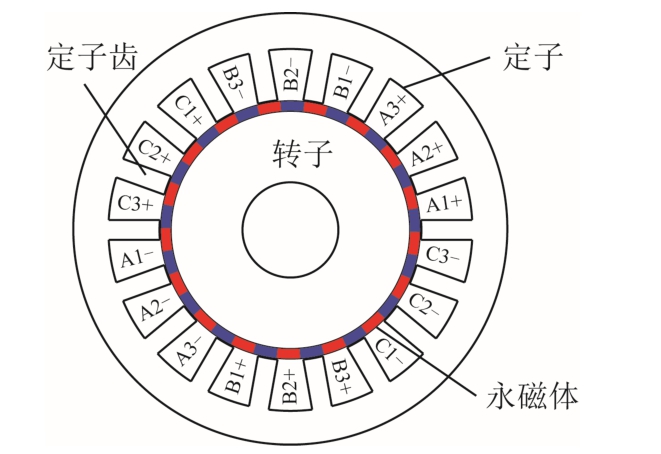
图1 Lipo 提出的永磁电机
Fig.1 The permanent magnet machine proposed by Lipo
图2 所示为一台定子12 槽、转子10 极磁通切换永磁电机(Flux-Switching Permanent Magnet Machine, FSPM)[12],其电枢绕组和永磁体都位于定子,转子为简单凸极铁心,属于定子永磁无刷电机[5]。该电机定子上有12 块永磁体,形成6 对极的静止磁场,转子上有10 个极,根据其转速、电流频率等关系获得的等效主极对数等于4,既不等于定子永磁磁场极对数,也不等于转子极数,难以用经典电机学理论来解释。
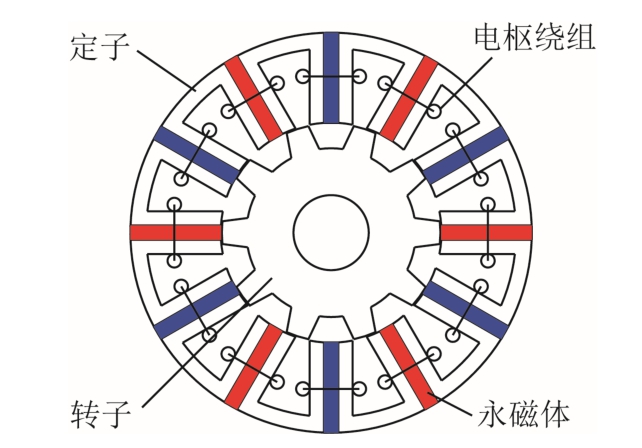
图2 12/10 极磁通切换永磁电机
Fig.2 The 12 slot/10 pole FSPM
事实上,上述电机都利用了“磁场调制原理”。文献[13]在深入分析上述新型电机工作原理的基础上,揭示了气隙磁场调制现象在电机中的普遍性,创立了电机气隙磁场调制理论,统一了电机运行原理,为电机运行原理和特性的分析与计算提供了一个全新的视角。电机气隙磁场调制理论将短路线圈、简单凸极和多层磁障对磁动势分布的影响用调制算子加以描述,使得任一具体的电机结构均可转换为统一的等效气隙模型。气隙磁场调制统一理论将电机中普遍存在的调制现象分为同步调制和异步调制,并指出电机机电能量转换过程中可能同时存在上述两种调制行为,而传统直流电机和同步电机主要利用同步调制并人为抑制异步调制,但大部分新型磁场调制电机主要利用人为增强异步调制[14]。
传统电机气隙磁场中,仅与励磁磁场主极对数相等的基波磁场产生有效电磁转矩,故只包含一种同步转矩或异步转矩分量。而近年来出现的基于磁场调制原理的新型拓扑结构电机,正是对额外有效谐波磁场的利用才使得这类电机平均转矩得到提升,故主电磁转矩中可能包含多个转矩分量。以简单凸极类磁场调制电机为例,该类电机虽然主要利用异步调制行为,但却能够生成同步转矩分量,调制行为与转矩成分的关系错综复杂、较难理解;另一方面,这类电机的调制行为与转矩特性具有相通性,因此可以统一进行归纳描述。无刷双馈电机(Brushless Doubly-Fed Machine, BDFM)转子包括短路线圈、简单凸极、多层磁障(径向及轴向)等多 种转子结构,是磁场调制电机重要一员,其本质是一类具有两个交流电气端口和一个公共机械端口的新型复合电机[1]。由于无刷双馈电机独特的复合特性,两个交流电气端口不同方式供电时可以运行在多种模式下。对应不同的运行模式、转子结构,BDFM 电磁转矩成分可能截然不同,其调制行为与转矩成分的关系更加复杂;而在特定的运行模式下,BDFM 与电励磁同步电机(Electrically Excited Synchronous Machine, EESM)具有相似性,即从磁场调制的角度解释了传统电机与新型磁场调制电机的内在联系。
文献[14]列举了常见简单凸极类磁场调制电机的同步调制和异步调制行为,但并未对转矩成分进行进一步的定义和分析。本文首次基于磁场调制理论阐述广义磁场调制电机中调制行为与转矩成分的定义及辩证关系,即同步/异步调制均能够分别生成同步转矩分量,而异步调制可以生成异步转矩分量。基于上述理论分析及定义,研究了BDFIM 可能的运行模式、存在条件及转矩构成,指出单馈同步模式下与EESM 的异同;定性分析多层磁障与短路线圈复合转子BDFM 拓扑结构和辅助短路线圈在磁场调制行为中发挥的作用,定量给出该电机调制算子,进而讨论复合转子给磁场耦合能力等方面可能带来的有益影响;最后,总结了FSPM 与BDFM 的相似性,并统一归纳简单凸极类磁场调制电机的调制行为及转矩特性。
1 调制行为及转矩成分的定义
1.1 同步调制与异步调制
根据电机气隙磁场调制统一理论,基本电机单元可规格化为“励磁源—调制器—滤波器”三要素的级联[13]。依初始励磁源与调制器的相对状态,可将调制行为定义为同步调制与异步调制,若调制器与励磁源存在相对运动,则为异步调制;若两者保持相对静止,则为同步调制。常见的异步调制行为有笼型感应电机(Squirrel Cage Induction Machine, SCIM)短路线圈、FRPM 电机凸极转子的异步调制行为等,异步调制电机结构如图3a 所示;常见的同步调制行为有同步磁阻电机多层磁障转子、内嵌式永磁同步电机( Interior Permanent Magnet Machine, IPM)凸极转子的同步调制行为等,其调制结构如图3b 所示。两种调制行为主要差异见表1。根据表1 特性对比可知:
表1 同步调制与异步调制之间的比较
Tab.1 Comparison between synchronous and asynchronous modulation behavior
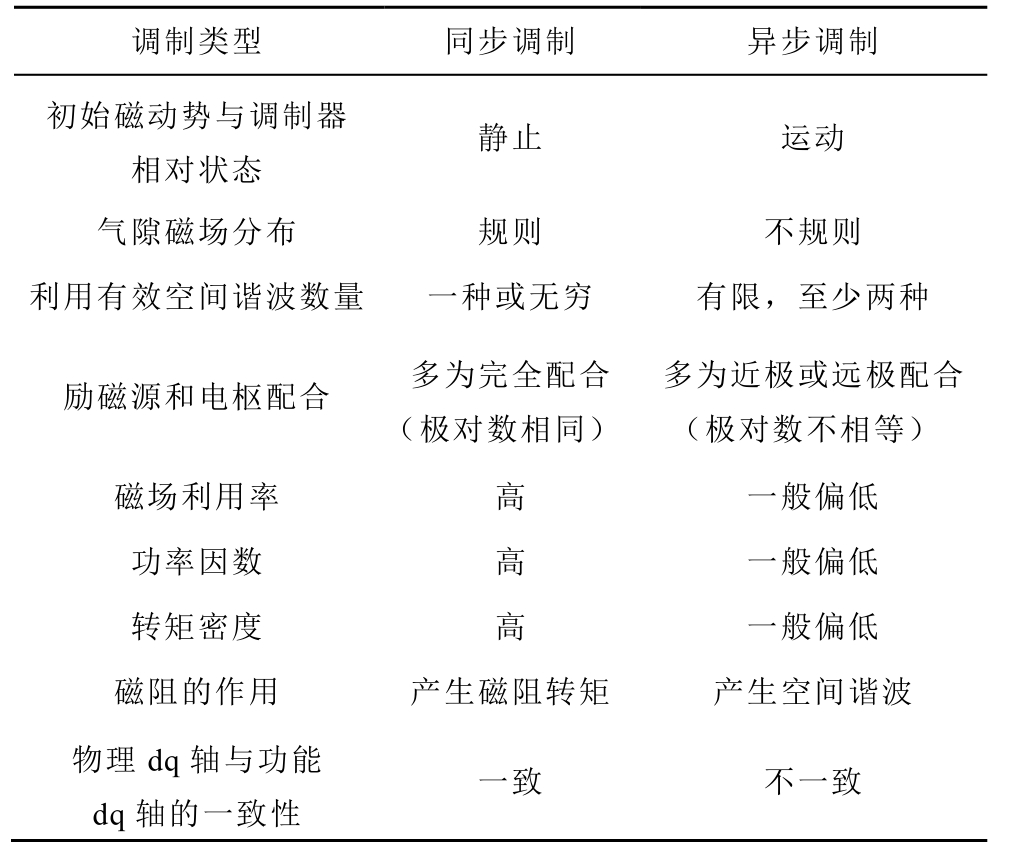
调制类型 同步调制 异步调制 初始磁动势与调制器相对状态 静止 运动 气隙磁场分布 规则 不规则 利用有效空间谐波数量 一种或无穷 有限,至少两种 励磁源和电枢配合 多为完全配合 (极对数相同) 多为近极或远极配合(极对数不相等) 磁场利用率 高 一般偏低 功率因数 高 一般偏低 转矩密度 高 一般偏低 磁阻的作用 产生磁阻转矩 产生空间谐波 物理dq 轴与功能 dq 轴的一致性 一致 不一致

图3 常见的磁场调制行为
Fig.3 The common magnetic field modulation behaviors
(1)同步调制类电机气隙磁场仅含一种有效谐波分量,多呈现规则正弦或矩形分布;而异步调制类电机气隙磁场包含大量谐波且幅值较高,分布并不规则。
(2)同步调制电机仅能利用 pf 对极有效谐波,但部分整距或接近整距电枢绕组电机例外,如有刷直流电机,其整距线圈具有很宽的频谱范围,允许矩形波初始励磁磁动势被调制后产生的几乎所有谐波分量通过,可理解为利用无穷种谐波。
(3)以FRPM 电机为例的异步调制电机可利用有限有效空间谐波,且以 pf 和  两种谐波为主,NRT 为转子极数。
两种谐波为主,NRT 为转子极数。
(4)磁场调制电机实质是牺牲了部分基波的幅值,而生成多种额外谐波分量,其中部分为能产生平均转矩的有效分量,但同样存在多种无效谐波分量,其基波磁场利用率一般较低;而传统电机除基波磁场外其余谐波磁场含量较低,其基波磁场利用率较高。
1.2 同步转矩和异步转矩分量
同步转矩与异步转矩分量的定义仅取决于建立该转矩分量的磁场来源及电机转速状态。若某转矩分量的生成机理如图4a 所示,由同一磁场来源建立,且转子与该磁场源作相对运动,即转子转速与该磁场同步速不相等,则该转矩为异步转矩;若某转矩分量由两个独立来源的极对数相同的磁场反应建立,且转子转速与两个磁场源的等效同步速相等,则该转矩为同步转矩,如图4b 所示。图中,Bf1、Bf2分别为励磁磁场、电枢磁场磁感应强度;ωf1、ωf2 分别为励磁磁场、电枢磁场的转速;ωsyn 为同步速;ωr电机转速;Te 为电磁转矩;M[Bf1]、M[Bf2]分别为励磁磁场、电枢磁场调制函数;Bf、B′f 分别为定子绕组建立的磁场、转子绕组感应磁场的磁感应强度。常见异步转矩成分有SCIM 定转子高次谐波磁场引发的异步附加转矩、BDFIM 简单异步转矩分量、双馈同步模式下异步转矩分量等;常见同步转矩成分有IPM 主电磁转矩、FSPM 等磁场调制电机转矩、BDFIM 双馈同步模式下同步转矩分量等。
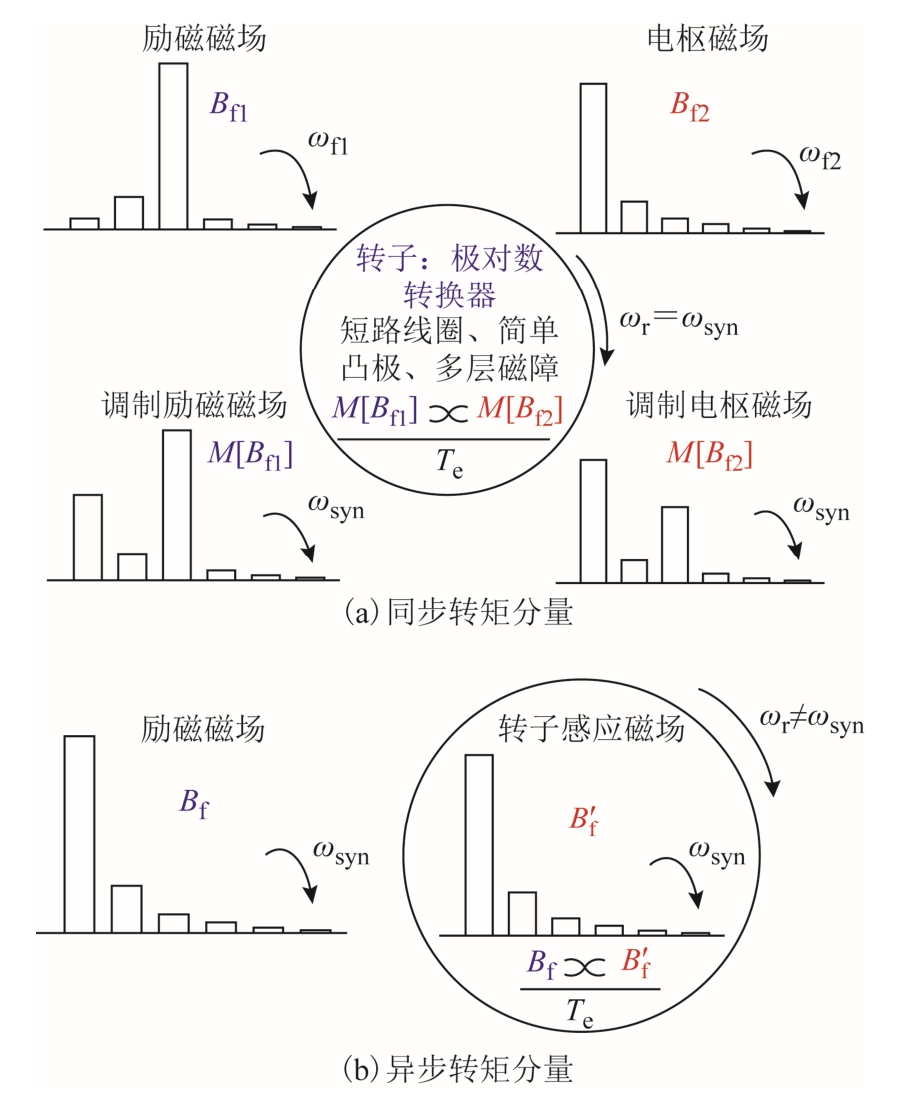
图4 同步转矩与异步转矩机理
Fig.4 Mechanism diagram of synchronous and asynchronous torque component
2 调制行为及转矩成分的关系
2.1 常见电机结构转矩成分解析
将常见电机的转矩成分归类见表2。传统电机可能利用同步调制行为或异步调制行为,但其物理dq 轴与功能dq 轴保持一致,即定转子极对数配合为完全配合;磁阻的存在仅生成磁阻转矩,并非改变气隙磁导从而产生额外有效谐波以提升平均转矩,即由磁阻调制出的谐波分量无效;故而气隙磁场中建立主电磁转矩的磁场分量仅与励磁磁场主极对数有关,即可利用的有效磁场谐波分量为一种,主电磁转矩仅包含一种同步转矩或异步转矩分量。
表2 常见电机的转矩成分定性解析
Tab.2 Qualitative analysis of torque components in common machines
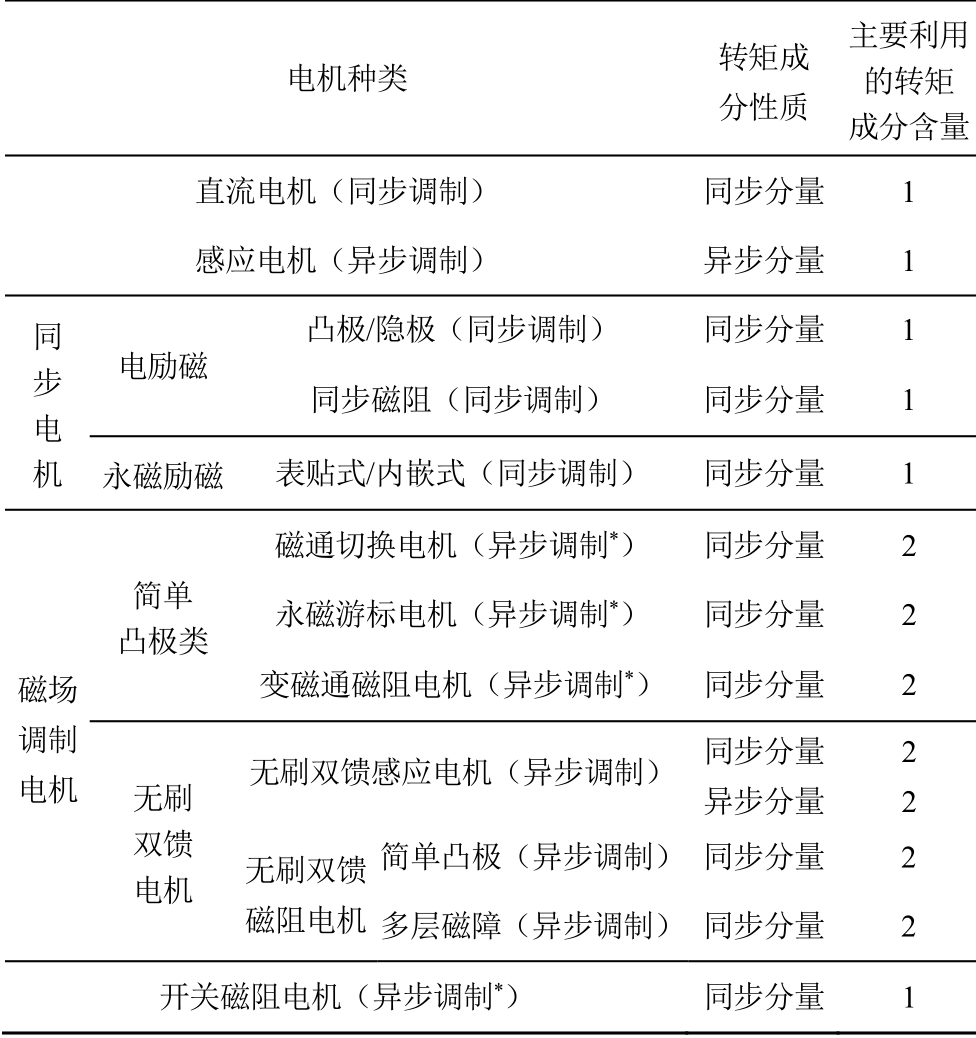
*表中仅列出改变初始磁动势幅值和空间频谱分布的主调制行为。
电机种类 转矩成 分性质 主要利用的转矩成分含量直流电机(同步调制) 同步分量 1 感应电机(异步调制) 异步分量 1 同步电机电励磁凸极/隐极(同步调制) 同步分量 1 同步磁阻(同步调制) 同步分量 1 永磁励磁 表贴式/内嵌式(同步调制) 同步分量 1 磁场调制电机简单 凸极类磁通切换电机(异步调制*) 同步分量 2 永磁游标电机(异步调制*) 同步分量 2 变磁通磁阻电机(异步调制*) 同步分量 2 无刷 双馈 电机 无刷双馈感应电机(异步调制) 同步分量异步分量2 2 无刷双馈磁阻电机简单凸极(异步调制) 同步分量 2 多层磁障(异步调制) 同步分量 2 开关磁阻电机(异步调制*) 同步分量 1
新型磁场调制电机主要利用异步调制行为,即依靠调制出的额外有效谐波以提升其平均转矩。由于励磁和电枢磁场极对数不相同,初始励磁、电枢磁动势的电角频率并不相同,因此必须满足转子转速与励磁、电枢磁场等效同步速相同,即转子转速在某一条件时,新型调制类电机能够建立励磁磁场与电枢磁场的电角频率的联系,从而发挥“磁场调制效应”[15]。另一方面,由于磁场调制现象的普遍性,无论是传统电机还是磁场调制电机,其同步速的定义应以调制后的磁场速度为准,如图4b 所示。
2.2 调制行为与转矩成分的辨证关系
由表2 可知,转矩成分性质与调制行为有关,调制行为指的是能改变初始磁动势幅值和空间频谱分布的主调制行为,具体分析如下:
(1)同步调制生成同步转矩分量。以图3a 所示的IPM 电机为例,其包含永磁励磁磁场、定子电枢磁场两个独立的磁场源;定子凸极性可以忽略不计,故为单位调制[14];初始励磁源与凸极转子保持相对静止,其调制行为是同步调制;两套磁场极对数相同并保持相对静止,且转子转速恒等于定子电枢绕组建立的旋转磁场同步速,故该IPM 电机仅包含一个同步转矩分量。
(2)异步调制生成同步转矩分量。以图3b 所示的FRPM 电机为例,定子凸极的同步调制行为仅改变静态永磁励磁磁场谐波幅值,而不影响其频谱分布[14];另一方面,由于励磁和电枢磁场极对数并不相等,则要求转子运行在两个磁场的等效同步速下,从而调制励磁磁场与调制电枢磁场能够相互作用产生平均电磁转矩。显然,FRPM 电机转子凸极对位于定子的永磁励磁源为异步调制,且主电磁转矩满足同步转矩定义,故异步调制可以生成同步转矩分量。
(3)异步调制生成异步转矩分量。参考图4b,以传统SCIM 电机为例,它仅包含一个定子磁场源,其主电磁转矩是由定子基波旋转磁场Bf 与由该磁场感应的转子电流所建立的转子基波磁场B′f 相互作用所产生,其本质是由同一磁场源建立而成;Bf与B′f 极对数相同,且无论转子实际转速是多少,B′f在空间相对于定子的转速总等于Bf 的同步转速,因而两者能够互相反应产生平均转矩;转子此刻相对于定子绕组建立的磁场作相对运动,即转子转速与定子旋转磁场同步速不相等,为异步运行(调制),故SCIM 仅包含一个异步转矩分量。
3 实例分析一:无刷双馈感应电机
3.1 运行模式及对应转矩分量
由于无刷双馈电机独特的复合特性,它可以运行在多种不同的模式下,具体见表3[16]。在级联异步模式下,两个电气端口中只有一个由交流供电,另一端口作短路处理,因而只存在一个频率子系统,且仅存在一套磁场源,故不会包含同步转矩分量。功率绕组(PW)或控制绕组(CW)短路处理相当于串接调速电阻阻值为零的特殊情形。以CW 侧短接为例,PW 通以交流电,转子相对于PW 建立的磁动势作相对运动,将在转子绕组感生磁场并与PW 磁场相互作用产生异步转矩分量。同理可知,CW 侧虽作短路处理,但同样会由于PW 建立磁场而感生极对数、频率与PW 相同的磁场,该磁场将在转子绕组感生磁场并与CW 侧磁场相互反应产生另一异步转矩分量。综上,无刷双馈电机运行于级联异步模式下,与异步电机运行原理类似,故部分文献称该状态为异步运行模式[17]。
表3 无刷双馈感应电机的运行模式及转矩成分
Tab.3 Operation mode and torque components of BDFIM

运行模式 存在条件 转矩成 分性质 转矩成分含量简单异步模式 PW(CW)交流供电, CW(PW)开路 异步分量 1 级联异步模式 PW(CW)交流供电, CW(PW)短路 异步分量 2 单馈同步模式 PW(CW)交流供电, CW(PW)直流供电 同步分量异步分量2 2 双馈同步模式PW 和CW 均为交流供电,并且满足式(1) 同步分量异步分量2 2
再以双馈同步运行模式为例,转子转速运行于PW 和CW 磁场等效同步速,使得PW 和CW 两个彼此独立的频率子系统合并为一个单一频率的系统,即满足
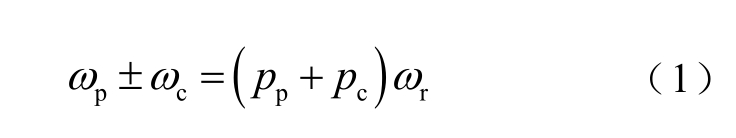
式中,ωp、ωc 分别为PW、CW 旋转磁场电角频率;ωr 为转子机械转速;pp、pc 分别为PW、CW 极对数。
图5 无刷双馈感应电机运行模式简化
Fig.5 Schematic diagram of operation mode of BDFIM
在该模式下,两个电气端口均由交流供电,并且满足双馈同步运行约束条件式(1),即PW、CW频率子系统合并为一个单频系统。由于转子相对于PW 或CW 建立的磁动势均作相对运动,故电磁转矩包含两个异步转矩分量,分别来自于功率侧和控制侧,由PW(CW)建立基波磁场和PW(CW)感应到转子产生的基波磁场相互作用产生。另一方面,PW(CW)侧磁场经转子调制后与CW(PW)侧磁场极对数相同,且频率一致、保持相对静止,相互反应生成同步转矩分量。故在双馈同步模式下,BDFIM 包含两个同步和两个异步转矩分量。
3.2 BDFIM 与EESM 的对比
部分文献指出,单馈同步模式下 BDFIM 与EESM 具有一定的相似性[18],但却未能给出具体的讨论分析。本文可从磁场调制及转矩成分的角度分析两者的异同,从而能够更好地理解传统电机与新型磁场调制电机的内在联系。单馈同步模式下BDFIM 与EESM 相似性主要体现在:
(1)磁场架构相同:两个电气端口均一套由直流供电励磁,一套由交流供电提供电枢磁场。
(2)调磁方式类似:该模式下BDFIM 可以如EESM 施加励磁、调节功率因数,其可调量只有电流幅值,故一般只能对无功功率进行调节。
(3)同步转矩分量为主:BDFIM 与EESM 均由两套独立磁场源生成转矩,且转子转速运行于等效同步速,满足生成同步转矩的条件。另一方面,当BDFIM 的PW 和CW 端电压给定时,忽略定子绕组电阻和漏电感,转子漏阻抗与转矩峰值成反比,且转子漏抗与转子电阻的比值影响异步转矩分量与同步转矩分量之间的比例[19]。其比值越大,转子漏阻抗角越接近π/2,异步分量所占比例越小。极限情况下,转子电阻为零,异步转矩分量将不出现在转矩表达式中,仅包含同步转矩分量。
BDFIM 与EESM 也存在差异性,体现在:
(1)BDFIM 可实现无刷化:BDFIM 通过调制方式实现无刷,在单馈同步模式下转子运行于亚自然同步速,能够建立PW 和CW 的单频关系。若BDFIM 运行于PW 同步速或CW 同步速,则不能正常起动工作,这也能够证明BDFIM 为异步调制行为主导的磁场调制电机,与同步电机工作原理存在本质差异。
(2)调制行为不同:EESM 转子调制器与励磁源相对静止,为同步调制,而BDFIM 为异步调制行为。
(3)转矩分量成分不同:由表2 可知,EESM 仅包含一个同步转矩分量,不包含异步转矩分量;而BDFIM 分别包含两个同步转矩和异步转矩分量。
4 实例分析二:复合转子无刷双馈电机
4.1 拓扑结构分析及磁场调制行为
在径向叠片转子铁心中加入磁障层,并在构成的磁障式转子中添加辅助短路线圈,便构成了多层磁障和短路线圈结合的复合转子[20-21],其拓扑结构如图6 所示。复合转子本质上旨在利用短路线圈绕组和多层磁障转子的双重调制增强转子的磁场转换能力,由于两个调制器与初始励磁磁动势均存在相对运动,且短路线圈调制器发挥磁场调制作用的基础就是转子运行在异步速,故该复合转子BDFM属于异步调制行为。但由于磁障结构的限制,导致辅助短路线圈导条较细且槽深较浅,导条趋肤效应明显且易饱和,使得短路线圈调制器磁场转换系数降低。
4.2 复合转子BDFM 调制算子
假设初始励磁磁动势为单位余弦
式中,p 为极对数;φ 为调制坐标系下的机械角度;ω 为定子电流频率。则多层磁障调制器对式(2)调制效果可表示为[22]
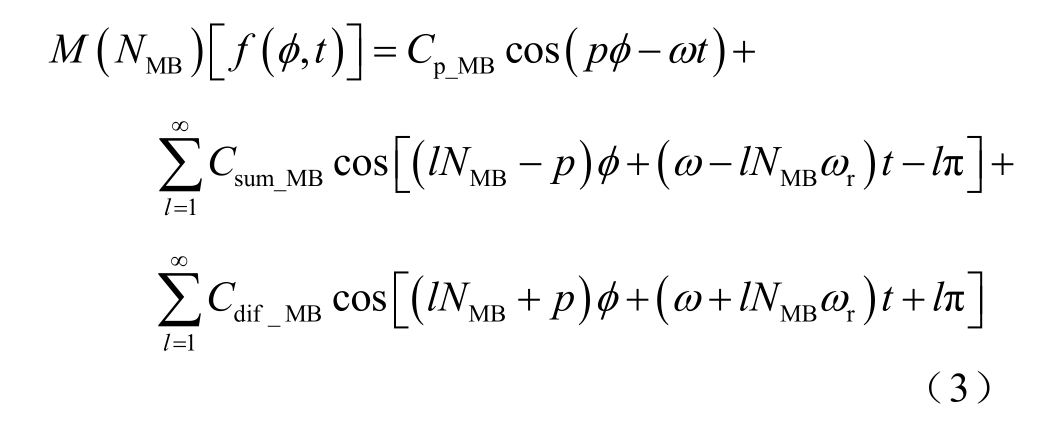
式中,NMB 为多层磁障极对数;Cp_MB、Csum_MB、Cdif_MB分别为p 对极、lNMB-p 对极、lNMB+p 对极为对应谐波的磁场转换系数;l 为谐波次数。
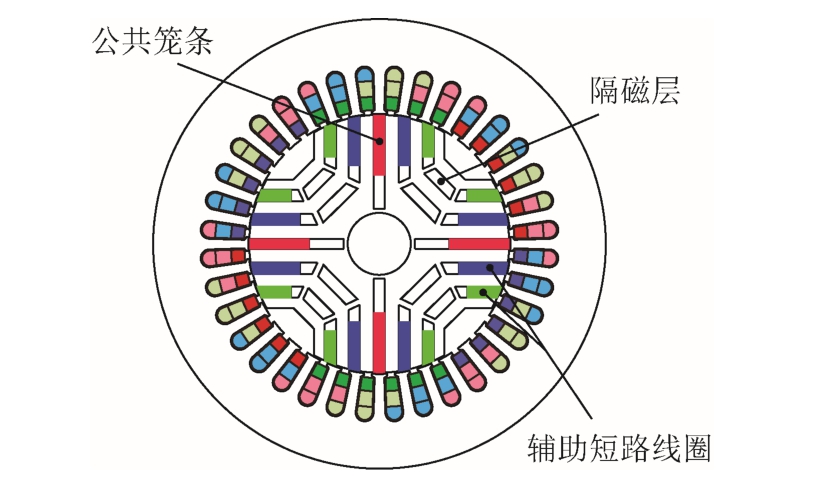
图6 复合转子无刷双馈电机拓扑结构
Fig.6 Topology of BDFM with composite rotor
短路线圈调制器对式(2)调制效果可表示为
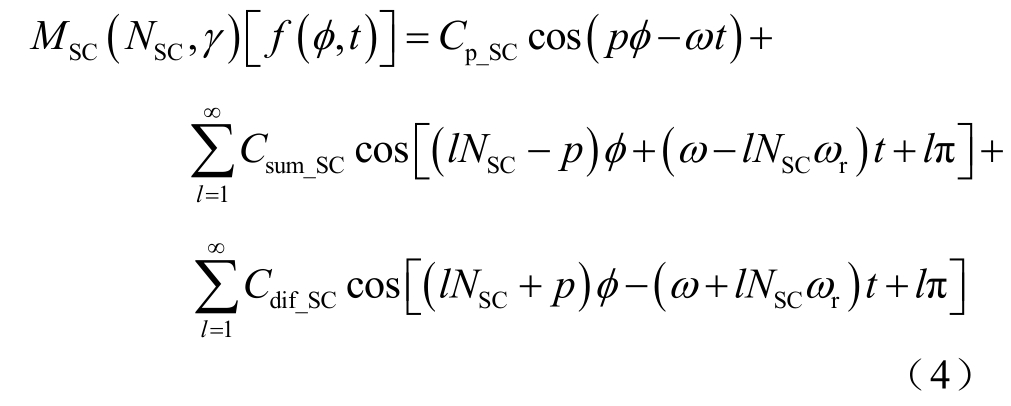
式中,NSC、γ 分别为短路线圈极对数和跨距; p_SCC 、![]() 分别为p 对极、 SClN p- 对极 SClN p+对极对应的谐波磁场转换系数。
分别为p 对极、 SClN p- 对极 SClN p+对极对应的谐波磁场转换系数。
由于复合转子中NMB 与NSC 相等,即多层磁障和短路线圈调制器产生的调制励磁磁动势频谱一致,满足空间叠加的条件。其调制算子为多层磁障和短路线圈调制算子的线性叠加,即
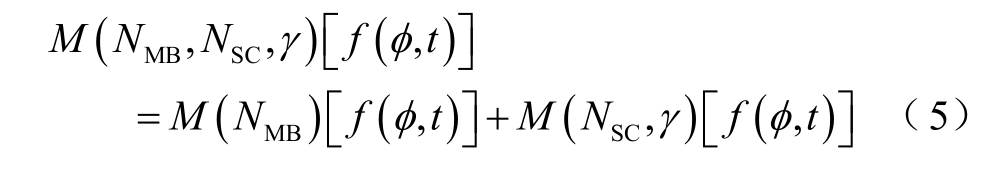
这与文献[20]中将复合转子两套调制器引发的气隙磁导变化线性叠加的结论一致。因此复合转子本质上是利用多层磁障和短路线圈的共同异步调制行为,相比普通多层磁障转子BDFM 增加了一套短路线圈调制器,从而能够提升相应的磁场转换系数,增强磁场转换能力即改善磁场调制效果。
由式(3)和式(4)可知,p 和lNMB-p 次有效谐波幅值得到提升,相对应的磁场转换系数为两种调制器系数的代数和,反映了磁场转换能力的增强。而无效谐波lNMB+p 次幅值变化规律未知,取决于该电机转子极数与转速,如式(3)和式(4)第三项所示,由两个调制器产生的lNMB+p 次谐波虽然极对数相同,但存在相位差。若相位差配合得当,则该次谐波在气隙中幅值较小;反之则可能引入幅值较高的无效谐波,给磁场调制带来不利影响。复合转子BDFM 的调制行为如图7 所示,其频谱如图8 所示。

图7 复合转子无刷双馈电机磁场调制行为
Fig.7 Modulation behavior of BDFM with composite rotor
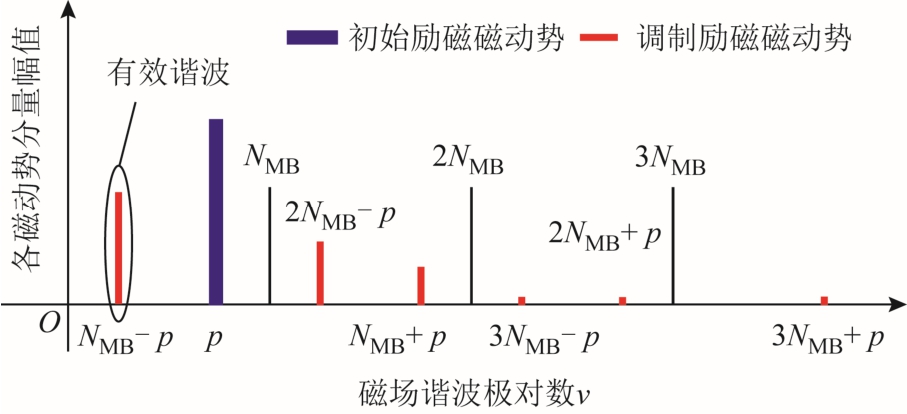
图8 复合转子无刷双馈电机频谱变化
Fig.8 Spectrum shift of BDFM with composite rotor
4.3 复合转子BDFM 有益效果及转矩分量
结合多层磁障与短路线圈调制特征,且考虑到 复合转子的本质,可总结其调制规律如下:
(1)复合转子能够有效提升磁场转换系数Cp 和Csum,从而改善磁场调制效果。
(2)复合转子调制器的磁场转换能力与极对数配合关系密切:在等效极对数NMB 相同的情况下,PW 与CW 极对数越接近,磁场转换能力越强,PW与CW 之间经转子形成的间接耦合关系越紧密。
(3)在等效极对数NMB 相同的前提下,当PW与CW 极对数相差为1 时,磁场转换能力最强,但实际中通常选择极对数相差为2 的组合以避免不平衡磁拉力的不良影响。
(4)复合转子BDFM 的PW 和CW 极对数以相同倍数变化并不会影响其磁场转换能力。
复合转子BDFM 定子绕组电感特性及转矩密度如式(6)~式(8)所示[22]。
CW 主自感可表示为
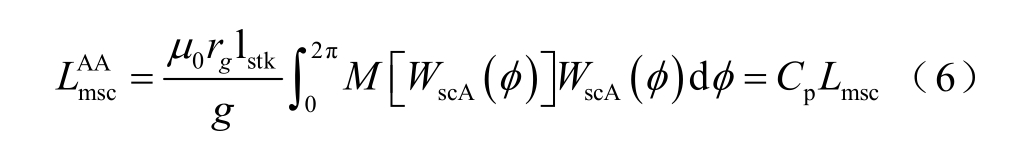
式中,μ0 为真空磁导率;rg 为气隙半径;lstk 为电机有效轴长;g 为气隙长度;M[WscA(φ)]和WscA(φ)分别为调制绕组函数和初始绕组函数;Lmsc 为自感常数量。
PW 与CW 相间互感可表示为
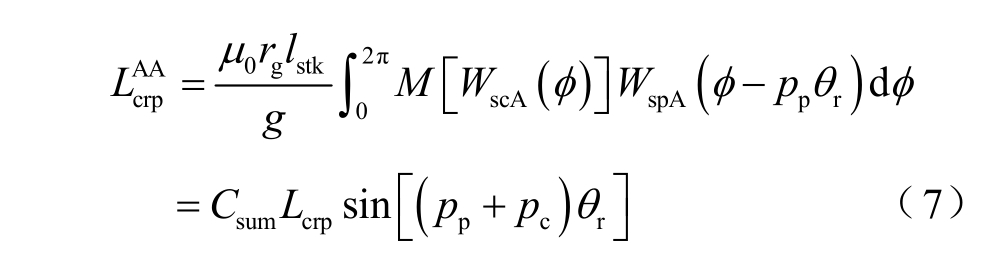
式中,θr 为转子机械位置角;Lcrp 为互电感常数量。
复合转子BDFM 转矩密度为

式中, f[ ]M B 和 fK 分别为调制磁负荷和电负荷;![]() 为电、磁负荷之间的功率因数。
为电、磁负荷之间的功率因数。
由于PW 与CW 之间的主自感、互电感分别由极对数为p、NMB-p 次磁场分量产生,磁场转换系数Cp 和Csum 的提升能够增加定子绕组电感幅值,从而反映出磁场调制效果的改善。同样道理,有效气隙磁通密度幅值增大,相应调制磁负荷幅值提升,平均转矩也会增加,这与文献[23]给出的结论一致。
另一方面,异步转矩分量的建立需要“感应额外磁场”,即要求转子中存在闭合回路以建立感应电流,闭合回路的形式可以为短路线圈,也可以是绕线结构。换言之,在单馈同步、双馈同步模式下,多层磁障转子BDFM 调制行为虽为异步调制,但无法建立异步转矩分量,其电磁转矩为两个同步转矩分量。而复合转子BDFM 由于转子增加了短路线圈闭合回路,拥有了类似BDFIM 的转矩特性,故电磁转矩包括两个同步转矩分量和两个异步转矩分量。额外增加的异步转矩分量也能够说明复合转子BDFM 转矩能力的提升。
5 实例分析三:磁通切换电机
FSPM 电机可认为是BDFM 的一种特殊情形,即永磁体阵列被能够产生相同磁动势分布的单相绕组所代替,此时 FSPM 电机等效为一台双凸极BDFM,其CW 为单相集中绕组、PW 为分数槽集中绕组,电机始终工作在自然同步转速。FSPM 电机转矩生成机理如图9 所示,图中,NRT 为转子极数。其励磁、电枢磁场主极对数不相同,但转子转速与两个磁场的等效同步速相同,满足产生同步转矩的条件,其中,调制电枢磁场与初始励磁磁动势极对数相同的磁场相互作用产生“基础”同步转矩分量,该分量与传统永磁同步电机利用励磁磁动势基波分量产生转矩机理相似;而调制励磁磁场中与初始电 枢磁动势极对数相同的磁场相互作用产生额外的“有效”同步转矩分量Te_eff,且正是由于能够利用除基波外的有效谐波磁通密度,FSPM 电机平均转矩才得以提升。
FSPM 电机以及FRPM 电机等简单凸极磁场调制电机磁场调制行为和转矩成分可描述为:
(1)永磁体阵列建立理想方波的初始励磁磁动势。
(2)初始励磁磁动势被定(转)子凸极同步调制,同步调制的作用使得基波幅值约变为原来的一半,但谐波的幅值都有明显增加,且被定(转)子齿调制后的励磁磁动势分布只包含一类谐波分量,其极对数为永磁体阵列极对数的奇数倍。
(3)随后励磁磁动势被转(定)子凸极异步调制,调制磁动势在等效气隙中产生一系列谐波,且包含三类谐波分量,其极对数分别为vp、vp+lNR(S)T 和vp-lNR(S)T,其幅值可以由三个磁场转换系数Cp、Csum和Cdif 进行表征。
(4)电枢绕组会选择性地与有效磁场谐波分量反应产生感应电动势,当与感应电动势频率相同的对称电流通入电枢绕组时便产生电磁转矩。
(5)由于简单凸极类磁场调制电机同时存在同步、异步调制行为,其中,同步调制行为仅改变初始励磁磁动势的幅值,而不影响气隙磁场频谱分布;而正是由于异步调制行为的存在,使得转子运行在励磁、电枢磁场等效同步速下,从而相互作用产生平均电磁转矩。
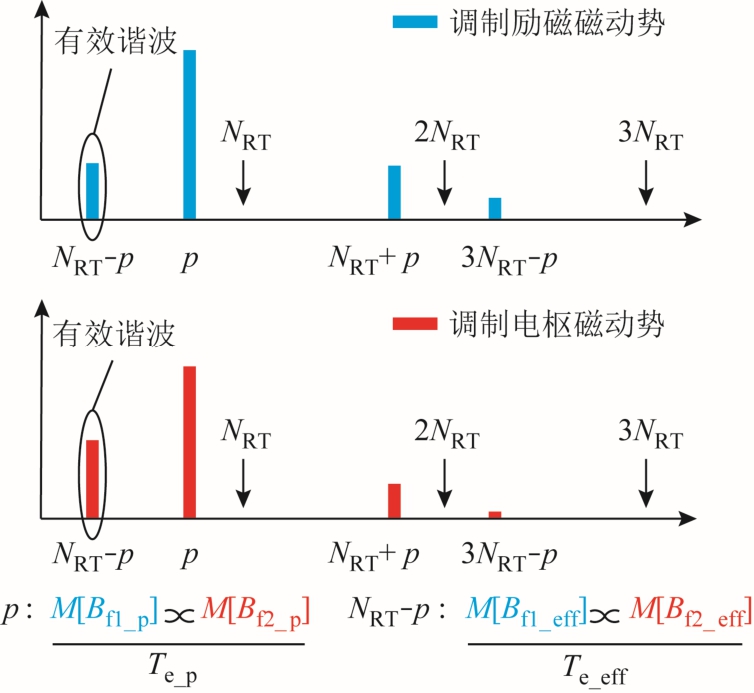
图9 磁通切换电机转矩生成机理
Fig.9 Torque production mechanism of FSPM
6 结论
本文定义、分析、归纳了广义磁场调制电机中的调制行为与转矩成分,并指出同步/异步调制均能够分别生成同步转矩分量,而异步调制可以生成异步转矩分量。基于此,研究了典型磁场调制电机的磁场调制行为和转矩成分。分析了BDFIM 可能的运行模式、存在条件及转矩构成,归纳BDFIM 与EESM 的相似性及差异性,从磁场调制行为和转矩成分的角度研究了调制类电机和传统电机的内在联系。总结了FSPM 电机与BDFM 的相似性,并统一描述了以FSPM 电机为代表的简单凸极类磁场调制电机的调制行为及转矩特性。
另一方面,作为电机三要素之一,调制器决定着电机调制磁动势分布规律、气隙磁场的谐波含量以及工作波阶次等,对磁场调制效果存在直接影响。本文定性分析了复合转子BDFM 拓扑结构和附加短路线圈在磁场调制行为中发挥的作用,指出该电机调制算子可叠加的本质原因,进而定量分析了复合转子给磁场耦合作用、电感特性、转矩密度等方面可能带来的有益影响。然而,如何通过合理分配混合式结构中几种调制器之间的比例,充分利用复合气隙磁场调制行为增强调制器磁场耦合能力,从而改善磁场调制效果,以使电机达到最佳电磁性能,是一个重要的理论问题,值得继续深入研究。
总之,本文基于磁场调制行为分析调制器之间复合调制的可能性,对理解和揭示调制器演化形式与单独作用机理具有深远意义,为指导电机系统的拓扑创新、性能分析、运行控制与综合设计奠定了理论基础。
[1] 程明, 韩鹏, 魏新迟. 无刷双馈风力发电机的设计、分析与控制[J]. 电工技术学报, 2016, 31(19): 37-53.
Cheng Ming, Han Peng, Wei Xinchi. Design, analysis and control of brushless doubly-fed generators for wind power application[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 37-53.
[2] 陈正方, 王淑红, 高若中, 等. 一种笼型转子无刷双馈电机的磁链观测方法[J]. 电工技术学报, 2018, 33(23): 5402-5409.
Chen Zhengfang, Wang Shuhong, Gao Ruozhong, et al. A flux linkage observation method of cage-rotor brushless doubly-fed machine[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5402-5409.
[3] Lawrenson P J, Stephenson J M, Blenkinsop P T, et al. Variable-speed switched reluctance motors[J]. IEEE Proceedings B-Electric Power Application, 1980, 127(4): 253-265.
[4] 马雯旻, 王杜, 曲荣海, 等. 基于有取向硅钢的轴向磁通开关磁阻电机准三维解析分析与设计[J]. 电工技术学报, 2018, 33(17): 4069-4077.
Ma Wenmin, Wang Du, Qu Ronghai, et al. Quasithree-dimensional analysis and design of an axial flux switched reluctance motor based on grain oriented silicon steel[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4069-4077.
[5] Cheng Ming, Hua Wei, Zhao Wenxiang, et al. Overview of stator-permanent magnet brushless machines[J]. IEEE Transactions on Industrial Electronics, 2011, 58(11): 5087-5101.
[6] 丁强, 王晓琳, 邓智泉, 等. 大气隙磁通切换无轴承永磁电机径向力绕组设计与比较[J]. 电工技术学报, 2018, 33(11): 2403-2413.
Ding Qiang, Wang Xiaolin, Deng Zhiquan, et al. Design and comparison of radial force winding configurations for wide air-gap flux-switching bearingless permanent-magnet motor[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2403-2413.
[7] Toba A, Lipo T A. Novel dual-excitation permanent magnet vernier machine[C]//Conference Record of IEEE IAS Annual Meeting, Phoenix, AZ, USA 1999, 4: 2539-2544.
[8] 李岱岩, 白保东, 杨晨, 等. 基于调磁块阵列的永磁游标电机研究[J]. 电工技术学报, 2018, 33(2): 359-366.
Li Daiyan, Bai Baodong, Yang Chen, et al. Study of permanent magnet vernier machine by using magnetic tuning block array[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 359-366.
[9] Chau K T, Zhang Dong, Jiang J Z, et al. Design of a magnetic-geared outer-rotor permanent-magnet brushless motor for electric vehicles[J]. IEEE Transactions on Magnetics, 2007, 43(4): 2504-2506.
[10] 周鹗. 电机学[M]. 北京: 水利电力出版社, 1988.
[11] 汤蕴璆. 电机学—机电能量转换[M]. 北京: 机械工业出版社, 1982.
[12] 程明, 张淦, 花为. 定子永磁型无刷电机系统及其关键技术综述[J]. 电工技术学报, 2014, 24(29): 5204-5220.
Cheng Ming, Zhang Gan, Hua Wei. Overview of stator permanent magnet brushless machine systems and their key technologies[J]. Transactions of China Electrotechnical Society, 2014, 24(29): 5204-5220.
[13] Cheng Ming, Han Peng, Hua Wei. General airgap field modulation theory for electrical machines[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6063-6074.
[14] Cheng Ming, Wen Honghui, Han Peng, et al. Analysis of airgap field modulation principle of simple salient poles[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 2628-2638.
[15] Wu Z Z, Zhu Z Q. Analysis of magnetic gearing effect in partitioned stator switched flux PM machines[J]. IEEE Transactions on Energy Conversion, 2016, 31(4): 1239-1249.
[16] Han Peng, Cheng Ming, Wei Xinchi, et al. Modeling and performance analysis of a dual-stator brushless doubly-fed induction machine based on spiral vector theory[J]. IEEE Transactions on Industrial Application, 2016, 52(2): 1380-1389.
[17] 张凤阁, 王凤翔, 王正. 不同转子结构无刷双馈电机稳态运行特性的对比实验研究[J]. 中国电机工程学报, 2002, 22(4): 52-55.
Zhang Fengge, Wang Fengxiang, Wang Zheng. Comparative experiment study on the performance of doubly-fed brushless machine with different rotor structures[J]. Proceedings of the CSEE, 2002, 22(4): 52-55.
[18] 于思洋. 兆瓦级复合转子无刷双馈风力发电机分析与设计方法研究[D]. 沈阳: 沈阳工业大学, 2018.
[19] 韩鹏. 双定子无刷双馈电机设计与驱动控制[D]. 南京: 东南大学, 2017.
[20] Zhang Fengge, Wang Hao, Jia Guanglong, et al. Effects of design parameters on performance of brushless electrically excited synchronous reluctance generator[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 9179-9189.
[21] 蒋晓东, 张凤阁, 周党生, 等. 双定子笼障转子无刷双馈发电机冷却空气流变特性数值分析[J]. 电工技术学报, 2019, 34(3): 466-473.
Jiang Xiaodong, Zhang Fengge, Zhou Dangsheng, et al. Numerical analysis of cooling air flow characteristic for double stator cage-barrier rotor brushless doubly-fed generator[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 466-473.
[22] Wen Honghui, Cheng Ming, Jiang Yunlei, et al. Analysis of airgap field modulation principle of flux guides [C]//IEEE Energy Conversion Congress and Exposition (ECCE), Portland, USA, 2018: 7302-7309.
[23] Zhang Fengge, Yu Siyang, Wang Yutao, et al. Design and performance comparisons of brushless doubly fed generators with different rotor structures[J]. IEEE Transactions on Industrial Electronics, 2019, 66(1): 631-640.