0 引言
对于众多具有直流特性的分布式电源和直流负载，将其通过DC-DC 变换器组成直流微电网是一种高效的能源利用方式。相比于交流微电网，由于省略了AC-DC 或DC-AC 中间环节，且无需考虑无功功率和谐波等问题，因此，直流微电网具有更高的效率和较低的控制复杂度[1]。而对于一些偏远低负荷地区的供电，考虑到输电成本较高的原因，可以通过组建孤岛型直流微电网解决当地居民的用电问题。但由于缺少大电网的支撑，需要利用储能系统来稳定直流母线电压。不同于由单一储能介质组成的储能系统，混合储能系统（Hybrid Energy Storage Systems, HESS）兼顾了功率密度高、能量密度大和运行寿命长的特点，近些年得到了广泛的关注[2-3]。
针对混合储能的控制问题，文献[4]提出了一种无互联通信的分层控制策略，其利用电压变化率作为全局信息载体，实现蓄电池和超级电容的功率分配，并由二次控制对底层控制进行修正补偿。文献[5]对母线电压进行分级，并利用多滞环控制和积分辅助控制，确定HESS 的工作方式。上述研究主要是围绕HESS 内部的功率分配问题，当直流微电网中含有多个HESS 时，就涉及HESS 间的控制问题。利用集中控制器，通过采集所有HESS 的信息并优化得出各自的功率需求，可以实现其协调经济运行，但集中式控制对通信要求较高，且灵活性和可靠性较差[6]。文献[7]则提出了一种分散式的HESS 控制方法，蓄电池和超级电容分别采用虚拟电阻和虚拟电容下垂控制，根据不同的虚拟参数实现不同和相同储能介质间的功率分配。文献[8]同样采用分散式控制结构，超级电容采用的是积分下垂控制，其本质上与虚拟电容下垂控制相同，但同样未考虑线路电阻的影响。不同于集中式控制，分布式控制不存在单点失效的风险，具有较高的可靠性。而相比于分散式控制，由于存在通信网络，可以实现协调配合，因此又具有较高的经济性。文献[9]在文献[7]基础上增加了二次电压调节，利用相邻蓄电池间的信息，控制其平均电压为额定值以改善线路电阻和虚拟电阻造成的电压偏差。而文献[10]同样考虑了线路电阻的影响，其利用分布式一致性理论，超级电容控制直流母线电压和自身荷电状态（State of Charge, SOC），蓄电池则负责调控超级电容端电压以及自身的SOC。
分布式控制器之间一般采用传统的通信方式，即时间触发通信，其以固定的周期进行采样和通信，并更新控制器的输出信号。在实际应用中，由于通信带宽有限，希望通信次数尽量的少。此外，为了延长控制器的使用寿命，也应减少控制器更新频率。近年来，出现了一种非周期采样控制方式——事件触发控制，其在保证控制性能的同时，降低了通信次数，在一定程度上避免了网络拥塞现象的出现[11]。且该控制对于非正常通信情况下的延时、数据丢包均具有较强的鲁棒性[12-13]，因此是一种较为高效的控制方式。这里需要说明的是，本文的研究重点是正常通信情况下多组HESS 的事件触发控制。文献[14]将事件触发引入到了二次电压控制中，避免了分布式电源间的连续通信。文献[15]为实现电压调节和电流均分，提出一种非线性的分布式控制器，并将触发函数与非负阈值相结合，改善了稳态触发灵敏度，但其在建立模型时需要提前知道线路参数。以上研究均采用基于连续通信和检测的触发控制，在得到触发函数后，还需要证明该触发控制系统具有正的最小事件间隔时间（排除Zeno 现象），但该证明过程往往较为复杂，特别是当系统存在外部干扰时，可能无法排除该现象[16]。为解决该问题，可以在现有时间触发机制的基础上，周期性地进行事件触发检测，从根本上避免发生Zeno 现象[17-18]。
不同于以上研究，本文以HESS 作为一个独立系统，提出一种基于事件触发机制的HESS 分层协调控制方法。底层控制采用虚拟电阻下垂控制，利用低通滤波器实现对蓄电池和超级电容的功率分配，并提出基于蓄电池SOC 的虚拟电阻调节和基于超级电容SOC 的电流补偿策略，实现HESS 协调安全运行。分布式控制层为下垂控制层提供电压补偿项，以同时实现对电压调节和电流均分的控制目标。为节约通信资源以及避免事件触发可能存在的Zeno 现象，提出了一种基于周期性通信的分布式事件触发控制方法，其利用Lyapunov 稳定理论推导出仅含有HESS 自身状态偏差量和相邻HESS 最近触发时刻状态量的事件触发函数，并通过设定触发函数的预判阈值，进一步减少了系统稳态运行时的通信次数。
1 系统构成
本文以孤岛型直流微电网为研究对象，其典型结构如图1 所示。该微电网含有光伏发电系统、直流负载以及多个HESS，均通过电力电子变换器与直流母线相连，并计及分布式电源与直流母线之间的线路电阻。同时，为实现多个HESS 间的分布式协调控制，还包含相应的通信网络。
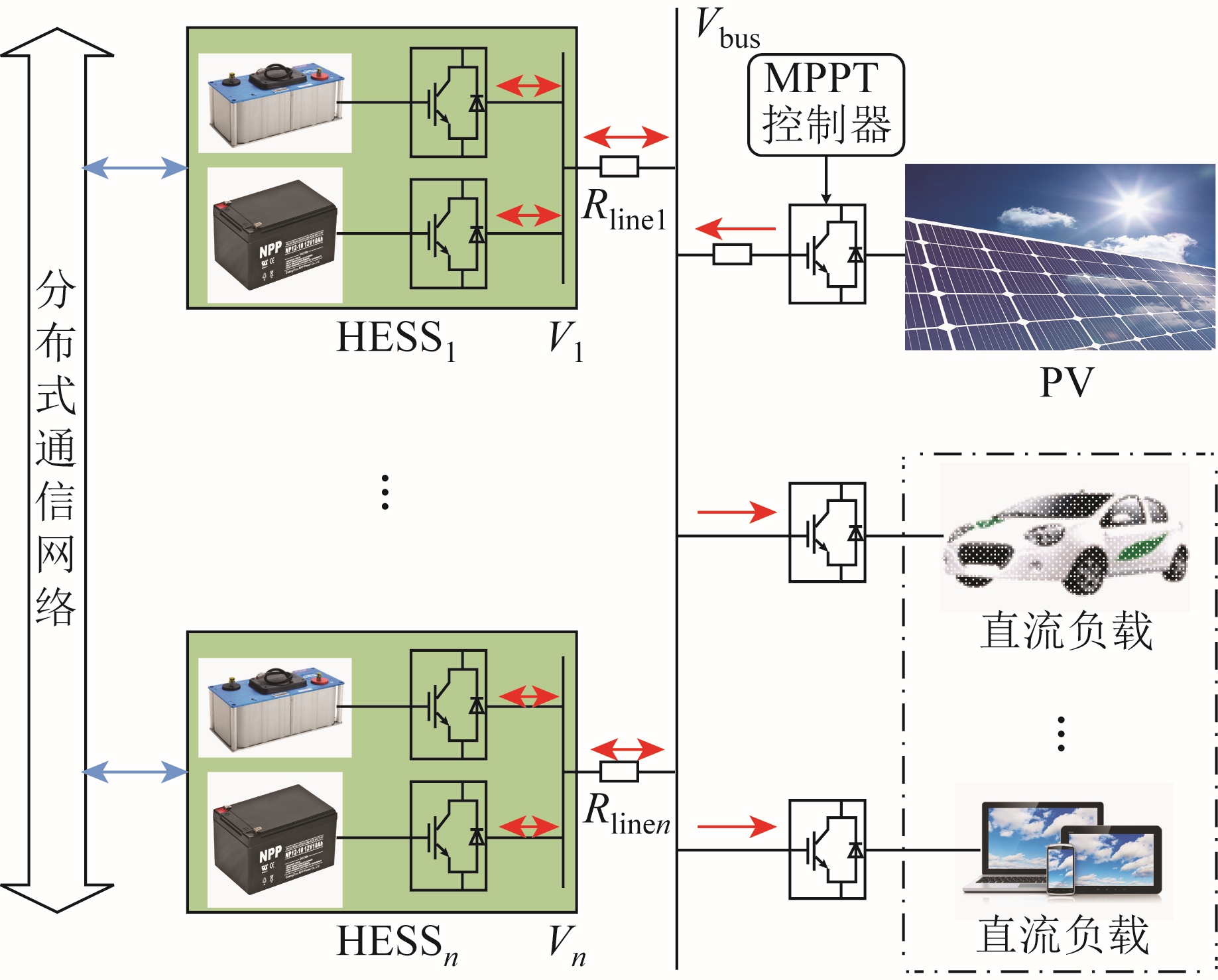
图1 含多混合储能系统的直流微电网
Fig.1 DC microgrid structure with multiple HESSs
为充分利用新能源，光伏系统工作于最大功率点跟踪（Maximum Power Point Tracking, MPPT）模式，其不参与HESS 间的分布式控制。HESS 则用于维持直流母线电压的稳定，解决供需两侧的随机性问题。不同于文献[19]中的HESS 结构，图1 中是一种模块化的储能结构，每个储能系统均由超级电容储能单元和蓄电池储能单元组成，并作为整体接入直流微电网，不同的HESS 间根据SOC 实现功率的协调分配。当负载或光伏系统发生突变时，HESS 内部由超级电容提供瞬时性的功率支撑，蓄电池则承担较为平缓的低频功率分量。
相对于直流微电网的物理层，图1 所示通信网络为信息层，通过稀疏通信网络可以实现相邻HESSi间信息的直接交换，以及非相邻HESSi 间信息的间接交换。利用图论理论对网络层进行抽象，本文所涉及的通信网络用无向图G=(V, E)描述，不考虑平行边和自回路。集合V 中的元素称为顶点或节点，顶点数量等于所接入的HESS 数量；集合E 中的元素称为边，表示HESSi 间存在直接的通信链路。对于一个顶点集
则称顶点i 与顶点j 相邻[20]。
2 混合储能系统分层协调控制
为实现超级电容与蓄电池的分频控制以及HESS 间的分布式控制，同时保证HESS 具有较好的可持续性，本节将介绍一种基于SOC 的直流微电网多HESS 分层协调控制方法。
2.1 HESS 下垂控制层
直流微电网中基于虚拟电阻的下垂控制函数为
式中，Vref 为直流母线额定电压；
为下垂控制器输出的参考电压；Rvi 为虚拟电阻；Ii 为HESS 电流。
在分布式控制系统中通过设置不同的虚拟电阻，可以实现直流微电网中不同分布式电源的功率分配。考虑图1 中的并联结构并计及线路电阻Rlinei，可以得到不同HESS 输出电流的关系为
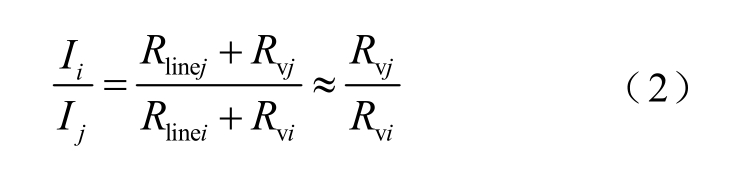
当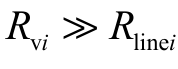
时，HESS 输出电流与虚拟电阻近似成反比，即
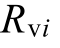越小的HESSi 所承担功率越大。因此通过调整参数Rvi 就可以实现功率在多个HESS间的比例分配。
2.1.1 基于蓄电池SOC 的虚拟电阻调节
当Rvi 设置较大时，虽然可以保证较高的功率分配精度，但会导致较大的稳态电压偏差。为使电压偏差满足电网运行要求，Rvi 需满足
式中，
为HESSi 虚拟电阻上限值；
换流器的额定电流；ΔVmax 为母线的最大允许电压偏差，本文取电压波动范围为额定电压的±5%。
HESS 中超级电容单元仅提供瞬时功率支撑，蓄电池单元承担低频功率分量。同时，又由于超级电容成本相对较高，为兼顾储能系统的经济性，往往配置蓄电池的容量远大于超级电容的容量。因此，对于HESSi 中Rvi 的设置，以HESSi 中蓄电池的SOC作为参考依据。考虑到蓄电池SOC 变化较为缓慢，且需同时满足式（3）约束条件，可采用式（4）计算Rvi 以实现较为合理的功率分配。
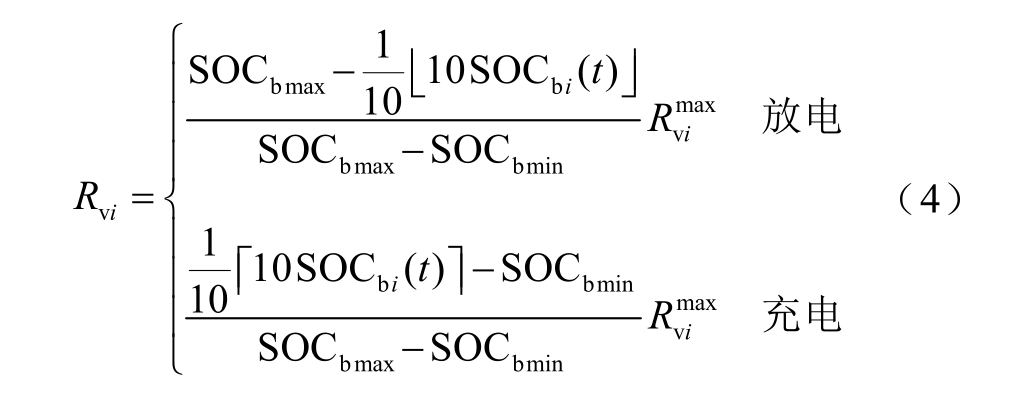
式中，
分别表示向下、向上取整运算；
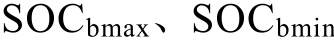分别为SOC 上、下限值，本文设置SOC 安全运行区间为[0.1, 0.9]。当HESS 既不充电也不放电时，Rvi 保持不变。
2.1.2 基于超级电容SOC 的电流补偿
虽然超级电容仅承担高频能量，但由于其容量较小，长时间运行时其SOC 可能接近SOC 上、下限。为避免影响HESS 的正常运行，需在必要时对超级电容进行调控。文献[7,9]均采用一种包含超级电容SOC 自恢复的控制方法，当发生阶跃变化后超级电容SOC 可以恢复至起始值。该方法虽然可以保证超级电容运行在安全区间，但降低了超级电容的容量利用率，且是一种被动控制。
为了充分利用超级电容的容量，将采用下述调节策略对超级电容SOC 进行补偿，并使其SOC 运行在上、下限内，保证HESS 正常运行，见图2 中的SOC 补偿调节模块。其中，超级电容SOC 参考值如式（5）所示，当其SOC 运行在安全区间内，电流补偿项δIi 为0，而当SOC 触及上、下限后δIi为非0 值。
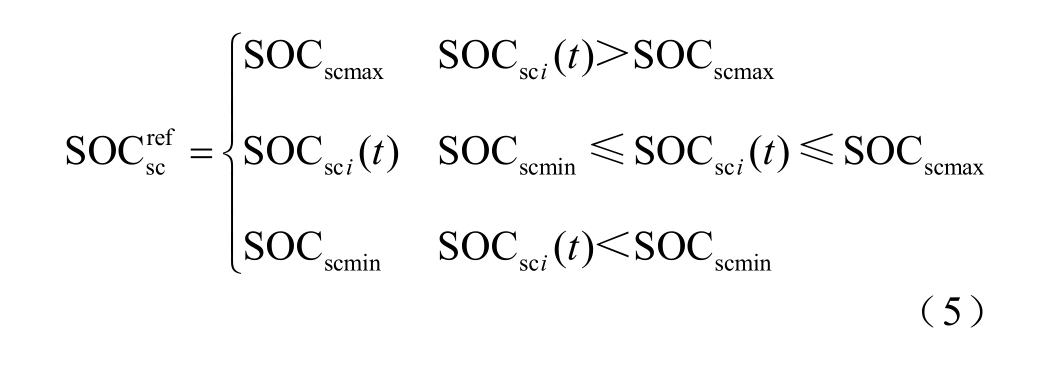
上述HESS 下垂控制层的控制框图如图2 所示，为实现HESS 中蓄电池（bat）与超级电容（sc）的协调配合，将电压环PI 控制器输出经一阶低通滤波器分解为蓄电池和超级电容的电流环PI 控制器参考值。其中，Vi 为HESSi 输出端电压，ui 为分布式控制层中所得到的电压补偿项。
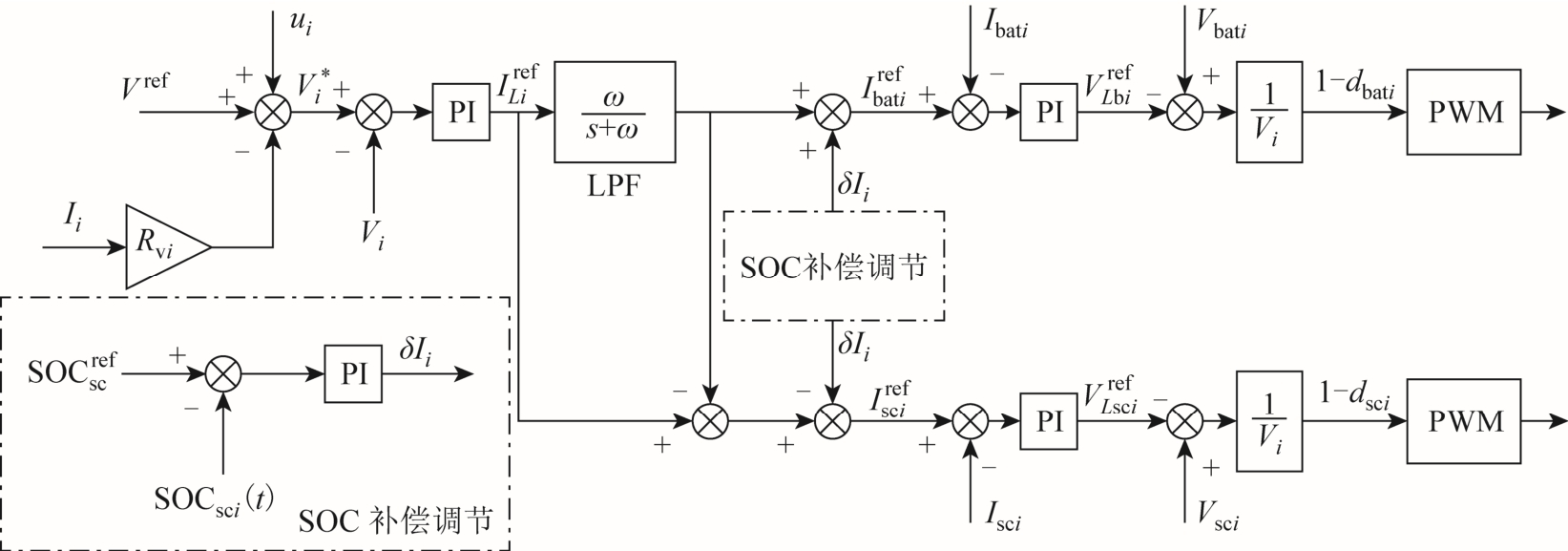
图2 HESS 下垂控制层
Fig.2 Droop control layer of HESS
2.2 HESS 分布式控制层
基于虚拟电阻的下垂控制虽然可以实现多个HESS 间的分布式控制，但由于线路电阻的存在，无法实现功率的精确分配，降低了微电网运行的经济性。因此，通过引入稀疏通信网络实现相邻HESS 间的信息交换，以改善相互间的协调性能和直流母线的稳态电压将是本节论述的重点。HESS分布式控制层包含两部分：平均电压调节和比例电流调节。
2.2.1 平均电压调节
当HESS 放电时，由于虚拟电阻Rvi 的存在，HESS 输出端电压低于额定电压且各不相等，经过线路电阻后导致母线电压进一步降低。为减弱该影响，可以使各HESS 输出端电压的平均值等于额定电压，故定义平均电压观测器为[21]
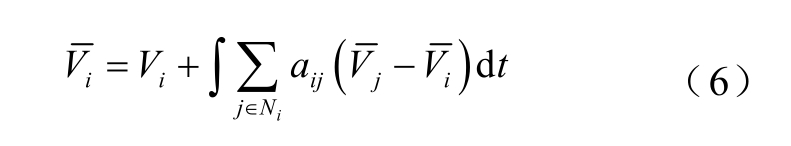
式中，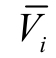
为HESSi 输出端平均电压；Ni 为HESSi 相邻储能单元的集合；aij 为与通信网络相关联的邻接矩阵A 的元素[22]。
将平均电压观测器输出与额定电压相比较，并送入积分控制器可得到电压补偿项
2.2.2 比例电流调节
由式（2）可知，期望各HESS 输出电流按给定虚拟电阻分配，即满足式（7）所示控制效果。
但是由于线路电阻存在且未知，下垂控制层无法实现该目标，为此引入比例电流调节模块。定义比例电流差值为
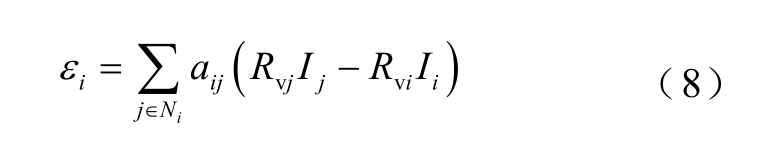
将该比例电流差值经积分控制器调节，可以得到电压补偿项
。因此，图2 中的ui 为
在式（1）中加入电压补偿项ui，可得到电压环参考值为
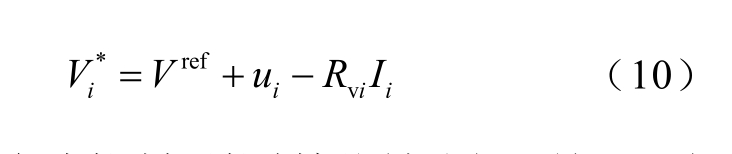
HESS 分布式控制层控制框图如图3 所示。由式（6）和式（8）可以看出，实现该层控制目标仅需要与相邻HESS 交换信息，并不存在集中控制器，是一个完全分布式的结构。从式（10）可以知道，该电压补偿项是对下垂控制的补充，当通信网络失效时，并不影响下垂控制层的正常运行。
图3 HESS 分布式控制层
Fig.3 Distributed control layer of HESS
3 分布式事件触发控制
上述分布式控制虽然可以实现对母线电压以及HESS 输出功率的有效调节，但是需要相邻HESS间进行周期通信。特别是当系统处于稳态时，控制信号变化不大，该周期通信过程并非必要，且占用了大量的通信资源，是一种经济性较差的被动控制方式。基于前文的控制结构，本节将介绍一种基于周期通信的分布式事件触发控制方式，该事件触发机制是建立在Lyapunov 稳定性理论上的，且与直流微电网状态密切相关，其仅在满足事件触发函数时发生通信并更新控制输出，在一定程度上降低了对通信资源的占用，是一种具有应用前景的主动控制方式。
3.1 事件触发函数设计
与传统固定周期的采样控制方式不同，事件触发控制只在某些特定时刻进行信号采样和传递。为避免Zeno 现象的发生，即避免在有限时间内发生无数次事件触发的现象，将采用一种建立在传统固定周期采样控制基础上的非周期事件触发控制。设采样周期为h，触发时刻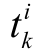
是采样时刻{0, h, 2h,…}的真子集。通常触发时刻是由一个触发函数确定的，当满足触发函数时则更新通信和控制信号。为了确定这些非周期离散触发时刻，下面将给出该事件触发函数的详细推导过程。
已知电压补偿项ui，则由分布式控制层给定的电压参考值为
下垂控制层相比于分布式控制层，具有更快的动态性能，认为其可以实现对分布式控制层给定参考电压的瞬时跟踪[23]。忽略下垂控制层的动态行为后，HESSi 输出端电压为
对式（12）求导并定义中间变量 
分别为
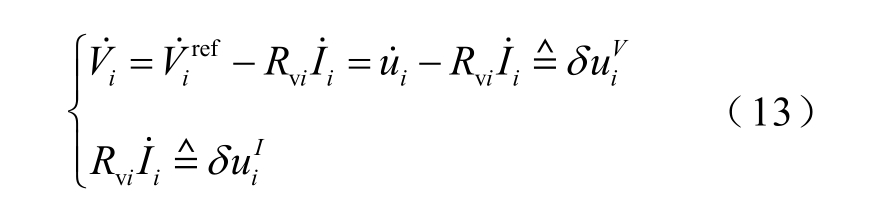
因此，电压补偿项ui 变为
由图3 可知
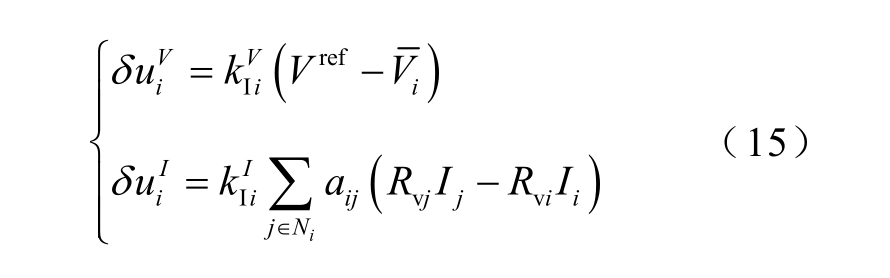
式中，
分别为平均电压调节和比例电流调节环节的积分系数，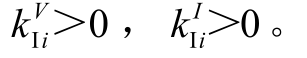
为便于后续推导，定义电压和电流偏差项为
对于式（16），在无向图中，
为常数，其导数等于0[24]。对式（16）分别求导数并利用式（6）、式（13）和式（15）的定义可得
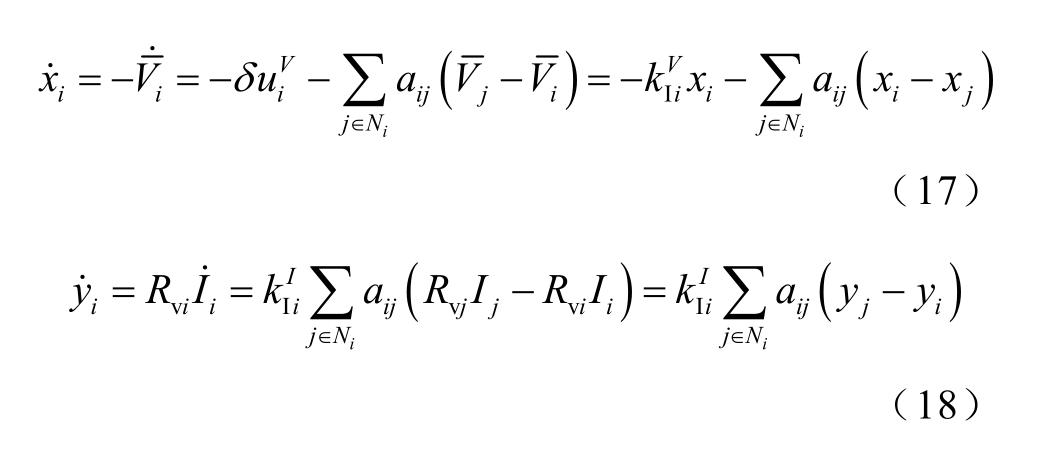
将式（17）和式（18）写成矩阵形式为
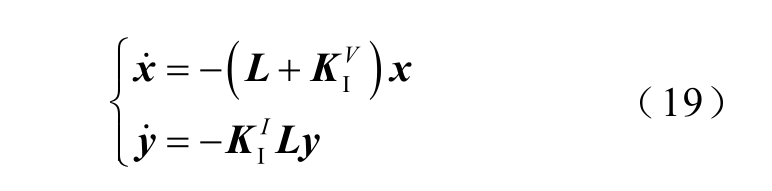
式中，L 为拉普拉斯矩阵；
为相应积分系数的对角矩阵。
式（19）可看作是leader-following 一致性算法和leaderless 一致性算法[25]。由拉普拉斯矩阵L 的性质，并利用LaSalle 不变原理，可得到以下结论：
1）矩阵 IVL+ K 正定，可知当t→+∞时，x(t)→0。
2）矩阵L 半正定，设Wy(t)为关于变量y 的
M E⊂ 是最大不变集，则当t→+∞时，有 y(t)→M。
本文算例部分取所有HESS 电压补偿项的积分系数相等，即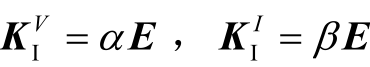
，E 为单位矩阵。定义状态量x 和y 与上一时刻状态量的偏差项为
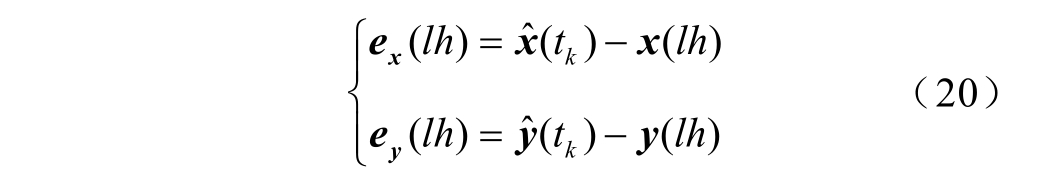
式中
为最新触发时刻的采样信号。
触发时刻的平均电压为
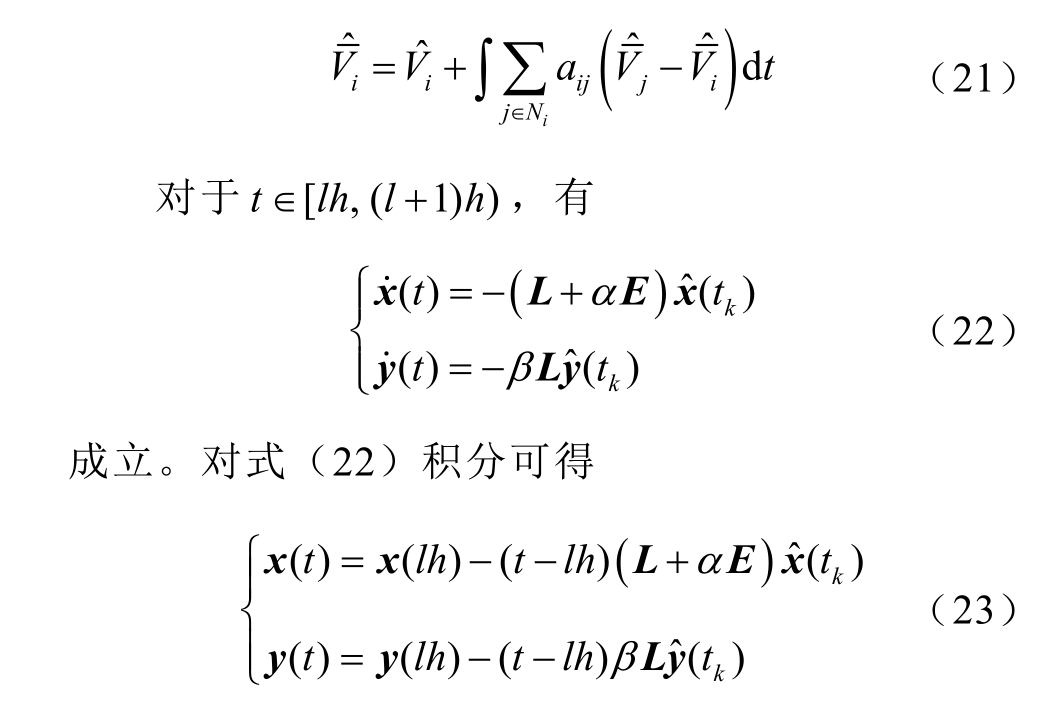
利用偏差项关系 
可将式（23）变为下述关于偏差项的方程。
对式（25）求导数并代入式（22）和式（24），可得
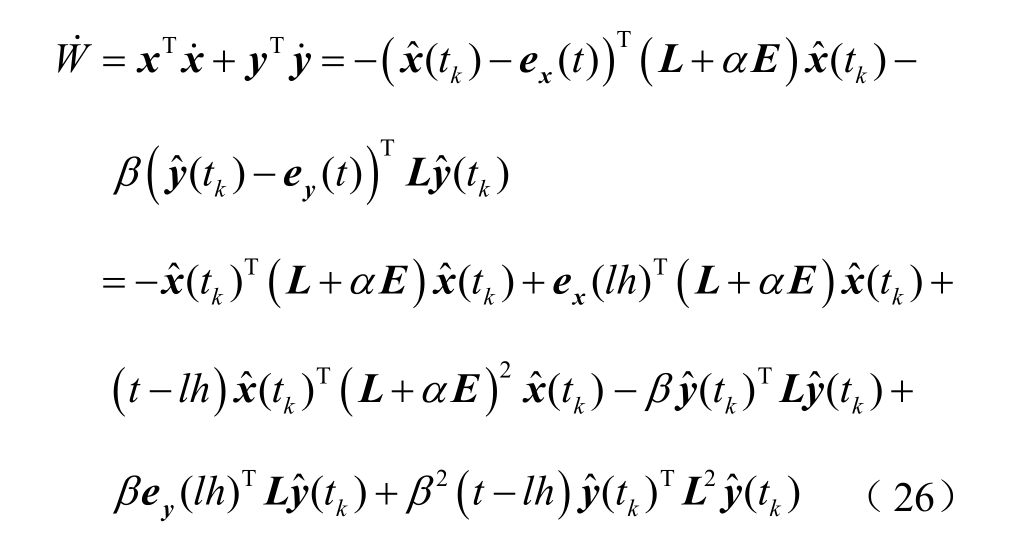
为表达清晰，忽略式（26）中的时间参数，并利用矩阵论相关知识可得
式中，λn 为L 阵最大特征值
为集合Ni 的阶数。
利用Young 不等式
令式（28）中b=2a。
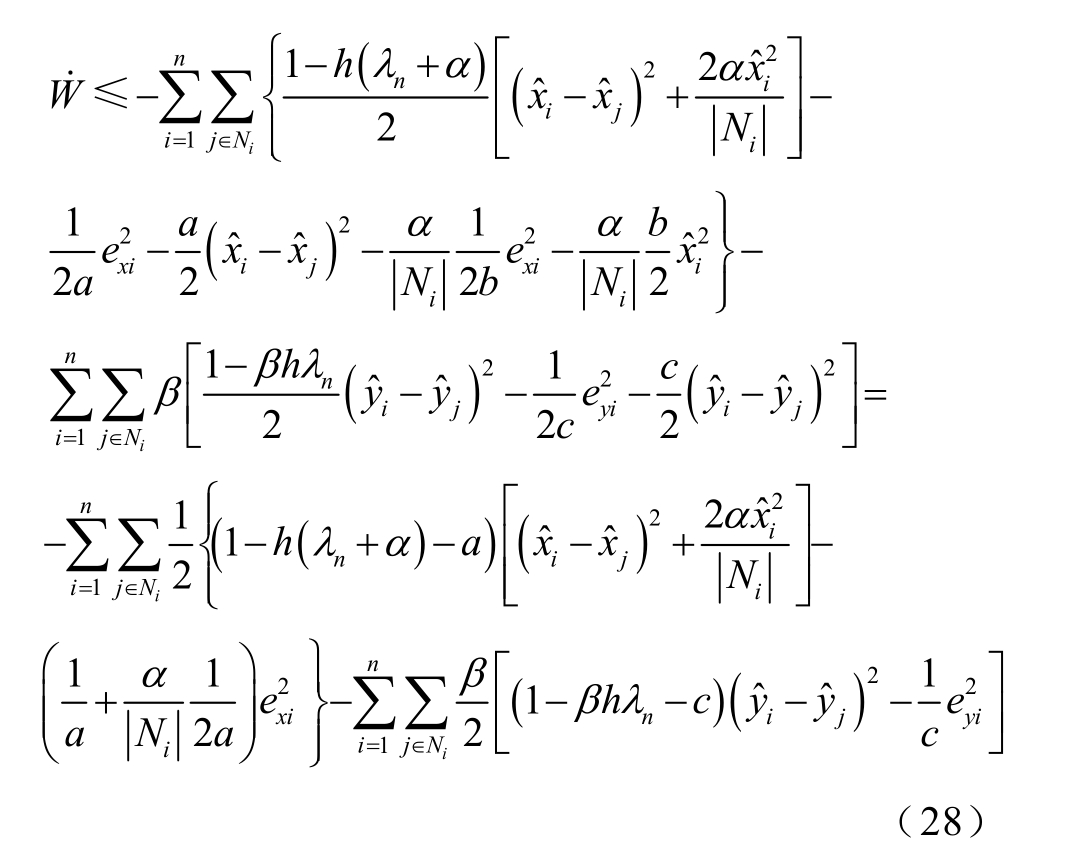
式中，
要计算特征值λn 就需要知道整个通信网络的连接情况，有时会较为困难，特别是当网络连接情况发生变化的时候，需要重新计算特征值λn。因此，可以利用文献[26]中所给出的L 矩阵最大特征值的上限 n nλ ≤ 进行估算，其弱化了对通信网络结构的要求，仅需要知道系统中运行的HESS 数量即可。因此式（30）可变为
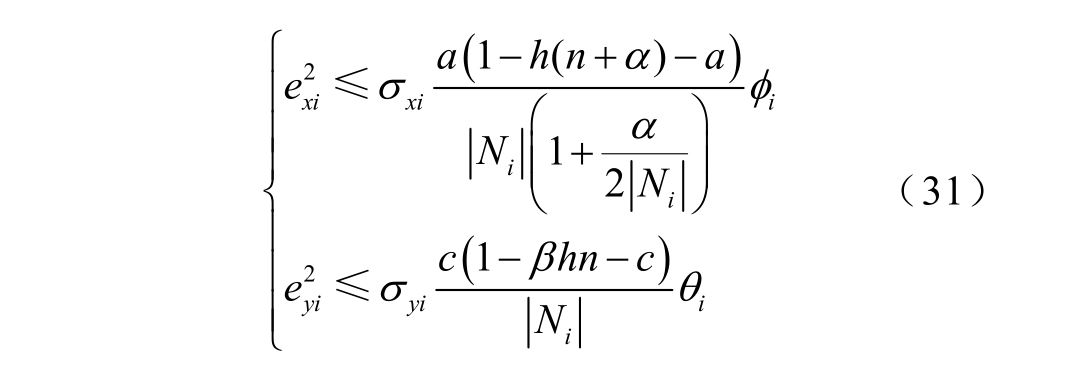
当a、c 取式（32）值时，不等式（31）右侧取最大值。
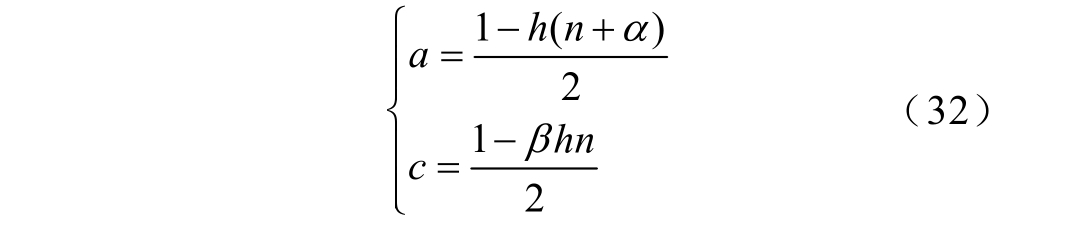
至此，可以得到分布式事件触发函数为
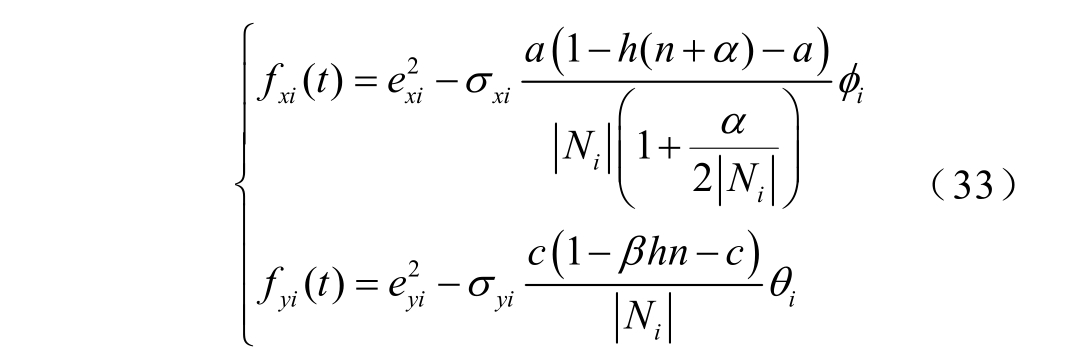
当 0W＞˙ 时触发通信，HESSi 下一次通信与控制的更新时刻为
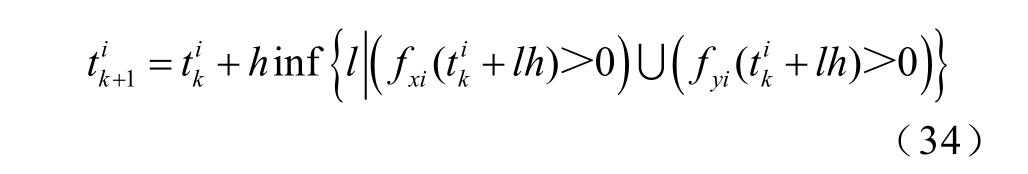
从式（34）可以看出，该触发函数不需要进行周期通信，其仅利用了自身状态偏差量和相邻HESS 的最新触发时刻的状态量。
3.2 事件触发控制的实现
从式（29）可以看出，随着平均电压和比例电流趋向于目标值，φi 和θi 将趋于0，触发函数式（34）将变得越来越敏感，这意味着事件被触发的频率也越来越高。即使系统处于稳态时，触发频率仍然较高，从而导致通信次数不能减少。为了进一步降低触发次数，定义两个非负的预判阈值e1 和e2，在执行触发函数式（34）之前，exi 和eyi 首先与e1 和e2进行比较，若满足式（35）则再判别是否满足事件触发条件，否则不执行式（34）[15]。
给出与上述控制方法相结合的基于事件触发机制的HESS 控制实现流程，如图4 所示。
图4 HESS 事件触发控制流程
Fig.4 Event triggered control flow chart of HESS
4 算例分析
为验证所提出控制方法的可行性和有效性，在Matlab/Simulink 环境下搭建了如图1 所示含有光伏发电系统、负载和3 组HESS 的孤岛直流微电网模型，系统及控制器参数见表1。系统中的物理参数是参考课题组已有的一套混合储能系统设定的，但适当增大了线路电阻参数，以使控制效果在仿真结果中对比明显；而各个PI 及I 控制器参数是通过仿真实验调试得到的。另外，需要指出的是，前文的推导过程并未用到表中的线路电阻，即控制算法与线路电阻无关。
表1 直流微电网及控制器参数
Tab.1 DC microgrid and controller parameters
参 数 数 值 直流微电网 Vref/V 220 Rline1, Rline2, Rline3/Ω 0.10, 0.12, 0.14 L/mH 3 C/μF 2 500 蓄电池 108V/108A·h 超级电容 96V/82.5F max v R /Ω 0.2 下垂控制层 电压环 kPV=2.8, kIV=92.2 蓄电池电流环 kPb=22.4, kIb=32.7 超级电容电流环 kPsc=1.4, kIsc=4.36 超级电容SOC 补偿项 kPSOC=300, kISOC=0.4 低通滤波器时间常数/s 1 分布式控制层 电压补偿项积分系数 α=2, β=200 通信周期h/μs 50
4.1 分层协调控制效果
本小节将对比传统下垂控制与引入分布式控制层后的控制效果。设三组HESS 初始SOC 分别为：HESS1 （ SOCb1=0.75 ； SOCsc1=0.90 ）， HESS2（SOCb2=0.65；SOCsc2=0.59），HESS3（SOCb3=0.65；SOCsc3=0.59）。三组HESS 的状态信息通过一个环形网络实现交换。初始母线电压为220V，分别在1s 时切除初始负载的50%，在4s 时增加初始负载的100%，在7s 时切除初始负载的100%。采用传统下垂控制和分层协调控制的直流母线电压变化情况如图5 所示。
图5 传统下垂控制与分层协调控制母线电压对比
Fig.5 Comparison of bus voltage between traditional droop control and hierarchical coordinated control
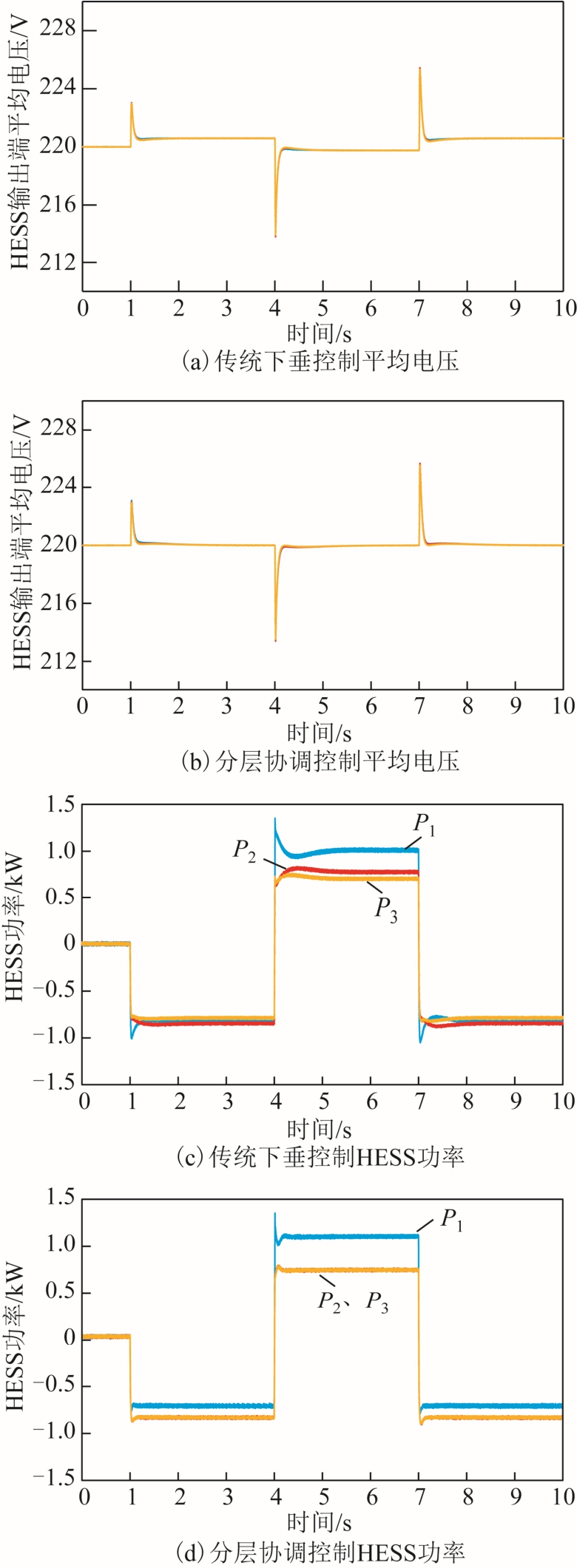
图6 HESS 输出端平均电压和功率对比
Fig.6 Comparison of HESS average voltage and power
由图5 可以看出，因为所设置的Rvi 满足约束条件，两种控制方法的母线电压均位于最大允许电压偏差内。由于电压补偿项ui 的存在，分层协调控制的Vbus2 更靠近额定电压。图5 中右下角的小图为Rvi变化曲线，HESS1 中蓄电池SOCb1 初始值最高，根据2.1.1 节基于蓄电池SOC 的虚拟电阻调节策略可知，Rv1 应在充电时最大、放电时最小，分别对应最小的充电功率和最大的放电功率，Rvi 变化曲线与之相符。
图6 为两种控制方法下的HESS 输出端平均电 压和吞吐功率曲线。其中，图6a 为传统下垂控制下的HESS 平均电压，其与母线电压变化趋势相同。图6b 为分层协调控制下的平均电压，显然在扰动发生后，三组HESS 的平均电压均能恢复至额定电压，该控制策略也是保证母线电压优于下垂控制的原因。图6c 为下垂控制下的三组HESS 功率曲线，HESS2和HESS3 设置的起始SOC 相同，承担的功率应该相等，但由于Rvi 和Rlinei 较为接近，其吞吐功率不能按照期望比例分配。而从采用分层协调控制后的图6d 可以看出，HESS2 和HESS3 的功率P2 和P3相等，表明比例电流调节的加入保证了较好的功率分配精度。
图7 为HESS1 和HESS2 内部功率分配以及超级电容SOC 变化曲线。由图7a 和图7b 可以看出，电压突变时超级电容提供瞬时功率支撑，蓄电池承担较为平缓的低频功率，且随着蓄电池出力增加，超级电容功率最终恢复至0。图7c 和图7d为对应的超级电容SOC 变化情况，为验证2.1.2节基于超级电容SOC 电流补偿策略的有效性，将HESS1 中超级电容的起始SOC 设置为接近0.9，当其超级电容的SOC 越过上限值后，SOC 补偿调节开始工作，与图7b 不同，图7a 中A 区域呈现出补偿过程，并导致图7c 中B 区域所示的SOC曲线恢复至90%以内。图7d 中SOC 处于正常运行区间，因此HESS2 中蓄电池和超级电容的内部功率无补偿过程。
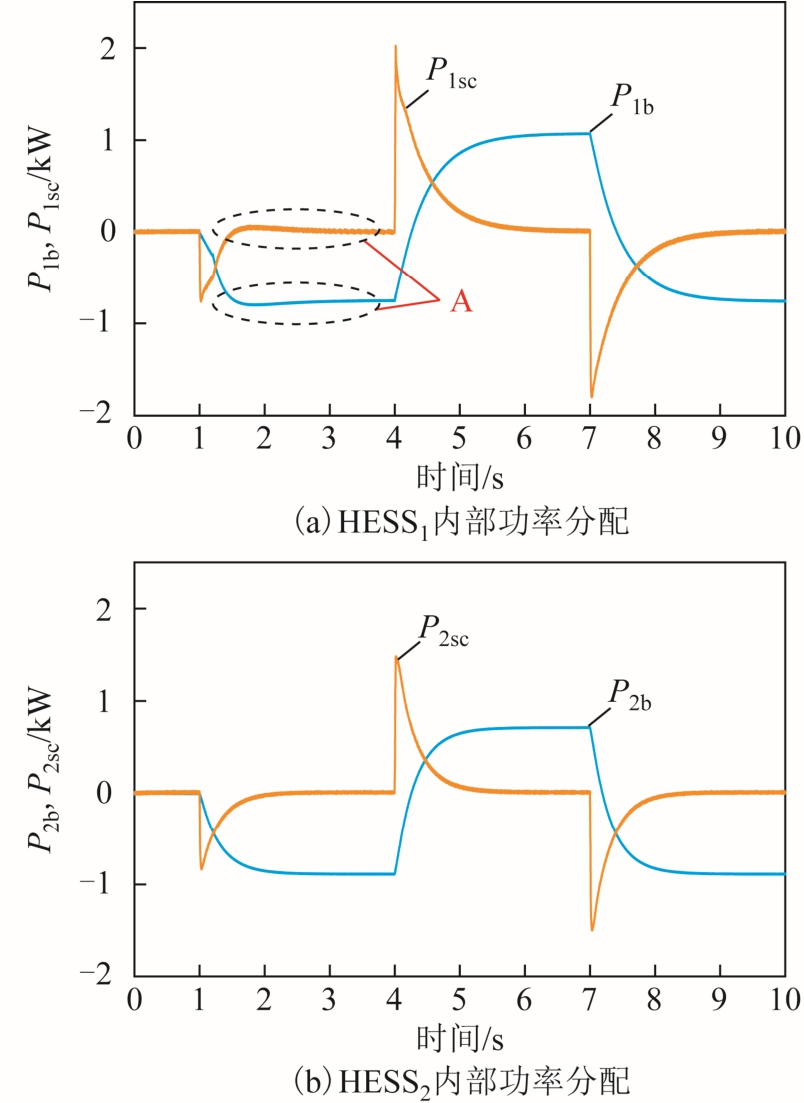
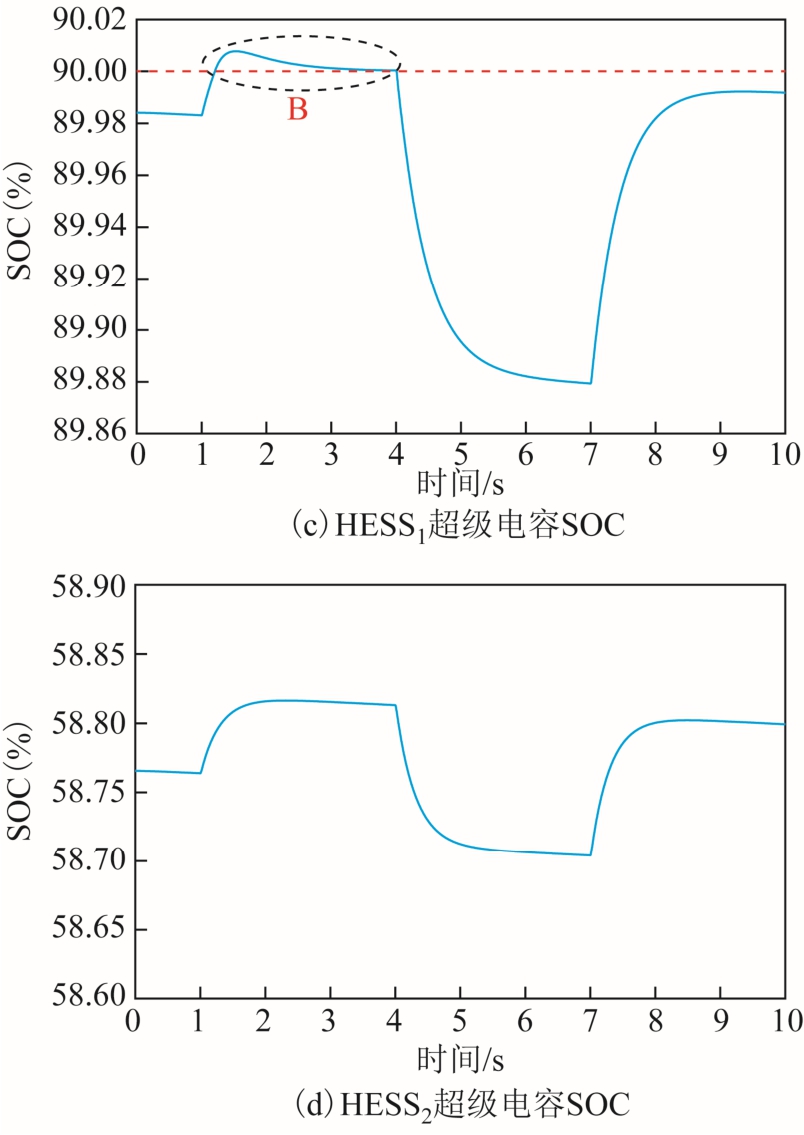
图7 HESS 内部功率及超级电容SOC 曲线
Fig.7 HESS internal power and supercapacitor's SOC curve
4.2 分布式事件触发控制效果
在分层协调控制的基础上引入事件触发机制，系统初始条件与4.1 节相同。图8 为不同阈值e1、e2 下母线电压波形。图8 中，右下角小图为电压稳态时5～6s 的电压波形。图8a 和图8b 的电压基本相同，随着阈值增大，图8c 中小图显示稳态时电压出 现了轻微波动。当阈值进一步增大，将会导致系统不稳定。
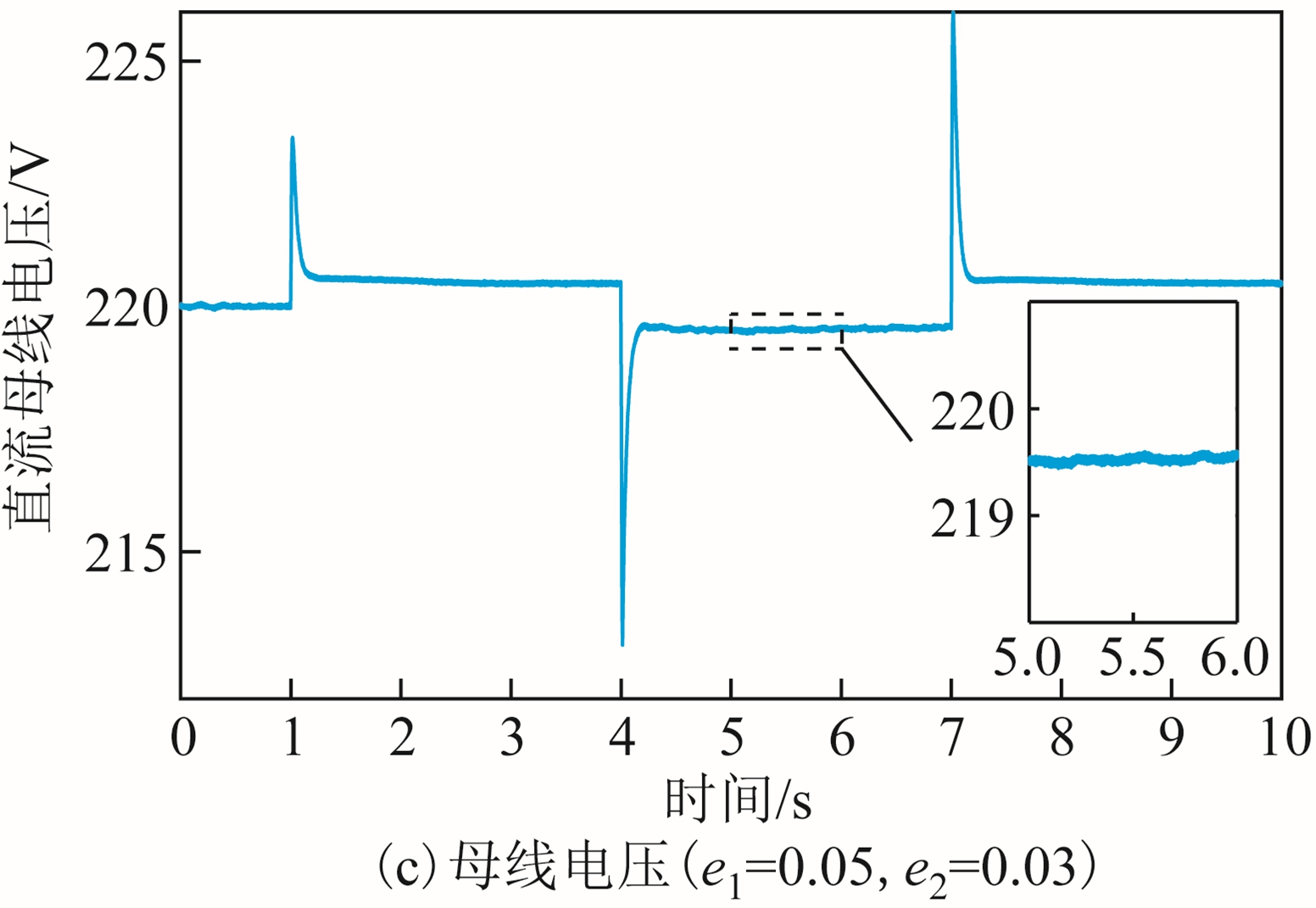
图8 不同阈值下母线电压
Fig.8 Bus voltages under different thresholds
图9 为与图8 相对应的在4s 附近的事件触发情况，即所发生通信的时刻。图9a 表明在阈值为0时，由于稳态时φi 和θi 趋于0，触发函数较为敏感， 稳态时的通信次数仍然较多。而随着阈值增大，稳态时通信频率降低，特别是在图9c 中，在4s 发生扰动前的稳态阶段，基本没有发生通信。在扰动发生后的4～4.005s 之间触发频率很高，之后触发频率呈现降低的趋势。这里需要强调的是，所有触发时刻的最小时间间隔均被限定为通信周期h，因此不存在Zeno 现象。
最后，为更清晰地说明事件触发机制的优势，对三组HESS 分别在无事件触发以及在三种不同阈值下事件触发的通信次数进行统计，如图10 所示。与周期性通信相比，事件触发控制的通信次数更少，而引入预判阈值后，通信次数可以进一步降低。
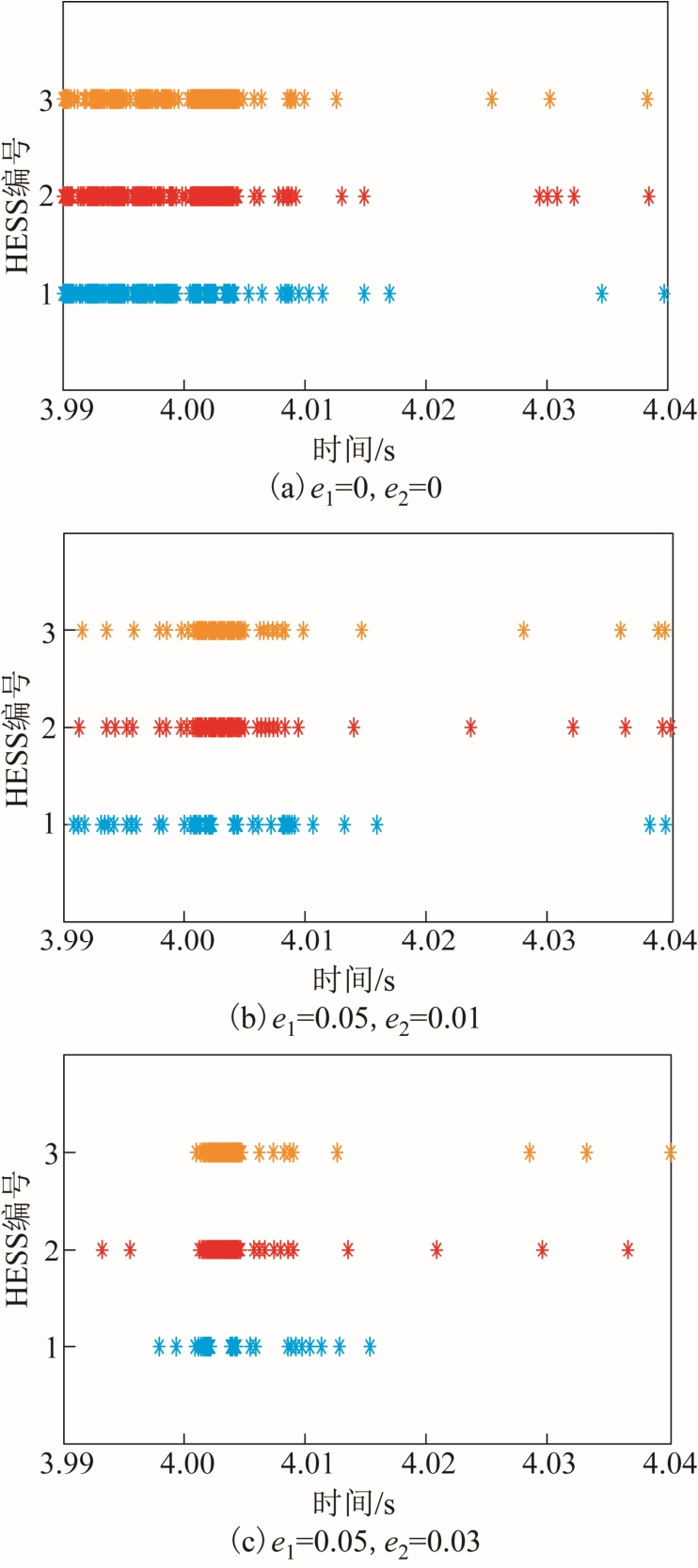
图9 不同阈值下4s 时刻的触发情况
Fig.9 Trigger points under different thresholds at 4s
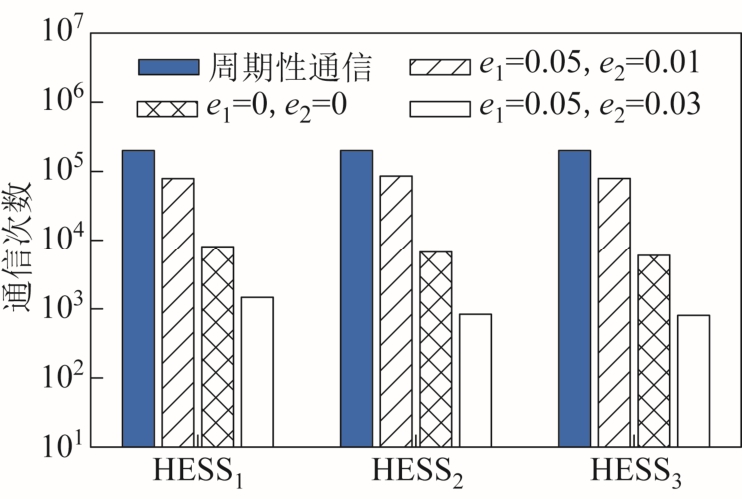
图10 通信次数对比
Fig.10 Communication frequency comparison
5 结论
本文针对孤岛型直流微电网中多HESS 控制问题展开研究，提出了一种基于事件触发机制的分层协调控制方法。下垂控制层采用低通滤波器实现超级电容和蓄电池的功率分配，并通过制定基于SOC 的控制策略实现HESS 间的协调安全运行。分布式控制层则利用稀疏通信网络对HESS 的平均电压和比例电流进行调节，以解决因虚拟电阻和线路电阻导致的母线电压偏差较大和功率分配精度差的问题。在此基础上，利用Lyapunov 稳定理论提出了一种建立在周期性通信之上的分布式事件触发控制方法，其从根本上避免了Zeno 现象的产生。该方法仅利用本地HESS 的状态偏差量和相邻HESS 最新触发时刻的状态量进行事件触发检测，并通过设定事件触发的预判阈值以进一步减少系统稳态时的事件触发次数。最后在Matlab/Simulink 环境下搭建了相应直流微电网模型，并验证了上述方法的有效性和可行性。
[1] 张勇军, 刘子文, 宋伟伟, 等. 直流配电系统的组网技术及其应用[J]. 电力系统自动化, 2019, 43(23): 39-49.
Zhang Yongjun, Liu Ziwen, Song Weiwei, et al. Networking technology and its application of DC distribution system[J]. Automation of Electric Power Systems, 2019, 43(23): 39-49.
[2] 马伟, 王玮, 吴学智, 等. 平抑光伏并网功率波动的混合储能系统优化调度策略[J]. 电力系统自动化, 2019, 43(3): 58-66.
Ma Wei, Wang Wei, Wu Xuezhi, et al. Optimal dispatching strategy of hybrid energy storage system for smoothing power fluctuation caused by grid-connected photovoltaic[J]. Automation of Electric Power Systems, 2019, 43(3): 58-66.
[3] 张继红, 王洪明, 魏毅立, 等. 含复合储能和燃气轮发电机的直流微电网母线电压波动分层控制策略[J]. 电工技术学报, 2018, 33(6): 1238-1246.
Zhang Jihong, Wang Hongming, Wei Yili, et al. Hierarchical control strategy of voltage fluctuation in DC microgrid consisting gas-turbine generator and composite energy storage[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1238-1246.
[4] 杨捷, 金新民, 吴学智, 等. 直流微网中混合储能系统的无互联通信网络功率分配策略[J]. 电工技术学报, 2017, 32(10): 135-144.
Yang Jie, Jin Xinmin, Wu Xuezhi, et al. A wireless power sharing control strategy for hybrid energy storage systems in DC microgrids[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 135-144.
[5] 刘志博, 刘兴杰. 独立直流微网中混合储能系统的改进多滞环控制策略[J]. 电工技术学报, 2018, 33(3): 490-497.
Liu Zhibo, Liu Xingjie. Improved multi-hysteresis control strategy of hybrid storage system in a stand-alone DC microgrid[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 490-497.
[6] 苏浩, 张建成, 冯冬涵, 等. 模块化混合储能系统及其能量管理策略[J]. 电力自动化设备, 2019, 39(1): 127-133, 140.
Su Hao, Zhang Jiancheng, Feng Donghan, et al. Modular hybrid energy storage system and its energy management strategy[J]. Electric Power Automation Equipment, 2019, 39(1): 127-133, 140.
[7] Xu Qianwen, Xiao Jianfang, Wang Peng, et al. A decentralized control strategy for autonomous transient power sharing and state-of-charge recovery in hybrid energy storage systems[J]. IEEE Transactions on Sustainable Energy, 2017, 8(4): 1443-1452.
[8] Lin Pengfeng, Wang Peng, Xiao Jianfang. An integral droop for transient power allocation and output impedance shaping of hybrid energy storage system in DC microgrid[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 6262-6277.
[9] Shi Mengxuan, Chen Xia, Zhou Jianyu, et al. Advanced secondary voltage recovery control for multiple HESSs in a droop-controlled DC microgrid[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 3828-3839.
[10] 周建宇, 闫林芳, 刘巨, 等. 基于一致性理论的直流微电网混合储能协同控制策略[J]. 中国电机工程学报, 2018, 38(23): 6837-6846.
Zhou Jianyu, Yan Linfang, Liu Ju, et al. A cooperative control strategy for DC microgrid based on consensus algorithm[J]. Proceedings of the CSEE, 2018, 38(23): 6837-6846.
[11] Nowzari C, Garcia E, Cortés J. Event-triggered communication and control of networked systems for multi-agent consensus[J]. Automatica, 2019, 105: 1-27.
[12] Zhu Wei, Jiang Zhongping. Event-based leader- following consensus of multi-agent systems with input time delay[J]. IEEE Transactions on Automatic Control, 2015, 60(5): 1362-1367.
[13] Wang Xiaofeng, Lemmon M D. Event-triggering in distributed networked control systems[J]. IEEE Transactions on Automatic Control, 2011, 56(3): 586-601.
[14] 肖湘宁, 王鹏, 陈萌. 基于分布式多代理系统的孤岛微电网二次电压控制策略[J]. 电工技术学报, 2018, 33(8): 1894-1902.
Xiao Xiangning, Wang Peng, Chen Meng. Secondary voltage control in an islanded microgrid based on distributed multi-agent system[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1894-1902.
[15] Han Renke, Meng Lexuan, Guerrero J M, et al. Distributed nonlinear control with event-triggered communication to achieve current-sharing and voltage regulation in DC microgrids[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 6416-6433.
[16] Borgers D P, Heemels W P M H. Event-separation properties of event-triggered control systems[J]. IEEE Transactions on Automatic Control, 2014, 59(10): 2644-2656.
[17] Meng Xiangyu, Chen Tongwen. Event based agreement protocols for multi-agent networks[J]. Automatica, 2013, 49: 2125-2132.
[18] Nowzari C, Cortés J. Distributed event-triggered coordination for average consensus on weight-balanced digraphs[J]. Automatica, 2016, 68: 237-244.
[19] Zhao Hongshan, Guo Wei. Hierarchical distributed coordinated control strategy for hybrid energy storage array system[J]. IEEE Access, 2019, 7: 2364-2375.
[20] Bapat R B. Graphs and matrices[M]. London: Springer Press, 2014.
[21] Nasirian V, Moayedi S, Davoudi A, et al. Distributed cooperative control of DC microgrids[J]. IEEE Transactions on Power Electronics, 2015, 30(4): 2288-2303.
[22] 郭伟, 赵洪山. 基于改进分布式一致性算法的电池储能阵列分组控制策略[J]. 电工技术学报, 2019, 34(23): 4991-5000.
Guo Wei, Zhao Hongshan. Grouping control strategy of battery energy storage array system based on an improved distributed consensus algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4991-5000.
[23] Liu Xiaokang, He Haibo, Wang Yanwu, et al. Distributed hybrid secondary control for a DC microgrid via discrete-time interaction[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 1865-1875.
[24] Zuo Shan, Davoudi A, Song Yongduan, et al. Distributed finite-time voltage and frequency restoration in islanded AC microgrids[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 5988-5997.
[25] Saber R O, Fax J A, Murray R M. Consensus and cooperation in networked multi-agent systems[J]. Proceedings of the IEEE, 2007, 95(1): 215-233.
[26] Merris R. Laplacian matrices of graphs: a survey[J]. Linear Algebra and Its Applications, 1994, 197-198: 143-176.