0 引言
随着柔性化电能输送需求的提升和电力电子技术的进步[1]，基于电压源换流器（Voltage Source Converter, VSC）的柔性直流输电工程在不断发展。目前我国已建成南汇、厦门两端、南澳三端以及舟山五端柔性直流输电等多个工程[1-2]。由于VSC 具有高度可控性和良好适应性[3]的优点，可将风电、光伏等新能源大规模接入交直流系统[4]。伴随新能源的大规模接入以及负荷复杂程度的提高，含VSC 交直流电网中注入功率的不确定性问题日益凸显[5-6]。因而，含VSC 的交直流系统潮流结果应当体现不确定注入功率对电网状态量的影响[5]，以便为电网的运行调控提供必要的参考。
随着对不确定潮流需求的提升，产生了多种不确定潮流的分析方法，主要有概率潮流法[6]、模糊潮流法[7]和区间潮流法[8]三种方法。其中，概率潮流法和模糊潮流法在实际工程中，较难获取其准确的概率分布或隶属函数[9]。区间潮流法分析较为简便，然而在不确定度较高时会存在状态区间过大即过于保守的现象[8]。为此，以区间潮流法为基础的仿射算法被提出，以中心值加噪声元的形式保存各不确定变量之间的联系和依赖性，以降低区间算法的保守性[10]。自文献[10]首次将仿射算法应用于不确定潮流计算以来，它在电力系统可靠性分析、潮流计算等方面发挥了重要作用[11]。文献[11-13]对基于仿射算法的配电网展开研究，由于配电网前推回代法无需考虑三角函数的仿射运算，因此没有解决仿射潮流中的三角函数问题。文献[14]针对交流输电网进行了区间-仿射潮流计算，但区间-仿射算法之间的转换导致了仿射噪声元的增加，并割裂了仿射数不确定量之间的不确定性传递关系，难以实现不确定输入变量对系统输出影响的量化分析。
随着含VSC 的交直流系统快速发展，在交直流潮流研究方面的研究已较为广泛[15-20]。计算方法总体上可分为统一迭代法[15-16]和交替迭代法[17-19]。文献[15-16]在分析了系统的稳态特性与基本控制方式的基础上形成了统一迭代潮流算法。文献[17- 19]对换流器在交流侧与直流侧进行等效，建立了适用于多端直流输电的交替迭代潮流算法。其中，文献[18]考虑VSC 下垂控制方式，分析了其对潮流分布的影响。
以上潮流求解模型中，交替迭代法可以相对容易地实现交流网络潮流计算程序的扩展。然而，现有交直流系统潮流计算研究中对不确定潮流的研究较少。文献[5]采用概率潮流的方式对含风电场的交直流系统进行了不确定潮流分析，但为形成有效的状态量概率分布，求解过程需要重复多次潮流计算，计算耗时过长。
因此，在现有研究基础上，本文针对交直流系统提出了一种基于仿射算法的不确定潮流算法。该方法首先确定了三角函数的仿射运算法则，而后基于仿射原理，对含VSC 的交直流系统中各个部分建立了仿射潮流模型。其中，考虑VSC 电压下垂控制方式在内的多种控制方式建立了VSC 的仿射化求解模型，进而，基于交替迭代法形成了交直流系统的仿射潮流模型，并结合 P-Q 分解法实现其快速求解。该算法可利用仿射算法不确定量之间的不确定性传递关系量化分析随机变量对系统状态量的影响。算例验证所提算法模型简洁、求解快速、结果较为准确，克服了交直流系统不确定潮流求解复杂的缺陷。
1 仿射算法
1.1 仿射算法简介
在仿射算法中，不确定量采用一阶多项式的形式来表示[12]，记为
式中， 0x 为仿射数中心值； ix 为噪声元系数； iε 为噪声元，其取值范围为[-1, +1]。
仿射数也可通过式（2）转为区间数形式[21]。
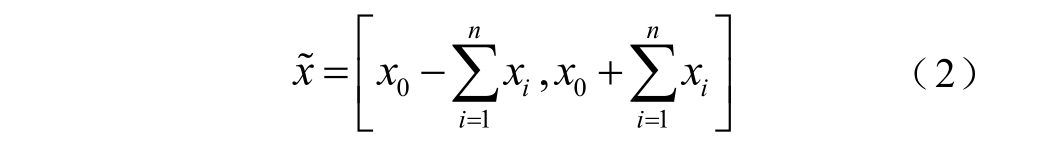
如 果 给 定 仿 射 数 
以及实数α，则仿射数之间基本的运算法则可表示为[21]
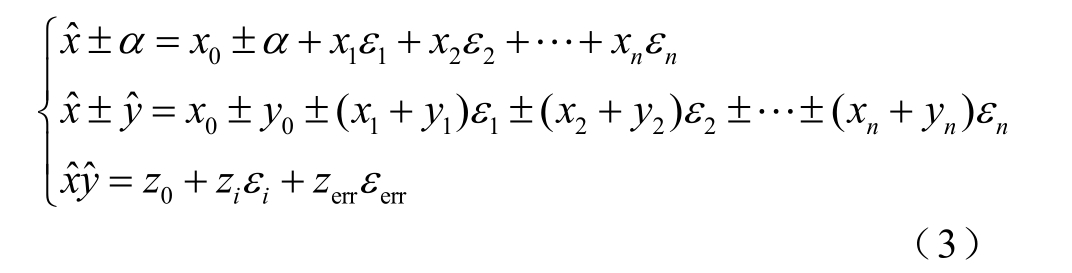
式中，
为乘法仿射运算过程中新产生的噪声元。
对 于除 法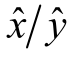
等 价 于
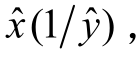若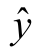
对应 的区 间数为 
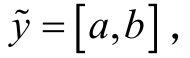则
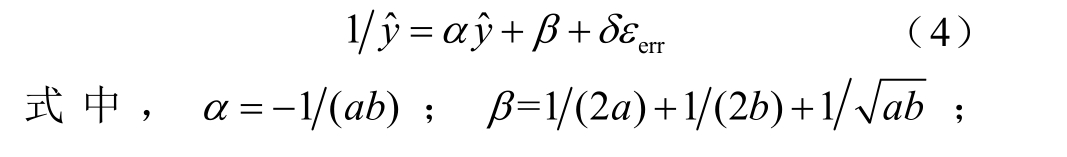
1.2 三角函数的仿射算法
仿射算法为线性运算，因此三角函数无法直接进行仿射运算。为实现其仿射化运算，本文基于潮流计算中相位不超过
，且相位差一般不超过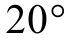
的性质[22]，应用切比雪夫最佳逼近理论[23]进行等效处理（线性化原理详见附录），实现了三角函数的仿射化运算。对于一个对应区间为[ a ,b ]的仿射数
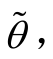，三角函数仿射运算法则可表示为
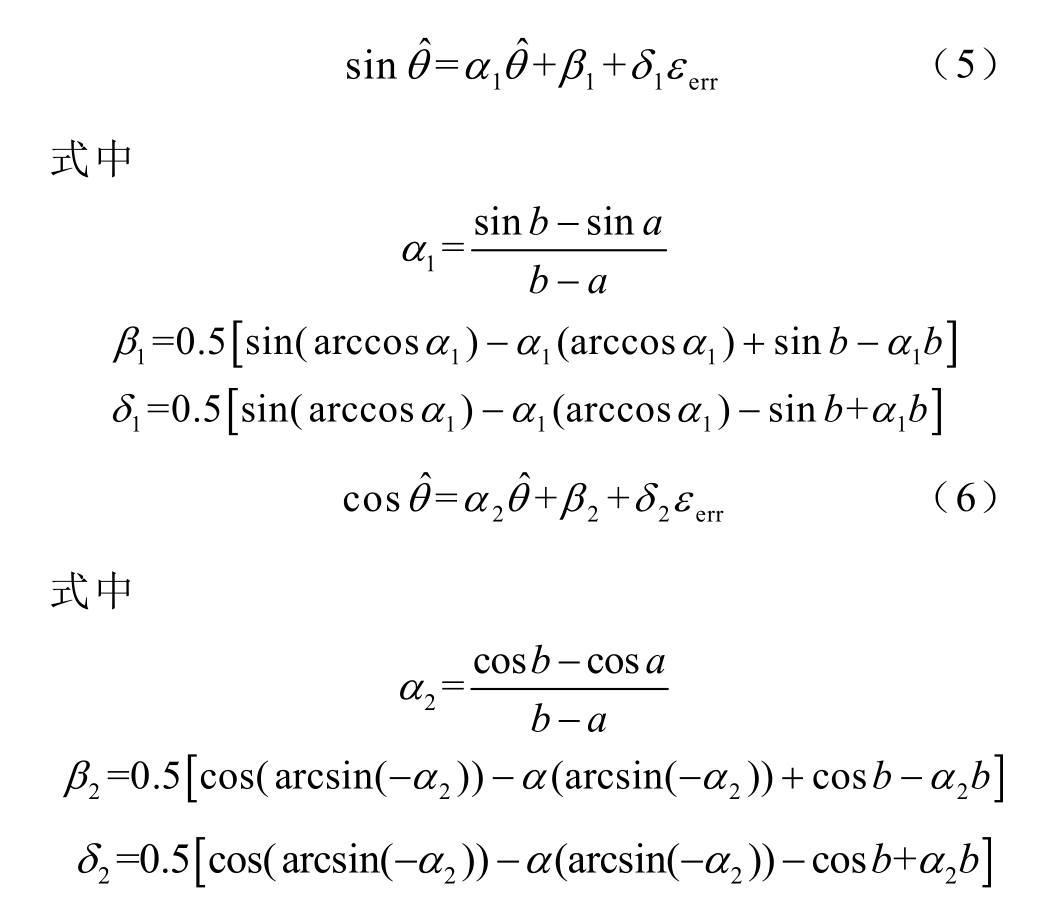
以
的仿射值进行三角函数仿射算法的计算精度验证，由切比雪夫线性化方法的性质可知，其最大误差点存在于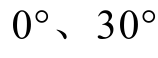
以及该近似函数与原函数同斜率的点，正弦和余弦函数求解的最大误差均为δ=0.004 5。可见，该三角函数线性化后的仿射数结果与实际结果相比误差较小。
1.3 不确定输入变量对系统状态量的影响力指标
由仿射数的运算规则可以看出，表征不确定性的噪声元具有可追踪性[10-13]，即根据噪声元系数的变化，可以计算该不确定因素对结果造成的不确定度。基于此特性，可以定义不确定输入变量对系统状态量的影响力指标。
假设m 个状态量
对应的n 个输入变量相互独立，分别为
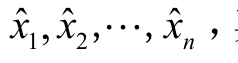其中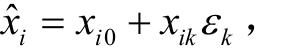 
则对于该状态量有
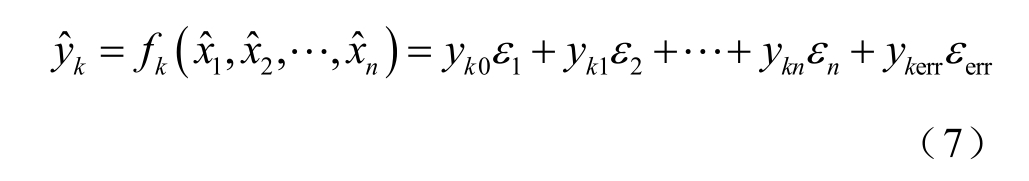
式中，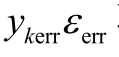 
项为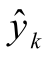
计算过程中产生的计算误差。 由此，每个噪声元 εi 对状态
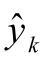的不确定影响度可用文献[12]中所定义的影响力指标来度量。
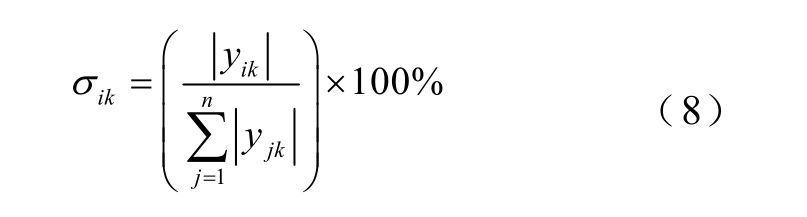
为分析某噪声元对系统整体不确定性带来的影响，定义噪声元对系统影响力指标为
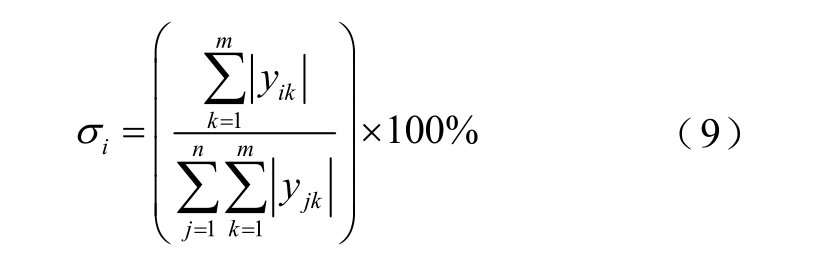
2 VSC 的潮流模型
2.1 VSC 稳态模型
VSC 可实现交直流变换[24-25]，其单相结构如图1 所示。为便于表述，本文规定从交流侧流向直流侧为功率正方向。
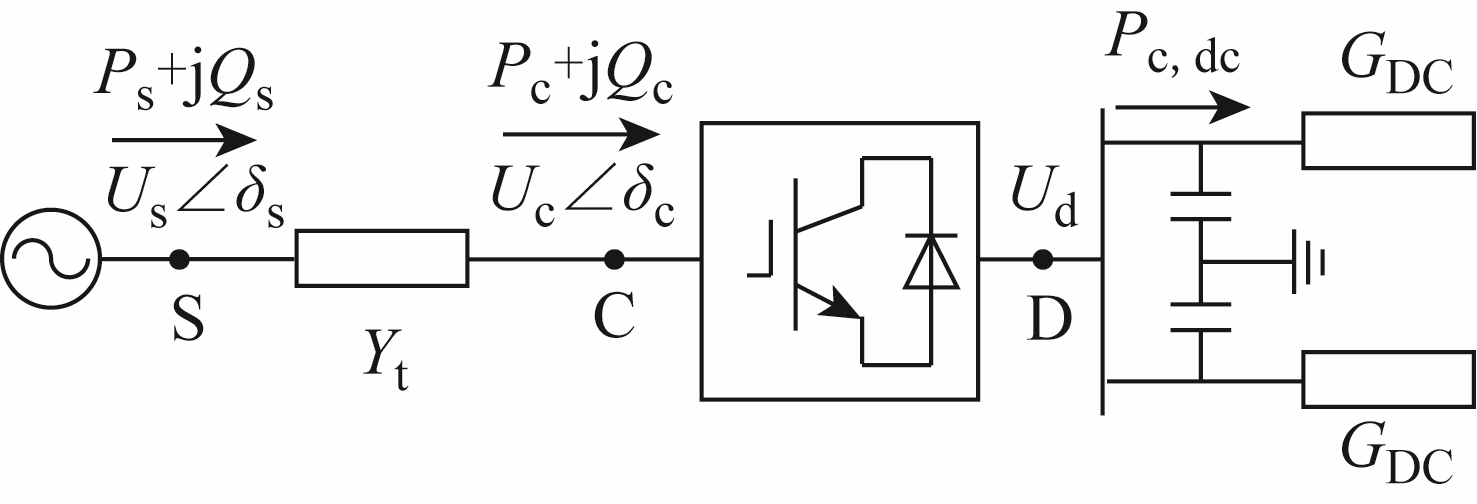
图1 VSC 换流站结构
Fig.1 Structure of VSC converter
图1 中，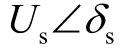
为交流网络侧母线S 处电压，
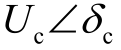为换流器交流侧母线C 处电压， Yt 为换流器复合导纳，表征变压器等效导纳和换流器等值导纳。
根据图1 所示电路，容易得到交流网络母线S处的注入功率为
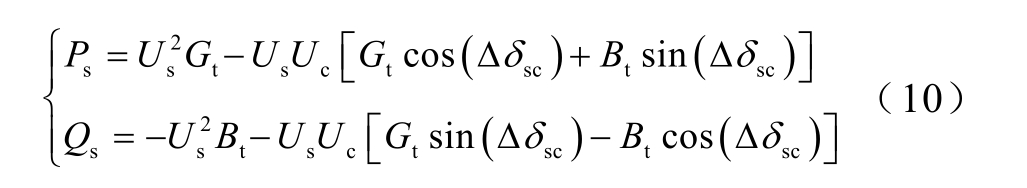
式中，Gt 为换流器复合电导；Bt 为换流器复合电纳；
换流器交流侧C 处的注入功率为
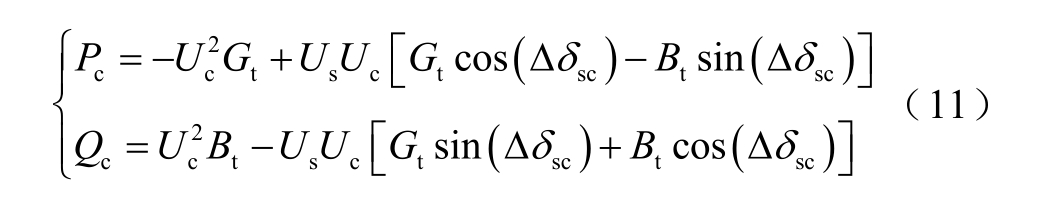
在VSC 直流侧，VSC 注入直流网络的有功功率为
式中， c,lossP 为换流器的功率损耗。
2.2 VSC 的损耗
换流器在进行电能变换时会产生开关损耗和导通损耗等功率损耗，其数值与换流器的电流值 cI 相关，可表示为[15]
式中，
损耗参数a、b、c 为常数[26-27]。
2.3 VSC 的控制方式
VSC 的求解模型与它的控制方式有关。VSC 可以独立地控制两类控制量[25]：有功类控制量和无功类控制量。从两类控制量中各选取一个控制量，可以组合形成VSC 的控制方式。VSC 的控制方式及其在直流侧的节点类型见表1。
表1 VSC 控制模式
Tab. 1 VSC control mode
模式 有功类控制量 无功类控制量 直流节点类型1 交流侧注入有功Ps 交流侧注入无功Qs Ⅰ 2 交流侧注入有功Ps 交流侧节点电压Us 3 直流侧节点电压Ud 交流侧注入无功Qs Ⅱ 4 直流侧节点电压Ud 交流侧节点电压Us 5 电压下垂控制 交流侧注入无功Qs Ⅲ 6 电压下垂控制 交流侧节点电压Us
表1 中的电压下垂（U-P）控制方式[18]，即控制 dU 与 c,dcP 满足
式中，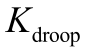
为下垂控制参数，
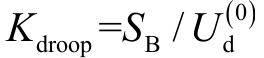， S B为系统功率基准值；
分别为初始运行点参数，取基准值。
表1 中，按照VSC 在直流侧的控制属性，将节点类型分为Ⅰ、Ⅱ、Ⅲ三种。直流节点类型I 为P节点，即节点注入有功功率给定，待求相应节点电压值。直流节点类型Ⅱ为Ⅴ节点，即直流松弛节点，该类型节点的节点电压给定，待求量为该节点VSC的注入功率。Ⅲ类型节点的直流节点电压与直流节点功率满足式（14）关系，本文在直流侧进行求解时，将Ⅲ类型节点按Ⅴ节点处理，而后应用式（14）更新电压值。故若无特殊说明，将Ⅱ、Ⅲ类型节点统称为直流网络的Ⅴ节点。
3 交替迭代法下交直流系统仿射潮流计算
3.1 交直流系统仿射潮流的计算方法
3.1.1 交流网络仿射潮流计算
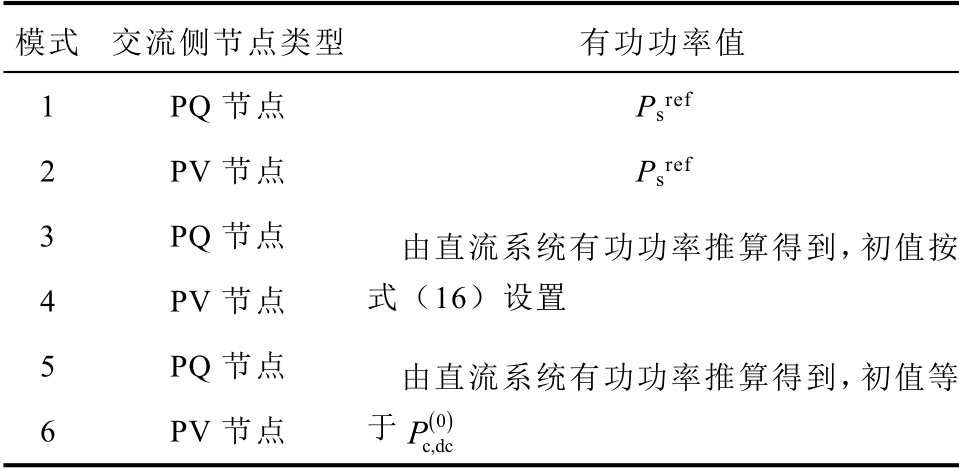
含有VSC 的交流网络与纯交流网络潮流模型的区别主要体现在对与VSC 偶联的S 节点的处理上。对于表1 所示的六种模式，其等效节点类型和首次运算时有功功率参考值获取方法见表2，无功功率或电压参考值均取给定值。
表2 VSC 交流侧参数取值表
Tab. 2 VSC AC side parameter value table
注：上标ref 表示VSC 的给定值。
模式 交流侧节点类型 有功功率值 1 PQ 节点 Psref 2 PV 节点 Psref 3 PQ 节点 由直流系统有功功率推算得到，初值按式（16）设置 4 PV 节点 5 PQ 节点 由直流系统有功功率推算得到，初值等于 ( )0 c,dc P 6 PV 节点
首次运算时，交流节点S 在控制模式3～6 下有功功率Ps 并非控制量，需要设置初值。对于控制模式3 或模式4，其直流侧节点为V 节点，一般直流网络仅有一个节点采用这一控制模式来实现功率平衡。此时，可假设直流网络无损[17]，并根据所有VSC 节点注入直流网络的有功功率之和为零这一规律，设置其初值
即
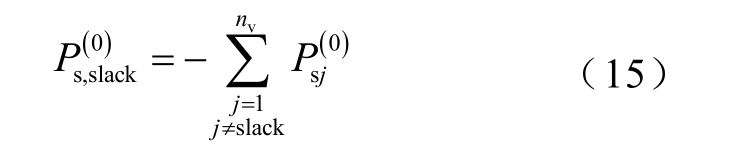
式中，nv 为系统中VSC 的数量；slack 为V 节点，即直流松弛节点。
对于控制模式5 或模式6，同样忽略VSC 中各元件损耗，令其初值
与VSC 直流侧
给定的初值
设含有不确定注入功率的交流网络共有n 个节点，其中含有m 个PQ 节点，将潮流方程中电压幅值、电压相位均以仿射数形式进行运算，从而交流网络中节点i 的功率方程可对应表示为
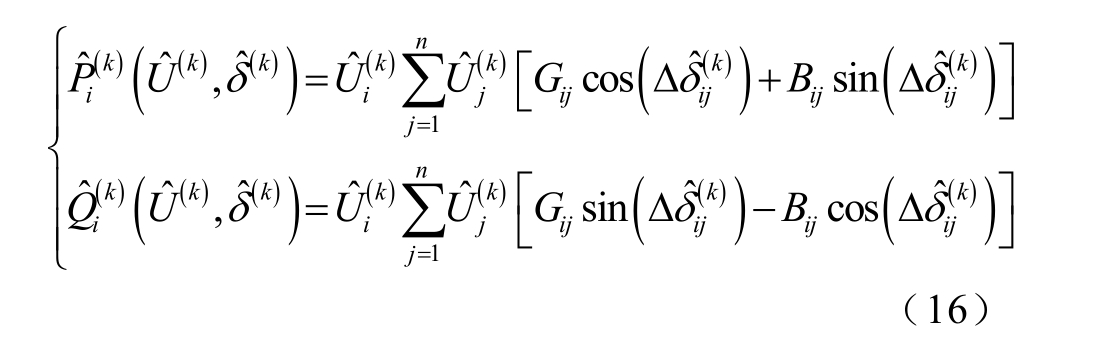
式中，
为迭代次数。
设交流网络PQ 节点注入功率为
可将其表示为
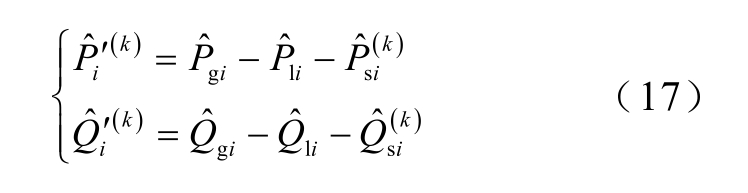
式中，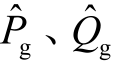
分别为发电机注入的有功、无功功率；
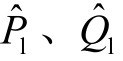分别为负荷消耗的有功、无功功率；
为VSC 与交流侧节点的交换功率，纯交流节点的值为0。
由此，交流网络的修正方程可以表示为
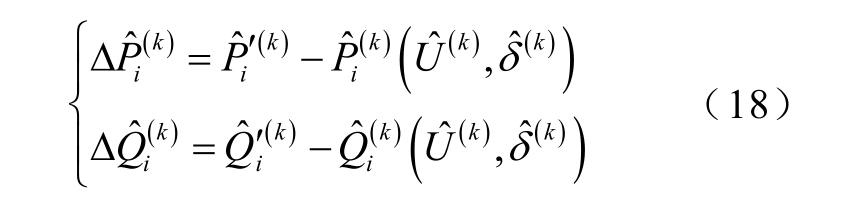
进而，依据潮流计算P-Q 分解法，式（18）的修正方程可以表示为
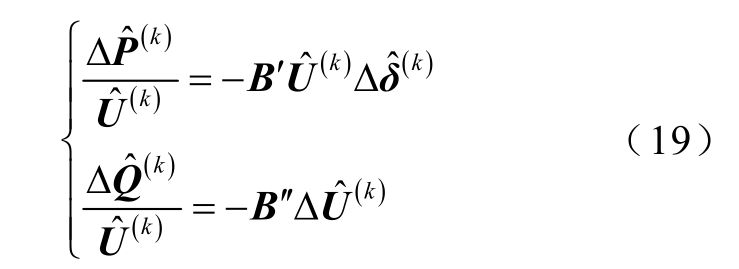
其 中 
式中，矩阵 B ′、B ′均由节点导纳矩阵虚部构成；B′为n-1 阶，即不含平衡节点对应行列；B ′为m 阶，即不含平衡节点和PV 节点所对应行列。
需要说明的是，本文采用P-Q 分解法而不是牛顿-拉夫逊法（以下简称牛-拉法）求解潮流方程的原因是，牛-拉法的雅可比矩阵每次迭代均需更新，其计算过程中包含大量的乘、除、三角函数运算，此类函数运算会产生额外误差项的运算，而额外误差项的积累放大导致了计算速度的降低与计算精度的降低[21]。P-Q 分解法的雅可比矩阵为常数阵，因此，交直流系统仿射潮流的求解采用P-Q 分解法可以较好地避免额外误差项的运算与误差放大。后文将会对此给出算例验证。
利用式（20），求取此次迭代电压幅值与相位修正量的仿射数，进而实现电压幅值与相位的更新。
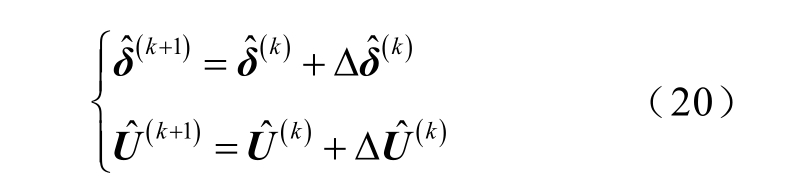
上述迭代过程中，实现了交流网络内不确定性信息的传递。
仿射潮流中交流网络的收敛条件为：迭代前后电压幅值与相位小于允许误差：
3.1.2 换流器参数计算过程
在交流电网状态量迭代更新后，可得到与VSC相连的交流节点S 处的仿射数形式的节点电压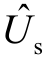 
和交流节点注入VSC 的功率
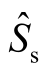。由此，换流器支路电流和电压的仿射值为
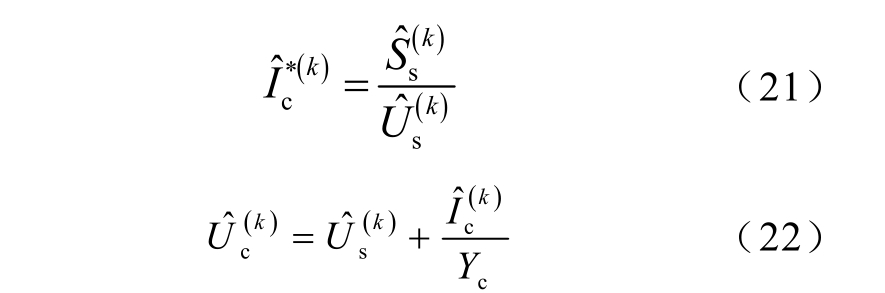
继而，换流器交流侧C 点功率可表示为
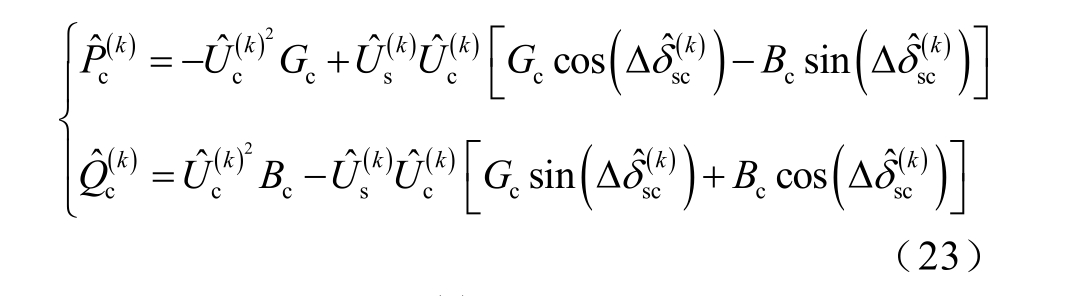
考虑换流器的损耗 
可得注入直流网络的有功功率为
3.1.3 直流网络潮流计算过程
假定直流网络共有nd 个节点，前md 个为P 节点（I 类型节点），节点i 仿射形式的节点功率方程为
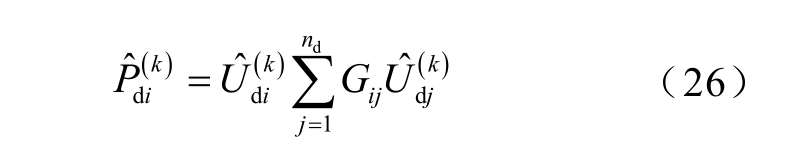
同时，节点i 注入有功功率的仿射数可表示为
式中，
分别为节点i 的电源功率和负荷功率 的 仿 射 值。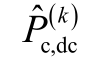
的值是由交流侧潮流迭代更新结果推导得到的，由此实现了交流网络噪声元不确定性向直流网络的传递。
由此，在仿射形式下，直流网络的修正方程可表示为
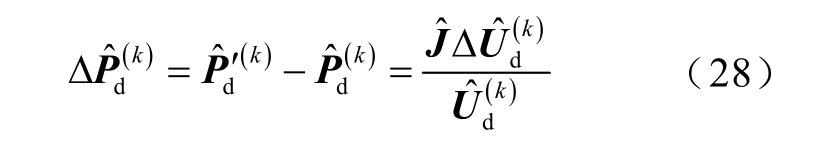
其中
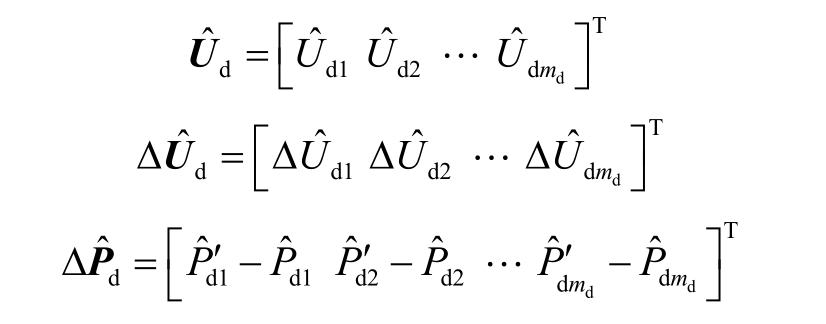
式中，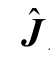
为md 阶雅各比矩阵，其对角及非对角元素分别为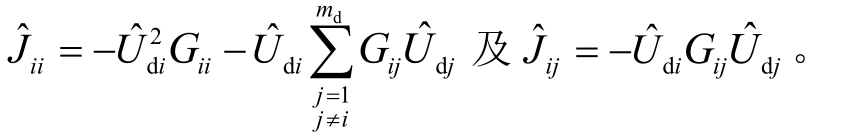
利用修正方程式（28），可求得电压修正值，从而得到新的直流电压值为
对于直流网络潮流，其收敛标准为：Ⅰ类型节点前后两次求解得到的电压差值小于容许误差
3.1.4 直流Ⅴ节点参数更新
对于直流Ⅴ节点，即Ⅱ、Ⅲ类型节点，在直流网络Ⅰ类型节点电压值更新后，可以通过式（26）求解更新节点的有功功率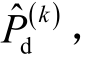 
而后直流Ⅴ节点利用式（30）求得相应
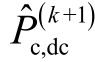为
Ⅲ类型节点获得值后，利用式（31）求得相应节点的电压更新值，以便下次迭代。
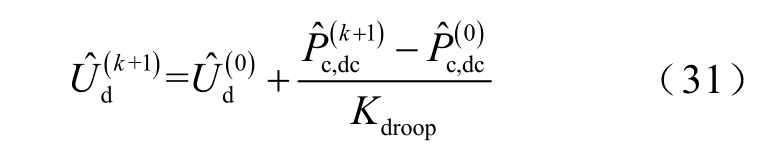
在获得VSC 注入Ⅱ类型及Ⅲ类型节点的功率值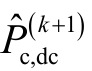 
后，通过式（32），可求得VSC 直流侧C 点功率值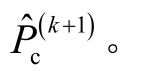
进一步，结合换流器参数和支路结构参数，可以推导得到VSC 与交流侧节点S 的交换功率
实现新一轮的交替迭代。
3.2 交替迭代法求解流程
交直流系统交替迭代法求解流程如图2 所示。
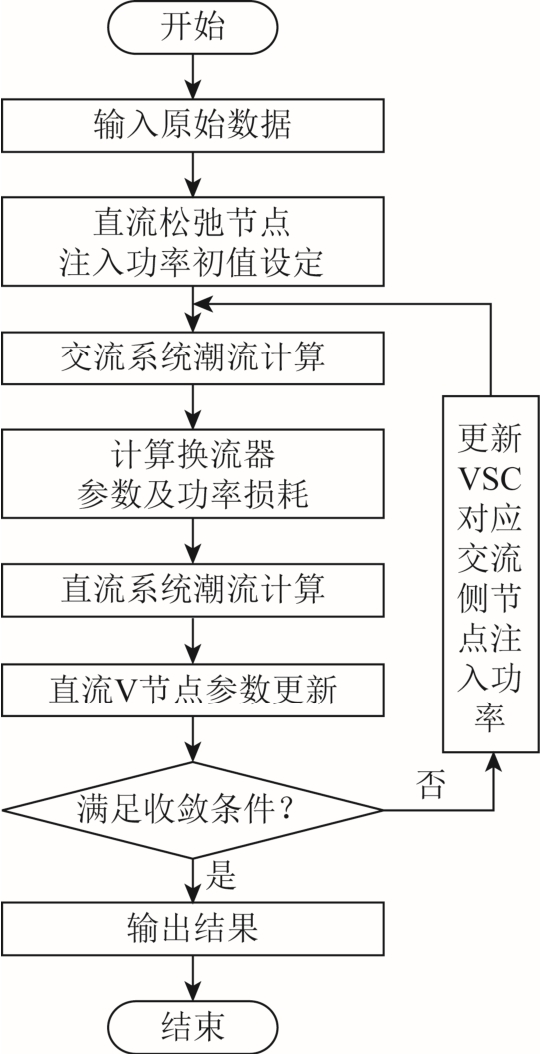
图2 交直流系统交替迭代法流程示意图
Fig.2 Alternating iterative method for solving AC/DC power flow
其各步骤说明如下：
1）输入系统参数。
2）通过式（15）确立直流松弛节点与交流侧交换的功率初值，置迭代标志位m1=0，m2=0。
3）通过式（16）～式（20）完成对交流网络的一次迭代求解，并进行收敛判断，若不符合收敛条件，设置标志位m1=1。
4）通过式（21）～式（25）完成对VSC 的参数运算，得到VSC 与直流网络的交换功率
5）通过式（26）～式（29）完成直流网络一次潮流迭代，并进行迭代收敛判断，若有不符合收敛条件的节点，设置标志位m2=1。
6）对直流网络的Ⅴ节点（Ⅱ类型和Ⅲ类型节点）利用式（26）求解
并通过式（31）更新Ⅲ类型节点电压，通过式（32）计算Ⅴ节点的
进而得到
7）判别此次交直流系统潮流的迭代计算是否满足收敛条件：若m1+m2=0 则说明交直流系统均已收敛，潮流计算结束，输出求解结果；若不满足，m1、m2 清零，返回步骤3）继续迭代。
在交直流潮流中，输入功率的不确定性对系统电压的影响可以由修正方程体现。同时，在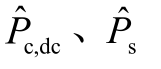
的更新过程中，潮流计算分别完成了不确定噪声元在交流侧和直流侧的相互传递。
4 算例分析
为验证本文所提出的交直流系统仿射潮流计算方法的有效性，在Matlab 2014a 仿真平台上对算法进行了测试。
4.1 算法性能测试
测试系统由两个交流网络通过4 节点直流网络相连构成，算法系统如图3 所示。其中，1 号交流网络为IEEE 14 节点网络，2 号交流网络为IEEE 30节点网络，具体电气连接如附图2 所示。
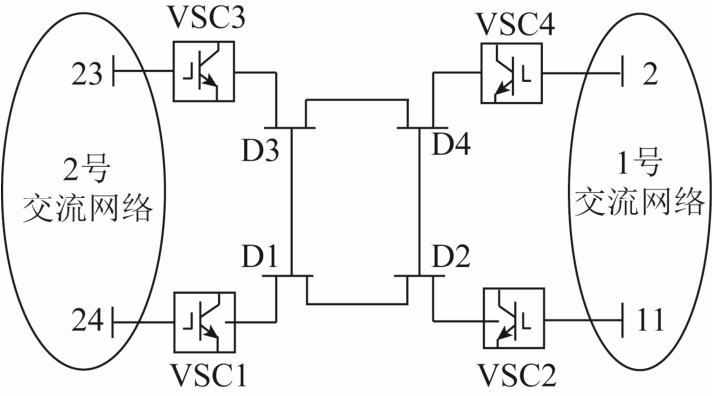
图3 算例系统简化示意图
Fig.3 Simplified structure of the case study system
设系统额定容量 NS 为100MV·A。直流线路参数见表3。同时，设置各VSC 参数相同，其复合阻抗为
损耗系数a、b、c 分别为
收敛精度为 ξ= 10- 5。文中所有计算均采用标幺值。
表3 直流网络线路参数
Tab.3 DC network line parameters
首端节点号 末端节点号 电阻R(pu) 1 2 0.015 1 3 0.015 2 4 0.010 3 4 0.015
4.1.1 算法性能对比
假设1 号交流网络9 号节点、2 号交流网络7号和21 号节点注入功率存在波动，分别为[26.55+ j14.94, 32.45+j18.25]、[20.52+j9.81, 25.08+j11.99]及[15.75+j10.08, 19.25+j12.32]，单位kV·A,从而其对应仿射形式表示的注入功率可表示为29.5+j16.6+ (2.95+j1.66)ε1 、 22.8+j10.9+(2.28+j1.09)ε2 、 17.5+ j11.2+(1.75+j1.12)ε3，单位kV·A。四个VSC 的控制模式及控制参数见表4。
表4 VSC 控制模式及相关参数
Tab.4 VSC control mode and related parameters
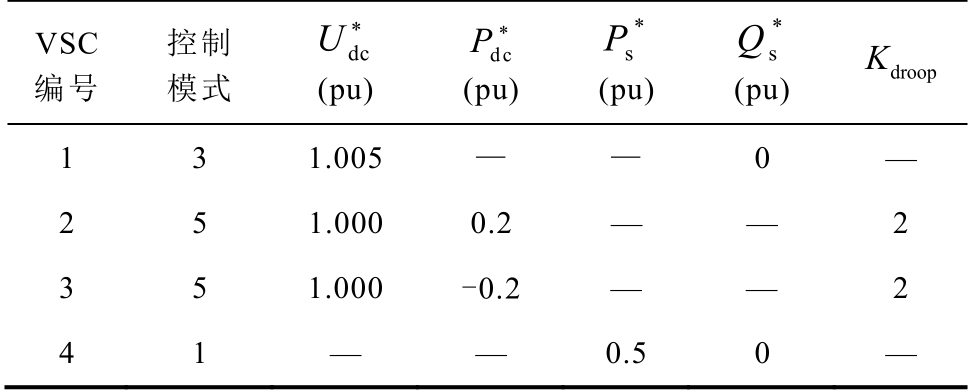
VSC 编号 控制模式 dc U *(pu) dc P *(pu) *sP(pu) *s Q(pu) droopK 1 3 1.005 — — 0 — 2 5 1.000 0.2 — — 2 3 5 1.000 -0.2 — — 2 4 1 — — 0.5 0 —
表5 部分节点电压幅值计算结果
Tab. 5 Partial node voltage amplitude results
系统号 节点号 电压幅值(pu) 电压相位/(°) 下限 上限 下限 上限 1 号交流网络 9 1.030 1.043 -11.812 -10.727 10 1.032 1.037 -11.746 -10.714 11 1.032 1.042 -10.883 -9.953 2 号交流网络 4 1.019 1.029 -6.166 -5.671 7 1.012 1.037 -8.678 -8.183 9 1.035 1.039 -7.899 -7.544
表6 VSC 参数计算结果
Tab. 6 VSC parameter calculation results
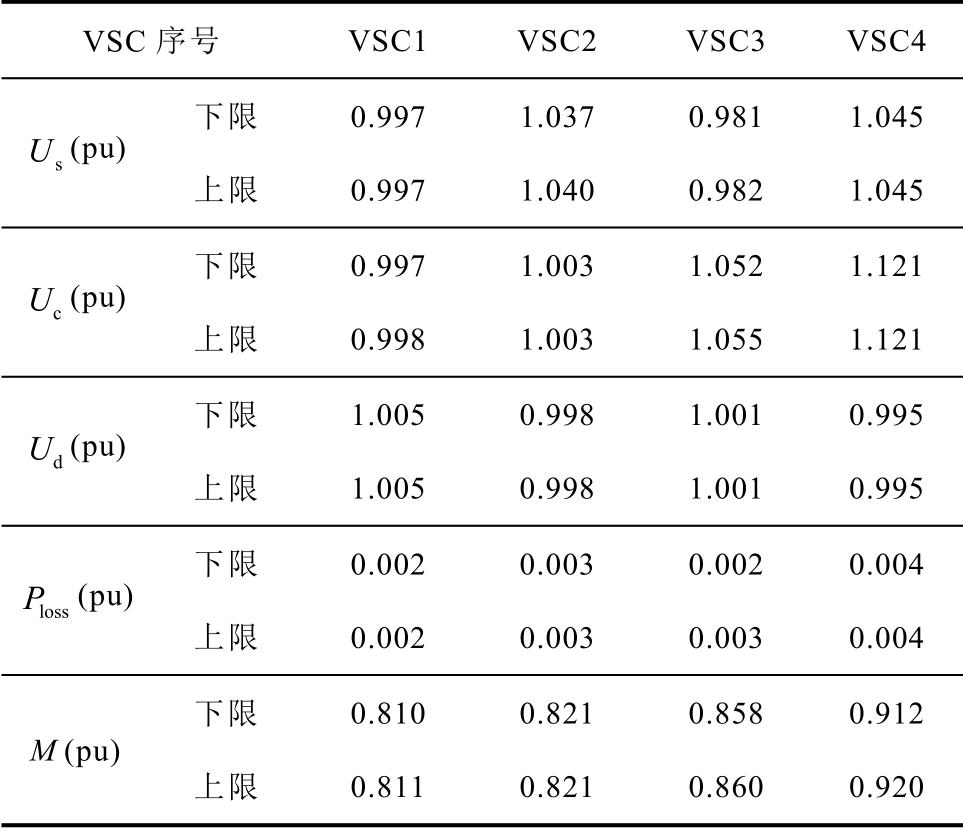
VSC 序号 VSC1 VSC2 VSC3 VSC4 s U (pu) 下限 0.997 1.037 0.981 1.045 上限 0.997 1.040 0.982 1.045 c U (pu) 下限 0.997 1.003 1.052 1.121 上限 0.998 1.003 1.055 1.121 d U (pu) 下限 1.005 0.998 1.001 0.995 上限 1.005 0.998 1.001 0.995 loss P (pu) 下限 0.002 0.003 0.002 0.004 上限 0.002 0.003 0.003 0.004 M (pu)下限 0.810 0.821 0.858 0.912 上限 0.811 0.821 0.860 0.920
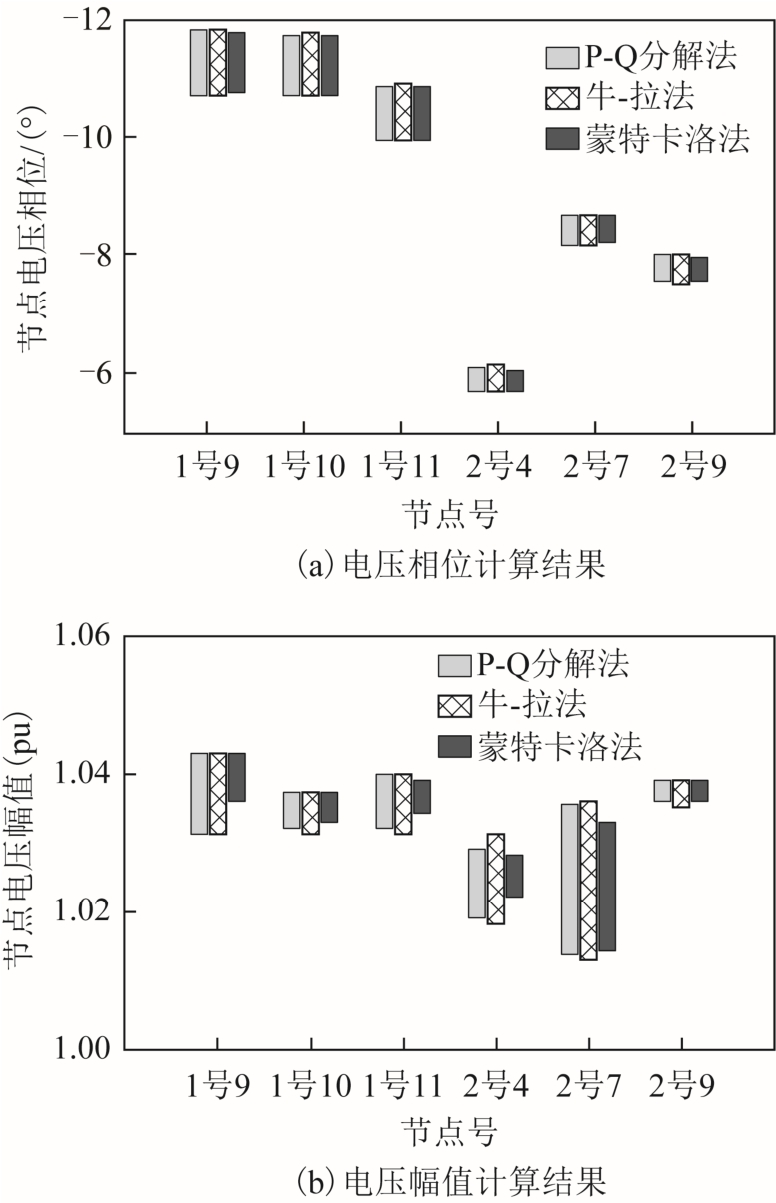
图4 不同算法结果对比图
Fig.4 Comparison of results of different algorithms
表7 不同算法的比较
Tab.7 Comparison of different algorithms
算法类型 结果 计算时间/s P-Q 分解法 收敛 1.34 牛-拉法 收敛 6.21 蒙特卡洛法 收敛 651.24
潮流计算结果见表5 和表6。考虑到仿射数结果查看不便，表中结果以区间形式表示。为体现该算法优良性能，与牛-拉仿射算法和蒙特卡洛模拟法结果进行了对比。图4 为三种方法下部分节点的电 压值对比结果，表7 为各算法的计算时间对比。其中，表7 中各方法的处理时间为从输入原始数据到潮流计算收敛的时间。此外，本文中所采用的蒙特卡洛法在不确定注入功率区间内以均匀分布随机抽样，进行104 次P-Q 分解法潮流计算，取各结果中的最小、最大值作为最终结果的下界与上界。
通过对比P-Q 分解法与牛-拉法的计算结果可以看出，基于P-Q 分解法的仿射算法计算时间更短，并且，P-Q 分解法所得到的不确定区间更窄，表现出了更好的计算精度，验证了P-Q 分解法在仿射潮流计算中的良好性能。
另外，对P-Q 分解法和蒙特卡洛法计算结果进行比较：P-Q 分解法的结果完全包含蒙特卡洛的计算结果，且结果的保守性不大，即P-Q 分解法结果具有完备性，同时其计算速度较蒙特卡洛法有百倍级差别。
综上分析，采用P-Q 分解法求解仿射潮流可在较短时间内获得不确定功率注入范围内的所有可能结果，保守性较小、效率高。
4.1.2 算法收敛性验证
为进一步验证 P-Q 分解法下交直流仿射潮流算法的良好性能，本节将采用更大的算例系统对其进行验证。本节的算例系统将图3 系统的1 号交流网络替换为IEEE 118 节点网络，其他结构及参数不变。
假设1 号交流网络11 号节点、60 号节点和70号节点注入功率分别为[63+j20.7,77+j25.3]、[70.2+ j2.7,85.8+j3.3]、[15.75+j10.08,19.25+j12.23]，单位kV·A,即其仿射形式的注入功率为：70+j23+(7+ j2.3)ε1、78+j3+(7.8+j0.3)ε2、66+j22+(6.6+j2.2)ε3和17.5+ j11.2+(1.75+j1.12)ε4，单位kV·A。同时，图5 和表8 给出了潮流结果并与蒙特卡洛模拟法进行了对比，以验证该算例下潮流计算收敛结果的正确性。
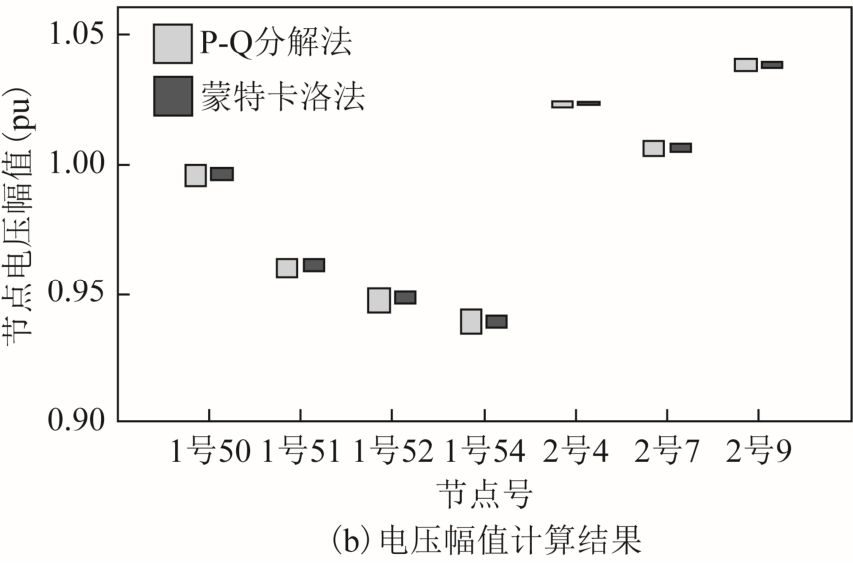
图5 潮流计算结果
Fig.5 Power flow calculation results
表8 计算结果对比
Tab.8 Comparison of different algorithms
算法类型 结果 时间/s P-Q 分解法 收敛 7.19 蒙特卡洛法 收敛 6 014.579
在此情况下，P-Q 分解法7.19s 实现收敛，结果能够包含蒙特卡洛模拟法的计算结果，说明该算法在该算例下依然具有很好的快速性、收敛性和完备性，进一步验证了该算法的性能。
4.2 不确定输入变量对系统状态的影响力分析
为研究交直流系统中不确定输入变量对系统造成的影响，在不考虑换流器容量限制等其他因素的影响下，对图3 所示算例进行不确定输入变量对系统状态的影响力指标的量化分析。节点注入功率波动假设如下：1 号交流网络3 号、4 号、9 号节点的注入功率较其确定值存在 10%± 的波动，分别以噪声元ε1、ε2、ε3 表征其波动量。其他参数设置不变。
图6、图7 给出了测试情景下各网络节点电压的计算结果，图8 所示为噪声元对状态变量影响力指标计算结果，并得到噪声元对系统影响力指标结果见表9。
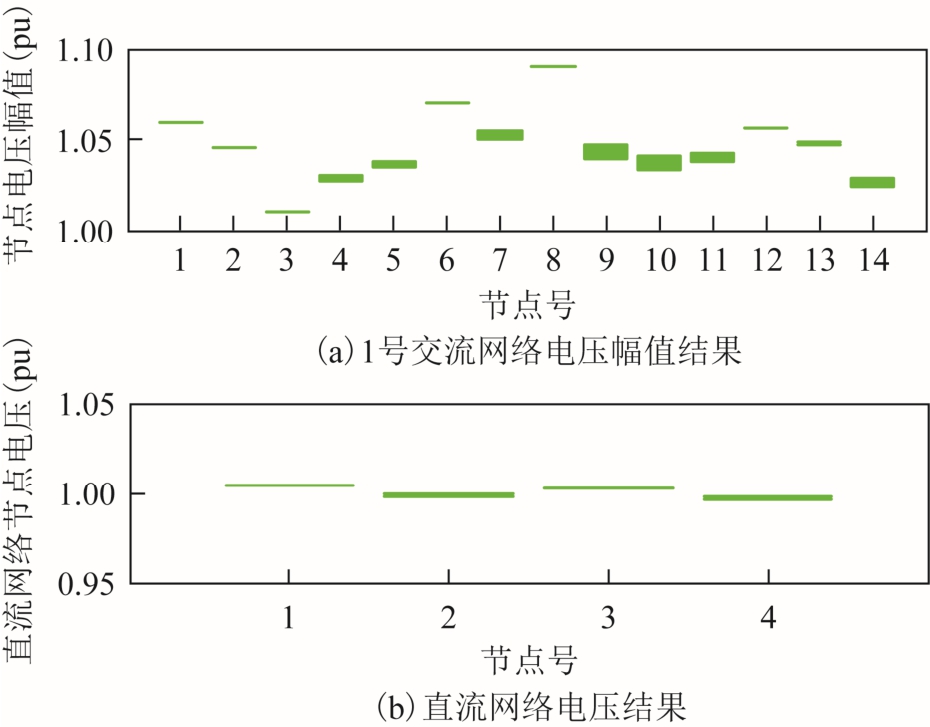
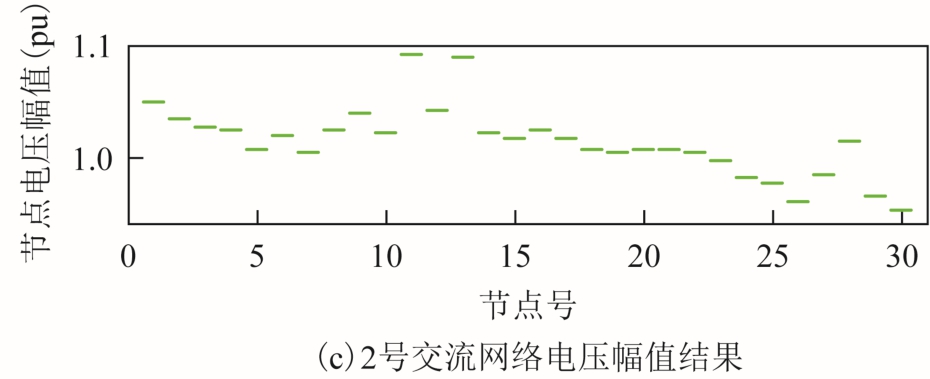
图6 节点电压幅值计算结果
Fig.6 Calculation results of voltage amplitude
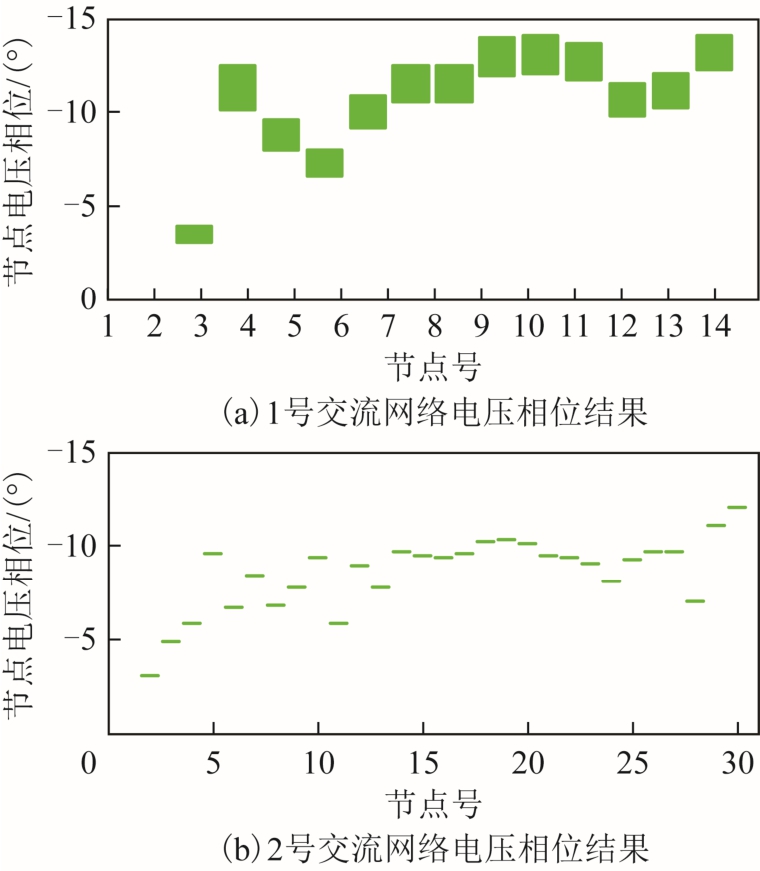
图7 节点电压相位计算结果
Fig.7 Calculation results of voltage phase angle
图8 1 号交流网络节点电压不确定性影响力指标
Fig.8 Voltage uncertainty influence index results of No.1 AC network
表9 噪声元影响力指标结果
Tab.9 Results of influence index of noise element （%）
噪声元1 噪声元2 噪声元3 电压幅值 5.6 17.4 77.0 电压相位 45.4 26.1 28.5
通过图6、图7 所示结果可以看出，1 号交流网络节点电压波动较为明显，直流网络及2 号交流网络的节点电压波动较为微弱。此外，4.1.2 节中的算例结果也可进一步验证该结论，图5 结果中 IEEE 118 节点网络（即不确定注入功率所在网络）电压幅值及相位结果的波动区间更明显。这是由于VSC控制量的存在，实现了交直流变量间一定程度的解耦，不确定输入变量的影响会被削弱。下文将着重分析不确定输入变量对所在的1 号交流网络的不确定性影响力指标水平。
通过对图8 和表9 影响力指标的分析可以得到：
1）噪声元对各自所在节点的不确定影响力较大，比如噪声元3 对其所在的9 号节点的电压幅值、相位影响力均较大，分别为86.67%、37.34%。
2）通过表9 噪声元对系统影响力指标分析，能够得到对系统不确定性影响最大的输入变量是噪声元3(ε3)所在的9 号节点，对系统电压幅值和相位整体的不确定性贡献分别达到77%和28.5%。因此，本指标的运算可以帮助工作人员正确寻找到对系统不确定水平影响最大的不确定注入功率，从而有针对性地实施优化方案。
3）不确定注入功率的数值大小不是影响系统不确定性的主要原因，本算例3 号节点的不确定注入功率数值最大，但对系统不确定性影响力最大的是9 号节点所对应的噪声元3(ε3)。
4）不确定注入功率的影响规律对电压幅值和电压相位不同。算例中，在扰动波动幅度相同条件下，电压幅值受9 号节点注入功率的噪声元3(ε3)影响最大，电压相位受各噪声元的影响则相对平均。由于噪声元3(ε3)所在的9 号节点与网络中各节点均有较强的电气连接，推测电压幅值的波动主要受电气连接强度的影响；而不确定注入功率对电压相位的影响则主要取决于功率波动幅值。
为进一步验证结论4 的准确性，设定3、4、9 号节点注入功率分别存在±20%、±10%和±5%的波动，对应为噪声元ε1、ε2 和ε3 的噪声系数（对比情境）。仿真计算得到噪声元对状态变量影响力指标计算结果如图9，噪声元对系统影响力指标结果见表10。
图9 对比情景1 下1 号交流网络电压不确定性 影响力指标图
Fig.9 Voltage uncertainty influence index result of No.1 AC network under the contrast situation
表10 对比情景1 下噪声元影响力指标结果
Tab.10 Results of influence index of noise element under the contrast situation （%）
噪声元1 噪声元2 噪声元3 电压幅值 11.2 16.3 72.5 电压相位 69.2 19.9 10.9
从图9 和表10 的结果可以看出尽管噪声元3(ε3)具有最小的功率波动输入，但依然对系统各节点电压幅值波动影响最大，达到72.5%；而电压相位波动则主要受噪声元波动幅度最大的噪声元 1(ε1)的影响。因此可以验证，以上关于噪声元对电压幅值和电压相位影响力最相关因素的分析是合理的。
通过以上分析可知：通过对交直流系统仿射潮流的量化分析，能够获取各不确定注入功率对系统影响的量化值，同时也可获知对各节点不确定性影响力最大的不确定注入功率；电力系统中节点电压的不确定性既受各节点波动幅度大小的影响，也受噪声元在电网中位置的影响，波动幅度对电压相位影响力显著，而电压幅值的波动则主要受噪声元位置的影响。因此，在电网出现电压波动越限等问题时，通过本文潮流分析方法，可以找到对电网状态量不确定性影响大的噪声元，系统工作人员可针对性地根据相应节点的波动特点实施对应的防控措施，提高电网运行的安全性。
5 结论
本文建立了一种含VSC 的交直流系统仿射潮流算法，方法基于交替迭代法形成了交直流系统的仿射潮流模型，并结合P-Q 分解法实现了模型的快速求解。算例验证，该算法可为含有不确定输入变量的交直流系统提供快速、可靠的仿射潮流结果，同时利用不确定输入变量对系统状态量影响力指标可实现不确定输入变量影响力的量化分析。算例分析表明，含VSC 的交直流系统中，交流网络中不确定注入功率对其所在网络影响力最大；噪声元波动幅度对电压相位影响力显著，而电压幅值的波动则主要受噪声元所在位置的影响。因此，该算法可为系统工作人员提供有效的决策参考，具有较高的实用价值。
附 录
实现三角函数的仿射运算重点在于寻求一个合适的线性函数替代原函数。本文采用切比雪夫线性逼近法[21]进行线性化函数的求取。如附图1 所示。
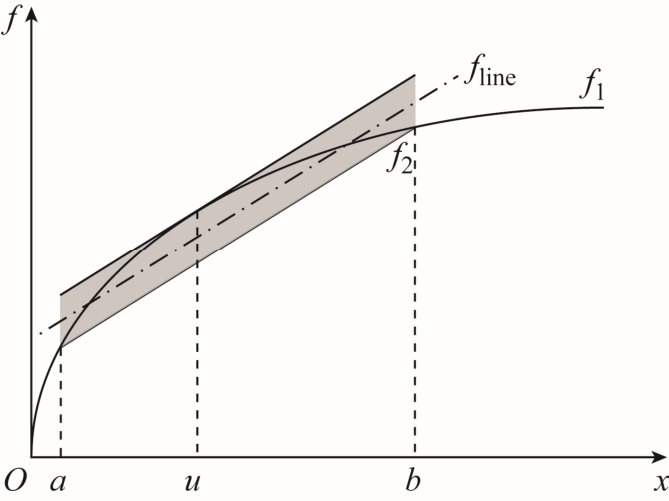
附图1 线性化原理
App.Fig.1 The principle of linearization
对于某非线性函数 1f，若已知其自变量范围在[a, b]内，则其线性化函数求解过程如下：
首先求取过(a, 1f(a))和(b, 1f(b))两点的函数 2f ，其斜率为
然后求取原函数上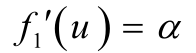
的点u，进一步求取
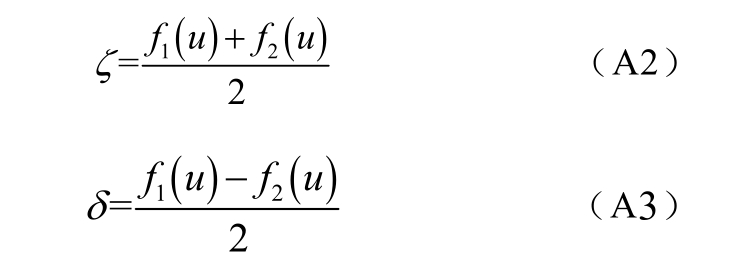
因此，可以获得其线性化近似函数为
由切比雪夫线性逼近的性质可知，最大误差点存在于a、b、u 三点，最大误差为δ。
在获取线性化函数 linef 后，其仿射运算只需要将自变量x 替换为相应的ˆx便可以简便的运算。
算例系统电气连接图如附图2 所示。
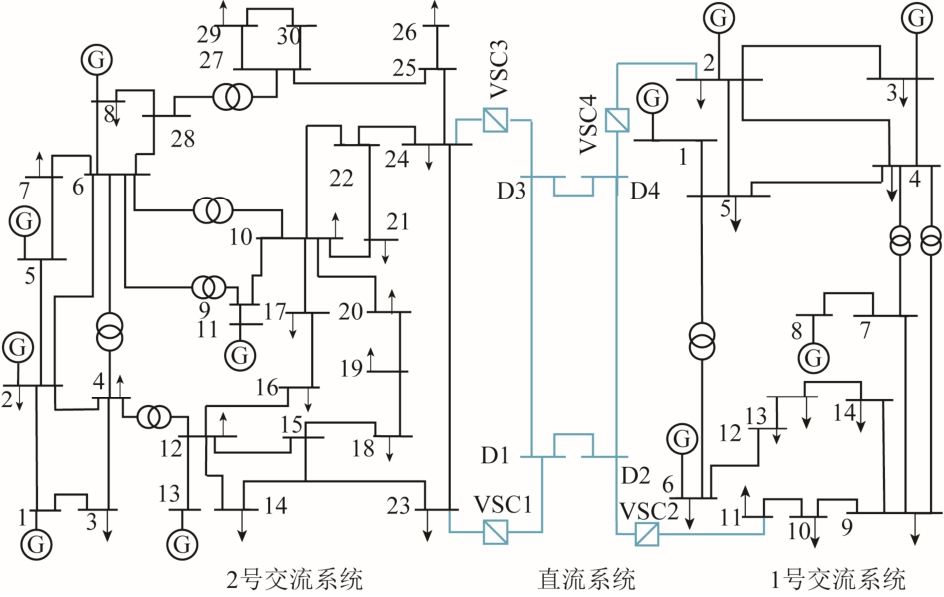
附图2 算例系统电气连接图
App.Fig.2 Electrical connection of case study system
[1] 刘振亚. 全球能源互联网[M]. 北京: 中国电力出版社, 2015.
[2] 李兴源, 曾琦, 王渝红, 等. 柔性直流输电系统控制研究综述[J]. 高电压技术, 2016, 42(10): 3025-3037.
Li Xingyuan, Zeng Qi, Wang Yuhong, et a1. Summary of research on flexible direct current transmission system control[J]. High Voltage Technology, 2016, 42 (10): 3025-3037.
[3] 杨仁炘, 施刚, 蔡旭. 海上全直流型风电场的电压源型控制[J]. 电工技术学报, 2018, 33(增刊2): 546-557.
Yang Renxin, Shi Gang, Cai Xu. Voltage source control of offshore full DC wind farm[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 546-557.
[4] 刘英培,杨小龙,梁海平,孙海新,赵玮.适用于混合多端直流输电系统的非线性下垂控制策略[J].电力系统自动化, 2018, 42(22):178-191.
Liu Yingpei, Yang Xiaolong, Liang Haiping, et al. Nonlinear droop control strategy for hybrid multi-terminal DC systems[J]. Automation of Electric Power Systems, 2018, 42(22):178-191.
[5] 孙玉树, 张国伟, 唐西胜, 等. 风电功率波动平抑下的 MPC 双储能控制策略研究[J].电工技术学报, 2019, 34(3): 571-578.
Sun Yushu, Zhang Guowei, Tang Xisheng, et al. Research on MPC and daul energy storage control strategies with wind power fluctuation mitigation[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 571-578.
[6] 曹佳, 严正, 李建华, 等. 含风电场交直流混联系统的概率潮流计算[J]. 电力自动化设备, 2016, 36(11): 94-101.
Cao Jia, Yan Zheng, Li Jianhua, et al. Probabilistic power flow calculation for AC-DC hybrid system with wind farms[J]. Electric Power Automation Equipment, 2016, 36(11): 94-101.
[7] Kumar S, Chaturvedi D K. Optimal power flow solution using fuzzy evolutionary and swarm optimization[J]. International Journal of Electrical Power & Energy Systems, 2013, 47(47): 416-423.
[8] Adusumilli BS, Raj V, Boddeti K K. Modified affine arithmetic-based power flow analysis with uncertainty[J]. IET Generation Transmission & Distribution, 2018, 12(18): 4225-4232.
[9] 韩亮. 计及间歇式电源不确定性的电力系统区间—仿射分析方法[D]. 天津: 天津大学, 2014.
[10] Vaccaro A, Canizares C A, Villacci D. An affine arithmetic-based methodology for reliable power flow analysis in the presence of data uncertainty[J]. IEEE Transactions on Power Systems, 2010, 25(2): 624-632.
[11] Wang Yang, Wu Zaijun, Dou Xiaobao, et al. Interval power flow analysis via multi-stage affine arithmetic for unbalanced distribution network[J]. Electric Power Systems Research, 2017, 142: 1-8.
[12] 王守相, 韩亮. DG 出力不确定性对配电网影响力分析的复仿射数学方法[J]. 中国电机工程学报, 2014, 34(31): 5507-5515.
Wang Shouxiang, Han Liang. Complex affine arithmetic based method for the analyses of DG's uncertainty influence on distribution network[J]. Proceedings of the CSEE, 2014, 34(31): 5507-5515.
[13] 韩亮, 王守相. 含光伏风电的基于仿射算法的配电三相潮流计算[J]. 电网技术, 2013, 37(12): 3413-3418.
Han Liang, Wang Shouxiang. Affine algorithm-based calculation of three-phase power flow in a distribution network connected with PV generation and wind generation[J]. Power System Technology, 2013, 37(12): 3413-3418.
[14] 丁涛, 崔翰韬, 顾伟, 等. 基于区间和仿射运算的不确定潮流算法[J]. 电力系统自动化, 2012, 36(13): 51-55, 115.
Ding Tao, Cui Hantao, Gu Wei, et al. An uncertainty power flow algorithm based on interval and affine arithmetic[J]. Automation of Electric Power Systems, 2012, 36(13): 51-55, 115.
[15] Mohamadreza B, Mehrdad G. A multi-option unified power flow approach for hybrid AC-DC grids incorporating multi-terminal VSC-HVDC[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2376-2383.
[16] Chai Runze, Zhang Baohui, Dou Jingming, et al. Unified power flow algorithm based on the NR method for hybrid AC-DC grids incorporating VSCs[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4310-4318.
[17] 张潼,王毅,翟明玉,等.含电压源换流器的交直流混联电网状态估计快速解耦法[J].电力系统自动化, 2018, 42(21): 70-78.
Zhang Tong, Wang Yi, Zhai Mingyu, et al. Fast decoupling method for state estimation of AC-DC hybrid grid with voltage source converter[J]. Automation of Electric Power Systems, 2018, 42(21): 70-78.
[18] Wang W Y, Barnes M. Power flow algorithms for multi-terminal VSC-HVDC with droop control[J]. IEEE Transactions on Power Systems, 2014, 29(4): 1721-1730.
[19] Beerten J, Cole S, Belmans R. Generalized steady-state VSC MTDC model for sequential AC-DC power flow algorithm[J]. IEEE Transactions on Power Systems, 2012, 27(2): 821-829.
[20] 陈厚合, 王长江, 姜涛, 等. 基于端口能量的含VSC-HVDC 的交直流混合系统暂态稳定评估[J]. 电工技术学报, 2018, 33(3): 498-511.
Chen Houhe, Wang Changjiang, Jiang Tao, et al. Transient stability assessment in hybrid AC-DC systems with VSC-HVDC via port energy[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 498-511.
[21] Pirnia M, Cañizares C A, Bhattacharya K, et al. A novel affine arithmetic method to solve optimal power flow problems with uncertainties[J]. IEEE Transactions on Power Systems, 2014, 29(6): 2775-2783.
[22] 何仰赞. 电力系统分析[M]. 武汉: 华中工学院出版社, 2002.
[23] Stolfi J, Figueiredo L H D. Self-validated numerical methods and applications[J]. Am J Psychiatry, 1997, 112(9): 673-677.
[24] 关维德, 黄守道, 黄小庆. 一种基于改进模块化多电平换流器的中压风电系统及其控制方法[J]. 电工技术学报, 2018, 33(16): 3782-3791.
Guan Weide, Huang Shoudao, Huang Xiaoqing. A medium-voltage wind power system based on an improved modular multilevel converter and its control method[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3782-3791.
[25] 吴杰, 王志新. 多端柔性直流输电系统的改进下垂控制策略[J]. 电工技术学报, 2017, 32(20): 241-250.
Wu Jie, Wang Zhixin. Improved droop control strategy for multi-terminal flexible DC transmission systems[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 241-250.
[26] Hong R. Architecture of Nan'ao multi-terminal VSC-HVDC system and its multi-functional control[J]. CSEE Journal of Power & Energy Systems, 2015, 1(1): 9-18.
[27] Ou K, Rao H, Cai Z, et al. MMC-HVDC simulation and testing based on the real-time digital simulator and physical control system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(4): 1109-1116.