0 引言
随着配电网规模的不断扩大，大力发展风电和光伏发电等分布式电源（Distribution Generation, DG）已成为未来电网的发展方向[1]。在获取经济效益的同时，为了应对DG 的接入问题，传统配电网必须向具备潮流主动控制能力和与负荷互动能力的主动配电网（Active Distribution Network, ADN）转变[2]。此外，电动汽车（Electric Vehicle, EV）作为一种全新的交通工具，在环保和节能方面具有重要的作用，因此也得到了广泛的应用。但电动汽车充电站的接入将带来充电负荷，其选址问题不仅与EV用户出行的便利有关，也将影响配电网的稳定性[3]。因此，为了更好地解决能源危机和环境问题，建立EV 充电站与配电网的协调规划模型[4]将更具意义。
近年来，与EV 充电站选址相关的研究成果已有不少。文献[5]以投运至目标年综合费用最小为目标，引入加权Voronoi 图来对EV 充电站进行规划；文献[6]以最小化电动汽车日充电等待时间和最小化年建设运维成本为目标，提出基于动态交通仿真的高速公路电动汽车充电站规划方法。另一方面，ADN 规划技术的发展也日渐成熟。文献[7-8]采用规划层和运行层相结合的双层规划思路，分别以网架动态重构和计及时序性的分布式光伏并网为重点，展开ADN 双层规划。为了更好地对ADN 进行优化控制，文献[9-13]在规划中添加了多种主动管理手段，包括馈线升级与新建、储能系统（Energy Storage System, ESS）、静止无功补偿器（Static Var Compensation, SVC）、有载调压变压器（On-Load Tap Changer, OLTC）等。
以上文献虽在充电站规划或ADN 规划上做了大量工作，但就EV 和ADN 的协同规划方面还有所欠缺。此外，考虑EV 充电问题的ADN 系统含有大量的不确定元素，主要包括交通网络中的用户充电需求、配电网络中的负荷需求和DG 出力。现有研究多采用随机规划法或鲁棒优化法来建立相关不确定性模型。
随机规划法通常以场景期望值法[9]或是基于概率密度分布函数的机会约束规划法[14]来建立模型。前者为了保证精度，通常需要大量的场景数据，进而降低计算效率，无法适用于大规模优化问题；后者不仅难以获得准确的概率密度分布，且属于非凸规划，需转为确定性模型才可求解，过程相对复杂。相比之下，鲁棒优化基于确定性集合来建立不确定性模型，不仅易于实现，而且不需大量的数据或是被概率分布所限制。因此，鲁棒优化在处理不确定性模型中更具优势且得以广泛应用。文献[15]针对风电与价格型需求响应存在的不确定性，提出了一种适用于预调度方案可行性检测的鲁棒调度方法。文献[16-17]均考虑了风电出力的不确定性，分别以无功优化和配电网扩展规划为重点进行鲁棒优化。
目前，国内外关于鲁棒优化在充电站选址或是ADN 规划中还鲜有应用。文献[18]对DG 和负荷建立了一定保守度的不确定性时序集合，构建了主动配电网分层鲁棒规划模型。文献[19]采用基约束鲁棒方法，考虑EV 充电需求的不确定性，建立了充电站选址决策模型。前者虽考虑了场景的鲁棒性，但本质上仍属于场景法，不属于鲁棒优化的范畴；后者虽应用了鲁棒优化，但没有考虑EV 充电对配电网的影响，也没有涉及ADN，模型偏于简单。
针对以上不足，本文通过耦合单元来联系ADN和交通网，考虑系统中主要的不确定性元素，提出了一种含EV 充电站选址决策的ADN 二阶段鲁棒规划模型。为了充分体现ADN 的特点，模型考虑了OLTC、SVC、ESS、DG 的联合运行，需求侧负荷削减以及弃风弃光等。因模型中含有大量的非线性项，本文通过Big-M 法和二阶锥规划技术对其进行松弛。另一方面，针对鲁棒规划所呈现的min-max-min形式的二阶段优化问题，采用列约束生成（Column and Constraint Generation, CCG）与Benders 分解相结合的二阶段法进行求解。最后，以一个改进的耦合系统为例进行仿真。仿真结果表明，模型的不确定度将对规划结果产生较大的影响。当合理选择不确定度的数值时，二阶段鲁棒规划将比确定性规划更具经济价值。
1 电动汽车充电站选址建模与网络耦合
1.1 充电站选址决策模型
EV 充电站选址问题主要与交通网络中需求点的需求量、需求点与选址点之间的距离有关。本文基于p-中值模型[19]，考虑充电站的建站固定成本和交通充电成本，以年总成本最小化为目标来确定充电站选址决策模型，具体形式表达为
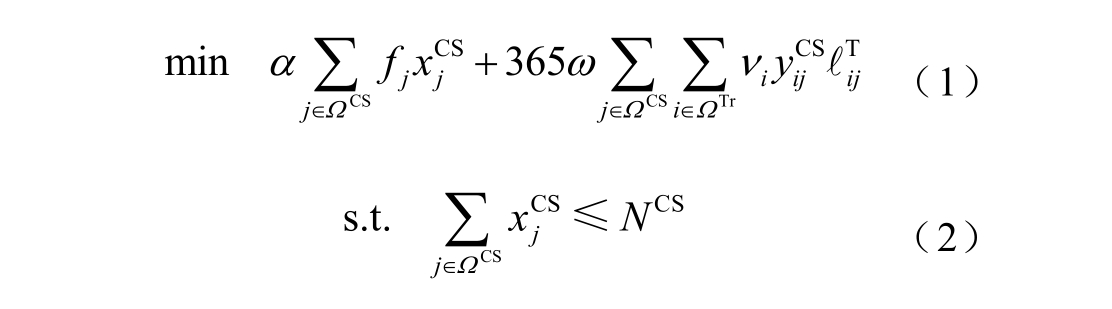
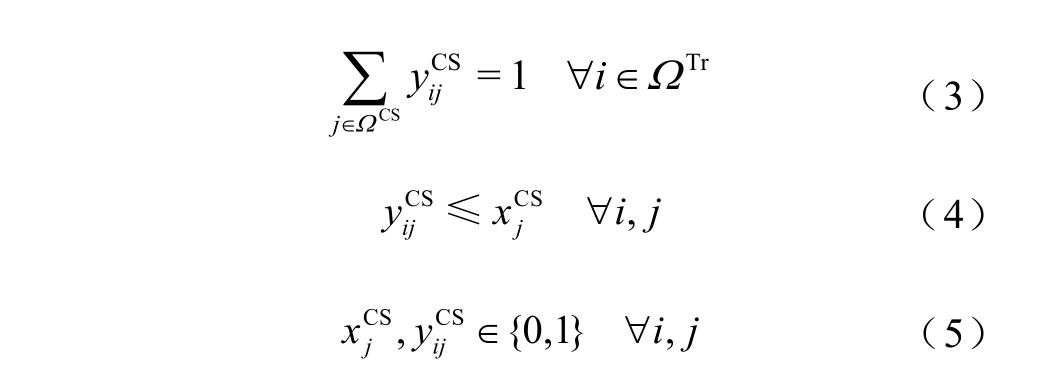
式中，α 为投资年值化系数，与投资年限和贴现率有关；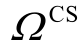
和 
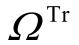分别为充电站建站候选点集合、交通网络需求点集合； f j为候选点j 建设充电站所需的固定成本；
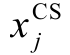为充电站选址的二值决策变量，当节点j 建站时，其为1，否则为0；ω 为单位路程充电成本；
为需求点的需求权重，即该点EV 平均每天需要的充电服务次数，与EV 数量和类型有关；
为二值变量，当需求点i 在候选点j 充电时为1，否则为0；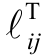
为交通网络中节点i 与j 相连的最短路径距离，可由Floyd 算法[20]求得；
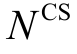为充电站可建的最大个数。
上述约束中，式（3）表示任意需求点的充电需求必须由一个充电站满足；式（4）表示只有建站点才可以提供充电服务。
1.2 电-交耦合单元
交通网络充电服务势必会带来充电负荷，影响配电系统的运行。为了较好地融合交通网和配电网，基于能源集线器[21]的思想，本文引入多个电-交耦合单元来联系两个系统，其具体表现形式及与各网络的关系如图1 所示。
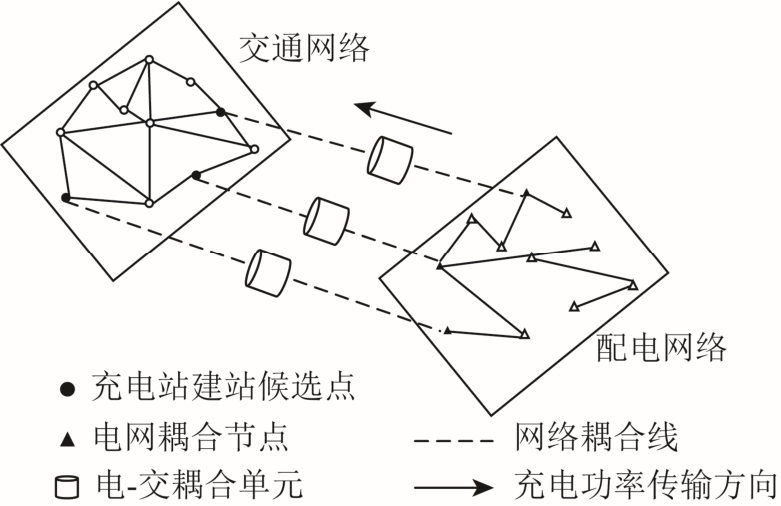
图1 电-交耦合单元示意图
Fig.1 Diagram of the electric-traffic coupling unit
为了便于实现充电需求与充电功率的转换，耦合线相连的两个耦合节点在地理位置上较为靠近。在耦合单元中，充电站的全天充电功率描述为
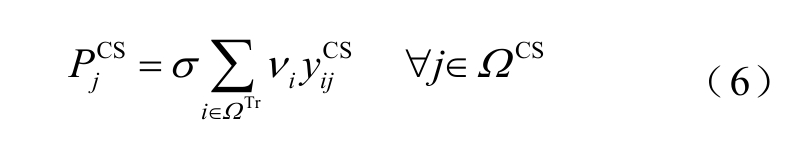
式中，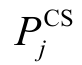
为第j 个充电站平均每天的充电功率；σ为需求与功率之间的转换系数，即单次充电功率。
这部分充电功率将沿着耦合线叠加到对应电力节点的负荷功率上，进而抬高节点原有的负荷水平。充电站的选址结果将影响到式（6）中二值变量的取值，进而影响配电网各个耦合节点的负荷功率，从而实现两层网络间环环相扣的关系。
2 基于耦合单元的主动配电网规划模型
本文以电力为主体并融合考虑EV 充电站选址决策的交通系统，进一步展开ADN 规划。其中，模型的运行层将考虑负荷、DG（本文主要指风力发电(Wind Turbine Generator, WTG)和光伏发电(Photovoltaic Generator, PVG)）以及EV 用户充电的时序特性，基于多场景技术[9,18,22]来计算目标函数。具体的时序特性曲线见附图1。
2.1 目标函数
目标函数不仅包括式（1）中的交通成本，还要考虑配电网的投资成本和运行成本。配电网的投资成本包含配电线路升级与新建成本，OLTC、SVC、DG、ESS 设备投资费用；运行成本主要指主网购电费用、网损费用以及主动削减费用（负荷削减、弃风弃光等），具体表示为
式中，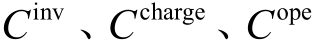
分别为系统的总投资成本、交通充电成本、运行成本；
分别为升级线路和新建线路的备选集合
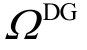为各设备投资的备选节点集合；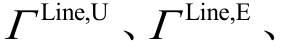
为各投资设备的备选类型集合；
类型集合；
为各投资设备的二进制或整数决策变量；
各设备不同型号t 的单位投资成本；
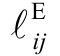为配电线路ij 的长度；
类型DG 下型号t 设备的单台容
分别为运行场景、所有线路、主网发电节点、风机节点、光伏节点、负荷节点集合；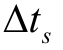
为场景s 在一年中的累积运行时间；
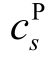为分时电价；
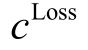为单位网损费
分别为WTG、PVG、有功和无功负荷的单位削减费用；
路电流和电阻；
分别为对应节点j 的主网供电功率、风机发电数据、风机实际出力、光伏发电数据、光伏实际出力、有功和无功负荷削减量。
2.2 约束条件
约束条件除了交通系统的式（2）～式（5）外，还要包括ADN 的投资约束和运行约束。
2.2.1 投资约束
投资决策变量约束主要包括：①各设备要保证线路或节点在候选类型集合中只能选择一种型号进行投资，且为了减小新建线路成本，对于某个新增的负荷节点，只可以选择一条线路进行新建；②DG节点和SVC 节点应设置设备接入台数限值。
因此，具体投资约束式为
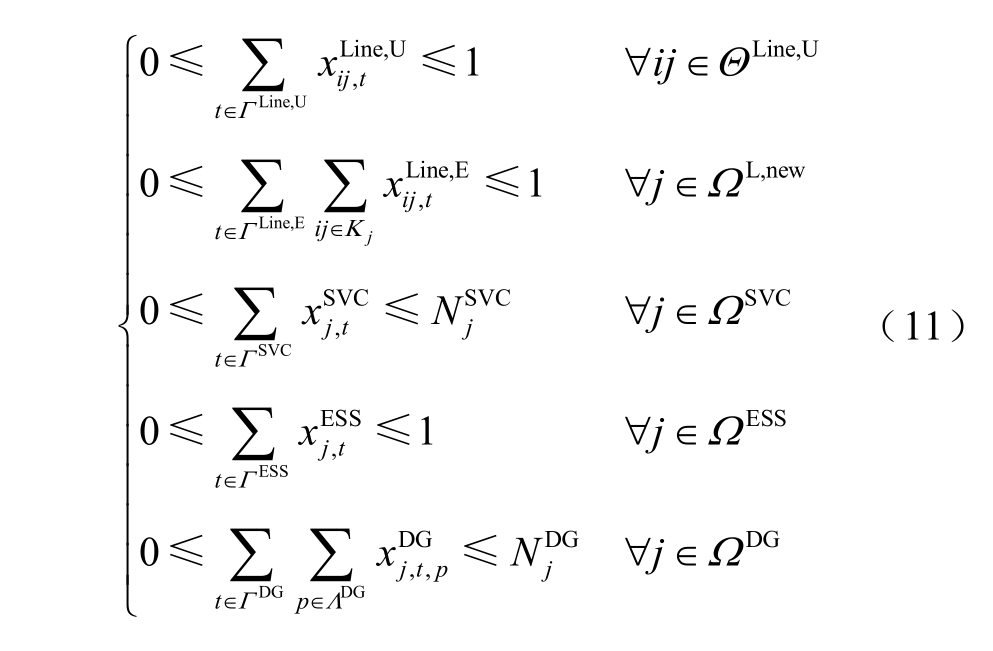
式中，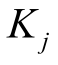
为新增负荷节点j 可连接的备选新建线路集合；
为新增负荷节点集合；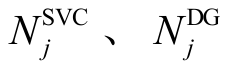 
分别为SVC、DG 节点可安装设备台数的最大值。
2.2.2 运行约束
1）潮流平衡约束及安全约束
原始的潮流平衡方程以及安全运行约束包含较多的非线性项[18]。为了能够采用解析方法有效求解模型，本文采用文献[9,23]中的二阶锥松弛技术，将相关约束式转换为二阶锥形式。
首先对支路电流和节点电压两个变量作等式变换，变换形式为
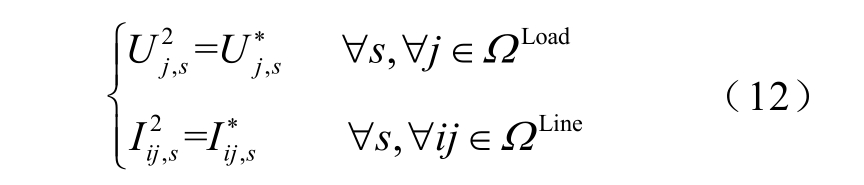
式中，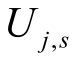
为场景s 下节点j 的电压幅值；
为替换变量。
因此，系统运行成本式（10）则不存在电流二次方项。同时基于Big-M 法，可将具体约束表示为
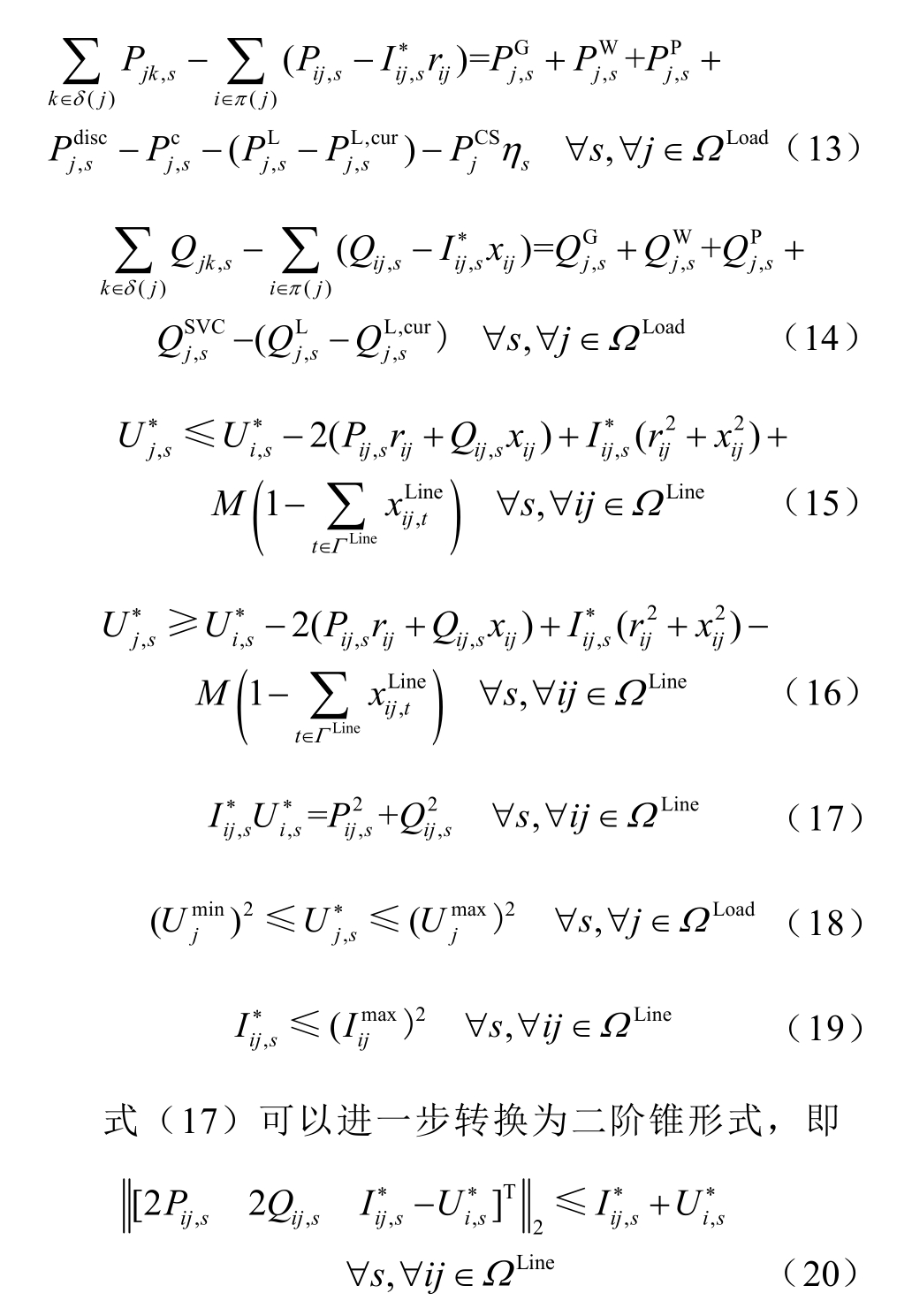
式中，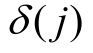
为以节点j 为首节点的支路末节点集合；
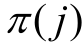为以节点j 为末节点的支路首节点集合；
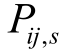和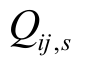
分别为场景s 下流过支路ij 的有功和无功功率；
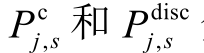分别为场景s 下ESS 节点j 的充电和放电功率；
分别为场景s 下节点j 的有功负荷和无功负荷；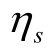
为场景s 下EV 用户充电比例，由对应的时序特性曲线可知；
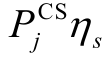即为场景s 下节点j 的EV 充电功率；x ij为支路ij 的电抗
分别为场景s 下节点j 的主网、WTG、
提供的无功功率；M 为很大的常数；
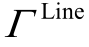为规划方案包括的所有升级和新建线路各自对应的设备类型；
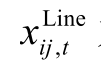为对应的投资变量；
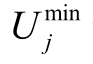分别为节点j 的电压幅值上、下限；
为支路ij 的电流幅值限值。
2）OLTC 运行约束
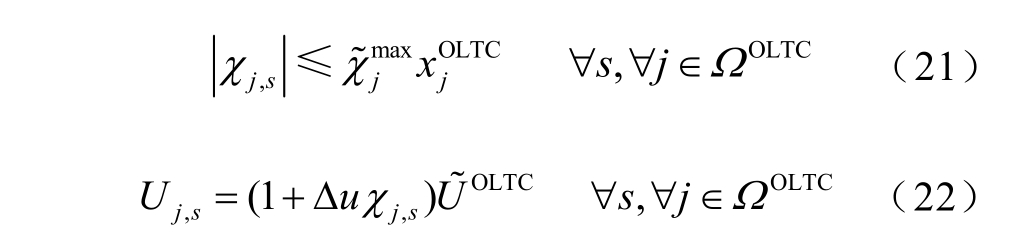
式中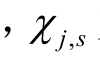
为场景s 下第j 个OLTC 的调压档位
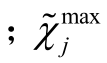为第j 个OLTC 的最大档位；Δ u 为一个档位对应的电压差值；
为调档前的电压幅值。
3）SVC 运行约束
式中，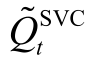
为型号t 的SVC 单台最大容量。
4）ESS 运行约束
（1）充放电状态约束
（2）充放电功率约束
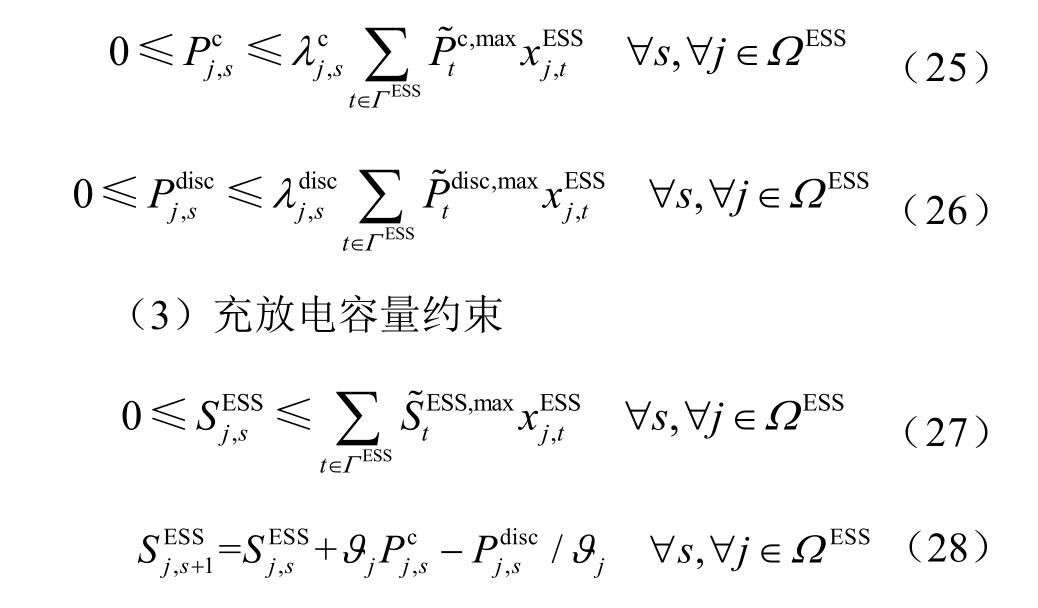
式中，
为二进制整数变量，分别代表ESS的充电状态和放电状态，约束（24）表示同一场景下同一ESS 只能充电或放电；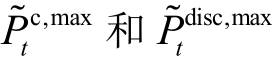 
分别为型号t 的ESS 最大充电功率和放电功率；
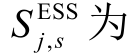场景s 下第j 个ESS 的当前容量；
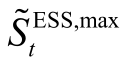为型号t 的ESS 最大容量；
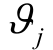为充放电效率系数，由于充放电过程存在功率损耗，实际充电量会有所减少，而放电量会增加，因此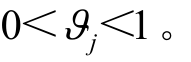
5）DG 相关运行约束
主要包括弃风弃光约束、渗透率约束以及无功功率控制约束。DG 无功功率的控制范围与当前时刻的有功出力有关。当容量固定时，弃风弃光手段的实现将减小DG 有功出力，此时无功功率的可调范围也将增大。具体约束为
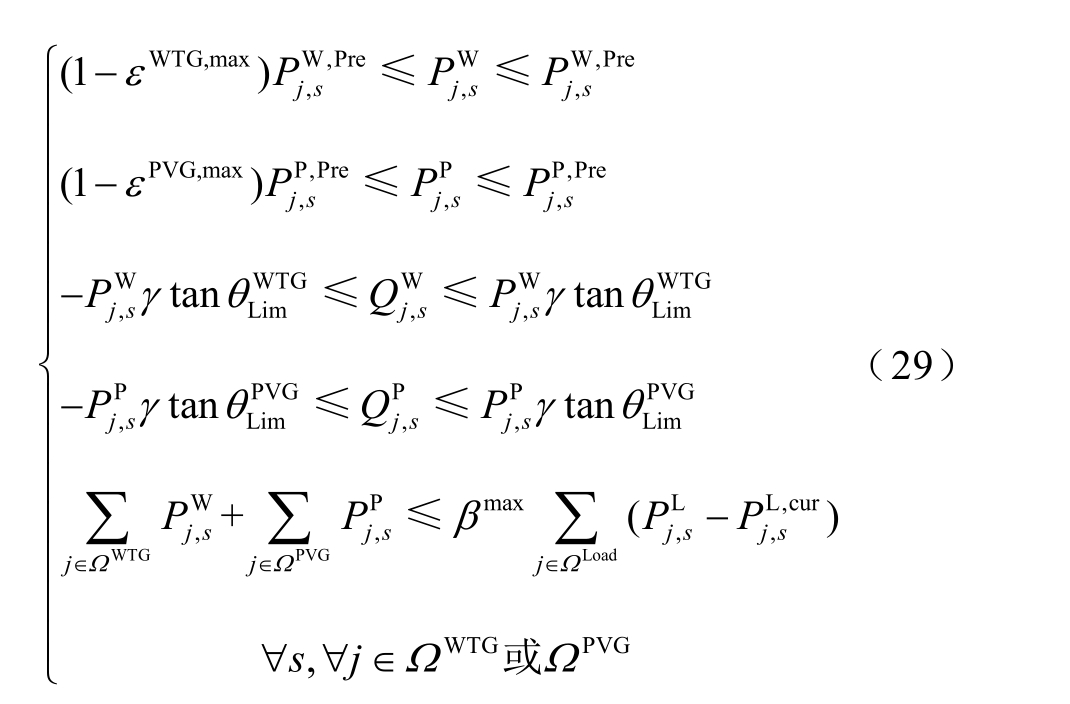
式中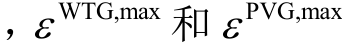
分别为风机和光伏的最大削减比例；
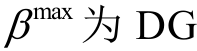在每个场景运行的最大渗透率；
分别为风机和光伏极限运行状态下的功率因数角；为了避免运行在极限状态，DG 无功出力需要设置裕度γ，本文取0.8。
6）负荷削减约束
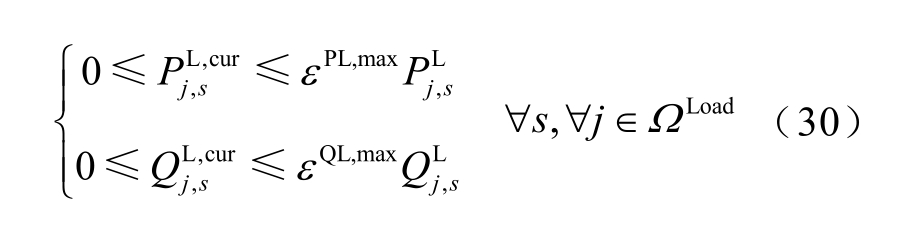
式中，
分别为有功和无功负荷的最大削减比例。
2.3 模型线性化
通过以上分析可知，上述模型还存在若干非线性表达式。为了能够有效建立鲁棒优化模型，应该对这部分约束式进行松弛处理。
1）OLTC 运行约束
为了满足二阶锥形式，约束式（22）需要引入新的辅助变量并转换为如下形式[23]
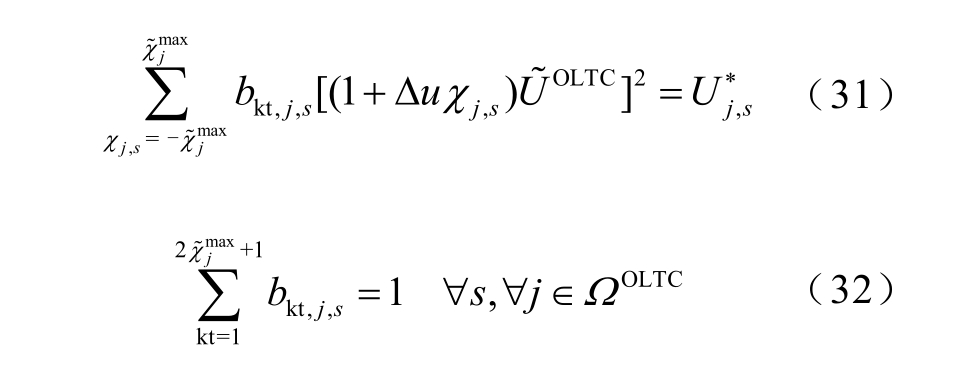
式中， kt, ,j sb 为辅助二进制变量。
约束式（32）表示每个OLTC 在场景s 下只能选择一个抽头档位，且该档位对应的编号为kt。与该编号对应的 kt, ,j sb 取1，其他均取0。
2）ESS 充放电功率约束
约束式（25）、式（26）存在状态变量和投资决策变量相乘的非线性项，可以通过式（33）来线性化。
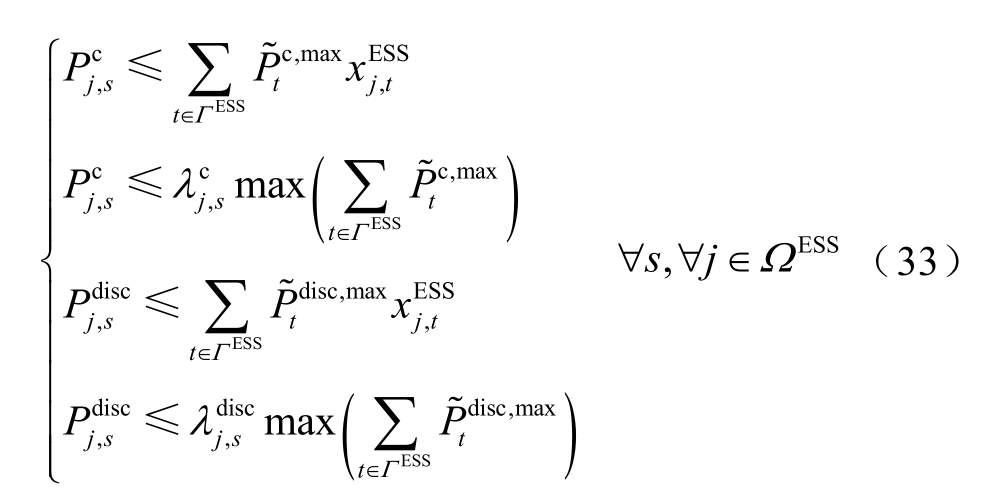
3 二阶段鲁棒规划模型及其求解方法
将确定性规划模型线性化后，针对耦合系统中配电负荷、DG 和EV 充电需求的不确定性，本文提出了考虑充电站的ADN 二阶段鲁棒规划模型，并通过CCG-Benders 法来求解。
3.1 二阶段鲁棒规划模型
3.1.1 不确定集合
较多文献都采用盒子模型来考虑鲁棒变量的不确定性[15,17,24-25]，且部分文献中只可取不确定区间的边界值，大幅度缩减了鲁棒变量的可行域。针对这个不足，本文令变量在不确定区间中自由寻优，以此来扩大可行域，具体表现形式为
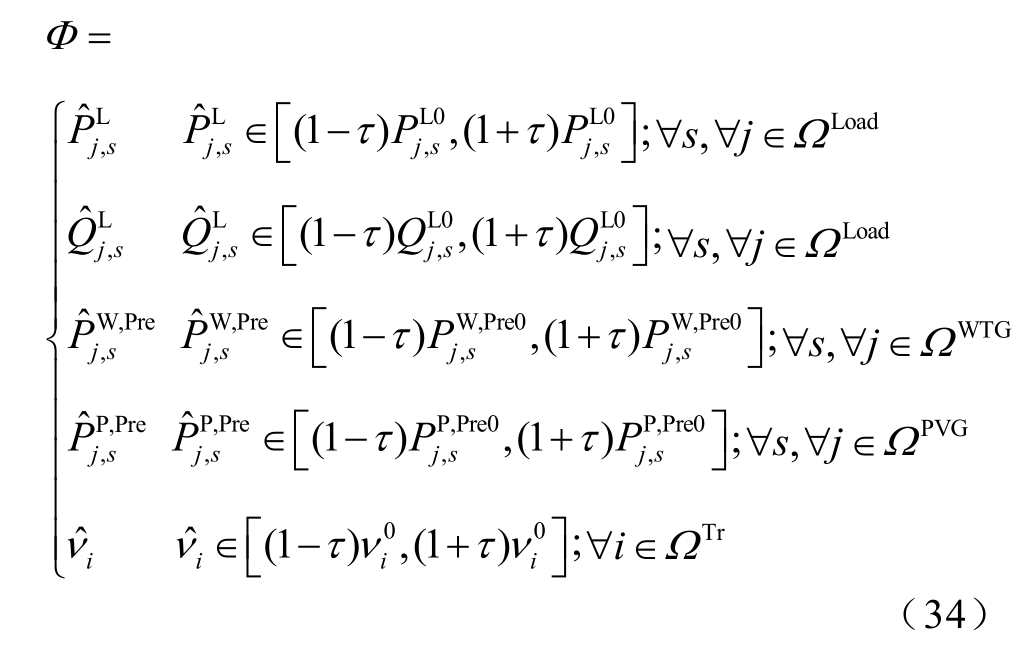
式中，Φ 为不确定集合；τ 为鲁棒模型的不确定度；上标0 为鲁棒变量的基准值。
在鲁棒模型中，不确定度是一个用以表征鲁棒变量波动范围大小的系数，其值越大，变量的不确定性越大。由式（34）可知，不确定度可以由变量的最大正偏移量除以基准值得到。为简化分析，本文假设所有鲁棒变量具有相同的不确定度。
3.1.2 鲁棒优化数学模型
经线性化后的原模型目标函数由式（7）～式（10）确定，具体约束包括式（2）～式（5）、式（11）、式（13）～式（16）、式（18）～式（21）、式（23）、式（24）、式（27）～式（33）。
考虑鲁棒变量的不确定性，原模型可以写成鲁棒形式，即
式中，一阶段变量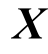
包括直接投资决策列向量和间接二进制列向量，即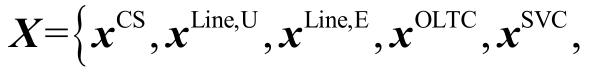
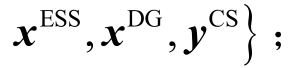二阶段鲁棒变量Z 如式（34）集合内所示；原模型中剩余的运行层列向量从属于二阶段运行变量
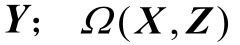为二阶段max-min 优化问题中运行变量的可行域。采用CCG-Benders 法求解时，
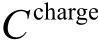中的ν i已在二阶段优化过程中被识别，并作为已知参数代回一阶段。因此， charge C 中仅含一阶段变量，归入一阶段目标函数中进行计算；式（36）和式（37）与式（2）～式（5）、式（11）相对应；式（38）为二阶段运行约束，对应于式（13）～式（16）、式（18）～式（21）、式（23）、式（24）、式（27）～式（33）。
3.2 CCG-Benders 二阶段求解方法
由于本文的二阶段问题可能无法收敛，基于这种情况产生的Benders 对偶最优割平面无法有效求解原问题[15]。因此，本文采用CCG 与Benders 分解相结合的二阶段法来分解原问题。
设当前的迭代次数为k+1 次，将式（35）～式（38）稍作改写并分解为一阶段主问题MP1 和二阶段子问题SP1，如式（39）、式（40）所示。
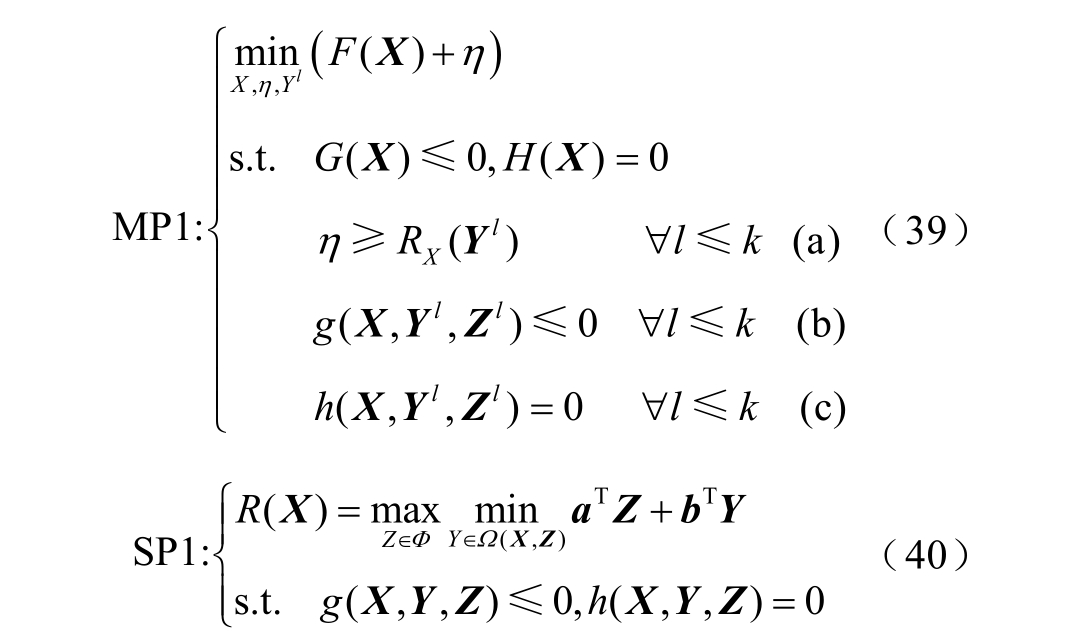
式中， F ( X )为投资成本和交通充电成本之和；η 为代替SP1 的辅助变量；l 为历史迭代次数；
分别为第l 次迭代由割平面引入的新变量和识别出的不确定参数；式（39a）为历代产生的所有最优割平面集合；式（39b）和式（39c）共同组成历代产生的所有可行割平面集合；R ( X )为二阶段目标函数；a 和b 为系数向量。
经过分解，一阶段主问题MP1 不含非线性条件，且属于混合整数规划问题，可以通过CPLEX 进行求解。其求解步骤介绍如下：
1）设鲁棒优化问题的初始上下界分别为正无穷和负无穷，上下界的最大相对误差为ε1max。
2）求解MP1，取出第k 次迭代产生的最优解，
更新问题的下界值
在初次迭代中，由于割平面均为空集，仅令0η≥ 即可。
3）将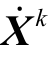 
作为已知参数代入SP1 并进行求解，取出最优解，即 
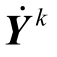和第k 次迭代识别出的不确定参数 
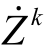，更新问题的上界值 U 1 = F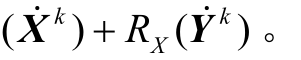 
4）判断迭代是否收敛。若 (U 1 -L1 )/ U 1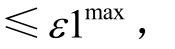 
则迭代收敛， 
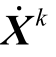为MP1 的最优解；否则向一阶段返回识别出的不确定参数
并增加相关约束，然后令 1k k= + ，返回步骤2）继续迭代。
3.3 子问题SP1 求解方法
二阶段子问题SP1 属于max-min 优化问题，且含有不确定集合，现有的数学求解方法或优化软件均无法直接求解。本文采用弱对偶和二阶锥对偶定理[16]，并结合外层逼近（Outer Approximation, OA）法[26]进行求解。
为了将内层min 问题转换为对偶形式，首先展开式（40）中的约束条件，如式（41）所示。
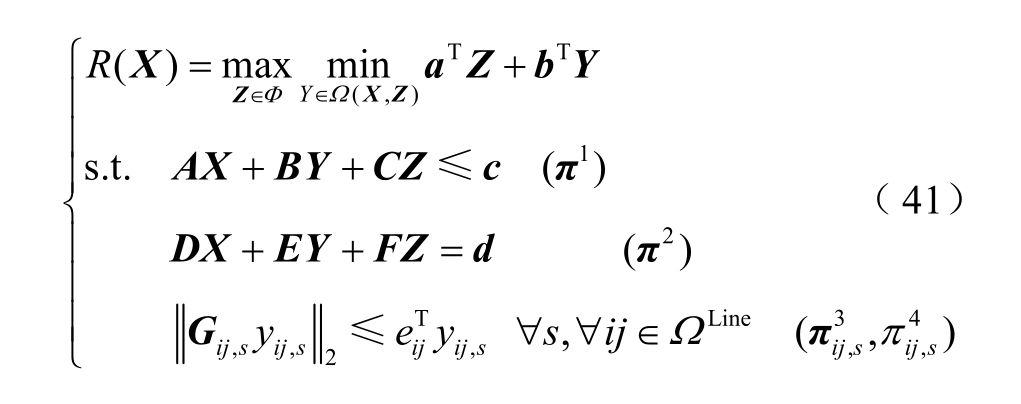
式中，
为适当维度的系数矩阵；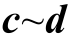
为系数向量；e 为系数；y ij ,s为二阶锥约束中的相关运行变量；
分别为不等式约束和等式约束的对偶列向量；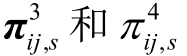
分别为场景s 下第ij 个二阶锥约束对应的对偶列向量和对偶乘子。
经对偶处理后，式（41）可改写为式（42）所示的max 型优化问题。
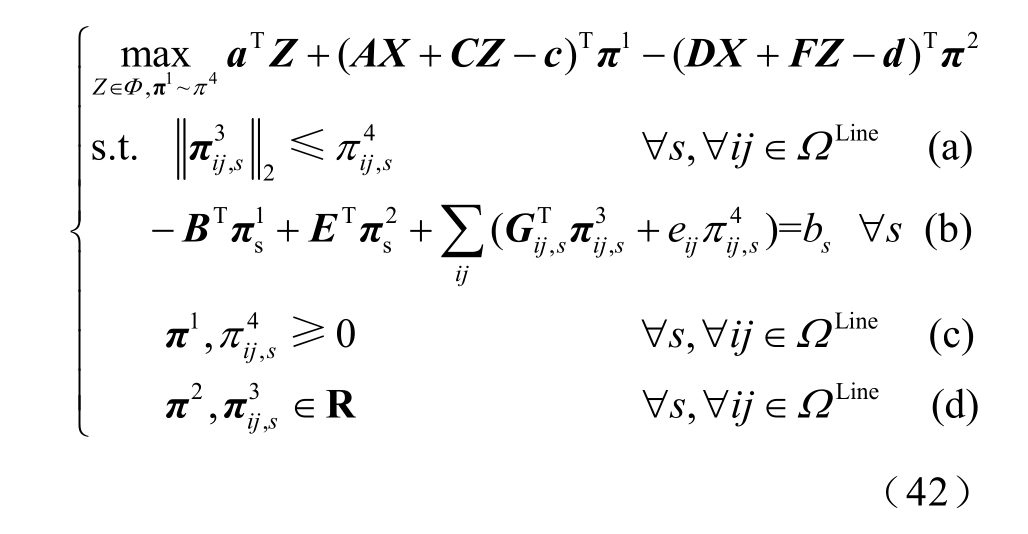
式中，R 为实数集。
在求解二阶段子问题时，X 作为已知参数代入，只需求取不确定参数Z 和各个对偶变量即可。但式（42）中存在两者相乘的双线性项，使得模型再次非线性化。这里继续采用Benders 分解将SP1 分为内层主问题MP2 和松弛子问题SP2，并通过OA 法来线性化MP2。其具体表达式如式（43）、式（44）所示，式（43）对应MP2，式（44）对应SP2。
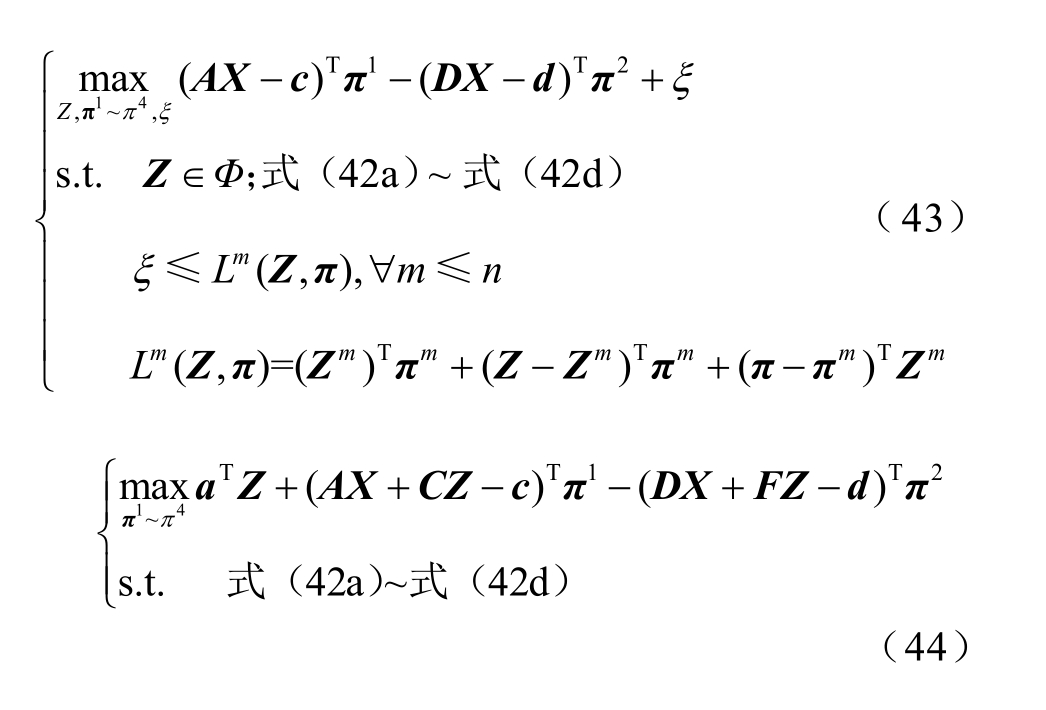
式中，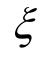
为双线性项的辅助变量；m 和n分别为历史迭代次数和当前迭代次数；
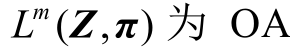法在第m 次迭代中产生的最优割平面，将其在最优解
处展开便得到式（43）的最后一行等式。
经处理后，式（43）和式（44）均线性可解，二阶段子问题SP1 便可通过CPLEX 进行求解。其具体求解步骤如下：
1）设二阶段子问题的初始上、下界分别为正无穷和负无穷，上、下界的最大相对误差为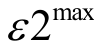 
，最大迭代次数为 maxn 。初次迭代时，令不确定参数 
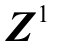取基准值。
2）求解SP2，取出第n次迭代产生的最优解 nπ ，对应的目标函数值用以更新问题的下界值L2。
3）将
作为已知参数代入MP2，构造并添加最优割平面约束，然后求解MP2。求出的目标函数值用以更新问题的上界值U2，并把最优解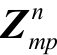 
作为二阶段识别出的关键场景。
4）判断 (U 2 - L 2 )/ U 2 ≤ ε2max以及 n ≥ nmax是否成立。若满足其中一个条件，则认为迭代结束，将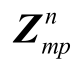
作为关键参数返回给一阶段；否则令 n = n+ 1，
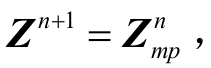返回步骤2）继续迭代。当迭代结束时，若
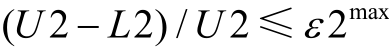仍未成立，则说明二阶段子问题在最大迭代数内一直无法收敛，识别出的 
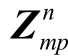为不可行解。
4 算例仿真分析
4.1 算例说明
本文以一个由改进的33 节点配电系统[9]和25节点交通系统[21]耦合而成的网络为例进行仿真分析，其拓扑结构见附图2。算例中共设置了10 个耦合单元，各耦合节点的连接情况见附表1。
交通系统中，各节点平均每天的需求权重见附表2；假设建设充电站所需的固定成本为40 万美元，建站的最大数量为 6；每次充电的单位路程成本为7 元，单次充电功率为10kW。配电系统中，新增负荷节点编号为34-37；原有线路的额定功率为0.5MW；DG 节点最多可安装5 台设备，且最大渗透率设为35%；SVC 节点最多可安装3 台设备；节点电压限值取0.95(pu)和1.05(pu)；规划年限为10 年，折现率为10%，投资年值化系数取0.162 8；相关投资设备的可选类型及对应费用见附表3～附表7；网损、负荷削减、弃风弃光等单位成本以及分时电价参数参考文献[22]。求解算法中，一阶段迭代最大相对误差设为 0.5%，二阶段迭代为0.2%。
4.2 仿真结果及其分析
将鲁棒模型的不确定度设为0.2，算例对应的仿真结果见表1 和表2，CCG-Benders 法的收敛过程如图2 所示。
表1 中，括号外的数字代表网络节点或馈线编号；括号内代表相应的设备数量。从规划结果来看，在交通系统中，充电站选址决策遵循分块集中的原 则，避开网络中最为拥挤的节点，选择边角区域中较为集中的节点进行建站。这是为了保持较小的权重距离，进而缩减交通充电成本。在配电系统中，为了满足鲁棒模型中最坏场景的运行约束条件，馈线升级以及设备投资都偏向于更贵的型号，且DG设备的投入台数均达到最大。
表1 规划方案结果
Tab.1 Results of the planning scheme
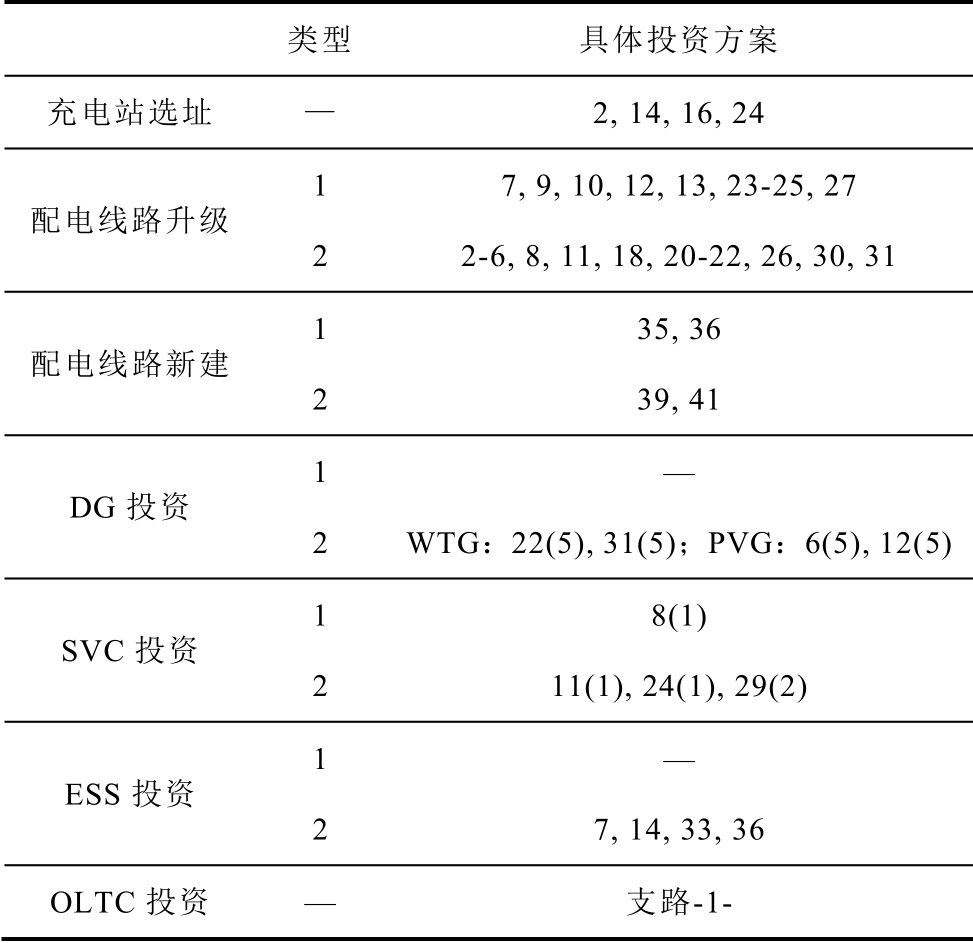
类型 具体投资方案 充电站选址 — 2, 14, 16, 24 配电线路升级 1 7, 9, 10, 12, 13, 23-25, 27 2 2-6, 8, 11, 18, 20-22, 26, 30, 31 配电线路新建 1 35, 36 2 39, 41 DG 投资 1 — 2 WTG：22(5), 31(5)；PVG：6(5), 12(5)SVC 投资 1 8(1) 2 11(1), 24(1), 29(2) ESS 投资 1 — 2 7, 14, 33, 36 OLTC 投资 — 支路-1-
表2 规划方案费用
Tab.2 Costs of the planning scheme （单位：105 美元）
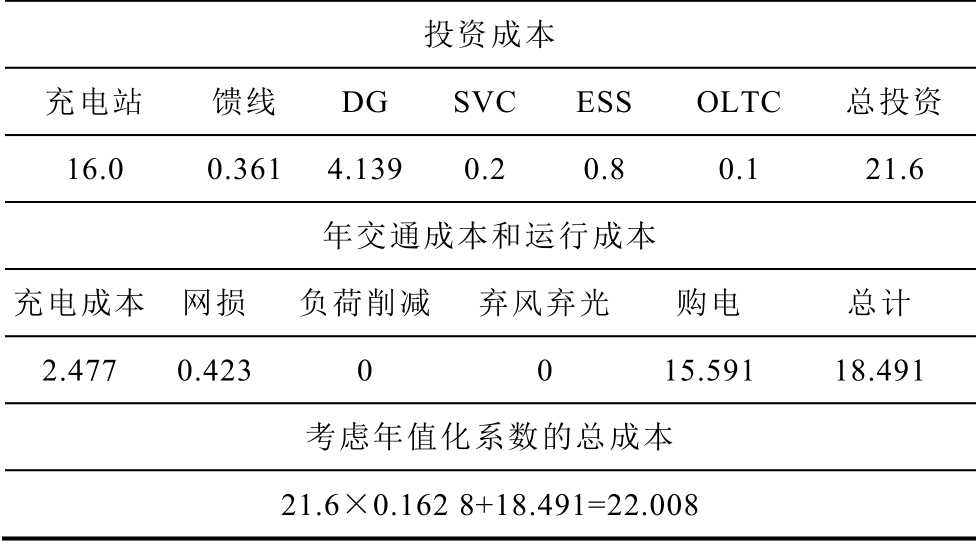
投资成本 充电站 馈线 DG SVC ESS OLTC 总投资16.0 0.361 4.139 0.2 0.8 0.1 21.6 年交通成本和运行成本 充电成本 网损 负荷削减 弃风弃光 购电 总计 2.477 0.423 0 0 15.591 18.491 考虑年值化系数的总成本 21.6×0.162 8+18.491=22.008
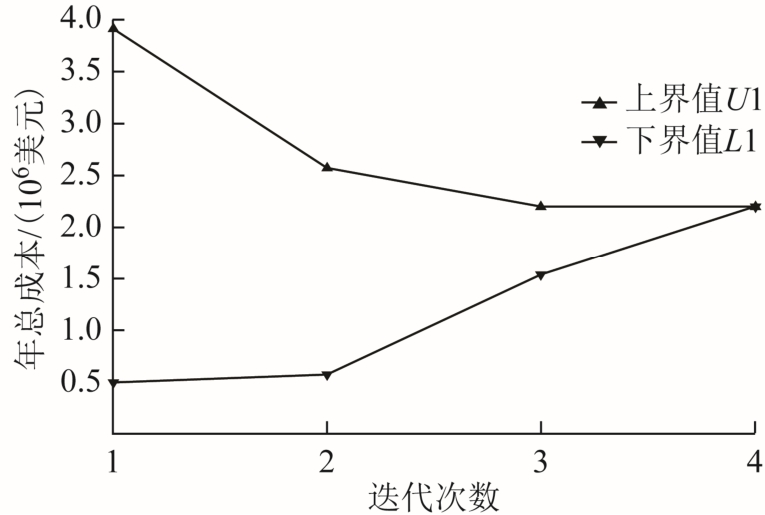
图2 算法收敛过程
Fig.2 The convergence procedure for the algorithm
另一方面，图2 给出了一阶段主问题和子问题对应目标函数值的变化情况。当模型的不确定度为0.2 时，优化过程在第四代便成功收敛，求解时间为99.024h，上、下界差值的相对误差为0.08%。与将投资层和运行层分开处理计算的智能方法[18]相比，本文所提的CCG-Benders 法不仅能有效求解二阶段鲁棒规划模型且具备较高的求解效率。
为了进一步说明鲁棒优化模型的有效性，本文同时对不考虑鲁棒的确定性模型进行了求解，并将两者的规划成本进行比对。确定性模型的投资方案见附表8，相关规划成本对比见表3。
对比表1～表3 和附表8 可以发现：
1）在设备投资方面，由于考虑了耦合系统中配电负荷、DG 和EV 充电需求的不确定性，鲁棒模型不仅增加了充电站和各设备的投资数量，还将各设备参数偏于更优的方向进行投资。因此，其相应的年投资成本要比确定性模型投入得更多。
表3 相关规划成本对比
Tab.3 Comparison for the related planning cost （单位：105 美元）
相关成本 鲁棒模型 确定性模型 年投资成本 3.517 2.381 年交通充电成本 2.477 2.576 网损成本 0.423 0.345 负荷削减成本 0 0.036 弃风弃光成本 0 0.379 主网购电成本 15.591 17.204 年总成本 22.008 22.921
2）由于投资方案更为保守，鲁棒模型不仅能够有效减少主网购电量，还能避免负荷削减和弃风弃光等现象，降低了年运行成本。同时，充电站建站数量的增加也减小了交通系统中的权重距离，使得年交通充电成本有所缩减。
3）相比确定性规划模型，当不确定度取0.2时，二阶段鲁棒规划模型虽然投资得更多，但其他成本的降低使其在规划年限内可以有效回收投资成本，并使年总成本降低了3.98%。可见，鲁棒模型在该不确定度下的规划结果更具经济价值。
为了说明各投资设备的作用，图3～图5 分别给出了规划方案相关功率及电压的运行分布曲线。
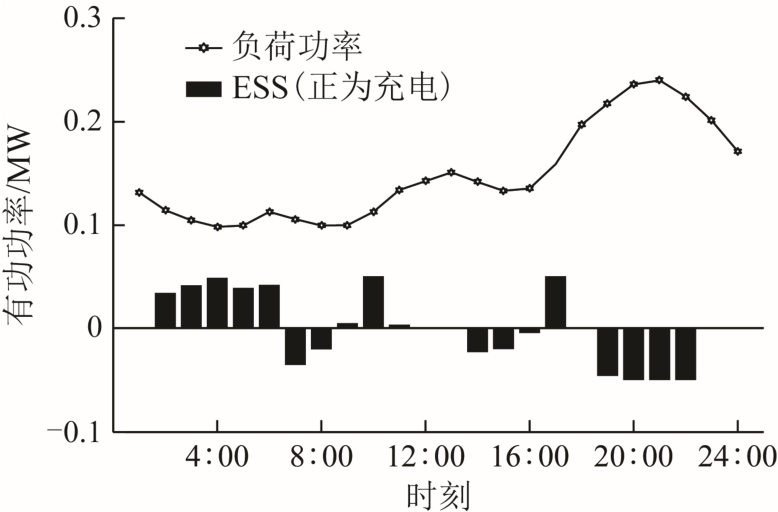
图3 节点36 有功功率运行分布
Fig.3 Active power operation profile of Node 36
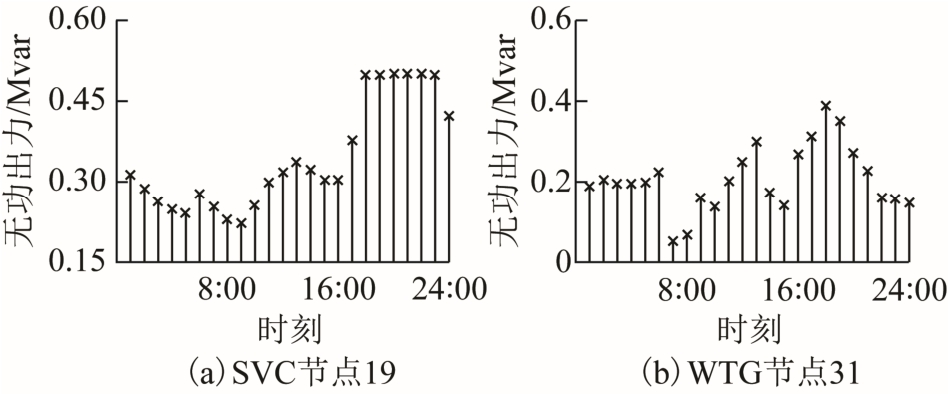
图4 无功功率运行分布
Fig.4 Reactive power operation profile
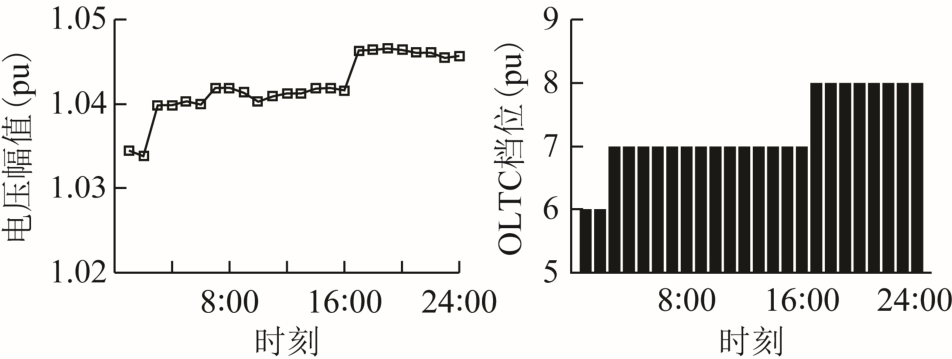
图5 OLTC 档位及节点电压分布
Fig.5 Profiles of node voltage and tap position of OLTC
1）由于避免了负荷削减和弃风弃光，鲁棒模型主要通过ESS 来实现有功功率的调整。由图3 可见，ESS 主要集中在凌晨以及电价较低的时段进行充电（如2:00～6:00 和9:00～11:00），此时负荷水平也相对较低；相反，当电价较高或处于负荷高峰（如7:00～8:00 或19:00～22:00）时，ESS 将及时放电。因此，储能措施可以有效削减高峰负荷并提高各发电能源的利用率，进而降低主网购电成本。
2）在无功功率运行方面，主要通过SVC 和DG无功控制来实现。由图4a 可见，SVC 无功出力曲线与负荷时序特性保持一致，且当系统处于负荷高峰时段（18:00～23:00），为了支撑电压降落，SVC处于满发状态。而DG 无功控制会更为复杂，其不仅与负荷水平有关，还受自身时序特性的影响。从图4b 可知，由于WTG 的时序值在18:00～23:00 间逐渐减小，即便遇到负荷高峰，无功出力也只能维持较高水平，不能达到满发状态。
3）为了便于分析OLTC 的作用，图5 给出了各场景的节点电压分布和抽头档位分布情况。由于OLTC 安装在变电站出口，2 号节点的电压经过调节后在各场景均会处于较高的水平。同时，为了适应较高负荷引起的电压降落，OLTC 抽头在17:00 以后调至较高的档位。
4.3 不确定度对鲁棒规划的影响
对二阶段鲁棒规划而言，不确定度是最为重要的参数之一。为分析其对优化结果和计算效率的影响，表4 给出了模型在不同取值下的规划成本、迭代次数及计算时间。
表4 各不确定度下的规划成本及算法求解信息
Tab.4 Comparison for the planning costs and solution information under different uncertainty
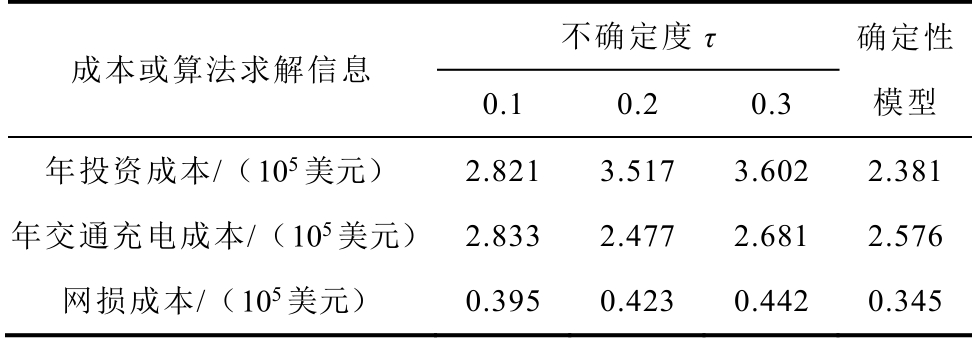
成本或算法求解信息 不确定度τ 确定性模型0.1 0.2 0.3 年投资成本/（105 美元） 2.821 3.517 3.602 2.381年交通充电成本/（105 美元） 2.833 2.477 2.681 2.576网损成本/（105 美元） 0.395 0.423 0.442 0.345
（续）
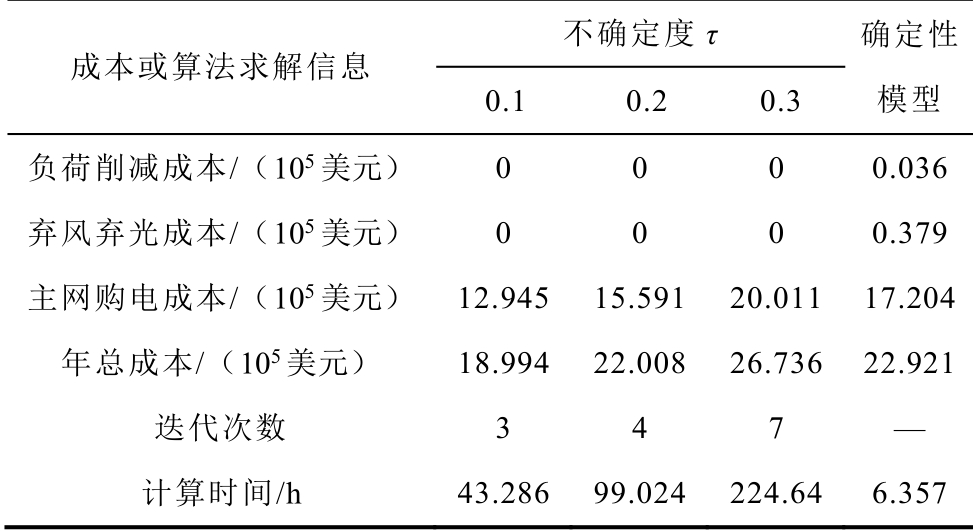
成本或算法求解信息 不确定度τ 确定性模型0.1 0.2 0.3 负荷削减成本/（105 美元） 0 0 0 0.036弃风弃光成本/（105 美元） 0 0 0 0.379主网购电成本/（105 美元） 12.945 15.591 20.011 17.204年总成本/（105 美元） 18.994 22.008 26.736 22.921迭代次数 3 4 7 — 计算时间/h 43.286 99.024 224.64 6.357
从表4 可以看出：
1）随着不确定度的增加，为了满足更坏场景的运行约束条件，规划的投资成本也会不断增大；相应地，其还会影响充电站的建站数量，进而影响交通充电成本。当建站数量不变时，τ 的增大会提高交通充电成本；随着充电需求继续波动，当需要建更多的充电站时，交通系统的加权距离可能会变小，使得交通充电成本降低。
2）τ 的增大还会增加网损和主网购电量，使得年运行成本进一步增加。以τ 取0.3 为例，当规划方案不能在规定年限内回收投资成本时，鲁棒模型在该不确定度下的经济效益就不如确定性模型。
3）τ 的取值会影响本文所提算法的计算效率。当取值过大时，模型的迭代次数会变大，且寻优过程的计算时间会随着一阶段主问题的约束条件增加而迅速延长，甚至无可行解。
在实际应用中，当二阶段鲁棒规划模型确定后，随着不确定度增加，规划方案的鲁棒性会增强，但也需付诸更多的经济成本来抵御不确定变量带来的风险。因此，在选取不确定度时，应在变量的不确定性以及经济成本之间做好权衡，既要体现其经济效益，又能使规划方案具备一定的鲁棒性。
5 结论
本文提出了含电动汽车充电站的主动配电网二阶段鲁棒规划模型，并结合Big-M 法和二阶锥松弛技术，基于CCG-Benders 法对模型进行了求解。该规划方法充分考虑了耦合系统中相关不确定元素以及OLTC、SVC、ESS 和DG 的联合投资运行，能够针对鲁棒规划问题为规划人员提供新的思路。基于算例仿真结果，可以得出以下结论：
1）在配电网规划中考虑多种投资设备的联合运行能够有效改善网络的功率和电压分布，充分体现了此类规划方案的优越性。
2）CCG-Benders 法能够有效求解含min-max- min 形式的二阶段鲁棒规划问题，且具备较高的求解效率。
3）当不确定度选取合理时，相比确定性模型，鲁棒规划模型可以有效降低运行成本和交通充电成本，并在规划年限内成功回收投资成本，更具经济价值。
4）对鲁棒规划模型而言，不确定度的增大会提高系统的年运行成本。当不确定度取得过大时，模型的迭代次数和寻优时间均会变得更大，甚至无可行解。因此，在实际应用中应合理选择不确定度的数值。
附 录
附表1 各单元节点对应关系
App.Tab.1 Node correspondence of each unit
单元编号 电力节点 交通节点 单元编号 电力节点 交通节点1 5 2 6 28 12 2 6 4 7 3 14 3 23 5 8 19 16 4 9 8 9 10 19 5 11 11 10 16 24
附表2 交通网络充电需求权重
App.Tab.2 Charging demand weights in the traffic system
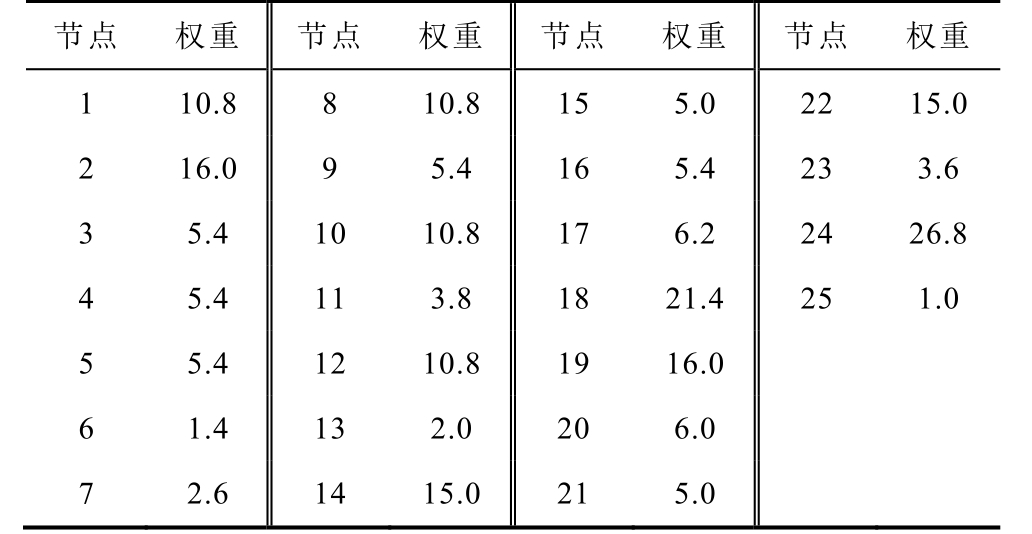
节点 权重 节点 权重 节点 权重 节点 权重1 10.8 8 10.8 15 5.0 22 15.0 2 16.0 9 5.4 16 5.4 23 3.6 3 5.4 10 10.8 17 6.2 24 26.8 4 5.4 11 3.8 18 21.4 25 1.0 5 5.4 12 10.8 19 16.0 6 1.4 13 2.0 20 6.0 7 2.6 14 15.0 21 5.0
附表3 备选配电线路型号参数
App.Tab.3 Parameters of candidate distribution lines
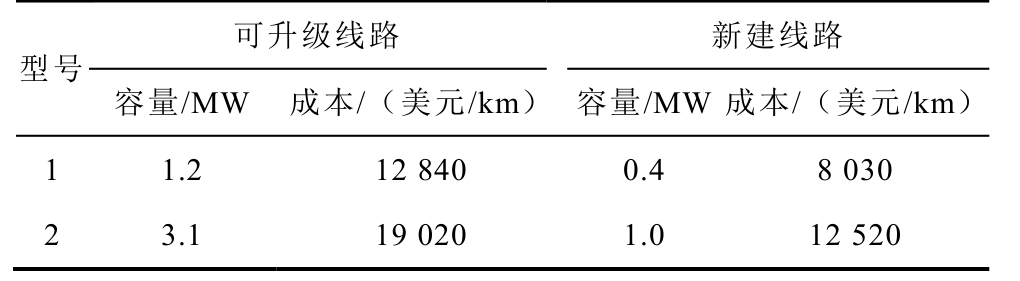
型号可升级线路 新建线路 容量/MW 成本/（美元/km） 容量/MW 成本/（美元/km）1 1.2 12 840 0.4 8 030 2 3.1 19 020 1.0 12 520
附表4 备选DG 型号参数
App.Tab.4 Parameters of candidate DGs
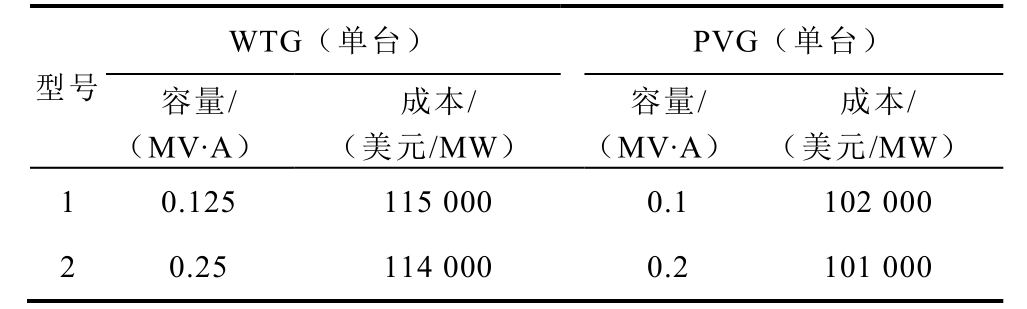
注：以上各型号的DG 额定功率因数均取0.85。
WTG（单台） 型号容量/ （MV·A）成本/ （美元/MW） PVG（单台） 容量/ （MV·A） 成本/ （美元/MW）1 0.125 115 000 0.1 102 000 2 0.25 114 000 0.2 101 000
附表5 备选OLTC 型号参数
App.Tab.5 Parameters of candidate OLTC
电压调节范围（pu） 费用/(美元/台) [0.94,1.06]：1±0.6%×10 10 000
附表6 备选SVC 型号参数
App.Tab.6 Parameters of candidate SVCs
型号 额定容量/Mvar 费用/(美元/台) 1 0.2 2 000 2 0.5 4 500
附表7 备选ESS 型号参数
App.Tab.7 Parameters of candidate ESSs
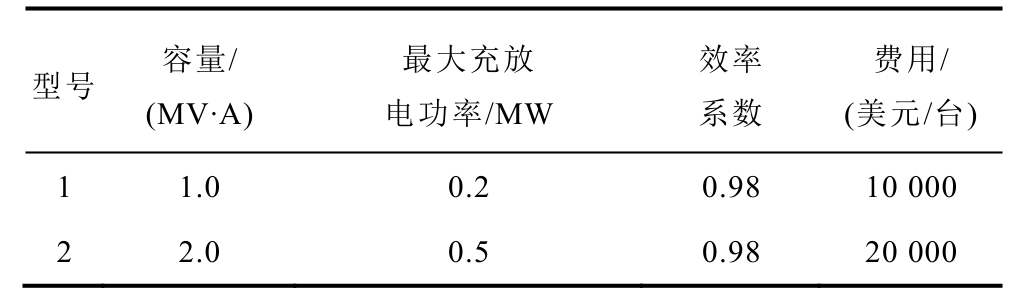
型号 容量/ (MV·A) 最大充放 电功率/MW 效率 系数 费用/ (美元/台)1 1.0 0.2 0.98 10 000 2 2.0 0.5 0.98 20 000
附表8 确定性模型规划方案
App.Tab.8 The planning scheme of the deterministic model
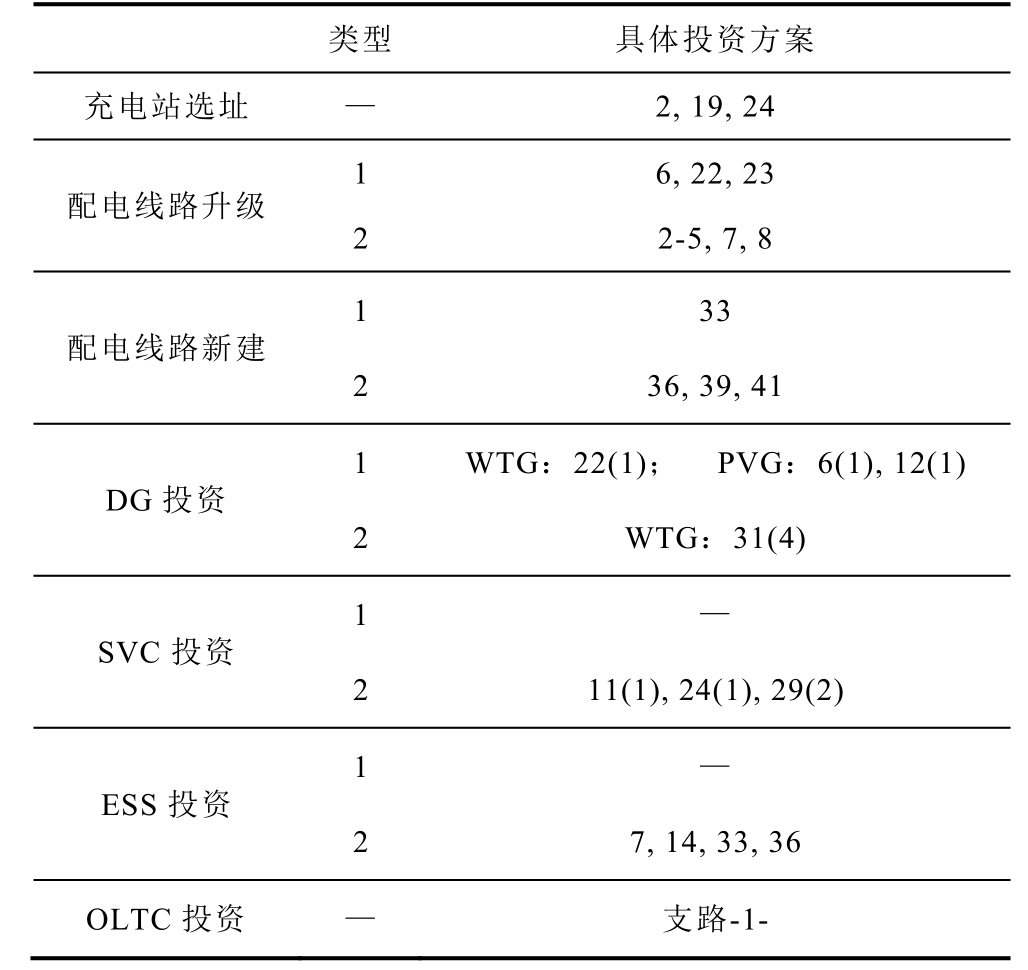
类型 具体投资方案 充电站选址 — 2, 19, 24 配电线路升级 1 6, 22, 23 2 2-5, 7, 8 配电线路新建 1 33 2 36, 39, 41 DG 投资 1 WTG：22(1)； PVG：6(1), 12(1) 2 WTG：31(4) SVC 投资 1 — 2 11(1), 24(1), 29(2) ESS 投资 1 — 2 7, 14, 33, 36 OLTC 投资 — 支路-1-
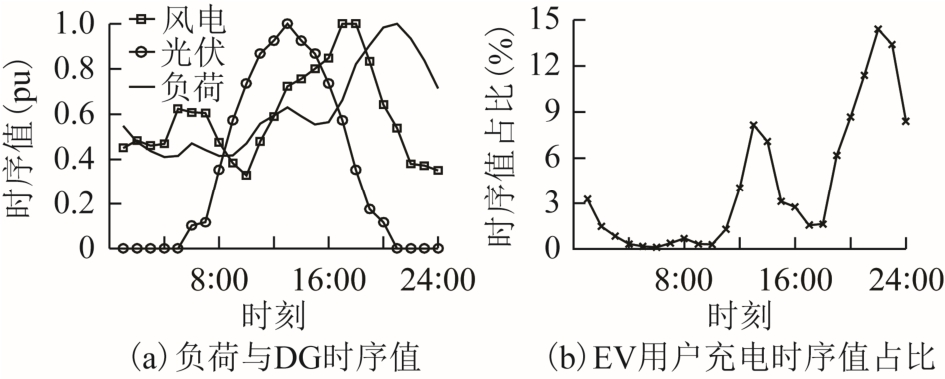
附图1 负荷、DG 及EV 用户充电的时序曲线
App.Fig.1 Timing curves of the load, DGs and EV charging
附图2 算例拓扑结构
App.Fig.2 Topology diagram of the example
[1] 范士雄, 蒲天骄, 刘广一, 等. 主动配电网中分布式发电系统接入技术及其进展[J]. 电工技术学报, 2016, 31(增刊2): 92-101.
Fan Shixiong, Pu Tianjiao, Liu Guangyi, et al. Technologies and its trends of grid integration of distributed generation in active distribution network[J]. Transactions of China Electrotechnical Society, 2016, 31(S2): 92-101.
[2] 曾鸣, 彭丽霖, 王丽华, 等. 主动配电网下分布式能源系统双层双阶段调度优化模型[J]. 电力自动化设备, 2016, 36(6): 108-115.
Zeng Ming, Peng Lilin, Wang Lihua, et al. Two-stage dual-level dispatch optimization model of distributed energy system in active distribution network[J]. Electric Power Automation Equipment, 2016, 36(6): 108-115.
[3] 刘柏良, 黄学良, 李军, 等. 含分布式电源及电动汽车充电站的配电网多目标规划研究[J]. 电网技术, 2015, 39(2): 450-456.
Liu Boliang, Huang Xueliang, Li Jun, et al. Multi-objective planning of distribution network containing distributed generation and electric vehicle charging stations[J]. Power System Technology, 2015, 39(2): 450-456.
[4] 管志成, 丁晓群, 张木银, 等. 考虑时序特性含电动汽车配电网分布式电源优化配置[J]. 电力系统保护与控制, 2017, 45(18): 24-31.
Guan Zhicheng, Ding Xiaoqun, Zhang Muyin, et al. Optimal allocation of distributed generation of distributed network containing electric vehicle considering timing characteristics[J]. Power System Protection and Control, 2017, 45(18): 24-31.
[5] 麻秀范, 王皓, 李颖, 等. 基于变权Voronoi 图和混合粒子群算法的电动汽车充电站规划[J]. 电工技术学报, 2017, 32(19): 160-169.
Ma Xiufan，Wang Hao，Li Ying，et al. Optimal planning of charging stations for electric vehicle based on weight-changed Voronoi diagram and hybrid particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society, 2017, 32(19): 160-169.
[6] 葛少云, 朱林伟, 刘洪, 等. 基于动态交通仿真的高速公路电动汽车充电站规划[J]. 电工技术学报, 2018, 33(13): 2991-3001.
Ge Shaoyun, Zhu Linwei, Liu Hong, et al. Optimal deployment of electric vehicle charging stations on the highway based on dynamic traffic simulation[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 2991-3001.
[7] 葛少云, 张有为, 刘洪, 等. 考虑网架动态重构的主动配电网双层扩展规划[J]. 电网技术, 2018, 42(5): 1526-1536.
Ge Shaoyun, Zhang Youwei, Liu Hong, et al. Bi-layer expansion programming method for active distribution network considering dynamic grid reconfiguration[J]. Power System Technology, 2018, 42(5): 1526-1536.
[8] 贾清泉, 赵美超, 孙玲玲, 等. 主动配电网中计及时序性与相关性的分布式光伏并网规划[J]. 中国电机工程学报, 2018, 38(6): 1719-1728, 1908.
Jia Qingquan, Zhao Meichao, Sun Lingling, et al. Planning for grid-connection of distributed PVs considering the sequential feature and correlation in active distribution network[J]. Proceedings of the CSEE, 2018, 38(6): 1719-1728, 1908.
[9] 谢仕炜, 胡志坚, 王珏莹, 等. 基于不确定随机网络理论的主动配电网多目标规划模型及其求解方法[J]. 电工技术学报, 2019, 34(5): 1038-1054.
Xie Shiwei, Hu Zhijian, Wang Jueying, et al. A multi-objective planning model of active distribution network based on uncertain random network theory and its solution algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1038-1054.
[10] 张旭升, 李瑞生, 黄利军, 等. 基于分层储能的主动配电网需求响应控制策略研究及实现[J]. 电力系统保护与控制, 2017, 45(15): 40-49.
Zhang Xusheng, Li Ruisheng, Huang Lijun, et al. Research and application on demand response based on hierarchical power storage[J]. Power System Protection and Control, 2017, 45(15): 40-49.
[11] 李燕, 胡志坚, 仉梦林, 等. 基于不确定网络理论计及经济性与可靠性的主动配电网规划[J]. 电力系统自动化, 2019, 43(16): 68-82.
Li Yan, Hu Zhijian, Zhang Menglin, et al. Active distribution network planning considering economy and reliability based on uncertain network theory[J]. Automation of Electric Power Systems, 2019, 43(16): 68-82.
[12] 马丽叶, 王玉翠, 王楚通. 主动配电网中计及网络重构的分布式电源鲁棒规划[J]. 电力系统自动化, 2018, 42(11): 94-101.
Ma Liye, Wang Yucui, Wang Chutong. Robust planning of distributed generators in active distribution network considering network reconfiguration[J]. Automation of Electric Power Systems, 2018, 42(11): 94-101.
[13] 刘佳, 徐谦, 程浩忠, 等. 计及主动配电网转供能力的可再生电源双层优化规划[J]. 电工技术学报, 2017, 32(9): 179-188.
Liu Jia, Xu Qian, Cheng Haozhong, et al. Bi-level optimal renewable energy sources planning considering active distribution network power transfer capability[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 179-188.
[14] 夏鹏, 刘文颖, 蔡万通, 等. 基于风电离散化概率序列的机会约束规划优化调度方法[J]. 电工技术学报, 2018, 33(21): 5069-5079.
Xia Peng, Liu Wenying, Cai Wantong, et al. Optimal scheduling method of chance constrained programming based on discrete wind power probability sequences[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 5069-5079.
[15] 仉梦林, 胡志坚, 李燕, 等. 基于可行性检测的考虑风电和需求响应的机组组合鲁棒优化方法[J]. 中国电机工程学报, 2018, 38(11): 3184-3194.
Zhang Menglin, Hu Zhijian, Li Yan, et al. A robust optimization method for unit commitment considering wind power and demand response based on feasibility testing[J]. Proceedings of the CSEE, 2018, 38(11): 3184-3194.
[16] Ding Tao, Liu Shiyu, Yuan Wei, et al. A two-stage robust reactive power optimization considering uncertain wind power integration in active distribution networks[J]. IEEE Transactions on Sustainable Energy, 2016, 7(1): 301-311.
[17] Amjady N, Attarha A, Dehghan S, et al. Adaptive robust expansion planning for a distribution network with DERs[J]. IEEE Transactions on Power Systems, 2018, 33(2): 1698-1715.
[18] 高红均, 刘俊勇, 魏震波, 等. 主动配电网分层鲁棒规划模型及其求解方法[J]. 中国电机工程学报, 2017, 37(5): 1389-1400.
Gao Hongjun, Liu Junyong, Wei Zhenbo, et al. A bi-level robust planning model of active distribution network and its solution method[J]. Proceedings of the CSEE, 2017, 37(5): 1389-1400.
[19] 谭欣欣. 基于鲁棒优化的电动汽车充电站选址决策研究[D]. 北京: 北京理工大学, 2016.
[20] Wei Dachuan. An optimized floyd algorithm for the shortest path problem[J]. Journal of Networks, 2010, 5(12): 1496-1504.
[21] 田园园, 廖清芬, 刘涤尘, 等. 面向综合能源供给侧改革的城市配网规划方法[J]. 电网技术, 2016, 40(10): 2924-2934.
Tian Yuanyuan, Liao Qingfen, Liu Dichen, et al. Planning of urban distribution network considering the integrated energy supply-side reform[J]. Power System Technology, 2016, 40(10): 2924-2934.
[22] 高红均, 刘俊勇. 考虑不同类型DG 和负荷建模的主动配电网协同规划[J]. 中国电机工程学报, 2016, 36(18): 4911-4922, 5115.
Gao Hongjun, Liu Junyong. Coordinated planning considering different types of DG and load in active distribution network[J]. Proceedings of the CSEE, 2016, 36(18): 4911-4922, 5115.
[23] Xie Shiwei, Hu Zhijian, Zhou Daming, et al. Multi-objective active distribution networks expansion planning by scenario-based stochastic programming considering uncertain and random weight of network[J]. Applied Energy, 2018, 219: 207-225.
[24] Dehghan S, Amjady N, Kazemi A. Two-stage robust generation expansion planning: a mixed integer linear programming model[J]. IEEE Transactions on Power Systems, 2014, 29(2): 584-597.
[25] Ruiz C, Conejo A J. Robust transmission expansion planning[J]. European Journal of Operational Research, 2015, 242(2): 390-401.
[26] Duran M A, Grossmann I E. An outer-approximation algorithm for a class of mixed-integer nonlinear programs[J]. Mathematical Programming, 1986, 36(3): 307-339.