0 引言
高速磁浮交通采用长定子直线同步电机驱动，具有速度快、能耗低的优点，适合远距离、高速运 输[1]。高速磁浮列车的牵引供电系统如图1 所示，位于轨道两端的变电站，通过馈电电缆向定子绕组供电，实际运行中有两种供电模式：单端供电模式和双端供电模式[2]。高速磁浮列车在加速阶段输出电压频率低于30Hz 以及在降速阶段输出电压频率 低于70Hz 时采用单端供电方式，即由轨道一端的变流器单独供电。列车速度到56km/h（对应输出电压频率30Hz）以上时，采用由线路两端变电站的变流器通过各自的馈电电缆同时向定子绕组段供电的双端供电模式。
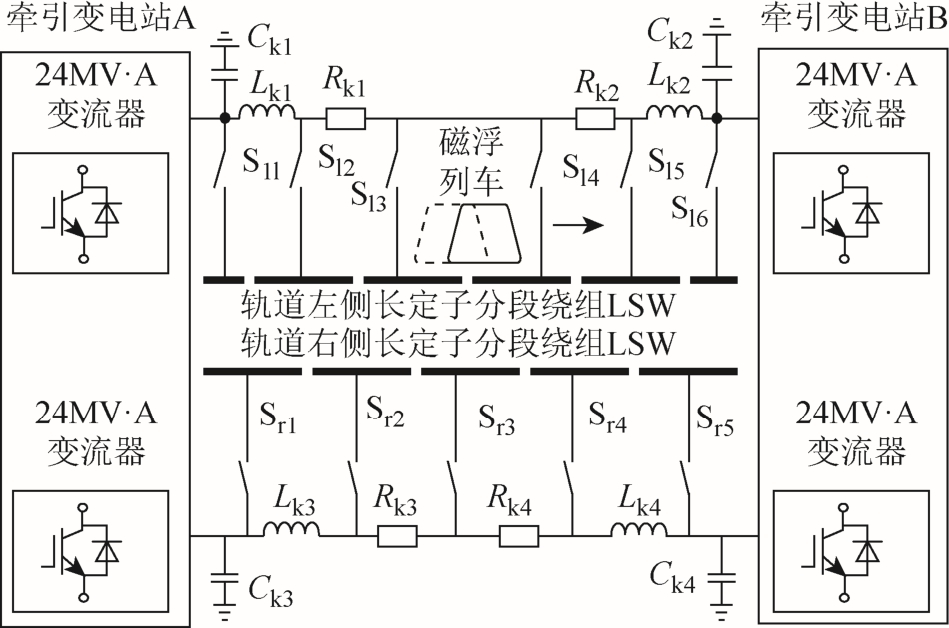
图1 磁浮列车牵引供电系统框图
Fig.1 Diagram of power supply system of maglev
当工作在双端供电模式时，磁浮列车在dq 坐标系下是强耦合、多输入多输出系统，dq 轴电流耦合严重，每台变流器电流不仅与自身的电流和电压交叉耦合项相关，还与另外一台变流器的电流、电压以及电机励磁电流相关。随着车速的增高以及运行过程中电机参数的变化，耦合越来越严重，不利于磁浮列车的稳定运行。特别是因为磁浮列车采用分段供电的方式，当磁浮列车从一个定子段过渡到另一个定子段时，列车一侧的定子会经历电流降为零再增大的过程。由于耦合作用的存在，使得定子电流产生尖峰[3]，因此需要对双端供电模式下的牵引控制策略展开研究。
传统的PI 电流控制忽略了交叉耦合项，动态性能差。文献[4]采用电压前馈解耦控制（Voltage Feedforward Decoupling Control, VFDC），利用电机参数计算前馈项来实现电流解耦，与传统PI 相比，动态性能有所提高，但在磁浮列车运行过程中，由于电机参数的变化，会导致解耦项不准确，系统动态性能受到影响。文献[5]采用基于内模的解耦控制器，鲁棒性好，但系统进入稳态前存在振荡。文献[6]采用基于扰动观测器的偏差解耦控制器，利用扰动观测器估算出的扰动补偿量，克服了偏差解耦的振荡问题，鲁棒性好，但扰动观测器在一定程度上依赖系统数学模型。文献[7]采用复矢量解耦控制器，动态性能好，但抗扰动能力较弱。文献[8]采用逆系统方法实现非线性反馈线性化解耦，具有良好的动态性能和稳定性，但它的实现需要精确的被控对象数学模型，并且计算比较复杂。
自抗扰控制器（Active Disturbance Rejection Control, ADRC）是一种对系统内扰和外扰鲁棒的控制器，不依赖数学模型[9]。自抗扰控制目前在电机控制领域取得了广泛的应用。文献[10]在异步电机中采用一阶ADRC 取代传统的速度环、电流环PI 控制器，取得了较好的控制效果。文献[11]提出一种基于ADRC 的位置-电流双环控制策略，对负载转矩、电机参数变化等扰动具有较好的抑制作用。文献[12]分析了永磁同步电机控制系统中控制增益对自抗扰控制器的影响。文献[13]设计了电流环非线性自抗扰控制器，提高了电流跟踪精度。文献[14]将自抗扰技术应用于永磁同步电机的速度环控制，实现了永磁同步电机自抗扰控制调速。
本文针对磁浮列车在双端供电模式下dq 轴电流耦合严重，换步过程中电流波动大的问题，提出一种基于自抗扰的牵引控制策略，并对传统自抗扰控制策略进行改进，提高了响应速度，降低了电流波动，最后通过仿真分析和基于RT-LAB 的高速磁浮半实物系统硬件在环实验，验证了算法的正确性。
1 双端供电模式下长定子直线同步电机数学模型
磁浮列车在双端供电模式下的原理如图 2 所示，两台变流器通过馈电电缆并联给长定子直线电机供电。其中ua、ub、uc 和ia、ib、ic 分别表示长定子直线电机定子绕组端部电压和定子绕组三相电流，ua1、ub1、uc1 和ia1、ib1、ic1 分别表示第一台变流器的输出电压和输出电流，ua2、ub2、uc2 和ia2、ib2、ic2 分别表示第二台变流器的输出电压和输出电流。
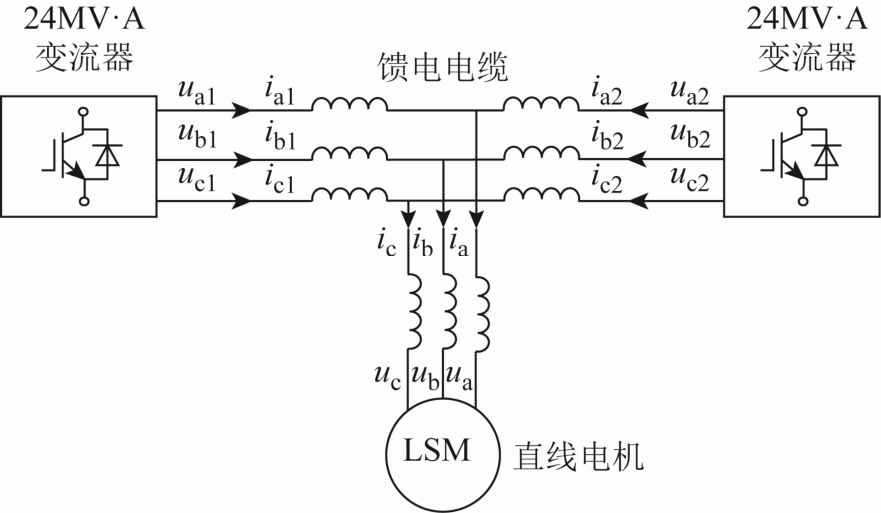
图2 长定子直线电机双端供电原理
Fig.2 Schematic diagram of long stator linear synchronous motor in the double feed mode
根据图2 建立了磁浮列车所用的长定子直线电机在双端供电模式时dq 坐标系下的数学模型为
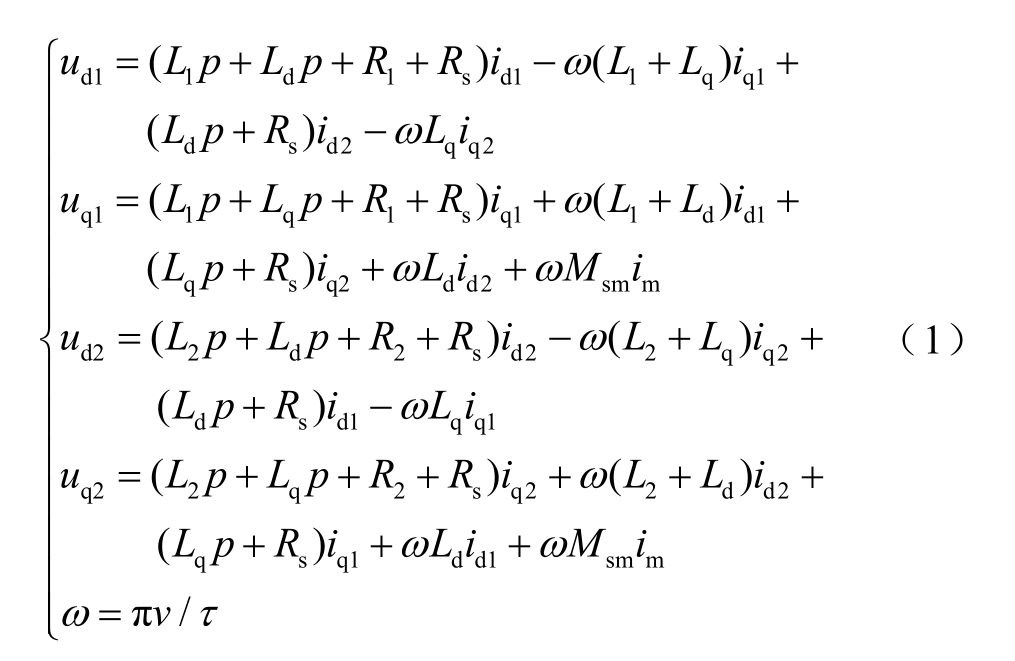
式中，ud1、uq1 和id1、iq1 分别为第一台变流器输出电压和输出电流在dq 坐标系下的分量；ud2、uq2 和id2、iq2分别为第二台变流器输出电压和输出电流在dq 坐标系下的分量；Ld、Lq 为定子绕组在dq 坐标系下的电感；R1、R2、L1、L2 为两侧馈电电缆参数；Rs 为定子电阻；Msm 为定子与动子间的互感；im 为励磁电流；v 为列车速度；τ 为极距；ω 为动子角速度；p 为微分算子。
由式（1）得到图3 所示的开环传递函数，可以看出在双端供电模式下，磁浮列车是强耦合、非线性、多输入多输出系统，dq 轴电流耦合严重，每台变流器电流不仅内部耦合，与自身的电流和电压交叉耦合项相关，而且外部耦合，与另外一台变流器的电流、电压和电机励磁电流相关。随着车速的增大以及运行过程中线路参数的变化，耦合作用的影响越来越大，不利于磁浮列车的稳定运行。
图3 单个变流器传递函数框图
Fig.3 Diagram of single inverter transfer function
实际上，对于磁浮列车所用的长定子直线电机而言，可以将两个变流器看作一个整体，以变流器输出电压之和与电压之差作为输入，以两个变流器共同输出的电流和环流作为状态变量，推导出状态方程式见式（2），其开环传递函数如图4 所示。
其中
图4 整体变流器传递函数框图
Fig.4 Diagram of whole inverter transfer function
由图4 可知，将两个变流器看作一个整体，变换过后耦合项简化，可以分为内部耦合项和馈电电缆耦合项，其中内部耦合项与电机参数和励磁电流有关，馈电电缆耦合项与馈电电缆的参数有关。
2 电压前馈解耦控制
在磁浮列车运行过程中，馈电电缆的参数随着行驶里程和电流频率等参数实时变化，根据文献[15]，电阻和电感的计算公式为
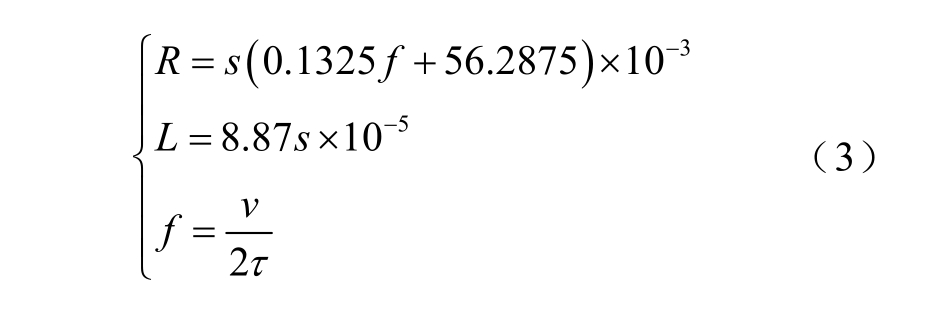
式中，v 为磁浮列车速度，m/s；s 为磁浮列车与牵引变流站的距离，km；R 为馈电电缆电阻值，Ω；L为馈电电缆电感值，H。
磁浮列车实际运行中，定子电流较大，而通过环流控制，环流一般较小，解耦补偿中馈电电缆参数可以根据式（3）计算。假定悬浮控制系统性能良好，励磁电流通常波动不大，与电机自身耦合项相比所占比例小。上述两部分耦合项都可以通过前馈解耦抵消，因此重点分析电机参数变化时电流环的解耦策略。
传统的电压前馈解耦控制原理如图5 所示，其中G1(s)、G2(s)为PI 控制器的传递函数，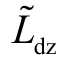
和
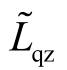为Ldz、Lqz 的估计值；
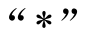表示指令值。
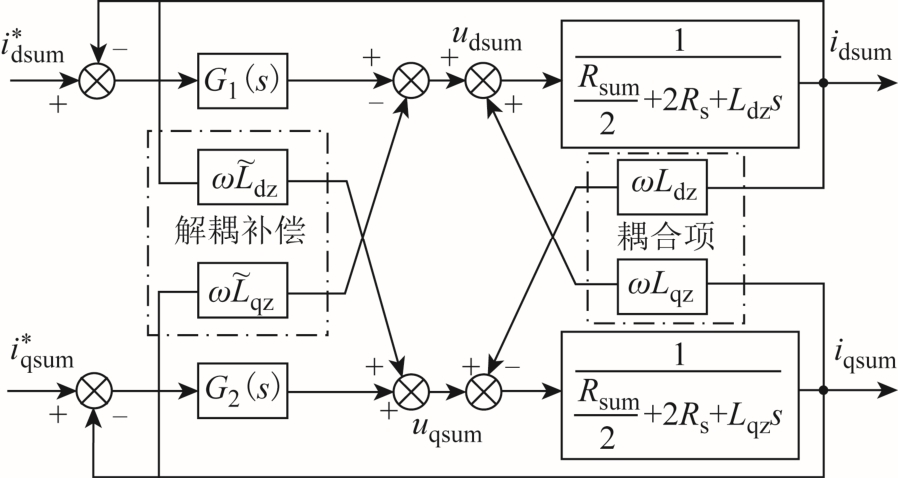
图5 电压前馈解耦原理
Fig.5 Schematic diagram of VFDC
忽略电流采样延时，根据图5 可以得到
其中
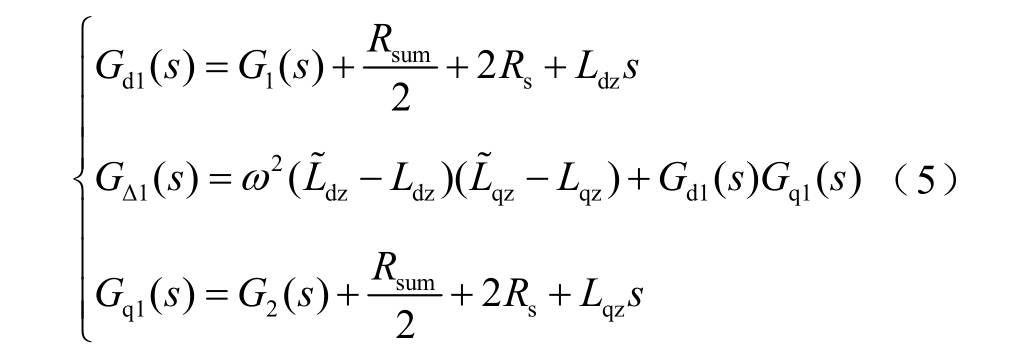
由耦合传递函数可知，只有当
时，才能实现完全解耦。磁浮列车在运行过程中，线路电感值会发生变化，导致估算值与实际值不一致，解耦补偿不能抵消实际的耦合量，因此不能完全解耦。随着车速的提高，耦合作用的影响越大。
3 基于自抗扰的电流解耦控制
3.1 自抗扰控制原理
自抗扰控制（ Active Disturbance Rejection Control，ADRC）是基于直接反馈线性化的思想，通过状态反馈将非线性系统转化成积分串联型线性系统，其优点在于该控制器不依赖对象的具体数学模型，在改善系统的稳定性、鲁棒性方面都有显著的效果[16]。传统的自抗扰控制器的结构如图6 所示，自抗扰控制器主要由三部分组成，包括跟踪微分器（Tracking Differentiator，TD）、扩张状态观测器（Extended State Observer，ESO）、非线性反馈控制率（Nonlinear State Error Feedback，NLSEF）。首先通过TD 依据被控对象的特性，安排合适的过渡过程，快速跟踪输入信号，并获得广义微分信号。然后通过ESO 实时估计系统的状态信息以及总扰动信息（包括系统未知扰动和未建模部分），并对扰动进行前馈补偿。最后通过NLSEF 用状态反馈规律把非线性系统变成积分串联型线性系统。
图6 自抗扰控制原理
Fig.6 Schematic diagram of ADRC
通过选择不同的TD、ESO、NLSEF 函数，可以得到多种类型的ADRC 控制器。磁浮列车电流需要快速跟踪指令变化，不需要安排过渡过程，因此不使用TD。此外，为了简化计算，本文采用二阶线性ESO，NLSEF 选择了比例反馈控制规律。
扩张状态观测器ESO
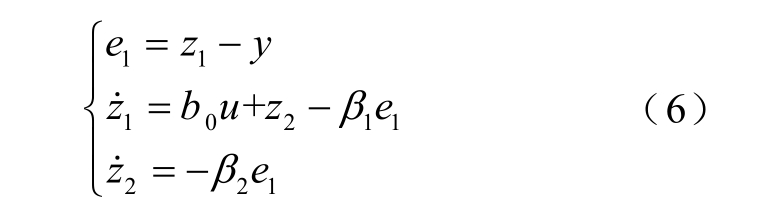
非线性状态误差反馈控制律NLSEF
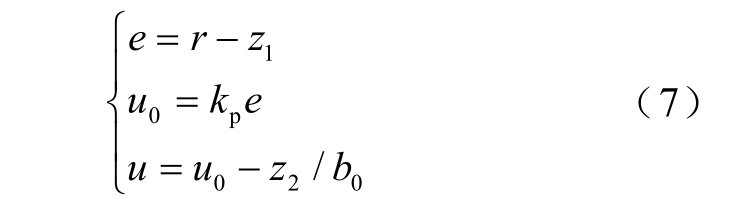
式中，r 为给定值； 1z 为对输出y 的观测值； 2z 为总扰动观测值；u0 为末补偿的系统输入；u 为最终的系统输入；b0 为控制增益估计值；β1、β2 为观测器系数；kp 为比例系数。
3.2 改进自抗扰控制原理
从图6 可以看出，传统的自抗扰控制器需要改变系统结构，不便于实现，因此本文提出一种改进型的自抗扰控制器，将传统算法重构，选取误差e与扰动f 作为状态变量，推导出控制器传递函数。
对于一阶系统式中，u 为系统输入，y 为系统输出，f 为总扰动，b 为控制增益。
误差e=r- y，r 为给定值，代入式（8）中，转化为
选取状态变量x1=e 和 2x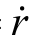 
f=-，式（9）转换为
对式（10）所示的对象，构造二阶线性ESO 为
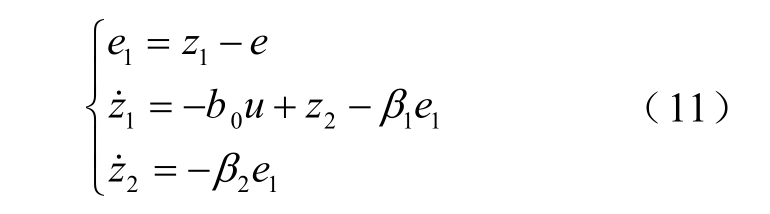
式中，z1 为误差e 的观测值；z2 为广义扰动x2 的观测值，由于观测器带宽的限制，观测值有一定的相位滞后，因此控制器选择原始的误差e作为输入，选择比例反馈控制规律为
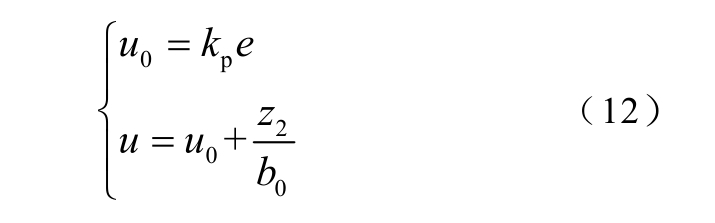
在观测器参数设计良好的情况下，可以认为z2≈x2，代入式（12）中得到
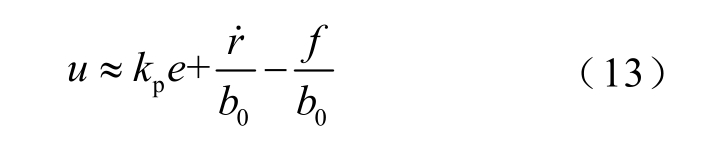
从式（13）可以看出，新的控制规律结合了比例反馈控制、输入微分前馈以及扰动补偿，具有优良的控制性能。将式（12）代入式（11）中，进行拉普拉斯变换，得到控制器传递函数为
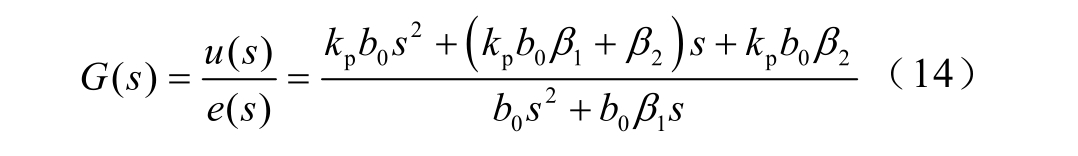
通过上述推导，可以得到改进的自抗扰控制器结构如图7 所示，相较于传统自抗扰控制器，取消了TD 环节，因为电流需要快速跟踪指令变化，不需要安排过渡过程。与此同时，算法具有以下两个优点：ESO 在观测扰动的同时观测了给定的微分，可以同时实现扰动补偿和输入微分前馈，提高了响应速度，减小了超调；控制器的输入变成了误差，在实际应用过程中，只需要将式（14）的传递函数进行离散化便能用程序实现，算法简单。
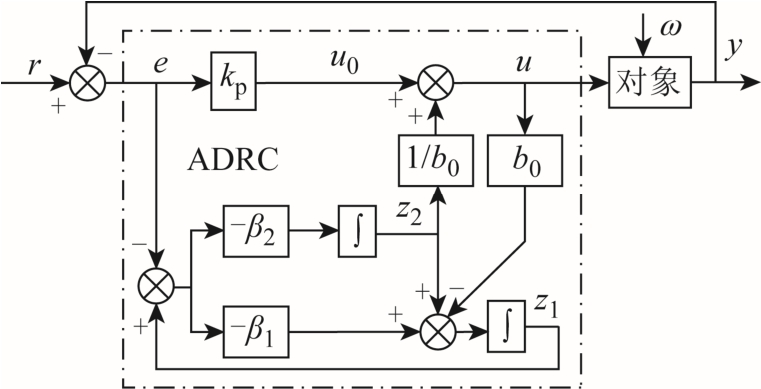
图7 改进的自抗扰控制原理
Fig.7 Schematic diagram of improved ADRC
3.3 基于自抗扰的电流解耦控制策略的设计
针对式（2）的四输入四输出强耦合系统，依靠模型参数进行前馈解耦的算法，解耦困难，鲁棒性差。本文引入自抗扰控制器，解决多输入多输出系统的耦合问题，计算简单，鲁棒性好。首先将式（2）的数学模型改为微分方程
令
将式（15）转换为
从式（16）可以看出，通过ESO 估算出总扰动f，进行前馈补偿后，原系统变成单输入单输出系统，idsum 只与u1 有关，iqsum 只与u2 有关，idsub 只与u3 有关，iqsub 只与 4u 有关，电流与控制量之间完全解耦。在x 和u 之间嵌入4 个自抗扰控制器，就能在不改变系统结构的前提下，实现电流快速准确跟踪指令值变化，因此基于自抗扰的电流控制框图如图8 所示。
3.4 改进自抗扰控制器参数设计和鲁棒性分析
由式（14）可以看出，改进的ADRC 控制器中有四个参数β1、β2、b0、kp 需要整定。控制器中参数β1、β2 按照线性ESO 带宽的概念进行整定[17]，选取β1=2ω0、β2=2ω02，ω0 为观测器带宽，ω0 越大，观测器对扰动估计的滞后越小，收敛越快，但过大的ω0会引入高频噪声，选取合适的ω0，保证LESO 的观测效果。b0 为控制增益估计值，当系统控制增益b已知时，选择b0=b，可以得到较好的控制性能。kp 为比例增益，其参数调节和PI 控制器参数类似。
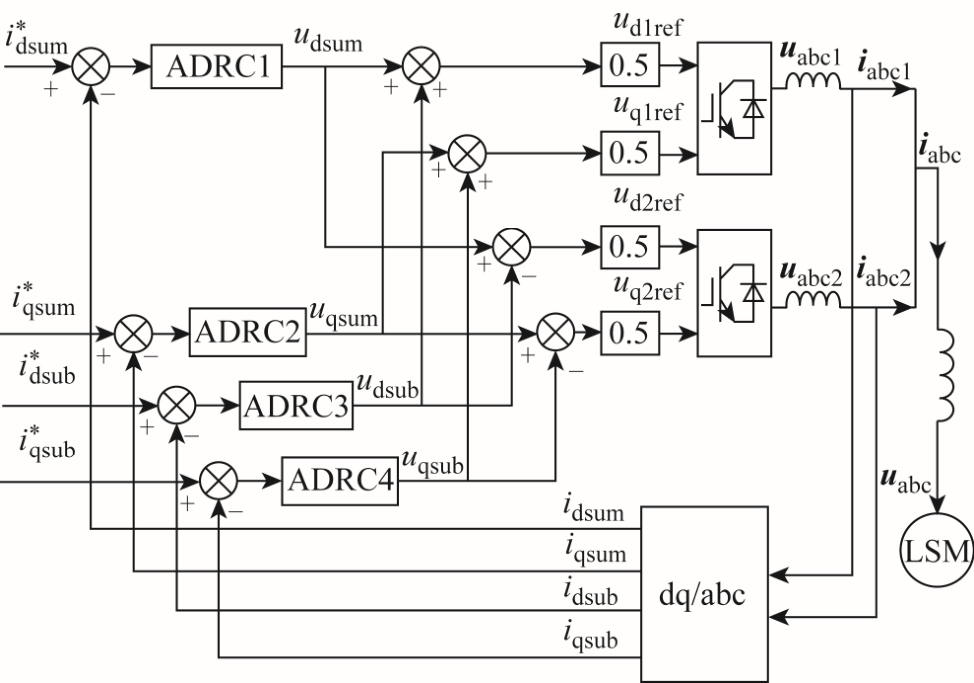
图8 基于自抗扰控制的电流控制框图
Fig.8 Diagram of current control based on ADRC
实验中首先根据数学模型大致估算控制增益，令b0=b，然后确定观测器带宽ω0，采用从小到大的方法进行调节，最后按照比例控制的经验调节kp，通过现场调试和修改参数，得到一组比较理想的控制器参数，参数整定简单。
由式（2）可知，在磁浮列车电流环中，真实控制增益b 为电感值的倒数，与线路参数有关，磁浮列车运行过程中，线路参数会发生变化。下面重点分析当线路电感变化，即b0 估计不准时自抗扰控制器的性能，b0 选取五组不同的值，其余参数按照下文表2所示，改进的自抗扰控制器的Bode 图如图9 所示。
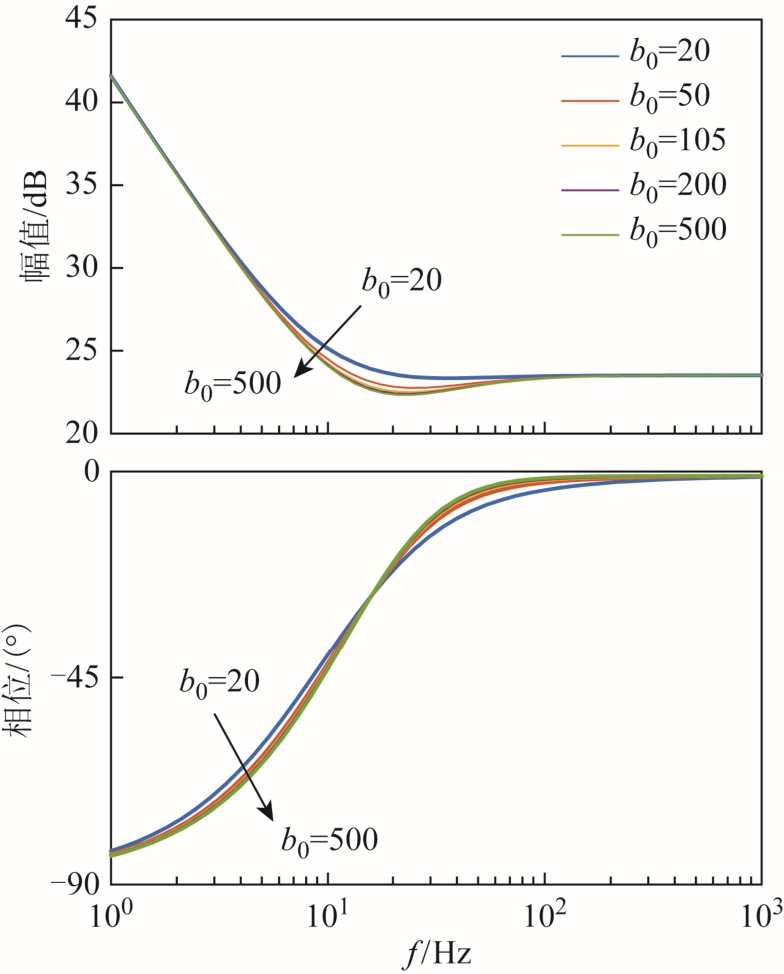
图9 改进自抗扰控制器传递函数图
Fig.9 Bode diagram of IADRC transfer function
可以看出，当控制器参数β1、β2、kp 整定过后，自抗扰控制器对参数b0 变化具有良好的鲁棒性，即使电感参数变化，参数b0 估计不准，解耦效果依旧良好，不会对实际对象控制效果产生影响。
4 系统仿真和实验研究
为了验证本文所提出的控制策略的有效性，在Matlab/Simulink 环境下搭建了仿真模型进行仿真分析，并在基于RT-LAB 的高速磁浮半实物系统上进行了硬件在环实验研究，实验平台如图10 所示，实验电机参数与仿真参数一致。电机参数见表1。
图10 高速磁浮牵引半实物系统
Fig.10 Semi-physical traction system of high-speed maglev
表1 长定子直线电机参数
Tab.1 Long stator linear motor parameters
参 数 数 值 定子电阻Rs/Ω 0.43 d 轴电感Ld/mH 3.061 q 轴电感Lq/mH 2.611 转子与动子间的互感Msm/mH 165 极距τ/ m 0.258 列车质量M/ kg 306 900 列车节数N 5 励磁电流im/A 27
4.1 仿真分析
在Matlab/Simulink 环境下搭建了仿真模型，与电压前馈解耦方法进行对比分析。自抗扰控制器参数见表2。PI 控制器参数kp=7，ki=7。dq 轴电流指令按照图11 的规律阶跃变化。
表2 自抗扰控制器参数
Tab.2 ADRC parameters
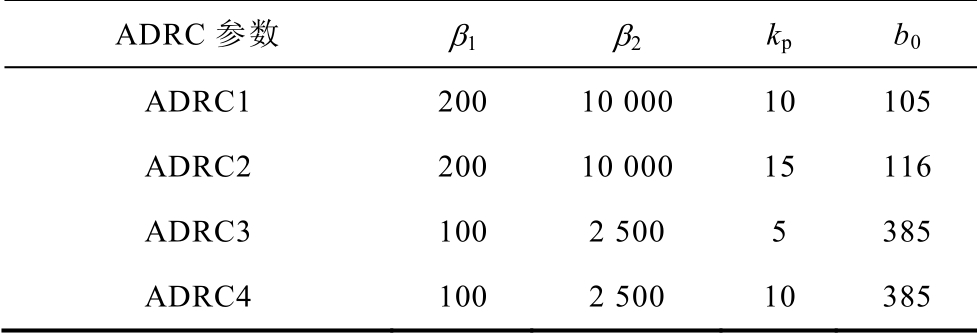
ADRC 参数 β1 β2 kp b0 ADRC1 200 10 000 10 105 ADRC2 200 10 000 15 116 ADRC3 100 2 500 5 385 ADRC4 100 2 500 10 385
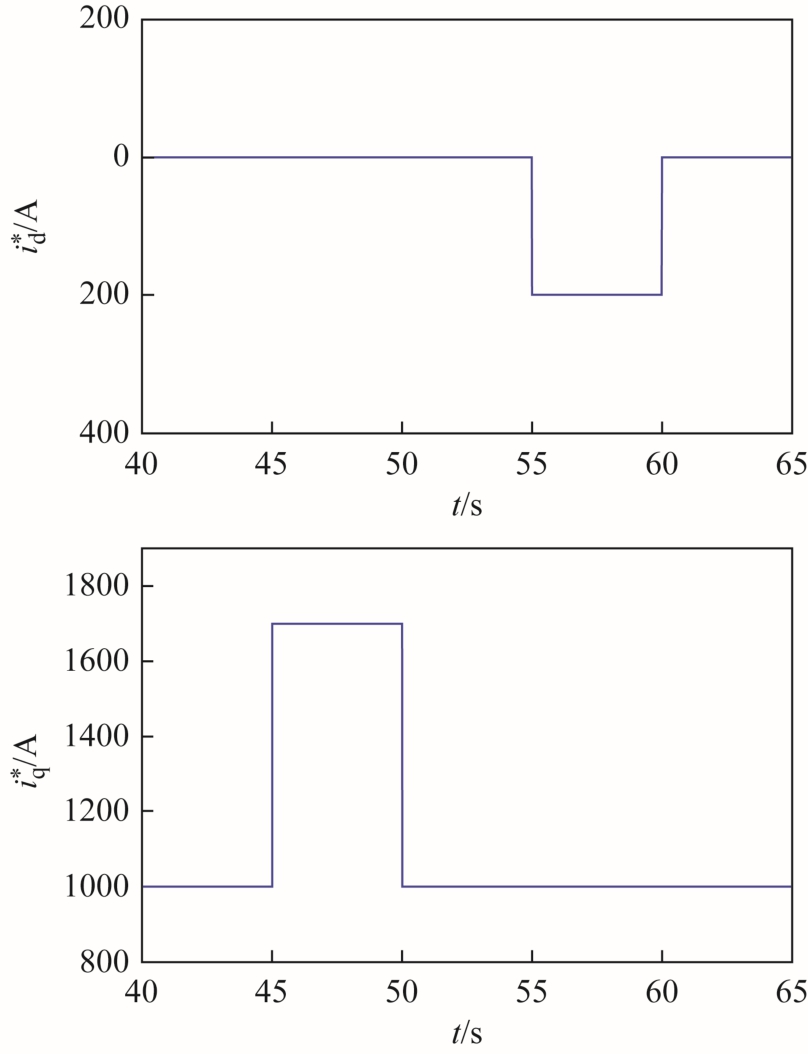
图11 dq 轴电流阶跃指令
Fig.11 Steps of dq axis current commands
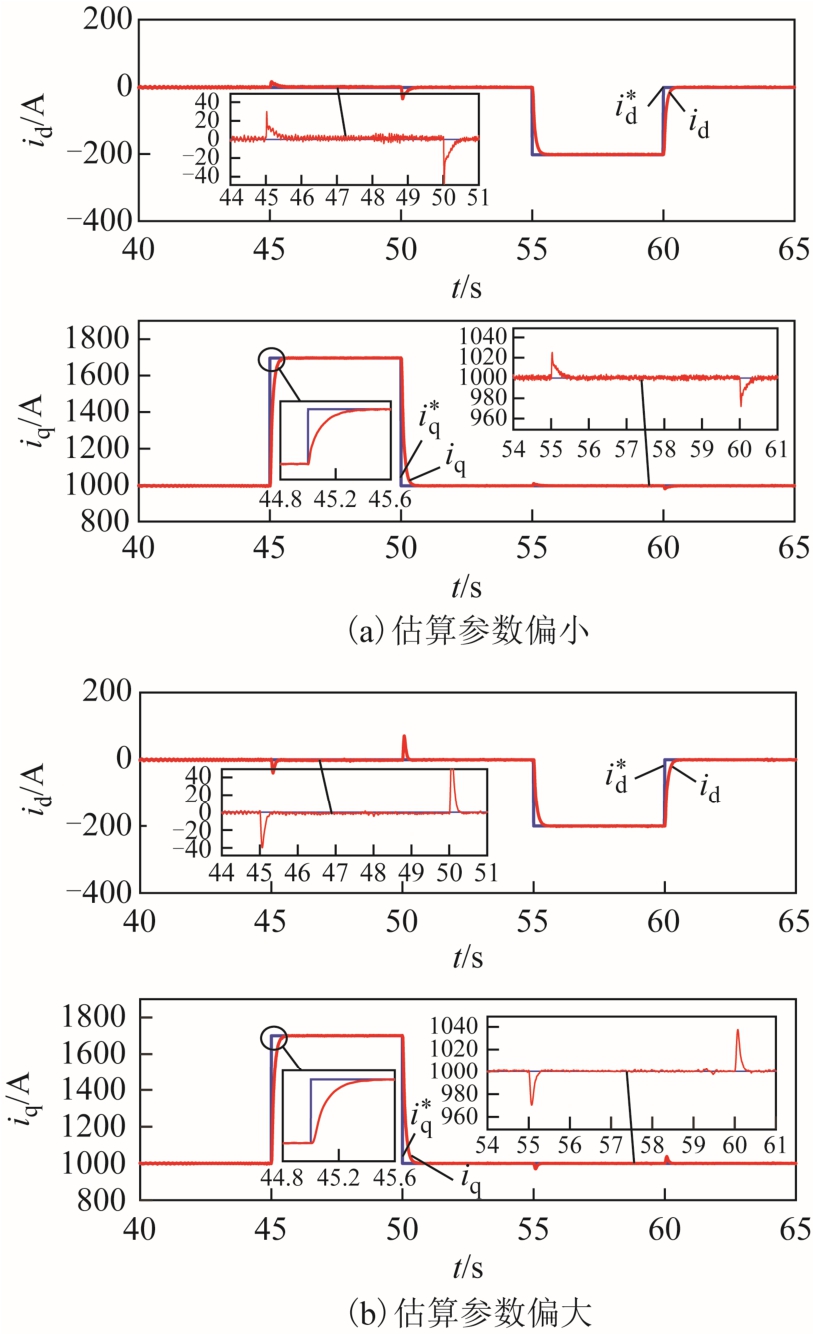
图12 采用VFDC 策略时电流响应波形
Fig.12 Current responses with VFDC
图12 为电压前馈解耦方法的参数估算分别为表1 的0.5 倍和2.0 倍时，dq 轴电流的响应曲线。可以看出，当估算参数不准时，dq 轴电流不能完全 解耦，任意轴电流突变会引起另一个轴电流产生波动，不能很好地跟踪指令变化，q 轴电流上升响应时间为0.4s。当估算参数偏大时，q 轴电流指令突变，d 轴电流波动60A；当估算参数偏小时，q 轴电流指令突变，d 轴电流波动40A。由此可见，dq 轴电流之间仍然存在耦合，电压前馈解耦鲁棒性差。
图13 为基于自抗扰解耦方法的参数估算分别为表1 的0.5 倍和2.0 倍时，dq 轴电流的响应曲线。可以看出，q 轴电流指令突变，d 轴电流波动不超过10A，dq 轴电流解耦效果好，与此同时q 轴电流上升响应时间为0.25s，比电压前馈解耦方法响应更快。因此可以证明，基于自抗扰的解耦算法具有良好的鲁棒性与动态性能。
图13 采用ADRC 策略时电流响应波形
Fig.13 Current responses with ADRC
4.2 实验验证
按照表2 的参数，在高速磁浮牵引半实物系统上进行了硬件在环实验，采用id=0 的转子磁场定向控制，实现了磁浮列车最高时速为600km/h 的加减速过程，速度曲线如图14 所示。实验过程中定子段长度为1.2km，定子换步方式采用两步法换步。变流器母线电压5 000V，采用SVPWM/SHE 切换调制策略，切换频率为115Hz。dq 轴电流和A 相电流通过上位机显示。
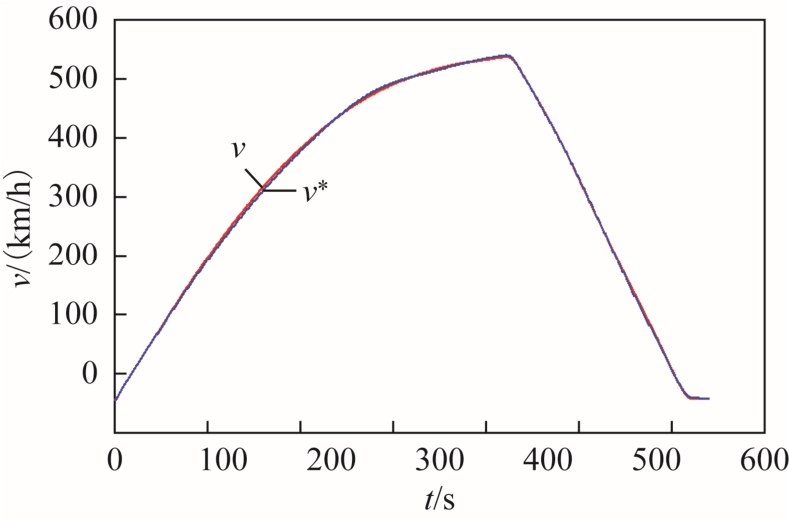
图14 磁浮列车速度曲线
Fig.14 The speed curve of high-speed maglev
图15 采用VFDC 策略时电流响应波形
Fig.15 Current responses with VFDC
由于磁浮列车采用分段供电的方式，当磁浮列车从一个定子段过渡到另一个定子段时，列车一侧的定子会经历电流降为零再增大的过程。由于dq 轴电流之间没有完全解耦，存在耦合作用，因此q 轴电流变化会对d 轴电流产生影响，定子电流存在周期性波动，对磁浮列车的稳定运行造成影响。
采用电压前馈解耦策略的电流响应曲线如图15 所示，由于估计参数与实际线路参数不一致，解 耦补偿不能抵消实际的耦合量，导致dq 轴电流不能完全解耦，在定子段换步过程中，d 轴电流波动剧烈，随着车速的升高，耦合越来越严重，高速时电流波动超过100A。从电流响应波形局部放大图可知，q 轴电流从开始下降到完全跟踪需要465ms，从开始上升到完全跟踪需要476ms，跟踪较慢，并且电流波动较大。
图16 为采用基于自抗扰解耦策略的电流响应曲线。在磁浮列车加速和减速过程中d 轴电流各有一个较大的尖刺，此时对照q 轴电流曲线，可知磁浮列车没有处于换步过程中，而车速为215km/h（对应的频率为115Hz），这是由于调制策略切换时对电流造成的冲击，与dq 轴电流耦合无关，电压前馈解耦策略也存在这个尖刺。这两个较大的尖刺可以通过后期优化调制策略改善。除此之外，在定子段换步过程中，d 轴电流周期性波动不大，即使高速时也不超过30A，dq 轴电流解耦效果好。从电流响应波形局部放大图可以看出，q 轴电流从开始下降到 完全跟踪需要410ms，从开始上升到完全跟踪需要427ms，系统响应速度更快。
综上所述，在磁浮列车运行过程中，当线路参数变化时，传统的电压前馈解耦控制策略由于估计参数与实际线路参数不一致，解耦补偿不能抵消实际的耦合量，解耦效果差；而基于自抗扰的解耦控制策略，在实现dq 轴电流解耦的同时，补偿了其他因素引起的扰动，降低了换步过程中的电流波动，有效地提高了系统的动态响应速度和抗干扰性能，表现出良好的鲁棒性。
图16 采用ADRC 策略时电流响应波形
Fig.16 Current responses with ADRC
5 结论
磁浮列车在双端供电模式下dq 轴电流耦合严重，而电压前馈解耦控制策略在参数变化时解耦效果差。因此本文在传统自抗扰控制策略的基础上，提出了基于改进自抗扰的牵引控制策略，该策略算法简单，易于实现，对参数变化具有良好的鲁棒性，降低了磁浮列车在换步过程中的电流波动，改善了系统的动态性能和稳态性能。通过仿真和硬件在环实验验证了基于自抗扰控制策略的有效性，该策略适用于高速磁浮列车的牵引控制。
[1] 吴祥明. 磁浮列车[M]. 上海: 上海科学技术出版社, 2003.
[2] 刘金鑫, 葛琼璇, 王晓新. 高速磁浮牵引控制系统半实物实验研究[J]. 电工技术学报, 2015, 30(14): 497-503.
Liu Jinxin, Ge Qiongxuan, Wang Xiaoxin, et al. Hardware-in-loop research of traction-system for high-speed maglev[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 497-503.
[3] 孙鹏琨, 葛琼璇, 王晓新, 等. 磁悬浮列车在双端供电模式下的无速度传感器控制[J]. 电工技术学报, 2018, 33(18): 4249-4256.
Sun Pengkun, Ge Qiongxuan, Wang Xiaoxin, et al. Research on speed sensorless control of maglev train with double-end power supply[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4249-4256.
[4] 刘金鑫, 葛琼璇, 王晓新, 等. 双端供电模式下高速磁浮列车牵引控制策略研究[J]. 电工电能新技术, 2015, 34(6): 16-21.
Liu Jinxin, Ge Qiongxuan, Wang Xiaoxin, et al. Research on control strategy of high-speed maglev train with double-end power supply[J]. Advanced Technology of Electrical Engineering and Energy, 2015, 34(6): 16-21.
[5] 周华伟, 温旭辉, 赵峰, 等. 基于内模的永磁同步电机滑模电流解耦控制[J]. 中国电机工程学报, 2012, 32(15): 91-99.
Zhou Huawei, Wen Xuhui, Zhao Feng, et al. Decoupled current control of permanent magnet synchronous motors drives with sliding mode control strategy based on internal model[J]. Proceedings of the CSEE, 2012, 32(15): 91-99.
[6] 李春鹏, 贲洪奇, 刘博, 等. 采用扰动观测器的偏差解耦控制方法[J]. 中国电机工程学报, 2015, 35(22): 5859-5868.
Li Chunpeng, Ben Hongqi, Liu Bo, et al. Deviation decouple control method based on disturbance observer[J]. Proceedings of the CSEE, 2015, 35(22): 5859-5868.
[7] Briz F, Degner M W, Lorenz R D. Analysis and design of current regulators using complex vectors[J]. IEEE Transactions on Industry Applications, 2000, 36(3): 817-825.
[8] Holtz J, Quan J, Pontt J, et al. Design of fast and robust current regulators for high-power drives based on complex state variables[J]. IEEE Transactions on Industry Applications, 2004, 40(5): 1388-1397.
[9] Han J. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.
[10] Li Jie, Ren Haipeng, Zhong Yanru. Robust speed control of induction motor drives using first-order auto-disturbance rejection controllers[J]. IEEE Transactions on Industry Applications, 2015, 51(1): 712-720.
[11] 刘春强, 骆光照, 涂文聪, 等. 基于自抗扰控制的双环伺服系统[J]. 中国电机工程学报, 2017, 37(23): 7032-7039.
Liu Chunqiang, Luo Guangzhao, Tu Wencong, et al. Servo systems with double closed-loops based on active disturbance rejection controllers[J]. Proceedings of the CSEE, 2017, 37(23): 7032-7039.
[12] 左月飞, 李明辉, 张捷, 等. 控制增益对永磁同步电动机自抗扰控制性能的影响[J]. 电工技术学报, 2016, 31(3): 58-65.
Zuo Yuefei, Li Minghui, Zhang Jie, et al. Influence of control gain on active disturbance rejection controller for PSSM[J]. Transactions of China Electrotechnical Society, 2016, 31(3): 58-65.
[13] 曾岳南, 曾祥彩, 周斌. 永磁同步电机传动系统电流环非线性自抗扰控制器的设计与稳定性分析[J]. 电工技术学报, 2017, 32(17): 135-143.
Zeng Yuenan, Zeng Xiangcai, Zhou Bin, et al. Nonlinear active disturbance rejection controller design for current loop of PMSM drive system and its stability analysis[J]. Transactions of China Electrotechnical Society, 2017, 32(17): 135-143.
[14] 周凯, 孙彦成, 王旭东, 等.永磁同步电机的自抗扰控制调速策略[J].电机与控制学报, 2018, 22(2): 57-63.
Zhou Kai, Sun Yancheng, Wang Xudong, et al. Active disturbance rejection control of PMSM speed control system[J]. Electric Machines and Control, 2018, 22(2): 57-63.
[15] 王娟. 磁悬浮列车用长定子直线同步电机特性研究与故障分析[D]. 北京: 中国科学院电工研究所, 2004.
[16] 韩京清. 自抗扰控制技术:估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008.
[17] Gao Z. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the 2003 IEEE American Control Conference, Denver, 2003, 6: 4989-4996.