0 引言
永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)的特点是具有较宽的调速范围、较高的机械强度、较大的功率密度和转矩,这使得永磁同步电机在轨道交通、风力发电、航空航天、新能源汽车等领域得到广泛的应用[1-3]。在实际应用中,受限于逆变器直流侧电压,PMSM 需要弱磁增速以拓宽调速范围并提高其稳定性[4-6]。
双电流调节器分别控制交轴电流和直轴电流,现有的弱磁控制策略主要有公式计算法[7-9]、查表法[10-12]、梯度下降法[13-16]和负直轴电流补偿法[17-18]等。当电机工作在弱磁区域时,随着转速的升高,两个电流调节器的耦合加强,调节器容易趋于饱和从而影响电机的性能[19]。
文献[20]提出了一种直接给定交轴电压的弱磁控制方法,不再尝试减小两个电流之间的耦合影响,而是利用电流耦合关系并通过调节直轴电流 di 来实现在弱磁区域的转矩和磁链控制。该方法只需要一个电流调节器,调节简单,动态响应快,但是电机不能充分利用逆变器直流侧电压,使得调速范围变窄,负载能力和电机效率有所下降。文献[21-22]通过离线计算和在线查表的方法得到交轴电压值,电机效率和带载能力得到提升,但是需要大量的实验数据,不易实现,可移植性差。
本文针对文献[20]提出的定交轴电压弱磁策略展开研究,提出了一种新的给定交轴电压的方法,引入虚拟电阻的概念,在保证系统动态响应的基础上提高了电机工作效率。
1 PMSM 数学模型
在同步参考坐标系下,永磁同步电机数学模型为
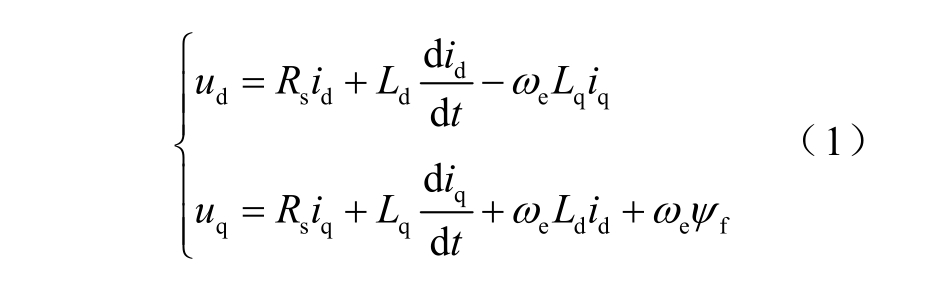
式中,ud、uq 分别为电机定子电压直轴、交轴分量;id、iq 分别为电机定子电流直轴、交轴分量;Ld、Lq分别为电机直轴、交轴电感;Rs 为电机定子电阻;ωe 为电机电角速度; fψ 为电机永磁体磁链。
永磁同步电机运行时最大输入电压受到逆变器直流侧电压及电机绝缘等级的限制,定子电压过高时会击穿绝缘层,损坏电机。故应满足的电压限制为
式中,Usmax 为电机定子端电压合成矢量的最大幅值。Usmax 取 dc 3U ,Udc 为直流母线电压。
另外,受系统温升约束,电机稳定运行时,定子电流合成矢量幅值不能超过最大允许幅值Ismax,即
PMSM 高速运行时,忽略定子电阻压降的影响,稳态电压可写成
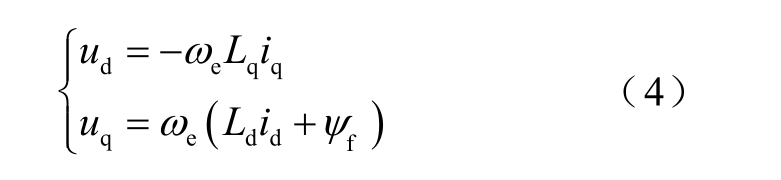
将式(4)代入式(2)得

PMSM 电磁转矩计算公式为
式中, p 为电机极对数。
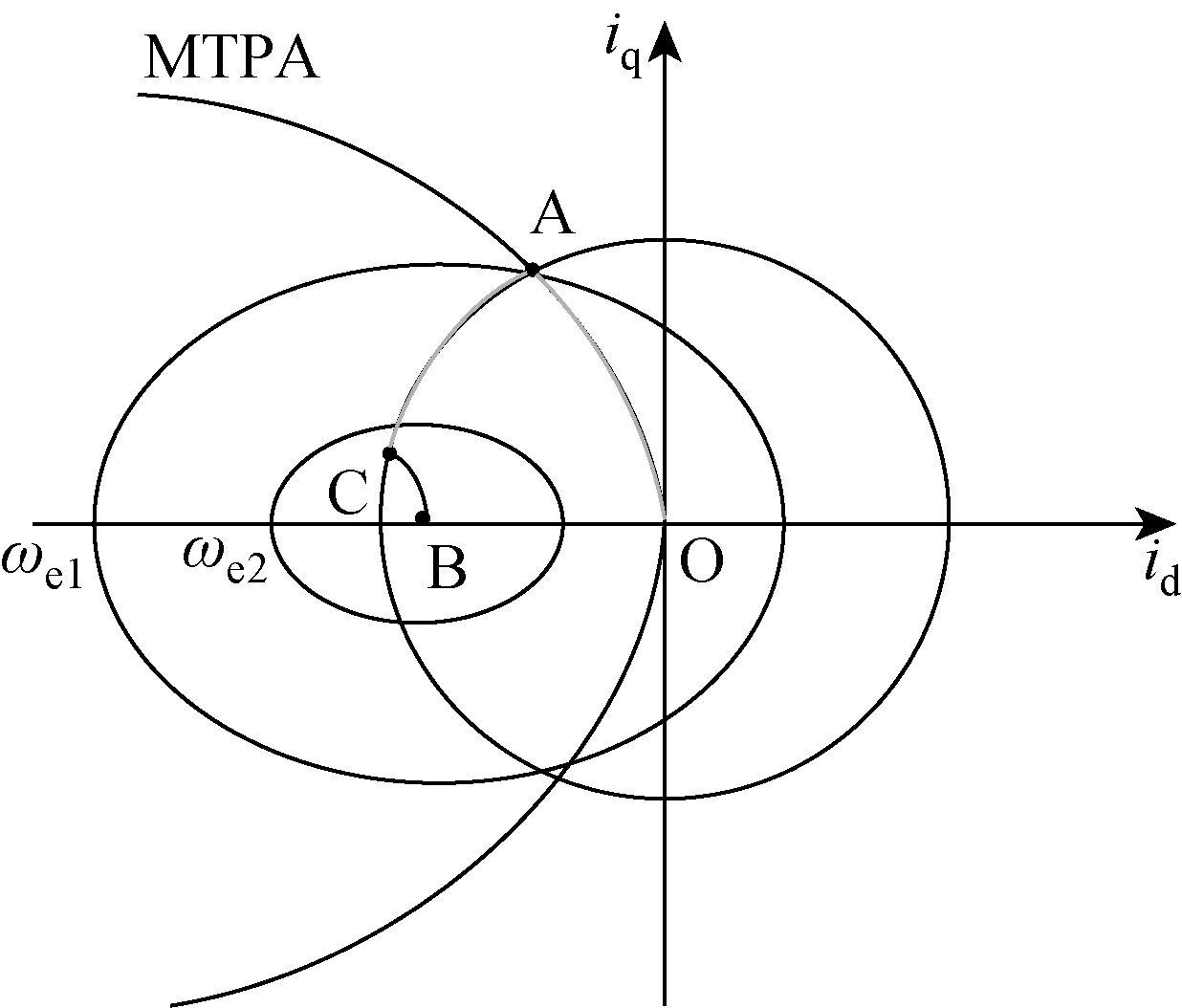
图1 PMSM 电流轨迹示意图
Fig.1 Current trajectory of PMSM
电机在id-iq 平面上的电流轨迹如图1 所示,电压限制椭圆与电流限制圆交集部分为即为该转速下电机稳定工作点的集合。当电机工作在恒转矩区时,即电机转速低于基速,电机工作点为电流限制圆与最大转矩电流比(Maximum Torque Per Ampere, MTPA)曲线的交点,即点A。由式(5)可知,随着转速升高,电压限制椭圆逐渐变小,当电机转速升高至基速时,电压限制椭圆与电流限制圆的交点与A 点重合,当电机转速高于基速时,逆变器直流侧电压达到最大值,不能继续升压,此时需要弱磁控制,使电机转速范围扩大。在弱磁开始阶段,电机工作点为电压限制椭圆与电流限制圆的交点,转速继续升高至电压限制椭圆与电流限制圆的交点和 电流限制圆与最大转矩电压比(Limit Voltage Maximum Torque, LVMT)曲线的交点重合后,电机工作点变为电流限制圆与LVMT 曲线的交点。
2 基于虚拟电阻的单电流调节器弱磁控制系统
传统单电流调节器弱磁控制方法的原理是交轴电压不通过电流调节器,直接给定交轴电压值作为交轴电流调节器的输出,而直轴电流的给定值由速度调节器控制,这就意味着最终的电压控制信号是由一个电流调节器和一个固定交轴电压信号组成的。由于直接给定电机交轴电压,根据交轴电压公式可知电机交、直轴电流满足

当电机在基速以下运行时,可以由MTPA 曲线得到电机在各负载状态下的稳态工作点,所以由速度控制器输出电机的交轴电流给定值后就可以通过计算获得直轴电流的给定值。当电机在基速以上运行时,如果采用固定交轴电压的算法,就可以通过式(7)计算得到电流之间的耦合关系。此时,由速度控制器输出电机的直轴电流给定值后就可以通过计算获得交轴电流的给定值。然后,再由直轴电流给定值通过电流调节器获得直轴电压给定值。这样,由于用交轴电压代表了电流耦合关系,就可以用一相电流指令和一相电压指令来确定电机电压控制信号,完成电机电流解耦控制。
传统的定交轴电压弱磁控制算法给定交轴电压U FWC为定值,电机工作点在加载过程中沿负载曲线移动,但是电机的带载能力与效率会互相矛盾。为简化图形,以表贴式永磁(Surface-mounted Permanent Magnet, SPM)电机为例进行分析,传统定交轴电压算法下电机运行状态分析如图2 所示。

图2 传统定交轴电压算法下电机运行状态分析
Fig.2 Analysis of PMSM operation under traditional fixed-q-axis voltage algorithm
电机在某一转速 eω 下给定交轴电压UFWC 时,负载曲线在id-iq 坐标系上与横轴交点为B 点,与电压极限圆对称轴交点为F 点,当电机想要达到最大带载能力时,需要取的交轴电压为UFWC1,此时电机电磁转矩为Te1,但是此时空载时电机工作在A 点,电机的定子电流已经很大,导致电机的效率变低;假设当电机想要最大限度地提高工作效率,则需要取的交轴电压为UFWC2,此时电机空载时工作点为B 点,该点为电机在空载时能达到的最小定子电流,相比A点电机效率显著提高,相比定交轴电压为UFWC1 时,负载线整体下移,即电机效率比之前升高,但是此时电机的带载能力变低,电机能够达到的最大电磁转矩减小为Te2。若要同时兼顾带载能力与电机效率,显然仅仅改变负载线公式中的交轴电压给定值UFWC不能解决问题,为此,本文提出虚拟电阻 sR′概念,通过改变 sR′与UFWC 同时改变负载线的斜率与截距,从而达到带载能力与电机效率的双重优化。
基于虚拟电阻的永磁同步电机单电流调节器弱磁控制系统框图如图3 所示。下面将对 FWCU 给定模块进行设计。
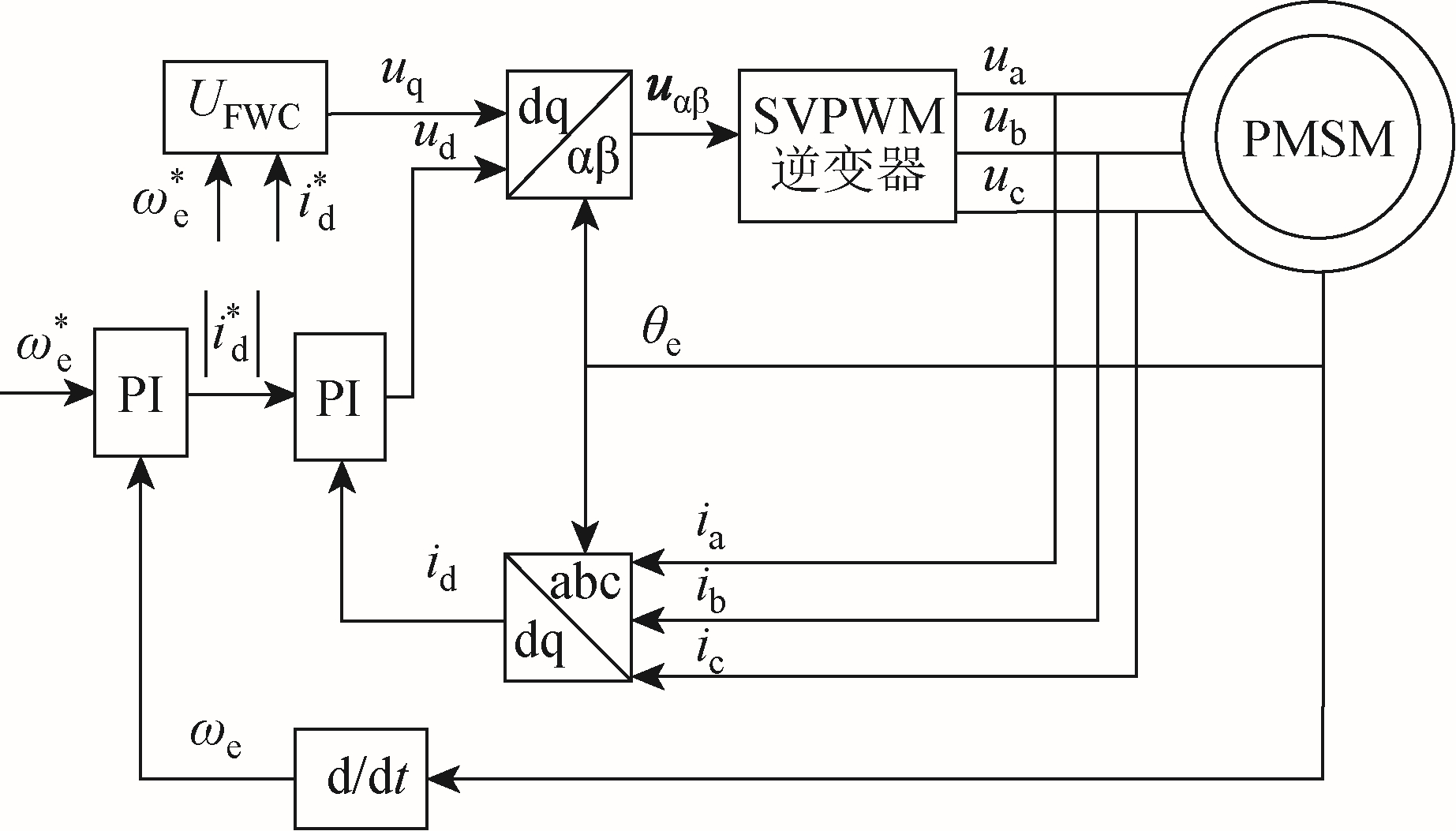
图3 基于虚拟电阻的永磁同步电机单电流调节器弱磁控制系统框图
Fig.3 Block diagram of flux-weakening control system for single-current regulator of PMSM based on virtual resistor
为简化分析,变换坐标轴为
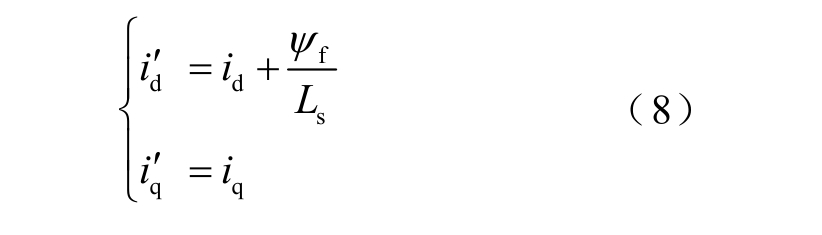
此时电机电压变为
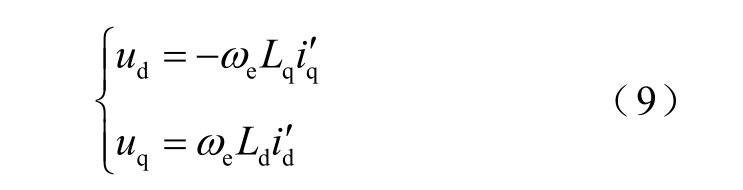
电压限制圆方程变为

由式(7)与式(8)可知,交轴电压取UFWC 时,交、直轴电流关系式在新的坐标系下变为
式(11)称为负载线公式,当交轴电压取UFWC时,随着负载的变化,电机的工作点沿式(11)所示曲线变化。
加入虚拟电阻 sR′ 后负载线公式变为

其中
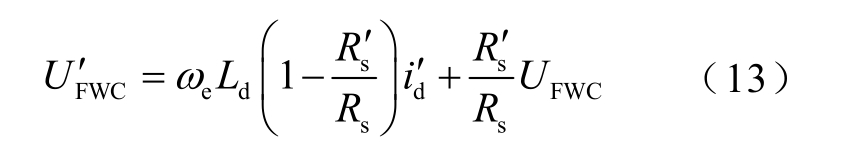
负载曲线与 iq′轴交点为![]()
![]()
弱磁控制算法下永磁同步电机工作状态分析如图4 所示。为表区分,式(11)所示负载曲线称为负载曲线1,图中用虚线表示,加入虚拟电阻后的负载曲线称为负载曲线2,用实线表示。若使两条负载曲线均能达到最大带载能力,即均过F 点,F点坐标为 ![]() 此时负载曲线1 的
此时负载曲线1 的![]()
![]() 负载曲线2的sR′ 为
负载曲线2的sR′ 为![]() 即负载曲线2 为
即负载曲线2 为


图4 弱磁控制算法下永磁同步电机运行状态分析
Fig.4 Analysis of PMSM operation under flux-weakening control algorithm
此时负载曲线1 与负载曲线2 均是恒过F 点的曲线,负载曲线1 通过改变 FWCU 的值,仅能改变截距,即使曲线上下移动,如图两条虚线所示。但负载曲线2 可以通过改变 FWCU′ 改变斜率。如图两条实线所示。
两条曲线重合时

故只要 FWCU′ 满足

加入虚拟电阻的负载曲线2 就能保证斜率小于负载曲线1,即当电机带载能力相同时负载曲线2代表的基于虚拟电阻的单电流调节器弱磁控制算法工作效率高于负载曲线1 代表的定交轴电压弱磁控制算法。
记

则k 的取值范围为

k 值取决于想要达到的优化效果,k 越大,电机工作效率优化效果越好。

图5 考虑定子电阻影响时电机运行状态分析
Fig.5 Analysis of PMSM operation considering stator resistor
考虑定子电阻影响时电机运行状态分析如图5所示。由图5 可知,若使负载线恒过F 点(F 点为电压限制圆与纵轴的交点),则能达到该转速下的最大转矩,而负载线与横轴交点越往右移,电机的工作效率越高,但是在实际情况中应考虑定子电阻影响。图中虚线代表电机考虑定子电阻影响时的电压限制圆,该圆与横轴交点为E′,故设计时应使负载线恒过E′点,从而最大程度地提高电机工作效率。
将F 点坐标 ![]() 代入负载线公式得
代入负载线公式得

E′点坐标为

将E′点代入负载线公式得到
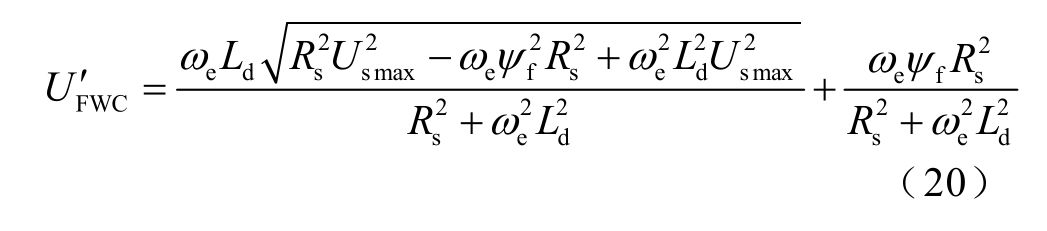
则此时电机的负载曲线可以同时兼顾电机带载能力与效率,此时负载线如图5 所示。故 UF′ WC 的取值上限变为

即k 的取值范围更新为

此时式(13)变为
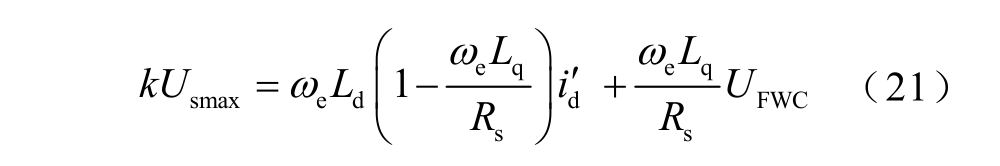
由此可推导得到电机兼顾带载能力与最大工作效率时的交轴电压给定值取为

此时

由式(22)和式(23)可知, FWCU 的选取与直流母线电压、电机转速以及直轴电流分量有关。
此时加入虚拟电阻的负载曲线为

3 仿真与实验结果分析
为了验证设计的基于虚拟电阻的单电流调节器弱磁控制算法的有效性,在PLECS 仿真软件中搭建基于虚拟电阻的永磁同步电机单电流调节器弱磁控制系统仿真模型。电机在恒转矩区采用id=0 控制,在恒功率区采用弱磁控制。其中,以恒速加载的形式近似得到电机在不同负载下稳态工作点。
3.1 仿真结果与分析
为了验证设计的基于虚拟电阻的单电流调节器弱磁控制算法的有效性,本文利用PLECS 仿真平台设计了如下几组仿真。
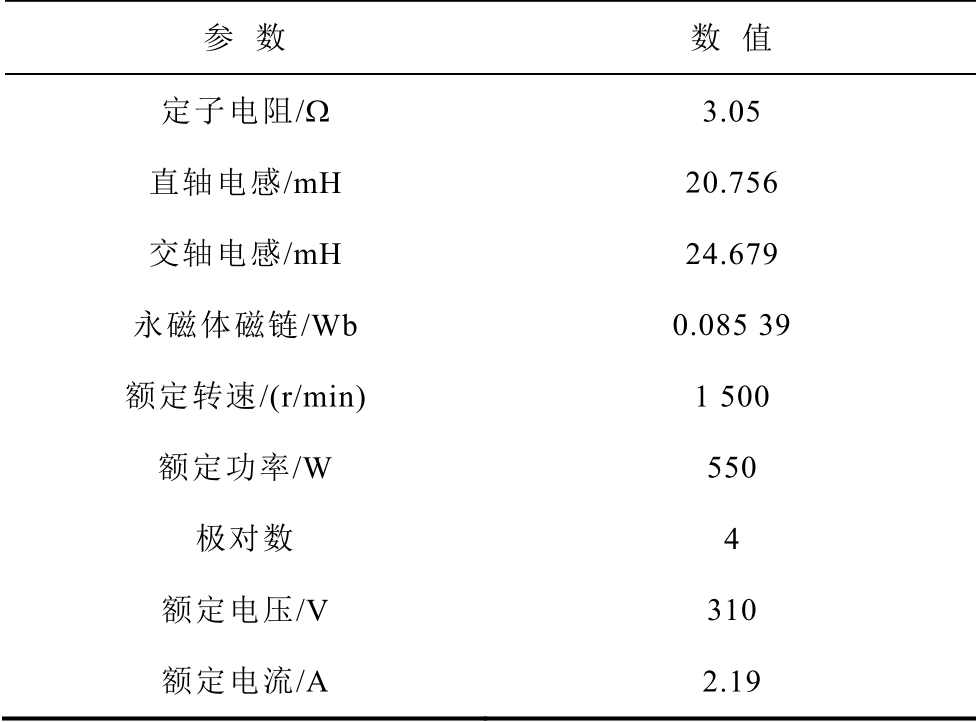
基于内置式永磁(Interior Permanent Magnet, IPM)电机改进的单电流调节器弱磁控制算法仿真模型参数见表1。
表1 仿真模型中内嵌式永磁同步电机的参数
Tab.1 Parameters of IPMSM in simulation model
参 数 数 值 定子电阻/Ω 3.05 直轴电感/mH 20.756 交轴电感/mH 24.679 永磁体磁链/Wb 0.085 39 额定转速/(r/min) 1 500 额定功率/W 550 极对数 4 额定电压/V 310 额定电流/A 2.19
仿真中,电机先采用id=0 控制加速至1 800r/min,然后通过算法切换模块将电机切换到恒功率运行,采用弱磁控制算法将转速升高至3 000r/min,在t=6s时,电机负载转矩开始以0.06N·m/s 的速度由0N·m升高至0.3N·m。分别采用传统定交轴电压单电流调节器弱磁控制算法与本文提出的基于虚拟电阻的单电流调节器弱磁控制算法进行恒速加载仿真。其中传统定交轴电压 FWCU 取36.5V。
加载时的电机仿真波形如图6 所示。以恒速加载的形式近似得到电机在不同负载下稳态工作点。
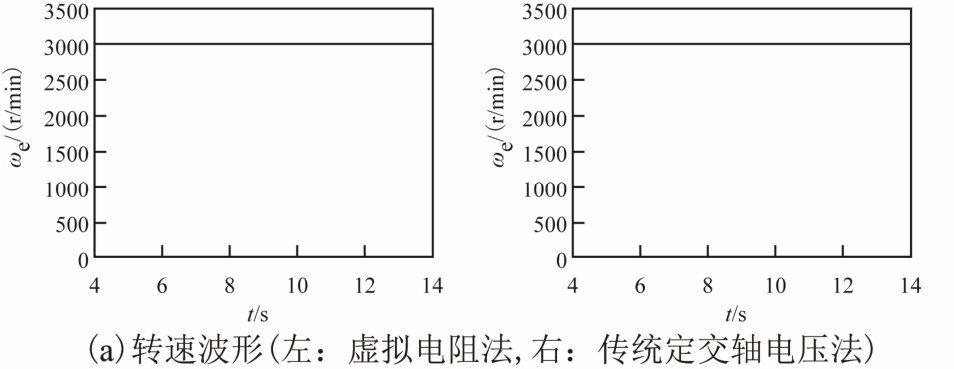

图6 转速为3 000r/min 时恒速加载时电机仿真结果
Fig.6 Simulation results with slope load at 3 000r/min
由图6 可知虚拟电阻法在相同负载下相比传统的定交轴电压方法效率显著提高。图6a 显示了在恒速加载时,两种控制方法下的电机传动系统转速均没有明显变化,电机处于稳定运行状态。从图6b 可 以看出电机输出的电磁转矩都能随着负载增加而同步增加。图6c 显示了电机在加载过程中的电机电流轨迹,可以看出,基于虚拟电阻的单电流调节器弱磁控制系统的电流轨迹相比传统定交轴电压控制的永磁同步电机弱磁控制系统整体下移,降低了电机工作时的损耗。从图6d 和图6e 中可以看出,空载时,虚拟电阻方法相电流幅值为0.891A,电阻损耗为1.211W,传统定交轴方法相电流幅值为2.705A,电阻损耗为11.158W,损耗减小89.1%,加载0.3N·m时,虚拟电阻方法相电流幅值为1.463A,电阻损耗为3.246W,传统定交轴方法相电流幅值为2.804A,电阻损耗为11.990W,损耗减小72.98%。从图6f 中可以看出,6~11s 恒速加载,基于虚拟电阻的方法能够极大地提高效率,在加载0.3N·m 时电机工作效率为71.1%,传统定交轴方法的效率为46.3%。
由仿真结果可知,本文设计的基于虚拟电阻的单电流调节器弱磁控制算法相对于传统的定交轴弱磁控制算法降低了电机工作时的损耗,效率显著提高。
3.2 实验结果与分析
本文搭建了永磁同步电机传动系统实验平台,如图7 所示。

图7 永磁同步电机传动系统实验平台
Fig.7 Experimental platform of PMSM drive system
永磁同步电机传动系统实验平台由强电驱动部分和弱电控制部分两大部分组成。强电驱动部分主要包括三相交流电源(AC380V)、三相隔离变压器、三相调压器、单相调压器、永磁同步电机及其驱动电路、伺服加载系统、散热系统。弱电控制部分包括直流电源、同步电机控制电路、伺服电动机控制电路以及PC 等。
实验时,给定转速3 000r/min。待电机在给定转速下稳定运行后,负载转矩由0N·m 增加至0.3N·m。实验进行两次,第一次实验时电机搭载传统单电流调节器弱磁控制算法。第二次实验时,电机搭载基于虚拟电阻的单电流调节器弱磁控制算法。实验波形如图8 所示。

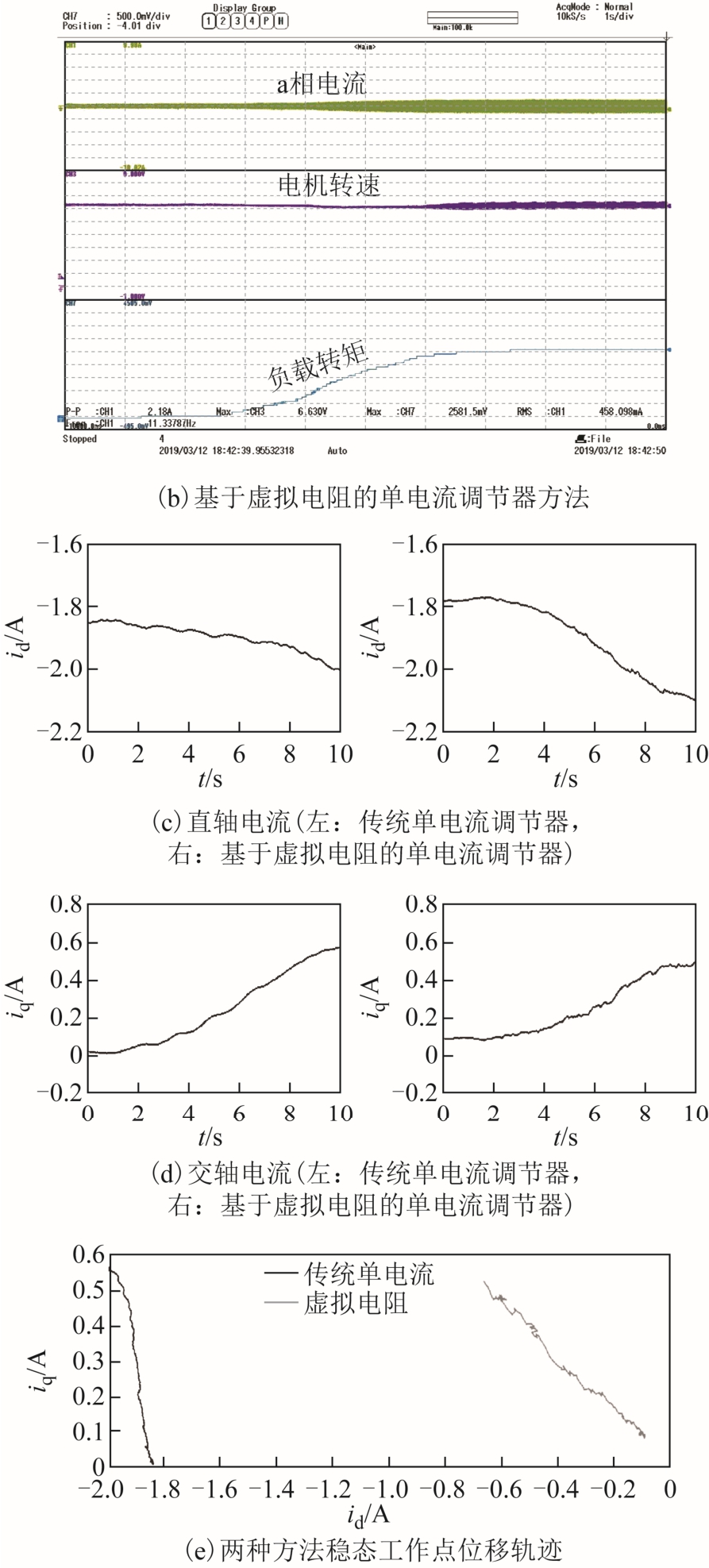
图8 传统单电流调节器与基于虚拟电阻的单电流调节器
Fig.8 Traditional single current regulator and virtual resistance based on single current regulator
图8 a、图8b 中三条曲线由上至下分别代表电机a 相电流、电机转速和负载转矩。其中转速波形转换单位为750r/min/V,转矩波形转换单位为0.1N·m/V。
由实验结果可知,加载过程中转速基本维持不变,可以认为电机状态处于稳态过渡状态。两种算法下直轴电流与交轴电流分别如图8c、图8d 所示。直轴电流主要反映电机的弱磁深度,交轴电流主要反映电机的电磁转矩。通过图8c、图8d 可知,传统单电流调节器无论是在空载还是带载时均具有很大的弱磁电流,而基于虚拟电阻的单电流调节器空载时几乎无弱磁电流,而是随着负载的增加逐渐增加弱磁电流。从图8e 可以直观地观察到传统单电流调节器下和基于虚拟电阻设计的单电流调节器下稳态工作点的位移轨迹。由图8e 显示,负载前后基于虚拟电阻的单电流调节器控制下电机的稳态工作点距离id-iq 平面的原点更近,电机的定子电阻损耗更小。
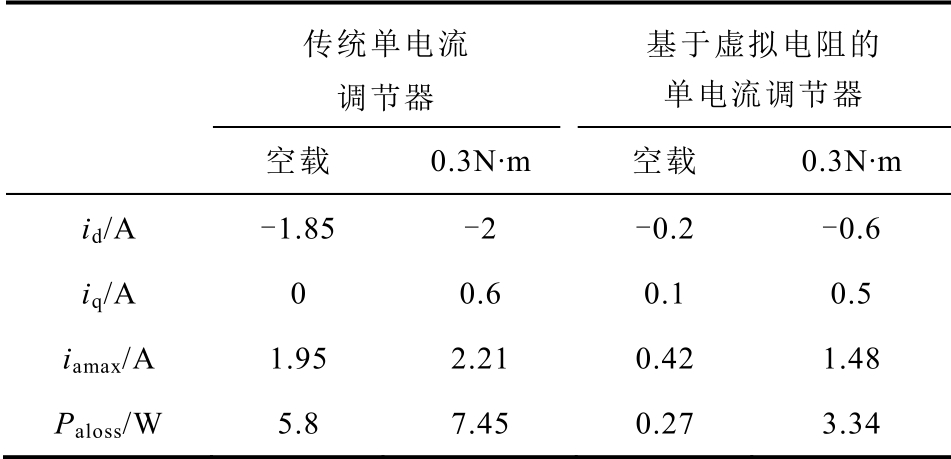
两种算法的加载实验结果见表2,本文提出的基于虚拟电阻的单电流调节器弱磁控制算法大大减少了定子电阻损耗,空载时以A 相电阻损耗为例,相对传统算法损耗减少95.34%,加载0.3N·m 时,损耗减少55.17%。
表2 弱磁控制实验结果
Tab.2 Experiment results of flux-weakening control schemes
传统单电流 调节器 基于虚拟电阻的 单电流调节器 空载 0.3N·m 空载 0.3N·m id/A -1.85 -2 -0.2 -0.6 iq/A 0 0.6 0.1 0.5 iamax/A 1.95 2.21 0.42 1.48 Paloss/W 5.8 7.45 0.27 3.34
以上实验证明了相比传统单电流调节器弱磁控制算法,基于虚拟电阻的单电流调节器弱磁控制算法能够有效地降低损耗。
4 结论
为了将单电流调节器系统中的弱磁电压定量化,在保证动态调速性能的同时提升工作效率,本文提出了从电流轨迹设计出发的单电流调节器弱磁电压给定方法。该方法依照稳态工作点预先设定的电流轨迹,根据单电流调节器的思想给出弱磁电压的表达式(式(22)),再将电流反馈值代入到式(22)中计算出弱磁电压的给定值。因此可以按照效率优化的要求设计电流轨迹,利用此算法获得弱磁电压的给定值,配合直轴电流调节器完成电机电压的给定,并搭建基于虚拟电阻的单电流调节器弱磁控制系统模型和实验平台。
仿真和实验结果表明,基于虚拟电阻的单电流调节器弱磁控制算法能够保证电机稳定运行,并在保证动态调速性能的同时满足效率优化的需求。
[1] 李崇坚. 交流同步电机调速系统[M]. 北京: 科学出版社, 2006.
[2] 高雅, 刘卫国, 骆光照. 牵引机车用永磁同步电机断电-重投控制系统研究[J]. 电工技术学报, 2016, 31(6): 100-107,117.
Gao Ya, Liu Weiguo, Luo Guangzhao. Research of power down-rejoining on control system for permanent magnet synchronous motor used in traction engines[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 100-107, 117.
[3] 徐奇伟, 孙静, 蒋小彪, 等. 混合动力车用复合结构永磁电机中磁场耦合[J]. 电工技术学报, 2017, 32(增刊2): 56-63.
Xu Qiwei, Sun Jing, Jiang Xiaobiao, et al. Magnetic coupling in compound-structure permanent-magnet motor for hybrid electric vehicle[J]. Transactions of China Electrotechnical Society, 2017, 32(S2): 56-63.
[4] 刘军锋. 感应电动机在弱磁区的高性能电流控制策略[J]. 电工技术学报, 2010, 25(7): 61-66.
Liu Junfeng. High performance current control strategy for induction motors in field-weakening region[J]. Transactions of China Electrotechnical Society, 2010, 25(7): 61-66.
[5] 侯利民, 申鹤松, 阎馨, 等. 永磁同步电机调速系统 H ∞鲁棒控制[J]. 电工技术学报, 2019, 34(7): 1478-1487.
Hou Limin, Shen Hesong, Yan Xin, et al. H∞ robust control of PMSM speed regulation system[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1478-1487.
[6] 张海洋, 许海平, 方程, 等. 基于负载转矩观测器的直驱式永磁同步电机新型速度控制器设计[J]. 电工技术学报, 2018, 33(13): 2923-2934.
Zhang Haiyang, Xu Haiping, Fang Cheng, et al. Design of a novel speed controller for direct-drive permanent magnet synchronous motor based on load torque observer[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 2923-2934.
[7] Morimoto S, Sanada M, Takeda Y. Wide-speed operation of interior permanent magnet synchronous motors with high-performance current regulator[J]. IEEE Transactions on Industry Applications, 1994, 30(4): 920-926.
[8] Pan C T , Sue S M . A linear maximum torque per ampere control for IPMSM drives over full-speed range[J]. IEEE Transactions on Energy Conversion, 2005, 20(2): 359-366.
[9] 王艾萌. 内置式永磁同步电动机的优化设计及弱磁控制研究[D]. 保定: 华北电力大学, 2010.
[10] Bae B H , Patel N , Schulz S , et al. New field weakening technique for high saliency interior permanent magnet motor[C]//38th IAS Annual Meeting on Conference Record of the Industry Applications Conference, Salt Lake City, UT, USA, 2003,DOI: 10.1109/IAS.2003.1257641.
[11] Doncker D , Lenke R W , Ulrichkwak R , et al. Field weakening control of interior permanent magnet machine using improved current interpolation technique[C]//IEEE Power Electronics Specialists Conference, Jeju, South Korea, 2006, DOI: 10.1109/pesc.2006.1712123
[12] Ottosson J, Alakula M. A compact field weakening controller implementation[C]//IEEE International Symposium on Power Electronics, Taormina, Italy, 2006, DOI: 10.1109/SPEEDAM.2006.1649859
[13] Yoon Y D , Lee W J , Sul S K . New flux weakening control for high saliency interior permanent magnet synchronous machine without any tables[C]// European Conference on Power Electronics & Applications, IEEE, Aalborg, Denmark, 2007, DOI: 10.1109/EPE.2007.4417350.
[14] 盛义发, 喻寿益, 桂卫华, 等. 轨道车辆用永磁同步电机系统弱磁控制策略[J]. 中国电机工程学报, 2010, 30(9): 74-79.
Sheng Yifa, Yu Shouyi, Gui Weihua, et al. Field weakening operation control strategies of permanent magnet synchronous motor for railway vehicles[J]. Proceedings of the CSEE, 2010, 30(9): 74-79.
[15] 丁强. 永磁同步电机矢量控制系统弱磁控制策略研究[D]. 长沙: 中南大学, 2010.
[16] 李珂, 顾欣, 刘旭东, 等. 基于梯度下降法的永磁同步电机单电流弱磁优化控制[J]. 电工技术学报, 2016, 31(15): 8-15.
Li Ke, Gu Xin, Liu Xudong, et al. Optimized flux weakening control of IPMSM based on gradient descent method with single current regulator[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 8-15.
[17] Kim S M, Sul S K. Speed control of interior permanent magnet synchronous motor drive for flux weakening operation[J]. IEEE Transactions on Industry Applications, 1995, 33(1): 43-48.
[18] Paicu M C , Tutelea L , Andreescu G D , et al. Wide speed range sensorless control of PM-RSM via “active flux model”[C]// IEEE Energy Conversion Congress & Exposition, San Jose, CA, USA, 2009, DOI: 10.1109/ECCE.2009.5316375.
[19] 张梓绥, 王琛琛, 游小杰, 等. 基于单Q 轴电流调节器的永磁同步电机电流轨迹控制[J]. 电工技术学报, 2018, 33(24): 5779-5788.
Zhang Zisui, Wang Chenchen, You Xiaojie, et al. Current locus control of permanent magnet synchronous motor based on single Q-axis current regulator flux-weakening method[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5779-5788.
[20] Chi Song, Xu Longya, Zhang Zheng. Efficiencyoptimized flux-weakening control of PMSM incorporating speed regulation[C]//IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 2007, DOI: 10.1109/PESC.2007.4342240
[21] Xu Longya, Zhang Yuan, Guven M K. A new method to optimize q-axis voltage for deep flux weakening control of IPM machines based on single current regulator[C]// IEEE 2008 International Conference on Electrical Machines and Systems, Wuhan, 2008: 2750-2754.
[22] Zhang Yuan, Xu Longya, Guven M K , et al. Experimental verification of deep flux-weakening operation of a 50 kW IPM machine by using single current regulator[C]//2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA , 2009, DOI: 10.1109/ECCE.2009.5316297