0 引言
随着电机和电力电子技术的不断革新与发展,直线作动器广泛应用于国防建设和国民经济的各个 领域[1-3]。传统直线作动器主要采用滚珠丝杆等机械执行机构,将旋转运动转换为直线运动[4-5]。然而,机械执行机构无法避免磨损、卡死和低运行精度等问题,直接影响到直线作动器的性能与使用寿命[6-7]。
直线电机经过多年的发展,具有高可靠、高精度、易维护和直接驱动等优势,为直线作动器的发展提供了新的思路[8-11]。但是,直线电机推力密度难以进一步突破[12]。为此,各国学者对新型直线电机 拓扑结构与设计方法进行了深入的研究与探索,如双定子结构、游标结构等[13-18];另外,从材料方面入手,将超导线圈等先进材料应用于直线电机 [19-21]。上述措施虽然可以在一定程度上提升直线电机的推力密度,但提升的空间有限,且增加了结构复杂性和制造成本。尽管如此,对于高端应用领域而言,直线电机推力密度仍显不足。
近年来,随着永磁磁力传动技术和机械加工工艺的进步与发展,永磁直线作动器的传输能力显著提升,已被引入到直线作动器领域,可以兼顾高推力密度和高可靠性等优点[22-24]。并且,随着磁性材料技术的不断发展,永磁直线作动器以其高能量转换、高可靠性、低振动、固有的过载保护等优点,在航空航天、国防军工、新能源发电等领域具有广阔的应用前景[25-27]。
本文回顾并总结了近年来国内外学者在高推力永磁直线作动器方面的研究,分类探讨磁力传动直线作动器的拓扑结构、工作机理与电磁特性。首先,对磁力传动技术应用于磁齿轮的一般性机理进行分析,结合国内外研究现状,对几种典型的磁力作动器的结构及特性进行阐述;然后,引入磁力丝杠直线作动器的概念,依据其结构和工作原理,对其拓扑结构和机械加工等关键技术问题进行剖析;最后,对应用前景进行分析,并探讨磁力丝杠直线作动器的发展方向。
1 磁场调制机理
2001 年,英国谢菲尔德大学D. Howe 教授首次将磁场调制机理引入到磁力齿轮结构中,提出了一种磁场调制式磁力齿轮,如图1 所示[28]。并且设计了原理样机,通过实验测试其转矩性能。东南大学程明教授首次将电磁电机统一规格化为励磁源—调制器—滤波器三个基本要素的级联,建立了电机“三要素”的数学表征方法,如图2 所示[29]。该方法突破了传统电机学理论的束缚,将广泛存在的 气隙磁场调制现象普遍化和理论化,提出并建立了电机气隙磁场调制的统一理论。该理论不仅适用于基于气隙磁场调制原理工作的游标电机、磁齿轮复合电机等,同样适用于有刷直流电机、感应电机和同步电机等传统电机,有望丰富、发展和完善电机学理论[29]。
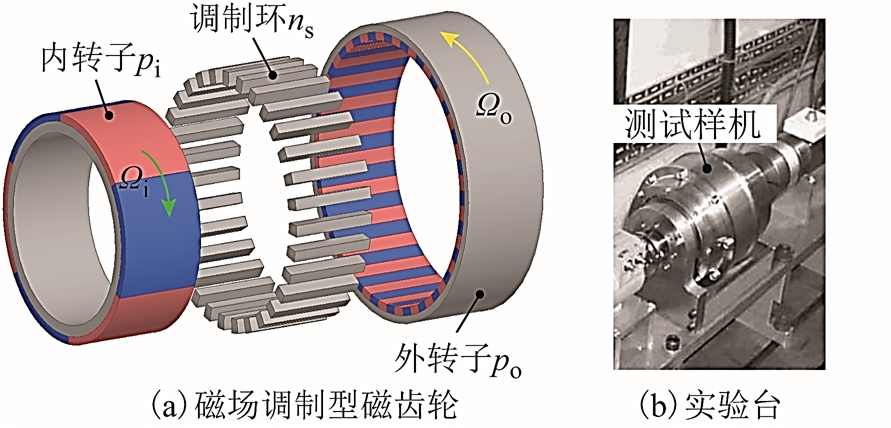
图1 磁场调制型磁齿轮
Fig.1 Field modulated magnetic gear

图2 电机气隙磁场调制理论示意图
Fig.2 Airgap field modulated theory for machines

图3 永磁磁场调制一般性机理
Fig.3 Principle of magnetic field modulated
在永磁磁场调制中,假定磁场调制装置中铁磁材料的磁导率是无穷大的,忽略其磁饱和现象;初始磁场仅由有效谐波组成,忽略其他高次谐波,如图3 所示。理想情况下,气隙在没有调制装置的作用下,仅含有pi 个周期的正弦分布波形,其气隙磁导率为μ0。当气隙中引入ns 对极的调制装置后,气隙磁导率被改变为ns 个铁磁材料磁导率μf 和ns 个空气磁导率μ0 交替的气隙磁导分布。经过调制后, 不难看出,该气隙磁场波形还是以pi 次谐波为主要趋势,但明显加入了ns±pi 的谐波次数。对调制波形进行磁动势(Magnetic Motive Force, MMF)分析后,气隙磁场主要谐波含量Np 可以表达为
因此,根据永磁磁场调制理论,磁齿轮的内、外永磁体极对数与调制环的极对数应该满足
式中,ns 为调制环的极对数;pi 和po 分别为内、外永磁体的极对数。
永磁磁场的调制作用实现了内、外转子和调制环之间的转矩和转速的传输。内转子、外转子和调制环,三者中固定其中任何一个部件,可以实现不同调制关系的转矩和转速的传输,其调制比为

式中,ωs、ωi 和ωo 分别为调磁环和内、外转子角速度。
以结构(ns=31,pi=3,po=28)为例,介绍磁场调制机理在旋转磁齿轮中的作用。永磁体磁场示意图如图4 所示,内层气隙在没有调磁环的作用下,永磁体阵列可以近似等效为单相整距绕组,在内层气隙中产生矩形波分布的初始磁动势,主要含有pi次及其奇数倍的谐波次数。引入极对数为 ns 的调磁环后,产生异步磁场谐波含量ns±pi,如图5 所示。磁场分量谐波次数必须与外转子极对数po 对应,从而实现转矩和转速的传输。反之亦然,外转子永磁体对内层气隙的调制原理同上述调制原理一致。

图4 永磁体磁场示意图
Fig.4 Permanent-magnetic field
在旋转磁齿轮结构中,调制后的气隙磁场谐波含量的表达式对式(1)进行补充,并且主要谐波次数Nm 表示为
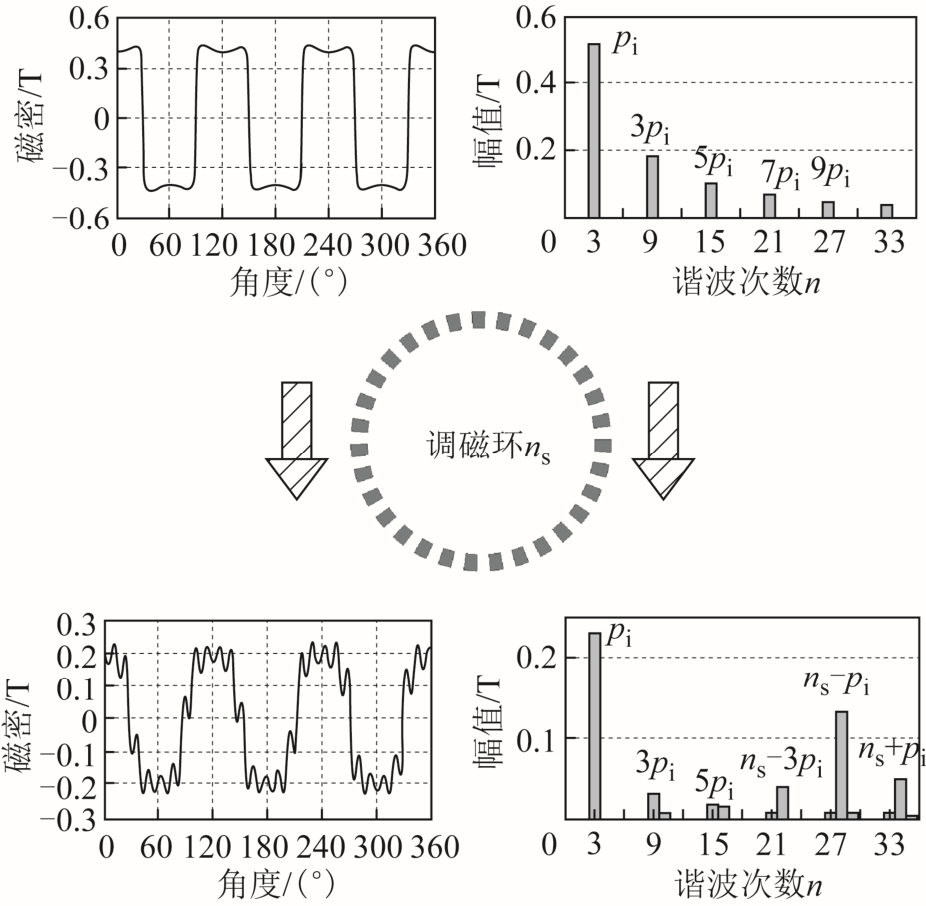
图5 磁场调制型磁齿轮工作机理
Fig.5 Operation principle of magnetic field modulated magnetic gear
式中,p 为内、外磁体极对数。
气隙磁场中的各次谐波的运动速度表示为
式中,ωr 为任一转子的转速。由式(5)可以看出,由于调制环的引入,磁场谐波速度发生了变化,从而形成运动速度和转矩变化的磁场调制式磁性齿轮。
基于磁场调制关系,其传动比表示为

2 单自由度磁力传动技术
2.1 旋转磁齿轮结构
磁场调制原理的引入,使得磁力齿轮得到了爆发式的关注。从此,开启了磁力传动技术发展的快车道,国内外学者集思广益,进一步设计开发磁路拓扑结构,提升磁力传动技术。2005 年,丹麦奥尔堡大学P. O. Rasmussen 教授提出了转子永磁体内置式结构,如图6a 所示,并设计一台样机原型,实测效率为96%,性能接近机械齿轮[30]。为了降低由调制产生的磁场谐波引起的涡流损耗和铁耗,进一步提出了一种无导磁轭型外转子结构,如图6b 所示,在不牺牲转矩性能的情况下,外转子损耗下降40%左右[31]。此外,国内学者提出了一种外转子轭部开槽结构,通过削弱奇数次谐波含量,有效降低转子铁耗,并对铁耗机理进行了剖析[32]。

图6 新型低损耗磁齿轮结构
Fig.6 Novel low-loss magnetic gear
香港大学K. T. Chau 教授与上海大学江建中教授合作开展了磁力齿轮方面的研究。提出将磁齿轮与永磁电机集成的思路,设计了磁齿轮复合电机[33-35],如图7a 所示,磁齿轮的高速转子与电机的转子集成设计作为复合转子,磁齿轮的外转子作为输出驱动,实现低速大转矩直接驱动,被广泛应用于电动汽车和风力发电领域。为了进一步提升磁齿轮的性能,南方科技大学蹇林旎博士在永磁齿轮结构的基础上,提出了Halbach 永磁阵列结构的磁齿轮。相比于现有结构,转矩密度提升13%,转矩脉动降低了67%。并且,气隙磁场更正弦,奇数次谐波含量更低,损耗也明显降低[36]。
相比于同心式结构,文献[37]介绍了一种磁场调制型轴向磁齿轮,实现了输入和输出轴之间的轴向隔离,轴向磁齿轮如图7b 所示。然而,由于其磁力耦合面积降低,进而导致其转矩密度略显不足。目前,随着磁场调制技术与磁性材料的发展,旋转磁齿轮可以实现超过250kN·m/m3 的转矩输出[38-39]。
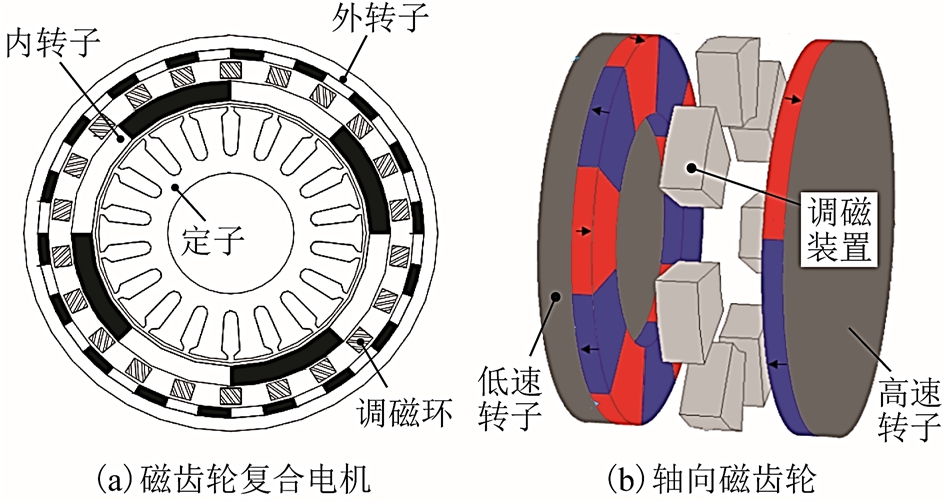
图7 磁齿轮复合结构与轴向磁齿轮
Fig.7 Magnetic gear machine and axial gear
2.2 直线磁齿轮结构
结合旋转磁齿轮的工作原理和转矩优势,国外学者将其扩展到直线作动器领域,提出了直线磁齿轮结构[40],如图8 所示。其工作原理与磁场调制型旋转磁齿轮一致,不同点是将磁场谐波由圆周方向转变为直线方向。经过磁场调制后,使得气隙中的工作谐波次数与内、外永磁体极对数相对应,从而实现推力的传输。由于磁场调制技术的引入,直线磁齿轮的推力密度可以达到1.7MN/m3,并设计加工了直线磁齿轮原理样机,实验验证了推力性能[41]。直线磁齿轮的提出,为永磁直线作动器的开发提供了新的借鉴。
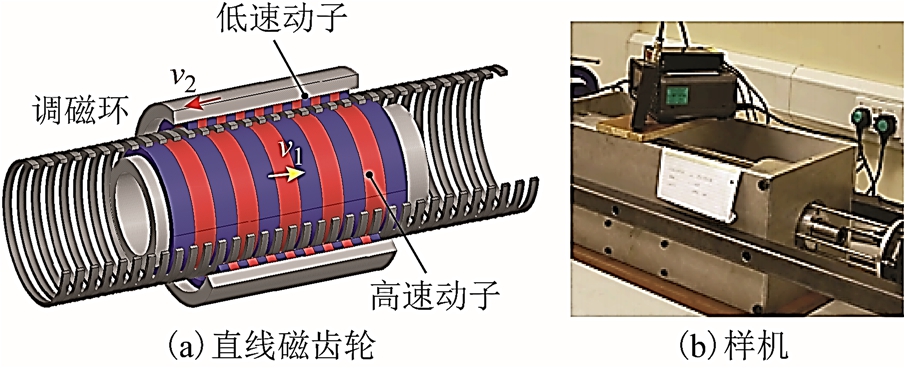
图8 磁场调制型直线磁齿轮
Fig.8 Field modulated linear magnetic gear
随后,东南大学程明教授、兰州理工大学包广清教授等将直线磁齿轮与直线电机结合,将其应用于波浪能的收集,直线磁齿轮复合结构如图9 所示[42-44]。在该结构中,由波浪能带动外动子低速往复运动,进而驱动内动子高速直线往复运动,从而实现电能的转换。但是,因该结构具有三层工作气隙,存在加工复杂、功率因数低的弊端。文献[45]提出一种应用于海洋发电的新型直线磁齿轮结构,其内、外动子磁体均采用Halbach 阵列结构,并将电枢绕组绕制在调磁环装置的空气槽中。该调磁装置不仅可以调制磁场,而且可以充当发电机的绕组。相比于现有的直线磁齿轮结构,该结构具有提升推力密度和简化机械结构的优势,Halbach 直线磁齿结构如图10 所示[45]。但是,该结构的绕组空间配置、散热等问题有待进一步研究。
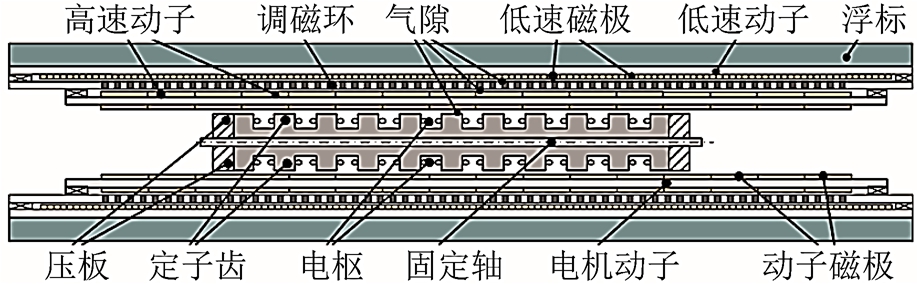
图9 直线磁齿轮复合结构
Fig.9 Linear magnetic gear integrated linear motor

图10 Halbach 直线磁齿轮结构
Fig.10 Linear magnetic gear with Halbach arrays
除了应用于海洋发电领域,文献[46]提出一种应用于车辆转向机构的磁齿轮直线作动器,如图11所示[46]。该结构将圆筒型永磁直线电机集成在直线磁齿轮的内部,并且两者共用一个高速动子,通过高速动子的低推力往复运动,实现低速外动子的高推力往复运动,进而驱动车辆的转向。值得注意的是,尽管直线磁齿轮技术兼顾了推力密度和可靠性,但是直线磁齿轮至少存在两个直线运动部件,直线轴承的安装和固定较为困难,直线磁齿轮如图12 所示[41],故存在体积大,空间利用率低的问题。若与直线电机复合设计,其加工难度、控制策略以及运行精度均存在较大困难。
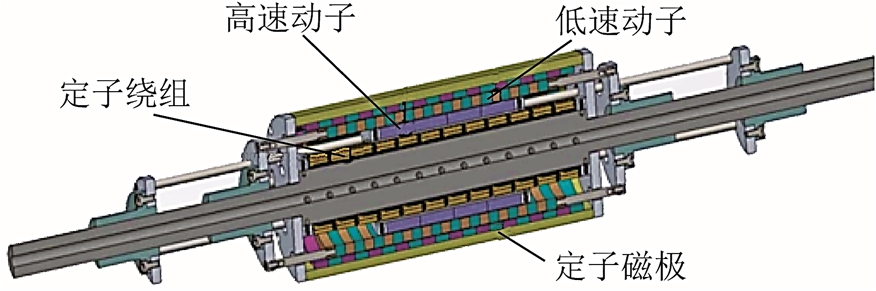
图11 磁齿轮直线电机结构
Fig.11 Magnetic gear linear machine
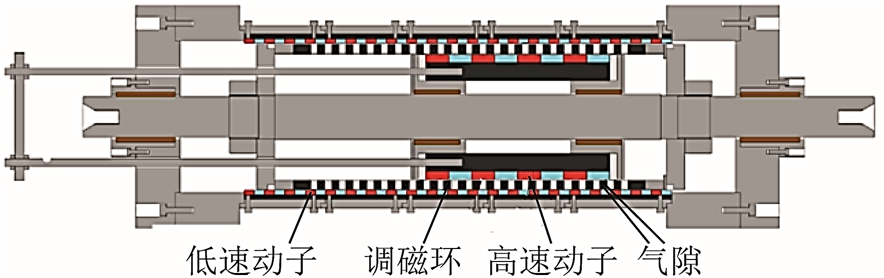
图12 直线磁齿轮装配结构
Fig.12 Linear magnetic gear assembly
3 多自由度磁力传动技术
3.1 旋转-直线作动器结构
2003 年,英国学者A. Turner 结合感应型和磁阻型直线-旋转作动器的原理,提出了应用于汽车挡位装置的直线-旋转作动器[47],如图13 所示。该作动器将永磁直线电机与永磁旋转电机机械结合,两类电机同时作用于一个输出轴上。分别通过驱动直线部分和旋转部分,实现直线-旋转运动。然而,该结构存在绕组利用率低、直线行程受限等问题。
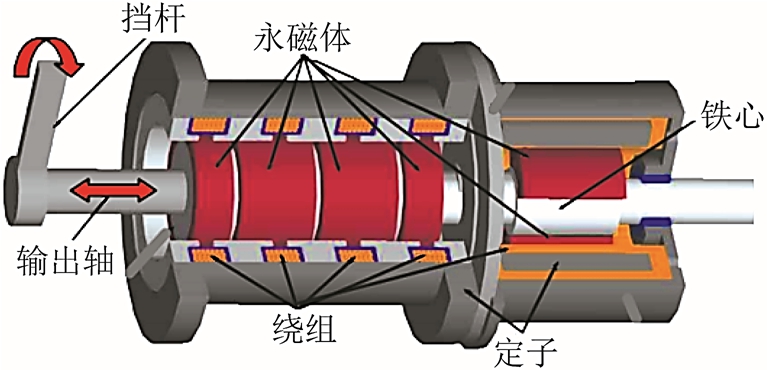
图13 永磁直线-旋转作动器雏形
Fig.13 Initial linear-rotary magnetic actuator
东南大学房淑华博士采用交错排列的动子磁极与三套独立的定子结合,提出一种旋转-直线型作动器[48-49],如图14a 所示。三套磁路相互独立的定子沿轴向排列,与交错排列的动子磁极作用,实现旋转-直线运动。同期,哈尔滨工业大学邹继斌教授设计了一种螺旋定子结构。其螺旋定子的绕组磁动势与动子磁动势作用,可以同时产生圆周方向的转矩和轴向方向的推力,实现螺进运动[50],如图14b 所示。然而,在上述两种旋转-直线作动器中,转矩和推力的解耦控制和端部效应是该类结构的研究重点。

图14 旋转-直线永磁作动器
Fig.14 Rotary-linear magnetic actuator
日本横滨国立大学Y. Fujimoto 教授,借助永磁直线电机的工作原理,提出了一种螺旋结构的作动器,如图15 所示。其定子和动子均采用螺旋设计,定子采用三相集中绕组,动子的螺旋侧面表贴有永磁体,从而实现动子的螺进运动[51-52]。上述旋转-直线作动器均采用电励磁磁场与永磁磁场相互作用。相比于永磁磁力传动,电励磁磁场的推力密度仍有较大的不足。然而,该类结构的提出,为螺旋式磁力丝杠作动器的拓扑结构的研究提供了全新的思路。

图15 螺旋式直线-旋转作动器
Fig.15 Helical linear-rotary actuator
3.2 高推力磁力丝杠作动器结构
美国学者W. A. Smith 在1998 年曾提出了磁力丝杠雏形,如图16 所示。通过磁力传输将旋转运动,转换为直线运动,并将其应用于心脏泵领域。但是,由于受限于当时的设计水平和永磁材料的发展,无法实现高性能的推力传输,并未引起人们的关注[53]。直到2011 年,英国谢菲尔德大学J. B. Wang教授首次提出了高推力密度永磁磁力丝杠直线作动器概念,高推力密度磁力丝杠作动器如图17 所示[54]。并且,对其电磁力进行了解析计算,解析结果与有限元分析高度吻合,推力密度可达10MN/m3以上。该结构由磁螺母(转子)和磁丝杆(动子)两部分构成,将N、S 极螺旋形充磁的磁体交替排列放置在磁螺母和磁丝杆上。

图16 磁力丝杠雏形的提出与应用
Fig.16 Proposal and application of magnetic screw
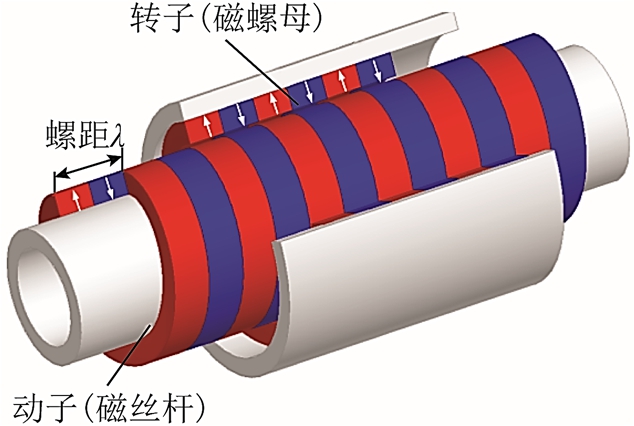
图17 高推力密度磁力丝杠作动器
Fig.17 High-performance magnetic screw
本节以单个导程λ 内含有1 对磁极的磁力丝杠模型为例,介绍螺旋气隙永磁磁力传动机理,螺旋磁路分布如图18 所示。磁丝杆采用螺旋形磁体结 构,所以在一个气隙圆周上存在径向和轴向两个方向的磁场分布。并且,由于采用单个导程内1 对极永磁体结构,其气隙磁场在一个360°的圆周内为一个完整的周期,螺旋磁路一个周期的磁通密度及其谐波分析结果如图19 所示。分别对圆周径向和轴向磁场进行MMF 分析,其磁场谐波主要次数均为1次。同时,磁螺母也采用同样的螺旋结构,其气隙磁场谐波次数与磁丝杆产生的谐波次数一致。因此,通过磁螺母的旋转运动,驱动磁丝杆直线运动,反之亦然。

图18 螺旋磁路分布
Fig.18 Distribution of helical field modulated

图19 螺旋磁路工作机理
Fig.19 Operation principle of helical field modulated

图20 嵌入式磁力丝杠结构
Fig.20 Embedded magnetic screw prototype
磁力丝杠工作原理与滚珠丝杠近似,在1 对极的磁力丝杠模型中,即磁螺母(转子)完整的旋转360°,磁丝杆(动子)随之移动一个螺距的位移λ,其磁场调制原理表示为
式中,Gr-t 为磁力丝杠的传动比;ωr 为转子角速度;vt 为动子速度;Ft 为动子推力;Tn 为转子转矩。
磁力丝杠直线作动器的问世,大幅提升了永磁直线作动器的推力密度,引起国内外学者的高度关注。2013 年,奥尔堡大学P. Q. Rasmussen 教授对磁力丝杠结构进行了深入研究,并提出了轴向磁体嵌入式结构,如图20 所示,提升了磁路结构的聚磁性能和力学性能。但是受限于加工水平,其样机螺旋 磁路采用在轭铁表面螺旋路径开孔,然后采用圆柱形磁体将孔依次填充。该样机螺旋磁路效果较差,磁体利用率低[55]。同期,还设计了应用于车辆主动悬挂系统的磁力丝杠作动器。通过控制磁丝杆和磁螺母的相对位置,提高车辆乘坐的舒适性和可靠性,并可以实现行驶过程中的能量回收[56]。
随后,美国学者S. Pakdelian 归纳总结了磁力丝杠的一般性设计方法,并且通过改变螺旋永磁体的极对数和磁力丝杠的导程,提出了单导程内变极对数的磁力丝杠结构,如图21a 所示。通过改变磁体极对数,可以调整螺旋磁场的调制比,并给出了基础结论[57]。哈尔滨工业大学高放博士对变极对数的磁力丝杠进行深入研究,对极对数和调制关系进行了补充与修改[58]。随后,S. Pakdelian 设计了磁力丝杠与旋转电机结合的实验平台,如图21b 所示。对磁力丝杠作动器进行了测试,结果显示,在低速传动领域,相比于同尺寸的圆筒型永磁直线电机,无论从推力密度、损耗、质量、体积、材料和成本方面,磁力丝杠直线作动器具有绝对的优势[59]。

图21 不同极对数的磁力丝杠及与实验平台
Fig.21 Magnetic screw with different poles and experiment platform
为了进一步提升磁力丝杠直线作动器的推力密度,2015 年,高性能磁力丝杠提出者J. B. Wang 教授与江苏大学开展合作研究,提出了Halbach 永磁阵列结构的磁力丝杠结构,如图22 所示。通过优化 永磁体的不同充磁方向,实现推力密度的最优配置[60]。相比于同尺寸的径向交替充磁结构,Halbach磁力丝杠的推力幅值提升72%,并减少了对导磁轭的依赖。
随后,国内学者结合永磁磁场调制原理,首次提出磁场调制式磁力丝杠结构[61-62],如图23a 所示。通过引入螺旋形调磁装置,将低速直线运动转换为高速旋转运动。该结构适合应用于长行程以及清洁能源转换领域,减少了长行程中动子永磁材料的使用。并且,可依据调制比的变化调整推力幅值和运动速度。2018 年,美国波特兰州立大学J. Z. Bird 教授设计开发了磁场调制式磁力丝杠样机,如图23b 所示,但是由于存在两层气隙,并且有三种螺旋配置,结构过于复杂,实测推力比预期下降50%[63]。

图22 Halbach 磁力丝杠结构及样机
Fig.22 Halbach magnetic screw and prototype
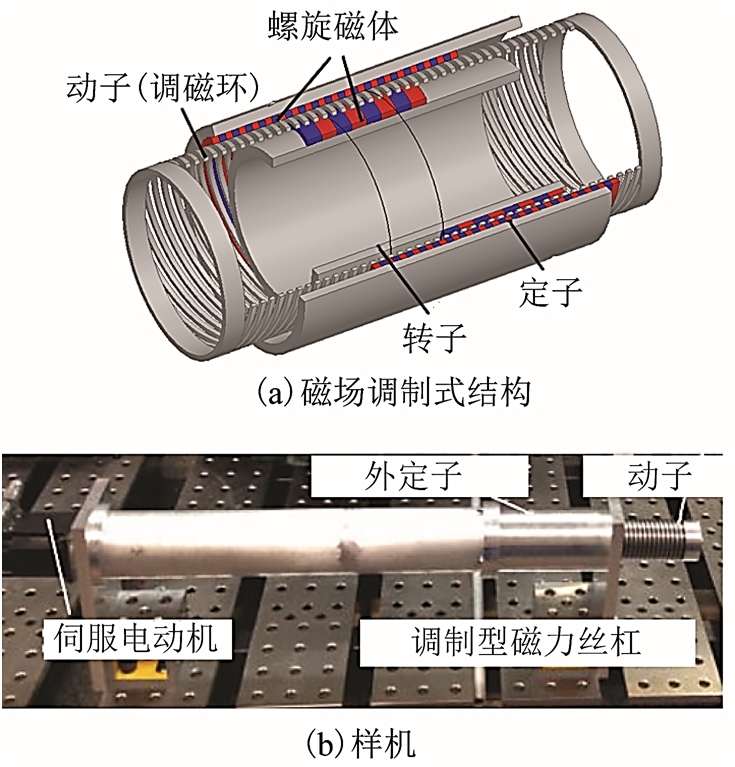
图23 磁场调制式磁力丝杠及样机
Fig.23 Modulated magnetic screw and prototype
近期,日本学者C. S. Cyusa 提出了一种基于磁力丝杠工作原理的RotLin 直线驱动器,如图24所示。该结构采用电机与磁力丝杠的复合设计,电机转子和磁螺母形成复合转子。复合转子既能与绕组作用产生转矩,又能与磁丝杆产生磁场耦合,实现直线往复运动[64]。但是,在该结构中复合转子磁路解耦问题和磁体利用率的问题仍然需要进一步的研究。
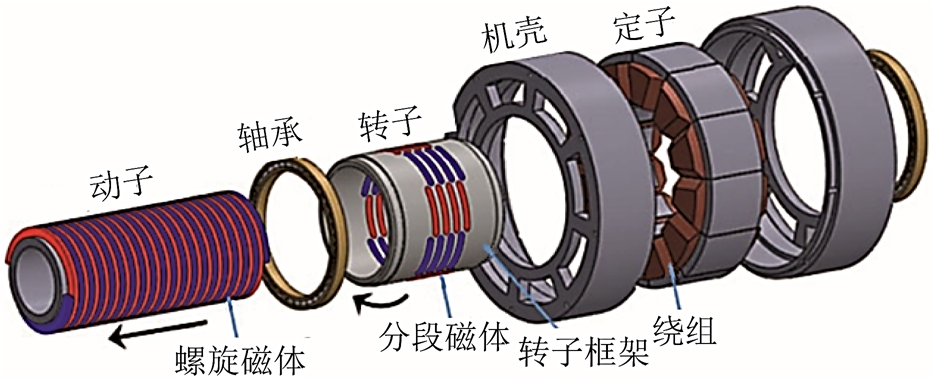
图24 RotLin 螺旋电机
Fig.24 RotLin helical machine
在永磁磁力丝杠的基础上,丹麦奥尔堡大学K. Lu教授与上海海事大学合作,提出了一种电磁式磁力丝杠。该磁丝杆由螺旋形槽和螺旋线圈组成,通过电励磁产生螺旋形磁场,如图25a 所示。该结构可以简化动子螺旋磁路的加工难度,节省了动子永磁材料的用量。并且,通过调整电流的幅值,及时应对负载的变化,控制带宽高。但是相比于永磁型结构,其推力密度下降75%左右[65]。同期,哈尔滨工业大学王骞博士提出了永磁-感应子式混合励磁磁力丝杠结构,使得磁力丝杠气隙磁场可调节,如图25b 所示。但是电励磁磁场相较于永磁磁场,其磁场密度远小于永磁磁场,使得电励磁产生的效果不够明显[66-67]。文献[68]将高温超导线圈引入电磁式磁力丝杠作动器中,可以提升混合励磁中电励磁性能。

图25 混合励磁磁力丝杠
Fig.25 Hybird excited magnetic screw
4 螺旋磁路加工技术
由于高性能永磁材料的质地较脆,可加工性较差,因此整体设计加工螺旋形磁体存在一定的困难。国内外学者对该问题进行了深入研究,文献[69]提出采用分段磁块沿圆周方向和轴向方向近似拼接为螺旋形磁场。通过有限元分析发现,为了获得近似理想的螺旋形磁路,每个圆周至少需要24 块弧度为15°的磁块,才可以实现近似螺旋,如图26a 所示。因此,制造大量分段磁块的磁性螺杆是一项繁琐、耗时而且昂贵的工作。并且,分段个数较多,对加工精度的掌控也比较困难。
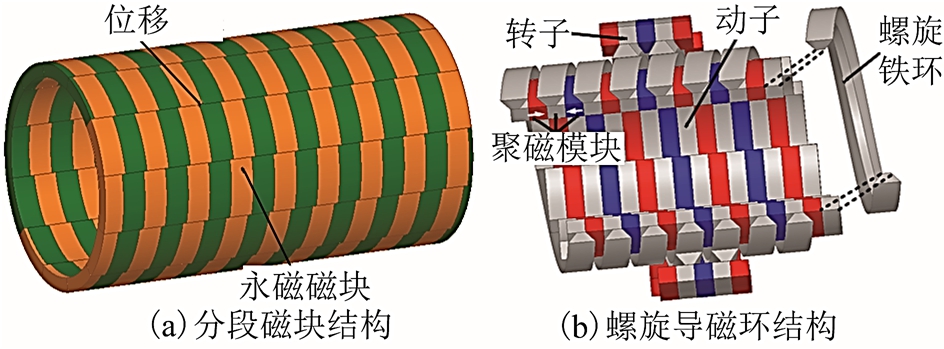
图26 螺旋磁路等效结构
Fig.26 Equivalent of helical magnetic poles
为了降低加工复杂度,提升螺旋磁路的完整性,文献[70]提出一种依据磁阻最小原理的磁体嵌入式结构,如图26b 所示。该结构将不同充磁方向的磁体与电工铁块结合,充磁方向指向电工铁块,由分段电工铁块的表面获得近似螺旋形磁路。由于电工铁材料的可加工性强,可以设计为整体螺旋形导磁环,铺设在电工铁块的表面,通过导磁环的磁阻最小路径,引出理想螺旋磁路。
2018 年,美国马萨诸赛大学学者采用了一种混合型磁材料实现螺旋形磁路的加工。该种材料具有较好的拉伸性,通过注射、粘接等加工方式,实现整体的螺旋效果。并且,采用该材料,设计加工了一台Halbach 阵列磁力丝杠,如图27 所示[71]。值得注意的是,该混合型磁材料的剩磁只有0.4T,采用该材料无法实现高推力密度的磁力传输。文献[72]指出,同样尺寸的磁力丝杠,采用钕铁硼材料(剩磁1.2T)与采用铁氧体等混合磁性材料(剩磁0.4T 左右),推力幅值相差7 倍左右,所以对高性能磁材料开展螺旋磁路技术的研究具有重要意义。
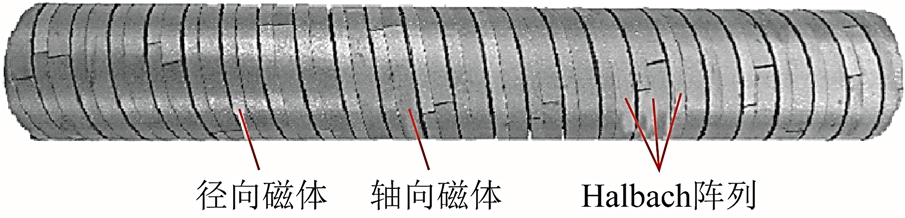
图27 混合型磁材料螺旋结构
Fig.27 Mixture materials helical structure

图28 脉冲型螺旋充磁器
Fig.28 Impulse magnetized machine
2019 年,英国学者K. Atallah 教授设计了一种脉冲型螺旋充磁结构,如图28 所示[73]。该结构通过螺旋线圈瞬时通入电流的方式,对烧结型钕铁硼材料进行充磁,提升了螺旋磁环的整体性[73]。但是,由脉冲电流产生的磁感应强度明显不足。笔者认为,该脉冲充磁方法不能达到高性能烧结型钕铁硼内禀矫顽力的3~5 倍,无法实现烧结型钕铁硼的饱和磁化[74-75]。因此,导致螺旋磁路剩磁不足。从实验结果 来看,采用此方案的样机实测推力比预期下降40%。
文献[76]提出了一种螺旋磁极的简化设计方法,依据螺旋导程,将永磁体圆弧进行斜切割处理,切割后的磁环,无需进行轴向方向的位移,可以近似精确地形成一组理想螺旋磁环,如图29a 所示。然而,现有的磁体充磁技术无法满足半圆环的理想径向充磁。文献[72]对该结构进行了重新设计,并加装了燕尾槽结构,极大地提升了磁体拼接精度、机械强度和表面圆度,进而保证气隙长度的均匀,如图29b 所示。随后,完成了高性能螺旋形磁路设计,如图30 所示。

图29 螺旋磁极的加工与改进
Fig.29 Process and improve of magnetic pole

图30 高性能螺旋磁路试制
Fig.30 Prototype of high-performance helical magnetic fields
5 磁力丝杠直线作动器的应用
目前,机械丝杠作为运动形态的转换部件被广泛应用于工业制造领域,但存在机械磨损、可靠性差等弊端。直线电机的提出,实现了高可靠性的优点,缺点是推力密度较低。相对而言,磁力丝杠直线作动器以其高推力密度、高可靠性等优势,在航空航天、交通、工业以及国防等众多领域具有较好的应用前景。
5.1 航空航天领域
磁力传动具有无需润滑、过载保护等优点,解决了航空航天装备在高海拔、高温低压环境下润滑困难的难题,极大地提高了系统可靠性。磁力丝杠直线作动器具有高推力密度的优势,在同样的推力需求下,有效降低了质量,提高了航空航天设备的机动性。图31 为一种舵机用磁力丝杠作动器原理模型,基于其高可靠、高推力的特性,在航空航天领域具有明显的优势。
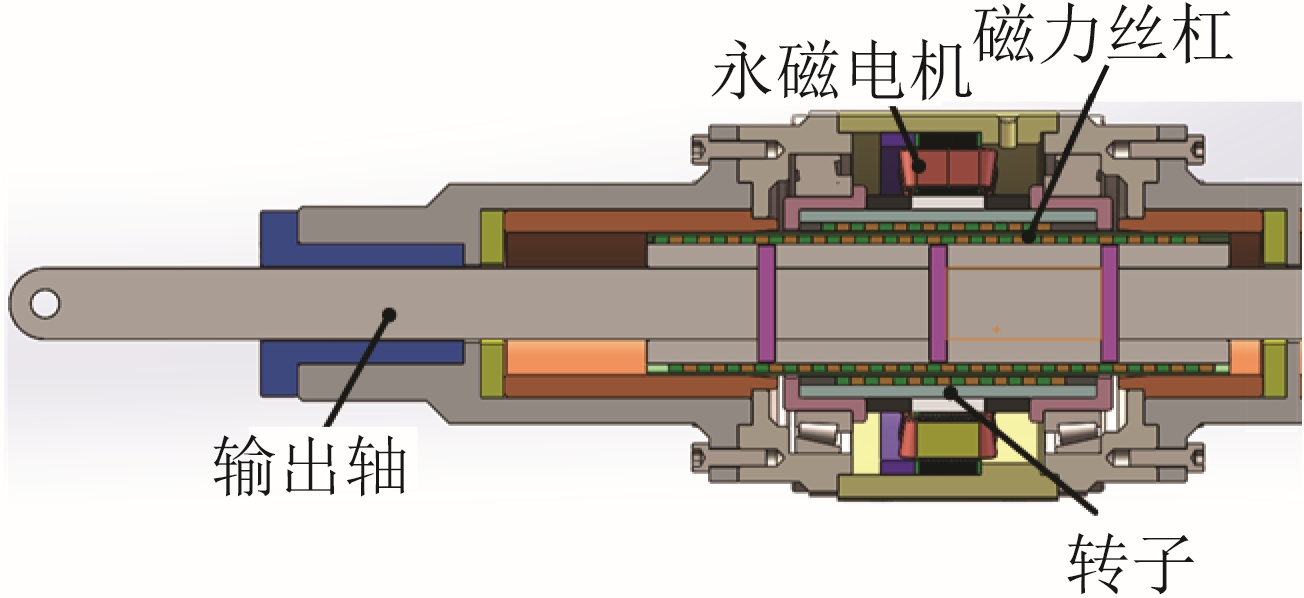
图31 应用于航空舵机的磁力丝杠
Fig.31 Magnetic screw used in aerospace
5.2 能源转换领域
将磁力丝杠作动器应用在振荡浮标和汽车悬架等应用背景的能源转换领域。通过磁力传动,将动子的低速、大推力直线运动转换为转子的高速、低转矩旋转运动,将旋转运动转换为电能。图32 所示为磁力丝杠系统应用于能源转换装置的理论模型,该装置将海洋波浪能[77]、汽车悬架系统的振动馈能[56],通过磁丝杆的直线运动,驱动磁螺母转动,实现能量的转换。

图32 应用于能源转换的磁力丝杠
Fig.32 Magnetic screw used in energy conversion
5.3 轨道交通领域
图33 展现了将磁力丝杠作动器在轨道交通中的应用。将磁螺母与外转子电机集成后,铺设在轨道上,磁动子部分安装在车厢底部。在列车起步时,轨道上的复合转子可以辅助驱动列车车厢,以克服冰雪路面的滑动;当列车需要爬坡或者克服风阻时,同样可以为列车提供动力。不仅是动力的输出,当列车需要制动或者是减速进站时,可以实现列车的动能到能源的转换。

图33 应用于列车驱动的磁力丝杠
Fig.33 Magnetic screw used in rail transport
6 结论
本文主要对高推力永磁直线作动器进行了综述。依据运动形态的不同,对磁性齿轮、旋转-直线式作动器和高推力磁力丝杠直线作动器的结构特点和运行机理进行了全面的分析。聚焦于高推力磁力丝杠直线作动系统,对其发展现状、加工技术以及应用前景进行了深入的研究和探索。总体而言,经过了近10 年的研究和发展,高性能磁力丝杠直线作动器的优势得到了充分地展现,其应用价值已经得到业内学者的肯定和关注,在航空航天等高、精、尖应用领域具有明显的优势。
磁力丝杠直线作动器作为一种概念和结构均新颖的磁力传动机构,仍有一些问题有待深入探讨,主要包括:
1)动态性能。磁力丝杠作为高推力直线传动系统的核心部件,既要实现高推力密度,又要兼具动态性能。由于采用磁力传动,存在刚度较低的问题,对阶跃信号和突变负载的响应不足。然而,动态性能的优劣,是该类作动器获得推广应用必须解决的问题之一。
2)计算精度与效率。磁力丝杠采用三维空间的螺旋结构,影响其推力性能的因素众多,往往借助有限元软件对其进行优化设计。然而,庞大的剖分网格、繁琐的建模,严重影响了计算的准确性和效率。因此,设计开发更准确、更快速的螺旋磁场解析模型具有实用价值,现有文献鲜有报道。
3)高性能螺旋磁路加工工艺。关于磁力丝杠特有的螺旋磁路的设计已经取得一定的成果,但主要还是采用分段装配等技术实现螺旋等效,增加了复杂度和误差。如何实现完整的高性能螺旋磁路加工,有待进一步探究。
4)与电机集成设计。将磁力丝杠直线作动器与电机进行一体化设计,形成结构紧凑的集成作动系统。需要对电机和磁力丝杠分别进行性能最优设计,采用多目标优化和等效磁网络等方法,获得最优的拓扑结构和参数。结合应用背景,挖掘磁力丝杠作动器与电机集成设计后的优势,并有针对性的开发新结构。
[1] Boldea I, Tutelea L, Xu W, Pucci M. Linear electric machines, drives, and MAGLEVs: an overview[J]. IEEE Transactions on Industrial Electronics, 2018, 66(9): 7504-7515.
[2] Hochwallner M, Pinto L P G, Krus P, et al. Tracking control for high-performance motion of a hydraulic infinite linear actuator[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(6): 2782-2793.
[3] Pan Donghua, Li Liyi, Wang Mingyi. Modeling and optimization of air-core monopole linear motor based on multi-physical fields[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9814-9824.
[4] 汤文成, 徐楠楠. 滚珠丝杆副发展及研究现状[J]. 机械设计与机械制造, 2016, 45(4): 11-14.
Tang Wencheng, Xu Nannan. Review on the research of ball screw[J]. Machine Design and Manufacturing Engineering, 2016, 45(4): 11-14.
[5] Liu Yilun, Xu Lin, Zuo Lei. Design, modeling, lab, and field tests of a mechanical-motion-rectifier-based energy harvester using a ball-screw mechanism[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(5): 1933-1943.
[6] Hanifzadegan M, Nagamune R. Tracking and structural vibration control of flexible ball-screw drives with dynamic variation[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(1): 133-142.
[7] Zhu H, Fujimoto H. Mechanical deformation analysis and high-precision control for ball-screw-driven stages[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(2): 956-966.
[8] Cao Ruiwu, Jin Yi, Lu Minghang, et al. Quantitative comparison of linear flux-switching permanent magnet motor with linear induction motor for electromagnetic launch system[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 7569-7578.
[9] Zhao Xing, Niu Shuangxia. Development of a novel transverse flux tubular linear machine with parallel and complementary PM magnetic circuit for precision industrial processing[J]. IEEE Transactions on Industrial Electronics, 2019, 66(6): 4945-4955.
[10] Yoon J, Lang J, Trumper D. Fine-tooth iron-core linear synchronous motor for low acoustic noise application[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9895-9904.
[11] Zeng Zhiqiang, Lu Qinfen. Investigation of novel partitioned-primary hybrid-excited flux-switching linear machines[J]. IEEE Transactions on Magnetics, 2018, 65(12): 9804-9813.
[12] Zhao Wenxiang, Zhu Jian, Ji Jinghua, et al. Improvement of power factor in a double side linear flux-modulation permanent-magnet motor for long stroke applications[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 3391-3400.
[13] 张静, 余海涛, 施振川. 一种波浪发电装置用低速双动子永磁直线电机运行机理研究[J]. 电工技术学报, 2018, 33(19): 4553-4562.
Zhang Jing, Yu Haitao, Shi Zhenchuan. Research on a tubular linear permanent magnet machines with dual translators for low speed wave energy conversion[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4553-4562.
[14] Sheng Tiantian, Niu Shuangxia. Design and analysis of a novel modular linear double-stator biased flux machine[J]. IEEE Transactions on Magnetics, 2018, 54(11): 8108905.
[15] Shi Chaojie, Qu Ronghai, Gao Yuting, et al. Design and analysis of an interior permanent magnet linear vernier machine[J]. IEEE Transactions on Magnetics, 2018, 54(11): 8106805.
[16] Bianchi N, Bolognani S, Corte D D, et al. Tubular linear permanent magnet motors: an overall comparison[J]. IEEE Transactions on Industry Applications, 2003, 39(2): 466-475.
[17] 许孝卓, 孙震, 汪旭东, 等. Halbach 交替极永磁同步直线电机特性分析[J]. 电工技术学报, 2019, 34(9): 1825-1833.
Xu Xiaozhuo, Sun Zhen, Wang Xudong, et al. Characteristic of a novel permanent magnet linear synchronous motor with Halbach array consequent pole[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1825-1833.
[18] Zhao Wenxiang, Ma Anqi, Ji Jinghua, et al. Multiobjective optimization of a double-side linear vernier PM motor using response surface method and differential evolution[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 80-90.
[19] 秦伟, 范瑜, 徐洪泽, 等. 高温超导运动磁场电磁Halbach 初级结构直线感应磁悬浮电机[J]. 电工技术学报, 2018, 33(23): 5427-5434.
Qin Wei, Fan Yu, Xu Hongze, et al. A linear induction maglev motor with HTS traveling magnetic electromagnetic Halbach array[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5427-5434.
[20] Shi Chaojie, Qu Ronghai, Kou Baoquan, et al. A novel HTS flux-reversal linear permanent magnet machine with a lower number of mover teeth and higher thrust density[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(3): 0601505.
[21] Ma Guangtong, Gong Tianyong, Zhang Han, et al. Experiment and simulation of REBCO conductor coils for an HTS linear synchronous motor[J]. IEEE Transactions on Applied Superconductivity, 2017, 27(4): 5201805.
[22] Zhu Z Q. Overview of novel magnetically geared machines with partitioned stators[J]. IET Electric Power Applications, 2018, 12(5): 595-604.
[23] 章跃进, 章君达. 偏心式谐波磁力齿轮气隙磁场分式线性变换解析模型[J]. 电工技术学报, 2018, 33(15): 3572-3577.
Zhang Yuejin, Zhang Junda. Analytical model of magnetic field of eccentric harmonic magnetic gear using fractional linear transformation method[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3572-3577.
[24] Johnson M, Gardner M, Toliyat H. A parameterized linear magnetic equivalent circuit for analysis and design of radial flux magnetic gears—part I: implementation[J]. IEEE Transactions on Energy Conversions, 2018, 33(2): 784-791.
[25] Filippini M, Alotto P. Coaxial magnetic gears design and optimization[J]. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9934-9942.
[26] 付兴贺, 王标, 林明耀. 磁力齿轮发展综述[J]. 电工技术学报, 2016, 31(18): 1-12.
Fu Xinghe, Wang Biao, Lin Mingyao. Overview and recent development of magnetic gears[J]. Transactions of China Electrotechnical Society, 2016, 31(18):1-12.
[27] Zhu Z Q, Khatab M, Li H, et al. A novel axial flux magnetically geared machine for power split application[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 5954-5966.
[28] Atallah K, Calverley S, Howe D. Design, analysis and realization of a high-performance magnetic gear[J]. IET Electric Power Applications, 2004, 151(2): 135-143.
[29] Cheng Ming, Han Peng, Hua Wei. General airgap field modulation theory for electrical machines[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6063-6074.
[30] Rasmussen P O, Andersen T O, Jorgensen F T, et al. Development of a high-performance magnetic gear[J]. IEEE Transactions on Industry Applications, 2005, 41(3): 764-770.
[31] Rasmussen P O, Frandsen T V, Jensen K K, et al. Experimental evaluation of a motor-integrated permanent-magnet gear[J]. IEEE Transactions on Industry Applications, 2013, 49(2): 850-859.
[32] Tian Ye, Liu Guohai, Zhao Wenxiang, et al. Design and analysis of coaxial magnetic gears considering rotor losses[J]. IEEE Transactions on Magnetics, 2015, 51(11): 8108304.
[33] 李祥林, 程明, 邹国棠, 等. 聚磁式场调制永磁风力发电机工作原理与静态特性[J].电工技术学报, 2014, 29(11): 1-9.
Li Xianglin, Cheng Ming, Chau K T, et al. Principle and analysis of a new flux-concentrating fieldmodulated permanent-magnet wind power generator [J]. Transactions of China Electrotechnical Society, 2014, 29(11): 1-9.
[34] 张东, 邹国棠, 江建中, 等. 新型外转子磁齿轮复合电机的设计与研究[J]. 中国电机工程学报, 2008, 28(30): 67-72.
Zhang Dong, Chau K T, Jiang Jianzhong, et al. Design and research of a novel magnetic-geared outer-rotor compact machine[J]. Proceedings of the CSEE, 2008, 28(30): 67-72.
[35] Jian Linni, Deng Zhengxing, Shi Yujun, et al. The mechanism how coaxial magnetic gear transmits magnetic torques between its two rotors: detailed analysis of torque distribution on modulating ring[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(2): 763-773.
[36] Jian L, Chau K T. A coaxial magnetic gear with Halbach permanent-magnet arrays[J]. IEEE Transactions on Energy Conversion, 2010, 25(2): 319-328.
[37] Wang Mingqiao, Tong Chengde, Song Zhiyi, et al. Performance analysis of an axial magnetic-fieldmodulated brushless double-rotor machine for hybrid electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2019, 66(1): 806-817.
[38] Shen Jianxin, Li Huayang, Hao He, et al. A coaxial magnetic gear with consequent-pole rotors[J]. IEEE Transactions on Energy Conversion, 2017, 32(1): 267-275.
[39] 刘晓, 赵云云, 黄守道, 等. 双磁场调制同轴磁齿轮瞬态和振动特性分析[J].电工技术学报, 2019, 34(9): 1865-1874.
Liu Xiao, Zhao Yunyun, Huang Shoudao, et al. Investigation of the transient and vibration characteristics of a dual-flux-modulator coaxial magnetic gear[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1865-1874.
[40] Atallah K, Wang J, Howe D. A high-performance linear magnetic gear[J]. Journal of Applied Physics, 2005, 97(10): 10N516.
[41] Holehouse R, Atallah K, Wang J. Design and realization of a linear magnetic gear[J]. IEEE Transactions on Magnetics, 2011, 47(10): 4171-4174.
[42] Li Wenlong, Chau K T, Jiang J Z. Application of linear magnetic gears for Pseudo-direct-drive oceanic wave energy harvesting[J]. IEEE Transactions on Magnetics, 2011, 47(10): 2624-2627.
[43] 包广清, 刘美钧. 一种新型永磁直线磁齿轮复合发电机的设计[J]. 电机与控制应用, 2016, 43(3): 8-15.
Bao Guangqing, Liu Meijun. Design of a novel magnetic-geared tubular linear permanent magnet generator[J]. Electric Machines and Control, 2016, 43(3): 8-15.
[44] Du Yi, Chau K T, Cheng Ming, et al. A linear magnetic-geared permanent magnet machine for wave energy generation[C]// International Conference on Electrical Machines and Systems (ICEMS), Incheon, South Korea, 2010: 1538-1541.
[45] Ho Sie, Wang Qingsong, Niu Shuangxia, et al. A novel magnetic-geared tubular linear machine with Halbach permanent-magnet arrays for tidal energy conversion[J]. IEEE Transactions on Magnetics, 2015, 51(11): 8113604.
[46] Liu C T, Hwang C C, Chiu Y W. Design of a coaxially magnetic-geared linear actuator for electric power steering system applications[J]. IEEE Transactions on Industry Applications, 2017, 53(3): 2401-2408.
[47] Turner A, Ramsay K, Clark R, et al. Direct-drive rotary-linear electromechanical actuation system for control of gearshifts in automated transmissions[J]. IEEE Transactions on Magnetics, 2003, 39(5): 3007-3009.
[48] 金平, 房淑华, 林鹤云. 基于磁场解析计算的直线旋转永磁作动器参数分析[J]. 中国电机工程学报, 2013, 33(18): 155-161.
Jin Ping, Fang Shuhua, Lin Heyun. Parameter analysis of linear and rotary permanent magnet actuators based on analytically magnetic field computation[J]. Proceedings of the CSEE, 2013, 33(18): 155-161.
[49] Guo Kaikai, Fang Shuhua, Lin Heyun, et al. 3-D analytical analysis of magnetic field of flux reversal linear-rotary permanent magnet actuator[J]. IEEE Transactions on Magnetics, 2017, 53(6): 8202205.
[50] 唐南君. 旋转-直线永磁执行器运行机理研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
[51] Fujimoto Y, Suenaga T, Koyama M. Contril of an interior permanent-magnet screw motor with powersaving axial-gap displacement adjustment[J]. IEEE Transactions on Industrial Electronics, 2014, 61(7): 3610-3619.
[52] Shukor A, Fujimoto Y. Direct-drive position control of a spiral motor as a monoarticular[J]. IEEE Transactions on Industrial Electronics, 2014, 61(2): 1063-1071.
[53] Vitale N G, Hirschman G B, Smith W A. Optimization of drive screw pitch in a pulsatile ventricle assist device[C]//IEEE Annual Northeast Bioengineering Conference (NEBC), Storrs, USA, 2001: 37-38.
[54] Wang Jiabin, Atallah K, Wang W. Analysis of a magnetic screw for high force density linear electromagnetic actuators[J]. IEEE Transactions on Magnetics, 2011, 47(10): 4477-4480.
[55] Holm R, Berg N, Rasmussen P O, et al. Design of a magnetic lead screw for wave energy conversion[J]. IEEE Transactions on Industry Applications, 2013, 49(6): 2699-2708.
[56] Berg N, Holm R, Rasmussen P O. Theoretical and experimental loss and efficiency studies of a magnetic lead screw[J]. IEEE Transactions on Industry Applications, 2015, 51(2): 1438-1445.
[57] Pakdelian S, Frank N, Toliyat H. Principles of the trans-rotary magnetic gear[J]. IEEE Transactions on Magnetics, 2013, 49(2): 883-889.
[58] Gao Fang, Wang Qian, Zou Jibin, et al. Development of equivalent 2-D finite-element models for accurate prediction of thrust force in permanent magnet lead screws[J]. IEEE Transactions on Magnetics, 2017, 53(11): 8207004.
[59] Pakdelian S, Deshpande Y, Toliyat H. Design of an electric machine integrated with trans-rotary magnetic gear[J]. IEEE Transactions on Energy Conversion, 2015, 30(3): 1180-1191.
[60] Ji Jinghua, Ling Zhijian, WangJiabin, et al. Design and analysis of a Halbach magnetized magnetic screw for artificial heart[J]. IEEE Transactions on Magnetics, 2015, 51(11): 8108604.
[61] 赵文祥, 凌志健, 吉敬华, 等. 一种磁场调制式磁力丝杠: 中国, CN 106341031 A[P]. 2017-01-18.
[62] Ling Zhijian, Ji Jinghua, Wang Fangqun, et al. Design and analysis of a field modulated magnetic screw for artificial heart[J]. AIP Advances, 2017, 7: 056717.
[63] Kouhshahi M, Kadel J, Bird J, et al. Designing and experimentally testing a magnetically geared lead screw[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 5736-5747.
[64] Cyusa C, Fujimoto Y. Enactment-based direct-drive test of a novel radial-gap helical RotLin machine[J]. IEEE Transactions on Industry Applications, 2018, 54(2): 1273-1282.
[65] Lu Kaiyuan, Wu Weimin. Electromagnetic lead screw for potential wave energy application[J]. IEEE Transactions on Magnetics, 2014, 50(11): 8205004.
[66] 高放. 永磁-感应子式磁力丝杠的电磁特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
[67] Gao Fang, Wang Qian, Zou Jibin. Analytical modeling of 3-D magnetic field and performance in magnetic lead screws accounting for magnetization pattern[J]. IEEE Transactions on Industrial Electronics, 2019, DOI:10.1109/TIE.2019.2931241
[68] Ling Zhijian, Zhao Wenxiang, Ji Jinghua, et al. Design and analysis of a new HTS electromagnetic screw[J]. IEEE Transactions on Magnetics, 2017, 53(11): 8203904.
[69] Pakdelian S, Frank N, Toliyat H. Magnetic design aspects of the trans-rotary magnetic gear[J]. IEEE Transactions on Energy Conversion, 2015, 30(1): 41-50.
[70] Ling Zhijian, Zhao Wenxiang, Ji Jinghua, et al. Design of a new magnetic screw with discretized PMs[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 0602805.
[71] Jenney K, Pakdelian S. Design and fabrication of the trans-rotary magnetic gear using quasi-Halbach arrays[C]//IEEE Industrial Electronics Society, Washington, USA, 2018: 18382153.
[72] Ling Zhijian, Ji Jinghua, Wang Jiabin, et al. Design optimization and test of a radially magnetized magnetic screw with discretized PMs[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 7536-7547.
[73] Mohamed H, Atallah K. Impulse magnetized magnetic screw[J]. IEEE Transactions on Magnetics, 2019, DOI: 10.1109/TMAG.2019.2890988.
[74] Glehn G, Steentjes S, Hameyer K. Pulsed-field magnetometer measurements and pragmatic hysteresis modeling of rare-earth permanent magnets[J]. IEEE Transactions on Magnetics, 2018, 54(3): 2100404.
[75] 鲁富强, 赵明静, 刘国征. 钕铁硼脉冲充磁过程的原理及参数变化分析[J]. 金属功能材料, 2017, 24(1): 32-34.
Lu Fuqiang, Zhao Mingjing, Liu Guozheng. Principle and parameter change analysis of NdFeB pulse magnetization process[J]. Metallic Functional Materials, 2017, 24(1): 32-34.
[76] Lu Kaiyuan, Xia Yongming, Wu Weimin, et al. New helical-shape magnetic pole design for magnetic lead screw enabling structure simplification[J]. IEEE Transactions on Magnetics, 2015, 51(11): 8204404.
[77] Qiao K, Wu W, Sun Z, et al. Wave power generation system based on magnetic lead screw[C]//European Conference on Power Electronics and Applications, Riga, Latvia, 2018: 18229210.