0 引言
电机分析方法主要包括磁路法、解析法和有限元法[1]。磁路法和解析法与电机经典理论紧密结合且计算速度快,因而在电机设计分析中有着广泛的 应用[2-3]。然而,当涉及电机复杂几何结构、严重的饱和情况,有限元法相比磁路法和解析法有着很大的优势。同样,有限元法的缺点也很明显,主要是计算速度较慢。为了提高有限元法仿真速度,一般利用电机几何对称性,只仿真电机部分模型,同时将三维模型转变为二维模型仿真[4]。但是,对于直线电机等磁路复杂的电机仿真仍需借助三维有限元仿真,计算成本昂贵[5-7]。
为了提高电机的性能同时兼顾经济性,通常基于有限元法,采用现代启发式优化算法对电机进行全局寻优[8]。常用的现代启发式优化算法包括遗传算法、模拟退火算法、粒子群算法和差分进化算法等[9-10]。这些优化算法都能够获得理想结果,但需要的仿真次数多,计算时间长,制约了电机开发进程。
基于代理模型的优化( Surrogate-Based Optimization, SBO)算法针对少数样本数据,利用代理模型拟合目标值与输入变量的数学关系,再借助加点准则(infill criterion)多次迭代,从而快速寻找到全局最优值[11]。该算法可以在很大程度上减少仿真次数,适合于有限元仿真和计算流体动力学仿真等高计算成本的应用场合[12-14]。代理模型主要包括Kriging 模型、多项式、径向基函数、支持向量回归模型等[15]。其中,基于Kriging 模型的高效全局优化(Efficient Global Optimization, EGO)算法应用最广[16]。EGO 算法每次迭代利用最大化改善期望(Expected Improvement, EI)加点准则只能添加一个新样本数据,限制了算法的收敛速度。为此,文献[17-18]利用EI 函数的多峰值性质,每次迭代添加的多个新样本数据对应EI 函数的多个极值点,并利用计算机并行运算能力,提高算法的收敛速度。此外,传统EGO 算法的EI 准则仍不能很好地平衡局部开发( local exploitation ) 和 全 局 搜 索( global exploration)。文献[19]在每次EGO 算法迭代时,使用不同的加权系数将EI 准则中的两项相加作为新的加点准则,在一定程度上加快了收敛速度。文献[20]提出了基于 EGO 的多目标优化(Multi-objective Optimization based EGO, EGO-MO)算法,将EI 准则中两项分别作为目标,使用多目标优化算法获得帕累托前沿(Pareto Front, PF),在PF 上选择多个点作为新样本数据。因而,该算法既利用了并行运算,也很好地兼顾了局部开发和全局搜索,加快了算法收敛速度。
磁通切换永磁(Flux-Switching Permanent Magnet, FSPM)电机的电枢绕组和永磁体都置于定子侧,其转子仅由导磁铁心构成。简单的结构、与转子永磁同步电机相近的转矩密度和效率使得FSPM 电机得到日益广泛的关注[21]。其直线形式也应运而生并得到深入研究[22-28]。文献[22]提出的新型模块化初级永磁型直线(Modular Primary Permanent Magnet Linear, MPPML)电机具有反电动势正弦、定位力小和容错能力强等优点。
本文在EGO-MO 算法的基础上,提出一种改进型 EGO-MO 算法,并应用于优化设计一台三相MPPML 电机。样机实验验证了分析结果。
1 电机结构和运行原理
一台三相MPPML 电机的截面如图1 所示。τm为动子极距,τs 为定子极距。动子由6 个E 形模块组成,模块之间是非导磁材料。两个U 形铁心所夹永磁体构成E 形模块,绕组为集中绕组。6 个E 型模块中永磁体交替充磁,充磁方向平行于运动方向。MPPML 电机的特殊之处是属于同一相的两个E 形模块间的距离λ1=(m±1/2)τs,m 是正整数。这种结构称之为磁路互补型结构,可以使电机反电动势的正弦性和推力波动均得到很大的改善。另外,相邻相E 形模块间的距离λ2=(j±1/3)τs,j 是正整数。可以根据动子长度最小原则来确定m 和j 取值。

图1 MPPML 电机结构
Fig.1 MPPML motor structure
MPPML 电机的运行原理可以通过图2 所示四个特征动子位置θe 处的A 相永磁磁场分布来简要说明。θe=0°时,A 相永磁磁通达到正向最大值。θe=90°时,永磁磁场被定子齿短路,导致A 相永磁磁通为0。θe=180°处A 相永磁磁通达到负向最大值。θe=270°时,永磁磁场再次被定子齿短路,A 相永磁磁通回到0。由此可见,随着动子位置的变化,电机相绕组磁通交替变化,并由此感应出反电动势。通入对应的交流电,电机可以输出有效的推力。
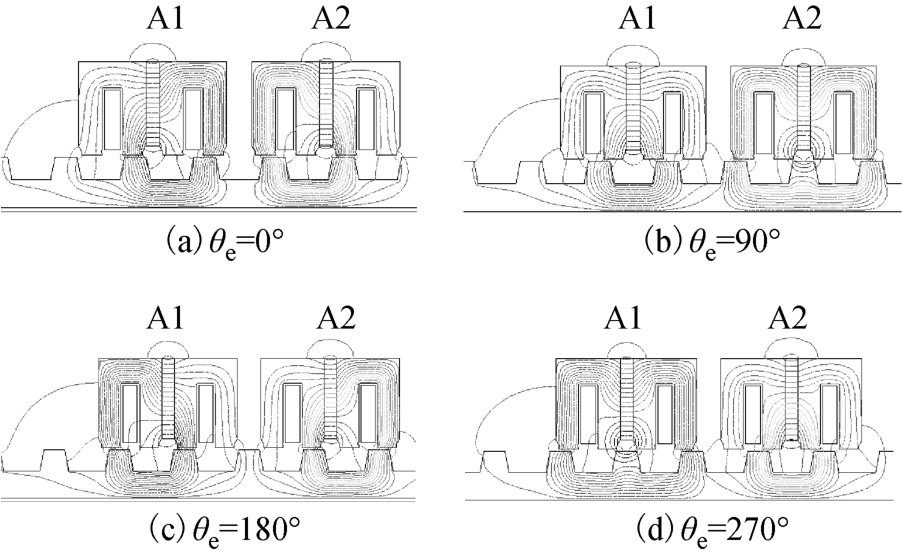
图2 MPPML 电机运行原理
Fig.2 Operation principle of MPPML motor
2 基于代理模型的优化算法
SBO 算法的一般流程如下:
(1)在设计空间内通过试验设计选取初始样本。
(2)对每个初始样本进行精确计算得到响应值。
(3)利用步骤(1)、(2)的数据建立代理模型。
(4)基于代理模型,采用加点准则获取下一个需要精确计算的样本。
(5)针对步骤(4)的样本进行计算得到响应值。
(6)将新样本数据并入现有样本数据,更新代理模型。
(7)不断重复步骤(4)~(6)直到满足收敛条件。
试验设计方法包括经典试验设计和现代试验设计方法[29-30]。经典试验设计包括全因子设计、中心组合设计和Box-behnken 设计等。一般针对确定性的计算机实验,试验设计方法主要采用现代试验设计方法,如拉丁超立方、蒙特卡罗和均匀设计。
2.1 Kriging 模型
Kriging 模型是一种插值模型,能同时给出未知函数的估计值和估计误差。对非线性和多峰函数能很好地近似拟合,这是Kriging 模型的一大优点。
Kriging 模型将未知目标函数看成一个高斯随机过程的具体实现。首先,定义X={x(1), x(2),…, x(n)}代表n 个样本,Y={y(1), y(2) ,…, y(n)}表示对应的响应值。
Kriging 模型(高斯随机过程)可以表示为
式中,μ 为是随机过程的均值;ε(x)为误差项,它的均值为零,方差是σ2。两个样本x(i)、x(j)间误差的相关性可以表示为
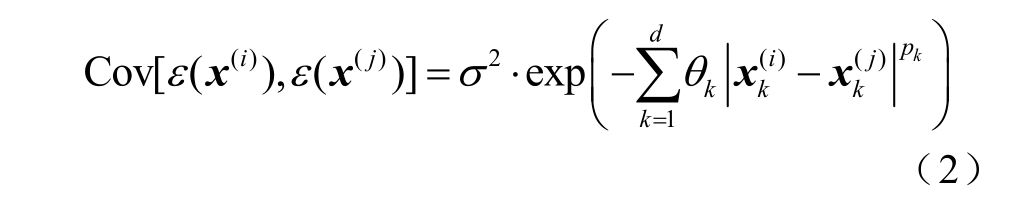
式中,d 为设计变量的维数;pk 和θk 为待估计参数。式(2)表明,相关性随着样本之间距离增大而减小。目标函数在未知点x 处的最佳线性无偏估计值 及其方均误差s2(x)分别为
及其方均误差s2(x)分别为
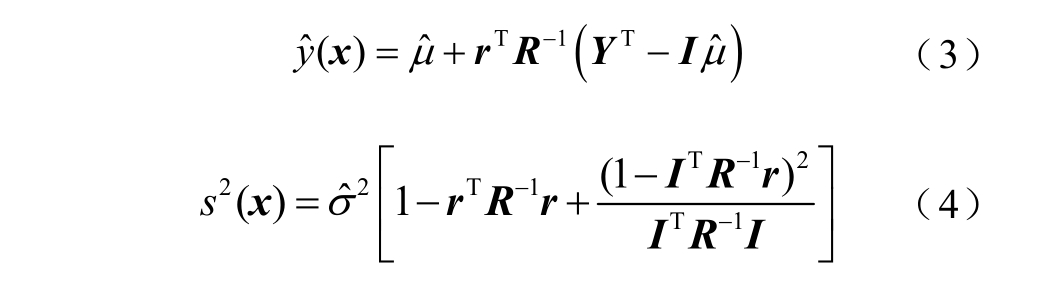
式中,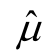 和
和 分别为μ、σ2的估计值;R 为n×n矩阵,其中(i,j)元素Rij= Cov[ε(x( i )),ε(x(j))];r 为n维列向量,其中元素ri=Cov[ε(x),ε( x(i))];I 为元素都为1 的n 维列向量。详细的公式推导过程可以参考文献[29]。
分别为μ、σ2的估计值;R 为n×n矩阵,其中(i,j)元素Rij= Cov[ε(x( i )),ε(x(j))];r 为n维列向量,其中元素ri=Cov[ε(x),ε( x(i))];I 为元素都为1 的n 维列向量。详细的公式推导过程可以参考文献[29]。
2.2 加点准则
加点准则主要包括最小化响应曲面准则、最小化置信下界函数准则、最大化改善概率准则和最大化EI 准则等[29]。理论证明了EI 准则能确保找到全局最优点,相比其他加点准则也有明显的优势。
目标函数在未知点x 处EI的数学表达式为
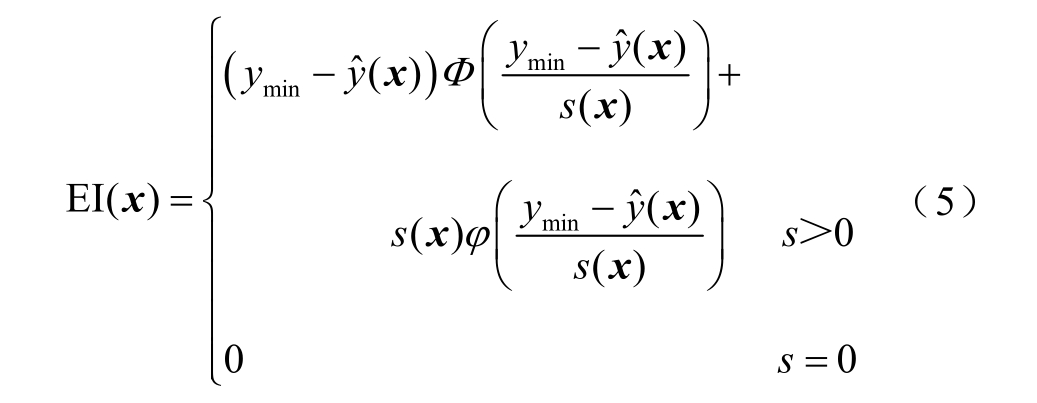
式中,ymin 为当前样本数据中最优值;Φ和φ分别为标准正态累积分布函数和标准正态分布概率密度函数。观察EI 第一项![]() 可知,未知点x 距离当前样本越近,
可知,未知点x 距离当前样本越近,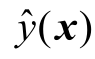 和s(x)越小,该项就越大,体现出局部开发;而未知点x 距离当前样本越远,s(x)越大,EI 第二项
和s(x)越小,该项就越大,体现出局部开发;而未知点x 距离当前样本越远,s(x)越大,EI 第二项![]() 越大,体现出全局搜索。可知,EI 加点准则兼顾了设计空间内的局部开发和全局搜寻,因而确保找到全局最优点。
越大,体现出全局搜索。可知,EI 加点准则兼顾了设计空间内的局部开发和全局搜寻,因而确保找到全局最优点。
下面将结合一个具体实例说明上述Kriging 建模和最大化EI 加点准则。Kriging 模型和EI 函数示意图如图3 所示。图中利用几个样本点建立Kriging模型。虚线是Kriging 模型给出的估计值的均值,两条点画线是根据模型的估计误差确定的估计值的置信区间。结合式(5)得到图中所示EI 函数波形。一般利用全局寻优算法,如遗传算法,确定EI 最大值点。在该点处将进行精确计算并更新Kriging 模型。图中所示EI 最大值点相比现有样本点是更接近原函数的最小值点。若按此迭代下去,全局最小值点是一定能找到的。

图3 Kriging 模型和EI 函数
Fig.3 Kriging model and EI function
2.3 改进型SBO 算法
现有最大化EI 加点准则每次只能确定一个点用于后续精确计算,没有利用好计算机并行计算的能力,导致寻优过程收敛速度慢。为了提高收敛速度同时兼顾局部开发和全局搜寻,文献[20]中EGOMO 算法将EI 的两项分别作为平衡局部开发和全局搜寻的目标,利用多目标优化算法寻优得到PF。假设需要加点Kc 个,先选取PF 上的两个极值点,后将PF 分成Kc-2 个聚类,在每个聚类上选取一个代表点。该方法的缺点在于PF 上选取代表点时没有考虑聚类点之间的距离,因而容易选取距离很近的代表点,导致代表点的代表性降低。同时,两个极值点的选取也不能必然导致收敛加快。
本文在文献[20]的基础上提出一种改进型的加点准则。具体实施步骤如下:
(1)将EI 的两项取负并看作两个目标,利用多目标优化算法,例如NSGA-II,获得PF。
(2)使用K 均态聚类(K-means clustering)算法将PF 划分为Kc 个聚类。
(3)在PF 每个聚类上选取代表点,代表点与现有样本以及其余聚类点的最小距离是最大的。
上述步骤(1)中取负是遵循优化惯例,将最大化问题转变成最小化问题。步骤(2)中的距离特指欧几里得长度。EI 两项构成的帕累托前沿如图4 所示PF,图中划分为4 个聚类。所选择的4 个代表点将利用计算机并行运算功能同时进行精确计算。本文将采用上述改进型加点准则的SBO 算法称之为改进型SBO 算法。
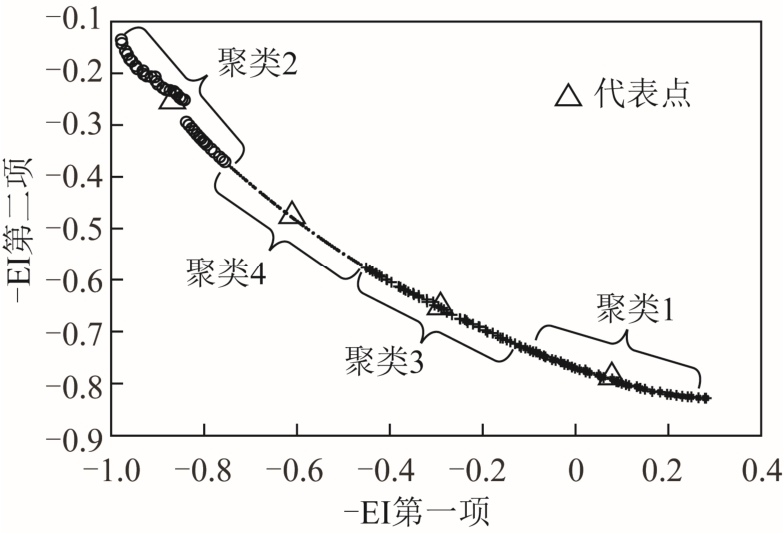
图4 EI 两项构成的帕累托前沿
Fig.4 Pareto front of the two items in EI
2.4 算法验证
为了验证所提出改进型SBO 算法的有效性,将针对一些测试函数展开优化,并对比传统的SBO 算法。初始样本的设计均采用拉丁超立方,初始样本的个数为测试函数输入变量维数的10 倍[16]。拉丁超立方使用Matlab 中的lhsdesign 函数进行设计。本文采用基于Matlab 的DACE 工具箱建立Kriging模型。PF 均分成4 个聚类。算法收敛条件为|(yminyglobal)/yglobal|≤0.01,其中yglobal 是全局最优值。
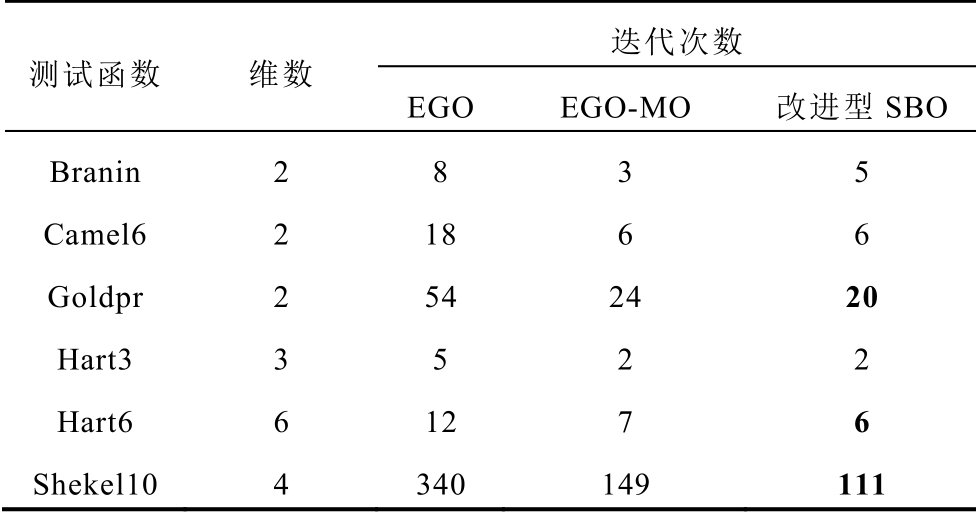
表1 中列出了测试函数在三种优化算法下满足收敛条件时需要的迭代次数。显然,相比传统EGO算法,EGO-MO 算法和本文提出的改进型SBO 算法收敛所需迭代次数都明显减少。除了Branin 函数,改进型SBO 算法相比EGO-MO 算法能以相同或者更少的迭代次数找到全局最优值。特别是局部极值点多达10 个的Shekel10 测试函数,本文提出的改进型SBO 算法具有明显优势。值得一提的是,现实中电机优化设计正是多极值点的问题。
表1 测试函数在不同优化算法下收敛迭代次数的比较
Tab.1 Iteration comparison of test functions under different optimization algorithms
测试函数 维数 迭代次数 EGO EGO-MO 改进型SBO Branin 2 8 3 5 Camel6 2 18 6 6 Goldpr 2 54 24 20 Hart3 3 5 2 2 Hart6 6 12 7 6 Shekel10 4 340 149 111
3 电机优化设计
将改进型SBO 算法应用于MPPML 电机优化之前,先定义电机设计参数,如图5a 所示。这里强调一下,本文定义的设计参数与文献[22]中定义略有不同。文献[22]中,动子齿宽、动子槽宽和永磁体下槽口宽都固定等于τm/4,如图5b 所示。而本文中没有此限定。磁通切换永磁电机的永磁体靠近气隙侧边缘易发生不可逆退磁。因此,为了减小退磁影响,永磁体高度hpm 比动子高度hm 要缩进2mm。另外,因为次级定子齿轭连接部宽度wsty 对电机性能影响较小,所以固定wsty=wst+2。此外,其余电机参数和所用材料与文献[22]中一致,见表2。
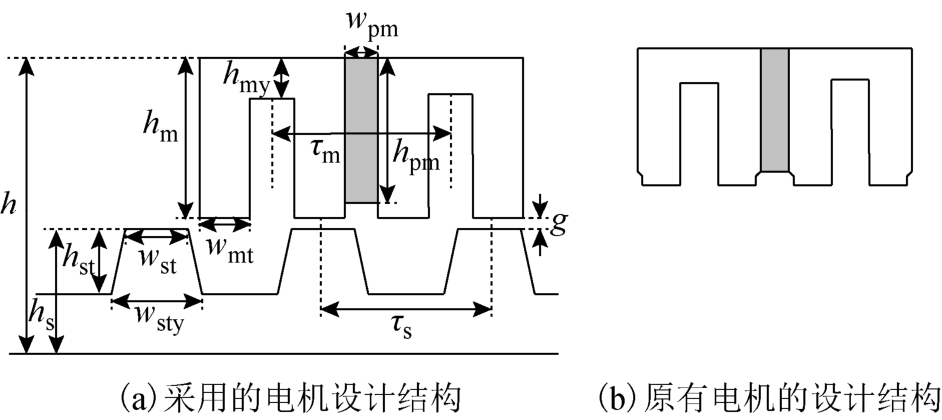
图5 电机设计结构和设计参数
Fig.5 Structure and design parameters of the motor
表2 MPPML 电机参数
Tab.2 Specification of the MPPML motor
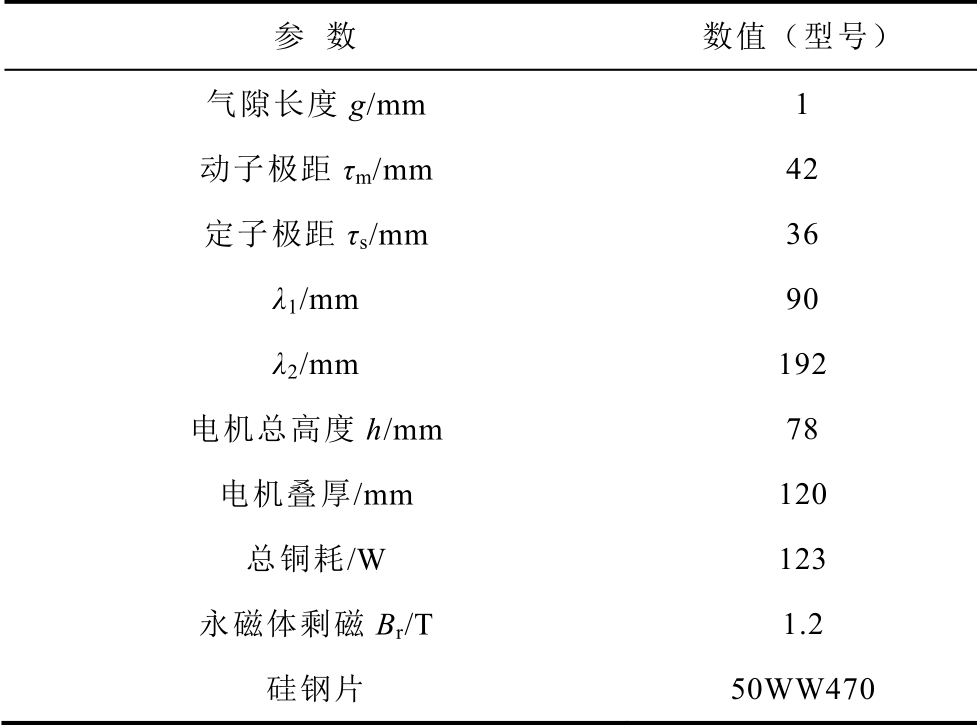
参 数 数值(型号) 气隙长度g/mm 1 动子极距τm/mm 42 定子极距τs/mm 36 λ1/mm 90 λ2/mm 192 电机总高度h/mm 78 电机叠厚/mm 120 总铜耗/W 123 永磁体剩磁Br/T 1.2 硅钢片 50WW470
为了优化方便,定义系数
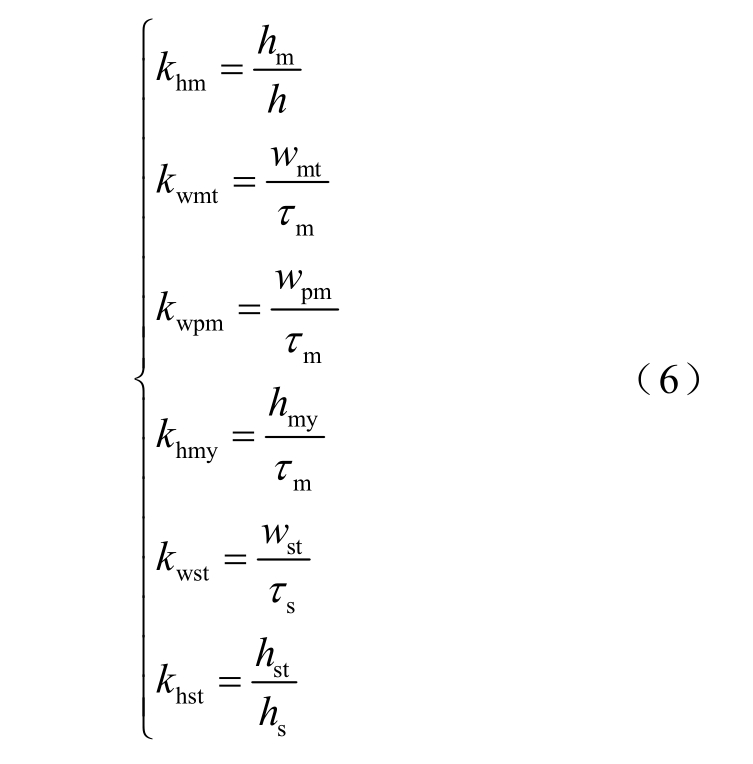
各个系数的变化范围在表3 中列出。
表3 系数变化范围
Tab.3 Variation range of coefficients
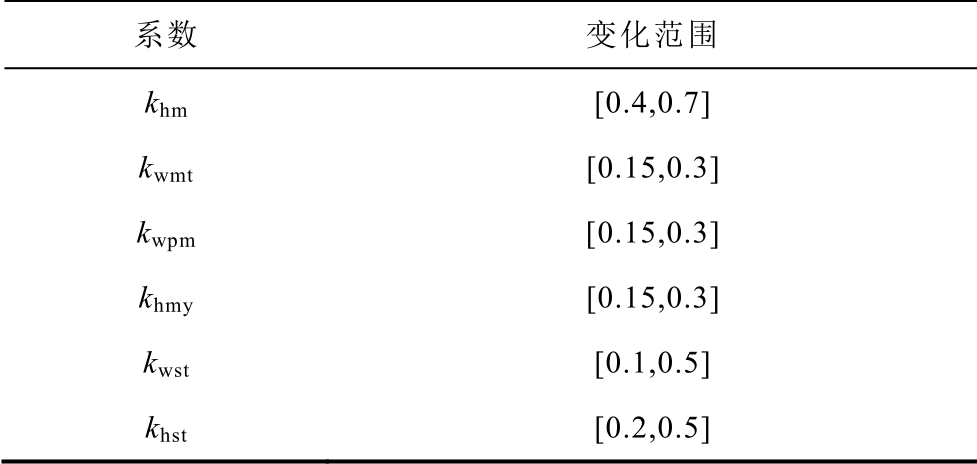
系数 变化范围 khm [0.4,0.7] kwmt [0.15,0.3] kwpm [0.15,0.3] khmy [0.15,0.3] kwst [0.1,0.5] khst [0.2,0.5]
电机优化目标是提高单位永磁体用量下的推力均值F,同时满足F≥800N 和推力波动率Fripple<0.08 这两个限制条件。其中,推力波动率的定义是推力峰峰值比推力均值。为了构造目标函数方便,单位永磁体用量下的推力均值用F/Spm 表示,其中,Spm=wpmhpm 是单块永磁体的横截面积。利用罚函数将限制条件和优化目标整合成一个优化目标为

式中,w1 和w2 为惩罚系数。为了满足限制条件,惩罚系数需比较大,这里w1=w2=10。
使用本文提出的改进型SBO 算法,初始样本的设计采用拉丁超立方,初始样本的个数为电机设计参数个数的10 倍,即60 个初始样本。考虑到计算机性能限制,将PF 划分为4 个聚类,即每次迭代是4 个有限元程序并行运算。这里MPPML 电机采用二维有限元模型分析,单个有限元仿真时长10min。优化目标和EI 项的收敛情况如图6 所示。图6a 所示为fobj 随迭代次数的变化情况。当迭代次数达到59 次时,图6b 所示PF 对应的EI 两项都足够小,认为达到收敛条件,不再继续迭代计算。fobj收敛于-2.738。为了验证改进型SBO 算法的优势,基于相同的初始样本,采用 EGO-MO 算法对MPPML 电机进行优化。相应fobj 随迭代次数的变化情况如图6a 所示,当迭代次数达到78 次时,图6b所示PF 对应的EI 两项都足够小,满足收敛条件,停止迭代计算。fobj 收敛于-2.735,是改进型SBO 算法寻优结果的0.998 9 倍。两种优化算法的寻优结果很接近,但改进型SBO 算法所需迭代次数明显更少,体现了该算法的快速性。
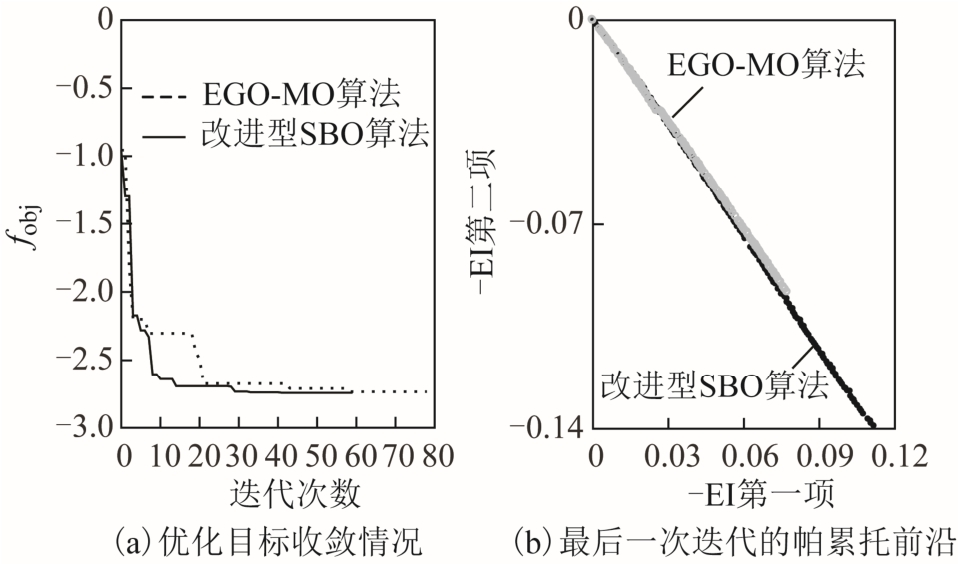
图6 优化目标和EI 项的收敛情况
Fig.6 Convergence of optimization objective and EI terms
为了进一步验证使用优化算法获得的结果是全局最优值,利用差分进化算法对MPPML 电机进行优化。差分进化算法的设置:选择方法是DE/rand/1/bin,种群数60,交叉常数0.9,权重因子0.8。经过30 代的计算演变,fobj 收敛于-2.753,是改进型SBO 算法寻优结果的1.005 5 倍。可知,两个优化结果极其接近,验证了改进型SBO 算法的寻优结果是全局最优值。值得注意的是,在改进型SBO 算法下,包括初始样本在内,一共运行了296 次有限元仿真,而差分进化算法运行了1 800 次有限元仿真。证明了改进型SBO 算法的高效性。
表4 中对比了前面所述三种优化算法的优化结果和文献[22]中的原有电机。图7 为四个电机的推力波形。可见,相比原有电机,基于改进型 SBO算法优化后的 MPPML 电机具有更小的推力波动率,且推力均值812.4N 比原有推力均值785.6N 增大3.4%,永磁体用量减小5.8%,从而F/Spm 提高9.78%。对比原有电机,优化后电机的功率因数从0.89 降为0.86,但效率却从84%提高到85%。此外,由于电机额定运行频率低,铁耗和永磁体涡流损耗较小,主要损耗是铜耗。对比改进型SBO 算 法优化后的电机,EGO-MO 算法优化后的电机的推力均值减小了0.73%,永磁体用量减少0.64%,导致F/Spm 减少0.11%。相应的效率有很小的变动,功率因数则从0.86 提高到0.88。而对比改进型SBO算法优化后电机,利用差分进化算法优化后电机的推力均值减小了0.32%,永磁体用量减小了0.85%,最终F/Spm 提高了0.55%。另外,这两种优化后电机的功率因数和效率相一致。可见,这两种优化算法结果极其相近。
表4 原有电机与优化后电机的性能比较
Tab.4 Performance comparison of four linear motors

参 数 原有电机优化电机 EGO-MO 算法 改进型SBO 算法差分进化算法动子高hm/mm 50 48.8 49.1 48.7动子齿宽wmt/mm 10.5 11.7 11.2 11.3永磁体宽wpm/mm 7 6.3 6.3 6.3 永磁体高hpm/mm 45 46.8 47.1 46.7动子轭高hmy/mm 14 11.7 11 11.6次级定子齿宽wst/mm 11.4 11.6 12.9 13 次级定子齿轭连接部宽度wsty/mm 16 13.6 14.9 15 次级定子齿高hst/mm 12 14 13.7 14.1次级定子高hs/mm 27 28.2 27.9 28.3次级成本(pu) 1 1.009 5 1.002 4 1.012相绕组匝数 116×2 140×2 154×2 149×2相电阻/Ω 1.14 1.37 1.51 1.47相电流有效值/A 6 5.47 5.21 5.29 B 相反电动势幅值(@1m/s)/V 64.65 70.1 72.16 70.9 B 相加载后电压幅值(@1m/s)/V 81.42 103.7 109.9 107.8铜耗/W 123 123 123 123铁耗(@1m/s)/W 18.4 19.1 19 19 永磁体涡流损耗(@1m/s)/W 3.55 1.17 1.12 1.14平均推力/N 785.6 806.5 812.4 809.8推力波动率(%) 8.2 6.5 6.8 6.8 效率(%) 84 84.9 85 85 功率因数 0.89 0.88 0.86 0.86推力/单块永磁体截面积/(N/mm2) 2.494 2.735 2.738 2.753
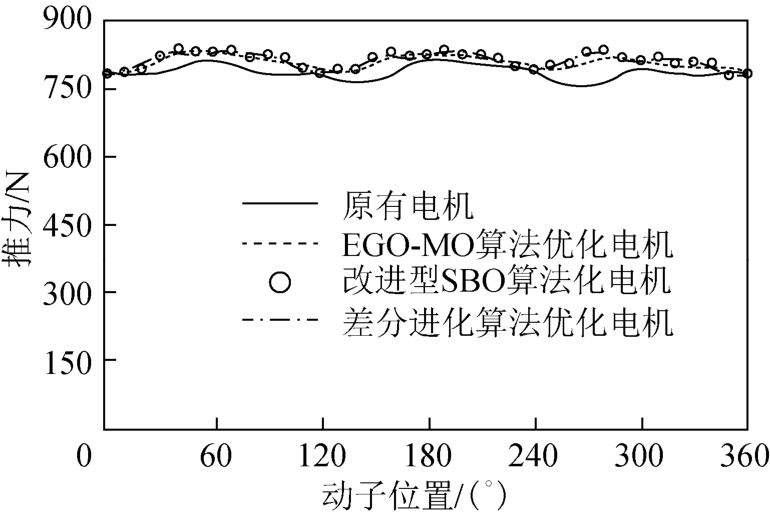
图7 三种优化算法和原有电机的推力波形
Fig.7 Thrust force of four motors
4 实验样机
为了验证上述有限元分析结果,加工制造了一台MPPML 电机,主要设计参数见表4 中所示原有电机参数。图8 为MPPML 电机样机照片。图9 中对比了0.692m/s 时有限元仿真所得反电动势波形与实验波形。为了考虑叠压系数影响和端部效应,采用三维有限元仿真。经比较A 相实验反电动势的幅值40V 比仿真反电动势幅值41.2V 小约2.9%,B 相实验反电动势的幅值40.2V 比仿真反电动势幅值42.1V 小约4.5%,C 相实验反电动势的幅值39.4V比仿真反电动势幅值41.2V 小约4.3%。可见,仿真波形与实验结果基本吻合,产生误差主要是因为样机使用硅钢片磁化曲线与仿真中所用磁化曲线存在差异。线切割等加工过程导致了实际硅钢片磁化性能的降低,这在仿真模型中没有考虑。

图8 MPPML 电机样机
Fig.8 Prototype of MPPML motor

图9 0.692m/s 电机空载反电动势波形
Fig.9 Back-EMF waveforms at 0.692m/s
将电机B、C 相绕组并联后与A 相绕组串联,通入5A 直流电,使用拉力传感器测得电机动子在不同位置下的推力波形如图10 所示。随着动子位置的变化,交轴电流逐渐增大后又逐渐减小。对应推力也先增大而后减小。对比三维有限元仿真结果,两者比较吻合。仿真值与测量值之间的误差一方面来源于电机所用滑块和导轨装配不佳,导致摩擦力随动子位置变化明显;另一方面是所用拉力传感器精度不高所带来的测量误差。
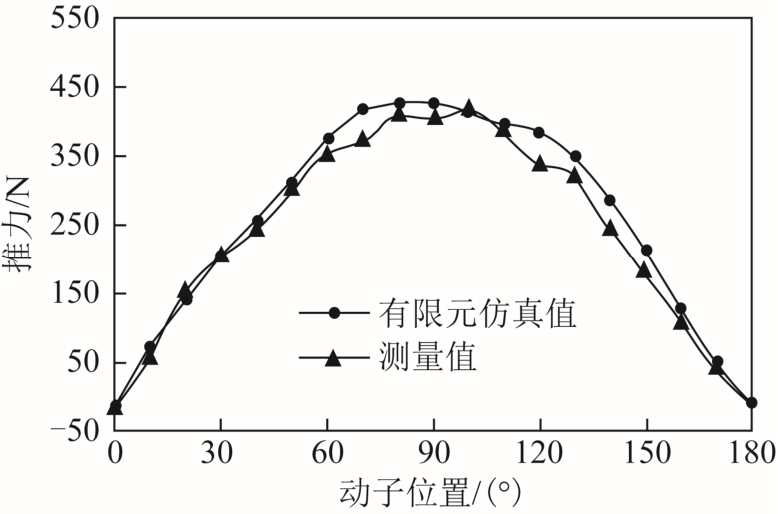
图10 静态推力
Fig.10 Static thrust force
5 结论
本文提出了一种改进型SBO 算法,每次迭代时将加点准则EI 的两项作为平衡局部开发和全局搜寻的目标,利用多目标优化算法得到PF,并将PF分成几个聚类,从不同聚类中选取需要精确计算的代表点。所提出优化算法很好地平衡了局部开发和全局搜寻,保证了优化目标的全局最优。结合并行运算,提高了优化算法的收敛速度。通过不同测试函数的验证,本文所提出的改进型SBO 算法相比现有EGO 算法和EGO-MO 算法都有一定的优势。一台三相MPPML 电机应用三种优化算法进行优化,EGO-MO 算法优化过程验证了所提算法寻优过程的快速性,差分进化算法优化结果验证了所提算法优化目标结果的全局最优性。在相同铜耗下,相比原有电机性能,优化所得电机具有更大的推力均值和更小的推力波动率,单位永磁体用量下的推力均值提高9.78%。
[1] Hendershot J R, Miller T J E. Design of brushless permanent-magnet machines[M]. New York: Magna Physics Publishing & Oxford University Press, 2010.
[2] Cheng M, Chau K T, Chan C C, et al. Nonlinear varying-network magnetic circuit analysis for doubly salient permanent-magnet motors[J]. IEEE Transactions on Magnetics, 2000, 36(1): 339-348.
[3] Zhu Z Q, Wu L J, Xia Z P. An accurate subdomain model for magnetic field computation in slotted surface-mounted permanent-magnet machines[J]. IEEE Transactions on Magnetics, 2010, 46(4): 1100-1115.
[4] Bramerdorfer G, Zăvoianu A, Silber S, et al. Possibilities for speeding up the FE-based optimization of electrical machines-a case study[J]. IEEE Transactions on Industry Applications, 2016, 52(6): 4668-4677.
[5] 鲍晓华, 刘佶炜, 孙跃, 等. 低速大转矩永磁直驱电机研究综述与展望[J]. 电工技术学报, 2019, 34(6): 1148-1160.
Bao Xiaohua, Liu Jiwei, Sun Yue, et al. Review and prospect of low-speed high-torque permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1148-1160.
[6] 刘细平, 李亚, 刘章麒, 等. 机械调磁式轴向永磁同步电机调磁特性分析与试验研究[J]. 电工技术学报, 2018, 33(5): 989-997.
Liu Xiping, Li Ya, Liu Zhangqi, et al. Analysis and experimental investigation on flux-adjusting characteristic for a mechanical flux-adjusting axial PM synchronous machine[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 989-997.
[7] 孙强, 张为堂, 花为. 一种车用双极性横向磁通永磁电动机[J]. 电机与控制学报, 2018, 22(8): 41-46.
Sun Qiang, Zhang Weitang, Hua Wei. Magnetic field of vehicle bipolar transverse-flux permanent magnet motor[J]. Electric Machines and Control, 2018, 22(8): 41-46.
[8] Bramerdorfer G, Tapia J A, Pyrhönen J J, et al. Modern electrical machine design optimization: techniques, trends, and best practices[J]. IEEE Transactions on Industrial Electronics, 2018, 65(10): 7672-7684.
[9] 鲁裕婷, 赵天乐, 都洪基, 等. 基于改进粒子群算法的含 DG 配电网无功优化[J]. 电力工程技术, 2018, 37(6): 69-74.
Lu Yuting, Zhao Tianle, Du Hongji, et al. Reactive power optimization of distribution network with distributed generation based on improved particle swarm optimization algorithm[J]. Electric Power Engineering Technology, 2018, 37(6): 69-74.
[10] 刘国海, 王艳阳, 陈前. 非对称V 型内置式永磁同步电机的多目标优化设计[J].电工技术学报, 2018, 33(增刊2): 385-393.
Liu Guohai, Wang Yanyang, Chen Qian. Multiobjective optimization of an asymmetric V-shaped interior permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 385-393.
[11] Forrester A I J, Keane A J. Recent advances in surrogate-based optimization[J]. Progress in Aerospace Sciences, 2009, 45: 50-79.
[12] Zhang Bangfu, Cheng Ming, Cao Ruiwu, et al. Analysis of linear flux-switching permanent magnet motor using response surface methodology[J]. IEEE Transactions on Magnetics, 2014, 50(11): 8103004.
[13] Taran N, Ionel D M, Dorrell D G. Two-level surrogate-assisted differential evolution multiobjective optimization of electric machines using 3-D FEA[J]. IEEE Transactions on Magnetics, 2018, 54(11): 8107605.
[14] Jouhaud J C, Sagaut P, Montagnac M, et al. A surrogate-model based multidisciplinary shape optimization method with application to a 2D subsonic airfoil[J]. Computers & Fluids, 2007, 36(3): 520-529.
[15] Wang G Gary, Shan S. Review of metamodeling techniques in support of engineering design optimization[J]. Journal of Mechanical Design, 2007, 129(2): 370-380.
[16] Jones D R, Schonlau M, Welch W J. Efficient global optimization of expensive black-box functions[J]. Journal of Global Optimization, 1998, 13: 455-492.
[17] Sóbester A, Leary S J, Keane A J. A parallel updating scheme for approximating and optimizing high fidelity computer simulations[J]. Structural and Multidisciplinary Optimization, 2004, 27(5): 371-383.
[18] Zhan Dawei, Qian Jiachang, Cheng Yuansheng. Balancing global and local search in parallel efficient global optimization algorithms[J]. Journal of Global Optimization, 2017, 67(4): 873-892.
[19] Sobester A, Leary S J, Keane A J. On the design of optimization strategies based on global response surface approximation model[J]. Journal of Global Optimization, 2005, 33(1): 31-59.
[20] Feng Zhiwei, Zhang Qingbin, Zhang Qingfu, et al. A multi-objective optimization based framework to balance the global exploration and local exploitation in expensive optimization[J]. Journal of Global Optimization, 2015, 61(4): 677-694.
[21] 李伟, 程明. 磁通切换电机的马尔科夫可靠性模型分析[J]. 电工技术学报, 2018, 33(19): 4535-4543.
Li Wei, Cheng Ming. Markov reliability model analysis for flux-switching permanent magnet machine[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4535-4543.
[22] 曹瑞武, 程明, 花为, 等. 磁路互补型模块化磁通切换永磁直线电机[J]. 中国电机工程学报, 2011, 31(6): 58-65.
Cao Ruiwu, Cheng Ming, Hua Wei, et al. Novel modularized flux switching permanent magnet linear machine with complementary magnetic circuits[J]. Proceedings of the CSEE, 2011, 31(6): 58-65.
[23] 黄磊, 胡敏强, 余海涛, 等. 双边长初级磁通切换永磁直线电机推力波动分析及抑制[J]. 电工技术学报, 2014, 29(11): 11-19.
Huang Lei, Hu Minqiang, Yu Haitao, et al. Analysis and suppression of the thrust ripple in a double-sided long primary flux-switching permanent magnet linear motor[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 11-19.
[24] 孔龙涛, 程明, 张邦富. 基于模型参考自适应系统的模块化磁通切换永磁直线电机无位置传感器控制[J]. 电工技术学报, 2016, 31(17): 132-139.
Kong Longtao, Cheng Ming, Zhang Bangfu. Position sensorless control of modular linear flux-switching permanent magnet machine based on model reference adaptive system[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 132-139.
[25] 孟高军, 袁野, 张亮, 等. 基于谐波抑制和扰动观测器的磁通切换永磁直线电机联合控制方法[J]. 电工技术学报, 2018, 33(9): 1957-1966.
Meng Gaojun, Yuan Ye, Zhang Liang, et al. A joint control method for linear flux-switching permanent magnet machine based on harmonic suppression and disturbance observer[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 1957-1966.
[26] 孟高军, 袁野, 孙玉坤, 等. 带定位力补偿的扩张观测器磁通切换永磁直线电机无位置传感器控制策略[J]. 电工技术学报, 2018, 33(17): 4091-4101.
Meng Gaojun, Yuan Ye, Sun Yukun, et al. Extended state observer with cogging force compensation for sensorless control strategy of linear flux-switching permanent magnet machine[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4091-4101.
[27] Wang Wei, Feng Yanan, Shi Yan, et al. Direct thrust force control of primary permanent-magnet linear motors with single DC-link current sensor for subway applications[J]. IEEE Transactions on Power Electronics, 2019, DOI:10.1109/TPEL. 2019. 2923378.
[28] Wang Wei, Feng Yanan, Shi Yan, et al. Fault-tolerant control of primary permanent-magnet linear motors with single phase current sensor for subway applications[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 10546-10556.
[29] Jones D R. A taxonomy of global optimization methods based on response surfaces[J]. Journal of Global Optimization, 2001, 21: 345-383.
[30] 赵靖英, 孙政樑, 姚帅亮, 等. 新型双电源转换开关直流速动电磁机构的设计与优化[J]. 电机与控制学报, 2018, 22(5): 52-62.
Zhao Jingying, Sun Zhengliang, Yao Shuailiang, et al. Design and optimization of DC electromagnetic mechanism with rapid action of new type of automatic transfer switching equipment[J]. Electric Machines and Control, 2018, 22(5): 52-62.