0 引言
对于弱电网中的多机并网系统而言,由于LCL滤波器的引入和多逆变器并联接入,会在逆变器的内部、逆变器之间,逆变器和电网之间形成谐波谐振[1-3],且随着并联台数增加,谐振频率向低频段偏移,极大地加剧了系统的谐波谐振风险[4-5],进而可能引发系统的全局谐振。因此,多逆变器并联谐振机理的分析以及谐振抑制方法的研究引起国内外学者的广泛关注[6-8]。
文献[9]分析了弱电网下电网阻抗的变化和逆变器并联数量的变化对 LCL型并网逆变器并联谐振特性的影响,并将LCL滤波系统谐振定义为LCL自身固有谐振和电网阻抗耦合产生的外部耦合谐振,得到了外部耦合谐振点随逆变器并联台数的增加向低频转移的结论。文献[10]通过开环传递函数描述多逆变器并联系统,指出随着逆变器并联数目增加,单台逆变器的等效电网阻抗增加,m台相同逆变器并联对单台逆变器而言等效电网阻抗扩大了m倍。
有源阻尼法是一种有效的谐振抑制方法,实现方式灵活方便,且不会增加额外功耗[11-13]。文献[14]提出了离散时间有源阻尼控制。文献[15-16]提出在控制器中加入滤波器,从而仅改变并网逆变器在谐振频率处的阻抗特性,避免谐振发生。文献[17]引入电容电压反馈和逆变器侧电感电流反馈,在逆变侧滤波电感和滤波电容支路串联或并联相应的电阻重塑并网逆变器的输出阻抗,抑制网络内谐波谐振。文献[18]提出反馈滤波器的电容电压微分量有源阻尼方法,而微分环节容易引入噪声干扰信号。文献[19]提出一种采用并网电流两次微分的反馈方法,实现谐振阻尼控制,无需增加额外传感器,但并网电流导函数会将噪声放大,造成系统振荡。以上文献都聚焦于多逆变器并联谐振的单点抑制方法的研究。然而,由于线路阻抗差异,每台逆变器本身的线路阻抗和自身的网侧滤波电感组合的该台逆变器等效网侧滤波单元阻抗不同,由等效LCL滤波单元引起的谐振点非固定不动。针对此问题,本文提出一种弱电网下多逆变器并网系统的全局高频振荡抑制方法,实现不同线路阻抗下多个谐振点的抑制。
本文首先在同步旋转坐标系下建立多逆变器并联的等效电路模型,研究了多逆变器并联谐振机理;然后提出基于公共耦合点(Point of Common Coupling, PCC)电压前馈和并网电流高频反馈相结合的弱电网下多逆变器并网系统的全局高频振荡抑制方法,通过仿真分析证明所提全局高频振荡抑制方法对多逆变器并联谐振抑制的有效性;之后搭建多逆变器并联实验平台,通过实验揭示多逆变器并联的谐振规律,并验证本文所提全局高频振荡抑制方法的有效性;最后,对本文所做工作进行了总结。
1 多逆变器并联的谐振机理分析
为研究多逆变器并联的谐振机理,本文首先建立考虑线路阻抗时单台三相并网逆变器在同步旋转坐标系下的等效电路模型,继而扩展到多台逆变器并联,建立考虑线路阻抗时多逆变器并联等效电路模型,通过分析不同激励源单独作用时逆变器输出并网电流响应特性,揭示多逆变器并联的谐振机理。
1.1 单台并网逆变器建模
三相LCL逆变器并网系统如图1所示。忽略逆变器直流侧电压的波动,用直流电源 udc代替直流侧前级;忽略线路等效电阻,线路阻抗可用线路等效电感Lline表示;iox(x=a, b, c)为逆变器侧输出电流;igx为网侧输出电流;uox为逆变器桥臂中点电压;ucx为滤波电容电压;ux为并网点电压;ugx为三相电网电压。建立三相LCL型并网逆变器在dq坐标系下的数学模型,下标“d”、“q”分别表示变量在d、q轴的分量。

图1 三相LCL逆变器并网系统
Fig.1 Grid-connected system of three-phase
LCL-type inverter
根据图1可得
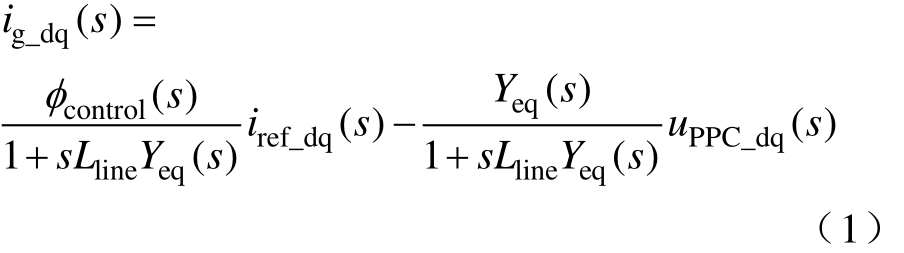
式中,φcontrol(s)为逆变器的诺顿等效受控电流源传递函数;Yeq(s)为逆变器的等效输出导纳;uPCC为PCC点电压。表达式为
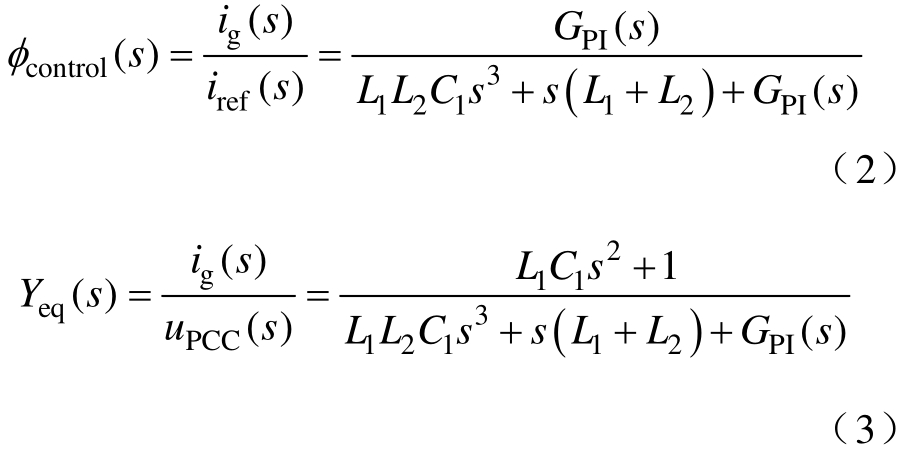
根据式(1)可建立三相并网逆变器在dq坐标系下的等效诺顿模型。逆变器诺顿等效电路模型如图2所示。

图2 逆变器诺顿等效电路模型
Fig.2 Norton equivalent circuit model of inverter
1.2 多台并网逆变器并联等效模型
N台并网逆变器并联运行时,其诺顿等效电路如图3所示。

图3 N台并网逆变器并联运行的诺顿等效电路
Fig.3 Norton equivalent circuit diagram for parallel operation of N grid connected inverters
根据节点电压法,可得第m台逆变器输出并网电流ig,m(s)为

由式(4)可知,多逆变器并联系统中,任意一台逆变器输出的电流由三部分组成:第一部分与逆变器自身的指令电流有关,其耦合关系强度用传递函数 Gself,m(s)表示;第二部分与其他逆变器的指令电流有关,其耦合关系强度用传递函数 Gpara,i,m(s)(其中 m≠i)表示;第三部分和电网电压有关,其耦合关系强度用传递函数Gseries,m(s)表示,具体传递函数关系为

通过分析3个激励源Gself,m(s)、Gpara,i,m(s)和Gseries,m(s)对逆变器输出电流的激励效果,揭示多逆变器并联谐振机理。
1.3 多逆变器并联谐振机理
每台逆变器本身的线路阻抗和自身的网侧滤波电感组合等效为该台的网侧滤波单元的阻抗,由于线路阻抗差异,每台逆变器等效的网侧滤波单元阻抗不同,因此由等效LCL滤波单元引起的自身谐振点非固定不动,引起的并联谐振点也非固定不动。
1.3.1 并网逆变器自身谐振特性
以第一台逆变器为例,分析逆变器自身谐振特性,逆变器自身谐振特性可以表示为

根据式(8),可以得到不同数量并网逆变器并联时,第一台逆变器自身激励效果 Gself,1(s)关于逆变器并联台数、谐波次数和幅值响应三维图,如图4所示。对每台逆变器而言,其线路阻抗可以和自身网侧滤波电感组合等效成每台的网侧滤波电感,由于每台等效的网侧滤波电感不同,因此由LCL耦合产生的谐振频率也不同。
1.3.2 并网逆变器之间并联谐振特性
第一台逆变器与其他逆变器的并联谐振可表述为

图4 自身激励效果Gself,1(s)三维图
Fig.4 Three-dimensional graph of Gself,1(s)
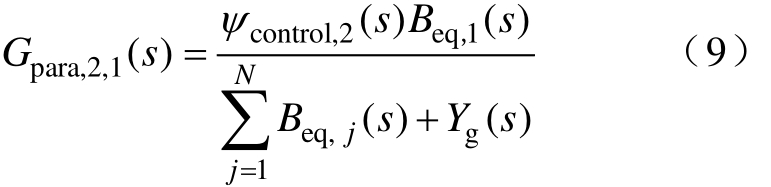
式中,Gpara,2,1(s)为第二台逆变器的指令电流iref_2对第一台逆变器输出并网电流ig,1的激励效果。
根据式(9),可以得到不同数量并网逆变器并联,逆变器并联激励效果Gpara,2,1(s)关于逆变器并联台数、谐波次数和幅值响应三维图,如图5所示。从图5可知,逆变器并联谐振特性存在两个谐振点,并且都不是固定谐振点,两个谐振点都随逆变器并联的数量变化而变化。
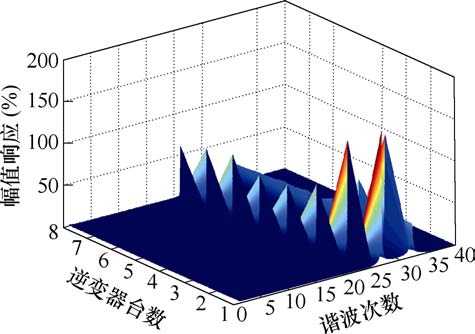
图5 并联激励效果Gpara,2,1(s)三维图
Fig.5 Three-dimensional graph of Gpara,2,1(s)
1.3.3 并网逆变器和电网间串联谐振特性
第一台逆变器与电网的串联谐振可表述为
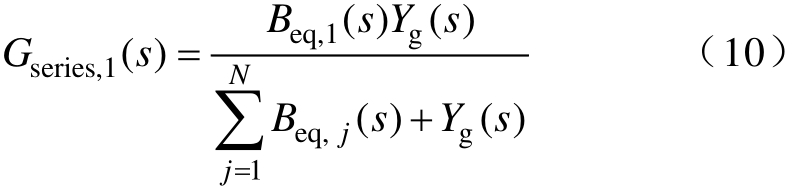
式中,Gseries,1(s)为电网电压对第一台逆变器输出的并网电流ig,1的激励效果。
根据式(10),可以得到不同数量并网逆变器并联,电网电压ug对第一台逆变器输出的并网电流ig,1的串联激励效果Gseries,1(s)关于逆变器并联台数、谐波次数和幅值响应三维图,如图6所示。

图6 串联激励效果Gseries,1(s)三维图
Fig.6 Three-dimensional graph of Gseries,1(s)
从串联谐振定义可知,研究串联谐振时,把每台逆变器输出的电压激励设置为 0,因此对电网侧而言,多台并联逆变器可以看作由LCL和线路阻抗组成的LCL网络,该LCL网络和电网阻抗组合可以等效为新的LCL网络,因此考虑线路阻抗时,串联谐振只存在一个由电网阻抗耦合产生的谐振点,其谐振频率随着逆变器台数的增加向低频转移。
2 弱电网下多逆变器并网系统的全局高频振荡抑制方法
并网逆变器自身谐振和并联谐振是逆变器本体以及逆变器间产生的谐振,因此采用逆变器内部的信号量反馈构造虚拟阻尼来抑制。而串联谐振是多并网逆变器与电网线路阻抗之间的谐振,考虑到多台并网逆变器经线路接入PCC,因此通过前馈电网与逆变器之间的PCC信号量来构造虚拟阻尼,以抑制多台并网逆变器与线路阻抗的串联谐振。
2.1 全局高频振荡抑制方法
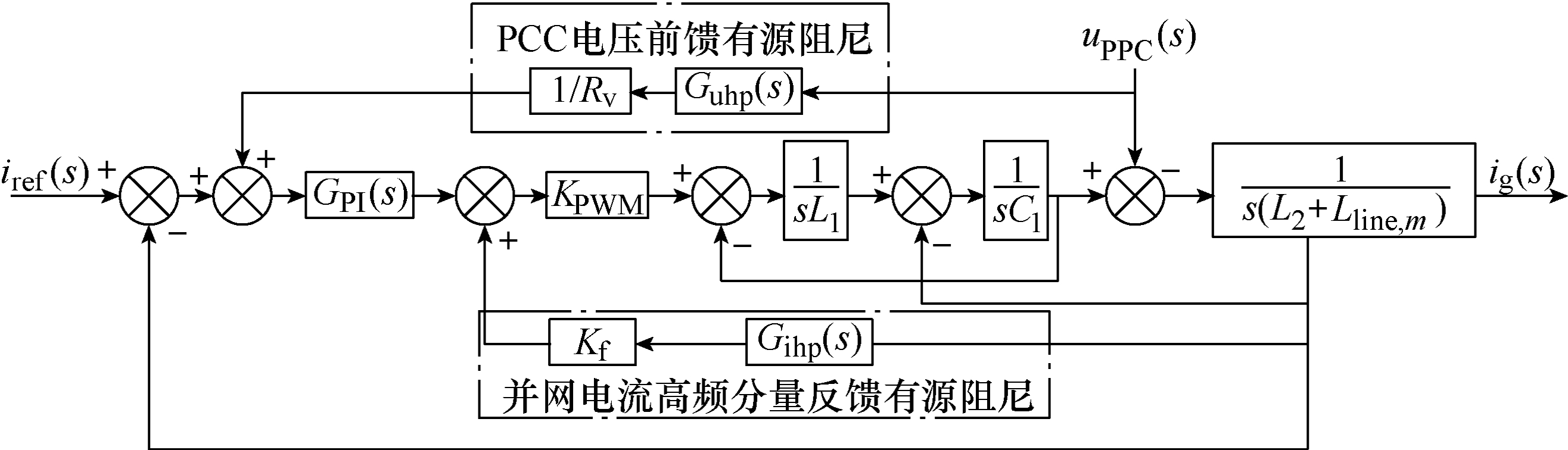
图7 全局高频振荡抑制方法
Fig.7 The global high-frequency oscillation suppression method
弱电网下多逆变器并网系统的全局高频振荡抑制方法如图7所示。Guhp(s)表示PCC电压前馈支路的高通滤波器,用于提取PCC处电压的高次谐波成分;Gihp(s)表示并网电流反馈支路的高通滤波器,用于提取并网电流的高次谐波。
2.1.1 PCC电压前馈
以第m台逆变器为例分析全局高频谐振抑制方法,PCC电压前馈有源阻尼等效电路如图8所示。

图8 PCC电压前馈有源阻尼等效电路
Fig.8 PCC voltage feedforward active damping
PCC处不施加PCC电压前馈有源阻尼时,有
式中,A(s)为不施加PCC电压前馈有源阻尼时构成并网电流的逆变器电压分量导纳;L(s)为不施加 PCC电压前馈有源阻尼时构成并网电流的电网电压分量导纳。

根据式(12)可求得系统谐振频率为
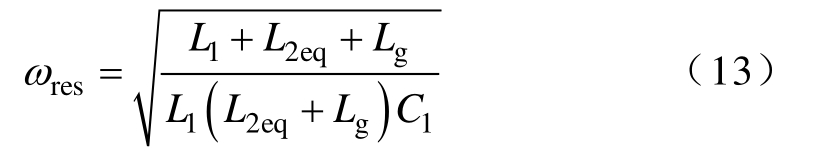
在PCC并联虚拟电阻Rv,即施加PCC电压前馈有源阻尼时,并网电流ig,m表达式为
式中,ginv_iuϕ(s)为施加PCC电压前馈有源阻尼时构成并网电流的逆变器电压分量导纳;gg_iuλ(s)为施加 PCC电压前馈有源阻尼时构成并网电流的电网电压分量导纳。其中
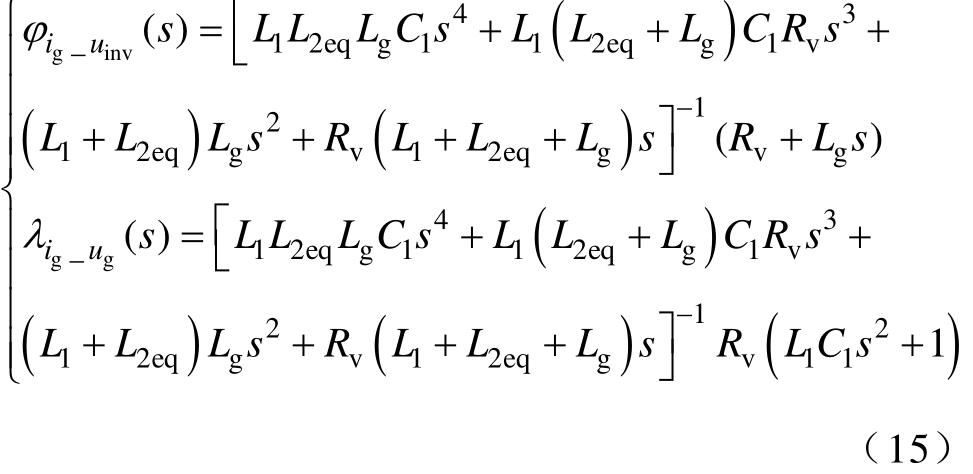
根据式(15)可知,引入PCC电压前馈,增加了系统阻尼,可有效抑制电网电压背景谐波和逆变器输出谐波造成的逆变器并联系统谐振。
2.1.2 并网电流高频分量反馈
针对并网逆变器自身谐振及并联谐振,本文提出并网电流高频分量反馈有源阻尼谐振抑制方法,如图9所示。

图9 并网电流高频分量反馈有源阻尼控制框图
Fig.9 Active damping control diagram of high-frequency component feedback for grid-connected current
引入反馈控制时,逆变器输出并网电流ig和逆变器调制信号ud的传递函数关系为
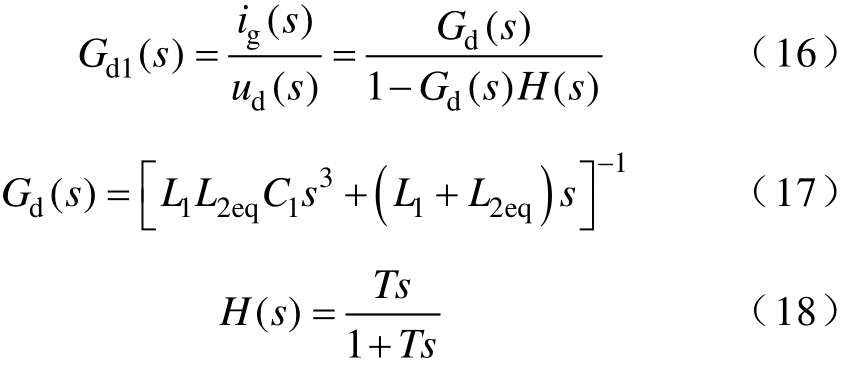
根据式(16)可知,Gd(s)即为LCL滤波器的传递函数,LCL发生谐振时,在谐振频率ωres处,Gd(jωres)幅值为无穷大,可通过负反馈控制实现对谐振峰的有效抑制,则需使Gd(jωres)H(jωres)的实部为负数,并且反馈深度越深,谐振抑制能力越强。在谐振频率ωres处,Gd(s)的相位处于第二、三象限,Gd(s)实部始终为负数,因此需要满足在谐振频率ωres处 H(jωres)>0。由式(18)可知,在全频段内H(jω)都位于第一象限,为了保证 LCL型逆变器在整个频率范围的稳定运行,可以通过提取谐振频率附近的高次谐波分量作负反馈控制,抑制谐振,实现系统稳定可靠运行。
并网电流高频分量反馈等效变换的控制框图如图10a所示,从图10a可以看出,并网电流高频分量反馈可以等效为在电容两端并联虚拟阻抗Zd,有
根据式(19)可知,Zd由虚拟电阻Rd和虚拟电容 Cd并联构成,Rd、Cd的大小由Kf决定,电阻Rd和Kf负相关,Cd和Kf正相关,有

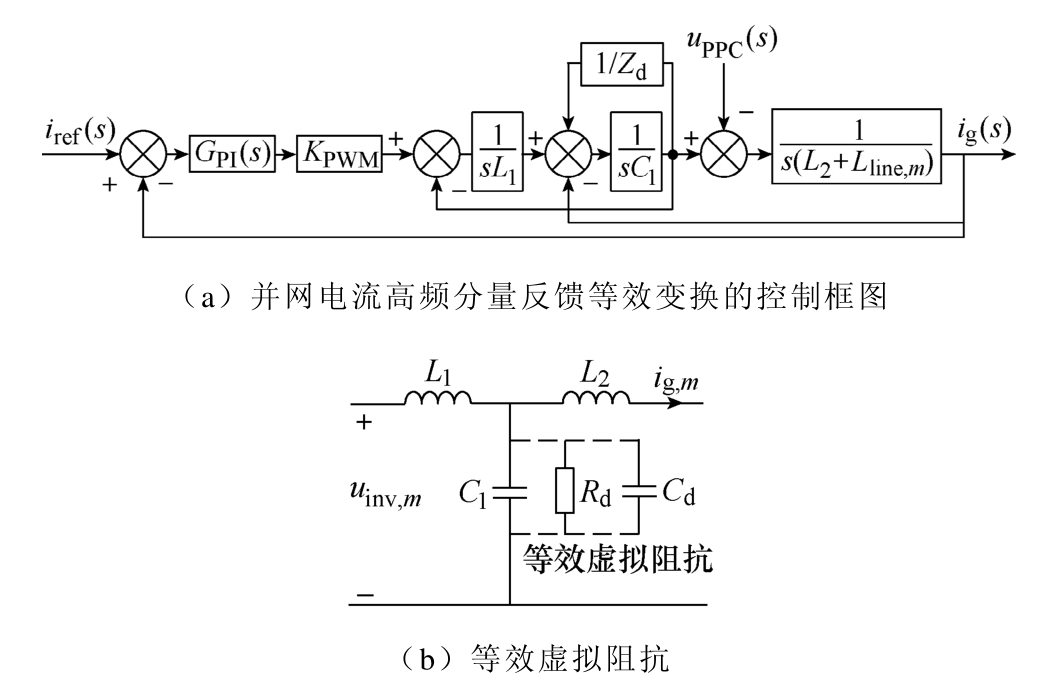
图10 并网电流高频分量反馈控制的等效示意图
Fig.10 Schematic diagram for high-frequency component feedback control of grid connected current
并网电流高频分量反馈的等效虚拟阻抗模型如图 10b所示,将等效虚拟阻抗 Zd和滤波电容 C1合并,可以得到并网电流高频分量反馈有源阻尼控制时滤波单元LCL的传递函数表达式为

根据式(21)推导出LCL滤波器的阻尼系数为
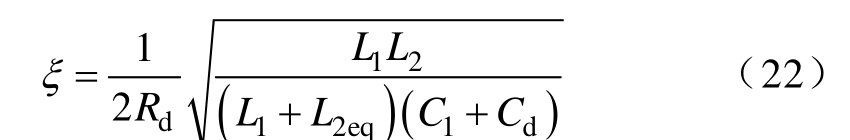
通常ξ =0.707,联立式(20)、式(22),可求得Kf =0.005。因此,根据式(20)可得Rd、Cd的取值。
本文采用一阶高通滤波提取高次谐波,仅增加高频处的系统阻尼,因此可以有效削弱有源阻尼方法对基波附近频段处稳定性的影响。
2.2 仿真分析
为得到较好的系统谐振抑制效果并满足系统稳定性和并网电流的控制精度要求,Rv=5Ω,逆变器台数、谐波次数和幅值响应的关系如图11所示。

图11 弱电网全局高频振荡抑制方法控制下多逆变器并网系统的三维图(Rv=5Ω)
Fig.11 Three-dimensional graph of mutil-inverter system using global high-frequency oscillation suppression method under weak grid (Rv=5Ω)
2.2.1 自身谐振抑制仿真分析
仿真工况和 1.3节一致,在第一台逆变器的指令电流中加入各个频次的谐波电流,而且含量均为3%。施加全局高频振荡抑制方法,考虑3台逆变器并联运行的工况,观察第一台逆变器输出的并网电流波形和频谱,通过对比不施加全局高频谐振抑制方法时并网电流波形和频谱,验证全局高频谐振抑制方法的有效性。
3台并网逆变器并联运行时,施加全局高频谐振抑制方法时第一台逆变器输出的并网电流波形和频谱如图12所示。施加全局高频谐振抑制方法和不施加全局高频谐振抑制方法时第一台逆变器输出并网电流的详细对比情况见表 1。施加该抑制方法后第一台并网电流畸变率降为 2.99%,有效抑制了逆变器自身谐振,并网电流波形得到极大改善。
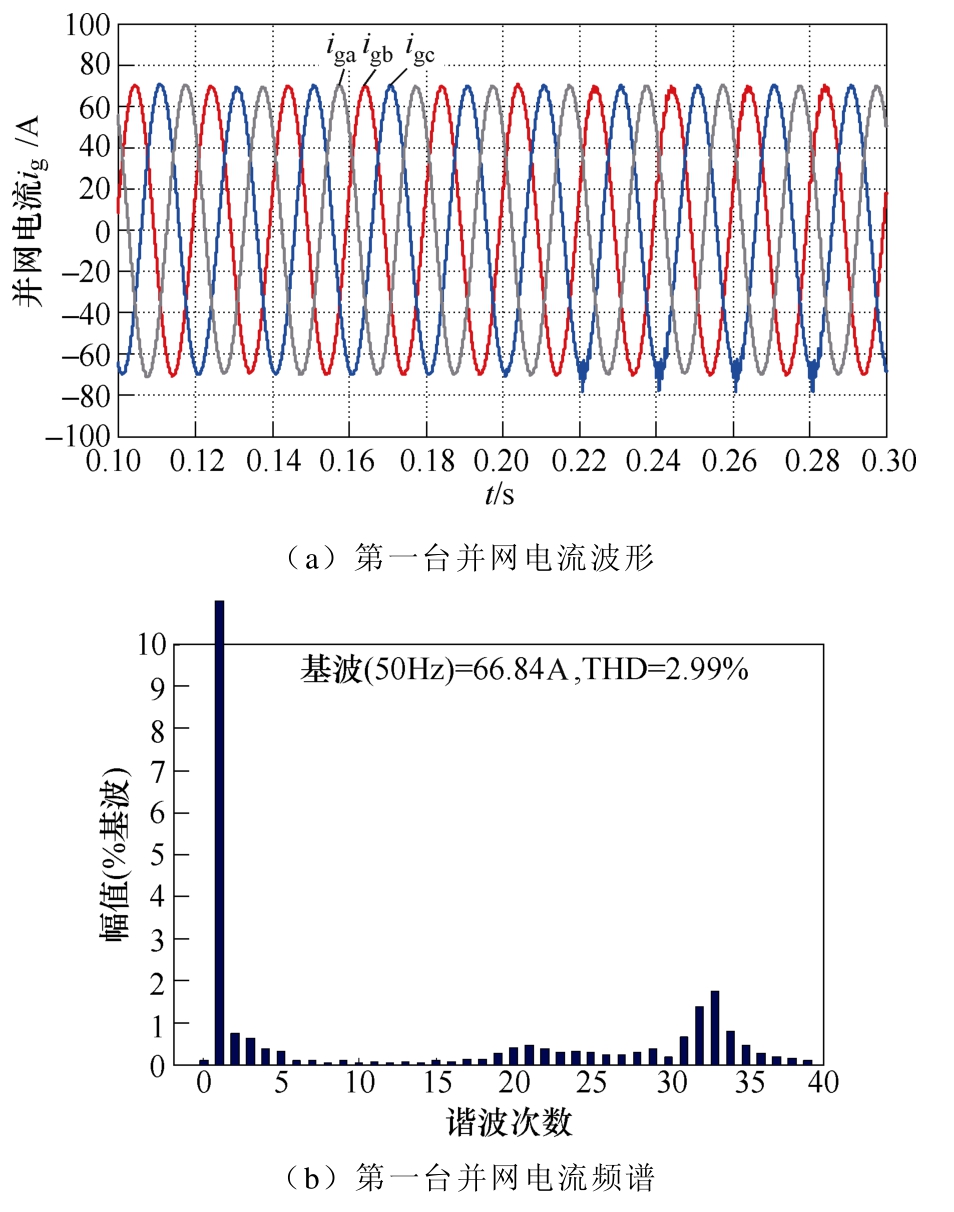
图12 全局高频谐振抑制方法下第一台逆变器并网电流波形和频谱
Fig.12 The grid-connected current waveforms and frequency spectrum of the first inverter under global high-frequency oscillation suppression strategy
表1 有/无全局高频谐振抑制方法时逆变器自身谐振
Tab.1 Self resonance of inverter with and without global high-frequency oscillation suppression strategy

第一台逆变器运行工况 畸变率(%)无全局高频谐振抑制方法 10.07施加全局高频谐振抑制方法 2.99
2.2.2 并联谐振抑制仿真分析
在第一台逆变器指令电流中加入各个频次的谐波电流,含量都为3%,仿真工况和1.3节一致,3台逆变器并联时,施加全局高频谐振抑制方法,第二台逆变器输出并网电流波形和频谱如图13所示。

图13 全局高频谐振抑制方法下第二台逆变器并网电流波形和频谱
Fig.13 The grid-connected current waveforms and frequency spectrum of the second inverter under global high-frequency oscillation suppression strategy
施加全局高频谐振抑制方法时,第二台逆变器并网电流波形和频谱如图13所示,可以看出,输出的并网电流畸变率降为 2.35%,全局高频谐振抑制方法极大改善了并网电流的波形质量,谐振抑制效果显著。施加全局高频谐振抑制方法和不施加全局高频谐振抑制方法的详细对比情况见表2。
表2 有/无全局高频谐振抑制方法时逆变器并联谐振
Tab.2 Parallel resonance of inverter with and without global high-frequency oscillation suppression strategy

第二台逆变器运行工况 畸变率(%)无全局高频谐振抑制方法 10.43施加全局高频谐振抑制方法 2.35
2.2.3 串联谐振抑制仿真分析
为了形象地表征逆变器和电网之间的串联谐振机理以及验证有源阻尼方法对逆变器和电网串联谐振的抑制效果,在电网电压中加入各个频次的谐波电压,含量相同且都不足 2%。考虑 3台并联时,观察第一台逆变器输出的并网电流波形和频谱,并和电网未加入谐波电压工况作对比。具体仿真过程:0.1~0.2s,不向电网中投入谐波电压源;0.2~0.3s,向电网电压中投入各个频次的谐波电压源。
施加全局高频谐振抑制方法,3台逆变器并联运行,第一台逆变器输出的并网电流和频谱如图14所示。第一台逆变器输出并网电流的畸变率降低为1.39%,电流波形改善明显。施加全局高频谐振抑制方法和不施加全局高频谐振抑制方法的对比情况见表3。

图14 全局高频谐振抑制方法下第一台逆变器并网电流波形和频谱
Fig.14 The grid-connected current waveforms and frequency spectrum of the first inverter under global high-frequency oscillation suppression strategy
表3 有/无全局高频谐振抑制方法时逆变器串联谐振
Tab.3 Series resonance of inverter with and without global high-frequency oscillation suppression strategy

第一台逆变器运行工况 畸变率(%)无全局高频谐振抑制方法 4.48施加全局高频谐振抑制方法 1.39
可知施加全局高频谐振抑制方法后,逆变器输出并网电流波形得到显著改善。
仿真表明了该全局高频谐振抑制方法对并网逆变器自身谐振、并联谐振、串联谐振抑制的有效性。
3 实验验证
为验证本文所提全局高频谐振抑制方法的有效性,搭建了包括三台并网逆变器并联的实验平台,每台逆变器额定运行功率为 30kW,开关频率为10kHz。实验平台如图15所示。

图15 多逆变器并联系统
Fig.15 Multi-inverter parallel system
不施加全局高频谐振抑制方法时,在第一台逆变器的指令电流上叠加谐波电流指令,可以得到单台运行、两台、三台并联运行时逆变器输出并网电流的波形和频谱图。
图16为单台并网逆变器独立工作,不施加全局高频谐振抑制方法时的实验结果,此时并网电流畸变率为9.5%,逆变器自身谐振频次位于第28次。

图16 无全局高频谐振抑制并网电流波形和频谱(单台)
Fig.16 Grid-connected current waveforms and spectrum without global high-frequency oscillation suppression strategy (one set)
不施加全局高频谐振抑制方法,两台并网逆变器并联运行时,实验结果如图17所示,第一台逆变器并网电流畸变率为6.5%,谐振频次位于第25次和第34次;第二台逆变器并网电流畸变率为7.1%,谐振频次位于第25次和第34次。
图18为三台并网逆变器并联运行,不施加全局高频谐振抑制方法时的实验结果,第一台逆变器输出并网电流畸变率为7.9%,谐振频次位于第24次和第 34次;第二台逆变器输出并网电流畸变率为5.9%,谐振频次位于第24次和第34次。

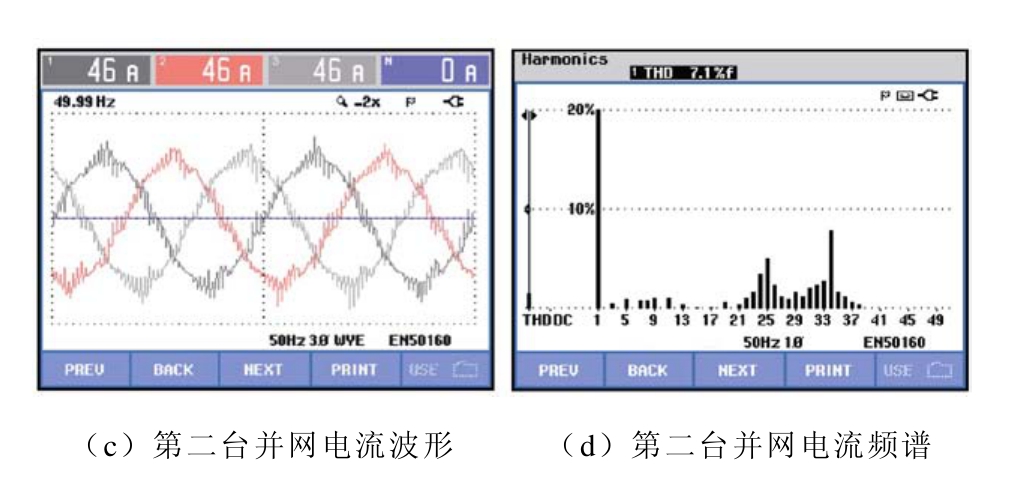
图17 无全局高频谐振抑制并网电流波形和频谱(两台)
Fig.17 Grid-connected current waveform and frequency spectrum without global high-frequency oscillation suppression strategy (two sets)

图18 无全局高频谐振抑制并网电流波形和频谱(三台)
Fig.18 Grid-connected current waveform and frequency spectrum without global high-frequency oscillation suppression strategy (three sets)
施加全局高频谐振抑制方法,在第一台逆变器的指令电流上叠加谐波电流指令,可以得到三台逆变器并联时逆变器输出并网电流波形和频谱如图19所示。
三台并网逆变器并联运行,施加全局高频谐振抑制方法和不施加全局高频谐振抑制方法的实验结果见表4和表 5。通过对比可知,施加全局高频谐振抑制方法时,第一台和第二台并网电流畸变率分别从7.9%和5.9%降为3.0%和2.7%,并网电流波形质量得到明显改善。实验验证了本文所提全局高频谐振抑制方法的有效性。

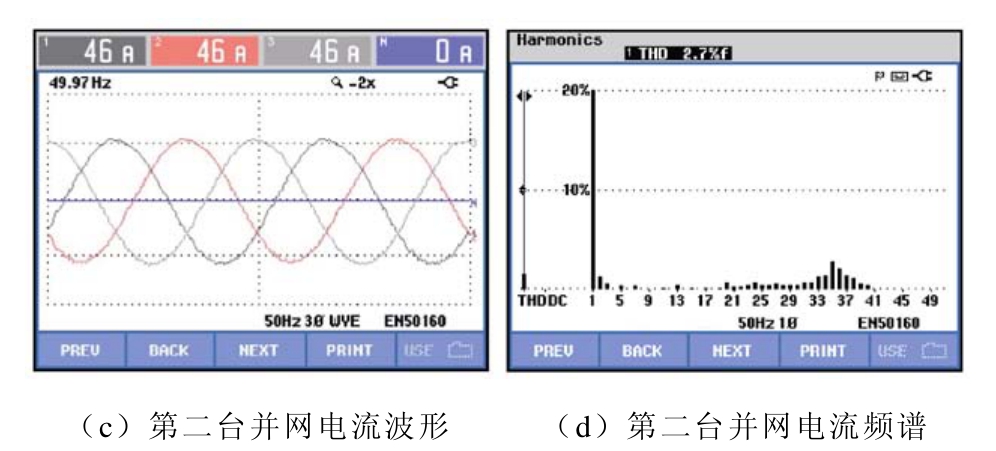
图19 全局高频谐振抑制并网电流波形和频谱(3台)
Fig.19 Grid-connected current waveform and frequency spectrum with global high-frequency oscillation suppression strategy (three sets)
表4 有/无全局高频谐振抑制方法时逆变器自身谐振
Tab.4 Self resonance of inverter with and without global high-frequency oscillation suppression strategy

第一台逆变器运行工况 畸变率(%)无全局高频谐振抑制方法 7.9施加全局高频谐振抑制方法 3.0
表5 有/无全局高频谐振抑制方法时逆变器并联谐振
Tab.5 Parallel resonant of inverter with and without global high-frequency oscillation suppression strategy

第二台逆变器运行工况 畸变率(%)无全局高频谐振抑制方法 5.9施加全局高频谐振抑制方法 2.7
4 结论
本文建立了多台并网逆变器并联模型,分析了多逆变器并联的自身谐振、串联谐振、并联谐振机理,针对多逆变器并联时谐振点因线路阻抗差异而有所不同的情况,提出了一种弱电网下多逆变器并网系统的全局高频振荡抑制方法,该方法引入PCC电压全局变量和并网电流高频分量到逆变器控制环节,通过理论分析与仿真验证,可实现多逆变器系统的高频振荡抑制。最后,在实验平台的基础上,进行多逆变器并联实验,通过实验揭示了多逆变器并联谐振机理,并验证了本文所提全局高频谐振抑制方法的有效性。
[1] 陈燕东, 王伊, 周乐明, 等. 弱电网下 LCL逆变器阻尼谐振抑制与功率快速调节方法[J]. 电工技术学报, 2018, 33(11): 2564-2574.Chen Yandong, Wang Yi, Zhou Leming, et al.Damping resonance suppression and fast power regulation method for LCL-type inverter under weak grid[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2564-2574.
[2] 陈燕东, 罗安, 陈智勇, 等. 一种快速无功支撑的阻容性逆变器并联控制方法[J]. 中国电机工程学报, 2014, 34(30): 5296-5305.Chen Yandong, Luo An, Chen Zhiyong, et al. A rapid reactive power control method for parallel inverters using resistive-capacitive output impedance[J]. Proceedings of the CSEE, 2014, 34(30): 5296-5305.
[3] Wu Wenhua, Chen Yandong, Luo An, et al. A virtual inertia control strategy for DC microgrids analogized with virtual synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2017, 64(7): 6005-6016.
[4] 方天治, 张先云, 黄淳, 等. 输入串联输出并联LCL型并网逆变器系统的目标多重化控制策略[J].电工技术学报, 2019, 34(6): 1189-1200.Fang Tianzhi, Zhang Xianyun, Huang Chun, et al.Control strategy to reach multiple objectives for input-series output-parallel LCL-type grid-connected inverter system[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1189-1200.
[5] Chen Yandong, Xie Zhiwei, Zhou Leming, et al.Optimized design method for grid-current-feedback active damping to improve dynamic characteristic of LCL-type grid-connected inverter[J]. International Journal of Electrical Power & Energy Systems, 2018,100: 19-28.
[6] 李维波, 徐聪, 许志豪, 等. 基于自适应虚拟阻抗的舰用逆变器并联策略[J]. 高电压技术, 2019,45(8): 2538-2544.Li Weibo, Xu Cong, Xu Zhihao, et al. Inverter parallel control strategy based on variable virtual impedance[J]. High Voltage Engineering, 2019, 45(8):2538-2544.
[7] 陈杰, 刘名凹, 陈新, 等. 基于下垂控制的逆变器无线并联与环流抑制技术[J]. 电工技术学报, 2018,33(7): 1450-1460.Chen Jie, Liu Ming’ao, Chen Xin, et al. Wireless parallel and circulation current reduction of droopcontrolled inverters[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1450-1460.
[8] 朴政国, 户永杰, 郭裕祺. 一种基于并联谐振的高频隔离型并网逆变器[J]. 电工技术学报, 2018,33(2): 322-330.Piao Zhengguo, Hu Yongjie, Guo Yuqi. Highfrequency isolated grid-connected inverter based on parallel resonance[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 322-330.
[9] 严干贵, 常青云, 黄亚峰, 等. 弱电网接入下多光伏逆变器并联运行特性分析[J]. 电网技术, 2014,38(4): 933-940.Yan Gangui, Chang Qingyun, Huang Yafeng, et al.Analysis on parallel operational characteristics of multi photovoltaic inverters connected to weakstructured power system[J]. Power System Technology, 2014, 38(4): 933-940.
[10] Juan L A, Mikel B, Jesus L, et al. Modeling and control of N-paralleled grid-connected inverters with LCL filter coupled due to grid impedance in PV plants[J]. IEEE Transactions on Power Electronics,2011, 26(3-4): 770-785.
[11] 姚骏, 谭义, 杜红彪, 等. 孤岛模式下逆变器并联系统的谐振特性分析及其抑制策略研究[J]. 电工技术学报, 2016, 31(23): 199-210.Yao Jun, Tan Yi, Du Hongbiao, et al. Analysis of resonant characteristics and resonance suppression strategy of inverter parallel system in islanding mode[J]. Transactions of China Electrotechnical Society, 2016, 31(23): 199-210.
[12] 方天治, 黄淳, 陈乃铭, 等. 一种提高弱电网下LCL型并网逆变器鲁棒性的相位超前补偿策略[J].电工技术学报, 2018, 33(20): 4813-4822.Fang Tianzhi, Huang Chun, Chen Naiming, et al. A phase-lead compensation strategy on enhancing robustness of LCL-type grid-tied inverters under weak grid conditions[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4813-4822.
[13] 陈新, 韦徵, 胡雪峰, 等. 三相并网逆变器 LCL滤波器的研究及新型有源阻尼控制[J]. 电工技术学报, 2014, 29(6): 71-79.Chen Xin, Wei Zheng, Hu Xuefeng, et al. Research on LCL filter in three-phase grid-connected inverter and novel active damping control strategy[J]. Transactions of China Electrotechnical Society, 2014, 29(6):71-79.
[14] Martin W, Tobias B, Rodrigo A, et al. Discrete-time active damping of LCL-resonance by proportional capacitor current feedback[J]. IEEE Transactions Industry Applications, 2014, 50(6): 3911-3920.
[15] Liu Huakun, Xie Xiaorong, Li Yu, et al. Mitigation of SSR by embedding subsynchronous notch filters into DFIG converter controllers[J]. IET Generation Transmission & Distribution, 2017, 11(11): 2888-2896.
[16] Mauricio Cespedes, Sun Jian. Mitigation of invertergrid harmonic resonance by narrow-band damping[J].IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(4): 1024-1031.
[17] 曾正, 赵荣祥, 吕志鹏, 等. 光伏并网逆变器的阻抗重塑与谐波谐振抑制[J]. 中国电机工程学报,2014, 34(27): 4547-4558.Zeng Zheng, Zhao Rongxiang, Lü Zhipeng, et al.Impedance reshaping of grid-tied inverters to damp the series and parallel harmonic resonances of photovoltaic systems[J]. Proceedings of the CSEE,2014, 34(27): 4547-4558.
[18] Malinowski M, Bernet S. A simple voltage sensorless active damping scheme for three-phase PWM converters with an LCL filter[J].IEEE Transactions on Industry Electronics, 2008, 55(4): 1876-1880.
[19] 陈东, 张军明, 钱照明. 带LCL滤波器的并网逆变器单电流反馈控制策略[J]. 中国电机工程学报,2013, 33(9): 10-16.Chen Dong, Zhang Junming, Qian Zhaoming. Single current feedback control strategy for grid-connected inverters with LCL filters[J]. Proceedings of the CSEE, 2013, 33(9): 10-16.