0 引言
电压源型逆变器（Voltage-Sourced Inverter,VSI）是可再生能源并网和交直流电网互联的重要接口。随着电力系统中可再生能源接入比例的增加和直流配用电技术的发展，当前依靠同步发电机维持电压与频率稳定的电力系统将变得更依赖于逆变器的控制[1-3]。考虑可靠性的要求，逆变器应具备在孤岛情况下向系统负载提供电源支撑的能力，这对逆变器输出电压的质量提出了更高的要求。
逆变器控制中应用最为广泛的电压电流双环控制，其输出等效为一个带内阻抗的非理想电压源，输出电压随负载电流的变化而波动，逆变器的输出外特性差。为抑制逆变器输出电压的波动，最直接的方法是提高逆变器控制系统的环路增益，但控制性能与系统稳定性相互制约，导致控制效果不尽如人意[4]。
为避免因增大控制增益可能导致的系统失稳问题，使用电流传感器采集负载电流信息进行前馈补偿成为一种简单易行的方法。实际工程中多采用比例前馈补偿的方式[5]，此方法削弱了低频电流对输出电压的影响，但对于中高频谐波电流的抑制效果并不明显。采用比例微分前馈方式理论上可以在整个频域内抑制负载电流的影响[6-8]，但前馈环节引入的附加阻抗特性必须完全拟合原有逆变器输出阻抗特性才能消除负载电流对输出电压的影响。使用传感器采集负载电流信息进行前馈补偿的方法不仅增加了传感器、信号传输和处理电路等成本（尤其是在大功率场合），还占用了处理器的ADC接口资源，其准确度也受传感器和信号处理电路精度的影响。
为节约传感器及其对应信号处理电路等资源，结构简单的扰动观测器（Disturbance Observer,DOB）[9]得以提出用于观测负载电流。文献[10]忽略电流内环的动态特性，将电流内环近似为一个单位增益的理想比例环节，导致其 DOB缺少了电流内环标称模型的设计，模型的精确性不足。文献[11]在 DOB中设计了电流内环的标称模型，但其电流内环受输出电压的影响，电流内环与电压外环存在耦合关系，加大了 DOB的设计难度，增加了控制过程的计算量。文献[12]将负载电流和直流母线电压幅值波动视为系统扰动，将传统 DOB变换为附加型 DOB嵌入单相逆变器的控制之中，简化了各传递函数的计算过程，但与传统 DOB相比，附加型DOB弱化了控制系统设计的二自由度（2 Degree of Freedom, 2 DOF）原则[13]。需要指出的是，文献[12]展示了仿真和实验波形却未给出仿真和实验所用的控制参数，文献[10]直接给出了控制参数却未给出参数选择的过程和理由，而文献[11]中控制参数的选择通过调试的方式完成。现有基于 DOB的逆变器控制方法存在共同的问题：控制参数的确定方法不具备普适性和可移植性。
此外，一些先进的控制算法如提高系统响应速度的无差拍控制（deadbeat control）[14]和抑制周期性干扰的重复控制（repetitive control）[15]等也被用于提高逆变器的性能。但无差拍控制导致系统对参数和负荷的变化敏感，系统的稳定性有所欠缺。而重复控制由于延迟因子的存在，控制效果有限，需要与其他控制相配合才能充分发挥其优点，特别地，文献[16]结合DOB的低频扰动抑制能力强与重复控制的抗周期性干扰能力强的优点，设计了基于内模原理的扰动观测器，在提升逆变器动态性能的同时，有效地提高了输出电压的跟踪精度和波形质量，为DOB性能的改进提供了新的研究思路。
为提高系统的动态和稳态性能，且不引入复杂的控制，本文提出一种易于实现、适合工程应用的基于 DOB的逆变器负载电流前馈控制策略，并给出具备普适性和可移植性的参数设计方法。首先充分利用已采集的输出电压信息，通过电压前馈补偿实现电流内环与电压外环的解耦，简化了传统双环控制的设计和分析。在此基础上，将负载电流设定为系统外部扰动量建立逆变器负载电流扰动观测模型，通过将 DOB观测所得负载电流前馈至电压外环补偿器的输出端，提高了输出电压对负载电流的抗扰动能力，增强了逆变器输出外特性。分析表明，与传统双环控制相比，本文所提控制策略可以使被控对象标称化，从而对参数摄动具备更强的鲁棒性。仿真和实验结果验证了所提控制策略的有效性和所设计系统的鲁棒性。
1 传统电压电流双环控制
1.1 LC滤波型逆变器主电路结构及数学模型
图1为LC滤波型三相逆变器的主电路结构，交流侧输出经 LC滤波器连接至负载 ZL。图中，Lf为滤波电感，Cf为滤波电容，Rf为滤波电感的电阻，ron为IGBT的导通电阻。
图1 逆变器主电路结构
Fig.1 Circuit structure diagram of inverter
对于图1所示逆变器主电路，dq旋转坐标系下的数学模型为
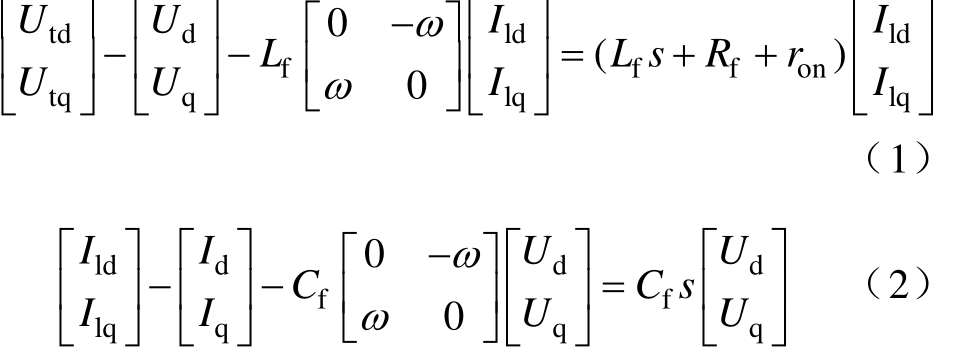
式中，Utd, Utq、Ud, Uq、Ild, Ilq、Id, Iq分别为三相桥输出电压、逆变器输出电压、电感电流、逆变器输出电流的d轴和q轴分量。
1.2 电流内环电压前馈补偿策略
根据式（1），电流内环的解耦控制如图2所示。为消除物理系统中输出电压对电流内环输出的影响，在控制系统电流补偿器的输出端进行电压前馈补偿，加入电压前馈补偿后，解耦的电流内环等效控制框图如图 3所示。其中，kI(s)=kpI+kiI/s为电流内环的PI补偿器，由图3可得电流内环的闭环传递函数为
图2 加入电压前馈补偿的电流控制框图
Fig.2 Current control block diagram with voltage feedforward compensation
图3 电流控制解耦后的等效控制框图
Fig.3 Equivalent control block diagram of current control
1.3 传统电压电流双环控制
将电流内环等效成一个增益为 GcI(s)的控制环节后，根据式（2），可得逆变器的传统双环控制系统如图4所示。当频率较小时，电流环应实现对参考电流的稳定无差跟踪，即GcI(s)≈1，从而可得图5所示解耦后的等效控制系统，其中，kU(s)=kpU+kiU/s为电压外环的PI补偿器。由图5可知，采用传统电压电流双环控制的逆变器，其输出电压不仅取决于电压参考值，也受输出电流的干扰。
图4 传统双环控制框图
Fig.4 Traditional dual loop control block diagram
图5 双环控制解耦后的等效框图
Fig.5 Equivalent block diagram of dual loop control
2 基于DOB的负载电流前馈控制
2.1 DOB的基本原理
适用于本文的前馈型 DOB结构如图 6所示。其中，X(s)为系统输入，Y(s)为系统输出，P(s)为被控对象的实际模型，Pn(s)为被控对象的标称模型，D(s)为系统外部扰动，ξ (s)为噪声干扰，Q(s)为低通滤波器，H(s)为控制系统的PI补偿器。
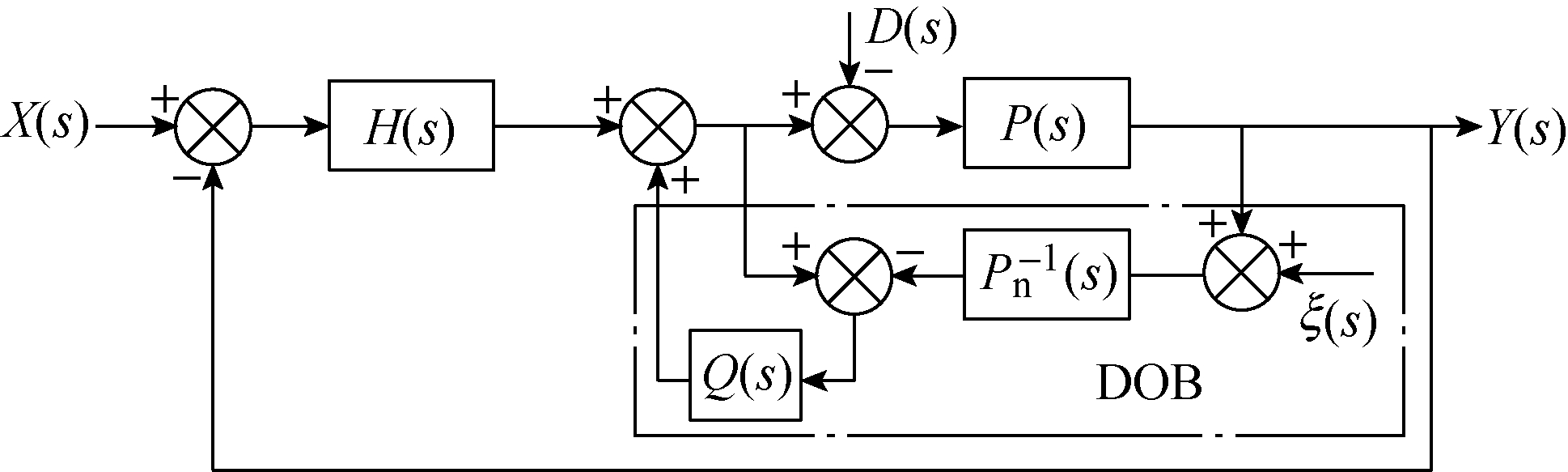
图6 前馈型DOB结构图
Fig.6 DOB with feedforward type
根据图6，DOB未投入时，输出Y(s)的表达式为
其中
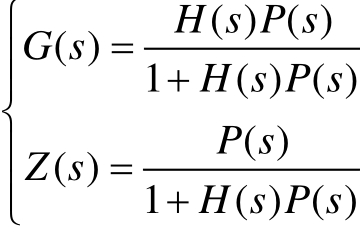
此时系统输出 Y(s)由系统输入 X(s)与系统外部扰动D(s)共同决定，D(s)将影响Y(s)对X(s)的指令跟踪。
DOB投入后，输出Y(s)的表达式为
其中
对于式（5），当Q(s)=1时，系统输出Y(s)关于各输入量的传递函数为
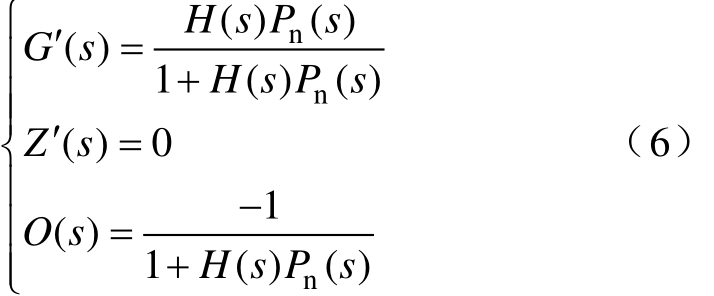
式（6）表明，当 Q(s)=1时，系统扰动 D(s)将不对Y(s)产生影响，并且加入DOB可以使实际被控对象标称化，从而保证系统对参数摄动有较好的鲁棒性。但Q(s)=1将导致系统对噪声干扰敏感，并且由于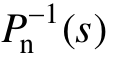 
的引入使DOB失去作用[16]。
当Q(s)=0时，系统输出Y(s)关于各输入量的传递函数为
此时系统的输入输出特性与不加 DOB时一致，Q(s)=0表明高频噪声得到抑制。因此，将Q(s)设计为低通滤波器，即可在消除系统外部低频扰动的同时也抑制高频噪声的干扰。
2.2 低通滤波器的设计要求
2.2.1 滤波器形式要求
对于式（8）所示被控对象，有
低通滤波器Q(s)可设计为
式中，τf为滤波器的时间常数。为保证DOB在物理上的实现，应保证
同时为减小滤波器带来的延时，k j- 的值应尽可能小。
2.2.2 滤波器时间常数设计要求
根据2.1节的分析，为达到引入DOB的期望效果，滤波器时间常数的确定应至少满足下列两个条件：①τf足够小，以保证其截止频率 ω b＞ ωd ，ωd为外部扰动的角频率；②同时τf足够大，以保证其截止频率
为噪声的角频率，ωs为保证控制系统稳定的约束角频率。为保证较好的噪声滤波效果和稳定性，同时抑制外部扰动的影响，可取
2.3 基于DOB的负载电流前馈控制原理
基于图5所示的双环控制系统和图6所示的前馈型 DOB结构，将负载电流视为系统扰动，提出基于 DOB的负载电流前馈控制，如图 7所示。其中，GncI(s)和Cnf分别为电流内环与滤波电容的标称模型。为引入DOB，用电流环输入端的等效扰动电
等效替代负载电流I[11]，If为DOB观测所得扰动电流前馈量。此时被控对象的标称模型为
图7 基于DOB的负载电流前馈控制框图
Fig.7 Block diagram of DOB based load current feedforward control
由式（3）和式（11）可知被控对象为二阶系统，根据2.2节及文献[18]的分析，可选用低通滤波器形式为
对于图 7所示控制系统，不加 DOB时，结合式（4），可得输出电压U的传递函数为
其中
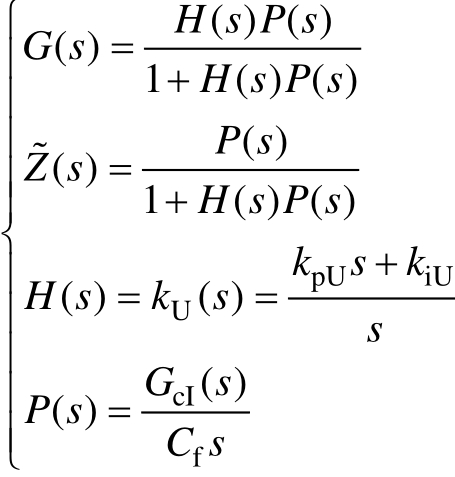
此时逆变器的输出电压U不仅由参考值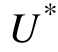
决定，还受到负载电流扰动I~的影响，且U随负载的投切而变化。
加入 DOB后，结合式（5），可得输出电压 U的表达式为
其中
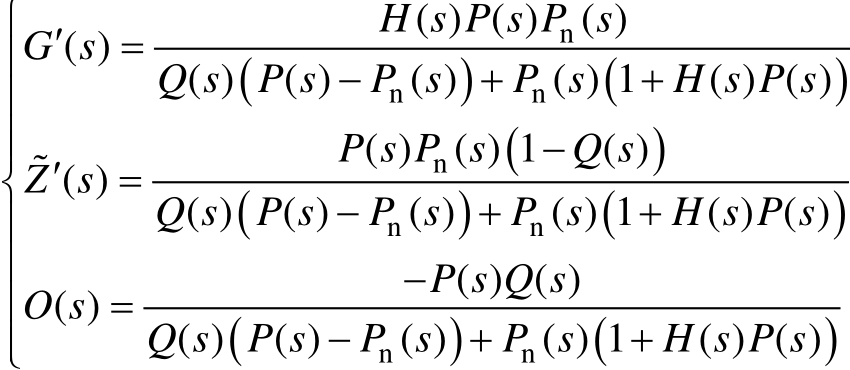
对于式（14），根据2.1节分析可知，若将Q(s)设计为低通滤波器，则上述基于 DOB的负载电流前馈控制可在消除负载电流扰动影响的同时也抑制高频噪声的干扰，使逆变器输出电压U只与参考值U*相关。
3 控制参数设计方法
3.1 电流内环补偿器参数
电流内环补偿器参数的设计应在保证电流准确跟踪的同时提高快速响应能力。由图3可知，电流环的开环传递函数为
观察到开环传递函数的固有极点s=-(Rf+ron)/Lf接近原点，这将导致开环增益的幅值和相位在低频处便开始下降，从而增大电流内环的稳态误差，于是通过设置零点s=-kiI/kpI抵消此极点，即令
此时系统的闭环传递函数变为
式中，τI为电流闭环传递函数的时间常数
由式（16）、式（17）可得电流环补偿器PI参数的设计式为
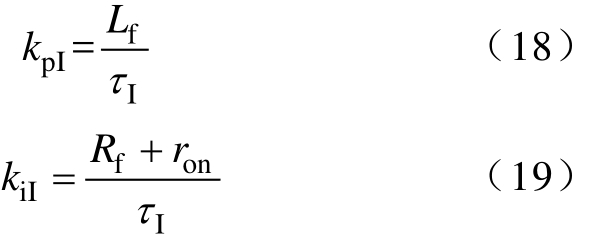
由式（18）和式（19）可知，电流内环补偿器的设计取决于时间常数Iτ，Iτ的取值应足够小以提高电流环的快速响应能力，同时应足够大以保证控制系统的带宽 I1τ远小于逆变器的开关角频率（一般小于开关角频率的1/10）[19]。
3.2 电压外环补偿器参数设计
电压外环补偿器参数的设计应在实现电压准确跟踪的同时保证控制系统有足够的稳定裕度。对于图7所示控制系统，假设前馈电流If能实现对电流扰动I~的跟踪，则系统的开环传递函数为
对于此开环传递函数有两个零极点、一个实极点的三阶系统，使用“对称优化法（symmetrical optimum）”[20]计算对应的相位裕度γ和剪切频率cω，有
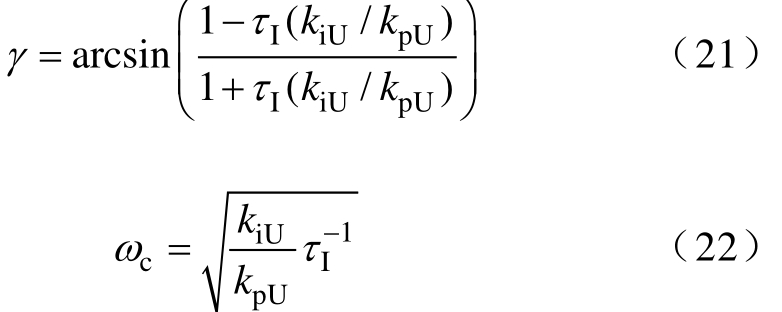
式（20）需要满足
即满足 k pU =Cfωc 。再结合式（21）和式（22）可得电压外环PI参数为
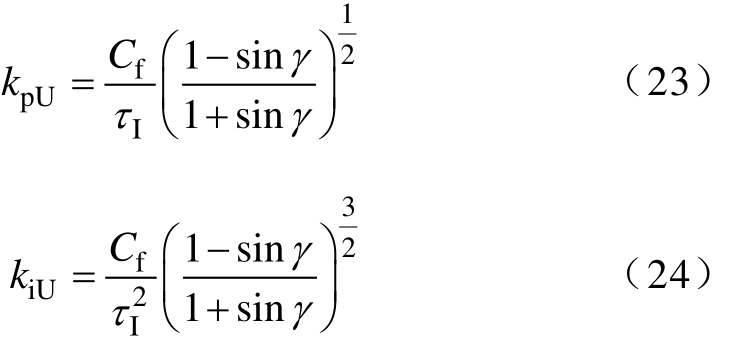
由式（23）和式（24）可知，电压外环补偿器参数的设计取决于控制系统相位裕度γ的选择，为保证控制系统的稳定性，γ应控制在4050°°～ 。
3.3 滤波器时间常数设计
对于式（12）所示二阶滤波器，其截止频率为
代入式（10），可得τf的取值范围为
本文将负载电流视为系统扰动，稳态时在 dq旋转坐标系下的角频率ωd=0；为避免DOB的引入对双环控制系统的稳定性造成影响，应取 ω s =ωc，从而保证加入 DOB后的前馈控制系统仍具备与双环控制系统近似的剪切频率及相位裕度；对于zω，由于噪声干扰的不确定性及复杂性，在参数计算阶段暂不考虑噪声的干扰，而是在仿真和实验阶段根据仿真及实验现象对τf进行调试，具体调试方法见第5节的仿真与实验部分。此外，在满足式（26）的前提下，τf的取值应尽可能小，以保证DOB在负载突变时对负载电流的快速跟踪，改善系统的动态特性。
3.4 系统稳定性分析
仿真和实验所用电路参数及根据3.1～3.3节所提参数设计方法计算所得的控制参数见表1。
根据表 1所示参数，画出滤波器时间常数τf取不同值时电压开环传递函数的伯德图，如图8所示。由图8可知，与未加DOB时相比，加入DOB后低频段的开环增益变大，说明低频段的电压跟踪能力更强，稳态跟踪误差更小；高频段的曲线重合，其特性相同，与 2.1节的理论分析一致。同时，由伯德图可证实，本文取滤波器时间常数τf =5ms
并不会减小控制系统的稳定裕度，这也表明所提滤波器时间常数设计方法的可行性。
表1 系统参数设置
Tab.1 System parameters
参 数 数 值直流侧电压Udc/V 800输出电压幅值指令U*/V 311输出电压频率指令f */Hz 50 IGBT导通电阻ron/mΩ 10滤波电感电阻Rf/mΩ 68.25滤波电感Lf/mH 0.54滤波电容 Cf/μF 9开关频率fs/kHz 10负载/Ω 50电流闭环时间常数τI/ms 0.2电流环比例系数kpI 2.7电流环积分系数kiI 391.25双环控制相位裕度γ /(°) 45电压开环剪切频率ωc/(rad/s) 2 066.7电压环比例系数kpU 0.018 6电压环积分系数kiU 15.99滤波器时间常数τf/ms 5
图8 电压开环传递函数伯德图
Fig.8 Bode plot of opened-loop voltage transfer function
同理可以画出图9所示负载电流扰动闭环传递函数的幅频特性伯德图，加入 DOB后，低频段的闭环幅频增益非常小且明显小于未加入 DOB时的闭环幅频增益，说明所提参数设计方法可有效抑制负载电流扰动的干扰；且滤波器时间常数τf越小，负载电流对输出电压的影响越小，所以在满足系统稳定和噪声抑制的前提下，可选择尽量小的τf。
图9 负载电流闭环传递函数伯德图
Fig.9 Bode plot of closed-loop load current transfer function
4 鲁棒性分析
当系统受到外部干扰和参数摄动的影响时，被控对象的实际模型可以用标称模型的乘性摄动形式描述为
式中，ΔP(s) 为未知摄动。假设ΔP(s)是稳定的，并且其上限已知，则根据小增益定理，系统鲁棒稳定的充分条件[21]为
式中，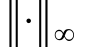
为H∞范数； K ( s)为控制器的传递函数。对于图7所示系统，有
由于未知摄动ΔP(s)难以确定，且电流扰动作用于电压外环，其主要受滤波电容参数Cf摄动的影响，所以对于鲁棒性的分析，可以分别求出基于DOB的前馈控制与传统双环控制的传递函数对电容参数Cf摄动的灵敏度，然后根据灵敏度的大小关系，判断其鲁棒性的强弱[22]。
4.1 灵敏度分析
逆变器的输出电压主要取决于参考电压输入以及负载电流扰动，输出电压对Cf的灵敏度可转化为输出电压关于参考电压的传递函数和关于扰动电流的传递函数对Cf的灵敏度问题。
4.1.1 G(s)对Cf的灵敏度
不加 DOB时，输出电压关于参考电压的传递函数G(s)关于Cf的对数灵敏度为
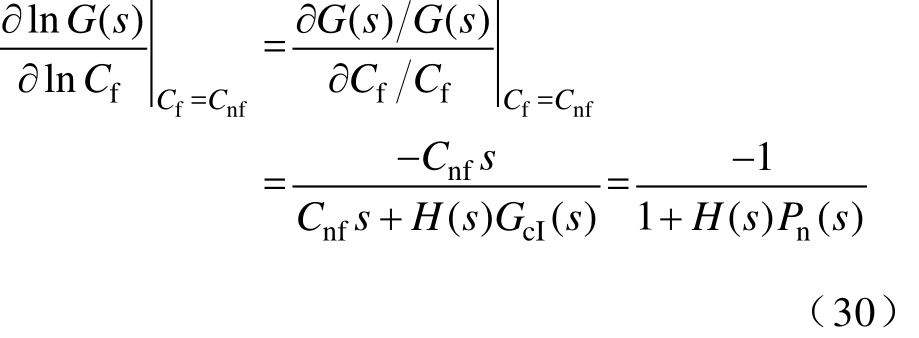
加入DOB后，()G s′关于Cf的对数灵敏度为
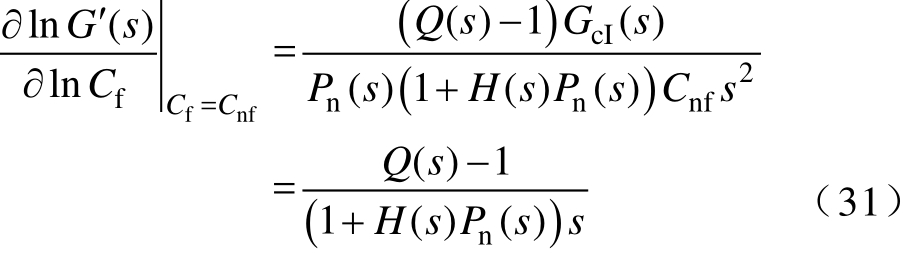
4.1.2 Z(s)对 Cf的灵敏度
不加 DOB时，输出电压关于扰动电流的传递函数Z(s)关于Cf的对数灵敏度为
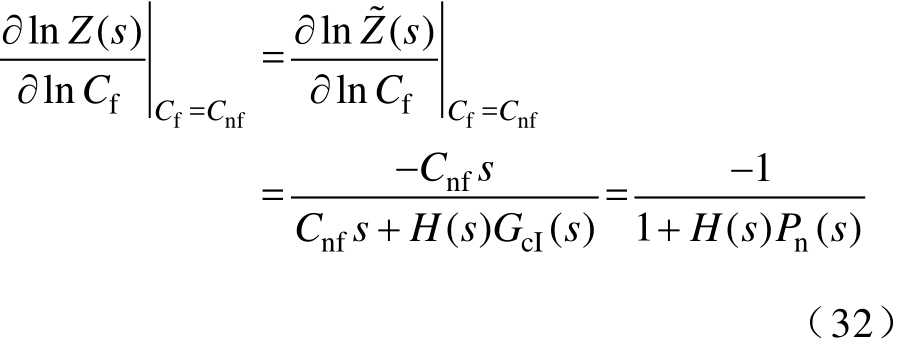
加入DOB后，Z(s)′关于Cf的对数灵敏度为
4.1.3 灵敏度对比分析
对比式（30）与式（32）、式（31）与式（33）可知，不加DOB时输出电压对 Cf的灵敏度可用式（30）或式（32）表示，加入 DOB后输出电压对Cf的灵敏度可用式（31）或式（33）表示。将表 1中的参数代入式（30）与式（31），画出不加 DOB以及加入DOB后输出电压对Cf摄动灵敏度的伯德图，如图10所示。由图10可知，在整个频段内，加入DOB后输出电压对于Cf灵敏度的幅频增益明显低于不加DOB时输出电压对于Cf灵敏度的幅频增益，表明加入DOB后输出电压受Cf参数摄动的影响较小，基于 DOB的前馈控制鲁棒性更强，与2.1节的分析相符。
图10 输出电压对Cf的灵敏度的伯德图
Fig.10 Bode plot of the sensitivity of the output voltage to Cf
4.2 电容参数摄动时系统稳定性分析
为进一步分析所提前馈控制方法在电容参数摄动时系统的稳定性问题，绘出电容参数摄动时电压闭环传递函数()G s′的根轨迹，如图11所示。由图11可知，当电容参数Cf在(0.2～2.0)Cnf范围内摄动时，系统的极点始终位于左半s平面，系统的鲁棒稳定性强。
图11 Cf摄动时系统的根轨迹图
Fig.11 Root locus of the system when the Cf is perturbed
5 仿真与实验
5.1 仿真分析
使用PSCAD/EMTDC对所提基于DOB的负载电流前馈控制方法的有效性和鲁棒性进行验证。系统参数设置见表1，仿真过程如下：逆变器首先空载运行，0.2s时投入负载，0.35s时切除负载。
5.1.1 所提控制策略的有效性验证
1）稳态性能分析
图 12、图 13分别为采用传统控制策略和采用本文所提前馈控制策略的仿真波形。观察图12，采用传统电压电流双环控制方法，当0.2s负载投入时电压峰值下降至290V左右，而在0.35s负载切除后电压恢复至 311V，输出电压受负载电流的影响较大。图13中，采用本文所提控制策略的逆变器，在负载投切过程中DOB观测所得前馈扰动电流ifa可以迅速地跟踪负载电流ia的变化，从而补偿负载电流导致的输出电压偏移，使稳态输出电压峰值维持在311V。仿真波形表明，采用本文所提前馈控制策略，可以减小因负载投切带来的输出电压偏移，系统的稳态性能更好。为了进一步对比分析逆变器的稳态性能，在PSCAD中使用快速傅里叶变换（Fast Fourier Transformation, FFT）元件及方均根值（Root Meam Square, RMS）元件分析稳态输出电压的总谐波畸变率（Total Hormonic Distortion, THD）和跟踪误差（e(RMS)）[16]，其结果见表2。
图12 传统双环控制仿真波形
Fig.12 Simulation waveforms of traditional dual loop control
图13 本文所提前馈控制仿真波形
Fig.13 Simulation waveforms of proposed feedforward control
表2 逆变器稳态性能的仿真对比
Tab.2 Simulation results of steady-state performance of inverter
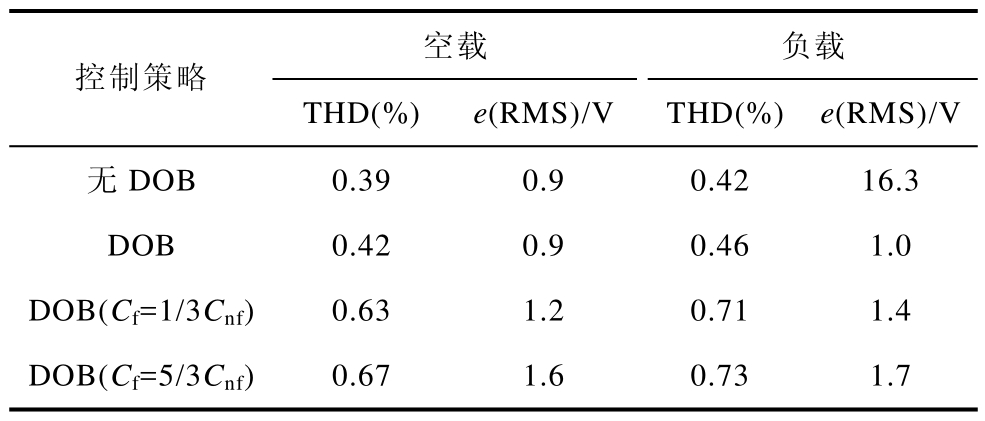
空载 负载控制策略THD(%) e(RMS)/V THD(%) e(RMS)/V无DOB 0.39 0.9 0.42 16.3 DOB 0.42 0.9 0.46 1.0 DOB(Cf=1/3Cnf) 0.63 1.2 0.71 1.4 DOB(Cf=5/3Cnf) 0.67 1.6 0.73 1.7
由表2可知，负载情况下，本文所提基于DOB的控制策略可以将电压的 e(RMS)由 16.3V降至1.0V，显著地提高了逆变器的稳态特性，而且本文所提方法通过选取合适的τf并不会过多地增加输出电压的THD。事实上，由于DOB在观测负载电流时不可避免地引入了噪声干扰，其THD会稍大于无DOB的控制方法，但仿真中可以通过观察前馈扰动电流ifa的波形情况逐步增大τf至ifa波形良好，即若取τf =5ms时，DOB观测所得扰动电流ifa波形畸变或毛刺过多，说明观测噪声对ifa产生了较大影响，此时可逐步增大τf至消除观测噪声的干扰，得到良好的扰动电流ifa波形，从而抑制噪声干扰对电压波形畸变的影响。
2）暂态性能分析
在 dq坐标系下观察负载投切时输出电压的动态变化过程，对比图12b与图13b发现，采用本文所提控制策略后，投入负载时电压波动的过调量由11V降低至 6V，到达第二个波动峰值的时间由0.001s缩短至0.000 75s。同样，切除负载时电压波动的过调量也由 11V降低至 6V，到达第二个波动谷值的时间由0.001s缩短至0.000 75s。仿真波形表明，采用本文所提前馈控制策略，能明显抑制负载投切过程中的电压波动，缩小电压波动的恢复时间，输出电压的暂态性能更好。理论上，若ifa能实现对ia的即时无差跟踪，则负载的投切将不再导致输出电压的波动，但DOB中滤波器的引入导致 ifa对ia的跟踪存在延时，从而使得本文所提控制策略虽能抑制电压波动，但不能完全消除电压波动。
5.1.2 所提控制策略的鲁棒性验证
对所提前馈控制系统，在电容参数分别摄动至1/3Cnf（3μF）及 5/3Cnf（15μF）时仿真研究其鲁棒稳定性。图14与图15所示仿真结果表明，电容参数摄动会导致DOB观测所得电流ifa对负载电流 ia的跟踪存在偏差，但66.67%的参数摄动不会导致系统的失稳，与4.2节的理论分析结果相符。
图14 Cf =1/3Cnf时所提前馈控制仿真波形
Fig.14 Simulation waveforms of proposed feedforward control when Cf =1/3Cnf
图15 Cf =5/3Cnf时所提前馈控制仿真波形
Fig.15 Simulation waveforms of proposed feedforward control when Cf=5/3Cnf
5.2 实验验证
以TI公司TMS320F28335为核心处理器，搭建图 16所示的实验平台对所提控制策略进行物理实验验证，实验参数见表 1。物理实验过程如下：逆变器首先空载运行，在电压达到某一峰值附近时刻投入负载，然后在电压达到另一峰值附近时刻切除负载。
图16 基于TMS320F28335的逆变器实验平台
Fig.16 Experimental platform based on TMS320F28335
5.2.1 所提控制策略的有效性验证
1）稳态性能分析
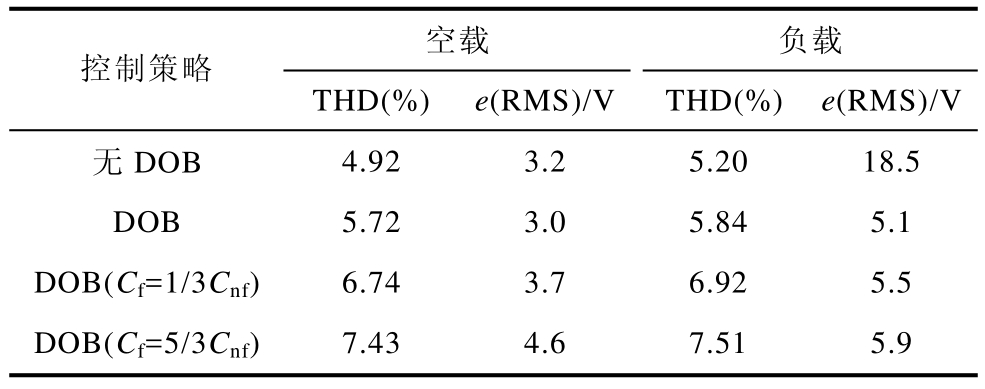
图 17、图 18分别为采用传统控制策略和采用本文所提前馈控制策略的实验波形。观察图17a与图 17c，采用传统控制策略，输出电压随负载投切而偏移，电能质量差。图18中，利用DSP的DAC接口输出前馈扰动电流ifa信号并使用示波器进行显示。观察图18a、图18c可知，前馈电流ifa实现了对负载电流ia的跟踪，从而减小负载电流导致的输出电压偏差，使逆变器在带载情况下保持稳态输出电压峰值为 311V左右。利用示波器导出实验波形数据后，在 Matlab中对稳态输出电压的 THD和e(RMS)进行计算，其结果见表3。
图17 传统双环控制实验波形
Fig.17 Experimental waveforms of traditional dual loop control
图18 本文所提前馈控制实验波形
Fig.18 Experimental waveforms of proposed feedforward control
表3 逆变器稳态性能的实验对比
Tab.3 Experiment results of steady-state performance of inverter
空载 负载控制策略 THD(%) e(RMS)/V THD(%) e(RMS)/V无DOB 4.92 3.2 5.20 18.5 DOB 5.72 3.0 5.84 5.1 DOB(Cf=1/3Cnf) 6.74 3.7 6.92 5.5 DOB(Cf=5/3Cnf) 7.43 4.6 7.51 5.9
观察表3数据，负载情况下，本文所提策略将电压的 e(RMS)由 18.5V降至 5.1V，验证了本方法在提高逆变器稳态特性方面的有效性。由于硬件实验中噪声以及传感器精度的影响，实验电压波形的THD相比于仿真波形电压的THD较高，但对比实验中各控制方法下的THD，本文所提方法在大幅提升电压跟踪精度的情况下并未过多地增加输出电压的畸变率。且实验过程中同样可以通过对τf的调试降低观测噪声对负载电流扰动观测的影响。
2）暂态性能分析
为更好地对比输出电压的动态变化过程，放大观察负载投切时的波形。对比图17b与图18b、17d与图18d可见，使用本文所提电流前馈控制方法，因负载投切导致的输出电压波动更小、电压波形的正弦度更好，即采用本文所提基于 DOB的负载电流前馈控制方法，可以抑制负载投切过程中的电压突变，改善输出电压的暂态性能。
5.2.2 所提控制策略的鲁棒性验证
同样，在电容参数分别摄动至1/3Cnf（3μF）及5/3Cnf（15μF）时实验观察所提前馈控制系统的鲁棒稳定性，实验波形如图19所示。图19所示实验结果表明，电容参数摄动即使达到66.67%也不会导致逆变器系统失稳，所提控制策略的鲁棒性强。
图19 Cf摄动时所提前馈控制实验波形
Fig.19 Experimental waveforms of proposed feedforward control when Cf is perturbed
6 结论
本文结合传统双环控制和扰动观测器的特点，在不增加额外投资的情况下提出了一种设计简单，适合工程应用的负载电流前馈控制策略。仿真与实验结果证明该方法具有以下优点：
1）具备普适性和可移植性，推导所得控制参数的计算公式适用于任意三相桥式逆变器，有助于推动DOB技术在逆变器中的产业化应用。
2）大幅减小逆变器输出电压的跟踪误差，使逆变器在不同带载情况下具备跟踪输出电压为给定指令值的能力。
3）改善逆变器输出电压的暂态性能，有效抑制因负载突变带来的电压波动问题，提升电压波动的恢复速度。
4）增强系统的鲁棒稳定性，在滤波电容参数摄动66.67%时逆变器仍能维持稳定运行。
[1] Quintero J, Vittal V, Heydt G T, et al. The impact of increased penetration of converter control-based generators on power system modes of oscillation[J].IEEE Transactions on Power Systems, 2014, 29(5):2248-2256.
[2] 易文飞, 张艺伟, 曾博, 等. 多形态激励型需求侧响应协同平衡可再生能源波动的鲁棒优化配置[J].电工技术学报, 2018, 33(23): 5541-5554.Yi Wenfei, Zhang Yiwei, Zeng Bo, et al. Robust optimization allocation for multi-type incentivebased demand response collaboration to balance renewable energy fluctuations[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5541-5554.
[3] 贺悝, 李勇, 曹一家, 等. 考虑分布式储能参与的直流配电网电压柔性控制策略[J]. 电工技术学报,2017, 32(10): 101-110.He Li, Li Yong, Cao Yijia, et al. Flexible voltage control strategy of DC distribution network considering distributed energy storage[J]. Transactions of China Electrotechnical Society, 2017, 32(10):101-110.
[4] Liserre M, Teodorescu R, Blaabjerg F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values[J]. IEEE Transactions on Power Electronics, 2006, 21(1):263-272.
[5] 方天治, 阮新波, 肖岚, 等. 一种改进的分布式逆变器并联控制策略[J]. 中国电机工程学报, 2008，28(33): 30-36.Fang Tianzhi, Ruan Xinbo, Xiao Lan, et al. An improved distributed control strategy of parallel inverters[J]. Proceedings of the CSEE, 2008, 28(33):30-36.
[6] Li Weiwei, Ruan Xinbo, Pan Donghua, et al. Fullfeedforward schemes of grid voltages for a three-phase, LCL-type grid-connected inverter[J].IEEE Transactions on Industrial Electronics, 2013,60(6): 2237-2250.
[7] Qi Yu, Peng Li, Huang Zeyi, et al. Feedforward control of output current for three-phase voltage source inverter (VSI) with transformer[C]//IEEE Applied Power Electronics Conference & Exposition,Fort Worth, TX, 2014: 2318-2322.
[8] 尹球洋, 王学华, 徐林. 一种实用前馈在逆变器带非线性负载中的应用[J]. 电力电子技术, 2018,52(7): 1-6.Yin Qiuyang, Wang Xuehua, Xu Lin. A practical feedforward for inverters with nonlinear loads[J].Power Electronics, 2018, 52(7): 1-6.
[9] Chen Wenhua, Yang Jun, Guo Lei, et al. Disturbanceobserver-based control and related methods-an overview[J]. IEEE Transactions on Industrial Electronics, 2016, 63(2): 1083-1095.
[10] Unan S, Gorgun H, Bakan F. Disturbance observer based control of three phase UPS inverter[C]//IEEE Control & Automation, Marraketh, 2010: 321-326.
[11] Lou Guannan, Gu Wei, Wang Jianjun, et al. A unified control scheme based on a disturbance observer for seamless transition operation of inverter-interfaced distributed generation[J]. IEEE Transactions on Smart Grid, 2017, 9(5): 5444-5454.
[12] 程丽敏, 李兴源. 基于扰动观测器的电压源型逆变器控制[J]. 电工技术学报, 2011, 26(8): 113-118.Cheng Limin, Li Xingyuan. Disturbance observer based PWM inverter control[J]. Transactions of China Electrotechnical Society, 2011, 26(8): 113- 118.
[13] Zhong Qingchang, Normey-Rico J E. Control of integral processes with dead-time. 1. disturbance observer-based 2 DOF control scheme[J]. IEE Proceedings-Control Theory and Applications, 2002,149(4): 285-290.
[14] Kawabata T, Miyashita T, Yamamoto Y. Dead beat control of three phase PWM inverter[J]. IEEE Transactions on Power Electronics, 1990, 5(1):21-28.
[15] Li Ming, Li Wenjuan, Liu Cheng, et al. Comparison of two repetitive control strategies of UPS inverter on saber[C]//IEEE International Forum on Strategic Technology, Harbin, China, 2011: 575-579.
[16] Wu Yuheng, Ye Yongqiang. Internal model based disturbance observer with application to CVCF PWM inverter[J]. IEEE Transactions on Industrial Electronics, 2017, 65(7): 5743-5753.
[17] Joo Y, Park G, Back J, et al. Embedding internal model in disturbance observer with robust stability[J].IEEE Transactions on Automatic Control, 2016,61(10): 3128-3133.
[18] Choi Y J, Yang K J, Chung W K, et al. On the robustness and performance of disturbance observers for second-order systems[J]. IEEE Transactions on Automatic Control, 2003, 48(2): 315-320.
[19] Yazdani A, Iravani R. Voltage-sourced converters in power systems: modeling, control, and applications[M]. New Jersey: IEEE Press/John Wiley, 2010:219-223.
[20] Vukosavic S N. Digital control of electrical drives[M].Boston: Springer Science Business Media, 2007:89-95.
[21] Ogata K. Modern control engineering[M]. New Jersey: Publishing House of Elec, 2011: 612-620.
[22] 李春鹏, 贲洪奇, 刘博, 等. 采用扰动观测器的偏差解耦控制方法[J]. 中国电机工程学报, 2015,35(22): 5859-5868.Li Chunpeng, Ben Hongqi, Liu Bo, et al. Deviation decouple control method based on disturbance observer[J]. Proceedings of the CSEE, 2015, 35(22):5859-5868.