0 引言
近年来，随着光伏、风能等新能源发电的普及以及电动汽车（Electrical Vehicle, EV）、不间断电源（Uninterruptable Power Supply, UPS）和LED等直流用电设备在生活领域和工商业领域的广泛应用[1-3]，基于现代电力电子技术的直流配电系统得到广泛关注。在解决新能源发电与直流负荷的接口问题上，直流配电系统无需额外的 DC-AC变换器，可以更高效地实现直流电能传输与电压转换。同时，相比于交流配电系统，直流配电系统不需要考虑频率与无功功率，因而具有控制简单的优点[4-6]。
在直流配电系统中，需要以隔离双向 DC-DC变换器（Isolated Bidirectional DC-DC Converter,IBDC）作为核心部件的固态变压器（Solid-State Transformer, SST）来控制功率流动，调节直流母线电压[7-10]。研究表明，在众多的 IBDC拓扑中，双有源桥（Dual Active Bridge, DAB）变换器因其控制简单、电气隔离、功率密度高和易于实现软开关等优点，具有较高的研究价值[8,11]。典型的DAB的拓扑结构如图1所示，它由高频变压器，一次、二次侧支撑电容C1和C2，电感L（外接电感加变压器漏感）和一次、二次侧的桥式电路H1、H2组成。其中，高频变压器电压比为k∶1。DAB作为功率传输的重要单元，其功率转换效率是直流配电系统的关键问题之一，因此采用合适的控制策略，建立准确的模型，以保障对控制变量进行准确便利的选取，对实现变换器的高效运行具有重要意义。
图1 DAB拓扑结构
Fig.1 Topology of DAB
目前 DAB主要采用移相控制策略，移相控制策略中，功率传输的灵活性与控制复杂程度息息相关，一般来说，随着控制自由度的增加，传输功率的调节更加灵活但控制复杂程度增大。文献[12]对DAB采用各种移相控制传输功率灵活性进行了比较，其中扩展移相控制虽然只拥有H1、H2桥间的外移相角和H1桥自身的内移相角两个控制自由度，控制简单却具有较高的传输功率灵活度。文献[13]详细分析了采用扩展移相控制（Extended Phase Shift,EPS）控制DAB的工作原理，并通过理论与实验验证了在相同传输功率下，EPS控制能够选取不同的运行点始终保证比传统移相控制的回流功率要小，但是并未涉及移相角与 DAB回流功率或电流应力特性之间的关系分析。文献[14]在文献[12]的基础上进一步开展的研究工作表明，多自由度情况下移相角的选取会更加灵活且复杂，同时指出在不同电压转换比时，DAB功率传输效率与控制效果不同，实际工程中应考虑变换器的电压转换比。为了提高DAB效率，文献[15-16]研究了从回流功率优化角度的控制策略。文献[17-19]基于电流应力优化提出了相应的控制策略，上述控制策略仅从 DAB单一特性的角度进行优化，公式推导过程也较为复杂。文献[20]提到在某些工况下减小电流应力的同时回流功率会增大，而现有文献并未针对移相角与回流功率和电流应力特性的相互作用关系进行详细分析。
针对上述问题，本文提出一种 DAB采用 EPS控制下的移相角优化选取与分析方法，对 DAB的两个移相角进行优化选取，利用优化选取的移相角对传输功率建模，可以简化对传输功率的分析过程与移相角的计算选取。同时为了提高DAB的效率，详细分析优化选取的移相角、输入输出电压的电压比与回流功率和电流应力特性的关系，进一步明确更优的移相角范围，提供移相角的计算与选取步骤，最后通过仿真和实验验证理论分析的正确性。
1 基于新移相角的DAB传输功率模型
假定功率由 V1传递至 V2侧为正向功率传输，由于 DAB的功率双向流动特性及自身结构的对称性，为了简化分析，以 V1＞kV2、正向功率传递为例，根据H1、H2桥间的移相角大小不同，采用EPS控制的DAB具有如图2所示的两种典型工作波形。其中，T为半个开关周期，器件开关频率f =1/(2T)，vH1为桥 H1交流侧电压，vH2为折算到一次侧的 H2交流侧电压，vL和iL分别为电感两端电压和电感电流。图2中，当H1桥交流侧电压vH1与电感电流方向相反时，会出现功率流回到输入侧的现象，如图2中阴影部分所示，文献[13]定义该部分功率为回流功率。实际上当DAB工作于图2b所示的状态时，两个移相角选取条件苛刻，电流应力较大，且当H1桥的内移相角较小时，回流功率大，变换器效率低，在实际应用中较少涉及。因此从实用角度出发，本文的后续章节将围绕图2a所示工作状态进行分析。若基于同样的思路对图2b的工作情况进行分析，过程类似，本文不再进行推导。
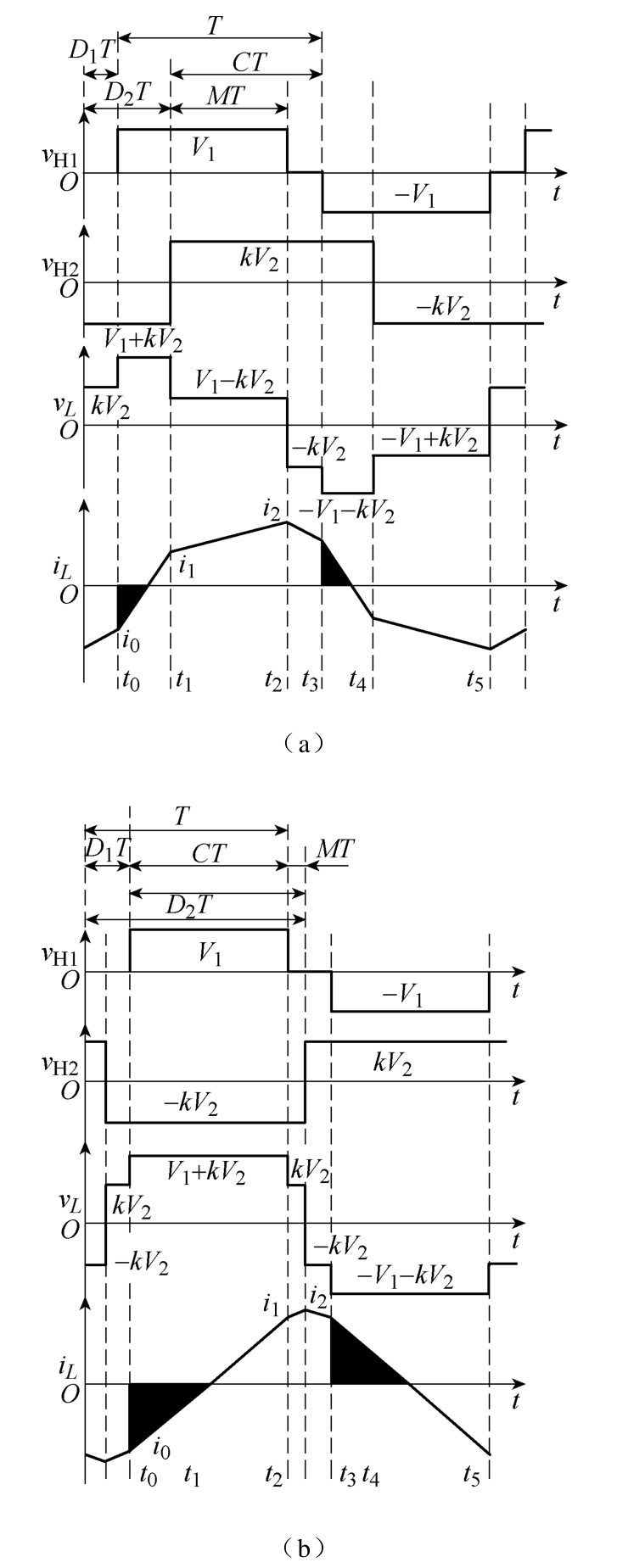
图2 EPS控制DAB主要波形
Fig.2 Crucial waveforms of DAB in EPS control
1.1 传输功率模型
不同于现有文献中通过两个移相角对 DAB的稳态特性进行分析，如图2a中D1T和D2T所示，本文定义电感两端电压为±(V1-kV2)的时间为 MT，电压为±(V1-kV2)和±kV2的时间之和为 CT，如图 2a所示，则其中C的取值范围为[0, 1]，M的取值范围为[0, C]。
以电感两端电压为 V1+kV2时刻为起始点进行分析，根据 DAB半个周期中不同时间段电感两端电压特性及其对称工作的特点，可以列写下述方程
解式（1）～式（3），可得
式中，n为实际输入电压与输出电压折算到变压器一次电压的比值，n=V1/(kV2)。电流应力imax=i2。定义 P为变换器在一个开关周期中内的平均功率，则有
而依据现有文献分析方法[13]，传输功率表达式为
式中，D1为桥 H1的内移相角；D2为桥 H1与 H2间的外移相角，且有0≤D1≤D2≤1。
由式（8）可以看到，通过D1和D2所建立的传输功率表达式具有较强的耦合性，在利用移相角分析传输功率特性与参数选取时复杂度较大。而由式（7）可以看到，通过参数M和C所建立的传输功率表达式中只具有关于两参数各自的表达项，即M(1-M)与C(1-C)两项，而不存在类似于式（8）中所存在的两参数乘积项D1D2，极大地减小了参数耦合度。
在不考虑参数范围时，从数学角度分析，式（7）中M(1-M)与C(1-C)两项皆为关于对称轴为0.5、开口向下的一元二次函数，在参数小于 0.5时，表达式的最终值随参数的增大而增大；参数大于0.5时，表达式的最终值随参数的增大而减小。若根据该特性将参数范围划分为三个区域：①C, M∈[0, 0.5)、M≤C；②C, M∈[0.5, 1.0]、M≤C；③C∈[0.5, 1.0]、M∈[0, 0.5]，从数学原理上可知，三个区域的传输功率范围相同。在此基础上研究不同区域DAB的相关特性，即传输功率控制的灵活度、回流功率与电流应力特性等，可以更简明清晰地反映移相角对DAB特性的影响，为移相角的选取提供更明确的范围。
1.2 传输功率特性
以 SPS控制时最大传输功率值 PN=kV1V2/(8fL)为传输功率基准值，将传输功率表达式（7）标幺化得到
图3 标幺化传输功率
Fig.3 Standard transmission power diagram
将标幺化传输功率表达式（9）通过三维曲线表示如图3a所示。为了便于观察比较，将三维图分割为三个子区间并转化为2D图，分别如图3b～图3d所示，传输功率为图中阴影部分。其中图3b对应移相角参数区间为C, M∈[0, 0.5)、M≤C；图3c对应参数区间为C, M∈[0.5, 1.0]、M≤C；图3d对应参数区间为C∈[0.5, 1.0]、M∈[0, 0.5]。
从图3中可以看到，三个区域的传输功率范围都相同，且与SPS控制相比未发生变化。以阴影区域面积的大小表示传输功率控制的灵活度，阴影区面积大表示控制的灵活度高，则在 C∈[0.5, 1.0]、M∈[0, 0.5]区间控制的灵活度最高，C, M∈[0, 0.5)、M≤C与C, M∈[0.5, 1.0]、M≤C两个区间控制灵活度相同且灵活度较小。
2 基于新移相角的DAB特性分析
由第1节的分析可知，采用分区域分析传输功率特性时，三个区域的传输功率范围都相同且 C∈[0.5, 1.0]、M∈[0, 0.5]区间控制的灵活度最高。然而满足传输功率只是最基本的要求，在保证传输功率的前提下 DAB还应具备较高的效率。回流功率与电流应力作为衡量 DAB性能的两个重要指标，它们的特性与移相角的选取息息相关，本节将分区域分析回流功率和电流应力特性与移相角的关系。
2.1 电流应力特性
电流应力的大小很大程度上影响了器件的选型与成本。由式（6）可知，EPS控制电流应力 imax的特性不仅与M和C有关，还与电压转换比n的取值范围有关。为了简化分析，根据式（6）构建电流应力辅助函数，有
在实际应用中，通常n的取值是固定的，当1≤n＜2和 n≥2时，根据式（10）可知，电流应力的特性与M的关系是不同的。分别取n=1.5和n=2.5为例，绘制电流应力辅助函数三维图分别如图 4a和图5a所示。同样为了便于观察比较，将1≤n＜2和n≥2的三维图分割为三个子区间并转化为2D图，分别如图 4b～图 4d和图 5b～图 5d所示。其中图4b和图5b中移相角参数区间C, M∈[0, 0.5)、M≤C；图4c和图5c中区间为C, M∈[0.5, 1.0]、M≤C；图4d和图5d中区间C∈[0.5, 1.0]、M∈[0, 0.5]。
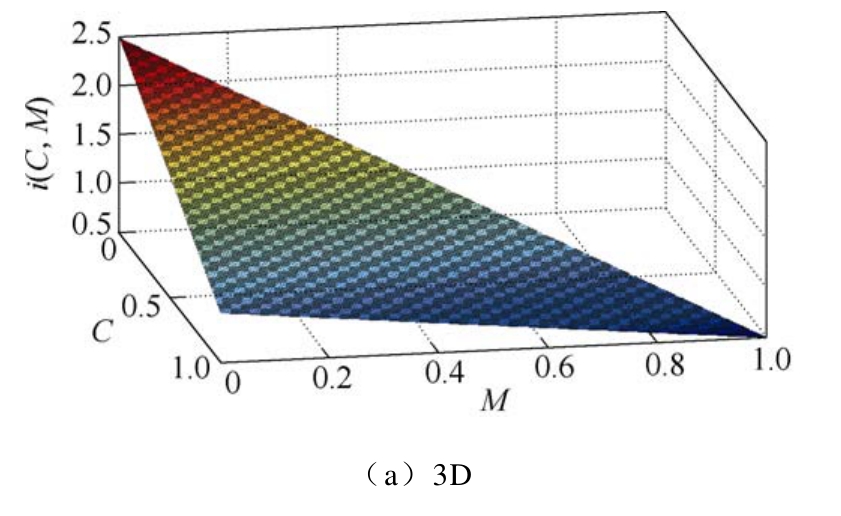
图4 1≤n＜2时电流应力特性
Fig.4 Current stress when 1≤n＜2
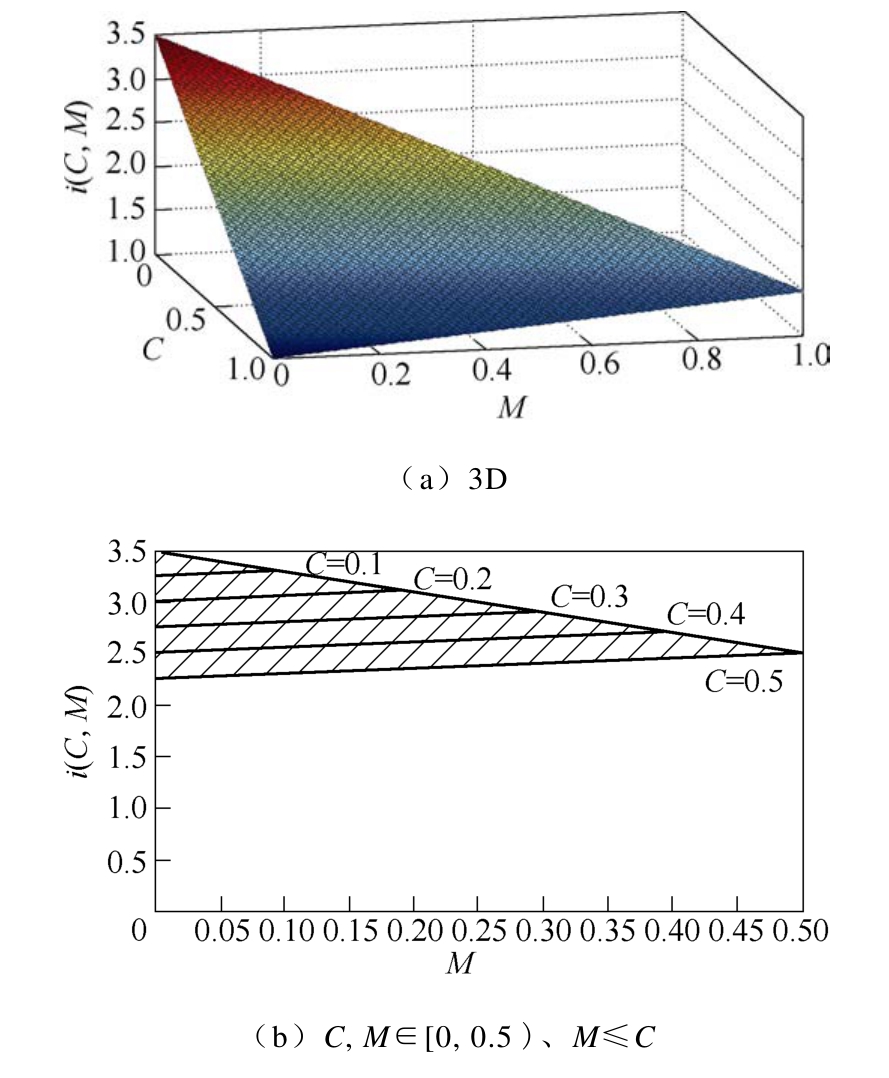
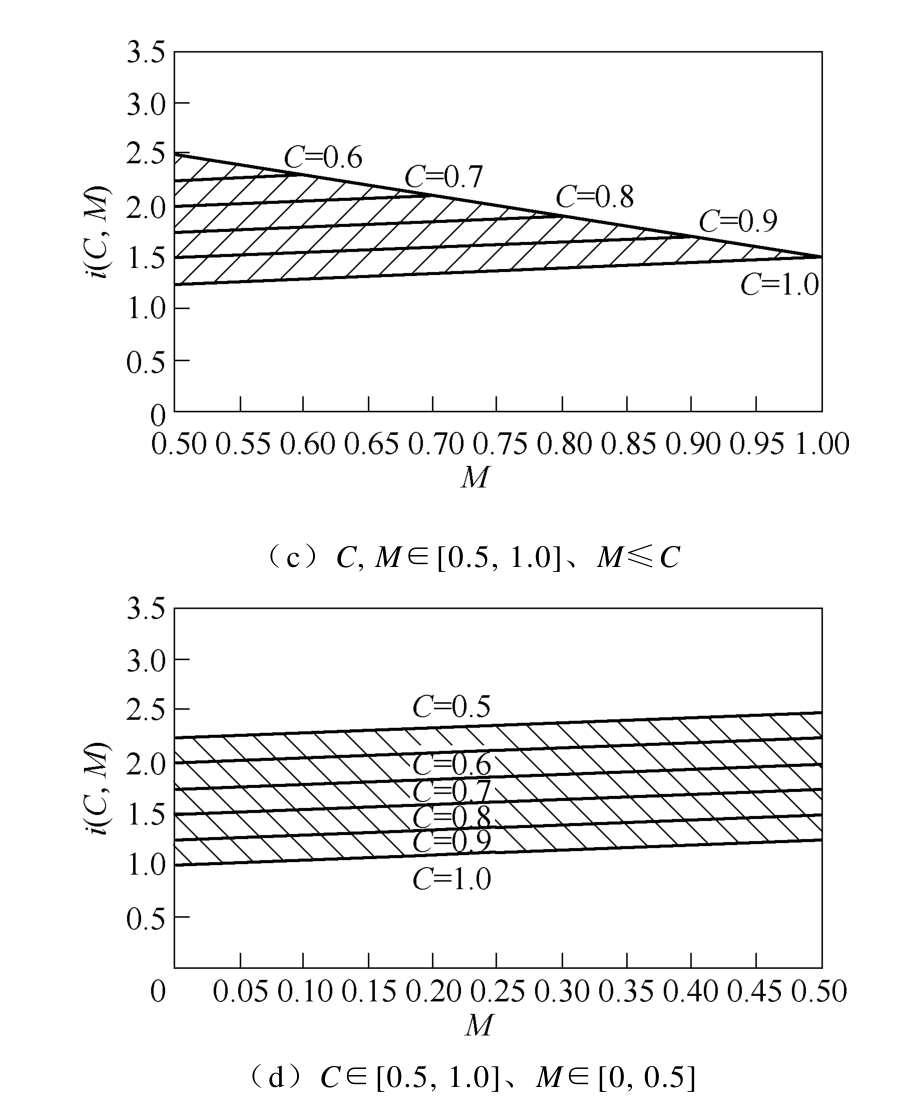
图5 n≥2时电流应力特性
Fig.5 Current stress when n≥2
由图4a和图5a可以看到，当M不变时，随着C的增大，电流应力都将减小；而当C不变时，1≤n＜2时电流应力随着M的增大而减小，n≥2时电流应力随着M的增大而增大。从图4b～图4d和图5b～图 5d可以看到，当移相角在区间 C, M∈[0, 0.5)、M≤C时电流应力始终较大；而在不同 n的范围下，电流应力特性在区间C, M∈[0.5, 1.0]、M≤C和区间C∈[0.5, 1.0]、M∈[0, 0.5]各有优势。结合图 3c和图 3d可以看到，当 1≤n＜2，移相角在区间 C, M∈[0.5, 1.0]、M≤C时，电流应力特性整体上较好，尤其当 DAB处于轻载时优势明显，此时M和C的取值都很大且接近于1，电流应力非常小；而当 n≥2，移相角在区间 C∈[0.5, 1.0]、M∈[0, 0.5]时，电流应力特性整体上较好，同样在轻载时效果显著，此时M很小且接近于0，C较大且接近于1。
2.2 回流功率特性
当传输功率需求发生改变时，移相角也发生变化，电感两端的电压波形随之改变，因而电感电流波形呈现不同的特点。而回流功率特性根据电感电流波形的不同而有所区别。对于EPS控制而言，电感电流根据节点电流 i0和 i1状态不同，有 i0≥0、i1＞0，i0＜0、i1≥0和 i0＜0、i1＜0三种状态，此时DAB三种工作状态波形如图6所示，图中阴影部分为存在回流功率时段。
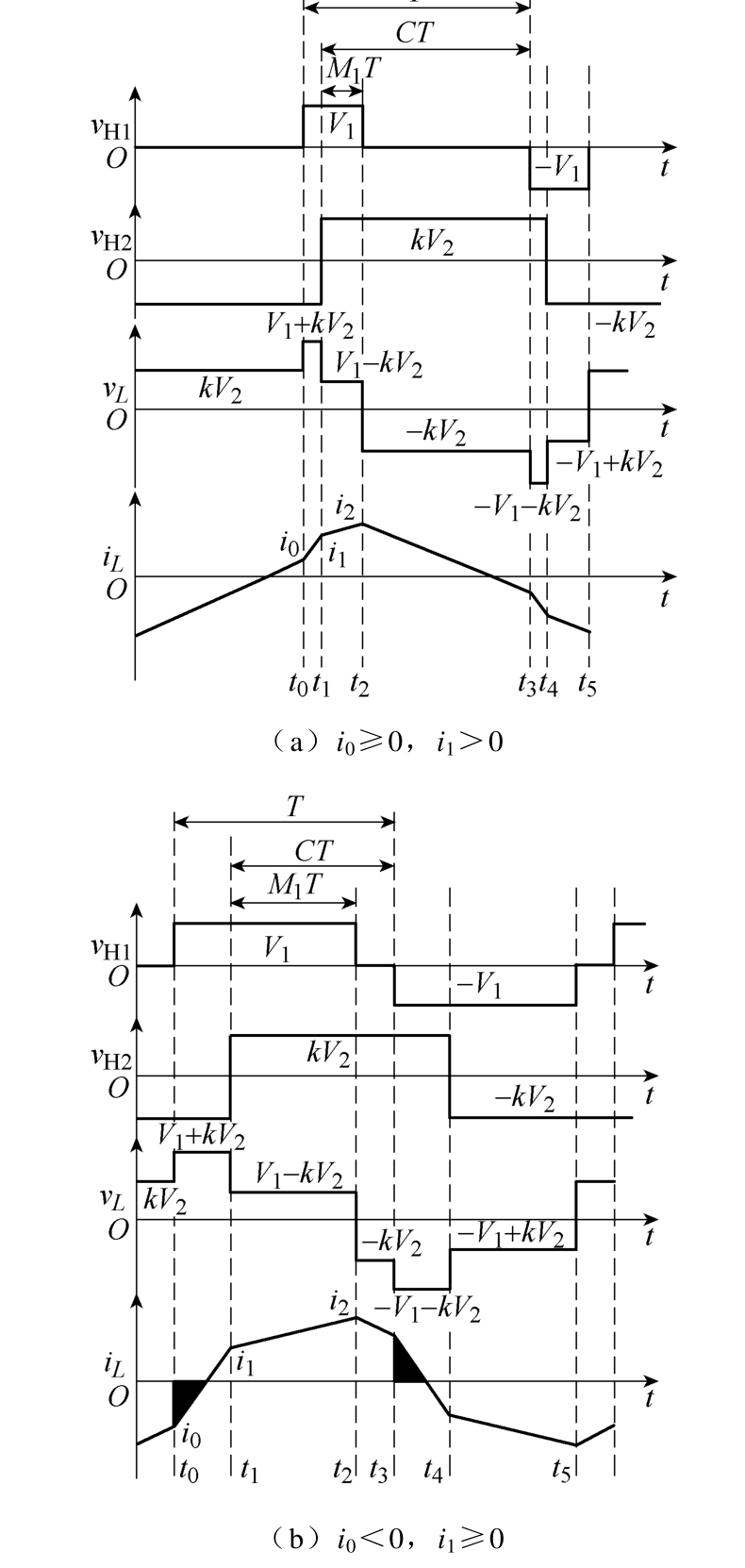
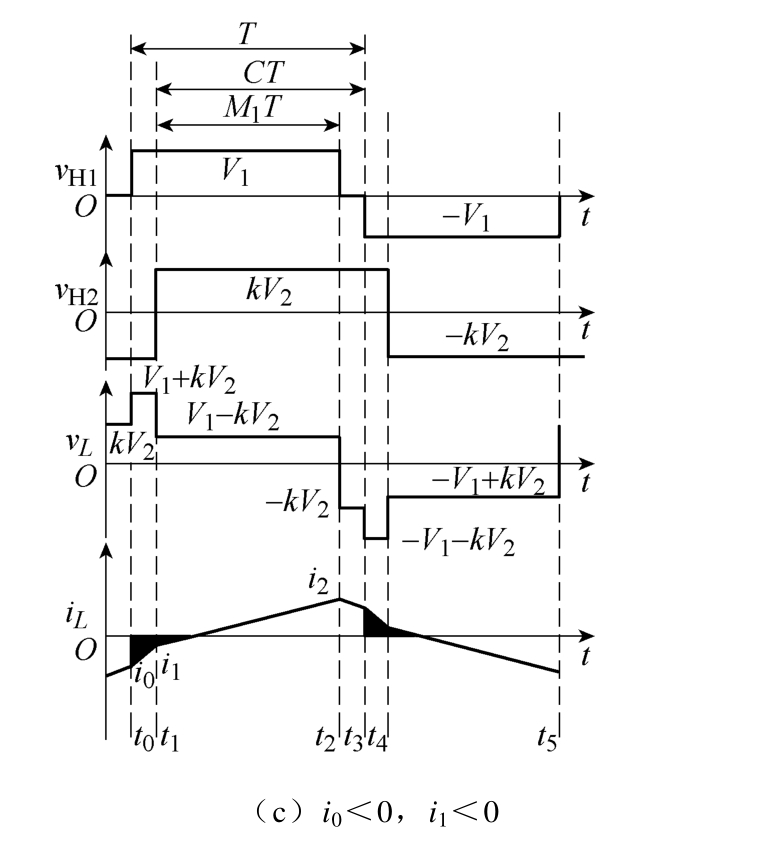
图6 不同状态DAB波形
Fig.6 Waveforms of DAB in different states
当传输功率一定时，回流功率越大，所需正向传递的功率也越大，这不仅会导致变换器效率下降，同时也会对功率器件有更高的要求。由于EPS控制时传输功率调节灵活性较高，若能选取合适的移相角，保证在相同传输功率时拥有较小的回流功率，则可提升 DAB的性能。对于处于不同工作状态的DAB回流功率 Pcir特性及全范围内参数C和M的关系见表 1。结合表 1和图 6，对不同工作状态的DAB回流功率特性进行分析。
在 n固定的情况下，满足一定的传输功率条件时：
（1）选取合适的C和M，可以实现DAB的零回流功率工作，即工作于i0≥0、i1＞0状态。
表1 不同工作状态回流功率特性
Tab.1 Characteristic of backflow power under working states
工作状态 M C Pcir i0≥0，i1＞02 1 1 0 1 C-+ -＜ ≤ ≤M n C n 2 1 1 3 2＜ ≤ ≤ 0 n C n++i0＜0，i1≥0 i0＜0，i1＜0■ + - + -■■■■0 2 1 1 1 1＜ ＜＜ ＜C C M C n n MC-1 CM C n+-＜ ＜1[0, 1.0]＜ ＜ ≤1 1 1 2 2 n C n+C M n kVV- + + -⋅+1 2 1 2 (1 C)16 1[]2 fL n 2 ( 2)(1 )1 16 ( 1)]2 2 1 2 kVV n M nM n C fL n n n C n n C n+ - - - +-{[( ) ( ) }2+ - - + - + +4 4 2 6 4 ( 1)2 2 2
（2）当DAB工作于i0＜0、i1≥0状态时，此时DAB所有开关可以实现零电压开通工作，该状态下回流功率表达式与电流i0的大小有关。根据式（4）构建电流i0的辅助函数，其表达式为
由于 i0＜0恒成立，因此辅助函数 i0(C, M)＞0恒成立。由式（11）可知，随着C的增大，i0(C, M)减小；随着M的增大，i0(C, M)增大。
（3）而当DAB工作于i0＜0、i1＜0状态时，根据表 1中回流功率表达式与 i0＜0、i1＜0状态的限制条件可知，回流功率为开口向上的一元二次函数，其对称轴 M=[1-(n-2)(1-C)]/n在 n＞1时恒小于1-1/n+C，因此回流功率为关于M的增函数。而将该回流功率表达式按照C进行降幂次整理，得到关于C的开口向上的一元二次函数，由于 i0＜0、i1＜0时M＞1-C+1/n＞1/n，因此函数对称轴为
回流功率同样为关于C的减函数。
综合上述分析，当 DAB工作于有回流功率的状态时，回流功率皆为关于M的增函数、关于C的减函数。取 n=2.5为例绘制全参数范围内的回流功率特性三维图如图7a所示，三个子区间的2D图分别如图7b～图 7d所示。从图中可以看到，当移相角在区间C, M∈[0, 0.5)、M≤C时，回流功率普遍较大，DAB的特性较差；而在 C∈[0.5, 1.0]、M∈[0, 0.5]区间，DAB可以在一定的参数范围内实现零回流功率工作。为了便于观察，结合表1与图3d，绘制区间C∈[0.5, 1.0]、M∈[0, 0.5]上DAB工作状态与传输功率的关系如图8所示。可以看到，当DAB的标幺化传输功率不大时，可以工作于零回流功率状态。
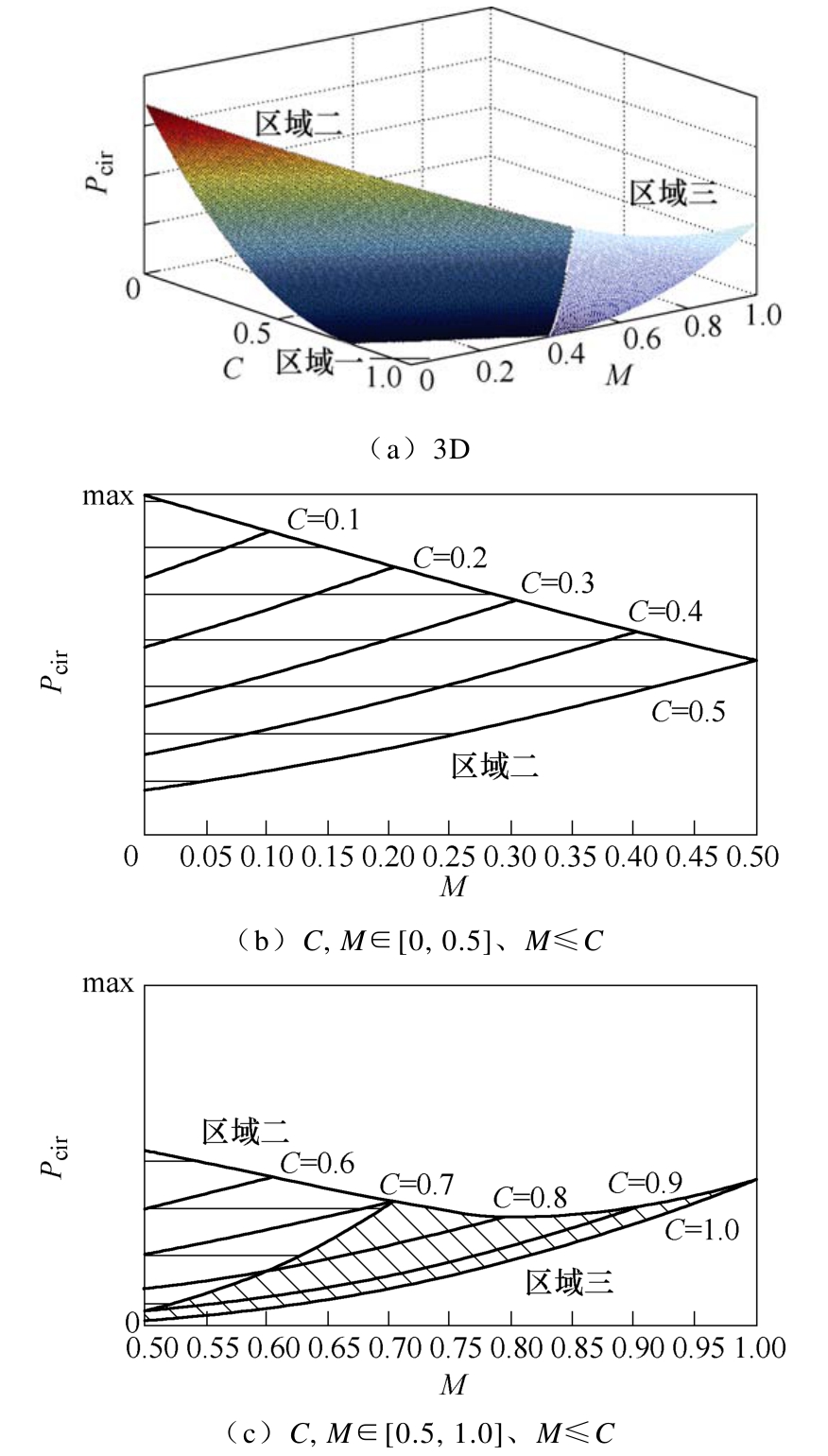
图7 回流功率特性
Fig.7 Characteristic of backflow power
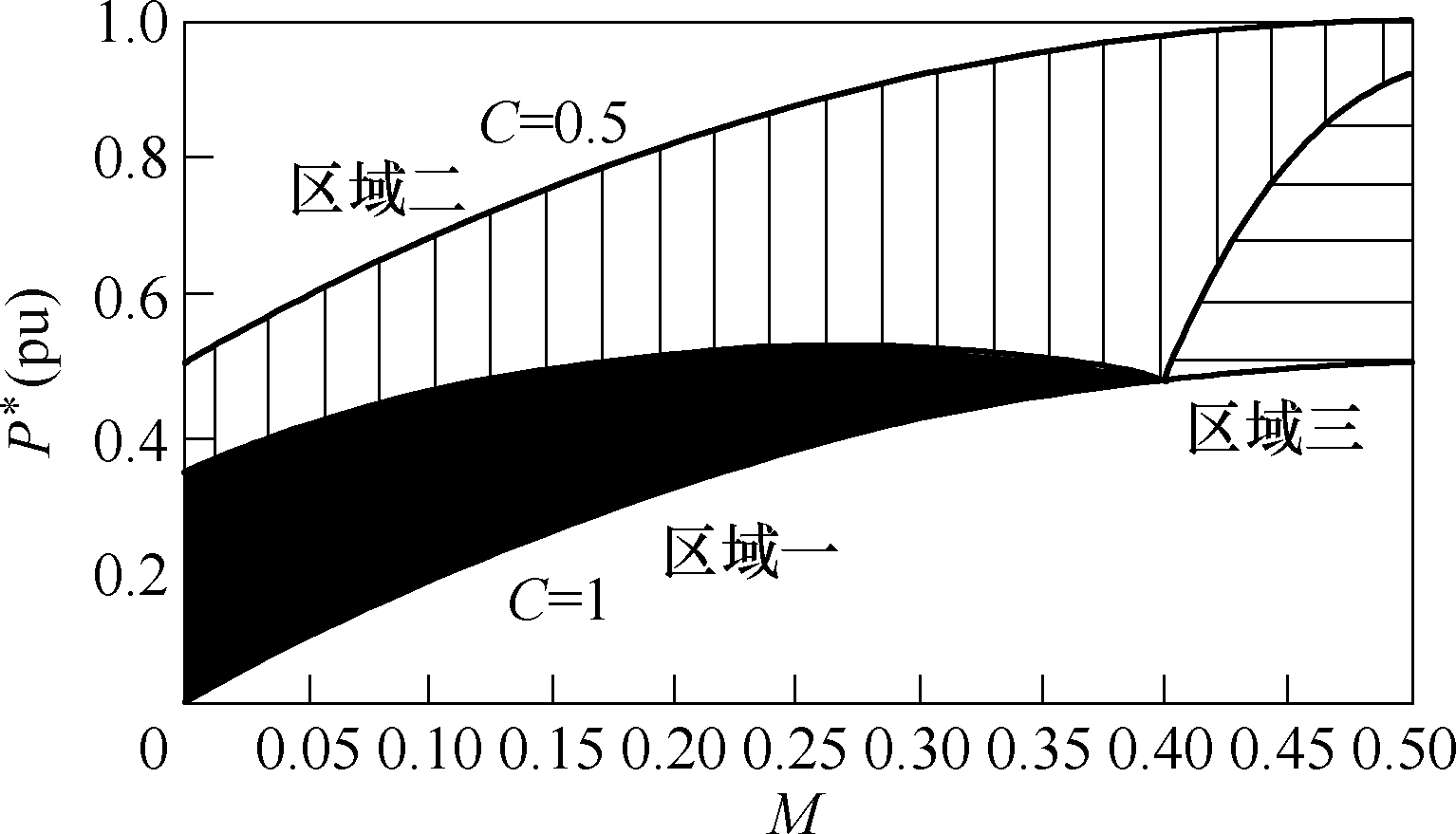
图8 工作状态与传输功率关系
Fig.8 The relationship between working states and transmission power
3 移相角计算与选取
通过上述章节中将移相角范围分为三个区域，分别对三个区域的传输功率、电流应力和回流功率特性的分析可知，三个控制区间都拥有同样的传输功率范围，而在传输功率灵活性、电流应力与回流功率特性的性能上，三个区间有所不同。其中传输功率灵活性在区间 C∈[0.5, 1.0]、M∈[0, 0.5]时最高；回流功率特性在区间C∈[0.5, 1.0]、M∈[0, 0.5]时整体上较好，且 DAB能在一定的参数范围内实现零回流功率工作；电流应力特性则根据n的范围不同，在区间 C, M∈[0.5, 1.0]、M≤C和 C∈[0.5, 1.0]、M∈[0, 0.5]上各有优势。因此由上述分析可知，移相角的选取首先排除在区间 C, M∈[0, 0.5)、M≤C中进行。
而在区间 C, M∈[0.5, 1.0]、M≤C和 C∈[0.5, 1.0]、M∈[0, 0.5]上，由传输功率表达式可知，对应于同一传输功率和同一C值，可能具有两个M的值分别在区间 M∈[0.5, 1.0]和 M∈[0, 0.5]中，由前述分析，此时当M∈[0, 0.5]时，回流功率特性较好，电流应力仅在 1≤n＜2时比在 M∈[0.5, 1.0]时大，且当 DAB处于轻载时差距尤为显著。而由图7c和图7d可知，轻载时在M∈[0.5, 1.0]区间，C和M 都接近于 1，此时电流应力非常大；而在 M∈[0, 0.5]区间，C接近于1，M接近于0，此时回流功率很小甚至为 0。考虑到轻载时，回流功率占正向传输功率的比重更大，因此本文优先保证 DAB具有较小的回流功率。
综合上述分析，本文对移相角的选取在区间C∈[0.5, 1.0]、M∈[0, 0.5]中进行。首先，确定满足传输功率要求的移相角范围：假设所需传输功率为P0，标幺化后为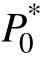 
= P0/PN。输入输出电压、电感和变压器等电路参数固定。
（1） 
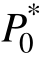∈[0, 0.5]时。对于每一固定 C值，当M=0时标幺化传输功率最小，其表达式为
由图 3d可知，标幺化传输功率最大值随着 C的增大而减小，因此当 
= 
时，根据式（13）可得解 Cmin∈[0.5, 1.0]。当 C=1，M=0.5时，有
=0.5(pu)。因此当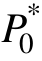 
∈[0, 0.5] (pu)时，选取任意C0∈[Cmin, 1.0]代入式（9），求解关于M的一元二次函数得到 M0∈[0, 0.5]，则 C0、M0皆满足传输功率为P0的要求。
（2）
∈[0.5, 1.0]时。对于每一固定C值，当M=0.5时标幺化传输功率达到最大值，此时标幺化传输功率最大值关于C的表达式为
当 
= 
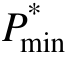时，根据式（14）可得解 Cmax∈[0.5, 1.0]。且由于标幺化传输功率最大值随着C的增大而减小，当 
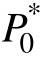∈[0.5, 1.0]时，选取任意 C0∈[0.5, Cmax]代入式（9），求解关于 M 的一元二次函数得到 M0∈[0, 0.5]，则 C0、M0皆满足传输功率为P0的要求。
本文在控制时，C0最终选取优化区间内的中间值，实际上在整个优化区间内 DAB回流功率与电流应力特性差距不大。在已知电路参数和确定传输功率大小的情况下，采用EPS控制时满足传输功率要求的DAB移相角范围选取流程如图9所示，DAB控制框图如图10所示。
4 仿真与实验
4.1 仿真
图9 移相角选取流程
Fig.9 Process of parameters selection
图10 DAB控制框图
Fig.10 Block diagram of DAB control
通过 Matlab/Simulink仿真验证理论分析的正确性。仿真参数设定输入电压120V，输出电压80V，变压器电压比为1，电感L=0.6mH，器件开关频率f =2kHz。根据传输功率基准值可求得PN=kV1V2/(8fL)=1 000W。假设所需传输功率P0=800W，根据第3节的分析，此时移相角的选取流程如图11所示。
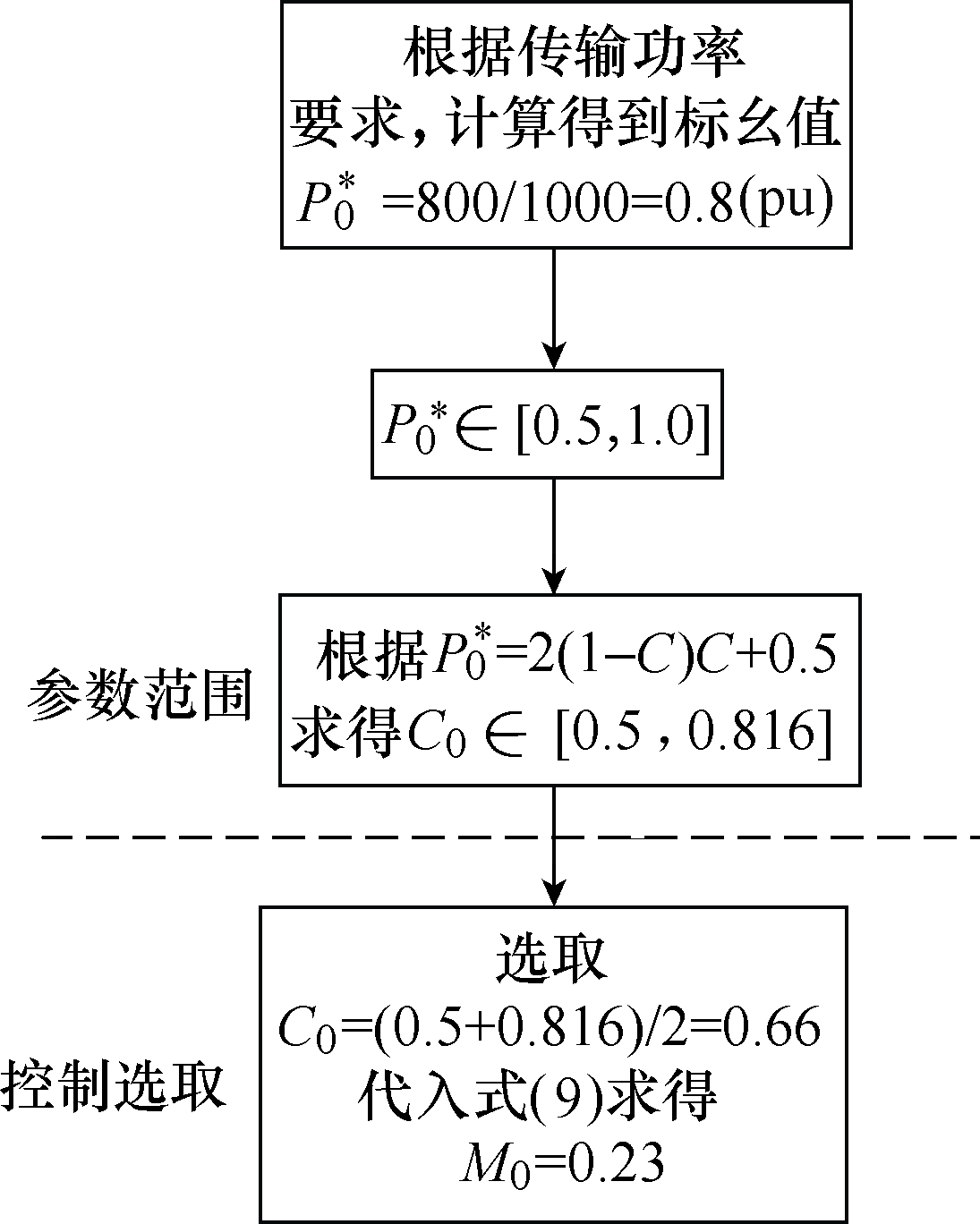
图11 移相角计算与选取
Fig.11 Calculation and selection of parameters
仿真时分别取 C1=0.4、C2=0.7和 C3=0.66，代入式（9）求得 M1=0.2、M2=0.255和 M3=0.23，其中 C3是参数范围的中间值，C2是根据表 1计算后选取的 i0≥0、i1＞0 状态与 i0＜0、i1≥0 状态临界处附近值，C1选取了区间 C, M∈[0.5, 1.0]、M≤C中的值。仿真结果分别如图 12～图14所示，图中阴影部分表示有回流功率存在。
图12 C1=0.4，M1=0.2时电压电流波形
Fig.12 Waveforms of voltage and current when C1=0.4, M1=0.2
图13 C2=0.7，M2=0.255时电压电流波形
Fig.13 Waveforms of voltage and current when C2=0.7, M2=0.255
图14 C3=0.66，M3=0.23时电压电流波形
Fig.14 Waveforms of voltage and current when C3=0.66, M3=0.23
根据图 12～图 14可以看到，选取相同区域的电感电流波形，当在区间 C, M∈[0.5, 1.0]、M≤C中选取时，回流功率与电流应力明显较大，而在区间C∈[0.5, 1.0]、M∈[0, 0.5]内选取时差距较小。实际上根据电流应力与回流功率表达式可以求得当取C1=0.4，M1=0.2时电流应力 imax1=30A，回流功率Pcir1=392W；取C2=0.7，M2=0.255时电流应力imax2=22A，回流功率 Pcir2=37.4W；取 C3=0.66，M3=0.23时电流应力 imax3=23A，回流功率 Pcir3=57W。控制算法中选取的C值，即C3，虽然不能保证DAB的性能最优，但是整体效果较好。若在此基础上对控制器算法加以改进，可进一步提升DAB的性能。
当传输功率由800W跳变为450W时，其暂态波形如图15所示。稳定后局部方法虚线框部分波形如图16所示。实际上当传输功率为450W时，根据图9所示流程可求得控制器中两参数C=0.83，M =0.1。此时根据电流应力表达式可得imax=20A，而根据表 1可得此时零回流功率状态临界条件为 C＞0.714，0＜M＜0.27，因此此时DAB工作于i0＞0、i1＞0状态，与仿真波形一致。
图15 功率跳变时电压电流波形
Fig.15 Waveforms of voltage and current when power changes
图16 传输功率为450W时电压电流波形
Fig.16 Waveforms of voltage and current when P0=450W
4.2 实验
为了验证理论分析的正确性，实验中电路参数与仿真时相同，当传输功率P0=800W，即传输功率标幺值分别为0.8时，分别选取不同的C0进行验证。首先当P0=800W，根据4.1节的分析，分别取C1=0.4，M1=0.2；C2=0.7，M2=0.255和 C3=0.66，M3=0.23三种情况，所得电压电流实验波形如图 17～图 19所示。
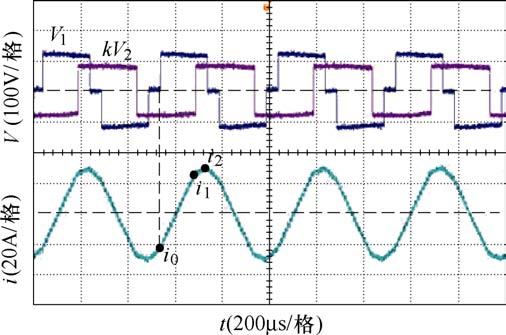
图17 C1=0.4，M1=0.2电压电流实验波形
Fig.17 Experimental waveforms of voltage and current when C1=0.4, M1=0.2
图18 C2=0.7，M2=0.255电压电流实验波形
Fig.18 Experimental waveforms of voltage and current when C2=0.7, M2=0.255
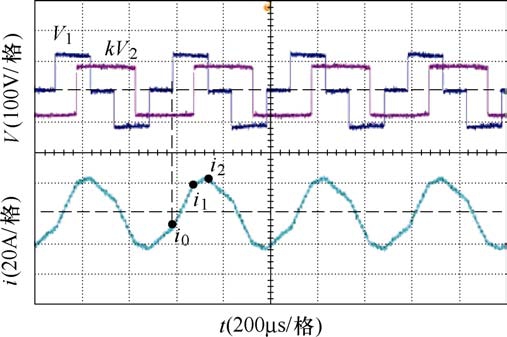
图19 C3=0.66，M3=0.23电压电流实验波形
Fig.19 Experimental waveforms of voltage and current when C3=0.66, M3=0.23
由图17～图19可以看到，取C1=0.4，M1=0.2，即图17所示波形电感电流与C2=0.7，M2=0.255和C3=0.66，M3=0.23，即图 18和图 19所示电感电流波形差距较大，其电流应力与回流功率都较大。而图18和图19中电感电流波形差距很小，与仿真所得结论一致。当选取移相角在区间C, M∈[0.5, 1.0]、M≤C中进行控制时，DAB的性能较好，且区间内选取不同参数造成的差异较小。
图20所示为负载发生变化，功率由800W变为450W后DAB稳定工作时的波形，可以看到根据本文设计的控制器，此时 DAB工作于零回流功率状态，电流应力略大于20A，DAB拥有较好的性能，与仿真分析一致。
图20 C1=0.83，M1=0.1电压电流实验波形
Fig.20 Experimental waveforms of voltage and current when C1=0.83, M1=0.1
5 结论
本文提出了一种扩展移相控制下的 DAB移相角优化选取与分析方法，利用新的移相角重新建立DAB的传输功率模型，可以利用一元二次函数的性质，简化传输功率的分析与移相角计算选取。在对电流应力与回流功率特性的分析中，回流功率与两移相角呈单调的变化关系，而电流应力与两移相角的关系受电压转换比 n的影响呈现不同的单调特性，因此当1＜n＜2时，优化电流应力与优化回流功率时有着难以规避的矛盾。综合考虑回流功率与电流应力的特性，在满足传输功率要求前提下可以将两移相角的取值范围确定在一个较小的范围内，此范围内移相角可以保障 DAB具有较好的特性。最后，仿真和实验验证了理论的正确性。然而本文采用更优的控制策略，该部分内容将在后续的工作中进行。
[1] Hugo Neves de Melo, João Pedro F Trovão, Paulo G Pereirinha, et al. A controllable bidirectional battery charger for electric vehicles with vehicle-to-grid capability[J]. IEEE Transactions on Vehicular Technology, 2018, 26(1): 114-123.
[2] Marco Martins, Marina S Perdigão, Andre M S Mendes, et al. Analysis, design, and experimentation of a dimmable resonant-switched-capacitor LED driver with variable inductor control[J]. IEEE Transactions on Power Electronics, 2017, 32(4):3051-3062.
[3] He Yuqing, Chen Yuehui, Yang Zhiqiang, et al. A review on the influence of intelligent power consumption technologies on the utilization rate of distribution network equipment[J]. Protection and Control of Modern Power Systems, 2018, 3(3):183-193.
[4] Harish Suryanarayana, Scott D Sudhoff. Design paradigm for power electronics-based DC distribution systems[J]. IEEE Transactions on Industrial Electronics, 2017, 5(1): 51-63.
[5] Wang Yu, Song Qiang, Sun Qianhao, et al. Multilevel MVDC link strategy of high-frequency-link DC transformer based on switched capacitor for MVDC power distribution[J]. IEEE Transactions on Industrial Electronics, 2017, 64(4): 2829-2835.
[6] 江道灼, 郑欢. 直流配电网研究现状与展望[J]. 电力系统自动化, 2012, 36(8): 98-104.Jiang Daozhuo, Zheng Huan. Research status and developing prospect of DC distribution network[J].Automation of Electric Power Systems, 2012, 36(8):98-104.
[7] 涂春鸣, 肖凡, 袁靖兵, 等. 级联型电力电子变压器直流电压二次纹波抑制策略[J]. 电工技术学报,2019, 34(14): 2990-3003.Tu Chunming, Xiao Fan, Yuan Jingbin, et al. DC ripple voltage suppression strategy for cascaded power electronic transformer[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2990-3003.
[8] Liu Jianqiang, Yang Jingxi, Zhang Jiepin, et al.Voltage balance control based on dual active bridge DC/DC converters in a power electronic traction transformer[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1696-1714.
[9] 张雪垠, 徐永海, 肖湘宁. 适用于中高压配电网的高功率密度谐振型级联 H桥固态变压器[J]. 电工技术学报, 2018, 33(2): 310-321.Zhang Xueyin, Xu Yonghai, Xiao Xiangning. A high power density resonance cascaded H-bridge solid-state transformer for medium and high voltage distribution network[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 310-321.
[10] 张明锐, 刘金辉, 金鑫. 应用于智能微网的SVPWM固态变压器研究[J]. 电工技术学报, 2012,27(1): 90-97.Zhang Mingrui, Liu Jinhui, Jin Xin. Research on the SVPWM solid state transformer applied in smart micro-grid[J]. Transactions of China Electrotechnical Society, 2012, 27(1): 90-97.
[11] Cao Lingling, Loo K H, Lai Y M. Output-impedance shaping of bidirectional DAB DC-DC converter using double-proportional-integral feedback for nearripple-free DC bus voltage regulation in renewable energy systems[J]. IEEE Transactions on Power Electronics, 2016, 31(3): 2187-2199.
[12] 谷庆, 袁立强, 聂金铜, 等. 基于开关组合规律的双有源桥 DC-DC变换器传输功率特性[J]. 电工技术学报, 2017, 32(13): 69-79.Gu Qing, Yuan Liqiang, Nie Jintong, et al. Transmission power characteristics of dual-active-bridge DC-DC converter based on the switching combination rules[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 69-79.
[13] Zhao Biao, Yu Qingguang, Sun Weixin. Extendedphase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid[J].IEEE Transactions on Power Electronics, 2012,27(11): 4667-4680.
[14] Gu Qing, Yuan Liqiang, Nie Jintong, et al. Current stress minimization of dual-active-bridge DC-DC converter within the whole operating range[J].IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(1): 129-142.
[15] 杨超, 许海平, 张祖之, 等. PWM 与移相结合控制下的混合三电平隔离型双向 DC-DC最小回流功率控制研究[J]. 电工技术学报, 2019, 34(15): 3186-3197.Yang Chao, Xu Haiping, Zhang Zuzhi, et al.Minimum backflow power control of the hybrid three level isolated Bi-directional DC-DC converters based on PWM-phase-shifting control[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3186-3197.
[16] 侯聂, 宋文胜, 王顺亮. 全桥隔离DC/DC变换器相移控制归一化及其最小回流功率控制[J]. 中国电机工程学报, 2016, 36(2): 499-506.Hou Nie, Song Wensheng, Wang Shunliang.Normalization of phase shift control and minimum reflux power control of full-bridge isolated DC/DC converters[J]. Proceedings of the CSEE, 2016, 36(2):499-506.
[17] 曾进辉, 孙志峰, 雷敏, 等. 双重移相控制的双主动全桥变换器全局电流应力分析及优化控制策略[J]. 电工技术学报, 2019, 34(12): 2507-2518.Zeng Jinhui, Sun Zhifeng, Lei Min, et al. Global current stress analysis and optimal control strategy of DAB converter based on dual-phase-shift control[J].Transactions of China Electrotechnical Society, 2019,34(12): 2507-2518.
[18] Li Jingxin, Wang Dongzhi, Wang Wei, et al.Minimize current stress of dual-active-bridge DC-DC converters for electric vehicles based on lagrange multipliers method[J]. Energy Procedia, 2017, 105:2733-2738.
[19] Song Chaochao, Chen Alian, Chen Jie, et al. Currentstress-optimized strategy of dual active bridge DCDC converter with dead-time effect in singlephase-shift control[C]//IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 2017: 1013-1018.
[20] 金莉, 刘邦银, 段善旭. 三电平双有源全桥 DC-DC变换器回流功率最小的移相控制[J]. 电工技术学报, 2018, 33(24): 5864-5873.Jin Li, Liu Bangyin, Duan Shanxu. Minimum reflux power strategy of three-level dual active bridge DC-DC converter with phase shift control[J]. Transactions of China Electrotechnical Society, 2018,33(24): 5864-5873.