0 引言
近年来,模型预测控制在电力电子与电力传动领域得到广泛关注和研究[1-3]。区别于常规的矢量控制等策略,模型预测控制直接根据电压源逆变器(Voltage Source Inverter, VSI)允许输出的电压矢量和负载的离散数学模型,预测下一周期的控制目标状态,并根据所建立的目标函数选择最优的电压矢量进行作用,从而实现闭环控制。由于模型预测控制实现比较简单,控制比较容易,可实现多目标优化控制,因此已被广泛的应用于光伏并网、电机驱动控制等领域[4-5]。
无论是在光伏并网系统,还是在电机驱动系统中,VSI功率开关管的高速开关都会产生较大的高频共模电压,进而危害系统的运行可靠性和安全性[6-7]。为此,诸多学者开展了VSI的共模电压抑制策略研究。文献[8-9]从VSI拓扑改造的角度研究了共模电压抑制策略,然而,这会增加系统的硬件成本。文献[10-11]从改变 PWM策略的角度研究了共模电压抑制策略,但其实现较复杂。
为了避免增加硬件成本,并降低计算复杂度,近年来,诸多学者开展了基于模型预测控制的 VSI共模电压抑制方法研究。考虑到模型预测控制易于实现多目标优化控制,文献[12-16]通过在目标函数中增加共模电压抑制项,以实现共模电压抑制的目标。然而,这类方法需要设计权重系数来平衡多个控制目标,而权重系数的设计较复杂。
为了实现VSI的共模电压抑制,并避免使用权重系数,文献[17-20]提出了基于电压矢量预选的VSI共模电压抑制方法,其思想是仅采用产生共模电压较小的电压矢量进行目标函数优化和 VSI控制;由于其没有考虑死区的影响,导致VSI实际输出的共模电压依然含有较多的电压尖峰。文献[21]考虑了死区影响,但没有充分利用两电平VSI的6个非零电压矢量,导致电流的总谐波畸变率(Total Harmonic Distortion, THD)较大。文献[22]通过深入分析死区的影响,进一步提出了一种改进的考虑死区影响的VSI共模电压抑制方法;该方法在每个控制周期只采用一个非零电压矢量工作,导致其电流THD依然较大。
为了在不增加硬件成本的前提下实现共模电压抑制,并降低电流THD,本文针对两电平VSI提出了一种虚拟矢量模型预测共模电压抑制方法。首先,给出了常规单矢量模型预测共模电压抑制法的基本原理。其次,引入了虚拟矢量的概念,并设计了一种基于虚拟矢量的 VSI模型预测共模电压抑制方法。再次,分析了死区和控制延时对所述虚拟矢量模型预测共模电压抑制方法的影响,并进行了改进。最后,提出了一种改进的VSI虚拟矢量模型预测共模电压抑制方法,并进行了仿真和实验验证。
1 常规单矢量模型预测共模电压抑制法
考虑到无论是在光伏发电并网系统,还是在电机驱动系统中,VSI输出所接的负载均为反电动势负载,因此本文以VSI输出接反电动势负载为例进行研究,其电路拓扑及电压矢量如图1所示。

图1 VSI的电路拓扑及电压矢量
Fig.1 Topology and voltage vectors of the VSI
1.1 共模电压的定义
共模电压常定义为VSI负载与直流侧中点之间的电压,如图1a中的uno所示。其与VSI开关状态Si(i=a, b, c)和直流电压udc之间的关系满足式中,当 i相上管导通,下管关断时,Si=1;当 i相上管关断,下管导通时,Si=0。
三相 VSI共有 8个电压矢量,如图 1b所示。结合式(1)可知,零矢量 u0产生的共模电压为-udc/2,零矢量 u7产生的共模电压为udc/2,奇矢量u1、u3和u5产生的共模电压为-udc/6,而偶矢量u2、u4和u6产生的共模电压为udc/6。由此可见,两个零矢量产生的共模电压峰值最大[19]。因此,为了抑制VSI的共模电压,通常需要避免使用零矢量。
1.2 常规单矢量共模电压抑制法的原理
常规基于电压矢量预选的VSI单矢量模型预测共模电压抑制方法在每个控制周期中仅选择一个非零矢量进行作用,其执行步骤如下。
第一,VSI在αβ 坐标系上的数学模型可表示为
式中,u为 VSI的输出电压矢量;i为 VSI的输出电流矢量;e为负载反电动势;R为负载电阻;L为负载电感。u(k)=[uα (k) uβ (k)]T,e(k)=[eα (k) eβ (k)]T,i(k)=[iα (k) iβ (k)]T。
第二,为了实现电流预测和延时补偿,需要对式(2)进行离散化。离散化后可得
将当前时刻作用的矢量 u(k)代入式(3)预测k+1时刻的电流矢量i(k+1),以实现延时补偿。
第三,在得到i(k+1)之后,可根据VSI的 6个非零电压矢量u(k+1)进一步预测k+2时刻的电流矢量i(k+2),满足
式中,考虑到e变化较慢,可近似认为e(k+1)=e(k)。
第四,为了评估6个非零电压矢量的电流控制效果,可建立式(5)的目标函数,并将6个非零电压矢量所预测得到的 6个不同的电流矢量 i(k+2)依次代入式(5)进行目标函数计算,从而得到6个不同的 gn(n=1, 2, 3, 4, 5, 6)。
式中,i*(k+2)为设定的电流参考值。
第五,通过比较6个不同的目标函数gn,确定使目标函数最小的电压矢量作为最优矢量。
为了进一步消除因死区而产生的共模电压尖峰,文献[22]研究了电压矢量预选方法,以将共模电压限制在±udc/6之间。由于该方法每个控制周期仅使用一个非零电压矢量,本文称之为单矢量法。虽然该单矢量法可以实现共模电压抑制,但其电流THD较大。为此,本文引入了虚拟矢量,以在实现共模电压抑制的同时进一步降低电流THD。
2 虚拟矢量模型预测共模电压抑制方法
2.1 虚拟矢量的定义
文献[23]引入了虚拟矢量的概念,以改善三相PWM 整流器的控制性能。其中,所述虚拟矢量由相邻的两个非零电压矢量和一个零电压矢量合成。由于零电压矢量所产生的共模电压较大,因此本文仅采用两个相邻的非零电压矢量合成虚拟矢量,所述的虚拟矢量定义为
式中,un和un+1分别为VSI相邻的两个非零电压矢量;t1n和t2n分别为这两个矢量的作用时间,且满足t1n+t2n=Ts,Ts为控制周期。
图1b给出了6个虚拟矢量的分布,当两个相邻非零电压矢量的作用时间发生改变时,所定义的虚拟矢量将沿着电压矢量六边形的6个边移动。与常规的单矢量法相比,虚拟矢量的引入增加了模型预测控制系统备选电压矢量的自由度,从而有助于提高预测控制精度,降低电流THD。
2.2 矢量作用时间的求取
为了确定6个虚拟矢量所在的位置,本文结合调制模型预测控制的思想来计算合成虚拟矢量的非零电压矢量作用时间[24],如下所述。
考虑到电压矢量un所对应的目标函数gn越大,其作用时间 t1n就需要越小,因此可近似认为 t1n与gn呈反比[24],由此可得合成虚拟矢量的非零电压矢量作用时间计算方法[24],即
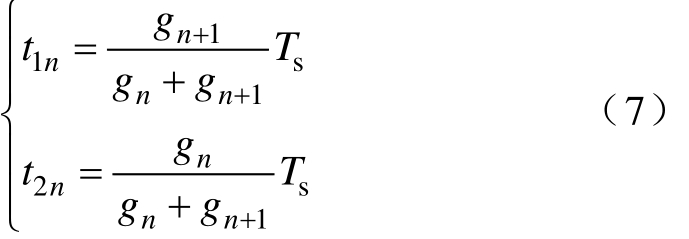
在由式(3)~式(5)计算得到6个非零电压矢量的目标函数后,可再根据式(7)计算各个非零电压矢量的作用时间,然后代入式(6),可确定 6个虚拟矢量的位置。最后再将6个虚拟矢量依次代入式(3)~式(5)进行电流预测和目标函数优化,并最终选择使 gn最小的虚拟矢量 Vn作为最优矢量进行作用,从而可实现虚拟矢量模型预测控制。
2.3 虚拟矢量的实现
文献[23]通过设计PWM发波,实现了虚拟矢量输出,本文也采用该原理实现虚拟矢量的输出。以虚拟矢量V1为例进行分析,其由矢量u1和u2合成。图2给出了其脉冲调制原理。图中,所定义的对称三角波周期为Ts,幅值为M。当调制波大于三角波时,输出PWM信号为高电平,否则为低电平。

图2 脉冲调制原理
Fig.2 Pulse modulation principle
当虚拟矢量 V1作用时,a相上管始终导通,c相下管始终导通,因此a相的比较值ua为三角波的峰值M,c相的比较值uc=0,而b相的比较值ub则由u1的作用时间t11决定。
由图2和三角形相似关系可得
同理,当其他虚拟矢量作用时,也可以采用类似的方法得到三相比较值,其结果见表1。
表1 三相电压比较值
Tab.1 Comparison values of the three phase voltages
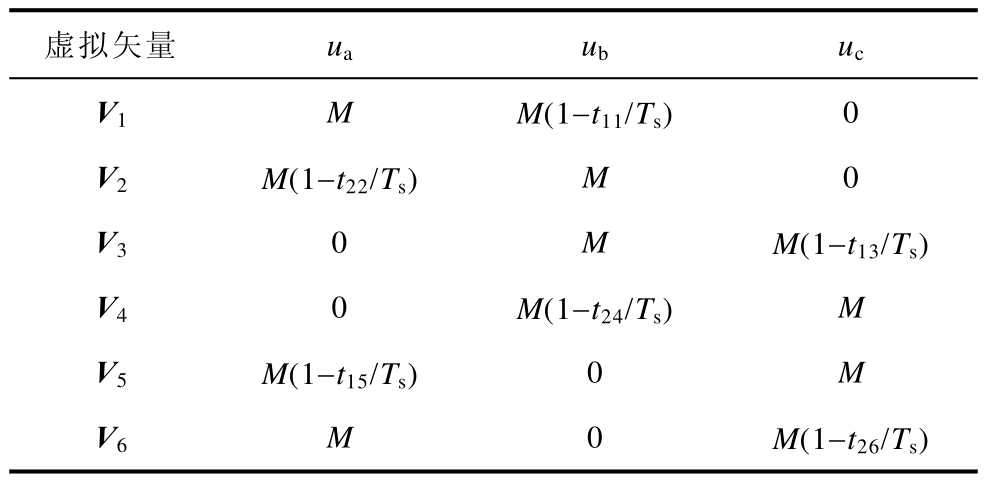
虚拟矢量 ua ub uc V1 M M(1-t11/Ts) 0 V2 M(1-t22/Ts) M 0 V3 0 M M(1-t13/Ts)V4 0 M(1-t24/Ts) M V5 M(1-t15/Ts) 0 M V6 M 0 M(1-t26/Ts)
由表1可见,在求得最优虚拟矢量后,即可根据其对应的非零电压矢量作用时间 t1n和 t2n求取三相比较值ua、ub和uc,从而实现对应的脉冲输出。
3 死区影响分析与改进
由图2可知,当虚拟矢量V1作用时,其对应的脉冲序列为 u2-u1-u2,而其他虚拟矢量作用时,其对应的脉冲序列如图3所示。由图3可见,无论采用哪一个虚拟矢量作用,其实际输出的脉冲序列都起于偶矢量,终于偶矢量。这意味着当不同控制周期内不同虚拟矢量进行切换时,其本质都是偶矢量在进行切换。而偶矢量进行切换时会出现VSI两个桥臂同时换流的情况,这有可能会因死区而产生等效零矢量,进而产生共模电压尖峰。因此,必须分析死区的影响,并对虚拟矢量的切换方法进行限制。

图3 脉冲序列示意图
Fig.3 Diagram of the pulse sequences
文献[22]通过将三相电流划分为 6个扇区,详细分析了死区的影响。本文同样定义三相电流由直流侧流向交流侧为正方向,并将三相电流平面划分为6个扇区,见表2,其中,Q代表电流扇区。
表2 电流扇区划分
Tab.2 Current sector division
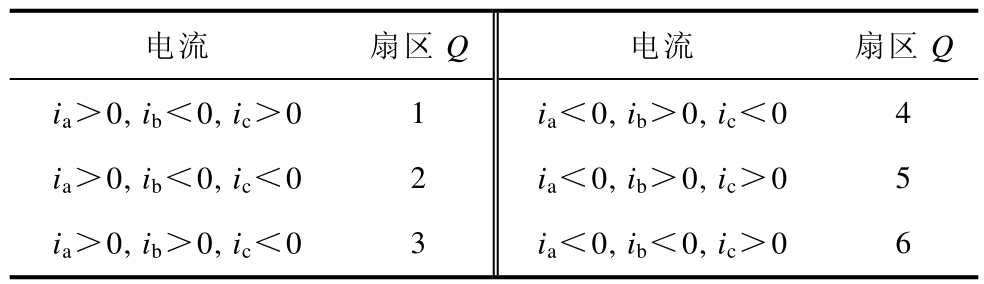
电流 扇区Q 电流 扇区Q ia>0, ib<0, ic>0 1 ia<0, ib>0, ic<0 4 ia>0, ib<0, ic<0 2 ia<0, ib>0, ic>0 5 ia>0, ib>0, ic<0 3 ia<0, ib<0, ic>0 6
采用与文献[22]相同的分析方法可得在特定的电流扇区内会产生等效零矢量的虚拟矢量切换组合,见表3。由表 3可见,为了避免等效零矢量的出现,在进行虚拟矢量切换时,必须考虑电流所在的扇区。例如,在电流扇区2内,不允许虚拟矢量V1或V2与V5或V6进行切换。考虑表3所示的矢量切换限制后,可得本文提出的虚拟矢量预选方法,如图4a所示;单电压矢量预选方法如图4b所示。
表3 产生等效零矢量的虚拟矢量切换组合
Tab.3 Switching combinations of virtual vectors that can generate equivalent zero vectors

电流扇区Q 切换电压矢量 产生的等效零矢量2 1 2 5 6 V V V V u7( ) ( )↔V V V V u7 6 3 4 5 6 4 1 2 3 4( ) ( )↔V V V V u7( ) ( )↔

图4 电压矢量预选方法
Fig.4 The voltage vector preselection method
4 延时影响分析与改进
由图4可知,为了完全将共模电压限制在±udc/6之内,必须准确进行电流扇区判断和电压矢量预选。然而,由于模型预测控制系统存在固有的一拍滞后延时,导致 k时刻选择的最优电压矢量只能在 k+1时刻作用。而当所选择的最优矢量在k+1时刻作用时,由于控制延时的影响,电流的扇区有可能会发生变化,这就有可能会出现表3所示的切换情况。
例如,当上一周期的最优矢量为V1,且电流处于扇区3时,由图4a可知,所有的6个虚拟矢量都可以作为备选矢量。假如经过目标函数优化后,V3为最优虚拟矢量,它将在下一周期作用于 VSI。而当V3作用时,由于一拍滞后的影响,a相电流有可能已经由大于零变为小于零,此时,电流扇区相应的会由 3变为 4,出现了在电流扇区 4内 V1向 V3切换的情况。由表3可知,此时会产生等效零矢量u7,进而会产生共模电压尖峰。因此,必须避免这种情况的出现。
同时,模型预测控制的电流纹波较大,电流过零点较难判断,给电流扇区的判断带来了影响。为此,本文进一步提出了一种基于滞环的电流扇区划分方法,并定义当任意一相电流瞬时值的绝对值小于δ 时为电流扇区 7。改进型的电流扇区划分方法见表4,表中δ 是一个小正数。
表4 改进型的电流扇区划分方法
Tab.4 Improved current sector division method
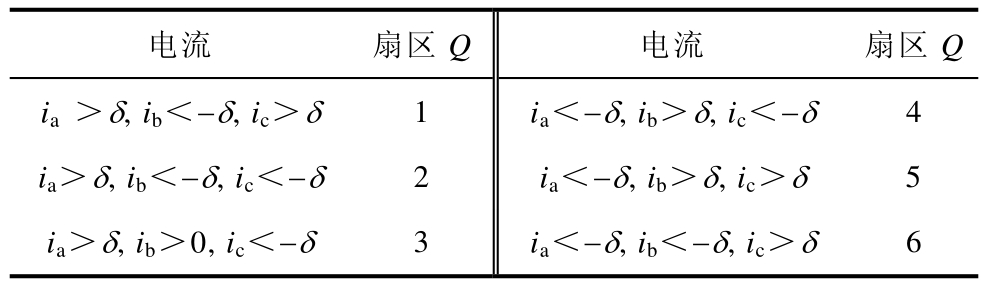
电流 扇区Q 电流 扇区Q ia >δ, ib<-δ, ic>δ 1 ia<-δ, ib>δ, ic<-δ 4 ia>δ, ib<-δ, ic<-δ 2 ia<-δ, ib>δ, ic>δ 5 ia>δ, ib>0, ic<-δ 3 ia<-δ, ib<-δ, ic>δ 6
当电流处于扇区7时,即意味着某相电流处于过零点附近,此时由于一拍滞后延时和电流纹波的影响,导致电流扇区较难准确判断。为了避免由于扇区判断错误而导致共模电压尖峰的产生,由图4a可知,此时只能允许 V1和 V2进行切换,V3和 V4进行切换,V5和 V6进行切换,而任意需要根据电流扇区决定是否允许切换的虚拟矢量都不允许进行切换。这虽然可以避免共模电压尖峰的产生,但明显降低了逆变器输出电流的可控性。
电流可控性分析示意图如图5所示。假如此时电流处于扇区7,且上一周期使用的虚拟矢量为V1,此时,为了避免出现共模电压尖峰,下一周期仅允许使用虚拟矢量V1和V2,而V1和V2只能向着图5中的四边形ABCD所覆盖的方向改变电流[25]。由图5可见,此时电流控制误差只会越来越大,甚至出现明显畸变。

图5 电流可控性分析示意图
Fig.5 Schematic diagram of current controllability analysis
为此,在电流处于扇区7时,可直接采用文献[21]所设计的单电压矢量预选方法,以避免电流出现明显畸变,并消除共模电压尖峰,如图4b所示。
当电流处于扇区 7,且上一周期使用的电压矢量为V1时,由图3可知,其终矢量为u2;由图4b可知,此时可选择u1、u2、u3和u5作为备选矢量。当选择u5时,由图5可见,电流将朝线段BE所指方向进行改变,其控制误差也会明显减小,从而避免了电流出现畸变的情况。
综上可得一种基于虚拟矢量的VSI模型预测共模电压抑制方法,其执行框图如图6所示。

图6 所提方法的执行框图
Fig.6 Implementation block diagram of the proposed method
5 电流变化分析与滞环设计
由第 4节的分析可知,电流滞环宽度δ 决定了图4所示的虚拟矢量法和单矢量法的作用范围,因此其选择和设计十分重要。本文对电流在一个周期内的变化量进行了详细分析,并最终给出了电流滞环宽度δ 的选择方法。
当虚拟电压矢量作用于VSI时,VSI的数学模型可以表示为
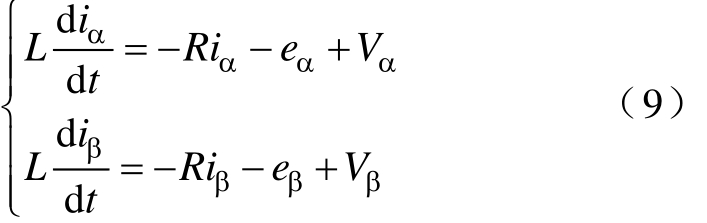
式中,Vα、Vβ 分别为 VSI 输出的虚拟矢量在αβ 坐标系上的分量。
考虑到VSI的输出基波频率远小于采样频率,且负载电阻R非常小,由式(9)可近似得到
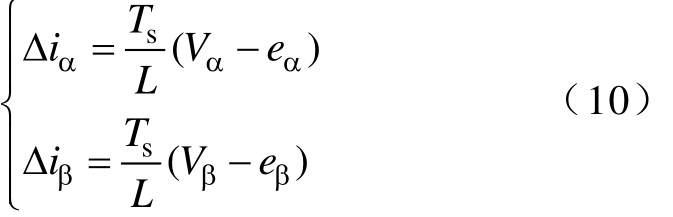
式中,Δiα、Δiβ 分别为 iα、iβ 在单个控制周期内的变化量。
将式(10)变换到abc坐标系上,可得
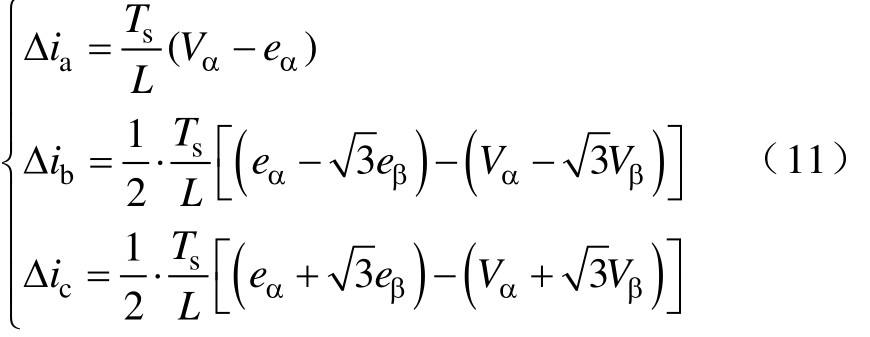
式中,Δia、Δib、Δic分别为三相电流在单个控制周期内的变化量。
以下对电流变化量进行分析。首先,假设反电动势满足
式中,E为反电动势幅值;θ 为反电动势的角度。
当虚拟矢量作用时,由式(6)可知,其对应的电压值满足
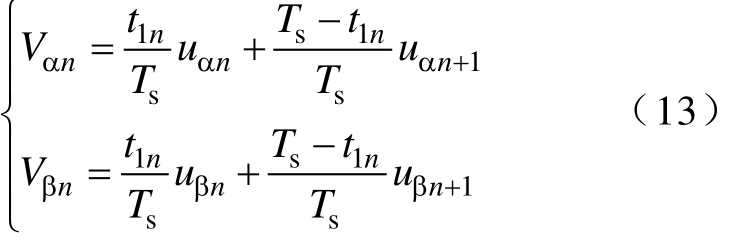
式中,uαn、uβn和 uαn+1、uβn+1分别为电压矢量 un和un+1对应的电压值。
取 E=56V,Ts=1/15 000s,udc=250V,L=20mH,图7给出了虚拟矢量V1作用时三相电流在一个控制周期内的变化量。


图7 电流单周期内的变化量分析
Fig.7 Variation analysis of the current in a single period
由图 7a可知,当虚拟矢量 V1作用时,在θ =180°时,Δia最大;随着电压矢量u1的作用时间 t11逐渐由0增大到Ts,虚拟矢量V1逐渐由u2向u1移动,Δia也逐渐增大;当 t11=Ts时,虚拟矢量 V1与u1和a相同相,Δia达到最大值,为0.742 2A,如图7a所示。同理,在θ =240°,t11=0时,虚拟矢量V1与 u2重合,与 c相反相,|Δic|达到最大值,也为0.742 2A,如图7c所示。
结合式(11)~式(13)也可得到,当θ =180°,t11=Ts时,Δia达到最大值,且满足
同理,当θ =240°,t11=0 时,|Δic|达到最大值,且满足
当其他虚拟矢量作用时,也可得到三相电流在单周期内的最大变化量,均满足式(14)和式(15)。经过计算可得,其最大值与图7相同,均为0.742 2A。
为了避免因控制延时而导致选择电压矢量时和最优电压矢量作用时的电流扇区不一致,应该保证在电流滞环宽度δ 大于电流单周期内的最大变化量时选择图4a所示的虚拟矢量预选方法,而在δ 小于电流单周期内的最大变化量时选择图 4b所示的电压矢量预选方法。为此,可根据下式选择δ,即
式中,k为增益系数,满足k≥1。
6 仿真与实验结果
6.1 仿真结果
为了验证所提方法的有效性,基于Matlab/Simulink建立了仿真系统,并进行了仿真研究。仿真中,VSI直流侧电压设为 250V,交流反电动势幅值设为56V,频率为 50Hz,负载电感为 20mH,负载电阻为0.05Ω,控制周期设为1/15 000s,死区时间为2μs。仿真中本文所提方法和文献[22]所提单矢量法的电流滞环δ 均设为0.75A。
仿真时,采用锁相环得到反电动势的角度,并将反电动势矢量定向在d轴上。图8给出了d轴电流为8A,q轴电流为0时的三相电流和共模电压的仿真结果。图8a为不考虑死区影响时的虚拟矢量法的仿真结果,为方便起见,这里称之为方法 1。图8b为在电流扇区7内仅使用两个虚拟矢量以克服死区影响,而在其他电流扇区内则使用图4a所示方法的仿真结果,为方便起见,这里称之为方法 2。图8c为本文最后提出的改进型虚拟矢量法(见图6)的仿真结果。图8d为文献[22]所提单矢量法的仿真结果。

图8 四种方法的稳态仿真结果
Fig.8 Steady-state simulation results of the four methods
由图8a可见,不考虑死区影响时,虽然实际电流可以得到较好控制,但其共模电压存在较多的电压尖峰,且该尖峰值均为udc/2,这与表3所示的分析结果一致。由图8b可见,当在电流扇区7内只采用两个虚拟矢量时,由于备选电压矢量太少,导致电流出现失控现象,三相电流在过零点附近,即扇区7内出现明显畸变,这也与理论分析一致。由图8c和图8d可见,本文所提方法和文献[22]所提单矢量法均既能实现共模电压抑制,又可以避免电流畸变。但是,由图9所示的电流THD可见,由于所提方法使用了虚拟矢量,其在电流扇区1~6内每个控制周期同时有两个非零电压矢量作用,因此其电流THD明显减小。

图9 电流THD仿真结果
Fig.9 Simulation results of the current THD
6.2 实验结果
为了进一步验证所提方法的有效性,建立了实验平台,并进行了实验研究,实验平台如图10所示。该平台采用Myway的APL-II型可编程双向直流电源作为直流侧,采用 Ametek的可编程交流电源来模拟交流反电动势负载。直流侧电压、反电动势幅值、RL参数、控制周期及死区时间均与仿真一致。实验中,由于实际VSI非线性特性的影响,导致其电流纹波比理论值大,因此文献[22]和本文所提方法的电流滞环δ 均设为0.9A。

图10 实验平台
Fig.10 Experimental platform
图11 和图12对比研究了常规单矢量法和本文所提方法的稳态电流控制效果。图11给出了反电动势频率为50Hz,d轴电流为8A,q轴电流为0时的实验结果。其中,图11a为常规单矢量法的实验结果,图11b为本文所提虚拟矢量法的实验结果。


图11 稳态实验结果(50Hz,8A)
Fig.11 Steady state experimental results (50Hz, 8A)

图12 稳态实验结果(20Hz,8A)
Fig.12 Steady state experimental results (20Hz, 8A)
由图11可见,常规单矢量法和本文所提虚拟矢量法均可以将共模电压完全抑制在±udc/6之内。然而,与常规单矢量法相比,本文所提方法由于在电流扇区 1~6内的每个控制周期里同时使用了两个非零电压矢量,因此其电流纹波明显较小。
图12给出了反电动势频率为20Hz时同样条件下两种方法的稳态实验结果。对比可见,本文所提虚拟矢量法仍然具有较低的电流纹波,这进一步验证了所提方法的有效性。
图 13进一步对比了稳态下这两种方法的电流THD值。图13a为反电动势频率为50Hz时的实验结果,图13b则为20Hz时的实验结果。由图13可以清晰地看到,本文所提方法在实现共模电压抑制的同时,可以明显减小电流THD,这进一步验证了其有效性。

图13 电流THD对比
Fig.13 Comparison of the current THD
图 14进一步对比了这两种方法的动态响应结果。实验时,反电动势频率设为50Hz,d轴电流由3A突增为8A。由图14可见,两种方法均可以实现共模电压抑制,且均具有较好的动态响应过程,这也验证了所提方法的有效性。

图14 实验结果对比
Fig.14 Comparison of dynamic state experimental results
7 结论
针对两电平VSI常规单矢量模型预测共模电压抑制法存在电流THD较大的问题,本文提出了一种基于虚拟矢量的VSI模型预测共模电压抑制方法。详细分析了死区、控制延时对所提方法的影响,并进行了改进,从而可将共模电压完全限制在±udc/6之内。此外,还详细分析了电流滞环宽度的设计方法,从而为所提方法的具体实现奠定了理论基础。仿真和实验结果均表明,与单矢量模型预测共模电压抑制法相比,本文所提方法在实现共模电压抑制的同时,通过使用虚拟矢量,明显降低了电流THD,提高了电流的动稳态控制性能。
[1] 姚骏, 刘瑞阔, 尹潇. 永磁同步电机三矢量低开关频率模型预测控制研究[J]. 电工技术学报, 2018,33(13): 2935-2945.Yao Jun, Liu Ruikuo, Yin Xiao. Research on 3-vector model predictive control with low switching frequency of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 2935-2945.
[2] 徐艳平, 王极兵, 张保程, 等. 永磁同步电机三矢量模型预测电流控制[J]. 电工技术学报, 2018,33(5): 980-988.Xu Yanping, Wang Jibing, Zhang Baocheng, et al.Three-vector-based model predictive current control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(5):980-988.
[3] 尚姝钰, 陈豪, 姜素霞, 等. 基于模型预测控制的有源电力滤波器开关损耗优化设计[J]. 轻工学报,2017, 32(2): 103-108.Shang Shuyu, Chen Hao, Jiang Suxia, et al.Optimized design of active power filter switching loss based on model predictive control[J]. Journal of Light Industry, 2017, 32(2): 103-108.
[4] 黄文涛, 花为, 於锋. 考虑定位力矩补偿的磁通切换永磁电机模型预测转矩控制方法[J]. 电工技术学报, 2017, 32(15): 27-33.Huang Wentao, Hua Wei, Yu Feng. A model predictive torque control scheme for flux-switching permanent magnet machines with cogging torque compensation[J]. Transactions of China Electrotechnical Society, 2017, 32(15): 27-33.
[5] 李伟, 张勇军, 肖雄. 实时电感辨识的模型预测并网逆变器控制方法[J]. 电工技术学报, 2018, 33(15):3450-3460.Li Wei, Zhang Yongjun, Xiao Xiong. The model predictive grid-connected inverter control method based on real-time inductance identification[J].Transactions of China Electrotechnical Society, 2018,33(15): 3450-3460.
[6] 尹靖元, 金新民, 杨捷, 等. 开绕组电机驱动用双三电平逆变器的共模电压差抑制[J]. 电工技术学报, 2016, 31(15): 178-186.Yin Jingyuan, Jin Xinmin, Yang Jie, et al. The differential common mode voltage elimination of dual three-level converter for open-end winding motor drives[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 178-186.
[7] 黄守道, 张文娟, 高剑, 等. 准谐振控制器在抑制永磁同步电动机共模电压上的应用[J]. 电工技术学报, 2013, 28(3): 93-98.Huang Shoudao, Zhang Wenjuan, Gao Jian, et al.Application of quasi-resonant controller for suppressing the common-mode voltage of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 93-98.
[8] 王宝诚, 郭小强, 杨勇, 等. 阻抗源四桥臂光伏逆变器共模特性研究[J]. 电工技术学报, 2018, 33(24):5848-5855.Wang Baocheng, Guo Xiaoqiang, Yang Yong, et al.Common mode behavior for Z-source four-leg inverter[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5848-5855.
[9] 郭小强, 贾晓瑜. 非隔离型级联 H5光伏逆变器共模漏电流特性分析[J]. 电工技术学报, 2018, 33(2):361-369.Guo Xiaoqiang, Jia Xiaoyu. Analysis of common mode leakage current for transformerless cascaded H5 PV inverter[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 361-369.
[10] 郭小强, 王学惠, 杨勇, 等. 三相六开关三电平光伏逆变器漏电流抑制[J]. 电工技术学报, 2018,33(14): 3255-3263.Guo Xiaoqiang, Wang Xuehui, Yang Yong, et al.Leakage current attenuation of three-phase six-switch three-level photovoltaic inverter[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3255-3263.
[11] 王汝田, 赵艳锋, 母兴军, 等. 五相双级矩阵变换器共模电压的抑制策略[J]. 电力自动化设备, 2018,38(8): 45-51.Wang Rutian, Zhao Yanfeng, Mu Xingjun, et al.Modulation strategy of common-mode voltage for five-phase two-stage matrix converter[J]. Electric Power Automation Equipment, 2018, 38(8): 45-51.
[12] Vargas R, Rodriguez J, Rojas C A, et al. Predictive control of an induction machine fed by a matrix converter with in-creased efficiency and reduced common-mode voltage[J]. IEEE Transactions on Energy Conversion, 2014, 29(2): 473-485.
[13] Duran M J, Riveros J A, Barrero F, et al. Reduction of common-mode voltage in five-phase induction motor drives using predictive control techniques[J].IEEE Transactions on Industry Applications, 2012,48(6): 2059-2067.
[14] Kouro S, Cortes P, Vargas R, et al. Model predictive control-a simple and powerful method to control power converters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1826-1838.
[15] Rojas C A, Aguirre M, Kouro S, et al. Leakage current mitigation in photovoltaic string inverter using predictive control with fixed average switching frequency[J]. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9344-9354.
[16] Vargas R, Ammann U, Rodriguez J, et al. Predictive strategy to control common-mode voltage in loads fed by matrix converters[J]. IEEE Transactions on Industrial Electronics, 2008, 55(12): 4372-4380.
[17] 郭磊磊, 金楠, 申永鹏. 一种基于优化电压矢量选择的电压源逆变器模型预测共模电压抑制方法[J].电工技术学报, 2018, 33(6): 1347-1355.Guo Leilei, Jin Nan, Shen Yongpeng. A mode predictive common-mode voltage suppression method for voltage source inverter based on optimum voltage vector selection[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1347-1355.
[18] Hoseini S K, Adabi J, Sheikholeslami A. Predictive modulation schemes to reduce common-mode voltage in three-phase inverters-fed AC drive systems[J]. IET Power Electronics, 2014, 7(6): 840-849.
[19] Mun S, Kwak S. Reducing common-mode voltage of three-phase VSIs using the predictive current control method based on reference voltage[J]. Journal of Power Electronics, 2015, 15(3): 712-720.
[20] Guo Leilei, Zhang Xing, Yang Shuying, et al. A model predictive control based common-mode voltage suppression strategy for voltage source inverter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6115-6125.
[21] Kwak S, Mun S. Common-mode voltage mitigation with a predictive control method considering dead time effects of three-phase voltage source inverters[J].IET Power Electronics, 2015, 8(9): 1690-1700.
[22] Guo Leilei, Jin Nan, Gan Chun, et al. An improved model predictive control strategy to reduce common-mode voltage for two-level voltage source inverters considering dead-time effects[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5):3561-3572.
[23] 康劲松, 李旭东, 王硕. 计及参数误差的永磁同步电机最优虚拟矢量预测电流控制[J]. 电工技术学报, 2018, 33(24): 5731-5740.Kang Jinsong, Li Xudong, Wang Shuo. Optimal virtual vector predictive current control for permanent magnet synchronous motor considering parameter Errors[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5731-5740.
[24] Vijayagopal M, Zanchetta P, Lillo L D, et al. Control of a direct matrix converter with modulated model predictive control[J]. IEEE Transactions on Industry Applications, 2017, 53(3): 2342-2349.
[25] 李兵强, 林辉. 面装式永磁同步电机电流矢量直接控制技术[J]. 中国电机工程学报, 2011, 31(增刊1):288-294.Li Bingqiang, Lin Hui. Direct control of current vector for surface-mounted permanent magnet synchronous motor[J]. Proceedings of the CSEE,2011, 31(S1): 288-294.