0 引言
相比于传统两电平逆变器，在中压、大功率场合，多电平逆变器已成为极具吸引力的替代方案，在相同的工作状态下，多电平逆变器可利用传统功率器件，而不需价格相对昂贵的新型功率器件，而且由于输出电压为多电平波形，使得输出波形质量更优，具有更小的电压变化率[1]。因此，多电平逆变器在大功率驱动器、静止无功补偿、柔性交流输电、可再生能源发电等领域得到广泛应用[2-6]。
级联H桥（Cascaded H-Bridge, CHB）型逆变器作为一种基本多电平拓扑，具有易于模块化拓展、无需中点电位控制和飞跨电容稳压控制的特点，但拓扑结构中需多个独立电压源，通常采用多绕组移相变压器结合二极管不控整流供电的方式，该方式下对各级联单元的输出功率提出了相应要求。当各级联单元输出功率相同时，通过设置移相变压器二次绕组的移相角，可消除变压器输入侧电流的低次谐波；当各级联单元输出功率不均衡时，通过设计移相角来消除输入侧谐波电流变得困难，导致大量的谐波电流注入电网，尤其是大功率应用场合，将对电网造成较大不利影响[7-8]。
为实现级联单元间的功率均衡，文献[9]基于阶梯波调制策略，通过不同级联单元开关模式的交换，控制各级联单元在固定时间内包含相同的基本电压波形，实现了单元间的功率均衡控制，但在低频调制中，低次谐波含量较高，影响逆变器输出电压的波形质量。载波移相（Carrier Phase Shift, CPS）调制策略的输出功率均分效果较好[10]，但线电压谐波较差；载波同相层叠（Phase Disposition, PD）调制策略输出线电压谐波特性最优[11]，但不能实现级联单元间的功率均衡控制。针对 PD调制策略下的功率均衡问题，文献[12-13]基于传统 PD载波，以载波周期为单位，改变相邻载波周期内的载波偏移量，在构成的新载波周期内可实现单元间的功率均衡控制，但载波偏移量的变化，会额外增加功率器件的开关次数，导致开关损耗增加。文献[14]提出错位等周期循环法，以实现单元间的功率均衡控制，通过改变各串联 H桥单元的控制脉冲宽度和循环次序，减少了开关动作次数，但该方法需计算各级联单元的输出脉冲宽度，同时需对各单元输出脉冲的起始时刻进行调整，实现相对复杂。文献[15]提出了一种具有PD和CPS优点的空间矢量调制策略，但随着电平数的增加，空间矢量调制技术实现和应用较为困难。文献[16]提出一种改进模型预测控制方法，可改善级联单元间的功率分配，但该方法需进行大量计算才能实现准确预测，计算过程复杂。
本文以三单元CHB型逆变器为研究对象，首先分析传统载波层叠调制策略下的功率不均衡问题；其次，指出基于载波控制自由度，可实现级联单元输出的重分配，依据该特性，文中提出基于 1/4和1/2输出周期脉冲循环的两种功率均衡方案；同时，为简化实现过程，对所提的两种功率均衡方案进行两次优化，并将优化后功率均衡方案和原始方案以及传统方法进行比较。最后，利用实验结果验证本文所提功率均衡方案的正确性与可行性。
1 CHB型逆变器的传统调制策略
1.1 CHB型逆变器
图1所示为三单元CHB型逆变器，各级联单元拓扑相同，均为H桥结构，级联单元i直流侧电压Udci=E（i=1, 2, 3），交流侧输出电压为 uoi；逆变器输出电压和电流分别为uo和io。
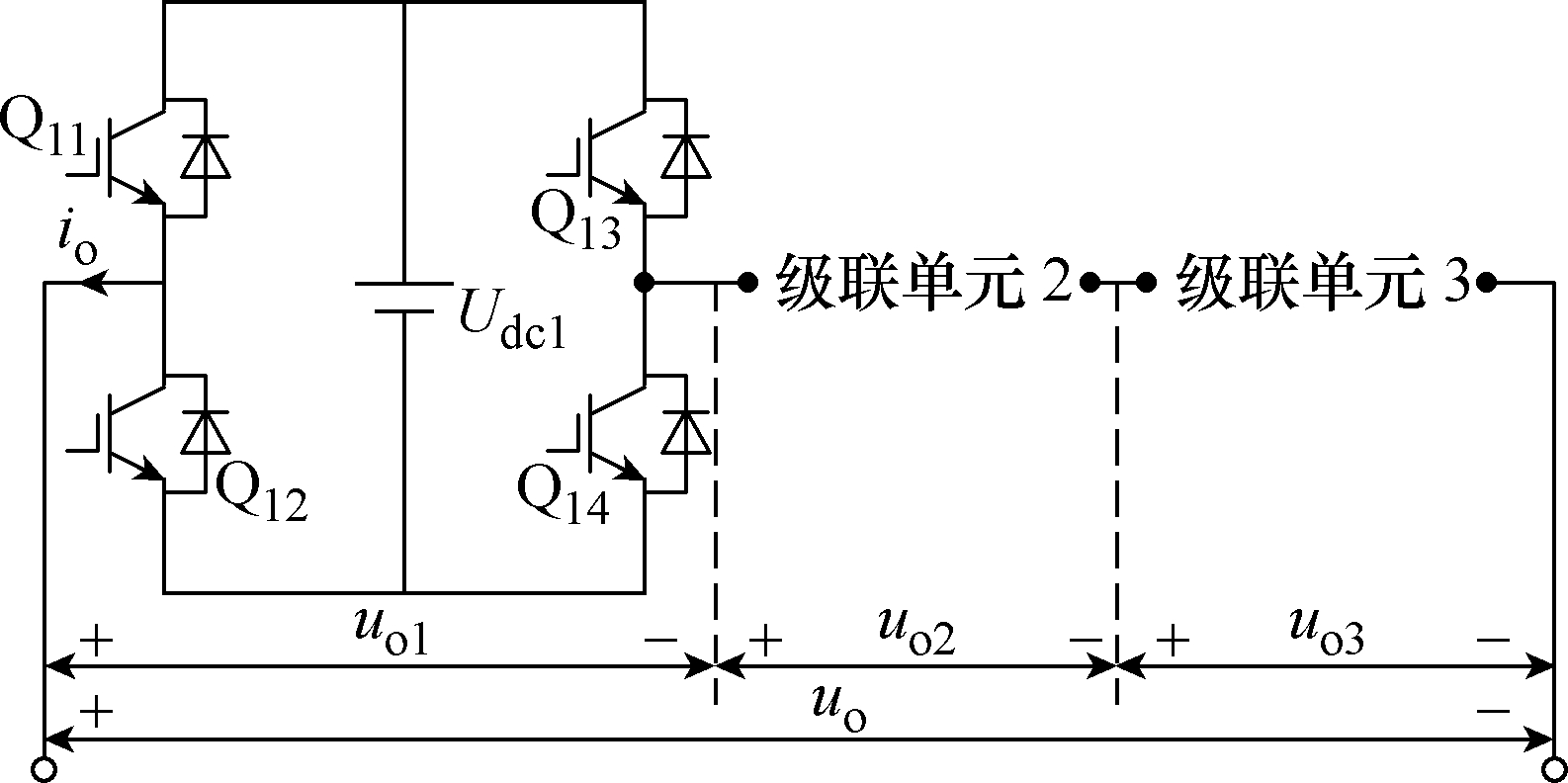
图1 三单元CHB型逆变器
Fig.1 Three cells cascaded H-bridge inverter
忽略逆变器输出电流io中的谐波成分，只考虑基波成分，设其表达式为
式中，I为逆变器输出电流幅值；ϕ 为功率因数角。
逆变器输出电压 uo可由级联单元输出电压 uoi表示为
级联单元i输出电压uoi存在±E、0三种电平，对于三单元 CHB型逆变器而言，共可输出±3E、±2E、±E、0七种电平。由于逆变器输出电平存在多种组合方式，因此，可在保证逆变器输出不变的情况下，通过主动改变各级联单元的输出，实现特定的控制需要。
1.2 传统调制策略及其功率不均问题
图 2所示为载波层叠调制原理。图中，utri+与utri-为级联单元i的载波信号，分布于时间轴上下两侧；调制比为m时，设正弦调制波uref表达式为
图2 载波层叠调制原理
Fig.2 Principle of carrier disposition modulation
在正半周前1/4周期，定义调制波uref与载波分层线 E和 2E的交点分别对应时间轴上的开关角θ1和θ2，其表达式为
当载波频率远大于调制波频率时，基于状态空间平均法，在开关周期内，可用输出电压的平均值代替其瞬时值。因此，采用图2所示调制策略时，级联单元 1～3的输出电压开关周期平均值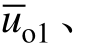
波形如图3所示。从图中可以看出，各级联单元具有不同的输出电压平均值曲线，则级联单元 1～3具有不相等的输出电压基波分量。在 CHB型逆变器中，级联单元平均输出功率正比于输出电压基波分量幅值，因此，采用传统载波层叠调制策略，级联单元间存在功率不均衡问题。尤其在低调制度的情况下，将会存在输出功率为零的级联单元，功率不均衡问题尤为明显。
图3 级联单元输出电压开关周期平均值
Fig.3 Average output voltage of cascaded cells in switching cycle
逆变器输出电压uo的开关周期平均值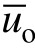
为
根据式（1）、式（5）可计算得到逆变器平均输出功率为
2 级联单元输出重分配机制
为保证逆变器输出线电压谐波特性最优，本文以传统载波同相层叠调制策略为基础[17]，对各级联单元输出进行重分配，以达到功率均衡的目的。
2.1 基于控制自由度的输出重分配
由正弦脉宽调制（Sinusoidal PWM, SPWM）原理可知，输出电压波形由调制波与载波共同决定，而二者均存在多个控制自由度。本节基于载波垂直偏移量自由度，分析载波不同垂直偏移量对级联单元输出的影响。
级联单元i为单极性调制，输出极性取决于正、负半周期，输出波形取决于调制波和与其相交截的载波。此时，定义交截载波相对于时间轴的垂直偏移量为Δli，当交截载波位于时间轴上侧时，Δli取值为1, 2, 3；当交截载波位于时间轴下侧时，Δli取值为-1, -2, -3。以正半周为例，图4给出了两种不同的载波分布情况，分别定义为情况1和情况2。
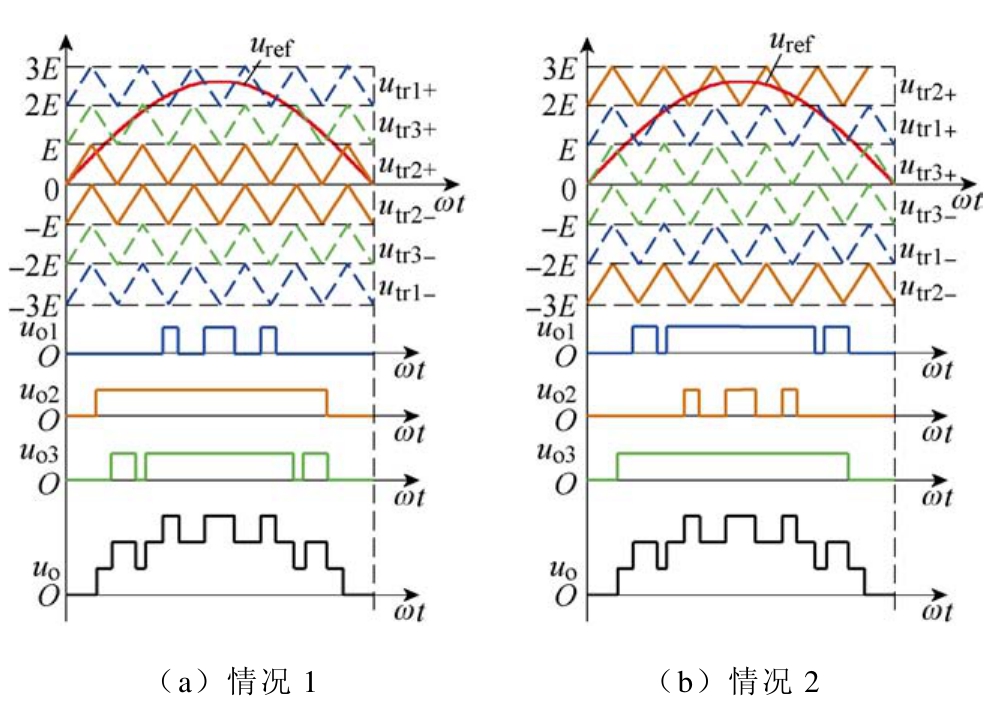
图4 不同Δli下的输出电压
Fig.4 Output voltage under different Δli
从图 4中可以看出，图4a对应级联单元 1～3交截载波的偏移量分别为Δl1=3、Δl2=1、Δl3=2；图4b对应级联单元 1～3交截载波的偏移量分别为Δl1=2、Δl2=3、Δl3=1。显然，图 4a与图 4b载波分布和级联单元输出不同，但二者对应相同的逆变器输出。当载波分布为其余情况或逆变器输出位于负半周期时，可得到相同的结论。因此，通过交截载波垂直偏移量Δli的调整，可仅改变单元输出，根据该特点，便可在不影响逆变器总功率输出的情况下，实现各级联单元输出功率的重新分配。
2.2 级联单元输出电压平均值
为便于下文计算级联单元的平均输出功率，本节给出级联单元输出电压开关周期平均值通式。以2/3＜m≤1为例，当Δli取值不同时，级联单元 i的输出电压开关周期平均值
如图5所示。
图5 不同Δli下级联单元i输出电压平均值
Fig.5 Average output voltage of cell i under different Δli
结合图 5，在第 x个输出周期，输出电压开关周期平均值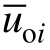
关于偏移量Δli和时间ωt的通式为
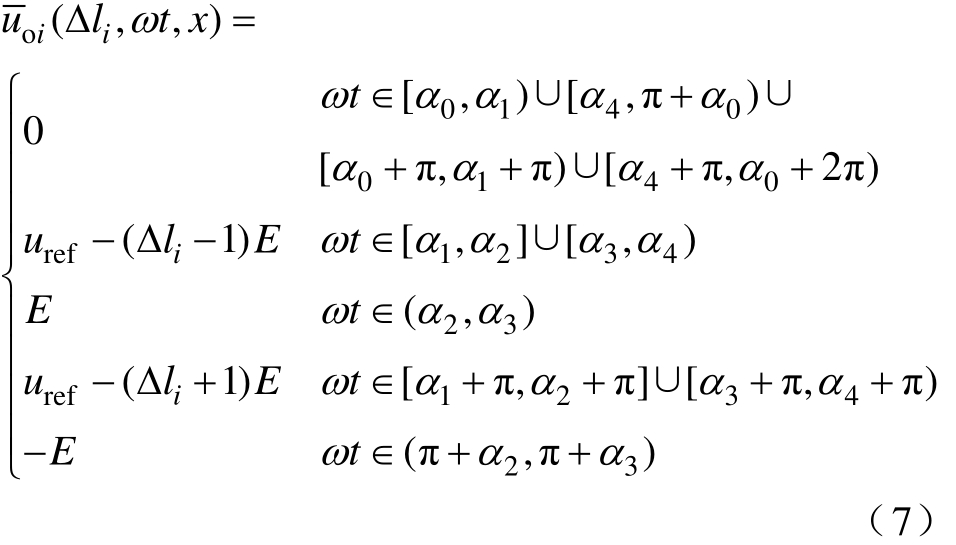
式中， 开关角α0、α1、α2、α3、α4表达式为
3 输出周期脉冲循环新型功率均衡方案
以 2.1节理论为基础，本文通过载波空间分布的调整，实现输出脉冲的循环，进而对级联单元输出功率进行控制。根据脉冲循环基本单位的不同，下文提出两种功率均衡解决方法及其优化方案。
3.1 基于1/4输出周期脉冲循环功率均衡方案
以1/4输出周期（To/4）为基本单位进行脉冲循环，得到图6所示功率均衡方法。由图6可知，相比于图2所示传统调制策略，级联单元i载波不再单一分布在某一特定层域，而是随着时间推移，在不同载波层域循环分布，但逆变器输出电压uo未发生变化，仅级联单元输出电压uoi改变。
以级联单元1为例，在区间[0, 3π]内，与调制波uref相交截载波的垂直偏移量Δl1依次为3、1、-2、-3、1、2。此时，由式（7）可得输出电压开关周期平均值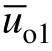
表达式为
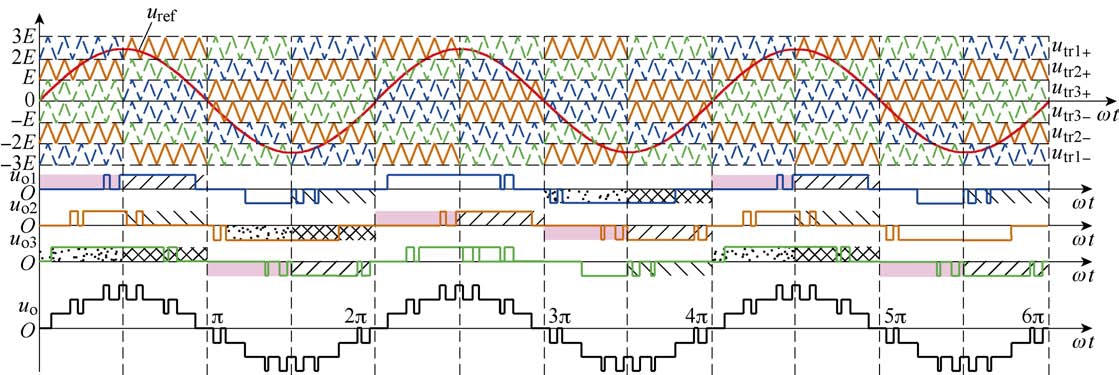
图6 基于1/4输出周期脉冲循环的功率均衡方案
Fig.6 Power balance method based on pulse circulation in quarter output period
结合式（1）与式（13），可计算得到级联单元1在前、后 3To/4内的平均输出功率 Po1(3To/4)1、Po1(3To/4)2分别为
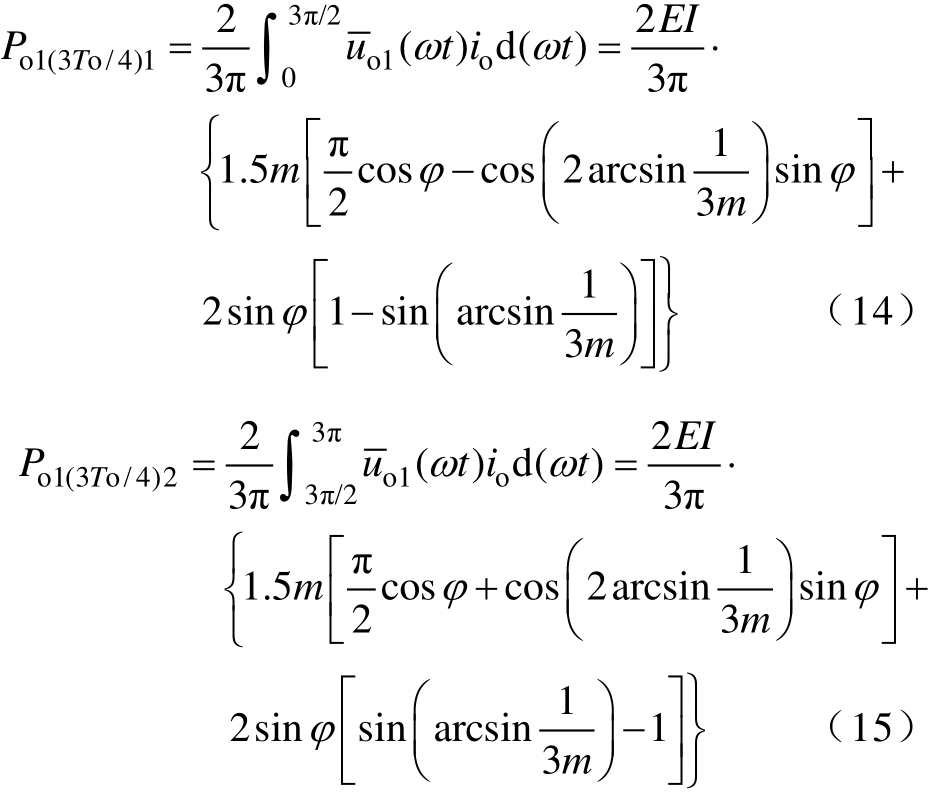
从式（14）和式（15）中可以看出，当功率因数角ϕ =0 时，Po1(3To/4)1=Po1(3To/4)2=0.5mEIcosϕ =Po/3，表明此时级联单元1在3To/4内获得均分功率；当功率因数角ϕ ≠0时，P(3To/4)1、P(3To/4)2不等于Po/3，即无法在3To/4内获得均分功率，但此时3To/2内的平均输出功率Po1(3To/2)为
此时，级联单元1在3To/2内可获得均分功率。
级联单元2、3以及区间[3π, 6π]内各单元的平均输出功率计算同理，可得到相同结论。
综上可知，级联单元1～3可实现功率均衡，且功率均衡时间与ϕ 相关。经分析可知，当ϕ ≠0时，在功率均衡时间3To/2内，每个级联单元均可输出6种以To/4为单位的独立基本电压，对应6种不等的基本功率；当ϕ =0时，在功率均衡时间3To/4内，每个级联单元均可输出3种以To/4为单位的独立基本电压，对应3种不等的基本功率，这是图6所示方案可实现功率均衡的本质原因。
3.2 基于1/2输出周期脉冲循环功率均衡方案
以To/2为基本单位进行脉冲循环，得到图7所示功率均衡方法。此时，载波调整的基本单位由To/4变为To/2，且仅级联单元输出电压uoi改变。
同样地，以区间[0, 3π]内的级联单元1为例，此时与调制波相交截载波的垂直偏移量Δl1依次为3、-2、1。由式（7）可得输出电压开关周期平均值
表达式为
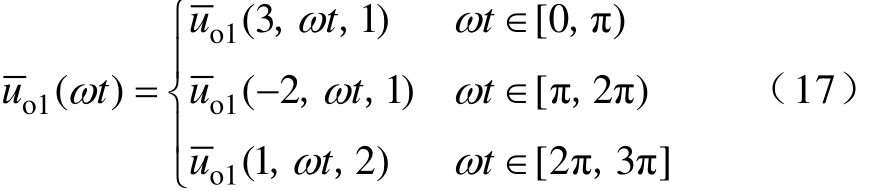
结合式（1）与式（17），可得前、后3To/4内的平均输出功率Po1(3To/4)1、Po1(3To/4)2分别为
图7 基于1/2输出周期脉冲循环的功率均衡方案
Fig.7 Power balance method based on pulse circulation in half output period
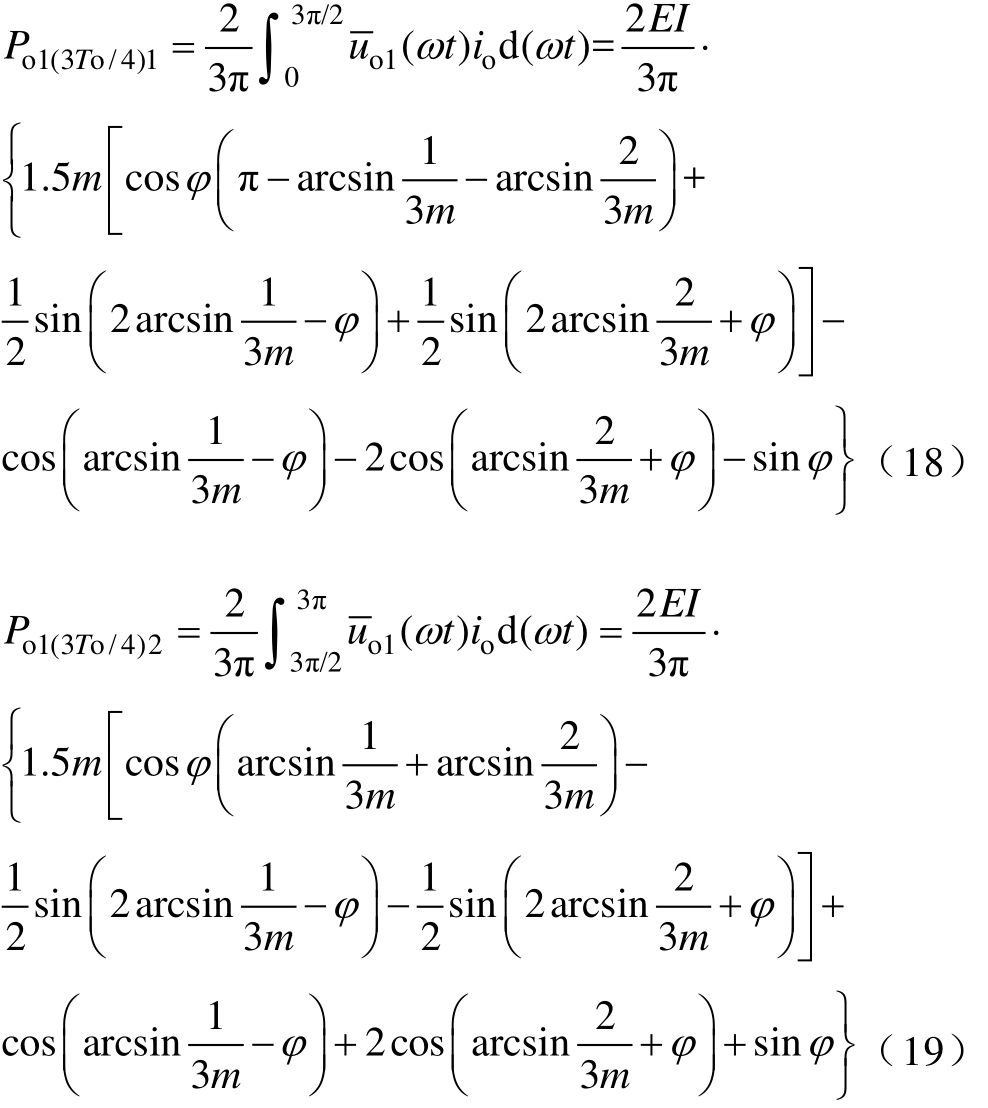
从式（18）、式（19）中可以看出，无论功率因数角ϕ 是否为零，在3To/4内，Po1(3To/4)1、Po1(3To/4)2均不等于 Po/3，表明级联单元1无法在 3To/4内获得均分功率。但3To/2内的平均输出功率Po1(3To/2)为
可以看出，此时级联单元1在3To/2内可获得均分功率。
级联单元2、3以及区间[3π, 6π]内各单元的平均输出功率计算同理，可得到相同结论。
综上可知，级联单元1～3可实现功率均衡，且功率均衡时间与ϕ 无关。经分析可知，在功率均衡时间3To/2内，每个级联单元均可输出 3种以To/2为单位的独立基本电压，对应3种不等的基本功率，这是图7所示方案可实现功率均衡的本质原因。
4 功率均衡方案优化
4.1 功率均衡方案的一次优化
本文提出的两种功率均衡方案在调制过程中均需要6个载波信号，调制实现相对复杂。本节对所提两种功率均衡方案的载波个数进行优化。
2.1 节分析表明，对于级联单元i而言，与调制波无交截的载波属于冗余载波，去除该冗余载波并不会对级联单元输出产生影响。因此，分别去除正半周期时间轴以下的载波和负半周期时间轴以上的载波，并将负半周期调制波与载波同时向上平移3E，得到基于 1/4和 1/2输出周期脉冲循环的一次优化方案，分别如图8和图9所示。从图中可以看出，两种功率均衡方案此时调制仅需分布于时间轴之上的载波，载波数量减少为原来一半，调制波由uref变为um，um表达式为
对比图6与图8、图7与图9可知，载波个数的减少，并未对级联单元及逆变器输出电压波形产生影响，因此，级联单元间的功率均衡特性和逆变器的输出特性保持不变。
4.2 功率均衡方案的二次优化
经上述优化，调制所需载波数量明显减少，但两种优化方案的载波调整次数仍较多，给载波的生成造成一定困难。为此，本节进一步对载波调整次数进行优化，得到基于 1/4和 1/2输出周期脉冲循环的二次优化方案，分别如图10和图11所示。
图12所示为优化前后，在3To内，不同级联单元的载波调整次数对比。显然，经优化后，两种功率均衡方案各级联单元的载波调整次数均大幅减少，简化了调制实现难度。但优化后，级联单元间的功率分配情况有待进一步分析。
图8 基于1/4输出周期脉冲循环的一次优化方案
Fig.8 Optimized method based on pulse circulation in quarter output period
图9 基于1/2输出周期脉冲循环的一次优化方案
Fig.9 Optimized method based on pulse circulation in half output period
图10 基于1/4输出周期脉冲循环的二次优化方案
Fig.10 Further optimized method based on pulse circulation in quarter output period
图11 基于1/2输出周期脉冲循环的二次优化方案
Fig.11 Further optimized method based on pulse circulation in half output period
图12 优化前后的载波调整次数
Fig.12 Carrier adjustment times before and after optimization
为便于分析，定义第x个输出周期从左至右的每个 1/4输出周期分别为区域 A(2x-1)1、A(2x-1)2、A(2x)1、A(2x)2。对于基于1/4输出周期脉冲循环的功率均衡方案而言，由图8与图10可知，载波调整次数优化前后，区域 A22至区域 A62内的载波分布及级联单元输出不同。
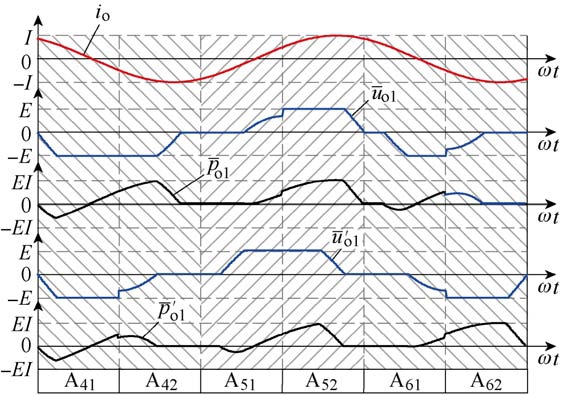
图13 [3π, 6π]内级联单元1输出功率（To/4）
Fig.13 Output power of cell 1 in interval [3π, 6π] (To/4)
图13 所示为[3π, 6π]内，级联单元1的功率波形。图中，
分别为图8、图10载波分布下级联单元输出电压平均值与功率。
基于电压波形及逆变器输出电流波形的对称性，并结合图13，表1所示为图8与图10中级联单元1输出功率的对应关系。由表1可知，从图8～图10载波调整次数优化的过程中，级联单元1的功率变化属于每个 3To/2的内部调整，整体上每个3To/2的平均输出功率不变。级联单元2和3同理，因此，级联单元间的功率均衡特性及功率均衡时间不变。
表1 输出功率对应关系（To/4）
Tab.1 Relationship of output power (To/4)
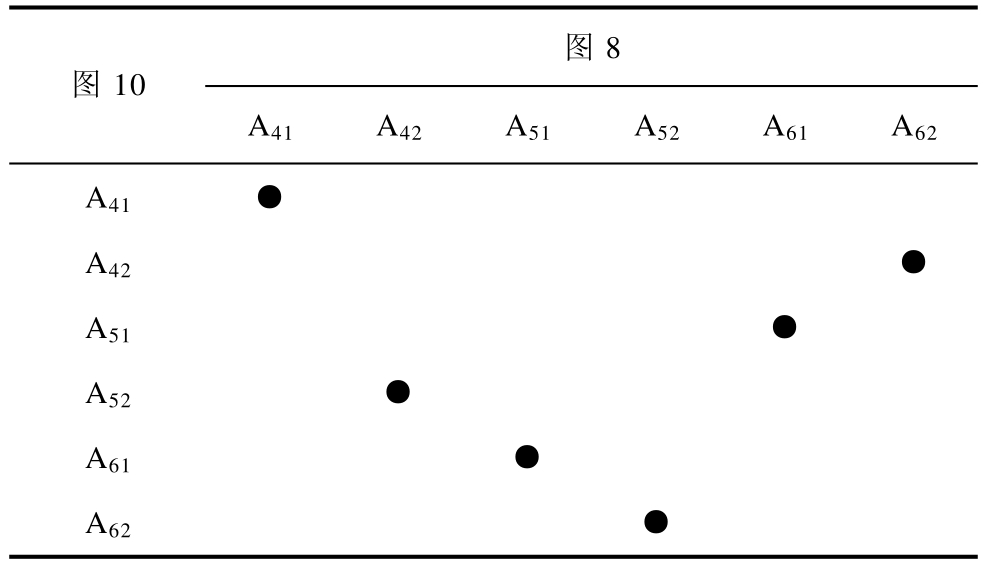
注：“●”—平均输出功率相等区域。
图8图10 A41 A42 A51 A52 A61 A62 A41 ●A42 ●A51 ●A52 ●A61 ●A62 ●
对于基于1/2输出周期脉冲循环功率均衡方案而言，由图9与图11可知，载波调整次数优化前后，仅区域A41～A62内的载波分布及级联单元输出不同。图14所示为[3π, 6π]内，级联单元1的功率波形。图中，
分别为图9、图11载波分布下级联单元输出电压平均值与功率。
图14 [3π, 6π]内级联单元1输出功率（To/2）
Fig.14 Output power of cell 1 in interval [3π, 6π] (To/2)
结合图14，表2所示为图9与图11中级联单元1输出功率的对应关系。可得与表1相同结论，各级联单元的功率变化仅属于每个 3To/2的内部调整，整体上 3To/2的平均输出功率不变，同样功率均衡特性及功率均衡时间不变。
表2 输出功率对应关系（To/2）
Tab.2 Relationship of output power (To/2)
注：“●”—平均输出功率相等区域。
图9图11 A41+A42 A51+A52 A61+A62 A41+A42 ●A51+A52 ●A61+A62 ●
前文分析均以调制比 m＞2/3为例，当 m≤2/3时，亦能得到相同结论，因此所提方案均能够在任意调制比和功率因数角下，控制级联单元在 3/2个输出周期内实现功率均衡。
5 功率均衡方案对比及拓展
本文提出的基于 1/4和 1/2输出周期脉冲循环的功率均衡方案均能实现级联单元间功率均衡控制。下文将对两种功率均衡原始方案及其优化方案在载波循环方式、载波循环周期、载波循环周期内的对称中线、3个输出周期（3To）内的载波调整次数、级联单元输出电压循环周期、功率均衡时间等方面进行对比分析。
表3给出了两种功率均衡方案的对比结果。从表中可以看出，每种功率均衡方案经一次和二次优化后，相比于各自原始方案在载波个数、载波调整次数两方面得到了逐步优化；此外，两种功率均衡方案无论是原始方案对比，还是优化方案对比，基于 1/2输出周期脉冲循环的功率均衡方案相比于基于1/4输出周期脉冲循环的功率均衡方案，其在3To内的载波调整次数明显较少，如原始方案、一次优化方案、二次优化方案中，基于 1/2输出周期脉冲循环功率均衡方案的载波调整次数依次为36次、12次、8次，而基于 1/4输出周期脉冲循环功率均衡方案的载波调整次数依次为66次、30次、20次；同时，优化前后，级联单元输出电压循环周期相同，且均能在 3To/2内实现功率均衡，但在功率因数角ϕ =0时，基于1/4输出周期脉冲循环功率均衡方案的均衡时间仅为3To/4。
本文将基于 1/4和 1/2输出周期脉冲循环的功率均衡方案与传统调制策略相比较，在同一直流侧电压和开关频率下，得到不同调制比下的各方案输出线电压总谐波畸变率（Total Harmonic Distortion，THD），见表4。从表4中可以看出，本文所提功率均衡方案下的输出线电压THD明显小于CPS调制策略，且与 PD调制策略相比，具有相同的输出线电压THD，因此线电压谐波特性最优。
表3 不同功率均衡方案对比
Tab.3 Comparison of different power balance methods
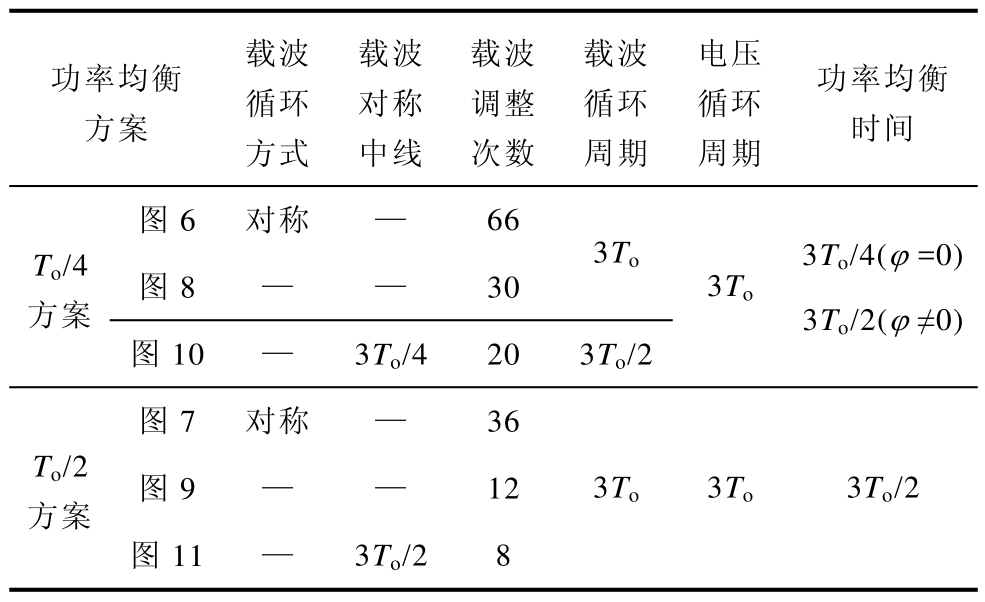
功率均衡方案载波循环方式载波对称中线载波调整次数载波循环周期电压循环周期功率均衡时间图6 对称 — 66 3To To/4方案 图8 — — 303To 3To/4(ϕ =0)3To/2(ϕ ≠0)图10 — 3To/4 20 3To/2图7 对称 — 36 To/2方案 图9 — — 123To 3To 3To/2图11 — 3To/2 8
表4 不同调制方法的THD对比
Tab.4 THD comparison of different modulation methods
THD(%)m To/4方案 To/2方案 CPS PD 0.74 15.31 15.31 22.19 15.31 0.60 17.38 17.38 28.72 17.38
综上所述，无论优化与否，本文所提任意一种新型功率均衡方案均可实现功率均衡和线电压谐波特性最优的双重控制目标。基于 1/2输出周期脉冲循环的功率均衡方案在载波调整次数方面具有优势；当ϕ =0时，基于1/4输出周期脉冲循环的功率均衡方案则在功率均衡时间方面具有优势，两种方案各具特点。
本文所提两种功率均衡方案均可推广应用至 n单元CHB型逆变器中，此时，经二次优化后的方案仅需n个载波，若载波以To/4为基本单位进行调整，则载波循环周期为nTo/2，且循环周期内载波波形关于t=nTo/4左右对称；若载波以To/2为基本单位进行调整，则载波循环周期为 nTo，且循环周期内载波波形关于 t=nTo/2左右对称；在任意功率因数角下，本文所提多种方案的功率均衡时间均为nTo/2，在功率因数角ϕ =0时，基于1/4输出周期脉冲循环功率均衡方案的功率时间将仅为nTo/4。
6 实验验证
经二次优化后的功率均衡方案具有最优效果，因此本文将对图10与图11对应的功率均衡方案进行实验验证。搭建三单元CHB型逆变器实验样机，其中，级联单元直流电压Udci=140V，开关频率fc=14kHz，调制比m=0.74，负载电阻RL=24Ω。
6.1 基于1/4输出周期脉冲循环功率均衡方案
图 15所示为级联单元输出电压 uo1、uo2、uo3的实验波形。从图中可以看出，以To/4为单位，存在6种独立基本电压，级联单元1～3在相同的3To/2内可包含上述6种基本电压；且各级联单元输出电压均为单极性，与前文理论分析一致。
图15 级联单元输出电压（To/4）
Fig.15 Output voltages of cascaded cells (To/4)
图 16所示为逆变器输出电压 uo、负载电阻端电压uL及逆变器输出电流io的实验波形。由图可知，逆变器输出电压为连续变化的七电平 PWM波形，经滤波后，负载电阻两端电压和逆变器输出电流波形正弦性良好，表明逆变器具有良好输出特性。
图16 输出电压及电流（To/4）
Fig.16 Output voltages and current (To/4)
图 17所示为级联单元 1～3的瞬时输出功率po1、po2、po3的实验波形。经测量，在3To/2内，级联单元 1～3平均输出功率 Po1(3To/2)=584.1W、Po2(3To/2)=578.6W、Po3(3To/2)=582.9W。因此，在3To/2内，各级联单元间实现了功率均衡。
6.2 基于1/2输出周期脉冲循环功率均衡方案
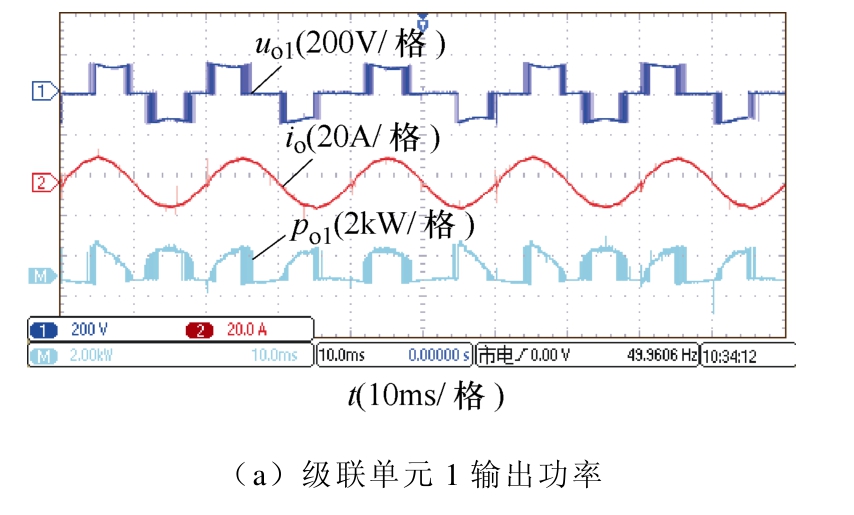
图17 级联单元输出功率（To/4）
Fig.17 Output power of cascaded cells (To/4)
图18 所示为级联单元输出电压uo1、uo2、uo3的实验波形。从图中可以看出，与基于 1/4输出周期脉冲循环的功率均衡方案不同，以To/2为单位，此时存在3种独立基本电压，级联单元1～3在相同的3To/2内可包含上述3种基本电压；同样，级联单元输出电压均为单极性，与前文理论分析一致。
图18 级联单元输出电压（To/2）
Fig.18 Output voltages of cascaded cells (To/2)
图 19所示为逆变器输出电压 uo、负载电阻端电压uL及逆变器输出电流io的实验波形。由图可知，逆变器输出电压为连续变化的七电平PWM波形，经滤波后，负载电阻两端电压和逆变器输出电流波形正弦性良好。
图19 输出电压及电流（To/2）
Fig.19 Output voltages and current (To/2)
图 20所示为级联单元 1～3的瞬时输出功率po1、po2、po3的实验波形。经测量，在3To/2内，级联单元 1～3平均输出功率 Po1(3To/2)=586.7W、Po2(3To/2)=578.6W、Po3(3To/2)=580.6W。因此，在3To/2内，各级联单元间实现了功率均衡。
图20 级联单元输出功率（To/2）
Fig.20 Output power of cascaded cells (To/2)
7 结论
在传统载波层叠调制策略下，CHB型逆变器可实现线电压谐波特性最优控制，但无法实现级联单元间的功率均衡控制。为实现两者的协调控制，本文提出基于 1/4和 1/2输出周期脉冲循环的功率均衡方案，并对两方案进行比较。理论分析和实验结果表明：
1）基于1/4和1/2输出周期脉冲循环的功率均衡方案，均能够在保证逆变器输出线电压谐波特性最优的前提下，实现单元间的功率均衡控制。
2）功率因数角ϕ ≠0时，两种功率均衡方案及优化方案的功率均衡时间均为3To/2；但功率因数角ϕ =0时，基于1/4输出周期脉冲循环的功率均衡方案及优化方案的功率均衡时间缩短为3To/4。
3）两种功率均衡方案经过各自的两次优化，在载波数量和载波调整次数方面均达到了良好的优化效果。
[1] Sahoo S K, Bhattacharya T. Phase-shifted carrierbased synchronized sinusoidal PWM techniques for a cascaded H-bridge multilevel inverter[J]. IEEE Transactions on Power Electronics, 2018, 33(1):513-524.
[2] Kandasamy K, Vilathgamuwa M, Tseng K J. Intermodule state-of-charge balancing and fault-tolerant operation of cascaded H-bridge converter using multi-dimensional modulation for electric vehicle application[J]. IET Power Electronics, 2015, 8(10):1912-1919.
[3] Reddy B P, A M R, Sahoo M, et al. A fault-tolerant multilevel inverter for improving the performance of a pole-phase modulated nine-phase induction motor drive[J]. IEEE Transactions on Industrial Electronics,2018, 65(2): 1107-1116.
[4] 陈玉, 文明浩, 尹项根, 等. 配电变压器集成式级联STATCOM原理与设计[J]. 电工技术学报, 2018,33(12): 2861-2872.Chen Yu, Wen Minghao, Yin Xianggen, et al.Principle and design of the cascaded STATCOM integrated with distribution transformer[J]. Transactions of China Electrotechnical Society, 2018,33(12): 2861-2872.
[5] Zabalza J C, Moreno P I, Madariaga D, et al. Voltage balancing control in 3-level neutral-point clamped inverters using triangular carrier PWM modulation for FACTS applications[J]. IEEE Transactions on Power Electronics, 2013, 28(10): 4473-4484.
[6] Ge Baoming, Liu Yushan, Abu-Rub H, et al. Stateof-charge balancing control for a battery-energystored quasi-Z-source cascaded multilevel inverter based photovoltaic power system[J]. IEEE Transactions on Industrial Electronics, 2018, 65(3): 2268-2279.
[7] Hammond P W. A new approach to enhance power quality for medium voltage AC drives[J]. IEEE Transactions on Industry Applications, 1997, 33(1):202-208.
[8] Rech C, Pinheiro J R. Line current harmonics reduction in multipulse connection of asymmetrically loaded rectifiers[J]. IEEE Transactions on Industrial Electronics, 2005, 52(3): 640-652.
[9] Tolbert L M, Peng Fangzheng, Cunnyngham T, et al.Charge balance control schemes for cascade multilevel converter in hybrid electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2002, 49(5):1058-1064.
[10] Monopoli V G, Marquez A, Leon J I, et al. Improved harmonic performance of cascaded H-bridge converters with thermal control[J]. IEEE Transactions on Industrial Electronics, 2019, 66(7): 4982-4991.
[11] Carrara G, Gardella S, Marchesoni M, et al. A new multilevel PWM method: a theoretical analysis[J].IEEE Transactions on Power Electronics, 1992, 7(3):497-505.
[12] Angulo M, Lezana P, Kouro S, et al. Level-shifted PWM for cascaded multilevel inverters with even power distribution[C]//Proceedings of 2007 IEEE Power Electronics Specialists Conference, Orlando,FL, 2007: 2373-2378.
[13] Gupta K K, Bhatnagar P, Vahedi H, et al. Carrier based PWM for even power distribution in cascaded H-bridge multilevel inverters within single power cycle[C]//Proceedings of 2016 Annual Conference of the IEEE Industrial Electronics Society, Florence,Italy, 2016: 6470-6475.
[14] 卫三民, 刘丛伟, 孙旭东, 等. 串联 H 桥多电平变频器中的功率平衡方法[J]. 电工技术学报, 2003,18(1): 64-67.Wei Sanmin, Liu Congwei, Sun Xudong, et al. A new power balancing method for cascaded H-bridge multilevel inverter[J]. Transactions of China Electrotechnical Society, 2003, 18(1): 64-67.
[15] 李继华, 阮新波, 王学华. 级联型多电平逆变器线电压谐波优化的 SVPWM 策略[J]. 电工技术学报,2014, 29(6): 120-128.Li Jihua, Ruan Xinbo, Wang Xuehua. A SVPWM strategy with optimal line-to-line voltage harmonic spectrum for cascaded multilevel inverters[J].Transactions of China Electrotechnical Society, 2014,29(6): 120-128.
[16] Wilson A, Cortés P, Kouro S, et al. Model predictive control for cascaded H-bridge multilevel inverters with even power distribution[C]//Proceedings of 2010 IEEE International Conference on Industrial Technology, Vina del Mar, Chile, 2010: 2171-2176.
[17] Leon J I, Kouro S, Franquelo L G, et al. The essential role and the continuous evolution of modulation techniques for voltage-source inverters in the past,present, and future power electronics[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5):2688-2701.