0 引言
近年来,由于全球环境污染及能源危机等问题日益严重,储量丰富、清洁无污染的可再生能源的开发利用越来越受到人们的重视[1-2]。在可再生能源利用系统中,电力电子逆变器是其电能变换与传输的关键环节[3]。多电平逆变器由于其输出电能质量高、总谐波畸变率(Total Harmonic Distortion, THD)小、开关器件的电压应力低以及需要较小的输出滤波器等优点得到了广泛的研究[4-5]。传统多电平逆变器包括二极管钳位型[6]、飞跨电容型[7-8]以及级联H桥[9]三种典型结构。二极管钳位型和飞跨电容型逆变器分别使用大量钳位二极管和钳位电容提高输出电平数量,但是这两种逆变器结构较为复杂,控制难度大,并且存在电容电压不平衡的问题。级联H桥型逆变器通过串联模块化结构得到更高数量的输出电平,但是较多的开关器件和直流输入电源增加了系统成本,限制了其应用范围。
为了克服传统逆变器结构的不足,减小系统的器件数量和控制复杂度,开关电容技术近年来被应用到多电平逆变器结构中。开关电容结构是一种典型的无磁性结构,其由一定数量的开关器件和分压电容组成,通过开关控制电容的工作状态,实现电能的变换与传输,具有体积小、效率高、功率密度大等优点[10-11]。文献[12]提出一种单输入源开关电容五电平逆变器结构,所提逆变器允许使用单个直流输入源产生多电平波形,并且具有提高输入电压的能力,然而其有限的五电平输出将产生较多的输出谐波。文献[13]提出一种集成开关电容技术的级联七电平逆变器结构,该逆变器利用分压电容代替级联结构的直流电源,减少了逆变器直流输入电源的数量,但是增加了开关器件的数量。文献[14]提出一种降低开关器件数量的开关电容七电平逆变器,该逆变器利用串联电容器之间的配合工作减少了开关器件的数量,但是其需要较复杂的调制算法控制串联电容器的平衡。
为了在更少的器件数量条件下产生更多的输出电平,近年来,开关电容九电平逆变器得到了大量研究。文献[15]提出基于开关电容结构的单相九电平逆变器,这个逆变器只需要一个直流电源即可同时完成升压与逆变两个过程,逆变器升压能力强,但是这种方法所用器件数量较多,增加了系统成本。文献[16]中所提开关电容逆变器能够减少开关器件的数量,并且降低开关器件的电压应力,但是其需要较多的分压电容,并需增加额外的电容电压平衡电路来控制分压电容的电压平衡。文献[17]提出一种级联开关电容结构的单相九电平逆变器,该逆变器由开关电容前端和H桥后端组成,具有器件数量少、控制简单等优点;但是该逆变器中每个级联单元均需要一个独立的直流输入电源,所需电源数量较多,限制了其应用范围。文献[18]提出的单相开关电容九电平逆变器具有更简洁的拓扑结构,需要更少的器件数量,但是该结构升压能力较低,并且需要采用两种控制算法实现逆变器中电容电压的平衡,增加了控制复杂度及传感器数量。在开关电容逆变器结构中,电容是逆变器的重要组成部分,电容电压波形直接影响到逆变器的输出波形,因此对逆变器电容电压的平衡控制至关重要。文献[19]通过增加辅助电压控制电路使电容电压稳定在期望的水平,原理简单,控制容易,但这种方法需要大量的附加设备,增加了系统成本。文献[20]通过一种改进的脉宽调制方式控制逆变器中电容电压的平衡,其无需增加额外的电压控制电路,并能有效抑制电容的纹波波动,但这种方式增加了系统的控制复杂度。
在上述研究的基础上,本文提出一种基于开关电容结构的单电源九电平逆变器。该逆变器结构简单,通过一个直流输入电源、两个电容以及少量开关器件即可产生九电平波形,所需功率器件数量少;能够实现电容电压的自均衡,系统控制简单,不需要额外的均压电路及复杂的控制算法。通过特定谐波消除法对逆变器进行调制,逆变器具有较低的器件开关频率和较少的输出谐波。文中给出了逆变器的工作原理、调制策略、电容自均压分析、电容参数分析以及拓扑比较分析。最后,通过实验对所提九电平逆变器的正确性及可行性进行验证。
1 逆变器拓扑结构和工作原理
1.1 拓扑结构
本文提出的开关电容多电平逆变器拓扑结构如图1所示,其由单个直流输入电源、开关电容电路、辅助双向开关和全桥电路组成。开关电容电路由开关管S5~S7、二极管VD1、VD2、以及分压电容 C1、C2构成;辅助双向开关由S8、S9组成;全桥电路由开关管S1~S4组成。该结构中,开关电容电路实现电源与电容之间的串并联转换,产生阶梯波电平;辅助双向开关连接开关电容电路和全桥电路,增加额外的电平输出;全桥电路实现输出电平的正负极性转换。
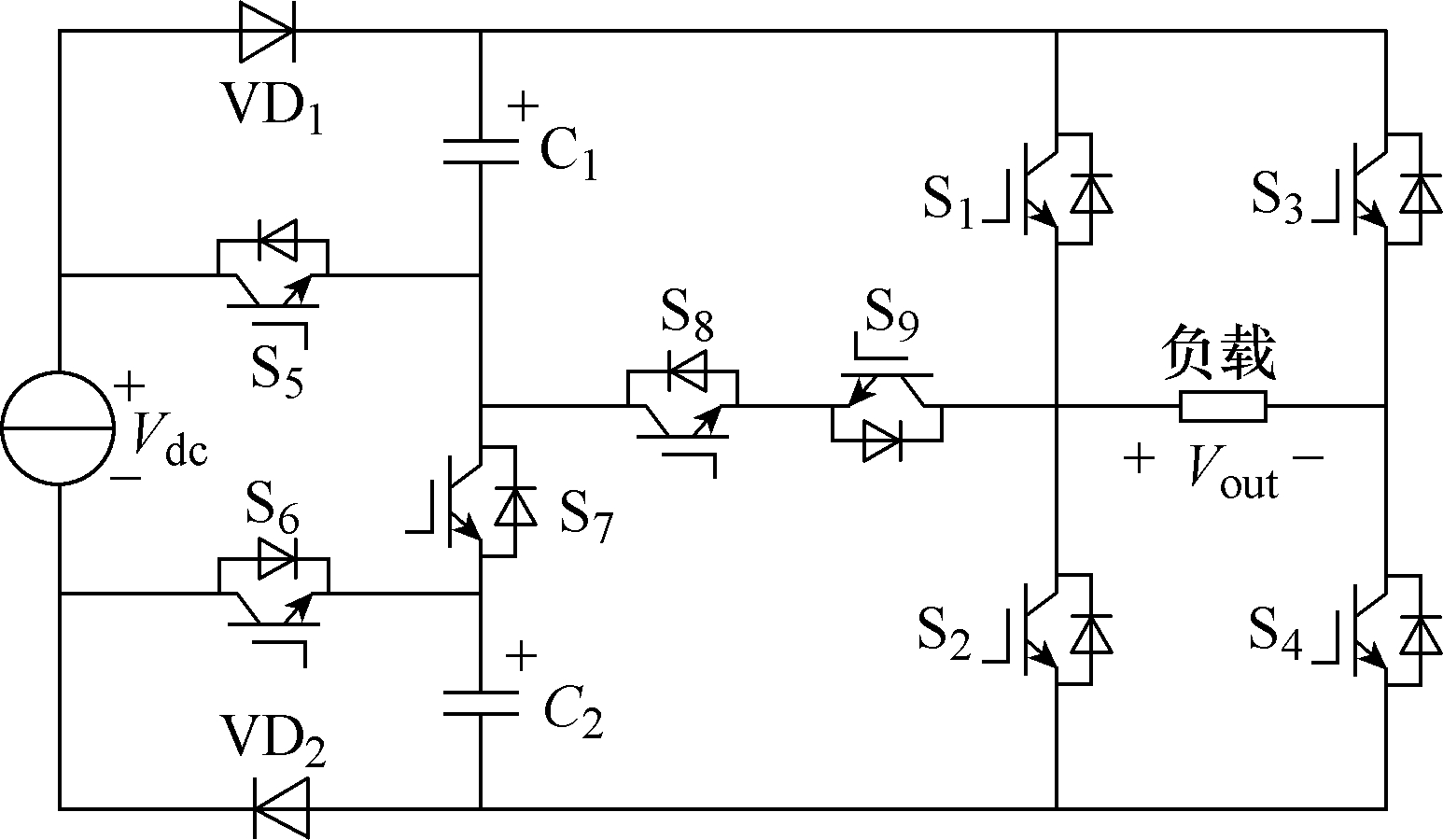
图1 逆变器拓扑结构
Fig.1 Topology of the proposed inverter
1.2 工作原理
在所提逆变器结构中,直流输入电源为Vdc,分压电容C1与C2的电压为Vdc/2。基于开关电容结构,通过合理的开关组合,所提逆变器能够输出九种电平:+2Vdc、+3Vdc/2、+Vdc、+Vdc/2、0、-Vdc/2、-Vdc、-3Vdc/2、-2Vdc。逆变器九种输出电平所对应的工作模态如图2所示。九种工作模态下逆变器各个功率器件的工作状态见表 1,其中包括开关管的开关状态、二极管的通断状态以及电容的充放电状态。为简便分析,做出如下假设:①逆变器中所有开关器件都是理想的,没有通态电阻和正向导通压降;②逆变器中电容容量足够大,两电容电压保持额定电压不变;③电容预充电已完成,系统进入稳态。逆变器具体的工作原理分析如下所示。
表1 逆变器功率器件工作状态
Tab.1 Operating status of each power device
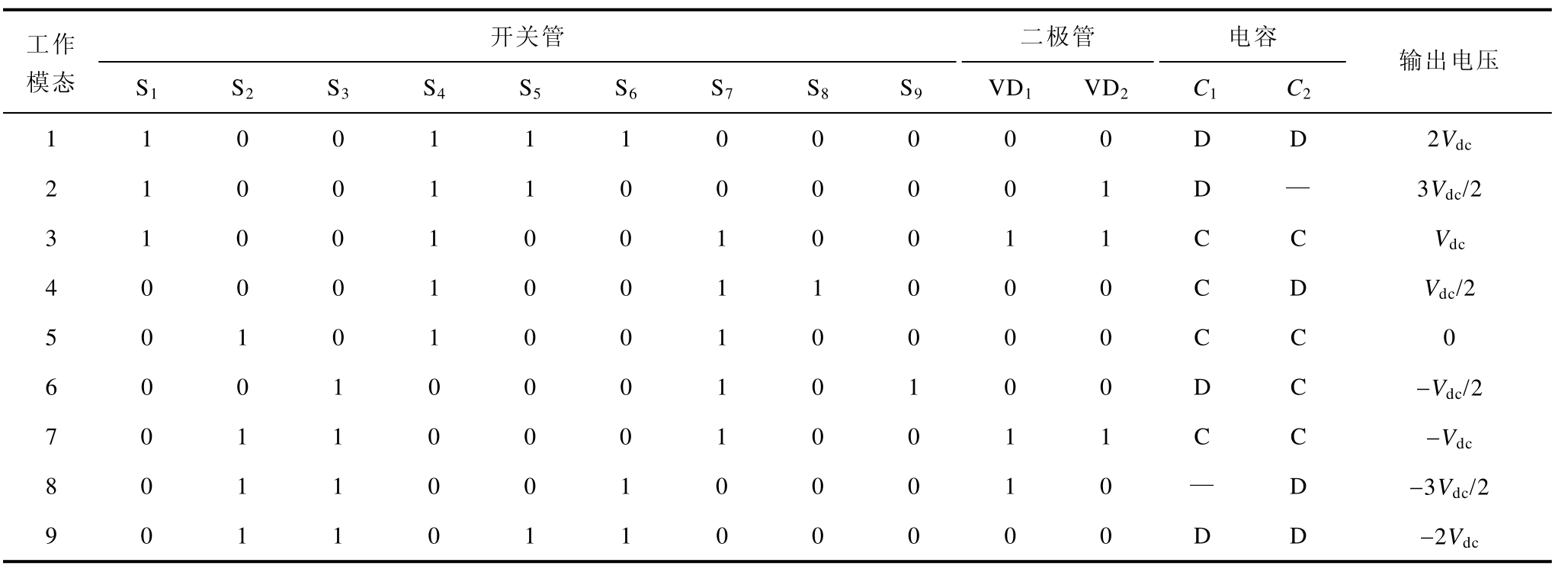
注:开关管的1和0表示开关管导通和关断;二极管的1和0表示二极管正向导通和反向截止;电容的C、—、D分别表示电容的充电、保持和放电状态。
工作模态 S1 S2 S3 S4 S5 S6 S7 S8 S9 VD1 VD2 C1 C2开关管 二极管 电容 输出电压1 1 0 0 1 1 1 0 0 0 0 0 D D 2Vdc 2 1 0 0 1 1 0 0 0 0 0 1 D — 3Vdc/2 3 1 0 0 1 0 0 1 0 0 1 1 C C Vdc 4 0 0 0 1 0 0 1 1 0 0 0 C D Vdc/2 5 0 1 0 1 0 0 1 0 0 0 0 C C 0 6 0 0 1 0 0 0 1 0 1 0 0 D C -Vdc/2 7 0 1 1 0 0 0 1 0 0 1 1 C C -Vdc 8 0 1 1 0 0 1 0 0 0 1 0 — D -3Vdc/2 9 0 1 1 0 1 1 0 0 0 0 0 D D -2Vdc
模态1:如图2a所示,开关管S1、S4、S5、S6导通,其余开关管关断。二极管 VD1、VD2分别被电容C1、C2反向截止。直流电源Vdc串联电容C1、C2对负载供电。此时逆变器输出电平为+2Vdc。
模态2:如图2b所示,开关管S1、S4、S5导通,其余开关管关断。二极管VD2正向导通,VD1被电容C1反向截止。直流电源Vdc串联电容C1对负载供电。此时逆变器输出电平为+3Vdc/2。
模态3:如图2c所示,开关管S1、S4、S7导通,其余开关管关断。二极管 VD1、VD2正向导通。此时,直流电源 Vdc通过二极管 VD1、VD2以及开关管S7对串联电容C1与C2进行充电;另一方面直流电源 Vdc通过 S1、S4对负载供电。此时逆变器输出电平为+Vdc。
模态4:如图2d所示,开关管S4、S7、S8导通,其余开关管关断。此时,电容 C2通过开关管 S4及辅助双向开关对负载供电。此时逆变器输出电平为+Vdc/2。
模态5:如图2e所示,开关管S2、S4、S7导通,其余开关管关断。直流电源 Vdc通过二极管 VD1、VD2以及开关管S7对串联电容C1与C2进行充电。开关管S2、S4的导通构成续流回路。此时逆变器输出电平为0。
模态6:如图2f所示,开关管S3、S7、S9导通,其余开关管关断。此时,电容 C1通过开关管 S3及辅助双向开关对负载供电。此时逆变器输出电平为-Vdc/2。
模态7:如图2g所示,开关管S2、S3、S7导通,其余开关管关断。二极管 VD1、VD2正向导通。此时,直流电源 Vdc通过二极管 VD1、VD2以及开关管S7对串联电容C1与C2进行充电。与此同时,直流电源 Vdc通过开关管 S2、S3对负载供电。此时逆变器输出电平为-Vdc。
模态8:如图2h所示,开关管S2、S3、S6导通,其余开关管关断。二极管VD1正向导通,VD2被电容C2反向截止。直流电源Vdc串联电容C2对负载供电。此时的逆变器输出电平为-3Vdc/2。
模态 9:如图 2i所示,开关管 S2、S3、S5、S6导通,其余开关管关断。二极管 VD1、VD2分别被电容C1、C2反向截止。直流电源Vdc串联电容C1、C2对负载进行供电。此时逆变器输出电平为-2Vdc。

图2 逆变器九种工作模态
Fig.2 Various operating modes of the proposed inverter
2 调制策略与电容分析
2.1 调制策略分析
针对提出的开关电容九电平逆变器,为获得更高的输出波形质量和较低的器件开关频率,本文采用特定谐波消除法对该逆变器进行调制。
特定谐波消除法基于波形合成原理,用阶梯波逼近正弦波,通过优化开关器件的开关时刻,特定地消除目标谐波,进而使输出电压总谐波含量降低;并且,该调制方式下,开关器件的开关频率与基波频率相近,能有效降低开关器件的开关频率[21]。特定谐波消除的原理如图3所示,根据波形合成原理,九电平阶梯波可以看成4个与输出阶梯波同频率的方波 Voi(i=1, 2, 3, 4)叠加而成,方波的幅值和初始导通角分别为±Vdc/2 和θi,其中:0<θ1<θ2<θ3<θ4<π/2。
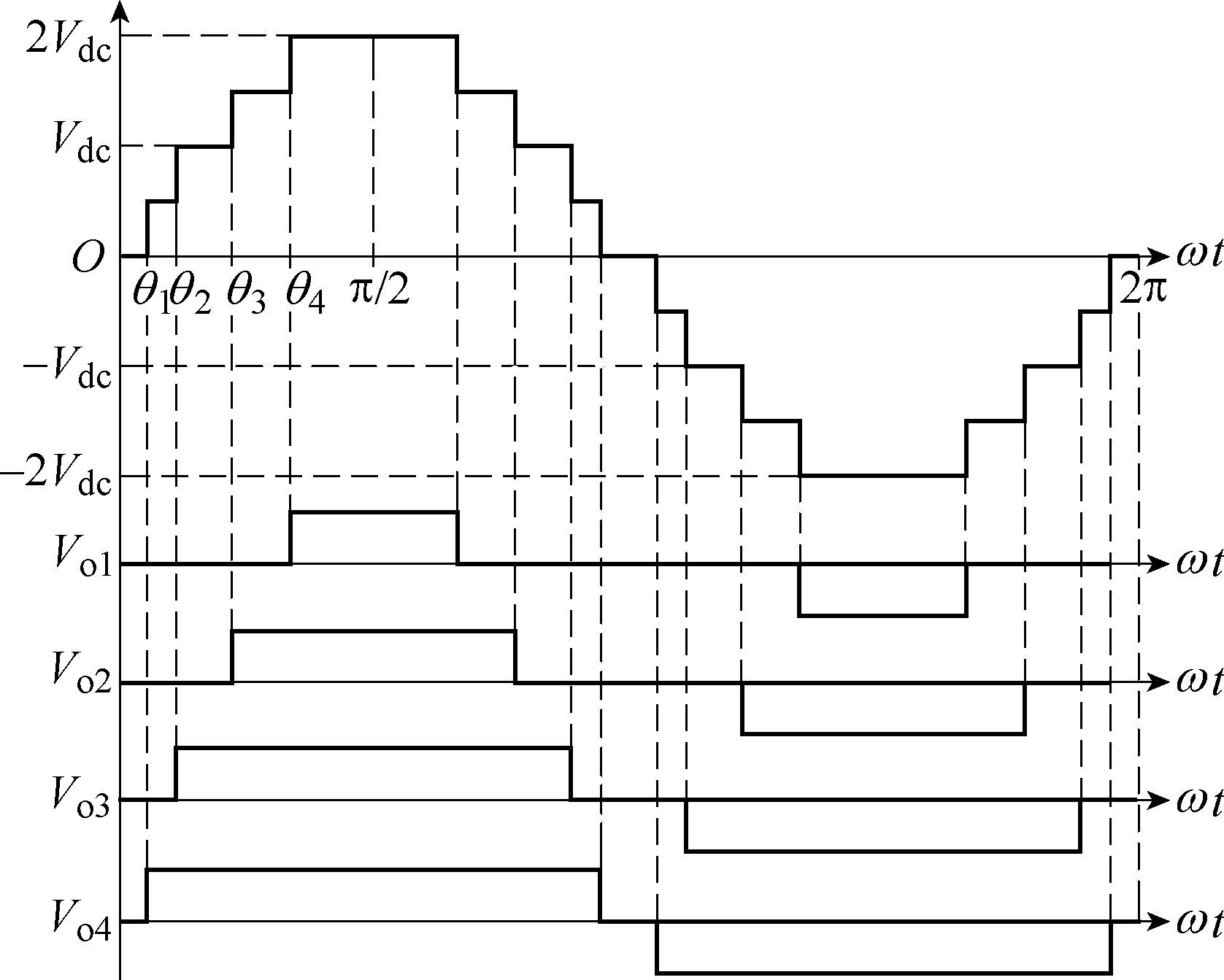
图3 特定谐波消除原理图
Fig.3 Principle diagram of specific harmonic elimination
方波Voi的傅里叶展开式可表示为
式中,ω 为输出波形角频率。
输出电压波形是由各个方波叠加形成的,则
输出电压Vo的傅里叶展开式可表示为
基波幅值调制度Mof为
输出波形的THD为

在逆变器输出电压波形中,低次谐波占谐波总畸变的主导地位,因此选择性地消除低次谐波能够大幅改善输出电压的波形质量。这里选择消除5、7、11次谐波,则各个方波初始导通角的数学计算方程组为
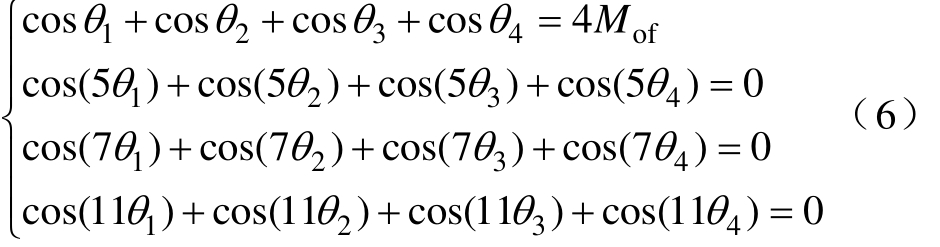
计算上述方程组得到各个初始导通角度,消除特定目标谐波,逆变器输出电压波形的 THD为9.92%,逆变器较多的输出电平和特定谐波消除调制方式使逆变器输出电压谐波含量较低。
根据特定谐波消除法的调制原理及表1中开关器件的工作状态,可得逆变器开关器件S1~S9的工作波形,如图4所示。
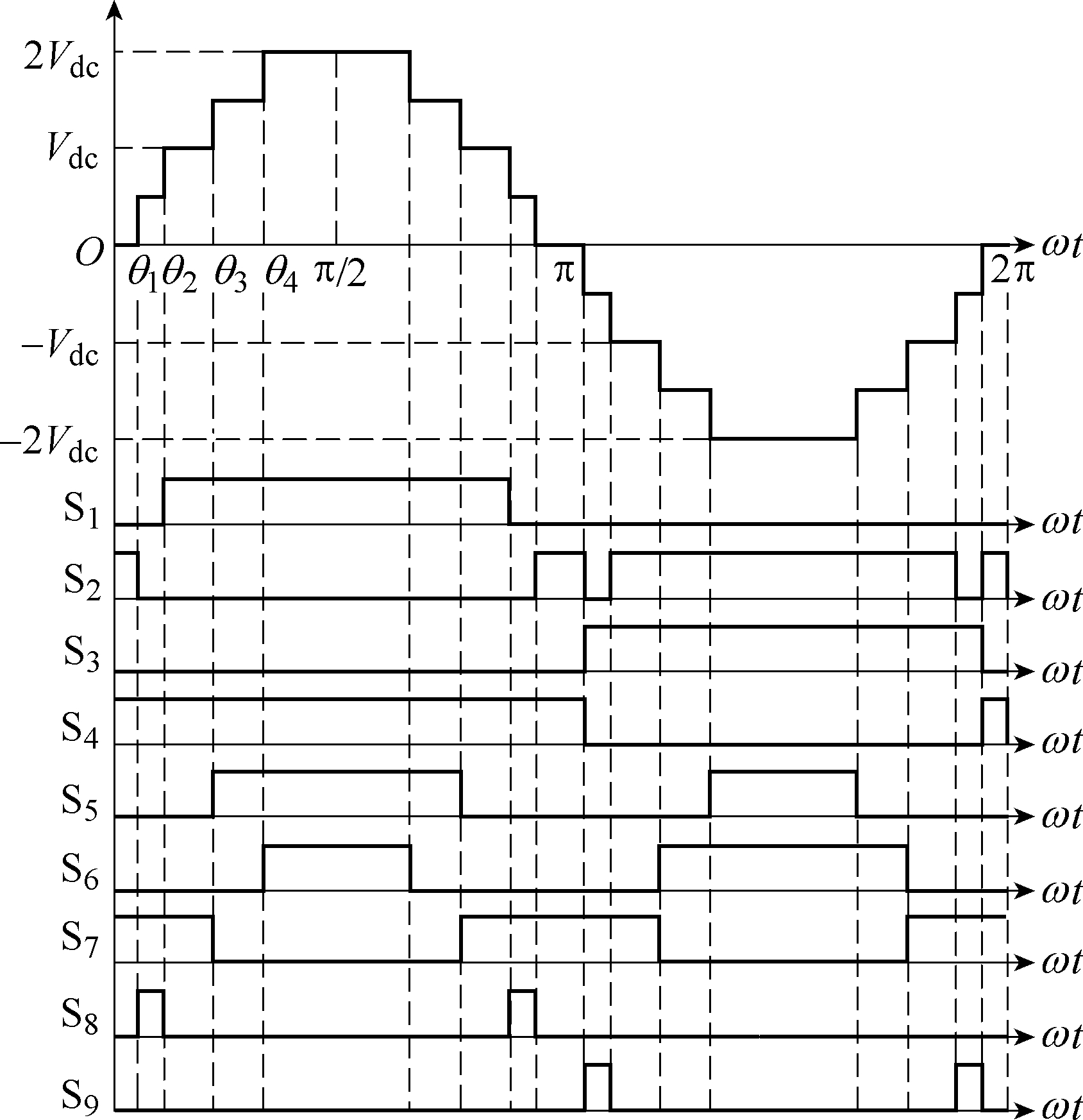
图4 逆变器的工作波形
Fig.4 Operational waveforms of the proposed inverter
2.2 电容自均压
由所提逆变器的工作原理可知,逆变器中两电容的充电电路不包含负载,电容的充电时间和充电电流均与负载无关,充电状态下电源直接并联电容对其进行充电,电容能够迅速达到额定电压状态。逆变器电容电压平衡的本质是电容的充放电量相等。图5给出了一周期内两电容的充放电工作状态及其对应的电容电压工作波形。
由图 5中可知,电容 C1的放电区间分别为[θ3,π-θ3]、[π+θ1, π+θ2]、[π+θ4, 2π-θ4]和[2π-θ2, 2π-θ1],放电电流为逆变器的负载电流 io。因此一周期内电容C1的总放电量为

图5 电容C1与C2的工作状态
Fig.5 Working state diagram of capacitance C1 and C2
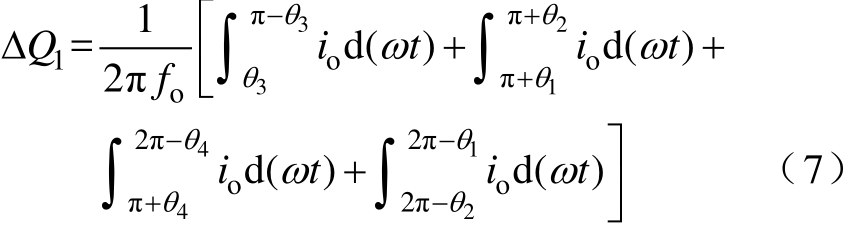
由于逆变器的调制区间正负对称,且对称调制区间内逆变器的工作状态对称相等,因此式(7)可简化为
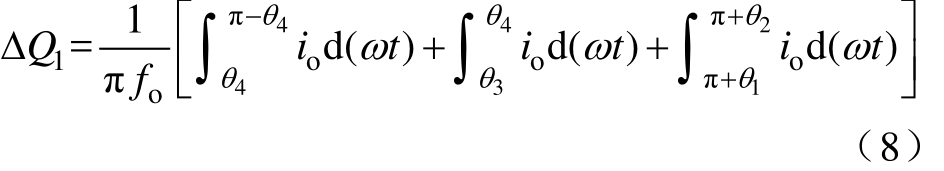
设逆变器的负载为Ro,式(8)可进一步计算为
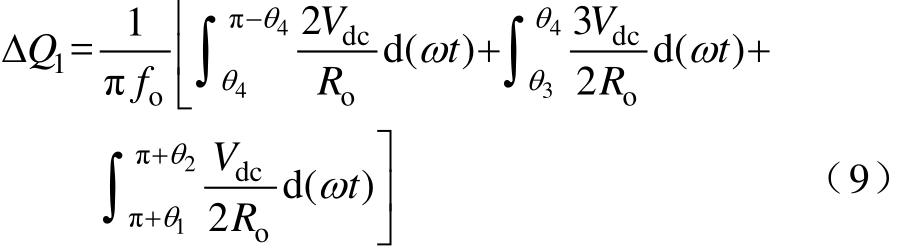
则一周期内电容C1的总放电量为
电容 C2的放电区间分别为[θ1, θ2]、[θ4, π-θ4]、[π-θ2, π-θ1]以及[π+θ3, 2π-θ3],放电电流为逆变器的负载电流io,电容C2的总放电量可计算为
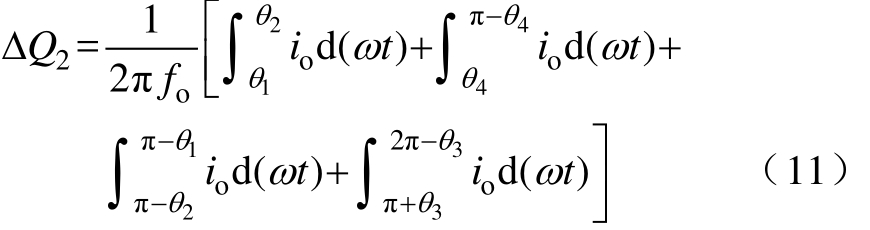
进一步计算式(11)得
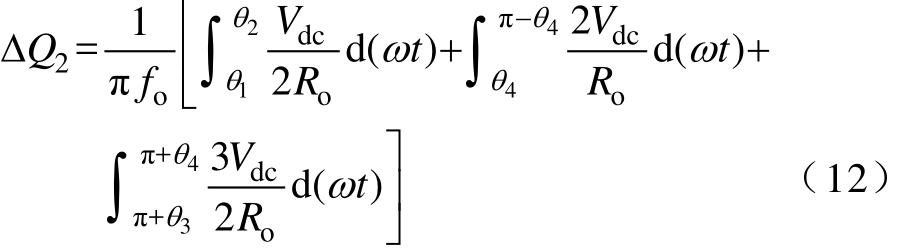
则一周期内电容C2的总放电量为
由上述对电容C1与C2放电量的计算结果可知,一周期内两电容的总放电量相等,即
因此,所提逆变器能够实现电容电压的自均衡。
2.3 电容参数设计
逆变器中电容参数的设计原则往往根据电容电压的纹波不大于电容额定电压的10%来设定,电容电压纹波主要由电容最大连续放电量决定。由表 1和图 5可知,电容 C1的最大连续放电区间为[θ3,π-θ3],放电电流为 io;电容 C2的最大连续放电区间为[π+θ3, 2π-θ3],放电电流为 io。电容 C1与 C2的最大连续放电区间长度以及对应的工作状态相同,因此电容 C1与 C2的最大连续放电量相同。为简便分析,这里仅对电容 C1进行计算。电容 C1的最大连续放电量为
在[θ3, θ4]和[π-θ4, π-θ3]工作区间内,逆变器输出电压为 3Vdc/2;在[θ4, π-θ4]工作区间内,逆变器输出电压为 2Vdc。逆变器负载为 Ro,则电容 C1最大连续放电量QΔ为

进一步计算式(16)可得
按照逆变器电容电压纹波不大于电容额定电压10%的设计原则,两电容的电容值均应满足
式中,VC为电容的额定电压。
因此,在允许的电容纹波条件下逆变器所需电容的最小值为
式中,ΔUrip为电容的纹波,且ΔUrip≤(10%)VC。
由上述分析可知,电容的最小值与输出频率、负载以及电容纹波呈反比,因此输出频率与负载越大,逆变器所需电容就越小;反之电容越大,电容纹波越小,负载容量越大,并且较大的电容值可以延长电容的使用寿命。但是,过大的电容会增加系统成本及占地面积,因此需要均衡成本与性能之间的关系,选择合适的电容值。
3 拓扑比较分析
为全面比较所提逆变器结构的性能,表2给出了所提逆变器与最近提出的几种开关电容九电平逆变器的参数对比。
表2 逆变器拓扑参数对比
Tab.2 Parameter comparisons with several inverter topology
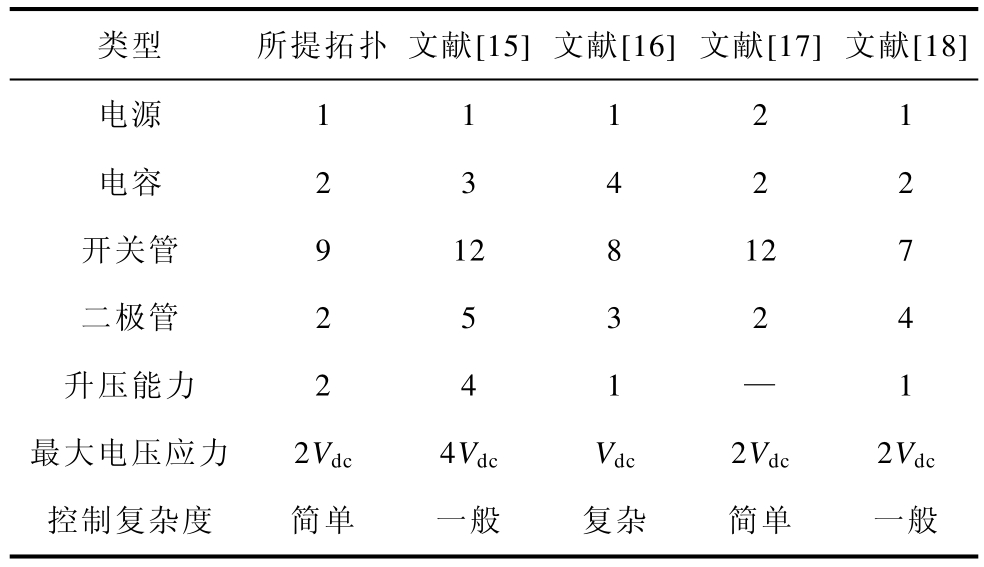
类型 所提拓扑 文献[15] 文献[16] 文献[17]文献[18]电源 1 1 1 2 1电容 2 3 4 2 2开关管 9 12 8 12 7二极管 2 5 3 2 4升压能力 2 4 1 — 1最大电压应力 2Vdc 4Vdc Vdc 2Vdc 2Vdc控制复杂度 简单 一般 复杂 简单 一般
由表2中对比可以看出,与现有开关电容九电平逆变器相比,所提逆变器结构在输出九电平时所用的器件总数较少,这有利于简化拓扑结构,降低系统成本;所提逆变器控制简单,不需要复杂的调制算法及额外的控制回路即可实现电容电压的平衡。与所提逆变器相比,文献[15]所提逆变器结构的升压能力更强,但是其需要更多的功率器件,并且开关器件的电压应力较大;文献[16]中所提逆变器的开关器件电压应力更低,但是该逆变器需要更多的分压电容,并需要增加额外的电压控制电路来实现串联电容器的电压平衡;文献[17]所提逆变器拓扑简洁,控制简单,但需要较多的直流输入电源,限制了其应用范围;文献[18]所提逆变器需要两种调制算法之间的配合实现电容电压的平衡,这相对增加了系统控制复杂度,并需要较多的传感器。
基于上述对比,所提逆变器结构具有器件数量少、控制简单、单电源输入、电容自均压以及开关器件电压应力较低等优点,具有一定的应用优势。
4 实验结果及分析
为了验证所提逆变器结构及其调制策略的正确性与可行性,本文通过一台小型实验样机对所提逆变器的工作原理及工作特性进行验证分析,实验平台如图 6所示,实验设备参数见表3。下面分别对逆变器的稳态和动态工作性能进行验证分析。

图6 实验平台
Fig.6 Experimental platform
表3 实验器件及参数
Tab.3 Experimental devices and parameters
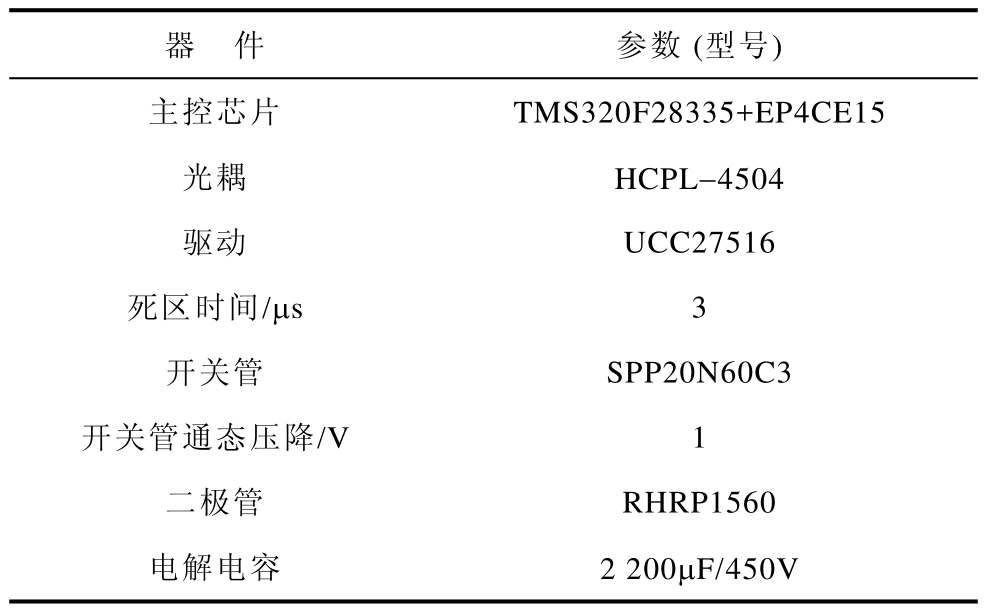
器 件 参数 (型号)主控芯片 TMS320F28335+EP4CE15光耦 HCPL-4504驱动 UCC27516死区时间/μs 3开关管 SPP20N60C3开关管通态压降/V 1二极管 RHRP1560电解电容 2 200μF/450V
4.1 稳态实验分析
为了验证所提逆变器结构的可行性及其理论分析的正确性,在输出频率为工频与高频时对逆变器的稳态工作特性进行验证分析。本实验中,逆变器输入电压为30V,电容为2 200μF,负载为100Ω,输出频率为50Hz和1kHz。
图 7给出了输出频率为 50Hz时逆变器输出电压和负载电流的实验波形,从图中可以看出,逆变器输出电压及对应的负载电流为理想的九电平阶梯波,验证了该逆变器结构及其调制策略的可行性与正确性。
图 8所示为输出频率为 50Hz时电容 C1与 C2的电压实验波形,由图8中可见,系统进入稳态后,两电容电压趋于常量,稳定在额定电压附近,电压纹波波动较小,满足纹波设定要求,验证了逆变器电容电压的自均衡。
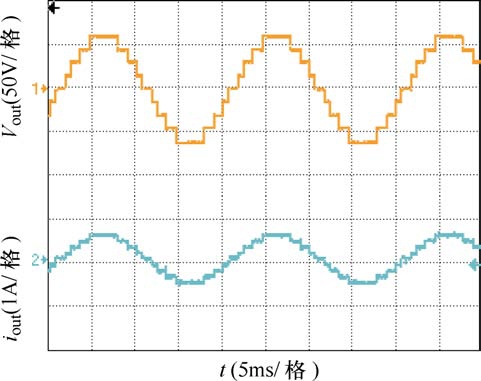
图7 逆变器输出电压和负载电流实验波形
Fig.7 Experimental waveforms of the output voltages and load current
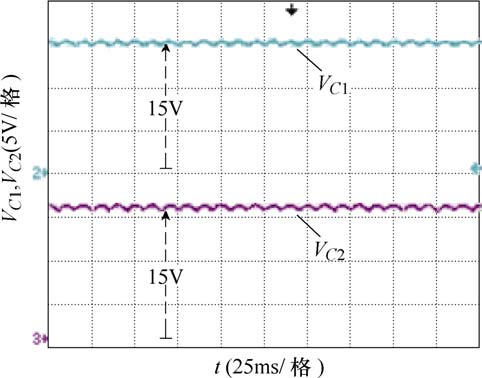
图8 电容电压实验波形
Fig.8 Experimental waveforms of the capacitor voltages

图9 输出频率为1kHz时逆变器输出电压与电容电压实验波形
Fig.9 Experimental waveforms of output voltage and capacitor voltages when the output frequency is 1kHz
图9 为输出频率 1kHz时逆变器输出电压与电容电压实验波形,从图中可知,当逆变器工作在高频时,逆变器输出电压波形理想,两电容电压波形稳定维持在额定电压位置,证明所提逆变器能够工作在高频工作环境。
图 10为逆变器各个开关器件的驱动信号实验波形,其工作波形与理论分析一致,进一步验证了逆变器调制策略的正确性。
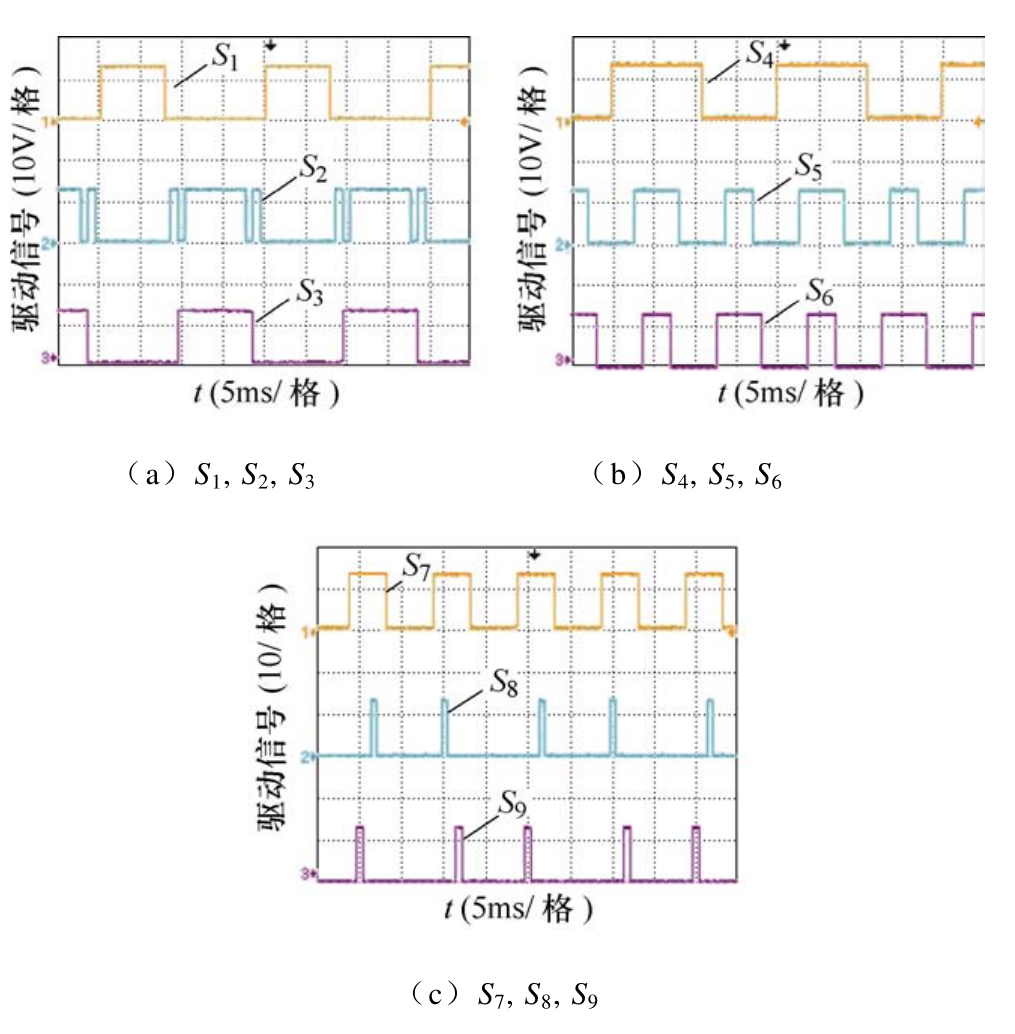
图10 驱动信号实验波形
Fig.10 Experimental waveforms of driving signals
4.2 动态实验分析
为了验证所提逆变器结构的动态工作性能及电容电压平衡能力,结合实际应用场景,进行了基于负载电流变化与输入电压变化的动态实验验证。本实验中,直流输入电压为 10V和 30V,电容值为2 200μF,负载为15Ω,输出频率为1kHz。
图11给出了负载变化时逆变器输出电压、负载电流以及两电容电压的动态实验波形。从图中可以看出,当逆变器负载从 0~15Ω 变化时,逆变器负载电流从0到±4A变化,变换前后逆变器输出电压保持稳定,变换后电容电压纹波变大,但波形保持稳定,证明所提逆变器具有较强的电容电压平衡能力。

图11 负载Ro变化的动态实验波形
Fig.11 Dynamic experimental waveforms of load Ro variation
图12 给出了输入电压变化时逆变器输出电压、负载电流以及两电容电压的动态响应波形。图 12a为逆变器输入电压从10V到30V变化时的动态实验波形;图12b为逆变器输入电压从30V到10V变化时的动态实验波形。由图中可以看出,当逆变器输入电压跳变时,逆变器两分压电容的电压波形变化同步,进入稳态后两电容电压保持平稳,并稳定在输入电压一半位置,证明了所提逆变器结构良好的自均压能力。

图12 输入电压变化的动态实验波形
Fig.12 Dynamic experimental waveforms of input voltage variation
5 结论
本文提出了一种基于开关电容结构的单电源九电平逆变器。所提逆变器结构通过电源与电容的串并联转换输出更多的电平。与最近提出的几种开关电容多电平逆变器相比,所提拓扑结构减少了功率器件的数量,降低了开关器件的电压应力。逆变器电容自均压的优点简化了控制策略,无需复杂的控制算法及额外的均压电路即可将电容电压控制在期望的水平。针对所提新型九电平逆变器,给出了能够减小器件开关频率与输出电压谐波含量的特定谐波消除调制策略,并对其调制原理进行了详细分析。通过一台小型实验样机对逆变器的工作性能进行实验验证,实验结果表明,所提逆变器结构具有良好的稳态和动态工作性能,在可再生能源利用等领域具有广泛的应用前景。
[1] 武平, 郭巍, 晋春杰, 等. 浅谈我国电力与能源现状及解决途径[J]. 电气技术, 2018, 19(5): 1-14.Wu Ping, Guo Wei, Jin Chunjie, et al. Analysis on the current situation of electricity and energy in China and its solution[J]. Electrical Engineering, 2018,19(5): 1-14.
[2] 易文飞, 张艺伟, 曾博, 等. 多形态激励型需求侧响应协同平衡可再生能源波动的鲁棒优化配置[J].电工技术学报, 2018, 33(23): 5541-5554.Yi Wenfei, Zhang Yiwei, Zeng Bo, et al. Robust optimization allocation for multi-type incentivebased demand response collaboration to balance renewable energy fluctuations[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5541-5554.
[3] 蒋冠前, 李志勇, 杨慧霞, 等. 柔性直流输电系统拓扑结构研究综述[J]. 电力系统保护与控制, 2015,43(15): 145-153.Jiang Guanqian, Li Zhiyong, Yang Huixia, et al.Research review on topological structure of flexible HVDC system[J]. Power System Protection &Control, 2015, 43(15): 145-153.
[4] 沈虹, 郭忠南, 关红磊, 等. 单相四开关多电平光伏逆变器研究[J]. 电工技术学报, 2018, 33(8):1775-1782.Shen Hong, Guo Zhongnan, Guan Honglei, et al.Research on single-phase four-switch multilevel PV inverter[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1775-1782.
[5] 曾君, 吴佳磊, 刘俊峰, 等. 一对基于开关电容原理的多电平高频逆变器[J]. 电工技术学报, 2018,33(6): 1312-1319.Zeng Jun, Wu Jialei, Liu Junfeng, et al. A pair of highfrequency multilevel inverters based on switchedcapacitor technique[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1312-1319.
[6] 吴可丽, 夏长亮, 张云, 等. 二极管钳位型三电平逆变器共模电压抑制[J]. 电工技术学报, 2015,30(24): 110-117.Wu Keli, Xia Changliang, Zhang Yun, et al.Common-mode voltage suppression for neutralpoint-clamped three-level inverter[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 110-117.
[7] 张云, 孙力, 吴凤江, 等. 电容箝位型非对称 H 桥五电平逆变器正弦脉宽调制控制[J]. 中国电机工程学报, 2009, 29(21): 40-45.Zhang Yun, Sun Li, Wu Fengjiang, et al. SPWM control of capacitor-clamped five level inverter comprised of asymmetric H bridge[J]. Proceedings of the CSEE, 2009, 29(21): 40-45.
[8] 刘朋, 陈昌松, 段善旭. 带飞跨电容的三电平全桥直流变换器输入中点电压的自平衡分析[J]. 电工技术学报, 2018, 33(18): 4335-4344.Liu Peng, Chen Changsong, Duan Shanxu. Selfbalance mechanism analysis of the neutral point voltage in three-level full bridge DC-DC converter with flying capacitors[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4335-4344.
[9] 陈仲, 许亚明, 袁涛, 等. 级联型逆变器载波循环功率均衡控制方法及比较[J]. 电工技术学报, 2018,33(20): 4802-4812.Chen Zhong, Xu Yaming, Yuan Tao, et al. Power balance control methods and comparative study using carrier rotation technique for the cascaded inverter[J].Transactions of China Electrotechnical Society, 2018,33(20): 4802-4812.
[10] 丘东元, 张波. 开关电容变换器组成原理及发展趋势[J]. 电气应用, 2007, 26(9): 6-12.Qiu Dongyuan, Zhang Bo. Switched capacitor converter and its developing trends[J]. Electrotechnical Application, 2007, 26(9): 6-12.
[11] 侯世英, 陈剑飞, 孙韬, 等. 基于开关电容网络的DC-DC变换器[J]. 电工技术学报, 2014, 29(10):90-97.Hou Shiying, Chen Jianfei, Sun Tao, et al. DC-DC converters based on switched-capacitor network[J].Transactions of China Electrotechnical Society, 2014,29(10): 90-97.
[12] Ranjan A, Gupta K K, Kumar L, et al. A switchedcapacitors based multilevel boost inverter with single input source[C]//IEEE India International Conference on Power Electronics, Delhi, India, 2012: 1-6.
[13] Sun Xiaofeng, Wang Baocheng, Zhou Yue, et al. A single DC source cascaded seven-level inverter integrating switched- capacitor techniques[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11):7184-7194.
[14] Choi J, Kang F. Seven-level PWM inverter employing series-connected capacitors paralleled to a single DC voltage source[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3448-3459.
[15] 谭国俊, 张旭, 薛映霞, 等. 投切电容式单相九电平逆变器研究[J]. 中国电机工程学报, 2017, 37(8):2351-2360.Tan Guojun, Zhang Xu, Xue Yingxia, et al. Research of switch capacitor single-phase nine-level inverter[J].Proceedings of the CSEE, 2017, 37(8): 2351-2360.
[16] Samanbakhsh R, Taheri A. Reduction of power electronic components in multilevel converters using new switched capacitor-diode structure[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11):7204-7214.
[17] Liu Junfeng, Cheng K W, Ye Yuanmao, et al. A cascaded multilevel inverter based on switchedcapacitor for high-frequency AC power distribution system[J]. IEEE Transactions on Power Electronics,2014, 29(8): 4219-4230.
[18] Sekar R M, Jayakumar D N, Mylsamy K, et al. Single phase nine level inverter using single DC source supported by capacitor voltage balancing algorithm[J]. IET Power Electronics, 2018, 11(14): 2319-2329.
[19] Ebrahimi J, Babaei E, Gharehpetian G B. A new multilevel converter topology with reduced number of power electronic components[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 655-667.
[20] Zhang Yun, Li Jing, Li Xinmin, et al. A method for the suppression of fluctuations in the neutral-point potential of a three-level NPC inverter with a capacitor-voltage loop[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 825-836.
[21] 孙醒涛, 孙力, 张云, 等. 一种新型电压型逆变器拓扑结构及其 PWM 控制方法[J]. 电工技术学报,2008, 23(7): 75-80.Sun Xingtao, Sun Li, Zhang Yun, et al. Topology and PWM control method of a novel voltage-source inverter[J]. Transactions of China Electrotechnical Society, 2008, 23(7): 75-80.