0 引言
磁耦合无线电能传输(Magnetic Coupling Wireless Power Transfer, MC-WPT)技术是基于电磁感应耦合原理实现一定距离的非接触式能量传输,由于其便捷、安全、灵活等特点受到了学者和企业的广泛关注,现已经应用于家电、医疗、消费电子和交通运输等各个领域[1-7]。
近年来,MC-WPT技术开始逐渐应用于移动式负载(如电动车行进中无线充电、物流系统搬运小车、仓储系统传输机构、变电站巡检机器人等[8-13]),即动态无线供电(Dynamic Wireless Power Transfer,DWPT)系统。在DWPT系统中,有图1和图2所示的两种常用供电模式。图1所示为全程单导轨供电模式[8-9]。当用电设备行驶在发射导轨上方时,拾取线圈可以获得持续的能量。但是,单导轨供电模式的缺点在于:因能量发射导轨长度远大于拾取线圈尺寸而使得耦合系数较小且产生较大的磁场暴露问题,因此不适用于长距离应用。图2所示为分段导轨(多阵列线圈)(为了方便描述,以下发射导轨和发射线圈统称发射导轨)供电模式。多个发射导轨依次铺设在用电设备的移动路径上,可以实现移动设备的分段供电,从而解决全程单导轨供电模式存在的问题。在这种供电模式中,有两种变换器驱动模式。图2a所示的单变换器驱动模式[10-12]下,多个发射导轨共用一个变换器,可以实现多发射导轨的同步驱动,但是需要增加导轨切换电路以降低非工作导轨的损耗。同时,该驱动模式对变换器容量要求较高,且系统冗余度较低,因此也不是长距离应用的最佳驱动方案。图2b所示的多变换器驱动模式[13]可以实现各发射导轨的独立控制,且系统具有较高的冗余度,相较而言更适用于长距离应用。但是,该驱动模式需要大量的变换器,从而增加了系统成本和维护难度。

图1 全程单导轨供电模式
Fig.1 Single track supply mode

图2 分段导轨(多阵列线圈)供电模式
Fig.2 Segmented track (multi-coil array) supply mode
作为MC-WPT系统的电能变换器,除了常用的桥式、推挽和E类逆变器,目前已见报道的拓扑还有矩阵变换器[14-15]、多电平逆变器[16-17]、三相逆变器[18-19]和多逆变器并联[20-21]等。上述拓扑的研究主要是以系统功率提升为目标,均具有较多的开关器件或直流储能元件,且多为单输出拓扑,更适用于驱动单个发射导轨。Boost逆变器作为一种集成式单级升压逆变器,可同时实现升压和逆变功能,具有开关器件少、结构与控制策略简单等特点,常用于隔离DC-DC电源、光伏逆变以及感应加热等[22-24]。本文在 Boost半桥逆变器的基础上,提出一种适用于DWPT系统的双输出逆变器。相比于图2b中的多变换器驱动模式,该逆变器可以产生两路相同的输出,用以驱动两段发射导轨,从而减少逆变器的数量,并简化系统控制。另一方面,作为逆变器本身,相比于MC-WPT系统常用的逆变器,在更少的开关器件下仍然能够保证相同的电压输出能力,从而可以进一步减少单个逆变器中开关器件的数量。因此本文所提双输出逆变器适用于分段导轨(多阵列线圈)模式的长距离动态无线供电系统。需要说明的是,基于本文所提逆变器的DWPT系统实际上是由多个结构和参数相同的子系统组合而成,每个子系统均包含逆变器和两段发射导轨。各子系统本身的运行特性和规则是相同的。本文针对单个子系统进行了研究与分析,其结果同样适用于其他子系统,进而可以扩展到整个系统。
1 双输出逆变器
1.1 拓扑结构
基于双输出逆变器的DWPT电路拓扑如图3所示。双输出逆变器由两个开关器件S1、S2及其反并联二极管 VDS1、VDS2、电感 L和电容 C组成。能量发射端采用具有恒流输出特性的 LCC谐振补偿网络。两个 LCC网络由补偿电容 Cf1、Cf2、Cp1、Cp2和补偿电感Lf1、Lf2组成。Lp1和Lp2为发射导轨。能量拾取端采用串联谐振补偿方式,Ls为拾取线圈,Cs为补偿电容。为了简化分析且不失一般性,拾取线圈后级的负载以电阻 R来代替。M1、M2和 M12为拾取线圈与发射导轨之间的互感以及两个发射导轨之间的交叉互感。uin和iin分别为逆变器输入电压和电流,uC和iC分别为C的电压和电流,iL为L的电流,iS1和iS2分别为S1和S2的电流。u1和 u2分别为逆变输出电压,i1和 i2分别为逆变输出电流,ip1和ip2分别为发射导轨电流。is为负载电流,uR为负载电压。在后文的分析中,除特殊说明外,图中各电流均以箭头标注的方向为正参考方向,各电压以符号“+”所在的一端为正参考端。

图3 基于双输出逆变器的DWPT电路拓扑
Fig.3 Topology of DWPT circuit based on the dual-output inverter
DWPT系统中,一般设计各能量发射端之间的参数具有对称性,即 Lf1=Lf2=Lf、Cf1=Cf2=Cf、Cp1=Cp2=Cp、Lp1=Lp2=Lp。系统谐振角频率表达式为
式中,f0为系统谐振频率。
1.2 工作原理
定义Zr1和Zr2为两个发射导轨中的等效反射阻抗。双输出逆变器采用 PWM 控制策略,定义 T(T=2π/ω0)和 D 分别为逆变器工作周期和开关占空比。定义ub的表达式为
逆变器主要工作波形及各工作模态下的等效电路如图4和图5所示。

图4 逆变器主要工作波形
Fig.4 Main operating waveforms of the inverter

图5 逆变器各工作模态等效电路
Fig.5 Equivalent circuits of each operating mode of the inverter
图 5中所标注的各电流方向为其实际方向。td为 S1和 S2驱动信号的死区时间。逆变器在一个工作周期内共有11个工作模态,各工作模态分析如下:
1)模态 1:t0≤t<t1。t0时刻,S2关断。S2中的电流iS2转移到S1中并流经VDS1,即为iS1。同时,u1下降为零,u2上升为 ub。iC改变极性,C进入充电状态。此模态下,iL开始由最大值线性下降。
2)模态 2:t1≤t<t2。t1时刻,S1开通。由于u1已经被 VDS1钳位为零,因此 S1可实现零电压软开关(Zero Voltage Switching, ZVS)开通。此模态下,iL继续线性下降。同时,可得出 S1实现 ZVS开通的条件为
如果式(3)不满足,S2关断时,u2被VDS2钳位为零,则可实现S2的ZVS关断。
3)模态 3:t2≤t<t3。t2时刻,i1反向过零,i2正向过零,随后i1开始反向增大,i2开始正向增大。此模态下,iL继续线性下降。
4)模态 4:t3≤t<t4。t3时刻,iS1正向过零,由 VDS1转移至 S1,S1开始导通。此模态下,iL继续线性下降。
5)模态 5:t4≤t<t5。t4时刻,电流 iC反向过零,C进入放电状态。此模态下,iL继续线性下降。
6)模态 6:t5≤t<t6。t5时刻,S1关断。iS1转移到S2中并流经VDS2。u2下降为零,u1上升为ub。iC改变极性,C进入充电状态。此模态下,iL开始由最小值线性上升。
7)模态 7:t6≤t<t7。t6时刻,S2开通。由于u2已经被VDS2钳位为零,因此S2可实现ZVS开通。此模态下,iL继续线性上升。同时,可得出S2实现ZVS开通的条件为
如果式(4)不满足,S1关断时,u1被VDS1钳位为零,则可实现S1的ZVS关断。
8)模态 8:t7≤t<t8。t7时刻,iS2正向过零,由 VDS2转移至 S2,S2开始导通。此模态下,iL继续线性上升。
9)模态 9:t8≤t<t9。t8时刻,iC和 i2反向过零,i1正向过零,C进入放电状态。此模态下,iL继续线性上升。
10)模态 10:t9≤t<t10。t9时刻,iC 和 i2正向过零,i1反向过零,C进入充电状态。此模态下,iL继续线性上升。
11)模态 11:t10≤t<t11。t10时刻,iC和 i2再次反向过零,i1再次正向过零,C再次进入放电状态。此模态下,iL继续线性上升。t11时刻,S2关断,逆变器进入下一个工作周期。
2 性能分析
2.1 逆变输出电压增益
假设C非常大,在一个工作周期内,uC保持不变。S1开通时,电感电压 uL=-UC;S2开通时,uL=Uin。稳态下,L满足伏秒平衡原则,即
结合式(2)和式(5),Ub可表示为
根据图4,以t0为初始时刻,忽略死区时间td,则u1和u2的傅里叶级数展开为
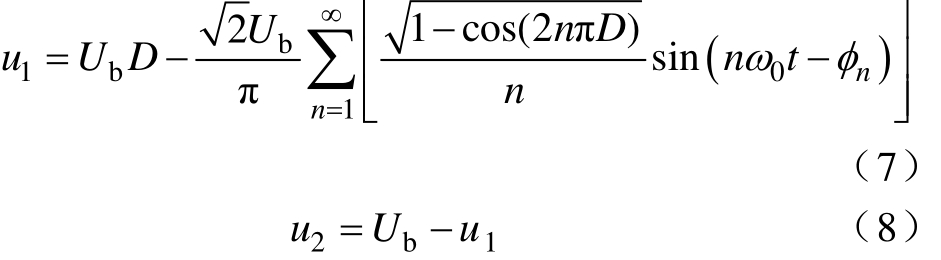
式中,φn=arctan[cot(nπD)]为 u1和 u2的 n次谐波的相位。u1和u2的n次谐波相量表达式为
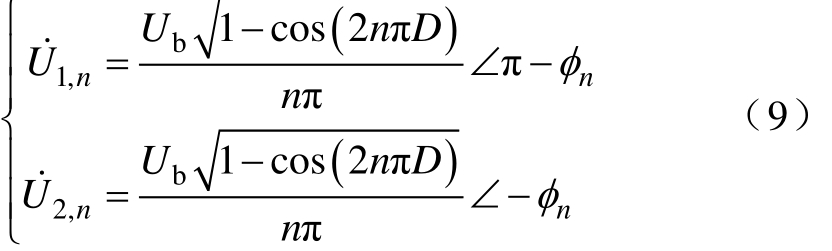
从式(9)可以看出,双输出逆变器的两路输出电压大小相等,方向相反。由于LCC网络具有较好的滤波特性,导轨电流近似正弦波,因此能量主要通过基波进行传输。定义逆变输出电压增益为

图6 Gv-p与D的关系
Fig.6 The relationship between Gv-p and D
Gv-p与D的关系如图6所示。在实际运行中,当D=1时,iL会持续上升,最终导致逆变器因电流过大而损坏。为了使逆变器具有足够的安全工作裕度,图中设置D的变化范围为0~0.9。可以看出,Gv-p与 D呈正相关,且存在 Gv-p|D=0.5=0.9,Gv-pmax=1.39。表 1为双输出逆变器与部分现有逆变器的对比。从表中可以看出,本文所提双输出逆变器在更少的开关器件数量下具有更宽的输出电压增益范围,从而保证了电压输出能力。
表1 双输出逆变器与部分现有逆变器的对比
Tab.1 Comparison of dual-output inverter with some existing inverters

拓扑 电压增益 输入 输出 开关器件电压型全桥 0~0.9 1 1 4矩阵变换器[15] 0~0.64 1 1 8多电平逆变器[16] 0~1.35 1 1 8三相逆变器[18] 0~0.78 1 3 6双输出逆变器 0~1.39 1 2 2
2.2 系统输出功率
利用基波等效,可将图3简化为图7所示的等效电路。图 3中,i2和 ip2的相位与 i1和 ip1相反,在实际应用中,需要改变逆变器第二路输出网络的连接方向,从而使 ip1和 ip2保持同相。因此,为了方便分析,在本小节中,对i2和ip2进行反相处理。

图7 系统等效电路
Fig.7 Equivalent circuit of the system
根据KVL定律,系统方程表达式为

其中
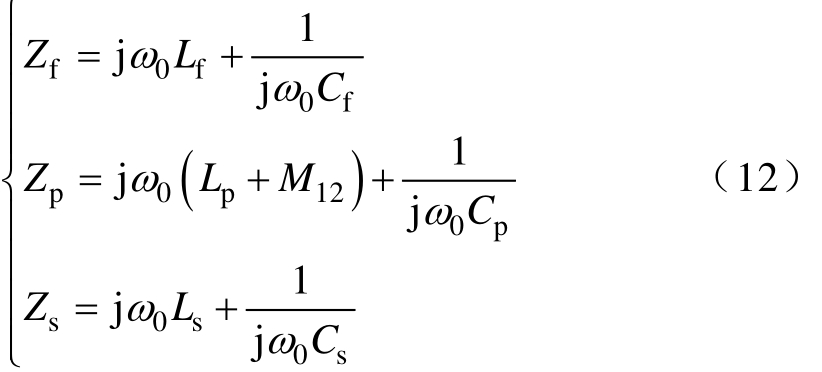
将式(1)和式(12)代入式(11),可解得
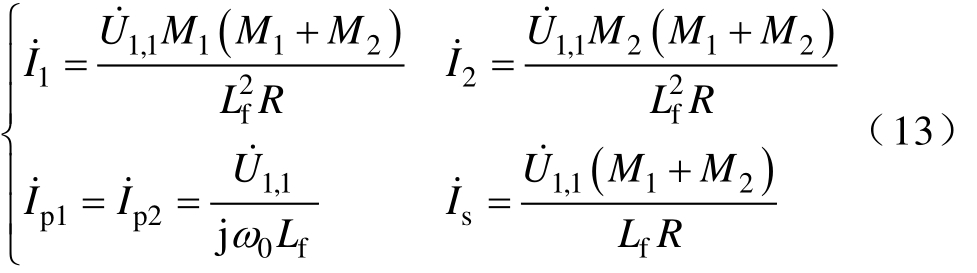
从式(13)可以看出, p1I˙和 p2I˙大小相等,相位相同,且与R、M1和M2无关。根据式(13),可以推导出系统输出功率为
以表2中的参数作为系统指定参数,图8a所示为Po与D和 M1+M2之间的关系。可以看出,在谐振状态下,Po与D和M1+M2呈正相关。图8b所示为D=0.5时,Po与M1和M2之间的关系。可以看出,Po与 M1和 M2呈正相关,且 M1和 M2对 Po的影响具有对称性。
表2 系统指定参数
Tab.2 Specified parameters of the system

参 数 数 值 参 数 数 值Uin/V 100 Lp/μH 100 L/μH 150 Ls/μH 130 C/μF 100 Cs/nF 26.97 Lf/μH 50 R/Ω 5 Cf/nF 70.12 M12/μH 5.7 Cp/nF 62.94 f0/kHz 85
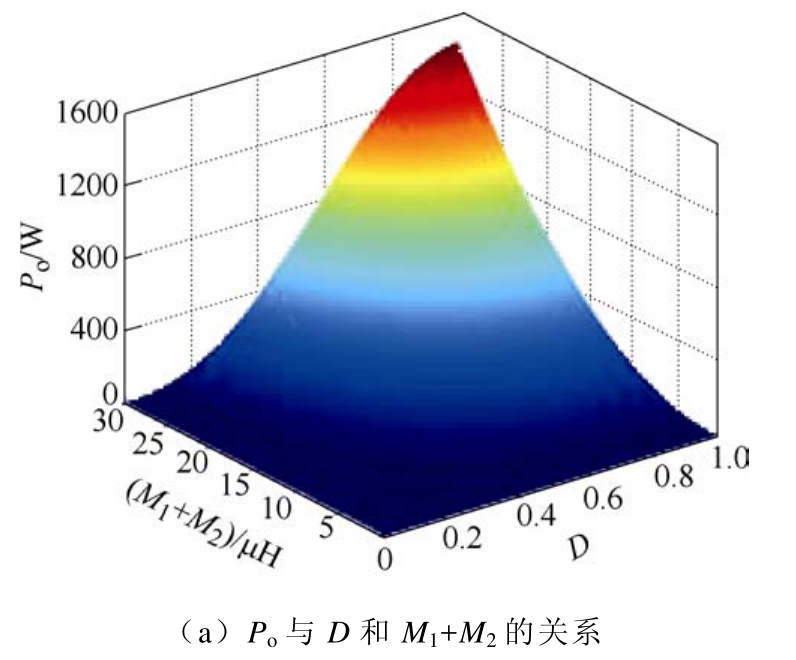

图8 Po与D、M1和 M2的关系
Fig.8 The relationship among Po with D, M1 and M2
2.3 开关器件应力及其软开关工作条件
根据图4,S1和S2的电压应力为
S1和S2的电流应力为
根据图4和图5,iS1和iS2的表达式为
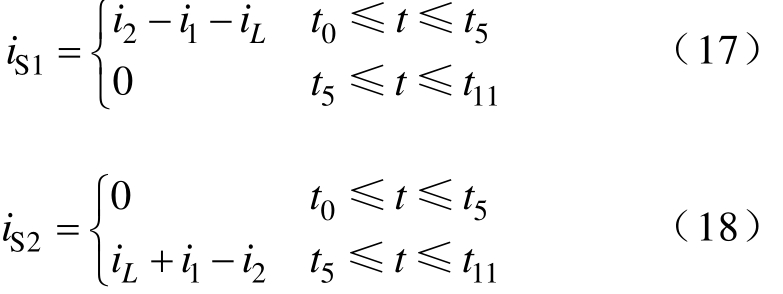
式中,t0=0;t5=(1-D)T;t11=T。
根据式(7)和式(13),i1和i2的基波表达式为
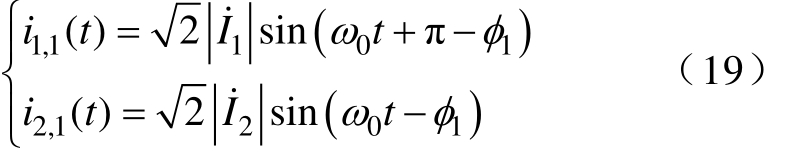
尽管LCC网络具有较好的低通滤波特性,但为了提高分析的准确性,仍需要计算i1和i2的高次谐波。根据文献[25]的分析,高次谐波下可对LCC进行如图9所示的简化。
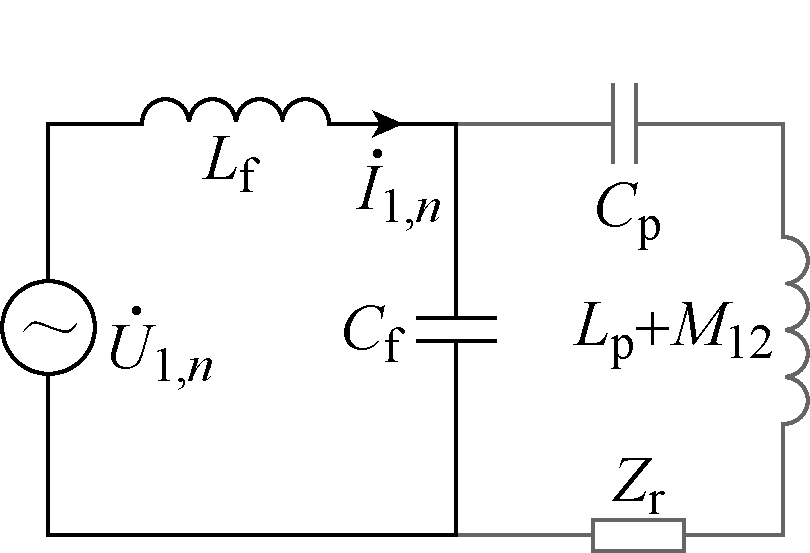
图9 高次谐波下LCC简化模型
Fig.9 Simplified model of LCC with high order harmonics
LCC在n次谐波下的阻抗表达式为
其中
因此,i1和i2的n次谐波表达式为
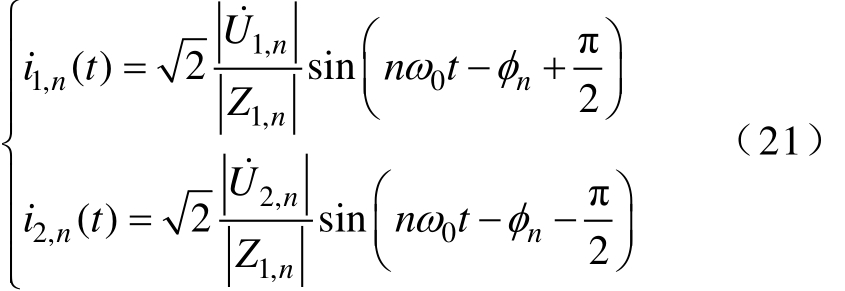
则i1和i2的总表达式为

假设系统无损耗,根据能量守恒定律,逆变器输入电流平均值Iin可表示为
式中,iLm为iL的平均值;iCm为iC的平均值,稳态下,iC满足安秒平衡,即iCm=0。则式(23)可改写为
S2开通时,iL线性增加,因此,iL的纹波为
最终,开关时刻iS2和iS1的表达式为

将式(13)、式(14)和式(19)~式(25)代入式(26),则可以得到开关器件的电流应力以及软开关工作状态。以表2中的参数作为系统指定参数,iS2(t0)与M1、M2和D的关系如图10所示。从图10可以看出,不管M1、M2和D取值如何,iS2(t0)总是大于零,即拾取线圈在移动过程中的任意位置处,S1均可以实现ZVS开通。同时,M1、M2和D越大,iS2(t0)就越大,开关器件的电流应力也就越大。图11为iS1(t5)与M1、M2和D的关系。图11a给出了不同占空比下,M1和M2的取值对iS1(t5)的影响;图11b为图11a中iS1(t5)的极性边界线。可以看出,M1+M2越大,即拾取线圈越接近于任一发射导轨的中心,越有可能实现 S1的 ZVS关断;M1+M2越小,即拾取线圈越接近于任一发射导轨的边缘时,越有可能实现S2的ZVS开通。

图10 iS2(t0)与M1、M2和 D的关系
Fig.10 The relationship among iS2(t0) with M1, M2 and D

图11 iS1(t5)与M1、M2和 D的关系
Fig.11 The relationship among iS1(t5) with M1, M2 and D
3 实验验证
为了验证理论分析的正确性和本文所提逆变器的可行性和优越性,按照表2中的参数搭建了如图12所示的实验装置进行实验验证。其中,现场可编程门阵列(Field Programmable Gate Array, FPGA)控制器用于产生可变占空比的PWM波,驱动S1和S2。双输出逆变器的尺寸为11cm×13cm。

图12 实验装置
Fig.12 The experimental setup

图13 耦合机构侧视图
Fig.13 Side view of the magnetic coupler
耦合机构的侧视图如图13所示。当拾取线圈沿着发射导轨移动时,互感会随着拾取线圈与发射导轨之间的相对位置x的变化而变化。设定当拾取线圈位于两个发射导轨的中间时,x=0。互感随x变化的测量值如图14所示。可以看出,M1和M2分别在x=-7.5cm和x=7.5cm处取得最大值。M1+M2基本上关于x=0对称,而M12则基本保持不变。

图14 互感随x变化的测量值
Fig.14 Measured mutual inductances vary with x
图15 所示为位置x为0和7.5cm、占空比D为0.3、0.5和 0.7时,逆变输出电压 u1、u2和导轨电流ip1、ip2波形。根据式(6),在D =0.3、0.5和0.7时,Ub的理论值分别为142.8V、200V和333.4V,实验中测得的值分别为140V、197V和330V,与理论值较为一致。ip1和ip2基本相等且相位相同,且与x无关,证明了本逆变器的双输出功能。需要说明的是,ip1和ip2之间的误差主要是由于实际系统中逆变器两路输出网络的参数不能严格一致而导致的。随着D的增大,导轨电流的有效值分别大约为2A、3.3A和4.4A。利用式(13)和式(10)推导出逆变输出电压增益分别为 0.534、0.881和 1.175,从而验证了双输出逆变器的电压输出能力。


图15 逆变输出电压和发射导轨电流波形
Fig.15 Waveforms of inverter output voltages and track currents
图16 所示为x为7.5cm和0,D为0.3、0.5和0.7时,S1和 S2的开关过程波形。其中,uS1和 uS2分别为 S1、S2的端电压。以 x=7.5cm,D=0.3为例进行分析。t0时刻,S1关断,驱动电压开始下降。t1时刻,S2开通,驱动电压开始上升,而在此之前uS2已经下降为零,因此,S2实现了 ZVS开通。t2时刻,S2关断,驱动电压开始下降。t3时刻,S1开通,驱动电压开始上升,而在此之前 uS1已经下降为零,因此,S1实现了ZVS开通。通过进一步分析不难发现,在其余波形图中 S1和 S2均实现了 ZVS开通。根据以上结果,结合图11和图14可以得出,在拾取线圈从发射导轨1移动到发射导轨2的整个过程中,双输出逆变器在不同的占空比下均可实现S1和S2的ZVS开通。


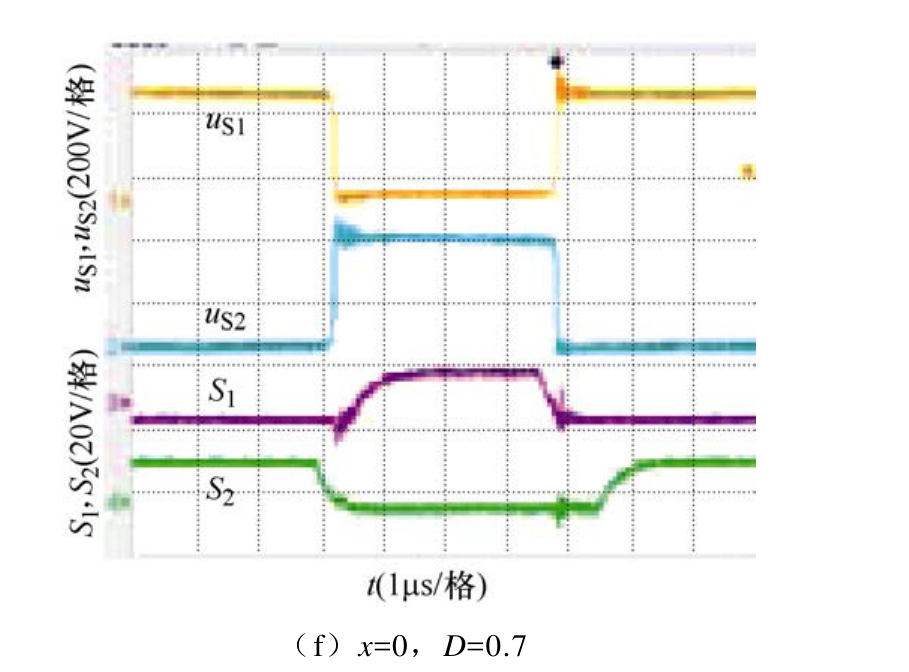
图16 不同x和D下S1和S2的开关过程
Fig.16 Switching process of S1 and S2 at different x and D
图17 给出了D=0.7时,拾取线圈移动过程中发射导轨电流ip1、ip2以及负载电压uR波形。图18为图17中拾取线圈不同x下的展开波形。可以看出,在拾取线圈的移动过程中,ip1和 ip2保持不变,uR则先减小后增大,在x=0处达到最小值。这一变化规律与式(14)、图8和图14的分析结果具有较高的一致性,也说明了本文所提双输出逆变器适用于DWPT系统。

图17 D=0.7时,拾取线圈移动过程中导轨电流和负载电压波形
Fig.17 Waveforms of track currents and load voltage in the moving process of pickup coil when D=0.7


图18 不同x下导轨电流和负载电压展开波形
Fig.18 Expansion waveforms of track currents and load voltage at different x
图19 为系统输出功率Po和效率η 的特性曲线。实验中采用的功率和效率测量设备为HIOKI PW6001-06功率分析仪。可以看出,在拾取线圈移动的过程中,Po会产生一定的波动,且D越大,Po的波动也就越大。当拾取线圈分别与两个发射导轨正对时,即 x=-7.5cm和 x=7.5cm时,Po达到最大值。根据式(14)和图 8,当 Lf和 R不变时,在相同的 U11下,即相同的 D下,Po与 M1+M2呈正相关。根据图 14,当x=-7.5cm和 x=7.5cm时,M1+M2均达到最大值,此时,Po也应达到最大值。实验结果与理论分析一致。从效率曲线可以看出,η 同样会随着拾取线圈的移动而产生波动,且在同一x下,随着D的增大,η 会有略微的下降。但总体而言,系统在不同的x和D下,均能保持较高的传输效率,且最大效率为90%以上。

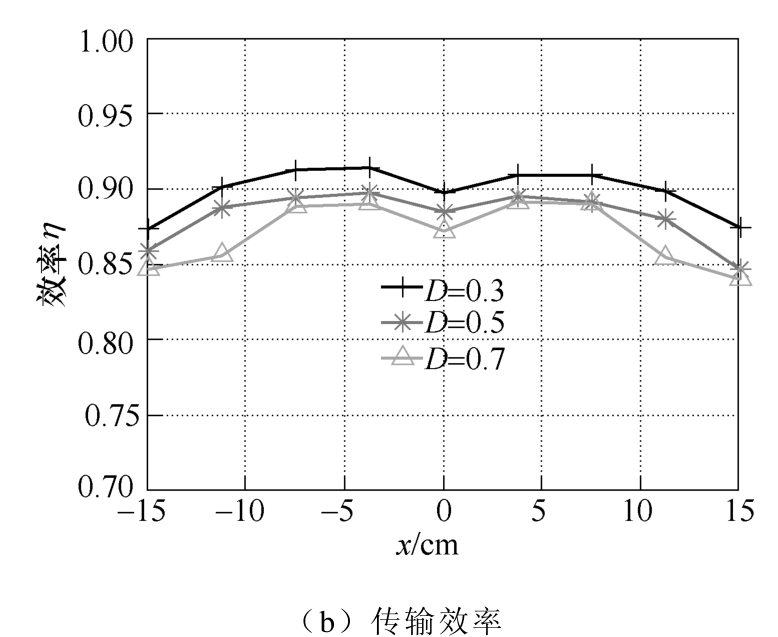
图19 系统输出功率和效率曲线
Fig.19 Curves of the system output power and efficiency
图 20所示为系统在 D=0.5,x=-7.5cm时负载变化波形。可以看出,负载变化时,除了iL会发生变化外,其他参数均保持稳定不变。而uR在负载变化过程中产生尖峰振荡的原因为:实验过程通过机械开关来改变电阻值,其在开关过程中会产生一定的抖动和噪声,从而影响了uR的波形。从图中可以看出,不管负载如何变化,系统响应时间都只有几个毫秒。实验结果说明,系统具有较快的动态响应速度,完全能够满足一般DWPT系统的要求。


图20 负载变化下uC、iL、ip1和uR的波形
Fig.20 Waveforms of uC, iL, ip1 and uR under load change
4 结论
本文提出了一种适用于DWPT系统的双输出逆变器。该逆变器可以产生两路相同的输出,用以驱动两段发射导轨(线圈),从而减少系统逆变器的数量,并简化系统控制。同时,该逆变器的输出电压增益范围为0~1.39,相比于MC-WPT系统部分常用逆变器,可以在更少的开关器件下保证电压输出能力,从而进一步减少单个逆变器中开关器件的数量。实验结果显示,基于本文所提双输出逆变器的DWPT系统可以在拾取线圈移动的过程中一直保持较高的传输效率,且最大传输效率为90%以上。同时,系统具有较快的动态响应速度,完全能够满足一般DWPT系统的要求。
[1] 杨庆新, 章鹏程, 祝丽花, 等. 无线电能传输技术的关键基础与技术瓶颈问题[J]. 电工技术学报,2015, 30(5): 1-8.Yang Qingxin, Zhang Pengcheng, Zhu Lihua, et al.Key fundamental problems and technical bottlenecks of the wireless power transmission technology[J].Transactions of China Electrotechnical Society, 2015,30(5): 1-8.
[2] 孙跃, 李云涛, 叶兆虹, 等. 三线圈ICPT系统中继线圈的位置优化[J]. 电工技术学报, 2016, 31(13):164-171.Sun Yue, Li Yuntao, Ye Zhaohong, et al. Optimization for relay coil location of 3-coil inductively coupled power transfer system[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 164-171.
[3] 陈琛, 黄学良, 谭林林, 等. 电动汽车无线充电时的电磁环境及安全评估[J]. 电工技术学报, 2015,30(19): 61-67.Chen Chen, Huang Xueliang, Tan Linlin, et al.Electromagnetic environment and security evaluation for wireless charging of electric vehicles[J]Transactions of China Electrotechnical Society, 2015,30(19): 61-67.
[4] 夏晨阳, 庄裕海, 童为为, 等. 自配置非对称磁路三相无线平面供电网[J]. 电工技术学报, 2014,29(7): 1-9.Xia Chenyang, Zhuang Yuhai, Tong Weiwei, et al.Self-configuration three-phase wireless power supply network with asymmetric magnetic circuit[J].Transactions of China Electrotechnical Society, 2014,29(7): 1-9.
[5] Wang Zhihui, Li Yupeng, Sun Yue, et al. Load detection model of voltage-fed inductive power transfer system[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 5233-5243.
[6] 苏玉刚, 吴学颖, 刘波, 等. 宽温度范围下感应耦合电能传输系统软开关技术[J]. 电工技术学报,2017, 32(16): 175-182.Su Yugang, Wu Xueying, Liu Bo, et al. Soft switching technology for ICPT system under the condition of wide temperature range[J]. Transactions of China Electrotechnical Society, 2017, 32(16):175-182.
[7] 郑心城, 陈为. 电动汽车无线充电的磁耦合结构综述[J]. 电气技术, 2017, 18(4): 9-15.Zheng Xincheng, Chen Wei. Overview of magnetic coupling structure in wireless charging for electric vehicle[J]. Electrical Engineering, 2017, 18(4):9-15.
[8] Choi S, Jeong S, Gu B, et al. Ultraslim S-type power supply rails for roadway-powered electric vehicles generalized models on self-decoupled dual pick-up coils for a large lateral tolerance[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6456-6468.
[9] Madawala U, Thrimawithana D. A bidirectional inductive power interface for electric vehicles in V2G systems[J]. IEEE Transactions on Industrial Electronics, 2011, 58(10): 4789-4796.
[10] 蒋成, 孙跃, 王智慧, 等. 电动汽车无线供电导轨切换模式分析[J]. 电力系统自动化, 2017, 41(12):188-193.Jiang Cheng, Sun Yue, Wang Zhihui, et al. Switching mode analysis of wireless supplying rail for electric vehicles[J]. Automation of Electric Power Systems,2017, 41(12): 188-193.
[11] 宋凯, 朱春波, 李阳, 等. 用于电动汽车动态供电的多初级绕组并联无线电能传输技术[J]. 中国电机工程学报, 2015, 35(17): 4445-4453.Song Kai, Zhu Chunbo, Li Yang, et al. Wireless power transfer technology for electric vehicle dynamic charging using multi-parallel primary coils[J]. Proceedings of the CSEE, 2015, 35(17):4445-4453.
[12] Zhou Shijie, Mi Chunting. Multi-paralleled LCC reactive power compensation networks and their tuning method for electric vehicle dynamic wireless charging[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6546-6556.
[13] Ko Y, Jang Y. The optimal system design of the online electric vehicle utilizing wireless power transmission technology[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(3):1255-1265.
[14] Bac N, Vilathgamuwa D, Madawala U. A SiC-based matrix converter topology for inductive power transfer system[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4029-4038.
[15] Weerasinghe S, Madawala U, Thrimawithana D. A matrix converter-based bidirectional contactless grid interface[J]. IEEE Transactions on Power Electronics,2017, 32(3): 1755-1766.
[16] Rodriguez J, Leeb S. A multilevel inverter topology for inductively coupled power transfer[J]. IEEE Transactions on Power Electronics, 2006, 21(6):1607-1617.
[17] 马林森, 李勇, 麦瑞坤. 基于二极管钳位五电平技术的 LCL型感应电能传输系统谐波分析[J]. 电工技术学报, 2017, 32(14): 175-183.Ma Linsen, Li Yong, Mai Ruikun. Harmonics analysis of a clamped diode multilevel technology in inductive power transfer system based on LCL topology[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 175-183.
[18] Covic G, Boys J, Kissin M, et al. A three-phase inductive power transfer system for roadwaypowered vehicles[J]. IEEE Transactions on Industrial Electronics, 2007, 54(6): 3370-3378.
[19] 邓其军, 刘姜涛, 陈诚, 等. 无线电能传输系统三相相移控制逆变器研发[J]. 电工技术学报, 2017,32(18): 52-61.Deng Qijun, Liu Jiangtao, Chen Cheng, et al.Development of a three-phase inverter with phaseshifted control for wireless power transfer system[J].Transactions of China Electrotechnical Society, 2017,32(18): 52-61.
[20] Hao Hao, Covic G, Boys J. A parallel topology for inductive power transfer power supplies[J]. IEEE Transactions on Power Electronics, 2014, 29(3):1140-1151.
[21] 麦瑞坤, 陆立文, 李勇. 两逆变器并联 IPT系统的环流消除方法研究[J]. 电工技术学报, 2016, 31(3):8-15.Mai Ruikun, Lu Liwen, Li Yong. Circulating current elimination of parallel dual-inverter for IPT systems[J]. Transactions of China Electrotechnical Society, 2016, 31(3): 8-15.
[22] 孙孝峰, 吴晓颖, 申彦峰, 等. 一种全功率范围零电压开通的电流型双向隔离 DC-DC变换器[J]. 电工技术学报, 2018, 33(10): 2282-2292.Sun Xiaofeng, Wu Xiaoying, Shen Yanfeng, et al. A novel current-fed bidirectional isolated DC-DC converter with full-operating-range ZVS[J]. Transactions of China Electrotechnical Society, 2018,33(10): 2282-2292.
[23] Abramovitz A, Zhao Ben, Smedley K. High-gain single-stage boosting inverter for photovoltaic applications[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3550-3558.
[24] Sarnago H, Lucia O, Burdio J. Interleaved resonant boost inverter featuring SiC module for high performance induction heating[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 1018-1029.
[25] Pantic Z, Bai Sanzhong, Lukic S. ZCS LCC-compensated resonant inverter for inductivepower-transfer application[J]. IEEE Transactions on Industrial Electronics, 2011, 58(8): 3500-3510.