0 引言
感应加热因与传统加热相比具有高效、节能和环保的优点,成为热处理领域首选的加热方式[1-4]。感应加热的原理是基于电磁感应现象[5-8],在加热器线圈中通入一定大小和频率的电流,交变电流产生交变磁场,根据法拉第电磁感应定律
式中,n为线圈匝数;dΦ/dt为单位时间内的磁通变化量(Wb/s)。故在工件上产生感应电压e,由于工件具有一定电阻,因此在工件上会产生涡流,利用涡流产生的焦耳热对工件进行加热[9-11]。
感应加热有纵向磁通感应加热和横向磁通感应加热两种基本形式[12]。纵向磁通感应加热产生的磁感线平行于被加热工件,适用于对管材、棒材等横截面积较大的工件进行加热;横向磁通感应加热产生的磁感线垂直于工件,适用于对横截面积较小的带材进行加热。随着热处理行业的发展,对金属带材如钢材进行加热处理成为行业发展趋势[13]。纵向磁通感应加热对带材进行加热时,由于带材横截面积较小,会出现涡流相互抵消的情况,故具有一定局限性,因此横向磁通感应加热技术被广泛应用[14]。
虽然横向磁通感应加热技术已经有了较大发展[15],但其也有缺点,即存在加热器出口处带材宽度方向上带材表面温度分布不均匀的问题[16-17]。这个缺点严重制约了横向磁通感应加热技术在热处理行业中的应用和推广。
感应加热装置中用于加热带材的交变磁场的有效值决定了带材表面温度的高低,装置漏磁大小决定了带材的加热效果和加热效率。漏磁大小与加热器结构有关,交变磁场的有效值是由其通过磁路的磁阻大小决定。
文献[17-20]比较了不同线圈结构对加热器出口处带材表面温度分布的影响,提出一种新型线圈结构。但是上述文献所用的是原有感应加热装置,此装置中漏磁较大,使得加热效果差、加热效率低,且磁场通过磁路的磁阻大,导致带材表面温度低。文献[21-22]研究利用优化算法对感应加热装置进行优化,文献[21]单独应用遗传算法进行加热装置优化;文献[22]将支持向量机和遗传算法相结合对加热装置进行优化。但是这两篇文献均没有涉及优化前后装置加热效率问题。文献[23]对线圈在带材宽度方向上相对位置变化对加热器出口处带材表面温度分布的影响进行了对比分析。但是该文献所采用的计算方法没有考虑带材材料参数随温度的变化。同时,该文献比较了不同激励电流大小和频率下加热器出口处带材表面温度分布情况。但是其只是通过单一变量法分别进行对比分析,没有优选出一组使温度分布均匀性最好的电流大小和频率的激励参数组合。
针对当前研究存在的问题,本文应用 MagNet和ThermNet软件以及Matlab软件在基于磁热耦合计算方法考虑带材运动和材料参数变化条件下对原有感应加热器进行设计改进,提出一种新型感应加热器。同时,对原有和新型装置的加热效率进行了对比分析。此外,基于新型装置,针对横向磁通感应加热技术存在带材温度分布不均匀的缺点,计算了不同激励电流大小和频率下加热器出口处带材表面的温度分布情况,优选出一组电流大小和频率的激励参数组合,使得加热器出口处带材表面温度分布均匀性最好。为实际热处理工业制作感应加热器和设置合适的激励参数提供了理论依据。
1 磁热耦合计算方法及装置加热效率
利用MagNet、ThermNet和Matlab软件进行磁热耦合计算分析过程中,当带材加热状态稳定后,加热器下方带材表面涡流分布不再发生变化,在无外界因素干扰的情况下,带材表面温度分布也不再变化。在加热过程中,由于带材连续运动,故运动到加热器出口之外的带材表面温度均为加热器出口处的温度。同样,处于加热器入口之外的带材表面温度均为带材的初始温度,即环境温度。综上,只需要研究加热器下方带材表面涡流和温度分布即可。
在实际工程中,被加热带材长度较长,但是在进行仿真计算时,若感应加热模型带材长度太长,当计算机系统的硬件资源如内存等不足时,可能会出现由于模型大、剖分细等原因使得求解失败的情况,故带材长度设置要在合理范围内。
由于感应加热装置在横向和纵向均对称,因此只需建立 1/4模型。将 1/4模型中加热器下方区域进行网格划分,磁热耦合计算区域如图1所示。
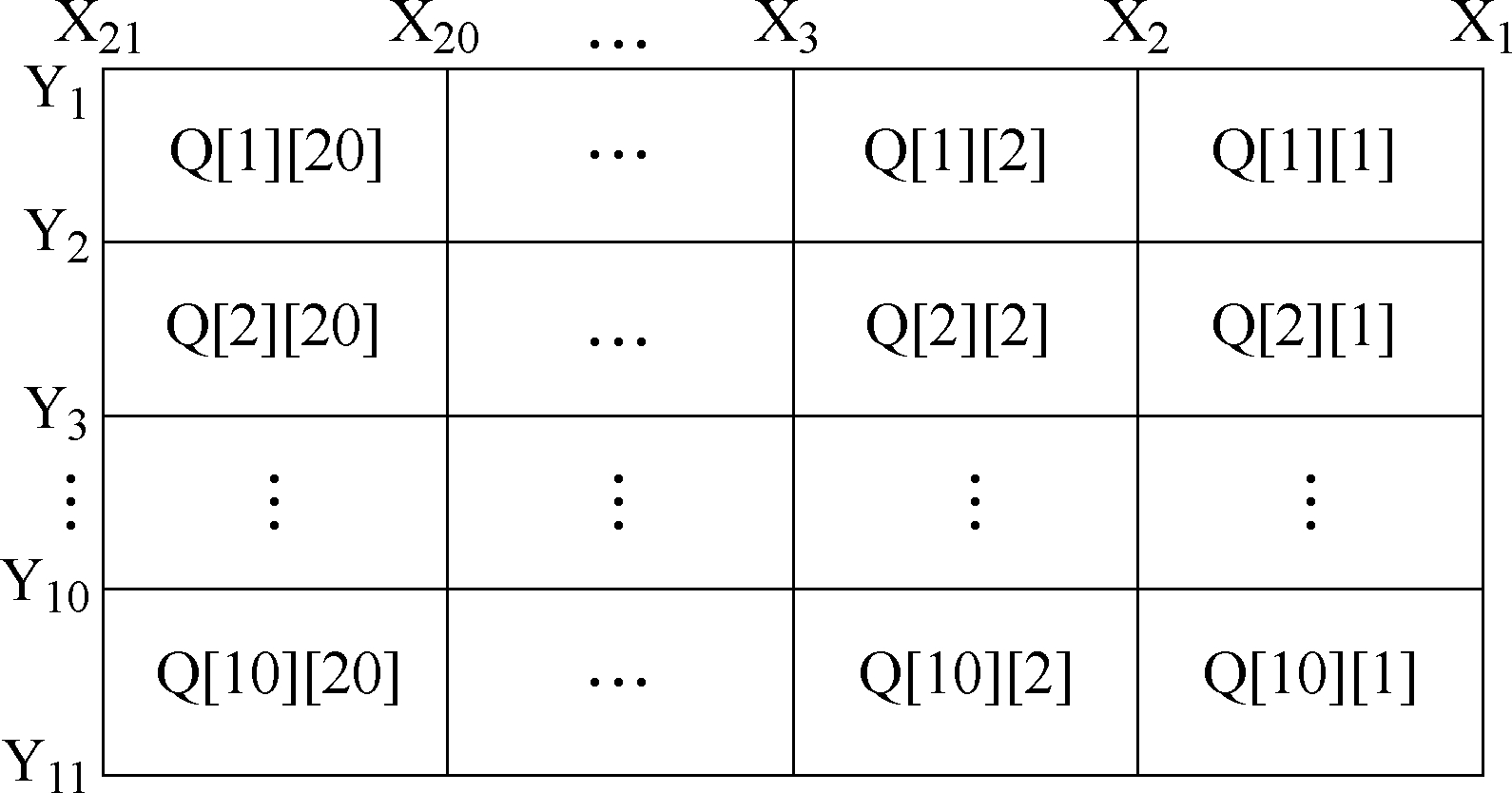
图1 磁热耦合计算区域
Fig.1 Calculation area of magnetic-thermal coupling
在图 1中,X1代表加热器入口,X21代表加热器出口,X2~X20代表纵向等间距的网格划分线。Y1代表带材边缘位置,Y11代表带材中线位置,Y2~Y10代表横向等间距的网格划分线。Xj与 Xj+1(j=1, 2,…, 20)之间距离均为 d=20mm。Yi与 Yi+1(i=1, 2,…, 10)之间距离均为l =30mm。每一部分区域![]() 示。
示。
在磁热耦合计算过程中,将带材的连续运动近似为步进运动,因为带材运动速度v不变,故每一次步进运动的计算时间均为t,且满足
本文建立的1/4模型中带材长度为400mm,宽度为300mm,整个带材是由长度为20mm,宽度为30mm的20×10个矩形带材构成,各个矩形带材的属性完全一致。利用上述方法建立的带材与加热器下方磁热耦合计算区域相对应,有利于提取温度。以下提取的温度 ![]() )均 为 每个矩形带材表面的中点温度。
)均 为 每个矩形带材表面的中点温度。
磁热耦合计算流程如图2所示。
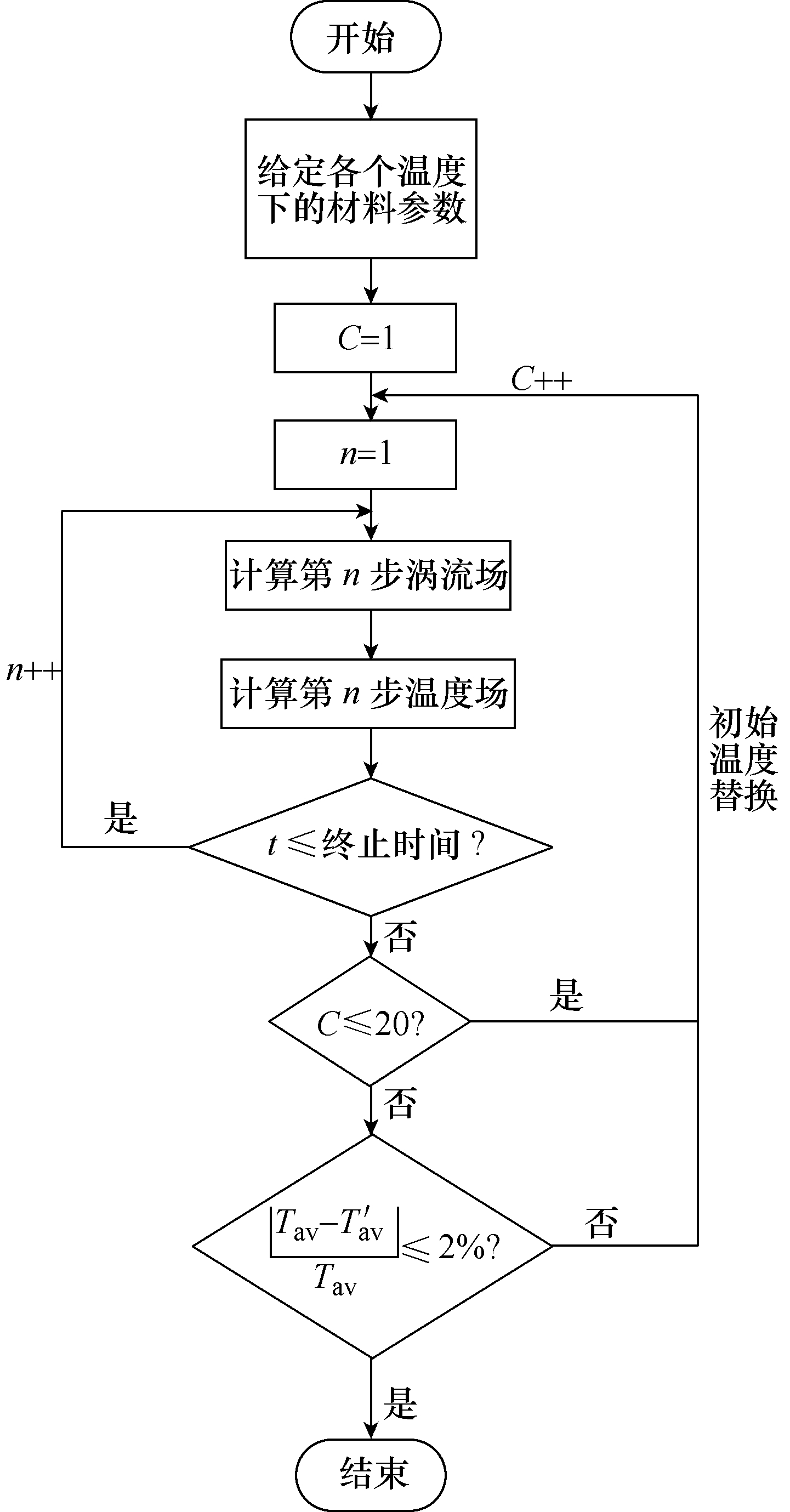
图2 磁热耦合计算流程
Fig.2 Calculation process of magnetic-thermal coupling
在开始计算前,需要将各个温度下的材料参数赋值给带材。计算开始,首先将带材第1列置于加热器下方Q[i][1],i∈ (1 ,10)位置,如图2中C=1,此时带材的初始温度为环境温度25℃,在时间t内进行涡流场和温度场耦合计算,图2中的n表示软件仿真计算时磁热耦合场的计算次数,到达终止时间后,将带材第1列到第19列的温度值提取出来,利用Matlab温度替换程序实现带材初始温度替换,进而实现带材材料参数随温度变化。然后将带材整体向前移动20mm,使带材第1列和第2列分别处于加热器下方 Q[i][2],Q[i][1],i∈ (1 ,10)位置,通过相同方法进行涡流场和温度场耦合计算和材料参数更新。当带材完全处于加热器下方时,提取带材第 2列到第20列的温度值,利用温度替换程序将温度赋值给带材第 1列到第19列,此时带材第 1列到第19列依次变为第2列到第20列,通过采点赋值的方法实现带材连续运动和材料参数随温度的变化。
通过大量计算分析可知,加热器下方带材表面温度稳定趋势是温度从加热器入口到出口逐渐稳定。故通过比较带材在加热器出口处,即Q[i][20],位置前后两次温度平均值的相对差值是否小于2%,来判断加热器下方带材表面温度是否稳定,计算公式如下
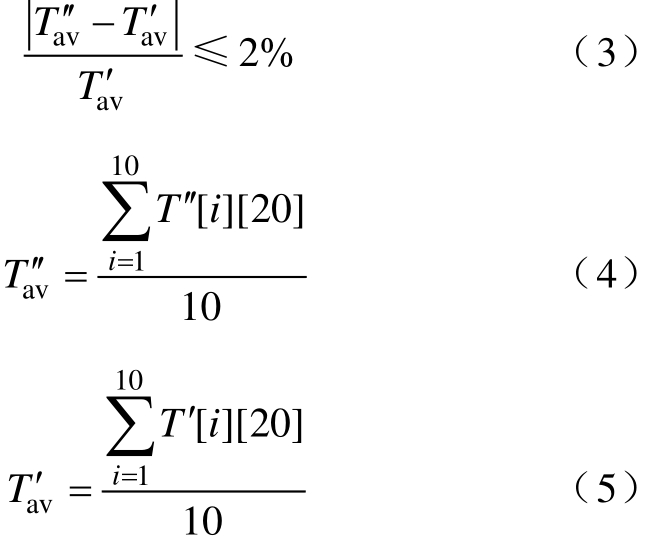
式中, avT′′和 avT′分别为后一次和前一次计算的加热器出口处的平均温度; T′′[i][20]和 T′[i][20]分别为后一次和前一次计算完毕后加热器出口处带材表面各采样点的温度值。
当两者的相对差值满足≤2%时,计算结束。当相对差值>2%时,继续取带材第2列到第20列的温度值进行初始温度替换,进而实现带材连续运动和材料参数实时变化。
当加热器下方带材表面温度全部稳定后,利用加热器出口处带材表面温度的相对不均匀度 Trel来判断加热装置优劣和加热效果好坏,计算公式为

式中,T[i][20]为带材表面温度全部稳定之后,加热器出口处带材表面各采样点的温度值;Tav为带材表面温度全部稳定之后,加热器出口处带材表面的平均温度。
感应加热装置的加热效率η 同样也是判断一个装置优劣的重要指标,计算公式为
式中,Q为加热状态稳定后在时间t1内从加热器出口运动出来的带材表面的涡流损耗(J);W为在时间t1内加热上述从加热器出口处运动出去的质量为m的带材所输入的有功激励(J)。选取处于加热器出口之外带材表面涡流损耗的原因是加热器下方带材表面温度高,带材会向加热器及其他区域传递热量,造成涡流损耗损失。Q计算公式为
式中,C是带材的比热容[J/(kg·)℃];m是带材表面温度达到稳定后在时间t1内从加热器出口运动出去的带材质量(kg);T1是带材的初始温度,取25℃;T2是温度稳定后加热器出口处带材表面的平均温度。
输入激励为正弦交流电,其瞬时值表达式为
故W的计算公式为
式中,|Z|为线圈阻抗的模。当带材表面温度全部达到稳定后,|Z|值可以在MagNet后处理页面中计算出来。
2 新型加热器设计
本节对原有感应加热器进行改进,设计出一种新型加热器结构。原有装置全模型图和 1/4模型图如图3所示。

图3 原有感应加热模型
Fig.3 Original induction heating model
以 1/4模型为例进行说明,该模型由铁心、线圈、带材、空气包以及磁力线垂直的边界条件组成。
铁心材料是 30Q130硅钢片,是一种厚度为0.3mm,理论最大铁心损耗为1.3W/kg的取向硅钢片。
线圈材料采用 T3铜,其具有较好的导电、耐腐蚀和加工性能。线圈结构采用双层六边形线圈,如图4所示。

图4 双层六边形线圈结构
Fig.4 Coil structure of double hexagon
该线圈结构的中段线圈与带材运动方向垂直,保证带材中段热源均匀。考虑到带材边缘对流、辐射散热的影响,边缘线圈采用三角形。经分析计算,该线圈结构能够使带材在加热器出口处产生更为均匀的温度分布,加热效果更好。
带材材料是45号钢,这是一种含碳量为0.42%~0.5%的优质碳素结构钢。而且,带材的材料参数如磁导率、电导率、比热容、热导率等均随着温度变化而变化。
2.1 设计原理
原有感应加热装置两个方向上的二维平面图及其部分磁感线分布如图5所示。
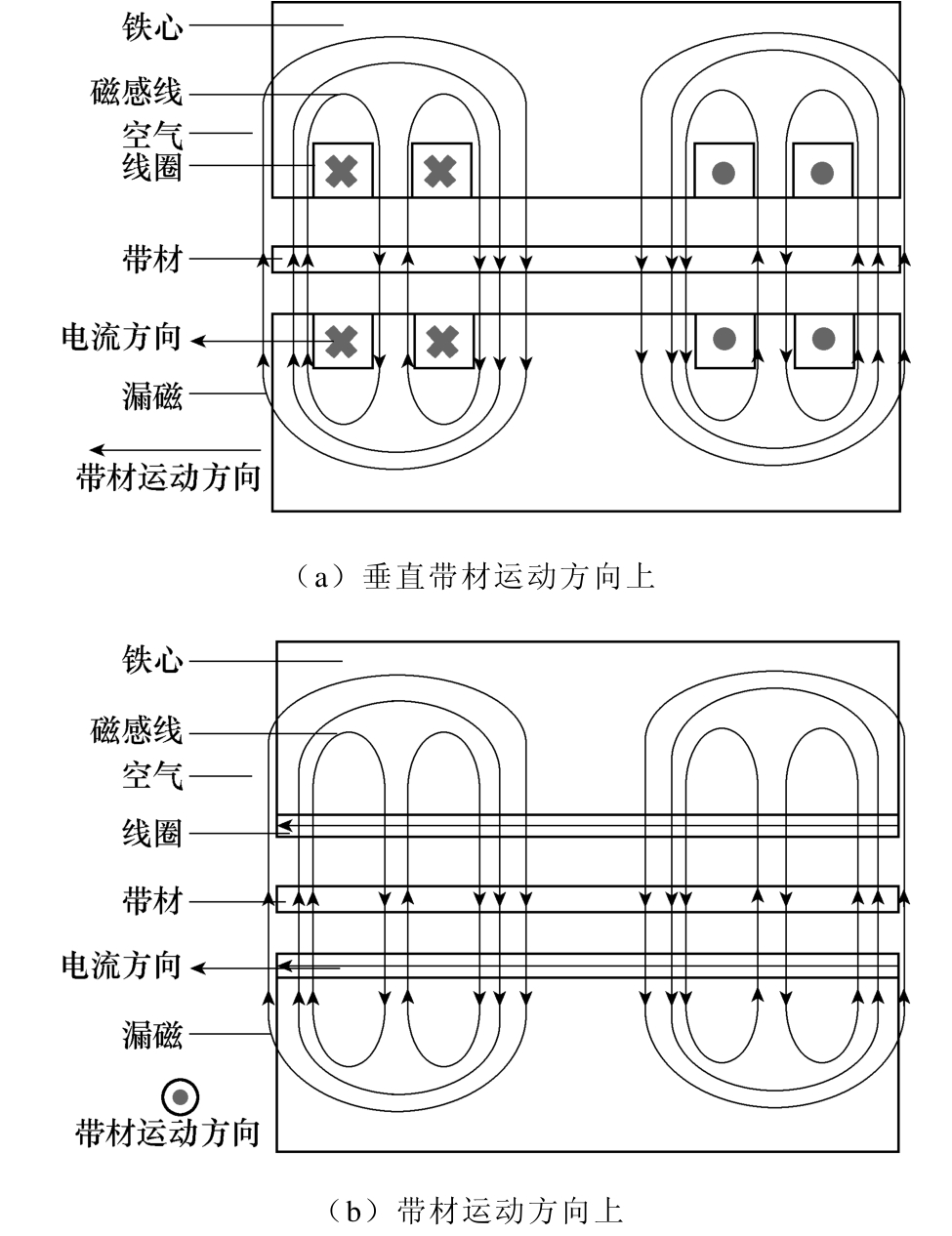
图5 原有感应加热装置二维平面图及其磁感线分布
Fig.5 Two-dimensional drawing of the original TFIH and its magnetic induction line distribution
在某一时刻,线圈中通入的交变电流方向见图5,根据右手定则,此时产生的部分磁感线如图 5所示。其中,图5a表示中段线圈产生的磁感线方向,图5b表示边缘线圈产生的磁感线方向。从图中可以看到,磁感线要通过两次上下加热器之间的气隙,故磁路中空气所占比例较大,因为空气的磁阻大,故原有装置中用于加热带材的交变磁场的有效值小,使得加热带材的热源小、带材温度低。同时,原有装置漏磁稍大,导致加热效果差、加热效率低。
针对原有装置存在的问题,本文提出一种新型加热器结构,新型装置全模型图和 1/4模型图如图6所示。

图6 新型感应加热模型
Fig.6 New induction heating model
新型装置是在原有装置的基础上,在带材宽度方向上的加热器边缘安装与铁心相同材料的铁轭,构成新型加热器结构且装置的其他变量保持不变。
新型装置带材运动方向上的二维平面图及其部分磁感线分布如图7所示。
根据磁感线会沿着磁阻小的磁路流通的原理,绘制了图7所示的部分磁感线分布。可知,中段线圈和边缘线圈产生的磁感线都会因通过铁轭流通而只通过一次上下加热器之间的气隙,故磁路中空气所占比例减小。由 2.2节计算结果可知,当加热状态稳定后,新型模型铁轭中磁通密度有效值的平均值为0.44T,通过查30Q130硅钢片材料参数中的磁化曲线可知铁轭磁导率约为 0.05H/m,而空气磁导率近似为真空磁导率μ0=4π×10-7H/m,故铁轭磁导率远远大于空气。磁阻计算公式为

图7 新型感应加热装置二维平面图及其磁感线分布
Fig.7 Two-dimensional drawing of the new TFIH and its magnetic induction line distribution
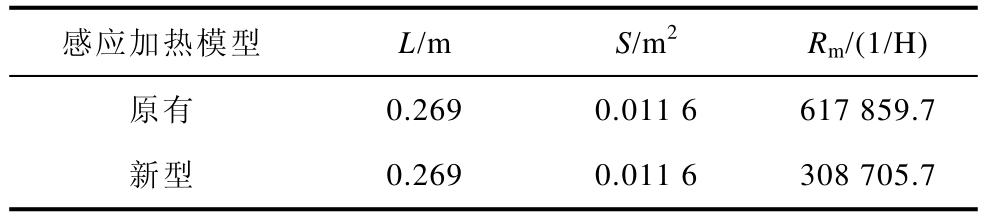
式中,Rm为磁路的磁阻(1/H);L为磁路长度(m);S为磁路横截面积(m2)。通过计算可以得到两个模型的磁阻对比见表1。
表1 原有模型与新型模型磁阻对比
Tab.1 Comparison of magnetic resistance between the original and new model
感应加热模型 L/m S/m2 Rm/(1/H)原有 0.269 0.011 6 617 859.7新型 0.269 0.011 6 308 705.7
由表1可知,原有模型磁路的磁阻是新型模型的两倍左右。综上,新型装置中用于加热带材的交变磁场的有效值大,使得加热带材的热源大,带材温度高。同时,新型感应加热器结构能够在一定程度上减小漏磁,因此可以改善带材的加热效果,提高装置加热效率。
2.2 计算结果
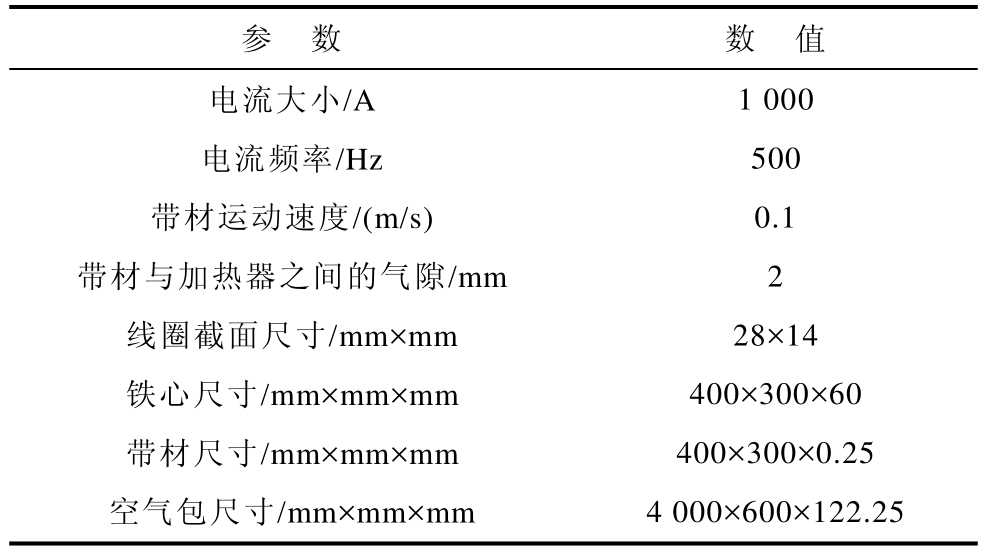
对原有装置加热器结构进行设计改进时,原有装置1/4模型设定的参数见表2。
表2 原有感应加热装置1/4模型参数
Tab.2 The parameters of 1/4 model of the original TFIH
参 数 数 值电流大小/A 1 000电流频率/Hz 500带材运动速度/(m/s) 0.1带材与加热器之间的气隙/mm 2线圈截面尺寸/mm×mm 28×14铁心尺寸/mm×mm×mm 400×300×60带材尺寸/mm×mm×mm 400×300×0.25空气包尺寸/mm×mm×mm 4 000×600×122.25
新型模型基于表2所示参数,其铁轭长度与铁心相同为400mm、铁轭厚度为29mm、铁轭与铁心之间的气隙为31mm。
基于第1节中提出的磁热耦合计算方法,在考虑带材运动和材料参数随温度变化的条件下,对原有和新型两种感应加热装置的 1/4模型在相同激励下进行计算分析,计算结果对比如下:
当加热状态稳定后,原有和新型模型中的磁感线分布如图8和图9所示。
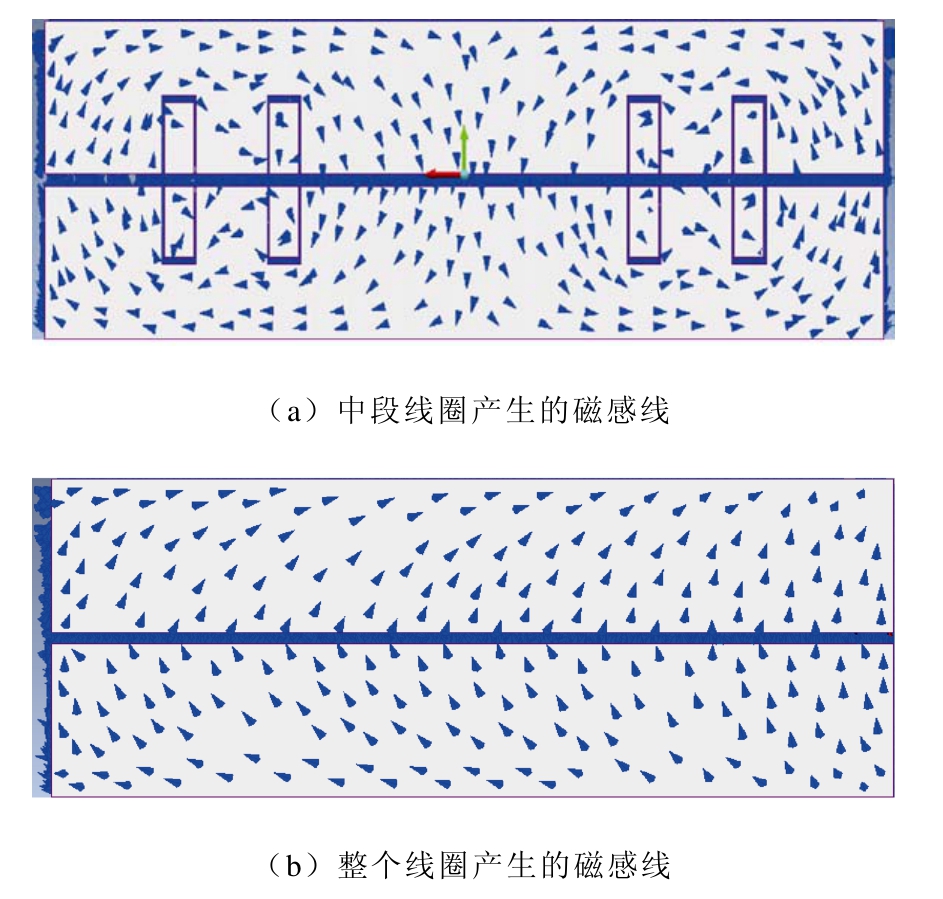
图8 原有感应加热模型磁感线分布
Fig.8 Distribution of magnetic induction line in the original induction heating model

图9 新型感应加热模型磁感线分布
Fig.9 Distribution of magnetic induction line in the new induction heating model
由于磁感线分布在 1/4模型中不能显示清楚,故选取1/2模型磁感线分布。观察图8可知,原有模型中磁感线通过的磁路空气所占比例较大,导致磁路磁阻大,使得用于加热带材的交变磁场的有效值小。同时,从图中可以看出,原有装置加热器边沿漏磁稍大。图9表明新型模型中无论是中段线圈还是边缘线圈,产生的磁感线在加热器铁心外围都通过铁轭流通,磁路中空气所占比例较小,导致磁路磁阻小,使得用于加热带材的交变磁场的有效值较大,且新型加热器结构在一定程度上减少了漏磁。同时,新型模型改善了两个线圈之间磁感线相互抵消的情况。图8和图9所示计算结果与2.1节设计原理的分析相符合,验证了原理的正确性。
当加热器下方带材表面温度全部达到稳定后,两个模型带材表面涡流分布云图如图10所示。

图10 涡流分布云图
Fig.10 The nephogram of eddy current distribution
图10 中,RMS|J|表示带材表面涡流值的方均根值。观察图10可知,两个模型的涡流分布都遵循“线圈投影规律”,即带材表面涡流主要分布在加热器线圈在带材上的投影区域内。
两个模型的涡流分布还满足加热器入口处带材表面涡流值大于出口处。原因是带材在加热过程中是连续运动的,观察温度分布云图可知,带材从加热器入口运动到出口是一个不断升温的过程,且带材材料参数中电导率和磁导率随着温度升高而减小,由于涡流大小与材料的电导率和磁导率呈正比,故加热器入口处带材表面涡流值大于出口处。
从图10中可以看出,新型模型带材表面涡流值整体上大于原有模型。因为新型模型中用于加热带材的交变磁场的有效值较大,在带材表面产生的感应电压大,从而带材表面涡流大。由软件计算结果可知,当带材表面温度达到稳定时前一次耦合计算过程中,两个模型中用于加热带材的平均磁通密度的有效值|B|在本次计算过程中随时间变化的大小对比如图11所示。

图11 平均磁通密度的有效值随时间变化的大小对比
Fig.11 Comparison of effective values of mean magnetic flux density with time
由图 11可知,新型模型中用于加热带材的|B|在本次耦合计算过程中均大于原有模型。由于激励电流为正弦交流电,故产生的交变磁场也随时间呈正弦变化,因此可以推出在带材整个加热过程中,新型模型中的磁通密度均大于原有模型。计算结果符合设计原理且与图 10中新型模型的涡流分布整体上大于原有模型的计算结果相对应。原有和新型模型中带材表面磁通密度分布如图12所示。


图12 磁通密度分布云图
Fig.12 The nephogram of magnetic flux density distribution
可以看出,新型模型带材表面的磁通密度整体上略大于原有模型,仿真计算结果符合设计原理。
当加热状态稳定后,两个模型带材表面热源分布云图如图13所示。

图13 热源分布云图
Fig.13 The nephogram of heat source distribution
观察图13可知,两个模型带材表面热源分布同样遵循“线圈投影规律”。由于在线圈拐角处涡流值较小,故拐角处热源值相对于线圈投影区域其他位置较低。同时线圈与带材边缘相交位置的热源值大于带材其他位置,这是因为“电磁场边缘效应”和边缘相交处时涡流值产生的影响大于带材边缘对流、辐射散热的影响。
同时观察到,两个模型中热源分布均满足加热器出口处带材表面热源值大于入口处。原因是在感应加热过程中,热源与温度是相互影响的关系,在加热器出口处带材表面温度值大于入口处且随着温度升高带材材料参数中电导率逐渐减小,并且减小的程度大于带材表面涡流值从加热器入口到出口减小的程度,被加热带材上单位体积的焦耳热功率Pv的计算公式为
式中,J为涡流(A/m2);σ 为电导率。故带材表面热源值在出口处大于入口处。
当带材的加热状态稳定后,加热器出口处带材表面的热源分布曲线如图14所示。

图14 加热器出口处带材表面热源分布
Fig.14 Heat source distribution on the surface of strip at the outlet of heater
从图14中可以看出,新型模型加热器出口处带材表面热源值整体上大于原有模型。可以发现,原有模型出口处带材表面的热源值波动较大,不平滑;新型模型出口处带材表面热源值波动较小,热源分布较平滑。
当加热状态稳定后,两个模型带材表面温度分布云图如图15所示。当加热状态稳定后,原有和新型模型加热器出口处带材表面温度分布情况如图16所示。
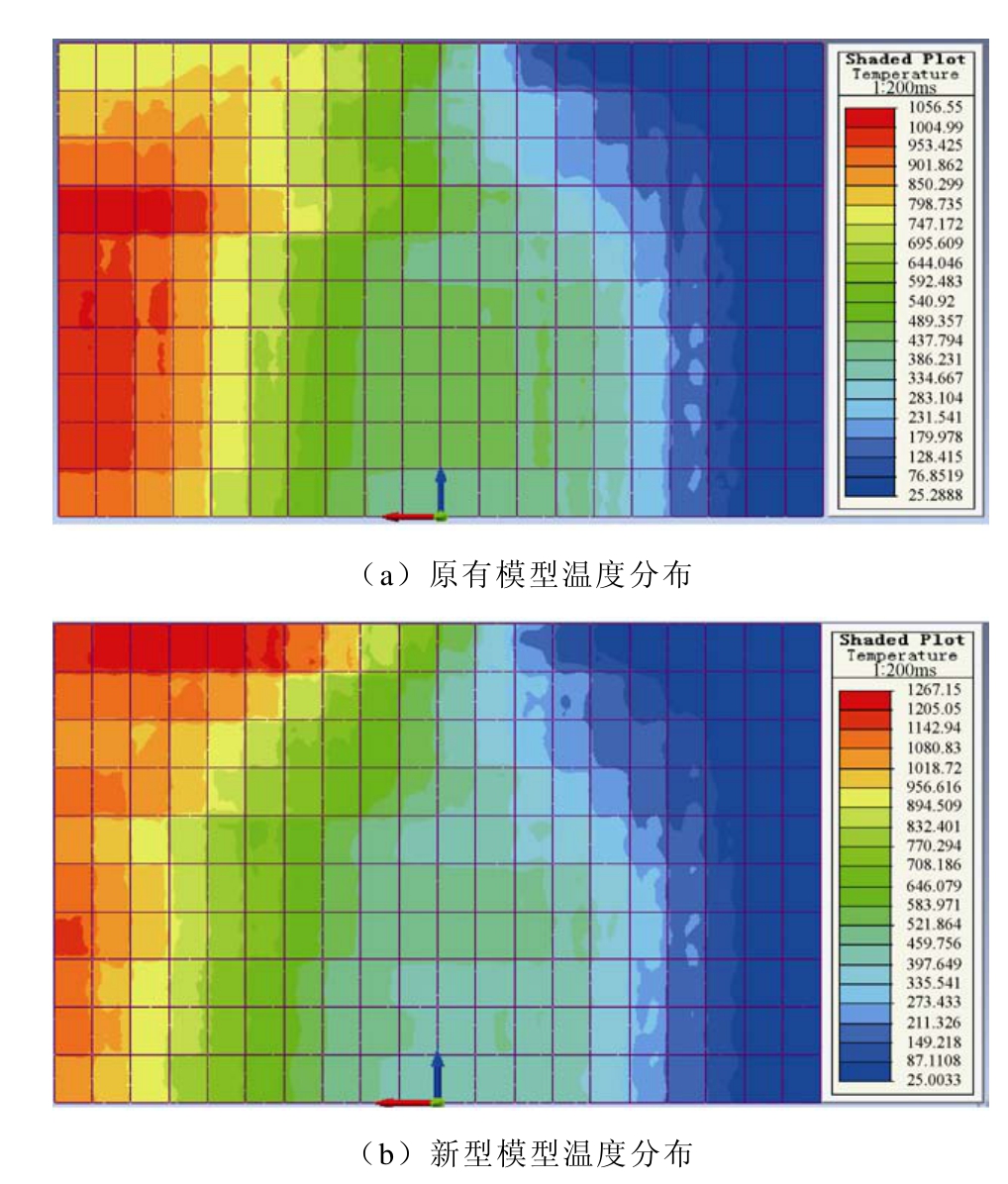
图15 温度分布云图
Fig.15 The nephogram of temperature distribution
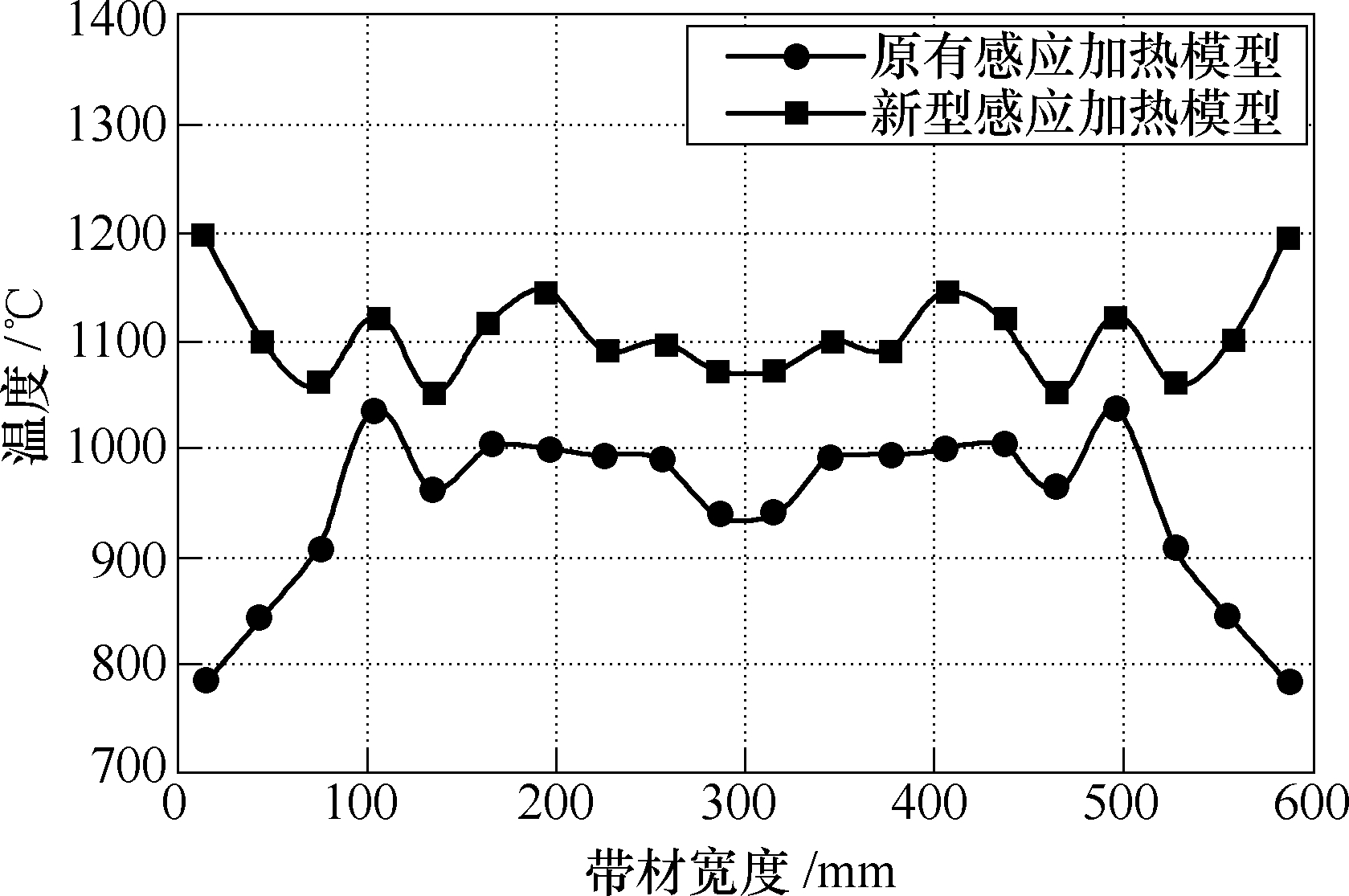
图16 加热器出口处带材表面温度分布
Fig.16 Temperature distribution on the surface of strip at the outlet of heater
观察图15和图16可知,两个模型中带材表面温度从加热器入口到出口不断升高且热量的传导使带材各部分温度分布更加平滑。新型模型由于“电磁场边缘效应”和线圈突出带材边缘以及铁轭结构的多重影响,使得带材边缘温度高于中线温度。但是,由于带材边缘与空气之间对流、辐射散热的影响,带材边缘温度并未明显高于中线部位,使得加热器出口处带材表面温度分布较为均匀。原有模型由于散热影响较大,造成带材边缘温度低于中线温度,温度分布均匀性差。
当带材表面温度全部达到稳定后,可以得到评价横向磁通感应加热装置优劣的四个参数值:加热器出口处带材表面最高温度Thigh、加热器出口处带材表面平均温度Tav、加热器出口处带材表面温度的相对不均匀度Trel以及装置加热效率η。两个模型的参数值对比见表3。
表3 感应加热装置优劣的评价参数
Tab.3 Evaluation parameters of advantages and disadvantages of the TFIH
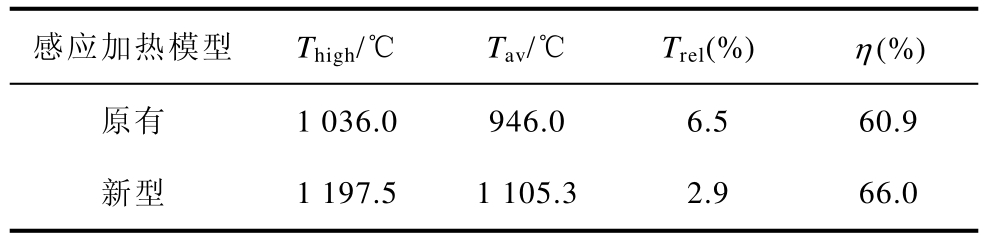
感应加热模型 Thigh/℃ Tav/℃ Trel(%) η (%)原有 1 036.0 946.0 6.5 60.9新型 1 197.5 1 105.3 2.9 66.0
由表 3可知,新型模型 Thigh比原有模型高161.5℃,Tav比原有模型高159.3℃,原因是新型模型带材表面涡流值、热源值整体上均大于原有模型,故带材表面温度值整体上也大于原有模型。同时还可以观察到,新型模型Trel比原有模型小3.6%,并且新型模型η 比原有模型高5.1%,这是由于新型加热器结构使得装置漏磁较少,以至于新型模型的加热效果和加热效率均优于原有模型。
综上所述,针对原有感应加热装置漏磁稍大且交变磁场通过磁路磁阻大的不足,在原有装置的基础上,在垂直带材运动方向的加热器边缘安装了使装置漏磁较小和使交变磁场流通磁路的磁阻变小的铁轭,设计了新型感应加热器结构,从而建立新型感应加热装置。采用磁热耦合计算方法,利用MagNet和ThermNet软件进行磁热耦合计算分析。计算结果表明:在相同激励下,新型装置能够使带材加热到更高温度。故在实际工程中,当要求将带材加热到某一指定温度时,新型装置需要的激励小,从而减少了感应加热装置电源的输出功率,节约工业能源。同时,新型装置能够在加热器出口处带材表面产生更为均匀的温度分布,改善了加热效果,并在一定程度上提高了装置的加热效率。而且,新型装置能够减少带材表面温度稳定时耦合场的计算次数。
本文提出的新型横向磁通感应加热器为实际工程加热器的制造提供了理论依据,具有很高的应用价值。
3 新型装置激励参数优选
3.1 激励电流大小优选
在对新型装置线圈通入激励电流的大小进行优选时,设置电流频率为 500Hz、带材运动速度为0.1m/s。计算比较了激励电流大小分别为 600A、800A、1 000A、1 100A、1 200A的情况下带材表面温度分布情况和装置加热效率,得到了不同激励电流大小下感应加热装置的评价参数值见表 4。不同激励电流大小下加热器出口处带材表面温度分布情况如图17所示。
表4 不同激励电流大小下装置的评价参数
Tab.4 Evaluation parameters of the TFIH under different excitation current magnitude
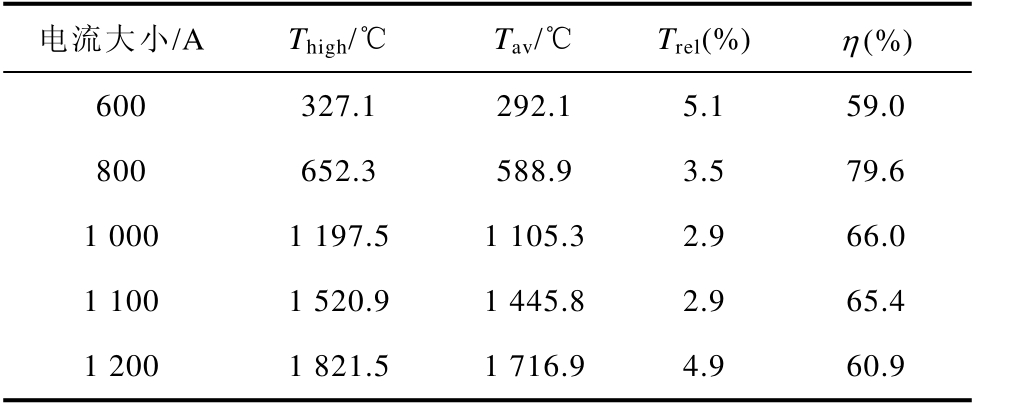
电流大小/A Thigh/℃ Tav/℃ Trel(%) η (%)600 327.1 292.1 5.1 59.0 800 652.3 588.9 3.5 79.6 1 000 1 197.5 1 105.3 2.9 66.0 1 100 1 520.9 1 445.8 2.9 65.4 1 200 1 821.5 1 716.9 4.9 60.9

图17 不同激励电流大小下温度分布曲线F
ig.17 Curves of temperature distribution under different excitation current magnitude
观察表 4和图 17可知,随着激励电流增大,Thigh和 Tav随之升高、Trel呈先减小后增大的趋势、η 则先增大后减小。同时,根据软件计算过程可知,随着激励电流增大,带材表面温度稳定时耦合场的计算次数不变。
综合以上数据及其分布规律,在以 Trel最小为原则的前提下,由于激励电流为1 000A时η 高于激励电流为1 100A的η,故3.2节优选激励电流频率时设置电流大小为1 000A。
3.2 激励电流频率优选
在对新型装置线圈通入激励电流的频率进行优选时,根据 3.1节的优选结果,设置电流大小为1 000A、带材运动速度为 0.1m/s。计算比较了激励电流频率分别为 100Hz、300Hz、500Hz、700Hz、900Hz的情况下带材表面温度分布情况和装置加热效率,得到了不同激励电流频率下感应加热装置的评价参数值见表 5。不同激励电流频率下加热器出口处带材表面温度分布情况如图18所示。
由表5和图18可知,当激励电流频率增大时,Thigh和 Tav随之升高、Trel呈先减小后增大的变化趋势。η 随着频率增大而逐渐降低,原因是线圈感抗与频率呈正比,当频率增大时,线圈感抗随之增大,使得线圈发热增大,从而造成装置的能量转换效率降低,即η 降低。随着激励电流频率增大,带材表面温度稳定时耦合场的计算次数不变。
表5 不同激励电流频率下装置的评价参数
Tab.5 Evaluation parameters of the TFIH under different excitation current frequency
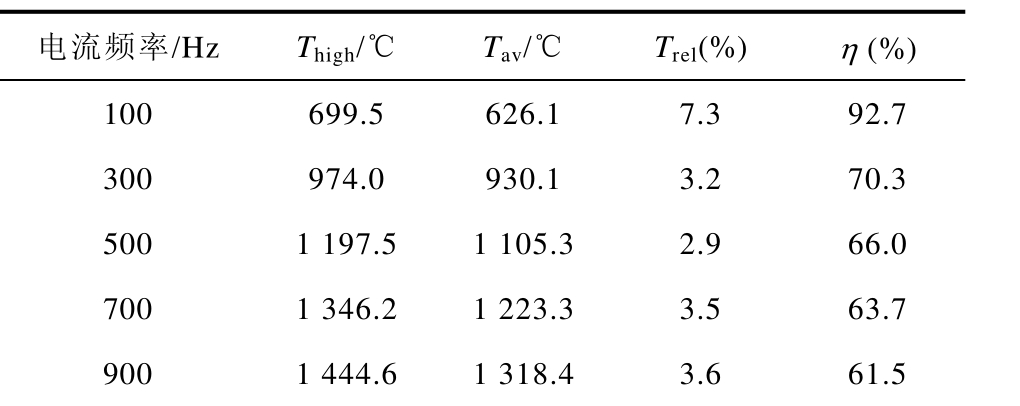
电流频率/Hz Thigh/℃ Tav/℃ Trel(%) η (%)100 699.5 626.1 7.3 92.7 300 974.0 930.1 3.2 70.3 500 1 197.5 1 105.3 2.9 66.0 700 1 346.2 1 223.3 3.5 63.7 900 1 444.6 1 318.4 3.6 61.5

图18 不同激励电流频率下温度分布曲线
Fig.18 Curves of temperature distribution under different excitation current frequency
综合以上数据及其分布规律,在以带材表面温度分布均匀程度最优为原则的前提下,由于当频率为500Hz时,Trel最小,故激励电流为 1 000A、频率为500Hz是最优的激励参数组合。
Matlab软件具有强大的数据处理能力,其曲面拟合功能可以对已有数据进一步细化处理,并在此基础上进行大量模拟计算,然后对数据进行曲面拟合。故基于表4和表5的计算数据,应用曲面拟合功能对感应加热装置的四个评价参数与激励电流大小和频率的关系分别进行曲面拟合,拟合结果如图19所示。
由图19可知,在图19a中,曲面拟合结果显示当激励电流大小和频率分别为1 000A和500Hz时,Trel的值最小,拟合结果验证了激励参数优选结果的正确性。在图19b和图19c中,拟合结果显示Thigh和 Tav的值随着激励电流大小和频率增大而增大,曲面拟合结果与参数优选时温度分布规律一致。图19d中的拟合结果显示随着电流大小增大,η 呈先增大后减小的变化趋势,且η 随着激励电流频率增大而减小,此结果与参数优选时加热效率分布规律完全一致。

图19 加热装置评价参数曲面拟合
Fig.19 Surface fitting of evaluation parameters of the TFIH
上述加热装置评价参数与激励电流大小和频率变化关系的曲面拟合结果验证了激励参数优选结果的正确性,证明了当激励电流大小为1 000A、频率为500Hz时,加热器出口处带材表面温度分布均匀程度最好,其相对不均匀度为2.9%,该温度均匀性能够有效满足实际工业生产的需要,解决了横向磁通感应加热装置带材温度分布不均匀的缺点,为实际热处理工业选择合适的激励参数组合提供了理论依据。
4 结论
本文针对原有横向磁通感应加热装置漏磁稍大且交变磁场通过的磁路磁阻大的缺点,对原有感应加热器进行设计改进,提出一种新型感应加热器。同时,基于新型装置和本文提出的磁热耦合计算方法,针对当前横向磁通感应加热技术存在带材表面温度分布均匀性差的缺点,对新型装置激励参数进行优选,给出一组最优的激励电流大小和频率。主要结论如下:
1)新型感应加热装置能够在加热器出口处产生更高、更均匀的温度分布。且与原有装置相比,新型装置具有更高的加热效率和更快的温度稳定速度。
2)在激励电流大小为 1 000A、频率为 500Hz的激励参数组合下,加热器出口处带材宽度方向上带材表面温度分布均匀性最好,其温度的相对不均匀度Trel为2.9%,该温度均匀程度能够有效满足实际工业生产的需要。
3)随着激励电流大小和频率增大,加热器出口处带材表面最高温度Thigh和平均温度Tav随之升高。
4)随着激励电流大小增大,装置加热效率η呈先增大后减小的变化趋势。随着激励电流频率增大,装置加热效率η 逐渐降低。
5)激励电流大小和频率变化不会影响带材表面温度稳定时耦合场的计算次数。
[1] Favennec Y, Labbe V, Bay F. Induction heating processes optimization a general control approach[J].Journal of Computational Physics, 2003, 187(1):68-94.
[2] 吴德会, 何天府, 王晓红, 等. 感应电能传输中矩形螺线线圈互感耦合的解析建模与分析[J]. 电工技术学报, 2018, 33(3): 680-688.Wu Dehui, He Tianfu, Wang Xiaohong, et al.Analytical modeling and analysis of mutual inductance coupling of rectangular spiral coils in inductive power transfer[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 680-688.
[3] 孙建亮, 邱丑武, 毕雪峰, 等. 感应加热与传统加热模式大型筒节加热效果研究[J]. 机械工程学报,2017, 53(10): 25-33.Sun Jianliang, Qiu Chouwu, Bi Xuefeng, et al. Study on heating effect of heavy cylinder with induction heating and conventional heating[J]. Journal of Mechanical Engineering, 2017, 53(10): 25-33.
[4] 王晓娜, 方旭, 唐波, 等. 脉冲式感应加热电源频率跟踪技术的研究与实现[J]. 电工技术学报, 2018,33(18): 4357-4364.Wang Xiaona, Fang Xu, Tang Bo, et al. Research and implementation of a frequency tracking technology for the pulsed induction heating power[J]. Transactions of China Electrotechnical Society, 2018,33(18): 4357-4364.
[5] 刘刚, 李炀, 陈垣, 等. 基于电磁-热耦合模型的架空导线温度分布和径向温差的计算与实验验证[J].电力系统保护与控制, 2018, 46(7): 7-13.Liu Gang, Li Yang, Chen Yuan, et al. Calculation and experiment verification on temperature distribution and radial temperature of overhead transmission line based on electromagnetic-thermal coupling fields[J].Power System Protection and Control, 2018, 46(7):7-13.
[6] 刘赟, 俞集辉, 程鹏. 基于电磁-热耦合场的架空输电线路载流量分析与计算[J]. 电力系统保护与控制, 2015, 43(9): 28-34.Liu Yun, Yu Jihui, Cheng Peng. Analysis and calculation on the ampacity of overhead transmission lines based on electromagnetic-thermal coupling fields[J]. Power System Protection and Control, 2015,43(9): 28-34.
[7] 黎镇浩, 曹全梁, 赖智鹏, 等. 电流丝法在电磁成形线圈电流和工件电磁力计算中的应用[J]. 电工技术学报, 2018, 33(18): 4181-4190.Li Zhenhao, Cao Quanliang, Lai Zhipeng, et al.Application of current filament method on the calculation of current and force in electromagnetic forming[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4181-4190.
[8] 李江涛, 孙义, 李擎宇, 等. 大电流开关柜温度分布特性的影响因素分析[J]. 电气技术, 2018, 19(9):12-18.Li Jiangtao, Sun Yi, Li Qingyu, et al. Analysis of influencing factors on temperature distribution characteristics of high current switchgear[J].Electrical Engineering, 2018, 19(9): 12-18.
[9] 张宇娇, 汪振亮, 徐彬昭, 等. 瞬态电磁-温度场耦合计算中自适应时间步长研究[J]. 电工技术学报,2018, 33(19): 4468-4475.Zhang Yujiao, Wang Zhenliang, Xu Binzhao, et al.Research on the adaptive time step in transient calculation of coupled electromagnetic and thermal fields[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4468-4475.
[10] 李宜伦, 王泽济, 杨仕友. 热轧带钢厂边部加热涡流-温度场仿真分析[J]. 电工技术学报, 2013, 28(增刊2): 105-110.Li Yilun, Wang Zeji, Yang Shiyou. Numerical simulation of the eddy current and temperature fields in the edge heating hot strip mill[J]. Transactions of China Electrotechnical Society, 2013, 28(S2): 105-110.
[11] 刘刚, 张瀚方, 池骋, 等. 二维电磁场-流体-温度场耦合仿真节点数据映射算法研究[J]. 电工技术学报, 2018, 33(1): 148-157.Liu Gang, Zhang Hanfang, Chi Cheng, et al. Research on node data mapping algorithm for the 2D coupling electromagnetic-fluid-thermal fields[J]. Transactions of China Electrotechnical Society, 2018, 33(1):148-157.
[12] 侯晓光, 李俊, 周月明. 宽幅带材横磁感应加热技术的发展[J]. 宝钢技术, 2016, 34(3): 7-15.Hou Xiaoguang, Li Jun, Zhou Yueming. Development of transverse flux induction heating for wide rang size strip[J]. Baosteel Technology, 2016, 34(3):7-15.
[13] 徐德超, 李俊, 孟庆格, 等. BH-IF钢超快速加热退火工艺[J]. 东北大学学报(自然科学版), 2014,35(10): 1412-1416.Xu Dechao, Li Jun, Meng Qingge, et al. Ultra-rapid heating annealing process of BH-IF steel[J]. Journal of Northeastern University(Natural Science), 2014,35(10): 1412-1416.
[14] 郭建龙, 胡坤太, 仇圣桃, 等. 连铸方坯感应加热数值模拟分析[J]. 特种铸造及有色合金, 2015,35(2): 184-188.Guo Jianlong, Hu Kuntai, Qiu Shengtao, et al.Numerical simulation of continuous casting square billet during induction heating process[J]. Special Casting & Nonferrous Alloys, 2015, 35(2): 184-188.
[15] Pang Lingling, Wang Youhua, Chen Tanggong. New development of traveling wave induction heating[J].IEEE Transactions on Applied Superconductivity,2010, 20(3): 1013-1016.
[16] 赵前哲, 柳亦兵, 刘衍平, 等. 铁磁性材料感应加热过程的数值分析[J]. 材料热处理学报, 2012,33(3): 151-155.Zhao Qianzhe, Liu Yibing, Liu Yanping. Numerical analysis for induction heating process of ferromagnetic materials[J]. Transactions of Materials and Heat Treatment, 2012, 33(3): 151-155.
[17] 孙于. 横向磁通感应加热器优化与耦合分析方法研究[D]. 天津: 河北工业大学, 2014.
[18] Wang Youhua, Wang Junhua, Pang Lingling, et al.An advanced double-layer combined windings transverse flux system for thin strip induction heating[J]. Journal of Applied Physics, 2011, 109(7):07E511.
[19] 孙于, 汪友华, 杨晓光, 等. 新型横向磁通感应加热线圈[J]. 电工技术学报, 2014, 29(4): 85-90.Sun Yu, Wang Youhua, Yang Xiaoguang, et al. A novel coil shape for transverse flux induction heating[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 85-90.
[20] 孙于, 汪友华, 杨晓光, 等. 横向磁通感应线圈结构研究[J]. 电工技术学报, 2014, 29(增刊1): 8-14.Sun Yu, Wang Youhua, Yang Xiaoguang, et al.Research on coil shape for transverse flux induction heating[J]. Transactions of China Electrotechnical Society, 2014, 29(S1): 8-14.
[21] 陈堂功. 遗传算法及其应用于电磁装置优化设计的研究[D]. 天津: 河北工业大学, 2006.
[22] 富坤. 支持向量机及其应用于感应加热装置优化设计的研究[D]. 天津: 河北工业大学, 2007.
[23] 汪友华, 郭春福, 陈龙, 等. 横向磁通感应加热带材温度场的计算分析[J]. 金属热处理, 2017, 42(11):178-182.Wang Youhua, Guo Chunfu, Chen Long, et al.Calculation and analysis of temperature field of steel strip with transverse flux induction heating[J]. Heat Treatment of Metals, 2017, 42(11): 178-182.