0 引言
变频器-感应电机系统是目前变频调速的主要形式，在工业生产、船舰驱动及轨道交通等领域广泛应用[1-3]。提高变频器的可靠性、电能变换效率和功率密度也成为各行业关注的焦点。传统电压型交-直-交变频器直流母线并联有大容量电解电容，电解电容本身的缺点导致变频器故障频发[4]、体积增大、维修成本上升。现有文献多侧重变频器-感应电机系统的能量回馈控制[5-6]，对变频器可靠性和功率密度有重要影响的电解电容研究不足。除滤波功能以外，电解电容还具有吸收感应电机回馈能量的作用，因此，分析感应电机能量回馈原理，探索减小变频器电解电容容量的理论依据，是实现小电容变频器的关键，具有重要的理论研究和实际应用价值。
按照能量处理方法，感应电机制动方式通常分为回馈制动、反接制动和能耗制动。回馈制动因提高了变频器的电能使用效率，近年来受到广泛研究。文献[7]提出一种直接功率和转矩一体化控制的能量回馈变频器，文献[8]提出基于电流幅相控制的变频器-电动机系统能量回馈控制方法，文献[9]提出基于直接电流控制的电机能量回馈控制方法。文献[7-9]共同特点是在直流母线与电网间设置一个三相逆变器实现能量回馈控制，因此增加了系统成本及复杂性。文献[10]提出基于脉冲宽度调制（Pulse Width Modulation, PWM）整流双功率因数校正（Power Factor Correction, PFC）模型的电机能量回馈控制方法，不仅能实现电动机能量回馈制动，还可实现网侧单位功率因数控制。但该方法采用PWM整流取代二极管整流，并未减小直流母线电容，导致设备成本和体积增加。文献[11]提出基于锁相环的调节整流角与调节励磁相结合的控制方法，实现负载换流逆变器驱动同步电机的回馈制动控制。但该方法用可控硅作为整流和逆变元件，降低了系统调速性能。文献[12-16]提出小电容三相逆变器控制方法，通过采用直流功率控制或输入电流控制实现网侧高功率因数控制。但这些文献提出的变频器网侧都为带储能电感的单相交流整流电路，不适用于三相交-直-交变频器。文献[17-18]提出带开关回馈电容的变频器控制方案，并对回馈能量进行了计算，但该文献并未分析感应电机磁场能量构成及变化特性，也没有物理实验验证。文献[19]提出一种空间电压矢量控制的开路零电压矢量概念，对三相逆变器在开路零电压矢量和短路零电压矢量下电动机磁场变化进行了分析，但也缺乏相应物理验证。文献[20-21]对感应电机三相突然短路实验进行了分析研究，总结了感应电机三相突然短路时定子电流和电磁转矩的变化情况。短路零电压矢量控制和感应电机三相突然短路本质上都属于电动机能耗制动，虽然电能使用效率不如能量回馈制动，但可减小变频器直流母线电解电容容量，有效提高了变频器可靠性和功率密度。
针对上述问题，本文提出一种直流母线带开关小电容的变频器-感应电机系统控制方法。首先提出开关小电容变频器电路结构，然后推导变频器不同开关状态下感应电机能量回馈特性，接着分析了电容参数计算方法及变频器控制方法，最后建立小电容变频器-感应电机实验系统进行实验分析。
1 小电容变频器-感应电机理论分析
1.1 小电容变频器系统结构
小电容变频器-感应电机系统结构如图1所示。与传统电压型交-直-交变频器直流母线并联大容量电解电容不同，小电容变频器直流母线并联一个开关电容，即绝缘栅极双极型晶体管（Insulated Gate Bipolar Transistor, IGBT）VT8与小容量电解电容C组成的串联支路，同时保留传统变频器直流母线的能耗制动回路（如图1中点画线框所示，R为制动电阻）。现有变频器直流母线大容量电解电容有储能和滤波两个基本功能。前者可吸收感应电机回馈能量并在负载电流增大、母线电压下降时释放能量，后者可滤除整流电路输出的6次谐波电压并减小直流母线电压脉动。小电容变频器直流母线电压允许在一定范围内波动，理想状态下期望母线电压为整流器输出的六脉波电压，感应电机回馈能量由开关电容吸收，电容参数计算无需考虑滤波问题，仅由一定条件下的感应电机回馈能量大小和直流母线电压最大允许变化量决定。因此，不同状态下感应电机能量回馈特性是设计小电容变频器的关键。
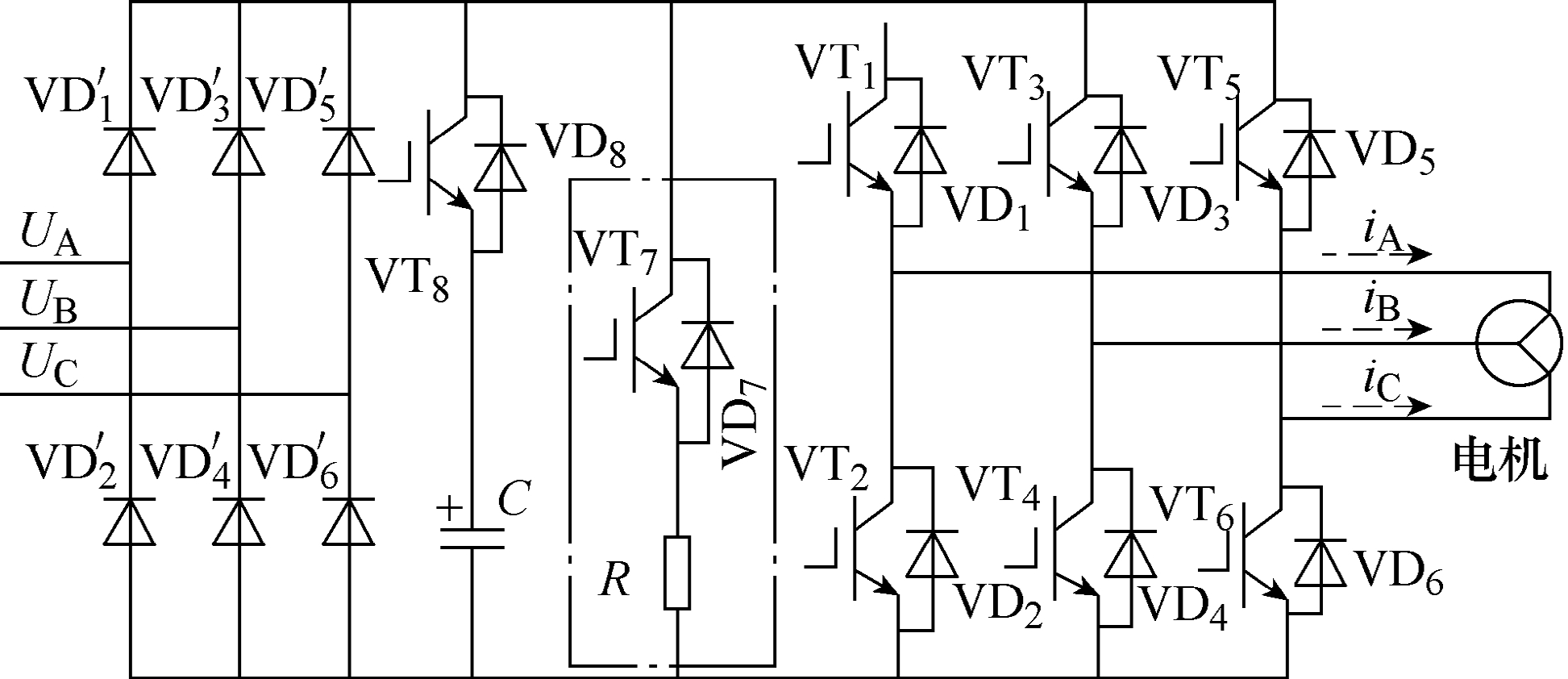
图1 小电容变频器-感应电机系统
Fig.1 Small capacitor frequency converter-induction motor system
1.2 变频器-感应电机能量回馈特性
根据感应电机四象限运行特性，其运行状态可分为正向电动、正向制动、反向电动和反向制动。为简化分析，本文仅考虑转子正转时的正向电动和正向制动运行状态。在感应电机正向制动运行时，电机电磁转矩为负，电机处于发电运行状态，转子动能转变为电能由电机回馈至变频器，受变频器整流二极管单向导电性限制，该部分能量只能由直流母线电解电容吸收。但转子动能较大，电机回馈能量会造成电容电压较大的泵升进而危及设备安全。当感应电机长时间运行在正向制动状态，变频器需要设置能耗制动回路防止直流母线电压过高，如图1中点画线框所示。在回馈能量导致变频器直流母线电压上升到安全设定值时触发 VT7，把回馈能量消耗在电阻R上。对于感应电机正向制动状态的能量吸收，传统变频器和本文提出的小电容变频器都采取能耗制动，与变频器电解电容的大小无直接关系。因此，小电容变频器电容容量选取仅需考虑正向电动运行状态下的能量回馈。
在正向电动运行时，感应电机吸收的平均功率为正，宏观上能量从变频器流向感应电机，但从瞬时功率来看，感应电机与变频器之间的能量流向与逆变器开关状态有关，具体分析如下。
如图1所示，逆变器采用电压空间矢量脉宽调制（Space Vector Pulse Width Modulation, SVPWM）技术。根据文献[16]，在逆变器 8个电压矢量基础上，引入 VT1～VT6全部关断时的电压矢量为开路零电压矢量（如因死区设置导致的 VT1～VT6同时关断），并称原来的零电压矢量为短路零电压矢量。在感应电机正向电动运行时，定子电流为连续近似正弦波电流，在逆变器不同开关状态时，感应电机能量流向不同，对应瞬时功率的正负也不同。为简便描述，不妨设图1所示虚线方向为感应电机定子三相电流的参考方向，并设瞬时电流 iA＜0, iB＞0,iC＞0，定义感应电机从直流母线吸收的瞬时功率为P，则包括开路零电压矢量在内，逆变器九种开关状态下的感应电机能量流向可分为四类，如图2所示，图2中实线箭头为实际电流流向。图2a～图2c为第一类运行状态，感应电机吸收的瞬时功率为正，P＞0。如图2a所示，在电压矢量（0 0 1）工作时，导通器件为 VT2、VD4和 VT5，直流母线电流 id与VT5实际电流相同，P＞0；如图2b所示，电压矢量（0 1 0）工作时导通元件为VT2、VT3和VD6，直流母线电流id与VT3实际电流相同，P＞0；如图2c所示，电压矢量（0 1 1）工作时导通器件为VT2、VT3和VT5，直流母线电流id与VT2电流相同，P＞0。图 2d～图 2f为第二类，P＜0，电机向直流母线电容回馈能量。如图2d所示，在电压矢量（1 0 0）工作时，导通器件为 VD1、VD4和 VD6，直流母线电流 id与 VD1实际电流一致，P＜0；同理可分析图2e和图2f，电压矢量（1 0 1）和（1 1 0）工作时都有P＜0，感应电机向变频器直流环节回馈能量。图2g为第三类，即零电压矢量（1 1 1）或（0 0 0）工作，在电压矢量（1 1 1）工作时，导通器件为VD1、VT3和 VT5，在该时间段内，感应电机等效三相定子绕组短路，此时直流母线与感应电机直接瞬时功率为零，感应电机能量以电机绕组铜耗、铁心铁耗等形式消耗。电压矢量（0 0 0）与电压矢量（1 1 1）作用效果相同。图2h为第四类，即VT1～VT6全部关断，此时逆变器等效为三相不可控整流桥，在假设电流状态时，导通器件为 VD1、VD4和 VD6，直流母线电流id与VD1实际电流相同，P＜0。
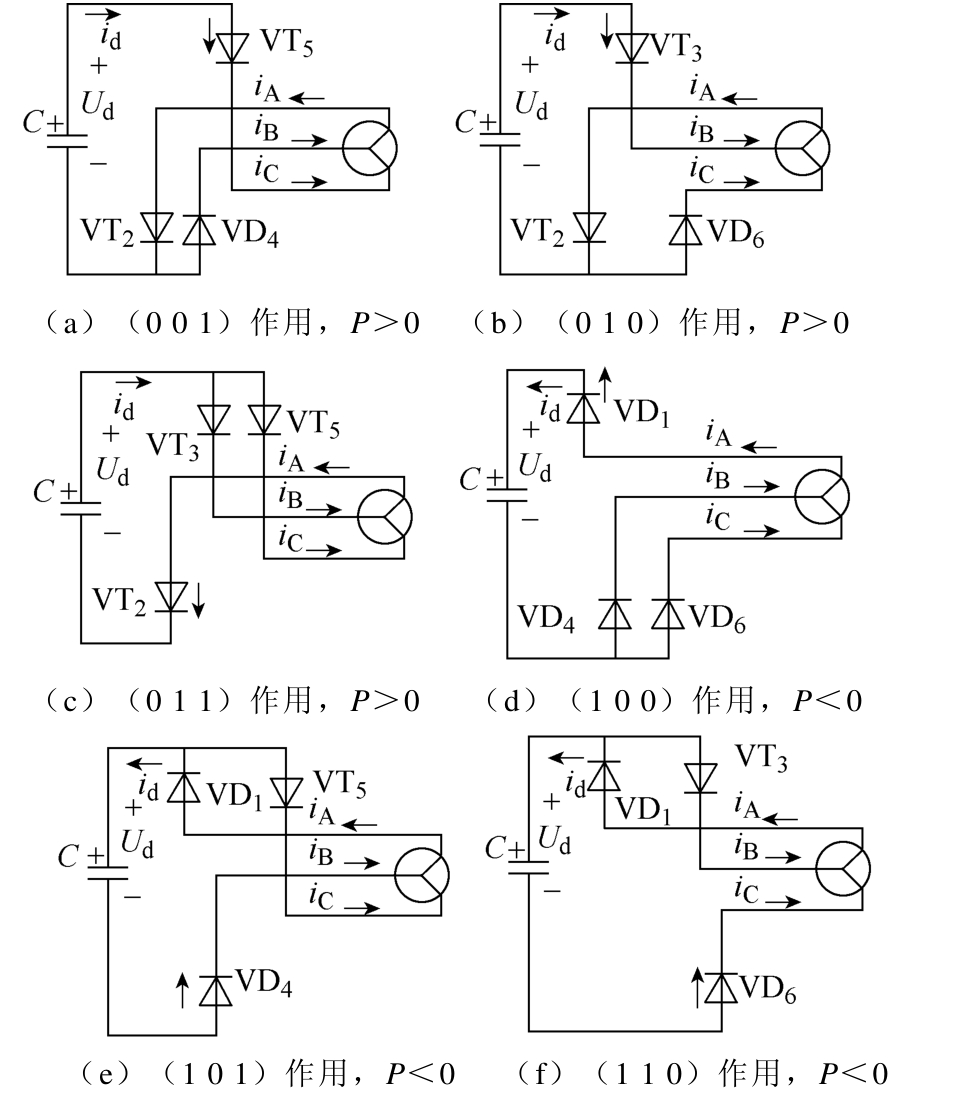
图2 不同开关状态下变频器-感应电机系统等效电路
Fig.2 The equivalent circuits of frequency converterinduction motor system under different switch states
上述分析结果与诸多文献通过逆变器开关器件实际导通数的判断结果一致，即开关器件实际导通数大于等于2时，P＞0，感应电机从变频器直流母线吸收能量；开关器件实际导通数小于2时，P＜0，感应电机向变频器直流母线回馈能量。不同之处是本文细分出零电压矢量和 VT1～VT6全部关断的开路零电压矢量的工作状态。
对比图2d～图2h，感应电机能量回馈时，瞬时功率与感应电机定子一相电流有关。欲计算感应电机回馈能量进而确定所需电容参数，需求解能量回馈时感应电机定子一相电流。以图2d为例，回馈电流id=iA，并假定该状态一直持续到回馈电流下降为零。忽略感应电机非线性因素，根据叠加原理将图2d等效为感应电机稳态运行定子三相突然短路（即图2g所示短路零矢量作用）和感应电机零初始状态下直流母线电压Ud单独作用的叠加。等效电路如图3 所示，约束条件为 iA≤0，iA=Ai′′+Ai′。
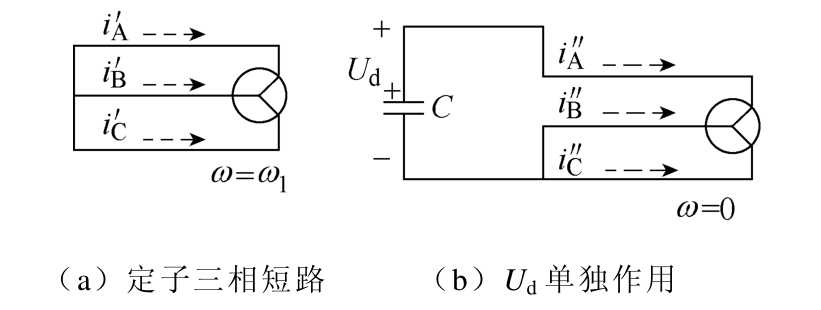
图3 电机能量回馈时等效电路
Fig.3 The equivalent circuits of induction motor when energy flowing back
首先分析图3a所示电路。由文献[17]可知电动机在空载时回馈能量最大，符合计算电动机定子突然三相短路的假设条件，忽略定子电阻，各类参数均归算到定子侧，并省略归算之后的上标“' ”，根据文献[20-21]得定子A相电流为
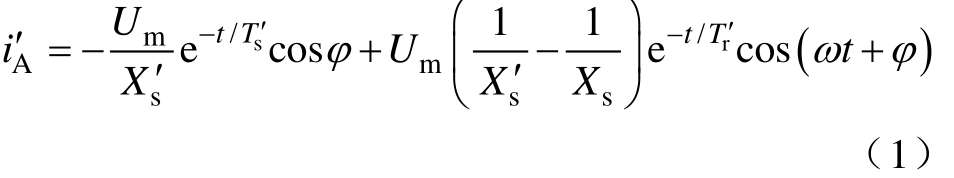
式中，Um为定子相电压幅值；Xs、 sX′分别为定子总电抗和暂态电抗，
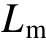分别为定子漏感、互感；sT′为定子暂态时间常数，
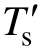≈Lls/Rs，Rs为定子电阻；rT′为转子暂态时间常数，
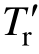≈Llr/Rr，Llr为转子漏感，Rr为转子电阻；ϕ 为短路时定子A相电流相位；ω 为转子角频率。式（1）由两部分组成：一是直流衰减分量，幅值受短路瞬间定子A相电流相位ϕ 影响，该分量以定子暂态时间常数 sT′衰减；另一分量是由转子旋转产生的交流分量，其幅值以转子暂态常数 rT′衰减。
在图3b所示感应电机零初始状态下Ud单独作用时，可视为转子不转动投入电网，由定、转子电压和磁链方程可得
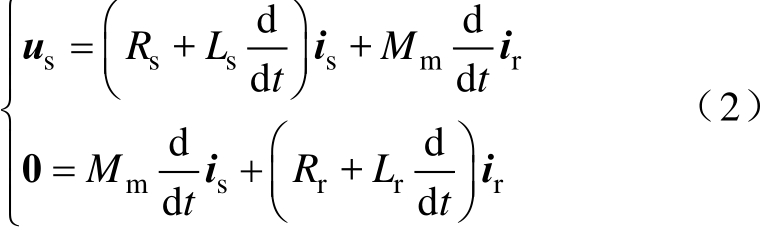
式中，us为定子电压空间矢量；is和 ir分别为定子和转子电流的空间矢量；d/dt为微分算子；Ls和 Lr分别为定子、转子绕组的总自感；Rs和Rr分别为定子、转子每相绕组电阻；Mm=3/2Msr，Mm和 Msr分别为坐标变换前、后定子和转子绕组间互感。对式（2）取拉普拉斯变换，并设Us(s)=L(us)，Is(s)=L(is)，Ir(s)=L(ir)，ψs(s)=L(ψs)，ψs为定子磁链。在零初始状态下可得
化简式（3）并结合感应电机磁链方程可得
式中，转子暂态时间常数 rT′= rL′/Rr， rL′为转子暂态电感，
分别为定子、转子漏感；Tr为转子时间常数，Tr=Lr/Rr。联合式（3）和式（4），得
式中，Ls(s)为定子运算电感，Ls(s)=Ls(1+srT′)/(1+sTr)。由式（5）可得
根据图2d所示等效电路，可知电压矢量us为
式中，Usm=2Ud/3；1、α、α2分别为定子三相绕组轴线上的单位空间矢量，1=ej0°, α =ej120°, α2=ej240°。对式（7）取拉普拉斯变换得：Us(s)=Usm/s，将其代入式（6），并借助 
和
化简得到定子电流 Is为
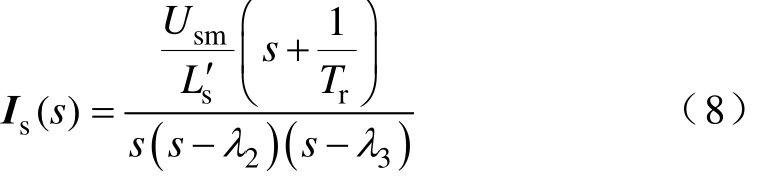
其中
式中，λ2、λ3均为负值，对应主磁场和漏磁场衰减系数，根据文献[22]，λ2≈-RsRr/[(Rs+Rr)Lm], λ3≈-(Rs+Rr)/(Llr+Lls)。由式（8）可得定子A相电流为
式中， Ai′′由一个直流稳态分量和两个直流衰减分量组成。第一个衰减分量系数较小，对应主磁场衰减分量；另一个衰减分量系数较大，对应漏磁场衰减分量。为简化计算，取 Rs=Rr，Ls=Lr，Lls=Llr，式（10）可简化为
式中，λ2较小，而能量回馈持续时间较短，式（11）第二部分可认为近似恒定，进一步简化为
综合式（1）和式（12），根据叠加原理可得开路零电压矢量作用下定子A相电流为
对比式（1）和式（13）可知，短路零电压矢量作用下定子电流衰减较快，而开路零电压矢量作用下受直流母线电压影响定子电流衰减较慢。由此得到，利用短路零电压矢量作用下的能耗制动，可快速消耗电动机回馈能量，从而减小回馈能量对储能电容的需求。受开路零电压矢量作用下二极管的单向导电性限制，式（13）的约束条件是iA≥0。因此，在假定初始状态（iA＜0, iB＞0, iC＞0）下，开路零电压矢量作用时定子A相电流自然衰减到零。
由式（13），可得 A相电流由初值衰减到零时电动机回馈能量为
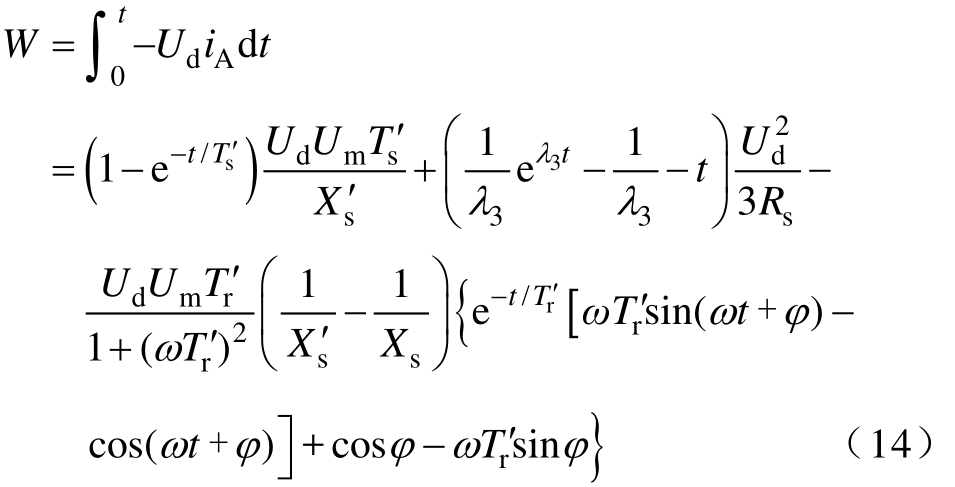
式（14）第一部分为定子电流自由衰减回馈的能量，该部分能量来自定子磁场储能；式（14）第二部分为直流母线向定子磁场转移能量，阻碍定子磁场衰减，当回馈电流为零时，受二极管关断影响，直流母线停止向定子磁场储能；式（14）第三部分对应转子动能产生的回馈能量。根据文献[22]，在开路零电压矢量作用下，转子电流按指数规律衰减。在转子旋转时，转子磁链切割定子绕组并在定子回路产生感应电流，转子动能及转子磁场能量以交变形式回馈至直流母线电容。但转子时间常数远小于电动机惯性时间常数，转子电流很快下降为零而转子转速基本不变，转子动能回馈较少。因此，感应电机稳态时回馈能量主要为定子磁场储能。
1.3 小电容参数计算
根据前面分析可知，在感应电机正向制动时处于发电运行状态，因转子动能较大，感应电机回馈至母线电能较大，必须采取能耗制动，因此小电容参数计算无需考虑电机的回馈制动能量，只以吸收感应电机正向电动运行时的回馈能量为依据。
为求取吸收感应电机正向电动运行时回馈能量所需的电容容量，需要知道最大回馈能量 Wm和电容电压允许变化量ΔU。因此首先计算最大回馈能量时间。为简化计算，取ϕ =0即回馈电流最大，令dW/dt=0，考虑能量回馈时间较短，对dW/dt=0计算后的指数函数线性化，可求得回馈能量最大时的时间为
把tm代入式（14）即可求得最大回馈能量。以感应电机参数为例（见附录），可得tm≈0.1ms，代入式（14）得感应电机稳态运行最大回馈能量Wm=0.307 2J。若能量回馈时允许变频器直流母线电压上升ΔU，由电容储能公式CU2/2即可计算吸收感应电机正向电动运行的回馈能量所需电容值，取ΔU=100V可得 C≥5.1μF。而传统变频器按直流母线纹波电压5%计算，所需电解电容C=3 500μF。
1.4 小电容变频器控制方法
如图1所示小电容变频器输出采用SVPWM控制。根据脉冲调制原理可知，伏秒积相同的脉冲电压对惯性负载的作用效果相同。因此，小电容变频器因直流母线电压脉动对感应电机转速的影响，可由SVPWM控制技术降到最低，有效降低了直流电压脉动带来的影响。
直流母线开关电容及能耗制动回路的控制方法如图4所示。图4中，ud为直流母线电压采样电压，UL为变频器输入线电压有效值，ΔU为直流母线电压相对线电压峰值的允许增加量。VT7为图 1中能耗制动回路开关器件，VT8为图 1中电容支路的开关器件。图4所示控制方法确保在小电容变频器直流母线电压高于三相整流桥输出电压峰值 L2U 时触发导通 VT8，用小容量电解电容吸收感应电机回馈能量。当回馈能量较大，在允许电压升高范围内小电容不足以全部吸收，此时直流母线电压将继续上升而达到 L2U+ΔU值，则触发导通 VT7进行能耗制动，确保母线电压在安全范围内。
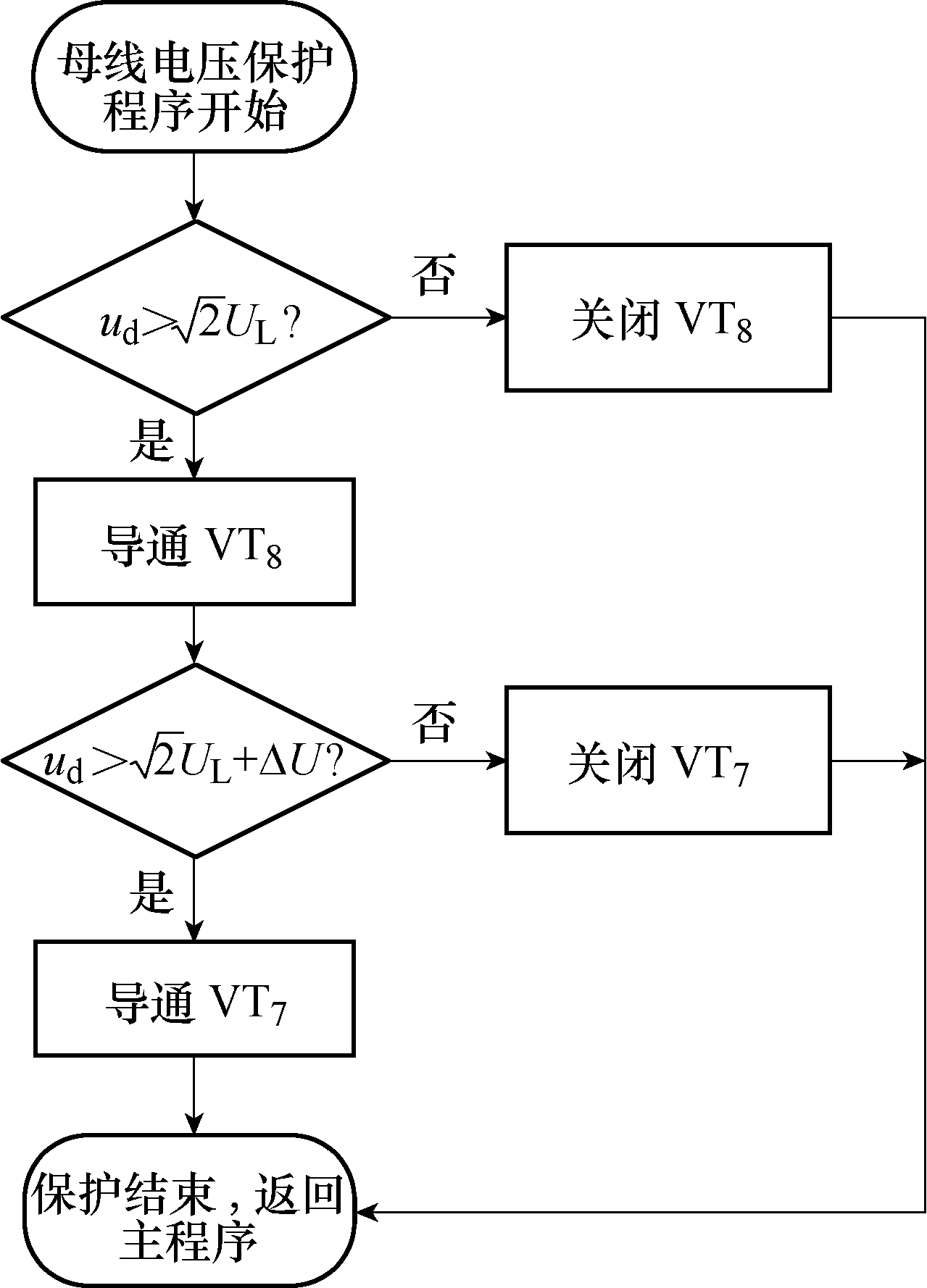
图4 小电容变频器直流母线电压控制流程
Fig.4 Control flow chart for DC-link voltage of small capacitor frequency converter
2 实验分析
2.1 仿真分析
为了验证上述理论分析，以附录所示22kW感应电机在 Matlab/SimPowersystem环境下建立小电容变频器-感应电机系统仿真模型，考虑实际效果，图 1中小电容 C=51μF，其他仿真参数：UL=380V，ΔU=100V，仿真步长1×10-7s，可得一系列仿真结果。
图5为感应电机稳态运行定子三相突然短路时A相电流分量 Ai′对比波形。图5a为理论分析结果，即按式（1）计算所得。图 5b为仿真结果，即在Matlab/SimPowersystem环境下建立仿真模型，待感应电机稳定运行，在0.998s定子A电流最大时切换到短路零电压矢量控制所得结果。图5结果显示，计算结果与仿真结果基本一致。图5电流波形外包络线为一衰减分量，对应式（1）的第一部分，该分量按定子暂态时间常数 sT′衰减。图5电流波形还包含一个正弦衰减分量，对应于式（1）的第二部分，衰减角频率为电源角频率，幅值按转子暂态时间常数 rT′衰减。
图5 感应电机定子三相突然短路时A相电流 Ai′
Fig.5 The A-phase current of an induction motor at the time of stator three-phase windings being short circuits suddenly
图6 为感应电机转子静止接入直流母线电压的定子电流分量 Ai′′对比波形，图6a为理论分析结果，即按式（12）计算得到，图6b为图3b所示等效电路的仿真结果。图6波形显示，仿真结果与理论分析一致。转子静止接入直流母线电压，感应电机反电动势为零，定子电流按指数规律上升，上升速度受λ3影响，即与漏磁场系数有关。因定子电阻值较小，理论上该电流稳态值较大。
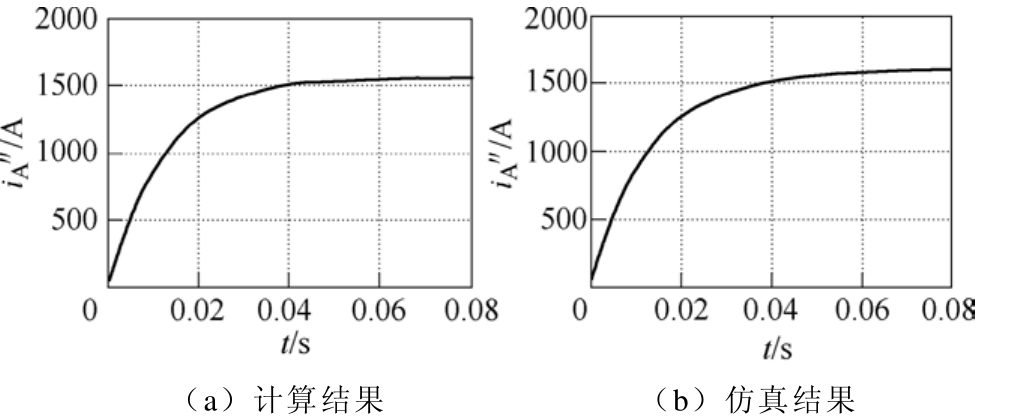
图6 感应电机转子静止接入直流母线电压的A相电流 Ai′′
Fig.6 The A-phase current of an induction motor fed by DC-bus voltage keeping rotor still
图7 为感应电机正向电动运行时，在假设状态下（即图1电机三相电流参考方向iA＜0, iB＞0, iC＞0时)，电压矢量（1 0 0）工作时的定子A相电流波形，也是直流母线回馈电流id的波形。图7电流波形即为图5和图6叠加结果。其中，图7a为理论分析结果，即按式（13）计算所得。图7b为相应仿真结果，即感应电机达到稳态且A相电流达反向峰值时，电压矢量（1 0 0）工作时变频器直流母线回馈电流波形。由图7可见，感应电机回馈电流持续时间较短，同时受开关器件导通方向限制，在同一开关状态下，实际电流衰减到零后不会反向。图 7a为理论计算结果，没有开关器件导通方向的约束，因此在大约0.1ms之后电流开始反向。而图7b仿真结果受开关器件导通方向限制，回馈电流衰减趋近于零但不会反向。同时为观察清楚，图7横坐标并未与图5和图6保持一致。
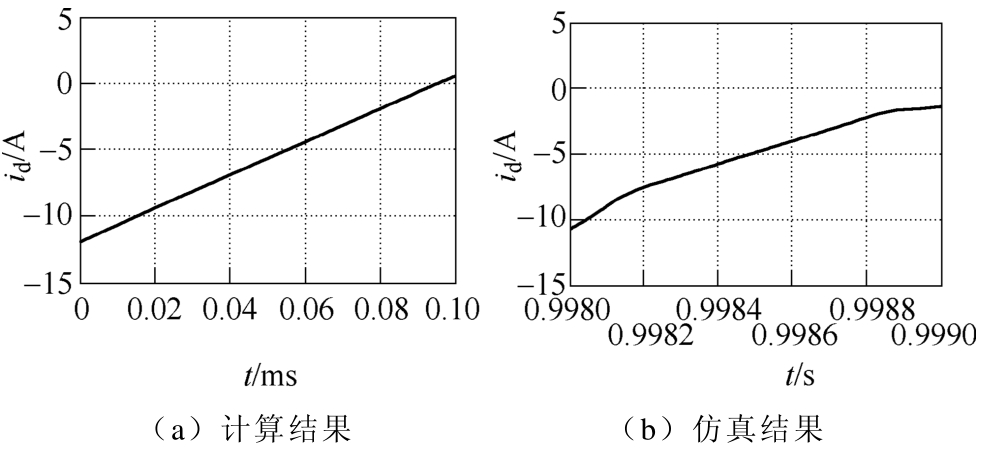
图7 感应电机正向电动运行电压矢量（1 0 0）工作时回馈电流
Fig.7 Feedback current of an induction motor in forward operation while the voltage vector (1 0 0) being working
图8 为前述假设状态下电压矢量（1 0 0）作用下变频器直流母线回馈能量波形。图8a为理论计算结果，即按式（14）计算所得。图8b为相应仿真结果。为简化计算过程，回馈能量时假定直流母线电压恒定。对比图 8a和图 8b，忽略理论分析过程的简化操作导致的误差，仿真结果与理论分析结果基本一致，其峰值即为感应电机正向电动运行时最大可能回馈能量。
上述分析过程假定能量回馈状态一直持续到回馈电流下降为零，实际工作中，变频器开关状态不停地变换，开关频率越高，感应电机回馈能量持续时间越小，特别是零电压矢量的插入，使得感应电机磁场储能衰减较快，电机总体回馈能量更小。
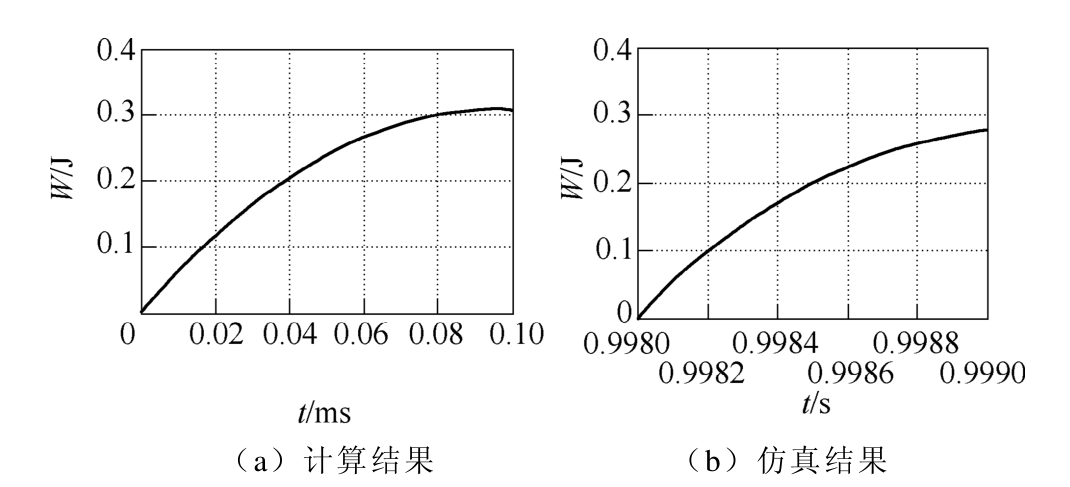
图8 感应电机正向电动运行电压矢量（1 0 0）工作时回馈能量
Fig.8 Feedback energy of an induction motor in forward operation while the voltage vector (1 0 0) being working
图9 为小电容变频器驱动感应电机空载起动过程电机转速和变频器直流母线电压波形。图9波形显示，在0.5s之前感应电机处于加速过程，并在大约0.5s达到额定转速。因感应电机起动过程电流较大，电机回馈能量也较大，相应的小电容变频器直流母线电压泵升较高，但直流母线电压控制在638V（即 L2U+ΔU）以下，在0.5～0.7s之间，转子转速处于超调阶段，感应电机运行在回馈制动状态，感应电机向小电容变频器直流母线回馈能量较大导致母线电压高于638V，能耗制动回路导通工作，确保变频器直流母线电压保持在安全范围之内。在 0.7s以后电机转速运行平稳，因空载运行时感应电机负载电流较小，电机回馈能量也较小，小电容变频器直流母线电压无明显升高。
图9 小电容变频器驱动感应电机空载起动过程
Fig.9 Starting process of an induction motor driven by small capacitor frequency converter without load
图 10为传统变频器驱动感应电机空载起动过程电机转速及变频器直流母线电压波形。对比图10和图 9，传统变频器与小电容变频器转速影响基本一致，在0.5s之前的转速上升过程，传统变频器因直流母线储能电容较大，母线电压增加量较小。但在0.5～0.7s转速超调过程，传统变频器也存在回馈制动导致母线电压泵升较大的问题，在0.7s以后受电机空载运行影响，传统变频器直流母线大容量电解电容储能释放较慢，母线电压下降也较慢。
图10 传统变频器驱动感应电机空载起动过程
Fig.10 Starting process of an induction motor driven by the traditional frequency converter without load
图 11为小电容变频器驱动感应电机负载 50%起动过程的电机转速和变频器直流母线电压波形。与图9相比，因电机负载增加，电机起动过程延长，转速上升时间由0.5s增加到约1s。同时感应电机转速超调量较小，电机在转速超调时的回馈能量较小，变频器直流母线电压泵升较小。但受负载电流增加，感应电机1s以后的稳态运行阶段的回馈能量较大，导致小电容变频器直流母线电压纹波比空载要大。
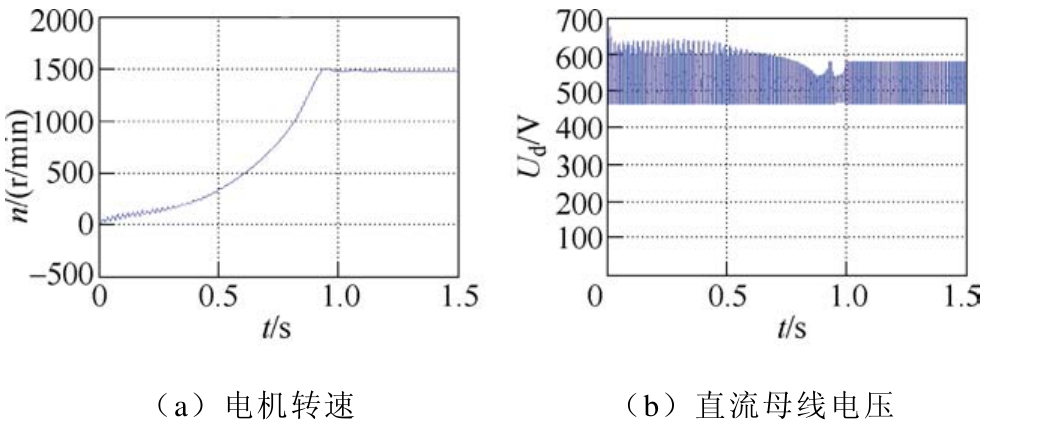
图11 小电容变频器驱动感应电机负载50%起动过程
Fig.11 Starting process of an induction motor driven by small capacitor frequency converter with 50% load
图 12为传统变频器驱动感应电机负载 50%起动过程的电机转速和变频器直流母线电压波形。图12a显示电机转速上升平稳，与图11性能一致。图12b所示变频器直流母线电压纹波较小，特别是感应电机运行稳定后，得益于直流母线大容量电容的储能，变频器直流母线电压近似恒定。
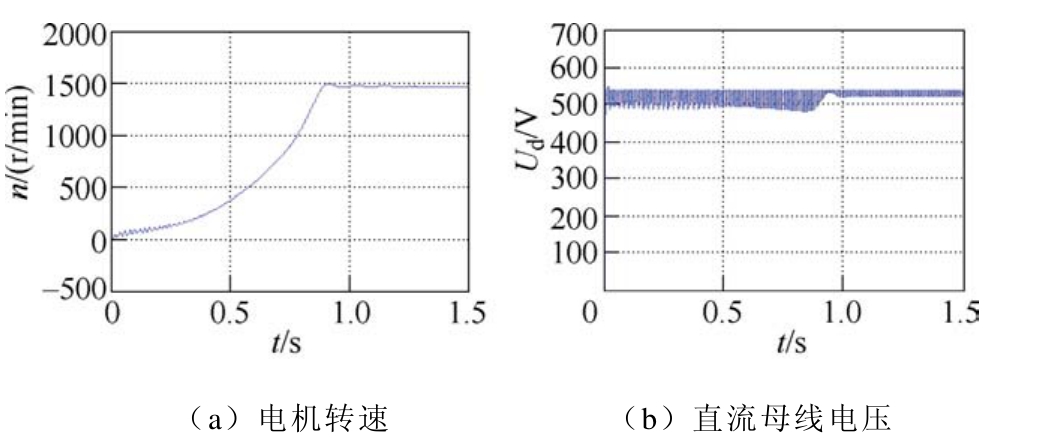
图12 传统变频器驱动感应电机负载50%起动过程
Fig.12 Starting process of an induction motor driven by the traditional frequency converter with 50% load
再分别对比图9～图12，在相同负载下，小电容变频器-感应电机系统的转速响应与传统变频器-感应电机系统的转速响应基本一致，小电容变频器直流母线电压虽有一定幅度波动，但都在理论设计及安全范围之内。仿真结果验证了小电容变频器的可行性。
2.2 物理实验
为进一步验证上述结论，建立物理实验系统如图13所示。图中小电容变频器基于STM32F103芯片设计，IGBT选用仙童 FGA25N120ANTD。负载为带测速发电机的3kW交流机组，电机参数：PN=3kW、UN=380V、n=1 480r/min。为便于安全测试，变频器由三相隔离变压器和自耦调压器串联供电,小电容变频器直流母线并联一组两个 400V/470μF电解电容串联，作为对比的传统变频器电容为三组、每组两个400V/470μF电解电容串联。
图13 变频器-感应电机实验系统
Fig.13 Experimental system of the frequency converter-induction motor
图14 为变频器驱动感应电机起动时，变频器直流母线电压波形。图14a显示，小电容变频器直流母线电压有明显下降，且放大后呈六脉波特点。原因是感应电机起动过程负载电流较大，变频器-感应电机系统由隔离变压器和自耦变压器供电，受电源内阻压降影响所致。六脉波的特点则是因为小电容储能较少，感应电机所需能量由变频器前端整流器提供，电容电压跟随整流器输出的六脉波电压。在电机起动完成后电机电流减小，变频器直流母线电压恢复且电压纹波较小。图14a同时显示，在起动过程及起动完成后，感应电机回馈能量造成的小电容变频器直流母线电压泵升较小，这与实验样机电解电容值比理论值偏大有关。
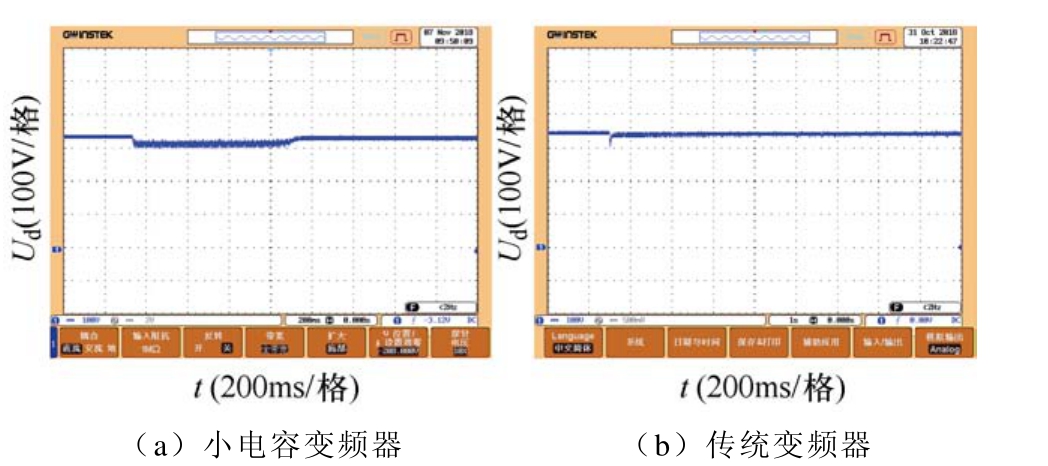
图14 感应电机起动时变频器直流母线电压
Fig.14 DC-link voltage of frequency converter in starting process of an induction motor
图14 b显示，起动瞬间受感应电机起动电流影响较大，传统变频器直流母线电压也有瞬时下降，但得益于大容量电解电容储能的补充，直流母线电压迅速恢复且起动过程母线电压纹波较小。对比图14a和图14b，感应电机起动过程小电容变频器直流母线电压动态时降落较大，稳态时与普通变频器基本一致，主要原因是小电容变频器直流母线小容储能较小，感应电机起动过程所需能量全部由电源供给，导致电源内阻压降增大，从而导致变频器供电电压减小。上述实验结果符合理论分析。
图 15为感应电机稳定运行时变频器直流母线电压波形。图15a波形呈现六脉波电压特点，无明显电压泵升，验证了小电容变频器-感应电机系统稳态时回馈能量较小、小电容变频器直流母线电压近似为整流器输出电压的理论预期。图15b波形无明显波动，说明传统变频器得益于大电容的储能和滤波，能保持直流母线电压近似恒定。
图15 感应电机稳态时变频器直流母线电压
Fig.15 DC-link voltage of frequency converter while induction motor being in a steady state
图 16为感应电机转速动下降时变频器直流母线电压波形。图16a波形显示，感应电机转速下降时回馈能量较大，小电容变频器直流母线电压有明显增加。图16b显示在电机转速动态降落过程，传统大电容变频器基本保持直流母线电压恒定，这与实验样机电解电容较大有关。
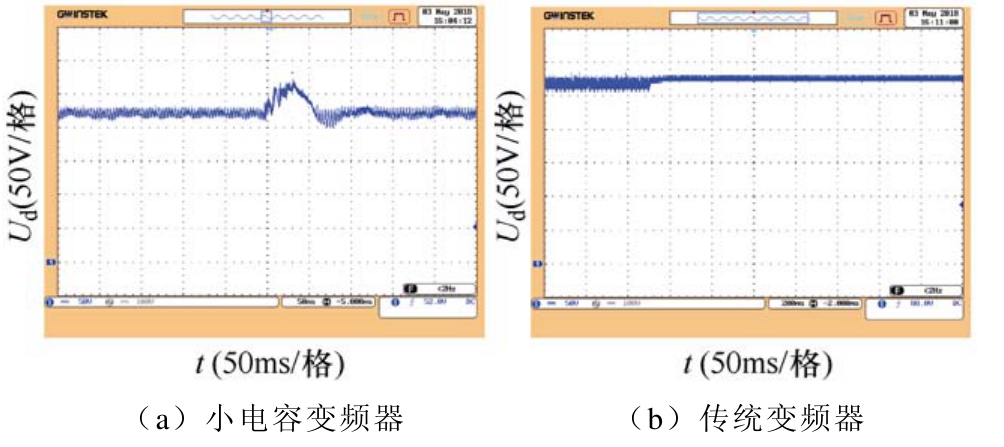
图16 感应电机转速下降时变频器直流母线电压
Fig.16 DC-link voltage of frequency converter while induction motor speed being reducing
图17 a和图17b分别为小电容变频器和传统变频器驱动感应电机起动过程转子转速波形。对比可以发现，两种情况下转子转速上升都比较平稳，但受小电容变频器直流母线电容储能较少影响，图17a所示电机转速上升时间较长，图 17b所示转速上升较快，稳态下转速波动基本一致。上述分析结果说明，小电容变频器稳态性能与传统变频器基本一致，但动态响应速度略低于传统变频器。
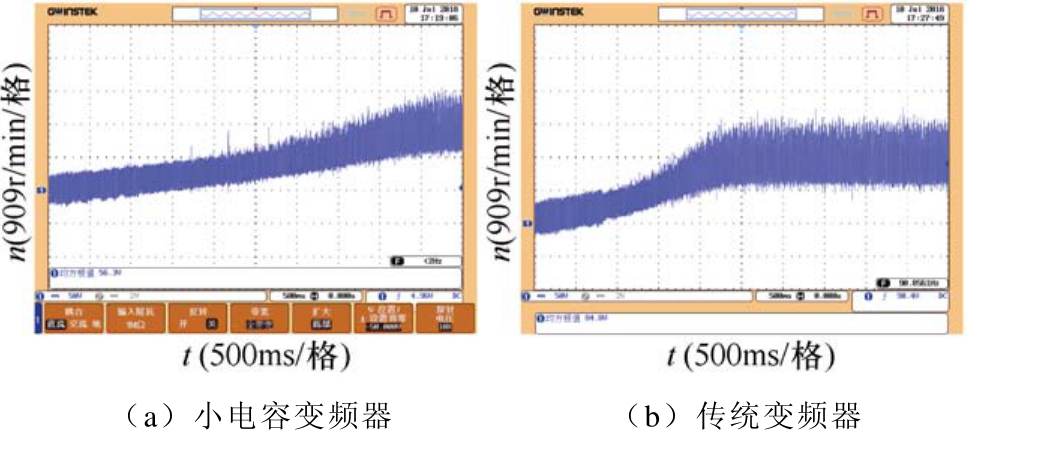
图17 感应电机转速波形
Fig.17 Rotor speed of induction motor
3 结论
本文从感应电机稳态运行时能量回馈特性入手，分析了变频器在不同开关状态下的瞬时功率特性，推导电机正向电动运行时的回馈电流及回馈能量方程，给出了小电容参数计算依据。研究结果显示：
1）感应电机正向电动运行时回馈能量与逆变器开关状态有关，回馈电流大小等于感应电机一相电流，回馈时间持续较短，回馈能量也较小。
2）在允许变频器直流母线电压有一定增加量时可减小传统变频器所需的电解电容容量。
3）小电容变频器采用 SVPWM 控制时可有效抑制直流母线电压脉动造成的影响。
4）小电容变频器-感应电机系统稳态性能与传统变频器-感应电机系统基本一致，但动态响应速度较慢。
5）实验结果验证了小电容变频器的可行性。
附 录
电机参数为：PN=22kW, UN=380V, nN=1 470r/min,IN=42.9A, fN=50Hz, Lm=81.2mH, Rs=0.115 2Ω, Rr=0.120 3Ω, Lsσ≈Lrσ=1.443mH, J=0.58kg·m2。
[1] 魏文婧, 胡海涛, 王科, 等. 基于铁路功率调节器的高速铁路牵引供电系统储能方案及控制策略[J].电工技术学报, 2019, 34(6): 1290-1299.Wei Wenjing, Hu Haitao, Wang Ke, et al. Energy storage scheme and control strategies of high-speed railway based on railway power conditioner[J].Transactions of China Electrotechnical Society, 2019,34(6): 1290-1299.
[2] 刘和平, 刘庆, 张威, 等. 电动汽车用感应电机削弱振动和噪声的随机PWM控制策略[J]. 电工技术学报, 2019, 34(7): 1488-1495.Liu Heping, Liu Qing, Zhang Wei, et al. Random PWM technique for acoustic noise and vibration reduction in induction motors used by electric vehicles[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1488-1495.
[3] 张冬冬, 郭新志, 安睿驰, 等. 基于 DFT的感应电机转子谐波磁通密度高效分离方法及负载条件下变频电机转子铁耗特性[J]. 电工技术学报, 2019,34(1): 75-83.Zhang Dongdong, Guo Xinzhi, An Ruichi, et al. A separation method of rotor flux density harmonics based on DFT and fine analysis rotor iron losses in inverter-fed induction motors[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 75-83.
[4] 王立乔, 崔舒敏, 陈梅. 功率解耦型无电解电容PFC电路并联补偿控制[J]. 电工技术学报, 2019,34(3): 516-528.Wang Liqiao, Cui Shumin, Chen Mei. Parallel compensation control of power factor corrector without electrolytic capacitor by power decoupling[J].Transactions of China Electrotechnical Society, 2019,34(3): 516-528.
[5] 卢东斌, 欧阳明高, 谷靖, 等. 电动汽车永磁同步电机最优制动能量回馈控制[J]. 中国电机工程学报, 2013, 33(3): 83-91, 12.Lu Dongbin, Ouyang Minggao, Gu Jing, et al.Optimal regenerative braking control for permanent magnet synchronous motors in electric vehicles[J].Proceedings of the CSEE, 2013, 33(3): 83-91, 12.
[6] Yin Lu, Zhao Zhengming, Lu Ting, et al. An improved DC-link voltage fast control scheme for a PWM rectifier-inverter system[J]. IEEE Transactions on Industry Application, 2014, 50(1): 462-473.
[7] 张华强, 孟凡华, 梁志平. 直接功率和转矩一体化控制的能量回馈变频器[J]. 电机与控制学报, 2013,17(10): 19-26.Zhang Huaqiang, Meng Fanhua, Liang Zhiping.Direct power and torque integration control for energy feedback converter[J]. Electric Machines and Control, 2013, 17(10): 19-26.
[8] 张承慧, 李珂, 杜春水, 等. 基于幅相控制的变频器能量回馈控制系统[J]. 电工技术学报, 2005,20(2): 41-45.Zhang Chenghui, Li Ke, Du Chunshui, et al. An energy-feedback control system of inverter based on phase and amplitude control[J]. Transactions of China Electrotechnical Society, 2005, 20(2): 41-45.
[9] 宋小亮, 蔚兰, 陈国呈, 等. 基于直接电流控制的电机能量回馈器研究[J]. 电力电子技术, 2010,44(5): 49-51.Song Xiaoliang, Yu Lan, Chen Guocheng, et al. The study of motor energy feedback system based on direct current control[J]. Power Electronics, 2010,44(5): 49-51.
[10] 尹忠刚, 钟彦儒, 刘静. 基于 PWM 整流器双 PFC模型的电机能量回馈系统[J]. 电力自动化设备,2010, 30(1): 36-40.Yin Zhonggang, Zhong Yanru, Liu Jing. Motor energy feedback system based on dual-PFC model of PWM rectifier[J]. Electric Power Automation Equipment, 2010, 30(1): 36-40.
[11] 韩啸, 高强, 寇佳宝, 等. 负载换流逆变器驱动同步电机能量回馈的研究[J]. 电气传动, 2018, 48(1):13-18.Han Xiao, Gao Qiang, Kou Jiabao, et al. Research on energy feedback control of synchronous motor driven by load commutated inverter[J]. Electric Drive, 2018,48(1): 13-18.
[12] Hyun-Sam Jung, Seung-Jun Chee, Seung-Ki Sul, et al.Control of three-phase inverter for AC motor drive with small DC-link capacitor fed by single-phase AC source[J]. IEEE Transactions on Industry Applications, 2014, 50(2): 1074-1081.
[13] 霍军亚, 王高林, 赵楠楠, 等. 无电解电容电机驱动系统谐振抑制控制策略[J]. 电工技术学报, 2018,33(24): 5641-5648.Huo Junya, Wang Gaolin, Zhao Nannan, et al.Resonance suppression control strategy of elec-trolytic capacitor-less motor drives[J]. Transactions of China Electrotechnical Society, 2018, 33(24):5641-5648.
[14] Yeongrack Son, Jung-Ik Ha. Discontinuous grid current control of motor drive system with singlephase diode rectifier and small DC-link capacitor[J].IEEE Transactions on Power Electronics, 2017, 32(2):1324-1334.
[15] Zhou Yufei, Huang Wenxin, Hong Feng. Singlephase input variable-speed AC motor system based on an electrolytic capacitor-less single-stage Boost three-phase inverter[J]. IEEE Transactions on Power Electronics, 2016, 31(10): 7043-7052.
[16] 周玉斐, 黄文新, 赵健伍. 单相交流输入的无电解电容抽头电感单级升压逆变器在交流调速系统中的应用[J]. 中国电机工程学报, 2014, 34(12):1836-1843.Zhou Yufei, Huang Wenxin, Zhao Jianwu. An adjustable-speed system with single-phase AC input based on electrolytic capacitor-less tapped-inductor single-stage Boost inverters[J]. Proceedings of the CSEE, 2014, 34(12): 1836-1843.
[17] 段明亮, 荣为青, 孟彦京. 一种带开关回馈电容变频器的仿真研究[J]. 电子技术应用, 2017, 43(12):133-136, 142.Duan Mingliang, Rong Weiqing, Meng Yanjing.Simulation research on a switched feedback capacitor inverter[J]. Power Supply Technology and Its Application, 2017,43(12): 133-136, 142.
[18] 孟彦京, 李宏涛, 张君燕. 一种新型小电容变频器及其调制技术的研究[J]. 微特电机, 2018, 46(7):66-70.Meng Yanjing, Li Hongtao, Zhang Junyan. Research on a novel small capacitance inverter and its modulation[J]. Small & Special Electrical Machines,2018, 46(7): 66-70.
[19] 孟彦京, 周鹏, 马汇海, 等. SVPWM中的开路零矢量及其对磁链轨迹的影响研究[J]. 电气传动, 2016,46(1): 19-23.Meng Yanjing, Zhou Peng, Ma Huihai, et al. Study of open-circuit zero voltage vector and its effect on flux trajectory in SVPWM[J]. Electric Drive, 2016, 46(1):19-23.
[20] 张海涛, 赵争鸣, 孟朔, 等. 三电平变频调速系统的三相短路制动仿真与实验分析[J]. 中国电机工程学报, 2004, 24(8): 59-63.Zhang Haitao, Zhao Zhengming, Meng Shuo, et al.The simulation and experimental analysis of shortcircuit breaking for 3-level inverter-motor systems[J].Proceedings of the CSEE, 2004, 24(8): 59-63.
[21] 汤蕴璆, 王成元. 交流电机动态分析[M]. 2版. 北京: 机械工业出版社, 2015.
[22] 谢仕宏, 孟彦京, 陈君, 等. 感应电机离散变频转矩脉动原因及改进方法[J]. 电机与控制学报, 2018,22(10): 103-111.Xie Shihong, Meng Yanjing, Chen Jun, et al. Cause and improvement of the discrete variable frequency torque ripple of induction motor[J]. Electric Machines and Control, 2018, 22(10): 103-111.