0 引言
随着先进制造业的发展，数控领域对伺服系统的高精度、高响应要求逐步提高。近年来，永磁同步电机因结构简单、功率密度高、运行可靠等优点被广泛应用。然而，永磁同步电机具有多变量、非线性、强耦合的特点，并且在其运行过程中，电机定子电阻、电感以及负载转矩实时变化，常规的PI控制技术已无法满足当前数控领域对系统转速实时跟踪性和鲁棒性的要求[1-2]。近年来，随着控制理论的发展，利用非线性控制方法设计新的方案相继出现，如滑模变结构控制[3]、反馈线性化控制[4]、自抗扰控制[5]以及反步控制[6]等。其中，反步控制方法因易与自适应参数估计技术相结合以降低系统内外扰动的影响而受到国内外学者的广泛关注。
反步控制为20世纪90年代初提出的以Lyapunov稳定性理论为基础的控制方法。该方法通过引入虚拟控制变量，将原始高阶系统分解为串级子系统，逐一对其构造合适的 Lyapunov函数并推导虚拟控制律，保证系统渐近收敛，最终导出实际的控制律及自适应律[7-8]。然而，单纯的反步控制系统尚无法满足系统对内外扰动鲁棒性以及高动态响应的性能要求。主要包括两大原因：①要实现电流、转速的精确控制，需以反步控制系统内部参数的准确性为前提[9-10]。然而，电机定子电阻、电感等内部参数会在电机运行过程中随着温度的变化发生摄动，电流、转速跟踪性能下降，系统对电机内部参数摄动的鲁棒性无法保证；②反步控制器中涉及的控制参数较多，为了简化控制器设计，倘若将这些参数设置为固定值，或者根据不同的转速工况给定与当前转速成一定比例的设定值，尚不考虑控制器参数对系统性能的影响，控制系统动态性能将受到一定限制[11-12]。针对第一个问题，一般通过设计相应的估计器对电机内部参数摄动量进行实时估计，将其补偿至控制器输出，保证电流跟踪的准确性。如文献[13]将自适应控制与反步控制相结合，提出一种基于自适应参数估计器的永磁同步电机自适应反步控制方法，通过定子电阻和负载转矩估计对控制系统输出进行实时校正，实现系统对电阻参数摄动和外部负载扰动的鲁棒性控制。然而，电机定子交直轴电感相互耦合，自适应律推导存在极大困难。因此，如何保证反步控制系统对电感参数摄动的鲁棒性有待进一步的研究。针对第二个问题，众多文献将模糊控制[14-15]或者神经网络控制[16-17]与自适应反步控制相结合，通过模糊控制器调节反步控制器中相关参数来改善系统的动态性能。如文献[18-19]将模糊控制与自适应反步控制相结合，利用模糊控制器在线整定反步控制器中的参数，进一步提高控制系统动态性能。然而，这些文献大多仅仅单纯考虑系统对转速动态响应的要求，对于电机运行过程中电感参数摄动对系统控制性能的影响考虑不够充分。因此，如何在反步控制系统拥有优良动态响应性能的同时保证其对内部电感参数摄动的鲁棒性能需进一步研究。
针对上述问题分析，为同时保证永磁同步电机伺服系统优良的动态响应性能与较强的参数摄动鲁棒性能，提出一种永磁同步电机模糊自整定自适应积分反步控制方法。将dq轴电流误差积分项引入自适应反步控制器控制律中，构成自适应电流误差积分反步控制器，实现对dq轴电流给定的精确跟踪，提高dq轴电流控制系统对内部参数摄动的鲁棒性。在此基础上，设计模糊推理模块应用于自适应积分反步控制器，系统根据电机转速误差及其变化率自适应在线整定转速反馈增益及自适应增益，进一步提高系统的转速动态响应性能。实验结果表明，与传统PI控制及传统反步控制相比，本文提出的模糊自整定自适应积分反步控制策略转速动态响应更为优良，对外部负载扰动和内部电感参数摄动有着较强的鲁棒性。
1 自适应反步控制器设计
永磁同步电机在dq旋转坐标系下的数学模型为
式中， ud、 uq分别为dq旋转坐标系下的电压分量；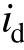
、iq分别为dq旋转坐标系下的电流分量； Ld、 Lq分别为定子dq轴电感；Rs为定子电阻；ωr为转子机械角速度；np为极对数；ψf为转子给定磁链；p为微分算子。
对式（1）作适当变换，得到
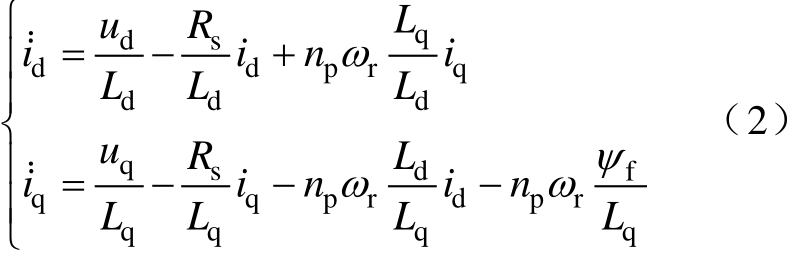
永磁同步电机的电磁转矩表达式为
机械运动方程为
式中，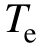
为电机输出电磁转矩；
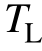为电机输出端负载转矩；J为电机输出轴转动惯量；B为电机输出轴阻尼系数。
结合式（3）和式（4），得到
采用反步控制方法对永磁同步电机转速进行控制，具体步骤如下。
（1）定义永磁同步电机转速跟随误差为
式中， *rω为给定电机转速。对转速误差求导，得到
定义Lyapunov函数为
对其求导，得到
对式（9）作适当变换，得到
式中，kω为转速反馈增益，且有 k ω＞0 。将负载转矩 TL、转动惯量J视为不确定性量进行估计，定义理想虚拟控制变量
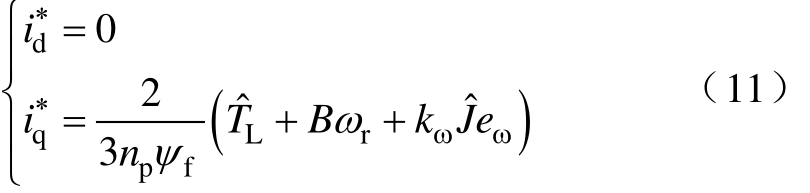
式中，
、Jˆ分别为电机负载转矩估计和转动惯量估计。
定义电机负载转矩估计误差
电流跟随误差 de、 qe为
结合式（11）和式（12），重新整理式（7），得到
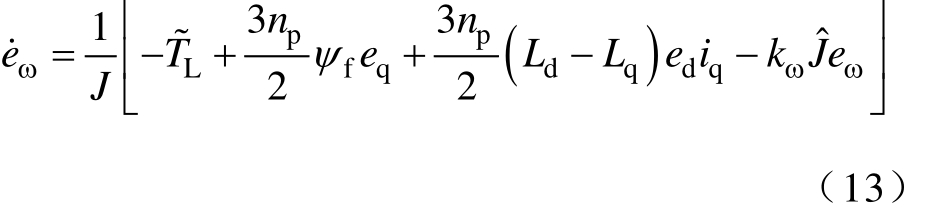
对dq轴电流跟随误差进行求导，得到
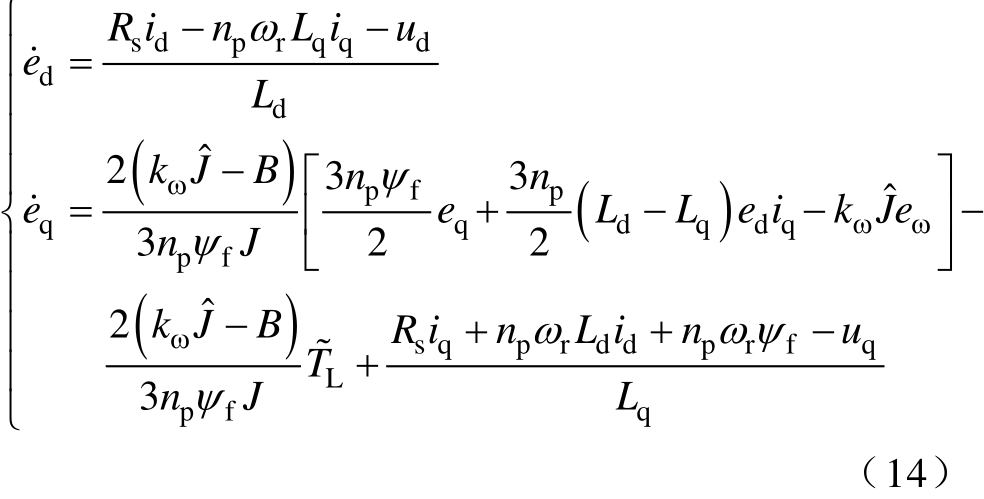
（2）定义Lyapunov函数为
式中，
为转动惯量估计误差；γ1、γ2为自适应增益； km为转矩电流微分增益，对其求导，得到
式中，
为正常数。为保证系统渐近收敛，需满足 V˙ ≤ 0 ，则控制律及自适应律分别选取为
将上述控制律及自适应律代入式（16），得到
考虑到kω、 dk和 qk均为正常数，则 0V˙≤ ，系统渐近收敛。
2 自适应电流误差积分反步控制器设计
电机运行过程中，反步控制系统中定子交直轴电感参数值会发生摄动，考虑到定子交直轴电感相互耦合，自适应律推导存在极大困难，dq轴电流跟随误差将随之增大。针对此问题，将dq轴电流跟随误差积分项引入控制律中，设计自适应电流误差积分反步控制器，以降低电感参数摄动对dq轴电流控制的影响。定义Lyapunov函数为
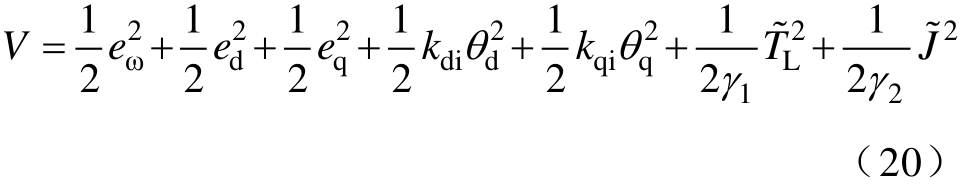
式中，
为d轴电流误差积分；θq=
dτ为q轴电流误差积分； kdi和 kqi分别为dq轴电流误差积分增益，且有 kdi＞0 ， kqi＞0 ，对其求导，得到
式中，
，为保证系统稳定性，选取控制律和自适应律分别为
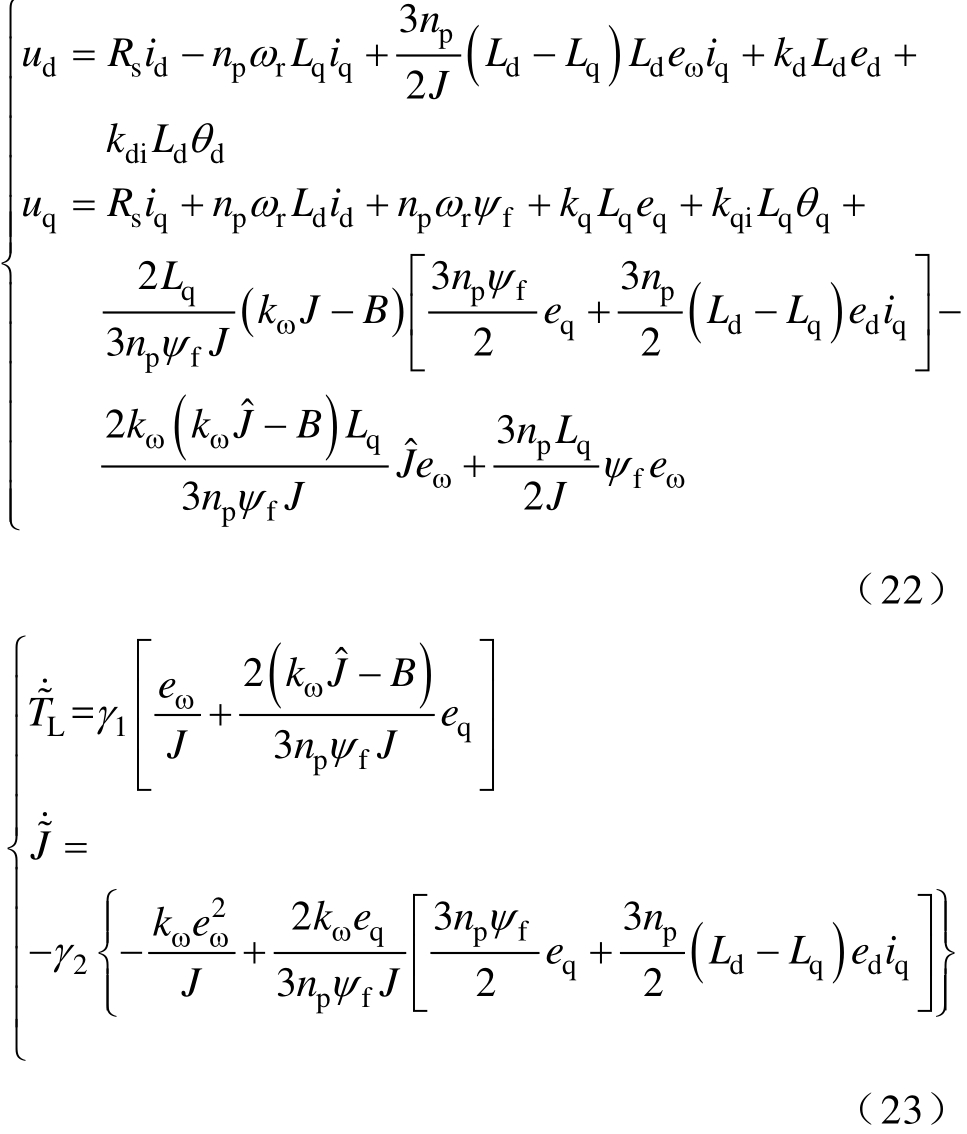
将上述控制律及自适应律代入式（21），得到
考虑到kω、 dk和 qk均为正常数，则 0V˙≤ ，系统渐近收敛。
根 据 式（20）可 知 ，
正 定 ， 且
具 有 无 穷 大 上 界 。 由 于 V ˙≤ 0 ， 则
考 虑 到
非递增有界，由此得到
另 外，由 于
且
均有界，则V˙˙有界，故V˙一致连续。根据Lyapunov引理，当
根据Barbalat引理可得，eω、 ed和 eq均收敛至零，即
系统实现转速、电流的精确跟踪。
3 模糊自整定自适应积分反步控制器设计
永磁同步电机控制系统中的反馈增益均为固定值，但电机的运行工况实时变化，在一定程度上限制了电机的动态性能。针对该问题，在自适应电流误差积分反步控制的基础上，根据电机转速误差eω及其变化率 ce自适应在线调整转速反馈增益kω以及自适应增益1γ值，在保证电感参数摄动鲁棒性的前提下进一步提高永磁同步电机控制系统的转速动态响应性能。
模糊推理模块的输入eω、ce和输出kω、1γ的模糊子集均对应[负大, 负中, 负小, 零, 正小, 正中, 正大]，即[NB, NM, NS, ZE, PS, PM, PB]。模糊系统隶属度函数选取三角曲线形式，即eω、 ce对应[-1,-2/3, -1/3, 0, 1/3, 2/3, 1]，kω、1γ对应[0, 1/3, 2/3, 1,4/3, 5/3, 2]，如图1a和图1b所示，分别为eω和kω的隶属度函数曲线，并且ce和1γ的曲线分别与eω和kω相同。
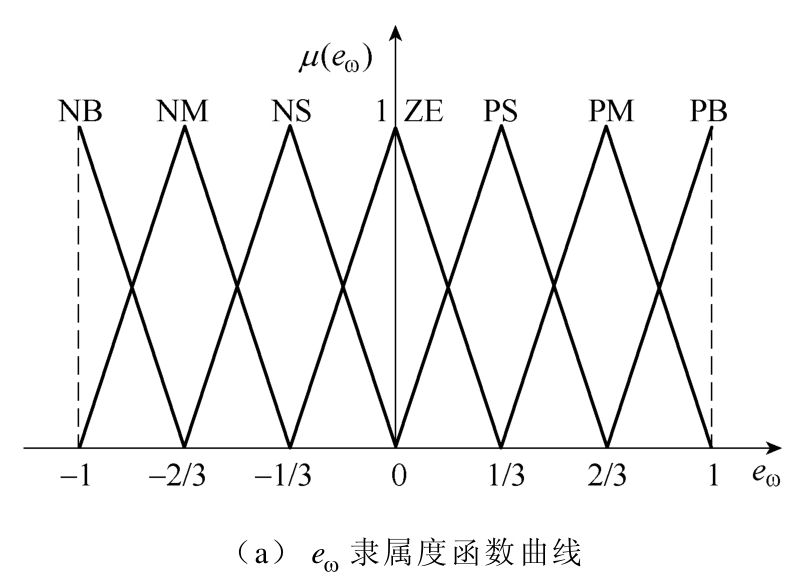
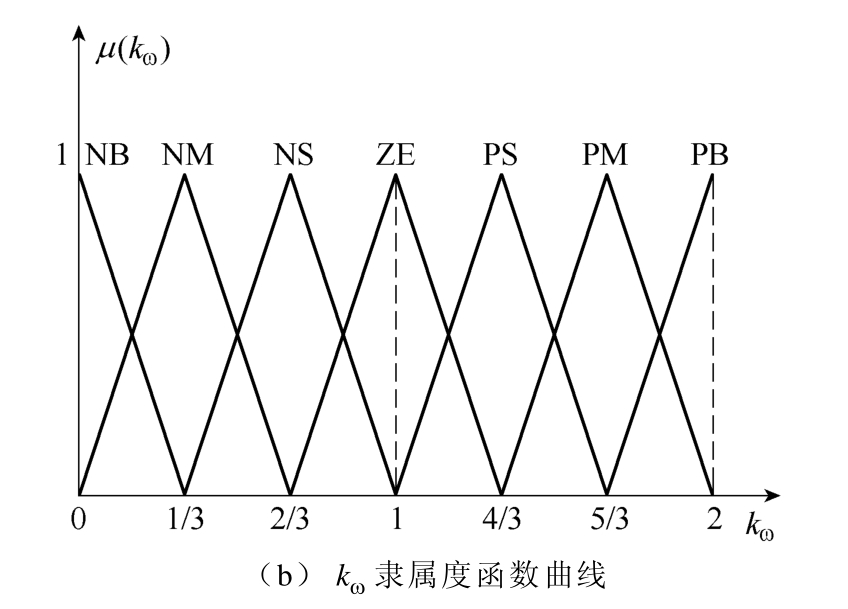
图1 隶属度函数曲线
Fig.1 Membership function curves
kω和1γ可近似认为是传统PI控制器中的比例项和积分项。对于kω的模糊设计规则，当eω和 ce处于正向较大区间时，电机输出电磁转矩远小于负载转矩，应选取较大的kω值，增大eω反馈对控制律的影响，增大输出电磁转矩，从而使得eω迅速趋于零。对于1γ的模糊设计规则，当eω和ce处于正向较大区间时，为避免较大的转速超调，应选取较小的1γ值，以削弱积分项的作用；当eω和 ce处于负向较大区间时，为减小系统静差，应选取较大的1γ值，以增强积分项的作用。同理，设计出其他区间内的模糊设计规则。kω和1γ模糊规则建立见表1和表2。
表1 ωk模糊规则
Tab.1 Fuzzy rules of kω
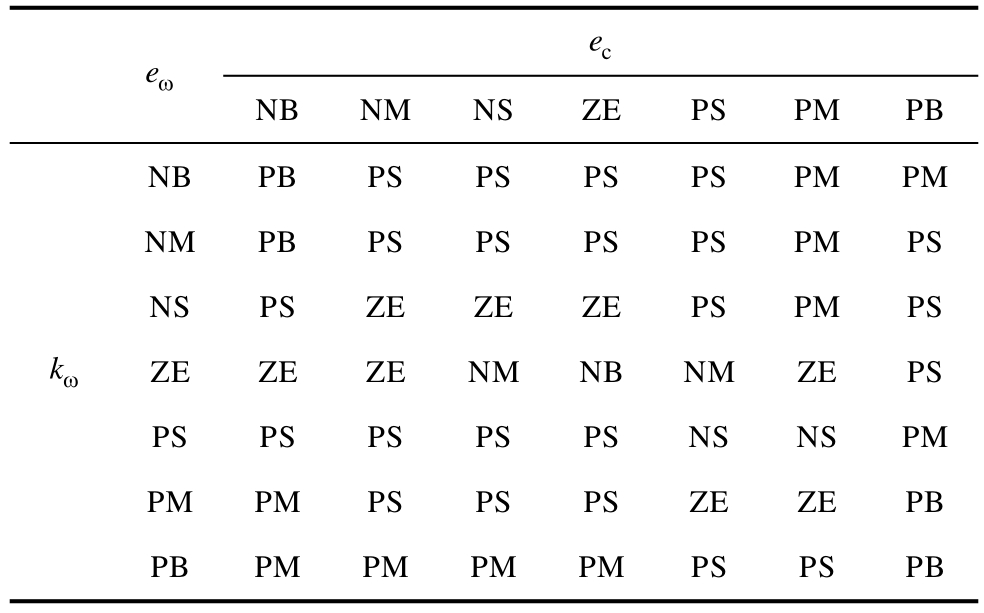
e eω c NB NM NS ZE PS PM PB NB PB PS PS PS PS PM PM kω NM PB PS PS PS PS PM PS NS PS ZE ZE ZE PS PM PS ZE ZE ZE NM NB NM ZE PS PS PS PS PS PS NS NS PM PM PM PS PS PS ZE ZE PB PB PM PM PM PM PS PS PB
表2 1γ模糊规则
Tab.2 Fuzzy rules of 1γ
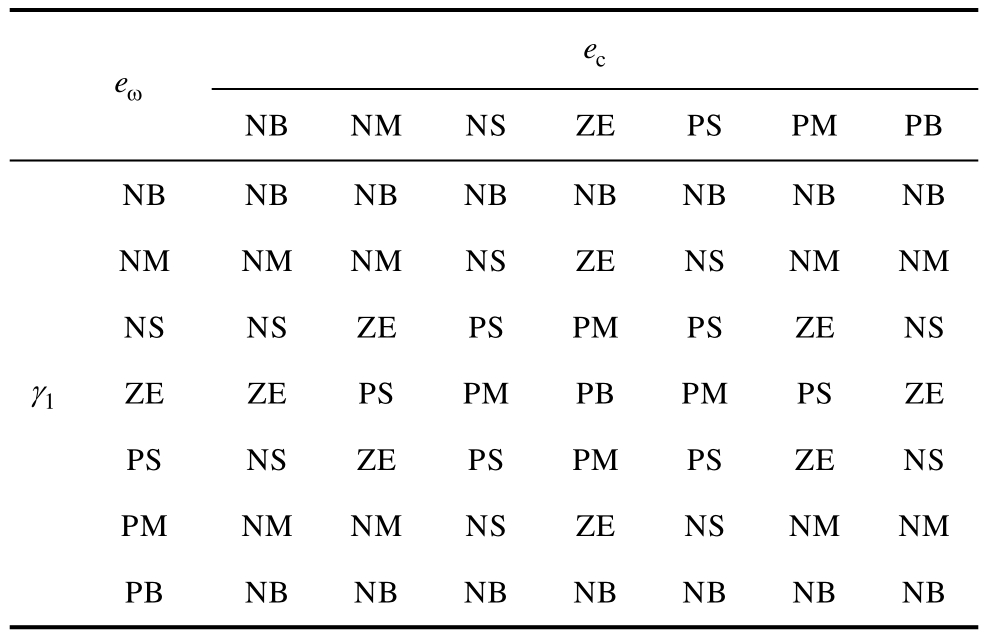
e eω c NB NM NS ZE PS PM PB NB NB NB NB NB NB NB NB 1γ NM NM NM NS ZE NS NM NM NS NS ZE PS PM PS ZE NS ZE ZE PS PM PB PM PS ZE PS NS ZE PS PM PS ZE NS PM NM NM NS ZE NS NM NM PB NB NB NB NB NB NB NB
综上所述，永磁同步电机模糊自整定自适应积分反步控制系统结构框图如图2所示。
图2 模糊自整定自适应积分反步控制系统结构框图
Fig.2 Structure of fuzzy self-tuning adaptive integral backstepping control system
4 实验结果及分析
在永磁同步电机交流调速平台上，对本文提出的模糊自整定自适应积分反步控制策略进行了相应的实验验证，实验平台如图3所示，具体包括被控永磁同步电机、驱动器以及测功机。其中，永磁同步电机选用中空电机，方便从内部进线。通过测功机控制器给定被控永磁同步电机固定数值的负载转矩，用于模拟外部负载扰动。
图3 实验平台
Fig.3 Experimental platform
对应的被控永磁同步电机参数见表3。
表3 电机参数
Tab.3 Motor Parameters
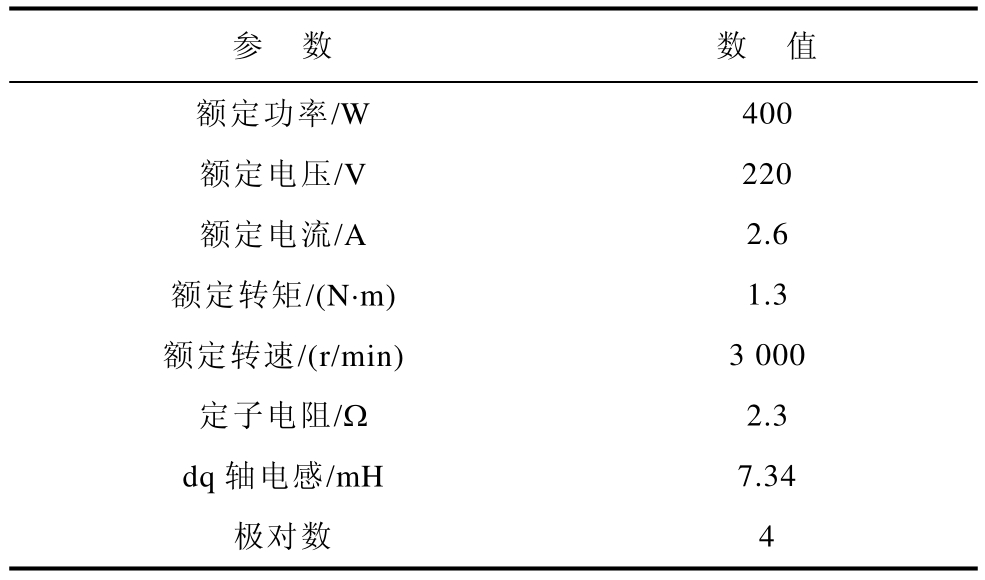
参 数 数 值额定功率/W 400额定电压/V 220额定电流/A 2.6额定转矩/(N·m) 1.3额定转速/(r/min) 3 000定子电阻/Ω 2.3 dq轴电感/mH 7.34极对数 4
为更为直观地体现模糊自整定自适应积分反步控制的优势所在，实验将其分别与传统PI控制方法和传统反步控制方法进行对比。其中，传统PI控制器中转速环比例参数 pkω选取为 800，积分参数 ikω选取为1 000。电流环比例参数 Ipk选取为1 000，积分参数 Iik选取为300；传统反步控制器中的转速反馈增益kω选取为60，dq轴电流调节参数 dk和 qk分别选取为300和40；模糊自整定自适应积分反步控制器中的转速反馈增益kω以及自适应增益1γ根据电机转速误差eω及其变化率 ce自适应在线调整，dq轴电流调节参数 dk和 qk选取与传统反步控制器相同，dq轴电流误差积分增益 dik和 qik分别选取为150和100。对比分外部扰动和内部参数摄动两种情况，通过给定负载突变模拟外部扰动，通过控制器电感分别选用0.8和1.2倍实际电感模拟内部参数摄动。
图4为电机起动过程中的a相电流响应波形对比，在100ms时刻给定电机以3 500r/min的转速起动，其中图4a为传统PI控制下的响应波形，图4b为传统反步控制下的响应波形，以及图4c为模糊自整定自适应积分反步控制下的实验波形。对比图4a～图4c可知，传统PI控制和传统反步控制下的相电流分别经过200ms和260ms左右达到稳态，对比模糊自整定自适应积分反步控制下的相电流起动波形，其仅仅经过大约100ms便可达到稳态值，由此验证了模糊自整定自适应积分反步控制起动过程中的电流动态响应性能要优于传统 PI控制和反步控制。
图4 起动过程相电流对比
Fig.4 Phase current comparison druing starting process
为验证模糊自整定自适应积分反步控制的动态性能以及针对外部负载扰动的鲁棒性，在0.2s时刻给定电机2 000r/min的阶跃转速起动，在0.6s时刻通过测功机控制器突加额定负载，在1.6s时刻突卸额定负载。图5所示为外部负载扰动下的dq轴电流及转速响应对比，包括传统PI控制（见图5a）、传统反步控制（见图5b）以及模糊自整定自适应积分反步控制（见图5c），其中实际转速通过尼康24位绝对值编码器计算获取。如图5a所示，在电机起动时间段，电机dq轴实际电流均存在较大毛刺。综合考虑响应与超调两方面因素，转速环和电流环 PI参数经反复调试达到理想值。在此情况下，大约经过 0.1s，电机实际转速达到稳态值，并且存在大约500r/min的转速超调。在突加额定负载瞬间，电机实际转速存在250r/min的向下波动，经0.05s调节至稳态。d轴实际电流毛刺加重，q轴给定电流和实际电流经过 0.08s调节至额定电流值，并且存在0.5A左右的超调，实际电流能够较好地跟随给定，转矩脉动加大。在突减额定负载瞬间，电机实际转速存在250r/min的向上波动，同样经0.05s调节至稳态，此时dq轴实际电流毛刺削弱。对比图 4b传统反步控制，在电机起动瞬间，转速超调降低至150r/min，但调节时间依旧较长，达到0.15s。在突加以及突减额定负载瞬间，电机转速存在 150r/min的波动，额定负载下的实际转速及转矩脉动较传统PI控制有所减弱。对比图 4c模糊自整定自适应积分反步控制，由于系统通过模糊推理模块自适应在线整定反馈增益，在电机起动瞬间，电机实际转速几乎瞬间无超调地达到稳态值，转速动态响应性能大幅度提高。同样，在突加以及突减额定负载瞬间，电机转速无明显波动。在突加负载瞬间，转矩电流快速无明显超调地达到额定值，转矩脉动小，在突减负载瞬间，转矩电流依旧无明显超调，由此体现出模糊自整定自适应积分反步控制在转速动态性以及抗负载扰动性方面的优越性。
图5 外部负载扰动下的dq轴电流及转速响应对比
Fig.5 Comparison of dq axis current and speed responses under external load disturbance
同理，为验证模糊自整定自适应积分反步控制针对内部参数摄动的鲁棒性，控制器分别选取dq轴定子电感为实际电感的0.8和1.2倍实际电感，dq轴电流及转速响应对比分别如图6和图7所示，同样包括传统 PI控制（见图 6a和图 7a）、传统反步控制（见图 6b和图 7b）以及模糊自整定自适应积分反步控制（见图6c和图7c）。如图6a和图7a所示，电感参数摄动下的dq轴电流较图5a振荡加剧，dq轴电流实际值依然能够跟随给定值。经分析，由于电感参数存在误差系统下的电流环 PI参数依旧选用图5a中无误差的参数，当系统数学模型发生变化时，PI控制器的控制效果会受到影响，此时需对系统电流环 PI参数重新调试才能达到理想的控制效果。如图6b和图7b所示，电感参数摄动下的dq轴电流较图 5b不仅存在明显的振荡，并且dq轴实际电流值较给定电流值存在明显的静差。经分析，传统反步控制基于理想的永磁同步电机数学模型，其对电机内部参数敏感，控制器中的定子电感误差影响了dq轴电流的控制效果。对比图6c和图7c模糊自整定自适应积分反步控制，图6c和图7c较图5c在电流振荡以及静差方面无明显变化，表明电感参数误差对系统电流控制影响较小。经分析，由于系统将dq轴电流跟随误差积分项引入控制律中，定子电感误差引起的电流静差将通过积分项被补偿，控制器对系统模型精确度的依赖大幅度降低。
图6 内部参数摄动下的dq轴电流响应对比（控制器dq轴电感选取0.8倍实际电感）
Fig.6 Comparison of dq axis current responses under internal parameter perturbation (dq axis inductance of the controller is selected as 0.8 times of the actual inductance)
图7 内部参数摄动下的dq轴电流响应对比（控制器dq轴电感选取1.2倍实际电感）
Fig.7 Comparison of dq axis current responses under internal parameter perturbation (dq axis inductance of the controller is selected as 1.2 times of the actual inductance)
5 结论
本文提出一种永磁同步电机模糊自整定自适应积分反步控制方法，将dq轴电流跟随误差积分项引入控制律中，设计自适应积分反步控制器。与此同时，设计模糊推理模块应用于自适应积分反步控制器，根据电机转速误差及其变化率自适应在线整定转速反馈增益以及自适应增益值。该控制方法能有效提高永磁同步电机伺服系统的动态响应性能，解决内部参数摄动和外部负载扰动对系统影响的问题。对比传统PI控制、传统反步控制与模糊自整定自适应积分反步控制，实验结果表明，与传统 PI控制及传统反步控制相比，本文提出的控制策略转速动态响应更为优良，对外部负载扰动和内部电感参数摄动有着较强的鲁棒性。
[1] 张海洋, 许海平, 方程, 等. 基于负载转矩观测器的直驱式永磁同步电机新型速度控制器设计[J].电工技术学报, 2018, 33(13): 2923-2934.Zhang Haiyang, Xu Haiping, Fang Cheng, et al.Design of a novel speed controller for direct-drive permanent magnet synchronous motor based on load torque observer[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 2923-2934.
[2] 刘宁, 夏长亮, 周湛清, 等. 基于比例增益补偿的永磁同步电机转速平滑控制[J]. 电工技术学报,2018, 33(17): 4007-4015.Liu Ning, Xia Changliang, Zhou Zhanqing, et al.Smooth speed control for permanent magnet synchronous motor using proportional gain compensation[J].Transactions of China Electrotechnical Society, 2018,33(17): 4007-4015.
[3] 崔家瑞, 高江峰, 张波, 等. 永磁同步电机滑模变结构鲁棒控制[J]. 电机与控制学报, 2016, 20(5):84-89.Cui Jiarui, Gao Jiangfeng, Zhang Bo, et al. Robust control of synchronous motor based on sliding mode variable structure[J]. Electric Machines and Control,2016, 20(5): 84-89.
[4] Aghili F. Optimal feedback linearization control of interior PM synchronous motors subject to timevarying operation conditions minimizing power loss[J]. IEEE Transactions on Industrial Electronics,2018, 65(7): 5414-5421.
[5] 曾岳南, 曾祥彩, 周斌, 等. 永磁同步电机传动系统电流环非线性自抗扰控制器的设计与稳定性分析[J]. 电工技术学报, 2017, 32(17):135-143.Zeng Yuenan, Zeng Xiangcai, Zhou Bin, et al.Nonlinear active disturbance rejection controller design for current loop of PMSM drive system and its stability analysis[J]. Transactions of China Electrotechnical Society, 2017, 32(17): 135-143.
[6] 赵希梅, 吴勇慷. 基于自适应修正拉盖尔递归神经网络的永磁直线同步电机反推控制[J]. 电工技术学报, 2018, 33(10): 2392-2399.Zhao Ximei, Wu Yongkang. Backstepping control based on adaptive modified laguerre recurrent neural network for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(10): 2392-2399.
[7] Kokotovic P V. The joy feedback: nonlinear and adaptive[J]. Control Systems Magazine, 1992, 12(3):7-17.
[8] Kokotovic P V, Krstic M, Kanellakopoulos I.Backstepping to passivity: recursive design of adaptive systems[C]//IEEE Conference on Decision and Control, Tucson, USA, 1992: 3276-3280.
[9] Cai Jianping, Wen Changyun, Su Hongye, et al.Adaptive backstepping control for a class of nonlinear systems with non- triangular structural uncertainties[J]. IEEE Transactions on Automatic Control, 2016, 62(10): 5220-5226.
[10] Zhou Jing, Wen Changyun, Zhang Ying. Adaptive backstepping control of a class of uncertain nonlinear systems with unknown backlash-like hysteresis[J].IEEE Transactions on Automatic Control, 2004,49(10): 1751-1759.
[11] Linares-Flores J, García-Rodríguez C, Sira-Ramírez H, et al. Robust backstepping tracking controller for low-speed PMSM positioning system: design,analysis, and implementation[J]. IEEE Transactions on Industrial Informatics, 2015, 11(5): 1130-1141.
[12] Morawiec M. The adaptive backstepping control of permanent magnet synchronous motor supplied by current source inverter[J]. IEEE Transactions on Industrial Informatics, 2012, 9(2): 1047-1055.
[13] 张兴华, 唐其太. 考虑参数和负载不确定性的内置式永磁同步电机自适应反步控制[J]. 控制与决策,2016, 31(8): 1509-1512.Zhang Xinghua, Tang Qitai. Adaptive backstepping control of interior permanent magnet synchronous motors considering parameter and load uncertainties[J].Control and Decision, 2016, 31(8): 1509-1512.
[14] 刘栋良, 崔言飞, 赵晓丹, 等. 基于反推控制的永磁同步电动机速度的模糊控制[J]. 电工技术学报,2014, 29(11): 38-44.Liu Dongliang, Cui Yanfei, Zhao Xiaodan, et al.Fuzzy control of speed of permanent magnet synchronous motor based on backstepping control[J].Transactions of China Electrotechnical Society, 2014,29(11): 38-44.
[15] Lin Chih-Min, Li Hsin-Yi. Intelligent control using the wavelet fuzzy CMAC backstepping control system for two-axis linear piezoelectric ceramic motor drive systems[J]. IEEE Transactions on Fuzzy Systems, 2013, 22(4): 791-802.
[16] Liu Sheng, Guo Xiaojie, Zhang Lanyong. Robust adaptive backstepping sliding mode control for six-phase permanent magnet synchronous motor using recurrent wavelet fuzzy neural network[J].IEEE Access, 2017, 5: 14502-14515.
[17] Lin Faa-Jeng, Teng Litao, Chen Chengyan, et al.FPGA-based adaptive backstepping control system using RBFN for linear induction motor drive[J]. IET Electric Power Applications, 2008, 2(6): 325-340.
[18] 杨明. 船舶电力推进永磁同步电机非线性反步控制器设计与优化研究[D]. 大连: 大连海事大学, 2012.
[19] 花熙文. 永磁同步电机的模糊反步自适应调速策略研究[D]. 南京: 南京航空航天大学, 2016.