0 引言
技术的快速发展对工业精密定位平台提出了一些基本要求，如高精度定位、快速定位、响应速度快、抗干扰能力等[1-2]。而永磁直线同步电机（Permanent Magnet Linear Synchronous Motor, PMLSM）自身具有这些特性，广泛应用于工业机器人、数控机床和XY平台驱动系统等自动化设备中[3-4]。由于省去了中间的机械传动机构，负载扰动、参数变化等不确定性因素会使PMLSM的位置跟踪性能下降，如何提高系统的控制精度成为关键[5-6]。因此，在高精度伺服控制系统中，必须设计控制器对这些不确定性进行抑制，使系统具有强鲁棒性，提高系统的控制性能。
众所周知，滑模控制（Sliding Mode Control,SMC）具有良好的暂态性能、对参数变化的鲁棒性和对扰动的不敏感性等优点[7]。SMC的鲁棒性是利用大切换控制增益来实现的，但经常产生抖振现象，这是SMC的一个主要缺点，可能会破坏系统性能[8-9]。为了解决抖振问题，国内外相关学者进行研究并取得一些成果。文献[10]采用动态积分滑模控制削弱抖振，提高了系统的鲁棒性，但当外部扰动过大时，系统的跟踪性能很难得到保证。文献[11]将自适应控制和鲁棒滑模控制相结合，对系统不确定性进行估计，提高了跟踪性，削弱了抖振，但系统的收敛性比较慢。文献[12]提出了一种非线性系统的非奇异终端滑模控制，消除了传统终端滑模控制中存在的奇异性问题，保证了跟踪误差在有限时间内收敛，提高了跟踪性能，但当出现外部扰动时会导致系统不稳定。
为此，本文设计了自适应非奇异快速终端滑模控制（Adaptive Nonsingular Fast Terminal Sliding Mode Control, ANFTSMC）方法。非奇异快速终端滑模控制（Nonsingular Fast Terminal Sliding Mode Control, NFTSMC）能够实现系统有限时间收敛，提高了收敛性，避免了奇异性，同时利用自适应来实时估计系统中总的不确定性，提高了系统的鲁棒性。通过实验证明所提出的控制方案能在短时间内将位置跟踪误差快速收敛于零附近，削弱了抖振且提高了控制精度。
1 PMLSM 数学模型
PMLSM通常采用dq轴电流控制，q轴超前d轴90°电角度，则电磁推力 eF表示为
式中，id、iq、Ld、Lq分别为d、q轴电流和电感；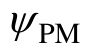
为永磁体磁链； np为极对数；τ为极矩。
根据磁场定向原理，取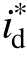 
= 0 ，为了设计方便，假设 L d = Lq = L ，则电磁推力可简化为
式中，Kf为电磁推力系数。
PMLSM的机械运动方程为
式中，M为PMLSM的动子质量；B为粘滞摩擦系数；v为动子速度；F为扰动，包括系统外部扰动、端部效应、参数变化及非线性摩擦力等。
不考虑F时，动态方程为
式中， d( t)为动子位置； 
为控制器输出， qu i= ，即推力电流。考虑F时，动态方程为
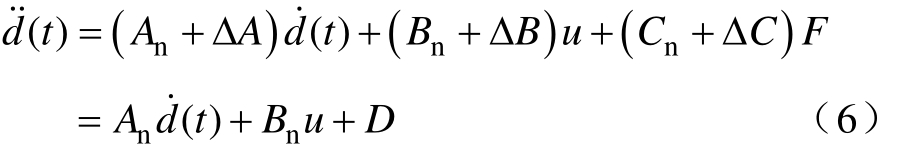
式中， C n =-1/M；ΔA、ΔB和ΔC分别为系统参数M和B引起的不确定量；D为系统不确定性总和，表示为
这里假设D有界，即
，δ为不确定性总和D的上界，为一正常数。
2 PMLSM 控制系统设计
基于ANFTSMC的PMLSM伺服系统框图如图1所示。图1中ANFTSMC采用NFTSMC和自适应控制相结合的方法设计。
设计控制器使PMLSM伺服系统在受不确定性影响时，实际信号 d ( t)能够跟踪任意输入信号
定义跟踪误差为
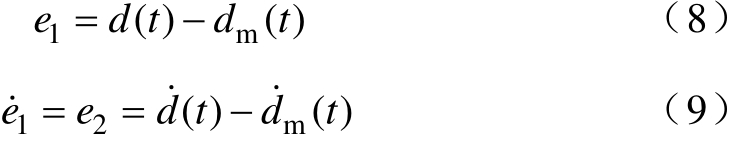
图1 基于ANFTSMC的PMLSM伺服系统框图
Fig.1 Block diagram of PMLSM servo control system based on ANFTSMC
式中，
依据泰勒级数展开定理，假设自适应控制输入不包含加速度函数，总的不确定性的上界是只包含位置和速度的函数，可以得出如下结论
式中，a0、a1、a2都是正数。
2.1 非奇异快速终端滑模控制器设计
针对PMLSM伺服系统位置跟踪控制问题，采用NFTSMC方法，目的是避免奇异性和提高系统的收敛速度，从而使PMLSM伺服系统对不确定性具有较强的鲁棒性能。下面对滑模面和控制律进行设计。
定义滑模面
式中，k1、k2为正常数；1＜β＜2, α＞β；sign(⋅)为符号函数。
当系统状态远离平衡状态时，
和
相比，占主导地位优势，从而保证了较高的收敛率，而且当系统状态接近平衡状态时，
保证了系统在有限时间内的收敛性。
对 s ( t)求导得
选择合适的滑模面后，设计等效控制律，s˙( t)=0是状态轨迹停留在滑模面 s( t) = 0 的必要条件，在不考虑不确定性的情况下，由式（10）和式（13）得
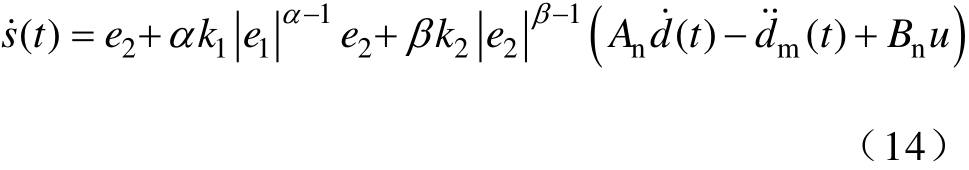
令s˙( t)=0得等效控制律为
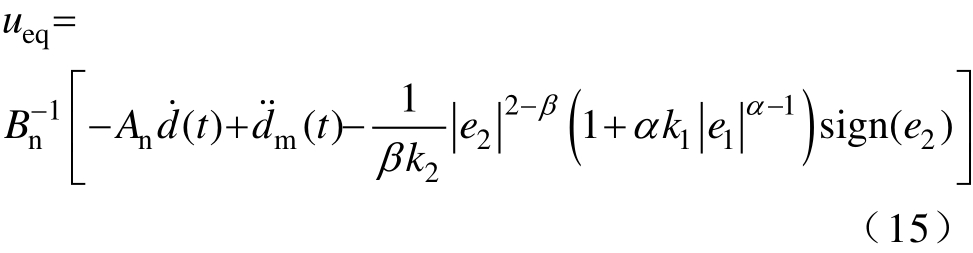
切换控制律为
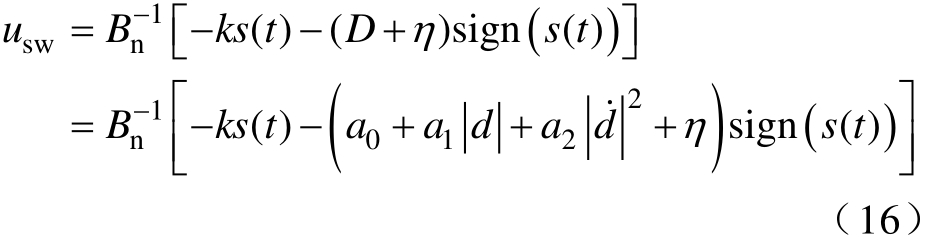
式中，
且是小的常数；k为切换增益，
2.2 自适应非奇异快速终端滑模控制器设计
在实际应用中，系统不确定性的未知上界是很难获得的。本文采用自适应控制来估计系统不确定性的未知上界，用
变为
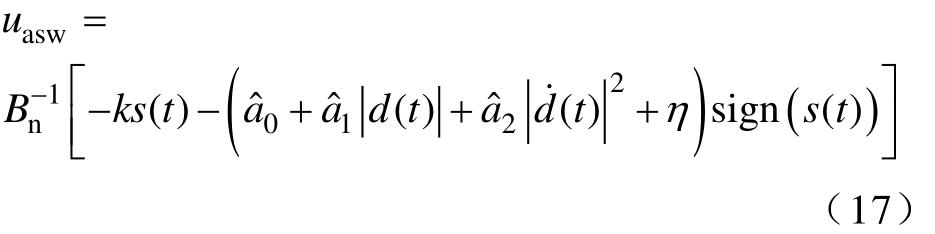
因此，总的控制律表示为
由Lyapunov稳定性定理可知，系统的状态渐近地收敛于滑模面 () 0s t= 。也就是说，在不确定性存在的情况下，系统状态依然能够收敛到滑模面，最终稳定在滑模面，即系统的鲁棒性得到提高。
3 系统实验分析
图2为PMLSM控制系统硬件结构。实验装置包括DSP、PC、整流器、IPM、PMLSM、直线光栅尺等。该实验DSP型号为TMS320F2812A，DSP通过 JTAG串口与 PC之间进行数据信息传输，对提出的控制算法进行处理。将处理完的控制信号输入IPM，然后再传递给PMLSM。
图2 PMLSM控制系统硬件结构
Fig.2 Hardware frame map of PMLSM control system
为验证ANFTSMC方法的有效性，分别采用SMC、NFTSMC和ANFTSMC三种方法对PMLSM伺服系统进行实验研究。PMLSM参数： M = 1 6.4kg ，B=8.0N⋅ s m，Kf= 5 0.7N/A， R =2.1Ω ， τ = 3 2mm，Ld = Lq = 4 1.4mH， Ψ f = 0 .09Wb。通过实验多次调试参数，系统处在最佳运行状态。SMC的参数：λ=15，β=400，ϕ=0.05。NFTSMC的参数：α=2，β=5 3，η=0.5，k1=1，k2=1，k= 8 000，a0 =9.5，a1=2.2，a2=2.8。ANFTSMC的参数：α=2，β=5 3，η=0.5，k1=1，k2=1，k=100，μ0=130，μ1=1，μ2=0.1。
在相同条件下，选取两种不同的输入信号，结合系统的响应曲线来验证PMLSM控制系统的各项性能指标。①幅值为1mm的阶跃信号，在 0.5s突加50N的恒定负载扰动（负载扰动占负载比例为40%）；②幅值为1mm，频率为0.16Hz的正弦信号；③幅值为1mm的阶跃信号，给定变化的负载扰动。
实验一：在情况①下，三种控制方法的PMLSM伺服系统位置跟踪曲线和位置误差曲线如图3a、图3b所示。通过位置跟踪曲线对比，在 0.15s时ANFTSMC和NFTSMC系统均已达到稳定状态，响应速度比 SMC更快，位置跟踪性能更好。在 0.5s突加扰动，ANFTSMC不仅能更快速地恢复到稳定状态，而且系统位置跟踪曲线偏离给定曲线的趋势最小，鲁棒性明显提高。图3c为三种控制方法的位置误差速度曲线，由图可知，在电机起动的瞬间，SMC位置误差速度曲线达到最大值约为 18mm/s，而 NFTSMC和 ANFTSMC最大值约为 15mm/s；NFTSMC和ANFTSMC比SMC的位置误差速度先趋近于零，表明NFTSMC和ANFTSMC比SMC具有更快的收敛性；从局部放大图看，ANFTSMC比NFTSMC和SMC的位置速度偏差都小。图3d、图3e分别为NFTSMC、ANFTSMC位置误差加速度曲线，在电机起动瞬间 NFTSMC比 ANFTSMC具有更大的误差加速度；当达到稳定状态时，NFTSMC的位置误差加速度的最大值接近于 50m/s2，而ANFTSMC的位置误差加速度的最大值基本稳定在20m/s2左右；在 0.5s突加扰动后，NFTSMC和ANFTSMC的位置误差加速度都比加入扰动前的位置误差加速度小，表明系统具有强鲁棒性。综上所述，ANFTSMC方法使系统具有更强的鲁棒性和更好的跟踪性，抖振现象得到改善。
图3 阶跃输入的SMC、NFTSMC和ANFTSMC位置曲线
Fig.3 Position curves of SMC, NFTSMC and ANFTSMC for step input
实验二：在情况②下，三种控制方法的PMLSM伺服系统位置跟踪曲线如图4a所示，系统位置误差曲线如图 4b～图4d所示。由图可见，在电机起动运行瞬间，SMC系统位置跟踪曲线的最大误差是3.6μm，然后逐渐稳定在2μm左右，收敛速度比较慢，抖振现象比较严重。而NFTSMC系统从电机起动运行，跟踪误差就一直稳定在1.5μm左右，抖振现象得到改善；与 SMC系统相比，省去了逐渐趋于稳定的过程，提高了系统快速收敛性。ANFTSMC系统跟踪误差始终保持在0.5μm左右；与NFTSMC相比，自适应控制的引入使抖振现象得到了明显的改善，进而使PMLSM伺服系统具有更好的跟踪精度和鲁棒性能。
图4 正弦波输入的SMC、NFTSMC和ANFTSMC位置曲线
Fig.4 Position curves of SMC, NFTSMC and ANFTSMC for sinusoidal input
实验三：在情况③下，给定变化的负载扰动曲线如图5a所示。由图可见，所加的扰动是非周期性扰动，更贴近于工程实际状况。PMLSM 伺服系统的三种控制方法的系统位置跟踪曲线如图5b所示，ANFTSMC和NFTSMC的收敛速度快于SMC且先到达期望轨迹。在变扰动情况下，明显看出 SMC偏离期望轨迹的幅度最大，跟踪性能和鲁棒性能都最差。从局部放大图可知，ANFTSMC的位置跟踪曲线基本上没有偏离期望轨迹曲线，而NFTSMC明显偏离期望轨迹曲线，表明ANFTSMC具有较好的跟踪性能和较强的鲁棒性能。图 5c是位置误差曲线，ANFTSMC和NFTSMC的误差比SMC的误差先趋近于零，表现出较快的收敛速度。在大约 1.3s后，SMC的误差开始明显波动变化，而ANFTSMC的误差没有明显的变化且几乎为零。
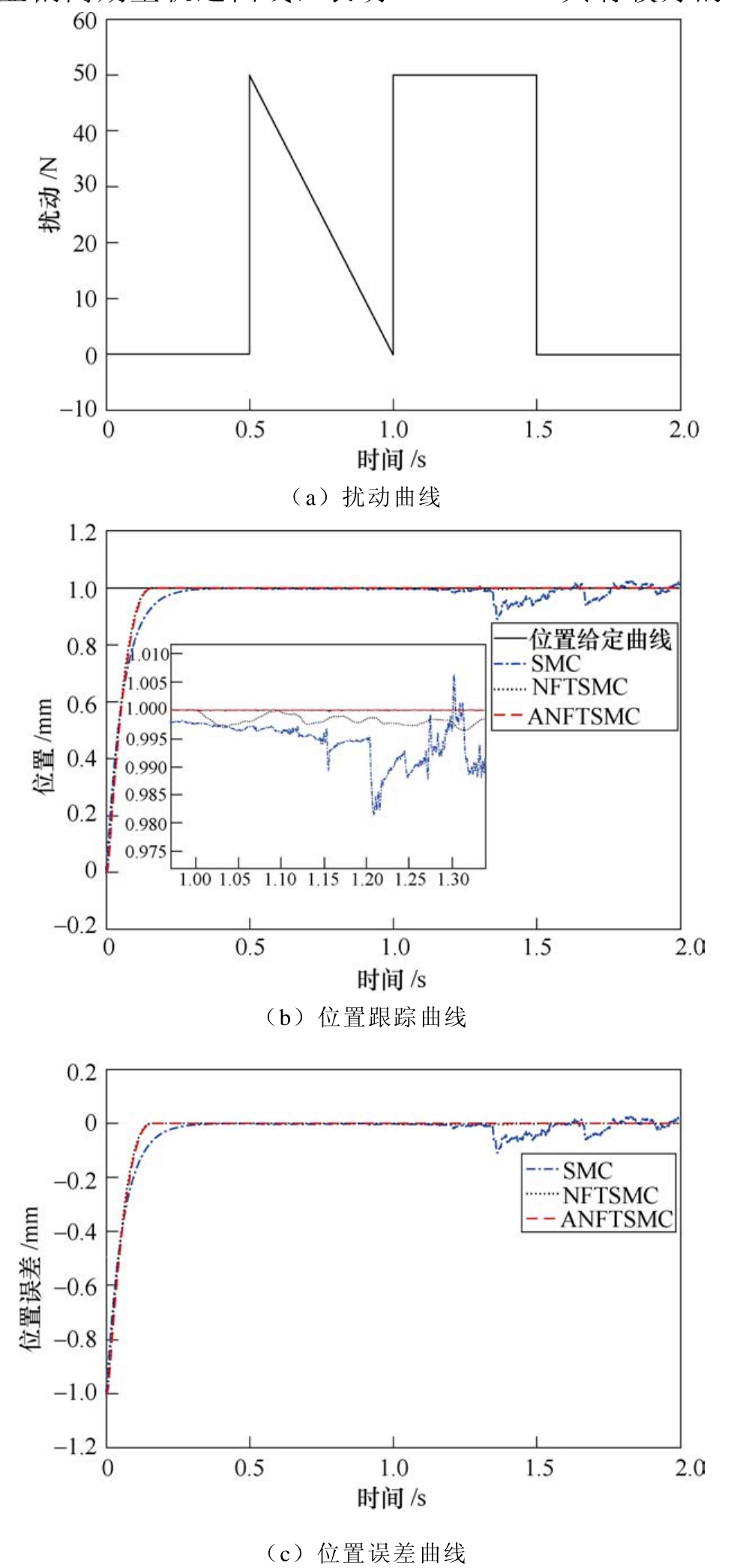
图5 阶跃输入的SMC、NFTSMC和ANFTSMC位置曲线
Fig.5 Position curves of SMC, NFTSMC and ANFTSMC for step input
4 结论
为改善PMLSM伺服系统位置跟踪控制精度，采用ANFTSMC方法可以在有限时间内使系统状态快速收敛到稳定状态。当系统状态远离稳定状态时，不仅实现了快速收敛，而且避免了终端滑模的奇异性问题。用只需测量位置和速度的自适应控制对系统不确定性参数进行实时估计，削弱了抖振，提高了鲁棒性，更适合于数控机床的实际应用。通过理论和实验分析得出，ANFTSMC系统具有以下优点：①系统跟踪性能好，具有较强的鲁棒性；②有效削弱了抖振；③系统跟踪误差小，收敛速度更快。
[1] Chen Mei-Yung, Lu Jian-Shiun. High-precision motion control for a linear permanent magnet iron core synchronous motor drive in position platform[J].IEEE Transactions on Industrial Informatics, 2014,10(1): 99-108.
[2] 王丽梅, 张宗雪. H型精密运动平台交叉耦合模糊PID同步控制[J]. 沈阳工业大学学报, 2018, 40(1):1-5.Wang Limei, Zhang Zongxue. Cross-coupled fuzzy PID synchronous control for H-type precision motion platform[J]. Journal of Shenyang University of Technology, 2018, 40(1): 1-5.
[3] Zhong Jinghua, Yao Bin. Adaptive robust precision motion control of a piezoelectric positioning stage[J].IEEE Transactions on Control Systems Technology,2008, 16(5): 1039-1046.
[4] 赵希梅, 王晨光. 永磁直线同步电机的自适应增量滑模控制[J]. 电工技术学报, 2017, 32(11): 111-117.Zhao Ximei, Wang Chenguang. Adaptive incremental sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 111-117.
[5] Ting Chensheng, Chang Yongnong, Shi Bowei, et al.Adaptive backstepping control for permanent magnet linear synchronous motor servo drive[J]. Electric Power Applications IET, 2015, 9(3): 265-279.
[6] 朱国昕, 雷鸣凯, 赵希梅. 永磁同步电机伺服系统自适应迭代学习控制[J]. 沈阳工业大学学报, 2018,40(1): 6-11.Zhu Guoxin, Lei Mingkai, Zhao Ximei. Adaptive iterative learning control for permanent magnet synchronous motor servo system[J]. Journal of Shenyang University of Technology, 2018, 40(1): 6-11.
[7] Hama T, Sato K. High-speed and high-precision tracking control of ultrahigh-acceleration movingpermanent-magnet linear synchronous motor[J].Precision Engineering, 2015, 40: 151-159.
[8] 赵希梅, 赵久威. 永磁直线同步电机的智能互补滑模控制[J]. 电工技术学报, 2016, 31(23): 9-14.Zhao Ximei, Zhao Jiuwei. Intelligent complementary sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2016, 31(23): 9-14.
[9] Mondal S, Mahanta C. Chattering free adaptive multivariable sliding mode controller for systems with matched and mismatched uncertainty[J]. ISA Transactions, 2013, 52(3): 335-341.
[10] Sun Baiqing, Ge Xiuwei, Sun Yibiao. Dynamical integral sliding mode control for permanent magnet ring torque motor[J]. Advanced Materials Research,2011, 383-390: 799-804.
[11] Panah P G, Ataei M, Mirzaeian B, et al. A robust adaptive sliding mode control for PMLSM with variable velocity profile over wide range[J]. Research Journal of Applied Sciences Engineering & Technology, 2015, 10(9): 997-1006.
[12] Tran M D, Kang H J. Nonsingular terminal sliding mode control of uncertain second-order nonlinear systems[J]. Mathematical Problems in Engineering,2015, 2015(2): 1-8.