0 引言
近年来,内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor, IPMSM)在功率密度、效率等方面的优势使其获得了广泛的应用[1-3]。为了提高运行效率、降低运维成本、增强运行可靠性,采用无位置传感器控制方式的永磁同步电机驱动系统是永磁电机控制技术发展的主流趋势[4-22]。
根据电机运行范围适用性的不同,无传感器控制技术主要分为中高速模型法[4-8]和零低速凸极特性跟踪法[9-22]两类。模型法主要利用反电动势或者磁链信息对转子位置进行估计。这类方法在中高速范围取得了较好的效果,但在低速运行时反电动势或者磁链信息的信噪比低,难以较为准确地提取转子位置信息。凸极性跟踪法主要是通过外加高频激励信号,利用电机自身的凸极特性来获取转子位置。由于此类方法是对电机凸极特性的跟踪,具有较强的电机参数鲁棒性,在零低速运行范围内能够获得较好的转子位置观测精度。凸极性跟踪法的代表性方法为高频注入法,并且根据注入信号的不同又可将其分为脉振高频注入法[10-13]、方波高频注入法[14-16]和旋转高频注入法[17-21]三类。脉振高频注入法观测器调节困难[11],方波高频注入法存在较大的高频损耗及噪声,且脉振高频注入和方波高频注入都存在起动发散风险[12-13]。相比而言,旋转高频注入法更易于调试和实现[11]。然而,在实际工程应用中,旋转高频注入法受到数字控制延时和滤波器延时的影响[17, 21],若不能采取有效的补偿措施,其转子位置观测精度将受到限制。
为提高旋转高频注入法的位置观测精度,文献[17]利用群时延理论对相位延迟进行补偿,但其补偿效果受滤波器设计和转速的影响。文献[20]采用全通滤波器消除控制延时,但受到电流检测精度的限制,且其反正切求取位置的计算方案易受到噪声干扰。文献[21]中针对转子初始位置辨识提出了通过正序高频电流信息实现对控制和解调延时的统一补偿策略,提升了电机初始位置辨识精度。然而,静止坐标系下的提取方案限制了其对电机转速的适应性。在电机运转时,因转子旋转的影响使得静止坐标系下正、负序高频电流呈现出不同的频率,使得解调延时对正、负序高频电流相位的影响也将不同,限制了通过正序电流相位信息对负序电流相位误差补偿的精确度,且反正切求取补偿角度的方案易受到噪声干扰。
为进一步提升位置观测精度,本文对旋转高频注入法的解调算法进行了进一步研究,提出了一种基于估计同步旋转坐标系的解调算法。尽管高频信号的注入仍以静止坐标系为参考坐标系,但解调算法却在估计的同步旋转坐标系下实施。分析表明,在同步旋转坐标系下,正、负序电流呈现出相同的频率,从而可以如同电机处于静止状态一样,有效地利用高频正、负序电流的相位信息,实现延时影响的自动校准,提升电机转子位置的跟踪准确性。通过在 18kW IPMSM 测试台上的实验验证了本方案的有效性和相比静止坐标系下解调方案的优势。
1 静止坐标系解调算法
1.1 传统旋转高频注入法
图1为基于旋转高频电压注入的IPMSM无位置传感器控制系统结构框图,其位置信号的获取源于对高频响应电流信号的解调。图1中, 为估计的电角速度,
为估计的电角速度,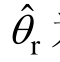 为估计的转子位置角。
为估计的转子位置角。
静止坐标系下注入的高频电压信号可表示为
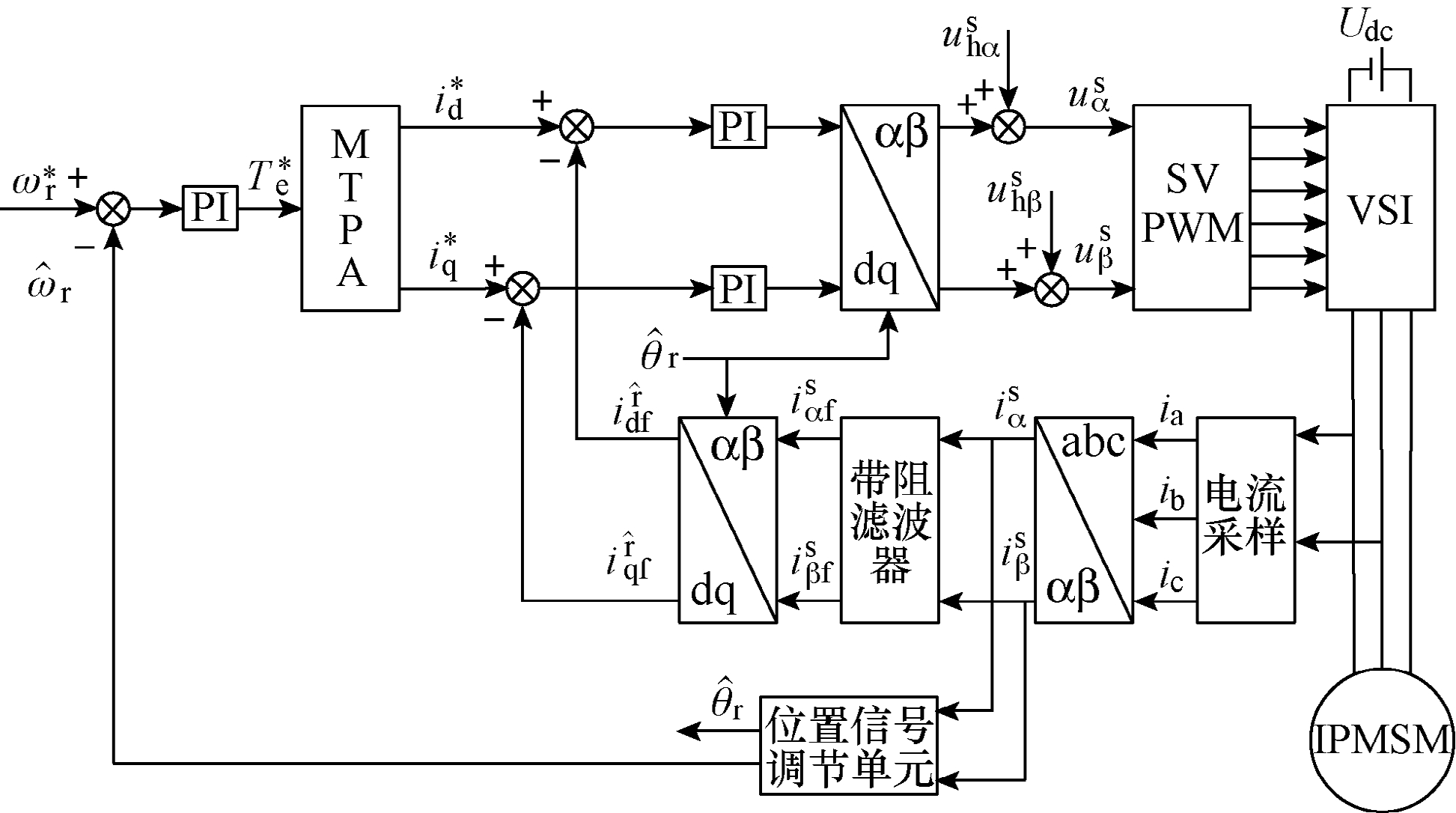
图1 IPMSM无位置传感器控制系统
Fig.1 Position sensorless control system of IPMSM
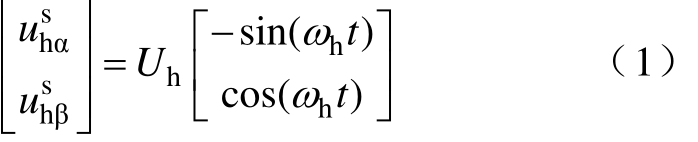
式中,![]() 分别为两相静止坐标系下注入的高频电压;Uh为高频电压幅值;ωh为高频电压的角速度。
分别为两相静止坐标系下注入的高频电压;Uh为高频电压幅值;ωh为高频电压的角速度。
静止坐标系下IPMSM高频电压方程可表示为
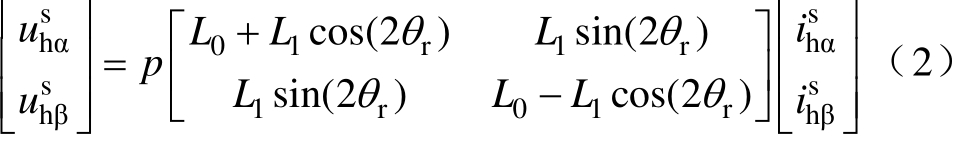
式中,![]() 分别为两相静止坐标系下的高频电流;
分别为两相静止坐标系下的高频电流;![]() 为均值电感;
为均值电感;![]() 为差值电感;dL、qL分别为直、交轴电感;rθ为转子位置角,若以rω表示转子旋转电角速度,则rr0tθωθ=+,其中0θ表示转子的初始位置,为简化表述在全文公式推导中将初始位置设置为0°,即rrtθω=;p为微分算子。
为差值电感;dL、qL分别为直、交轴电感;rθ为转子位置角,若以rω表示转子旋转电角速度,则rr0tθωθ=+,其中0θ表示转子的初始位置,为简化表述在全文公式推导中将初始位置设置为0°,即rrtθω=;p为微分算子。
将式(1)代入式(2),可将高频电流表示为
式中, hpI、 hnI 分别为正、负序高频电流幅值,即![]()
传统旋转高频注入法解调流程如图 2[18]所示。图2中,BPF为带通滤波器,HPF为高通滤波器,PLL为锁相环。
图2 传统旋转高频注入法解调流程
Fig.2 Diagram of the conventional demodulation with rotating HF signal injection method
虽然传统旋转高频注入法具有良好的稳定性,但其位置解调精度受数字控制延时和滤波器延时的限制[21]。
1.2 基于静止坐标系补偿算法
文献[21]中针对转子初始位置辨识提出了通过正序高频电流信息实现对控制和解调延时的统一补偿策略,提升了电机初始位置辨识精度。其具体的解调流程如图3所示,即通过同步旋转滤波器实现正、负序高频电流提取。通过正序分量的相位信息对由负序分量得到的转子位置角的相位误差进行补偿。滤波延时不仅对负序分量,而且对正序分量均产生相位延迟影响。因此,所获得的高频电流可表示为
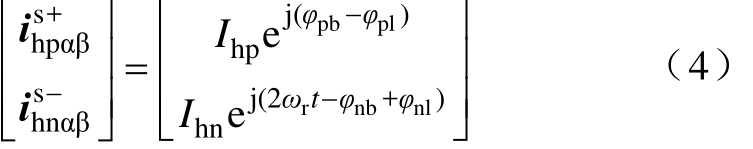
式中,![]() 分别为基于静止坐标系补偿算法提取的正、负序高频电流;pbϕ、nbϕ分别为BPF对正、负序高频电流产生的相移;plϕ、nlϕ分别为低通滤波器(Low Pass Filter, LPF)对正、负序高频电流产生的相移。
分别为基于静止坐标系补偿算法提取的正、负序高频电流;pbϕ、nbϕ分别为BPF对正、负序高频电流产生的相移;plϕ、nlϕ分别为低通滤波器(Low Pass Filter, LPF)对正、负序高频电流产生的相移。
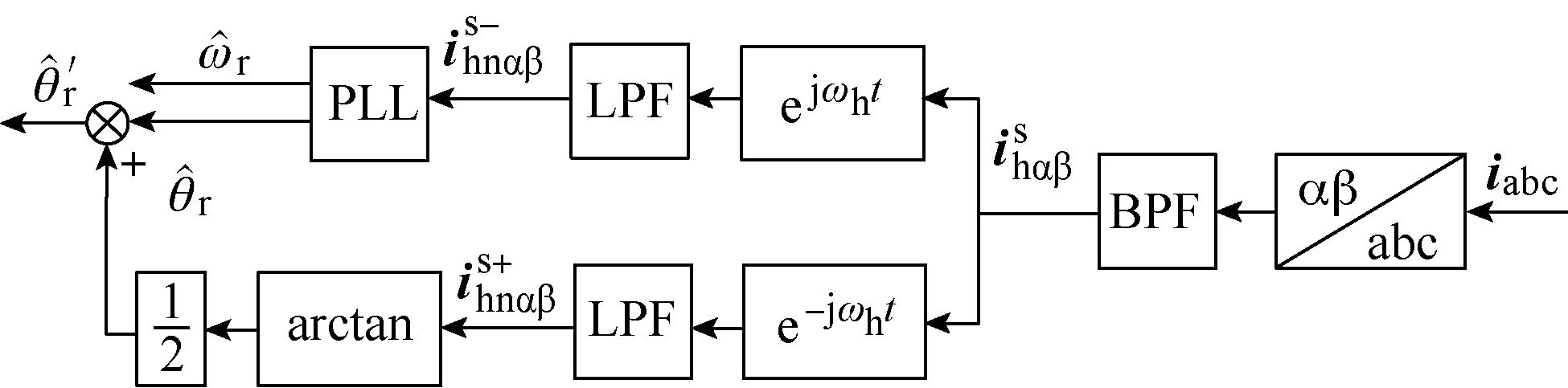
图3 静止坐标系补偿算法解调流程
Fig.3 Diagram of the demodulation with phase compensation in the stationary reference frame
此外,在对控制系统进行离散化数字实现时,通常会引入约 1.5sT的控制延时[22],其中 sT表示开关周期。考虑控制延时的影响,式(3)可表示为
式中,![]() ,为正序高频电流受控制延时产生的相移;
,为正序高频电流受控制延时产生的相移; ![]() 为负序高频电流受控制延时产生的相移。
为负序高频电流受控制延时产生的相移。
因此,考虑数字控制延时和滤波器延时,通过图3所示的流程提取的高频电流可表示为
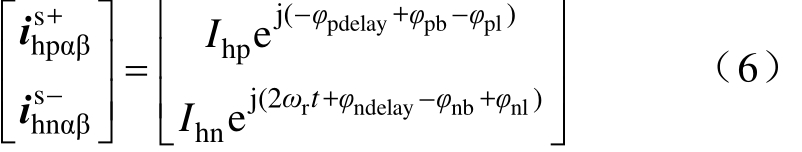
当电机静止时,正、负序高频电流呈现出相同的频率,因而控制延时,BPF和LPF对正、负序高频电流产生相同的相位影响,从而实现延时的精确校准。但在电机运转时,式(3)中r0ω≠,因而在αβ静止坐标系下,正、负序高频电流呈现出不同的频率,从而造成控制延时、滤波器延时对正、负序高频电流相位的影响也将不同,限制了通过正序电流相位信息对负序电流相位误差补偿的精确,且转速越高补偿精度越差。这里以注入600Hz高频信号且电机运行于20Hz的情况为例,设计BPF中心频率为600Hz,品质因数为2,其相频响应如图4a所示;设计截止频率为 100Hz,品质因数为 0.707的二阶LPF,其相频响应如图4b所示。此时,滤波器对负序电流的相位延迟为-46.2°,若不进行补偿,观测位置误差将达到-23.1°。滤波器对正序电流的相位影响为-3.8°,补偿后位置误差仍高达-25°。由上述分析可以得到,此补偿方案仅在初始位置辩识阶段具有良好的位置观测精度,然而对低速情况并不适用。

图4 滤波器相频响应
Fig.4 Phase response of filter
2 旋转坐标系解调算法
2.1 正、负序高频电流提取
为解决电机运转状态下解调延时对正、负序电流所产生的相位影响不一致的问题,本文提出了一种基于估计同步旋转坐标系ˆˆ d-q的高频电流提取和解调方案。图5给出了各坐标系之间的位置关系。在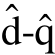 坐标系下高频电流可表示为
坐标系下高频电流可表示为

图5 各坐标系之间的位置关系
Fig.5 Diagram of different reference frames
式中,![]() 坐标系下提取的高频电流。
坐标系下提取的高频电流。
考虑到估计坐标系最终将跟踪实际同步旋转坐标系,即![]() 结合式(7)表达式可知,在
结合式(7)表达式可知,在![]() 坐标系下,正、负序高频电流最终将具有相同的频率。在d-q坐标系下,通过BPF获取高频电流信号后,本文设计了如图6所示基于ˆˆ d-q坐标系的对称正、负序高频电流分离方案,通过正、负序同步滤波器实现正、负序电流的分离。考虑到在注入高频电压不变的情况下,高频电流的大小受到电机电感参数的影响,进而影响到观测性能的问题[4],这里分别对正、负序高频电流进行了标幺化处理,最终得到的正、负序电流分量可表示为
坐标系下,正、负序高频电流最终将具有相同的频率。在d-q坐标系下,通过BPF获取高频电流信号后,本文设计了如图6所示基于ˆˆ d-q坐标系的对称正、负序高频电流分离方案,通过正、负序同步滤波器实现正、负序电流的分离。考虑到在注入高频电压不变的情况下,高频电流的大小受到电机电感参数的影响,进而影响到观测性能的问题[4],这里分别对正、负序高频电流进行了标幺化处理,最终得到的正、负序电流分量可表示为
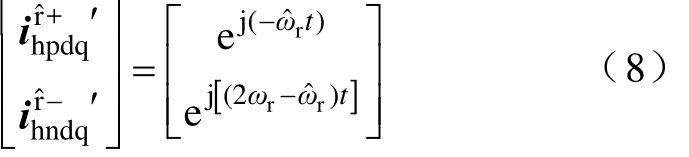
式中,![]() 分别表示提取的正、负序高频电
分别表示提取的正、负序高频电![]() 对应 的 标幺值 。
对应 的 标幺值 。
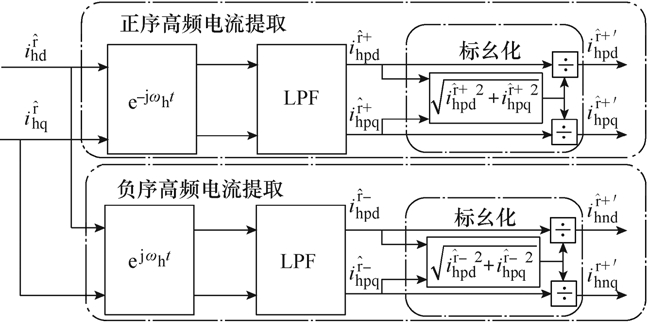
图6 正、负序电流的提取流程
Fig.6 Flow chart of the positive and negative sequence current extraction
2.2 误差分析及位置观测
2.2.1 数字控制延时
对式(5)进行坐标变换,可以得知在ˆˆ d-q坐标系下,控制延时对正、负序高频电流的影响大小。考虑控制延时的影响,式(8)可表示为

2.2.2 高频电流的提取
与静止坐标系的解调算法不同,本方案通过BPF提取高频电流信号是在估计同步旋转坐标系下实施的,此时正、负序高频电流呈现出相同的频率,因而BPF对正、负序高频电流所产生的相位影响也将相同。在与静止坐标系补偿算法误差分析相同的注入频率和运行频率情况下,估计同步旋转坐标系下BPF对正、负序高频电流的相位影响如图7a所示。
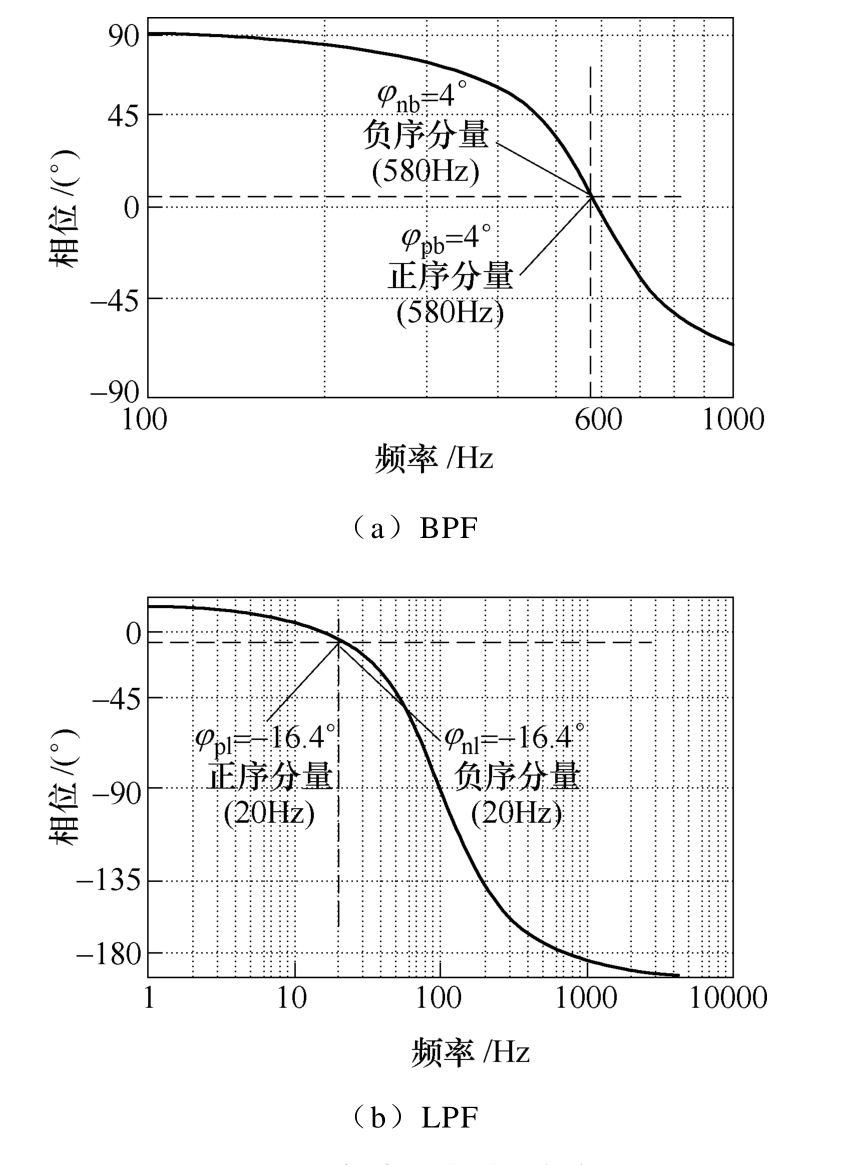
图7 滤波器相频响应
Fig.7 Phase response of filter
考虑BPF的影响,式(8)可表示为
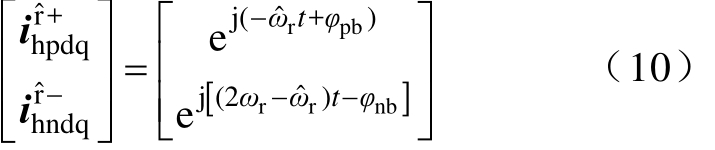
与静止坐标系补偿算法不同,![]()
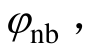 且不受转速的影响。
且不受转速的影响。
2.2.3 正、负序电流分离
正、负序高频电流的分离是通过高频正、负序同步滤波器实现的,即在高频正序同步坐标系中通过LPF提取正序分量,在高频负序同步旋转坐标系中通过LPF提取负序分量。分析不难发现,正、负序高频电流分别在高频正、负序同步旋转坐标系中呈现出相同的频率,均为rω。因而,在经过相同的LPF时,也将产生相同的相位延迟,如图7b所示。
考虑LPF的影响,式(8)可表示为
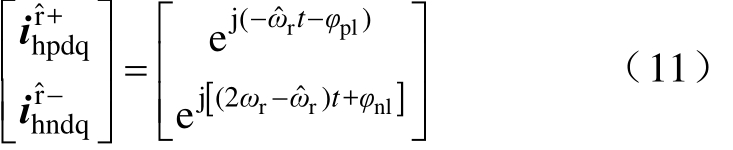
式中,当![]()
2.2.4 转子位置观测
在综合考虑数字控制延时和滤波器延时后,式(8)可表示为

式中,pϕ为控制和解调滤波延时对正序高频电流所产生的总相位差;nϕ为控制和解调滤波延时对负序高频电流所产生的总相位差。
对式(12)所示正、负序电流进行叉乘运算可得

式中 ,![]() 表 示锁相误 差 ;
表 示锁相误 差 ;![]()
![]() 表示残差。
表示残差。
依据式(13)可设计相应的PLL,如图8所示。显然,在PLL收敛后,位置误差大小为/2ε,为进一步消除这一残差,可在观测位置中引入补偿项。同样,以注入600Hz高频信号且电机运行频率为20Hz,开关频率为8 400Hz的情况为例进行分析,pdelay/2ϕ=![]() 补偿量仅占控制延时造成的误差的6.7%,其值较小,且与转速成线性相关,易于补偿。最终使得无论在零速还是低速情况下,控制和解调滤波延时对位置检测误差的影响都得以消除。
补偿量仅占控制延时造成的误差的6.7%,其值较小,且与转速成线性相关,易于补偿。最终使得无论在零速还是低速情况下,控制和解调滤波延时对位置检测误差的影响都得以消除。
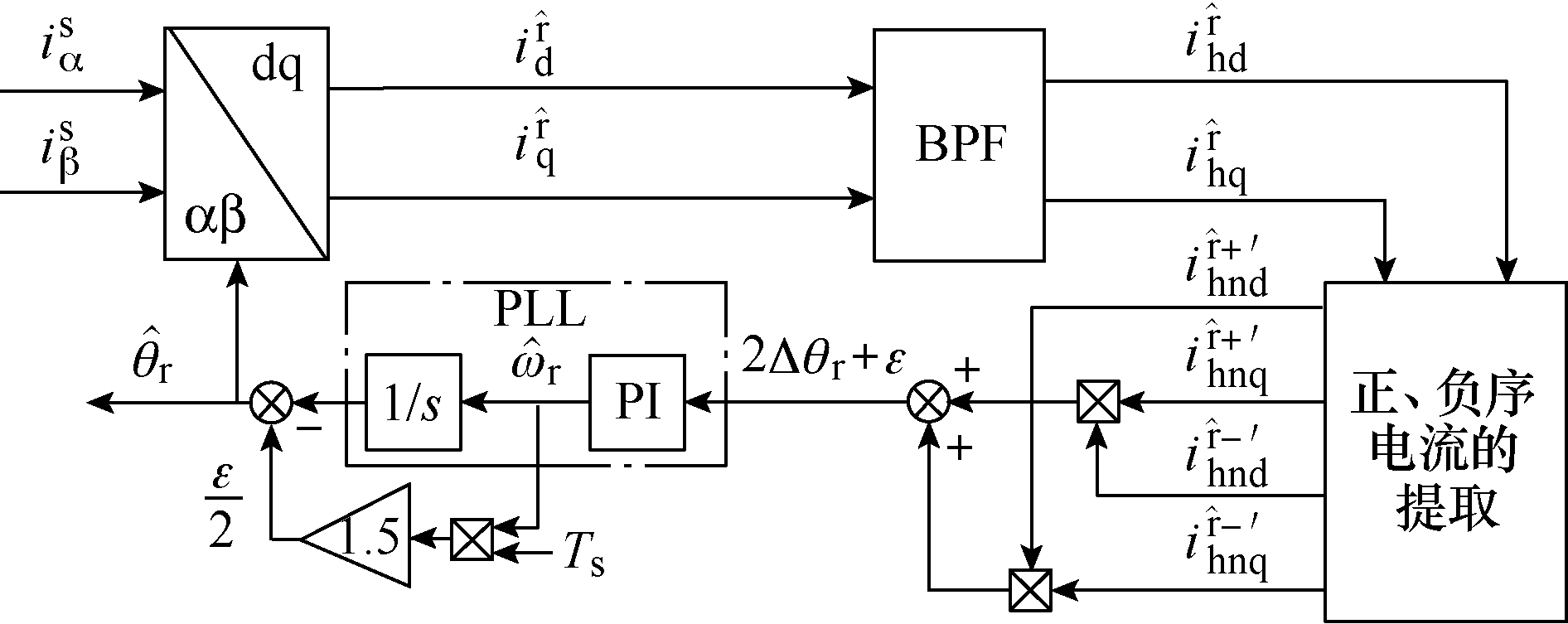
图8 基于旋转坐标系的解调流程
Fig.8 Demodulation implemented on the SRF
3 实验验证
为了验证所提同步旋转坐标系解调算法的有效性,在图9所示的IPMSM实验平台上进行了验证,所用IPMSM主要参数在表1给出。图9中感应电机(Induction Motor, IM)为陪试电机,由变频器控制,两电机同轴相连,IPMSM电机控制器的主控芯片为32位DSP TMS320F28335,注入的旋转高频电压信号频率为600Hz,幅值为57V。
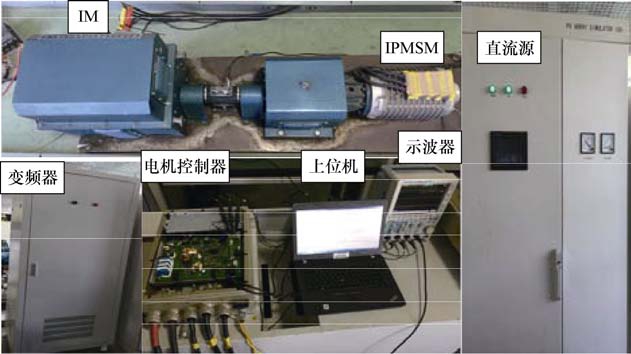
图9 IPMSM矢量控制实验平台
Fig.9 Experimental platform for vector-controlled IPMSM
表1 IPMSM实验平台参数
Tab.1 Experimental platform parameters of IPMSM
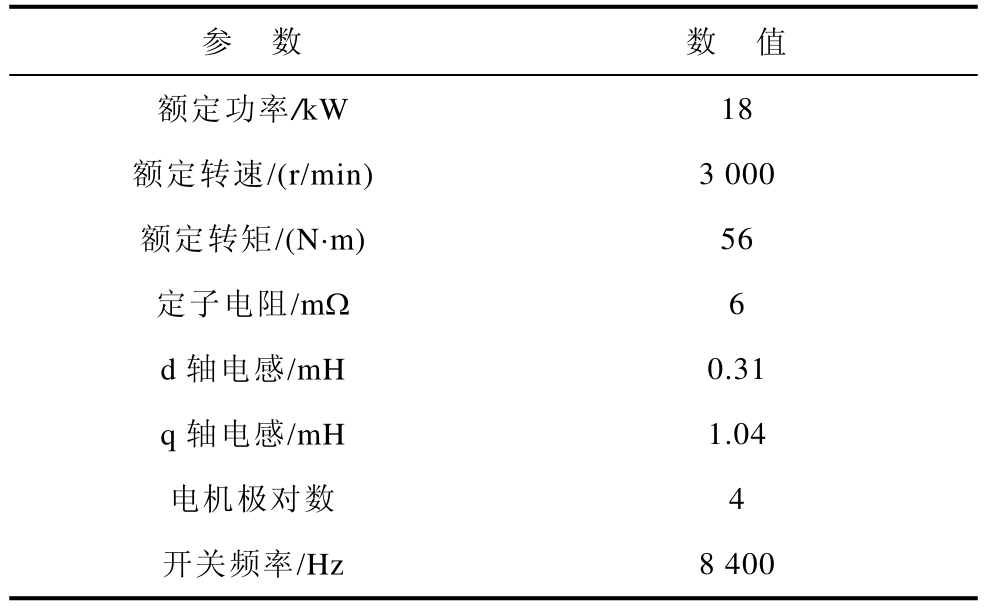
参 数 数 值额定功率/kW 18额定转速/(r/min) 3 000额定转矩/(N·m) 56定子电阻/mΩ 6 d轴电感/mH 0.31 q轴电感/mH 1.04电机极对数 4开关频率/Hz 8 400
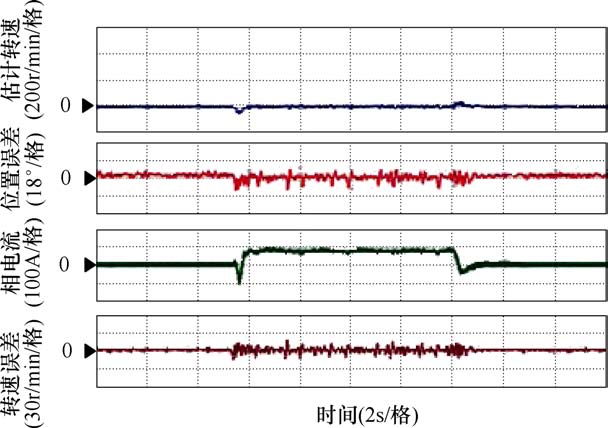
图10 零速突加突减额定负载
Fig.10 Dynamic response under step increase and decrease of the rated load at 0r/min
图10 为IPMSM运行于无传感器控制模式下,转速为0r/min时,突加减额定负载的扰动响应过程中估计转速、位置误差、相电流、转速误差波形。显然,即便在大小为额定负载的剧烈扰动下,所设计的无位置传感器控制系统依然保持着较好的控制精度,转速误差不超过 16r/min,位置误差控制在10°以内。
图11为电机发生正、反转及零速运行的实验结果,整个过程中没有出现明显的速度波动,位置误差控制在10°以内。
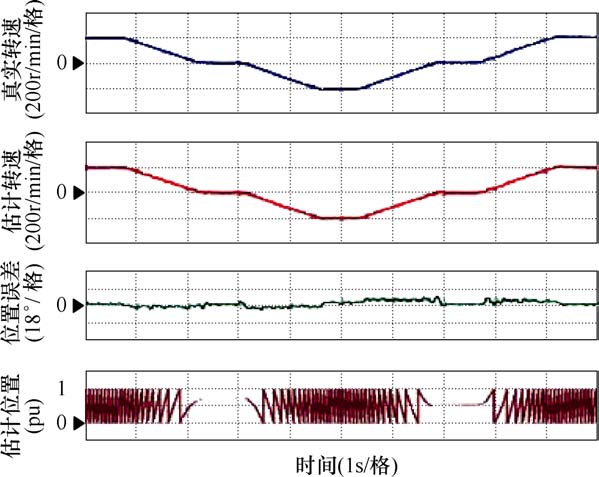
图11 正转-零速-反转
Fig.11 Process of forward-standstill -reverse
为了验证本文所提解调算法的位置观测精度以及相比静止坐标系解调算法的优势,以下将给出一系列对比实验结果。这里,为了保证相同的工况,对比实验均是两个算法独立于控制系统所得到的结果,此时矢量控制算法所用转子位置为实测位置。
图12为200r/min突加减额定负载两种算法的对比实验。基于静止坐标系的补偿算法突加减额定负载位置误差波动幅度大,整个过程位置误差波动范围[1.6°, 21.0°]。而基于旋转坐标系的解调算法突加减额定负载过程中位置误差波动范围为[-7.0°,6.6°],位置误差波动范围同比下降29.9%。显然,旋转坐标系解调算法提升了旋转高频注入法对负载扰动的鲁棒性。
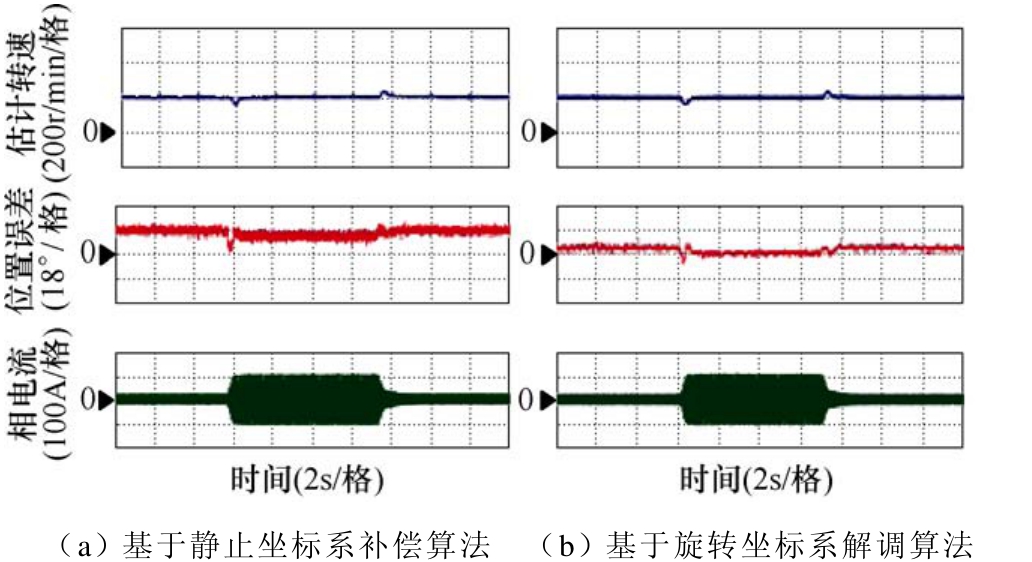
图12 200r/min突加突减额定负载对比
Fig.12 Comparison of dynamic response under step increase and decrease of the rated load at 200r/min
图 13为 0r/min-400r/min-0r/min升降速过程中两种解调算法的对比实验结果。不难看出,静止坐标系补偿算法的位置误差随转速的变化呈现明显的变化,位置误差最大可达 35°;而旋转坐标系解调算法位置误差没有出现明显的变化,位置误差控制在8°以内,最大位置误差同比下降77.1%,具有较好的速度适应性。

图13 0r/min-400r/min-0r/min对比实验
Fig.13 Comparison of the operation at 0r/min-400r/min-0r/min
为了进一步验证数字控制延时和滤波器延时对传统旋转高频注入法、静止坐标系补偿算法和同步旋转坐标系解调算法的影响,图14给出了不同注入频率和不同转速下三种方案的位置观测误差,并在图15中对误差分布情况进行了描述。图14和图15结果表明,传统的旋转高频注入法受控制延时和滤波器延时的影响最大;静止坐标系补偿算法在零速时能够较为准确地对延时误差进行补偿,但是当电机运转,静止坐标系下正序、负序高频电流频率不同,限制了补偿精度;本文所提出的算法在不同的注入频率、不同转速情况下均取得良好的位置辩识效果,有效消除了控制延时和滤波器延时对位置辩识产生的影响。
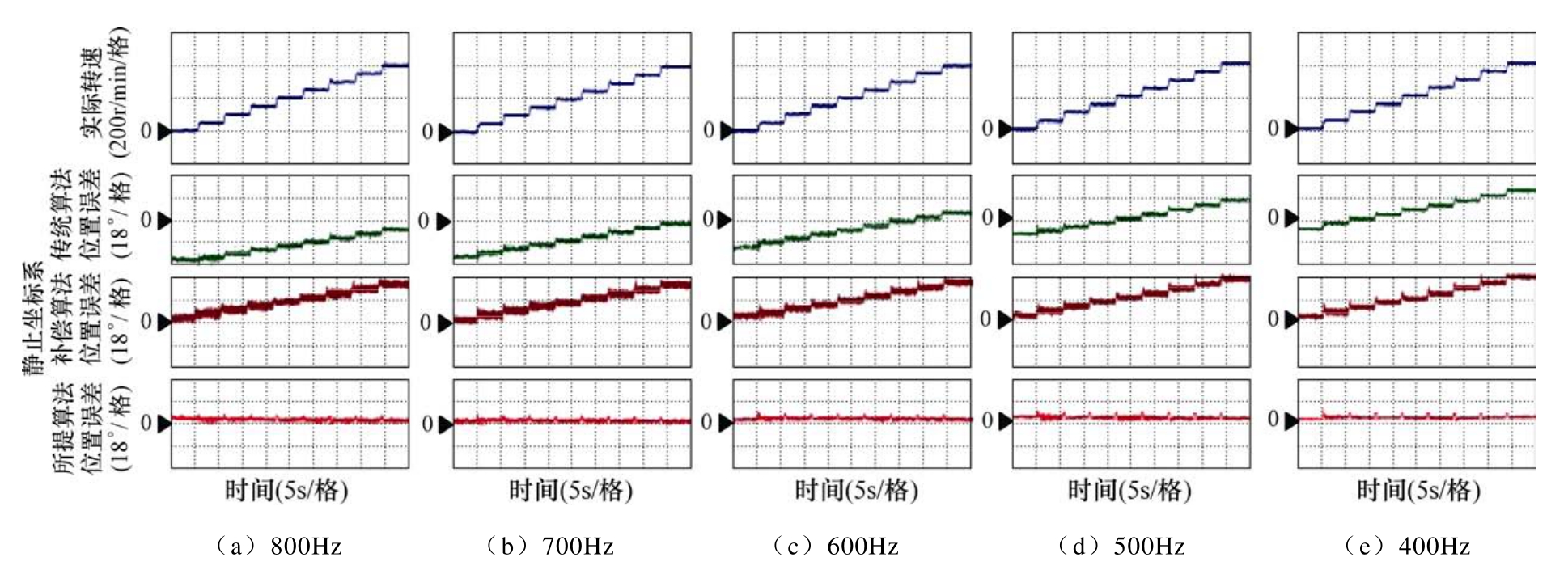
图14 不同注入频率和不同转速对比
Fig.14 Comparison of different injection frequency and different speed

图15 不同注入频率不同转速下位置误差分布
Fig.15 Position error distribution at different injection frequency and different speed
4 结论
本文对旋转高频注入法的解调算法进行研究,针对观测精度受到数字控制延时和解调滤波延时影响的问题,提出了一种基于旋转坐标系的高频电流信号提取和位置解调方案。本方案同样在静止坐标系下进行高频电压信号的注入,但高频信号提取和位置解调过程却以估算的同步旋转坐标系为参考,通过正、负序高频电流相位关联信息进行叉乘运算,在获取位置信息的同时实现了解调延时和控制延时的自动校准,提升了旋转高频注入法的位置解调精度。18kW IPMSM的实验结果验证了本方案的有效性和相比静止坐标系下解调方案的优势。
[1] Li Haoyuan, Zhang Xing, Yang Shuying, et al.Analysis and design of IPMSM drive system based on visualization technique in discrete time domain[C]//IEEE Energy Conversion Congress and Exposition,Cincinnati, USA, 2017: 1940-1946.
[2] 章金晶, 汤宁平. 永磁同步电动机电感参数测量的研究综述[J]. 电气技术, 2018, 19(2): 1-5.Zhang Jinjing, Tang Ningping. The review of inductance parameters of measurement permanent magnet synchronous motor[J]. Electrical Engineering,2018, 19(2): 1-5.
[3] Dutta R, Rahman M F. Design and analysis of an interior permanent magnet (IPM) machine with very wide constant power operation range[J]. IEEE Transactions on Energy Conversion, 2008, 23(1):25-33.
[4] 王高林, 李卓敏, 詹瀚林, 等. 考虑逆变器非线性的内置式永磁同步电机转子位置锁相环观测器[J].电工技术学报, 2014, 29(3): 172-179.Wang Gaolin, Li Zhuomin, Zhan Hanlin, et al. Phaselocked-loop rotor position observer for IPMSM considering inverter nonlinearity[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 172-179.
[5] Song Xinda, Fang Jiancheng, Han Bancheng, et al.Adaptive compensation method for high-speed surface PMSM sensorless drives of EMF-based position estimation error[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1438-1449.
[6] 王要强, 冯玉涛, 秦明, 等. 表贴式永磁同步电机全阶滑模观测与控制策略[J]. 电工技术学报, 2018,33(24): 1-12.Wang Yaoqiang, Feng Yutao, Qin Ming, et al. Fullorder sliding mode observation and control strategy for surface permanent magnet synchronous motor[J].Transactions of China Electrotechnical Society, 2018,33(24): 1-12.
[7] 刘计龙, 肖飞, 麦志勤, 等. IF控制结合滑模观测器的永磁同步电机无位置传感器复合控制策略[J].电工技术学报, 2018, 33(4): 919-929.Liu Jilong, Xiao Fei, Mai Zhiqin, et al. Hybrid position-sensorless control scheme for PMSM based on combination of if control and sliding mode observer[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 919-929.
[8] 田素立, 赵瑞杰, 李朝锋, 等. 永磁同步电机角度软锁相环估算方法研究[J]. 电力系统保护与控制,2017, 45(18): 108-113.Tian Suli, Zhao Ruijie, Li Chaofeng, et al. Research of angle soft phase-locked loop estimation method of permanent magnet synchronous motor[J]. Power System Protection and Control, 2017, 45(18): 108-113.
[9] 黄科元, 周李泽, 周滔滔, 等. 一种增强可靠性的永磁同步电机初始角检测[J]. 电工技术学报, 2015,30(1): 45-51.Huang Keyuan, Zhou Lize, Zhou Taotao, et al. An enhanced reliability method for initial angle detection on surface mounted permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 45-51.
[10] 尹忠刚, 张彦平, 张延庆, 等. 采用免疫高频脉动信号注入的 PMSM 转速辩识方法[J]. 电工技术学报, 2016, 31(增刊2): 243-254.Yin Zhonggang, Zhang Yanping, Zhang Yanqing, et al. High frequency pulsating signal injection for permanent magnet synchronous machines based on immune algorithm[J]. Transactions of China Electrotechnical Society, 2016, 31(S2): 243-254.
[11] 田兵, 安群涛, 孙东阳, 等. 基于磁饱和效应的表贴式永磁同步电机初始位置检测方法[J]. 电工技术学报, 2016, 31(1): 155-164.Tian Bing, An Quntao, Sun Dongyang, et al. Initial position estimation for surface permanent magnet synchronous motors based on magnetic saturation effect[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 155-164.
[12] Liu J M, Zhu Z Q. Novel sensorless control strategy with injection of high-frequency pulsating carrier signal into stationary reference frame[J]. IEEE Transactions on Industry Applications, 2014, 50(4):2574-2583.
[13] Luo Xin, Tang Qipeng, Shen Anwen, et al. PMSM sensorless control by injecting HF pulsating carrier signal into estimate fixed-frequency rotating reference frame[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2294-2303.
[14] Wang Gaolin, Yang Lei, Zhang Guoqiang, et al.Comparative investigation of pseudorandom highfrequency signal injection schemes for sensorless IPMSM drives[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2123-2132.
[15] Liu J M, Zhu Z Q. Sensorless control strategy by square-waveform high-frequency pulsating signal injection into stationary reference frame[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(2): 171-180.
[16] 张国强, 王高林, 徐殿国. 基于无滤波器方波信号注入的永磁同步电机初始位置检测方法[J]. 电工技术学报, 2017, 32(13): 162-168.Zhang Guoqiang, Wang Gaolin, Xu Dianguo.Filterless square-wave injection based initial position detection for permanent magnet synchronous machines[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 162-168.
[17] Liu Jinbo, Nondahl T, Schmidt P, et al. An on-line position error compensation method for sensorless IPM motor drives using high frequency injection[C]//2009 IEEE Energy Conversion Congress and Exposition, San Jose, USA, 2009: 1946-1953.
[18] 李浩源, 张兴, 杨淑英, 等. 基于旋转高频注入的内置式永磁同步电机初始位置检测算法[J]. 电工技术学报, 2018, 33(8): 1723-1731.Li Haoyuan, Zhang Xing, Yang Shuying, et al. A detecting algorithm for initial position of interior permanent magnet synchronous motor based on rotating high frequency injection[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1723-1731.
[19] 刘景林, 鲁家栋. 基于相电流正负序分量相角差的高精度内置式永磁同步电机转子初始位置检测方案[J]. 电工技术学报, 2016, 31(23): 63-69.Liu Jinglin, Lu Jiadong. High-precision estimation method of initial rotor position for IPMSM based on phase difference of positive an negative sequence current component[J]. Transactions of China Electrotechnical Society, 2016, 31(23): 63-69.
[20] Kim S I, Im J H, Song E Y, et al. A new rotor position estimation method of IPMSM using all-pass filter on high-frequency rotating voltage signal injection[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6499-6509.
[21] 杨健, 杨淑英, 李浩源, 等. 基于旋转高频电压注入的永磁同步电机转子初始位置辩识方法[J]. 电工技术学报, 2018, 33(15): 3547-3555.Yang Jian, Yang Shuying, Li Haoyuan, et al . Initial rotor position estimation for IPMSM based on high frequency rotating voltage injection[J]. Transactions of China Electrotechhnial Society, 2018, 33(15): 3547-3555.
[22] Holmes D G, Lipo T A, Mcgrath B P, et al.Optimized design of stationary frame three phase AC current regulators[J]. IEEE Transactions on Power Electronics, 2009, 24(11): 2417-2426.