0 引言
交直流输变电设备的绝缘特性是制约其向更高电压等级和更大容量发展的关键因素之一[1-2]。空间电荷积聚是导致绝缘内部局部电场畸变的重要因素,进而影响绝缘材料的老化和击穿过程[3-4]。针对空间电荷积聚的研究,特别依赖于电荷测试技术的发展,目前常用的测试方法包括电声脉冲法(Pulsed Electro-Acoustic, PEA)、压力波法和热方法等[5]。其中,PEA 的测试硬件系统相对简单,且能在临近击穿条件下使用,因而得到了广泛应用[6]。
利用PEA 测试空间电荷时,为提高电极和试样声阻抗的匹配性,通常在试样和高压电极间加入半导电电极[7]。受限于PEA 测试系统和试样本身的特性,往往需要对测试结果中的畸变部分进行后期恢复处理。最早由T. Takada 在假定试样与半导电电极声阻抗相等的条件下,分别对衰减系数和电压-电荷转换系数做了详细推导[8-9]。然而近几年的声阻抗实际测试结果表明,半导电电极和试样的声阻抗必然存在一定差异[10-11]。考虑到PEA 测试信号的微弱性以及被测试样的多样化,认为两者相等可能会导致恢复结果与实际情况存在较大偏差,进而影响对试样内部畸变电场的判断。此外,根据静电场下的泊松方程[12],试样畸变电场的计算不仅需要准确恢复试样内部电荷分布,还需要保证试样与电极界面处的电荷计算准确,同时根据IEC 标准,界面电荷的准确表征也有助于测试系统的校正过程[13]。因此,需要基于上电极与试样的声阻抗差异来改进现有的波形恢复过程,提出适用的界面与空间电荷波形恢复算法。
此外,由于设备绝缘多为不同介质组成的复合绝缘结构,多层介质中空间电荷的测试也受到国内外学者的关注[14-15]。R. Bodega 详细分析了双层介质中不同位置处测试波形的传播过程[16]。进一步,文献[17]推导了双层介质内部测试波形的衰减恢复算法。但这些研究多基于试样与电极声阻抗相等这一假设条件恢复计算空间电荷,且缺乏相应的界面测试波形准确恢复方法。考虑到研究多层介质中空间与界面电荷影响下的畸变电场的必要性,需首先基于电极声阻抗特性确定多层介质中界面与空间电荷的准确恢复算法。
本文基于电声脉冲法测试波形的畸变原理与恢复过程,分析了考虑上电极与试样声阻抗差异时试样内部空间电荷和界面电荷的恢复原理。进一步结合衰减系数和电压-电荷转换系数的推导,提出了单层和双层介质测试波形的改进恢复算法,并通过不同上电极材料下单层介质的电荷恢复结果、与以往恢复算法的对比分析以及双层介质的恢复结果,对改进算法的精确度和适用性进行了验证。
1 单层介质中测试波形的改进恢复算法
应用电声脉冲法测量空间电荷的基本原理为:对被测试样施加连续的电脉冲,使试样内部积聚电荷承受的静电力发生变化,电荷发生位移并产生压力波,压力波经下电极传播后由压电传感器转换为电信号,最后被示波器记录。通过分析处理记录的电信号,可得到沿介质厚度方向的空间电荷分布。
在实际测试过程中,压力波通常会受到测试系统和试样本身的影响而发生畸变,使得测试结果往往与实际电荷分布并不相同。图1 所示为测试过程中通常需要考虑的三个问题,包括过冲、衰减和电荷量的转换等。
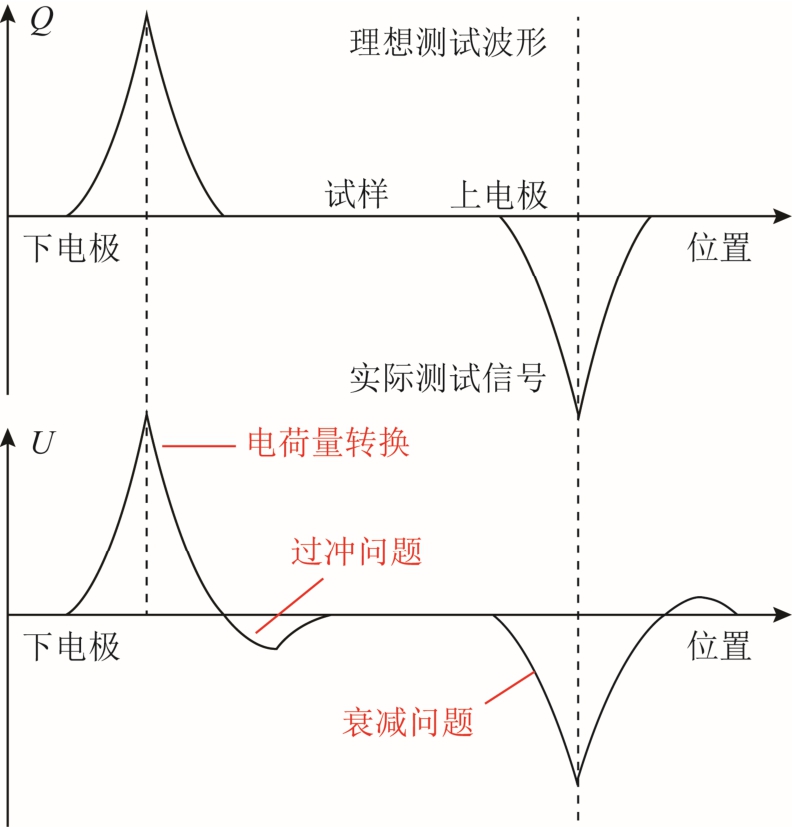
图1 理想波形与实际测试信号的对比
Fig.1 Comparison between the ideal and actual signals
针对上述畸变问题,以往恢复算法往往基于上电极与声阻抗相等这一基本假设条件进行推导,该假设条件对实际恢复过程的影响可借鉴仿真模型进行分析。根据文献[18]中基于PEA 硬件系统搭建的传输线模型,可将测试中压力波的传播过程等效为传输线模型中的电压传播过程,如图2 所示为相应的模型结构。为方便起见,图2 中仅画出了上电极到下电极间的等效模型,且假设测试试样仅在两个界面处有感应电荷积聚。此外,两个匹配电阻仅用于匹配相邻传输线的波阻抗,能够保证传播到该位置处的压力波信号不发生反射,进而便于记录和分析。
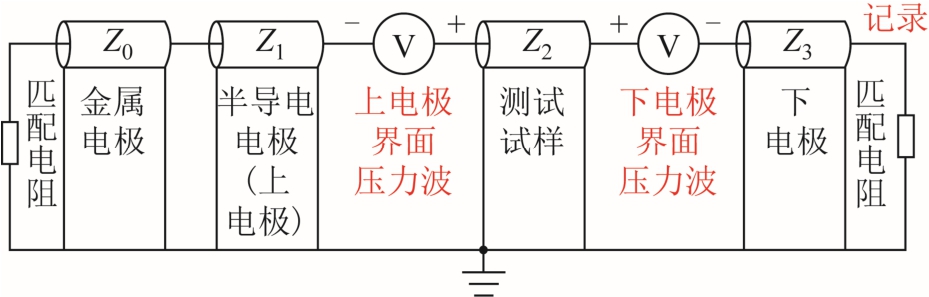
图2 界面处压力波产生和传播的等效传输线模型
Fig.2 Equivalent model for the generation and propagation process of interfacial pressure waves
脉冲激励下两个电极界面的压力波信号用幅值为600V 的指数信号近似模拟,声阻抗相等时的仿真参数借鉴文献[18]中的设定参数,并进一步通过改变上电极与试样声阻抗的比例,记录了不同声阻抗匹配模式下传播到下电极后的压力波分量,仿真结果如图3 所示。图中上下电极界面记录结果的差异,主要是由上电极界面压力波在试样中传播时的衰减畸变和透射过程造成的。
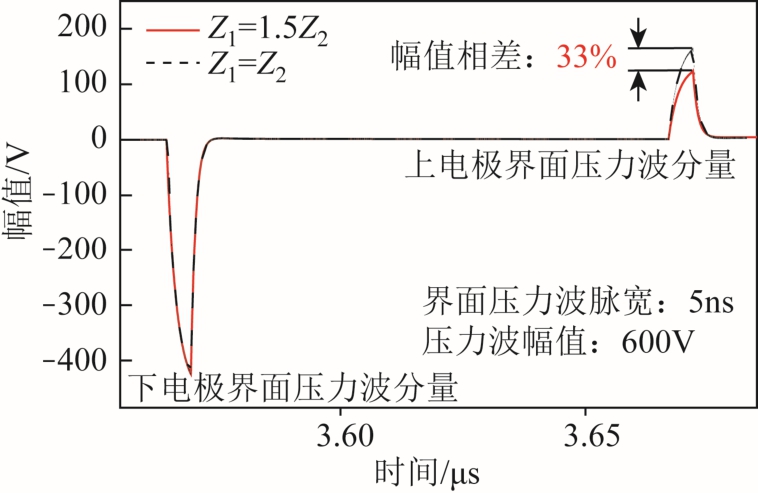
图3 不同声阻抗匹配模式下下电极后的压力波对比
Fig.3 Comparison of pressure waves after the ground electrode for different acoustic impedances
由图3 可见,与声阻抗相等时的仿真结果相比,声阻抗不相等时记录的上电极界面压力波分量在幅值上会有明显变化。由于该记录波形代表输入到传感器中的压力波,实际测试波形必然受到上电极与试样声阻抗参数的影响。同时,文献[10-11]中的测试结果显示上电极与试样声阻抗存在一定的差异,以往恢复算法基于的阻抗相等条件与实际情况并不相符,因而需要进行针对性的改进。
对于测试信号中的过冲问题,通常是由压电传感器电容和放大器输入阻抗形成的滤波电路造成,由于两项参数与压力波的传播过程无关,过冲恢复不受声阻抗参数的影响。
压力波的衰减主要指压力波在有损介质中传播时产生的损耗,通常表现为图1 所示的测试波形脉宽展宽和幅值降低。不同位置处压力波的传播过程如图4 所示。其中,上电极界面处信号的衰减过程与试样内部信号的过程相同,主要由试样的衰减系数决定,系数的求解主要由上、下电极界面处的测试波形决定。由于以往算法中认为上电极和试样的声阻抗相同,经推导得到的衰减系数计算公式中并不会体现压力波传播过程中的声阻抗变化[9]。
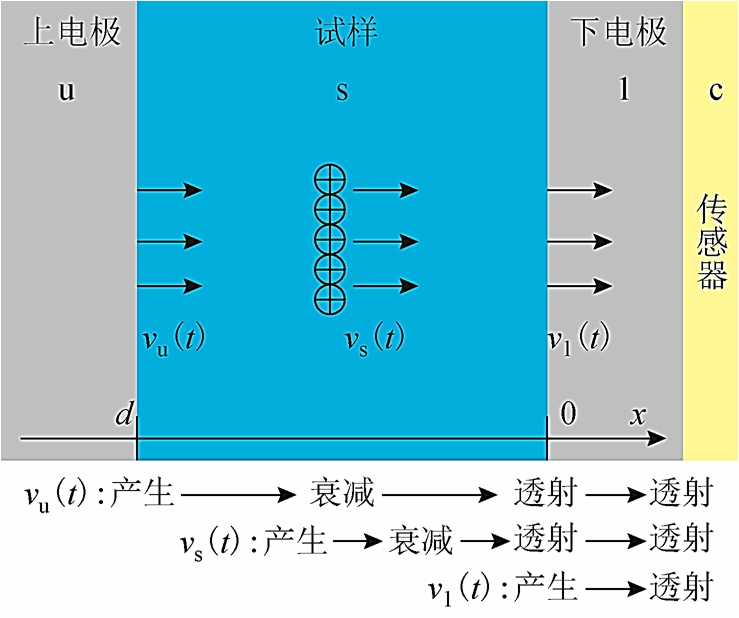
图4 单层试样中不同位置处压力波的传播过程
Fig.4 Propagation process of the pressure waves at different position in a single-layer sample
电荷量的转换是将过冲和衰减恢复后的电压波形转换为实际的电荷分布。在推导电压-电荷转换系数时,需要基于图4 所示的测试信号的产生和传播过程。考虑到电极与试样声阻抗的差异,需要讨论试样不同位置处的电压-电荷转换系数。
由上述分析可知,测试结果中受上电极与试样声阻抗特性影响的恢复计算,主要包括衰减恢复和电荷量的转换两个过程,由此本文重点对这两个恢复过程进行推导。
1.1 考虑声阻抗差异的衰减系数推导
由图2 可知,不同位置处的压力波主要经过了产生、衰减和透射三类过程。当压力波在介质a 和b 的界面处产生或透射时,b 中传播的压力波幅值分别与产生系数Ga-b 和透射系数Ta-b 有关。Ga-b 和Ta-b 分别为[16]
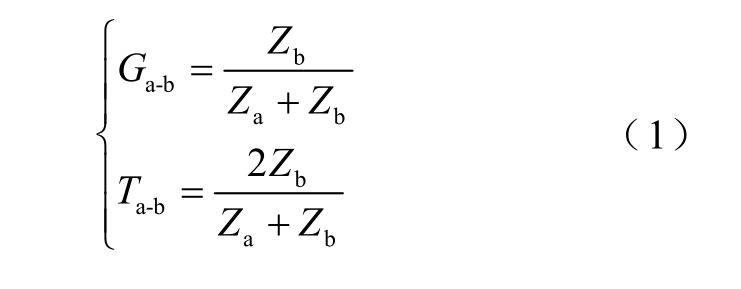
式中,Z 为介质的声阻抗,可由材料密度和声速的乘积进行计算。若压力波在介质内部产生,则产生系数等于0.5。
实际测试时获得的电压信号v(t)由上电极与试样界面处信号vu(t)、试样内部信号vs(t)和下电极与试样界面处信号vl(t)组成,即
基于图2,并结合T. Takada 等在文献[9]中对压力波形成和传播阶段的详细推导过程,上、下电极和试样界面处的测试信号与对应位置处的压力波信号之间的关系可由式(3)表示(由于衰减恢复一般在频域内进行,公式采用频域形式)。
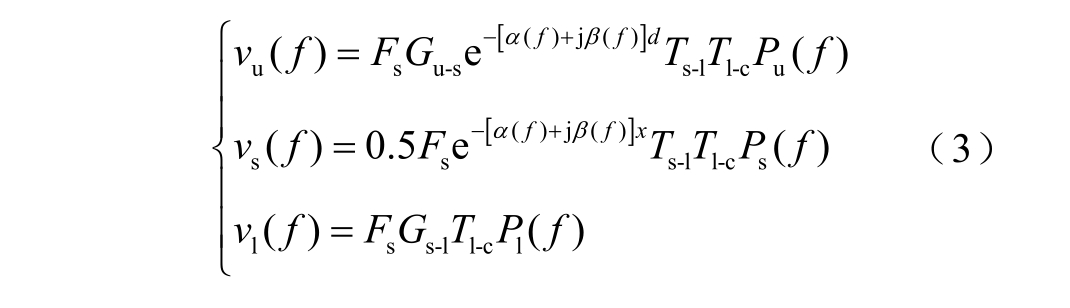
式中,Fs 为系统常数,主要与传感器的电容、放大器的传递函数及压电传感器的转换系数等参数有关,即由系统本身特性所决定;α(f )和β(f )分别为被测试样的衰减系数和色散系数,β(f )=2πf/u(f ),u(f )为压力波中不同频率分量的传播速度;d 为试样厚度;Pu(f)、Ps(f)和Pl(f)分别为上电极界面、试样内部和下电极界面处的电荷振动产生的初始压力波信号。
由于在恒定温度下压力波中各频率分量的传播速度相同[19],通常只需要对试样的衰减系数进行求解。在低电场条件下,由静电感应原理,上、下电极与试样界面处的面感应电荷量相等,此时在电脉冲作用下两位置处的压力波幅值和脉宽相同,即Pu(f)=Pl(f)。但实际测试中,上电极和试样界面处产生的信号会在经过整个试样过程中发生衰减,而下电极处的界面波形在传播过程中不经过试样,因此不受试样衰减系数的影响。据此,结合式(3)中上、下电极处的信号结果进行推导,可得单层试样内的衰减系数为

当上电极采用半导电电极时,若认为电极和试样的声阻抗相等,即2Gu-s=1,此时得到的衰减系数公式和以往的计算公式相同[20]。但考虑到电极和试样声阻抗存在差异,界面处的产生系数不能忽略。
1.2 试样内不同位置处的电压-电荷转换系数
由于脉冲电场的持续时间相对于压力波的传播时间非常短,可以认为脉冲电场是场强幅值为ep 的冲激函数,此时在脉冲电场的作用时间ΔT 内,各位置处的测试信号与对应的电荷密度之间的关系为[9]
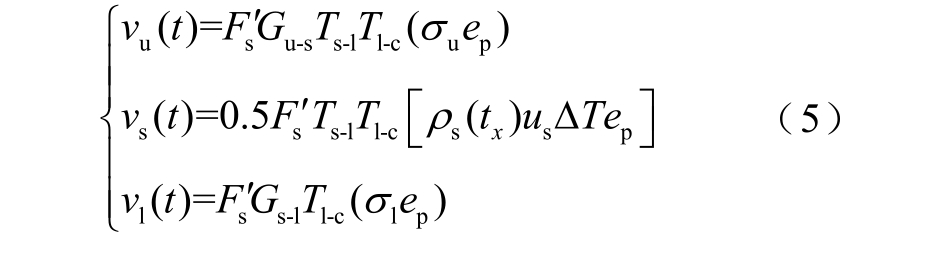
式中, sF′为Fs 和电荷量与压力波的转换系数的乘积,仍是一个系统常数,由测试系统的硬件决定;σu 和σl 分别为上、下电极界面处的面感应电荷密度;ρs 为试样内的体电荷密度;us 为试样内的压力波传播速度。
理想情况下,测试得到的界面处感应面电荷应为一个幅值为σ 的脉冲函数。然而实际测试中,受限于测试系统的分辨率等因素,实际得到的面电荷分布往往会以具有一定脉冲宽度ΔT 的体电荷形式表现出来,如图1 中的测试波形所示。对脉宽为ΔT的下电极处的信号进行积分,可以得到系统常数 sF′的计算公式。进一步,将测试的面电荷分布近似看作一个具有ΔT 宽度的方波[13],理想面电荷密度和对应测试信号中的体电荷密度之间的关系为
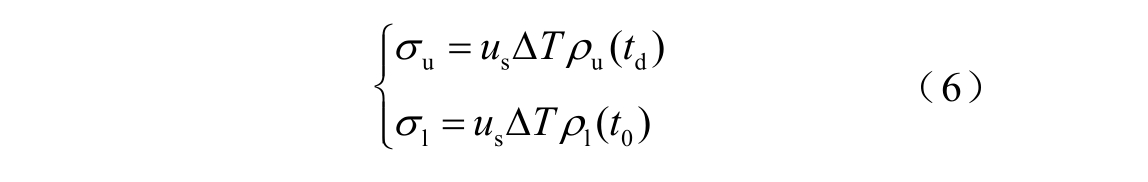
本文定义Ku、Ks、Kl 分别为上电极界面、试样和下电极界面处的电压-电荷转换系数,即
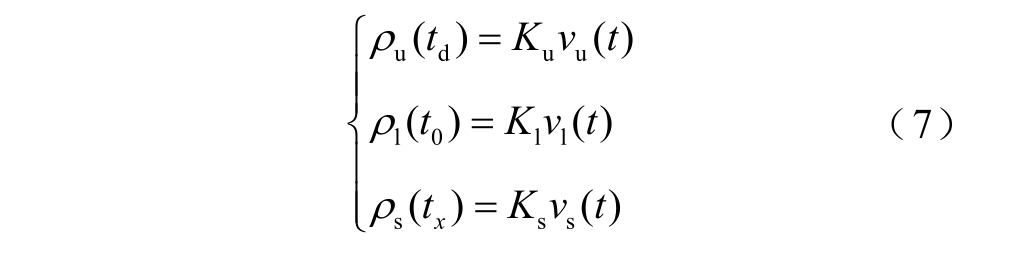
将式(6)和式(7)代入到式(5),并根据产生系数和透射系数的转换关系,可以得到
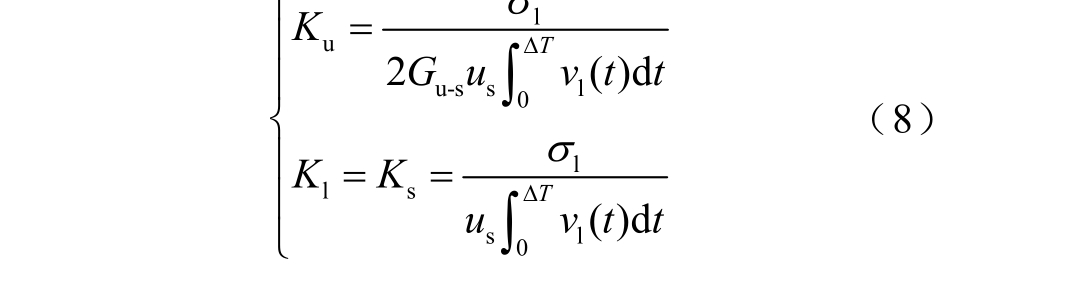
其中,在直流极化电压Udc 下,电极与试样界面处的感应面电荷密度为
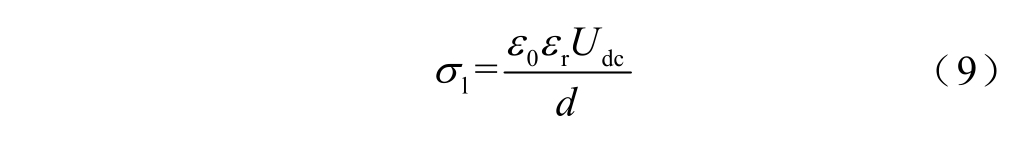
式中,εr 为试样的介电常数。
由式(8)可知,通过定义界面理想面电荷密度与实际测试的体电荷密度间的关系式,电极声阻抗这一影响因素纳入到了电压-电荷转换系数的计算公式中。另外,当试样和电极的声阻抗相等时,各位置处的电压-电荷转换系数相等,并且与以往的计算公式相同[21]。但实际由于声阻抗的差异性,上电极界面处的转换系数会有所变化。
综上所述,当考虑上电极与试样的声阻抗差异时,需要对衰减系数和电压-电荷转换系数进行修正。由于改进算法仅对两个参量的计算公式进行修正,在恢复流程方面与以往恢复算法没有区别,在此不再赘述。恢复流程中的过冲畸变恢复可参阅文献[19,22],衰减畸变恢复可借鉴文献[23]中的恢复过程。
此外,改进算法与以往算法的适用范围相同,主要适用于直流条件和不存在温度梯度的极化情况。当所加极化电压的波形、尺度和温度等因素影响介质密度和声速时,则会影响介质的声阻抗特性,此时需要考虑相关复杂测试条件对介质衰减恢复与电荷量校正过程的影响。另外,上述改进恢复算法也可推广应用于双层/多层介质中测试波形的改进算法推导过程中,详见附录中的说明。
2 改进恢复算法的验证与应用
2.1 不同电极材料下改进恢复算法的验证
本文验证算法准确度的基本原理为:采用两种声阻抗差异较大的半导电上电极对同一个试样进行测试,因此经恢复算法处理后的不同电极下的试样电荷分布结果和电荷总量应该基本相同。据此设定的测试流程为:在20kV/mm 平均电场强度下对聚酰亚胺(Polymide, PI)试样加压4h 后进行20min 的短路,然后在低于10kV/mm 的参考低电场下,先采用半导电乙丙橡胶电极对深陷阱电荷进行测试,测试完成后立刻改用半导电硅电极进行测试。由于电极更换时间很短,在此过程中试样内部电荷不会发生较大的变化。
测试所用电极和试样的特性见表1,其中被测PI 试样厚度为250μm。所用PEA 硬件系统中,脉冲源脉冲宽度为5ns,最大输出幅值为600V。压电传感器选用厚度为10μm 的聚偏氟乙烯(Polyvinylidene Fluoride, PVDF)薄膜,放大器的频带宽度为0.001~500MHz。测试过程中,每次测试1 000 组用于平均的数据来提高测试结果的信噪比。此外,为了避免频域内较小的高频分量导致恢复后波形出现的振荡,本文将恢复信号的频率分量设定在100MHz以内[19]。
表1 不同上电极和被测试样的特性
Tab.1 Characteristics of different electrodes and samples
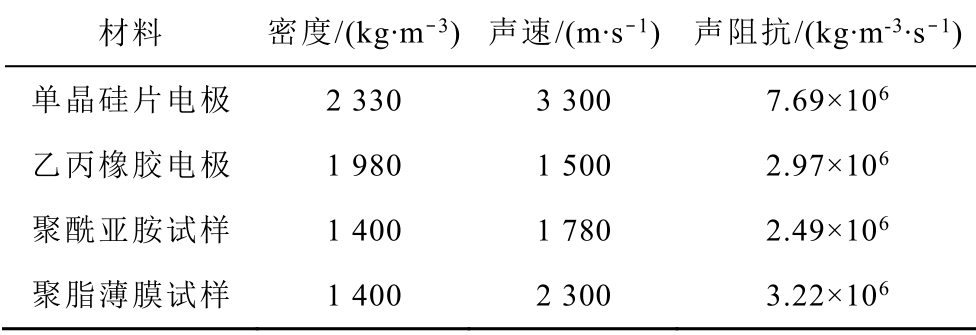
材料 密度/(kg·m-3) 声速/(m·s-1) 声阻抗/(kg·m-3·s-1)单晶硅片电极 2 330 3 300 7.69×106 乙丙橡胶电极 1 980 1 500 2.97×106 聚酰亚胺试样 1 400 1 780 2.49×106 聚脂薄膜试样 1 400 2 300 3.22×106
不同半导电电极下的参考波形和实测波形的测试结果如图5 所示。图5 可知,两种电极下测试结果的差异性主要体现在上电极与试样界面处的波形上。两组参考波形和测试波形的波峰、脉宽都有一定的差异,说明不同半导电电极的使用会影响上电极界面处的测试波形,这与文献[24]中提到的半导电电极可能会改变界面电荷分布特性的观点相同。 测试所用上电极的声阻抗越大,上电极界面处波形的幅值会越低,这主要是因为较高的电极声阻抗会导致低的信号产生系数。但试样内和下电极界面处的波形基本不受影响。

图5 PI 试样在参考电场和实测电场下的测试波形
Fig.5 Measured waveforms of the PI samples under the reference and measured electric fields
图6 a 和图6b 分别为采用不同恢复算法时得到的电荷结果。由恢复结果可知,以往算法处理后两种电极下试样内部电荷出现较大的差异,尤其是接近上电极位置处的衰减距离更长的空间电荷差异明显,而经改进算法处理后的两种实测波形的恢复结果基本相同。同时,以往算法下两种电极测试结果的相对偏差达到了 48.31%,而改进算法下偏差仅为1.65%。结合前述提到的恢复算法处理后不同电极下同一试样的电荷测试结果和电荷总量应该基本相同这一验证原理,上述恢复结果表明本文改进的恢复算法具有更高的准确度。此外,考虑到也有研究指出半导电电极可能会影响电荷向试样内的注入过程,进而导致试样电荷积聚结果与实际环境下的积聚结果不同[25],本文改进的恢复算法可以推广应用到考虑绝缘实际运行条件的金属电极下的电荷测试中。
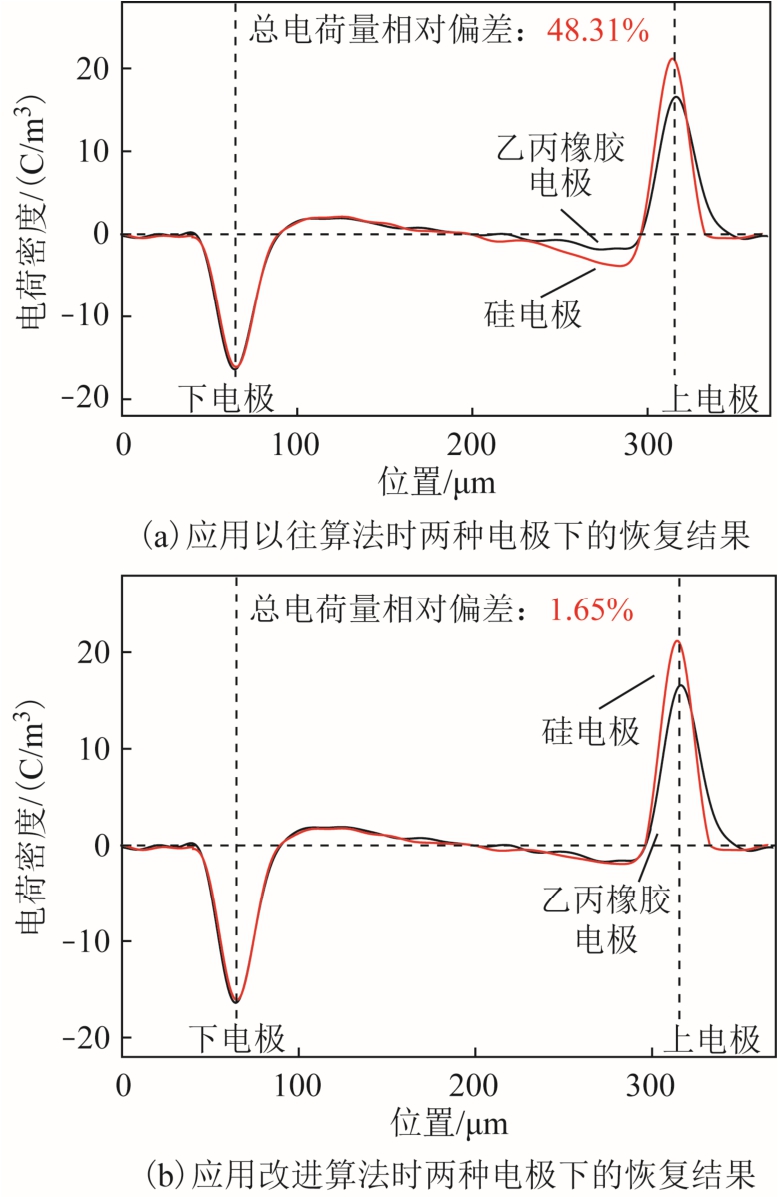
图6 不同电极下应用不同算法时的恢复波形
Fig.6 Recovery waveforms using different recovery algorithms under the two electrodes
波形恢复结果中,临近两侧电极的位置都有异极性电荷的积聚,这主要是试样的内部杂质在高场条件下发生电离形成的,并且大量电荷也被试样内部的深陷阱所捕获。此外,乙丙橡胶电极下的上电极界面恢复结果小于单晶硅片下的恢复结果,说明不同半导电电极对试样的界面感应电荷确实存在不可忽略的影响。
2.2 改进恢复算法与以往恢复算法的对比
为了研究半导电电极与试样声阻抗差异对恢复结果的影响,采用单晶硅电极测试了在外施电场26 kV/mm 下极化4h 后PI 试样内部的空间电荷分布,原始测试波形如图7a 所示。
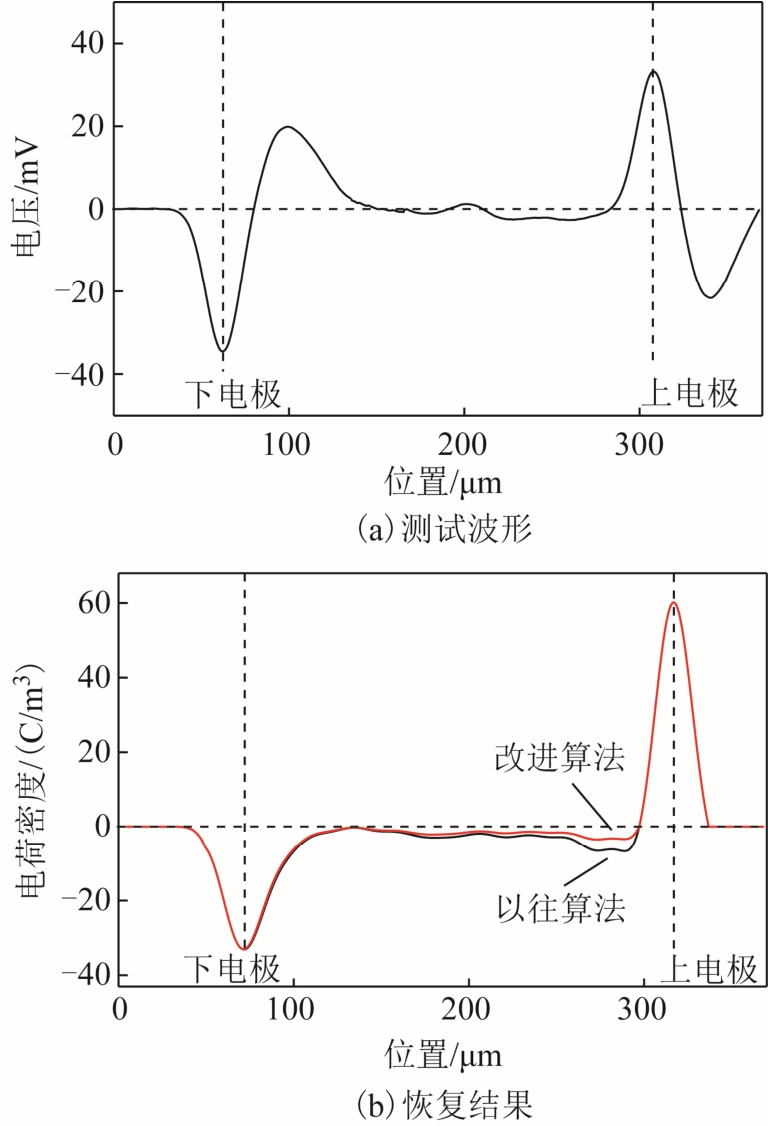
图7 不同恢复算法下单层试样的测试波形和恢复结果
Fig.7 Measured and recovery waveform of a single-layer sample using different recovery algorithms
对原始测试波形采用以往的恢复算法与本文改进的恢复算法进行处理,恢复结果如图7b 所示,应用改进的恢复算法得到的电荷积聚结果小于以往恢复算法求解的结果。这是由于本文所用半导电电极的声阻抗大于试样的声阻抗,因此界面产生系数大于不考虑声阻抗差异时的产生系数。由式(4)可知,此时求解的衰减系数的绝对值相对于以往方法计算的结果偏小,因而采用改进算法恢复的结果较小。
恢复结果中,试样内部和临近上电极附近积聚了一定量的负极性电荷,说明由接地电极注入的电荷和杂质电离形成的电荷不断向上电极迁移,而相对地,由上电极注入的正极性电荷量较少。受试样内部积聚电荷的影响,电极界面处的电荷表现为下电极电荷幅值降低且上电极电荷幅值增加。另外,两种恢复算法下界面处的恢复波形基本相同,说明算法中声阻抗差异的计入并不会对单层介质上电极界面处的波形恢复产生影响。由前面推导的单层介质衰减系数和电压-电荷转换系数计算式(4)和式(8)分析可知,声阻抗对界面波形恢复的影响会在两个恢复过程中相互抵消。但多层介质衰减系数和转换系数的计算过程比较复杂,由声阻抗造成的影响不能忽略。
根据泊松方程,对恢复的电荷结果进行积分,可以得到受试样内部电荷影响的畸变电场分布,如图8 所示。对比两种方法下的恢复结果可知,采用以往方法得到的结果会过高估计试样内部的电场畸变程度。同时考虑到在长时间的高电场极化条件下,试样内部存在大量的积聚电荷,此时以往恢复算法计算的电场结果与实际电场会存在很大的偏差,进而影响对试样击穿过程的准确判断。另外,考虑到暂时没有标准规定半导电电极材料的选择,不同的电极试样搭配可能会导致以往恢复结果与实际结果存在更大的偏差。因此,即使采用半导电电极进行测试,也必须将电极声阻抗和试样声阻抗的差异代入到恢复计算中。
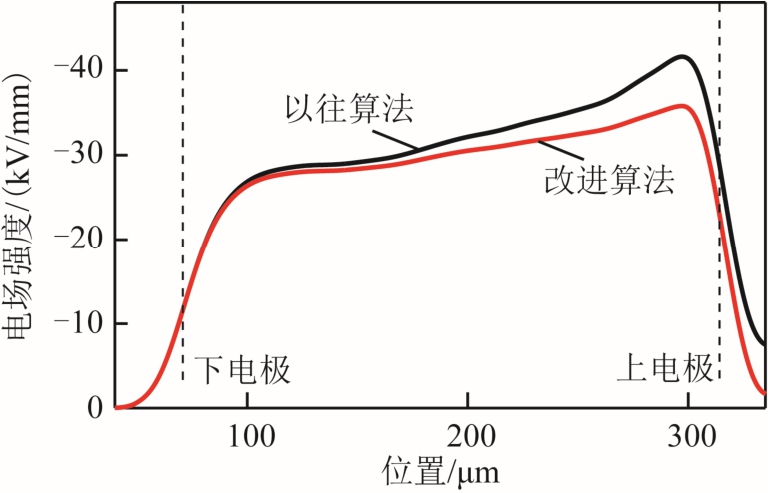
图8 不同恢复算法下畸变电场的计算结果
Fig.8 Calculation results of electric field using different recovery algorithms
进一步,本文定义了空间电荷总量偏差 Q∆ 和最大畸变场强偏差 maxE∆ 来表示改进算法在恢复计算时准确性的提高程度,如式(10)所示。
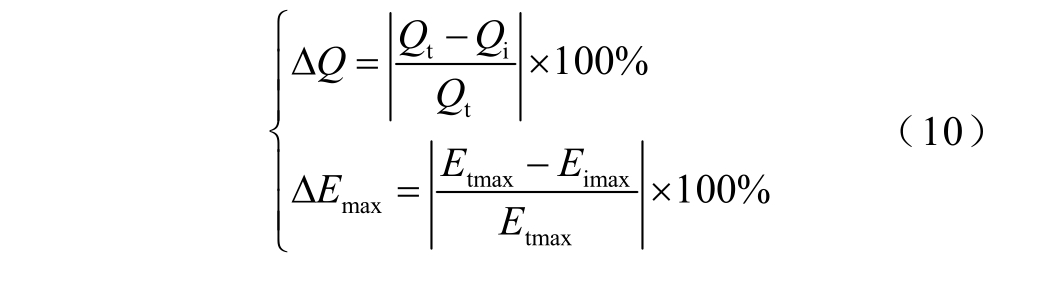
式中,Qt 和Qi 分别为采用以往算法和改进算法时恢复结果中的空间电荷总量(不包含界面电荷);Etmax和Eimax 分别为采用两种算法时场强恢复结果中的最大畸变电场强度。
将上述恢复结果代入式(10)中,计算可得空间电荷总量偏差和畸变场强偏差分别为 33.47%和13.99%,说明两种算法的计算结果存在较大的偏差。同时结合前述改进算法的验证过程,说明改进算法在很大程度上提高了恢复计算过程的准确性。
2.3 多层介质中改进恢复算法的适用性
基于附录描述的双层介质测试波形的恢复算法,在16kV/mm 外施电场下测试并恢复了聚酯薄膜(Polyethylene Terephthalate, PET)和PI 膜组成的双层介质,其中PET 膜厚度为350μm,PI 膜厚度为250μm,两者声阻抗的相关参数见表1。双层介质中间涂覆了一层硅油,用以消除空气间隙和改善两介质间的声学接触。
测试和恢复结果如图9 所示。对比两个结果可知,测试中的过冲和衰减问题都得到了较好的恢复。恢复结果中,两种介质内部和界面处都有负极性电荷的积聚,其中临近下电极的电荷积聚可能主要由杂质电离导致,临近上电极的电荷积聚主要来源于同极性电荷的注入。而两种介质界面处的恢复结果,除了受不连续的介电常数影响外,电极注入和杂质电离形成的负极性电荷也迁移到该位置处。恢复结果的合理性,验证了改进算法在恢复多层介质空间电荷和界面电荷的畸变测试波形时的适用性。

图9 改进恢复算法下双层介质的测试波形和恢复结果
Fig.9 Measured and recovery waveforms of a doublelayer sample using improved recovery algorithm
3 结论
1)基于电声脉冲法等效传输线模型,仿真指出上电极与试样声阻抗的差异会影响传播到压电传感器的压力波分量幅值。结合试样内部不同位置处压力波的传播过程,进一步分析指出该差异会影响恢复计算中衰减恢复和电荷量的转换两个恢复过程。
2)通过分析衰减系数和电压-电荷转换系数的推导过程,提出了考虑上电极声阻抗影响下的单层介质界面/空间电荷的改进恢复算法。不同上电极材料下测试波形的对比恢复结果验证了本文改进算法具有更高的准确度,且适用于不同电极下测试波形的恢复过程。
3)与以往算法的对比结果发现,若认为半导电电极与试样的声阻抗相等,电荷恢复结果和畸变电场计算结果与实际情况可能会存在较大的偏差。
4)基于考虑声阻抗差异的双层介质电压-电荷转换系数的推导,实现了双层介质测试结果的有效恢复,验证了本文改进的恢复算法及其推导过程能够推广应用到多层介质空间电荷与界面电荷的波形恢复中。
附 录
与单层介质相比,多层介质中不同位置处电荷产生的压力波在传播过程中可能会发生多次衰减和透射,因而更为复杂。其中,双层介质中不同位置处压力波的传播过程如附图1 所示。
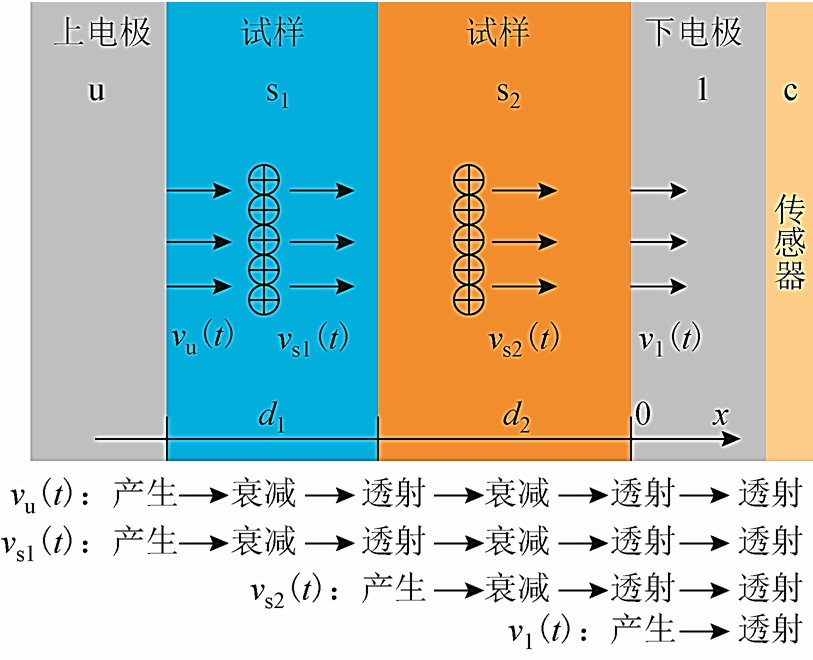
附图1 双层介质中不同位置处压力波的传播过程
App.Fig.1 Propagation process of pressure waves at different position in a double-layer sample
对于双层介质测试波形的衰减恢复过程,文献[17]基于试样内部的静电力特性已对衰减系数作了详细的推导。由于衰减恢复过程多在频域内进行,本文将双层介质中衰减系数的求解转换为频域形式,如式(A1)所示。
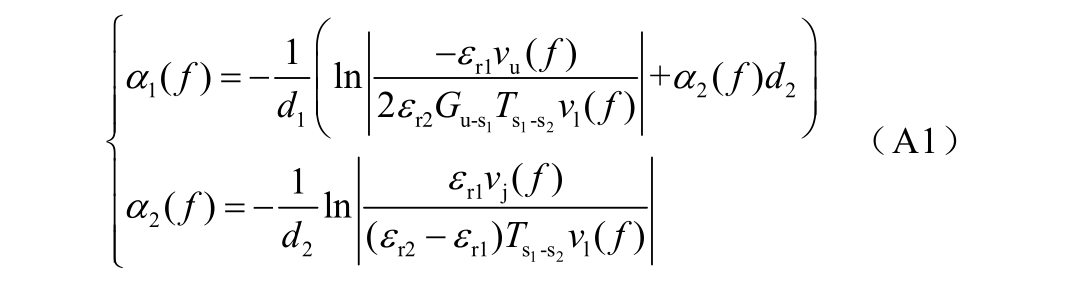
式中,vj(f)为双层介质界面处的测试波形,在低电场条件下主要由相邻介质间不相等的介电常数引起[25]。
进一步,考虑到界面压力波的产生与透射过程和试样内压力波的过程相异,下面将对双层介质中电压-电荷转换系数进行推导。
根据附图1,测试得到的各位置处的压力波信号为
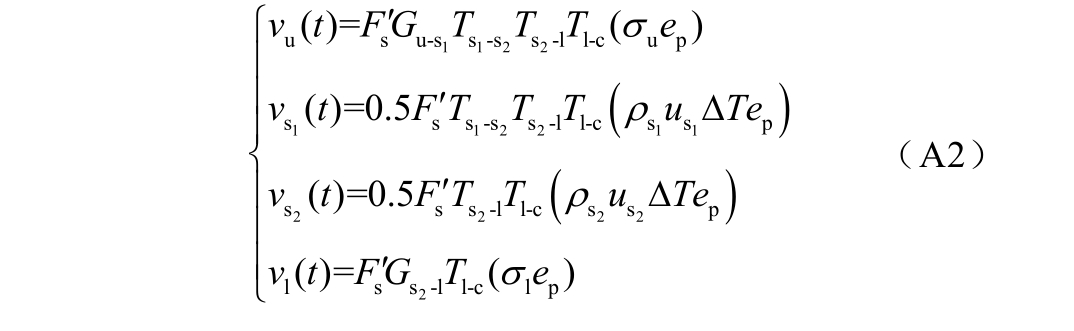
与单层介质中的推导过程相同,首先在∆T 时间内对下电极界面处的信号进行积分,推导得到此时常数 sF′的表示形式,并结合面电荷密度与体电荷密度的转换关系及电压-电荷转换系数的定义,经推导可得双层介质中各位置处的转换系数为
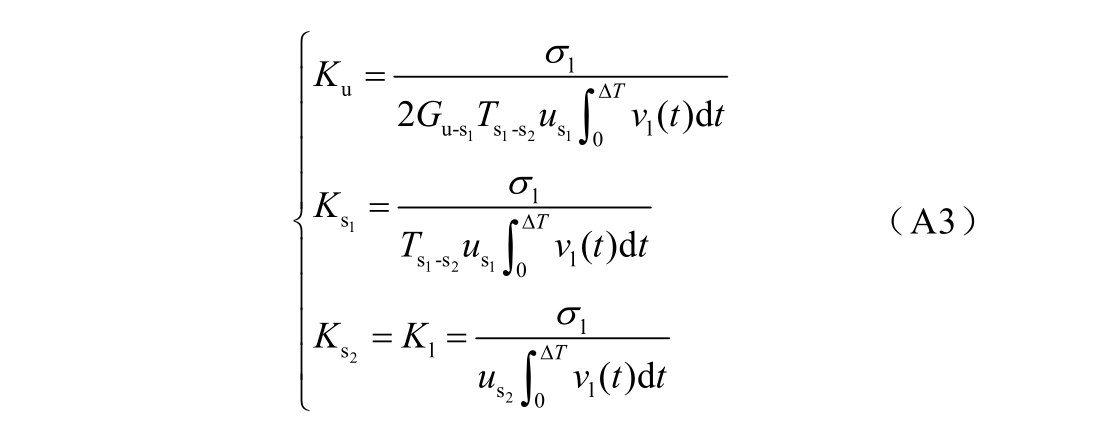
由式(A3)可见,不同位置处电压-电荷转换系数的差异主要由声阻抗导致的各项系数以及各层介质中的不同声速造成。另外,双层介质中下电极与试样界面处的感应电荷密度为
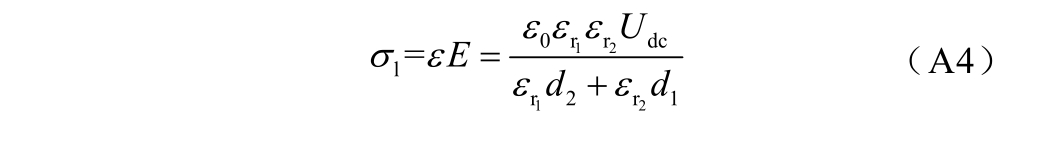
此外,当双层介质的厚度与声速关系满足式(A5)时,试样 2s 中的反射压力波不会叠加在有效测试信号中,此时波形恢复过程不需要考虑反射信号的影响[16]。
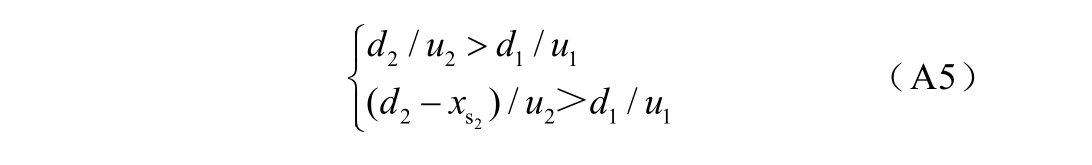
[1] 鲁杨飞, 李庆民, 刘涛, 等. 高频电压下表面电荷分布对沿面放电发展过程的影响[J]. 电工技术学报, 2018, 33(13): 3059-3070. Lu Yangfei, Li Qingmin, Liu Tao, et al. Effect of surface charge on the surface discharge evolution for polyimide under high frequency voltage[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3059-3070.
[2] Tanaka Y. Space charge distribution measurement using PEA method-encounter with unexpected behavior[C]//International Conference on Properties and Applications of Dielectric Materials, Xi’an, China, 2018: 1-10.
[3] 李亚莎, 代亚平, 花旭, 等. 杂质对交联聚乙烯电缆内部电场和空间电荷分布影响[J]. 电工技术学报, 2018, 33(18): 4365-4371. Li Yasha, Dai Yaping, Hua Xu, et al. The Influence of impurities on electric field and space charge distribution in XLPE cable[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4365-4371.
[4] 王威望, 李盛涛, 刘文凤. 聚合物纳米复合电介质的击穿性能[J]. 电工技术学报, 2017, 32(16): 25-36. Wang Weiwang, Li Shengtao, Liu Wenfeng. Dielectric breakdown of polymer nanocomposites[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 25-36.
[5] 周远翔, 王宁华, 王云杉, 等. 固体电介质空间电荷研究进展[J]. 电工技术学报, 2008, 23(9): 16-25. Zhou Yuanxiang, Wang Ninghua, Wang Yunshan, et al. Review of research on space charge in solid dielectrics[J]. Transactions of China Electrotechnical Society, 2008, 23(9): 16-25.
[6] 廖瑞金, 柳海滨, 柏舸, 等. 纳米SiO2/芳纶绝缘纸复合材料的空间电荷特性和介电性能[J]. 电工技术学报, 2016, 31(12): 40-48. Liao Ruijin, Liu Haibin, Bai Ge, et al. Space charge characteristics and dielectric properties of nano-SiO2/aramid paper composite[J]. Transactions of China Electrotechnical Society, 2016, 31(12): 40-48.
[7] Fukunaga K. Progress and prospects in PEA space charge measurement techniques[J]. IEEE Electrical Insulation Magazine, 2008, 24(3): 26-37.
[8] Li Ying, Aihara M, Murata K, et al. Space charge measurement in thick dielectric materials by pulsed electroacoustic method[J]. Review of Scientific Instruments, 1995, 66(7): 3909-3916.
[9] Li Ying, Yasuda M, Takada T. Pulsed electroacoustic method for measurement of charge accumulation in solid dielectrics[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1994, 1(2): 188-195.
[10] Fukuma M, Funo R, Murakami Y, et al. Measurement of acoustic property for signal recovery in PEA method[C]//International Conference on Electrical Insulating Materials, Kyoto, Japan, 2011: 69-72.
[11] Wadamori M, Fukuma M, Maeno T, et al. Proposal of numerical analysis model of acoustic wave propagation and generation on PEA method[C]// International Conference on Properties and Applications of Dielectric Materials, Nagoya, Japan, 2003: 863-866.
[12] 张博雅, 张贵新. 直流GIL 中固-气界面电荷特性研究综述Ⅰ: 测量技术及积聚机理[J]. 电工技术学报, 2018, 33(20): 4649-4662. Zhang Boya, Zhang Guixin. Review of charge accumulation characteristics at gas-solid interface in DC GIL, part I: measurement and mechanisms[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4649-4662.
[13] IEC/TS 62758. Calibration of space charge measuring equipment based on the pulsed electro-acoustic (PEA) measurement principle[S]. Geneva, Switzerland: International Electrotechnical Commission, 2012.
[14] 兰莉, 吴建东, 王雅妮, 等. 低密度聚乙烯/乙丙橡胶双层介质的界面空间电荷特性[J]. 中国电机工程学报, 2015, 35(5): 1266-1272. Lan Li, Wu Jiandong, Wang Yani, et al. Space charge property at the interface in low density polyethylene/ethylene propylene rubber double layered insulation[J]. Proceedings of the CSEE, 2015, 35(5): 1266-1272.
[15] 郝建, 黄博, George Chen, 等. 空间电荷在多层结构油纸绝缘混合体系的积聚规律及其对电场分布的影响[J]. 高电压技术, 2017, 43(6): 1973-1979. Hao Jian, Huang Bo, George Chen, et al. Space charge accumulation behavior of multilayer structure oilpaper insulation and its effect on electric field distribution[J]. High Voltage Engineering, 2017, 43(6): 1973-1979.
[16] Bodega R, Morshuis P H F, Smit J J. Space charge measurements on multi-dielectrics by means of the pulsed electroacoustic method[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2006, 13(2): 272-281.
[17] 兰莉, 尹毅, 吴建东. 双层介质的电声脉冲法空间电荷波形恢复[J]. 中国电机工程学报, 2016, 36(2): 570-576. Lan Li, Yin Yi, Wu Jiandong. Recovery of space charge waveform in multi-layer dielectrics by means of the pulsed electro-acoustic method[J]. Proceedings of the CSEE, 2016, 36(2): 570-576.
[18] Chahal J S, Reddy C C. Modeling and simulation of pulsed electroacoustic measurement method[J]. IEEE Systems Journal, 2014, 8(4):1283-1292.
[19] 吴超一, 钟力生, 王霞, 等. 脉冲电声法空间电荷测量波形恢复的数据处理[J]. 中国电机工程学报, 2005, 25(16): 137-140. Wu Chaoyi, Zhong Lisheng, Wang Xia, et al. Data Processing of space charge waveform recovery in PEA method[J]. Proceedings of the CSEE, 2005, 25(16): 137-140.
[20] Murkami Y, Sugiyama T, Kasashima T, et al. Signal recovery of space charge distribution using acoustic property in PEA method[C]//IEEE International Conference on the Properties and Applications of Dielectric Materials, Sydney, Australia, 2015: 344-347.
[21] 周凯, 吴广宁, 刘君, 等. 基于电声脉冲法的空间电荷直接测量仪的研制[J]. 仪器仪表学报, 2008, 29(10): 2110-2115. Zhou Kai, Wu Guangning, Liu Jun, et al. Development of space charge direct measurement device for polymer insulation based on PEA[J]. Chinese Journal of Scientific Instrument, 2008, 29(10): 2110-2115.
[22] 蔡川, 李旭光, 尹毅, 等. 空间电荷测量信号恢复中的频域反卷积技术及实现[J]. 电工技术学报, 2009, 24(10): 165-169. Cai Chuan, Li Xuguang, Yin Yi, et al. Frequency domain deconvolution technique and its implementation in the recovery of the space charge signal[J]. Transactions of China Electrotechnical Society, 2009, 24(10): 165-169.
[23] Vázquez A, Chen G, Davies A E, et al. Space charge measurement using pulsed electroacoustic technique and signal recovery[J]. Journal of the European Ceramic Society, 1999, 19(6): 1219-1222.
[24] Sugiyama T, Uqbah M, Ishikawa A, et al. Development of a space charge measurement method without a semiconducting electrode[C]//International Symposium on Electrical Insulating Materials, Niigata, Japan, 2014: 397-400.
[25] Bodega R, Morshuis P H F, Smit J J. Space charge signal interpretation in a multi-layer dielectric tested by means of the PEA method[C]//IEEE International Conference on Solid Dielectrics, Toulouse, France, 2004: 1-4.