0 引言
随着柔性高压直流输电的快速发展,直流交联聚乙烯(Cross-Linked Polyethylene, XLPE)电缆凭借其优良的绝缘性能得到越来越多的应用。我国多个高压直流输电项目陆续投入运行[1-3],亟需完善在线监测和故障预警系统,以保证供电的可靠性。局部放电(Partial Discharge, PD)作为判断电力设备状态的一项重要指标已被国际电工委员会(IEC)列入检测标准[4],但是直流电缆局部放电的模式识别和故障诊断研究仍有待深入。
早在20 世纪90 年代,国外就有学者研究了直流电压下局部放电的机理。荷兰Delft 理工大学的F. H. Kreuger 和M. J. P. Jeroense 都对直流电压下局部放电中的空间电荷分布和电场分布做了详细的讨论[5-6]。U. Fromm 进一步研究了有关放电重复次数n、放电量q 和相邻两次脉冲时间间隔∆t 的图谱,并将其应用于局部放电类型的分类[7];A. Pirker 提出使用NoDi*模式图来区分不同缺陷的直流电压下的局部放电[8]。国内也有不少学者对直流局部放电的模式识别做了一些研究,主要集中在储能电容器[9]、气体绝缘金属封闭开关设备[10]、变压器油纸绝缘[11]上,但是涉及XLPE 电缆的研究相对较少[12]。文献[13]研究了直流电压下的不同缺陷的XLPE 电缆局部放电的放电量和放电重复率差异。文献[14]研究了电树枝和局部放电的关系,将电树枝的长度与局部放电阶段进行了一一对应。文献[15]采用非下采样轮廓变换和支持向量机。文献[16]采用压缩感知算法对不同缺陷的直流电缆局部放电进行了模式识别。但是现阶段的直流局部放电模式识别中常用偏斜度、互相关系数[12, 17]等统计算子进行特征提取,依赖人工经验,在随机性很强的直流电缆局部放电信号的分类中有一定局限性,而卷积神经网络(Convolutional Neural Network, CNN)则使用不断学习的卷积核,在提取图像固有特征的过程中自我改进,在不需要人为提取统计算子的基础上完成自适应特征提取。目前,该方法已在变压器[18]、交流电缆[19]等模式识别中取得了一定的应用,但是鉴于直流电压下的局部放电缺少相位信息,该方法在直流局部放电中鲜有应用。
为此,本文利用CNN 针对线芯尖端毛刺、绝缘内部气隙、绝缘表面划痕和外半导电层爬电四种典型绝缘缺陷的局部放电信号进行模式识别研究。首先搭建试验系统检测四类缺陷电缆的局部放电信号,再对局部放电信号进行消噪处理,最后对CNN 进行训练并实现缺陷分类。本文着重研究不同的求解器参数、神经网络结构和训练样本数量对CNN 识别效果的影响,并与传统模式识别方法进行了比较。
1 试验系统及过程
1.1 试验系统的搭建
本文采用的试验系统如图1 所示[15]。其中DC输出高压直流,C1 为滤波电容,R 为保护电阻,使用HAEFELY DDX 9121b 直流局部放电检测仪捕捉局部放电信号,检测阻抗、耦合电容 C2 均符合IEC60270 等国际标及仪器规范。信号采集的触发阈值为10pC,HFCT 传感器通频带为3~50MHz,示波器带宽2GHz,采样率设置为1GS/s。
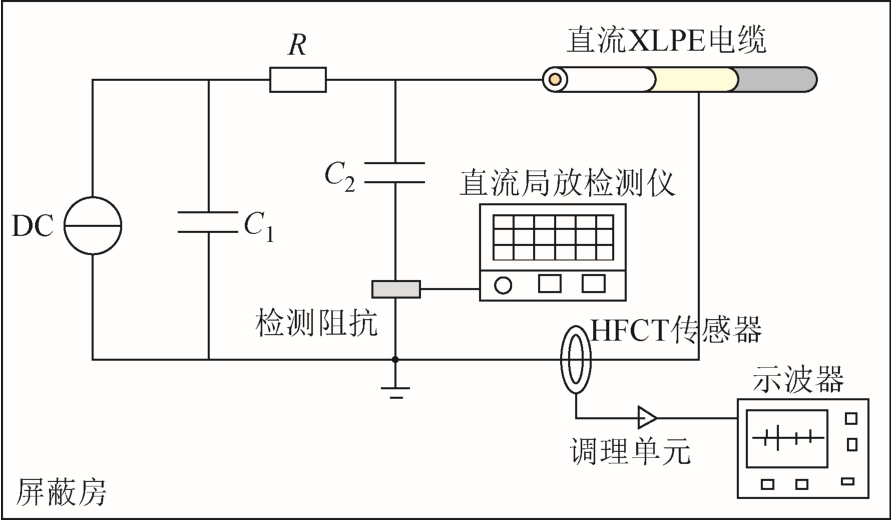
图1 直流电缆局部放电试验系统
Fig.1 Partial discharge test system of DC cable
试验所采用的电缆型号为YJV-120mm2,XLPE层厚度为4.5mm。设计四类典型绝缘缺陷模型如图2 所示,分别为[15]:①电晕模型,扎入1.5mm 长度的金属针,曲率半径为100μm;②气隙模型,在XLPE 表面扎出若干微孔,再用环氧树脂密封;③划痕模型,在XLPE 表面划出宽2mm、长10mm、 深1mm 的划痕;④爬电模型,在一端剥除外半导电层时留有宽3mm、长10mm 的残留。
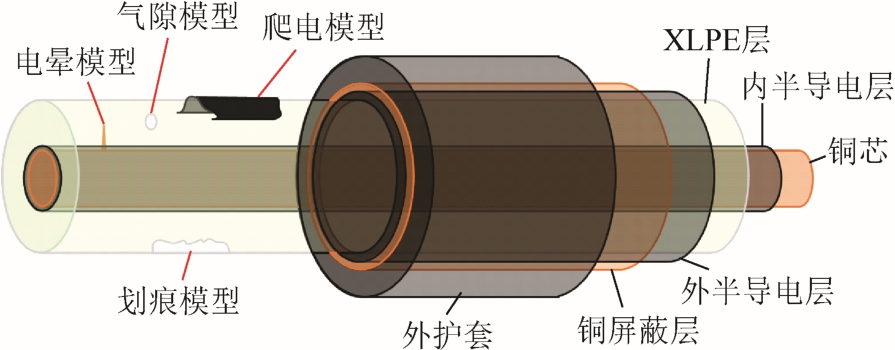
图2 XLPE 电缆的四种缺陷模型
Fig.2 Four defect models of XLPE cable
1.2 局部放电信号的采集与分析
试验统一施加负极性电压,环境温度在(293±5)K 范围内,背景噪声限制在3 mV 以下。分别对四种缺陷类型的电缆采用阶梯升压法[20],直至出现稳定的局部放电信号,并在该电压下采集局部放电信号序列。
各缺陷的稳定起始放电电压为:电晕缺陷为-19.3kV,气隙缺陷为-20.5kV,划痕缺陷为-21.7kV,爬电缺陷为-22.5kV。发现电晕缺陷下起始电压最低,可能原因为尖端处电场畸变严重,局部放电更加容易发生;爬电缺陷起始电压最高,可能原因为外半导电层断口处较为平整,电场畸变较为轻微。
接下来处理各类缺陷的局部放电信号:首先提取连续的300 个脉冲波形的峰峰值q 和相邻两个脉冲之间的时间间隔∆t;再进行消噪处理,直流电压下的局部放电有很强的随机性,可能会出现一些异常的时间间隔∆t,这些偶然数据可能会造成严重的数据偏差,因此本文利用置信区间理论进行消噪处理[16]。
式中,∆ti 为第i 次测量值;mean(∆t)为测量序列的平均值;st(∆t)为标准偏差,满足该条件即断定为偶然数据。接下来对剔除偶然数据后的脉冲序列做出典型特征图谱,图3 所示为不同放电量q 的放电次数、不同脉冲时间间隔∆t 的放电次数以及三维放电密度 图谱H(q, ∆t),用来分析不同缺陷的局部放电特征。


图3 直流电缆四类典型缺陷的特征图谱
Fig.3 Characteristic spectrum of four typical defects of DC cables
由上述特征图谱可以发现四类典型缺陷有一定的区别。电晕缺陷放电量较大且放电间隔较短,推测与局部电场畸变较大有关,强电场发射电子容易产生电树枝,在XLPE 低密度区域引发电子雪崩,促使局部放电的发生[14]。气隙缺陷放电分散性较大,可能是由于气隙与XLPE 交界面各处的局部电场强度不同导致自由电子出现的弛豫时间分散性较大,从而放电时间间隔差距也相对较大。划痕缺陷放电量有较为明显的多个区间,推测是由于划痕各处粗糙度不同,几处曲率半径较小的划痕处易发生局部放电。爬电缺陷放电时间间隔较长,可能是由于缺陷处电场强度较小,一次放电后积累的空间电荷中和时间要长,对应的恢复时间较长,导致相邻两次放电的时间间隔较长。各类缺陷特征图谱的差异也佐证了模式识别的可行性。
2 基于CAFFE 的局部放电模式识别
2.1 CAFFE 方法
卷积神经网络框架(Convolutional Architecture for Fast Feature Embedding, CAFFE)是UC Berkeley的贾扬清提出的一个深度学习框架[21],核心算法是卷积神经网络CNN。该方法的基本思想是利用一个卷积核不断地对二维图像的各个区域进行卷积操作以提取局部的特征,再将各个特征进行组合映射,最终得到一个专属的特征向量,如图4 所示。该方法一经提出就在计算机的图像识别领域引起很大的 轰动,现已成为人脸识别[22-23]中广泛使用的深度学习框架。
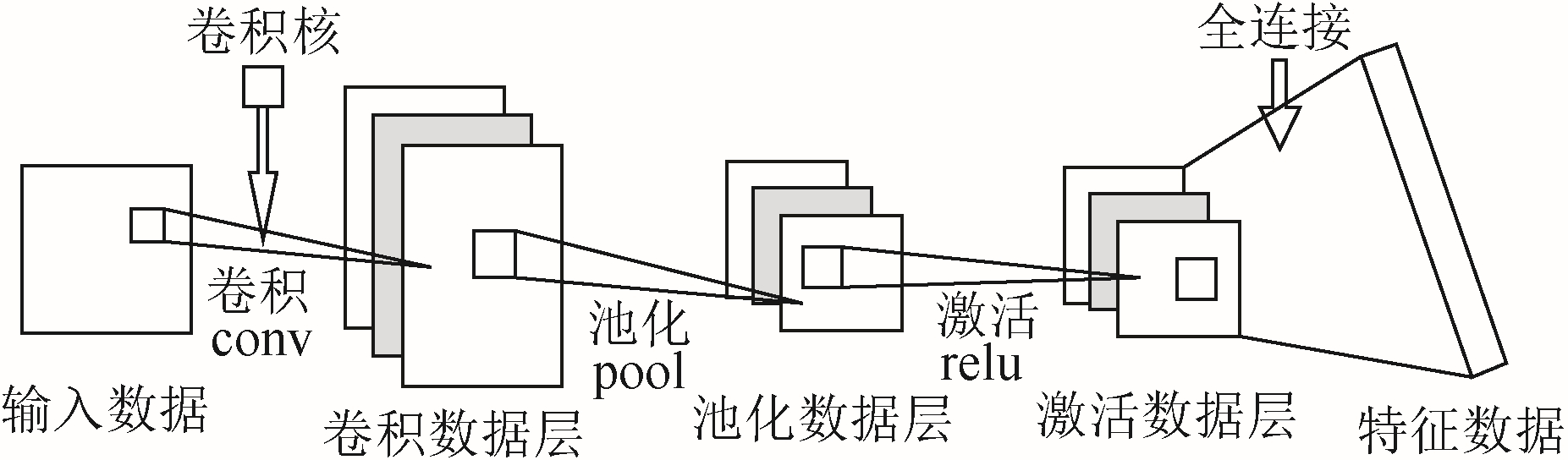
图4 卷积神经网络结构
Fig.4 Network diagram of CNN
CAFFE 包含三个核心模块:Blob、Layer 和Net。其中Blob 是用于存储数据的N 维向量;Layer 是神经网络的核心,定义了例如卷积、池化、损失的层结构;Net 定义了一个以Blob 为输入和输出,由多层Layer 组合的有向无环图的完整网络。图5 为CAFFE 自带的网络结构模型Quick-CIFAR-10 的数字分类器的网络结构图。
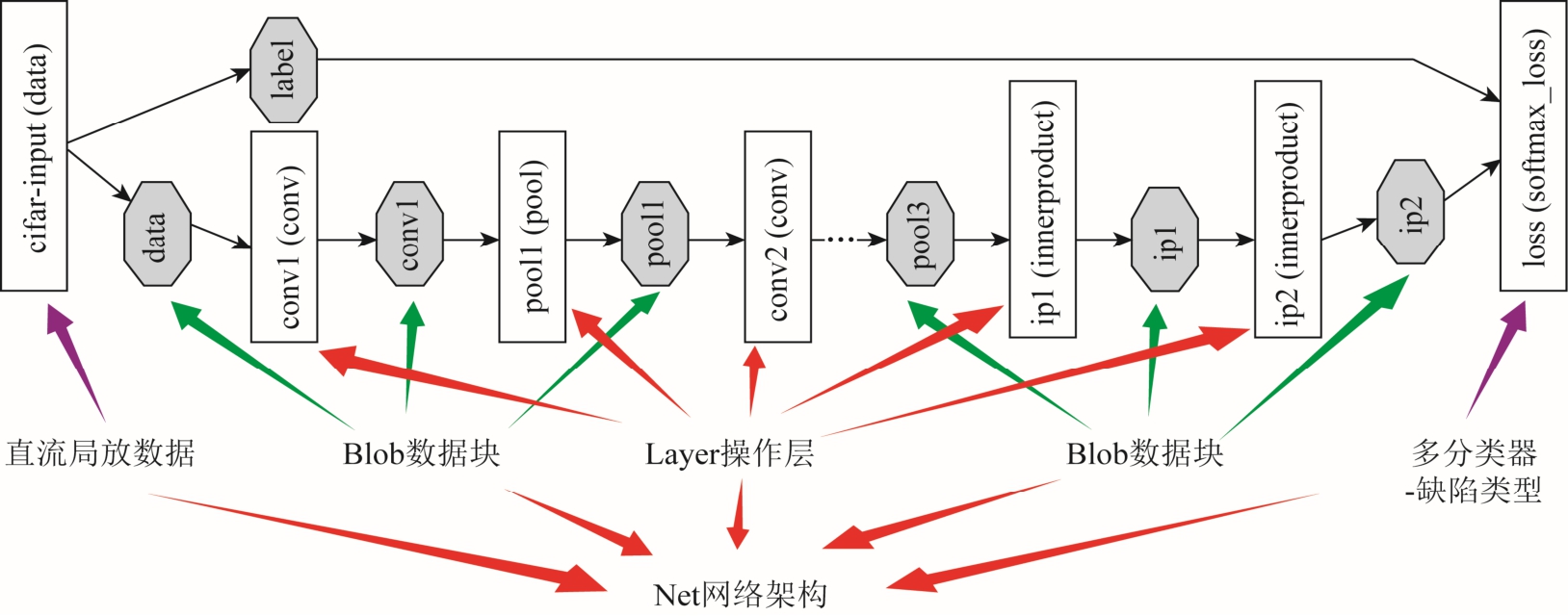
图5 Quick-CIFAR-10 的结构
Fig.5 Network diagram of Quick-CIFAR-10
Layer 作为卷积神经网络的核心,根据其种类的不同拥有不同的功能[21]。例如,卷积层用于提取图像中的特征值,池化层用于数据降维,激活函数用于处理非线性问题,SoftMax 用于计算损失值对模型参数进行更新。
CAFFE 的任务就是将样本数据集通过构建的网络框架,不断训练调整框架中的参数,包括提取特征的卷积核参数,目标是使最终的损失值低于一定值或者正确率高于一定值,最后完成训练的CAFFE 模型就是满足要求的所需多分类问题的解。
2.2 局部放电模式识别步骤
本文利用CAFFE 作为四类绝缘缺陷直流XLPE电缆的局部放电模式识别的核心算法框架。模式识别流程如图6 所示,具体实施步骤如下。
1)数据处理:将1.2 节中试验得到的由波形表示的示波器数据进行消噪滤波处理,将处理后的数据以时间为横轴,脉冲峰峰值为纵轴得到如图3 所示的特征图谱并归一化,以此作为数据样本。
2)构建数据集:CAFFE 的训练需要训练样本和测试样本,本文选择四种缺陷,每种70 个训练样本和40 个测试样本,总共280 个训练样本和160 个测试样本。
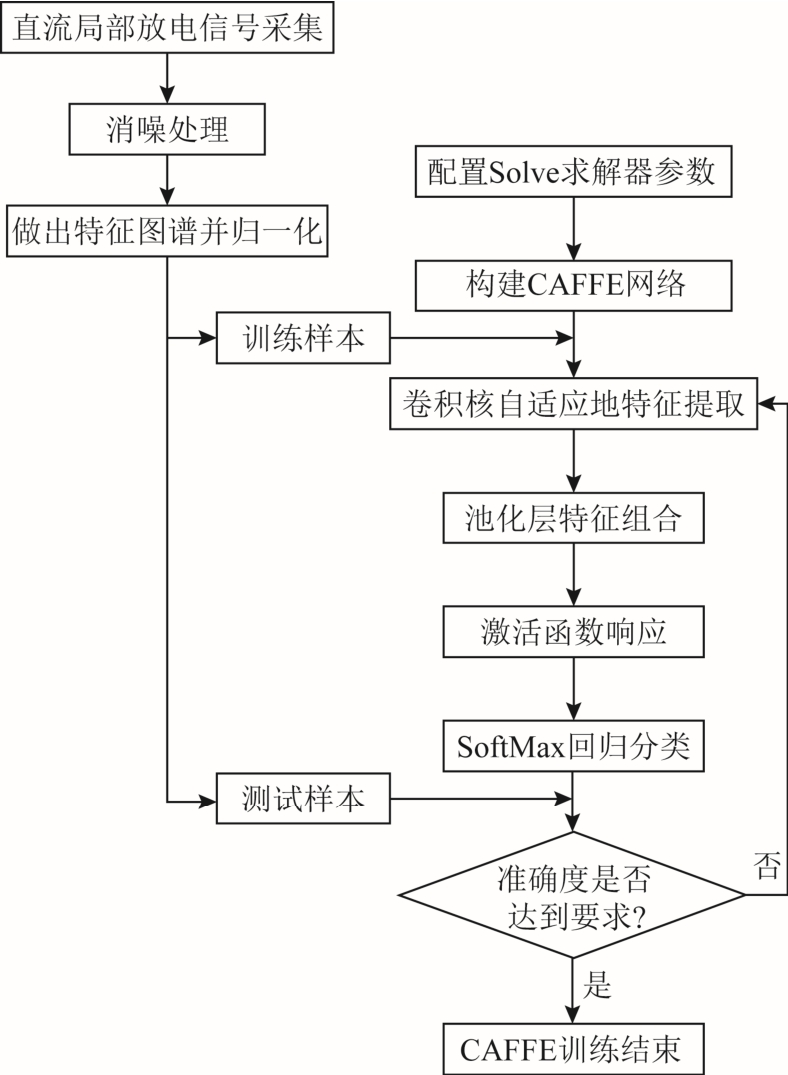
图6 模式识别流程
Fig.6 The flow chart of pattern recognition
3)设置CAFFE 的求解器参数:设置CAFFE 求解器Solver 的参数,例如初始学习率、学习率模式、最大迭代次数等。
4)构建CAFFE 网络结构:构建CAFFE 的网络结构,包括使用的卷积层层数、池化函数、激活函数的选择。
5)训练CAFFE 网络:将训练样本和测试样本作为输入,通过CAFFE 网络进行卷积、池化、激活、回归操作更新网络参数,最后得到训练完成的CAFFE 卷积神经网络。
3 模式识别结果及分析
训练CAFFE 网络最为关键的两步为配置训练用的求解器solver 的参数和构建CAFFE 的网络结构,下面将对两者分别进行分析以寻找最优配置。
3.1 求解器参数的最优配置
Solver 求解器参数的配置主要是学习率和迭代次数的设置。训练过程的学习率又由初始学习率和学习率模式决定。学习率模式分为固定学习率模式和衰减学习率模式,其中衰减学习率模式是学习率随着迭代过程的进行逐渐衰减,衰减的参数由衰减系数γ和衰减单位步长s 确定,公式为li=lbase×γi/s。其中li 代表第i 次的学习率,lbase 表示初始学习率。迭代次数主要由训练样本数量和网络结构复杂度决定,经过测试本文选择6 000 次的迭代次数。
本节采用Quick-CIFAR-10 作为测试学习率参数对训练效果影响的基准网络架构,分别对固定学习率和衰减学习率模式下的初始学习率为1×10-5、5×10-5、1×10-6 和5×10-6 的求解器进行训练,并设置衰减学习率模式下的衰减系数γ=0.9,衰减单位步长s=500,典型训练效果如图7 所示,其中横轴均为迭代次数。四种缺陷下识别正确率及平均识别正确率的结果见表1。为了便于观察,图8 展示了不同学习率配置下的平均识别正确率。其中识别正 确率的计算方法为正确识别缺陷类型样本的个数除以总样本的个数,平均识别正确率为四种缺陷的识别正确率取平均值。


图7 典型学习率配置在迭代过程中的训练效果
Fig.7 Training results of typical learning rate configuration during iterative procedure
表1 不同学习率配置下四种缺陷及平均识别正确率
Tab.1 The accuracy of four defects and average by different learning rate configuration
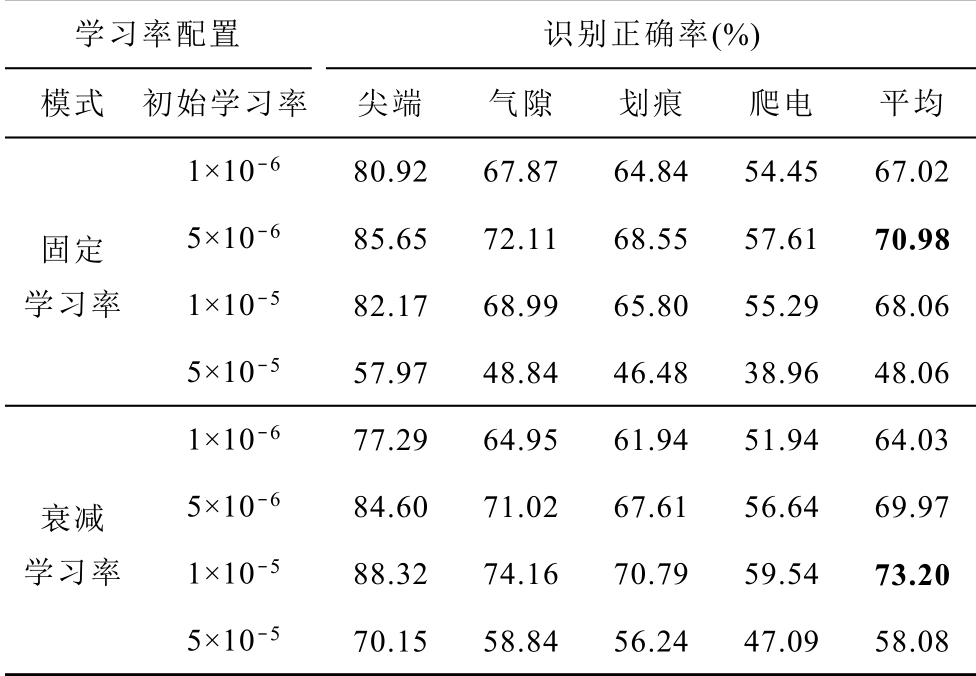
学习率配置 识别正确率(%) 模式 初始学习率 尖端 气隙 划痕 爬电 平均固定学习率1×10-6 80.92 67.87 64.84 54.45 67.02 5×10-6 85.65 72.11 68.55 57.61 70.98 1×10-5 82.17 68.99 65.80 55.29 68.06 5×10-5 57.97 48.84 46.48 38.96 48.06 衰减学习率1×10-6 77.29 64.95 61.94 51.94 64.03 5×10-6 84.60 71.02 67.61 56.64 69.97 1×10-5 88.32 74.16 70.79 59.54 73.20 5×10-5 70.15 58.84 56.24 47.09 58.08

图8 不同学习率配置下平均识别正确率效果图
Fig.8 Average accuracy by different learning rate configuration
由图7 可以看出两组典型学习率配置下平均识别正确率随迭代次数的增加呈上升趋势,到6 000 次迭代基本趋于平稳,说明6 000 次迭代后CAFFE 网络已训练完成。另外固定学习率模式下正确率波动明显比衰减学习率模式大。分析原因,初始的学习率较大可以让网络中的各参数较快地逼近最优值,但是随着迭代次数的增加各参数已逐渐趋向于最优值,如果学习率依旧较高则有可能使参数在最优值附近振荡,而逐步地降低学习率可以使参数更容易逼近最优值。
由表1 可以看出相同学习率配置下,不同缺陷的识别正确率不一定相同,8 种不同学习率配置下尖端缺陷的识别正确率均为最高,爬电缺陷的识别正确率均为最低。分析原因,由图3 可以看出尖端缺陷的放电特征图谱H(q, ∆t)有一个较为集中的主峰,较为容易区分,而爬电缺陷的放电特征图谱H(q, ∆t)则分散性较大,可能会与气隙缺陷、划痕缺陷的图谱相混淆,导致识别正确率相对较低。另外,可以看出平均识别正确率能较好地反映该学习率配置下的综合识别效果,因此本文将以平均识别正确率作为识别效果的评判标准。
由图8 可以发现固定学习率和衰减学习率模式下,初始学习率对网络训练效果影响较大,固定学习率下初始学习率为5×10-6 时正确率最高,衰减学习率下初始学习率为1×10-5 时正确率最高。分析原因,衰减学习率下学习率随着迭代次数增加而减小,因此最优配置的初始学习率较固定学习率高。另外在最优配置下衰减学习率的正确率高于固定学习率,结合图7 得出的衰减学习率下网络参数振荡较小,说明衰减学习率模式的训练效果优于固定学习率模式,因此接下来分析CAFFE 网络结构对训练效果影响时选择衰减学习率模式。
3.2 CAFFE 网络结构的最优配置
CAFFE 的训练效果十分依赖网络的结构,网络结构中最主要的是Layer 层,接下来将以Alexnet 网络结构为基准,比较不同卷积层层数、激活函数的选择对CAFFE 训练效果的影响。
相较于Quick-CIFAR-10 网络的结构,Alexnet 网络更加复杂,在图像识别领域取得了更好的效果[24]。由于两者网络结构存在不同,因此最佳学习率配置也有所不同,本文通过在衰减学习率模式下设置不同的初始学习率来寻找Alexnet 网络中学习率的最佳配置,结果如图9 所示。可以看出衰减学习率模式下初始学习率为1×10-3 时Alexnet 网络训练效果最优,平均识别正确率达到了85.11%,比最优配置下的Quick-CIFAR-10 高出12.10%。接下来将以该求解器参数配置作为基准测试不同网络结构对训练效果的影响。

图9 Alexnet 网络不同初始学习率下平均识别 正确率效果
Fig.9 Recognition effect by different initial learning rate in Alexnet
CAFFE 网络结构主要包括卷积层、池化层、激活函数和SoftMax 等,其中,池化层和SoftMax 的选择比较固定,而对卷积层和激活函数的研究较为活跃。因此本文主要考虑卷积层层数和激活函数的选择对训练效果的影响。
卷积层用于提取图像的特征,是CNN 中的核心。它通过卷积核实现了对二维矩阵的遍历式卷积操作,对于图像的操作可以理解为滤波的过程,卷积的定义式为
式中,I(x,y)为输入二维矩阵中x 行y 列的数据值;w(x,y)为滤波用的卷积核;a、b 为卷积核的大小参数。该操作的实质是将一个卷积核在输入的二维矩阵上滑动,每次都将覆盖区域进行加权求和作为该区域的新值,以期得到矩阵各部分的特征值。对于直流电缆局部放电信号特征图谱的操作,卷积层的作用就是提取特征图谱每一部分的特征信息,例如轮廓、角点等边缘突变值,公式为
式中,xlj 为第l 层神经元j 的输出;f(·) 为激活函数;Mj 为与神经元j 相关的输入集合;![]() 为第l 层神经元j 与上一层神经元i 对应的卷积核;Bl 为偏置。因为每种缺陷的特征图谱有其固有的特性,即各部分的统计特性相类似,卷积核可以将某一部分学习到的特征应用于另一部分。该层的输出为包含各部分特征的矩阵,再经过池化层的特征组合、激活函数提取激活区域等操作即可识别不同缺陷的特征图谱。
为第l 层神经元j 与上一层神经元i 对应的卷积核;Bl 为偏置。因为每种缺陷的特征图谱有其固有的特性,即各部分的统计特性相类似,卷积核可以将某一部分学习到的特征应用于另一部分。该层的输出为包含各部分特征的矩阵,再经过池化层的特征组合、激活函数提取激活区域等操作即可识别不同缺陷的特征图谱。
激活函数是用来模拟人类神经元接受刺激后是否激活的过程,通过增加非线性单元使模型能处理非线性的问题。早期常用的激活函数有 tanh、Sigmoid 函数,现在Relu 激活函数因其最大程度保留数据特征、拥有不饱和非线性特性和梯度下降收敛快的优势逐渐成为常用激活函数,具体定义为
此外,还有众多Relu 的变种,例如指数线性单元ELU,拥有较高的鲁棒性,定义为
式中,α 为可调节参数,本文中取α=1。另外Google Brain 基于对现有的激活函数分析,在2017 年提出新的激活函数Swish,该激活函数具备无上界有下界、平滑、非单调的特性,定义为
式中,β 为可调节参数,本文中取β=1。
本文将通过改变CAFFE 网络中卷积层层数并选择不同的激活函数来测试不同网络结构对训练效果的影响。接下来将综合对比3 层、5 层、7 层卷积层网络和Relu、ELU、Swish 激活函数对Alexnet 网络训练效果的影响,平均识别正确率如图10 所示。
由图10 可以看出,卷积层层数和激活函数选择对CAFFE 训练效果均有一定的影响,三种激活函数都在卷积层层数为5 时训练效果最好,不同卷积层层数下三种激活函数表现各有优劣。Quick-CIFAR-10 网络中卷积层为3 层,发现与同为3 层卷积层的Alexnet 网络识别正确率相差不大,只低了3.16%,而不同卷积层层数之间的差距最大甚至超过了20%,说明卷积层层数对识别效果影响较大。在相同卷积层层数下激活函数的选择对识别效果也有 一定的影响,最大差距能到8.32%。可以看出卷积层数为5 层,选择Swish 激活函数是直流局部放电模式识别中Alexnet 网络的最优网络结构配置。
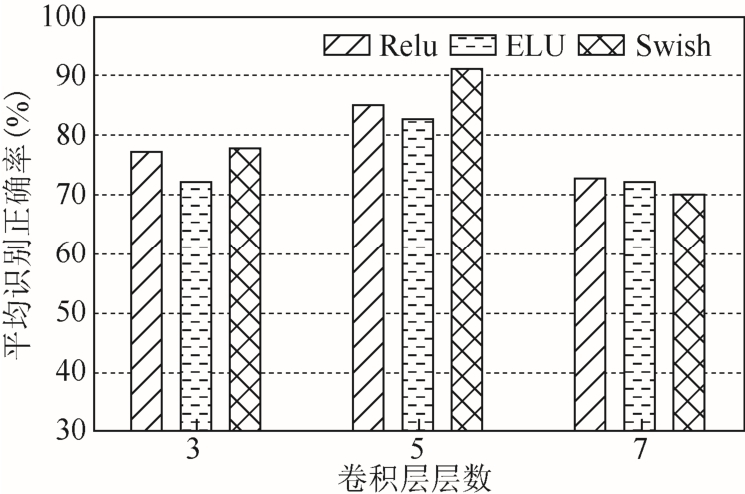
图10 不同卷积层层数和激活函数时平均识别正确率
Fig.10 Recognition effect by different numbers of convolutional layers and different activation functions
另外直流下局部放电的强随机性可能导致训练过程中出现过拟合的情况,即对噪声过于敏感。过拟合的判别方法是交叉验证法,计算不同样本的训练误差Jtrain 和交叉验证误差Jcv,如果两者差距过大,表明出现过拟合情况。

式中,θ 为模型的参数;hθ 为模型函数。为了防止过拟合情况的发生,本文使用Dropout 层随机地让网络某些隐层节点的权重不工作,抑制了噪声的干扰。在5 层卷积、Swish 激活函数的Alexnet 网络中添加Dropout 层后最终的平均识别正确率为91.32%,相对于未添加Dropout 层的90.78%,提高了0.54%,虽然在识别正确率上影响不大,但是对于以后现场海量数据的识别可以起到防止过拟合的作用。最终改进后的Alexnet 网络如图11 所示。

图11 改进后的Alexnet 网络结构
Fig.11 Network diagram of modified Alexnet
改进后的Alexnet 网络的识别混淆矩阵(confusion matrix)见表2,可以看出:爬电缺陷和气隙缺陷是CNN 模式识别误差的主要来源,其中爬电缺陷的样本有10.78%被误识别为气隙缺陷,气隙缺陷样本有8.03%被误识别为爬电缺陷,是混淆矩阵中两个最大的误识别率,很大程度上降低了平均识别正确率。另外,尖端缺陷与气隙缺陷、划痕缺陷之间没有误识别率,这也符合图3 中尖端缺陷的特征图谱与另外两者差异较大的分析。
表2 改进后的Alexnet 网络的识别混淆矩阵
Tab.2 Confusion matrix of the modified Alexnet network (%)
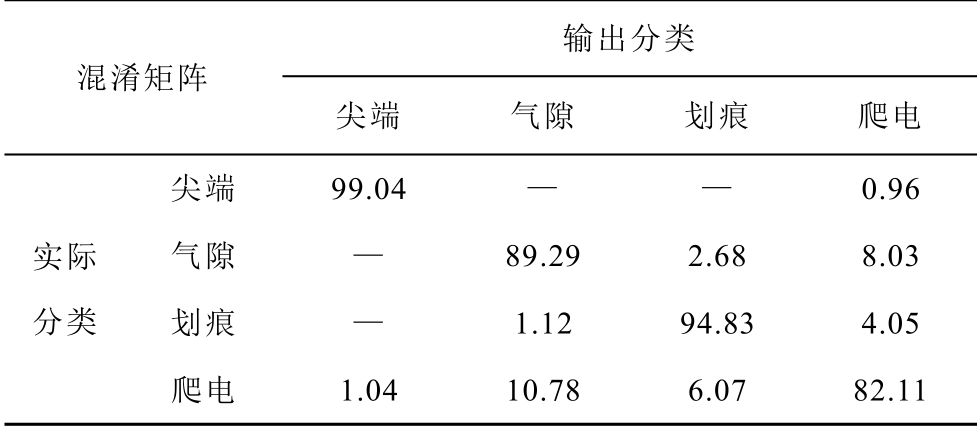
混淆矩阵 输出分类 尖端 气隙 划痕 爬电 实际分类 尖端 99.04 — — 0.96 气隙 — 89.29 2.68 8.03 划痕 — 1.12 94.83 4.05 爬电 1.04 10.78 6.07 82.11
3.3 训练样本数量对识别效果的影响
CNN 算法通过训练样本对网络中各个卷积核的权值参数进行训练以达到最优识别效果,训练样本数量的大小可能会对识别效果产生一定的影响。本文利用每种缺陷训练样本数量分别为40、50、60、70 来对改进的Alexnet 网络进行训练,分析不同的训练样本数量对识别效果的影响。识别效果如图12所示,可以发现随着训练样本数量的增加,平均识别正确率在增加,识别正确率方差在缩小,并且两者都呈现指数形式,体现出了边际递减效应。如果继续增加训练样本数量,识别效果可能会更好,但是提升效果可能越来越小,并且训练时间可能会大幅增加,因此本文最终选择每种缺陷的训练样本数量为70 个。
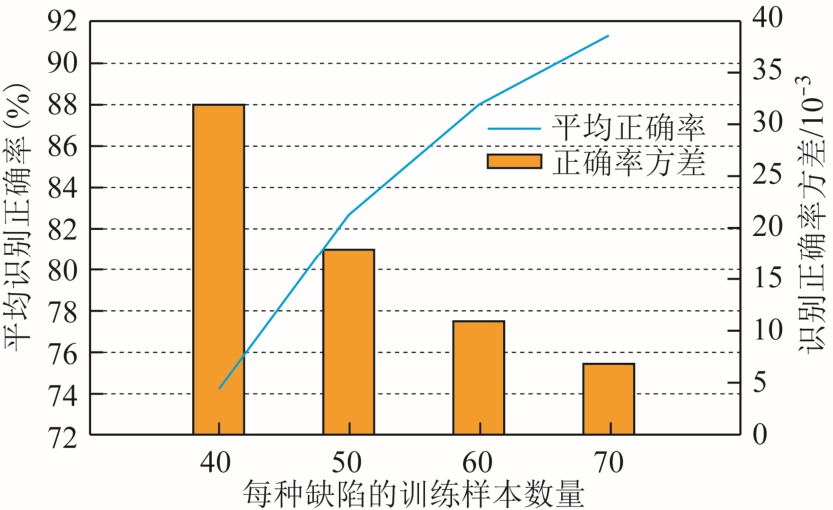
图12 不同训练样本数量对识别效果影响
Fig.12 Recognition performance by different numbers of training samples
3.4 与传统模式识别算法的比较
为了印证采用改进后的Alexnet 网络的CNN 算法对直流电缆局部放电的识别效果,本文将其与反向传播神经网络(Back Propagation Neural Network,BPNN)和支持向量机(Support Vector Machine, SVM)进行了比较。表3 给出了BPNN、使用径向基函数(Radial Basis Function, RBF)的SVM 以及采用最优学习率配置下的Quick-CIFAR-10、Alexnet 和改进的Alexnet 网络的CNN 的平均识别正确率和训练时长。可以发现传统的模式识别算法BPNN 和SVM的训练时间要短于CNN,但是识别正确率要低于使用Alexnet 网络的CNN,其中识别正确率较高的SVM 要比使用改进后的Alexnet 网络的CNN 低8.97%,差距较大。分析原因,BPNN 和SVM 是传统的浅层分类器,对于强随机性的直流局部放电信号的高维特征提取有所欠缺,导致识别正确率偏低。另外对比采用不同网络结构的CNN 可以发现不同的网络结构对训练效果影响较大,对训练时间也有一定的影响。虽然改进后的Alexnet 网络训练时间相较于原始的Alexnet 略微要长,但是识别正确率高出了 6.21%,具有较大的优势,说明改进后的Alexnet 网络结构相较于原先纯粹应用于分类物体的图像识别的Alexnet 网络更适合直流XLPE 电缆的局部放电模式识别,最终识别正确率能达到91.32%。
表3 不同模式识别框架的平均识别正确率和训练时间
Tab.3 Final average accuracy and training time of different pattern recognition frameworks
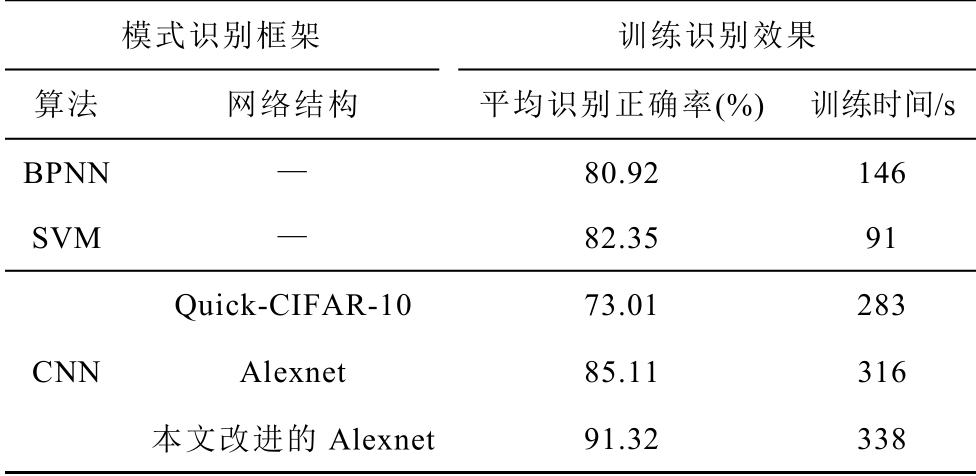
模式识别框架 训练识别效果 算法 网络结构 平均识别正确率(%) 训练时间/s BPNN — 80.92 146 SVM — 82.35 91 CNN Quick-CIFAR-10 73.01 283 Alexnet 85.11 316 本文改进的Alexnet 91.32 338
4 结论
本文针对直流XLPE 电缆的四类典型绝缘缺陷的局部放电信号进行了模式识别研究,分析了不同求解器参数、网络结构和训练样本数量对CNN 识别效果的影响,并与传统模式识别算法进行了比较,得到以下结论:
1)四类绝缘缺陷的局部放电特征图谱H(q,Δt)具有一定的典型性:尖端缺陷呈现较为集中的单一主峰,气隙缺陷和爬电缺陷则分散性较大,划痕缺陷可观测到两个主峰。CAFFE 方法利用卷积神经网络CNN 能自适应提取图像特征的特点,无需人为提取特征参数。
2)通过改变初始学习率、学习率模式、卷积层层数、激活函数选择可以发现求解器Solver 配置参数和CAFFE 网络结构对训练效果影响较大,本次实验中采用衰减学习率模式、5 层卷积、Swish 激活函数时训练效果最优。不同的训练样本数量对识别效果也有一定的影响,存在边际递减效应。综合考虑识别效果和运算效率,本文设定每种缺陷的训练样本数量为70 个。
3)相比于传统模式识别算法BPNN 和SVM,采用改进的Alexnet 网络的CNN 能捕捉到强随机性的直流局部放电图谱更高维的信号特征,平均识别正确率至少高出前者8.97%,达到91.32%。
4)本文直流电缆局部放电信号的采集在屏蔽房内进行,降低了外部干扰,现场采集的局部放电信号必定含有大量的噪声,因此本文提出的方法对不同噪声强度下局部放电信号的模式识别的有效性仍有待进一步研究。
[1] 何金良, 党斌, 周垚, 等. 挤压型高压直流电缆研究进展及关键技术述评[J]. 高电压技术, 2015, 41(5): 1417-1429. He Jinliang, Dang Bin, Zhou Yao, et al. Reviews on research progress and key technology in extruded cables for HVDC transmission[J]. High Voltage Engineering, 2015, 41(5): 1417-1429.
[2] 杜伯学, 李忠磊, 杨卓然, 等. 高压直流交联聚乙烯电缆应用与研究进展[J]. 高电压技术, 2017, 43(2): 344-354. Du Boxue, Li Zhonglei, Yang Zhuoran, et al. Application and research progress of HVDC XLPE cables[J]. High Voltage Engineering, 2017, 43(2): 344-354.
[3] 钟力生, 任海洋, 曹亮, 等. 挤包绝缘高压直流电缆的发展[J]. 高电压技术, 2017, 43(11): 3473-3489. Zhong Lisheng, Ren Haiyang, Cao Liang, et al. Development of high voltage direct current extruded cables[J]. High Voltage Engineering, 2017, 43(11): 3473-3489.
[4] 周远翔, 赵健康, 刘睿, 等. 高压/超高压电力电缆关键技术分析及展望[J]. 高电压技术, 2014, 40(9): 2593-2612. Zhou Yuanxiang, Zhao Jiankang, Liu Rui, et al. Key technical analysis and prospect of high voltage and extra-high voltage power cable[J]. High Voltage Engineering, 2014, 40(9): 2593-2612.
[5] Kreuger F H. Industrial high DC voltage[D]. Delft: Delft University of Technology, 1995.
[6] Jeroense M J P. Charges and discharges in HVDC cables[D]. Delft: Delft University of Technology, 1997.
[7] Fromm U. Interpretation of partial discharges at DC voltages[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1995, 2(5): 761-770.
[8] Pirker A, Schichler U. Partial discharge measurement at DC voltage-Evaluation and characterization by NoDi* pattern[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(3): 883-891.
[9] 吴广宁, 李晓华, 冉汉政, 等. 高压脉冲造成储能电容器老化的直流局部放电测试技术[J]. 电工技术学报, 2010, 25 (7): 172-178. Wu Guangning, Li Xiaohua, Ran Hanzheng, et al. Partial discharge under DC condition with pulse discharge degradation of high voltage storage capacitors[J]. Transactions of China Electrotechnical Society, 2010, 25(7): 172-178.
[10] 齐波, 魏振, 李成榕, 等. 交直流复合电场中油纸绝缘沿面放电现象及特征[J]. 电工技术学报, 2016, 31 (10): 59-67. Qi Bo, Wei Zhen, Li Chengrong, et al. The phenomena and characteristics of oil-paper insulation surface discharge under AC and DC voltage[J]. Transactions of China Electrotechnical Society, 2016, 31(10): 59-67.
[11] Li Yuan, Zhang Qiaogen, Ding Yuqin, et al. Effect of cellulose impurities on partial discharges in oilpressboard insulation under DC voltage[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(4): 2271-2273.
[12] 秦雪, 钱勇, 许永鹏, 等. 基于2D-LPEWT 的特征提取方法在电缆局部放电分析中的应用[J]. 电工技术学报, 2019, 34(1): 170-178. Qin Xue, Qian Yong, Xu Yongpeng, et al. Application of feature extraction method based on 2D-LPEWT in cable partial discharge analysis[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 170-178.
[13] Gu Xiao, He Shuang, Xu Yang, et al. Partial discharge detection on 320 kV VSC-HVDC XLPE cable with artificial defects under DC voltage[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(3): 939-946.
[14] Liu Mechen, Liu Yunpeng, Li Yanda, et al. Growth and partial discharge characteristics of electrical tree in XLPE under AC-DC composite voltage[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(4): 2282-2290.
[15] Xu Yongpeng, Qian Yong, Yang Fengyuan, et al. DC cable feature extraction based on the PD image in the non-subsampled contourlet transform domain[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(2): 533-540.
[16] Yang Fengyuan, Sheng Gehao, Xu Yongpeng, et al. Partial discharge pattern recognition of XLPE cables at DC voltage based on the compressed sensing theory[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(5): 2977-2985.
[17] 陈焕栩, 解浩, 张建文, 等. 基于灰度共生矩阵纹理特征的局部放电模式识别[J]. 电力系统保护与控制, 2018, 46(5): 25-30. Chen Huanxu, Xie Hao, Zhang Jianwen, et al. Partial discharge pattern recognition based on texture feature of gray level co-occurrence matrix[J]. Power System Protection and Control, 2018, 46(5): 25-30.
[18] 于生宝, 何建龙, 王睿家, 等. 基于小波包分析和概率神经网络的电磁法三电平变换器故障诊断方法[J]. 电工技术学报, 2016, 31 (17): 102-112. Yu Shengbao, He Jianlong, Wang Ruijia, et al. Fault diagnosis of electromagnetic three-level inverter based on wavelet packet analysis and probabilistic neural networks[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 102-112.
[19] 杨帆, 王干军, 彭小圣, 等. 基于卷积神经网络的高压电缆局部放电模式识别[J]. 电力自动化设备, 2018, 38 (5): 123-128. Yang Fan, Wang Ganjun, Peng Xiaosheng, et al. Partial discharge pattern recognition of high-voltage cables based on convolutional neural network[J]. Electric Power Automation Equipment, 2018, 38(5): 123-128.
[20] 聂洪岩, 张潮海, 顾哲屹, 等. 局部放电条件下干式空心电抗器匝间绝缘的电老化特性研究[J]. 电工技术学报, 2018, 33(13): 3071-3079. Nie Hongyan, Zhang Chaohai, Gu Zheyi, et al. The research on electrical aging characteristics of turn-toturn insulation of dry-type air core reactor under partial discharge[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3071-3079.
[21] Jia Yanqing, Shelhamer E, Donahue J, et al. Caffe: convolutional architecture for fast feature embedding[C]// ACM International Conference on Multimedia, Orlando, FL, USA, 2014: 675-678.
[22] Yan Kewen, Huang Shaohui, Song Yaoxian, et al. Face recognition based on convolution neural network[C]// Chinese Control Conference, Dalian, China, 2017: 4077-4081.
[23] Turchenko V, Luczak A. Creation of a deep convolutional auto-encoder in Caffe[C]// 2017 9th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Bucharest, 2017: 651-659.
[24] 常亮, 邓小明, 周明全, 等. 图像理解中的卷积神经网络[J]. 自动化学报, 2016, 42(9): 1300-1312. Chang Liang, Deng Xiaoming, Zhou Mingquan, et al. Convolutional neural networks in image understanding[J]. Acta Automatica Sinica, 2016, 42(9): 1300-1312.