0 引言
在电力系统分析中,架空输电线路往往采用单段集中参数模型[1-2]。在该模型下,假设输电线路沿线电流密度和材料特性是均匀的,并忽略线路沿线气象数据时空变化导致的导体温度的变化,输电线路参数通常采用导体温度为20℃时对应的电阻和电抗值[3]。实际上沿线气象数据具有显著的时空变化特性,导致导体温度往往异于20℃[4]。架空输电线路是电网的主要构成要素,线路参数的变化必将影响系统的运行状态[5]。
架空输电线路沿线气象数据,一方面可通过实地测量直接得到[6],如华东电网500kV 瓶武5905 线安装了3 个测试点,实现了环境温度、风速、风向和日照强度的就地测量;另一方面可通过我国气象部门发布的各种气象数值预报产品得到[7-8]。如中国目前发展的 GRAPES(global/regional assimilation and prediction system) 全球/区域一体化数值预报系统。规格为格点距离10km×10km,每天数值预报发布2 次(夜间00:00 点/中午12:00),每隔3h 输出未来72h 预报。文献[9]基于GRAPES 数值天气预报对线路热载荷能力进行了研究。文献[10]的气象数据取自山东大学(威海)天文台,由7 年的气象数据统计分析可知,风速的最大值为22.7m/s,最高环境温度为42.0℃,最低环境温度为-13.5℃,年最大温差达到了48.9℃,气象参数具有显著的季节性,尤其是周围环境温度。文献[11-12]指出,在局部地区寒潮的影响下,长度240km 的架空输电线路首末端环境温度差值达到了20℃,沿线气象数据的空间变化特性也是显著的。
架空线路导体温度决定于所处的气象环境及其载流值。气象数据的时空变化决定了线路导体温度的时空分布,在文献[13]中,线长7km,电压等级132kV 的架空输电线路,在1 月份的某周内,导体温度最低达到了0℃以下,最高达到了22℃。在文献[14]中,湖善2435 线冬季11 月份导体温度变化范围在10~40℃。在文献[15]中美国爱达荷州西部2 条138kV 和2 条230kV 输电线路应用了架空输电线路动态热定值技术,在该文献中通过某月实际测量的风速、环境温度和载流值计算导体温度,一个月内最低温度达到了0℃,最高温度达到了40℃以上。
通过上述分析可知,实际运行环境下由于沿线气象参数较强的时空变化特征,导体温度也呈现出显著的变化。但上述测量或计算沿线气象数据和导体温度的目的均是为了提高线路的热载流量,实现架空输电线路的增容运行。文献[16-18]提出了实时运行环境下电热耦合的潮流模型与应用。文献[19]基于动态热定值对配电网的可靠性进行研究。文献[20]基于沿线气象数据,提出计及线路热惯性效应的安全经济调度模型。文献[21]通过计算导体温度,建立了计及导线截面径向与周向传热路径的热网络模型。但上述文献没有考虑气象数据和导体温度的空间变化幅度与变化梯度。实际导体温度的空间变化必然导致线路电阻和电抗参数沿线的非均一性,影响系统运行状态。
为此,本文首先依据CIGRE 标准热平衡方程,给出依据风速、环境温度等实际气象数据计算导体温度的方法。在此基础上,对山东地区某220kV 架空线路及东北地区某500kV 线路气象数据和导体温度的时空分布进行了分析;其次建立了计及气象数据时间变化特性的季节性模型,计及气象数据空间变化特性的平均值模型、权重平均值模型和线路分段模型;再次依据线路参数与导体温度的关系,建立了计及气象数据时空变化的潮流模型和分解协调的求解算法;最后通过六种情景下的IEEE 5 节点系统运行状态及线路极限传输能力的分析与比较,验证了电力系统运行状态分析中考虑气象数据和导体温度时空分布的必要性。
1 CIGRE 标准热平衡方程
架空输电线路的温度受其载流量和周围气象条件(风速、风向、日照和温度等)的影响。其中,促使架空输电线路温度升高的主要因素是导体载流量引起的焦耳热和由于日照吸收的热量,而对输电线路起冷却作用的主要是风力因素导致的对流散热和导体温度与周围温差而产生的辐射散热。根据CIGRE 标准[22],架空输电线路的热平衡方程为

式中, cT 为架空输电线路的导体温度;T 为周围环境温度;V 为风速;φ 为风向角;θ 为太阳辐射角;sq 为日照吸热,其主要影响因素为θ ; rq 为由温差引起的辐射散热,其主要影响因素为 cT 和T ; cq 为由风速、风向引起的对流散热,其主要影响因素为cT 、T 、V 、φ;m 为导体质量;I 为载流量;R 为在温度 cT 下的导体电阻; pc 为导体比热容;t 为时间。sq 、 rq 和 cq 的详细表达参见文献[4]。
当输电线路载流量及其周围的气象条件处于稳定状态时,其发热量和散热量将处于平衡状态,此时稳态下的热平衡方程为
由于CIGRE 标准热平衡方程对于导体温度 cT来说不能表示为显函数,需要设定初始值,通过循环迭代,逐次渐近求得 cT 的近似解。迭代步长可以根据实际需求的求解精度来设定。
2 气象数据和导体温度的时空分布
处于运行条件下的输电线路,其周围气象条件是随着时间和空间的不同而变化的。针对架空输电线路气象数据和导体温度时间维度上的变化,本文取山东地区某220kV 架空线路,同时采用山东大学(威海)天文台,2016 年共8 784h 的整点风速和周围环境温度数据,计算LGJ400/50 导线的导体温度。风速和环境温度的频率分布直方图如图1 和图2 所示。风速的最大值为19.60m/s,平均值为6.42m/s,周围环境温度的最大值为 38.20℃,最小值为 -13.40℃,平均值为13.73℃。

图1 风速频率分布直方图
Fig.1 Frequency distribution histogram of wind speed
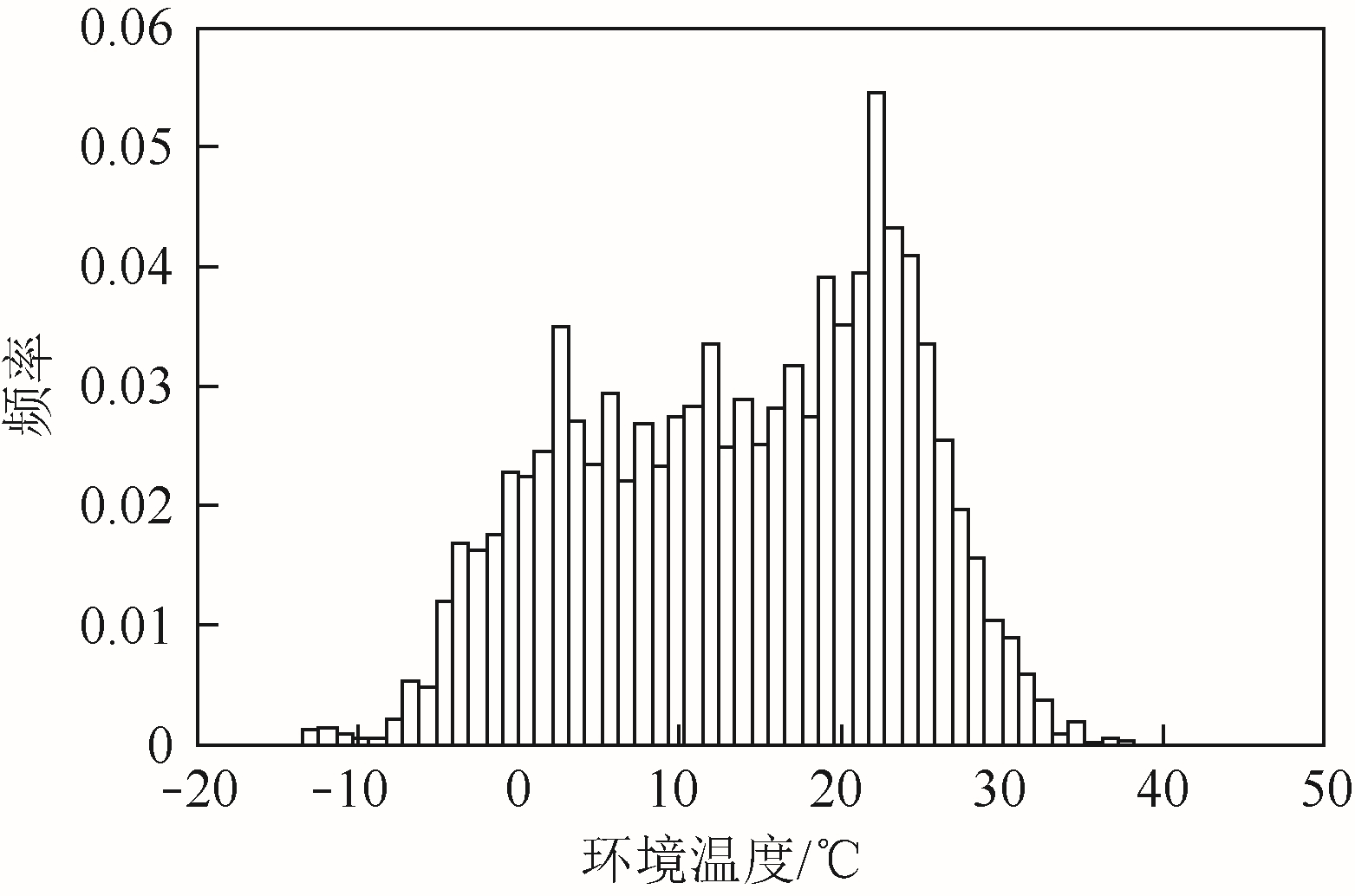
图2 周围环境温度频率分布直方图
Fig.2 Frequency distribution histogram of ambient temperature
设流经该导线电流为最大允许电流的75%,则在上述气象条件下,通过热平衡方程即式(2),可得全年导体温度的变化与分布如图3 所示。其中,导体的最大温度86.45℃,最小温度-10.79℃,平均温度19.71℃。其中春、夏、秋、冬一年四季导体温度的最大值、最小值和平均值见表1。
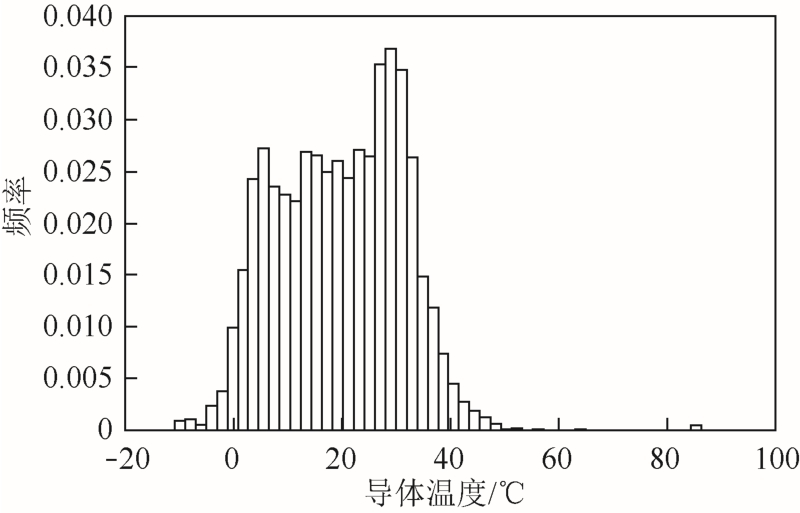
图3 导体温度频率分布直方图
Fig.3 Frequency distribution histogram of conductor temperature
表1 不同季节导体温度值
Tab.1 Conductor temperature in different seasons

季节 最大值/℃ 最小值/℃ 平均值/℃ 季 56.46 2.50 19.27 季 86.45 19.56 32.26 秋季 53.0 -0.62 21.36 冬季 21.84 -10.79 5.81
通过上述分析可见,由于气象数据的变化引起导体温度的变化幅度较大,在上述一年内导体温度的变化幅度达到了97.24℃,并呈现出显著的季节性。因此,如果在电力系统的分析与计算中忽略导体温度的变化(取恒定值20℃),必然导致分析结果存在误差。
针对架空输电线路气象数据和导体温度空间维度上的变化,本文取用东北地区某500kV 架空线路,该线路全长411.4km,根据该线路1 012 座杆塔的经纬度坐标,得到该线路的地理方位如图4 所示。
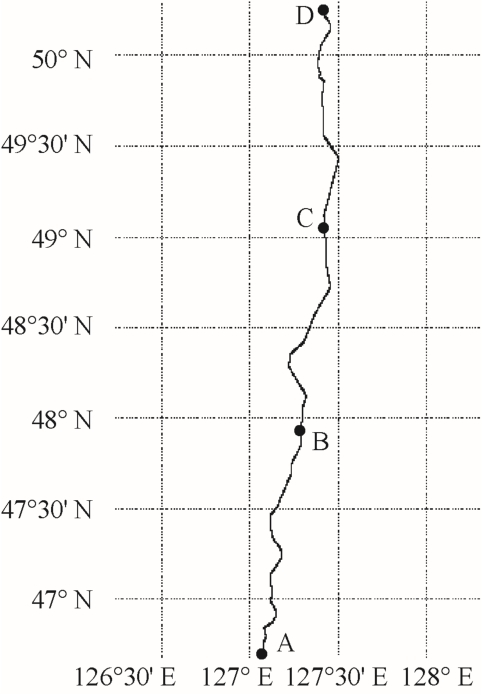
图4 某500kV 线路地理方位
Fig.4 A 500kV line diagram
图4 中相应经度和纬度的交叉点共有234 个,为中国气象数据网GRAPES 气象预报产品的数值预报点,而A、B、C、D 为沿纬度均分的输电线路上的4 个点,利用上述234 个交叉点,采用反距离插值技术,可得输电线路上A、B、C、D 点的周围环境温度和风速,2016 年7 月7 日0:00 点的数据见表2。设流经该导线电流为最大允许电流的75%,通过热平衡方程式(2)可得上述4 个测量点的导体温度。从表2 可见,当环境温度较稳定,风速空间变化较大时,输电线路首末端导体温差达到了22.67℃。
表2 2016 年7 月7 日0:00 点导体温度的空间分布
Tab.2 The conductor temperature spatial distribution at 0:00 July 7, 2016
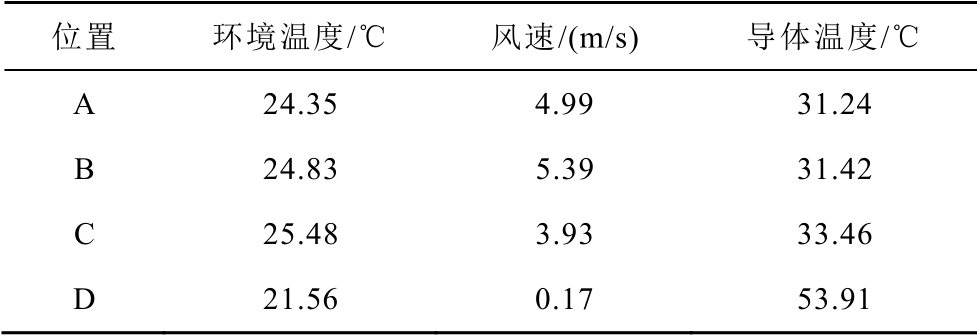
位置 环境温度/℃ 风速/(m/s) 导体温度/℃ A 24.35 4.99 31.24 B 24.83 5.39 31.42 C 25.48 3.93 33.46 D 21.56 0.17 53.91
表3 给出了2017 年2 月28 日12:00 点,上述4 个点的周围环境温度和风速,沿线风速较稳定,但是线路首末端周围环境温度相差17.63℃。从中可以看出,当风速较稳定,环境温度空间差异性较大时,输电线路首末端导体温差也达到20.61℃。
通过上述分析可知,架空线路气象数据和导体温度均存在显著的时空分布特性,导体温度的时空变化必然导致输电线路参数的时空变化,进而影响整个系统的潮流状态。导体温度的时空分布是由气象数据的时空变化引起的,为此有必要建立描述架空线路气象数据时空分布特性的表征模型。
表3 2017 年2 月28 日12:00 点导体温度的空间分布
Tab.3 The conductor temperature spatial distribution at 12 Feburary 28, 2017

位置 环境温度/℃ 风速/(m/s) 导体温度/℃ A 7.50 3.18 16.19 B -4.17 2.28 6.14 C -3.97 2.75 5.24 D -10.13 5.80 -4.42
3 气象数据时空变化的表征模型
气象数据、导体温度及线路负荷都存在一定的季节性,本文建立了考虑气象数据时间维度变化的季节性模型,按不同的季节取不同的气象数据值。根据表1,春季和秋季导体温度接近电力系统常规分析中设定的20℃,为此春季和秋季不考虑气象数据的变化,而采用导体温度的恒定值20℃;考虑到夏季的高温度和低风速情景,夏季的环境温度取为38℃,风速设定为0.5m/s;考虑到冬季的低温度和高风速情景,冬季的环境温度取为-20℃,风速设定为18m/s。
为了描述沿线气象数据空间分布的不均匀性,本文给出气象数据空间分布的三种表征模型:平均值、权重平均值和线路分段模型。
1)平均值——输电线路首末端气象数据平均值。

式中,Tbeg、Vbeg 分别为输电线路首端环境温度、风速;Tend、Vend 分别为输电线路末端环境温度、风速。
2)权重平均值——基于气象数据测量点在线路中位置的加权值。

式中,N 为环境温度测量点的总数;a 为线路上的某个测量点(a=1,…,N); ∆x a , a+1为测量点a 和下一个测量点a+1 之间的线路长度;l 为线路的总长度。
3)线路分段模型。
以沿线变化梯度较稳定的环境温度为分段依据,如图5 所示,Mst 为环境温度测量装置所在位置标志。

图5 线路分段模型下的温度分布
Fig.5 Conductor temperature distribution under segmentation model
线路的分段方法具体如下:
1)根据Mst1、Mst2、Mst3 和Mst4 这4 个位置处的环境温度值,假设任意两个测量位置之间,温度沿着距离x 的分布是线性单调的,由此可确定4 个测量点之间的温度分布,如果线路送端xS 与受端xR 并不是环境温度测量装置的所在位置,则可根据测量点之间的温度分布确定送端xS 与受端xR 处的环境温度值TS 和TR。
2)在输电线路任意一个分段内允许的最大温度差 ![]() 确定的情况下,以分段数最少为目标对输电线路进行分段,从线路送端xS 开始,当温差达到
确定的情况下,以分段数最少为目标对输电线路进行分段,从线路送端xS 开始,当温差达到![]() 时确定x1,xS 与x1 之间为输电线路的第一段,第一段气温T1 为此段内T(x)的平均值,以此方法逐步确定各段距离及各段的环境温度值。
时确定x1,xS 与x1 之间为输电线路的第一段,第一段气温T1 为此段内T(x)的平均值,以此方法逐步确定各段距离及各段的环境温度值。
4 计及线路气象数据变化的电网潮流
假设某条输电线路或输电线路某段l 首末端节点为i 和j,忽略对地电纳,则该线路有功和无功潮流为
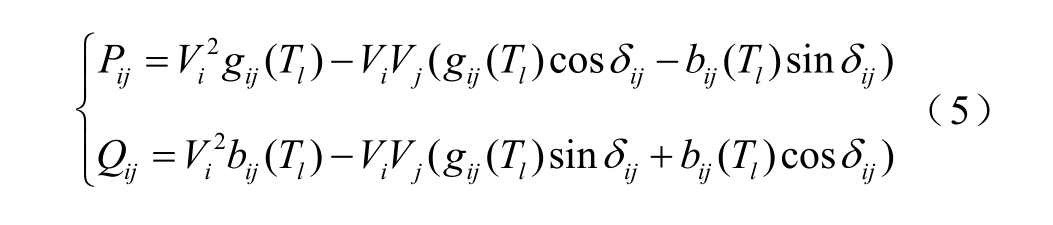
流经该段线路的电流为

式中, Tl 为某输电线路或线路某段l 的导体温度; Vi和 V j为节点i 和节点j 的电压幅值; δij = δ i - δj 为节点i 和节点j 的电压相位差; g ij和 bi j分别为与该段输电线路串联阻抗等效的导纳参数, g i j=ri j /( r i j2+xi2j)和bi j=-xi j /(r i j2+xi2j)均与输电线路的导体温度有关。
式中, T0 为参考温度,通常取 T0 =20℃; ri j(T 0 )为参考温度下的电阻值; ri j(T l )为实际温度 Tl 下的电阻值;α 为电阻的温度系数,由导体的物理材质决定。导线的电抗值也与温度相关,其主要是由线路弧垂引起的导线长度变化引起的,线路电抗与导体温度之间存在复杂的非线性关系,本文采用相关研究普遍应用的文献[12]的处理方法,见式(8)。
式中,xi j(T 0 )为线路在导体参考温度 T0 下的电抗;xi j (T l )为线路在导体实际温度 Tl 下的电抗;β 为电抗温度系数。
电力系统在运行时,电源的电流或功率通过系统各输配电元件(线路、变压器等)流入负荷,系统的潮流方程为

式中, GiP 和 GiQ 分别为节点i 电源的有功和无功注入功率; LiP 为 LiQ 分别为节点i 的有功和无功负荷;j i∈ 代表节点j 与节点i 直接相连,但是不包括节点i。从式(9)可以看出,输电线路导体温度的变化,将直接导致系统潮流的变化,但架空线路导体温度决定于其所处的气象环境及其载流值。在式(9)中,导体温度及载流值均是未知量,但二者之间的约束关系为式(2)所示的导体的热平衡方程。本文采用分解协调的求解思路,计算步骤如图6 所示。
分解协调的求解方法将潮流方程与热平衡方程自然地分解开来,由系统潮流计算和热平衡方程计算两个独立子程序组成。当计算导体热平衡方程时,接收潮流计算所得的导体载流值,通过热平衡方程的反复迭代求解导体温度;当计算潮流方程时,接收由热平衡方程计算所得的导体温度,通过反复迭代求解潮流方程得到导体的载流值。依此反复求解,直到收敛。该分解协调算法中,两个子程序的数据相互独立,分别采用各自合适的迭代算法和收敛精度,子程序之间通过接口传递数据完成计及输电线路沿线气象数据变化的潮流计算。

图6 分解协调的算法流程
Fig.6 Decomposition and coordination algorithm flow chart
5 算例分析
本文采用一个改进的5 节点电力系统作为算例。网络结构如图7 所示,其中节点4 和节点5 为电源所在节点,支路4-2 和支路3-5 为变压器所在支路,不涉及气象条件时空分布问题。而支路2-3、1-3、2-1 为架空线路,本文所提方法和计算结果的分析主要体现于这3 条线路。线路电压等级为220kV,输电线路采用LGJ-400/50 型导线,其中铝线部分截面积为399.73 mm2,导体直径为27.63mm。系统中线路2-3、1-3、2-1 的长度分别为300km、300km、120km。线路的电阻和电抗温度系数为0.003 9(1/℃)。
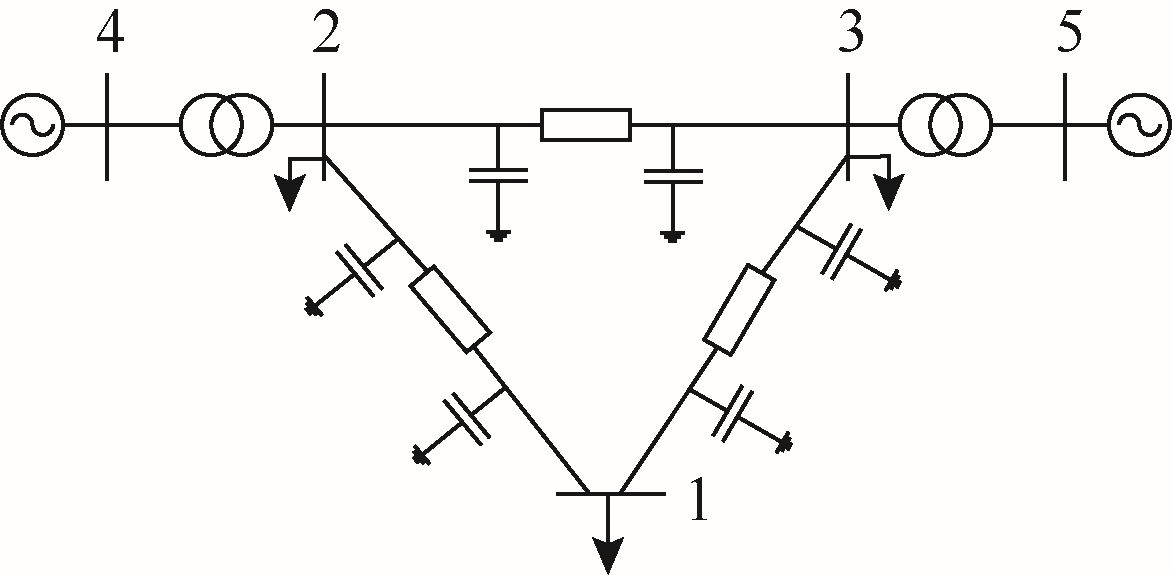
图7 网络结构
Fig.7 Network structure
为了说明输电线路沿线气象数据对系统潮流和网络损耗等系统运行状态的影响,本文针对输电线路沿线气象数据时空分布的不同表征模型,对如下六种情景进行了分析与计算:
基准情景:不考虑输电线路沿线气象条件的变化,假定该电网系统中的各条输电线路导体温度均为20℃。此为电力系统常规分析与计算采用的线路参数值。为此设定该情景为基准情景。
情景1:考虑到气象数据变化的季节性,在炎热的夏季,输电线路沿线环境温度通常较高,风速较低。本文夏季取环境温度为38℃,风速为0.5m/s。
情景2:在寒冷的冬季,输电线路沿线环境温度通常较低,风速较高。本文冬季取环境温度为-20℃,风速为18m/s。
情景3:考虑沿线气象参数空间分布的不均匀性,设环境温度为20℃,风速为0.5m/s,节点3 处发生寒流,环境温度骤变为0℃,风速骤变为10m/s。在此情景中,由于线路首末端气象参数值不同,采用平均值的表征模型确定气象参数值。
情景4:气象条件的设置与情景3 相同,假设线路1-3 与线路2-3 存在将线路三等分的两个气象测量点,测量点环境温度分别为2℃和-4℃,风速分别为12.5m/s 和16.5m/s。在此情景中,采用权重平均值的表征方法确定气象参数值。
情景5:气象条件和测量点的设置与情景4 相同,采用线路分段模型。依据周围环境温度,取6℃温度阈值进行分段,则线路2-3、1-3 都可分为5 段。其中,支路2-3 分段为2-6、6-7、7-8、8-9 和9-3;支路1-3 分段为1-10、10-11、11-12、12-13、13-3。分段后的系统为13 节点系统,其中,每段环境温度及风速取决于每段首末平均值,则分段结果如图8 和表4 所示。

图8 支路2-3 与支路1-3 环境温度分段结果
Fig.8 Ambient temperature segmentation results of branch 2-3 and branch 1-3
表4 支路2-3 与支路1-3 分段结果
Tab.4 Segmentation results of branch 2-3 and branch 1-3
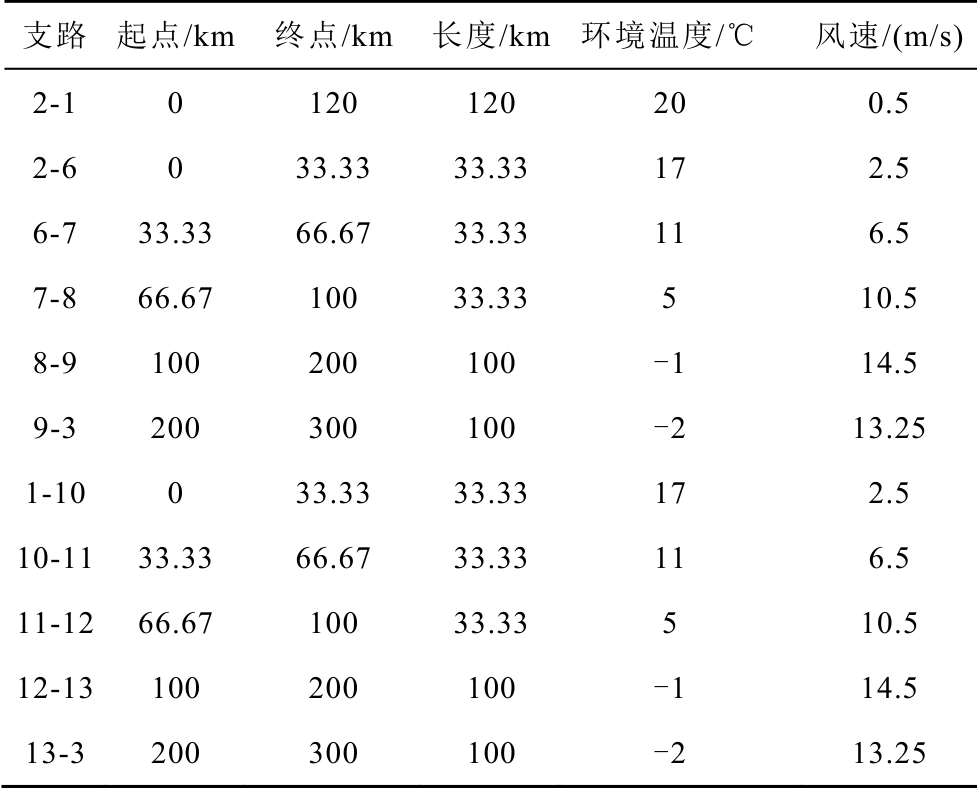
支路 起点/km 终点/km 长度/km 环境温度/℃ 风速/(m/s)2-1 0 120 120 20 0.5 2-6 0 33.33 33.33 17 2.5 6-7 33.33 66.67 33.33 11 6.5 7-8 66.67 100 33.33 5 10.5 8-9 100 200 100 -1 14.5 9-3 200 300 100 -2 13.25 1-10 0 33.33 33.33 17 2.5 10-11 33.33 66.67 33.33 11 6.5 11-12 66.67 100 33.33 5 10.5 12-13 100 200 100 -1 14.5 13-3 200 300 100 -2 13.25
5.1 系统潮流
分别针对上述六种情景,采用图6 所示分解协调算法,计算计及气象数据变化的电网潮流。潮流计算的初始条件为:1 号节点负荷有功功率为320MW,无功功率为80Mvar;2 号节点负荷有功功率为160 MW,无功功率为40Mvar;3 号节点负荷有功功率为240MW,无功功率为60Mvar;4 号节点为PV 节点;5 号节点为平衡节点。潮流初始化包括设置导体温度初始值,在此取为20℃,用于算法的首次迭代。设置合理的导体温度初始值,将会使算法的迭代次数减少,在本算例中一般经过3~6 次全局迭代,可得各个支路导体温度与线路参数。表5 给出了支路1-3 在六种情形下的导体温度和电阻、 电抗和电纳参数值。
表5 六种情景下支路1-3 的导体温度与线路参数
Tab.5 The conductor temperature and line parameters of the branch 1-3 under 6 cases

情景 支路 导体温度/℃ r(pu) x(pu) b(pu)基准情景 1-3 20 0.044 7 0.251 0 0.408 8情景1 1-3 56.63 0.051 1 0.286 9 0.408 8情景2 1-3 -17.73 0.038 1 0.214 1 0.408 8情景3 1-3 15.40 0.043 9 0.246 5 0.408 8情景4 1-3 5.95 0.042 3 0.237 3 0.408 8情景5 1-10 25.91 0.005 1 0.028 5 0.045 4 10-11 15.93 0.004 9 0.027 5 0.045 4 11-12 8.60 0.004 8 0.026 9 0.045 4 12-13 1.88 0.013 8 0.077 8 0.136 3 13-3 1.00 0.013 8 0.077 5 0.136 3
从表5 可以看出,情景1 的导体温度最高,为56.63℃,情景2 的导体温度最低,为-17.73℃,二者的温差达到了74.36℃。在情景5 中,支路1-3 首末端导体温度差值也达到了24.91℃。由此可见,导体温度的时空变化幅度较大。电阻及电抗与导体温度呈线性关系,情景1 的导体温度最高,导致电阻及电抗最大;情景2 的导体温度最低,导致电阻及电抗最小;情景5 中,随着导体温度的逐渐降低,电阻及电抗也逐渐减小。本文忽略了导体温度对导线对地电容的影响。
节点电压、相角、有功功率、电流及系统有功损耗的计算结果见表6。
表6 六种情形下的潮流计算结果
Tab.6 The power flow results under 6 cases

情景 节点电压幅值(pu) 节点电压相角/(°) 支路潮流/MW 支路电流/A 有功损耗/MW 1 2 3 1 2 3 2-1 3-1 2-3 2-1 3-1 2-3 基准情景 0.909 5 1.026 1 1.041 8 -31.86 -20.54 -12.14 200.64 136.81 60.64 565.52 353.1 158.37 19.05 情景1 0.852 0 1.012 3 1.031 2 -37.13 -22.55 -12.44 203.38 139.95 63.38 604.84 374.71 166.62 25.34 相差 -6.32% -1.34% -1.02% -16.54% -9.79% -2.47% 1.37% 2.3% 4.52% 6.95% 6.12% 5.21% 33.02% 情景2 0.945 5 1.035 3 1.048 0 -27.94 -18.70 -11.95 198.35 135.32 58.33 541.07 343.14 152.15 14.97 相差 3.96% 0.9% 0.6% 12.3% 8.96% 1.57% -1.14% -1.09% -3.81% -4.32% -2.82% -3.93% -21.42%情景3 0.893 2 1.024 4 1.038 0 -32.62 -20.04 -12.22 197.46 141.63 57.46 562.90 370.29 150.86 20.49 相差 -1.79% -0.17% -0.36% -2.39% 2.43% -0.66% -1.58% 3.52% -5.24% -0.46% 4.87% -4.74% 7.56% 情景4 0.898 3 1.026 3 1.038 6 -31.88 -19.48 -12.20 195.70 142.88 55.69 554.66 372.85 146.43 19.84 相差 -1.23% 0.02% -0.31% -0.06% 5.16% -0.49% -2.46% 4.44% -8.16% -1.92% 5.59% -7.54% 4.15% 情景5 0.901 0 1.027 0 1.039 0 -31.61 -19.29 -12.18 195.19 143.09 55.19 551.66 382.13 144.67 19.51 相差 -0.93% 0.09% -0.27% 0.78% 6.09% -0.33% -2.72% 4.59% -8.99% -2.45% 8.22% -8.65% 2.41%
可以看出,情景1 与基准情景相比,节点1 的电压变化最大,电压幅值的差额达到了-6.32%,相位差额达到了-16.54%。这是因为节点1 离电源较远,电压支撑能力较弱。支路2-3 的有功潮流相差最大,达到了4.52%。支路2-1 的电流相差最大,达到了6.95%。情景1 的系统有功损耗与基准情景差额达到了33.02%,变化是非常显著的,这是因为线路的电阻参数受导体温度变化影响较大,而系统有功损耗主要是由导体电阻流经电流产生的焦耳热引起的;情景2 与情景1 相比,导体温度与基准情景相差较小,所以电压及潮流相比情景1 相差较小,但有功损耗的差别也达到了-21.42%。情景1 与情景2考虑了沿线气象条件的季节性变化,由此可见,气象条件的季节性对系统潮流的影响不容忽略,尤其是对系统有功损耗的影响。
情景3、情景4 和情景5 考虑了沿线气象参数的空间分布不均匀性。在此三种情景中,分别采用不同的气象数据表征模型,考虑气象参数沿线空间分布的不均匀性。情景3 中架空输电线路首末端环境温度平均值为-10℃,风速为5.25m/s;而情景4 中输电线路沿线已知环境温度权重平均值为2.67℃,风速权重平均值为11.42m/s。情景4 与情景3 相比,支路潮流的最大差额达到了-3.08%,电流的最大差额达到了-2.94%,有功损耗差额为-3.17%。情景5 中采用线路分段模型,情景5 相对于情景3 支路潮流的最大差额达到了-3.95%,电流的最大差额达到了-4.10%,有功损耗的差额为-4.78%。
另外,在本文算例中,设支路1-2 导体温度为常规计算值20℃,当支路1-3 和支路2-3 导体温度平均值或加权平均值与常规计算所采用导体温度相差15℃时,系统有功损耗计算差值也达到了5%,也进一步说明在系统状态分析中有必要考虑导体温度的时空分布特性。从表6 计算结果可见,采用不同的气象数据表征模型,系统运行状态的分析结果相差还是显著的。不同模型表征气象条件时空分布的精确度不同,越精确,潮流计算结果越准确,但是计算规模越大,计算过程越复杂。
阈值温度不同则线路的分段数不同。表7 给出了不同分段数下的支路2-3 潮流及系统有功损耗。随着阈值温度的降低,分段数逐渐增加。当由3 段增加到5 段时,有功功率变化-0.58%,电流变化-0.88%,有功损耗变化-0.81%;由5 段增加到7 段时,有功功率变化-0.16%,电流变化0.17%,有功损耗变化0%,变化已不明显。随着分段数的增加,潮流计算将会更加准确,然而系统节点数及计算规模也将变大。因此本算例采用折中的5 段进行研究。
表7 不同分段数下的支路2-3 潮流及系统有功损耗
Tab.7 Power flow of branch 2-3 and active loss of system under different segment numbers

阈值温度/℃ 分段数/段 有功功率/MW 电流/A 有功损耗/MW 10 3 55.51 145.96 19.67 6 5 55.19 144.67 19.51 4 7 55.10 144.92 19.51
5.2 极限传输功率
为了研究输电线路沿线气象参数分布对系统极限传输能力的影响,1 号节点的有功、无功负荷按照同一比例增长,其余的节点负荷不变。负荷增量由各发电机出力大小按比例分配,采用连续潮流方法得到基准情景与其他五种情景的PV 曲线,如图9 所示。表8 和表9 详细列出了极限传输功率值与其对应的电压值。

图9 1 号节点PV 曲线及其局部放大图
Fig.9 PV curves of bus 1 and its zoomed in curves
表8 计及气象数据季节性变化的极限传输功率
Tab.8 The limit power transfer under meteorological data seasonal variation
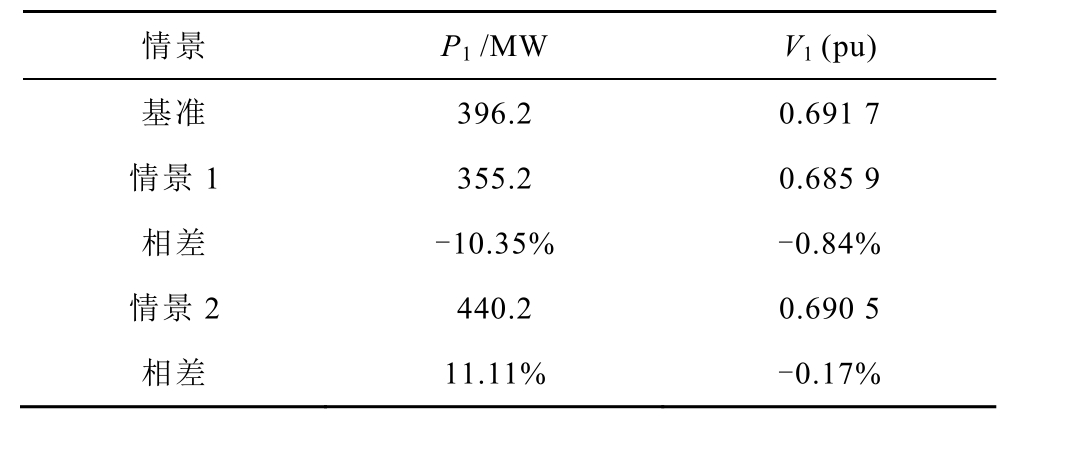
情景 P1 /MW V1 (pu) 基准 396.2 0.691 7 情景1 355.2 0.685 9 相差 -10.35% -0.84% 情景2 440.2 0.690 5 相差 11.11% -0.17%
表9 计及气象数据空间分布的极限传输功率
Tab.9 The limit power transfer under meteorological data spatial variation
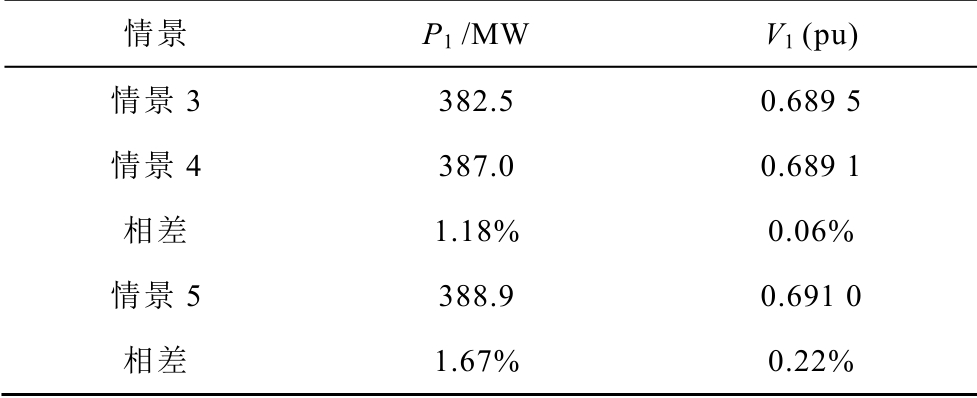
情景 P1 /MW V1 (pu) 情景3 382.5 0.689 5 情景4 387.0 0.689 1 相差 1.18% 0.06% 情景5 388.9 0.691 0 相差 1.67% 0.22%
情景1 和情景2 反映了季节性变化下的线路功率传输特性。基准情景的导体温度恒为20℃,极限传输功率为396.2MW;情景1 的环境温度为38℃,风速为0.5 m/s,极限传输功率为355.2MW,与基准值相差-10.35%;情景2 的环境温度为-20℃,风速为18 m/s,极限传输功率为440.2MW,与基准情景相差11.11%。可以看出,季节性的气象条件变化对线路极限传输功率有很大影响,计及气象条件的变化可有效提高系统极限传输功率计算的准确性。
在表9 中,情景3、情景4 和情景5 环境温度为20℃,风速为0.5m/s,节点3 处发生寒流,环境温度骤变为0℃,风速骤变为10m/s,上述三种情景为计及了气象数据空间分布的极限传输功率。情景3 采用平均值模型,极限传输功率为382.5MW,与基准情景相差-3.46%;情景4 极限传输功率为387.0MW,情景4 采用加权平均值模型,与情景3 的平均值模型相比相差1.18%,传输功率相差4.5MW;情景5 分段模型与情景3 平均值模型相比相差1.67%,极限传输功率相差6.4MW。以上三种情景的对比说明了描述气象数据空间分布的表征模型不同,计算结果还是相差较大的。每种模型的适应条件与实际气象数据的变化速率及变化幅度、架空线路长度、电网地理位置与结构参数等诸多因素有关,需针对实际电网,利用真实气象数据进行实证研究。
6 结论
本文通过输电线路导体温度时空分布的验证分析,在合理设定的基础上提供了一种考虑气象时空分布特性的线路传输特性分析方法。输电线路设定为固定的单段集中参数模型,所得到的线路潮流及极限传输功率与实际情况偏差较大。本文通过实例验证了输电线路沿线气象参数具有显著的时空变化特性,建立了考虑气象参数时间分布的季节性模型,和考虑气象参数空间分布的平均值、加权平均值及线路分段模型。在上述模型的基础上对线路潮流及极限传输功率做了具体的分析,计算结果表明气象数据的时空分布对系统运行状态有重要的影响,在对电网状态进行分析时有必要计及气象参数的时空分布特性。
[1] 张刘春. ±1100kV 特高压直流输电线路防雷保护[J]. 电工技术学报, 2018, 33(19): 4611-4617. Zhang Liuchun. Lightning protection of ±1100kV UHVDC transmission line[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4611-4617.
[2] 黎鹏, 阮江军, 黄道春, 等. 模拟山火条件下导线-板间隙击穿特性影响因素分析[J]. 电工技术学报, 2018, 33(1): 195-201. Li Peng, Ruan Jiangjun, Huang Daochun, et al. Influence factors analysis of the conductor-plane gap breakdown characteristic under simulation forest fire condition[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 195-201.
[3] 陈珩. 电力系统稳态分析 [M]. 3 版. 北京: 中国电力出版社, 2007.
[4] 张辉, 韩学山, 王艳玲. 架空输电线路运行载流量分析[J]. 电网技术, 2008, 32(14): 31-35. Zhang Hui, Han Xueshan, Wang Yanling. Analysis on current carrying capacity of overhead lines being operated[J]. Power System Technology, 2008, 32(14): 31-35.
[5] 倪识远, 胡志坚, 傅晨宇. 单回不对称输电线路分布参数的测量方法[J]. 电工技术学报, 2018, 33(5): 1086-1095. Ni Shiyuan, Hu Zhijian, Fu Chenyu. A method for measuring the distributed parameters of single-circuit asymmetric transmission line[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1086-1095.
[6] 张启平, 钱之银. 输电线路实时动态增容的可行性研究[J]. 电网技术, 2005, 33(7): 18-21. Zhang Qiping, Qian Zhiyin. Study on real-time dynamic capacity increase of transmission line[J]. Power System Technology, 2005, 33(7): 18-21.
[7] 周海松, 陈哲, 张健, 等. 应用气象数值预报技术提高输电线路动态载流量能力[J]. 电网技术, 2016, 40(7): 2175-2178. Zhou Haisong, Chen Zhe, Zhang Jian, et al. Application of meteorological numerical forecast technology for improving transmission line capability[J]. Power System Technology, 2016, 40(7): 2175-2178.
[8] 陈德辉, 神学顺. 新一代数值预报系统GRAPES 研究进展[J]. 应用气象学报, 2006, 17(6): 773-777. Chen Dehui, Shen Xueshun. Recent progress on GRAPES research and application[J]. Journal of Applied Meterological Science, 2006, 17(6): 773-777.
[9] 殷治军. 基于气象数据的架空输电线路热载荷能力研究[D]. 济南: 山东大学, 2017.
[10] 王艳玲, 严志杰, 梁立凯, 等. 气象数据驱动的架空线路载流的动态定值分析[J]. 电网技术, 2018, 42(1): 315-322. Wang Yanling, Yan Zhijie, Liang Likai, et al. Dynamic rating analysis of overhead line loadability driven by meteorological data[J]. Power System Technology, 2018, 42(1): 315-322.
[11] Cecchi V, Knudson M, Miu K. System impacts of temperature-dependent transmission line models[J]. IEEE Transactions on Power Delivery, 2013, 28(4): 2300-2308.
[12] Cecchi V, Leger A, Miu K, et al. Incorporating temperature variations into transmission-line models[J]. IEEE Transactions on Power Delivery, 2011, 26(4): 2189-2196.
[13] Jupe S, Kadar D, Murphy G, et al. Application of a dynamic thermal rating system to a 132kV distribution network[C]//IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies, Manchester, England, 2011: 1-8.
[14] 徐青松, 季洪献, 侯炜, 等. 监测导线温度实现输电线路增容新技术[J]. 电网技术, 2006, 30(增刊): 171-176. Xu Qingsong, Ji Hongxian, Hou Wei, et al. The novel technique of transmission line’s capacity increase by means of monitoring conductor’s temperature[J]. Power System Technology, 2006, 30(S): 171-176.
[15] Greenwood D, Gentle J, Smyers K. A comparison of real-time thermal rating systems in the U.S. and the U.K.[J]. IEEE Transactions on Power Delivery, 2014, 29(4): 1849-1858.
[16] 丁希亮, 韩学山, 张辉, 等. 电热协调潮流及输电线路温度变化过程分析[J]. 中国电机工程学报, 2008, 28(19): 138-144. Ding Xiliang, Han Xueshan, Zhang Hui, et al. Analysis on electrothermal coordination power flow and transmission line temperature variation process[J]. Proceedings of the CSEE, 2008, 28(19): 138-144.
[17] 王孟夏, 韩学山, 黄金鑫, 等. 计及电缆热特性的电热耦合潮流计算[J]. 电力系统自动化, 2016, 40(11): 73-79. Wang Mengxia, Han Xueshan, Huang Jinxin, et al. Electro-thermal power flow calculation considering thermal properties of cable [J]. Automation of Electric Power Systems, 2016, 40(11): 73-79.
[18] 董晓明, 梁军, 韩学山, 等. 计及输电线路温度变化的连续潮流模型与计算[J]. 电力系统保护与控制, 2012, 40(23): 36-41. Dong Xiaoming, Liang Jun, Han Xueshan, et al. Model and calculation of continuation power flow considering change of transmission line temperature[J]. Power System Protection and Control, 2012, 40(23): 36-41.
[19] 王艳玲, 梁立凯, 韩学山, 等. 计及动态热定值的配电网可靠性分析[J]. 中国电机工程学报, 2017, 37(5): 1400-1417. Wang Yanling, Liang Likai, Han Xueshan, et al. Distribution network reliability analysis considering dynamic thermal rating[J]. Proceedings of the CSEE, 2017, 37(5): 1400-1417.
[20] 冯凯, 应展峰, 陈汹, 等. 计及线路热惯性效应的模型预测控制安全经济调度模型[J]. 电工技术学报, 2018, 33(8): 1875-1883. Feng Kai, Ying Zhanfeng, Chen Xiong, et al. Model predictive control security economic dispatch model considering transmission line thermal inertia effect[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1875-1883.
[21] 胡剑, 熊小伏, 王建. 基于热网络模型的架空输电线路径向和周向温度计算方法[J]. 电工技术学报, 2019, 34(1): 139-152. Hu Jian, Xiong Xiaofu, Wang Jian. Radial and circumferential temperature calculation method of overhead transmission lines based on thermal network model[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 139-152.
[22] CIGRE. Thermal behavior of overhead conductors[R]. CIGRE WG12, ELECTRA(144), 1992.