0 引言
近年来，全球正大力发展分布式可再生能源发电，但其随机性和间歇性的特点使得并网面临巨大挑战，导致弃风、弃光率居高不下。如何提高新能源利用率成为当前的研究热点[1-3]。需求响应（Demand Response, DR）作为一种灵活性资源参与电力系统的调峰和备用，通常被认为是储能设备的低成本替代，充分挖掘DR 潜力，通过DR 来适应可再生能源发电大规模接入系统，将成为未来智能电网的发展趋势[4-6]。
分布式发电技术的发展为DR 的实施提供了有利的应用平台。当系统出现意外事件时，通过采用先进的测量技术和通信系统，需求侧资源能够及时做出反馈，调整用电需求，实现源荷之间的供需平衡。同时将DR 项目纳入电力系统的经济调度中，能够达到削峰填谷[7-8]、节能减排等效果[9]。当前形势下，国内外已有诸多学者对计及DR 的优化调度问题进行了研究。在国内，文献[10]以最大消纳风电和系统运行成本最小为目标，建立了计及大规模风电和需求响应参与的电力系统随机调度模型，用以解决风电出力的不确定性；文献[11]利用分布式系统内部需求侧负荷来解决电力市场交易时所面临的新能源出力波动问题，证明了对负荷进行调度，能够很好地抵消新能源机组的随机性，使系统获得更高收益。国外电力市场较国内更为开放，其研究目标更多地聚焦在紧急需求响应、能量市场等方面。文献[12]提出了一种DR 资源对系统短期充裕性影响分析的评估模型，研究了紧急需求响应在削减高峰负荷、提高负载因数等方面取得的成效，说明了DR 资源能够有效提高系统的可靠性；文献[13]分析了辅助服务DR 项目在n-k 安全约束机组组合中的应用，作为一种备用方式，因其平抑新能源波动性的快速响应优势，得到了一定应用。目前，我国正在进行电力市场改革，电价及激励政策尚未完善，有必要针对中国具体国情，将DR 资源纳入日前调度计划，加强需求侧与供电侧的互动，提高电力系统运行的经济性和可靠性。
此外，大多数调度策略在优化管理过程中并没有深入研究系统内不确定因素导致的收益风险。投资组合理论等风险度量方法可用于权衡资产收益和风险的关系，且已在电力系统优化调度领域得到了广泛应用。文献[14]详细归纳了随机规划模型中常用的风险度量方法，包括利润方差法、风险价值（Value-at-Risk, VaR）法、条件风险价值（Conditional Value-at-Risk, CVaR）法等。其中CVaR 作为一种有效的风险度量手段已经被广泛应用于电力系统的风险管理。文献[15]采用CVaR 方法，提出了基于风险规避的优化运行框架，以提高风电等随机性电源接入后系统在电力市场中的收益。文献[16]为了提高分布式电源和DR 接入系统的收益，根据不确定性随机变量的分布信息，利用CVaR 建立系统风险评估体系。文献[17]计及了可再生能源出力及市场电价不确定性，搭建了风险约束的随机规划模型，将CVaR 风险作为约束条件，对系统面临的风险进行约束，进而提高系统运行可靠性。但CVaR 方法在应用过程中需满足不确定性随机变量服从某一确定分布，这与实际应用不符。在工程实际中，存在新能源出力和电价等不确定因素，而且由于环境、市场以及预测技术的限制，很难获得其分布的准确信息，一般只能掌握其部分信息。因此，用以描述随机变量的分布本身也具有不确定性，导致CVaR 理论在评估风险过程中产生不可忽视的误差，这也限制了CVaR 理论的应用，CVaR 对只掌握部分随机变量分布信息的情况并不适用。
本文在已有研究基础上，进一步提出了基于最差条件风险价值（Worst-case Conditional Value-at-Risk，WCVaR）理论的收益-风险组合优化调度模型，利用WCVaR 理论处理不确定性随机变量分布信息不完全问题，进而量化可再生能源出力、负荷以及市场电价不确定性给资源调度管理带来的低收益风险。同时，将需求响应和可靠性指标融入日前调度模型中，协调解决发电侧和需求侧的供需互动问题，实现系统经济和可靠运行。通过仿真算例验证了所提模型的可行性和有效性。
1 基于激励补偿机制的DR 建模
随着电力市场的逐渐开放，在需求侧我国普遍实行了基于价格型需求响应的峰谷分时电价政策，而针对激励型响应政策尚未完善，需展开进一步研究。本文在分时电价的基础上，引入激励补偿机制，构建多时段DR 模型，鼓励用户主动参与系统优化调度，保证电网经济性与安全性。
本文假设分布式系统运营商（Distributed System Operator, DSO）负责分布式系统优化调度。DSO 从分布式单元（Distributed Generator, DG）发电企业和需求响应用户购买电量，并按照实时电价向用电负荷售电。按照此种模式，DSO 根据自身收益来确定最优购电组合计划，制定能量和备用市场中的发电资源分配策略。图1 为需求响应参与系统调度的框架图，图中η 表示用户需求响应参与度，激励补偿越高，用户参与需求响应的主动性越强，η 越大。
图1 计及DR 的日前调度计划框架
Fig.1 Day-ahead scheduling framework considering DR
1.1 单时段DR 模型
单时段DR 指某一时段内，在激励机制作用下，用户主动调整负荷，但无法将用电需求转移到其他时段。
实施需求响应后，t 时段用户j 的电力需求将从D0 j ,t 变为 D Dj ,R t，则
式中，D∆,j t为用户j 在t 时段需求响应前后的负荷之差。
为提高用户参与程度，规定在出现最高负荷时，DSO 将给予用户 *A 元/（MW·h）的补偿，根据各时段负荷水平差异，实时调整激励价格。定义“DR 比例系数” tΓ 为各时段负荷与负荷最大值之比，即
式中，T 为调度周期。则各时段的补偿价格 tA 为
式中， *A 为最高补偿价格。则t 时段用户j 参与DR获得的报酬为
t 时段用户j 的DR 收益S 为
式中，B ( D Dj ,Rt)为t 时段未实施补偿前用户j 用电量等于 D Dj ,Rt 时的收益；Prt 为DR 下t 时段的电价。收益 B ( D D j ,Rt )表示为
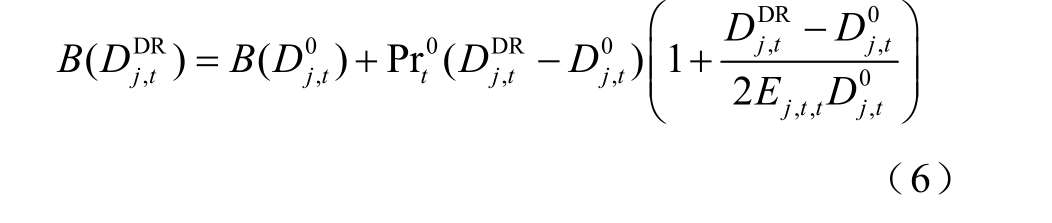
式中，Ej , t ,t为自弹性系数；P rt0 为响应前t 时段电价；B( D 0j ,t )为用电量等于 D 0j ,t 时的收益。
由式（5）和式（6）可知，收益S 近似为开口向下的抛物线函数，当 ∂S ∂D D ,Rt = 0时，收益S 取到最大值。
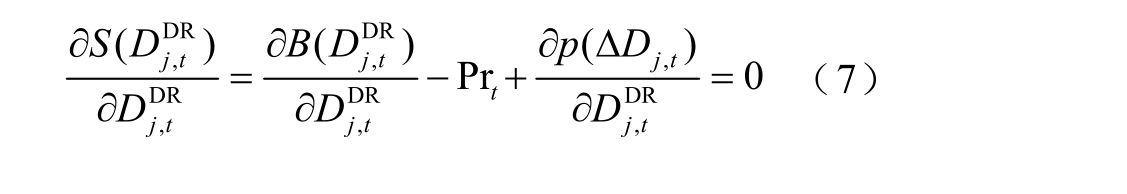
联立式（4）和式（7）得
进一步，根据式（6）和式（8）有
则计及需求响应后，t 时段用户j 的用电需求调整为
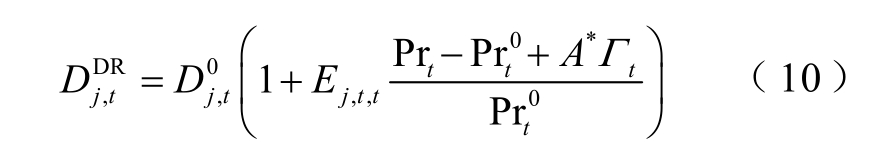
1.2 多时段DR 模型
多时段DR 是指在激励机制的作用下，用户可将当前的用电负荷转移至其他时段，实现负荷多时段转移。
与建立单时段模型类似，多时段下，t 时段用户j 的需求为
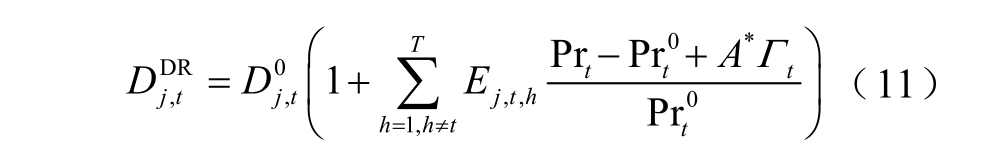
式中E,j t h 为交叉弹性系数。
1.3 组合DR 模型
引入“DR 响应系数”η 作为用户参与DR 项目的参与度。一般情况下认为ηt 与At 成正比，但在系统实际调度过程中，居民及工商业用户的必须用电不会因为价值或激励的调整而减少，因此导致用户参与度存在饱和阈值，即响应超过这个数值，用户就没有更进一步的响应了。因此本文设定 maxPrt 为饱和阈值，用以约束参与度ηt，ηt 可表示为
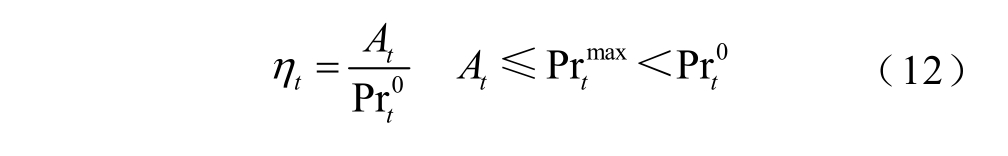
联立式（10）～式（12），t 时段用户j 实际参与需求响应的负荷为
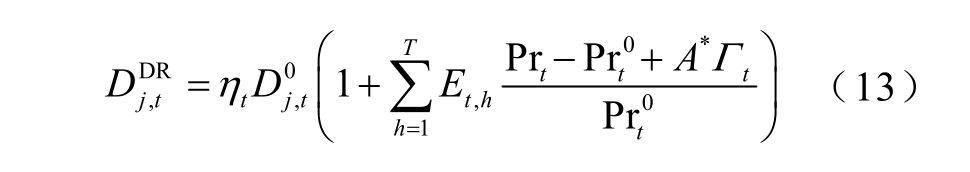
t 时段的实际负荷为
2 可靠性指标计算及转换
可靠性评估作为电力调度的重要组成部分，对电网的安全稳定运行起着重要作用。近年来，在欧美等多个电力市场中，概率性旋转备用（Spinning Reserve, SR）评估方法得到了广泛应用。本文采用电量不足期望（Expected Energy Not Served, EENS）评价系统短期可靠性。EENS 用以衡量系统当前的备用容量水平，当EENS 较小时，备用容量较大，可靠性水平较高。
为简化模型，假定系统失负荷仅由发电机组故障停运引起，考虑在日前调度过程中，机组发生多重故障的概率非常小，故本文在计算EENS 时，仅计及双重故障，t 时段系统EENSt 表示为
式中，P .i t为t 时段机组i 出力；SRt 为t 时段系统的旋转备用容量，
；R,i t 为机组i 在t 时段 的备用容量；δ i , t= 1表明t 时段机组i 切机将导致备用不足，系统失负荷，反之，δ i , t = 0，即系统处于安全状态，不会失负荷；si S ,t 和si D ,t分别为单机和双机故障下机组i 的失负荷贡献系数； pi S ,t 和 pi D ,t分别为发生单机和双机故障的概率；NG 为常规机组数量。
通过对用户进行调查统计，获取失负荷价值（Values of Lost Load, VOLL）。将可靠性指标EENS 转换为经济性指标，实现市场环境下电网运行过程中可靠性与经济性的相互平衡。期望停电损失成本为
3 风险管理
由于存在新能源机组出力、负荷以及电价的不确定性，会导致分布式发电系统在能量市场中的收益出现不同水平的波动，具有一定的风险特征，且在发电调度管理过程中采取不同的风险态度，收益会产生较明显的差异。因此本文引入WCVaR 方法，该方法能够在仅知道随机变量属于某一分布集合的情况下，合理权衡风险与收益。
3.1 最差条件风险价值理论概述
令 f ( x , y )为风险管理过程中的收益函数，其值由决策变量 x ∈ χ⊆Rn和随机变量 y ∈Rm决定， y的概率密度函数为 p ( y )，则收益函数不低于其阈值ζ 的概率为
对于给定的 x ∈χ，Ψ ( x , ζ )为收益函数 f ( x , y)的累积分布函数，且Ψ ( x , ζ )是关于ζ 的非增函数。
给定置信水平 α ∈ (0,1)的风险价值VaR α ( x )为
式中，VaR α ( x )值为Ψ ( x, ζ ) =α时，由ζ 值组成的非空区间右端点。
那么，置信水平α 下的条件风险价值CVaRα ( x)可表示为
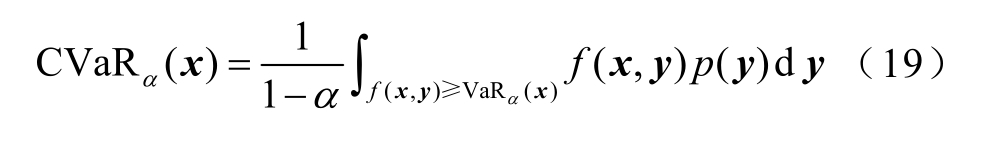
由式（19）直接计算CVaR α ( x )非常困难，Rockafellar-Uryasev 在文献[18]中通过构造函数F ( x , ζ )来计算CVaRα ( x )，即
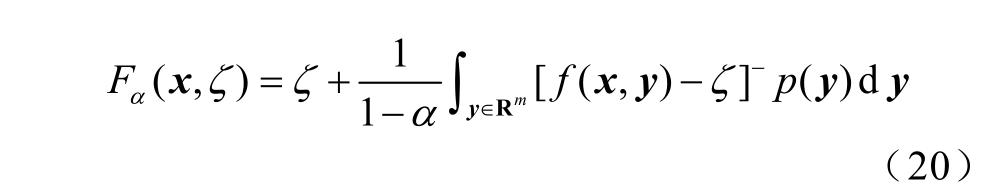
式中，
则有
在随机规划过程中，通过生成满足随机变量统计特征的可行情景集合来模拟随机变量y ，令
为情景集合，则有
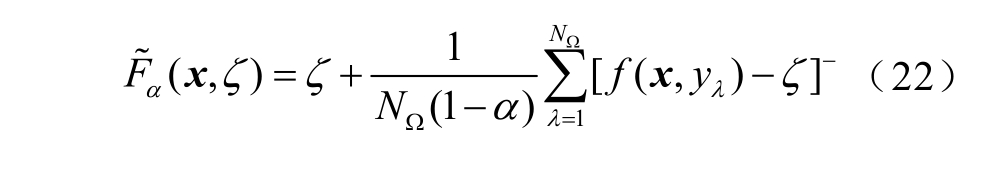
式中，NΩ 为集合中场景总数。
在实际过程中，决策者不可能掌握随机变量概率分布的准确信息。针对此种情况，提出了最差条件风险价值（WCVaR）概念，评估仅知道随机变量概率分布所属可能集合时的风险。
定义1 设随机变量y 的概率密度函数 (∈℘y)p ，℘为部分信息已知下的某分布集合，对任意 χ∈x 的WCVaR 定义为
联立式（22）和式（23）得
3.2 随机变量分布集合的处理
设随机变量y 的概率密度函数 ( )p ∈℘y ，即
式中，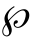
为不同分布 pl ( y )所构成的集合；m为分布的可能数量。
利用场景技术描述随机变量的不确定性，场景生成方法采用拉丁超立方法[19]。定义 lΩ 为 ( )lp y 分布下随机变量y 的场景集合，如式（26）所示，每 个场景发生的概率为 lλπ ，并满足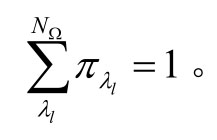
式中，q 为随机变量种类；λl为场景集合中的某一场景。
3.3 离散界约束下的WCVaR 模型转换与求解
定义2 若场景空间中的随机变量y 为
其场景点的概率满足 
称 lΩ 为离散分布。
在WCVaR 模型中，由于环境因素影响和技术手段有限，实际中难以获得概率密度函数 ( )p y 的准确表达式，此时，为了确定y 的场景点概率 0π 的可信度，需将 0π 放入一个给定的不确定集合。
假设π 为某一不确定集合，即
式中，π 0为名义概率分布（最有可能概率分布）；ε为偏差向量；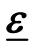
和
为常数向量。则称π 为界约束集，称随机变量y 服从离散界约束分布， e Tε = 0保证π 为某一概率分布。
根据 pl ( y )的分布集合℘，离散界约束集边界规定为
根据定义2，离散界约束分布下的WCVaR 风险值为
其中
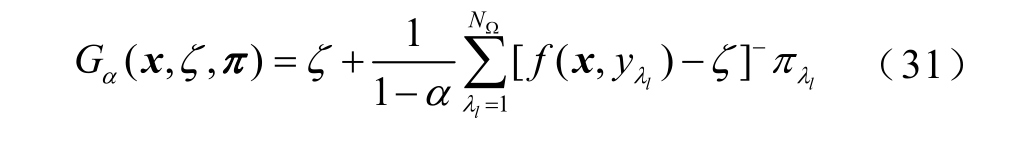
引入辅助变量 zλ l = f ( x, yλ l)-ζ，式（31）转换为
由
则有
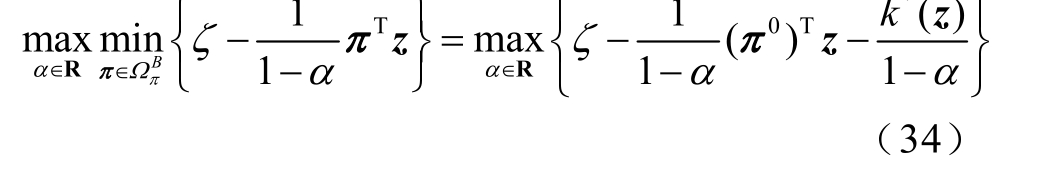
式中， (k* z )为下述线性规划问题的最优值。
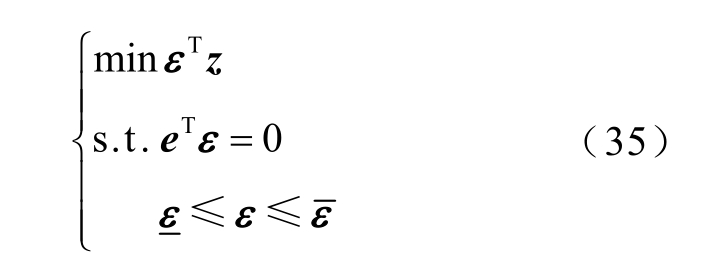
采用Lagrange 对偶定理，将式（35）转换为其对应的凸半定规划问题。
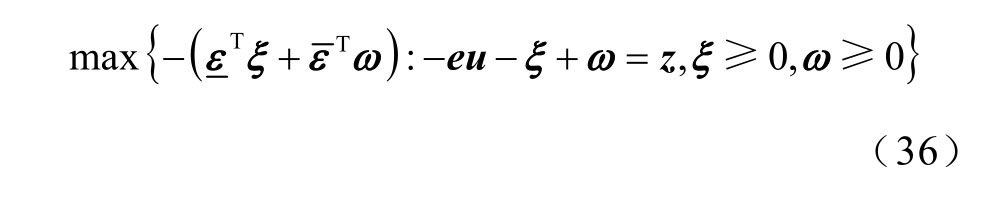
由此，含有max-min 复杂的NP 难问题，在离散界约束条件下，利用拉格朗日对偶原理，可以将所提模型转换为确定性的凸半定规划问题。在离散界约束分布下，风险值WCVaR 转换为如下模型
4 考虑WCVaR 的收益-风险组合优化模型
4.1 目标函数
本文利用WCVaR 建立收益-风险组合优化模型，其目标函数包含两部分，即
第一部分为实时运行过程中各场景下的期望收益，由于随机变量的概率分布仅知道部分信息，因此分布式系统的收益也是未知的。当随机变量属于离散界约束分布时，分布式系统的最差期望收益等于在所有已知分布中的收益最小值， 即
其中 E( profit λl )为场景集合 Ω l下的期望收益，其目标函数为
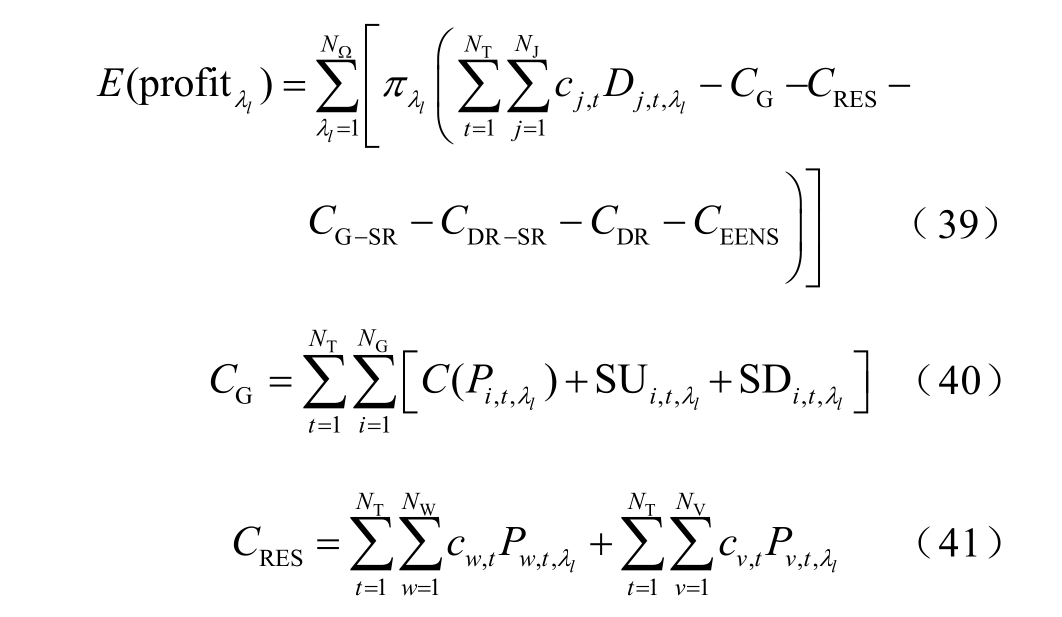
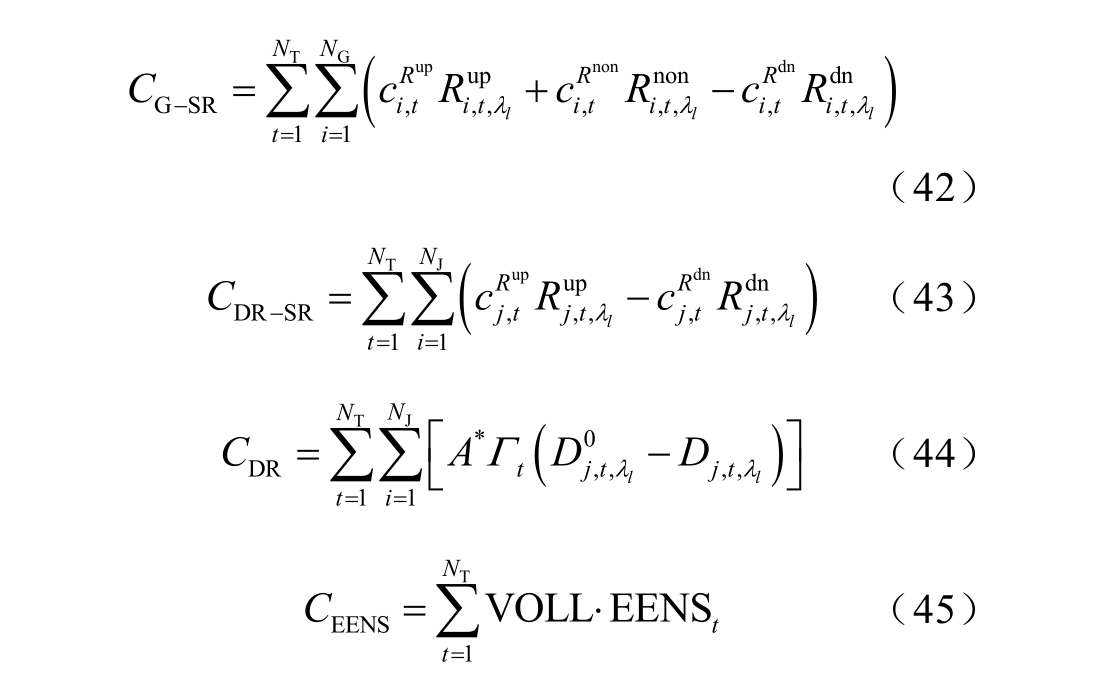
式中， c j ,t为向用户出售的电价； D j , t,λ l 为 λl 场景下t 时段用户j 的净负荷； CG 为常规机组购电成本，包括发电成本 C ( P i , t,λl )和起停成本 SU i , t ,λl 、 SD i , t ,λl ；C RES 为新能源购电成本，包括风电成本 c w, t Pw , t ,λ l 和光伏成本 cv ,t Pv , t,λ l ； N W和 N V分别为风机和光伏机组数量； c w, t和 cv ,t分别为风电和光伏的购电价格； Pw , t,λ l和 Pv , t,λ l 分别为 λl 场景下t 时段风机w 和光伏v 出力；C G - SR 为向常规机组购买备用的成本； ci R ,tu p 、ci R,tn on和c R ,td n 分别为t 时段机组i 提供上旋转备用、非旋转备用和下旋转备用的报价； Ri u , tp,λ l 、 R in , o t ,nλ l 和R id , tn, λ l 分别为λl 场景下t 时段向机组i 分配的上旋转备用、非旋转备用和下旋转备用量； CD R - SR为向DR 用户购买备用的成本； c Rj ,utp 和 c Rj ,dtn 分别为t 时段用户j 提供上、下旋转备用的报价； R uj ,p t ,λ l 和 R dj ,n t,λ l 分别为 λl 场景下t时段向用户j 分配的上、下旋转备用量； C DR为DR成本。
第二部分为风险度量项，需要特别说明的是，本文 WCVaR 风险模型中的 f ( x , y )为收益函数profitλl ，WCVaRα(x)近似为具有较低收益的概率为(1 - α) × 1 00%的情景集合所对应的期望收益，故其表示的是运营商面临的低收益风险，并非代表损失，因此调度计划的WCVaR α ( x )越大，代表风险越小，其与传统代表损失的风险意义并不相同。
4.2 约束条件
1）系统功率平衡约束
2）常规机组约束
（1）发电机输出功率约束
式中， Pi min和 Pi max分别为机组i 出力的下限和上限；γ i ,t 为t 时段机组i 的运行状态， γ i , t= 1表示开机，γ i , t = 0表示停机。
（2）机组启停约束
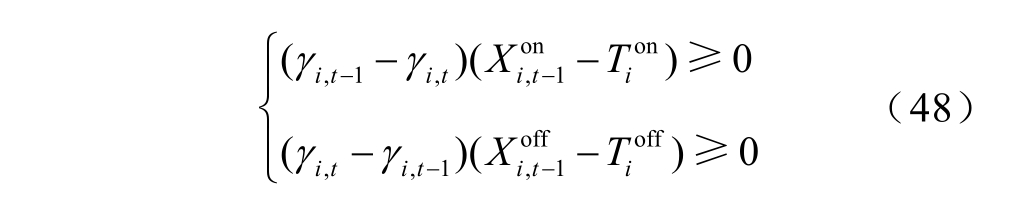
式中，X io , nt - 1 和 X io , ftf-1 分别为 t- 1时段机组i 已连续开机和停机的时段数； Ti on和 Ti off分别为机组i 的最小开机和停机时段数。
（3）机组爬坡约束
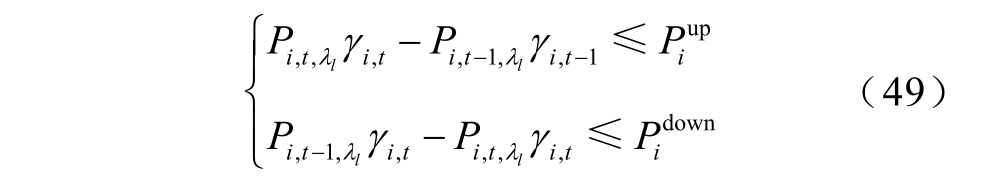
式中，P i up和 Pid own分别为机组i 的上、下爬坡限制。
3）需求响应约束
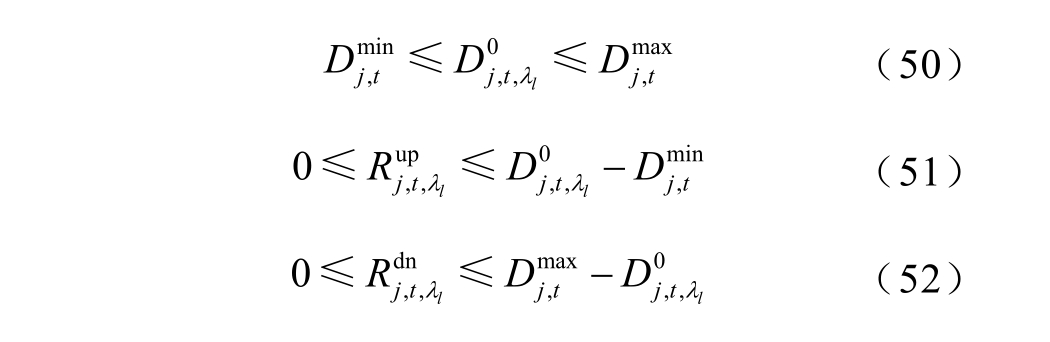
式中， 
和
分别为t 时段用户j 的最小和最大负荷。
4）系统备用约束
式中， riu, tp,λ l 、 ri d, tn,λ l 和 ri n, toλ nl 分别为 λl 情景下t 时段实际调用机组i 的上旋转备用、下旋转备用和非旋转备用。同样可得到DR 提供的备用约束条件为
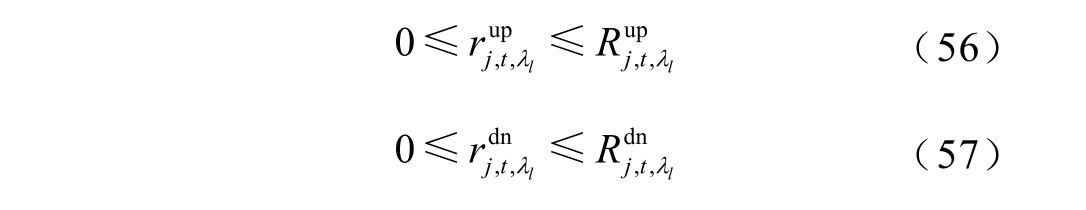
式中，
和
分别为 λl 情景下t 时段实际调用用户j 的上旋转备用和下旋转备用。
5）可靠性约束
本文考虑系统运行的可靠性约束主要体现为各时段下的电量不足期望小于某一限值，即
式中，EENS max为最大电量不足期望值。
5 仿真分析
5.1 参数设置
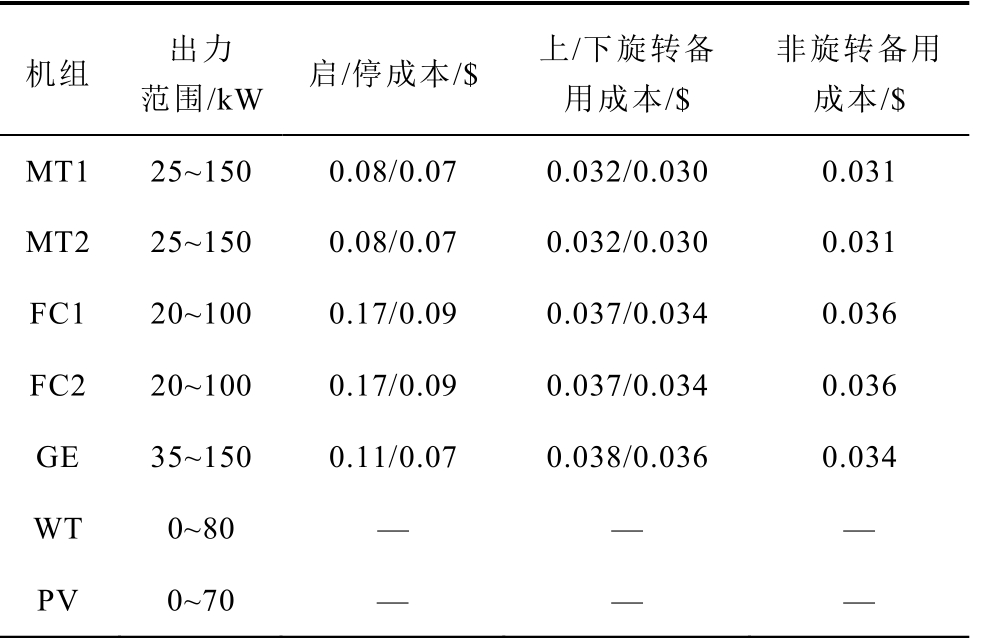
本文以改进的CIGRE16 节点低压分布式自治微网系统为例[20]，对所提模型进行分析，图2 为其拓扑结构，系统包含两台微型燃气轮机（MT1 和MT2），分别接入节点2 和12；两台燃料电池机组（FC1 和FC2），分别接入节点7 和14；一台内燃机组（GE），接入节点8；三台参数相同的风电机组（WT1、WT2 和WT3）接入节点6、9 和16；两台参数相同的光伏机组（PV1 和PV2）接入节点5 和10，各分布式电源具体参数见表1。在节点2、3、4、5、8、11、13 和15 接入8 组聚合负荷（L1～L8），均包含DR 负荷，响应负荷数据来自PJM 公司[21]。
图2 系统结构
Fig.2 Diagram of system structure
表1 机组参数
Tab.1 The parameters of generators
机组 出力 范围/kW 启/停成本/$ 上/下旋转备用成本/$ 非旋转备用成本/$ MT1 25～150 0.08/0.07 0.032/0.030 0.031 MT2 25～150 0.08/0.07 0.032/0.030 0.031 FC1 20～100 0.17/0.09 0.037/0.034 0.036 FC2 20～100 0.17/0.09 0.037/0.034 0.036 GE 35～150 0.11/0.07 0.038/0.036 0.034 WT 0～80 — — — PV 0～70 — — —
此外，利用拉丁超立方法模拟风电、光伏、负荷以及电价等随机变量的不确定性，生成2 000 场景，并采用K-means 算法削减至25 个场景。削减后各场景下各变量的取值如图3 中灰色实线所示。图中黑色虚线为变量的均值，即对应变量的预测值。
图3 随机变量场景
Fig.3 Scenarios of each stochastic parameters
5.2 数值结果与分析
本文仿真设置两种模式。模式1：DR 不参与系统优化；模式2：DR 参与系统优化。
α=0.95、VOLL=1$/(kW·h)时，在模式1 和模式2 两种情况下，不同风险规避水平下DSO 期望收益-WCVaR 的近似有效边界如图4 所示。
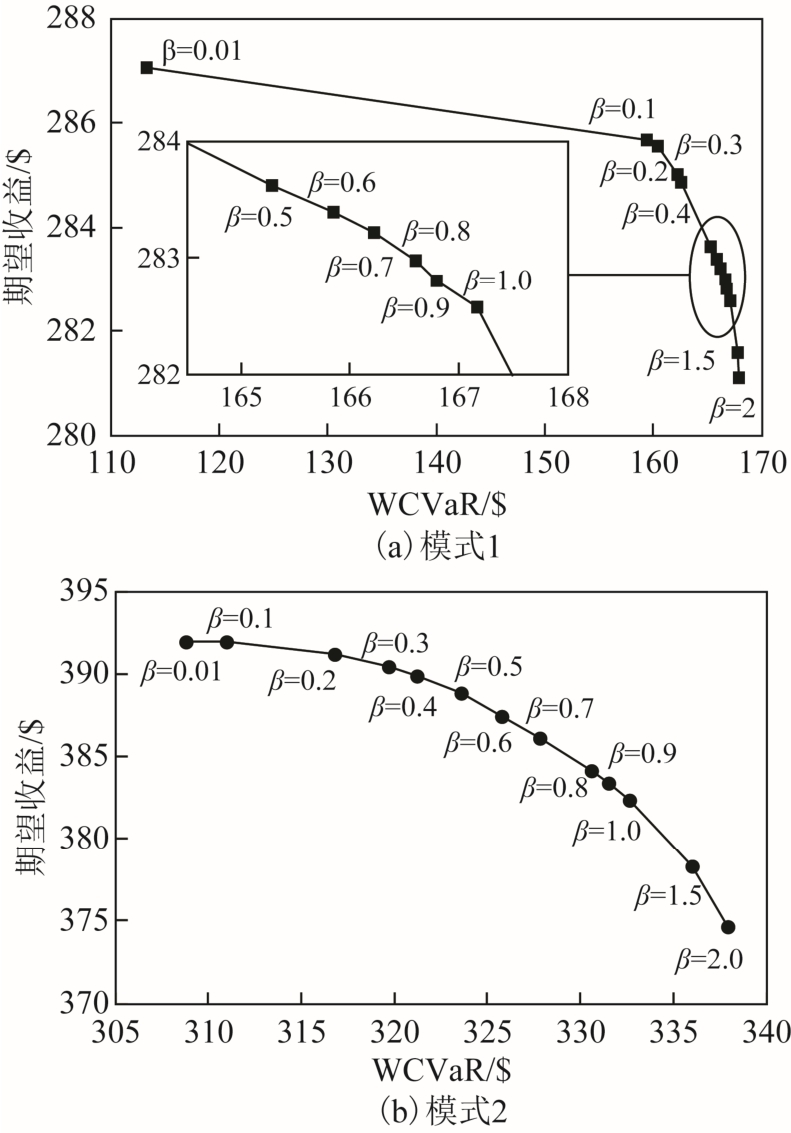
图4 系统期望收益和WCVaR 有效前沿
Fig.4 Efficient frontier of expected profit versus WCVaR with different patterns
图4 中收益-WCVaR 曲线均满足随着β 值增加，WCVaR 值增加而期望收益降低，这是因为风险规避参数增加，DSO 愿意以较低的收益换取较低的风险 水平。对比分析模式1 和模式2 可知，模式2 中β增加时，其收益降低率低于模式1，图4a 中，当β由 0.01 变化为 0.1，收益并未产生较大变化，但WCVaR 大幅增加，进一步增加β 值，DSO 期望收益下降较明显，而WCVaR 并未产生明显变化，即风险偏好程度较低时，随着风险规避参数增加，收益降低缓慢；当风险偏好程度较高时，较小的风险水平降低都会造成较严重的收益减少。表明无DR参与时，过度追求风险规避其效果并不理想，会导致收益减少严重，而风险并未产生明显变化；DR 参与时，收益-WCVaR 前沿变化较均匀，DSO 可以根据风险偏好来确定系统运行状态。
图5 为VOLL 取不同值时，两种模式下的期望收益和EENS 成本曲线。
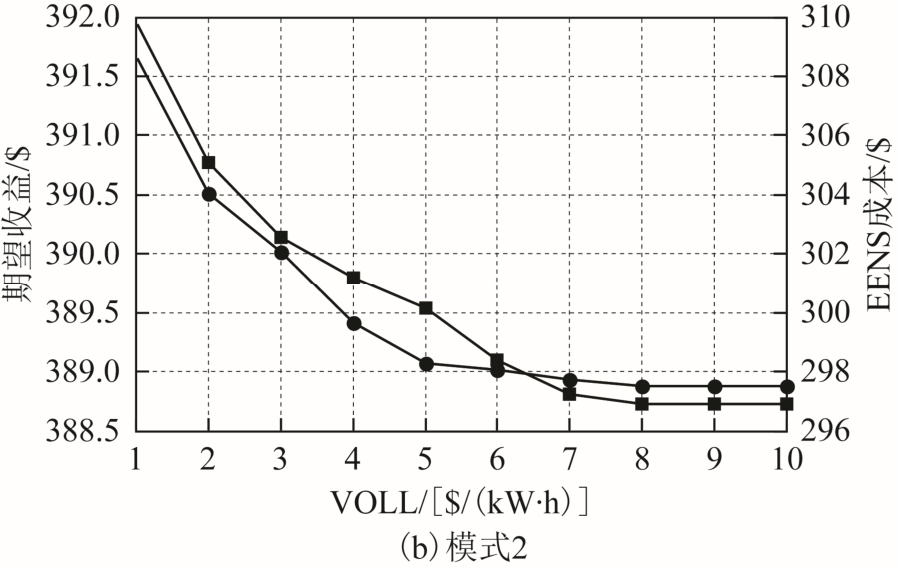
图5 不同VOLL 值下的期望收益与EENS 成本
Fig.5 Expected profit and cost of EENS under different VOLL values
从图5 中可以看出，模式1 中随着VOLL 值增加，EENS 成本在逐渐增加，尽管增加VOLL 值可以起到降低EENS 的作用，但DSO 需承担更多的EENS 成本。通常情况下，相比于设定较高的VOLL 值，购买额外备用的单价要低于强迫中断负荷而支付的补偿单价，所以随着VOLL 值增加，发电成本较高的机组逐渐承担这部分负荷，期望收益逐渐降低，甚至会出现负值。模式2 中，由于DR 的参与，可以缓解负荷高峰时段的强迫中断负荷。
图6 为不同VOLL 值下期望收益-WCVaR 有效前沿(β=0.01)，表2 为对应的系统各项指标。
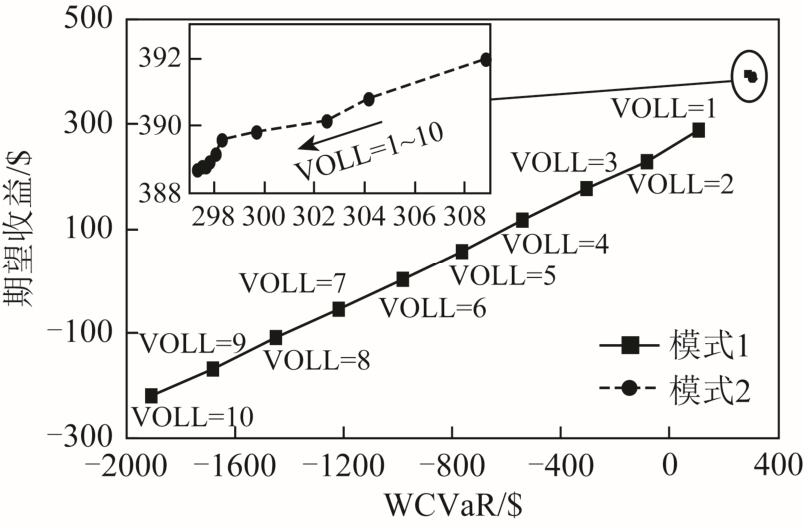
图6 不同VOLL 值下期望收益-WCVaR 有效前沿
Fig.6 Efficient frontier of expected profit versus WCVaR for different VOLL values
表2 不同VOLL 值对应的期望收益和可靠性水平指标
Tab.2 Expected profit and reliability level versus different VOLL
VOLL 期望收益/$ 总备用成本/$ 模式1 模式2 EENS/(kW·h) EENS 成本/$ 模式1 模式2 DGs 提供 DR 提供 DGs 提供 DR 提供 模式1 模式2 模式1 模式2 1 287.60 392.00 140.00 0 110.32 40.14 61.32 2.21 61.32 2.21 2 228.10 390.80 144.23 0 111.48 42.36 58.43 0.93 116.86 1.86 3 175.21 390.16 146.22 0 111.71 42.97 56.77 0.45 170.31 1.35 4 115.70 389.80 148.20 0 112.03 43.25 54.31 0.38 217.24 1.52 5 56.20 389.60 149.11 0 112.88 43.35 53.09 0.30 265.45 1.50 6 3.31 389.16 150.18 0 113.32 43.43 52.28 0.22 313.68 1.32 7 -56.20 388.92 151.22 0 113.48 44.33 51.05 0.13 357.35 0.91 8 -109.10 388.80 152.36 0 113.88 45.52 49.22 0 393.76 0 9 -168.60 388.76 153.37 0 113.88 45.52 49.22 0 442.98 0 10 -221.49 388.68 154.78 0 113.88 45.52 49.22 0 492.20 0
不难看出，两种模式下，期望收益和WCVaR 值均随VOLL 设定值的提高而降低。在模式1 中，从VOLL=1$/(kW·h)增至VOLL=10$/(kW·h)过程中，收益从287$降低至-221$，下降了177%；而在模式2中，仅仅降低了0.85%。不难理解，DR 参与调度后，DR 用户在高峰负荷时可以为系统提供备用容量，以降低较严重情况下的中断负荷量，相应的EENS成本也随之降低，DR 在提高DSO 收益和降低风险方面具有一定作用。
由表2 中各项数据分析得到，DSO 期望收益和系统运行可靠性受VOLL 影响，DSO 在调度过程中可根据VOLL 值的选取来保证系统运行可靠性。
表3 为调度周期内，不同VOLL 值下由DG 和DR 提供的上旋转备用（U-SR）、下旋转备用（DSR）和非旋转备用（N-SR）容量情况。从表中数据分析可知，提高VOLL 设定值，能够提高系统总备用水平，且当DR 参与调度后，可以提供一部分备用容量，减少了向价格较高的DG 单元购买备用容量，在一定程度上降低系统运行成本。通过改变VOLL 值，可以调整系统资源、备用以及EENS之间的平衡点。换言之，当VOLL 值增加时，提高系统备用水平较中断负荷更加经济。因此，在VOLL 取值较大情况下，系统的上、下旋转备用水平较高。
表3 VOLL 对总备用容量的影响
Tab.3 Impact of VOLL on the total reserve
模式 VOLL/ [$/(kW·h)] 备用容量/W U-SR (DGs) D-SR (DGs) N-SR (DGs) U-SR(DR)D-SR(DR)1 1 730 2 398 1 201 0 0 5 799 2 420 1 294 0 0 10 851 2 425 1 363 0 0 2 1 573 1 398 1 435 151 1 141 5 619 1 398 1 446 220 1 150 10 622 1 398 1 449 248 1 156
为了更直观地分析VOLL 值对系统备用水平的影响，图7 给出了VOLL=1$/(kW·h)和5$/(kW·h)下各个时段由DG 和DR 提供的系统上旋转备用水平。总的来说，为了避免不确定性带来的影响和提高系统可靠性水平，在VOLL 值较高水平下，系统总旋转备用水平也较高。
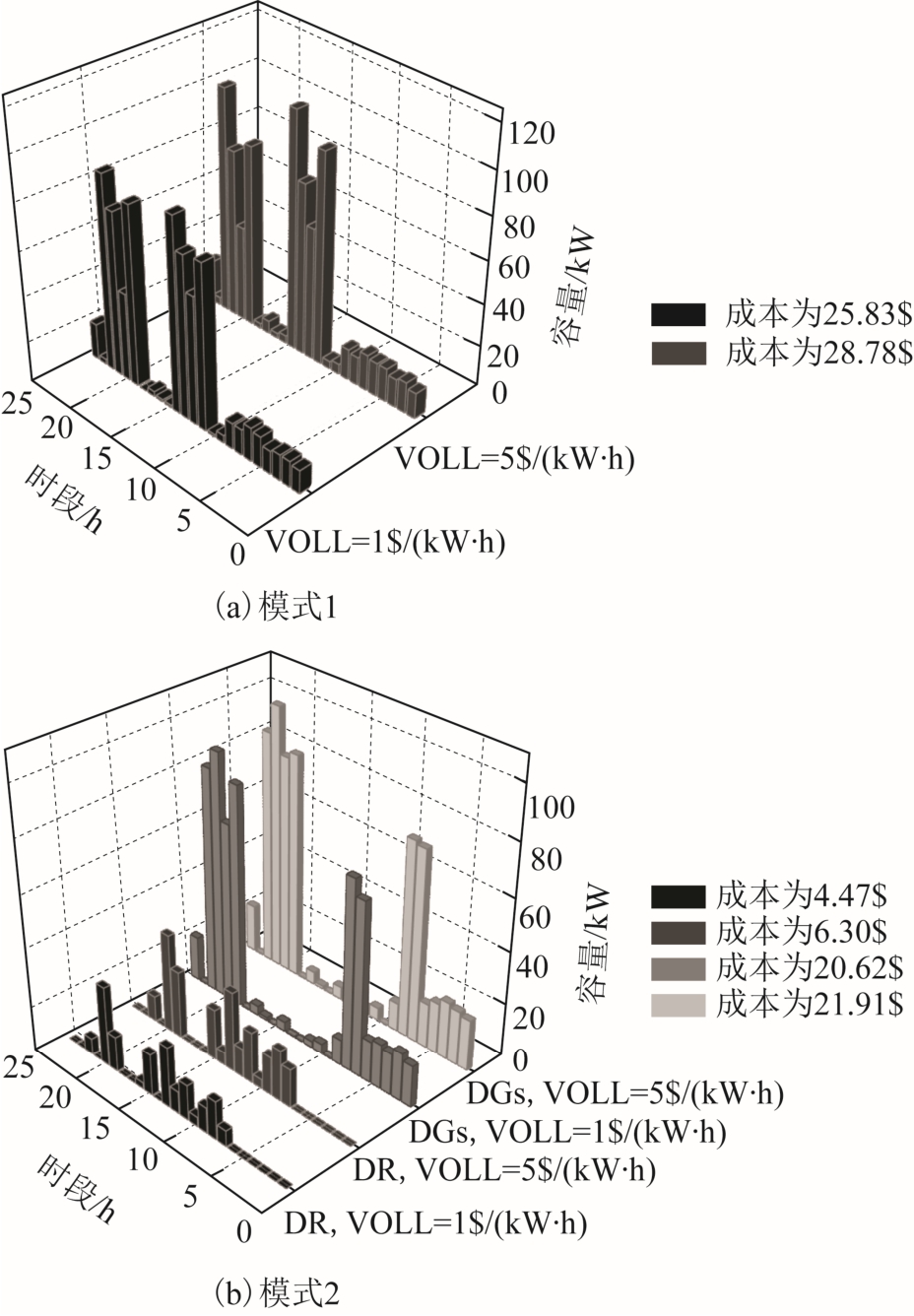
图7 各时段系统上旋转备用水平(β=0.01)
Fig.7 Hourly up-SR(β=0.01)
表4 为不同风险规避参数下的系统各项指标。 分析各项数据可知，总备用成本随β 增大而增加，主要由于DSO 为了降低严重情况下的强迫负荷中断，有必要购买更多的备用。此外，在β 逐渐增大过程中，EENS 和EENS 成本逐渐降低，尽管收益在一定程度上也逐渐降低，但此时系统的可靠水平也较高。
表4 不同风险规避参数下的期望收益和可靠性水平
Tab.4 Expected profit and reliability level versus different risk aversion parameter
β 期望收益/$ 总备用成本/$ EENS/(kW·h) EENS 成本/$ 模式1 模式2 模式1 模式2 DGs 提供 DR 提供 DGs 提供 DR 提供 模式1 模式2 模式1 模式2 0.01 66.35 393.42 146.29 0 113.41 42.25 57.37 0.38 286.85 1.90 0.1 64.28 392.03 147.56 0 112.69 46.42 56.48 0.27 282.40 1.35 0.5 60.26 386.13 149.65 0 111.36 54.13 56.00 0.23 280.00 1.15 1.0 57.67 380.38 151.48 0 110.55 63.26 55.42 0.17 277.10 0.85 1.5 53.20 375.94 152.98 0 109.46 70.14 54.88 0.14 274.40 0.70 2.0 50.45 369.01 154.33 0 108.01 72.38 54.00 0.09 270.00 0.45
表5 为不同风险规避参数下的系统各部分备用水平。可以看出，在较高风险规避参数时，为减少负荷中断的情况，系统总备用水平较高。模式1 中，β 由0.01 增至2.0 时，系统的上、下以及非旋转备用分别增加了14.5%、0.70%和24.2%；而模式2 中，由于DR 加入，由DGs 提供的备用与模式1 相比较低，特别是下旋转备用。
表5 不同风险规避参数下系统备用水平
Tab.5 Reserve for different parameters
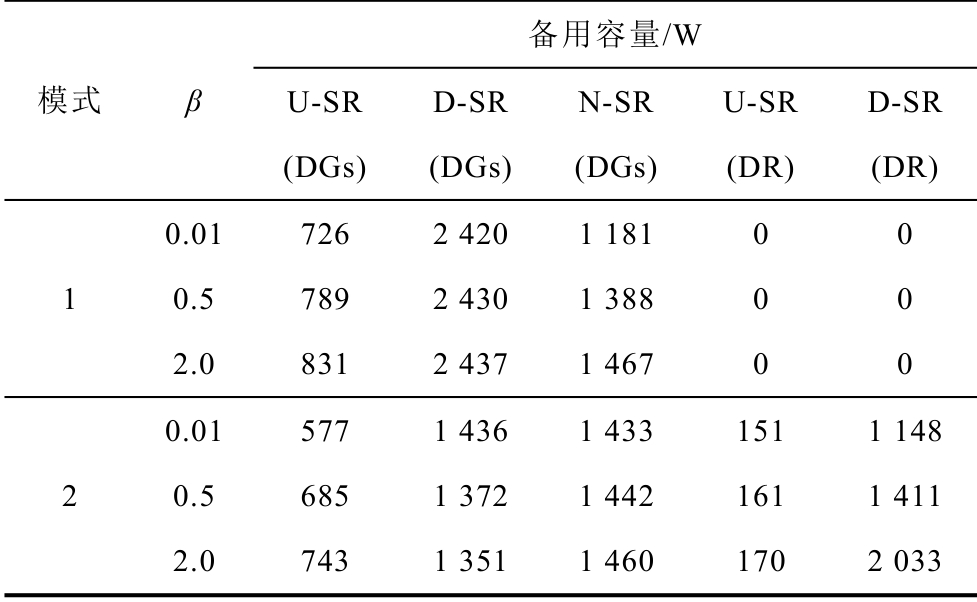
模式 β 备用容量/W U-SR (DGs) D-SR(DGs)N-SR (DGs) U-SR (DR) D-SR(DR) 1 0.01 726 2 420 1 181 0 0 0.5 789 2 430 1 388 0 0 2.0 831 2 437 1 467 0 0 2 0.01 577 1 436 1 433 151 1 148 0.5 685 1 372 1 442 161 1 411 2.0 743 1 351 1 460 170 2 033
图8 为β=0.01 和β=2.0 时，系统上旋转备用情况。从图中可以看出，β=2.0 时由DGs 和DR 提供的备用均高于β=0.01 时，即随着风险规避参数的提高，系统的总备用容量增加。
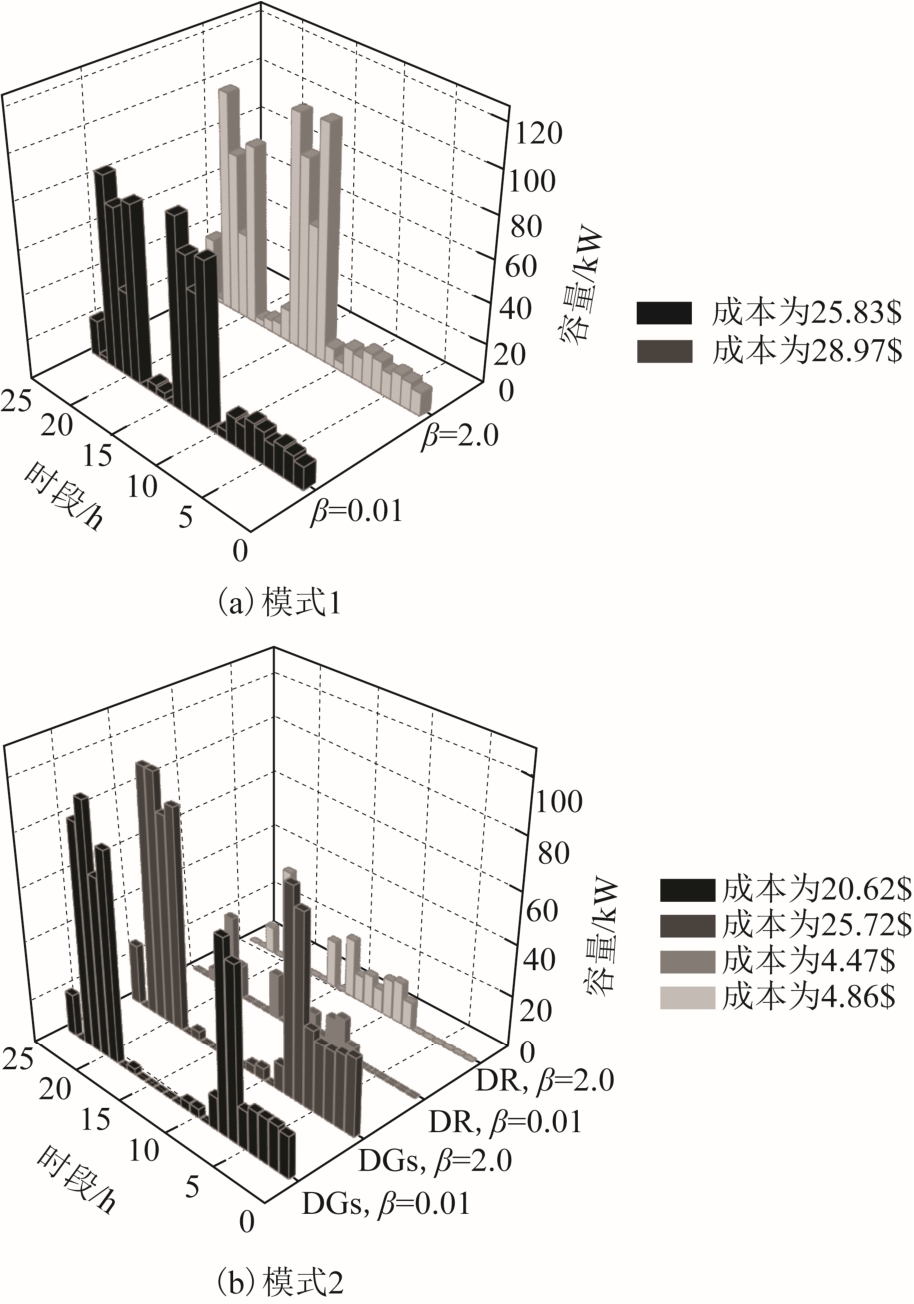
图8 各时段系统上旋转备用水平（VOLL=1$/(kW·h)） Fig.8 Hourly up-SR(VOLL=1$/(kW·h))
图9 给出了不同风险规避参数下的系统EENS成本变化情况。在两种模式下，随着β 的增大，EENS成本均降低，这是因为β 逐渐增大，系统采取了更加安全可靠的运行方式，提高了系统备用水平，减少强迫负荷中断情况发生，且由于DR 的接入，系统备用水平更高，故模式2 下EENS 成本整体较模式1 低。在模式1 中，VOLL 值由1 变为5 时，EENS 成本分别降低了10.7%和19%；而模式2 中，则分别降低了42%和77%。随着风险规避参数的增加，系统运营商为了更好地规避风险，进而购买更多的备用容量，此时，购买额外备用容量相比于因中断负荷而进行的补偿来说更加经济，因而，DR 参与调度后，EENS 成本大幅度降低。
图9 不同风险规避参数下的EENS 成本
Fig.9 Cost of EENS for different parameters β
6 结论
本文聚焦于不确定因素对发电调度会产生影响的现实问题，综合考虑了需求响应资源、可靠性以及风险收益等相关因素，建立了最差条件风险价值（WCVaR）的收益-风险组合模型。通过模型求解和算例分析得出以下结论：
1）新能源出力、负荷以及电价的不确定性大大增加了系统低收益风险，利用WCVaR 建立的收益-风险模型，对不确定性随机变量产生的潜在风险进行评估，更直观地描述收益与风险之间的关系，为系统运营商制定能量分配策略提供参考。
2）所提模型在日前调度基础上融入需求响应项目，建立供需互动机制，在一定程度上能够降低系统风险，最大化运行收益。
3）模型中引入了可靠性指标，并通过期望停电损失将可靠性指标转换为经济性指标，实现了系统运行经济性与安全性的有效统一。
4）为避免确定性概率分布在评估风险时存在的误差，在随机变量部分分布信息已知情况下建立的WCVaR 指标，更能真实反映系统的实际收益风险，且经Lagrange 理论简化的模型具有线性规划形式，理论上可保证其同解性，易于计算实现，有一定的应用价值。
[1] 易文飞, 张艺伟, 曾博, 等. 多形态激励型需求侧响应协同平衡可再生能源波动的鲁棒优化配置[J]. 电工技术学报, 2018, 33(23)： 5541-5554. Yi Wenfei, Zhang Yiwei, Zeng Bo, et al. Robust optimization allocation for multi-type incentive-based demand response collaboration to balance renewable energy fluctuations[J]. Transactions of China Electrotechnical Society, 2018, 33(23)： 5541-5554.
[2] 周强, 汪宁渤, 何世恩, 等. 高弃风弃光背景下中国新能源发展总结及前景探究[J]. 电力系统保护与控制, 2017, 45(10)： 146-154. Zhou Qiang, Wang Ningbo, He Shien, et al. Summary and prospect of China's new energy development under the background of high abandoned new energy power [J]. Power System Protection and Control, 2017, 45(10)： 146-154.
[3] 孙欣, 方陈, 沈风, 等. 考虑风电出力不确定性的发用电机组组合方法[J]. 电工技术学报, 2017, 32(4)： 204-211. Sun Xin, Fang Chen, Shen Feng, et al. An integrated generation-consumption unit commitment model considering the uncertainty of wind power[J]. Transactions of China Electrotechnical Society, 2017, 32(4)： 204-211.
[4] 孙建军, 张世泽, 曾梦迪, 等. 考虑分时电价的主动配电网柔性负荷多目标优化控制[J]. 电工技术学报, 2018, 33(2)： 401-412. Sun Jianjun, Zhang Shize, Zeng Mengdi, et al. Multiobjective optimal control for flexible load in active distribution network considering time of use tariff[J]. Transactions of China Electrotechnical Society, 2018, 33(2)： 401-412.
[5] 唐学军, 韩佶, 苗世洪, 等. 基于需求侧响应的多类型负荷协调控制模型[J]. 电力系统保护与控制, 2017, 45(16)： 116-123. Tang Xuejun, Han Ji, Miao Shihong, et al. Coordinated control model of multi-type load based on demand response [J]. Power System Protection and Control, 2017, 45(16)： 116-123.
[6] Parvizimosaed M, Farmani F, Anvarimoghaddam A. Optimal energy management of a micro-grid with renewable energy resources and demand response[J]. Journal of Renewable & Sustainable Energy, 2013, 5(5)： 3395-3409.
[7] 田世明, 王蓓蓓, 张晶. 智能电网条件下的需求响应关键技术[J]. 中国电机工程学报, 2014, 34(22)： 3576-3589. Tian Shiming, Wang Beibei, Zhang Jing. Key technologies for demand response in smart grid[J]. Proceeding of the CSEE, 2014, 34(22)： 3576-3589.
[8] 许汉平, 李姚旺, 苗世洪, 等. 考虑可再生能源消纳效益的电力系统“源-荷-储”协调互动优化调度策略[J]. 电力系统保护与控制, 2017, 45(17)： 18-25. Xu Hanping, Li Yaowang, Miao Shihong, et al. Optimization dispatch strategy considering renewable energy consumptive benefits based on “source-loadenergy storage” coordination in power system[J]. Power System Protection and Control, 2017, 45(17)： 18-25.
[9] 李力行, 苗世洪, 孙丹丹, 等. 多利益主体参与下主动配电网完全信息动态博弈行为[J]. 电工技术学报, 2018, 33(15)： 3499-3509. Li Lixing, Miao Shihong, Sun Dandan, et al. Dynamic games of complete information in active distribution network with multi-stakeholder participation[J]. Transactions of China Electrotechnical Society, 2018, 33(15)： 3499-3509.
[10] 刘文颖, 文晶, 谢昶, 等. 考虑风电消纳的电力系统源荷协调多目标优化方法[J]. 中国电机工程学报, 2015, 35(5)： 1079-1088. Liu Wenying, Wen Jing, Xie Chang, et al． Multiobjective optimal method considering wind power accommodation based on source-load coordination[J]. Proceedings of the CSEE, 2015, 35(5)： 1079-1088.
[11] 夏榆杭, 刘俊勇, 冯超, 等. 计及需求响应的虚拟发电厂优化调度模型[J]. 电网技术, 2016, 40(6)： 1666-1674. Xia Yuhang, Liu Junyong, Feng Chao, et al. Optimal scheduling model of virtual power plant considering demand response[J]. Power System Technology, 2016, 40(6)： 1666-1674.
[12] Zhou Y, Mancarella P, Mutale J. Modelling and assessment of the contribution of demand response and electrical energy storage to adequacy of supply[J]. Sustainable Energy Grids & Networks, 2015, 3(3)： 12-23.
[13] Aghaei J, Alizadeh M I. Robust n-k contingency constrained unit commitment with ancillary service demand response program[J]. IET Generation Transmission & Distribution, 2014, 8(12)： 1928-1936.
[14] Zheng Qipeng, Wang Jianhui, Liu A L. Stochastic optimization for unit commitment： a review[J]. IEEE Transactions on Power Systems, 2015, 30(4)： 1913-1924.
[15] Moghaddam I G, Nick M, Fallahi F, et al. Risk-averse profit-based optimal operation strategy of a combined wind farm-cascade hydro system in an electricity market[J]. Renewable Energy, 2013, 55(4)： 252-259.
[16] Shayeghi H, Sobhani B. Integrated offering strategy for profit enhancement of distributed resources and demand response in microgrids considering system uncertainties[J]. Energy Conversion & Management, 2014, 87： 765-777.
[17] Rezaei N, Kalantar M. Stochastic frequency-security constrained energy and reserve management of an inverter interfaced islanded microgrid considering demand response programs[J]. International Journal of Electrical Power & Energy Systems, 2015, 69： 273-286.
[18] Zhu S, Fukushima M. Worst-case conditional valueat-risk with application to robust portfolio management[J]. Operations Research, 2009, 57(5)： 1155-1168.
[19] Zhou Yijia, Li Yang, Xu Lijun, et al. Inseparable robust reward-risk optimization models with distribution uncertainty[J]. Japan Journal of Industrial & Applied Mathematics, 2016：1-14.
[20] Mohan V, Singh J G, Ongsakul W. Sortino ratio based portfolio optimization considering evs and renewable energy in microgrid power market[J]. IEEE Transactions on Sustainable Energy, 2016, 8(1)： 219-229.
[21] Metered load data： 2016 hourly loads [DB/OL]. [2017-01-05]. http：//www.pjm.com/markets-and-operations/ ops-analysis/historical-load-data.aspx.