0 引言
为了应对能源危机和环境污染问题,以风电为代表的可再生能源在全球范围内得到快速发展与推广[1-2]。然而,风电的间歇性、不确定性等不友好特性[3-4],严重阻碍了其大规模应用。为此,全球多个国家已经相继启动了大规模储能系统的研发和建设。在诸多储能技术中,压缩空气储能(Compressed Air Energy Storage, CAES)和抽水蓄能是目前被认为比较适合大规模储能的技术。相比较而言,CAES的选址限制小,投资建设成本低,近年来受到广泛关注。
传统 CAES 电站在储能阶段利用电能压缩空气并存储,在发电阶段将存储的高压空气与燃料混合燃烧后驱动膨胀机发电,存在依赖化石燃料和系统效率低两大弊端。为了解决上述弊端,先进绝热压缩空气储能(Advanced Adiabatic Compressed Air Energy Storage, AA-CAES)应运而生。目前,全球已有多个国家已建成或即将建设AA-CAES 电站,其中德国筹划建设ADELE 示范电站,设计容量达300MW/1000MW·h[5],我 国 已 建 成 10MW AACAES 示范系统,下阶段计划建设100MW 级AACAES 系统[6]。
目前国内外已就CAES 电站的规划问题进行了一些研究。文献[7-9]从经济性角度出发,研究了CAES 电站应用于风电消纳的可行性。文献[10]根据风电并网标准,以平抑风电场功率波动为目标,对CAES 电站容量进行优化。文献[11]以功能成本最低为目标,对含CAES 电站的热电联供系统的容量进行了优化。文献[12]以减少岛屿风电场弃风为目标,提出了双模式CAES 电站的容量优化方法。
但是,上述文献均未考虑AA-CAES 电站的变寿命特性。而AA-CAES 电站优化规划结果与其使用寿命息息相关,同时,AA-CAES 电站的使用方式对其寿命影响较大,因此,有必要研究AA-CAES 电站使用方式对其寿命的影响机理。此外,上述文献中也未见针对大规模AA-CAES 电站的优化规划方法,而目前多座AA-CAES 电站已处于设计或研发阶段,因此,研究面向电力系统运行的AA-CAES 电站优化规划方法迫在眉睫。
本文首先研究了影响AA-CAES 电站寿命的主要因素,建立了AA-CAES 电站的变寿命模型,并分析了AA-CAES 电站调度运行方式对其使用寿命的影响机理。在此基础上,本文建立了AA-CAES 电站双层优化规划模型,上层计及AA-CAES 电站寿命对其日均投资成本的影响,对AA-CAES 电站的投资、运行维护成本与下层反馈的电网典型日运行成本之和进行优化;下层根据上层所确定的 AACAES 电站容量,进行电网典型日最优运行方式求解,并将最优运行结果反馈给上层。最后,基于修改的IEEE 30 节点系统和某地区的典型日数据进行仿真,并验证了该双层优化模型的有效性。
1 A A-CAES 电站寿命分析
AA-CAES 电站的全寿命周期成本与电站的使用寿命息息相关,而电站的使用方式将直接影响电站的使用寿命,因此,有必要详细分析AA-CAES 电站的变寿命特性。
AA-CAES 电站主要由压缩机、膨胀机、储气室、换热器、储热装置、电机和其他辅助元件等构成。通常情况下,压缩机、膨胀机和储气室对AA-CAES电站投资建设成本的影响较大[13-14]。其中,储气室在运行过程中的气压变化缓慢且平滑,温度变化范围较小[15],储气室整体热应力较小,因而忽略运行状态变化对储气室寿命的影响。根据以上分析,本文主要考虑AA-CAES 电站压缩机和膨胀机的变寿命特性。
1.1 AA-CAES 电站叶轮机寿命分析
叶轮机技术发展较早,且已广泛应用于大规模AA-CAES 电站的压缩机和膨胀机[5,13]。作为旋转部件,叶轮机的寿命受其使用方式的影响较大,主要影响因素包括:载荷变化、温度、加载模式、结构尺寸、加工工艺和工作环境[16]。其中,温度和载荷变化受运行工况的影响程度较高,其他因素在建设完成后基本固定不变。
对于温度对机械设备寿命的影响,在工程应用中一般通过引入一个温度影响因子Kd 进行表征[16]。
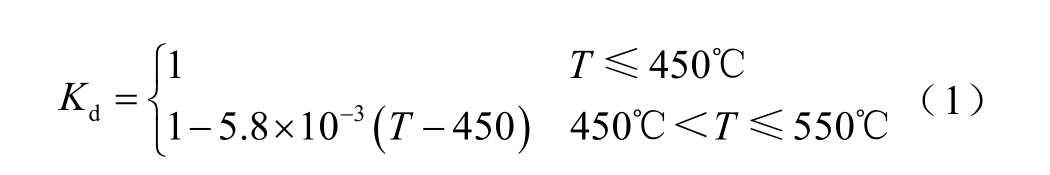
式中,T 为温度。
AA-CAES 电站叶轮机的工作温度范围通常小于450℃[15]。因而在AA-CAES 电站的运行过程中,温度变化对压缩机和膨胀机的寿命影响不大。
在载荷变化方面,叶轮机在起停和转速波动等载荷变化过程中会发生应变,导致叶轮机寿命损耗。通过对叶轮机载荷变化过程进行有限元分析,可以得到其应变大小,该应变对应的循环寿命次数可由式(2)计算[16]。
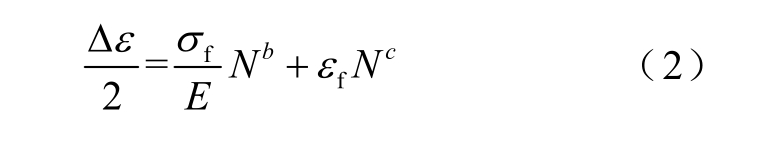
式中,∆ε 为材料应变;σf 为疲劳强度系数;E 为材料的弹性模量;N 为循环寿命次数;b 为强度因子;εf 为疲劳延性系数;c 为疲劳延性指数。
综上所述,本文主要考虑起停和正常工作时转速波动对AA-CAES 电站压缩机和膨胀机寿命的影响。
1.2 Miner 线性累积损伤理论
在工程实际中,设备所受到的载荷通常是多变的。Miner 线性累积损伤理论是一种用于计算多种载荷历程下寿命损耗的有效方法,其形式简单,使用便捷,且在多数情况下的寿命预测与试验结果有相当程度的吻合性,是目前应用最为普遍的寿命预测方法之一[17-18]。
Miner 线性累积理论可以阐述如下[17-18]。
设备经历k 种不同载荷时,其循环寿命为Ni(i=1,2,…,k)次,则有
1)单次循环造成的损伤为

式中,D 为损伤。
2)ni 次相同载荷循环造成的损伤为
3)k 个不同载荷下循环造成的损伤为

4)疲劳破坏发生条件
式(5)即为Miner 理论的基本表达式,疲劳破坏发生条件为

1.3 AA-CAES 电站寿命模型
本文考虑调度指令对AA-CAES 压缩机/膨胀机寿命的影响,并主要针对起停和转速波动对 AACAES 叶轮机造成的寿命损耗进行分析。
下面以24 时段调度中压缩机寿命损耗为例,开展分析。
1.3.1 起停造成的寿命损耗
起停的载荷历程可简单描述为“零转速—额定工作转速—零转速”的加载过程。AA-CAES 电站压缩机起停主要有两种情况:
(1)运行计划安排AA-CAES 电站起停的次数。由日前调度安排AA-CAES 电站压缩机起停次数为
式中,vC,t 为二进制变量,用于表示AA-CAES 电站是否处于压缩工况。当AA-CAES 电站处于压缩工况时vC,t=1;反之vC,t=0。
(2)AA-CAES 电站应提供备用时发生的起停次数。AA-CAES 电站作备用时可能会发生起停或工况转换。根据当地单日备用发生统计数据,因备用导致的压缩机平均日起停次数为
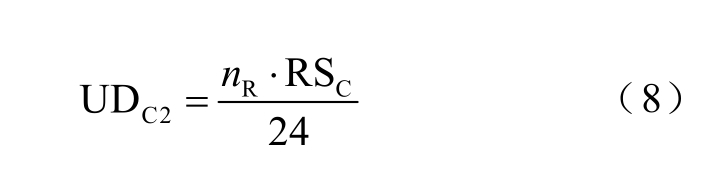
式中, Rn 为单日备用发生统计平均次数;RSC 为备用安排中压缩机发生开关机的次数。
AA-CAES 电站经历的起停加载过程数为开关机次数的一半。从而,基于Miner 线性累积损伤理论,起停造成的寿命损耗为
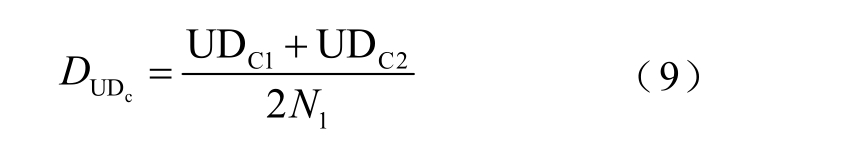
式中,N1 为起停载荷历程对应的压缩机循环寿命次数。
1.3.2 正常运行时转速波动造成的寿命损耗
在工程实际中,由于气动载荷、旋转失速和一些其他不稳定因素的影响,叶轮机在正常工作时常会出现小幅的转速波动,波动范围一般在叶轮机额定转速的±5%以内。此时载荷历程可简单地描述为“额定转速—超速—低速—额定转速”。正常运行时转速波动造成的疲劳损耗为

式中,N2 为转速波动载荷历程下的循环寿命次数;f FL为AA-CAES 正常运行时的波动频率(次/h);OPTC 为压缩机的运行时间。

以上是一天内压缩机因调度运行导致的疲劳损耗。根据Miner 线性累积理论,压缩机的寿命(年)为

式中, SECσ 为安全系数,其取值范围满足
膨胀机的寿命分析与压缩机类似,在此不再赘述。
2 考虑AA-CAES 电站变寿命特性的双层优化规划模型
由于AA-CAES 电站的日均设备投资成本与压缩机和膨胀机的寿命为非线性关系,且压缩机和膨胀机寿命与其运行计划也为非线性关系,因此,为了将非线性问题集中处理,本文采用双层优化结构,建立了考虑变寿命特性的AA-CAES 电站优化规划模型。本优化模型中,上层配置AA-CAES 电站的压缩功率、发电功率和容量,下层求解AA-CAES 电站应用于电网中的调度运行问题。
下面分别介绍两层的具体内容。
2.1 规划层
上层优化问题为规划层,决定储能功率和容量大小,决策变量为
式中,PC,r 和PG,r 分别为压缩机和膨胀机的额定功率;VST 为储气室体积。
2.1.1 优化目标
本文设定AA-CAES 电站由电网公司建设并管理,AA-CAES 电站综合容量规划的优化目标为:在满足系统需求和各类约束条件的前提下,使系统规划期间国民经济总支出最小[19]。因此规划层的目标函数为
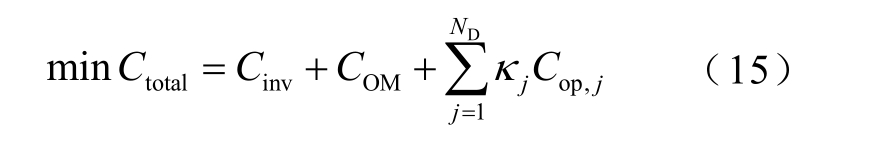
式中,Ctotal 为总成本;Cinv 为日均设备投资成本;COM 为AA-CAES 运行维护成本;ND 为典型日的种类数;Cop,j 为电网典型日j 的运行成本,是下层优化的目标函数,其大小受AA-CAES 电站规划的结果影响,又与电网调度运行方式有关;κj 为典型日j在一年中所占的比例。
压缩机和膨胀机具有较高的回收、再利用价值[20],日均设备投资成本中应考虑其残值回收。压缩机和膨胀机运行状况不同,其寿命一般不等,需要分情况讨论投资成本和残值回收,下面以回收压缩机的残值为例,即压缩机寿命大于膨胀机寿命的情况,介绍投资成本的计算方法。
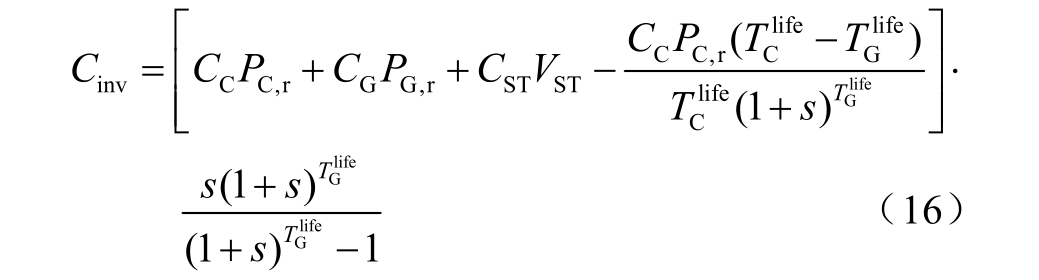
式中,CC 和 CG 分别为压缩机和膨胀机的成本系数;CST 为储气室的成本系数;TClife 和TGlife(年)分别为压缩机和膨胀机的寿命,其大小受下层优化的AA-CAES 电站调度结果影响;s 为折现率。
COM 为
式中,Com 为运行维护成本系数。
2.1.2 约束条件
受投资成本和AA-CAES 技术发展等条件限制,对其功率和容量限制为
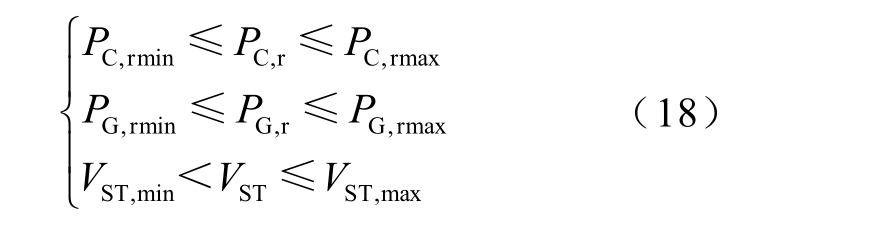
式中,PC,rmax 和PC,rmin 分别为压缩机额定功率的上、下限;PG,rmax 和PG,rmin 分别为膨胀机额定功率的上、下限;VST,min 和VST,max 分别为储气室体积最小值和最大值。
2.2 调度层
本文求解规划-调度双层问题,仅考虑日前调度,调度时段为24 段。下层优化问题为调度层,根据上层确定的AA-CAES 电站的额定功率和容量,求解电网的最优运行方式。下层的决策变量包括:常规机组的起停状态、出力、备用量;AA-CAES 电站的运行状态、功率、备用;弃风量等。
2.2.1 优化目标
以最小化典型日全天系统运行成本为目标函数,如式(19)和式(20)所示。需要指出的是,由于设定AA-CAES 电站由电网公司建设并管理,所以其运行成本将不包含购电成本和备用采购成本,其压缩过程消耗电量成本体现在同时段向常规机组购电的成本上。

式中,COP 为电网运行总成本;CG,e 为电网向常规机组购电的成本;CG,R 为电网向常规机组购买备用的成本;CWcur 为弃风成本;NG 为常规机组数量;bGi 和cGi为向常规机组i 购电的成本系数,与燃料参数类似;SGi,t 为常规机组i 在t 时段的起动成本;PGi,t 为常规机组i 在t 时段的出力;Rup Gi,t和Rdown Gi,t 分别为电网在t 时段向常规机组i 购买正备用和负备用的容量;αGi 和βGi 分别为常规机组i 的正/负备用容量购买单价;λW为弃风成本系数;Wt 为t 时段的弃风容量。
2.2.2 约束条件
1)系统功率平衡约束
式中,PW,t 和PL,t 分别为t 时段的风电和负荷预测值;PCAESC,t 和PCAESG,t 分别为t 时段CAES 电站压缩功率和发电功率。
2)系统备用约束
由于AA-CAES 电站的备用调节范围并不连续,电网需要从常规机组购买一定容量的备用对 AACAES 电站备用不可调节区进行填补,以保证系统备用容量可以从0 到所需值连续可调,约束表达式详见文献[21]。
本文同时考虑应对风电、负荷预测误差和常规机组故障的备用,备用约束为

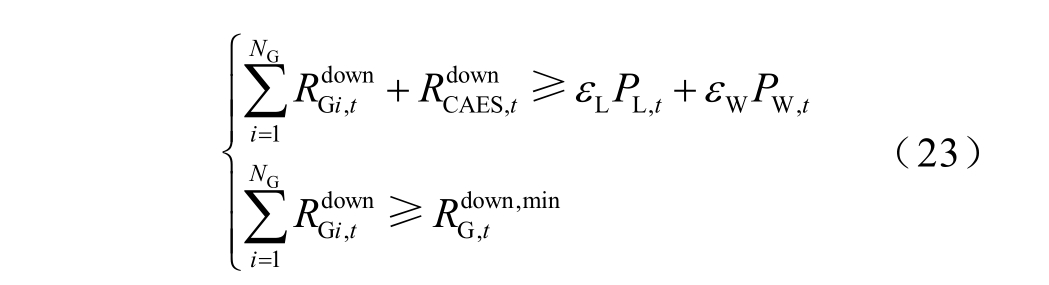
式中,εL 和εW 分别为负荷和风电的预测误差比例;max{PGi,t}为t 时段常规机组i 出力最大值。
3)AA-CAES 电站运行约束
AA-CAES 电站运行约束可见文献[21-23],包括压缩机约束、膨胀机约束、储气室约束、蓄热系统约束和运行工况约束等。需要说明的是,AA-CAES电站具有快速响应能力[5,21],因此在日前调度尺度下,可以忽略AA-CAES 电站的爬坡约束、起停时间约束和工况转换时间约束。
4)AA-CAES 电站备用特性
由于AA-CAES 电站具有工况切换迅速、起停时间短、爬坡速度快和幅值变化大等优势,因而适合在电力系统中承担备用任务[5,24]。AA-CAES 电站承担备用任务,当发生工况转换时会影响其使用寿命,因而有必要分析AA-CAES 电站在何种备用情况下会发生工况转换。
AA-CAES 电站处于压缩、停机或发电工况时的备用特性各不相同,备用模型详见文献[21]。
AA-CAES 电站仅能选择一种备用模式,当AACAES 电站处于压缩工况时,有如下约束:

式中,r 为二进制变量,用于表示AA-CAES 电站是否选用对应的模式作为备用;上标up 和down 分别为正备用和负备用;下标c、o、g 分别表示压缩工况、停机工况和发电工况之间的切换关系,如co 表示压缩工况转停机工况。当选择其中一种备用时,对应的r 为1;否则为0。
AA-CAES 电站停机时,备用模式约束为
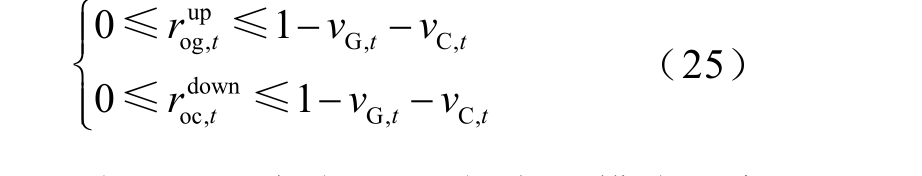
AA-CAES 电站处于发电工况时,备用模式约束为
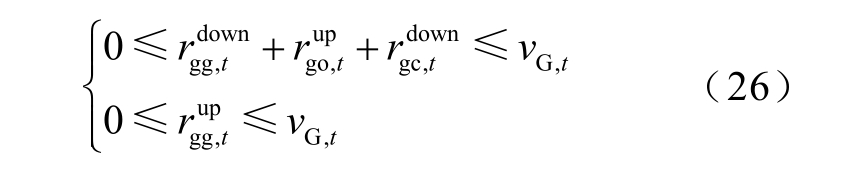
根据以上分析,AA-CAES 电站作备用时,压缩机开关机的次数为
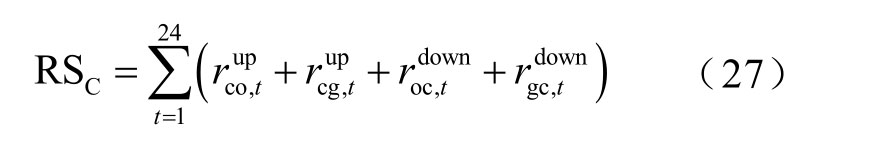
类似地,AA-CAES 电站作备用时,膨胀机开关机次数为
5)AA-CAES 电站储气室最终气压约束
约束条件如下[14]:
6)其他约束
本模型中,常规机组功率上下限约束、爬坡约束、最小起停时间约束和备用容量约束等详见文献[25]。
3 求解方法
粒子群优化(Particle Swarm Optimization,PSO)算法是一种进化计算技术,具有种群规模小、计算速度快、基本不依赖经验参数和鲁棒性好等特点,可以灵活地处理包含非线性约束的优化问题[26-27]。考虑PSO 的上述优势,本文上层优化问题采用PSO算法。当上层结果传给下层,即AA-CAES 的额定功率和容量确定时,下层优化可转换为混合整数线性规划(Mixed Integer Linear Program, MILP)问题,便于采用常规的商用化优化软件求解,本文采用Matlab 的YALMIP(R20180612)工具箱调用CPLEX 12.8.0 求解器对下层优化问题进行求解。
详细求解流程如图1 所示。图1 中可行性检测保证上层优化问题的功率、容量满足约束条件式(18),当功率或容量超过限值时将其修改为限值。粒子的适应度函数即为上层优化的目标函数。
4 算例分析
4.1 算例参数
AA-CAES 电站建设成本系数、运维成本系数、压缩机/膨胀机功率范围和储气室体积范围等规划层参数见附表1,其中AA-CAES 电站的建设成本系数和运维成本系数综合参考了文献[9,13-14];AA-CAES 电站功率限制和储气室容量限制参考了文献[5,13],折现率取8%。
调度层基于修改版的IEEE 30 节点系统进行仿真分析,常规机组调度参数见附表2[21, 24]。由于风电和负荷具有较明显的季节性[14],本文选取四季典型日的风电、负荷预测数据进行计算,并根据四季典型日在一年中所占的比例进行加权计算,得到电网一 年的日均运行成本,用于说明电网一年的运行情况。

图1 双层优化问题的求解流程
Fig.1 Flow chart of solving bi-level optimization problem
典型日数据如图2 所示,其中春秋季的负荷预测曲线一致,风电预测曲线不同。调度时段为24 段,即单位调度时长为1h。假设风电出力最大预测误差和负荷最大预测误差分别为20%和5%;单位弃风成本为200$/MW。AA-CAES 电站运行参数和变寿命特性参数[16]见附表3。
此外,需要说明的是,本文在优化规划时采用寿命周期内中后期的负荷曲线求取规划结果,以满足负荷增长的需求。该负荷曲线主要依据《城市电力规划规范GB/T50293-2014》中的预测方法获得。

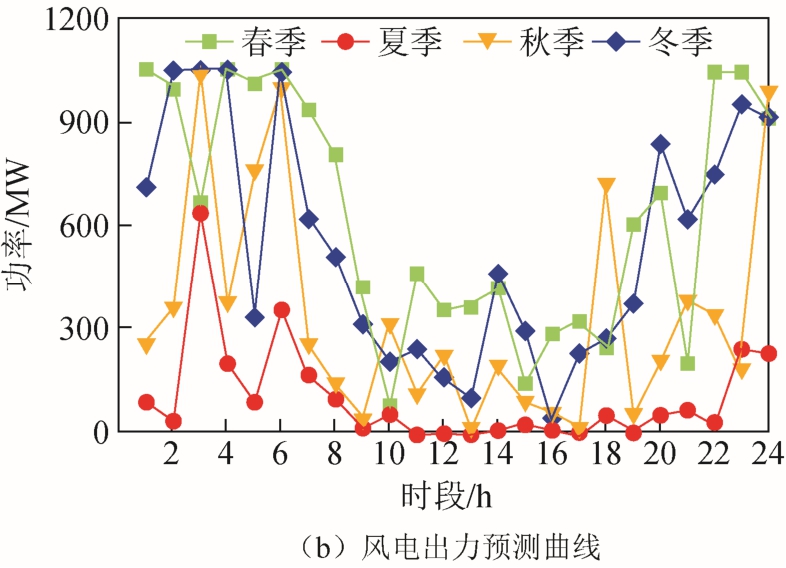
图2 风电出力和负荷的典型日预测曲线
Fig.2 Forecast curves of wind power output and load in typical days
4.2 结果分析
4.2.1 规划结果分析
为了验证该优化方法的有效性,本文设置了3个场景以作对比:场景1,即本文模型;场景2,不考虑AA-CAES 电站寿命变化,假定AA-CAES 电站的寿命为固定的60 年;场景2′,根据场景2 确定的AA-CAES 电站规划结果,采用本文的变寿命模型重新计算AA-CAES 电站的寿命和成本;场景3,不建立AA-CAES 电站。各场景除AA-CAES 电站设置不同之外,其他条件一致,各场景的规划层的仿真结果见表1。表1 中的电网运行成本为电网全年日均运行成本,该成本基于春、夏、秋、冬四个季节的典型日数据,并根据各季节典型日在一年中所占比例进行加权计算得到。
表1 规划结果
Tab.1 Planning results

参 数 场景1 场景2 场景2′ 场景3压缩功率/MW 276 278 278 — 发电功率/MW 303 308 308 — 储气室体积/(103m3) 1 687 1 744 1 744 — 总成本/$ 652 754 651 787 653 527 904 765日均设备投资/$ 58 417 57 741 59 481 — CAES 运维成本/$ 6 346 6 423 6 423 — 电网运行成本/$ 587 992 587 624 587 624 904 765压缩机寿命/年 55 假定60 53 — 膨胀机寿命/年 41 假定60 41 —
对比场景1 与场景3 可以看出,建立AA-CAES电站后电网的运行成本从904 765$降至587 992$,减少了316 773$(35%);AA-CAES 电站由于寿命较长,其日均设备投资成本仅为58 417$,日均设备投资成本与运行维护成本之和仅为64 763$。故建立AA-CAES 电站后,总成本下降了252 011$(27%),说明了AA-CAES 电站应用于电网具有良好的经济效益。
场景2 假定AA-CAES 电站的寿命为固定的60年,长于场景1 的41 年,则场景2 的单位容量日均设备投资成本小于场景1。场景2 AA-CAES 电站额定功率和容量的规划结果大于场景1,以期减小电网运行成本。从而场景2 的日均设备投资成本和电网运行成本均小于场景1。然而,场景2 中AA-CAES电站寿命预计过于乐观,将场景2 的AA-CAES 电站规划结果代入变寿命模型中考虑时,发现其寿命短于60 年,压缩机和膨胀机的寿命分别为53 年和41 年,对应的总成本为653 527 $,大于场景1 的总成本。说明场景2 不考虑AA-CAES 电站寿命变化,所得到的AA-CAES 电站功率、容量规划结果不是最佳的,其收益预期亦不准确。而本文模型可以根据AA-CAES 电站的使用寿命,确定更优的电站功率、容量,从而降低系统总成本。
4.2.2 AA-CAES 电站对电网运行成本的影响分析
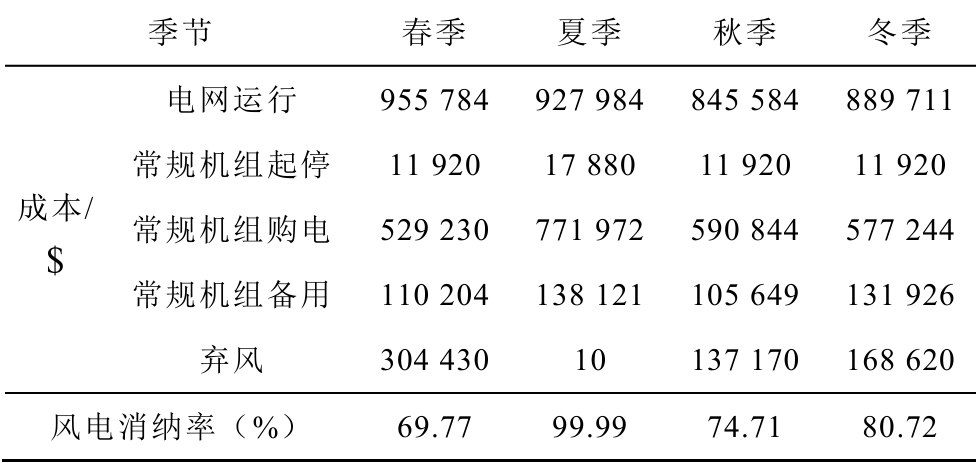
下面分析建立AA-CAES 电站对电网调度运行的影响。未建立AA-CAES 电站即场景3 的调度结果见表2,建立AA-CAES 电站即场景1 的调度结果见表3。
表2 场景3 的调度结果
Tab.2 Dispatching results of scenario 3
季节 春季 夏季 秋季 冬季 成本/$ 电网运行 955 784 927 984 845 584 889 711常规机组起停 11 920 17 880 11 920 11 920常规机组购电 529 230 771 972 590 844 577 244常规机组备用 110 204 138 121 105 649 131 926弃风 304 430 10 137 170 168 620风电消纳率(%) 69.77 99.99 74.71 80.72
表3 场景1 的调度结果
Tab.3 Dispatching results of scenario 1
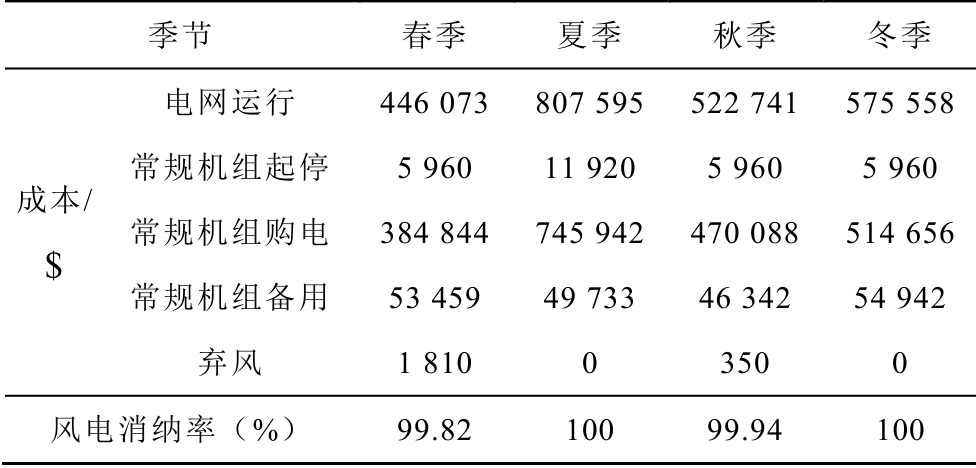
季节 春季 夏季 秋季 冬季 成本/$ 电网运行 446 073 807 595 522 741 575 558常规机组起停 5 960 11 920 5 960 5 960 常规机组购电 384 844 745 942 470 088 514 656常规机组备用 53 459 49 733 46 342 54 942弃风 1 810 0 350 0 风电消纳率(%) 99.82 100 99.94 100
对比表2 和表3 可以看出,建立AA-CAES 电站可以有效减少电网运行中的各项成本并提升风电消纳率。
1)对常规机组运行成本而言,由于常规机组动态特性差,起停、调节成本高,AA-CAES 电站建成后,可以有效减少常规机组的起停和调节,并使常规机组工作在经济性更好的区间。因而,常规机组的起停成本、购电成本和备用成本都下降了很多。其中以风电出力较大的春、秋、冬三个季节最为明显,这是因为风电比负荷波动大,且预测误差更大,为了消纳风电,常规机组付出的代价大。AA-CAES电站建成后代替常规机组承担了调节任务,因而削减常规机组的运行成本。
2)对风电消纳而言,由于常规机组爬坡速度慢,调节成本高,且存在最小起停时间的约束,因此未建立AA-CAES 电站时,在风电出力较大的季节,风电消纳率低,弃风成本较高。AA-CAES 电站建成后,利用其动态响应特性出色和容量大的优势,有效地消纳了风电,将风电全年消纳率由76%提升到99%以上,减少了弃风成本。
4.2.3 AA-CAES 电站运行情况分析
场景1 中各典型日的运行情况如图3 所示。图中,AA-CAES 电站的功率为负表示其工作在压缩工况,将AA-CAES 电站的负备用视为负值。
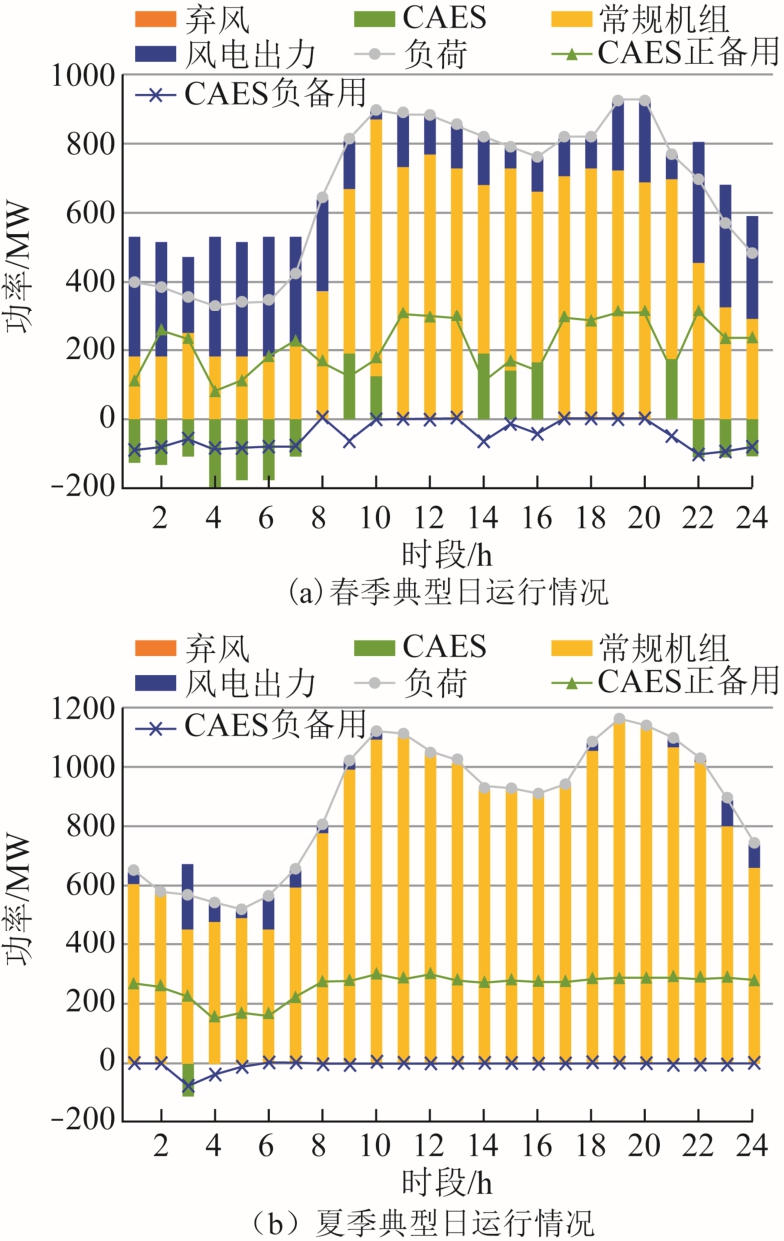
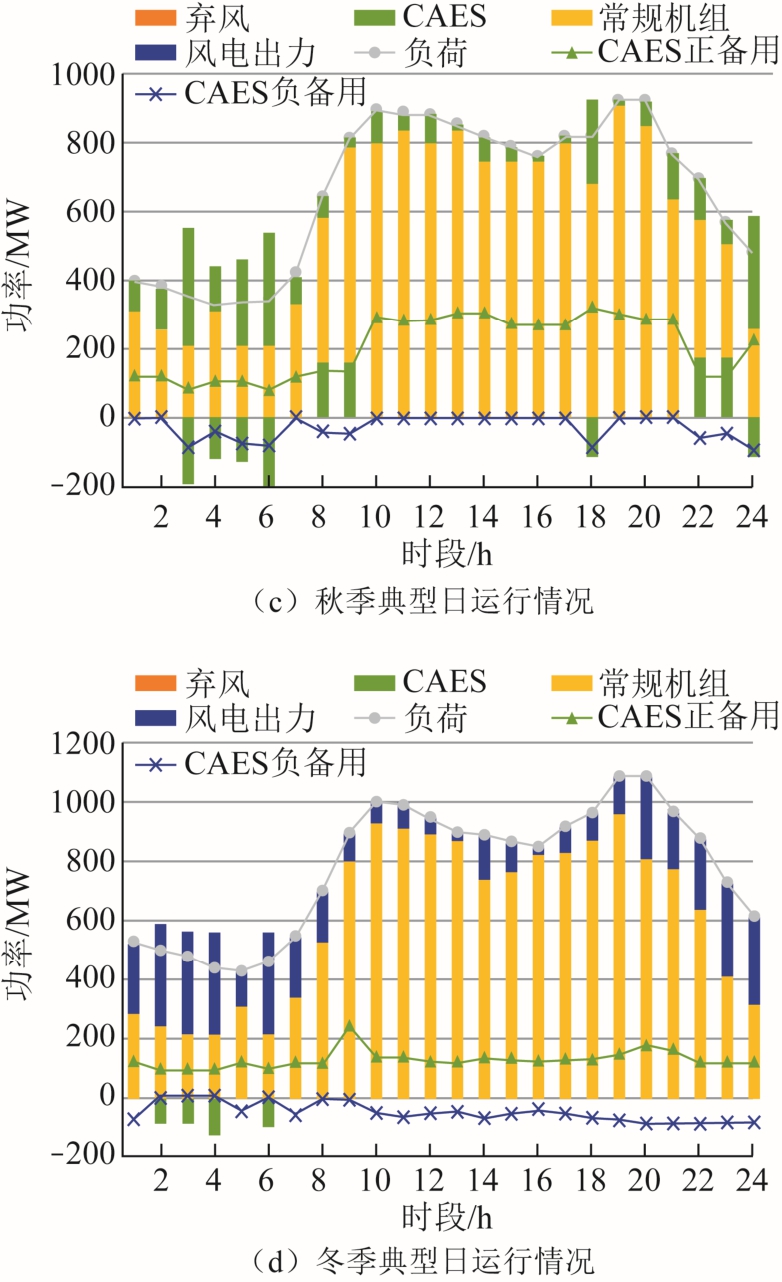
图3 场景1 中电网典型日运行情况
Fig.3 Grid operation in typical days of scenario 1
接下来分析AA-CAES 电站的运行工况和备用情况。由图3 可知,AA-CAES 电站并不是全天都 在开机状态,除了在风电出力较大且波动大的春季典型日中,运行了16h 之外,其他情况下运行时间都不超过1/3。即使AA-CAES 电站运行时,其发电或压缩功率也不会接近最大功率限值。这是因为在停机或上述运行功率时,AA-CAES 电站的向上和向下调节的能力都较强,从而其备用能力更强。这种情况下,AA-CAES 电站既能发挥其削峰填谷的作用,又承担了系统的备用任务。AA-CAES 在压缩、发电工况和停机时,都可以承担备用任务,且基本全天都在作备用,展现了其优异的备用能力。因备用而发生的AA-CAES 电站起停并不体现在其运行状态上,但在实际运行中,由风电和负荷预测误差发生备用调节的情况较为常见。因此考虑AACAES 电站作备用时,备用需求发生导致AA-CAES电站工况转换的情况,并计及这些情况发生的期望次数,将其对AA-CAES 电站寿命的影响考虑进优化模型中是切合实际且至关重要的。此外,由图3可知AA-CAES 电站作正备用的情形更多,膨胀机的起停更频繁,其寿命损耗比压缩机快,这与表1场景 1 膨胀机的寿命短于压缩机的寿命的结论是一致的。表4 是AA-CAES 电站全寿命周期内的寿命损耗情况。由表4 可知,压缩机和膨胀机起停造成的寿命损耗均大于持续运行造成的寿命损耗,且膨胀机由于起停更为频繁,其起停造成的损耗所占比例更大。
表4 AA-CAES 电站寿命损耗情况
Tab.4 The situation of AA-CAES’s life loss

损耗来源 比例(%) 压缩机起停 51.30 压缩机持续运行 48.70 膨胀机起停 76.44 膨胀机持续运行 23.56
5 结论
本文详细分析了影响AA-CAES 电站运行寿命的主要因素,并建立了其变寿命模型,基于该变寿命模型提出了一种AA-CAES 电站规划方法,最后,进行仿真验证,得到了以下结论:
1)AA-CAES 电站的持续运行和工况转换均会损耗其寿命,其中工况转换影响更大。AA-CAES 电站作正备用的情形较多,膨胀机起停更频繁,寿命损耗更大,因此膨胀机的寿命短于压缩机。
2)对AA-CAES 电站的功率和容量作规划时,考虑其变寿命特性,规划结果更优——系统总成本更小,预期收益更准确。
3)AA-CAES 电站应用于电力系统时,不仅具有削峰填谷的能力,还具有优异的备用能力,并且在压缩工况、发电工况和停机时都能承担备用任务。在本文算例中,AA-CAES 电站建成后,电网运行成本减小了35%,系统总成本减少了27%,风电消纳率由76%提升到99%以上。
附 录
附表1 规划层参数
App.Tab.1 Parameters of planning level

参 数 数 值 压缩机建设成本系数/($/MW) 3.9×105 膨胀机建设成本系数/($/MW) 3.25×105 最小储气室体积/(103m3) 10 额定压缩功率下限/MW 10 额定发电功率下限/MW 10 储气室建设成本系数/($/km3) 3.0×104 运行维护成本系数/($/MW) 10.96 最大储气室体积/(103m3) 2 000 额定压缩功率上限/MW 500 额定发电功率上限/MW 500
附表2 常规机组参数
App.Tab.2 Parameters of generators

参 数 机 组 G1 G2 G3 G4 G5 G6 最大出力/MW 350 240 200 250 350 230最小出力/MW 100 30 20 50 50 30 bGi/MW 34.4 48.8 58.8 46.0 30.0 50.4 Gi c /$ 130 110 120 110 120 100起动成本/$ 1 500 890 500 900 1 450 720爬坡速率/ (MW/min) 2.3 4.5 8.2 4.6 2.7 7.9 最小起停时间/h 4 2 2 2 4 2 G i α /($/MW) 19.28 15.28 14.28 17.96 22.12 13.12 Gi β /($/MW) 16.00 13.08 11.80 12.52 15.32 11.24
附表3 AA-CAES 电站参数
App.Tab.3 Parameters of AA-CAES plant

?
[1] 郭鹏, 文晶, 朱丹丹, 等. 基于源-荷互动的大规模风电消纳协调控制策略[J]. 电工技术学报, 2017, 32(3): 1-9. Guo Peng, Wen Jing, Zhu Dandan, et al. The coordination control strategy for large-scale wind power consumption based on source-load interactive[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 1-9.
[2] 赵冬梅, 殷加玞. 考虑源荷双侧不确定性的模糊随机机会约束优先目标规划调度模型[J]. 电工技术学报, 2018, 33(5): 1076-1085. Zhao Dongmei, Yin Jiafu. Fuzzy random chance constrained preemptive goal programming scheduling model considering source-side and load-side uncertainty[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1076-1085.
[3] 孙欣, 方陈, 沈风, 等. 考虑风电出力不确定性的发用电机组组合方法[J]. 电工技术学报, 2017, 32(4): 204-211. Sun Xin, Fang Chen, Shen Feng, et al. An integrated generation-consumption unit commitment model considering the uncertainty of wind power[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 204-211.
[4] 韩璐, 李凤婷, 王春艳, 等. 风电接入对继电保护的影响综述[J]. 电力系统保护与控制, 2016, 44(16): 163-169. Han Lu, Li Fengting, Wang Chunyan, et al. A survey on impact of wind farm integration on relay protection[J]. Power System Protection and Control, 2016, 44(16): 163-169.
[5] 梅生伟, 李瑞, 陈来军, 等. 先进绝热压缩空气储能技术研究进展及展望[J]. 中国电机工程学报, 2018, 38(10): 2893-2907. Mei Shengwei, Li Rui, Chen Laijun, et al. An overview and outlook on advanced adiabatic compressed air energy storage technique[J]. Proceeding of the CSEE, 2018, 38(10): 2893-2907.
[6] Wang Jidai, Lu Kunpeng, Ma Lan, et al. Overview of compressed air energy storage and technology development[J]. Energies, 2017, 10(7): 991.
[7] Cavallo A. Controllable and affordable utility-scale electricity from intermittent wind resources and compressed air energy storage (CAES)[J]. Energy, 2007, 32(2): 120-127.
[8] Swider D J. Compressed air energy storage in an electricity system with significant wind power generation[J]. IEEE Transactions on Energy Conversion, 2007, 22(1): 95-102.
[9] Fertig E, Apt J. Economics of compressed air energy storage to integrate wind power: a case study in ERCOT[J]. Energy Policy, 2011, 39(5): 2330-2342.
[10] 谭靖, 李国杰, 唐志伟. 基于压缩空气储能的风电场功率调节及效益分析[J]. 电力系统自动化, 2011, 35(8): 33-37. Tan Jing, Li Guojie, Tang Zhiwei. Design and economic analysis of compressed air energy storage based wind farm power regulation system[J]. Automation of Electric Power Systems, 2011, 35(8): 33-37.
[11] Safaei H, Keith D W, Hugo R J. Compressed air energy storage (CAES) with compressors distributed at heat loads to enable waste heat utilization[J]. Applied Energy, 2013, 103(1): 165-179.
[12] Zafirakis D, Kaldellis J K. Autonomous dual-mode CAES systems for maximum wind energy contribution in remote island networks[J]. Energy Conversion & Management, 2010, 51(11): 2150-2161.
[13] 张新敬, 陈海生, 刘金超, 等. 压缩空气储能技术研究进展[J]. 储能科学与技术, 2012, 1(1): 26-40. Zhang Xinjing, Chen Haisheng, Liu Jinchao, et al. Research progress in compressed air energy storage system: a review[J]. Energy Storage Science and Technology, 2012, 1(1): 26-40.
[14] 张俊. 含有压缩空气储能的微网规划与运行控制研究[D]. 济南: 山东大学, 2016.
[15] Wang Sixian, Zhang Xuelin, Yang Luwei, et al. Experimental study of compressed air energy storage system with thermal energy storage[J]. Energy, 2016, 103: 182-191.
[16] 王建男. 离心压缩机叶轮全寿命疲劳分析与安定性分析[D]. 大连: 大连理工大学, 2016.
[17] 陈传尧. 疲劳与断裂[M]. 武汉: 华中科技大学出版社, 2002.
[18] 刘惟信. 机械可靠性设计[M]. 北京: 清华大学出版社, 2000.
[19] 娄素华, 崔继纯. 考虑动态功能的抽水蓄能电站综合规划模型[J]. 电力系统自动化, 2009, 33(1): 27-31. Lou Suhua, Cui Jichun. An integrated planning model of pumped-storage station considering dynamic functions[J]. Automation of Electric Power Systems, 2009, 33(1): 27-31.
[20] 徐滨士. 再制造与循环经济[M]. 北京: 科学出版社, 2007.
[21] 李姚旺, 苗世洪, 尹斌鑫, 等. 考虑先进绝热压缩空气储能电站备用特性的电力系统优化调度策略[J].中国电机工程学报, 2018, 28(18): 5392-5404. Li Yaowang, Miao Shihong, Yin Binxin, et al. Power system optimal scheduling strategy considering reserve characteristics of advanced adiabatic compressed air energy storage plant[J]. Proceedings of the CSEE, 2018, 28(18): 5392-5404.
[22] 李姚旺, 苗世洪, 尹斌鑫, 等. 含先进绝热压缩空气储能电站的电力系统实时调度模型[J]. 电工技术学报, 2019, 34(2): 387-397. Li Yaowang, Miao Shihong, Yin Binxin, et al. Realtime dispatch model for power system with advanced adiabatic compressed air energy storage[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 387-397.
[23] Raju M, Khaitan S K. Modeling and simulation of compressed air storage in caverns: a case study of the Huntorf plant[J]. Applied Energy, 2012, 89(1): 474-481.
[24] Beaudin M, Zareipour H, Schellenberglabe A, et al. Energy storage for mitigating the variability of renewable electricity sources: an updated review[J]. Energy for Sustainable Development, 2010, 14(4): 302-314.
[25] 罗纯坚, 李姚旺, 许汉平, 等. 需求响应不确定性对日前优化调度的影响分析[J]. 电力系统自动化, 2017, 41(5): 22-29. Luo Chunjian, Li Yaowang, Xu Hanping, et al. Influence of demand response uncertainty on dayahead optimization dispatching[J]. Automation of Electric Power Systems,2017, 41(5): 22-29.
[26] 郑静, 文福拴, 李力, 等. 计及风电场和储能系统联合运行的输电系统扩展规划[J]. 电力系统自动化, 2013, 37(1): 135-142. Zheng Jing, Wen Fushuan, Li Li, et al. Transmission system expansion planning considering combined operation of wind farms and energy storage systems[J]. Automation of Electric Power Systems, 2013, 37(1): 135-142.
[27] 孙建军, 张世泽, 曾梦迪, 等. 考虑分时电价的主动配电网柔性负荷多目标优化控制[J]. 电工技术学报, 2018, 33(2): 401-412. Sun Jianjun, Zhang Shize, Zeng Mengdi, et al. Multiobjective optimal control for flexible load in active distribution network considering time-of-use tariff[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 401-412.