0 引言
多风电场公共连接点（Point of Common Coupling，PCC）电压畸变是各个风电场共同作用的 结果[1-5]。评估某一个风电场谐波发射水平时，系统侧包含其余风电场，加剧了背景谐波的不确定性。由于风机滤波器在某些谐波频率呈现低阻抗,增加了评估风电场谐波发射水平的复杂性[6-10]。
评估谐波发射水平的典型方法有波动量法[6,11]和线性回归法[12-13]。波动量法是根据PCC 谐波电 压、电流波动量比值实部符号判别谐波发射水平；线性回归法是通过求解方程回归系数估计谐波发射水平。这两种方法受背景谐波波动影响较大，在背景谐波平稳时计算结果误差小。对于某一风电场而言，系统侧包含其余风电场，背景谐波可能有较大波动，评估风电场谐波发射水平误差大。
文献[14]根据PCC 处谐波电流与背景谐波近似独立协方差为零的性质估计谐波发射水平。该方法在谐波源侧谐波阻抗远大于系统谐波阻抗时，有效地抑制了背景谐波变动对估计结果的影响。由于风机滤波器在某些谐波频率呈现低阻抗，PCC 处谐波电流与背景谐波相关性增强。文献[14]方法在评估风电场谐波发射水平时，计算结果误差较大。
文献[7]使用参考阻抗估计谐波发射水平，要求参考阻抗与实际阻抗接近。负荷投切、系统运行方式和电网参数是不断变化的，系统参考阻抗偏离实际值，影响估计结果。评估典型非线性用户谐波发射水平时，不考虑呈高阻抗特性的谐波源侧谐波阻抗。但风机滤波器在某些谐波频率呈低阻抗，评估风电场谐波发射水平时，风机滤波、箱式变压器和集电线等元件构成的等值阻抗不可忽略，将此阻抗定义为风电场侧附加谐波阻抗。当元件参数和网络拓扑确定，该阻抗基本保持不变。并网逆变器LCL 滤波器的网侧阻抗由箱式变压器和集电线构成，箱式变压器主导。集电线等值后，得到的风电场侧附加谐波阻抗近似值与实际值接近，可作为参考阻抗。
本文主要研究由直驱式永磁同步风力发电机（Direct-drive Permanent Magnet Synchronous Generator, D-PMSG）构成的D-PMSG 风电场的谐波发射水平[15-16]。提出了一种基于改进协方差特性评估D-PMSG 风电场谐波发射水平的方法。首先计算D-PMSG 风电场侧附加谐波阻抗，作为风电场侧参考阻抗。然后利用改进协方差特性建立了PCC 处谐波电压和电流偏差量与PCC 两侧谐波阻抗的表达式[17]，得到系统谐波阻抗，进而求出谐波发射水平。所提方法克服了文献[14]中PCC 处谐波电流和背景谐波相关性带来的误差。仿真和实测数据计算结果表明所提方法评估D-PMSG 风电场谐波发射水平能有效地抑制背景谐波干扰，计算结果更为合理。
1 谐波发射水平误差分析
以诺顿等效电路作为计算谐波源侧谐波发射水平误差的模型，如图1 所示。图中 SI˙为系统侧谐波电流源， CI˙为谐波源侧谐波电流源；ZS 为系统谐波阻抗，ZC 为谐波源侧谐波阻抗； PCCV˙ 和 PCCI˙ 分别为PCC处谐波电压和电流。
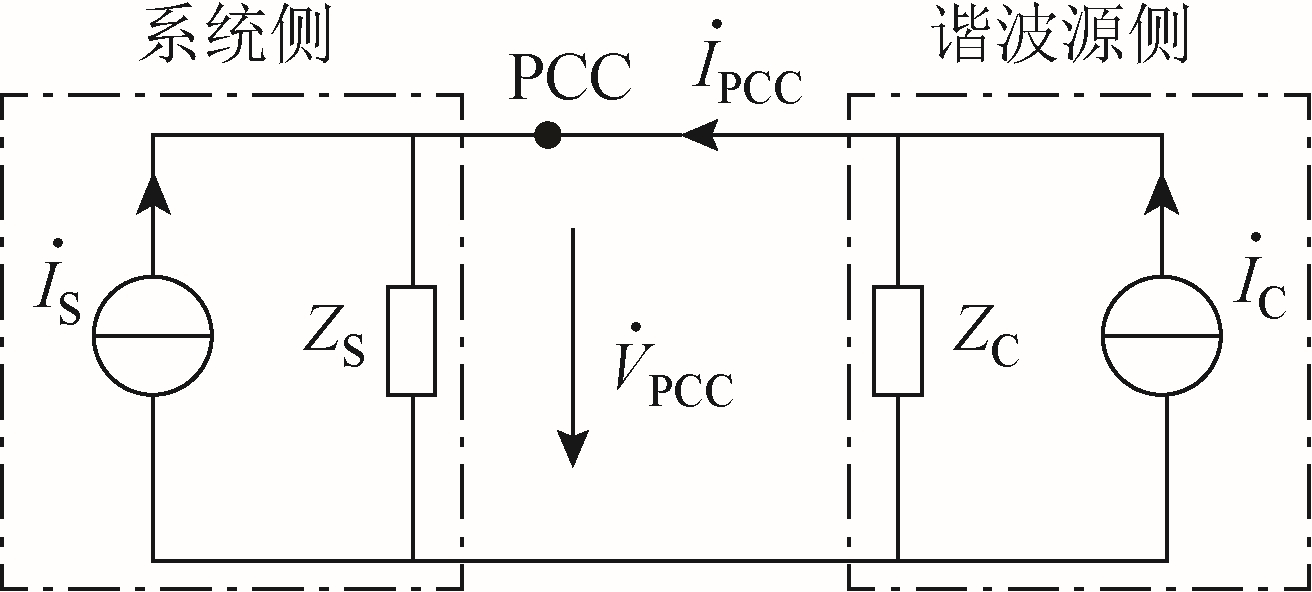
图1 系统和谐波源诺顿等效电路
Fig.1 Norton equivalent of system and harmonic source
谐波源侧的谐波电流源单独作用时，在PCC 处产生的谐波电压为谐波源侧的谐波发射水平。根据图1 求出谐波源侧的谐波发射水平幅值为
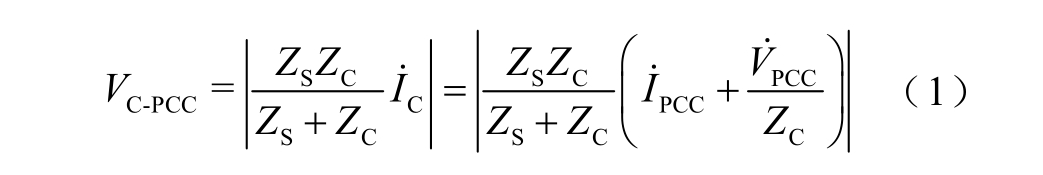
现有评估方法在谐波源侧谐波阻抗远大于系统谐波阻抗时，忽略谐波源侧谐波阻抗。对式（1）进行化简得到估计结果为
由式（1）和式（2）求出谐波发射水平相对误差为
由图1 可得PCC 谐波电压和电流表达式分别为
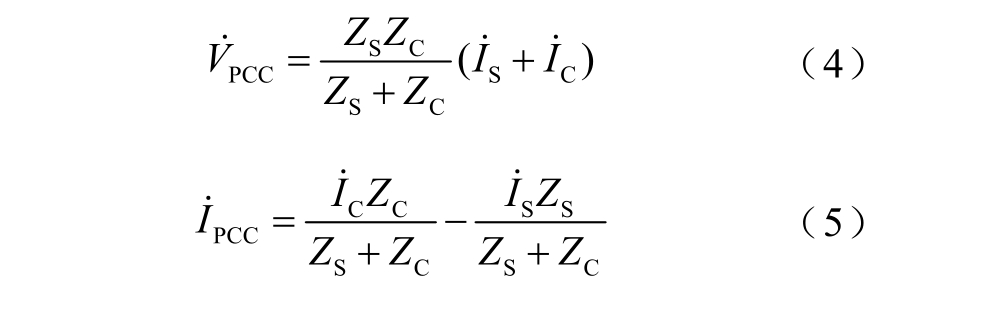
将式（4）、式（5）代入式（3）得到误差为
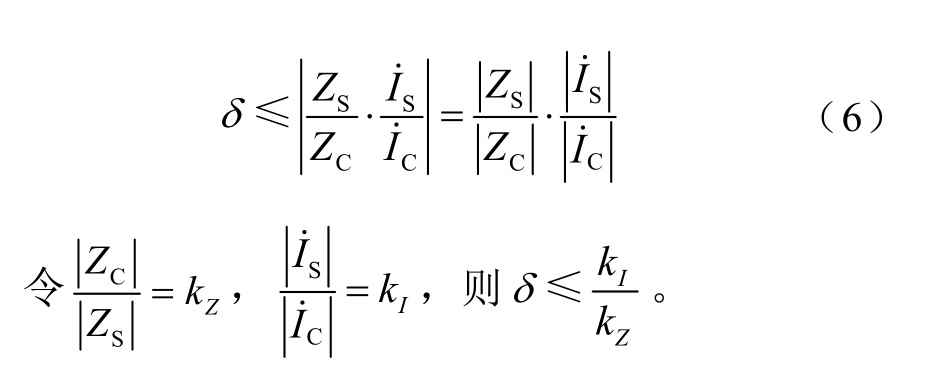
考虑PCC 两侧谐波阻抗比值kZ 对谐波发射水平误差δ 的影响。根据式（6）画出误差δ 最大值曲线如图2 所示，其中kI 取值分别为0.3、0.5、0.8和1.0。当kI 不变时，谐波发射水平相对误差最大值随着kZ 增大而减小。kZ＞10 时，谐波发射水平误差均小于10%，表明谐波源侧谐波阻抗远大于系统谐波阻抗时，估计谐波发射水平可以忽略谐波源侧谐波阻抗。
图2 误差曲线
Fig.2 Error curves
风机滤波器在某些谐波频率呈现低阻抗，PCC两侧谐波阻抗比值kZ 较小。评估D-PMSG 风电场谐波发射水平误差较大，谐波源侧谐波阻抗不可忽略，本文提出改进协方差法评估谐波发射水平。
2 基于改进协方差法的D-PMSG 风电场谐波发射水平评估方法
2.1 D-PMSG 风电场侧等效谐波模型建立
直驱风机采用全功率变流器，机侧变流器与网侧变流器由直流电容隔开，注入电网的谐波由逆变器产生。电压源型逆变器等效为谐波电压源[18]，本文将逆变器的非线性因素（功率开关管的脉宽调制过程、数字延时和死区效应等）考虑到谐波电压源中[19]。逆变器出口滤波器、箱式变压器和集电线等值为直驱风机附加谐波阻抗。直驱风机谐波模型简化为谐波电压源与直驱风机附加谐波阻抗串联的戴维南等效电路。
多台直驱风机并联的风电场并网结构如图 3所示。将单台直驱风机谐波模型推广到D-PMSG 风电场谐波模型，得到如图4 所示风电场侧的戴维南等效电路。
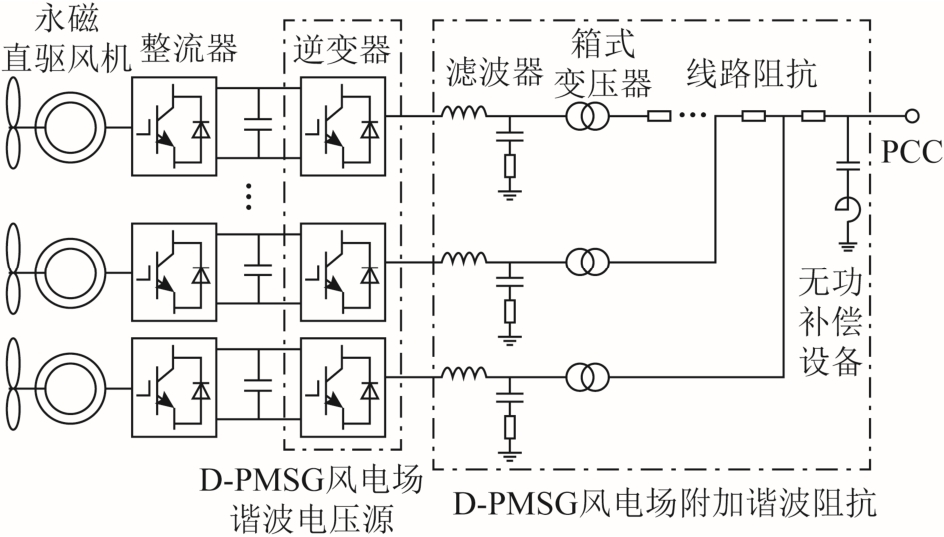
图3 D-PMSG 风电场谐波模型简化
Fig.3 Harmonic model simplification of D-PMSG wind farm
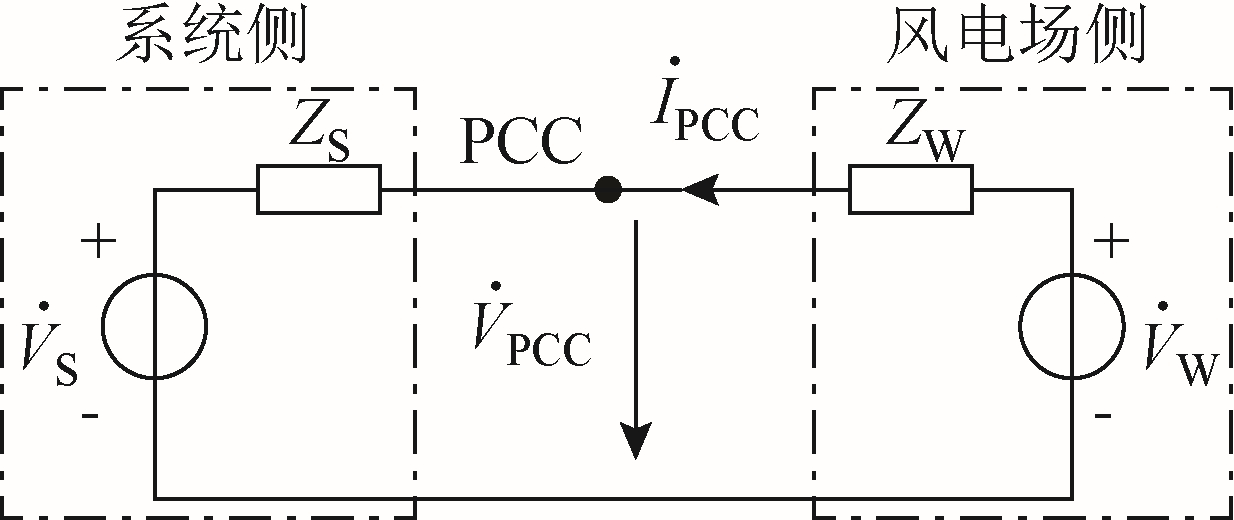
图4 系统和D-PMSG 风电场戴维南等效电路
Fig.4 Thevenin equivalent of system and D-PMSG wind farm
图4 中 WV˙ 为D-PMSG 风电场谐波等效的谐波电压源。ZW 为风电场侧附加谐波阻抗，可根据元件参数和网络拓扑计算得到。
2.2 改进独立矢量协方差法基本原理
计算某个D-PMSG 风电场在PCC 处谐波发射水平等效电路，如图4 所示。图中风电场侧是该DPMSG 风电场的谐波模型；系统侧为背景谐波等效的谐波模型，ZS 为系统谐波阻抗， SV˙为系统侧谐波电压源。
根据图4 可知D-PMSG 风电场谐波电压源为
对式（7）求均值得到
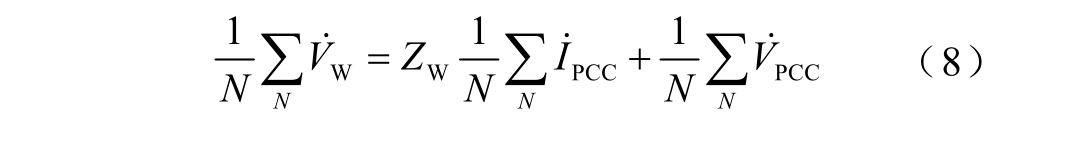
式（7）和式（8）相减得到D-PMSG 风电场谐波电压源的偏差量方程为
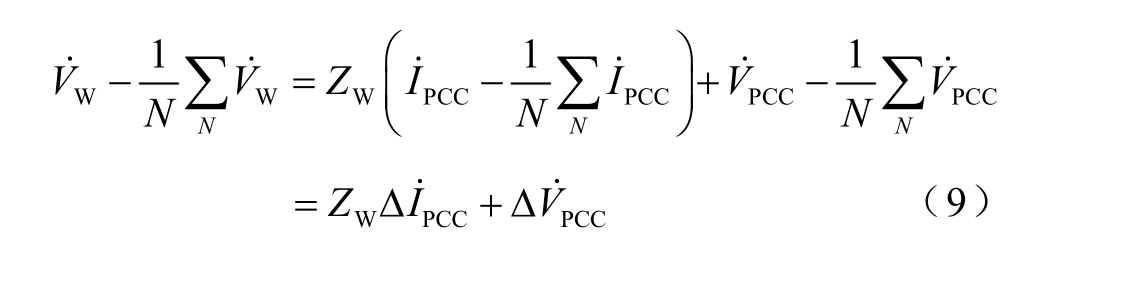
式（9）中PCC 处测量数据的偏差量表示为
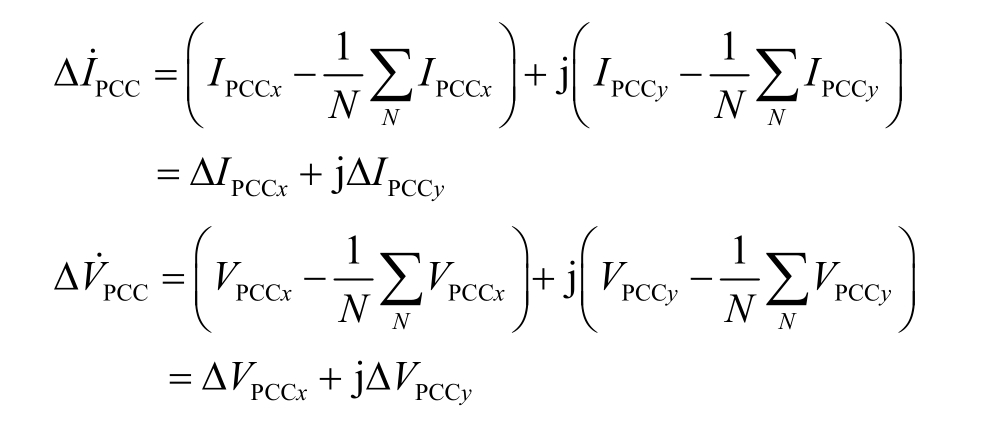
根据图4 电路列写方程
估计时间内系统谐波阻抗保持不变，对式（10）求均值得
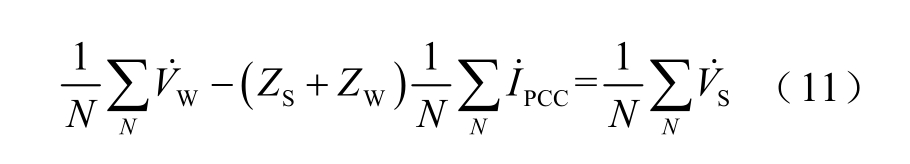
式（10）减去式（11）得到
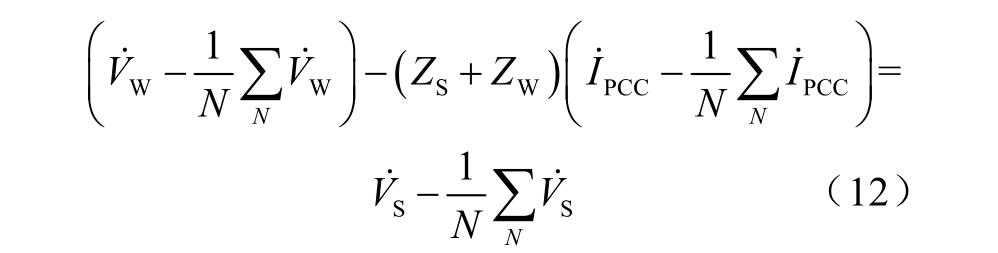
式（12）为两侧谐波源的偏差量方程。通常风电场谐波等效为谐波电压源，考虑了功率开关管脉宽调制过程、数字延时、死区效应和器件非理想特性等非线性因素。逆变器的控制特性受电网背景谐波影响，与背景谐波有一定相关性；其余非线性因素由逆变器自身特性造成，与背景谐波独立。在通常运行条件下，背景谐波影响程度较小，D-PMSG 风电场侧谐波源与背景谐波有弱相关性，因此认为它们近似独立，协方差近似为零。根据文献[14]的推导，抵消了系统谐波电压源的偏差量。其中D-PMSG风电场侧谐波源的偏差量由式（9）求出。得出关于PCC 谐波电压、电流偏差量与两侧谐波阻抗的表达式，求得ZS 为
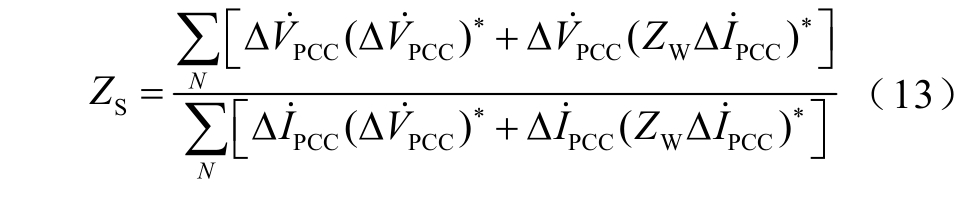
式中，*表示复数的共轭。
计算D-PMSG 风电场谐波发射水平为
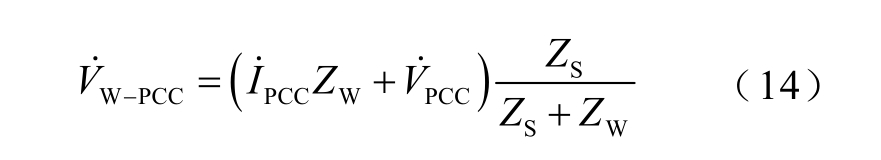
2.3 原协方差法误差分析
根据图4 用文献[14]提出的独立随机矢量协方差方法（简称原协方差法），认为 PCCI˙ 与 SV˙近似独立，求出系统谐波阻抗ZSO 为 N
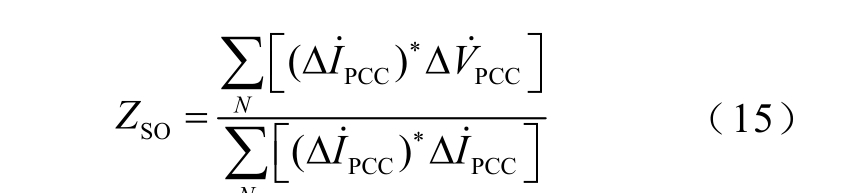
实际计算 PCCI˙ 与 SV˙的协方差值为
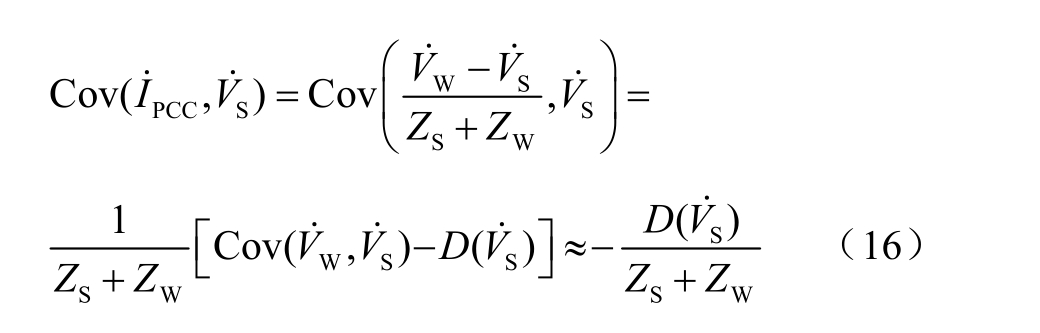
式中，(S )D V˙ 为 SV˙的方差。
将该协方差视为已知参数，对式（15）得到的系统谐波阻抗进行修正，计算结果为
比较式（15）和式（17）看出原协方差法计算结果ZSO 偏小。 PCCI˙ 与 SV˙的协方差是影响估计结果的直接原因，因此误差来自于D-PMSG 风电场侧附加谐波阻抗和背景谐波电压方差。D-PMSG 风电场侧附加谐波阻抗在某些谐波频率阻抗较小，背景谐波可能存在较大波动，使得式（16）协方差值绝对值大，求出的系统谐波阻抗偏小，根据式（14）计算D-PMSG 风电场谐波发射水平也偏小。
3 D-PMSG 风电场侧附加谐波阻抗计算
直驱风机逆变器出口电压为690V，经箱式变压器升压到35kV，通过集电线汇集到PCC 处。集电线长度存在差异，根据D-PMSG 风电场拓扑计算其附加谐波阻抗较为困难，考虑计算D-PMSG 风电场侧近似附加谐波阻抗。
直驱风机谐波模型如图5 所示，图中 VSCV˙ 为等效的谐波电压源，L1 为逆变器侧电感，C 为滤波电容，R 为阻尼电阻，ZT 箱式变压器谐波阻抗，ZL 集电线谐波阻抗。
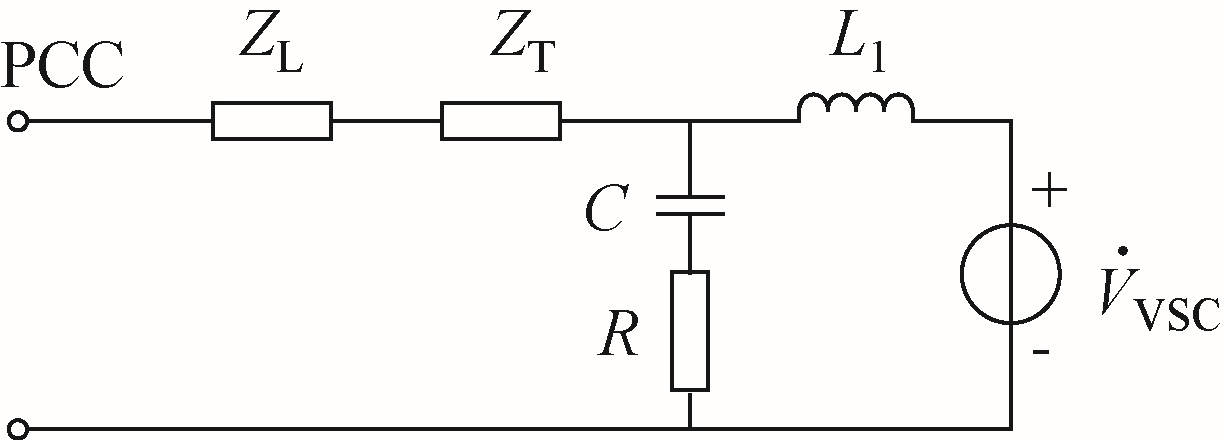
图5 直驱风机谐波模型
Fig.5 Harmonic model of D-PMSG
计算直驱风机附加谐波阻抗方法如下。
滤波电容C 串联阻尼电阻R 再与逆变器侧电感L1 并联构成LC 滤波器，其谐波阻抗为
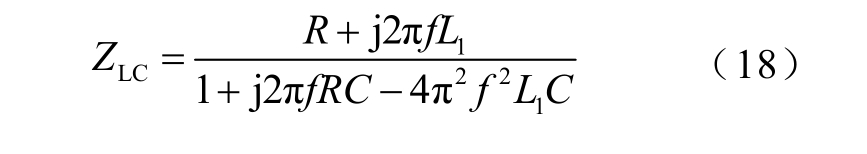
式中，f 为谐波频率。
忽略箱式变压器电阻，则
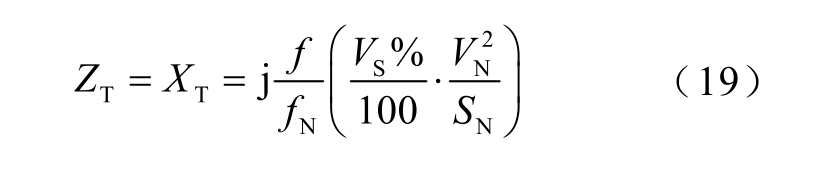
式中， NS 为额定容量；VN 为额定电压；VS%为短路电压； Nf 为基波频率。
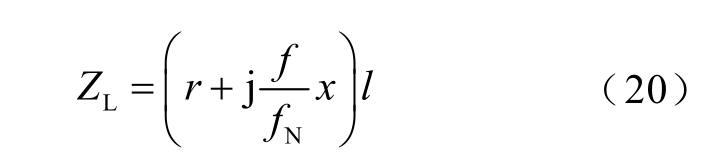
式中，r、x 分别为集电线单位长度电阻和电抗；l 为集电线长度。
则直驱风机附加谐波阻抗为
式中，ZL+ZT 看作LCL 滤波器的网侧阻抗。集电线的长度大多在2～20km，假设集电线长度均等效为10 km。在集电线长度为边界值和等效长度时，根据表1 中某D-PMSG 风电场参数，计算工频下直驱风机附加阻抗，结果见表2。
风机滤波器的网侧阻抗由集电线和箱式变压器 构成。它们的基波和谐波阻抗均呈感性，计算集电线阻抗的占比|ZL|/|ZL+ZT|。表2 中占比随集电线长度增加而增大，集电线长20km 时，占比为16.60%。得出风机滤波器的网侧基波阻抗由箱式变压器阻抗主导。
表1 D-PMSG 风电场参数
Tab.1 Parameters of D-PMSG wind farm
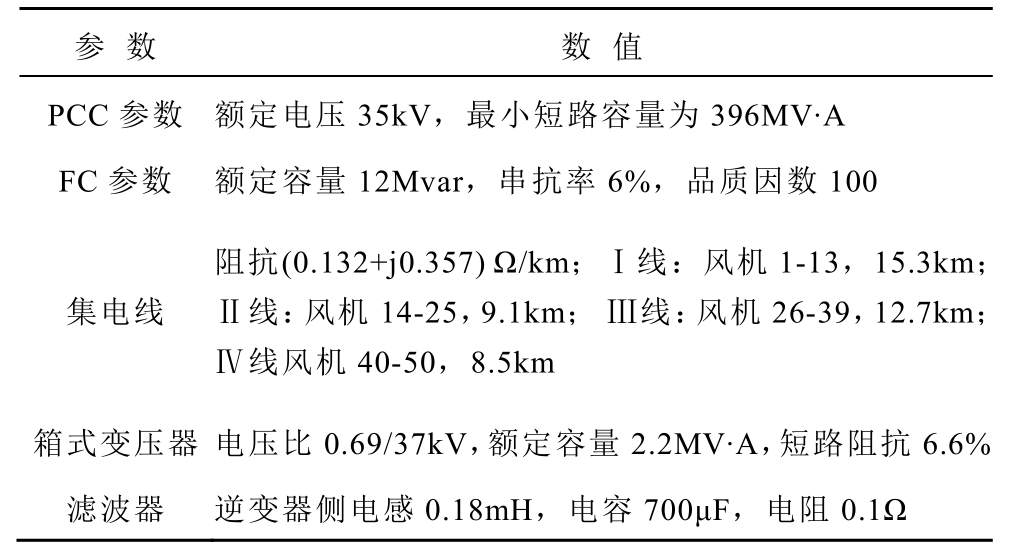
参 数 数 值 PCC 参数 额定电压35kV，最小短路容量为396MV·A FC 参数 额定容量12Mvar，串抗率6%，品质因数100 集电线 阻抗(0.132+j0.357) Ω/km；Ⅰ线：风机1-13，15.3Ⅱ线：风机14-25，9.1km； Ⅲ线：风机26-39，12.7Ⅳ线风机40-50，8.5km 箱式变压器 电压比0.69/37kV，额定容量2.2MV·A，短路阻抗6.6%滤波器 逆变器侧电感0.18mH，电容700μF，电阻0.1Ω
表2 直驱风机附加阻抗
Tab.2 D-PMSG additional impedance
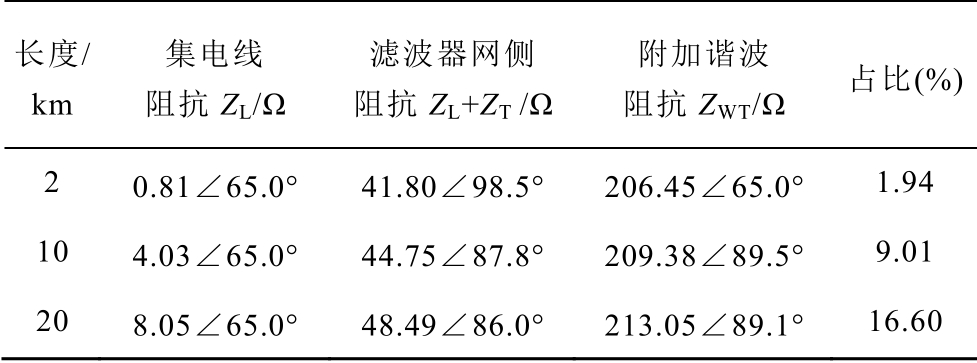
长度/ km 集电线 阻抗ZL/Ω 滤波器网侧 阻抗ZL+ZT /Ω 附加谐波 阻抗ZWT/Ω 占比(%)2 0.81∠65.0° 41.80∠98.5° 206.45∠65.0° 1.94 10 4.03∠65.0° 44.75∠87.8° 209.38∠89.5° 9.01 20 8.05∠65.0° 48.49∠86.0° 213.05∠89.1° 16.60
风电场PCC 处主要含有5、7、11、13 次谐波，在集电线长度不同时，计算了直驱风机附加5、7、11、13 次谐波阻抗，结果见表3。同一谐波频率下，阻抗相角的极差很小；阻抗幅值极差大，但远小于阻抗幅值，可以忽略。集电线长度变化对直驱风机附加谐波阻抗影响很小，将集电线长度等效为10km。
表3 直驱风机附加谐波阻抗
Tab.3 D-PMSG additional harmonic impedance
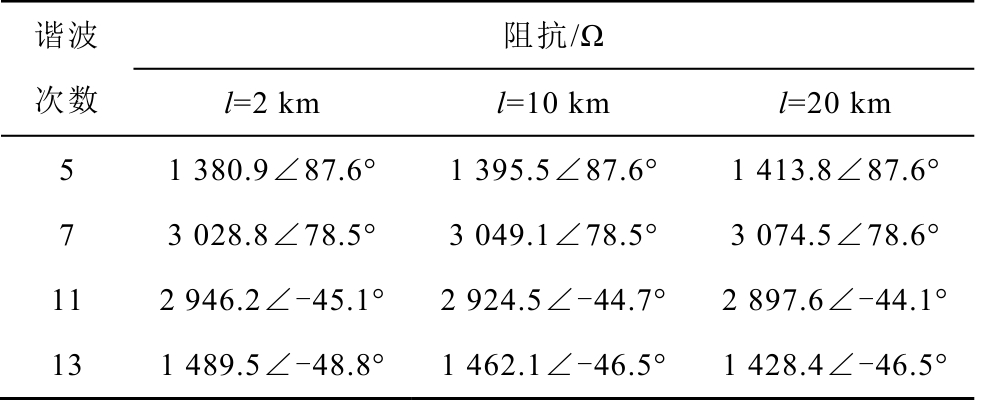
谐波次数阻抗/Ω l=2 km l=10 km l=20 km 5 1 380.9∠87.6° 1 395.5∠87.6° 1 413.8∠87.6°7 3 028.8∠78.5° 3 049.1∠78.5° 3 074.5∠78.6°11 2 946.2∠-45.1° 2 924.5∠-44.7° 2 897.6∠-44.1°13 1 489.5∠-48.8° 1 462.1∠-46.5° 1 428.4∠-46.5°
将以上结论推广到n 台直驱风机并联的风电场，计算D-PMSG 风电场侧附加谐波阻抗时，集电线长度等效为10km。此外，风电场通常使用相同型号的风机，各机组配置的滤波器、箱式变压器参数相同。因此考虑聚合风电场的各元件阻抗，得到近似的DPMSG 风电场侧附加谐波阻抗为
式中，ZLCagg 为LC 滤波器聚合阻抗；ZTagg 为箱式变压器聚合阻抗；ZLagg 为风电场集电线聚合阻抗；ZFC为无功补偿装置阻抗。
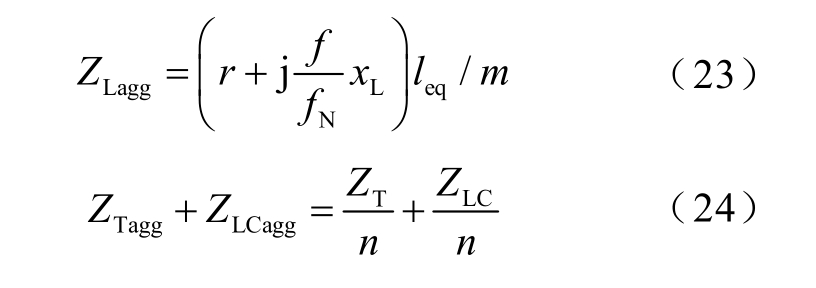
式中，leq 为等效长度，leq=10 km；m 为集电线数量。
由式（22）计算D-PMSG 风电场侧附加谐波阻抗近似值；根据风电场拓扑和元件参数，求出谐波节点阻抗矩阵，其中风电场 PCC 处自阻抗为 DPMSG 风电场侧附加谐波阻抗准确值。D-PMSG 风电场侧附加谐波阻抗及其误差见表4。随着谐波次数增加，相对误差的绝对值大致呈现增加趋势，DPMSG 风电场侧附加谐波阻抗幅值相对误差绝对值在10%内，相角相对误差绝对值在20%内。
表4 D-PMSG 风电场侧附加谐波阻抗及其误差 Tab.4 D-PMSG wind farm additional harmonic impedance and its error
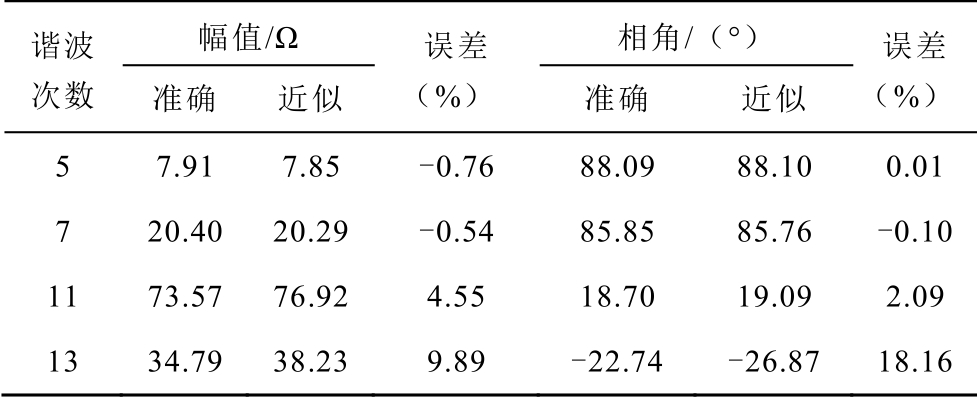
谐波 次数 幅值/Ω 误差 （%） 相角/（°） 误差（%）准确 近似 准确 近似 5 7.91 7.85 -0.76 88.09 88.10 0.01 7 20.40 20.29 -0.54 85.85 85.76 -0.10 11 73.57 76.92 4.55 18.70 19.09 2.09 13 34.79 38.23 9.89 -22.74 -26.87 18.16
4 仿真分析
为了验证本文方法的正确性，根据图4 戴维南等效电路建立仿真算例，生成PCC 处谐波电压电流数据，具体仿真参数设置如下[20]：
1） WV˙ 的幅值为100V，加上±20%随机波动和5%正弦半波变化； WV˙ 的相角为30°，加上±10%随机波动和10%正弦半波变化。背景谐波 SV˙的幅值为p| WV˙ |（p 取0.1、0.3、0.5、0.8 和1.0），幅值加上±10%随机波动和5%正弦半波变化； SV˙相角60°，加上±10%随机波动和10%正弦半波变化。
2）为使PCC 两侧阻抗与实际情况相符，ZS 选取系统5 次谐波阻抗的参考值17.285Ω（根据表1中PCC 参数计算得出），幅值加上20%正弦半波变化，相角为70°加上20%正弦半波变化；ZW 取表4中的近似值，幅值7.85Ω，相角88.1°，保持不变。
上述仿真模型生成1 000 组模拟数据，按每60组数据递推计算。系统谐波阻抗计算中，每60 组数据为一段，得到一个ZS；下一次往后递推一组数据得到新的60 组数据段，用来计算新的ZS，以此类推。计算D-PMSG 风电场谐波发射水平95%概率值时，首先利用各数据段计算的ZS，根据式（14）计算出D-PMSG 风电场谐波发射水平，再求出其95%概率值。
本文在不忽略谐波源侧谐波阻抗的情况下计算谐波发射水平，因此不再与文献[11-13]忽略谐波源侧谐波阻抗的方法进行比较。使用三种方法（方法1 为文献[20]的快速独立分量法，方法2 为文献[14]的原协方差法，方法3 为本文方法）计算了系统谐波阻抗幅值相对误差方均根值和D-PMSG 风电场谐波发射水平95%概率值（理论值为87.85V）相对误差，结果见表5。由于近似计算D-PMSG 风电场侧附加谐波阻抗有误差，ZW 取边界值（0.9×7.85）Ω 和（1.1×7.85）Ω，用方法3 计算得出结果见表6。
表5 三种方法计算结果误差对比
Tab.5 Contrast of calculation errors of three methods
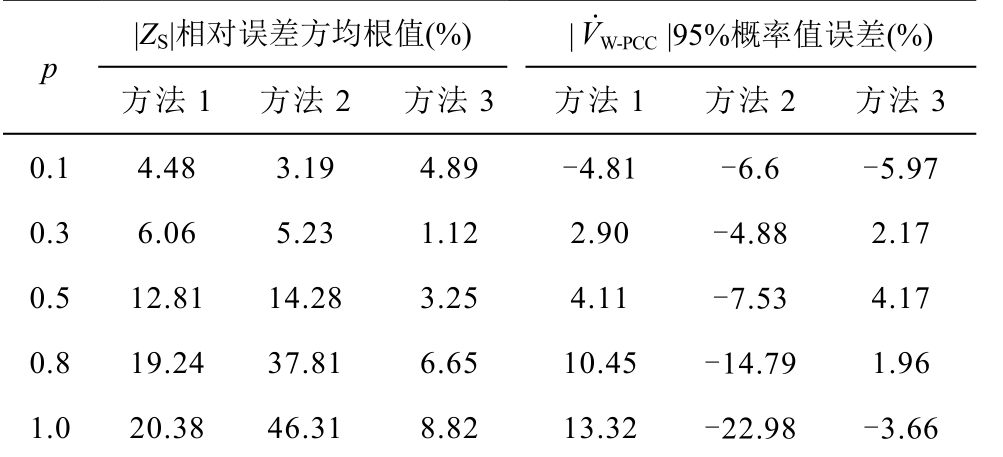
V˙ |95%概率值误差(%) |ZS|相对误差方均根值(%) | W-PCC p 方法1 方法2 方法3 方法1 方法2 方法3 0.1 4.48 3.19 4.89 -4.81 -6.6 -5.97 0.3 6.06 5.23 1.12 2.90 -4.88 2.17 0.5 12.81 14.28 3.25 4.11 -7.53 4.17 0.8 19.24 37.81 6.65 10.45 -14.79 1.96 1.0 20.38 46.31 8.82 13.32 -22.98 -3.66
表6 计算结果误差
Tab.6 Calculation errors
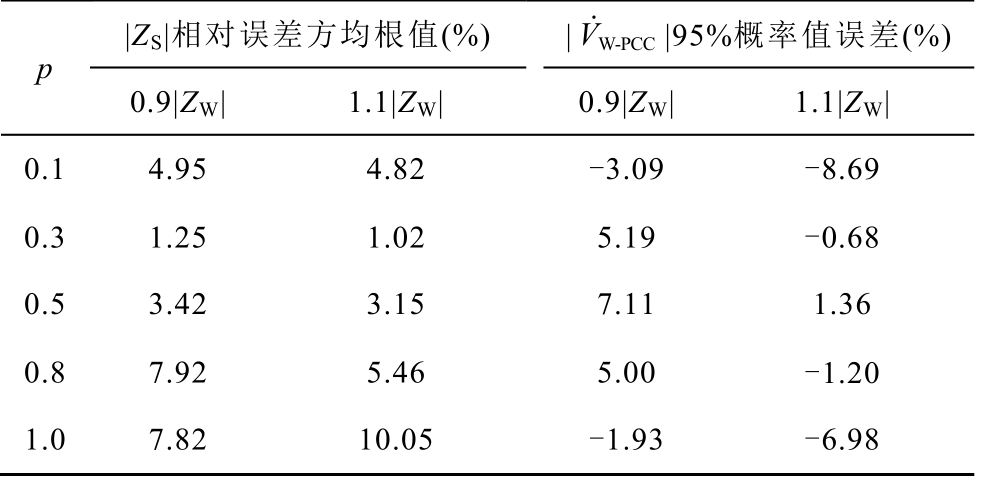
p |ZS|相对误差方均根值(%) | W-PCC V˙ |95%概率值误差(%)0.9|ZW| 1.1|ZW| 0.9|ZW| 1.1|ZW| 0.1 4.95 4.82 -3.09 -8.69 0.3 1.25 1.02 5.19 -0.68 0.5 3.42 3.15 7.11 1.36 0.8 7.92 5.46 5.00 -1.20 1.0 7.82 10.05 -1.93 -6.98
通过表5 的计算结果看出，当p 值增大时，即背景谐波增大，三种方法计算得到的系统谐波阻抗误差大致呈增大的趋势，方法3 的误差增长趋势最小。当p 值大于0.1，在相同背景谐波下，方法3 计算的系统谐波阻抗误差在三种方法中最小。用三种方法计算谐波发射水平误差，方法3 的计算结果误差都较小，说明方法3 较好地消除了背景谐波干扰。随着p 值增大，观测信号噪声增大，快速独立分量分析算法的分离效果下降，方法1 计算结果误差增大。方法2 计算谐波发射水平的相对误差全为负，说明计算结果相对于理论值偏小，仿真结果与2.3 节的理论分析相符。
对比表5、表6 中计算结果，同一p 值下系统谐波阻抗误差接近，谐波发射水平误差也同样接近，表明近似计算D-PMSG 风电场侧附加谐波阻抗产生的误差对估计系统谐波阻抗和谐波发射水平的影响都较小。
5 实测数据计算分析
某地区有三个风电场集中接入电网，评估其中一个D-PMSG 风电场谐波发射水平时，系统侧包含其余两个风电场，加剧了背景谐波的不确定性。该D-PMSG 风电场侧附加谐波阻抗已在第3 节进行计算，结果见表4。实测数据来自某D-PMSG 风电场35kV 母线（PCC），每30s 对采样数据做傅里叶变换，得到各次谐波的测量值。图6 是连续5h 内PCC处5 次谐波电压和电流幅值波形。采用仿真分析的三种方法对PCC 处5 次谐波数据按每30min 分段递推计算，得到系统谐波阻抗计算结果如图7 所示。
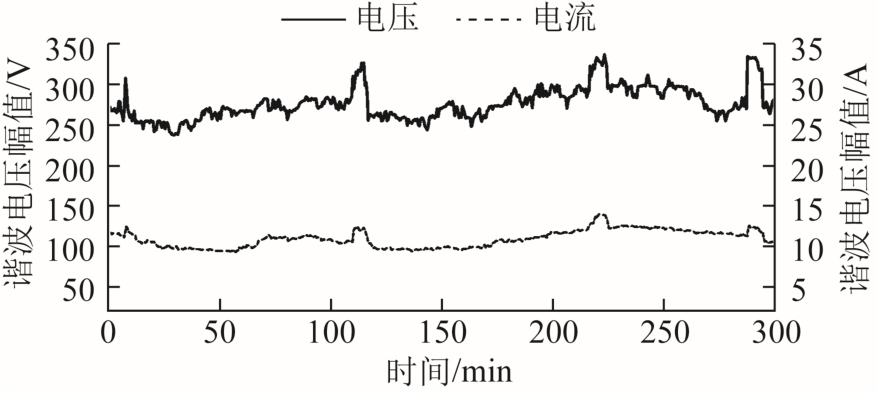
图6 谐波电压电流波形
Fig.6 Waveforms of the harmonic voltage and current
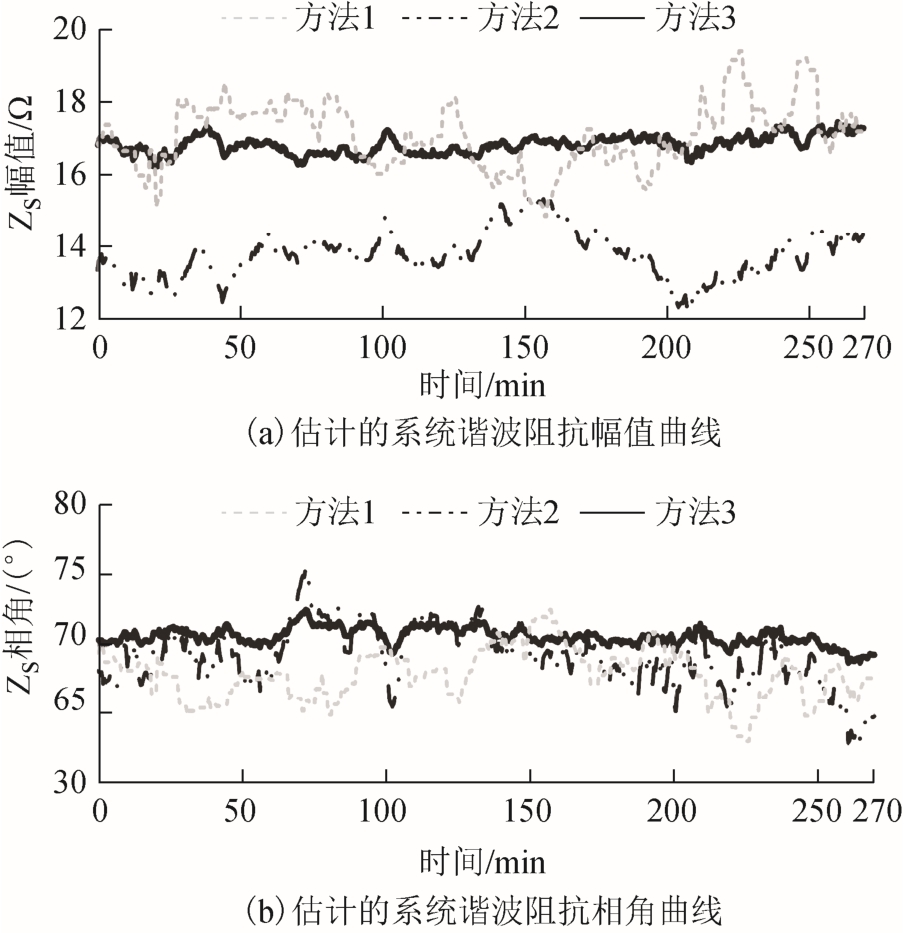
图7 系统5 次谐波阻抗估计值
Fig.7 Estimation of the 5th harmonic ZS
根据表1 中系统短路容量计算系统参考基波阻抗为3.457Ω，估算系统5 次谐波阻抗为17.285Ω。由图7 可知，本文方法计算得到的系统5 次谐波阻抗幅值与估算的阻抗幅值接近。方法1 利用快速独立分量分析算法计算系统谐波阻抗，D-PMSG 风电场背景谐波包含了风区其余风电场谐波源，加剧了背景谐波不确定性，源信号的分离效果降低，估计ZS 有较大误差。方法2 因为背景谐波和PCC 处谐波电流相关性增强，导致估计结果明显偏小。本文方法更好地消除了背景谐波的干扰，计算结果更合理。
用本文方法评估D-PMSG 风电场谐波发射水平，ZW 分别使用表4 中D-PMSG 风电场侧附加5 次谐波阻抗的准确值和近似值，结果见表7。系统谐波阻抗和D-PMSG 风电场谐波发射水平95%概率值计算结果的相对误差都很小，表明简化计算D-PMSG风电场侧附加谐波阻抗对谐波发射水平估计结果影响很小。
表7 ZS 和|
|评估误差对比
Tab.7 Contrast of ZS and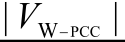 
errors
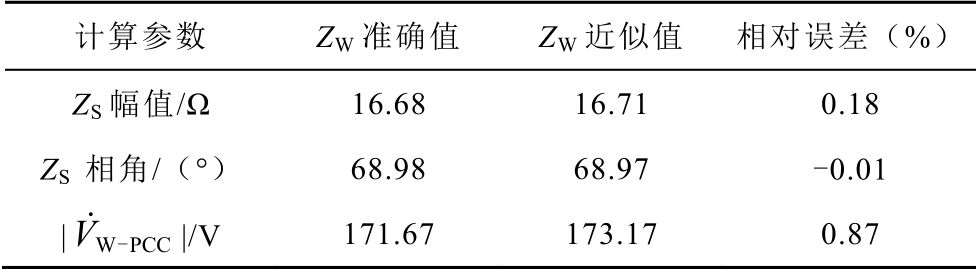
计算参数 ZW 准确值 ZW 近似值 相对误差（%）ZS 幅值/Ω 16.68 16.71 0.18 ZS 相角/（°） 68.98 68.97 -0.01 | W PCC V -˙ |/V 171.67 173.17 0.87
6 结论
1）本文计算系统谐波阻抗，考虑了D-PMSG 风电场侧附加谐波阻抗，克服了原协方差方法中PCC处谐波电流和背景谐波相关性对结果的影响。
2）在风机滤波器呈现低阻抗，D-PMSG 风电场侧附加谐波阻抗不可忽略的情况下，本文方法相较于快速独立分量法和原协方差法，更好地抑制了背景谐波的干扰。由仿真结果可以看出本文方法计算结果误差较小。通过评估某D-PMSG 风电场谐波发射水平，表明了本文方法的有效性。
3）本文方法需要根据D-PMSG 风电场元件参数计算其附加谐波阻抗，使得谐波发射水平评估过程繁琐。根据D-PMSG 风电场特征，寻求更简便的附加谐波阻抗计算方法值得进一步研究。
[1] Tentzerakis S, Paraskevopoulou N, Papathanassiou S, et al. Measurement of wind farm harmonic emissions[C]//IEEE Power Electronics Specialists Conference, Rhodes, Greece, 2008： 1769-1775.
[2] 甘磊, 吴臻, 谷纪亭, 等. 风电集群接入系统规划的混合整数线性模型[J]. 电工技术学报, 2017, 32(5)： 165-175. Gan Lei, Wu Zhen, Gu Jiting, et al. A MILP model for grid-connection transmission system planning of wind farm clusters[J]. Transactions of China Electrotechnical Society, 2017, 32(5)： 165-175.
[3] Liang Xiaodong. Emerging power quality challenges due to integration of renewable energy sources[J]. IEEE Transactions on Industry Applications, 2017, 53(2)： 855-866.
[4] 王深哲, 高山, 李海峰, 等. 含风电接入的电网规划方案电能质量评估[J]. 电工技术学报, 2013, 28(8)： 56-65. Wang Shenzhe, Gao Shan, Li Haifeng, et al. Evaluation of power quality in grid planning scheme with wind power integration[J]. Transactions of China Electrotechnical Society, 2013, 28(8)： 56-65.
[5] 何世恩, 郑伟, 智勇, 等. 大规模集群风电接入电网电能质量问题探讨[J]. 电力系统保护与控制, 2013, 41(2)： 39-44. He Shien, Zheng Wei, Zhi Yong, et al. Power quality issues of large-scale cluster wind power integration[J]. Power System Protection and Control, 2013, 41(2)： 39-44.
[6] Yang Honggeng, Pirotte P, Robert A. Harmonic emission levels of industrial loads statistical assessment[C]// CIGRE Proceedings： International Council on Large Electric Systems, Paris, France, 1996： 456-462.
[7] Xu W, Liu Yilu. A method for determining customer and utility harmonic contributions at the point of common coupling[J]. IEEE Transactions on Power Delivery, 2000, 17(1)： 210-216.
[8] Liang Shun, Hu Qiaohui, Lee W J. A survey of harmonic emissions of a commercially operated wind farm[J]. IEEE Transactions on Industry Applications, 2012, 48(3)： 1115-1123.
[9] 汤波, 林顺富, 陈光, 等. 居民配电网负荷谐波电流发射水平评估方法[J]. 电工技术学报, 2018, 33(3)： 533-542. Tang Bo, Lin Shunfu, Chen Guang, et al. The harmonic current emission level of the residential loads in the distribution network[J]. Transactions of China Electrotechnical Society, 2018, 33(3)： 533-542.
[10] 邱思语, 杨洪耕. 改进的加权支持向量机回归的谐波发射水平估计方法[J]. 电工技术学报, 2016, 31(5)： 85-90. Qiu Siyu, Yang Honggeng. Assessment method of harmonic emission level based on the improved weighted support vector machine regression[J]. Transactions of China Electrotechnical Society, 2016, 31(5)： 85-90.
[11] 龚华麟, 肖先勇, 刘亚梅, 等. 基于主导波动量筛选原理的用户谐波发射水平估计方法[J]. 中国电机工程学报, 2010, 30(4)： 22-27. Gong Hualin, Xiao Xianyong, Liu Yamei, et al. A method for assessing customer harmonic emission level based on the dominant fluctuation filtering principle[J]. Proceedings of the CSEE, 2010, 30(4)： 22-27.
[12] 张巍, 杨洪耕. 基于二元线性回归的谐波发射水平估计方法[J]. 中国电机工程学报, 2004, 24(6)：54-57. Zhang Wei, Yang Honggeng. A method for assessing harmonic emission level based on binary linear regression[J]. Proceedings of the CSEE, 2004, 24(6)： 54-57.
[13] 艾永乐, 王玉栋, 都静静, 等. 基于LTS 初值的稳健回归的谐波发射水平评估方法[J]. 电力系统保护与控制, 2015, 43(21)： 99-105. Ai Yongle, Wang Yudong, Du Jingjing, et al. A method for assessing harmonic emission level based on robust regression of LTS initial value[J]. Power System Protection and Control, 2015, 43(21)： 99-105.
[14] 惠锦, 杨洪耕, 林顺富, 等. 基于独立随机矢量协方差特性的谐波发射水平评估方法[J]. 电力系统自动化, 2009, 33(7)： 27-31. Hui Jin, Yang Honggeng, Lin Shunfu, et al. Assessment method of harmonic emission level based on covariance characteristic of random vectors[J]. Automation of Electric Power Systems, 2009, 33(7)： 27-31.
[15] 陈宝平, 林涛, 陈汝斯, 等. 直驱风电场经 VSCHVDC 并网系统的多频段振荡特性分析[J]. 电工技术学报, 2018, 33(增刊1)： 176-184. Chen Baoping, Lin Tao, Chen Rusi, et al. Characteristics of multi-band oscillation for direct drive wind farm interfaced with VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2018, 33(S1)： 176-184.
[16] 钟再敏, 江尚, 康劲松, 等. 永磁同步电机谐波电压与电流的耦合模型及前馈控制[J]. 电工技术学报, 2017, 32(18)： 131-142. Zhong Zaimin, Jiang Shang, Kang Jinsong, et al. A harmonic voltage and current coupling permanent magnet synchronous motor model and feedforward control[J]. Transactions of China Electrotechnical Society, 2017, 32(18)： 131-142.
[17] 程维虎, 来向荣. 复值随机变量的协方差与相关性[J]. 中央民族大学学报： 自然科学版, 2001,10(1)： 19-21. Cheng Weihu, Lai Xiangrong. Covariance and correlation coefficient of complex random variables[J]. Journal of the Central University for Nationalities： Natural Science Edition, 2001, 10(1)： 19-21.
[18] Badrzadeh B, Gupta M, Singh N, et al. Power system harmonic analysis in wind power plants-Part I： Study methodology and techniques[C]//IEEE Industry Applications Society Annual Meeting, Las Vegas, USA, 2012： 1-11.
[19] 杨洪耕, 肖先勇, 刘俊勇. 电能质量问题的研究和技术进展(二)——供电网谐波的测量与分析[J]. 电力自动化设备, 2003, 23(11)： 1-4. Yang Honggeng, Xiao Xianyong, Liu Junyong. Issues and technology assessment on power quality part2： measurement and analysis for harmonic in supply network[J]. Electric Power Automation Equipment, 2003, 23(11)： 1-4.
[20] 赵熙, 杨洪耕. 基于快速独立分量分析的系统侧谐波阻抗计算方法[J]. 电力系统自动化, 2015, 39(23)： 139-144. Zhao Xi, Yang Honggeng. Method of calculating system-side harmonic impedance base on FastICA[J]. Automation of Electric Power Systems, 2015, 39(23)： 139-144.