0 引言
随着能源互联网建设，高比例分布式风电直接或与冷热电联供系统（Combined Cooling, Heating and Power, CCHP）构成能量枢纽（Energy Hub, EH）接入配电网，主动配电网（Active Distribution Network, ADN）多能流耦合特征日益明显[1]。能源转型要求优先利用风电等可再生清洁能源，而风电兼具随机模糊不确定性[2]和波动性[3-4]，EH 如何对其优先利用、ADN 与EH 及主网有功双向交互、负荷三相不平衡等对潮流分布有重要影响，含能量枢纽主动配电网的潮流分析方法亟待研究。
考虑风电等可再生能源的配电网潮流方法可分两类：①计及其不确定性，如概率/随机潮流[5-8]、模糊潮流[9-10]，区间潮流[11-13]及概率区间潮流[14]等。概率/随机潮流根据已知随机变量的统计特征，运用蒙特卡洛模拟或半不变量法等获取待求量概率特征；模糊潮流基于模糊集理论获取待求量隶属函数；区间潮流利用区间刻画待求量上下界；区间概率潮流则将随机性和区间法相结合[14]。然而，事物不确定性客观上兼具随机性和模糊性[15]，如风速以随机模糊变量描述更科学[2]。②兼顾其波动性及随机性，如含风电场输电网动态潮流和动态随机最优潮流[16]、信息物理融合的主动配电网动态潮流方法[17]等，而兼顾风电随机模糊性和波动性配电网潮流方法尚未研究。
EH 是ADN 多能流耦合基本单元，含风电等EH建模及其优化[18]、综合能源系统混合潮流及其最优潮流[19-21]、含能量枢纽配电网潮流及其优化[22]等被研究，兼顾风电随机模糊性和波动性，改进其冷/热电耦合模式以优先利用风电尚未得到研究。关于三相不平衡的配电网潮流方法已相对成熟[23-25]，但综合考虑EH、ADN 及主网有功双向交互下配电网三相不平衡潮流方法尚未被探讨。
本文以日前计划为背景，考虑风电随机模糊性和波动性、冷/热电负荷波动性及负荷三相不平衡，通过各时段风电穿透水平、冷/热电负荷比较，提出适应负荷变化和风电穿透水平的EH 冷/热电耦合模式及风电供冷/热分配系数，以实现风电优先利用，进而获得EH 运行状态及其与ADN 随机模糊交换功率；考虑直接接入配电网风电和EH 交换功率，得到日内ADN 与主网的源、荷和孤岛交互状态及其交换功率；建立含风电优先利用EH 的主动配电网三相不平衡随机模糊动态潮流模型；提出随机模糊模拟、前推回代及三相解耦结合的模型求解算法；最后采用改进的IEEE 33 节点系统对文中模型和算法进行验证。
1 EH 优先利用风电冷/热电改进耦合模式及其与ADN 交换功率
1.1 兼顾随机模糊性和波动性的日风电出力模型
据文献[2]，以随机模糊变量描述风速，则随机模糊风电有功出力 wP~ 为
式中， v~t 为t 时段随机模糊风速；ρ 为空气密度；A 为风轮覆盖面积； C r为风机风能利用系数； Prated为风电机组有功功率的额定值； vc ut-in为切入风速；vc ut-out为切出风速； vr ated为额定风速。
采用随机模糊模拟生成日时间尺度风速，各时段风速为随机模糊变量，以风速各时段随机模糊期望值变化描述其波动性。设风电机组以恒功率因数运行且忽略机械损耗，t 时段风电出力为
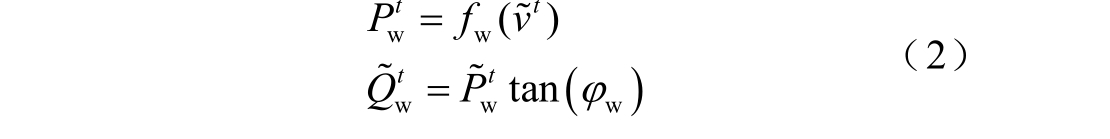
式中， ϕ w为风电机组的功率因数角； t = 1,2,… ,T， T 为时域长度，本文将一天24h 分96 时段，即T=96。
1.2 EH 优先利用风电改进冷/热电耦合模式及其与ADN 交换功率
图1 为由分布式风电、热电联供设备、中央空调系统（Air Conditioner, AC）和电力变压器等构成的EH。风电通过变流器对电负荷 Lte 和AC 供电，定义t 时段随机模糊性风电 P~w t供冷/热分配系数为 vwt（冷/热负荷按常规作为一个物理量 Lt h），则EH 与ADN 交换功率 
也为随机模糊变量。
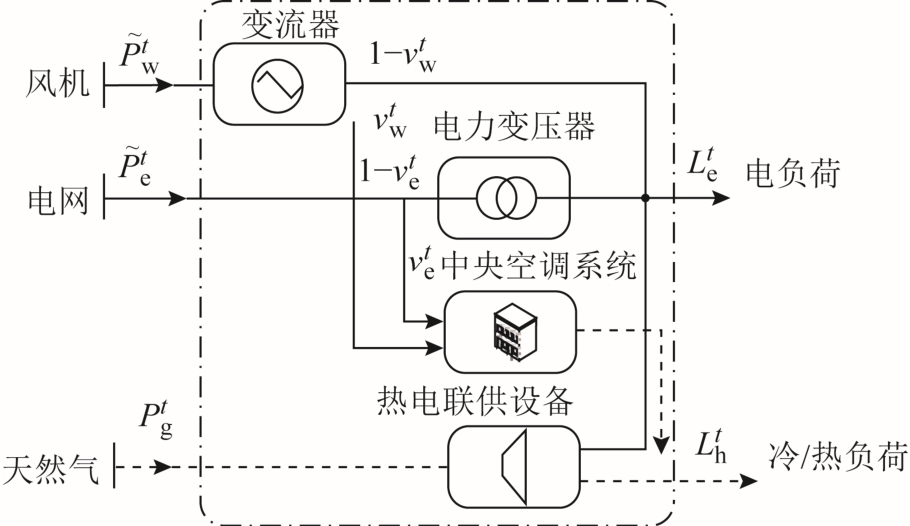
图1 含风电优先利用的EH 模型
Fig.1 EH model with preferential use of wind power
设t 时段 P~e t的供冷/热分配系数为 ve t ，则
和
分别为风电和ADN 输入到AC 的电能，t 时段EH 的输入输出耦合关系为
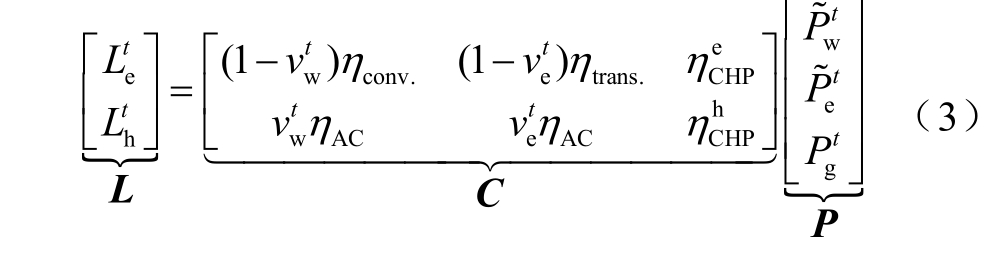
式中，η conv.为风电转换器的效率；η trans.为变压器的效率；η Ce HP 和η Ch HP分别为CHP 机组的制电和制冷/热效率；η AC为AC 制冷/热效率； Pg t 为t 时段天然气能量值。
可通过式（3）求取，若EH 以恒功率因数 cosϕEH 运行，则与ADN 无功交换功率
本文提出在日时间尺度潮流分析中，为优先利用风电，通过冷/热电负荷和风电随机模糊出力比较确定各时段耦合模式及风电供冷/热分配系数，对传统“以热定电”（Following the Thermal Load, FTL）、“以电定热”（Following the Electric Load, FEL）以及混合运行（Following Hybrid Electric-thermal Load, FHL）等耦合模式[26]改进。
1.2.1 模式A：改进FTL 模式
风电供冷/热分配系数 v wt 受t 时段风电不同穿透、CCHP 系统冷/热和电负荷需求状况及CHP 机组最大冷/热输出功率 
和电能输出功率影响，为优先利用风电，t 时段风电供冷/热分配系数 v wt 表示如下，具体推导过程参见附录。
当
时，风电全部通过AC 供冷/热负荷，即t 时段风电供热/冷分配系数 vwt = 1。
当 
时，t 时段 v wt 的值为
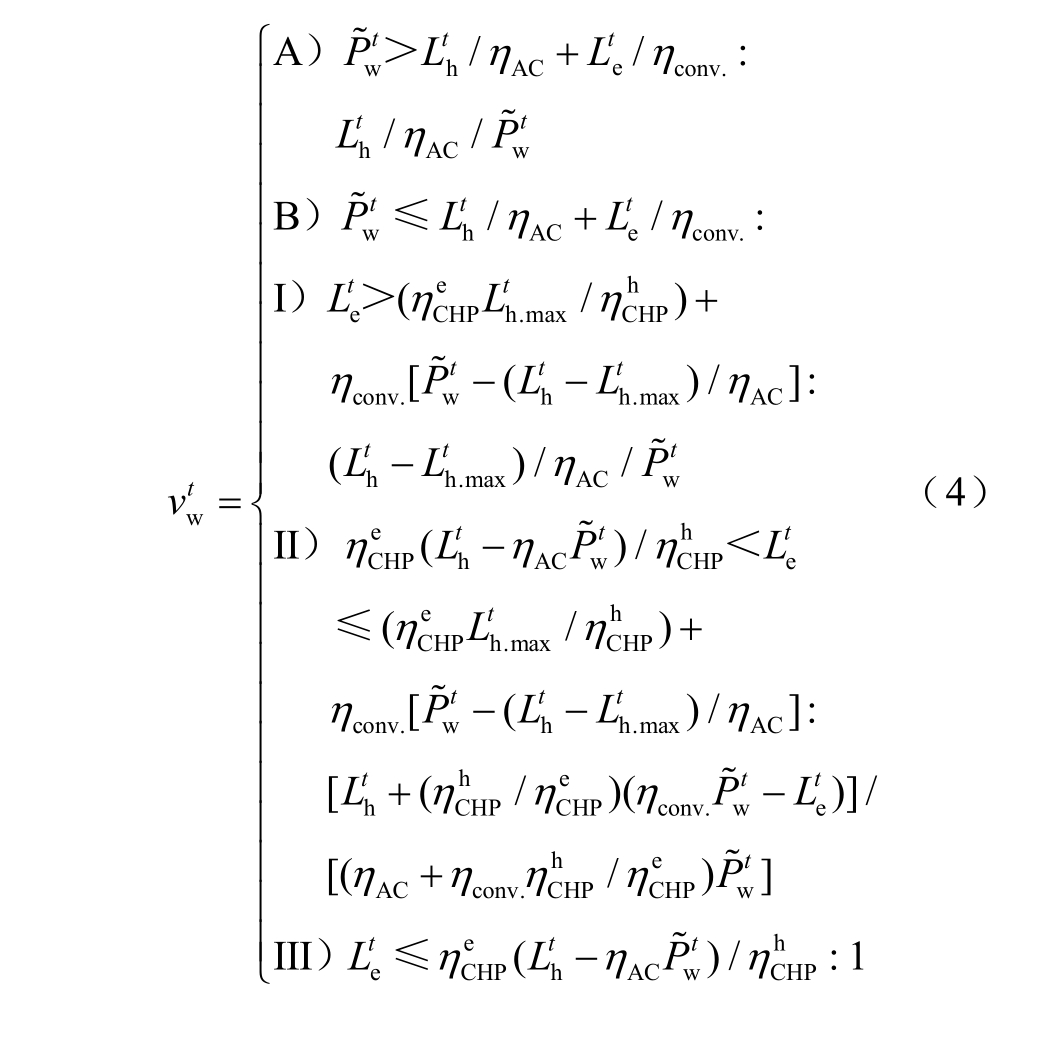
式中， Lt h .max为改进FTL 模式CHP 机组最大可能冷/热输出功率。Lt h≤Phm.CaHxP 时， Lt h.max = Lth；Lt h Phm.CaHxP时， Lth .max=Phm.CaHxP。
将式（4）求得的 v wt 代入EH 耦合关系式（3），可求解得到t 时段各种情况下的EH 与ADN 随机模糊交换功率 P~e t 如式（5）～式（7），定义 P~e t为负时EH 为电源状态，反之为负荷状态。
式中，
为电网输入到空调AC 的电功率； ∆ Lth和 ∆ Lte分别为电网补充EH 的冷/热电需求。
1.2.2 模式B：改进FEL 模式
类似可得t 时段改进FEL 模式下的风电供冷/热分配系数 v wt 和随机模糊交换功率
，参见附录式（A2）～式（A6）。
1.2.3 模式C：改进FHL 模式
电热需求比 tφ 为
电热需求比 tφ 的临界比值Φ 可设定为 CHP机组制电效率和制冷/热效率之比，即
考虑日内EH 负荷具有波动性，各时段电热需求比 tφ 不同，通过各时段电热需求比同临界比值比较，确定EH 各时段改进耦合模式。
以RMt 表示t 时段EH 的改进耦合模式，与t时段电热需求比 tφ 的关系为
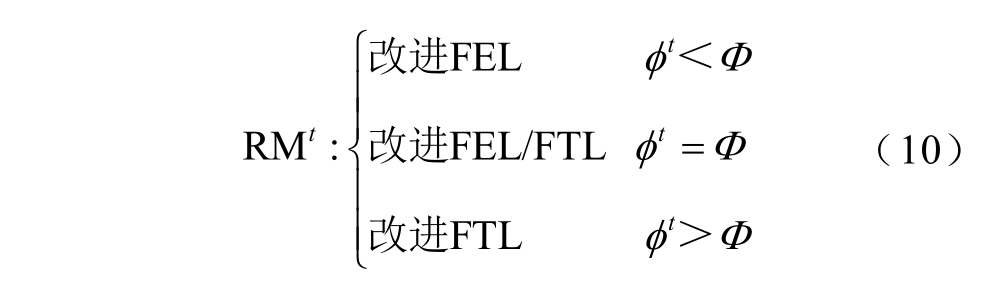
日时间尺度T 个时段EH 的改进耦合模式可表示为
2 含优先利用风电EH 的ADN 与主网交互状态模型
考虑直接接入配电网和EH 与AND 交换功率，t 时段ADN 根节点与主网交互有功功率为
式中，N 为配电网节点数；
为t 时段直接接入到配电网节点i 的风电机组随机模糊有功出力；
为接入到配电网节点i 的含风电EH 与配电网的随机模糊交换功率；P L t. i为节点i 有功负荷；P lotss 为配电网总网损。
A DN 为负荷；反之，为源；
AD N 为孤岛。
t 时段ADN 与主网联络线功率限额为
式中
分别为联络线有功功率上、下限。
3 含优先利用风电EH 的ADN 三相不平衡随机模糊动态潮流模型和算法
3.1 潮流模型
兼顾随机模糊性和波动性的日风电出力模型如文中1.1 节，考虑冷/热电负荷预测精度较高，本文暂仅考虑其波动性。通过配电网电负荷t-1 时段预测值及变化率预测值，得到t 时段电负荷为
式中， 
分别为t-1 和t 时段配电网第i 节点处、第r 相的有功负荷和相应的无功负荷及其变化率。
通过冷/热电负荷t-1 时段预测值及变化率预测值，得到t 时段EH 冷/热电负荷为
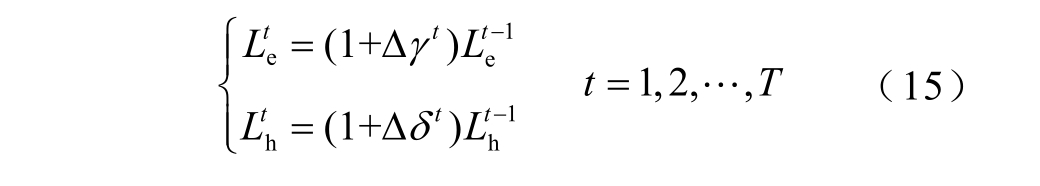
式中，
分别为t-1 时段EH 电负荷和冷/热负荷
为t 时段相应变化率。
任意t 时段ADN 系统有功和无功功率平衡。
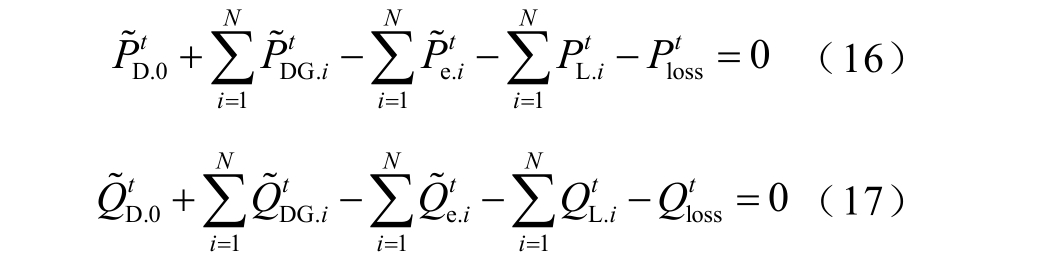
t 时段ADN 有功网损为
t 时段含EH 和分布式风电ADN 三相不平衡潮流节点功率方程为
式中， 
分别为t 时段配电网第i 节点处、第r 相的净有功功率和相应的无功功率； Gi j、 B ij 分别为节点间导纳的实部与虚部； U i、 θ ij 分别为节点电压幅值及相角。
3.2 潮流模型求解算法
风电接入节点以PQ 节点处理，结合随机模糊模拟、EH 冷/热电改进耦合模式及三相解耦前推回代算法对模型求解，步骤如下：
1）根据
时段k 和c 置信区间，采用随机模糊模拟技术模拟W 组t 时段直接接入ADN 和接入EH 的风电出力。根据t 时段EH 电热需求比，由式（11）选定相应EH 改进耦合模型，计算出风电供冷/热分配系数
以及对应的EH 与ADN 随机模糊交换功率
2）根据t-1 时段配电网三相负荷值 PL t.- i1 _r和t时段配电网负荷变化率 ∆μ t得到t 时段配电网三相负荷 PL t . i _r。根据t-1 时段EH 冷/热、电负荷Lth-1、Lte-1值和t 时段EH 冷/热、电负荷变化率得到t 时段EH 冷/热负荷 Lt h、电负荷 Lt e 。
3）设置 u= 1；设主动配电网根节点的电压为U˙ D.0，将三相不平衡主动配电网进行相间解耦转换为各独立相，其解耦模型参见文献[27]，给定A、B、C 三相全网电压初值集合
4）根据主动配电网的
结合步骤1）和步骤2）所得t 时段数据，采用前推回代算法分别并行计算t 时段A、B、C 三相的潮流，得到第u 次迭代的三相电压集合
5）判断三相潮流是否收敛。收敛条件是相邻两次迭代得到的全网电压偏差小于预设的收敛精 
度ε ，即，收敛进入步骤6），否 则 1u u= + 返回步骤3）。
6）判断潮流结果是否满足配电网潮流约束条件，满足进入步骤7）；不满足调节无功补偿装置、风电和EH 等参数，返回步骤3）。
7）根据潮流结果代入式（18）得到t 时段配电网网损 Pl otss，结合t 时段风电出力、配电网负荷和EH 交换功率，代入式（12）可得到t 时段输配交互功率
，判断t 时段ADN 运行状态。
正值表示t 时段ADN 作为电源向输电网输送功率，
负值表示t 时段ADN 作为负荷从输电网吸收功率，从而可分别得到电源和负荷状态下随机模糊动态潮流结果及其所处时段。
8）判断t 是否等于T，是则潮流计算结束，得到T 时段含风电优先利用EH 的主动配电网三相不平衡随机模糊动态潮流结果及各个时段EH 对其接入随机模糊风电的利用功率，再根据各个时段的风电出力、配电网负荷、EH 交换功率、计算网损
及步骤7）得到的
进而得到T 时段内EH 对其接入风电的平均风电利用功率、风电消纳量和消纳水平；否则 1t t= + 返回步骤1）。
具体流程如图2 所示。
4 算例仿真及结果分析
图2 算法流程
Fig.2 Algorithm flow chart
将标准IEEE 33 节点系统作如下修改：五组两台风机分别接入节点3、6、10、14、27，2 个含单台风机EH1、EH2 分别接入节点20、30，设风电和 EH 恒功率因数运行，风机参数见表1，EH 参数见表2，ADN 接线图如图3 所示，配电网基准电压取12.66kV，基准容量10MV·A，设平衡节点B 相相角为0，对负荷参数进行调整，扩展为三相，并假定线路空间对称，而三相负荷不平衡，配电网电负荷日变化率和EH 日冷/热电负荷如图4 所示。
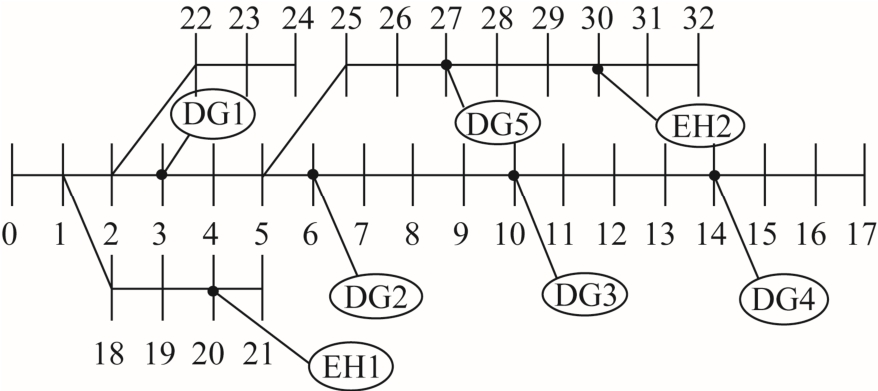
图3 算例网络接线图
Fig.3 Example network wiring diagram
以系统典型日96 时段为例，图5 为随机模糊模拟1 000 组96 时段单台风机出力及其随机模糊期望 值，设每台风机各个时段出力近似相等，可得单台风机日平均出力为356.25kW。
表1 风力发电参数
Tab.1 Parameters of wind generation
w cosϕ ratedP / kW cut-in v / (m/s) cut-out v / (m/s) rated v / (m/s) k c/(m/s) 0.93 500 3 25 13 [3.75,4.38, 6.32] [8.31,9.76,11.88,13.70]
表2 EH 参数
Tab.2 Parameters of EH
参数 conv.η trans.η ACη e CHP η h CHP η max e.CHP P /kW e h.CHP P /kW 数值 0.95 0.95 0.70 0.30 0.40 200 266
4.1 含优先风电利用EH 的ADN 三相不平衡随机模糊动态潮流结果
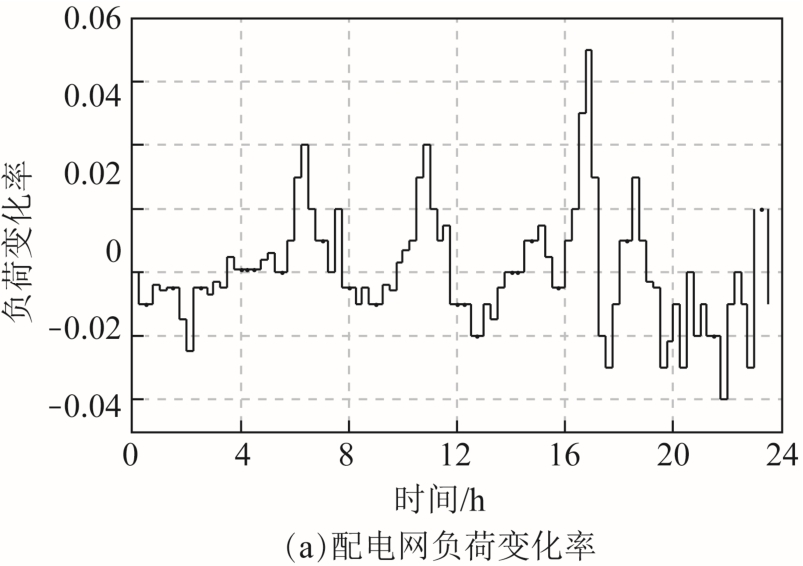
图4 ADN 电负荷变化率、EH 冷/热电负荷
Fig.4 Electric load change rate of ADN, EH’s cooling/ heating and electric load
表3 为本文方法得到的日时间尺度EH1 耦合模 式、风电供冷/热分配系数期望值及风电利用功率期望值，EH2 相关结果见附表1。
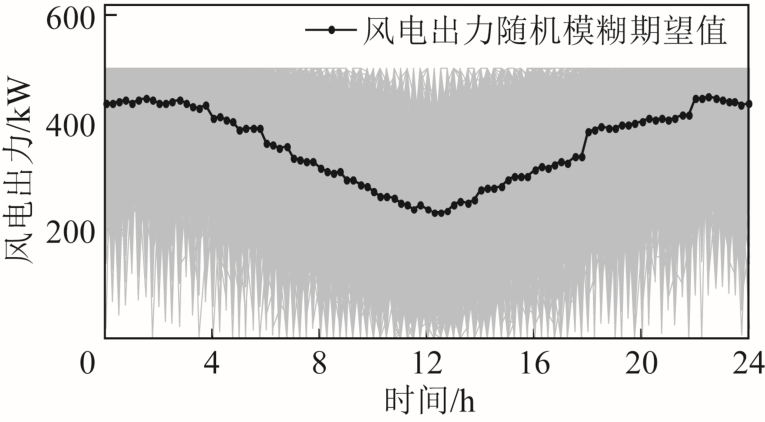
图5 随机模糊模拟风机出力
Fig.5 Wind turbine output by random fuzzy simulation
表3 EH1 日内耦合模式、风电供冷/热分配系数及风电利用功率结果
Tab.3 Intraday coupling mode, cooling/heating dispatch factor and utilization for wind power of EH1
时 段 耦合 模式 分配 系数 风电利 用功率/ kW 时 段 耦合 模式 分配 系数 风电利 用功率/kW 时 段 耦合 模式 分配系数风电利用功率/kW时段耦合模式分配系数风电利用功率/kW时段耦合模式分配 系数 风电利 用功率/ kW 时 段 耦合 模式 分配系数风电利用功率/kW 1 A 0.47 317.56 17 A 0.53 329.97 33 B 0.64 316.87 49 B 0.29 240.33 65 A 0.99 314.57 81 B 0.73 403.83 2 A 0.47 318.78 18 A 0.53 331.50 34 B 0.62 309.84 50 B 0.27 233.25 66 A 0.99 319.48 82 B 0.70 407.70 3 A 0.47 316.02 19 A 0.54 330.58 35 B 0.60 308.02 51 B 0.27 232.41 67 A 0.99 314.75 83 B 0.71 403.15 4 A 0.47 320.54 20 A 0.54 330.53 36 B 0.59 310.59 52 B 0.28 236.13 68 A 0.99 323.78 84 B 0.63 375.99 5 A 0.48 320.41 21 A 0.55 322.94 37 B 0.55 294.26 53 B 0.29 248.25 69 A 0.98 327.67 85 B 0.60 355.54 6 A 0.47 322.13 22 A 0.56 326.55 38 B 0.52 293.59 54 B 0.31 253.44 70 A 0.98 326.65 86 B 0.55 334.73 7 A 0.47 323.85 23 A 0.56 330.03 39 B 0.49 285.64 55 B 0.30 252.49 71 A 0.96 337.90 87 A 0.49 314.92 8 A 0.49 328.51 24 B 0.58 335.49 40 B 0.47 283.35 56 B 0.30 257.26 72 A 0.94 337.95 88 A 0.49 314.11 9 A 0.49 324.80 25 B 0.61 326.16 41 B 0.43 271.74 57 B 0.32 276.67 73 A 0.87 383.90 89 A 0.47 323.78 10 A 0.49 324.68 26 B 0.63 330.07 42 B 0.40 263.84 58 B 0.28 278.79 74 B 0.50 387.77 90 A 0.48 324.58 11 A 0.49 329.56 27 B 0.64 336.77 43 B 0.38 262.27 59 B 0.25 279.25 75 B 0.51 392.94 91 A 0.48 329.10 12 A 0.49 332.27 28 B 0.66 348.08 44 B 0.36 259.46 60 B 0.22 281.01 76 B 0.53 389.58 92 A 0.48 325.69 13 A 0.49 330.30 29 B 0.66 332.07 45 B 0.31 252.73 61 A 0.99 293.67 77 B 0.61 388.87 93 A 0.48 329.31 14 A 0.50 329.30 30 B 0.65 332.38 46 B 0.30 247.18 62 A 0.99 299.25 78 B 0.71 397.70 94 A 0.49 326.15 15 A 0.51 332.79 31 B 0.65 327.96 47 B 0.28 238.38 63 A 0.99 302.22 79 B 0.74 397.36 95 A 0.48 325.90 16 A 0.50 335.10 32 B 0.65 328.48 48 B 0.29 247.80 64 A 0.99 300.05 80 B 0.72 398.36 96 A 0.48 322.89
由表3 可见，EH 各时段对应不同的多能流耦合模式和供冷/热分配系数，同时段EH1、EH2 结果亦有差异，原因是各时段电热需求比不同、风电随机模糊性和波动性及EH 冷/热电负荷波动性。本文提出的改进多能流耦合模式通过各时段风电出力和EH 冷/热电负荷比较，调节供冷/热分配系数动态跟踪风电和冷/热电负荷，实现EH 优先利用接入风电。
图6 为各时段改进耦合模式和风电供冷/热分配系数下EH 与ADN 随机模糊交换功率期望值。由图6 可知EH 在0～36 和80～96 时段以电源状态
与ADN 交互，在时段36～80 以负荷状态
与ADN 交互，交互状态由各时段风电出力大小、EH 冷/热电负荷需求决定。
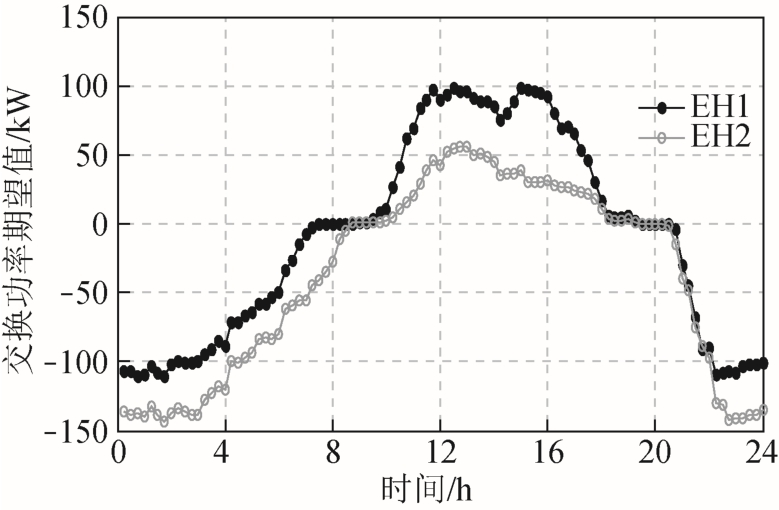
图6 96 时段EH 与ADN 随机模糊交换功率期望值
Fig.6 Expected value of random fuzzy exchange power between EH and ADN in 96 period
图7 为ADN 与主网各时段随机模糊交互功率 期望值。图8 和图9 分别为ADN 与主网以负荷状态?
（时段25～86）或电源状态
（时段1～ 24，87～96）交互的三相节点电压幅值和相角随机模糊期望值。各时段三相有功功率损耗和ADN 风电利用功率期望值（B 相为例）见附表2。
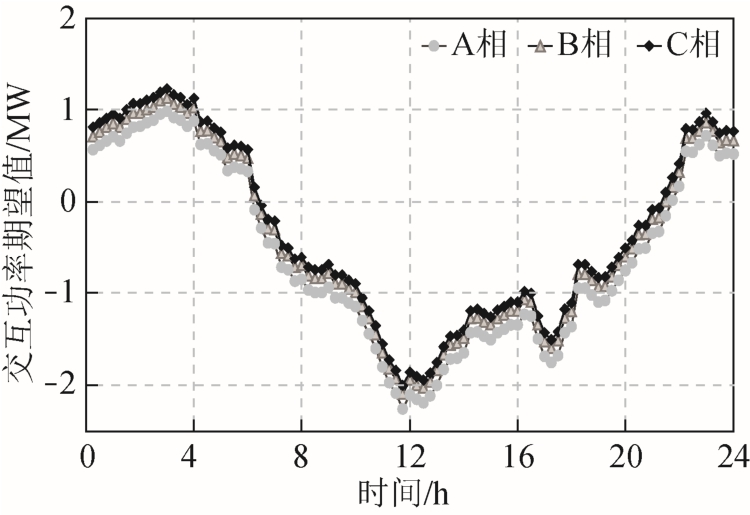
图7 96 时段ADN 与主网随机模糊交互功率期望值
Fig.7 Expected value of random fuzzy interactive power between ADN and transmission grid in 96 period
由图7 可知， ADN 与主网以负荷状态交互多发生在 6：00～22：00，以电源状态交互 多发生在0：00～6：00 和22：00～24：00，原因是6：00～22：00 分布式风电穿透功率相对于系统负荷较低，且此时段EH大多处于负荷状态，因此ADN 处于负荷状态，由主网供给电能缺额；而其他时段风电穿透功率相对较高，且EH 处于电源状态，ADN 处于电源状态向主网售电。结果表明，本文模型能有效反映ADN 与主网交互状态，由于三相不平衡负荷使得A、B、C 三相与主网随机模糊交互功率期望值存在差异。
图8 ADN 与主网负荷交互状态下三相电压幅值和相角随机模糊期望值
Fig.8 Random fuzzy expected value of three-phase voltage amplitude and angle in load interaction state between ADN and transmission network
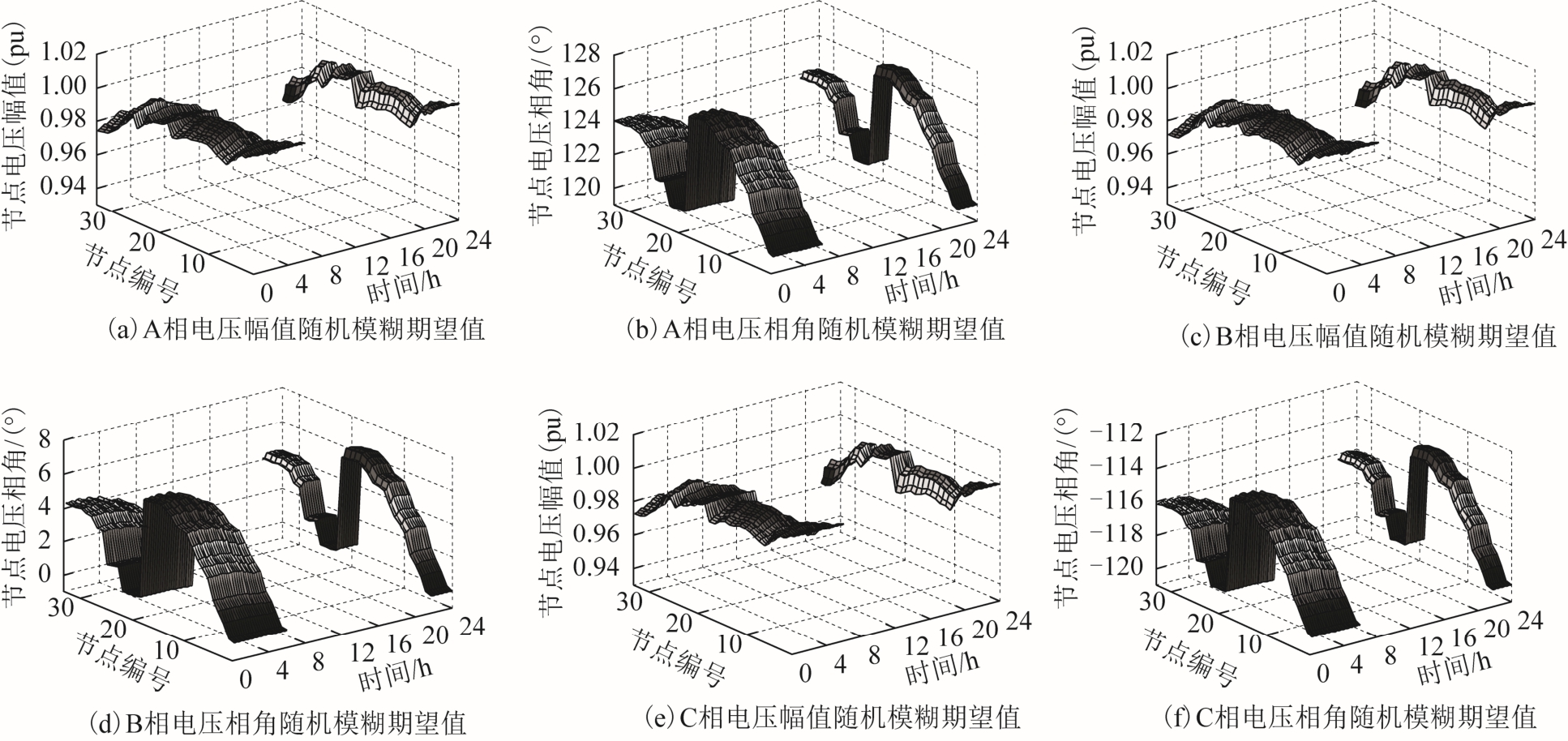
图9 AND 与主网电源交互状态下三相电压幅值和相角随机模糊期望值
Fig.9 Random fuzzy expected value of three-phase voltage amplitude and angle in power interaction state between ADN and transmission network
由图8、图9 可知，各时段电压幅值和相角随机模糊期望值潮流结果不同，不同交互状态下ADN三相随机模糊期望值潮流结果具有明显差异，表明本文方法能充分考虑风电穿透水平、EH 与ADN、ADN 与主网交互等因素对潮流分布影响，与传统方法相比，信息更加科学全面。
图10 为本文EH 改进多能耦合模式和常规耦合模式下日96 时段风电利用情况，定义同一时段EH风电利用功率与风电出力之比百分数为各时段EH 风电利用率，改进耦合模式和常规模式EH 各时段风电利用率如图11 所示。
图10 日时间尺下EH 风电利用情况
Fig.10 Utilization of wind power by EH in daily scale
图11 EH 风电利用率
Fig.11 Utilization rate of wind power by EH
由图10 和图11 可知，在风电相同出力情况下，改进耦合模式下各时段EH 风电利用功率和风电利用率都高于常规模式。经计算可得，EH1 在改进多能耦合模式下日平均风电利用功率为317.43kW，常规模式下日平均风电利用功率为222.00kW；EH2 在改进多能耦合模式下日平均风电利用功率为301.78kW，常规模式下日平均风电利用功率为208.kW。图10 阴影部分面积可表示EH 风电利用功率与时间的乘积，即日时间尺度下96 时段内EH 对其接入风电所消耗的电能，计算得到改进耦合模式下EH1 对风电电能消耗占风电机组总输出电能的89.1%、EH2 为84.7%，常规模式下EH1 对风电电能消耗占风电机组总输出电能的62.3%、EH2 为58.5%。
综上，本文方法提高了各时段EH 对风电的利用功率，日风电电能消耗也明显高于常规模式。
4.2 文中随机模糊动态潮流和随机动态潮流结果比较分析
4.2.1 潮流结果随机模糊特征提取及分析
采用核密度平均估计拟合节点电压幅值和相角的概率分布特征，发现其采用三峰正态分布可较好地描述。
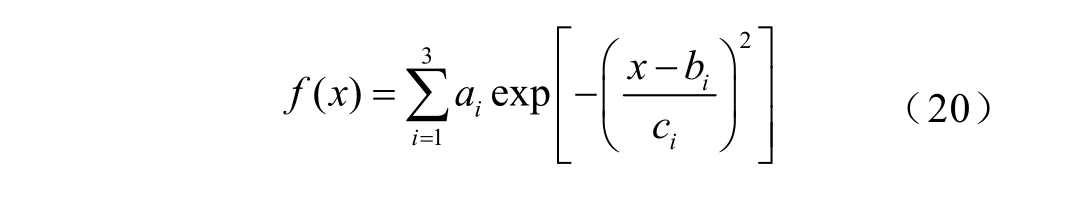
式中， ia 、 ib 和 ic 为拟合参数。
而随机模糊模拟1 000 组风速及100 次随机模糊动态潮流计算结果统计，发现电压幅值分布参数可分别用梯形和三角形模糊数表示，以18 时段节点10 的B 相参数 a3 、 b 3 、 c 3为例， a3 可采用梯形模糊变量 ξ a3 = (7.20,7.90,8.53,9.09)表示， b3 可采用三角形模糊变量 ξ b3 = (0.939,0.942,0.947)表示， c3 可采用梯形模糊变量 ξ c3=(0.030,0.031,0.035,0.038)表示，同理可提取节点电压相角随机模糊特征。
4.2.2 随机模糊动态潮流结果与随机动态潮流结果比较
以第36 时段B 相随机模糊动态潮流和随机动态潮流为例，依据该时段风速形状参数和尺度参数的置信区间，采用随机模糊模拟技术模拟出该时段1 000 组随机模糊风电出力。依据该时段确定风速分布参数，采用蒙特卡洛（Monte Carlo, MC）随机抽样方法模拟1 000 组随机风电出力。分别代入潮流模型进行潮流计算，以蒙特卡洛模拟风电出力得到的电压幅值与相角的最大和最小值作为潮流结果的上下限，如图12 所示。
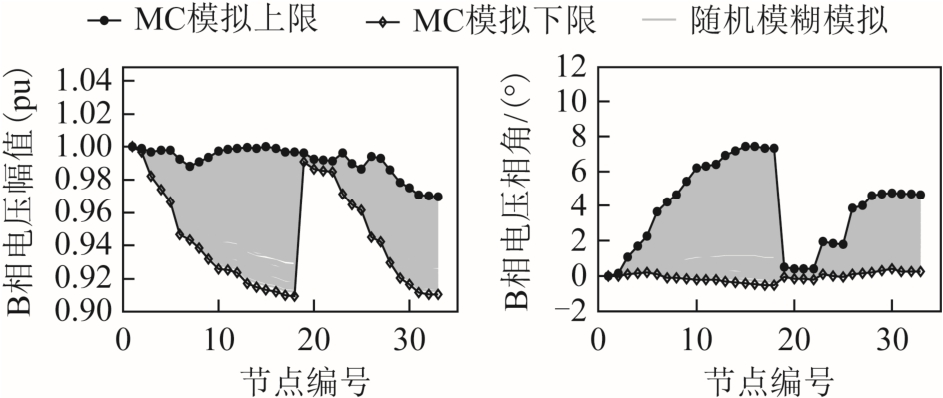
图12 两种潮流结果的电压幅值和相角
Fig.12 Voltage amplitude and phase angle of two power flow results
由图12 可知，利用本文方法得到的各节点电压幅值和相角处于该时段蒙特卡洛模拟风电出力获得的各节点幅值相角最大最小值范围之内，其他相和其他时段也可得此结论，表明本文方法可获得兼顾随机性和模糊性且能反映不同时间断面风电波动特性的潮流结果。
5 结论
提出了一种含优先利用风电能量枢纽三相不平衡主动配电网随机模糊动态潮流方法，得到以下结论：
1）本文方法能综合计及风电出力随机模糊不确定性和波动性及冷/热电负荷的波动性，能有效反映ADN 与EH 及主网的双向交互功率及不同交互状态，获得的日前计划潮流信息兼具随机模糊性及不同时间断面波动性，更加科学全面。
2）本文提出的EH 改进多能流耦合模式能有效跟踪风电、冷/热电负荷变化调节风电供冷/热分配系数，实现EH 风电就地优先利用。
本文暂从日前计划角度研究，考虑ADN 的主动管理及其双层优化潮流将后续研究。
附 录
模式A：风电优先利用EH 改进FTL 多能流耦合运行模式风电供冷/热分配系数建模分析：
1）当 
风电全部通过AC 供冷/热负荷，即风电供热/冷分配系数 w 1t v = ，若CHP 输出最大冷/热功率 
仍不满足需求，则从电网获取电能供给冷/热负荷。
2）当 
分为两种情况：
（1）当
，EH 系统冷/热和电负荷均可由风电出力供应，CHP 机组和电网可为备用，风电供热/冷分配系数
（2）当可分三种场景。
设
为改进FTL 模式下CHP 机组最大可能冷/热输出功率。
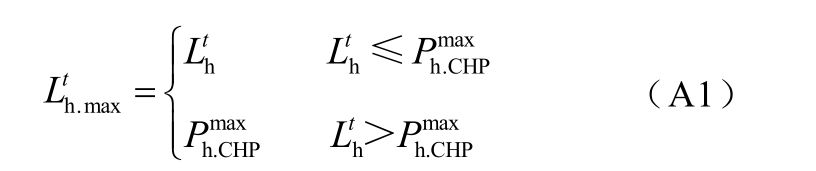
场 景 I： 当 
式中
分别为CHP 供给电负荷和冷/热负荷效率，即风电能满足EH 冷/热负荷需求，但剩余风电小于电能差额（即电负荷和CHP 最大冷热功率
时产生电能之差），此时CHP 输出冷/热功率 Lt h max，风电补充冷/热负荷缺额，剩余风电供给EH 电负荷，电网补充电负荷缺额且备用，则风电供热/冷分配系数为
场景II： 当 
且 
，即风电满足CCHP系统冷/热负荷需求后，剩余风电出力大于电能差额（即电负荷和CHP 最大冷热功率 Lth max时产生电能之差），且设此时CHP 机组电功率不能满足电负荷需求，则风电供热/冷分配系数 
场景III： 当 
即全部风电用于制冷/热，CHP 机组补充供给冷/热需求时输出电功率可以满足 EH 电负荷需求，则风电供热/冷分配系数w 1t v = 。
模式B：改进FEL 模式风电供冷/热分配系数 v wt 为
式中， Lte.max为改进FEL 模式下CHP 机组最大可能电输出功率。
改进FEL 模式下EH 与电网随机模糊交换功率模型为
附表1 EH2 日内耦合模式、风电供冷/热分配系数及 风电利用功率结果
App.Tab.1 Intraday coupling mode, cooling/heating dispatch factor and utilization for wind power of EH2
时段耦合模式分配系数风电利用功率/kW时段耦合模式分配 系数 风电利用功率/ kW 时段 耦合模式分配系数风电利用功率/kW 1 A 0.44 285.51 33 B 0.70 304.16 65 A 0.42 314.57 2 A 0.44 284.31 34 B 0.69 303.72 66 A 0.43 319.48 3 A 0.44 286.00 35 B 0.72 308.02 67 A 0.42 314.75 4 A 0.44 286.95 36 B 0.70 310.59 68 A 0.43 323.78 5 A 0.45 288.18 37 B 0.66 294.26 69 A 0.44 327.67 6 A 0.44 288.66 38 B 0.61 293.59 70 A 0.44 326.65 7 A 0.44 287.37 39 B 0.57 285.64 71 A 0.45 337.90 8 A 0.44 289.02 40 B 0.52 283.35 72 A 0.46 337.95 9 A 0.45 287.36 41 B 0.46 271.74 73 B 0.53 383.90 10 A 0.45 286.11 42 B 0.41 263.84 74 B 0.55 387.77 11 A 0.44 287.43 43 B 0.39 262.27 75 B 0.57 392.94 12 A 0.44 289.19 44 B 0.39 259.46 76 B 0.56 389.58 13 B 0.47 293.75 45 B 0.37 252.73 77 B 0.56 388.87 14 B 0.47 294.42 46 B 0.36 247.18 78 B 0.58 397.70 15 B 0.48 295.62 47 B 0.33 238.38 79 A 0.73 397.36 16 B 0.48 299.69 48 B 0.33 247.80 80 A 0.68 398.36
（续）
时时时段 耦合模式 分配 系数 风电利用功率/ kW 段 耦合模式 分配系数风电利用功率/ kW 段 耦合模式 分配系数风电利用功率/kW 17 B 0.51 299.76 49 B 0.33 240.33 81 A 0.66 403.83 18 B 0.51 299.50 50 B 0.31 233.25 82 A 0.63 405.76 19 B 0.51 297.02 51 B 0.30 232.41 83 A 0.61 390.55 20 B 0.52 297.73 52 B 0.31 236.13 84 A 0.60 365.95 21 B 0.54 295.07 53 B 0.33 248.25 85 B 0.61 351.44 22 B 0.54 298.90 54 B 0.35 253.44 86 B 0.58 325.98 23 B 0.54 297.08 55 B 0.34 252.49 87 B 0.55 317.31 24 B 0.54 301.42 56 B 0.35 257.26 88 B 0.52 306.21 25 B 0.58 294.71 57 B 0.38 276.67 89 B 0.46 300.17 26 B 0.58 293.82 58 B 0.38 278.79 90 B 0.46 298.57 27 B 0.59 291.52 59 B 0.38 279.25 91 A 0.44 291.00 28 B 0.59 294.90 60 B 0.38 281.01 92 A 0.44 289.33 29 B 0.61 285.10 61 B 0.40 293.67 93 A 0.44 287.93 30 B 0.62 287.01 62 B 0.40 299.25 94 A 0.44 285.90 31 B 0.63 289.30 63 B 0.40 302.22 95 A 0.44 285.00 32 B 0.65 298.13 64 B 0.40 300.05 96 A 0.44 284.69
附表2 各时段ADN 三相网损和风电利用功率期望值
App.Tab.2 Expected value of three-phase network loss and wind power utilization of ADN at each period
时段 网损/kW ADN 风电利用功率/kW 时段网损/kW ADN 风电利用/kW A 相 B 相 C 相 A 相 B 相 C 相1 261.3 282.8 252.6 4 450.4 49 201.0 218.2 198.5 2 874.0 2 262.5 283.8 253.8 4 411.1 50 196.1 212.7 193.8 2 791.9 3 262.6 283.7 254.1 4 377.4 51 189.9 206.0 187.6 2 777.4 4 263.4 284.4 254.7 4 400.3 52 186.2 202.1 183.8 2 818.5 5 257.9 278.5 249.4 4 354.8 53 184.0 200.1 181.1 2 952.7 6 263.2 283.9 254.6 4 364.7 54 184.5 200.4 181.4 3 004.9 7 266.1 286.9 257.5 4 368.4 55 180.5 196.3 177.5 2 993.4 8 261.7 281.9 253.3 4 304.4 56 180.8 196.8 177.6 3 049.0 9 254.0 273.2 245.8 4 212.5 57 183.3 200.1 179.5 3 278.3 10 256.0 275.1 247.8 4 177.5 58 185.0 201.9 181.1 3 300.1 11 258.0 277.1 249.8 4 198.3 59 187.8 204.9 183.9 3 303.5 12 258.7 277.7 250.5 4 183.0 60 192.6 210.0 188.6 3 323.5 13 252.9 271.6 245.0 4 137.1 61 197.1 215.4 192.7 3 473.2 14 249.6 268.0 241.7 4 107.2 62 201.0 219.7 196.4 3 543.0 15 245.6 264.0 237.8 4 121.7 63 201.3 219.9 196.6 3 574.2 16 250.5 269.2 242.6 4 159.4 64 200.2 218.6 195.6 3 541.4
（续）
时段网损/kW ADN 风电利用功率/kW 时段 A 相 B 相 C 相 A 相 B 相 C 相网损/kW ADN 风电利用功率/kW 17 231.7 249.6 224.3 4 063.2 65 208.1 227.4 203.1 3 703.6 18 233.3 251.4 225.9 4 068.8 66 214.4 234.4 209.2 3 773.0 19 228.4 246.2 221.2 4 034.1 67 223.7 244.9 218.7 3 748.7 20 226.5 244.4 219.4 4 037.1 68 247.0 270.6 241.7 3 877.9 21 217.4 235.0 210.5 3 971.6 69 256.0 280.6 250.5 3 932.0 22 218.4 236.1 211.5 4 009.9 70 248.5 272.5 243.0 3 915.5 23 218.7 236.3 211.8 3 994.4 71 244.9 268.5 239.1 4 037.6 24 220.0 238.0 213.0 4 036.2 72 240.5 263.8 234.6 4 033.4 25 205.0 222.8 198.6 3 937.4 73 263.5 289.2 256.0 4 563.2 26 208.7 227.5 202.3 3 983.4 74 266.4 292.5 258.7 4 622.6 27 209.3 228.3 203.0 3 973.2 75 277.4 304.8 269.5 4 707.5 28 212.5 231.9 206.0 4 029.0 76 279.8 307.4 272.1 4 675.0 29 203.2 222.1 197.4 3 837.7 77 277.4 304.8 269.7 4 664.5 30 202.2 221.0 196.5 3 831.8 78 280.5 308.1 272.4 4 765.5 31 203.0 222.2 197.4 3 805.1 79 273.5 300.2 265.5 4 731.2 32 202.4 221.5 196.8 3 814.0 80 269.8 295.8 261.9 4 710.3 33 197.9 216.4 192.8 3 694.5 81 269.5 295.4 261.4 4 764.2 34 191.5 209.4 186.5 3 625.5 82 266.3 291.4 258.1 4 751.6 35 189.3 207.1 184.4 3 612.8 83 264.2 289.2 256.0 4 731.7 36 189.7 207.3 184.8 3 625.1 84 263.9 288.4 255.6 4 674.2 37 178.7 195.5 174.3 3 452.1 85 257.3 281.2 249.2 4 599.8 38 180.2 196.8 175.7 3 431.7 86 257.2 280.7 249.0 4 561.2 39 176.2 192.4 172.0 3 341.2 87 255.9 279.0 247.6 4 541.9 40 175.3 191.5 171.2 3 328.4 88 250.8 272.6 242.7 4 423.9 41 173.2 189.1 169.4 3 203.4 89 270.1 292.7 261.1 4 586.7 42 172.8 188.6 169.2 3 120.5 90 270.2 292.8 261.2 4 576.5 43 182.7 199.1 179.2 3 113.0 91 273.2 295.6 264.1 4 547.9 44 191.5 208.8 188.2 3 095.9 92 268.0 289.5 259.2 4 446.4 45 197.8 215.4 194.8 3 018.6 93 267.5 289.5 258.6 4 514.3 46 201.4 219.0 198.7 2 956.5 94 268.1 290.5 259.2 4 526.5 47 205.6 223.2 203.3 2 854.6 95 266.0 288.1 257.2 4 495.6 48 201.2 218.9 198.4 2 964.1 96 262.2 283.8 253.5 4 451.2
[1] 王成山, 洪博文, 郭力, 等. 冷热电联供微网优化调度通用建模方法[J]. 中国电机工程学报, 2015, 33(31)： 26-33. Wang Chengshan, Hong Bowen, Guo Li, et al. A general modeling method for optimal dispatch of combined cooling, heating and power microgrid[J]. Proceedings of the CSEE, 2015, 33(31)： 26-33.
[2] 马瑞, 张强, 吴瑕, 等. 日风速随机模糊不确定模型[J]. 中国电机工程学报, 2015, 35(24)： 6351-6358. Ma Rui, Zhang Qiang, Wu Xia, et al. Random fuzzy uncertain model for daily wind speed[J]. Proceedings of the CSEE, 2015, 35(24)： 6351-6358.
[3] 刘艳, 叶茂, 顾雪平, 等. 基于概率分布列的风电参与黑启动时电力系统安全裕度分析[J]. 电工技术学报, 2018, 33(21)： 5059-5068. Liu Yan, Ye Mao, Gu Xueping, et al. Probability distribution column based security margin analysis of power system with wind power participating in black start[J]. Transactions of China Electrotechnical Society, 2018, 33(21)： 5059-5068.
[4] 沈小军, 周冲成, 吕洪. 基于运行数据的风电机组间风速相关性统计分析[J]. 电工技术学报, 2017, 32(16)： 265-274. Shen Xiaojun, Zhou Chongcheng, Lü Hong. Statistical analysis of wind speed correlation between wind turbines based on operational data[J]. Transactions of China Electrotechnical Society, 2017, 32(16)： 265-274.
[5] 张晓英, 王琨, 张蜡宝. 基于切片采样的风力发电并网系统概率潮流计算[J]. 电工技术学报, 2016, 31(23)： 100-106. Zhang Xiaoying, Wang Kun, Zhang Labao. Probabilistic load flow calculation based on slice sampling for wind farms integration system[J]. Transactions of China Electrotechnical Society, 2016, 31(23)： 100-106.
[6] 方斯顿, 程浩忠, 徐国栋, 等. 基于Nataf 变换含相关性的扩展准蒙特卡洛随机潮流方法[J]. 电工技术学报, 2017, 32(2)： 255-263. Fang Sidun, Cheng Haozhong, Xu Guodong, et al. A nataf transformation based on extended quasi monte carlo simulation method for solving probabilistic load flow problems with correlated random variables[J]. Transactions of China Electrotechnical Society, 2017, 32(2)： 255-263.
[7] Aien M, Fotuhi-Firuzabad M, Aminifar F. Probabilistic load flow in correlated uncertain environment using unscented transformation[J]. IEEE Transactions on Power Systems, 2012, 27(4)： 2233-2241.
[8] Soleimanpour N, Mohammadi M. Probabilistic load flow by using nonparametric density estimators[J]. IEEE Transactions on Power Systems, 2013, 28(4)： 3747-3755.
[9] 洪芦诚, 石立宝, 姚良忠, 等. 计及风电场发电功率不确定性的电力系统模糊潮流[J]. 电工技术学报, 2010, 25(8)： 116-122, 130. Hong Lucheng, Shi Libao, Yao Liangzhong, et al. Fuzzy modelling and solution of load flow incorporating uncertainties of wind farm generation[J]. Transactions of China Electrotechnical Society, 2010, 25(8)： 116-122, 130.
[10] Cortés-Carmona M, Palma-Behnke R, Jimenez-Estevez G. Fuzzy arithmetic for the DC load flow[J]. IEEE Transactions on Power Systems, 2010, 25(1)： 206-214.
[11] 胡健, 付立军, 马凡, 等. 基于仿射算术优化的不确定系统区间潮流快速分解法[J]. 电工技术学报, 2016, 31(23)： 125-131. Hu Jian, Fu Lijun, Ma Fan, et al. Fast decoupled power flow calculation of uncertainty system based on interval affine arithmetic optimization[J]. Transactions of China Electrotechnical Society, 2016, 31(23)： 125-131.
[12] 廖小兵, 刘开培, 张亚超, 等. 基于区间泰勒展开的不确定性潮流分析[J]. 电工技术学报, 2018, 33(4)： 750-758. Liao Xiaobing, Liu Kaipei, Zhang Yachao, et al. Uncertain power flow analysis based on interval Taylor expansion[J]. Transactions of China Electrotechnical Society, 2018, 33(4)： 750-758.
[13] Vaccaro A, Cañizares C A, Bhattacharya K. A range arithmetic-based optimization model for power flow analysis under interval uncertainty[J]. IEEE Transactions on Power Systems, 2013, 28(2)： 1179-1186.
[14] 鲍海波, 韦化, 郭小璇, 等. 考虑风电不确定性的概率区间潮流模型与算法[J]. 中国电机工程学报, 2017, 37(19)： 5633-5642. Bao Haibo, Wei Hua, Guo Xiaoxuan, et al. Model and algorithm of probabilistic interval power flow considering wind power uncertainty[J]. Proceedings of the CSEE, 2017, 37(19)： 5633-5642.
[15] 薛禹胜, 雷兴, 薛峰, 等. 关于风电不确定性对电力系统影响的评述[J]. 中国电机工程学报, 2014, 34(29)： 5029-5040. Xue Yusheng, Lei Xing, Xue Feng, et al. A review on impacts of wind power uncertainties on power system[J]. Proceedings of the CSEE, 2014, 34(29)： 5029-5040.
[16] 孙国强, 李逸驰, 向育鹏, 等. 计及风速时空相关性的含风电场电力系统动态随机最优潮流计算[J]. 中国电机工程学报, 2015, 35(17)： 4308-4317. Sun Guoqiang, Li Yichi, Xiang Yupeng, et al. Dynamic stochastic optimal power flow of wind integrated power system considering temporal and spatial correlation of wind speed[J]. Proceedings of the CSEE, 2015, 35(17)： 4308-4317.
[17] 孙辰, 刘东, 李庆生. 信息物理融合的主动配电网动态潮流研究[J]. 中国电机工程学报, 2016, 36(6)： 1509-1516. Sun Chen, Liu Dong, Li Qingsheng. Research on dynamic power flow of active distribution network based on cyber-physical fusion[J]. Proceedings of the CSEE, 2016, 36(6)： 1509-1516.
[18] 王毅, 张宁, 康重庆. 能源互联网中能量枢纽的优化规划与运行研究综述和展望[J]. 中国电机工程学报, 2015, 35(22)： 5669-5681. Wang Yi, Zhang Ning, Kang Chongqing. Review and prospect of optimal planning and operation of energy hub in energy internet[J]. Proceedings of the CSEE, 2015, 35(22)： 5669-5681.
[19] 徐宪东, 贾宏杰, 靳小龙, 等. 区域综合能源系统电/气/热混合潮流算法研究[J]. 中国电机工程学报, 2015, 35(14)： 3634-3642. Xu Xiandong, Jia Hongjie, Jin Xiaolong, et al. Study on hybrid heat-gas-power flow algorithm for integrated community energy system[J]. Proceedings of the CSEE, 2015, 35(14)： 3634-3642.
[20] 林威, 靳小龙, 穆云飞, 等. 区域综合能源系统多目标最优混合潮流算法[J]. 中国电机工程学报, 2017, 37(20)： 5829-5839. Lin Wei, Jin Xiaolong, Mu Yunfei, et al. Multiobjective optimal hybrid power flow algorithm for integrated local area energy system[J]. Proceedings of the CSEE, 2017, 37(20)： 5829-5839.
[21] Moeini-Aghtaie M, Abbaspour A, Fotuhi-Firuzabad M, et al. A decomposed solution to multiple-energy carriers optimal power flow[J]. IEEE Transactions on Power Systems, 2014, 29(2)： 707-716.
[22] 苗键强, 张宁, 康重庆. 能量路由器对于配电网运行优化的影响分析[J]. 中国电机工程学报, 2017, 37(10)： 2832-2839. Miao Jianqiang, Zhang Ning, Kang Chongqing. Analysis on the influence of energy router on the optimal operation of distribution network[J]. Proceedings of the CSEE, 2017, 37(10)： 2832-2839.
[23] 李红伟, 孙宏斌, 张安安, 等. 基于正序分量的含PV 节点的三相配网潮流算法[J]. 中国电机工程学报, 2012, 32(1)： 115-121. Li Hongwei, Sun Hongbin, Zhang Anan, et al. Positive-sequence component based three-phase unbalanced power flow solution for distribution system with PV nodes[J]. Proceedings of the CSEE, 2012, 32(1)： 115-121.
[24] 杨雄, 卫志农, 孙国强, 等. 主动配电网三相解耦潮流算法[J]. 电工技术学报, 2016, 31(2)： 186-195. Yang Xiong, Wei Zhinong, Sun Guoqiang, et al. Three-phase decoupled power flow algorithm for active aistribution networks[J]. Transactions of China Electrotechnical Society, 2016, 31(2)： 186-195.
[25] 苏申, 阮玉斌, 刘庆珍, 等. 配电网三相潮流计算方法研究[J]. 电气技术, 2017, 18(2)： 1-4, 35. Su Shen, Ruan Yubin, Liu Qingzhen, et al. Research review of three-phase power flow methods for distribution system[J]. Electrical Technology, 2017, 18(2)： 1-4, 35.
[26] Li Miao, Mu Hailin, Li Nan, et al. Optimal option of natural-gas district distributed energy systems for various buildings[J]. Energy and Buildings, 2014, 75： 70-83.
[27] 陈醒, 卫志农, 沈海平, 等. 基于双解耦的配电网三相不平衡快速潮流算法[J]. 电力自动化设备, 2017, 37(10)： 63-70. Chen Xing, Wei Zhinong, Shen Haiping, et al. Threephase unbalanced fast power flow calculation algorithm based on double decoupling for distribution network[J]. Electric Power Automation Equipment, 2017, 37(10)： 63-70.