0 引言
2017 年，我国累计风电装机容量达188GW，其中新增装机容量为19GW，占比10.1%[1]。随着风电渗透率的提高，风电的随机性、间歇性及波动性等不确定性给电网的规划[2]和运行[3-4]带来了很大的挑战。合理建立风电功率序列模型对电网的随机规划和调度以及可靠性评估等具有重要的意义。
风电功率序列建模可分为预测建模[5-6]和模拟建模[7-16]两类。预测建模是预测未来时刻的风电功率值，常被用于电网的短期调度，而模拟建模是模拟出与历史数据（序列）具有相似特征的人造风电功率序列，一般被用于中长期调度、电网随机规划、可靠性评估及概率潮流等研究[13]。目前，这些研究主要基于时序模拟技术[17-19]，即采用大量实测风电数据（数年甚至数十年的数据）进行仿真[9,16]。然而，对于许多新建风电厂，其实测数据的长度无法满足该技术的要求，此时模拟建模十分必要。此外，随着现代电力系统的复杂度、网密度及分布式资源渗透率的提高，即使存在相对大量的高质量历史风电数据，也不足以支持时序模拟技术的运用[9]，因此迫切需要开展模拟建模。鉴于该必要性和迫切性，本文主要研究模拟建模。根据研究对象不同，模拟建模又可分为直接建模与间接建模两类，其中直接建模是直接以历史风电功率数据为研究对象进行建模，而间接建模则是先通过历史风速数据建模，生成人造风速序列后，再基于风机功率曲线，将其转换为人造风电功率序列。前者与后者相比，具有无需建立复杂风速模型[20]和避免风-电转换过程引入误差[10]的优势。本文将以风电功率数据为研究对象，进行直接建模。
在具体建模方法方面，相比于自回归滑动平均、人工神经网络及支持向量机等方法[5-6,16]，蒙特卡洛模拟法[7-15]直接通过统计分析历史数据特征进行建模，能较好地阐释风电功率的物理特性，适用性更强。文献[7]将风电功率序列划分为风过程和片段，通过风过程反映风电功率的波动特征，但对风过程的划分具有一定的主观性。文献[8]在文献[7]的基础 上，利用自组织映射神经网络改进了风过程的划分方法，但需要大量的历史数据作为训练样本。文献[21]指出，基于马尔科夫链的蒙特卡洛法（Markov Chain Monte Carlo, MCMC）具有可利用有限历史数据进行时间序列建模的优势。文献[9]基于MCMC 法分别对风速和风电功率序列建模，较好地复现了历史序列的概率密度分布及自相关性等特征，并发现以风电功率序列进行建模的效果更好。文献[10]在文献[9]的基础上进一步探讨了风电功率的季节特性对建模效果的影响，并建议分季节进行建模。目前，基于传统MCMC 法进行风电功率序列建模时，存在以下问题[11-12]：①历史风电功率序列的状态转移概率矩阵一般具有山脊特点[12]，容易导致人造风电功率序列陷入某种状态中难以跳变，使得该状态的持续时间过长；②在确定人造风电功率状态序列中各状态样本的取值时，仅是从相应状态所代表的功率范围内随机均匀抽取一值作为该状态样本的功率值，这使得最终生成的人造风电功率序列在同一状态内的波动过于频繁；③容易丢失风电功率的波动及状态持续时间分布等时域特征。针对上述问题，文献[11-12]结合风电功率的时域特征，提出了持续与波动蒙特卡洛法，解决了问题②和③，但未能有效解决问题①，此外，该方法将状态转移过程中“状态跳变”与“状态持续（自跳变）”过程分离，人为假定某一状态在不同持续时间下跳变到其余各状态的概率之比不变，这使得其复现历史特征（尤其是转移特征）的效果有限。
对历史数据进行状态划分是MCMC 法的基础。现有关于MCMC 法的文献[9-15]，一方面，在状态划分前，未提及对历史序列进行滤波预处理，这可能导致历史序列中的样本对状态的隶属出现错误以及提取的风电功率波动特征中混杂了噪声。虽然已有学者对滤波方法开展了一些研究，但这些研究大多与随机变量（风电功率）建模彼此独立，对其适应性不强。目前，面向随机变量建模，开展滤波参数寻优方法的研究尚不多见，文献[9]初步探讨了滑动平均滤波窗口长度对人造风电功率序列的影响。另一方面，在状态划分时，主观预设状态数量，较少涉及关于状态数的最优决策研究。虽然在聚类领域，已有一些关于聚类数（状态数）的最优决策研究，但这些研究大多仅根据数据本身的分类精度确定最优状态数，未计及马尔科夫链（Markov Chain，MC）模型的建模质量，对MCMC 法建模的适应性不强。
针对上述问题，本文通过研究面向随机变量建模的滑动平均滤波窗口长度选取方法和建立状态数优化决策模型，提出风电功率序列的自适应状态划分策略，以避免主观划分历史风电功率序列的局限性。在此基础上，本文考虑状态持续时间对状态转移概率的影响以及风电功率的波动特征，提出一种改进的MCMC 风电功率序列建模方法。该方法不仅解决了传统MCMC 法的三个问题，而且避免了持续与波动蒙特卡洛法的不足。以德国某风电场2017 年历史风电功率数据[22]为例进行风电功率序列建模，说明该方法的科学性与有效性。
1 状态划分过程建模
将历史风电功率序列中所有样本划归不同的状态，得到历史风电功率状态序列是状态划分过程。针对以往研究[9-15]在建模过程中涉及的滤波方法及状态数决策模型对MCMC 法适应性不强的问题，本文提出面向随机变量建模的滑动平均滤波参数（窗口长度）寻优方法和构建计及MC 建模质量的状态数优化决策模型。在此基础上，提出风电功率序列的自适应状态划分策略，客观划分历史数据。
1.1 面向随机变量建模的滑动平均窗口长度的自适应选取方法
鉴于滑动平均滤波法[23]具有实现简单、平滑度高等特点，本文采用该方法对历史风电功率序列进行滤波，防止序列中样本对状态的隶属出现错误，然而滑动平均窗口长度的选取是一个难题。
文献[24]指出，滑动平均窗口长度的选择依赖经验，对于冲击性较大负荷，推荐长度为30min。文献[9]研究表明，滑动平均窗口长度越长，人造风电功率序列的自相关性越高。借鉴文献[9,24]的研究成果，本文提出面向随机变量建模的滑动平均窗口长度的自适应选取方法。该方法以文献[24]推荐长度为滑动平均窗口长度的初始值，基于文献[9]所述单调性确定搜索方向，以人造风电功率序列相对于历史风电功率序列在自相关函数（Autocorrelation Function，ACF）方面的方均根误差（Root Mean Squared Error, RMSE）eacf 最小为寻优目标，寻找最优窗口长度。具体步骤如下：
1）据历史数据的粒度δ，将滑动平均窗口长度Δ 初始化为([30/δ]×δ)min，并据式（1）求出eacf。 式中，f1(xi)和f2(xi)分别为人造和历史风电功率序列的ACF 在滞后数xi 处的取值；X 为设定的最大滞后数；Avg 为平均值算子。eacf 越小表示历史及人造风电功率序列在自相关性方面越接近。任一序列{v1, v2, …, vn}的ACF 在滞后数xi 处的取值 f acf (xi )为
式中，cov 和var 分别为卷积和方差算子；vt 为序列{v1, v2, …, in xv - }； it xv+ 为序列{ 1 ixv+ , v2, …, nv }。
2）如果人造风电功率序列的ACF 曲线在历史风电功率序列的ACF 曲线之上，则试探减小Δ 一个单位长度；反之，则试探增加Δ 一个单位长度；如果两者出现交叉，则依次试探减小及增加Δ 一个单位长度。
3）重复步骤2）直至找出最小的eacf 及其对应的最优窗口长度Δ。
1.2 基于状态数优化决策模型的状态划分方法
通过分类精度和贝叶斯信息准则（Bayesian Information Criterion，BIC）[9,25]指标评价状态划分的效果，进而对滤波后的历史风电功率序列建立状态数优化决策模型，可以相对客观地确定最优状态划分数量（聚类数）。在最优聚类数下，经状态划分（聚类），可得最优状态划分方案，即历史风电功率状态序列。
1.2.1 分类精度
应用K 均值聚类法[26]（或其他聚类法）将滤波后的历史风电功率序列划分为k 个类（状态），并求得各个类Ci(i=1,2,…,k)的聚类中心Pi,cluster，相应的分类精度可由平均聚类误差ecluster 表征为
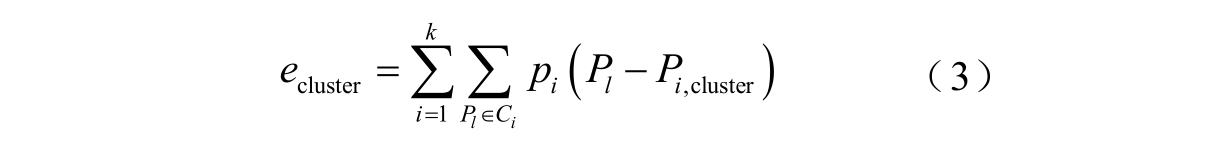
式中，pi 为状态i 的概率；Pl 为属于第i 个类的风电功率样本值，Pl∈Ci。ecluster 越小，表示分类精度越高。
1.2.2 贝叶斯信息准则
贝叶斯信息准则（BIC）作为一种综合权衡统计模型适用性和复杂性的指标，已被广泛应用于评价MC 模型的建模质量[25]。一般来说，在一组可供选择的模型当中，倾向于选择BIC 值较大的模型。BIC的计算公式[9,25]为
式中，BIC 为BIC 的值；L、φ 分别为MC 模型的对数似然函数值、独立参数数量，具体计算公式将在2.2 节给出；n 为历史序列中样本数量。
1.2.3 状态数优化决策模型
综合考虑分类精度及BIC 指标，构建如式（5）所示的状态数优化决策模型，求解该模型得到最优聚类数。
式中，krange 为聚类数k 的取值范围，可根据样本分布预设；α、β 为权系数，可由熵权法[27]确定。
1.3 自适应状态划分策略
综上所述，提出风电功率序列的自适应状态划分策略，流程如图1 所示。对历史风电功率序列进行滑动平均滤波处理后，基于状态数优化决策模型进行状态划分，得到历史风电功率状态序列。然后按照后文第2 节和第3 节中提出的方法生成人造风电功率序列，并根据eacf 自适应地调整滤波窗口长度，直至eacf 最小为止。
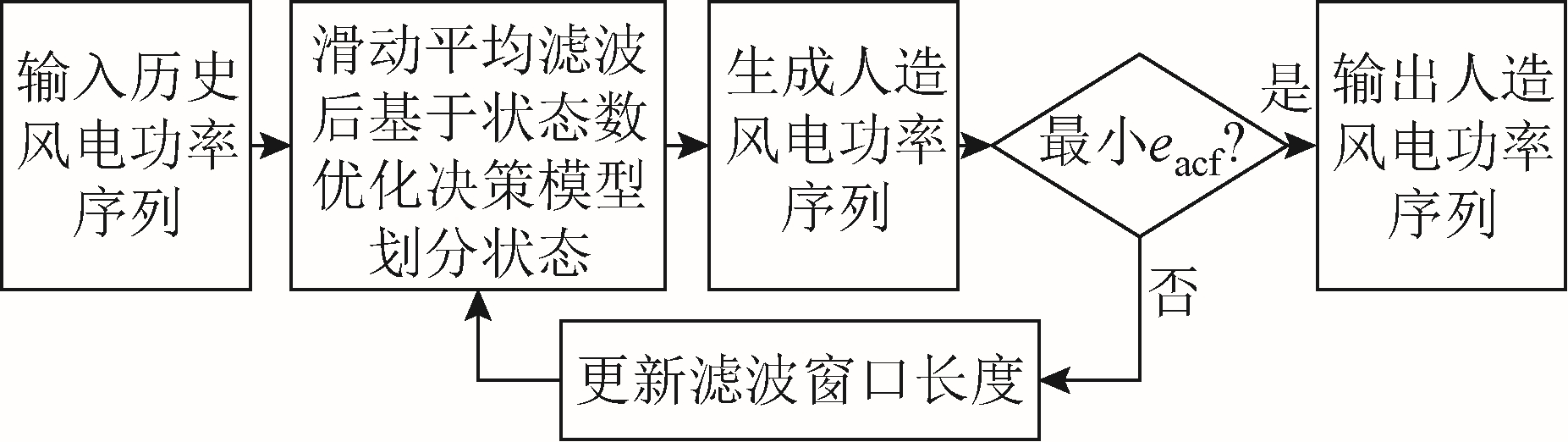
图1 风电功率序列的自适应状态划分策略
Fig.1 Strategy for self-adaptively dividing time series of wind power into different states
鉴于后文3.2 节中添加波动量及噪声的需要，在状态划分过程中，找出滤波前及滤波后的历史风电功率序列中对应于第i(i=1,2,…,k)类样本的上下限区间Pi,orig_interval 及Pi,interval。
2 状态转移过程建模
状态转移过程建模的流程为：获得历史风电功率状态序列后，统计分析状态的转移特征，进而基于蒙特卡洛模拟法对转移特征进行抽样，生成人造风电功率状态序列。
2.1 状态的转移特征分析
状态的转移特征可由状态的转移概率（自跳变及互跳变转移概率）直接表征，状态的持续时间间接体现。
2.1.1 状态持续时间概率分布
以经插值补缺、剔除异常点等处理后的德国某风电场2017 年春季风电功率监测数据为例，图2 展示了某一风电功率状态的持续时间概率分布直方图和相应的指数及逆高斯拟合曲线。
图2 某一状态的持续时间概率分布
Fig.2 Probability density of a certain state’s duration
从图2 可以看出，该状态的持续时间不服从指数分布。类似地，通过分析可以发现其他风电功率状态的持续时间亦不服从指数分布，这说明基于传统MCMC 法进行风电功率序列建模时，MC 模型的无后效性[28]假设并不合理。换言之，状态的转移概率会随着状态持续时间的推移而变化，因此，如果忽略状态持续时间对状态转移过程的影响，将难以保证建模的准确性。
2.1.2 状态转移概率
对于传统MCMC 法，任一状态的转移概率可由状态转移概率矩阵得到；对于持续与波动蒙特卡洛法，由于“状态持续（自跳变）”与“状态跳变”过程分离，模型中只有状态跳变概率矩阵[11]，因此需分别采用式（6）、式（7）求出状态在持续时间t 下的自跳变和跳变到另一状态的转移概率。
式中，li、t、Δt 分别为状态i 持续时间、已持续时间、还能持续的时间；p(li＞t+Δt|li＞t)为状态i 在已经持续了时间t 的情况下还能接着持续Δt 的概率，即自跳变转移概率。
式中，pij(t)为状态i 在持续时间t 下跳变到状态j 的转移概率；pjump ij 为状态跳变概率矩阵中第i 行第j 列的元素。
历史风电功率状态序列中某一状态的转移概率和传统MCMC 法以及持续与波动蒙特卡洛法中对应于该状态的转移概率，随着该状态持续时间的推移而变化的情况，如图3 所示。
图3 某一状态的转移概率
Fig.3 The transition probability of a certain state
从图3 中可以看出：①在传统MCMC 法中，该状态的自跳变和跳变到另一状态的转移概率一直保持恒定，与“历史转移概率”（历史转移特征）不符；②在持续与波动蒙特卡洛法中，该状态的自跳变和跳变到另一状态的转移概率只有在状态持续时间较短的部分相对符合“历史转移概率”的变化趋势，这是因为文献[11]采用逆高斯函数来拟合状态持续时间的概率分布，但逆高斯函数仅在状态持续时间较短的部分相对贴合历史状态持续时间的概率分布，而在持续时间较长的部分逐渐偏离，如图2 所示；③当状态持续时间较长时，在持续与波动蒙特卡洛法中，该状态的自跳变转移概率并未出现下降趋势，这说明该方法其实不能有效解决传统MCMC 法中“状态持续时间过长”的问题，其中未出现下降趋势是由逆高斯函数本身决定，与状态划分策略无关，证明过程见附录。
2.2 三维状态转移概率矩阵
针对传统MCMC 法和持续与波动蒙特卡洛法中状态转移概率的变化趋势与历史不符的问题，本文计及状态转移概率随状态持续时间增加而变化的实际情况，提出了三维状态转移概率矩阵，对历史转移特征进行描述。三维状态转移概率矩阵的三个维度（行、列、页）分别由状态、状态、状态持续时间构成，如图4 所示。矩阵中任一元素(i，j，l)表示状态i 在其持续时间为l 时，跳变到状态j 的转移概率。
图4 三维状态转移概率矩阵
Fig.4 3D state transition probability matrix
根据历史风电功率状态序列生成三维状态转移概率矩阵的方法如下：
1）设状态数和最大的状态持续时间分别为 k和lmax，建立大小为k×k×lmax 的三维状态转移频数矩阵N3dim，并将其初始化为零矩阵。
2）假设当前时刻的风电功率状态为i，状态i已持续的时间为l，如果下一时刻的状态为j，则矩阵N3dim 中的元素(i，j，l)加1。
3）重复步骤2）直至遍历完历史风电功率状态序列。
4）对三维状态转移频数矩阵N3dim 按行归一化，即可得到三维状态转移概率矩阵
从上述方法可以看出，在时间复杂度方面，生成三维状态转移概率矩阵与用传统MCMC 法生成二维状态转移概率矩阵一样，均为O(n)，即仅需遍历一次历史风电功率状态序列。
生成三维状态转移概率矩阵后，采用式（8）和式（9），即可求出1.2.2 节中MC 模型的对数似然函数值L 及独立参数数量φ。
式中，
分别为
中的元素(i, j, l)。
式中，k 为状态数；lmiax 为状态i 的最大持续时间。
2.3 解维修正
由于风电出力具有季节性且风电场规模往往随着社会经济水平发展逐年增大，因此MCMC 法常常选择某季度甚至更短时间跨度的历史数据作为研究对象[10,13]。此时研究对象的样本数量有限，使得经统计得到的状态转移概率可能出现部分异常。为此，本文提出解维修正方法对
进行修正：将
沿时间维度分解为k2 个转移概率时间维向量，依次对各时间维向量进行拟合修正，进而将修正后的时间维向量按原有顺序重新组合得到一个新的三维矩阵，最后将该三维矩阵按行归一化，即可生成修正后的三维状态转移概率矩阵P
本文仍用图3 来说明通过拟合由
解维得到的各转移概率时间维向量，可有效修正经统计得到的转移概率中的异常值。图3 展示的“历史转移概率”即为相应的某一转移概率时间维向量。从图中可以看出，“历史转移概率”的部分取值会出现异常，其中较为明显的异常如图中历史转移概率“异常点”所示。这些“异常点”主要表现为相应持续时间下对应的自跳变转移概率为1，而跳变到其他状态的转移概率为0。造成这一现象的原因是，有限的历史数据使得相应持续时间下没有出现跳变到其他状态的统计样本。由图2 可知，越长的状态持续时间出现的概率越小，当历史数据的样本量相对较少时，某一状态在持续时间较长时的自跳变或跳变到其他状态的统计样本可能不足，因此，“异常点”主要在状态持续时间较长时出现。针对上述问题，本文采用多项式函数，对“历史转移概率”进行拟合，拟合结果如图3 中“拟合曲线”所示。从图中可以看出，“拟合曲线”作为新的转移概率时间维向量，不仅符合“历史转移概率”的变化趋势，还能有效修正这些“异常点”。类似地，对其他的转移概率时间维向量进行拟合，对应的“拟合曲线”亦既符合相应的“历史转移概率”变化趋势，又可修正相应的“异常点”。因此，解维修正方法可有效修正转移概率中的异常值，弥补研究对象中样本量较少的不足。
此外，当状态持续时间过长时，图3a 中“拟合曲线”代表的某状态自跳变转移概率迅速减小；图3b 中“拟合曲线”代表的某状态跳变到另一状态的转移概率迅速增大。类似地，通过分析可以发现，其他的状态转移时间维向量对应的“拟合曲线”几乎都存在此现象，这说明基于三维状态转移概率矩阵生成的风电功率序列不会陷入某一状态中难以跳变。此现象亦符合实际物理过程，即在自然界中，当风速保持在某一水平的时间过长时，风速倾向于转移到另一水平。值得一提的是，对于稳定运行的风机，其出力在短时间内剧烈变化的概率很小，换言之，当前状态只能跳变到临近状态。这个特点使得大部分的时间维向量为零向量，大大简化了解维修正过程。
2.4 蒙特卡洛抽样
本文将适用于二维状态转移概率矩阵的蒙特卡洛抽样法[11]拓展到三维，利用三维状态转移概率矩阵生成三维状态转移累计概率矩阵
，进而基于该矩阵抽样生成人造风电功率状态序列。
根据
生成
的方法如下：
1）初始化
的零矩阵，记
的第l 页二维状态转移概率矩阵为Pl，并令l=1。
2）根据式（10），由Pl 生成大小为(k+1)×(k+1)的二维状态转移累计概率矩阵
后，将
赋给
中第l 页，并令l=l+1。
3）若l＞lmax，则停止；否则，重复步骤2）。
其中
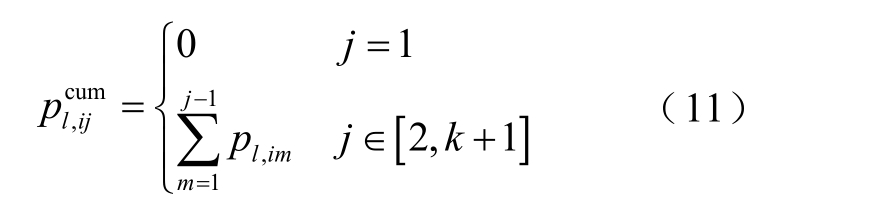
式中，pl,im 为Pl 中第i 行、m 列的元素。
基于
抽样生成给定仿真时长T 的人造风电功率状态序列的方法如下：
1）基于均匀分布生成区间[1,k]内的整数作为初始风电功率状态以及区间[0,1]内的随机数u。
2）假设当前时刻的风电功率状态为i 且状态i已持续了时间l，将u 与矩阵
中第l 页第i 行的元素进行比较，如果其落在(pcum l,ij , pcum l,i(j+1)]内，则下一时刻的状态为j。
3）重复步骤2）直至生成的人造风电功率状态序列的长度为T。
3 波动特征添加过程建模
波动特征添加过程建模是在尽量保持历史风电功率波动特征的基础上，将状态空间离散的人造风电功率状态序列还原为状态空间连续的人造风电功率序列。
3.1 波动量及噪声概率分布
风电功率的噪声为去噪前的功率值减去滑动平均去噪后的功率值，即
式中，ΔPt,noise、Pt 及Pt,smooth 分别为风电功率在时刻t 的噪声、功率值及去噪后的功率值。
风电功率的波动特征可由波动量[11,29]定义，如式（13）所示。
式中，ΔPt 为风电功率在时刻t 的波动量。
文献[11,29]研究表明，t location-scale 分布适合描述风电功率的波动量及噪声的概率分布，其概率密度函数为
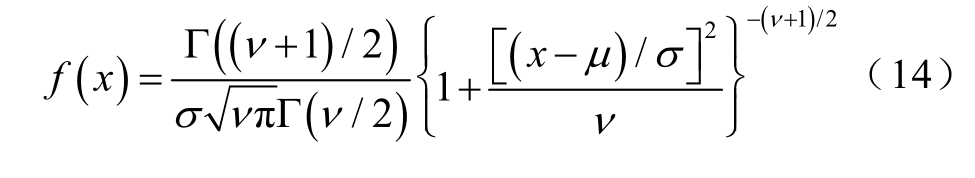
式中，Γ 为伽马函数；μ、σ、ν 分别为位置、尺度、形状参数。
3.2 添加波动量及噪声
利用式（14）获得风电功率波动量及噪声的概率密度函数ffluc、fnoise 后，对人造风电功率状态序列添加相应的波动量及噪声，即可生成包含噪声信息的人造风电功率序列。
针对现有MCMC 法[9-15]或直接添加白噪声，或添加混杂了噪声的波动量，造成人造风电功率序列的波动特征偏离历史功率特征的问题，本文在分离噪声及波动量的基础上，分开添加波动量及噪声，完善了现有的波动特征添加方法[9-13]，如下所示：
1）假设人造风电功率状态序列初始时刻的状态为i。基于均匀分布生成区间Pi,orig_interval 内的初始风电功率值P(t=1)。
2）假设m 时刻的状态为j，m+1 时刻的状态为s。基于波动量概率密度函数ffluc 随机生成ΔP，如果P(t=m)+ΔP 落在区间Ps,interval内，则进入步骤3）；否则，重新生成 ΔP，直至 P(t=m)+ΔP 落在区间Ps,interval 内为止。
3）基于噪声概率密度函数fnoise 随机生成一个ΔP'，如果P(t=m)+ΔP+ΔP'落在区间Ps,orig_interval 内，则下一个m+1 时刻的风电功率P(t=m+1)为P(t=m)+ ΔP+ΔP'；否则，重新生成ΔP'直至P(t=m)+ΔP+ΔP'落入区间Ps,orig_interval 内为止。
4）重复步骤2）和步骤3），直到生成的人造风电功率序列的长度为T。
4 风电功率序列建模流程
综合第1～3 节所述，基于改进MCMC 法的风电功率序列建模流程如图5、图6 所示，其中图5是建模流程的基本结构，而图6 是对图5 的详细描述。
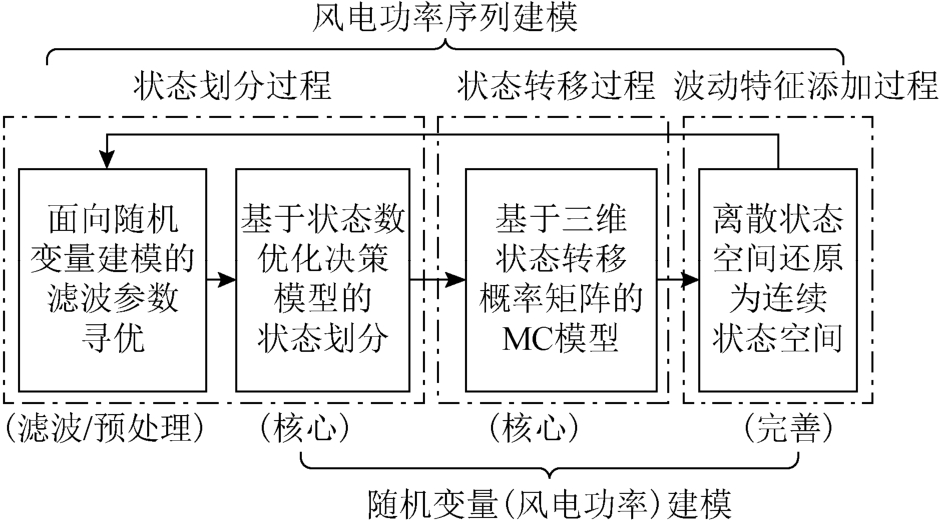
图5 基于改进MCMC 法的风电功率序列建模结构
Fig.5 Scheme for the improved MCMC method-based wind power time series modeling
本文中的风电功率序列建模，在研究内容上包括滤波及随机变量（风电功率）建模两部分，其中滤波是数据预处理环节，服务于随机变量建模，而随机变量建模是人造风电功率序列随机生成环节。在建模流程上可分为三步，依次为状态划分过程建模、状态转移过程建模及波动特征添加过程建模。
5 算例分析
5.1 数据来源
以经插值补缺、剔除异常点等处理后的德国某风电场2017 年15min 级风电功率监测数据[22]作为历史数据，按季度分别进行4 次仿真，各次仿真长度设置为相应季度历史数据长度的10 倍。其中，基于春季（3～5 月）历史数据的仿真结果见下文，其他季节的仿真结果见附录。
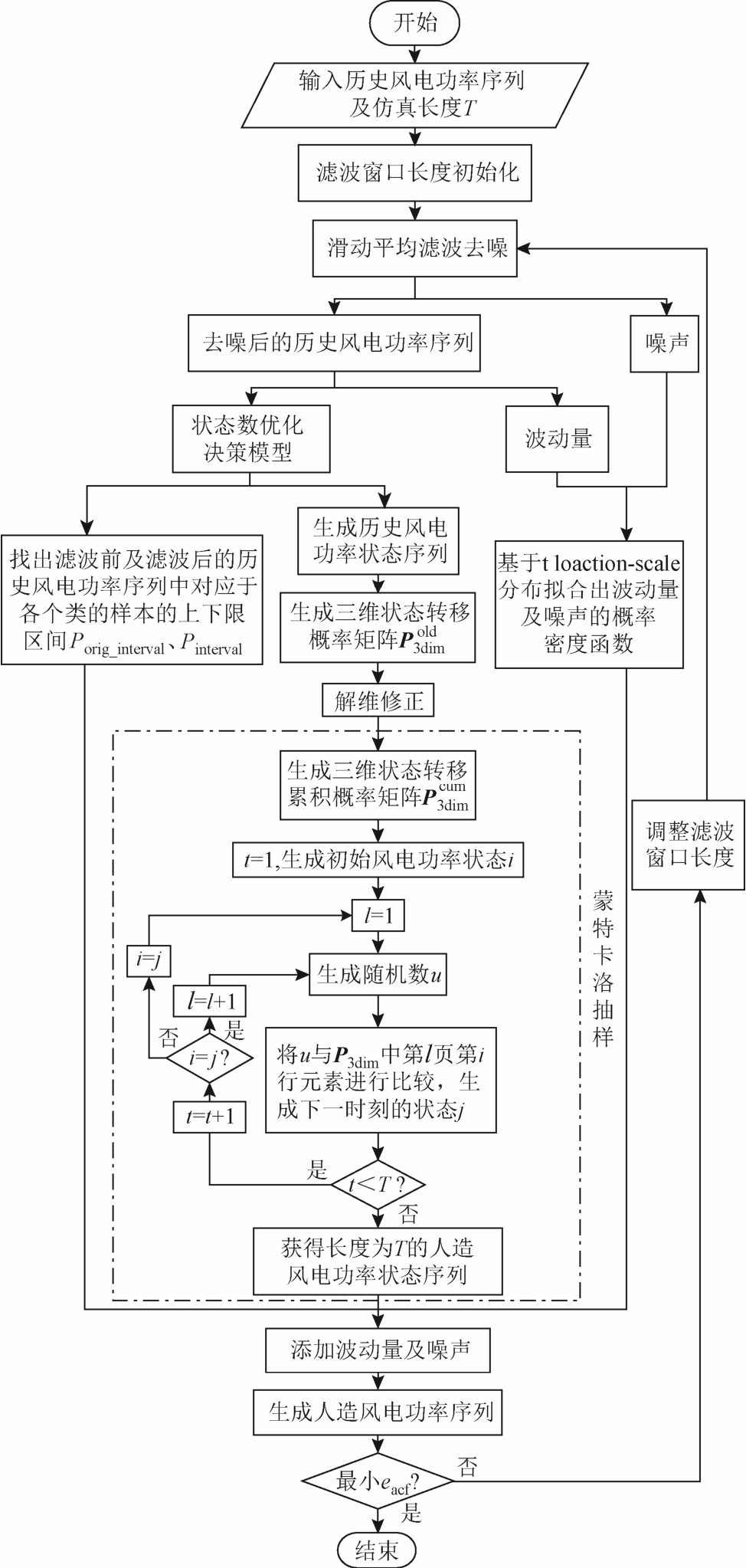
图6 基于改进MCMC 法的风电功率序列建模流程
Fig.6 Flow chart for the improved MCMC method-based wind power time series modelling
5.2 状态划分方案
应用前述风电功率序列的自适应状态划分策略对春季历史数据进行状态划分。根据eacf 最小，可确定最优滤波窗口长度为30min，如图7 所示。在该窗口长度下，图8 展示了归一化后的ecluster 及-BIC随聚类数的变化趋势。从图中可以看出，随着聚类数的增加，ecluster 先迅速减小而后减小趋势不再明显，-BIC 则近似线性增大。这说明，综合评价状态划分效果需折中考虑分类精度及MC 建模质量指标，且当聚类数大于一定值后，分类精度的提高效果不再明显，而建模质量却近似线性变差，故聚类数不宜过多。由式（5）得最优聚类数为14，在此聚类数下进行聚类，即得最优状态划分方案。对其他季节历史数据进行状态划分，可得类似结论，相应的最优滤波窗口长度和聚类数见附表1。
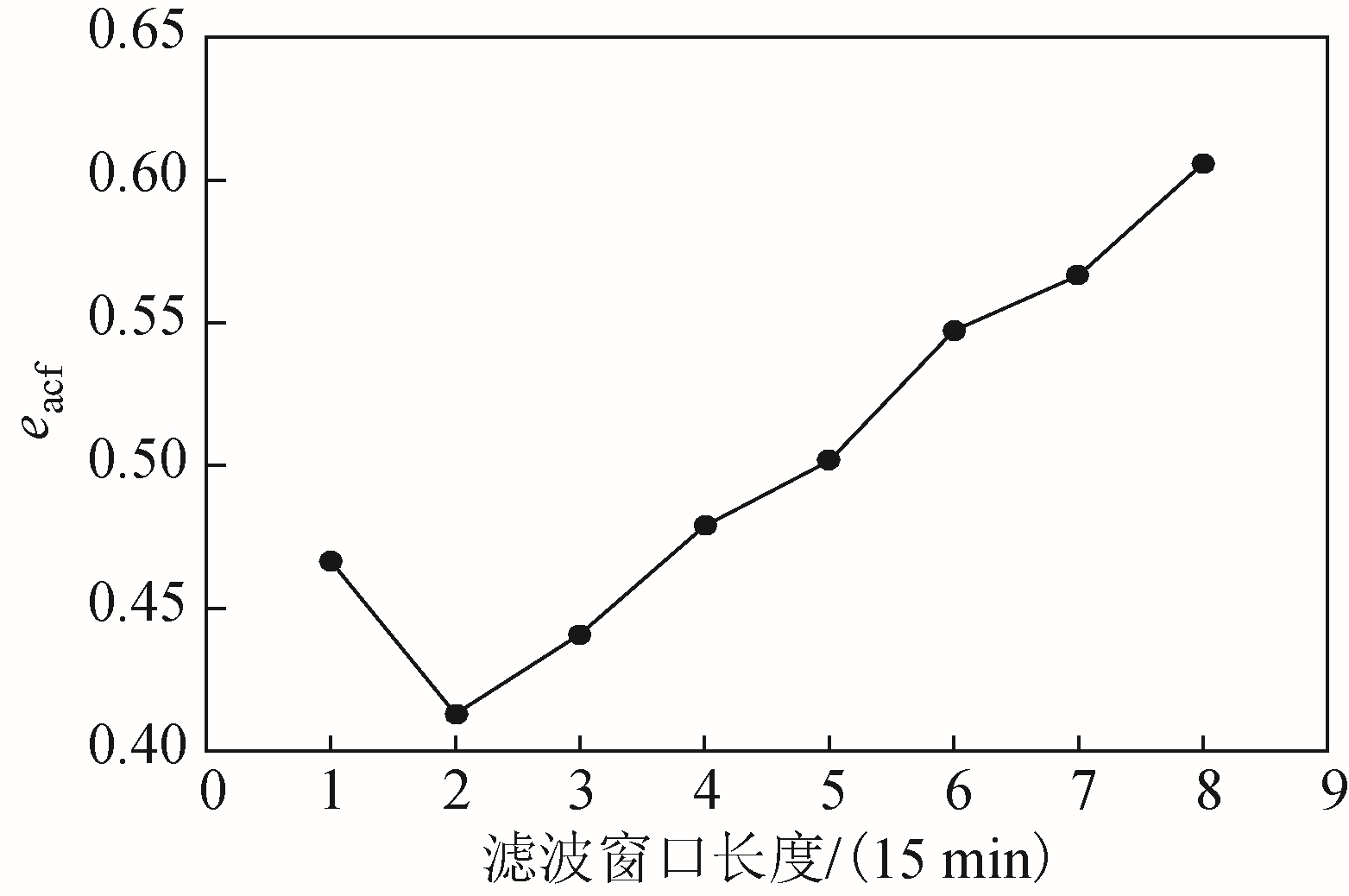
图7 eacf 随滤波窗口长度的变化趋势图
Fig.7 Trend of eacf with the variation of the filter window length
图8 状态划分效果评价指标趋势图
Fig.8 Trends of the state division assessment indexes
5.3 基于不同 MCMC 法生成的人造序列特征对比
本文从转移特征、波动特征、自相关性、功率值概率分布及状态持续时间概率分布等方面，将基于本文方法与传统MCMC 法及持续与波动蒙特卡洛法生成的人造序列进行特征对比。其中，对转移特征的对比已在2.1 节论述，本小节不再赘述。概率分布可由累计概率分布函数（ Cumulative Distribution Function，CDF）完整描述，不妨类似式（1）定量确定人造风电功率序列相对于历史风电功率序列在功率值概率分布方面的RMSE ecdf，而人造风电功率状态序列在多个状态持续时间概率分布方面的平均RMSE emean_dur，则可由式（15）确定。
式中，k 为状态数；ei,dur 为人造风电功率状态序列中状态i 在持续时间概率分布方面的RMSE，可用类似式（1）求出。
图9 展示了部分长度的历史风电功率序列及与其等长的部分长度人造风电功率序列（基于不同方法），图10 展示了历史及各人造风电功率序列的波动量概率密度拟合曲线。由图9 可以看出，本文方法、持续与波动蒙特卡洛法较好地解决了传统MCMC 法中“同一状态内波动过于频繁”的问题。但持续与波动蒙特卡罗法缺少滤波过程，使得基于该方法模拟出的波动特征易受噪声干扰而偏离历史，本文通过滤波分离波动量及噪声，有效解决了该问题。由图10 中本文方法相比于持续与波动蒙特卡洛法可以看出，对应的波动量概率密度曲线更贴合历史曲线。
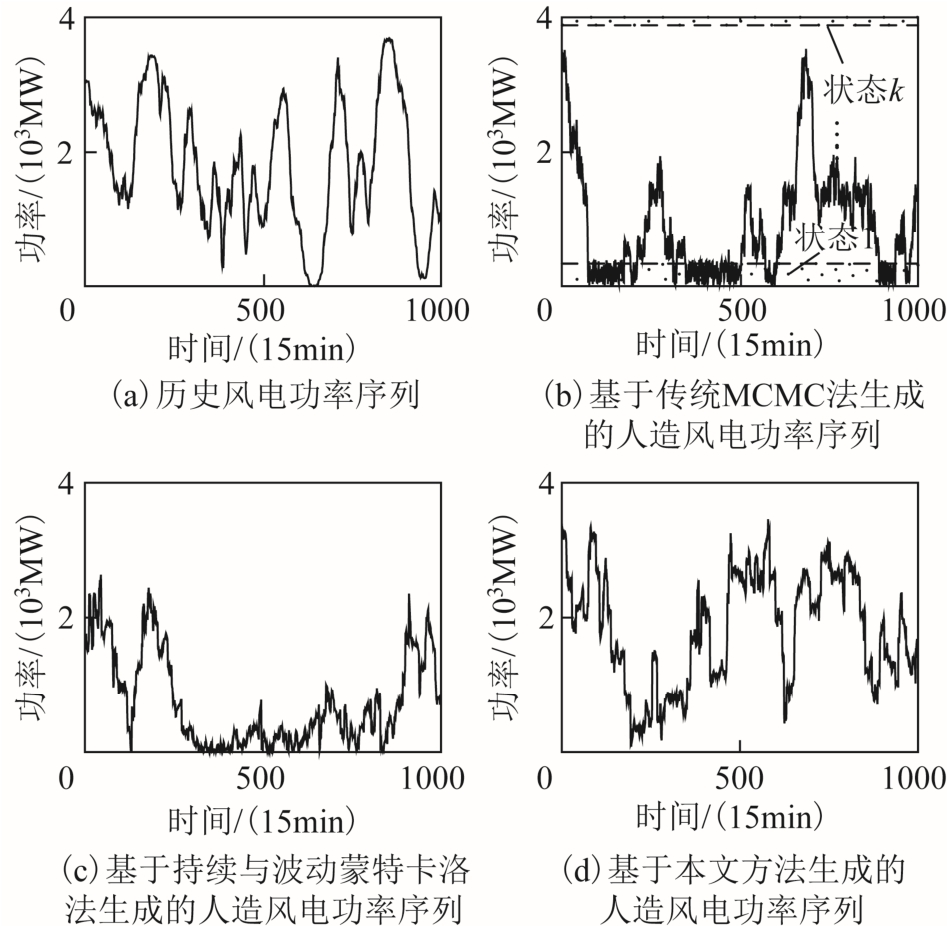
图9 部分长度的风电功率序列
Fig.9 A part of wind power time series
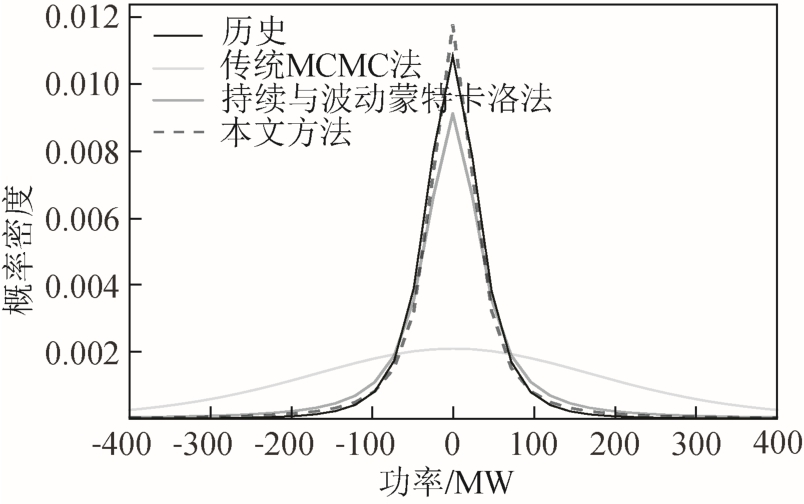
图10 波动量概率密度对比
Fig.10 Comparison of fluctuation quantity’s probability density
此外，由于状态数不宜过多，使得各状态对应 的样本区间相对较大，因此合理地添加波动特征（将离散状态空间还原为连续状态空间）是必要的。图10 中本文方法对应的波动量概率密度曲线最贴合历史曲线，说明相比现有方法，本文通过分开叠加波动量和噪声，防止噪声对波动量的干扰，更能达到合理添加波动特征的目的。
图11 和图12 分别为历史与人造风电功率序列在功率值概率分布及自相关性方面的对比。表1 定量地给出了人造序列在功率值概率分布、自相关性及状态持续时间方面的RMSE。由图11 和图12 可以看出，本文方法对应的风电功率CDF 曲线及ACF曲线均最贴近相应的历史曲线，说明本文方法能更好地复现历史功率值概率分布及相关性特征，这同时可由表1 中本文方法对应的ecdf 及eacf 最小看出。由于状态数量较多，不便绘图展示各状态持续时间的概率分布情况，故本文直接通过emean_dur 比较历史及人造风电功率状态序列的状态持续时间概率分布 特征。在表1 中，本文方法对应的emean_dur 最小，说明本文方法相比于现有方法更能复现历史状态持续时间概率分布特征。
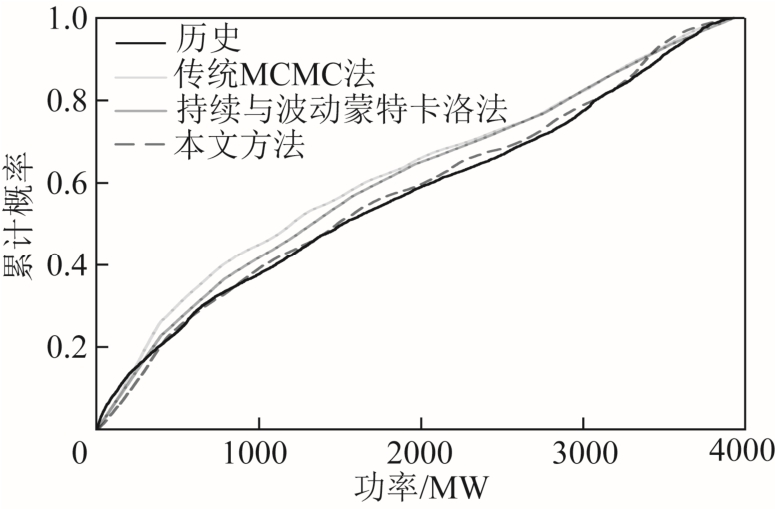
图11 风电功率值累计概率的对比
Fig.11 Comparison of wind power’s CDF
图12 自相关性对比
Fig.12 Comparison of ACF
表1 不同MCMC 法的对比
Tab.1 Comparison of different MCMC methods
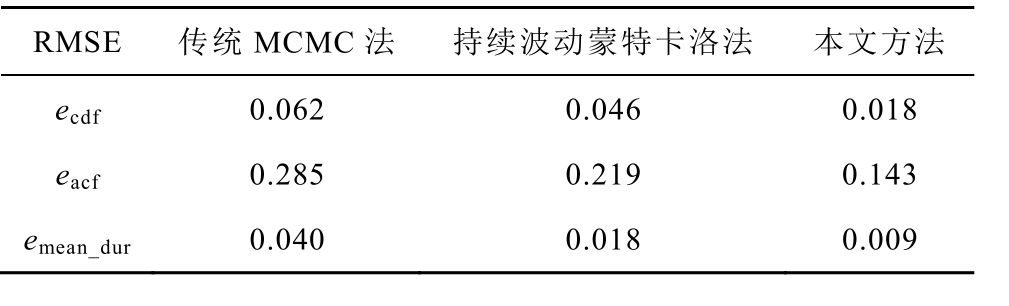
RMSE 传统MCMC 法 持续波动蒙特卡洛法 本文方法ecdf 0.062 0.046 0.018 eacf 0.285 0.219 0.143 emean_dur 0.040 0.018 0.009
附表2 定量地给出了在其他季节历史数据下，人造序列（基于不同方法）在功率值概率分布、自相关性及状态持续时间方面的RMSE。类似地，可以得出在其他季节历史数据下，本文方法依然能更好复现历史数据特征的结论。
5.4 不同滤波方法的对比
鉴于转移特征及波动特征的复现效果由随机变量（风电功率）建模直接决定，本小节从自相关性和风电功率值概率分布两方面对比不同的滤波方法（本文所提滤波方法、窗口长度固定为90min 的滑动平均滤波法和基于三层分解的小波滤波法[30]）。对比结果见表2 及附表3，其中表2 及附表3 分别对应春季及其他季节历史数据。
表2 不同滤波方法的对比
Tab.2 Comparison of different filtering methods
RMSE 滑动平均 （自适应） 滑动平均 （90min 窗口） 小波 （三层分解）ecdf 0.018 0.024 0.027 eacf 0.143 0.189 0.178
由表2 可以看出，相比于窗口固定的滑动平均滤波法和小波滤波法，本文滤波法对应的eacf 分别减小了0.046 及0.035，而ecdf 则相差不大，略微减少了0.006 及0.009。这说明相比于其他滤波方法，本文滤波方法能较为明显地提高随机变量建模对历史数据自相关性的复现程度，以及改善对风电功率值概率分布的复现效果。在其他季节历史数据下，由表3 亦可得出相同的结论。
表3 不同聚类工具的对比
Tab.3 Comparison of different clustering tools
计及MC 建模质量 未计及MC 建模质量 K 均值 模糊C 均值 K 均值 模糊C 均值状态数量 14 15 39 40 ecdf 0.018 0.017 0.013 0.012 eacf 0.143 0.147 0.211 0.214 emean_dur 0.009 0.009 0.018 0.019
5.5 不同聚类工具的对比
在状态数优化决策模型中计及MC 建模质量前后，相应于不同聚类工具（K 均值和模糊C 均值聚类法[31]）的仿真结果见表3 和附表4。其中，表3和附表4 分别对应春季和其他季节历史数据。
对比表3 的第二、三列可知，在本文所提的状态数优化决策模型中，应用不同的聚类工具对仿真结果影响不大。对比表3 的第二、四列或第三、五列可知：如果状态数优化决策模型中未计及MC 建模质量，将得到相对较大的状态数量；在较大的状态数量下，虽然风电功率值概率分布的复现效果略好，但自相关性、转移特征等均较差。这一结果与文献[13]的研究结果保持一致，原因是：较大的状态数量，虽然缓解了历史风电功率序列在离散化的过程中丢失风电功率值概率分布信息，但使得MC 建模质量恶化严重（见图8）。在其他季节历史数据下，由附表4 亦可得出相同的结论。
6 结论
针对现有MCMC 法存在的不足，本文提出了一种基于三维状态转移概率矩阵的改进 MCMC风电功率序列建模方法。通过算例分析得到以下结论：
1）与现有MCMC 法相比，本文建模方法能更好地复现历史数据的转移、波动、功率值概率分布、自相关性及状态持续时间概率分布等特征。
2）在风电功率序列的自适应状态划分策略中，提出的面向随机变量建模的滑动平均滤波窗口长度自适应选取方法，以随机变量建模输出结果反馈调节窗口长度，能提高随机变量建模对历史数据自相关性的复现程度，从而为滤波参数的寻优方法提供了一种新思路；建立的状态数优化决策模型综合考虑了分类精度及MC 模型建模质量指标，能实现状态数的最优决策，避免了根据经验预设状态数，主观划分历史数据的不足。
3）构建的三维状态转移概率矩阵能在不增加状态转移概率矩阵生成算法时间复杂度的基础上，计及状态持续时间对状态转移过程的影响，使得生成的人造风电功率状态序列在更好地复现历史转移特征的同时，不存在状态持续时间过长的问题。
4）本文方法可推广至其他随机变量建模之中，尤其适用于随机变量短时内无剧烈跳变的应用场景，如光伏出力及负荷大小序列建模等。
附 录
1. 命题证明
命题：在持续与波动蒙特卡洛法中，当某一状态的持续时间过长时，该状态的自跳变转移概率并不会减小。
证明：假设状态i 的持续时间li 服从逆高斯分布，记其概率密度和分布函数分别为f(x)、F(x)，其中
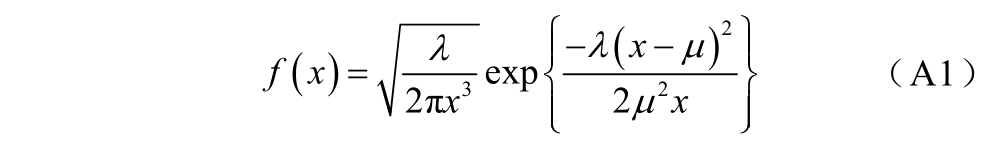
式中，μ为均值，μ＞0；λ为形状参数，λ＞0。
状态i 的自跳变转移概率可由式（6）求出，现重写为
当t→+∞时，F(t)→1，式（A2）最右项的分子、分母均趋近于0。由洛必达法则，有
即当t→+∞时，式（A3）趋向于恒定，故命题成立。 2. 仿真结果（夏秋冬季）
附表1 状态划分方案（夏秋冬季）
App.Tab.1 State division schemes (summer, fall, and winter)
季节 夏 秋 冬 窗口长度/min 45 45 60 状态数量 22 20 18
附表2 不同MCMC 法的比对（夏秋冬季）
App.Tab.2 Comparison of different MCMC methods (summer, fall, and winter)
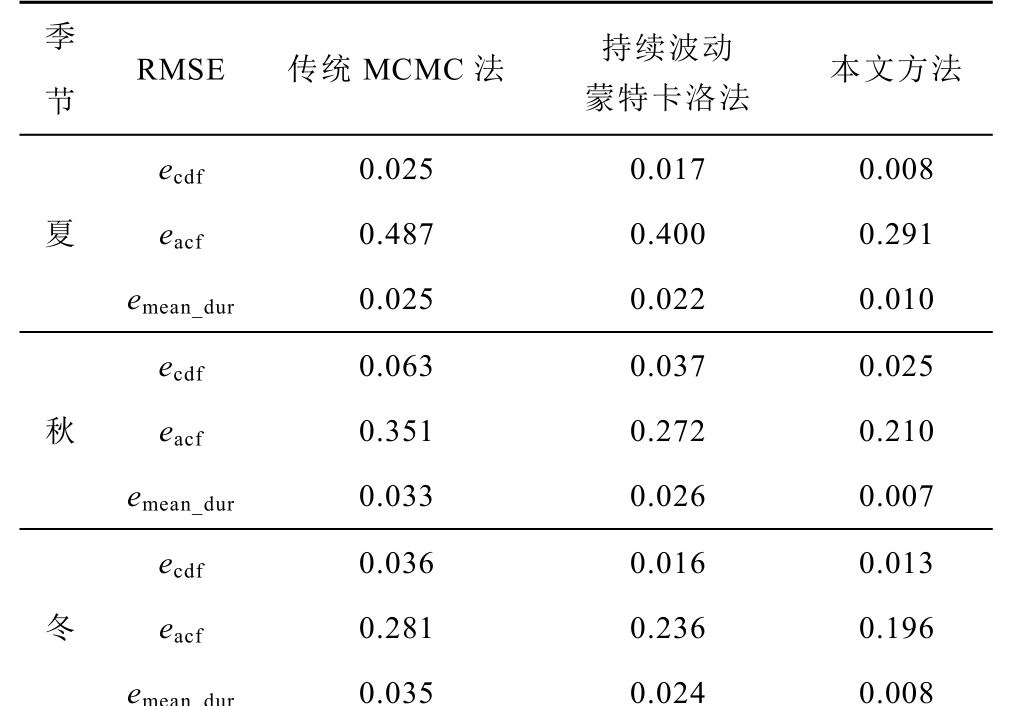
季节 RMSE 传统MCMC 法 持续波动 蒙特卡洛法 本文方法ecdf 0.025 0.017 0.008 夏 eacf 0.487 0.400 0.291 emean_dur 0.025 0.022 0.010 ecdf 0.063 0.037 0.025 秋 eacf 0.351 0.272 0.210 emean_dur 0.033 0.026 0.007 ecdf 0.036 0.016 0.013 冬 eacf 0.281 0.236 0.196 emean_dur 0.035 0.024 0.008
附表3 不同滤波方法的对比（夏秋冬季）
App.Tab.3 Comparison of different filtering methods (summer, fall, and winter)
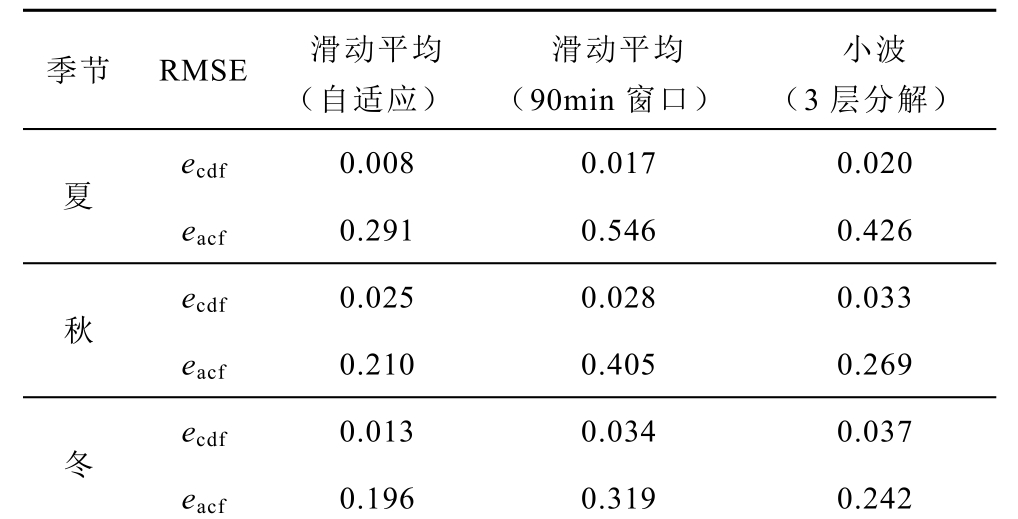
季节 RMSE 滑动平均 （自适应）滑动平均 （90min 窗口） 小波 （3 层分解）夏 ecdf 0.008 0.017 0.020 eacf 0.291 0.546 0.426 秋 ecdf 0.025 0.028 0.033 eacf 0.210 0.405 0.269 冬 ecdf 0.013 0.034 0.037 eacf 0.196 0.319 0.242
附表4 不同聚类工具的对比（夏秋冬季）
App.Tab.4 Comparison of different clustering tools (summer, fall, and winter)
季节 仿真结果计及MC 建模质量 未计及MC 建模质量K 均值 模糊C 均值 K 均值 模糊C 均值夏状态数量 22 23 47 47 ecdf 0.008 0.008 0.005 0.006 eacf 0.291 0.304 0.382 0.387 emean_dur 0.010 0.011 0.021 0.023 秋状态数量 20 22 45 46 ecdf 0.025 0.023 0.016 0.015 eacf 0.210 0.217 0.262 0.268 emean_dur 0.007 0.008 0.020 0.022 状态数量 18 19 43 44 冬ecdf 0.013 0.013 0.008 0.007 eacf 0.196 0.204 0.231 0.234 emean_dur 0.008 0.010 0.023 0.024
[1] GWEC. Global wind power statistical data 2017[R]. Brussels： GWEC, 2018.
[2] 胡源, 别朝红, 宁光涛, 等. 计及风电不确定性的多目标电网规划期望值模型与算法[J]. 电工技术学报, 2016, 31(10)： 168-175. Hu Yuan, Bie Zhaohong, Ning Guangtao, et al. The expected model and algorithm of multi-objective transmission network planning considering the uncertainty of wind power[J]. Transactions of China Electrotechnical Society, 2016, 31(10)： 168-175.
[3] 赵冬梅, 殷加玞. 考虑源荷双侧不确定性的模糊随机机会约束优先目标规划调度模型[J]. 电工技术学报, 2018, 33(5)： 1076-1085. Zhao Dongmei, Yin Jiafu. Fuzzy random chance constrained preemptive goal programming scheduling model considering source-side and load-side uncertainty[J]. Transactions of China Electrotechnical Society, 2018, 33(5)： 1076-1085.
[4] 张艺镨, 艾小猛, 方家琨, 等. 基于极限场景的两阶段含分布式电源的配网无功优化[J]. 电工技术学报, 2018, 33(2)： 380-389. Zhang Yipu, Ai Xiaomeng, Fang Jiakun, et al. Twostage reactive power optimization for distribution network with distributed generation based on extreme scenarios[J]. Transactions of China Electrotechnical Society, 2018, 33(2)： 380-389.
[5] 叶瑞丽, 郭志忠, 刘瑞叶, 等. 基于小波包分解和改进Elman 神经网络的风电场风速和风电功率预测[J]. 电工技术学报, 2017, 32(21)： 103-111. Ye Ruili, Guo Zhizhong, Liu Ruiye, et al. Wind speed and wind power forecasting method based on wavelet packet decomposition and improved Elman neural network[J]. Transactions of China Electrotechnical Society, 2017, 32(21)： 103-111.
[6] 孙国强, 卫志农, 翟玮星. 基于RVM 与ARMA 误差校正的短期风速预测[J]. 电工技术学报, 2012, 27(8)： 187-193. Sun Guoqiang, Wei Zhinong, Zhai Weixing. Short term wind speed forecasting based on RVM and ARMA error correcting[J]. Transactions of China Electrotechnical Society, 2012, 27(8)： 187-193.
[7] 刘纯, 吕振华, 黄越辉, 等. 长时间尺度风电出力时间序列建模新方法研究[J]. 电力系统保护与控制, 2013, 41(1)： 7-13. Liu Chun, Lü Zhenhua, Huang Yuehui, et al. A new method to simulate wind power time series of large time scale[J]. Power System Protection and Control, 2013, 41(1)： 7-13.
[8] 李驰, 刘纯, 黄越辉, 等. 基于波动特性的风电出力时间序列建模方法研究[J]. 电网技术, 2015, 39(1)： 208-214. Li Chi, Liu Chun, Huang Yuehui, et al. Study on the modelling method of wind power time series based on fluctuation characteristics[J]. Power System Technology, 2015, 39(1)： 208-214.
[9] Papaefthymiou G, Klockl B. MCMC for wind power simulation[J]. IEEE Transactions on Energy Conversion, 2008, 23(1)： 234-240.
[10] Wu Tong, Ai Xiaomeng, Li Weixing, et al. Markov chain monte carlo method for the modeling of wind power time series[C]//IEEE International Conference on Innovative Smart Grid Technologies, Tianjin, China, 2012： 1-6.
[11] 于鹏, 黎静华, 文劲宇, 等. 含风电功率时域特性的风电功率序列建模方法[J]. 中国电机工程学报, 2014, 34(22)： 3715-3723. Yu Peng, Li Jinghua, Wen Jinyu, et al. A wind power time series modelling based on its time domain characterisitcs[J]. Proceedings of the CSEE, 2014, 34(22)： 3715-3723.
[12] 吴桐. 风电功率的特性分析及其时间序列生成方法研究[D]. 武汉： 华中科技大学, 2013.
[13] 罗钢, 石东源, 陈金富, 等. 风光发电功率时间序列模拟的MCMC 方法[J]. 电网技术, 2014, 38(2)： 321-327. Luo Gang, Shi Dongyuan, Chen Jinfu, et al. A markov chain monte carlo method for simulation of wind and solar power time series[J]. Power System Technology, 2014, 38(2)： 321-327.
[14] 蒋平, 霍雨翀, 张龙, 等. 基于改进一阶马尔科夫链的风速时间序列模型[J]. 电力系统自动化, 2014, 38(19)： 22-27. Jiang Ping, Huo Yuchong, Zhang Long, et al. A wind speed time series model based on advanced first-order markov chain approach[J]. Automation of Electric Power Systems, 2014, 38(19)： 22-27.
[15] 丁明, 鲍玉莹, 毕锐. 应用改进马尔科夫链的光伏出力时间序列模拟[J]. 电网技术, 2016, 40(2)： 460-464. Ding Ming, Bao Yuying, Bi Rui. Simulation of PV output time series used improved markov chain[J]. Power System Technology, 2016, 40(2)： 460-464.
[16] 夏泠风, 黎嘉明, 赵亮, 等. 考虑光伏电站时空相关性的光伏出力序列生成方法[J]. 中国电机工程学报, 2017, 37(7)： 1982-1992. Xia Lingfeng, Li Jiaming, Zhao Liang, et al. A PV power time series generating method considering temporal and spatial correlation characteristics [J]. Proceedings of the CSEE, 2017, 37(7)： 1982-1992.
[17] Ummels B C, Gibescu M, Pelgrum E, et al. Impacts of wind power on thermal generation unit commitment and dispatch[J]. IEEE Transactions on Energy Conversion, 2007, 22(1)： 44-51.
[18] Silva A M L L, Sales W S, Da Fonseca Manso L A D F, et al. Long-term probabilistic evaluation of operating reserve requirements with renewable sources[J]. IEEE Transactions on Power Systems, 2010, 25(1)： 106-116.
[19] Wang Jianhui, Shahidehpour M, Li Zuyi. Securityconstrained unit commitment with volatile wind power generation[J]. IEEE Transactions on Power Systems, 2008, 23(3)： 1319-1327.
[20] 王丽婕, 廖晓钟, 高阳, 等. 风电场发电功率的建模和预测研究综述[J]. 电力系统保护与控制, 2009, 37(13)： 118-121. Wang Lijie, Liao Xiaozhong, Gao Yang, et al. Summarization of modeling and prediction of wind power generation[J]. Power System Protection and Control, 2009, 37(13)： 118-121.
[21] Dobakhshari A S, Fotuhi-Firuzabad M. A reliability model of large wind farms for power systems adequacy studies[J]. IEEE Transactions on Energy Conversion, 2009, 24(3)： 792-801.
[22] Tenne T. Offshore wind energy data from a German windfarm[DB/OL]. 2017-11-11. http：//www. tennettso. de/site/en/Transparency/publications/network-figures/ actual-and-forecast-wind-energy-feed-in.
[23] 郑君里. 信号与系统[M]. 北京： 高等教育出版社, 2011.
[24] 汪德星. 电力系统运行中AGC 调节需求的分析[J]. 电力系统自动化, 2004, 28(8)： 6-9. Wang Dexing. Analysis of AGC demand of power system operation[J]. Automation of Electric Power Systems, 2004, 28(8)： 6-9.
[25] 段江娇. 基于模型的时间序列数据挖掘[D]. 上海： 复旦大学, 2008.
[26] 李滨, 覃芳璐, 吴茵, 等. 基于模糊信息粒化与多策略灵敏度的短期日负荷曲线预测[J]. 电工技术学报, 2017, 32(9)： 149-159. Li Bin, Qin Fanglu, Wu Yin, et al. Short-term daily load curve forecasting based on fuzzy information granulation and multi-strategy sensitivity[J]. Transactions of China Electrotechnical Society, 2017, 32(9)： 149-159.
[27] 丁明, 过翌, 张晶晶, 等. 基于效用风险熵权模糊综合评判的复杂电网节点脆弱性评估[J]. 电工技术学报, 2015, 30(3)： 214-222. Ding Ming, Guo Yi, Zhang Jingjing, et al. Node vulnerability assessment for complex power grids based on effect risk entropy-weighted fuzzy comprehensive evaluation[J]. Transactions of China Electrotechnical Society, 2015, 30(3)： 214-222.
[28] 田铮. 随机过程与应用[M]. 北京： 科学出版社, 2007.
[29] 林卫星, 文劲宇, 艾小猛, 等. 风电功率波动特性的概率分布研究[J]. 中国电机工程学报, 2012, 32(1)： 38-46. Lin Weixing, Wen Jinyu, Ai Xiaomeng, et al. Probability density function of wind power variations[J]. Proceedings of the CSEE, 2012, 32(1)： 38-46.
[30] 鲁军, 李侠, 王重马, 等. 基于小波分析的MSMA振动传感器信号处理与故障检测[J]. 电工技术学报, 2015, 30(10)： 354-360. Lu Jun, Li Xia, Wang Zhongma, et al. Signal process and fault detection of MSMA vibration sensor based on wavelet analysis[J]. Transactions of China Electrotechnical Society, 2015, 30(10)： 354-360.
[31] 杨锡运, 刘玉奇, 李建林. 基于四分位法的含储能光伏电站可靠性置信区间计算方法[J]. 电工技术学报, 2017, 32(15)： 136-144. Yang Xiyun, Liu Yuqi, Li Jianlin, et al. Reliability confidence interval calculation method for photovoltaic power station with energy storage based on quartile method[J]. Transactions of China Electrotechnical Society, 2017, 32(15)： 136-144.