0 引言
分布式光伏发电具有清洁高效、就近利用和因地制宜等优势，近年来光伏发电在配电网中的装机容量不断扩大[1]。分布式发电并网技术规范要求电网故障时光伏发电须保持低电压穿越运行，同时优先向电网提供无功电流支持[2-4]。光伏发电并网点电压发生跌落时，须按低电压穿越要求保持不脱网运行，其注入的短路电流由并网点电压跌落和低电压穿越控制共同决定[5-6]；而并网电压严重跌落时光伏发电允许退出运行，此时光伏发电无短路电流注入电网[4]。光伏发电的低电压穿越建模是典型的灰箱问题，不同厂家和型号光伏逆变器的拓扑结构、控制策略及参数存在差异，使得光伏发电的低电压穿越能力存在模糊性[7]。同时，电网故障发生的随机因素导致光伏发电并网点电压跌落具有随机性，使得光伏发电故障期间的短路电流表现出不确定性，为此评估含分布式光伏发电主动配电网的短路电流随机变化范围和分布情况具有重要意义。
在光伏发电暂态建模方面，文献[8]研究了光伏发电在线性区和非线性区的故障暂态响应特性及控制环节的影响规律；文献[9]考虑光伏发电故障穿越控制建立其稳态短路电流计算模型，文献[10]分析了低电压穿越时序对光伏发电短路电流的影响，前述模型仅针对不同故障条件下光伏发电的稳态短路电流，尚未研究光伏发电在故障暂态阶段的等效模型。在短路电流计算方面，文献[11]提出了考虑光伏发电限流特性的辐射型配电网短路电流算法，文献[10,12-14]则利用叠加原理提出了含光伏发电配电网的三相短路电流和不对称电流的计算方法。但是前述方法均针对确定性的短路电流计算，未考虑系统故障等随机因素，也未计及光伏发电低电压穿越过程的不确定性，它们仅能得到最恶劣情况下系统的短路电流，无法获得光伏发电并网导致系统短路电流水平增加的变化区间。
在光伏发电低电压穿越方面，文献[15-16]提出基于正负序补偿和模型预测控制的光伏发电改进控制策略，以改善其在电网故障期间的控制性能；文献[17-19]通过对不同厂家光伏逆变器和实际光伏发电站的测试，建立了光伏发电低电压穿越的故障模型；文献[19]还分析了光伏发电低电压穿越过程的短路电流故障分量特征。但是前述文献主要对低电压穿越过程中光伏发电的电流特性进行建模，还未见相关文献对其低电压穿越能力的不确定性进行建模研究。目前，概率评估方法已应用于主动配电网电压稳定[20]、电压暂降[21]和潮流分析[22]等方面，将电网故障随机性建模、光伏发电短路电流计算及其低电压穿越不确定建模整合，即可对含分布式光伏发电主动配电网的短路电流水平进行概率评估。
为此，本文首先对光伏发电不脱网运行时的故障稳态特征进行分析，得到不同端电压跌落下其短路电流的输出特性；利用其低电压穿越的不确定性建立低电压脱网概率评估模型；最后综合考虑光伏发电短路电流输出特性、低电压脱网不确定性和系统故障信息等影响因素，对主动配电网短路电流进行概率评估。
1 光伏发电低电压穿越要求及故障特性
1.1 光伏发电低电压穿越要求
含光伏发电的电网故障时，并网点处电压即使出现大幅跌落，光伏发电仍会按照并网规程保持不脱网运行[4]。而逆变器作为光伏发电并网的核心部分，也是实现低电压穿越的重要元件，决定了光伏发电不脱网运行状态下的输出特性，其低电压穿越控制框图如图1 所示[23]。
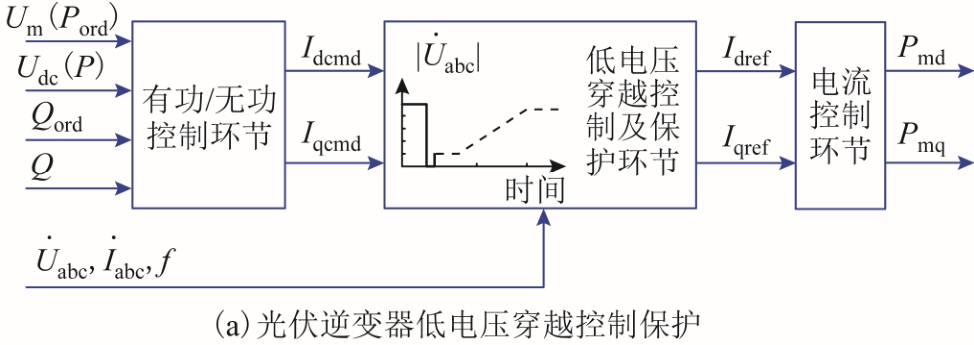
图1 光伏发电低电压穿越要求
Fig.1 Low voltage ride-through requirements of photovoltaic power generations
由图1a 可知，逆变器控制保护包括有功/无功控制环节、低电压穿越控制及保护环节、电流控制环节三部分。其中Um 和Udc 分别为光伏方阵最大功率点电压和逆变器直流侧电压；P、Q 和Pord、Qord 分别为逆变器输出的有功、无功功率和逆变器的有功、无功功率控制指令；经有功/无功控制环节后输出得到有功控制指令电流Idcmd 和无功控制指令电流 Iqcmd；再将采集到的逆变器交流侧三相电压相量 abcU˙ 、电流相量 abcI˙ 以及网侧频率 f 同时反馈至故障穿越控制及保护环节，计算获取逆变器交流侧电流d 轴分量参考值Idref 和q 轴分量参考值 Iqref；最后经电流控制环节获得在同步旋转 dq坐标系下，逆变器PWM 模块调制比d 轴分量Pmd和q 轴分量Pmq。
图1b 为低电压穿越控制及保护环节的详细控制框图，它描述了逆变器在电网故障及恢复过程中的暂态特性，以及逆变器的过/欠电压、过/欠频、过电流保护特性。根据文献[4]要求，光伏发电系统应具备低电压穿越能力，且在电网电压跌落过程中提供无功电流支撑。其主要根据逆变器交流侧三相电压
跌落程度的不同，首先确定逆变器交流侧q轴分量参考值Iqref，即对电网提供无功电流支撑，再依据Iqref 确定电流d 轴分量参考值Idref，并对有功电流进行限幅。图中Kmax 为最大电流输出倍数，Kq0和Kq 分别为逆变器零电压穿越和低电压穿越无功电流支撑系数，In 表示逆变器交流侧额定电流。
由图1a 可以看出，当端电压跌落并持续一段时间时，光伏发电极有可能面临脱网，而脱网后将无法向系统注入短路电流。单台光伏发电在不脱网运行时能产生的短路电流与其端电压跌落情况有关，因此下文将先对光伏发电故障期间稳态特性进行分析，为系统短路电流概率评估奠定基础。
1.2 光伏发电故障特性分析
光伏属于变流型电源，在电网故障阶段呈限流特性[6]。由图1b 中低电压穿越控制环节可知，逆变器交流侧电流输出参考值被进行了限幅处理，根据逆变器交流侧三相电压
跌落水平，确定不同跌落程度下的电流参考值，以此为出发点分析光伏发电在不同端电压跌落下的电流特性。
首先根据式（1）确定逆变器交流侧电流q 轴分量参考值Iqref，其中Iqref=Iqcmd=0，Kq 取1.5，Kq0 取1.05[4]。逆变器交流侧电流d 轴分量参考值Idref 通过式（2）决定，其中Idcmd 与有功功率P 和电压
的比值有关，即 
此处假设光伏运行于P=0.8(pu)，Kmax 取1.5，由式（2）可知无功电流Iqref 的支撑将对有功电流输出产生一定影响。
Iqref、Idref 和Iref 随端电压的变化趋势如图2a 所示。图中Iqref 随端电压跌落呈比例增大最后趋于恒定；而 Idref 随端电压跌落逐渐增大到极值后被限幅，由于无功电流的增长Idref 逐渐减小最后达到恒定值；Iref 为总电流指令值，即 
近似于光伏发电输出电流，随着端电压跌落逐渐增大，在达到1.5(pu)后限幅输出。由以上分析可知，通过式（1）和式（2）可确定在不同端电压跌落下，单台光伏发电机组不脱网运行时能输出的短路电流，并且由图2a 可知，光伏输出电流大小与其端电压呈非线性关系，与常规电源相比有很大差别。
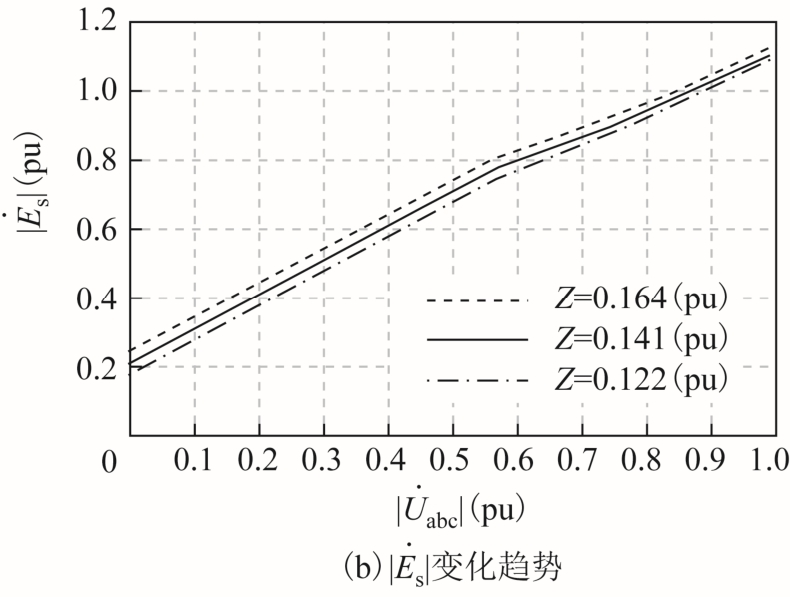
图2 Iqref、Idref、Iref 和 s| |E˙ 的变化范围
Fig. 2 Variation range of Iqref, Idref, Iref and s| |E˙
光伏发电端口可用戴维南等效电路表示，有等
式 
成立，其中 sE˙为等值内电动势，Z为虚拟控制阻抗，其大小由控制参数决定[5]。将测量到的不同虚拟控制阻抗值代入上述等式，画出内电势
随端电压
的变化趋势如图2b 所示。可以看出，内电动势呈现两个变化趋势，在未进入限流阶段时
随
下降缓慢，当输出电流限幅后电流保持恒定，
呈比例减小但仍稍大于端电压
2 光伏发电低电压穿越能力随机建模
2.1 低电压穿越不确定性区域
光伏发电的低电压穿越曲线（Low Voltage Ride Through Curve, LVRTC）如图3 粗实线所示，图中横轴表示电压跌落持续时间，纵轴表示电压幅值。当电网发生故障时，由光伏发电的端电压跌落程度以及持续时间共同决定其是否脱网。若位于LVRTC以下，即阴影区域内，光伏发电将从电网退出；反之处于并网运行状态。由于电网故障时更多关注的是故障初始阶段的短路电流，且故障清除时间通常在0.4s 以内[24]，故本文仅考虑0.4s 内光伏发电的运行情况。
图3 光伏发电低电压穿越曲线及试验结果
Fig.3 LVRTC and experimental results of photovoltaic power generations
利用群菱能源ACLT-1100 光伏低电压穿越测试装置，对型号为华威能源ES-5TLT、ES-8TLT 和ES-12TLT 三台5kW、8kW 和12kW 的小容量光伏逆变器进行低电压穿越能力测试[25]，分别在光伏发电输出功率为0.1Pn～0.3Pn 和不小于0.7Pn 两种工况下进行检测，且在相同电压跌落测试点重复测试1 次，取两台光伏逆变器多次测试数据的平均值，在图3中分别用不同的符号标注测试结果。其中ES-5TLT能在相同电压跌落程度下保持更长的不脱网运行时间，而ES-8TLT 在端电压跌落至0.3(pu)附近才能保持不脱网运行。
此外，图3 中不同的符号表示2011 年国网电力科学研究院对青海电网光伏电站的检测结果，包含两台艾默生 SSL0500 逆变器、一台阳光电源 SG 500KTL 逆变器和一台南瑞继保PCS-9563-500kW 逆变器。由图3 可知，SSL0500 逆变器对应两个检测结果，其中一台逆变器在端电压跌落至0.2(pu)后的0.07s 就已脱网，而另一台则在0.75s 后才脱网。
由以上分析可知不同型号逆变器的低电压穿越能力不同；即使逆变器型号相同，由于各生产厂家制造工业的差异，在低电压穿越能力测试中也有很大差异。综合考虑以上情况，可近似认为它们的低电压穿越能力在国家标准曲线附近区域波动，由此构成了一个不确定性区域如图4 所示。
图4 低电压穿越不确定性区域
Fig.4 Uncertainty region of LVRTC
图4 中粗实线为LVRTC 的前半部分，阴影区域为本文定义的不确定性区域，要得到此区域的范围，就需要确定图中上下界限两条实线所在位置。由于不同型号逆变器的低电压穿越能力各不相同，因此需要对多台逆变器进行测试，由试验数据确定上述区域范围，下文以逆变器两类测试结果进行分析。
对多台逆变器进行低电压穿越能力测试，其中部分逆变器在端电压跌落至0(pu)时，还能保持一定时间不脱网运行（类比前述ES-5TLT 逆变器），则可通过tmax 和Umin 确定区域的下边界，其中tmax 表示在多台逆变器测试结果中，端电压跌落至0(pu)时能保持不脱网运行的最长时间，Umin 表示不脱网运行时间大于tmax 的最小端电压；另一种情况则为部分逆变器在端电压未跌落至0(pu)时就已脱网（类比前述ES-8TLT 逆变器），此时区域的上边界由Umax确定，Umax 表示在多台逆变器测试结果中，能保持不脱网运行的最大端电压。
为方便分析，本文将不确定性区域分为A、B、C三个子区域，其中A 区是t 和U 的二维函数，由图4 可知A 区范围包括Umin＜U＜Umax且t＜tmax区域；B 区和C 区分别是t 和U 的一维函数，其中B 区范围包括U＜Umin 且t＜tmax 区域，C 区范围包括Umin＜U＜Umax 且t＞tmax 区域。此外，在不确定性区域上方的区域D(U＞Umax 部分)为不脱网运行区；剩余部分区域E(U＜Umin 且t＞tmax 部分)为脱网运行区。
2.2 光伏发电低电压脱网随机评估模型
光伏发电是否脱网由其端电压跌落程度和持续时间共同决定，在不确定性区域内可转换为概率问题，利用概率模型描述低电压穿越能力的随机性，进而对已知故障条件下的光伏脱网概率进行评估。
图4 中区域D 内光伏保持不脱网运行，而位于区域E 时光伏将从电网中切除。由于生产厂家、设备型号、运行环境等因素的影响，区域ABC 内光伏脱网概率是不确定的，即t 和U 都是随机变量。本文基于负荷电压耐受曲线的相关研究[26]，用正态分布函数表征随机变量t 和U 的随机性。设区域B 和区域C 内分别关于一维随机变量t 和U 的概率密度函数为fx(t)和fy(U)，具体表示为
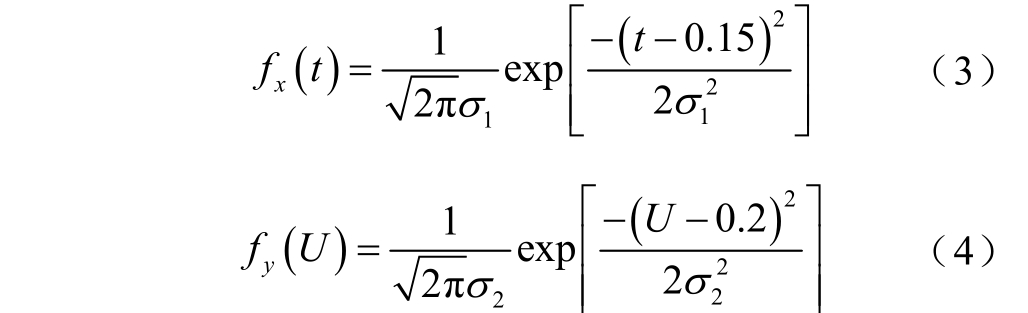
式中
1σ 和 2σ 分别为区域B 和区域C 的分布密度。由于t 和U 是两个相互独立的随机变量，则区域A 内关于随机变量t 和U 的联合概率密度函数可表示为
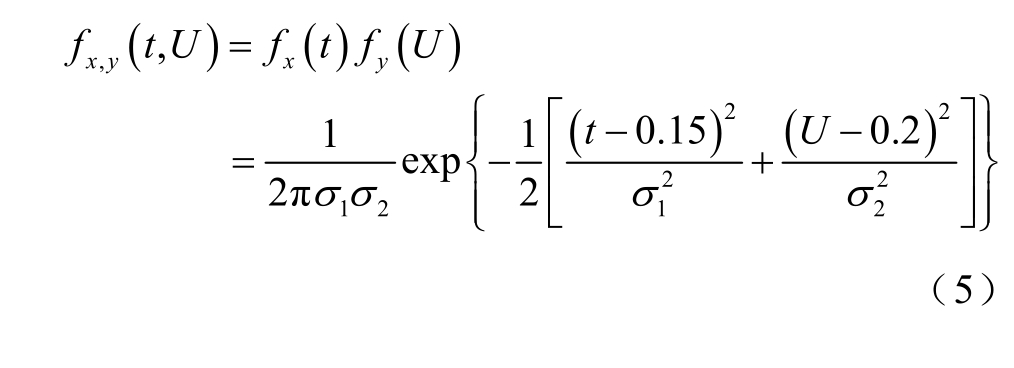
根据3σ 原则，可进一步求解 1σ 和 2σ 的值为
通过多次试验获取tmax、Umax、Umin 的值，代入式（6）求解 2σ ，结合式（3）～式（5）便可得到整个不确定区域内的概率密度函数。
假设光伏端电压跌落有s1～s5 五种情况，分别位于A、B、C、D、E 区域内，具体如图5 所示。其中s1 位于区域D 内，光伏保持并网运行，并向电网注入短路电流，即脱网概率为0；s2 在区域E 中，光伏从电网中退出，即脱网概率为1；U3 和t3 分别为s3 的电压跌落幅值和持续时间；t4 为s4 的电压跌落持续时间；U5 为s5 的电压跌落幅值。
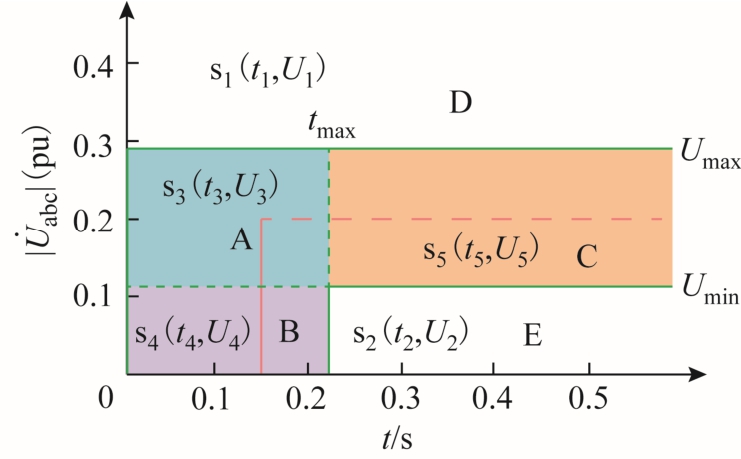
图5 光伏发电脱网评估
Fig.5 Evaluation of off-grid operation for photovoltaic power generations
当发生s1～s5 跌落时光伏的脱网概率分别表示为
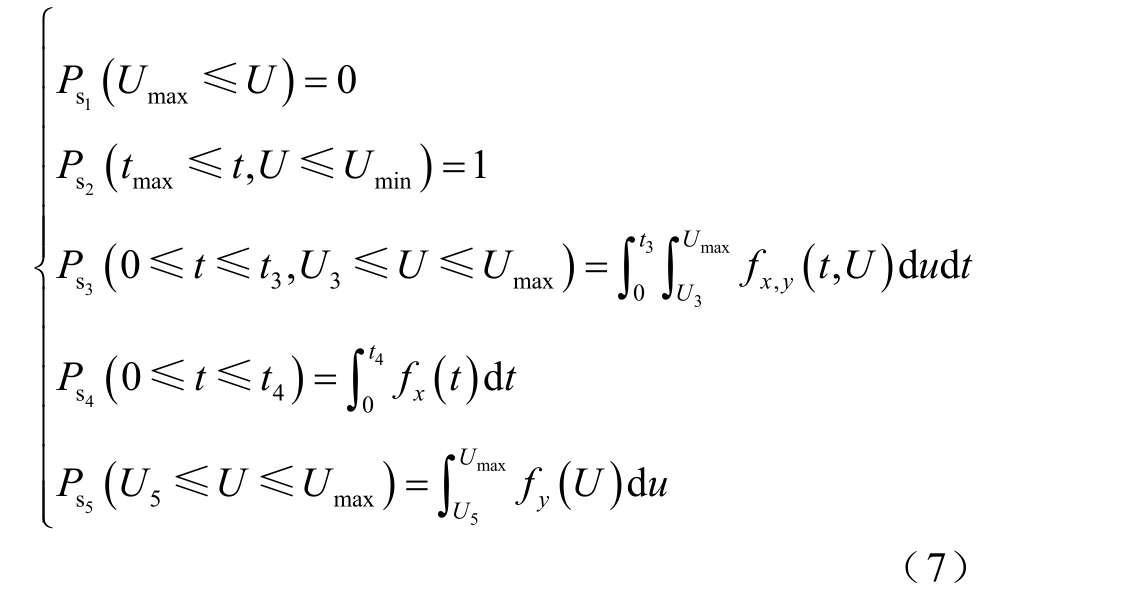
根据前述分析，假设光伏发电低电压穿越不确定性区域的边界Umin、Umax 和tmax 分别为0.1(pu)、0.3(pu)和0.2s，结合式（7）给出不同端电压跌落以及不同故障持续时间下，光伏发电脱网概率的三维图如图6 所示，图中纵坐标Ppv 表示光伏发电的脱网概率。由图可知，最下层区域和最上层区域分别对应图5 中的区域D 和区域E，它们的脱网概率Ppv分别为0 和1，其余区域的概率随端电压跌落和故障持续时间的改变而改变。
图6 光伏发电脱网概率三维图
Fig.6 Three-dimensional diagram of off-grid probability of photovoltaic power generations
由第1 节分析可知，在未考虑低电压穿越不确定性时，即电网故障后光伏发电保持不脱网，单台光伏发电机组能产生的短路电流仅由其端电压跌落程度决定。但实际光伏注入电网的短路电流受其是否脱网的影响而呈现出不确定性，通过本节分析可知，光伏发电在电网故障时是否脱网是由端电压跌落和故障持续时间共同决定的概率事件。
为客观表示光伏注入电网的真实短路电流，本文提出用光伏发电短路电流的期望值
对其进行描述，具体表示为
，其中Ipv 表示在某一电压跌落下，光伏不脱网运行时能提供的短路电流，电流大小由端电压决定；1-Ppv 表示在该故障情况下通过式（7）计算得到的不脱网概率，概率大小由端电压与故障持续时间共同决定；因此可认为光伏发电短路电流期望值
是关于端电压和故障持续时间的函数。假设光伏发电在额定功率下运行，电流限值为1.5(pu)，则在图6 的基础上画出光伏发电短路电流期望值
与端电压和故障持续时间的关系如图7 所示。
图7 pv I 与abc U˙ 、t 关系图
Fig.7 The diagram of pv I , abc U˙ and t
图7 中最上层区域和最下层区域分别对应图5中的区域D 和区域E，它们的光伏发电短路电流期望值
分别为1.5(pu)和1(pu)，其余区域的期望值随端电压跌落和故障持续时间变化而具有不确定性，需根据实际故障情况具体分析。
3 计及低电压穿越不确定性的短路电流概率评估
含有光伏发电的10kV 配电网馈线拓扑结构如图8 所示，其中Tl 为降压变压器，Zl、Z2 分别为两条馈线的线路阻抗。图8 中两条馈线均可能发生故障，且故障位置、故障类型等均具有随机性，并且各光伏发电机组在故障期间是否脱网具有不确定性，脱网的机组越多，它们注入故障点的短路电流越小，因此将进一步对系统短路电流的评估产生影响。为全面获取系统短路电流的变化区间和概率分布情况，需同时考虑光伏发电低电压脱网概率评估模型，以及系统中故障线路、故障类型、故障持续时间等一系列不确定性因素的影响。
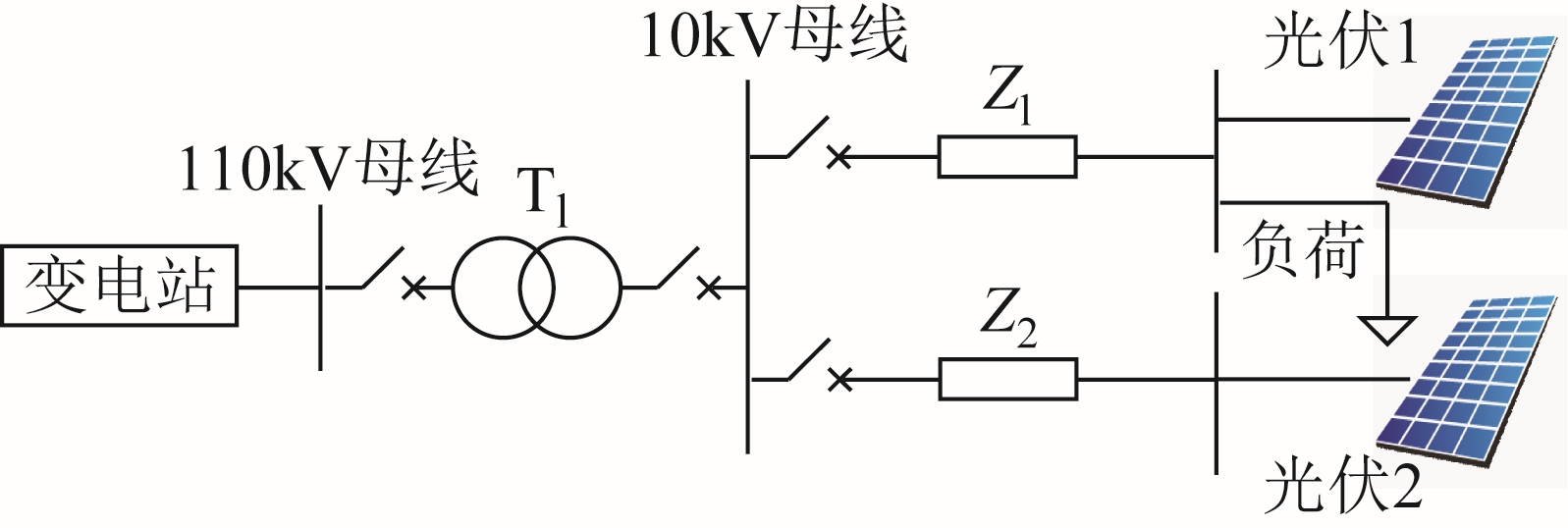
图8 含光伏发电的配电网馈线拓扑结构
Fig.8 Topology of distribution network feeder with photovoltaic power generations
为不失一般性，可认为每条线路故障率与其长度呈正比，且某条线路上各点发生故障的概率相同，即服从[0,1]的均匀分布。考虑到故障主要有三相短路、两相短路、两相接地短路、单相接地短路四种类型，需要对配电网故障情况进行统计分析，获取各种类型故障的发生概率，实际中较难得到真实数据，故假设电网中各类故障发生概率与文献[21]相同。故障持续时间与继电保护装置类型及动作时间有关，本文假定故障持续时间服从期望为0.18s、标准差为0.06s 的正态分布，且故障过渡阻抗服从期望为5Ω、标准差为1Ω 的正态分布[21]。
蒙特卡洛法可用于处理多维复杂系统的随机问题[21]，将不确定因素进行随机抽样，获取随机变量的值再进行迭代计算。本文基于蒙特卡洛模拟对电力系统短路电流进行概率评估，通过随机抽样的方法，以电网故障条件的不确定性抽样下光伏发电出现脱网事件的频率估计其概率，进而计算电网故障时光伏发电注入的短路电流概率分布及其期望值。同时结合光伏发电短路电流特性、低电压脱网概率模型以及故障信息等不确定性因素进一步对短路电流进行概率评估，具体流程如图9 所示。
图9 短路电流概率评估流程
Fig.9 Flow chart of short-circuit current probability assessment
计算流程主要按以下几个步骤进行：
1）设置抽样次数。
2）根据故障事件的分布特征，对故障线路、故障位置、故障类型、故障持续时间等故障信息进行第n 次随机抽样。
3）根据步骤2）中故障信息的抽样值计算系统中各节点的电压跌落值，并结合文中第1 节对光伏发电短路电流特性的分析，由其端电压跌落值确定在第n次抽样中光伏不脱网运行时能输出的短路电流Ipvn。
4）结合文中第2 节光伏低电压脱网概率模型，由端电压跌落程度和故障持续时间确定在第n 次抽样中光伏发电的脱网概率Ppvn，进而计算出光伏发电短路电流的期望值(1-Ppvn)Ipvn。
5）将期望值(1-Ppvn)Ipvn 代入短路计算程序，重新计算出故障点短路电流。
6）检验n 是否达到抽样次数，若未达到，则返回步骤2），进行第n+1 次抽样；若已经达到，则将n 次抽样得到的全部结果汇总，由此获得系统短路电流的概率分布图。
4 算例分析
本文以福建某地区配电网实际网架结构参数为例，在Matlab/Simulink 中搭建仿真模型，并采用本文方法获取光伏发电并网下电网的短路电流概率分布。由于通常忽略负荷对短路电流计算的影响，因此以下算例均在短路前空载条件下进行计算和仿真。
算例中各个光伏发电均由500kW 光伏发电机组组成，其中单台机组额定电压为315V，功率因数为1，机组参数见表1。其控制器均采用GB/T32826-2016 规定的低电压穿越控制及保护环节，电网故障时逆变器直流电压保持恒定，单台光伏逆变器输出电流上限为1.5 倍额定电流。考虑到实际运行中光伏发电出力随光照波动变化，仿真中选择正常运行和故障后所有光伏发电输入的光照强度均为1kW/m2，输入的环境温度为30℃，光伏发电的出力主要由光照强度决定。
表1 光伏发电机组基本参数
Tab.1 Basic parameters of photovoltaic power generations
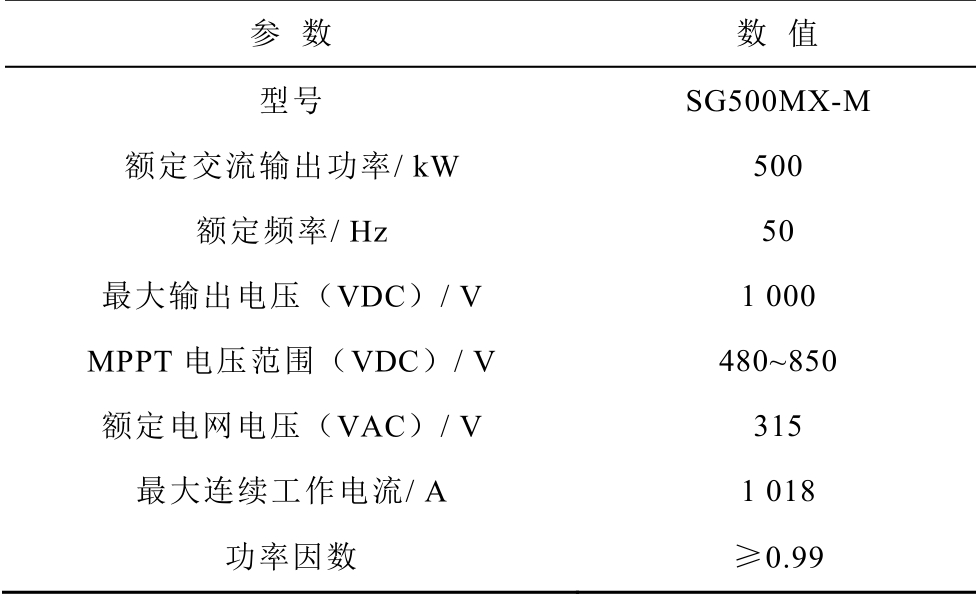
参 数 数 值 型号 SG500MX-M 额定交流输出功率/ kW 500 额定频率/ Hz 50 最大输出电压（VDC）/ V 1 000 MPPT 电压范围（VDC）/ V 480～850 额定电网电压（VAC）/ V 315 最大连续工作电流/ A 1 018 功率因数 ≥0.99
4.1 13 节点算例
福建某地区10kV 馈线网络结构如图10 所示，其中11、12、13、10 节点分别接入0.5MW、1MW、0.5MW、1.5MW 的光伏发电，通过Matlab/Simulink对线路进行故障仿真。
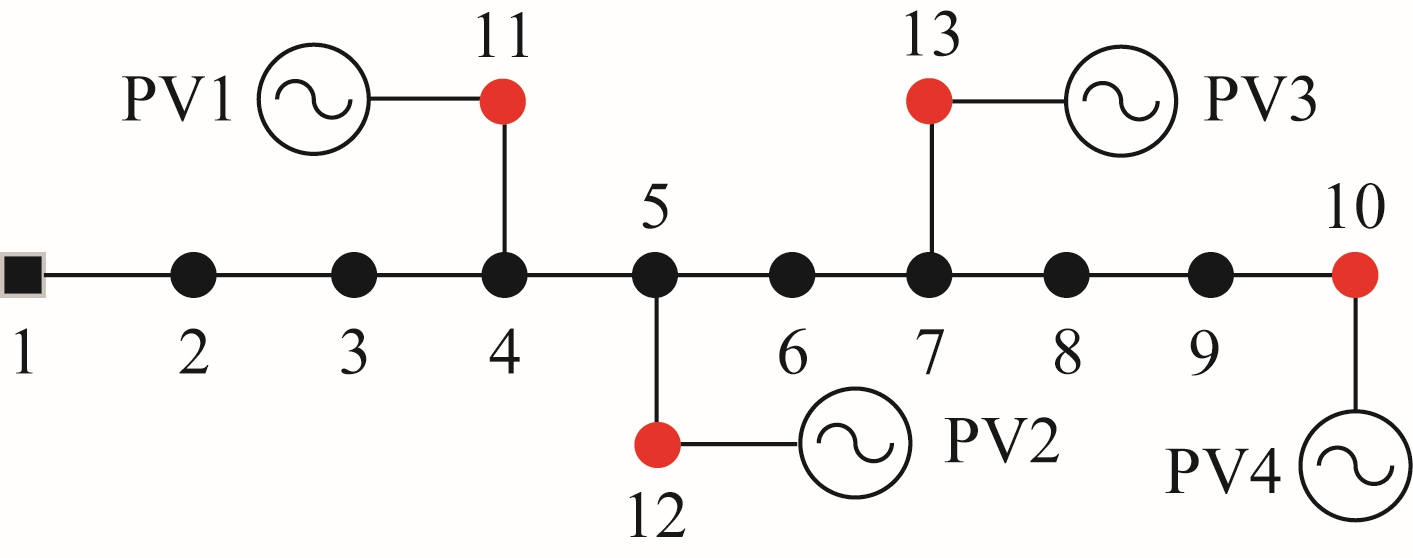
图10 13 节点网络结构
Fig.10 Network structure with 13 nodes
首先求解光伏发电的脱网概率模型，为计算简便，本文假设所有光伏发电在低电压穿越能力测试中Umin、Umax 和tmax 分别为0.1(pu)、0.3(pu)和0.2s，根据式（3）～式（6）确定概率密度函数中的参数，即 2σ =0.033，光伏发电低电压脱网概率模型为
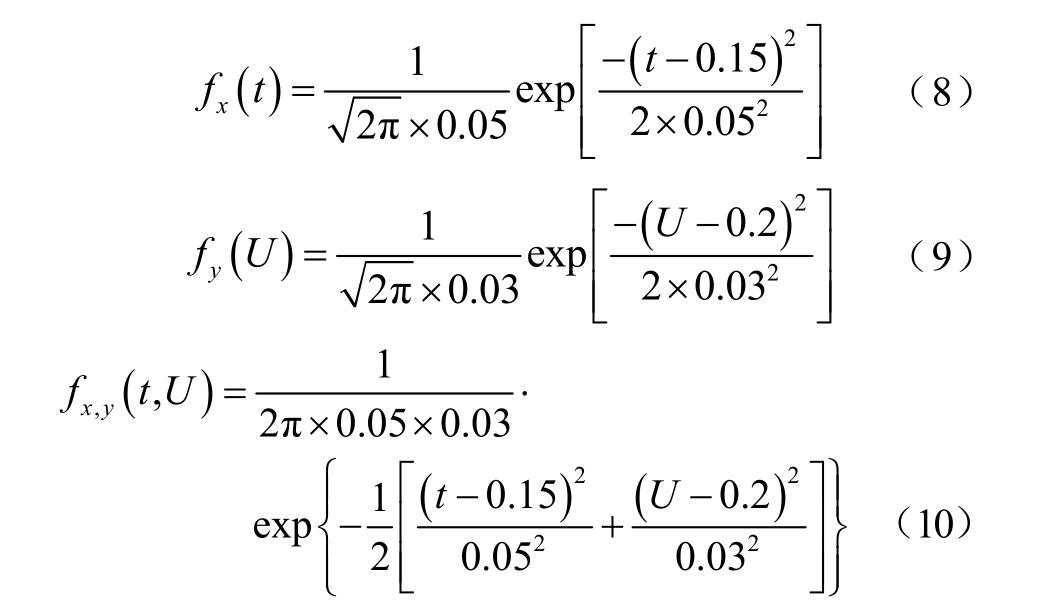
本文采用蒙特卡洛模拟进行随机抽样，根据每次抽样结果获得电网故障条件，再计算每次抽样条件下电网中各节点的电压大小，以得到不同节点的电压暂降值。本文算例中设置抽样次数为1000，利用这1 000 次抽样下的电压暂降数据可绘制光伏发电并网点电压直方图，以表示各节点电压跌落程度的概率分布。其中光伏并网点（即节点11、12、13、10）电压跌落情况如图11 所示。由图可知，4 个光伏发电端电压跌落至 0.5(pu)以下时出现的概率较大，部分光伏发电可能面临脱网，将对系统短路电流产生影响，因此有必要结合电压跌落时间，对系统短路电流进行概率评估。
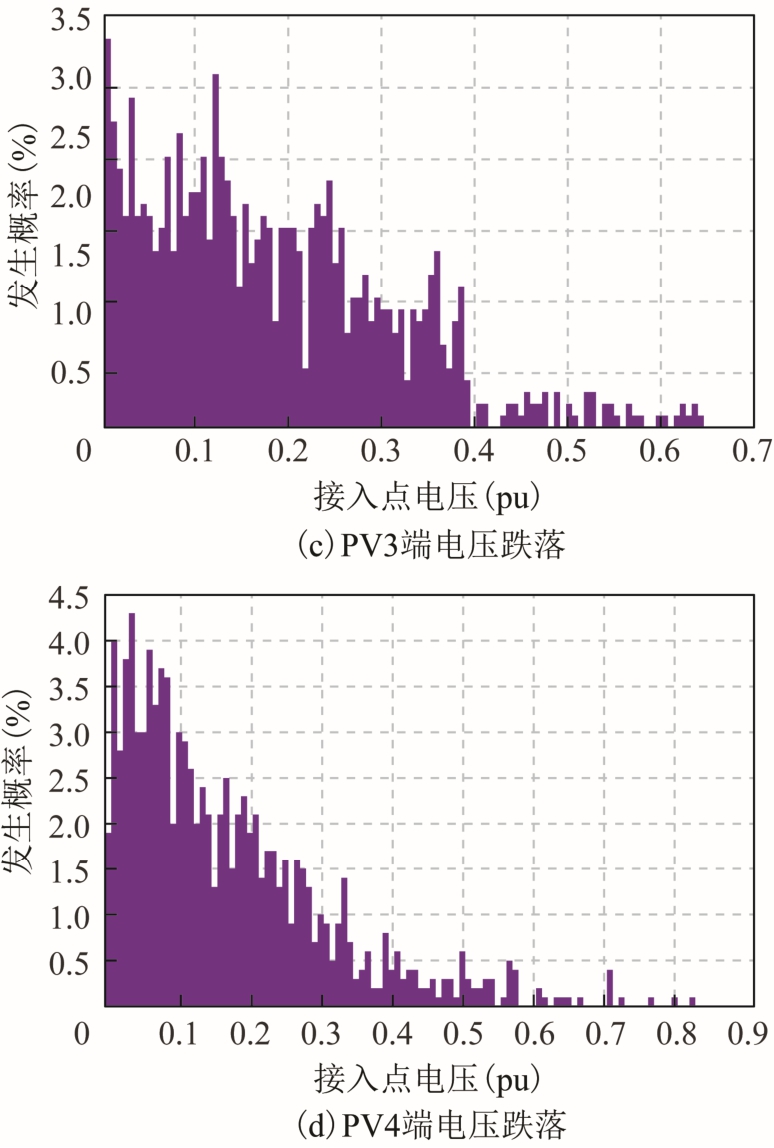
图11 光伏并网点电压跌落程度的概率分布
Fig.11 Probability distribution of voltage sag at gridconnected point of photovoltaic power generations
将每次抽样计算所得光伏端电压跌落值以及随机生成的故障持续时间代入其低电压脱网概率模型，可计算出各光伏的脱网概率Ppv，进而得到此特定条件下光伏发电输出电流的期望值(1-Ppv)Ipv。图12 显示了1 000 次抽样后系统中各光伏发电短路电 流期望值的概率分布结果。
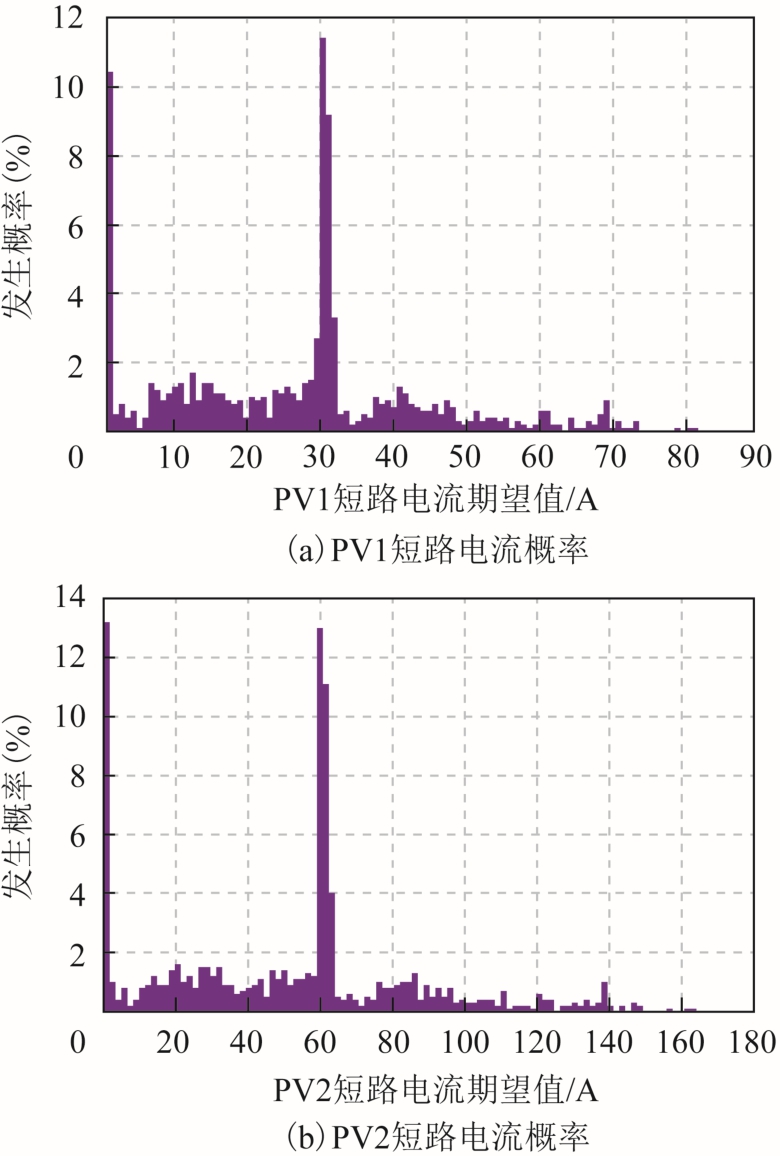
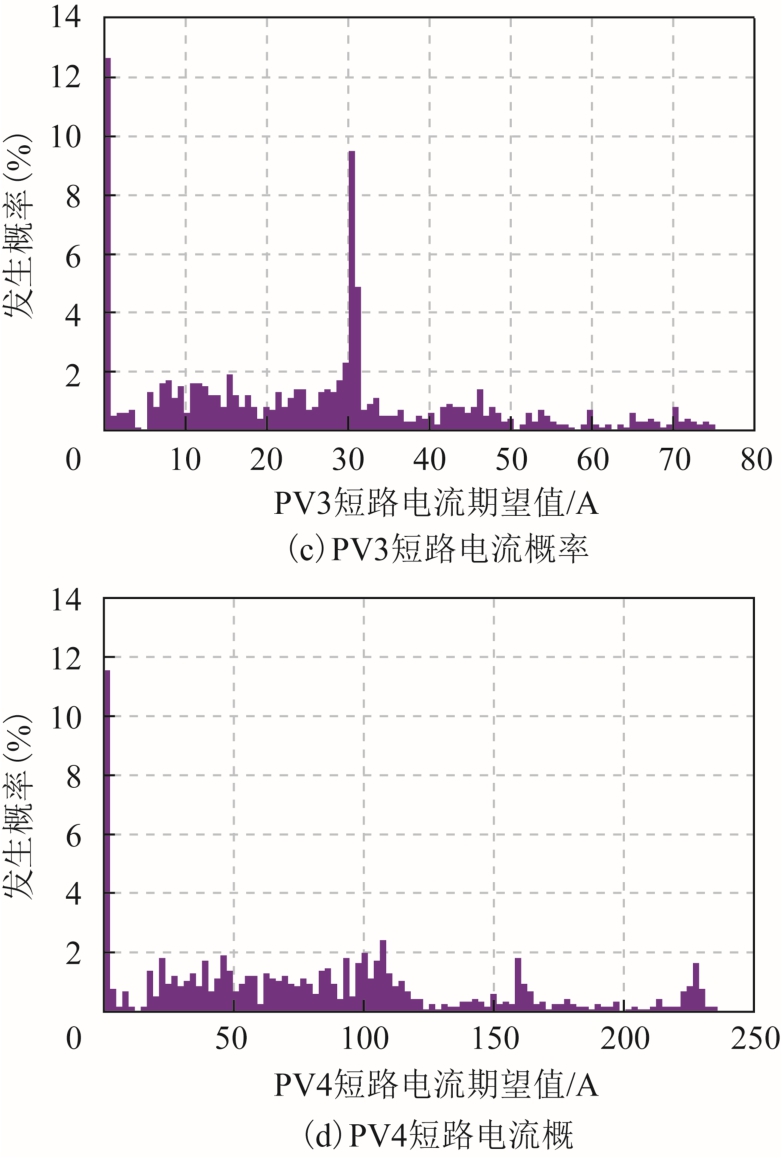
图12 光伏短路电流期望值的概率分布
Fig.12 Probability distribution of expected value of shortcircuit current of photovoltaic power generations
由图12 可以看出，各光伏发电短路电流期望值为0 这一事件发生概率较高，其中以光伏PV4 最为显著。由此说明实际运行中，光伏在故障期间极有可能面临脱网且输出电流为0，从而将影响对故障点短路电流的准确评估。因此需结合光伏实际脱网情况完善其电流输出结果，从客观角度更真实地反映光伏发电在电网故障期间的运行状态。此外光伏PV1、PV3 和PV2 短路电流期望值在30A 和60A 处的概率也呈现较高趋势，并且电流大小与其容量大小呈正相关，其中光伏PV2 的容量为PV1 和PV3的两倍，故短路电流也为两倍。
每次抽样将各光伏发电短路电流期望值代入短路计算程序，获取故障点以及流经各个节点的短路电流，1 000 次后所得短路电流概率分布情况如图13 和图14 所示。由图13 可知，光伏未接入区域整体较光伏接入区域偏左，说明光伏的接入将在一定程度上提高系统的短路水平。
当光伏接入时，故障点短路电流最大可接近7kA，但短路电流出现在0.5～1kA 区间的概率更大，这是由于系统发生单相故障的概率远远大于其他故障类型，而单相故障产生的短路电流最小。根据图13中概率分布情况可对系统电气设备进行合理的配 置，如确定系统断路器开断容量等。
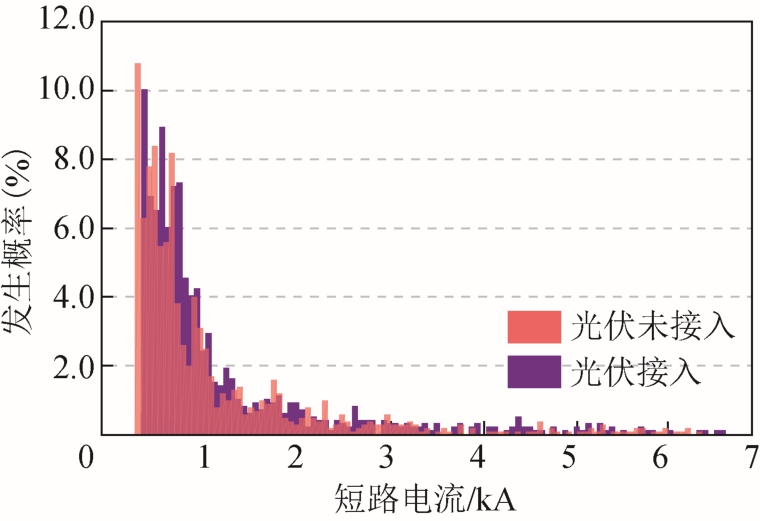
图13 故障点短路电流概率分布
Fig.13 Probability distribution of short-circuit current at fault points
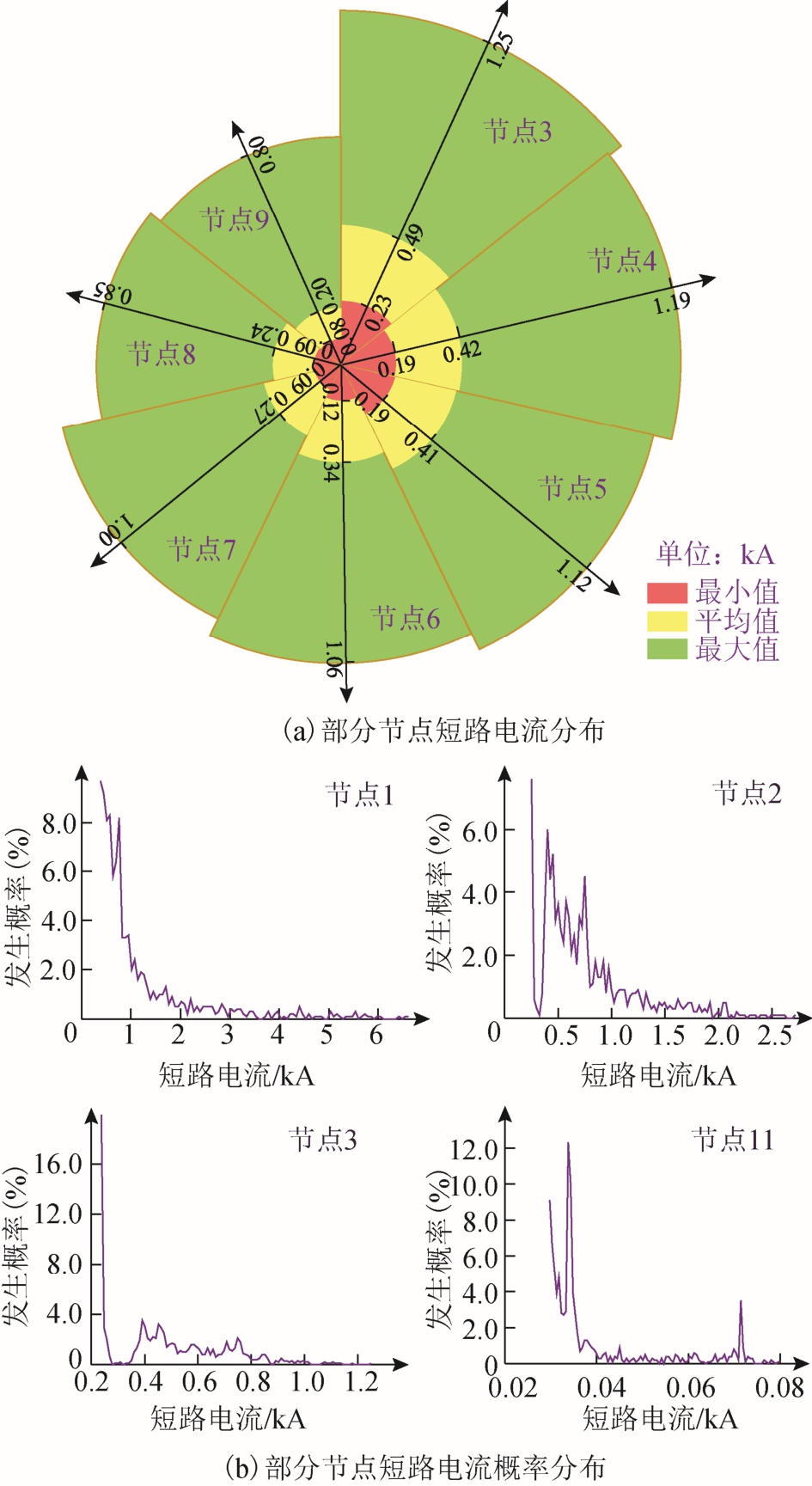
图14 部分节点短路电流分布情况
Fig.14 Distribution of short-circuit current at some nodes
在1 000 次抽样计算中，流经系统其余部分节点的短路电流统计结果如图14 所示。图14a 中每个 扇形区域对应一个节点的短路电流结果，扇形半径长度表示电流值大小；图14b 中列出流经节点1、节点2、节点3、节点11 的短路电流概率分布。由图可知，越靠近常规电源，流经该节点的短路电流越大，由于常规电源的短路容量远大于光伏发电，对短路电流的大小起主导作用。
4.2 50 节点算例
福建某地区10kV 馈线网络结构如图15 所示，其中空心圆节点为光伏发电接入点，光伏最小接入容量为0.5MW，最大为1.5MW。同样地，利用文中第3 节的方法对该网络进行1 000 次抽样仿真，获取系统短路电流概率分布，图16 和图17分别为故障点和流经其他节点的短路电流概率分布结果。
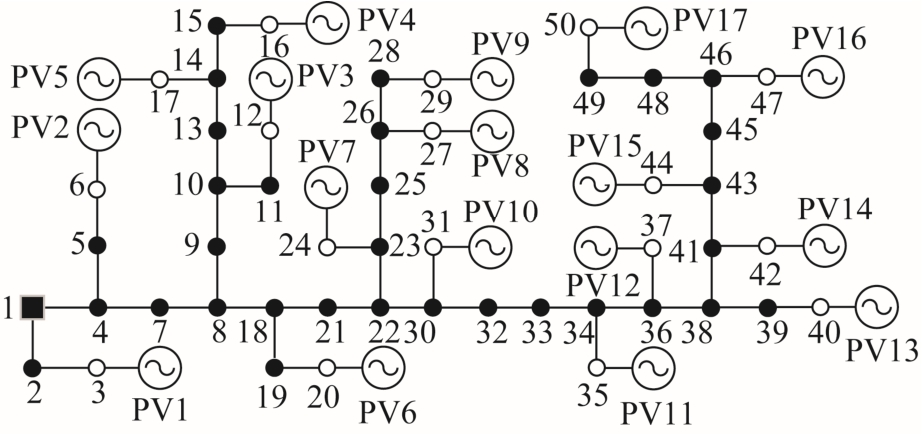
图15 50 节点网络结构
Fig.15 Network structure with 50 nodes
图16 故障点短路电流概率分布情况
Fig.16 Probability distribution of short-circuit current at fault points
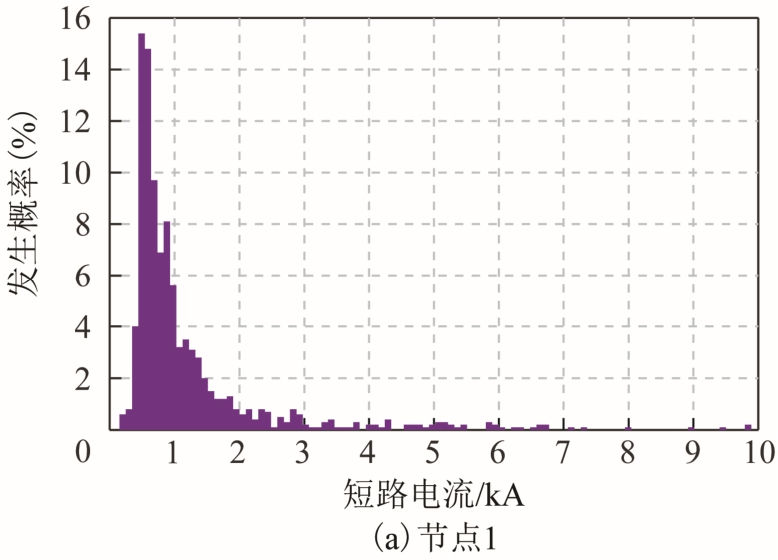
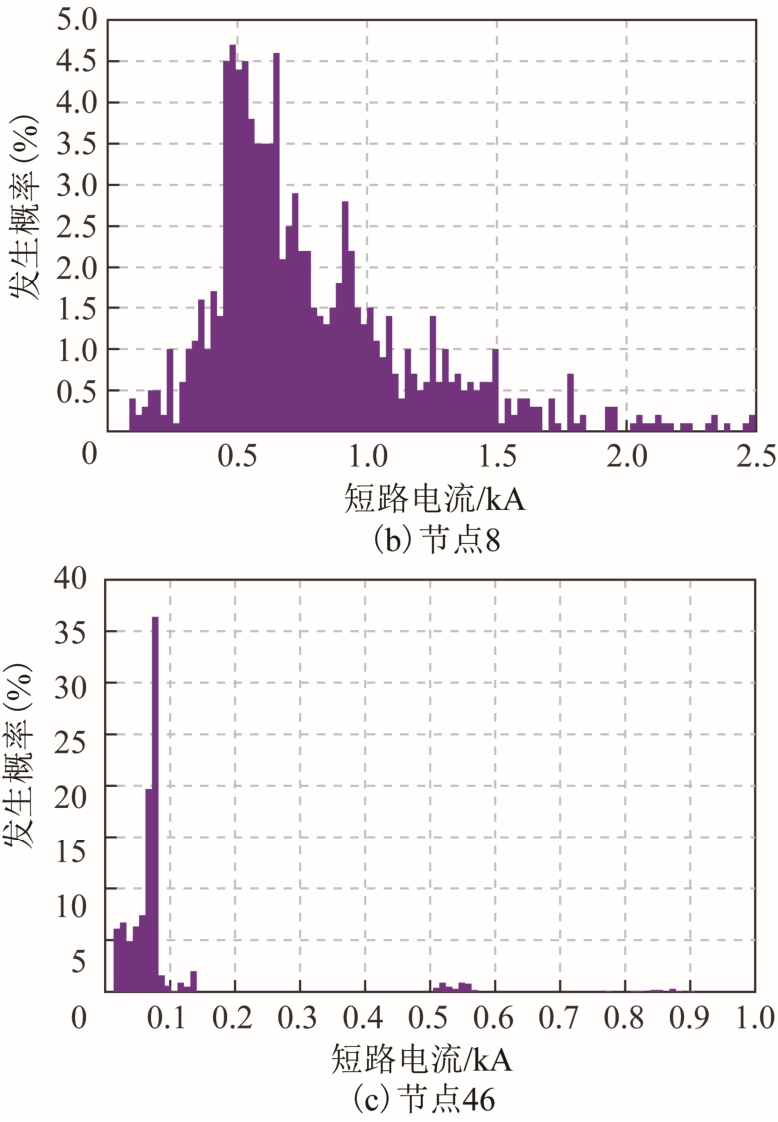
图17 部分节点短路电流概率分布情况
Fig.17 Probability distribution of short-circuit current at some nodes
由图16 可知，光伏发电并网将在一定程度上提高系统的短路水平，且该网络较13 节点网络中的光伏并网数量有所增加，因此对故障点短路电流影响更大。
综合对比图16 和图17 可知，由于故障点的短路电流由系统侧常规电源和各光伏发电共同提供，因此短路电流最大；而节点1～节点46 所承受的最大短路电流和最大概率短路电流均呈减小趋势，由于系统侧常规电源提供的短路电流远大于光伏发电，可认为节点距离常规电源越近，所承受的短路电流将会越大。
此外由图17 可知，各节点短路电流的概率分布各不相同，其中节点1 与节点46 概率分布比较集中，而节点8 的短路电流分布相对分散。这与系统整体拓扑结构有关，节点1 位于网络首端，与常规电源相连，节点46 处于网络末端，相邻节点有并网光伏，两者受常规电源或光伏发电的影响相对单一，短路电流分布也更集中。而图15 中节点8 处于网络中部，且连接支线较多，受常规电源与各光伏发电的共同影响，因此短路电流的分布更加分散。
为说明本文方法的正确性，收集了该配电系统变电站（即节点1）的历史短路电流数据共53 组，对其进行处理并绘制成直方图，与本文仿真结果进行对比，具体如图18 所示。由于获取的录波数据有限，且本文仿真设置的故障条件与该电网实际情况有所出入，故两者并未完全重合，但由图可知，两者的变化趋势大致相同，由此说明本文方法所得结果具有一定的正确性与参考性。
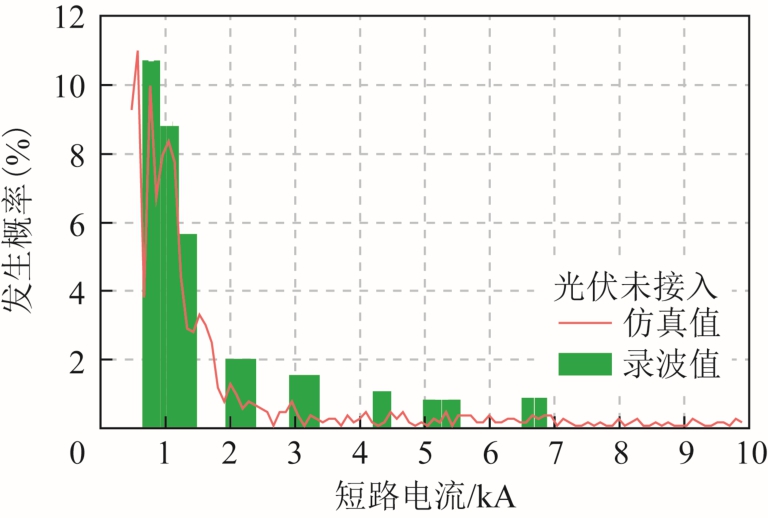
图18 节点1 仿真结果与录波数据统计结果对比
Fig.18 Comparison between simulation results and statistical results of recorded wave data at node 1
5 结论
本文分析在不同端电压跌落下，光伏发电并网运行时的故障电流特性，考虑低电压穿越能力的不确定性建立光伏低电压脱网随机评估模型，同时结合系统故障信息进一步提出计及低电压穿越不确定性的系统短路电流概率评估方法。从概率角度揭示了光伏发电脱网对系统短路电流的影响，与人为特定条件下的精确计算方法相比，本文方法既可评估系统最大短路电流，又可获取最大概率电流以及系统短路电流的概率区间，对系统电气设备的合理配置有一定参考价值。
[1] 孙玲玲, 赵美超, 王宁, 等. 基于电压偏差机会约束的分布式光伏发电准入容量研究[J]. 电工技术学报, 2018, 33(7)： 1560-1569. Sun Lingling, Zhao Meichao, Wang Ning, et al. Research of permitted capacity of distributed photovoltaic generation based on voltage deviation chance constrained[J]. Transactions of China Electrotechnical Society, 2018, 33(7)： 1560-1569.
[2] 贾科, 顾晨杰, 毕天姝, 等. 大型光伏电站汇集系统的故障特性及其线路保护[J]. 电工技术学报, 2017, 32(9)： 189-198. Jia Ke, Gu Chenjie, Bi Tianshu, et al. Fault characteristics and line protection within the collection system of a large-scale photovoltaic power plant[J]. Transactions of China Electrotechnical Society, 2017, 32(9)： 189-198.
[3] 范士雄, 蒲天骄, 刘广一, 等. 主动配电网中分布式发电系统接入技术及其进展[J]. 电工技术学报, 2016, 31(增刊2)： 92-101. Fan Shixiong, Pu Tianjiao, Liu Guangyi, et al. Technologies and its trends of grid integration of distributed generation in active distribution network[J]. Transactions of China Electrotechnical Society, 2016, 31(S2)： 92-101.
[4] 中国国家标准化管理委员会. 光伏发电站接入电力系统技术规定： GB 19964-2012[S]. 2012.
[5] 马静, 刘青, 吴佳芳, 等. 高比例变流型电源并网的输电系统三相短路电流计算[J]. 电力系统自动化, 2019, 43(5)： 83-91. Ma Jing, Liu Qing, Wu Jiafang, et al. Three-phase short-circuit current calculation for power transmission system with high penetration of converter-type sources[J]. Automation of Electric Power Systems, 2019,43(5)： 83-91.
[6] Hooshyar H, Baran M E. Fault analysis on distribution feeders with high penetration of PV systems[J]. IEEE Transactions on Power System, 2013, 28(3)： 2890-2896.
[7] 葛路明, 曲立楠, 陈宁, 等. 光伏逆变器的低电压穿越特性分析与参数测试方法[J]. 电力系统自动化, 2018, 42(18)： 149-156. Ge Luming, Qu Linan, Chen Ning, et al. Characteristic analysis of low voltage ride-through and parameter test method for photovoltaic inverter[J]. Automation of Electric Power Systems, 2018, 42(18)： 149-156.
[8] 孔祥平, 袁宇波, 黄浩声, 等. 光伏电源故障电流的暂态特征及其影响因素[J]. 电网技术, 2015, 39(9)： 2444-2449. Kong Xiangping, Yuan Yubo, Huang Haosheng, et al. Fault current transient features and its related impact factors of PV generator[J]. Power System Technology, 2015, 39(9)： 2444-2449.
[9] 刘素梅, 毕天姝, 王晓阳, 等. 具有不对称故障穿越能力逆变型新能源电源故障电流特性[J]. 电力系统自动化, 2016, 40(3)： 66-73. Liu Sumei, Bi Tianshu, Wang Xiaoyang, et al. Fault current characteristics of inverter interfaced renewable energy generators with asymmetrical fault ride-through capability[J]. Automation of Electric Power Systems, 2016, 40(3)： 66-73.
[10] 周念成, 叶玲, 王强钢, 等. 含负序电流注入的逆变型分布式电源电网不对称短路计算[J].中国电机工程学报, 2013, 33(36)： 41-49. Zhou Niancheng, Ye Ling, Wang Qianggang, et al. Asymmetric short-circuit current calculation for inverter interfaced distributed generators with negative sequence current injection integrated in power systems[J]. Proceedings of the CSEE, 2013, 33(36)： 41-49.
[11] Plet C A, Green T C. Fault response of inverter interfaced distributed generators in grid-connected applications[J]. Electric Power Systems Research, 2014, 106(1)： 21-28.
[12] 杨杉, 同向前. 含低电压穿越型分布式电源配电网的短路电流计算方法[J]. 电力系统自动化, 2016, 40(11)： 93-95. Yang Shan, Tong Xiangqian. Short-circuit current calculation of distribution network containing distributed generators with capability of low voltage ride through[J]. Automation of Electric Power Systems, 2016, 40(11) ： 93-95.
[13] 杨杉, 同向前, 刘健, 等. 含分布式电源配电网的短路电流计算方法研究[J]. 电网技术, 2015, 39(7)： 1977-1982. Yang Shan, Tong Xiangqian, Liu Jian, et al. Shortcircuit current calculation of distribution network with distributed generation[J]. Power System Technology, 2015, 39(7)： 1977-1982.
[14] 王守相, 江兴月, 王成山. 含分布式电源的配电网故障分析叠加法[J]. 电力系统自动化, 2008, 32(5)： 38-42. Wang Shouxiang, Jiang Xingyue, Wang Chengshan. A superposition method of fault analysis for distribution systems containing distributed generations[J]. Automation of Electric Power Systems, 2008, 32(5)： 38-42.
[15] 漆汉宏, 王晓娜, 魏艳君, 等. 消除有功振荡的改进低电压穿越方法[J]. 电工技术学报, 2014, 29(增刊1)： 416-423. Qi Hanhong, Wang Xiaona, Wei Yanjun, et al. An improved LVRT method for eliminating active oscillation[J]. Transactions of China Electrotechnical Society, 2014, 29(S1)： 416-423.
[16] 贾利虎, 朱永强, 孙小燕, 等. 基于模型电流预测控制的光伏电站低电压穿越控制方法[J]. 电力系统自动化, 2015, 39(7)： 68-74. Jia Lihu, Zhu Yongqiang, Sun Xiaoyan, et al. A control method of low voltage ride through for photovoltaic plant based on model current predictive control[J]. Automation of Electric Power Systems, 2015, 39(7)： 68-74.
[17] 刘美茵, 黄晶生, 张军军, 等. 基于BDEW 标准的光伏并网逆变器模型验证及误差分析[J]. 电力系统自动化, 2014, 38(13)： 196-201. Liu Meiyin, Huang Jingsheng, Zhang Junjun, et al. Model validation and error analysis of photovoltaic grid-connected inverter based on BDEW standard[J]. Automation of Electric Power Systems, 2014, 38(13)： 196-201.
[18] 王定国, 陈卓, 姚为正, 等. 光伏并网逆变器低电压穿越检测方案分析[J]. 电力系统保护与控制, 2014, 42(12)： 143-147. Wang Dingguo, Chen Zhuo, Yao Weizheng, et al. Analysis of grid-connected PV inverter low voltage ride through testing scheme[J]. Power System Protection and Control, 2014, 42(12)： 143-147.
[19] 焦龙. 新能源场站涉网性能验证试验研究[D]. 北京： 华北电力大学, 2016.
[20] 方家琨, 苗璐, 文劲宇, 等. 含风电-SMES 的电力系统暂态稳定概率评估[J]. 电力系统保护与控制, 2013, 41(1)： 176-182. Fang Jiakun, Miao Lu, Wen Jinyu, et al. Transient stability probability evaluation of power system incorporating with wind farm and SMES[J]. Power System Protection and Control, 2013, 41(1)： 176-182.
[21] 贾东梨, 刘科研, 盛万兴, 等. 有源配电网故障场景下的电压暂降仿真与评估方法研究[J]. 中国电机工程学报, 2016, 36(5)： 1279-1288. Jia Dongli, Liu Keyan, Sheng Wanxing, et al. Voltage sag simulation and evaluation in active distribution network with fault cases[J]. Proceedings of the CSEE, 2016, 36(5)： 1279-1288.
[22] 蒲天骄, 赵灿, 陈乃仕, 等. 基于D-S 理论的主动配电网不确定性潮流及运行风险分析[J]. 电力系统自动化, 2016, 40(12)： 53-61. Pu Tianjiao, Zhao Can, Chen Naishi, et al. D-S theory based uncertainty flow calculation and operational risk analysis for active distribution network[J]. Automation of Electric Power Systems, 2016, 40(12)： 53-61.
[23] 中国国家标准化管理委员会. GB/T32826-2016 光伏发电系统建模导则[S]. 2016.
[24] 周泽昕, 马世英, 汤涌, 等. 电力系统稳定计算中500kV 线路故障清除时间的研究[J]. 中国电力, 2002(2)： 47-51. Zhou Zexin, Ma Shiying, Tang Yong, et al. Study on fault clearing time of 500kV transmission line used in power system stability calculation[J]. Electric Power, 2002(2)： 47-51.
[25] 光伏发电站低电压穿越检测技术规程： Q/GDW 1926-2013 [S].
[26] 刘旭娜, 肖先勇, 汪颖. 电压暂降严重程度及其测度、不确定性评估方法[J]. 中国电机工程学报, 2014, 34(4)： 644-658. Liu Xuna, Xiao Xianyong, Wang Ying. Voltage sag severity and its measure and uncertainty evaluation[J]. Proceedings of the CSEE, 2014, 34(4)： 644-658.