0 引言
暂态失稳事故是破坏电力系统稳定运行,造成电网经济损失的主要原因之一[1]。如果调度控制中心在暂态故障清除后不能快速评估系统稳定程度,并针对失稳系统及时采取控制措施,故障将影响电网中的相邻区域,导致连锁故障发生,甚至演变为大规模停电事故[2-3]。工作人员根据经验判断系统稳定性并通过查询决策表完成控制的方式,需要较长操作时间,已经不能满足电网发展需求[4]。精准的紧急控制策略成为防止暂态事故扩大的前提[5],而暂态稳定性快速量化评估是最优紧急控制的基础。因此,研究快速精准的暂态稳定性量化分析方法具有重要现实意义。
暂态稳定评估是电力系统安全稳定分析的重要组成部分[6-7]。暂态稳定的主要分析方法包括时域仿真法[8]、直接法[9]和人工智能方法[10]。其中,时域仿真法通过求解微分代数方程组,确定状态量的变化曲线,稳定判定依赖于人工经验,缺少机理性和控制相关的有效信息,因此多被用作离线检验系统稳定性的方法[11]。随着数据挖掘技术的兴起,基于深度学习的人工智能算法被广泛应用于电力系统稳定性的在线预测,但是,该方法在建立量化分析准则时往往十分困难。快速的量化方法是精准有效地实现暂态稳定控制的先决条件,直接法通过建立辅助函数判断系统稳定性,不仅避免了大量的迭代计算,还可以求出系统的稳定裕度,量化分析电力系统的暂态稳定性。
故障因素与暂态稳定裕度息息相关[12],保护动作信息包含故障类型、故障位置以及故障持续时间等有效信息,综合考虑保护动作信息,可以使暂态稳定分析结果更加快速、准确。目前,计及故障因素的暂态稳定量化分析方法主要包括概率稳定分析方法[13-15]、能量函数法及基于扩展等面积法(Extended Equal-Area Criterion, EEAC)的暂态稳定裕度计算方法等。概率稳定分析方法将故障因素考虑成随机概率事件,通过计算稳定裕度的概率分布分析系统稳定性。该方法主要基于蒙特卡洛法,计算量偏大[16],并且在实际应用中工作人员根据计算得到的系统失稳概率,往往不能直观判断暂态稳定性。如果将网络拓扑结构简化成单机无穷大母线形式,则能量函数法和EEAC 方法具有相同的判稳机理[17]。文献[18-19]研究了不同故障持续时间对系统稳定性的影响。文献[20]根据EEAC 理论推导了两机系统暂态稳定裕度表达式,同时分析了不同故障位置下系统的稳定裕度。基于EEAC 的方法计算简单[21],求出的稳定裕度可以直接判断系统的稳定情况。但是,目前的研究多围绕三相短路展开分析,据电力系统的实际运行数据显示,三相短路故障在所有发生的故障类型中占比只有2%[22]。如果稳定评估和紧急控制过程均以三相故障为基础进行分析,结果将会过于保守,过度控制将给电网带来不必要的损失。因此,分析不对称短路下故障因素对稳定裕度的影响具有重要意义。
本文提出一种计及保护信息的暂态稳定裕度解析算法。首先,计算不对称短路情况下的附加阻抗,并对多机系统网络模型进行化简。在网络简化模型的基础上,根据等面积准则建立暂态稳定裕度指标。然后,提出聚合功角的分段模型,进一步推导得到暂态稳定裕度的解析表达式,分析不对称短路下故障位置和故障持续时间对稳定裕度的影响。最后,在四机系统和新英格兰系统中进行仿真分析,证明本文提出方法的有效性。
1 不对称故障模型
1.1 系统等效聚合模型
多机系统的发电机转子运动方程为
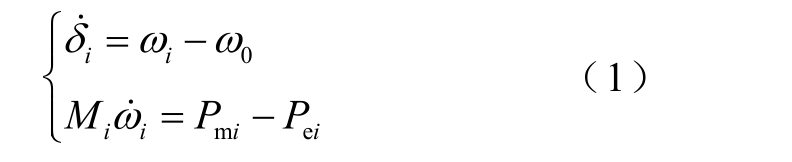
式中, miP 和 eiP 分别为第i 台发电机的机械功率和电磁功率,i=1,2,…,NG; iM 为转动惯量; iδ 和 iω 分别为发电机的功角和角速度。根据 CCCOI-RM[23]相关理论,当系统发生故障时,发电机会根据受到影响程度的不同分成主导失稳的临界机群和角度偏差较小的剩余机群,两个机群分别用“K”群和“T-K”群表示。计算两机群惯性中心,可以将式(1)转子运动方程聚合成两机系统形式
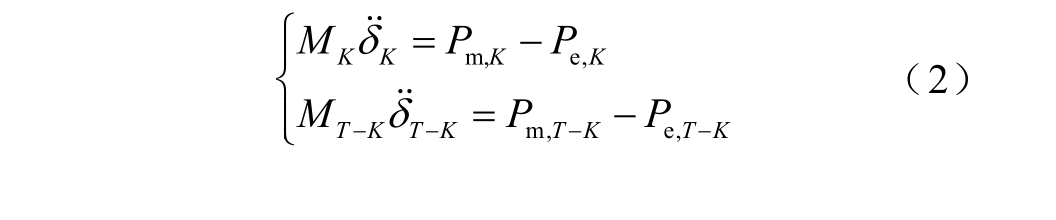
其中
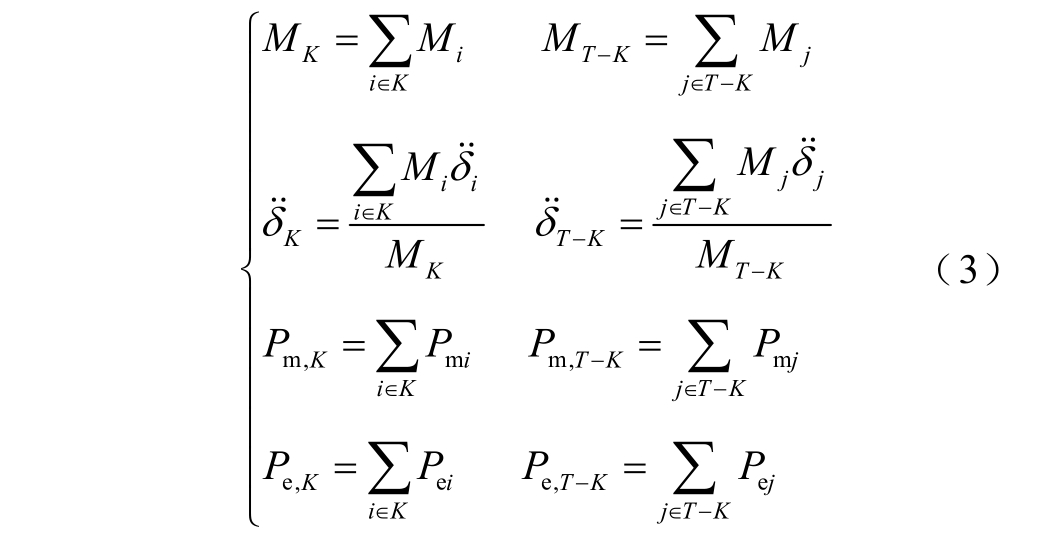
式(2)所示运动方程更侧重于定性分析发电机互补群之间的相对摇摆,为了定量分析系统稳定性,需要将式(2)等效成单机无穷大母线形式。本文在聚合过程中,假设系统故障后分为理想的两群,“K”群各发电机功角全部用“K”群的惯性中心功角代替,“T-K”群各发电机功角全部用“T-K”群的惯性中心功角代替。可以得到等效单机无穷大母线形式的转子运动方程为
其中

式中,Pmax 为等效单机无穷大系统发电机电磁功率峰值;γ为等效单机无穷大系统发电机功角偏移量;Pc 为等效单机无穷大系统发电机机械功率偏移量;Ei 为第i 台发电机的内电势;Gij、Bij 分别为只考虑发电机内节点的节点导纳矩阵的实部和虚部。
1.2 不对称短路附加阻抗
当线路r-j 发生故障时,考虑故障点f 的节点阻抗矩阵为
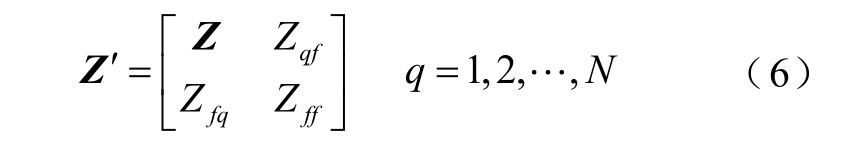
式中,Z 为未发生故障时的N 维节点阻抗矩阵,新增非对角元素 qfZ 和 fqZ 互为转置,可以通过推导求出。
式中,α 为故障位置距离线路首段的百分比。 新增对角元素为

式中,zL 为故障线路r-j 的阻抗。
在故障后已知负序网络和零序网络的情况下,根据式(6)~式(8)可以计算出负序阻抗矩阵和零序阻抗矩阵。假设仅在故障点注入单位电流,全网的电流表示为 I ′,根据式(9)可以分别计算出负序和零序网络的节点电压。
负序网络和零序网络的故障点电压在数值上分别等于系统的负序阻抗 2z 和零序阻抗 0z 。结合正序等效定则,不对称短路的附加阻抗z∆可以表示为
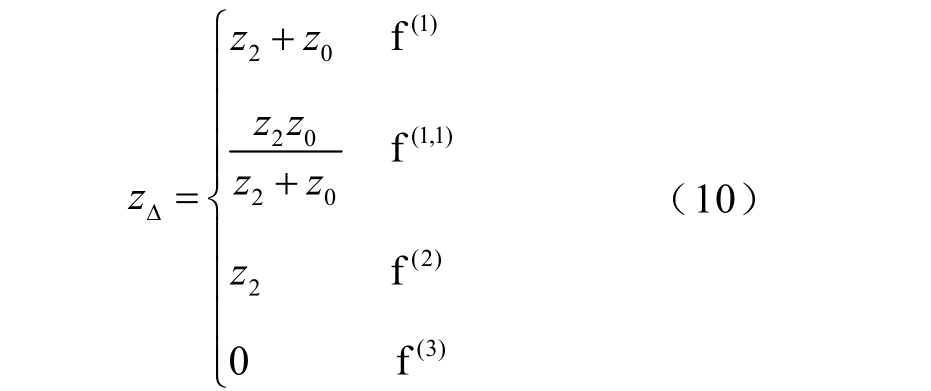
式中, f (1)、 f (1,1)、 f (2)和 f (3)分别表示网络发生单相短路、两相接地短路、两相相间短路和三相短路。
将节点导纳矩阵写成紧凑形式为
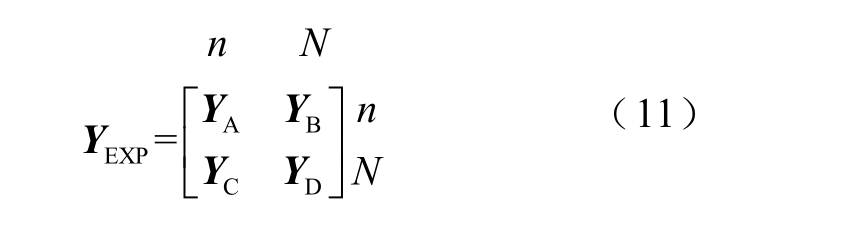
式中,YEXP 为考虑发电机内节点的拓展节点导纳矩阵; AY 为发电机内阻抗矩阵;YB 为考虑发电机内节点的拓展导纳矩阵非对角块,YB=[-YA 0];YC 为考虑发电机内节点的拓展导纳矩阵非对角块,YC=[-YA 0]T; DY 为计及发电机内阻抗、负荷等效阻抗和短路附加阻抗的节点导纳矩阵。则收缩导纳矩阵可以表示为
式中,Yred 为只含发电机内节点的收缩导纳矩阵。
2 故障后系统暂态稳定裕度分析
2.1 暂态稳定裕度的解析表达式
研究大扰动下系统的暂态稳定性问题,本质上就是研究扰动过程中系统内部积攒的能量是否可以在故障清除后完全转换和消耗。当系统严格等值成单机无穷大系统后,可以使用等面积法代替分析系统内部能量的变化。将减速面积和加速面积的差值定义为暂态稳定裕度指标
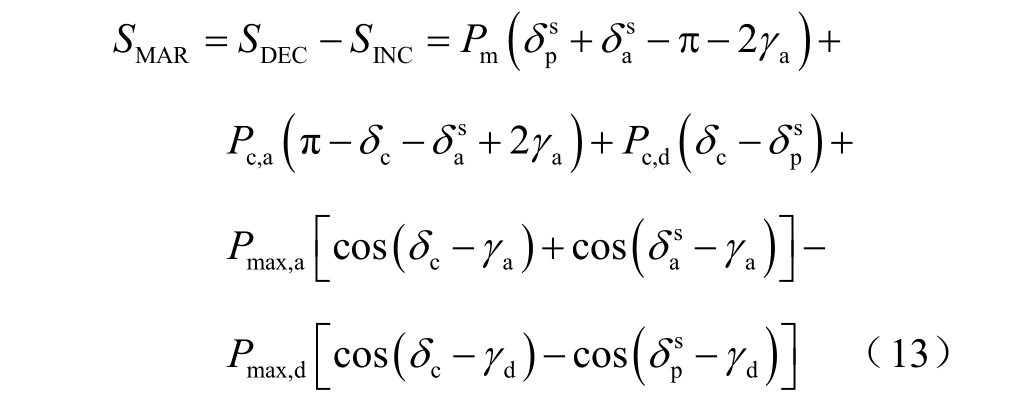
式中,下标p、d、a 分别表示故障前、故障中和故障后;δps和 δ as分别为故障前和故障后的稳定平衡点;cδ 为故障清除角。
2.2 等效功角的分段模型
对于式(4)所示的发电机摇摆方程,含有非线性成分sin(δ γ-) ,无法直接求解。本文采取分段线性处理的方法,将sin(δ γ-) 分解成多段线性函数,这样式(4)就退化成二阶线性微分方程。在下面的推导过程中使用δ′代替δ γ- 。对于每一段线性函数
式中,下标n 代表第n 段线性函数的参数值;kn 和bn 可以根据最小二乘拟合求出。用不同的线性函数代替不同区间的sinδ′后,式(4)可以简化为
求解功角过程如下。
1)计算发电机功角初始值,并确定相应区间对应的线性函数。
根据式(15)求出发电机功角为
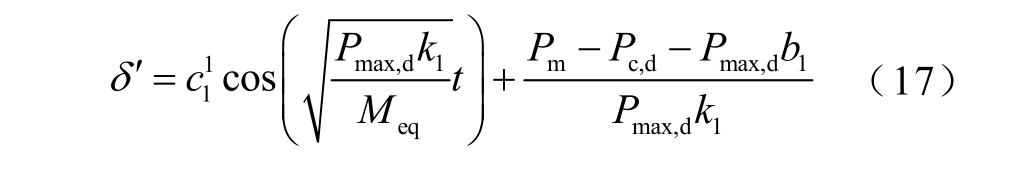
通过式(17)求出区间末端的功角变化率
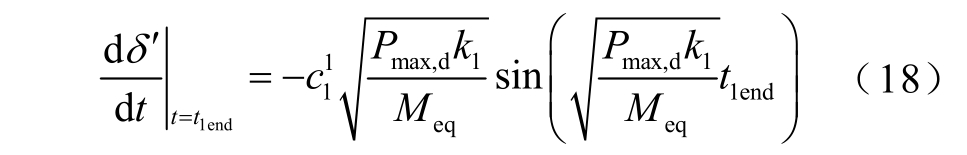
2)根据区间1 末端对应的功角变化率和时间可
以求出区间2 的功角表达式为
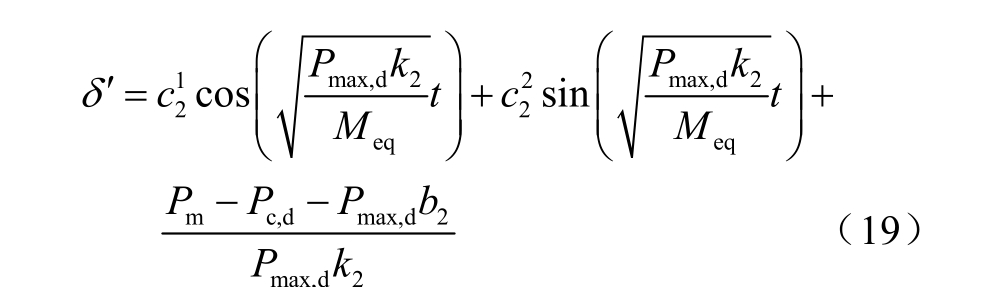
其中,c 1 2和 c2 2可以通过式(20)和式(21)进行求解。

3)重复步骤2)可以求出故障持续过程中的功角表达式。
4)故障清除后,根据网络模型修改参数,重复步骤1)~步骤3),可以求出故障后功角表达式。
故障清除角表达式可以表示为
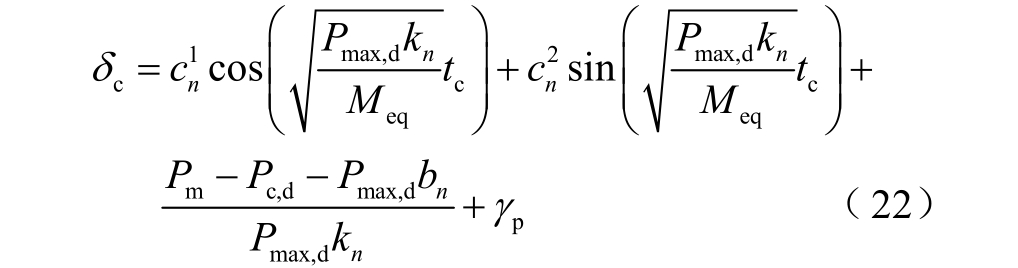
将等效发电机的故障清除角和对应参数代入式(13)可以求出系统稳定裕度。通过求取稳定裕度对各个变量的偏导数可以分析稳定裕度随各变量的变化趋势。
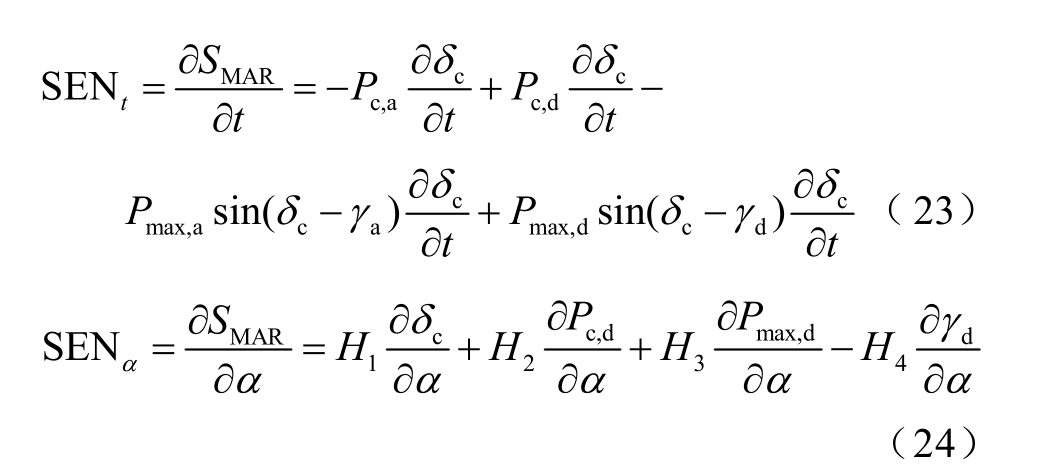
其中
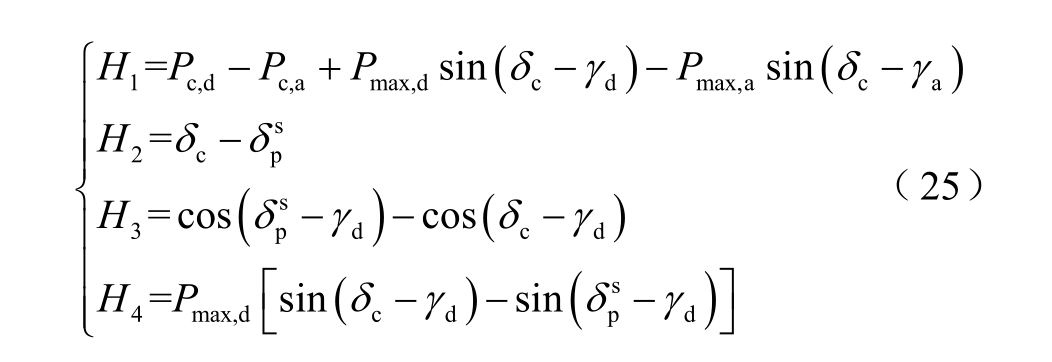
式中,SENt 为暂态稳定裕度对时间的灵敏度;SENα为暂态稳定裕度对故障位置的灵敏度。
根据式(5)可以得到

2.3 暂态稳定评估过程
继电保护系统对电力系统稳定运行起着至关重要的作用。电力系统中配置的计算机监控系统,通过GOOSE 实现保护信息的传输,GOOSE 报文在传输过程中使用专用传输通道[24-25],优先级高,传输延时一般不超过20ms[26],同时抗干扰能力强,可以有效避免传输通道阻塞造成的数据传输延时和数据缺失,保证保护信息的传输效率。充分利用量测数据与故障评估信息,可以更加快速准确地完成电力系统的稳定性评估。本文利用含故障位置以及故障持续时间的解析表达式,实现电力系统暂态稳定评估的流程如图1 所示。首先,通过获取的保护信息确定电网结构,求取网络简化模型。然后,使用2.1 节和2.2节中方法求出稳定裕度解析表达式,结合保护系统评估故障信息,在线确定电力系统的暂态稳定裕度。
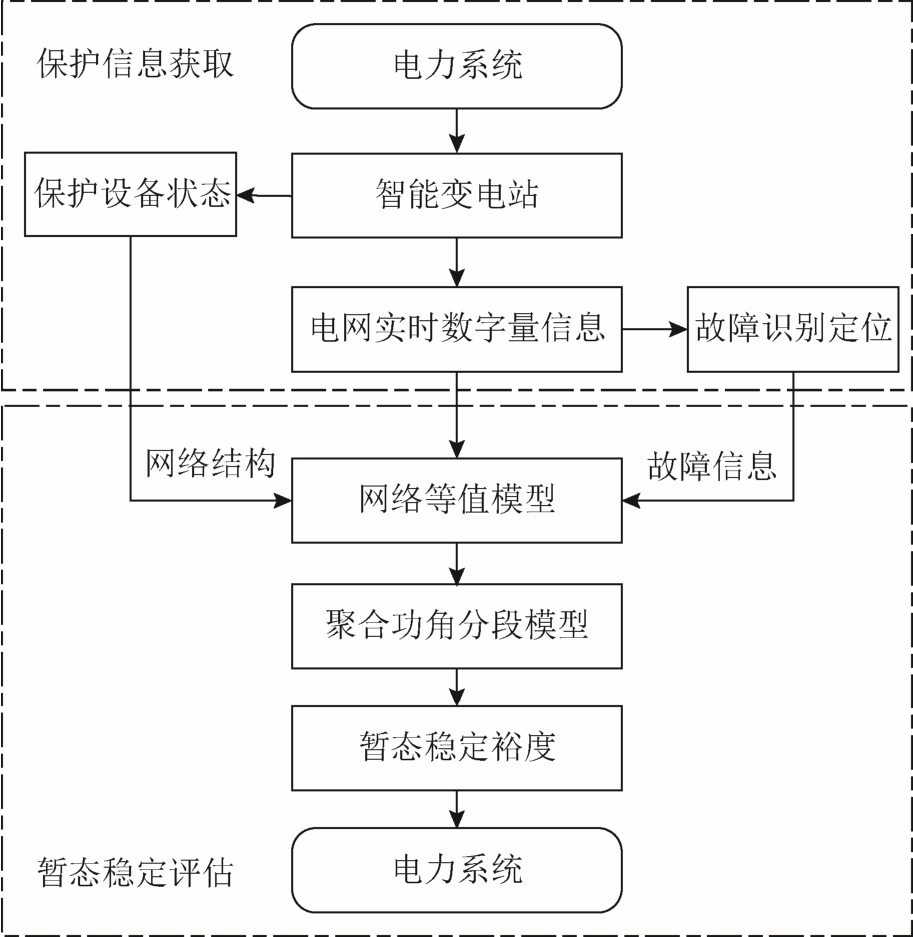
图1 暂态稳定评估流程
Fig.1 Flowchart of transient stability assessment
3 仿真结果与分析
3.1 四机系统仿真算例
采用四机两区系统作为测试系统,如图2 所示。线路8-9 中点在0.2s 设置两相接地故障,0.35s 将故障清除。该运行条件下的时域仿真曲线如图3 所示,各发电机的功角在故障清除后保持同步增长,系统稳运行。
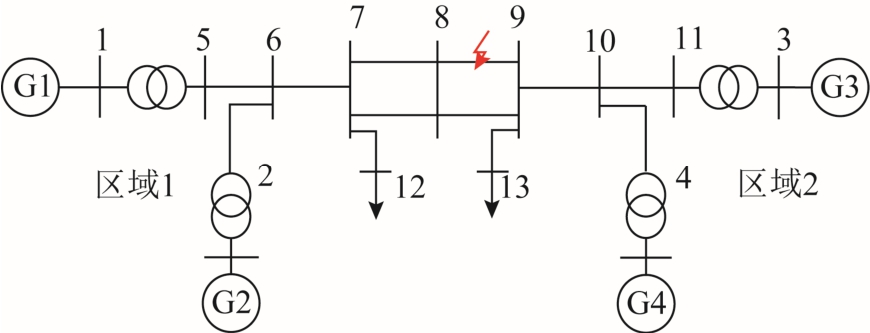
图2 四机两区系统
Fig.2 Four-machine two-area system
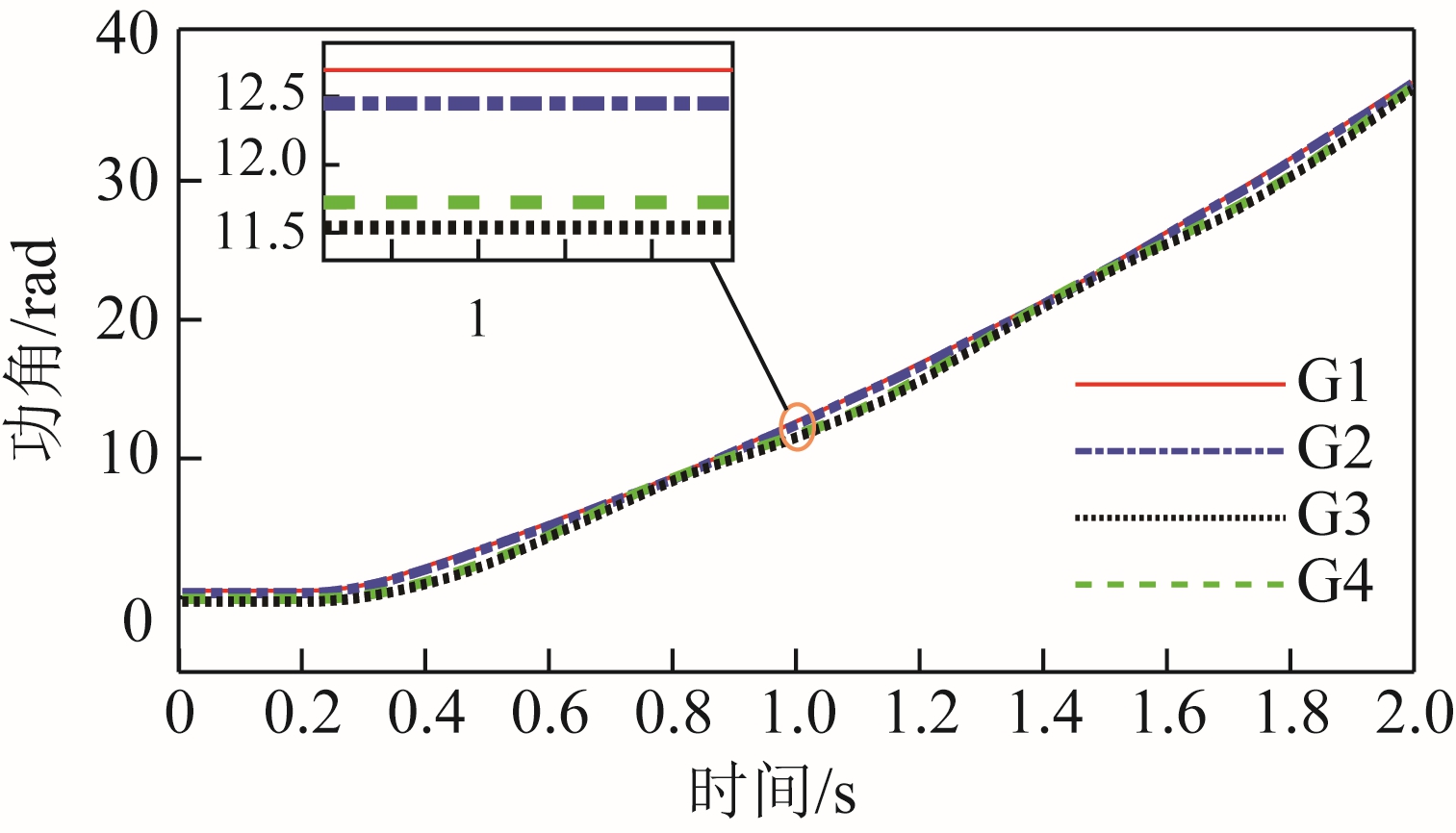
图3 0.35s 清除故障后的发电机转子摇摆曲线
Fig.3 Rotor swing curves of generators after clearing fault at 0.35s
为了分析聚合后的功角偏差,分别采用如下三种方法求取等效单机无穷大母线(One-Machine Infinite-Bus, OMIB)系统的功角曲线:
1)通过时域仿真求出每台发电机的功角,然后通过式(3)和式(5)对功角进行聚合,求出等效OMIB 系统的功角变化曲线。
2)采用1.1 节中聚合条件对多机系统进行等值,然后根据式(4)表示的等效OMIB 系统进行非线性仿真,求出功角变化曲线。
3)在方法2 中所述等值的基础上,直接采用2.2 节中方法对功角进行解析计算,求出一定范围内的功角变化曲线。
方法1 和方法2 均基于改进欧拉法迭代求解,方法3 则基于解析计算,三种方法的结果如图4 所示。在故障后的功角摇摆过程中,本文提出的方法与两种通过非线性仿真得到的结果相当接近。
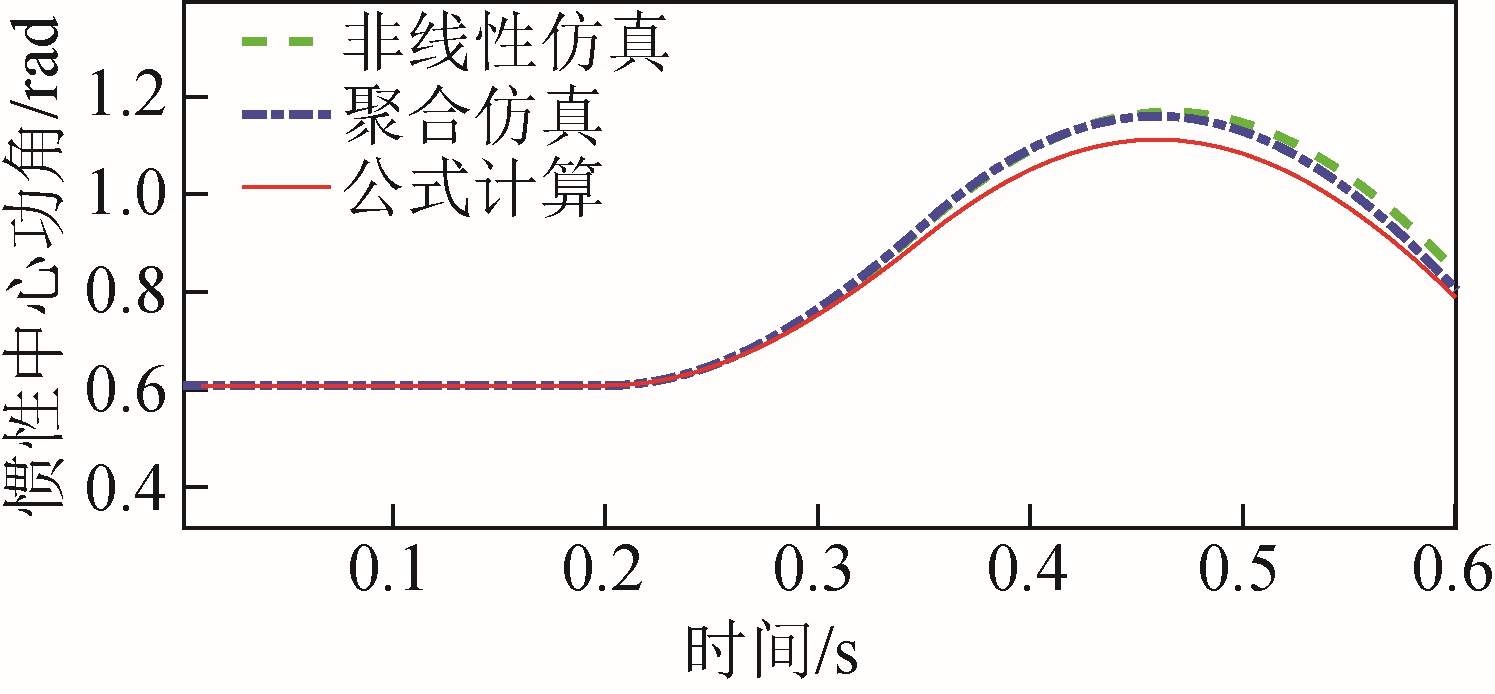
图4 故障后稳定运行的仿真结果
Fig.4 Simulation results under stable operation after fault
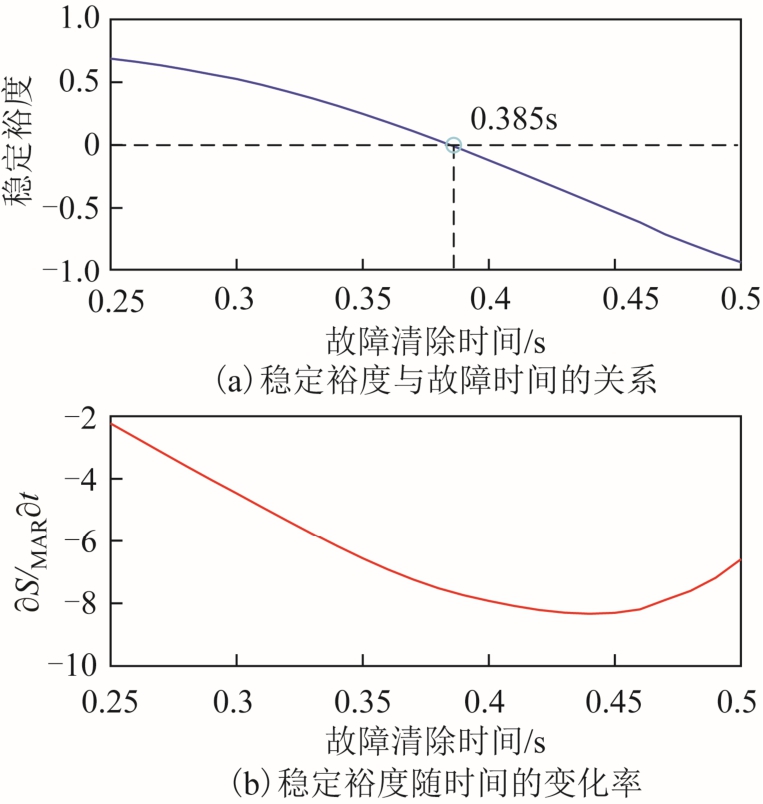
图5 稳定裕度随故障持续时间的变化关系
Fig.5 Relationship between stability margin and fault clearing time
线路8-9 距离首端60%处在0.2s 设置两相接地故障,故障清除时间在0.25~0.5s。根据式(13)和式(23)分别得到稳定裕度与故障时间的关系曲线如图5a 所示,稳定裕度随时间的变化率曲线如图5b所示。在仿真过程中稳定裕度对时间的偏导数恒小 于零,稳定裕度单调减小。在故障清除时间增加到0.385s 时,系统稳定裕度为零,说明系统处于临界稳定状态,通过时域仿真得到四机系统的功角变化曲线如图6 所示。图6a 表示故障清除时间为0.37s时的仿真曲线,从图中可以看出,故障清除后各发电机的功角保持同步增长,系统稳定运行。当故障清除时间增加到0.38s 时,仿真曲线如图6b 所示,发电机1、2 组成的超前群相对于发电机3、4 组成的机群摆开大,系统失稳。通过时域仿真得到的临界清除时间在0.37~0.38s,本文方法相比时域仿真法的误差为0.005~0.015s。
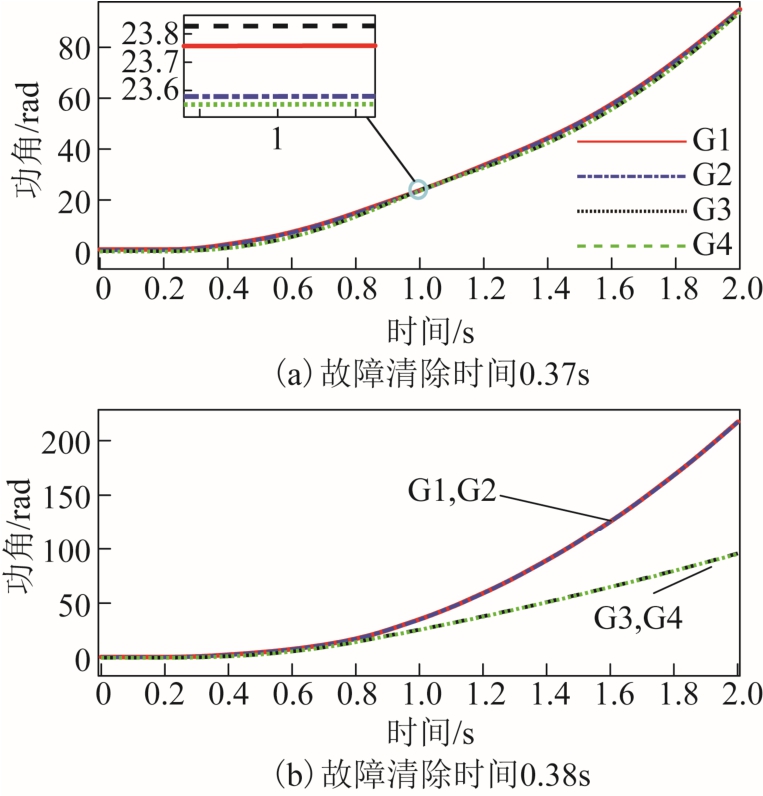
图6 不同故障清除时间下的发电机功角曲线
Fig.6 Rotor swing curves of generators after clearing fault at different times
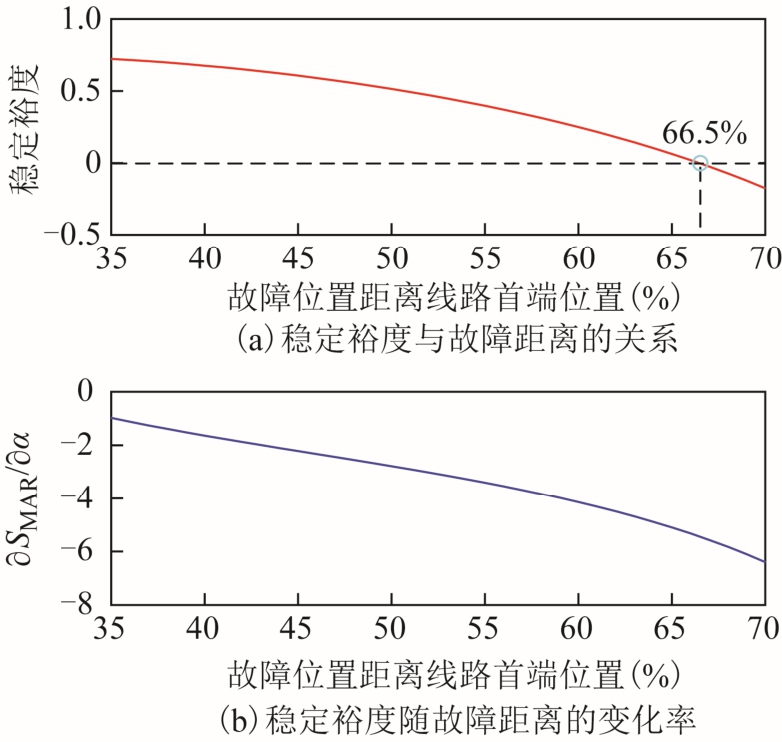
图7 稳定裕度随故障位置的变化关系
Fig.7 Relationship between stability margin and fault location
线路8-9 在0.2s 设置两相接地故障,0.35s 将故障清除,故障位置在距离线路首端35%~70%变化,得到稳定裕度随故障位置的变化关系如图7 所示。 随着故障位置距离线路首端距离的增加,稳定裕度持续减小并且呈现出凸状变化,与之对应,稳定裕度随故障位置的变化率为负并且在区间内单调减小。当故障位置达到线路的66.5%时,稳定裕度为零,系统处于稳定运行边界。通过时域仿真分别得到故障位置为64%和65%时的发电机功角曲线,如图8a 和8b 所示。当故障位置为64%时,发电机功角同步运行,系统稳定。故障位置为65%时,发电机功角摆开,系统失稳。在改变故障位置的情况下,本文方法相比时域仿真法的误差为1.5%~2.5%。

图8 不同故障位置下的发电机功角曲线
Fig.8 Rotor swing curves of generators after clearing fault at different locations
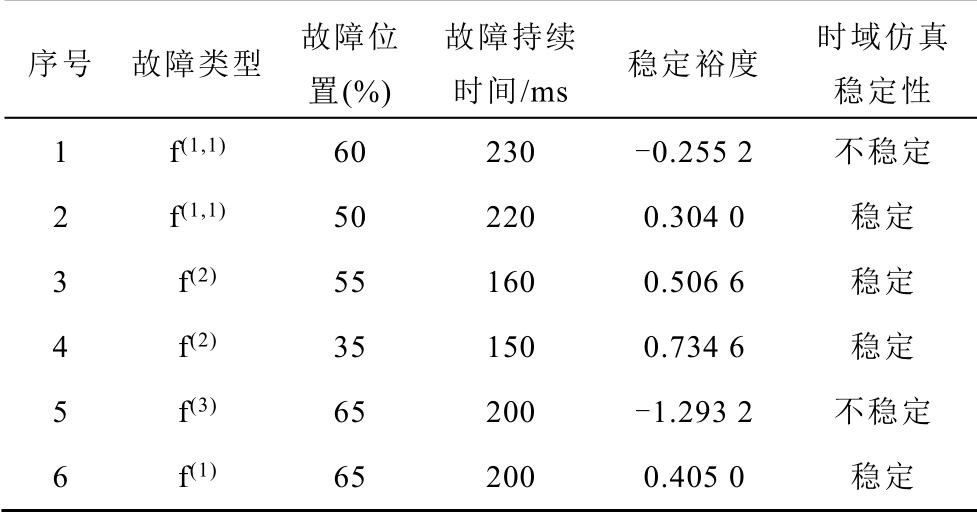
设置不同的故障位置,故障类型和故障持续时间,根据式(13)和式(22)可以求出系统的暂态稳定裕度,见表1。
表1 四机系统不同故障条件下的暂态稳定裕度
Tab.1 Transient stability margin under different fault conditions of four-machine system
序号 故障类型 故障位 置(%) 故障持续 时间/ms 稳定裕度 时域仿真稳定性 1 f(1,1) 60 230 -0.255 2 不稳定 2 f(1,1) 50 220 0.304 0 稳定 3 f(2) 55 160 0.506 6 稳定 4 f(2) 35 150 0.734 6 稳定 5 f(3) 65 200 -1.293 2 不稳定 6 f(1) 65 200 0.405 0 稳定
3.2 新英格兰系统仿真算例
采用新英格兰10 机39 节点系统作为测试系统,网架结构如图9 所示。
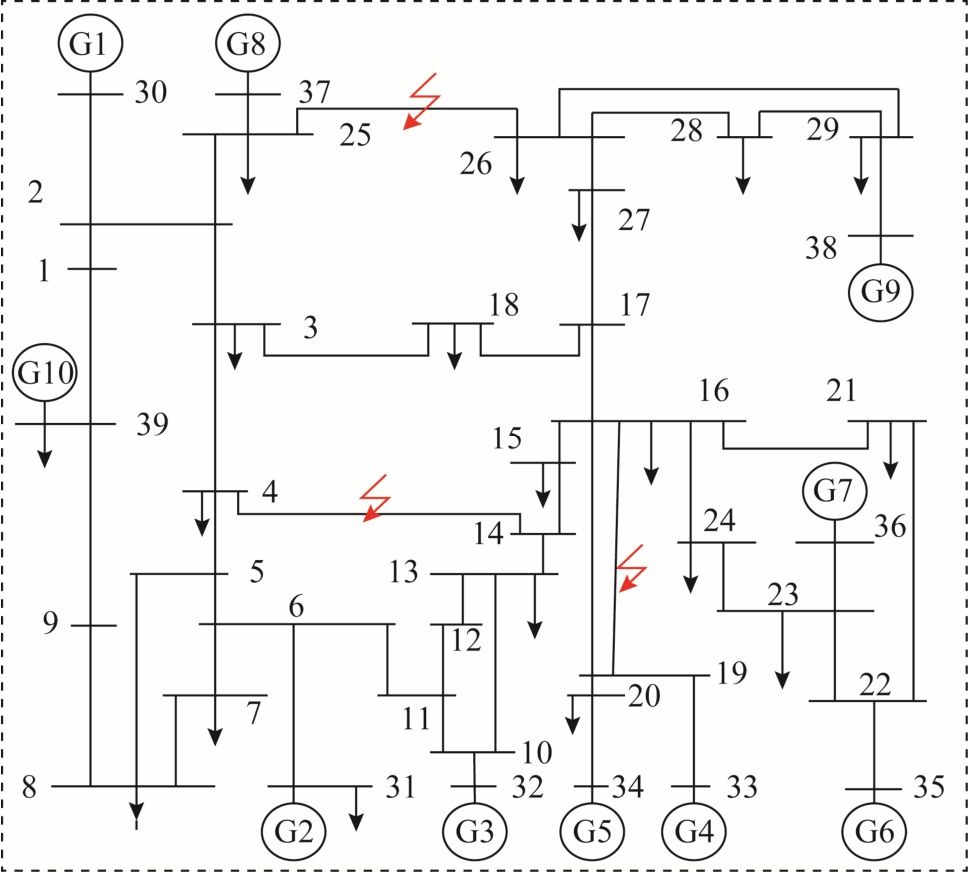
图9 新英格兰系统结构示意图
Fig.9 Configuration of New England power system
线路16-19 中点在0.5s 设置两相接地故障,0.8s将故障清除。通过3.1 节中所述三种方法求出的等值功角曲线如图10a 所示,时域仿真功角曲线如图10b 所示。故障清除后,以发电机4、5 组成的临界机群相对于其他发电机摆开,系统失稳。此时,由图10a 中的曲线可以看出,本文方法的计算结果与理论仿真结果非常接近。
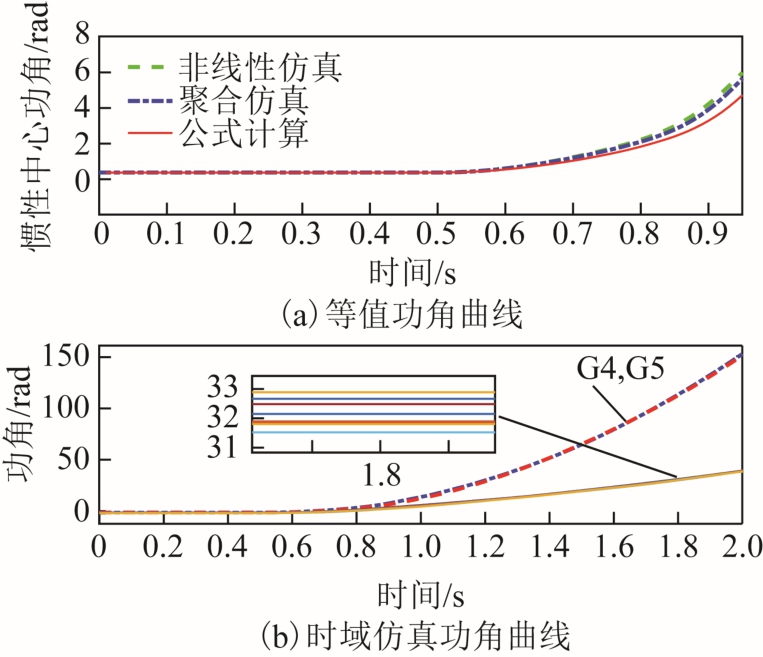
图10 故障后不稳定系统的仿真曲线
Fig.10 Simulation curves of unstable system after fault
本文利用含有故障位置和故障清除时间的解析表达式计算暂态稳定裕度,如果故障位置存在测量误差,暂态稳定裕度的计算结果将受到影响。故障位置量测误差对暂态稳定裕度的影响见表2。由表2 可知,故障位置无误差时,在线路16-19 中点在0.5s设置两相接地故障,使用本文提出的方法得到在故障清除时间为0.594s 时,暂态稳定裕度为0,系统处于临界稳定状态。使用时域仿真法,设置故障清除时间为0.58s 和0.59s,得到发电机功角曲线分别如图11a 和图11b 所示,系统的临界运行状态在0.58~0.59s 之间。因此,当故障位置无误差时,本文方法评估极限清除时间的误差在0.004~0.014s。
表2 故障位置量测误差对暂态稳定裕度的影响 Tab.2 Influence of fault location measurement error on transient stability margin
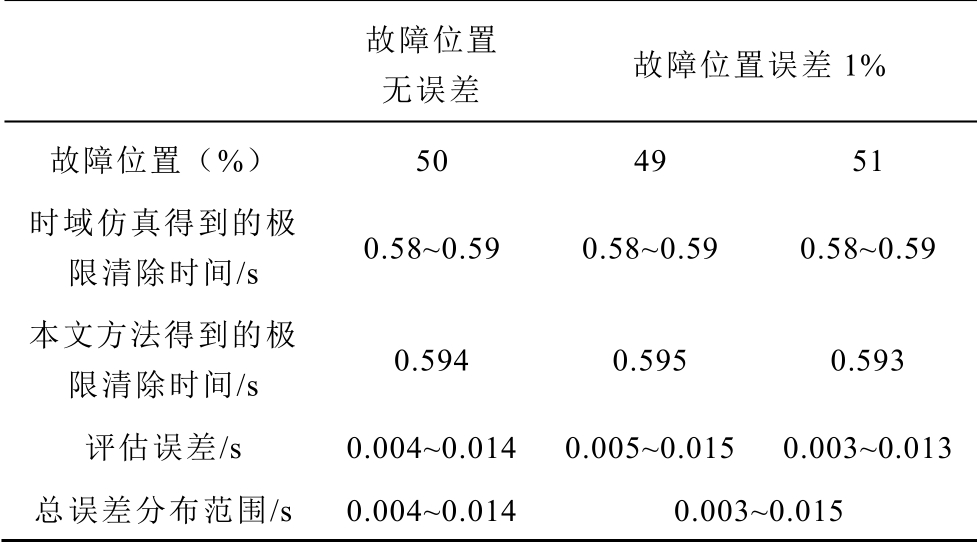
故障位置 无误差 故障位置误差1% 故障位置(%) 50 49 51 时域仿真得到的极限清除时间/s 0.58~0.59 0.58~0.59 0.58~0.59 本文方法得到的极限清除时间/s 0.594 0.595 0.593 评估误差/s 0.004~0.014 0.005~0.015 0.003~0.013总误差分布范围/s 0.004~0.014 0.003~0.015

图11 线路16-19 发生故障时的时域仿真曲线
Fig.11 Time domain simulation curves when the fault occurs on line 16-19
研究表明,故障位置的误差一般不超过1%[27-28],通过分析故障位置误差对本文方法的影响验证方法的有效性和准确性。假设线路16-19 中点发生故障,以故障位置距离线路首端49%、51%分别进行误差分析。当线路16-19 的49%处在t=0.5s 时发生两相接地故障时,使用本文方法得到的极限清除时间为0.595s,相比于时域仿真法的误差为0.005~0.015s;当线路16-19 的51%处在t=0.5s 发生两相接地故障时,使用本文方法得到的极限清除时间为0.593s,相比于时域仿真方法的误差为0.003~0.013s。综上所述,计及故障位置误差时,本文方法评估极限清除时间的误差在0.003~0.015s,可以看出,故障位置引起的误差对评估结果影响较小,在可接受范围内。
本文计及保护信息,针对不同故障类型,推导得到包含保护信息(故障类型、故障位置和故障持续时间)的暂态稳定裕度实用表达式。当系统中发生故障后,将保护系统提供的在线保护信息代入暂态稳定裕度实用表达式,直接得到故障后的暂态稳定裕度,有效避免时域仿真法求解微分代数方程的复杂计算过程。
在时域仿真过程中,当任意两台发电机功角差超过4π时,将系统的运行状态判定为失稳。若故障清除后2s 内发电机间的最大功角差仍未摆开超过4π,则认为系统稳定运行。以图11b 为例分析计算耗时,图中发电机4 和5 组成的临界机群相对于其他发电机摆开,当仿真时间达到1.2s 时,两机群间的最大功角超过4π。此时,使用Matlab R2016a 仿真耗时7.667s。在同样的故障条件下,使用本文提出方法进行暂态稳定裕度计算,耗时为0.464s。除此之外,在不同的故障位置和故障持续时间下,使用同样的比较方法进行10 次仿真计算,得到时域仿真方法的平均耗时为8.55s,本文方法的平均耗时为0.462s。需要指出,本文所述的仿真时间均为硬件设备在一定条件下的计算时间,如果对硬件设备进行更新,评估方法的耗时将进一步减少。
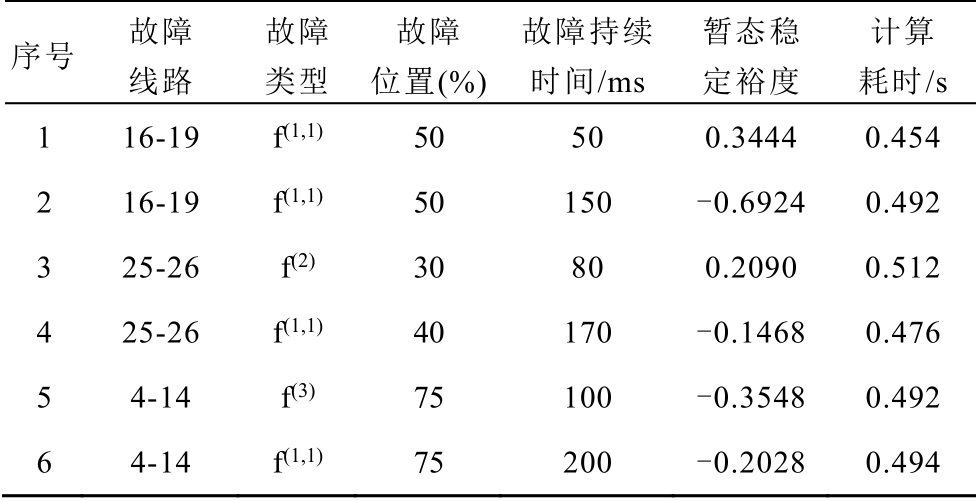
利用本文提出的分析方法,计算了不同故障条件下系统的暂态稳定裕度,见表3。对于序号3、4给出的故障信息,通过时域仿真得到相对应的发电机功角仿真曲线如图12 所示。对于序号3 的故障信息,故障清除后功角保持同步增长,系统稳定。对于序号4 的故障信息,故障清除后,发电机8 相对于其余发电机组成的机群摆开,系统失稳。两种运行情况下的仿真结果与稳定裕度指标表征的系统稳定性结果相同。序号5、6 对应的故障信息,同样可以通过仿真进行验证,不再赘述。
表3 新英格兰系统不同故障条件下的暂态稳定裕度
Tab.3 Transient stability margin under different fault conditions of New England test system
序号 故障 线路 故障类型故障 位置(%) 故障持续 时间/ms 暂态稳定裕度计算 耗时/s 1 16-19 f(1,1) 50 50 0.3444 0.454 2 16-19 f(1,1) 50 150 -0.6924 0.492 3 25-26 f(2) 30 80 0.2090 0.512 4 25-26 f(1,1) 40 170 -0.1468 0.476 5 4-14 f(3) 75 100 -0.3548 0.492 6 4-14 f(1,1) 75 200 -0.2028 0.494
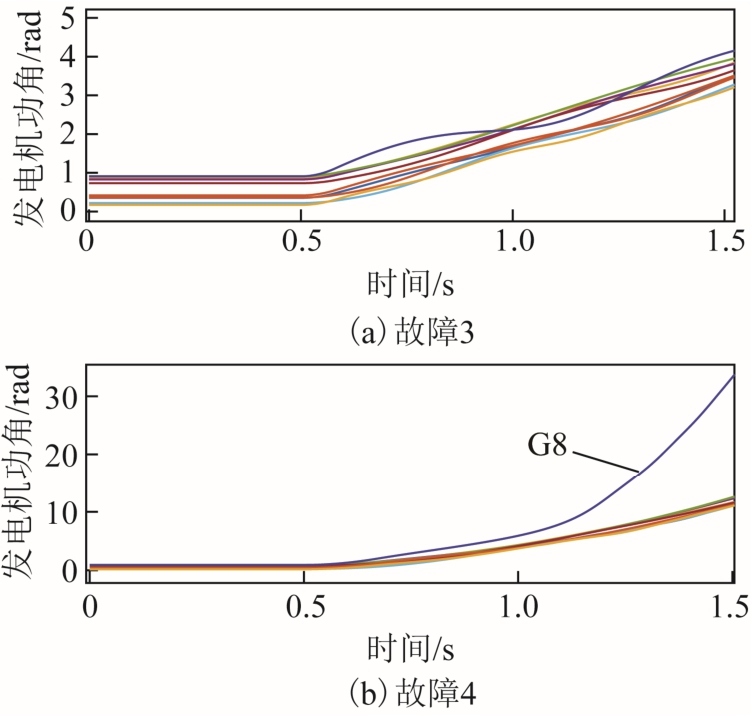
图12 线路25-26 发生故障时的时域仿真曲线
Fig.12 Time domain simulation curves when the fault occurs on line 25-26
计及励磁系统和调速系统进行暂态稳定分析时,本文计算结果将受到不同程度的影响。考虑励磁系统时,假设发电机励磁绕组的时间常数较大,故障后同步机的暂态电动势增长缓慢,当励磁倍数不高时,励磁系统对发电机暂态电动势影响较小[29]。在线路16-19 中点设置两相接地故障,0.65s 将故障清除,得到图13 所示的等效OMIB 系统功角特性曲线。通过本文方法计算的暂态稳定裕度为-0.692 4,时域仿真得到的不含励磁系统的减速面积与加速面积差值为-0.779 9,含励磁系统的减速面积与加速面积差值为-0.732 3。可以看出在这种假设下,励磁系统对结果的影响较小,与发电机暂态电动势为常数的结果十分相近。
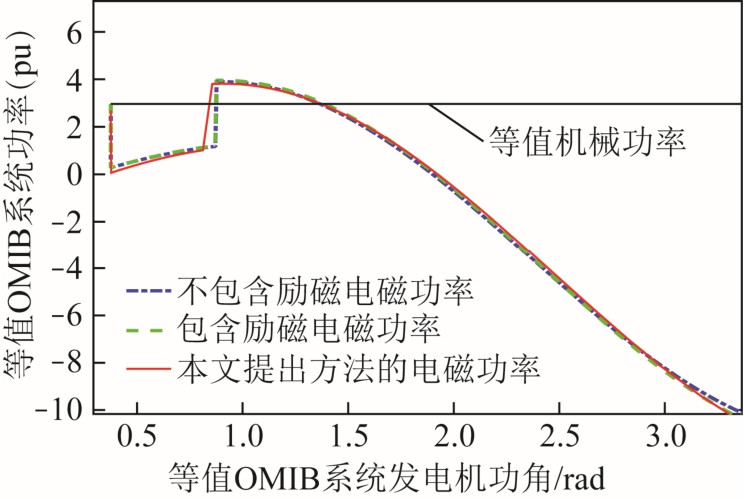
图13 励磁系统对暂态稳定裕度的影响 Fig.13 Effect of excitation system on transient stability margin
在分析调速器影响时,设置故障位置和故障清除时间与分析励磁系统时相同,得到图14 所示的等效OMIB 系统功角特性曲线。可以看出,当计及自动调速系统的作用时,等效发电机机械功率是受到较大影响的参数。机械功率的改变将导致加速面积和减速面积发生变化,影响最终暂态稳定裕度的计算结果。
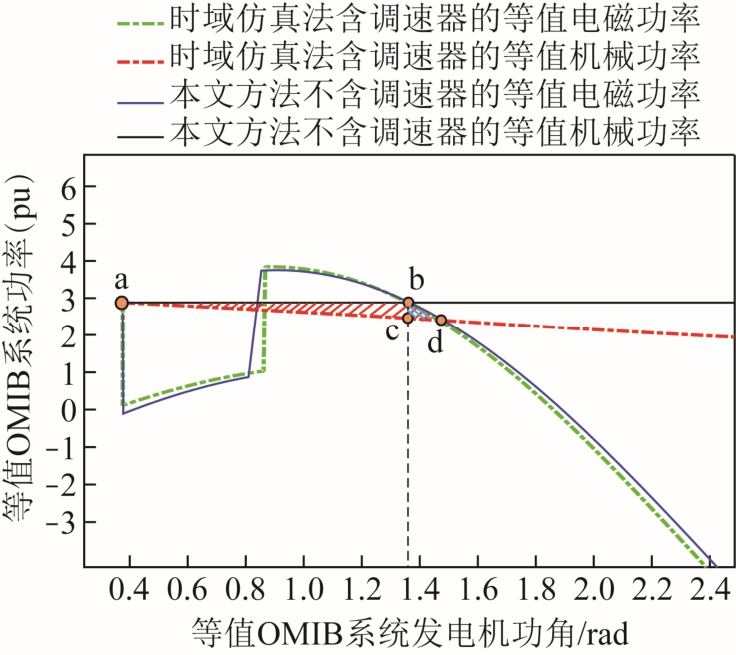
图14 调速器对暂态稳定裕度的影响
Fig.14 Effect of governor on transient stability margin
电网中每台发电机都会装设传感器,可以在线确定发电机机械功率。分析含有调速器的系统稳定裕度时,需要通过在线监测的机械功率对本文方法计算结果进行修正,计及面积偏差abd 给计算结果造成的影响。为了简化计算,使用abc 面积代替abd面积进行分析。在计算含调速系统的暂态稳定裕度过程中,本文方法的计算误差主要由电磁功率计算误差引起的面积偏差以及省略的bdc 面积共同组成。在图14 所示的算例中,修正后本文方法计算的暂态稳定裕度为-0.558 7,时域仿真得到含调速系统的减速面积与加速面积差值为-0.539 4。修正后的方法仍可以有效评估含调速系统的暂态稳定裕度。
4 结论
本文提出一种计及保护信息的暂态稳定裕度解析算法。该方法通过建立发电机聚合功角的分段模型确定了暂态稳定裕度解析表达式。分别在四机系统和新英格兰系统中进行仿真,分析了不同故障位置和故障持续时间下暂态稳定裕度的变化。选取临界稳定条件进行时域仿真,验证了所提方法的有效性。本文方法综合考虑保护动作信息,避免了仿真迭代过程的复杂计算,降低暂态稳定评估所需时间,使暂态稳定分析过程更加快速、准确。在已知保护信息的情况下,可以直接求出电力系统的暂态稳定裕度,为后续紧急控制提供了计算依据。
[1] Zweigle G C, Venkatasubramanian V M. Transient instability mitigation for complex contingencies with computationally constrained cost-based control[J]. IEEE Transactions on Smart Grid, 2016, 7(4): 1961-1969.
[2] 王振浩, 张明泽, 杜虹锦, 等. 考虑柔性直流落点约束的最优主动解列断面搜索算法[J]. 电工技术学报, 2017, 32(17): 57-66. Wang Zhenhao, Zhang Mingze, Du Hongjin, et al. A searching algorithm for optimal controlled islanding surfaces considering VSC-HVDC terminal constraint[J]. Transactions of China Electrotechnical Society, 2017, 32(17): 57-66.
[3] 顾雪平, 李少岩, 周光奇, 等. 计及特级负荷恢复的网架重构分时段全局优化方法[J]. 电工技术学报, 2017, 32(7): 138-149. Gu Xueping, Li Shaoyan, Zhou Guangqi, et al. Global optimization by multi-time-stage coordination for network reconfiguration considering vital load restoration[J]. Transactions of China Electrotechnical Society, 2017, 32(7): 138-149.
[4] 姜涛, 张明宇, 崔晓丹, 等. 电力系统静态电压稳定域边界快速搜索的优化模型[J]. 电工技术学报, 2018, 33(17): 4167-4179. Jiang Tao, Zhang Mingyu, Cui Xiaodan, et al. A novel optimization model to explore static voltage stability region boundary in bulk power systems[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4167-4179.
[5] 韦肖燕, 李欣然, 钱军, 等. 采用储能电源辅助的暂态稳定紧急控制方法[J]. 电工技术学报, 2017, 32(18): 292-306. Wei Xiaoyan, Li Xinran, Qian Jun, et al. Power system transient stability emergency control method assisted by energy storage[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 292-306.
[6] Wang Songyan, Yu Jilai, Zhang Wei. Transient stability assessment using individual machine equal area criterion part II: stability margin[J]. IEEE Access, 2018, 6: 38693-38705.
[7] 陈厚合, 王长江, 姜涛, 等. 基于投影能量函数和Pin-SVM 的电力系统暂态稳定评估[J]. 电工技术学报, 2017, 32(11): 67-76. Chen Houhe, Wang Changjiang, Jiang Tao, et al. Transient stability assessment in bulk power grid using projection energy function and support vector machine with pinball loss[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 67-76.
[8] 胡臻, 李欣然, 刘光晔, 等. 基于稳定影响度指标的电压稳定脆弱点分析[J]. 电工技术学报, 2017, 32(7): 150-157. Hu Zhen, Li Xinran, Liu Guangye, et al. Analysis of voltage fragility area based on the stability influence index[J]. Transactions of China Electrotechnical Society, 2017, 32(7): 150-157.
[9] Sun Qiuye, Huang Bonan, Li Dashuang, et al. Optimal placement of energy storage devices in microgrids via structure preserving energy function[J]. IEEE Transactions on Industrial Informatics, 2017, 12(3): 1166-1179.
[10] Siddiqui S A, Verma K, Niazi K R, et al. Real-time monitoring of post-fault scenario for determining generator coherency and transient stability through ANN[J]. IEEE Transactions on Industry Applications, 2017, 54(1): 685-692.
[11] 朱蜀, 刘开培, 秦亮, 等. 电力电子化电力系统暂态稳定性分析综述[J]. 中国电机工程学报, 2017, 37(14): 3948-3962, 4273. Zhu Shu, Liu Kaipei, Qin Liang, et al. Analysis of transient stability of power electronics dominated power system: an overview[J]. Proceedings of the CSEE, 2017, 37(14): 3948-3962, 4273.
[12] 杨帅, 王双杰. 含有分布式电源电网的故障特性影响因素分析[J]. 电气技术, 2015, 16(4): 22-25. Yang Shuai, Wang Shuangjie. Analysis of the influence factors of fault characteristics of the power network with distributed generations[J]. Electrical Engineering, 2015, 16(4): 22-25.
[13] Ju Ping, Li Hongyu, Gan Chun, et al. Analytical assessment for transient stability under stochastic continuous disturbances[J]. IEEE Transactions on Power Systems, 2018, 33(2): 2004-2014.
[14] 沈超, 方勇杰. 计及发电功率随机性的暂态稳定裕度概率分布计算[J]. 电力系统自动化, 2013, 37(19): 41-48. Shen Chao, Fang Yongjie. Calculation of transient stability margin distribution under random power injection conditions[J]. Automation of Electric Power Systems, 2013, 37(19): 41-48.
[15] 崔凯, 房大中, 钟德成. 电力系统暂态稳定性概率评估方法研究[J]. 电网技术, 2005, 29(1): 44-49. Cui Kai,Fang Dazhong,Zhong Decheng.Study on probabilistic assessment method for power system transient stability[J]. Power System Technology, 2005, 29(1): 44-49.
[16] 周海强, 鞠平, 薛禹胜, 等. 基于拟哈密顿理论的随机电力系统暂态稳定性分析[J]. 电力系统自动化, 2016, 40(19): 9-14. Zhou Haiqiang, Ju Ping, Xue Yusheng, et al. Transient stability analysis of stochastic power system based on quasi-hamiltonian system theory[J]. Automation of Electric Power Systems, 2016, 40(19): 9-14.
[17] 汪小明, 刘涤尘, 黄涌, 等. 基于能量函数法的电网暂态稳定性分析[J]. 电网技术, 2011, 35(8): 114-118. Wang Xiaoming, Liu Dichen, Wu Jun, et al. Energy function-based power system transient stability analysis[J]. Power System Technology, 2011, 35(8): 114-118.
[18] 任先成, 李威, 薛禹胜, 等. 互联电网失稳模式演化现象及其影响因素分析[J]. 电力系统自动化, 2013, 37(21): 9-16. Ren Xiancheng, Li Wei, Xue Yusheng, et al. Unstable modes evolution and its influencing factors analysis in interconnected power grids[J]. Automation of Electric Power Systems, 2013, 37(21): 9-16.
[19] Xue Yusheng. The mechanisms of unstable modes evolving with fault clearing time[C]//Proceedings of the 16th Symposium on Electrical Power Engineering, Kaohsiung, Taiwan, China, 1995: 522-527.
[20] 刘强, 薛禹胜, 董朝阳, 等. 线路故障位置对暂态稳定性的异常影响及其机理[J]. 电力系统自动化, 2007, 31(18): 1-5. Liu Qiang, Xue Yusheng, Dong Zhaoyang, et al. Abnormal effects of line fault location on transient stability and its mechanism[J]. Automation of Electric Power Systems, 2007, 31(18): 1-5.
[21] 陈长胜, 马世英, 郑超, 等. 基于暂态偏差能量的紧急控制效果超前评估方法[J]. 中国电机工程学报, 2018, 38(17): 5118-5125, 5308. Chen Changsheng, Ma Shiying, Zheng Chao, et al. The advance evaluation of emergency control based on transient deviation energy[J]. Proceedings of the CSEE, 2018, 38(17): 5118-5125, 5308.
[22] 李庚银. 电力系统分析基础[M]. 北京: 机械工业出版社, 2011.
[23] 薛禹胜.运动稳定性量化理论[M]. 南京: 江苏科学出版社, 1999.
[24] 姜宪国, 王增平, 李琛. 基于稀疏PMU 布点的广域保护全网时间同步方案[J]. 电力自动化设备, 2012, 32(9): 122-127. Jiang Xianguo, Wang Zengping, Li Chen. Wholenetwork time synchronization of wide-area protection based on sparse PMU placement[J]. Electric Power Automation Equipment, 2012, 32(9): 122-127.
[25] 孔令号, 焦彦军, 戴志辉. 基于灰色关联度的站域保护原理[J]. 电网技术, 2014, 38(8): 2274-2279. Kong Linghao, Jiao Yanjun, Dai Zhihui. A new substation area protection principle based on gray correlation degree[J]. Power System Technology, 2014, 38(8): 2274-2279.
[26] 殷志良. 基于IEC 61850 的变电站过程总线通信的研究[D]. 北京: 华北电力大学, 2005.
[27] 林富洪, 王增平, 曾惠敏. 基于测距函数相位特性的T 型高压线路故障定位原理[J]. 中国电机工程学报, 2011, 31(13): 107-113. Lin Fuhong, Wang Zengping, Zeng Huimin. A novel fault location algorithm based on phase characteristics of fault location function for three-terminal transmission lines[J]. Proceedings of the CSEE, 2011, 31(13): 107-113.
[28] 王增平, 林富洪. 基于同步相量测量的N 端输电线路故障测距新算法[J]. 电网技术, 2010, 34(5): 154-160. Wang Zengping, Lin Fuhong. A new fault location algorithm for N-terminal transmission lines based on synchronized phasor measurement[J]. Power System Technology, 2010, 34(5): 154-160.
[29] 常鲜戎, 赵书强. 电力系统暂态过程[M]. 北京: 机械工业出版社, 2010.