0 引言
随着风力发电在电力系统中的占比逐渐上升,其功率输出随风速改变带来的波动性给电力系统的安全稳定运行带来一系列的技术和经济上的挑战,因此,相关风电并网标准规定风电场必须服从电网调度中心的有功功率调度需求,控制其有功输出[1-3]。随着风力发电机组在技术与结构上的快速发展,风电场能够在输送电能的同时为电力系统提供多种辅助服务,如频率、电压支持及无功功率补偿等。
与传统的异步风力发电机组不同,双馈异步感应风力发电机组(Doubly-Fed Induction Generator, DFIG)能够在实现有功无功解耦控制的同时向网侧输送无功功率,因此在风电场中利用DFIG 的无功调控能力来实现风电场的实时无功控制已经成为一种共识[4]。DFIG 具有显著的优点,如较高的可控性、较小的变流器容量以及迅速的无功调节能力等[5]。
目前常用于风电场有功功率控制的方法有比例分配[6](Proportional Distribution, PD)和比例积分(Proportional-Integral, PI)控制等,这些方法操作简单易于实现,但引起的传输系统的功率损耗较大。文献[7]采用模型预测控制算法(Model Predictive Control, MPC)从整场、机群以及单机三个层次实现风电场内部的有功功率调度。文献[8-9]针对目前风电场的疲劳优化和有功功率控制两者不能兼顾的现状,建立了一种同时控制风电场的疲劳分布和有功功率的方法。文献[10-11]采用分布式MPC 算法分配风电机组的有功功率,系统仍然需要采用集中单元来实现风机有功功率的跟踪。文献[12]通过区域模糊推理来评估风电场的健康度,同时采用按能力权重分配算法来实现风电场内部的有功调度。
风电场的无功功率控制可用于补偿系统无功的同时降低机端电压的差异。文献[13-14]采用传统的PD 来控制风电场的无功功率;文献[15]在网络分析的基础上,提出了用于风电场的无功优化控制方法;文献[16-17]提出用粒子群优化算法降低传输系统和变压器的损耗来实现风电场的无功功率分配;文献[18]采用MPC 算法实现风电场的无功控制,确保所有节点电压维持在稳定范围的同时降低风电场内部传输损耗;文献[19]提出了一种基于共识协议的适用于风电场的分布式协同电压控制策略,为系统提供快速响应的同时分配无功功率,消除稳态电压误差。
上述研究成果有利于风电场功率控制的优化,但仍存在不足。本文提出一种用于双馈型风电场的有功无功协调优化控制(Active and Reactive Power Coordination Control, ARPCC)策略,该策略将双馈型风电场构建成一个基于线性潮流方程的最优潮流(Optimal Power Flow, OPF)模型,并且结合了DFIG内部无功分配策略,能够降低DFIG 机组产生的有功损耗和风电场集电线路产生的网络损耗,同时能够实现双馈型风电场的降载运行,满足风电并网的相关准则。
1 有功无功协调优化控制结构
1.1 风电场结构配置
图1 展示了典型风电场的结构配置。风场通过升压变压器与外部电网相连,电网通过平衡节点控制风电场的有功输出和实现对无功的调节。汇流母线与若干簇DFIG 风机相连,每条馈线由多台风机构成,风机等距离放置。该风电场的节点包括一个网侧的平衡节点、一个汇流母线节点和若干个风机节点。
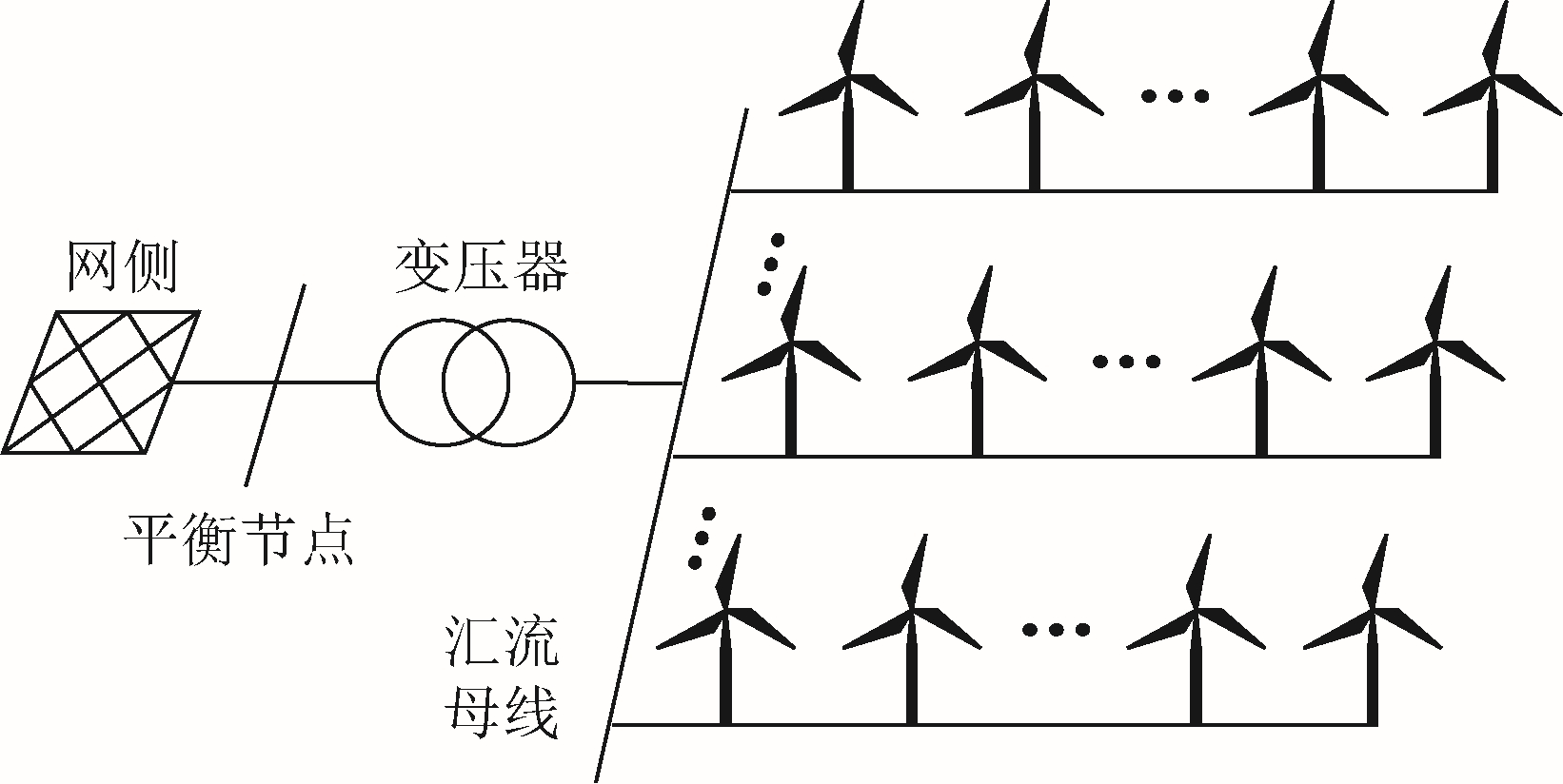
图1 风电场的典型结构配置
Fig.1 Typical configuration of wind farm
1.2 有功无功协调优化控制策略
双馈型风电场有功无功协调优化控制的控制框图如图2 所示,其中,ARPCC 控制器即为双馈风电场中的有功无功协调优化控制器,Pref WF和Qref WF是电力系统调度中心根据电网需求向双馈风电场发出的总有功功率和无功功率的参考值,控制器接收到调度指令后,将风电场反馈的测量数据(包括DFIG 风机当前时刻风速v i,风机前一时刻实际输出的有功 功率PWT,i和节点电压值ui)代入最小损耗目标函数,采用二次规划算法计算目标函数从而得到DFIG 的所需参数Q s、Q g和P WT的参考值,其中Qref s,i 和Qref g,i 分别是DFIG 的定子无功功率的参考值和网侧变流器无功功率的参考值,Pref WT,i是DFIG 风机当前时刻输出有功功率的参考值。
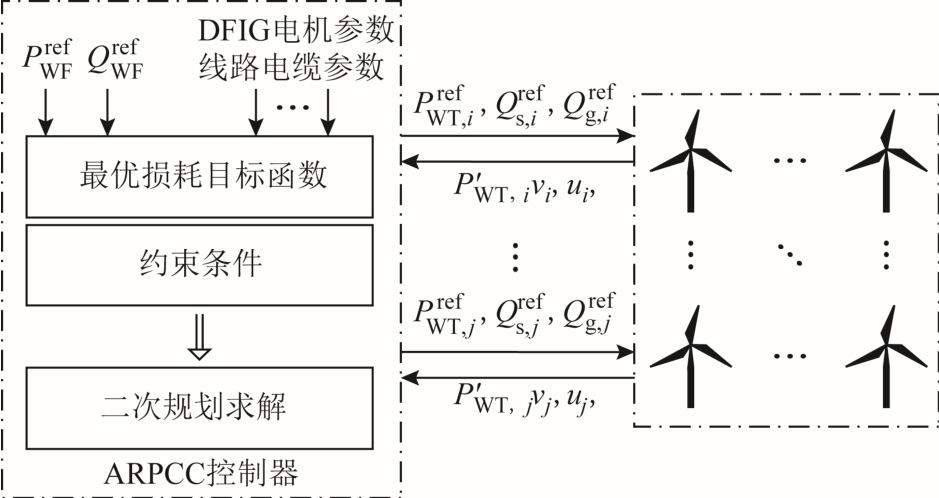
图2 有功无功协调优化控制框图
Fig.2 The diagram of active and reactive power coordination control for the DFIG wind farms
2 双馈型风电场的损耗模型
2.1 网络损耗
一般情况下,输电线路的有功功率损耗主要是指电流通过元件的电阻r 时产生的功率损耗,如图3 所示。
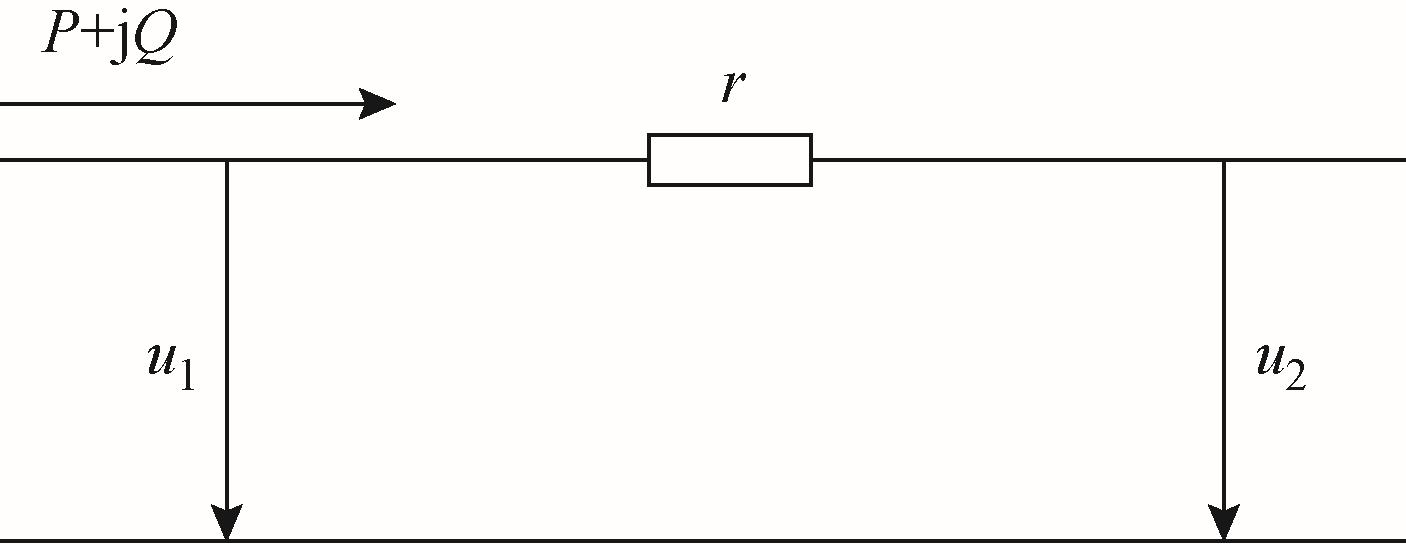
图3 风电场输电线路的等效电路
Fig.3 The equivalent circuit of transmission line in the wind farms
风电场中输电线路的有功功率损耗 Pt rlo ansss 可以表示为
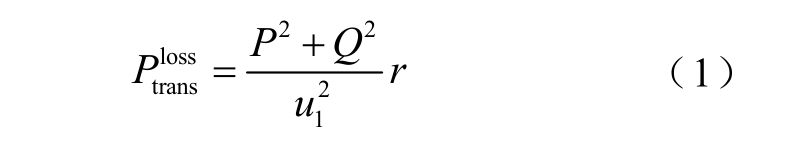
2.2 DFIG 铜耗
DFIG 风机结构如图4 所示。DFIG 风机是一种采用双馈感应电机作为发电机的风力发电机。DFIG的定子侧与电网直接相连,而转子侧通过背靠背PWM 变流器与外网进行电能交换,定子和转子上均有交流电通过从而实现了电机的双向供电,这也是其被称为双馈电机的原因。

图4 双馈感应风机的典型结构
Fig.4 Typical configuration of DFIG
忽略电机暂态过程,可以得到DFIG 电机在旋转同步坐标系(dq 坐标系)中的定子电压方程和磁链方程为
式中,usd、usq 和urd、urq 分别为定子电压us 和转子电压ur 在dq 坐标系中的d 轴和q 轴分量;电流i 和磁链ψ 的表示方法与电压类似;s 为转差率;rs 为定子的电阻;rr 为转子侧折算到定子侧的电阻值;xs 为定子绕组的电抗;xr 为转子侧折算到定子侧之后的电抗值;xm 为定子和转子绕组间的励磁电抗。
将同步旋转坐标系定向到dq 坐标系的q 轴上,则有usq=0 和usd= us,可根据定子侧的功率方程计算得到定子电流在d 轴和q 轴上的分量为

式中,Ps 和Qs 分别为DFIG 定子的有功和无功功率。
在风速已知时,转子电流的d 轴分量计算式为
式中,Psr= Pmecωs/ωr,ωs 和ωr 分别为定、转子的电压与电流之间的角频率,Pmec 为DFIG 所捕获的风功率;n 为转子与定子绕组间的匝数比。
网侧变流器所流经的电流计算式为
式中,igd 和igq 分别为流经网侧变流器的电流在d 轴和q 轴上的分量,经过推导可表示为
式中,Pg 和Qg 分别为网侧变流器提供的有功和无功功率。DFIG 中的功率关系为
式中,Ps 为定子有功功率。
由式(6)和式(7)推导可得到网侧变流器的电流在d 轴上的分量表达式为
流经定子、转子以及网侧变流器的电流在d 轴和q 轴上的分量可由式(2)~式(8)推导计算。
式中,x:=[Qs Qg]T,A、B 矩阵表示为
式中,a:=rs/xs,b:=xs/(r2 s +x2 s )。DFIG 的铜耗计算式为
式中,i2 s= i2 sd+ i2 sq;i2 r= i2 rd+ i2 rq。
2.3 变流器损耗
DFIG 中转子侧变流器和网侧变流器均采用脉宽调制(Pulse Width Modulation, PWM)变流器。变流器损耗以热能的形式扩散,会降低变流器的使用寿命,对系统造成不良影响,因此需要采取措施来降低其损耗。变流器损耗主要有开关损耗和通态损耗。开关损耗由变流器的导通和关断动作引起,通态损耗则由流经开关器件的电流引起的[20]。两种损耗计算公式为
式中,Ps 和Pc 分别为变流器的开关损耗和通态损耗;Ps,T、Ps,D 和Pc,T、Pc,D 分别为晶体管、二极管的开关损耗和通态损耗;irms 为变流器通过的正弦电流有效值;us,T 和us,D 为变流器的晶体管和二极管动作时引起的电压降落常数;uIGBT 为变流器开关器件的恒压降;rIGBT 为变流器的引线电阻。因此,变流器损耗可表示为
代入数据计算可得ac=0.004 5,bc=10.139 81。
对于转子侧变流器,irms 即为转子所通过的电流ir,对于网侧变流器,irms 即为流经网侧变流器的ig。
DFIG 中的变流器损耗计算式为
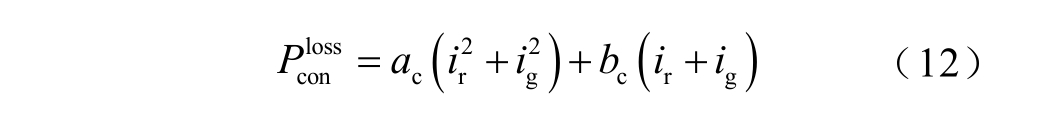
从而可以得到i 节点单台DFIG 的机组损耗为
2.4 线性潮流模型
根据图1 的风场拓扑,可以得到如图5 所示的双馈风电场的潮流示意图,图中箭头的指向即为正方向,其中,N 表示风电场中所有节点的集合,节点v 表示平衡节点,节点0 是汇流母线节点,下标ij 用来表示节点i 与节点j 之间的有向线段,则流经两个相邻节点之间的功率可用Pij+jQij 表示,单个节点的注入功率则用Pj+jQj 表示,相邻节点之间的线路阻抗用rij+jxij 表示,ui 是节点i 的电压值,NF 和NW 分别表示风电场中的馈线数量和每条馈线上的DFIG 数量。
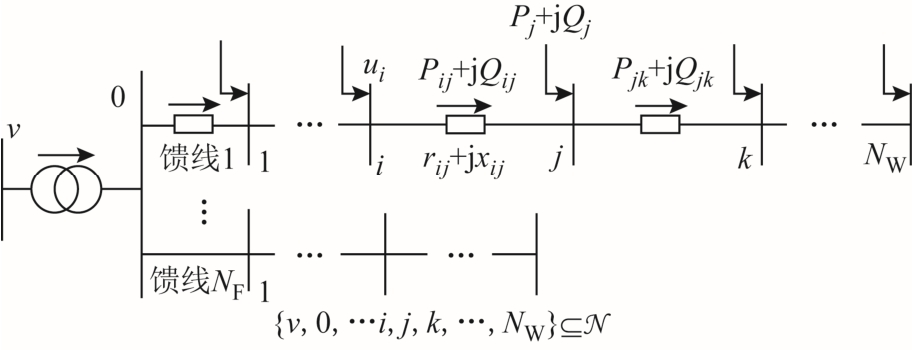
图5 双馈风电场的潮流示意图
Fig.5 The power flow diagram of the DFIG wind farm
对于图5 所示的辐射型拓扑的双馈风电场,可以得到潮流方程为

忽略潮流模型中的损耗,即将式(14)中的变量Iij 置零,可得到线性潮流模型为
式中,![]()

3 基于OPF 的有功无功协调优化控制
3.1 优化目标函数
根据线性潮流方程,以降低双馈风电场的线路损耗和 DFIG 机组损耗为优化目标,忽略节点电压的波动,可以得到以降低损耗为优化目标的双馈风电场的有功无功协调优化控制的模型,其目标函数为
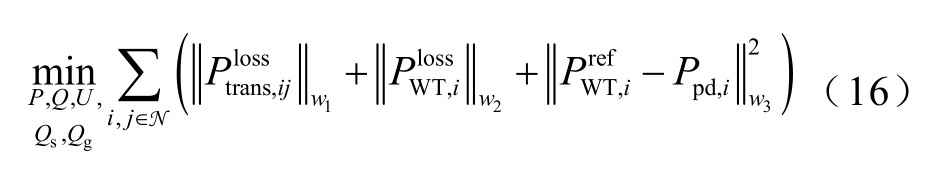
式中,Ppd,i 为按风机可用功率的比例计算得到的风机输出有功功率的参考值;每一项的下标w1、w2和w3 为权重因子,分别表示各项在目标函数中的比重,本文采用主客观综合赋权法根据各项的具体含义及其在目标函数中的占比来综合确定权重因子的取值。
3.2 等式约束
DFIG 节点的注入功率即为DFIG 机组实际的输出功率,即
式中, s,jQ 、 g,jQ 分别为节点j 的定子、网侧变流器的参与功率。
所有的节点电压都需要满足潮流方程,忽略变压器和电缆阻抗引起的电压降落,可得电压约束为
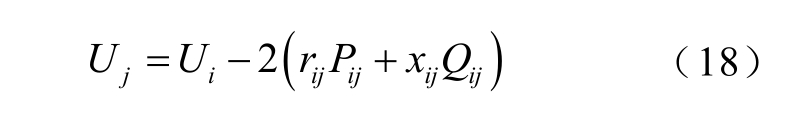
平衡节点的有功和无功功率即为风电场待分配的有功和无功功率参考值Pref WF和Qref WF,平衡节点的电压通过计算应为
由于位置的特殊性,位于每条馈线末端的风机节点并无相邻的下一个节点,因此其流向相邻的下一节点的潮流值为零,即该节点的注入功率与相邻的前一节点流向该节点的潮流值相等,即
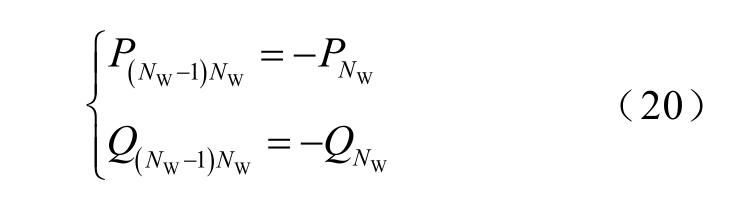
风电场风机输出的总有功功率和无功功率应跟随风电场设定的有功功率和无功功率的参考值,即为
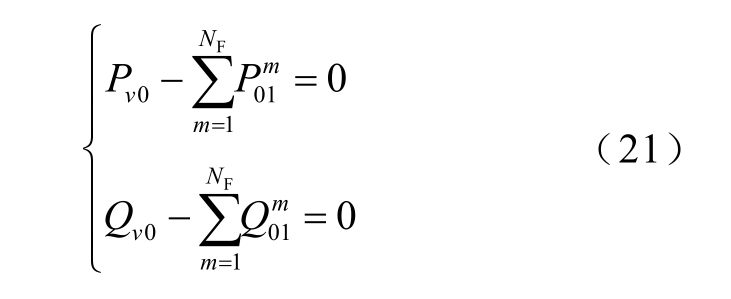
式中,上标m 表示节点所处的馈线位置。
3.3 不等式约束
风电场中的节点电压波动都应该保持在一定的范围内,即
式中,ε 为电压限制常数,根据ANSI 关于电压波动的相关准则,通常取ε =0.05。对式(22)进行相应的代数计算,可以得到Ui 的上、下限约束为
风电场中DFIG 输出的有功功率受限于当前时刻DFIG 可用的有功功率
式中,Pavi WT,j是风机当前时刻可用的有功功率,根据风机当前的风速求得。
DFIG 的定子和网侧变流器的无功输出之和即为DFIG 的实际输出功率,上、下限约束[14]为
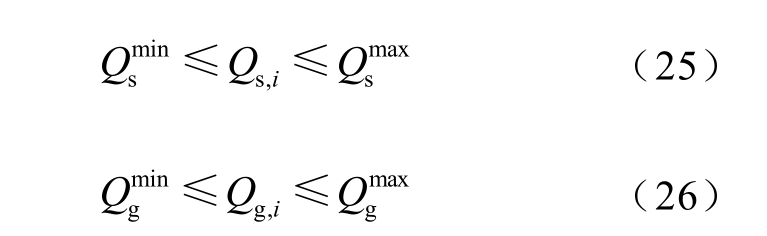
约束条件的取值为

式中,Sg 为网侧变流器的最大容量;irn 为转子电流的额定值,一般与变流器所选择的安全系数有关。
将本文所提出的目标函数和相应的约束转换为一个标准的二次规划问题,然后采用二次规划的方法来求解该目标函数[21]。
4 仿真验证
4.1 仿真平台
为了证明提出的双馈风电场有功无功协调优化控制策略降低损耗的效果,在Matlab/Simulink 仿真平台上搭建一个具有两条馈线的模拟双馈风电场,每条馈线由10×5MW DFIG 风机组成,模拟风电场的参数见表1。
表1 双馈风电场的仿真参数
Tab.1 The parameters of the DFIG wind farm

参 数 实际值 标幺值 DFIG 额定机械功率PWT 5MW 0.05 (pu) 定子额定相电压us(rms) 548.48V 0.017 (pu) 额定频率 50Hz 转子额定转速 1 170r/min 额定转差率 s -0.17 定子电阻 rs 1.552mΩ 1.42×10-4 (pu) 转子电阻 rr 1.446mΩ 1.33×10-4 (pu) 定子电抗 xs 2.133Ω 1.96×10-1 (pu) 转子电抗 xr 2.108Ω 1.91×10-1 (pu) 互感电抗 xm 1.733Ω 1.59×10-1 (pu) 滤波器电阻 rfil 6.79×10-4Ω 6.20×10-5 (pu) 线路电阻 rij 1.34×10-1Ω/km 1.23×10-2 (pu) 线路电抗 xij 1.29×10-1Ω/km 1.18×10-2 (pu) 升压变压器电阻rv0 2.18×10-2Ω 2.00×10-3 (pu) 升压变压器电抗xv0 1.306Ω 1.20×10-1 (pu) 风电场额定容量SWF 100MV·A 1.0 (pu) 基准电流IB 1 749.5A 1.0 (pu) 基准电压VB 33kV 1.0 (pu) 基准阻抗ZB 10.89Ω 1.0 (pu)
4.2 控制策略
4.2.1 策略1:ARPCC 策略
该策略同时考虑了双馈风电场的网络损耗和DFIG 机组的损耗,结合了最优线性潮流和DFIG 内部无功最优分配,优化目标如式(16)所示。
4.2.2 策略2:ARPCC 不考虑DFIG 机组损耗
该策略2 不考虑DFIG 机组损耗,采用最优线性潮流优化输出功率。DFIG 输出的无功功率均由定子提供,网侧变流器的输出无功功率设置为零,目标函数是去除DFIG 机组损耗项的式(16)。
4.2.3 策略3:比例控制策略
比例控制策略是传统的功率控制策略,控制方式简单易实现,DFIG 输出的有功无功功率参考值为
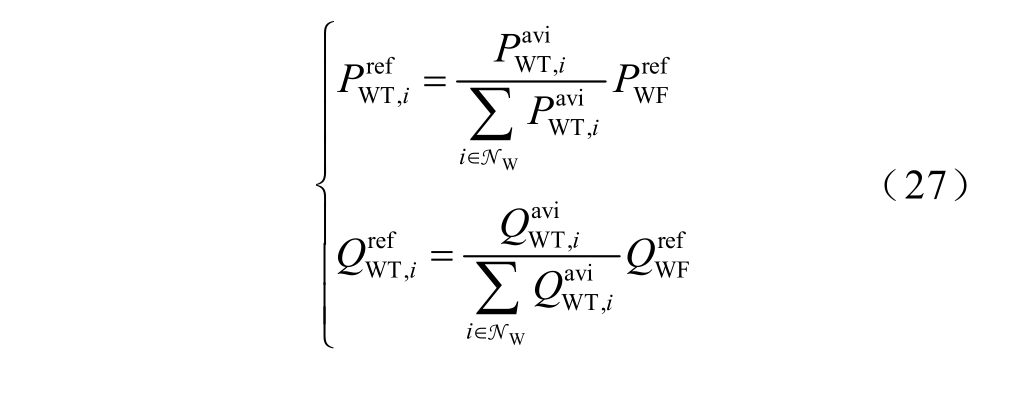
式中,NW 为风电场中DFIG 节点的集合。
4.3 控制效果
仿真时间设置为600s。图6 所示为双馈风电场可用有功功率Pavi WF和电网调度中心期望风电场输出的有功功率Pref WF曲线。从0~250s,Pavi WF在65~75MW之间波动,此时Pref WF约为Pavi WF/2;250s 后随着风速的增加,Pavi WF也逐渐上升,最高达到90MW,而此时Pref WF曲线也在逐渐上升,其上升速率高于Pavi WF曲线的增加速率,说明此时风电场的风能利用率在逐渐上升;400s 之后,Pavi WF和Pref WF两者曲线重合,双馈风电场此时满载运行。

图6 双馈风电场可用有功功率和期望输出有功功率
Fig.6 Total available active power and active power dispatch command of the DFIG wind farm
图7 是双馈风电场的实际输出有功功率和期望输出的有功功率曲线,证明了ARPCC 策略能够调节双馈风电场的有功功率输出,实现调度中心的有功调度需求,ARPCC 策略能够实现双馈风电场的降载运行,实际输出的有功功率与有功功率调度需求间的细微差异是由双馈风电场内部功率损耗引起的。
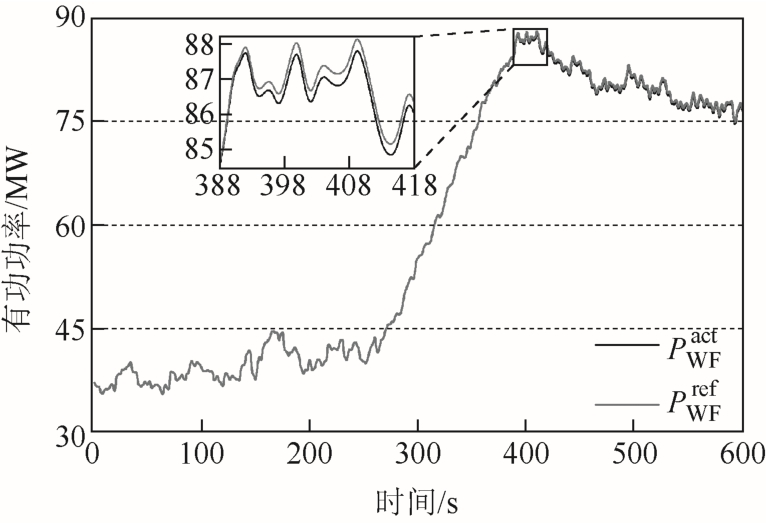
图7 双馈风电场实际输出有功功率和有功调度需求
Fig.7 Total output active power and active power dispatch command of the DFIG wind farm
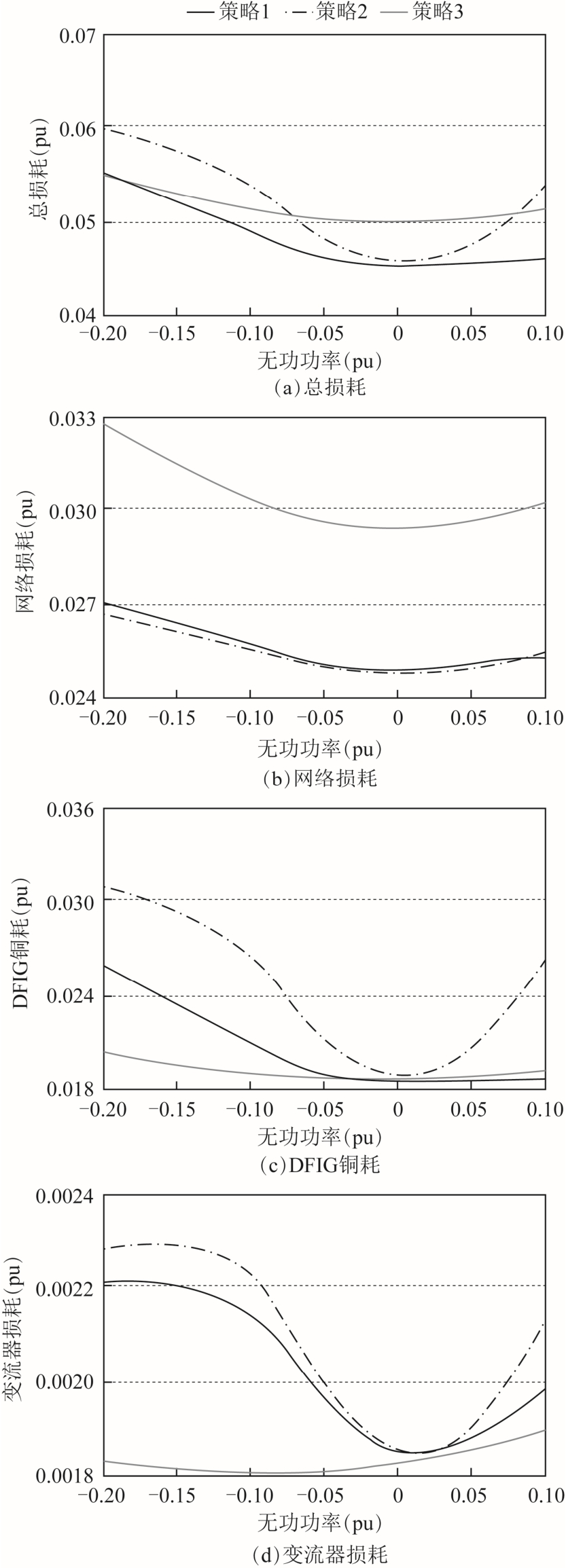
图8 风速恒定采用不同控制策略时的双馈风电场各种损耗比较
Fig.8 Comparisons of various losses of the DFIG wind farms under different strategies with constant wind speed
图8 是风速恒定、风电场的无功需求不同时,采用不同控制策略的双馈风电场多种损耗的曲线,风能利用率设定为80%,无功功率的参考值的范围设定为-0.2(pu) ~0.1(pu) 。从图8a 中可以看出,采用策略1 时双馈风电场的总损耗值低于策略2 和策略3,从而证明在风速恒定时,策略1 能够在实现 风电场不同的无功需求的同时降低风电场的损耗值。以双馈风电场无功参考值为-0.2(pu)为例,策略1 与策略2 相比其损耗下降百分比为13.23%,与策略3相比,其损耗下降百分比为15.03%。由图8b 可以看出采用策略1 和采用策略2 时,双馈风电场的网络损耗基本相同,而采用策略3 时风电场的网络损耗总是较大,说明策略1 在降低DFIG 的机组损耗时,其降低网络损耗的效果几乎不受影响。由图8c和图8d 可以看出当系统的无功功率设置为0 时,三种策略的DFIG 的铜耗和变流器损耗值基本相同,而随着无功的增加,策略3 的两种损耗与策略1 相比更低。
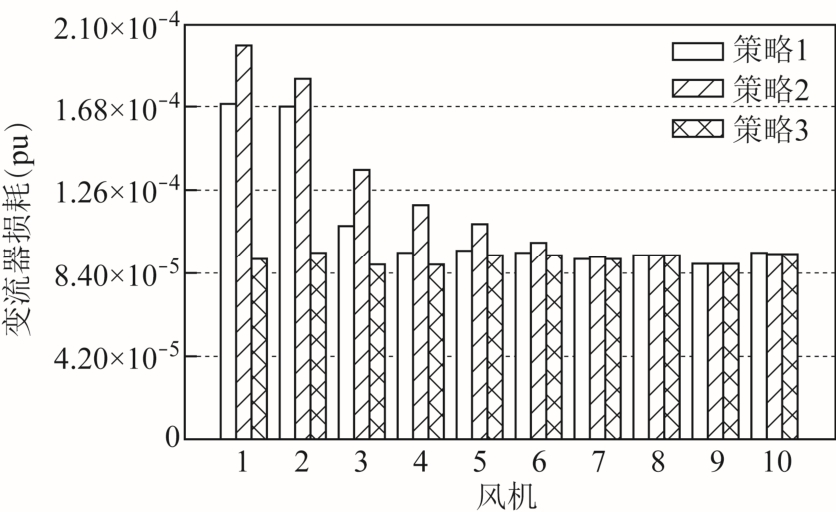
图9 第一条馈线上的10 台风机的变流器损耗分布
Fig.9 Converters loss of ten DFIG WTs at the 1st feeder
图9 所示为第一条馈线上的10 台风机的变流器损耗分布。图9 的运行条件为:无功功率参考值设置为-0.2(pu),风能利用率为80%,由于两条馈线具有对称性,图中仅包含第一条馈线上的DFIG 变流器损耗。从图9 可以看出,策略1 的部分DFIG 变流器损耗与策略3 相比较大,这是因为该部分DFIG无功功率较大,风机节点电压较低,电流增大,从而引起变流器损耗增加,其余DFIG 的变流器损耗则与策略3 的变流器损耗基本持平,因此总变流器损耗与策略3 相比更大。根据图9 中的数据简单计算可得,策略1 和策略2 相比,变流器损耗的下降百分比最高可达20.80%,结合图8b 可以看出,策略1能够同时降低网络损耗和DFIG 的变流器损耗。
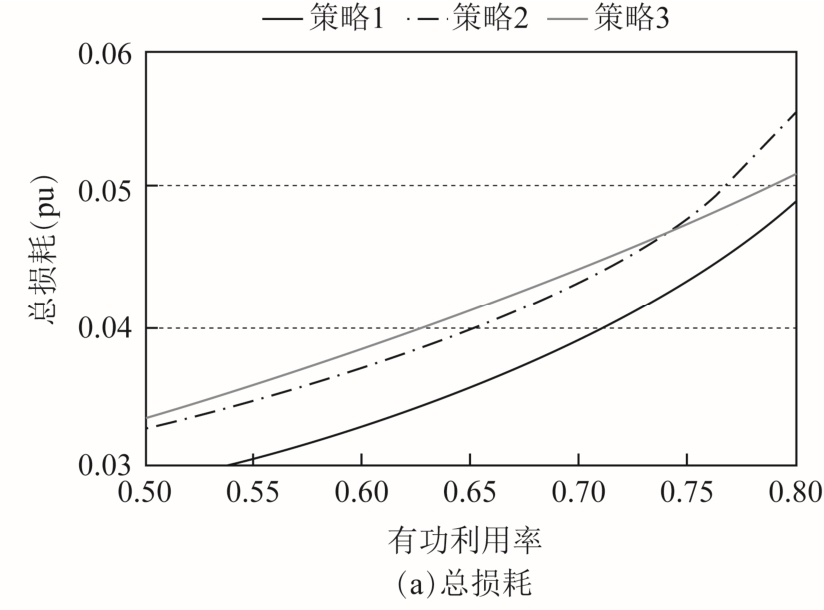

图10 双馈风电场无功需求恒定采用不同控制策略时的损耗比较
Fig.10 Loss comparisons of the DFIG wind farms with constant reactive power demand and different strategies
图10 所示为双馈风电场的无功需求恒定、有功调度需求不同时,采用不同控制策略的双馈风电场 多种损耗的曲线。风电场的有功功率参考值的范围设定为Pavi WF的50%~80%,风电场无功功率的参考值设定为-0.1(pu) 。图10a 证明策略1 能够实现双馈风电场的降载运行,同时还能降低风电场的功率损耗;从图10b 可以看出采用策略1 和策略2 时,双馈风电场的网络损耗基本相同,两种策略的网络损耗相差不超过6%;与策略3 相比,策略1 的网络损耗下降百分比最高可达64.71%;由图10c 和图10d 可知,策略1 的 DFIG 机组损耗与策略3 相比较高,这是因为策略1 在降低网络损耗时,会引起部分风机的无功功率增加,相应的节点电压降低,电流增大,从而导致DFIG 机组损耗(包括DFIG 铜耗和变流器损耗)增加。比较策略1 和策略2 的损耗曲线,可以清晰地看出采用策略1 时DFIG 的铜耗和变流器损耗都低于没有引入DFIG 机组损耗控制的策略2,是因为策略1 加入了DFIG 机组损耗控制,策略1 的DFIG 无功功率与策略2 相比较小,流经DFIG 的电流较低,所以策略1 的DFIG 机组损耗低于策略2。由此可以看出,策略1 能够同时降低网络损耗和DFIG 的机组损耗从而降低风电场的总功率损耗。
在设定的仿真时间范围内,图11 是双馈风电场在仿真平台中采用不同的控制策略模拟实际风电场运行时产生的总损耗曲线。图12 是双馈风电场采用策略1 与其余两种策略相比较的损耗减少值,例如:比较策略1 与策略2 时,采用策略2 的总损耗值减去相同时刻策略1 的总损耗值,从而得到策略1 损耗降低的数值。策略1 与策略2 相比,降低的总损耗值在300~400kW 之间波动,经计算可得,损耗下降百分比的范围为5% ~ 18%;策略1 与策略3 相比,损耗降低的程度约在320s 之后逐渐减弱,在400s 左右达到稳定,这是因为此时风电场从降载运行变为满载运行,有功功率对双馈风电场损耗的影响逐渐增加。从图12 中可以看出,双馈风电场满载运行时,与策略3 相比,采用策略1 依然能够降低 200kW 左右的功率损耗。通过上述的仿真结果和图6、图7 可以看出,策略1 在风电场不同的运行状况下都能够降低风电场的网络损耗以及DFIG 的机组损耗,延长相关器件的使用寿命,同时能够实现风电场的降载运行,满足风电场运行的多样性需求。
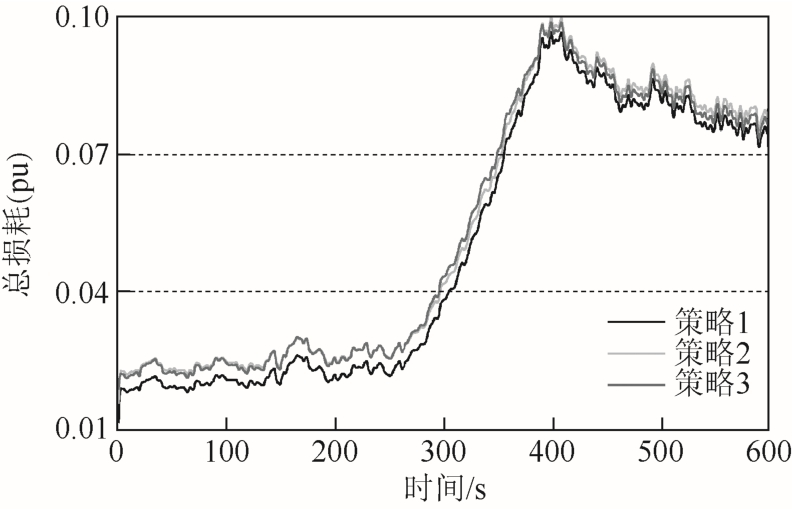
图11 风电场采用不同控制策略运行一定时间的总损耗
Fig.11 Total losses of the DFIG wind farms with different control strategies for a certain period of time

图12 风电场采用不同策略运行一定时间的损耗降低值
Fig.12 Loss reduction of the DFIG wind farms with different control strategies for a certain period of time
5 结论
本文提出了一种适用于双馈风电场的有功和无功协调优化控制的方法。仿真结果有效地证明了该方法能够在降低双馈风电场的总功率损耗的同时,分配风电场内部DFIG 机组的有功和无功功率,实现风电场的降载运行,满足风电场在不同情况下的运行需求。该方法的优点如下:
1)该方法将双馈型风电场构建成一个基于线性潮流方程的OPF 模型,结合了DFIG 内部无功优化分配策略,能够降低DFIG 机组产生的有功损耗和风电场集电线路产生的网络损耗。
2)与有功和无功功率单独控制相比,所提出的ARPCC 策略同时考虑了有功和无功功率对功率损耗的影响,因此它能够更大幅度地降低风电场的功率损耗,降载运行时依然能够降低系统的功率损耗从而延长变流器等器件的使用寿命。
3)该方法不需要增加额外设备,能够分配风电场内部DFIG 机组的有功无功功率,实现双馈型风电场的降载运行,满足风电并网的相关准则。
[1] Demailly F, Ninet O, Even A. Numerical tools and models for Monte Carlo studies of the influence on embedded generation on voltage limits in LV grids[J]. IEEE Transactions on Power Delivery, 2005, 20(3): 2343-2350.
[2] 国家电网公司. Q/GDW 432—2010 风电调度运行管理规范[S]. 北京: 中国电力出版社, 2010.
[3] 罗毅, 邵周策, 张磊, 等. 考虑风电不确定性和气网运行约束的鲁棒经济调度和备用配置[J]. 电工技术学报, 2018, 33(11): 2456-2467. LuoYi, Shao Zhouce, Zhang Lei, et al. Robust economic dispatch and reserve configuration considering wind uncertainty and gas network constraints[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2456-2467.
[4] 马少康, 耿华, 马进, 等. 双馈型风电场详细模型建模方法[J]. 电工技术学报, 2017, 32(增刊1): 1-10. Ma Shaokang, Geng Hua, Ma Jin, et al. An approach to establish detailed model of DFIG based wind farm[J]. Transactions of China Electrotechnical Society, 2017, 32(S1): 1-10.
[5] 刘瑞芳, 任雪娇, 陈嘉垚. 双馈异步风力发电机的轴电流分析[J]. 电工技术学报, 2018, 33(19): 4517-4525. Liu Ruifang, Ren Xuejiao, Chen Jiayao. Analysis of bearing currents in doubly-fed induction wind turbines[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4517-4525.
[6] 唐程辉, 张凡, 张宁, 等. 基于风电场总功率条件分布的电力系统经济调度二次规划方法[J]. 电工技术学报, 2019, 34(10): 2069-2078. Tang Chenghui, Zhang Fan, Zhang Ning, et al. Quadratic programming for power system economic dispatch based on the conditional probability distribution of wind farms sum power[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2069-2078.
[7] 叶林, 任成, 李智, 等. 风电场有功功率多目标分层递阶预测控制策略[J]. 中国电机工程学报, 2016, 36(23): 6327-6336, 6597. Ye Lin, Ren Cheng, Li Zhi, et al. Stratified progressive predictive control strategy for multiobjective dispatching active power in wind farm[J]. Proceedings of the CSEE, 2016, 36(23): 6327-6336, 6597.
[8] 苏永新, 段斌, 朱广辉, 等. 海上风电场疲劳分布与有功功率统一控制[J].电工技术学报, 2015, 30(22): 190-198. Su Yongxin, Duan Bin, Zhu Guanghui, et al. Fatigue Distribution and active power combined control in offshore wind farm[J]. Transactions of China Electrotechnical Society, 2015, 30(22): 190-198.
[9] Huang Sheng, Wu Qiuwei, Guo Yifei, et al. Bi-level decentralised active power control for large-scale wind farm cluster[J]. IET Renewable Power Generation, 2018, 12(13): 1486-1492.
[10] Spudić V, Conte C, Baotić M, et al. Cooperative distributed model predictive control for wind farms[J]. Optimal Control Applications & Methods, 2015, 36(3): 333-352.
[11] Zhao Haoran, Wu Qiuwei, Guo Qinglai, et al. Distributed model predictive control of a wind farm for optimal active power control-part II: implementation with clustering-based piece-wise affine wind turbine model[J]. IEEE Transactions Sustainable Energy, 2015, 6(3): 1-10
[12] 刘军, 张彬彬, 赵婷. 基于模糊评价的风电场有功功率分配算法[J]. 电工技术学报, 2019, 34(4): 786-794. Liu Jun, Zhang Binbin, Zhao Ting. Research on wind farm active power dispatching algorithm based on fuzzy evaluation[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 786-794.
[13] Xu Dianguo, Li Rui, Liu Yicheng, et al. Reactive power analysis and control of doubly fed induction generator wind farm[C]//2009 13th European Conference on Power Electronics and Applications, Barcelona, 2009: 1-10.
[14] 郎永强, 张学广, 徐殿国, 等. 双馈电机风电场无功功率分析及控制策略[J]. 中国电机工程学报, 2007, 27(9): 77-82. Lang Yongqiang, Zhang Xueguang, Xu Dianguo, et al. Reactive power analysis and control of doubly fed induction generator wind farm[J]. Proceedings of the CSEE, 2007, 27(9): 77-82.
[15] 严干贵, 孙兆键, 穆钢, 等. 面向集电系统电压调节的风电场无功电压控制策略[J]. 电工技术学报, 2015, 30(18): 140-146. Yan Gangui, Sun Zhaojian, Mu Gang, et al. Collector system voltage regulation oriented reactive power control strategy for wind farm[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 140-146.
[16] Kanna B, Singh S N. Towards reactive power dispatch within a wind farm using hybrid PSO[J]. International Journal of Electrical Power & Energy Systems, 2015, 69: 232-240.
[17] 刘云峰. 含双馈感应风机的配电网无功优化研究[D]. 郑州: 郑州大学, 2018.
[18] Guo Yifei, Gao Houlei, Wu Qiuwei, et al. Coordinated voltage control scheme for VSC-HVDC connected wind power plants[J]. IET Renewable Power Generation, 2018, 12(2): 198-206.
[19] Guo Yifei, Gao Houlei, Wu Qiuwei. Distributed cooperative voltage control of wind farms based on consensus protocol[J]. International Journal of Electrical Power & Energy Systems, 2019, 104: 593-602.
[20] Petersson A. Analysis, modeling and control of doubly-fed induction generators for wind turbines[D]. Chalmers: Chalmers University of Technology, 2005.
[21] Johan L. Modeling and solving uncertain optimization problem in YALMIP[C]// The International Federation of Automation Control, Korea, 2008: 1337-1341.