0 引言
在绿色能源日益提倡的今天,风力发电已成为世界优先发展的新能源之一。作为风力发电的主流发电机,交流励磁双馈发电机可以在电机转速变化时利用外电路控制转子电流频率实现变速恒频发电。此时变频器的能量能够双向流通,其功率也比较小,系统成本也相应减少,特别是对于高压发电系统,这种效果更加明显。但是其结构上存在电刷、集电环等,发电系统的可靠性较低。如在风力发电中,塔架多处于偏僻的地方,交通不便,经常维修十分困难[1-3]。
与交流励磁双馈发电机相比,无刷双馈电机(Brushless Double Fed Machine, BDFM)不仅具有交流励磁双馈发电机通过调节励磁电流的大小来实现变速恒压调节的功能,而且其结构上取消了电刷集电环装置,提高了系统的可靠性,减小了变频器所需的容量,降低了系统的成本,在风力发电领域具有较好的应用前景[4-8]。
无刷双馈电机具有特殊性,其定子上有两套极对数不同的绕组,一套为功率绕组,另一套为极对数不同的控制绕组[9-11]。对于定子上确定极对数分别为p1、p2 两套绕组,选取p1(p2)为功率绕组,p2(p1)为控制绕组尚无定论。文献[12]对1/3 对极电机两种极对数组合情况下空载电流进行了对比,最终选择功率绕组极对数pp=1、控制绕组极对数pc=3 的电机。文献[13]对1/3 对极电机两种极对数组合情况下气隙磁场进行了对比,结果表明功率绕组极对数为pp=1,控制绕组极对数为pc=3 的电机的基波含量较高,谐波含量较低。现有文献仅针对单个电机在某一运行点时的性能进行分析,不具有普遍性,且对出现性能偏差的原因没有解释。本文利用绕线转子无刷双馈电机的等效电路,推导出给定两套定子绕组极对数分别为p1、p2 情况下,取p1 对极为功率绕组、p2 对极为控制绕组,或者p2 对极为功率绕组、p1 对极为控制绕组,两种极对数组合时功率绕组输出相电压、转子电流与励磁电流之间的关系,并利用有限元法对2/4 对极和1/3 对极的无刷双馈发电机分别在两种极对数组合情况下进行数值计算及对比分析,结果表明功率绕组极对数较小的性能更好,最后通过实验验证了数值计算的正确性。
1 基于等效电路的理论推导
假定无刷双馈电机的定子铁心内径为D1,相数为m,定子两套绕组极对数分别为p1、p2。p1 对极对应的相串联匝数为Ns1,基波绕组系数为kws1,相电阻为r1,励磁电感为Lm1,漏电感为L1σ。p2 对极对应的相串联匝数为Ns2,基波绕组系数为kws2,相电阻为r2,励磁电感为Lm2,漏电感为L2σ。转子绕组槽数为Qz,转子相数mz=(p1+p2)/mp(mp 为定子两种极对数的最大公约数),相串联匝数为Nr,相电阻为rr,漏电感为Lrσ。kwr1 和kwr2 分别为转子绕组p1 对极磁场和p2 对极磁场各自的基波绕组系数,为保证研究的可信度,采用控制变量法保持控制绕组的励磁电流和功率绕组侧的负载不变,这里仅研究其发电机性能。无刷双馈电机的每相等效电路如图1 所示[14]。
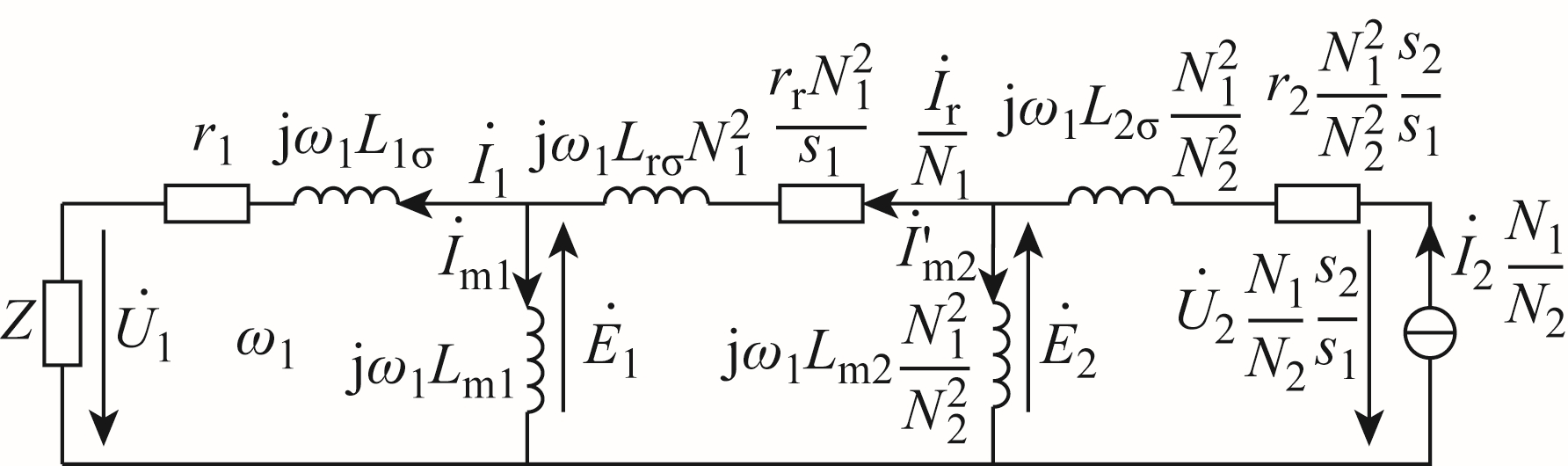
图1 无刷双馈电机的单相等效电路
Fig.1 Single-phase equivalent circuit of BDFM
图1 中参数均折算到一次侧,除了 m2I′˙ 为折算后的值,其余均为实际值。令功率绕组极对数pp=p1,频率为f1,电流角频率为 1ω ,接三相对称阻抗为Z的负载, 1U˙、 1I˙分别为负载上的电压和电流, 1E˙为其对应磁场的励磁电动势, m1I˙ 为流过Lm1 的电流;控制绕组极对数pc=p2,频率为 2f ,电流角频率为2ω ,励磁电流为 2I˙, 2E˙为折算后p2 对极磁场励磁电动势, m2I′ 为折算后流过Lm2 的电流。转子角速度为 rω , 1s 为p1 对极磁场对转子的转差率, 2s 为p2 对极磁场对转子的转差率。
N1 为p1 对极绕组对转子绕组p1 对极磁场的有效匝比,N2 为p2 对极绕组与转子绕组p2 对极磁场的有效匝比,即
由文献[15]可知,主电感为

式中,lef为电机铁心有效长度;δef为气隙有效长度;τp1=πD1/(2p1),τp2=πD1/(2p2)。令K=μ0D1lefm/(πδef),对于确定的电机,其为定值,则Lm1=Kk1(Ns1kws1)2/p12,Lm2=Kk2(Ns2kws2)2/p22,由于定子两套绕组在同一个电压等级,所以 N s 1 ≈ Ns2,且两套绕组的基波绕组系数近似相等,即 k w s1 ≈ kws2。k1、k2 为考虑铁心磁阻情况下的饱和系数,其中k1、k2≥1。为简化计算,这里令k1=k2,当电机饱和程度较低时k1=k2=1;当电机饱和程度较高时,k1=k2>1。
空载时图1 中负载阻抗Z 为无穷大,此时转子电流 rI˙、功率绕组输出电压 1U˙与控制绕组激励电流I˙2之间的关系式分别为

由于 ![]() 与其他项之和相比较小,可以忽略不计,同时再对式(5)进行恒等变换可得
与其他项之和相比较小,可以忽略不计,同时再对式(5)进行恒等变换可得

式中

由于此时电机饱和程度较低,饱和系数k1=k2=1,因此,无论功率绕组选择p1 对极或者p2 对极,其为定值。通过式(6)可知,在电机空载状态下,无论功率绕组选择p1 或者p2 对极,其输出电压和控制绕组励磁电流基本成正比。
基于图1 无刷双馈电机的每相等效电路可以得出方程

由于功率绕组接入电网,因此其频率f1=50Hz,电流角频率ω=2πf1;控制绕组频率满足f2=n(p1+p2)/ 60-f1,当电机转子转速一定时,无论功率绕组选择p1 对极或是p2 对极,f2 都为定值。
由式(7)可得转子电流 rI˙与励磁电流 2I˙的关系为

式中,X=-jT;Z1=Z+r11+jω1L1σ,由于负载阻抗Z 和主电抗之和远大于线圈自身电阻和漏抗,为方便计算,令 1Z Z≈ 。由于 1Z Z≈ ,式(8)中分母第二、三、五项数值较小,可以忽略,再将式(2)代入式(8)可得

式中,除了p1、kwr1 和kwr2 为变量,其余值基本不变,通常情况下,kwr1 和kwr2 相差较小,因此分母基本不变。对于实际常用的倍极比组合为1/3、2/4 的无刷双馈电机来说,功率绕组选择p1 或者p2 对极对转子电流影响较大,且功率绕组极对数越大,转子电流越大。
无刷双馈电机在稳定运行时,转子电流的频率满足fr=s1f1=-s2f2,式中

因此,转子电流频率为

将控制绕组电流频率 ![]() 代入式(12),可以得出在功率绕组极对数确定时,转子电流频率与转速之间的关系式为
代入式(12),可以得出在功率绕组极对数确定时,转子电流频率与转速之间的关系式为
运行范围是电机的一项重要指标,根据无刷双馈发电机的运行原则,电机的转子转速总是落在功率绕组旋转磁场转速和控制绕组旋转磁场转速之间,无刷双馈电机功率绕组的频率f1=50Hz 保持不变,控制绕组的频率随着转子转速的变化而变化。选择p1 对极为功率绕组时,考虑极端情况,功率绕组旋转磁场的转速、转子的转速、电机和控制绕组旋转磁场的转速将在60f1/p1 时保持同步,此时发电机系统不能正常发电,因此电机转子转速范围满足 0≤n<60f1/p1,选取较小极对数作为功率绕组,电机运行范围较大。
由式(7)还可以得出功率绕组输出电压 1U˙与控制绕组激励电流 2I˙之间的关系式为
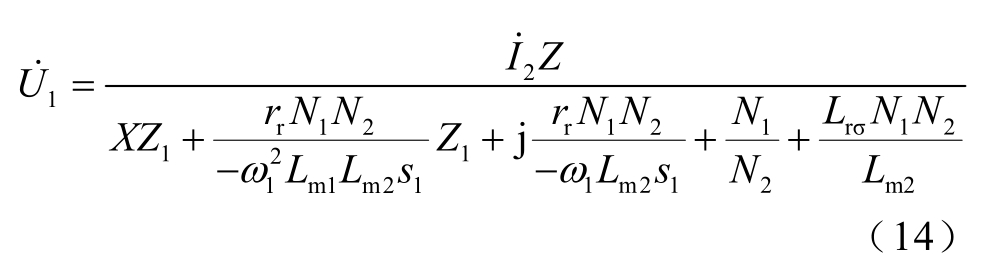
利用式(8)简化方法,式(14)可简化为

由式(15)可以看出在控制绕组侧加相同的励磁电流,功率绕组侧带相同负载阻抗Z 时,功率绕组侧输出电压随着有效匝比的增大而减小。当负载阻抗较大时,有效匝比可以忽略,此时电机的性能与空载状态类似,式(15)可以简化为式(6)。
功率绕组侧电流满足

其共轭表达式为

p1 对极绕组侧输出的有功功率为

式中,Re{·}为取实部。
p2 对极绕组侧输出的有功功率为

系统总输出功率为
为了发挥无刷双馈电机所需变频器容量较小的优点,其通常运行在自然同步转速附近[16]。此时无刷双馈电机约70%以上的功率由功率绕组来承担, 因此从无刷双馈电机的外部来看,其基本上相当于一台具有功率绕组极数的感应电机。显然,选用少极数的功率绕组比多极数的功率绕组更为有利,因为极数少比极数多的感应电机所需要的励磁功率要小,具有较高的功率因数和效率。
定子功率绕组磁动势的幅值为
当负载一定时,无论功率绕组选择p1 还是p2 对极,其回路电流I1 为定值,而由于磁动势的幅值与极对数成反比,所以功率绕组极对数越小,磁动势幅值越大,气隙磁场越强,因此功率绕组与转子绕组之间具有较强的耦合能力。
2 仿真研究
2.1 2/4 对极电机
本文采用有限元法进行仿真研究,样机以YZR315 电机为参照,电机极对数为2/4,转子绕组采用5 联等匝结构,其节距为7,各线圈的匝数为18匝,绕组联结方式如图2 所示。电机的基本参数见表1。定子两套绕组的并联支路数均为2,定子2 对极绕组的相串联匝数为60,基波绕组系数为0.927 1;定子4 对极绕组的相串联匝数为60,基波绕组系数为 0.945 2。空载状态下定子 2 对极励磁电感为155mH,定子4 对极励磁电感为40mH;转子绕组对应2 对极的绕组系数为0.688 6,对应4 对极的绕组系数为0.795 0,漏感为7.35mH。定义极对数组合形式pp=2、pc=4 为方案一,pp=4、pc=2 为方案二。

图2 5 联等匝转子绕组接线图
Fig.2 Equal-turn winding connection diagram of the rotor with 5 coils
表1 基本参数
Tab.1 Parameters of the prototype machine

参数 数值 定子外径/mm 520 定子内径/mm 390 气隙长度/mm 0.8 转子外径/mm 388.4 转子内径/mm 100 铁心长度/mm 455 定子槽数 72 转子槽数 54 自然同步转速/(r/min) 500
空载状态下,保持转子转速为600r/min 不变,两种方案转子电流与励磁电流之间仿真与计算的关系曲线如图3 所示,从图3 中可以看出,随着励磁电流的增大,两种方案的转子电流均增大,与励磁电流基本成正比关系,且两种方案的计算结果与有限元仿真结果基本相同。

图3 空载状态下转子电流与励磁电流之间仿真与计算的关系曲线
Fig.3 The curves of rotor current and excitation current including separate results of simulation and calculation in no-load condition
利用上述电感参数及有效匝比,可以计算出参数 0.1T ≈ ,根据式(6)能够绘制出空载状态下功率绕组相电压与控制绕组侧励磁电流之间的关系曲线,再通过有限元法算出两种方案的关系曲线如图4 所示。从图4 中可以看出,当励磁电流较小时,两种方案在同一励磁电流下的相电压仿真值均与计算值吻合得较好;当随着励磁电流增大到一定程度时,由于电机空载特性非线性[17],使得功率绕组侧输出电压增加较为缓慢,与计算值偏差会有所增加。对比两种方案可知,方案一的电机非线性程度较低,性能较好。

图4 空载状态下功率绕组相电压与控制绕组侧励磁电流的关系曲线
Fig.4 The curves of the relation between phase voltage of PW and excitation current of CW in no-load condition
为了研究空载状态下两种方案非线性程度不同的原因,这里以转子转速为600r/min,控制绕组加励磁电流37A 为例,在0.2~0.3s 期间,两种方案的转子电流波形如图5a 所示,其快速傅里叶变换(Fast Fourier Transform,FFT)的有效值如图5b 所示。

图5 转子电流波形及其FFT 分析
Fig.5 Waveforms of rotor current and its FFT analyzing
从图5 可以看出,方案二转子基波电流频率为10Hz,方案一的转子基波电流频率为30Hz,满足式(13)。方案二转子基波电流的有效值为8A,频率为30Hz 的谐波电流有效值为0.57A,而方案一的转子基波电流有效值为2.9A,仅为方案二转子基波电流的0.36 倍,频率为90Hz 的谐波电流有效值为0.35A,仅为方案二转子谐波电流的0.61 倍。由此可见方案一的转子基波和谐波电流均较小。
图6 为两种方案的定子齿部磁通密度分布图。对比图6a、图6b 可以看出,方案一的定子齿部磁通密度幅值普遍低于1.5T,最大值仅为1.55T;方案二的定子齿部磁通密度幅值有较大部分高于1.5T,最大值可达 1.7T,与方案一相比,最大值高出了0.15T。从电机的磁场来看,由于电机是空载状态,因此这时电机内部只存在两种磁场,一种是控制绕组产生的磁场,另一种是转子绕组产生的磁场。控制绕组励磁电流相同,产生的磁场基本相同,转子电流越大,电机的磁通密度越大,导致电机磁路的磁阻增加,空载曲线的非线性程度增大。

图6 定子齿部磁通密度分布
Fig.6 Distribution diagrams of the magnetic flux density in stator teeth
此时两种方案功率绕组的输出电压波形及其FFT 分析结果如图7 所示。从图7 中可以看出:方案一的功率绕组输出电压有效值约为220V,而方案二的功率绕组输出电压有效值仅为205V,与方案一相比降低了约6.8%。因此,方案一的磁通密度较低,达到额定电压需要的励磁电流较小,成本较低。

图7 空载功率绕组相电压波形及其FFT 分析
Fig.7 Phase voltage waveforms of PW in no-load condition and its FFT analyzing
对于方案二,其运行范围为0 ≤ n<7 50r/min,而方案一,其运行范围可达0 ≤ n<1 500r/min,显然方案一与方案二相比运行范围较大。
不同负载状态下,饱和系数与励磁电流关系曲线如图8 所示。从图中可以看出,方案二的饱和程度明显高于方案一;在负载电阻较大时,两种方案的饱和程度均较低;随着负载电阻的减小,两种方案的饱和程度均增加,且方案二的饱和程度与方案一相比增加的速率更快。在负载电阻为100Ω 时,方案一的饱和系数为 1.28,方案二的饱和系数为1.35,而当负载电阻为5Ω 时,方案一的饱和系数为2.08,方案二的饱和系数可达为2.86,是方案一的1.37 倍,饱和程度较高。

图8 饱和系数与励磁电流关系曲线
Fig.8 The curves between saturation coefficient and excitation current
不同负载情况下,两种方案转子电流与励磁电流的计算与仿真关系曲线如图9 所示。对比图9a、图9b 可知,方案二转子电流普遍高于方案一,且在负载电阻较大时相差倍数较高,负载电阻较小时相差倍数较小,两种方案的转子电流计算值与仿真值吻合得较好,验证了理论推导的正确性。图9a 中功率绕组输出相电压基本保持220V 不变,图9b 的功率绕组输出相电压曲线如图10 所示。

图9 转子电流与励磁电流关系曲线
Fig.9 The curves between rotor current and excitation current

图10 功率绕组侧相电压与控制绕组侧励磁电流的 关系曲线
Fig.10 The curves between phase voltage of PW and excitation current of CW
从图10 中可以看出,两种方案负载电阻越小所需励磁电流越大。从方案二的功率绕组侧相电压与控制绕组侧励磁电流的关系曲线可以看出,负载电阻在100~10Ω 之间,功率绕组侧相电压与方案一相比相对较低,这是因为负载电阻较大时,电机可近似看成空载状态,而方案二的非线性较高,因此电压相对较低,此时功率绕组侧相电压逐渐增加,当负载电阻在10Ω 附近时,方案二的功率绕组侧相电压达到最大值。根据式(16)可知,当负载电阻和励磁电流保持不变时,功率绕组侧相电压随着有效匝比的减小而增大,方案二的有效匝比为0.89,方案一的有效匝比为1.13,因此功率绕组侧相电压有一定增加。然而由于方案二的转子电流有效值为15A,方案一的转子电流有效值仅为10.5A,方案二的磁场密度较大,因此功率绕组侧相电压与方案一相比较低,基本符合式(16)所述规律。而当负载电阻从10Ω 到5Ω 时,功率绕组侧相电压会逐渐减小,这是由于方案二的转子电流与方案一相比较大,电机饱和程度较高,导致铁心磁压降增加,功率绕组侧输出电压偏低。
两种方案的系统输入和输出功率曲线如图 11所示。从图中可以看出方案二的输入功率高于方案一,而输出功率低于方案一,这主要是由于方案二的转子电流较大,导致系统铜耗和铁耗较高,因此其效率偏低。图中计算值与仿真值相差较小,但是由于计算值忽略了功率绕组侧的漏阻抗,因此计算值会略高于仿真值。

图11 系统输入和输出功率曲线
Fig.11 The curves of input and output power
为更好地比较两种方案在负载电阻较小时电机的性能,以功率绕组侧带5Ω 负载为例,在控制绕组加相同激励电流(幅值为105A)的情况下,图12 给出了此时两种方案的转子电流波形及其FFT 分析结果。
从图12 可以看出,两种方案转子电流的频率依然满足式(13),此时方案二转子基波电流的有效值为25.67A,频率为30Hz 谐波电流有效值为2.47A,而方案一转子基波电流的有效值仅为21.64A,频率为30Hz 谐波电流有效值也仅为1.7A,转子基波电流和谐波电流与方案二相比均较小,通过图10 可 知,两种方案此时功率绕组侧输出电压相差较小,控制绕组侧励磁电流相同,转子电流越大,电机的饱和程度越高。

图12 转子电流波形及其FFT 分析
Fig.12 Current waveforms of rotor and its FFT analyzing

图13 定子齿部磁通密度分布图
Fig.13 Distribution diagrams of the magnetic flux density in stator teeth
图13 给出了0.2s 时两种方案的定子齿部磁通 密度分布。由图 13a 可以看出方案一的齿部磁密仅有个别点超过1.8T,绝大部分磁密低于1.8T,而图13b 中方案二的齿部磁密有较大部分超过1.8T,电机过度饱和,会导致电机温升较高、振动和噪声增大。
两种方案功率绕组侧的输出电压波形如图 14所示。根据图14 不难发现,方案二的电压波形正弦性较差,电压谐波畸变率较高,其基波电压有效值约为217V,低于方案一,且谐波含量较大,谐波含量中频率为110Hz 的谐波电压有效值可达10.6V;而方案一谐波含量较小,频率为130Hz 的谐波电压有效值仅为5.9V,电机的饱和程度较低,发电性能较好。

图14 电压波形及其FFT 分析
Fig.14 The voltage waveforms and its FFT analyzing
2.2 1/3 对极电机
对于1/3 对极转子采用文献[9]所述新型混合式转子无刷双馈电机,样机以 YZR250 电机为参照,定义pp=1、pc=3 为方案三,pp=3、pc=1 为方案四。
空载状态时,功率绕组相电压与励磁电流的关系曲线如图15 所示。由式(6)可知,对于确定的电机,功率绕组相电压与功率绕组选择哪种极对数无关。从图中可以看出,方案三的仿真值与计算值基本吻合,说明理论推导同样适用于1/3 对极电机;而方案四在励磁电流较小时基本相同,励磁电流较大时相差较大。通过仿真可知,当控制绕组的励磁电流为 27A,此时方案三电机转子电流有效值为2.8A,功率绕组侧电压为220V;而方案四转子电流达到了17.5A,约为方案三的6.2 倍,功率绕组输出电压仅为186V,电机的磁通密度很高,磁路磁阻较大,空载非线性程度较严重。因此,在空载状态时,方案三具有较好的性能。

图15 功率绕组相电压与励磁电流的关系曲线
Fig.15 The curves between phase voltage of PW and excitation current of CW
不同负载情况下,两种方案的饱和系数曲线如图16 所示。从图中可以看出,随着负载电阻的减小,控制绕组的励磁电流逐渐增大,同时两种方案的饱和系数也逐渐增大,且方案四的饱和系数普遍高于方案三。图17 为相应条件下功率绕组侧相电压与励磁电流的关系曲线,方案四的功率绕组侧相电压明显低于方案三。由于方案四的转子电流始终大于方案三,在负载电阻为200Ω 时,方案四的转子电流为18.1A,而方案三的转子电流仅为3.3A,方案四的转子电流约为方案三的5.5 倍,电机的饱和程度较高,而方案三饱和程度较低,发电性能较好。

图16 饱和系数与励磁电流关系曲线
Fig.16 The curves between saturation coefficient and excitation current

图17 功率绕组侧相电压与控制绕组励磁电流的关系
Fig.17 The curves between phase voltage of PW and excitation current of CW
3 样机试验
为进一步验证解析计算的正确性,根据表1 参数,由长江航运集团电机厂制造了一台2/4 对极试验样机,试验平台如图18 所示。1/3 对极试验样机由皖南电机厂制造,试验平台如图19 所示。

图18 2/4 对极样机试验平台
Fig.18 Prototype of 2/4 pole pairs BDFM and the test rig

图19 1/3 对极样机试验平台
Fig.19 Prototype of 1/3 pole pairs BDFM and the test rig
利用上述两台样机分别进行试验研究,2/4 对极样机的试验过程分为两步:①将4 对极绕组作为功率绕组,2 对极绕组作为控制绕组,即将4 对极绕组与负载相连,2 对极绕组与变频器相连,分别测出空载和不同负载状态下4 对极绕组侧的输出电压;②对调两套绕组的连接方式,即将2 对极绕组与负载相连,4 对极绕组与变频器相连,分别测出空载和不同负载状态下2 对极绕组侧的输出电压。1/3 对极样机的试验过程与之类似。
测量得到方案一和方案二分别在空载和负载状态下功率绕组相电压和控制绕组励磁电流试验结果如图20 和图21 所示,方案三和方案四两种样机的实验结果如图22 和图23 所示。

图20 空载状态下2/4 对极功率绕组相电压与控制绕组侧励磁电流对比曲线
Fig.20 The curves of phase voltage of PW and excitation current of CW with 2/4 pole pairs in no-load condition

图21 不同负载下2/4 对极功率绕组侧电压与控制绕组侧励磁电流对比曲线
Fig.21 The curves of phase voltage of PW and excitation current of CW with 2/4 pole pairs in different load condition

图22 空载状态下1/3 对极功率绕组相电压与控制绕组侧励磁电流对比曲线
Fig.22 The curves of phase voltage of PW and excitation current of CW with 1/3 pole pairs in no-load condition

图23 不同负载下1/3 对极功率绕组侧电压与控制绕组侧励磁电流对比曲线
Fig.23 The curves of phase voltage of PW and excitation current of CW with 1/3 pole pairs in different load condition
从图20 和图21 可以看出,方案一和方案二两种方案的计算值、仿真值和实测值趋势基本相同,由于空载特性的非线性,仅在励磁电流较大时有所偏差;图22 和图23 中方案三和方案四两种方案利用三种方法计算的结果也基本相同,验证了解析方法和仿真的正确性,同时也说明该解析方法的通用性。三种结果存在一定偏差的原因主要有:①计算时在空载状态下忽略了 2 r 1 1 r N s ,负载状态下忽略了定子漏阻抗以及式(14)中对结果影响较小的项;②仿真时网格剖分的精度;③实测时机械摩擦损耗和风磨损耗的影响。
4 结论
文中通过对确定的电机在pp=p1、pc=p2和pp=p2、pc=p1 两种极对数组合下进行了理论分析、仿真计算和试验验证,得出如下结论:
1)对无刷双馈电机的单相等效电路进行推导,在空载状态下,无刷双馈电机的转子电流、功率绕组侧电压分别满足式(4)和式(6);在负载状态下,无刷双馈电机的转子电流、功率绕组侧电压分别满足式(9)和式(15);在两种状态下,转子频率与转速之间均满足式(13),电机的运行范围满足0≤n<60f1/p1。
2)对pp=2、pc=4 和pp=4、pc=2 两种极对数组合下的电机进行有限元仿真,对比分析可知,功率绕组极对数较小的转子电流小,定子齿部磁通密度较低,功率绕组侧电压较高,电机运行范围较广,负载状态下发出的功率相对较大。该结论同样适合pp=1、pc=3 和pp=3、pc=1 两种极对数组合下的电机。
3)试验结果表明理论推导和仿真计算的正确性,本文给出的结论对其他极对数组合的电机在确定功率绕组极对数方面也有一定的参考价值。
[1] 阚超豪. 绕线转子无刷双馈电机转子绕组设计和运行特性研究[D]. 武汉: 华中科技大学, 2010.
[2] 程源. 绕线转子无刷双馈电机特性研究[D]. 武汉: 华中科技大学, 2012.
[3] 黄长喜. 新型磁阻式无刷双馈电机研究及其应用[D]. 合肥: 合肥工业大学, 2016.
[4] Ren Taian, Kan Chaohao, Wu Hongbin, et al. The study of a wound brushless doubly fed machine based on a rotor with the reluctance effect[J]. IEEJ Transactions. on Electrical and Electronic Engineering, 2018, 13(2): 330-338.
[5] Han Li, Ou Xianpeng, Du Jiang, et al. Study of direct coupling in stator dual windings of brushless doublyfed machine[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 974-982.
[6] Chen Xi, Wang Xuefan. Proximate standing wave feature of magnetic field and its influence on the performance of wound rotor brushless doubly-fed machine[J]. IEEE Transactions on Energy Conversion, 2017, 32(1): 296-308.
[7] 张凤阁, 蒋晓东, 李应光, 等. 新型磁障转子无刷双馈电机热计算[J]. 中国电机工程学报, 2018, 38(9): 2745-2752. Zhang Fengge, Jiang Xiaodong, Li Yingguang, et al[J]. Thermal calculation on a brushless doubly-fed machine with a magnetic barrier rotor[J]. Proceedings of the CSEE, 2018, 38(9): 2745-2752.
[8] 张爱玲, 熊光煜, 刘振富, 等. 无刷双馈电机能量传递关系和功率因数特性的实验研究[J]. 中国电机工程学报, 2011, 31(6): 92-97. Zhang Ailing, Xiong Guangyu, Liu Zhenfu, et al. Experimental study on energy transmission and power factor characteristics of brushless doubly-fed machines[J]. Proceedings of the CSEE, 2011, 31(6): 92-97.
[9] 任泰安, 阚超豪, 吴红斌, 等. 新型混合式转子无刷双馈电机[J]. 中国电机工程学报, 2018, 38(9): 2753-2762. Ren Taian, Kan Chaohao, Wu Hongbin, et al. A new hybrid rotor of brushless doubly-fed machines[J]. Proceedings of the CSEE, 2018, 38(9): 2753-2762.
[10] 欧先朋, 韩力, 韩雪峰, 等. 两种不同笼型转子结构无刷双馈电机的稳态运行性能对比[J]. 电工技术学报, 2017, 32(23): 61-71. Ou Xianpeng, Han Li, Han Xuefeng, et al. Comparison of steady state operating performances on brushless doubly-fed machine with two different cage rotors[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 61-71.
[11] 张岳, 王凤翔, 邢军强, 等. 磁障转子无刷双馈电机[J]. 电工技术学报, 2012, 27(7): 49-54. Zhang Yue, Wang Fengxiang, Xing Junqiang, et al. Brushless doubly-fed machines with magnetic barrier rotor[J]. Transactions of China Electrotechnical Society, 2012, 27(7): 49-54.
[12] 陈昕, 王雪帆. 基于无刷双馈发电机的船舶独立发电系统励磁控制和性能分析[J]. 电工技术学报, 2017, 32(3): 120-129. Chen Xin, Wang Xuefan. Excitation control and performance analysis for BDFIG-based ship standalone power generation system[J]. Transactions of China Electrotechnical Society, 2017, 32(3):120-129.
[13] Zhang Fengge, Jia Guanglong, Zhao Yunwu, et al. Simulation and experimental analysis of a brushless electrically excited synchronous machine with a hybrid rotor[J]. IEEE Transactions on Magnetics, 2015, 51(12): 8115007.
[14] Roberts P C, McMahon R A, Tavner P J, et al. Equivalent circuit for the brushless doubly-fed machine (BDFM) including parameter estimation’[J]. IEE Proceedings of Electrical Power Appllication, 2005,152(4): 933-942.
[15] 程源. 无刷双馈发电机的电磁设计及其性能分析[D]. 武汉: 华中科技大学, 2009.
[16] 王秀平. 新型混合转子无刷双馈电机的电磁特性分析与实验研究[D]. 沈阳: 沈阳工业大学, 2014.
[17] 汤蕴缪, 罗应立, 梁艳萍. 电机学[M]. 北京: 机械工业出版社, 2008.